Cells navigate with a local-excitation, global-inhibition-biased excitable network

Abstract

Cells have an internal compass that enables them to move along shallow chemical gradients. As amoeboid cells migrate, signaling events such as Ras and PI3K activation occur spontaneously on pseudopodia. Uniform stimuli trigger a symmetric response, whereupon cells stop and round up; then localized patches of activity appear as cells spread. Finally cells adapt and resume random migration. In contrast, chemotactic gradients continuously direct signaling events to the front of the cell. Local-excitation, global-inhibition (LEGI) and reaction–diffusion models have captured some of these features of chemotaxing cells, but no system has explained the complex response kinetics, sensitivity to shallow gradients, or the role of recently observed propagating waves within the actin cytoskeleton. We report here that Ras and PI3K activation move in phase with the cytoskeleton events and, drawing on all of these observations, propose the LEGI-biased excitable network hypothesis. We formulate a model that simulates most of the behaviors of chemotactic cells: In the absence of stimulation, there are spontaneous spots of activity. Stimulus increments trigger an initial burst of patches followed by localized secondary events. After a few minutes, the system adapts, again displaying random activity. In gradients, the activity patches are directed continuously and selectively toward the chemoattractant, providing an extraordinary degree of amplification. Importantly, by perturbing model parameters, we generate distinct behaviors consistent with known classes of mutants. Our study brings together heretofore diverse observations on spontaneous cytoskeletal activity, signaling responses to temporal stimuli, and spatial gradient sensing into a unified scheme.

Many cells have an internal “compass” that enables them to sense, and move directionally along, gradients of extracellular chemicals, electric fields, or mechanical forces. Increasing evidence suggests that chemotaxis plays an extensive role in normal physiology (1). During embryogenesis, for example, chemoattractants guide primordial germ cells to proper locations, mediate the formation of organs, and control the wiring of the nervous system. In the adult, chemotaxis is needed for immune cell trafficking, wound healing, and stem cell homing to niches. Chemotaxis is also involved in the pathology of numerous diseases. For example, the migration of immune cells to specific sites plays a key role in inflammatory disorders such as asthma, arthritis, and vascular disease; and, in cancer metastasis, cells escape the primary tumor, enter the circulation, and emigrate to specific tissues (2, 3). Chemotactic behavior is virtually identical in human leukocytes and free-living amoebae, indicating that the process has ancient origins and that the basic mechanisms of gradient detection are shared among eukaryotic cells.

Chemotaxis can be conceptually divided into processes of motility, directional sensing, and polarity (see Box 1) (4, 5). Motility in amoeboid cells such as Dictyostelium and human leukocytes involves a periodic extension and retraction of pseudopodia coupled with regulated adhesion, which moves cells about in the absence of a gradient (6–8). Directional sensing refers to the ability of chemotactic cells to read the gradient and bias the motile machinery. Chemoattractants are recognized by G-protein-coupled receptors and associated G proteins that are uniformly distributed along the cell perimeter but, nevertheless, direct downstream signaling events toward or away from the high side of the gradient. For example, activation of Ras proteins and PI3-kinase, accumulation of phosphatidylinositol (3,4,5) phosphate (PIP₃), and new actin polymerization occur at the front while the PI3-phosphatase, PTEN, and myosin localize at the rear of the cell (9–12). Polarity is an elongated state where signaling events occur at and projections extend from the cell anterior, even in the absence of or in a uniform concentration of chemoattractant.

Box 1. Temporal and Spatial Responses of Chemotactic Cells.

Chemotaxis in amoeboid cells such as Dictyostelium and human leukocytes involves motility, directional sensing, and polarity as indicated above. Motility is achieved through a rhythmic extension of pseudopodia which propels cells in random directions. Directional sensing denotes the mechanisms that read the gradient and bias the extensions. Cytoskeletal inhibitors eliminate motility and polarity but do not prevent directional sensing: Signaling events occur in stable crescents facing toward the gradient even in immobilized cells. Polarity is an elongated state where projections extend mostly from the anterior, even in the absence of an external cue. Unpolarized cells are equally sensitive along the perimeter and will form a new front when exposed to a fresh gradient, whereas polarized cells gradually turn. However, a sufficiently steep gradient can elicit a new front from the rear of a polarized cell. When cells are exposed to a uniform increase in chemoattractant they immediately freeze, then round up or cringe within 30 s, as indicated below. Then they undergo a series of spreading responses and finally, after several minutes, resume random migration. Biochemical responses triggered by chemoattractant subside or adapt during continuous stimulation. Some adapting responses briefly decrease when the stimulus is added, whereas most transiently increase. The adapting responses are biphasic, corresponding to the cell behavior. As visualized with a PIP3 biosensor, the initial phase occurs uniformly around the perimeter and disappears at the cringe. The second phase consists of a series of patches at the tips of the spreading cells.

An important general characteristic of the physiological responses to chemoattractants is the tendency to subside during constant stimulation, a phenomenon referred to as adaptation (Box 1) (13, 14). The properties of adaptation have been characterized by studying the stimulus–response behavior of numerous signaling events (15, 16). Generally, the “front” responses, such as PIP₃ accumulation, transiently increase, whereas the “rear” ones decrease before returning to prestimulus levels. Regardless of their sign, responses are triggered by increases in receptor occupancy and adapt when occupancy is held constant. Cells respond again when occupancy is increased further or when the stimulus is removed and reapplied after a period of deadaptation. A few events, such as receptor phosphorylation and G-protein dissociation, do not adapt but persist as long as chemotactic stimuli are maintained (17–19).

Chemoattractant-mediated responses of Dictyostelium amoebae and human leukocytes are actually biphasic (Box 1). That is, there is an initial spike that declines sharply by 30 s followed by a weaker secondary response which occurs over the next several minutes (20–22). Importantly, at the time of the initial decline, cells are not yet adapted and will mount another biphasic response if the stimulus is removed and immediately reapplied. Only after 5 min or so, when the secondary responses have subsided, are cells adapted and completely refractory to immediate reapplication of chemoattractant (13). A key challenge for eukaryotic chemotaxis is to understand how these kinetically complex, adapting responses to uniform stimuli relate to the ability of cells to move continuously and directionally along gradients of chemoattractant and stably localize signaling events toward the high side.

Intriguingly, even in the absence of stimulation, the cortical cytoskeletons of amoebae as well as human neutrophils display excitability, which possibly underlies cell morphological changes including spontaneous motility (23–25). Observations by total internal reflection fluorescence microscopy (TIRFM) reveal propagating waves of recruitment of actin-binding proteins and suppressor of cAMP receptor (SCAR) subunits to the cell cortex which can be influenced by chemoattractant. It is generally recognized that propagating waves in biological systems involve an excitable network with diffusive contact among the elements (26). In neutrophils, this spontaneous activity appears to drive projections at the cell perimeter that move the cells, whereas the patterns observed thus far in Dictyostelium may be related to the formation of macropinosomes. Because signaling events are activated at the tips of pseudopodia of randomly migrating and spreading cells as well as at the rims of macropinosomes, it is conceivable that the entire biochemical network behaves in a coordinated fashion. Chemoattractants and other cues might bias this excitable network to direct migration and related cell morphological events.

Numerous models have been proposed to capture the fascinating behavior of chemotaxing cells (27). Several versions of reaction–diffusion models, designed to explain polarity, have generated responses that are greatly amplified relative to the external gradient but did not capture the ability of cells to rapidly readjust behavior to shifting stimuli. Arrieumerlou and Meyer obtained realistic chemotactic behavior by having receptor occupancy directly bias randomly generated pseudopodia (28). However, this system did not adapt and could not account for the observed excitability of the network. The local-excitation, global-inhibition (LEGI) model was proposed to explain the signaling responses of immobilized cells exposed to step increases as well as gradients of chemoattractant (29, 30). Although the LEGI scheme can predict the responses to any combination of step and gradient stimuli, it does not amplify the external gradient. A clever modification of the LEGI model, referred to as the “balanced inactivation model” introduced a threshold effect which increased the extent of amplification (31). However, neither of these models, in and of themselves, accounts for the dynamic behavior of chemotaxing cells.

Drawing on all of this previous work, we propose here the LEGI-biased excitable network hypothesis to account for the temporal and spatial responses of cells to chemoattractants. We suggest that upstream signaling components including chemoattractant receptor and G protein read the stimulus and produce a signal, according to a LEGI scheme, that serves as an input to a downstream excitable biochemical network that generates spontaneous pseudopodia. In the course of preparing this manuscript, a study appeared that used noise-driven FitzHugh–Nagumo equations to account for the appearance of the PIP₃ patches on cells, but no attempt was made to link the responses to chemotactic stimulation (32). This linkage was the motivation for the LEGI-biased excitable network hypothesis which applies to random motility, chemotaxis, as well as the temporal responses of cells to uniform stimuli.

Results

Biochemical Network Displays Spontaneous Excitability That Can Be Regulated by Chemoattractant.

Our previous observation that Ras activation and PIP₃ accumulation occur at the tips of pseudopodia prompted us to ask whether the excitable waves of cytoskeletal activity were accompanied by activation of other parts of the network. As before, we used RBD-GFP and PH_Crac-GFP as biosensors for Ras activation and PIP₃ accumulation and the SCAR complex subunit, Hspc300-GFP, to monitor cytoskeletal activity. As shown in Fig. 1 and Movies S1–S3, we observed patches of RBD-GFP, PH_Crac-GFP, and Hspc300-GFP recruitment to the basal surface of the cell. The patches were heterogeneous ranging from brief, limited flashes to large expanding waves. The dynamic character of these events was similar for all of the components but the Hspc300-GFP patches seemed to have a finer structure and more punctuate spots than the others.

Fig. 1.

Propagation waves of signaling events and excitability of the biochemical network. (A) Developed Dictyostelium cells overexpressing GFP-tagged PH_Crac, Raf1-RBD, and Hspc300 were imaged with a TIRF microscope, while undergoing random migration. Imaged regions shown are roughly 7 × 7 μm. The dynamic nature of these excitable waves is more clearly demonstrated in the corresponding Movies S1–S3. Time stamps are the number of seconds since movies started. (B) Synchronization of activity at different levels of the signaling network is demonstrated in cells coexpressing RBD-GFP and LimE-RFP (Left), or PH-GFP and LimE-RFP (Right). In each case, upper and lower panels show two independent examples (see Movies S4 and S5). (C) The intensity of Hspc300 in response to sudden application of a micropipette containing 10 μM cAMP at 25 s displays a sharp first peak followed by broad secondary activities (Movie S6). The lower graph shows the average intensity plotted over time.

RBD-GFP, PH_Crac-GFP, and Hspc300-GFP displayed similar patterns of dynamic behavior, which suggested to us that these occurred simultaneously, but others have reported wave-like distributions of PH_Crac-GFP that were not colocalized with the cytoskeletal events. To address this issue, we coexpressed RBD-GFP or PH_Crac-GFP with the actin-binding protein, LimE-RFP, and imaged the signaling events and new actin polymerization simultaneously. As shown in Fig. 1B and Movies S4 and S5, both RBD-GFP and PH_Crac-GFP dynamically colocalized with LimE-RFP. At a frame rate of 3 s, all of the events appeared to occur in the same place at the same time. Most of the excitable behavior we observed in moving cells displayed this pattern. Occasionally, we also observed situations where a broad PH_Crac-GFP signal was bounded by a thinner band of LimE-RFP, as has been reported (33, 34). In these instances, the waves appeared to be “stalled” within the boundary of the cell and may represent a different structure from the waves that expand to the edge.

As shown in Fig. 1C and Movie S6, uniform addition of chemoattractant triggered a rapid recruitment of each component to the cell surface, followed by an immediate reversal where the frequency of events briefly dropped below the prestimulus level. Often, for each of the biosensors, the first transient response was followed by a series of additional flashes at random sites. These secondary bursts, which were quite heterogeneous among cells, undoubtedly correspond to an often-observed second phase of biochemically monitored events and to the patches of PIP₃ accumulation detected by epifluorescence microscopy (see Box 1). We also examined Hspc300-GFP in cells tracking toward a cAMP-filled micropipette (Movie S7). In this case, most of the flashes of activity occurred toward the anterior of the cell. These observations suggest that many, if not all, components of the signaling network display similar excitable behavior which can be perturbed in a defined manner by chemoattractants.

A LEGI-Biased Excitable Network Model Was Formulated to Simulate Cellular Behavior.

We formulated a model to test the LEGI-biased excitable network hypothesis (see Fig. 2A and Box 2). The chemoattractant is sensed by a LEGI module, representing the chemoattractant receptor, associated G proteins, and modulators, that generates a response regulator as previously described. The response regulator serves as an input for a noise-driven excitable system, corresponding to the network of downstream biochemical events that control cytoskeletal activity. The entire excitable network is modeled simply as interactions of components X and Y, where X is autocatalytic and drives Y, which provides negative feedback to X. Stochastic fluctuations (noise) drive X, which motivates the basal behavior of the network. The response regulator also drives X, which couples the upstream and downstream modules. The half-times for the rise and fall of the inhibitor in the LEGI module were chosen to be much longer than those of the positive and negative feedback loops within the excitable network (∼2 min versus ∼10 s). Note that the excitable network can behave independently but the effects of the LEGI module on final activity are filtered by the downstream events. A brief outline of the model is found in Box 2; a formal description and an explanation of its major features are presented in the SI Text. Here we provide simulations run on the model and compare them to the wealth of legacy information of the behavior of chemotactic cells.

Fig. 2.

The LEGI-biased excitable network model and simulations of activity before and after addition of uniform stimuli. (A) The system consists of a LEGI module, in which an external signal, S, drives excitor, E, and inhibitor, I, which in turn control a response regulator, RR. The RR is a positive driver of an excitable network. The excitable network is represented, for simplicity, by interactions between variables X and Y and is triggered by stochastic noise. (B) Two-dimensional simulations of unstimulated (Upper) and stimulated systems (Lower). The stimulus was applied at 100 s. These images are of X; Y was slightly less noisy and lagged X but otherwise represented the behavior of the system identically. Movies S8 and S9 show two-dimensional, simultaneous simulations of X and Y. (C) Kymograph of a one-dimensional simulation in the absence of stimulation. This and all kymographs are plots of Y. Patches can occur simultaneously far apart in space (arrows ∼280 s) or close together which fuse and form a wider patch (arrowhead ∼500 s). Around the edges of some patches, prolonged small regions of high activity can be seen (e.g., triangles ∼450 and 840 s). (D and E) Response of model to addition of uniform stimuli denoted by the bar above the kymograph. In E, the parameters of the excitable network have been perturbed randomly. (F) Mean (red) level of activity of X around the perimeter of the cell for an aggregate of randomly perturbed cell models (n = 40). Shaded region denotes one SD away from the mean. The blue and green dotted lines are the individual traces of the simulations in D and E, respectively. Vertical lines are 60 s apart.

Box 2. The LEGI-Biased Excitable Network Hypothesis.

As shown in Fig. 2A, we propose that chemotaxis is mediated by two connected reaction–diffusion systems, designated LEGI and excitable network. The LEGI module represents the chemoattractant receptor, associated G proteins, and modulators. The excitable network represents the downstream biochemical responses that control cytoskeletal activity.

In the LEGI module, a signal (S) generates an excitor (E) and an inhibitor (I). A response regulator (RR) depends on the balance of E and I. The excitor reflects the local receptor occupancy, whereas the inhibitor depends more closely on the average level of receptor occupancy. As shown at left, the excitor changes faster than the inhibitor and so, when cells are exposed to a uniform stimulus, the response regulator rises transiently until the slower inhibitor catches up. The cells adapt perfectly at the front and back. The timescale of the inhibitor and response regulator are on the order ∼2 min. When a gradient is applied, there is an initial response. However, when it reaches a steady state, the excitor exceeds the inhibitor at the front of the cell while it is lower at the back. This difference leads to a response regulator that, relative to basal levels, is persistently higher at the front and lower at the back.

The response regulator drives an excitable network, a system in which perturbations can elicit responses that are much greater than the initial perturbation. Our simplified model of the excitable network consists of two components. The first, X, is triggered either by change in the LEGI response regulator or through stochastic noise fluctuations. These small initial deviations are amplified by an autocatalytic positive feedback loop where X produces additional X. Changes in X also drive the second component, Y, which in turn, provides negative feedback enabling a shutoff of the network. The diagram below shows two equivalent ways of representing the dynamics excitable network. On the left are the changes in each component as a function of time. On the right, in the phase-plane diagram, the line labeled “trajectory” plots changes in both values at the same time. The phase-plane diagram also shows “nullclines,” determined by setting the expressions for the rates of change of X and Y equal to zero, which helps predict the response of the system to perturbation. Vector arrows indicate the direction a trajectory must take.

In our model, X and Y are initially at equilibrium (point a). Noise or a change in the response regulator of the LEGI module alters the amount of X. If a small increase in X reaches a “threshold,” then positive feedback causes X to increase greatly (from a to b), forcing a delayed increase in Y which begins the shutoff of X (from b to c). This continues until X reaches its minimum (d) and then the system settles to its new equilibrium (e). The timescale for this response is relatively fast, ∼10 s.

In the phase-plane diagram, the system equilibrium is the point where the two nullclines meet (i.e., zero rate of change of X and Y; initially at point a). The increase in X raises the X nullcline which shifts the equilibrium to a new point (e). As the system is no longer in equilibrium, X and Y must change. Due to the positive feedback, X changes greatly and Y changes slightly, causing the system to move away from the new equilibrium toward point b. The high level of X leads to an increase in Y which counteracts X. At point b, X reaches its maximum as it crosses the new X nullcline. As Y continues to increase to point c, the decrease of X continues until the trajectory again crosses the X nullcline at point d. From there, the system settles to its new equilibrium (e).

Localized Patches of Activity Appear Randomly and Are Synchronized by the External Stimulus.

Fig. 2B and Movies S8 and S9 show two-dimensional simulations of spontaneous activity and responses to uniform stimuli. The parameters in the model were chosen to account for the typical size and duration of an observed patch of PIP₃ accumulation as well as the general features of the biochemical responses to uniform chemoattractant addition. The patterns of X and Y were similar except that X slightly preceded and was less diffuse than Y. In the absence of stimulation, initial points of spontaneous activity appeared and propagated into patches of various sizes and durations. When a patch expanded sufficiently and activity at its origin subsided, it appeared as a propagating wave (see Movie S8). A uniform stimulus generated a response over the entire field, which shut off rapidly and was followed by a series of secondary localized clusters of activity (see Movie S9). The evolution of the patterns varied in each simulation run with the same parameters due to the influence of stochastic noise. The performance of X or Y in the simulations closely matched that of the biosensors in cells as will be analyzed in greater detail below.

To facilitate tracking of the temporal and spatial responses of the model, all subsequent simulations were carried out on a circular domain and the activity of the simulated cell was represented as a kymograph of Y. As seen in the kymograph of a cell in the absence of stimulation, it is clear that patches of activity can appear simultaneously, either far from each other (Fig. 2C) or sufficiently close to give the appearance of a single, wider crescent. The patches spread out laterally and in some cases, a smaller secondary increase emerged at the edge of a patch. A uniform stimulus gave rise to a burst of activity that covered nearly the entire perimeter (Fig. 2D). This response declined rapidly by 30 s due to the negative feedback loop within the excitable network. A second phase of high activity then appeared, though it was not as consistent in space as the initial response. The frequency of patches remained higher than prestimulus levels for a few minutes, corresponding to the timescale of the LEGI module. During this period, increases in activity seen at the edges of patches were more common. Eventually, the system adapted and the spontaneous activity returned completely to the prestimulus level as the response regulator disappeared.

Similar patterns of spontaneous and stimulated activity appeared in simulations using randomly perturbed model parameters (Fig. 2E), though the frequency, sizes, and durations of the patches varied. To determine the form of the response of a population of cells, we measured the average level of activity around the perimeter for 40 cells that had randomly altered model parameters, and plotted the mean level of activity of X as a function of time (Fig. 2F). We saw a clear first peak, followed by a smaller second peak, and the activity returned to basal levels approximately 5 min after addition of the stimulus. The average profile was compared with the responses of two individual cells. In all cases, the first peak was evident, but the averaging of a heterogeneous population led to less distinct shutoffs and broader secondary peaks. Nevertheless, the similar behavior demonstrated the robustness of the model.

Spontaneous Activity Patches Display Adaptation to Multiple Stimuli.

We next considered the effect of removing a spatially homogeneous stimulus from an adapted cell (Fig. 3A). As seen earlier, after adding a stimulus it took about 5 min for the simulated cell to adapt and attain a prestimulus level of activity. Thereafter, the cell sustained this basal behavior until the stimulus was removed. The removal triggered a period of little or no activity, distinctly below the basal level. Eventually, about 5 min after removal of the stimulus, the spontaneous patches of activity reappeared and were maintained at the prestimulus level.

Fig. 3.

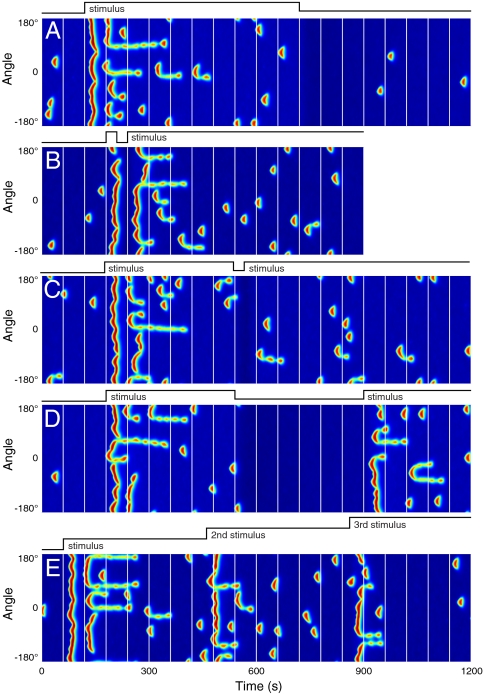
Response of the model to addition, removal, and combinations of uniform stimuli. (A) As indicated, a uniform stimulus was applied at 120 s and removed at 720 s. (B) As indicated, stimulus was applied for 30 s, removed for 30 s, and then reapplied. (C) As indicated, the stimulus was applied 360 s, removed for 30 s, and reapplied. (D) as indicated, the stimulus was applied for 360 s, removed for 360 s, and reapplied. (E) As indicated, three identical stimulus increments were applied 400 s apart, without intervening removals. Vertical lines are 60 s apart.

Because the LEGI module responds on longer timescales than the excitable network, multiple stimuli should give rise to different activity patterns depending on the timescales on which they are applied. We first subjected the model to a 30 s application of a stimulus, followed by a short removal (a further 30 s) before reapplying a persistent stimulus (Fig. 3B). Both stimuli generated similar, spatially uniform responses; the second was followed by secondary patches of activity and eventual adaptation to prestimulus levels. Changing the duration of the first stimulus to 360 s gave rise to quite a different behavior. As expected, there was a biphasic response to the first stimulus, followed by a return to basal activity and a suppression of basal activity when the stimulus was removed. Reapplying the stimulus 30 s later instantly mitigated the suppression but elicited no response as the system had now adapted (Fig. 3C). The responsiveness could be recovered by delaying application of the second stimulus for 360 s, sufficiently long to allow deadaptation to occur (Fig. 3D). Finally, we showed that the simulated cell responded and adapted repeatedly to sequential increments in the stimulus. In this case, successive increases elicited smaller bursts in activity (Fig. 3E). In general, the magnitude of the integrated response was proportional to the relative change in the stimulus.

Spontaneous Activity Patches Are Steered in the Direction of a Chemoattractant Gradient.

We next explored the response of the model to spatial gradients (Fig. 4A). The application of a chemoattractant gradient caused a sudden nearly equal increase in stimulus across the cell. Accordingly, it elicited a spatially uniform response, which disappeared as previously observed with uniform stimuli. Thereafter, a series of localized patches appeared with temporal regularity, primarily aligned with the external gradient. By measuring the average steady-state level of activity as a function of the angle along the perimeter for 20 cells, we determined that the external gradient was greatly amplified (Fig. 4B and Fig. S1). We also plotted the response regulator of the LEGI module which, as previously noted, is not amplified compared with the external gradient. We then repeated this simulation with a shallower gradient (approximately 6% versus 19% between the front and back) gradient. The initial response was quite similar, but the steady-state behavior was less regular in time and not as aligned with the external gradient (Fig. 4C). The average level of activity was smaller and broader than when responding to a steep gradient because the patches of activity were less frequent and less localized (Fig. 4D and Fig. S1). Nevertheless, the output of the coupled system is more amplified than the response regulator alone. Finally, we considered the effect of a quick shift in the direction of the gradient (Fig. 4E). After a brief suppression due to transient removal of the stimulus, changing the location of the gradient redirected the series of localized activity patches in the direction of the new gradient.

Fig. 4.

Response of the model to applied spatial gradients. (A) As indicated, a steep spatially graded stimulus centered at 0° was applied at 180 s. (B) The mean level of activity (red), standard deviation (gray), and the response regulator (blue) are shown as a function of angle for an aggregate of cells (n = 20). (C and D) The same simulations were run with a shallower gradient. (E) In this simulation, the direction of the (steep) gradient was changed from 0° (180–660 s) to 90° (at 670 s). Vertical lines are 60 s apart.

Altering LEGI or the Strengths of the Feedback Loops in the Excitable Network Produces “Phenotypes.”

To determine how the strengths of different feedback loops in the model affect the temporal and spatial behavior, we performed a number of simulations using systematically perturbed systems (Fig. 5 and Fig. S2). We first considered the effect of decoupling the two modules of the system, by removing the link between the LEGI system and the downstream excitable network. In these simulations, the typical spontaneous patches of activity were seen but they were unaltered by the external stimulus. When coupling was reduced by 75%, random bursts of activity continued but there were weak temporal responses to a stimulus increment and partial spatial restriction of the response to the gradient (Fig. 5B and Fig. S2B). We then explored the effects of prolonging the time course of the global inhibitor (i.e., delaying adaptation) within the LEGI module (Fig. 5C and Fig. S2C). In this altered system, the initial peak in activity was similar to that in wild type. However, the subsequent peaks were long lasting and periodic bursts of activity along nearly the entire perimeter were seen for an extended period of time both under spatially uniform and gradient inputs. In the latter, the periodic responses eventually aligned themselves with the external gradient.

Fig. 5.

Response of model to perturbations within the LEGI and excitable network modules. In these simulations, the nominal model (A) was systematically altered and the response to a uniform stimulus (Left) or a steep spatial gradient (Right) was calculated. (B) Connection between LEGI module and excitable network reduced by 75%. (C) Time course of the inhibitor in the LEGI module slowed down by a factor of 10. (D) Negative feedback reduced by 25%. (E) Negative feedback increased by 25%. The color scheme in each panel is autoscaled to maximize contrast. The absolute levels of activity can be seen in Fig. S2, which shows the corresponding aggregate data for multiple (n = 40) spatially uniform simulations. Vertical lines are 60 s apart.

Changing parameters within the excitable network also gave rise to distinctive behaviors. When the strength of the negative feedback loop was reduced, the spontaneous patches of activity were stronger and longer lasting, and multiple sites along the perimeter responded simultaneously. The responses to uniform stimuli were more intense; the secondary peaks were delayed but broader. These features made the responses appear to be less aligned with the gradient (Fig. 5D and Fig. S2D). Similar behavior was seen by increasing the positive feedback strength (Fig. S3). In contrast, increasing the negative feedback strength made the initial response smaller and nearly eliminated the secondary responses. It reduced the intensity of the patches during exposure to a gradient; however, they remained tightly confined in the correct direction (Fig. 5E and Fig. S2E). Finally, we halved the strength of the positive feedback loop in the excitable network. The response decreased in magnitude as might be expected. More interestingly, the second peak after the uniform stimulus disappeared and the response to the gradient was no longer periodic; rather, it pointed stably, but weakly, along the gradient.

Discussion

The LEGI-biased excitable network hypothesis incorporates many of the features and surmounts many of the difficulties posed by previous schemes of chemotaxis. Our formulation of the hypothesis simulates the propagating waves of signaling events seen on the basal surfaces and the dynamic patches of activity observed at the tips of pseudopodia in migrating cells. The model accounts for the kinetically complex responses of wild-type cells, the reactions to compound stimuli, as well as directional sensing of shallow spatial gradients. Assuming that the patches of activity are correlated with cellular projections that move cells, the model generates the dynamic behavior and explains the extraordinary sensitivity of chemotactic cells. Furthermore, systematic perturbation of the model parameters gives rise to activities consistent with phenotypes observed in known classes of mutants.

The output of the model is consistent with the unbiased extensions of pseudopodia displayed by Dictyostelium cells and neutrophils prior to stimulus addition, as well as the biphasic responses to increments in chemoattractant (see Box 1). During the initial peak, the high activity along the entire perimeter is consistent with the observed uniform activation of Ras and PI3K. One would expect pseudopodia to be extended everywhere, but in reality cells “freeze,” perhaps because cytoskeletal or membrane components are limited (not modeled here). The rapid shutoff of activity caused by the negative feedback loop in the excitable network corresponds to the cringe stage where Ras activity goes down, PIP₃ accumulation disappears, F actin depolymerizes, and the cells round up. The following period of increased event frequency matches the observed spreading responses where the tips of the extensions are labeled with patches of signaling and cytoskeletal proteins. Finally, the return to random activity brought about by adaptation of the LEGI module fits with the resumption of random migration observed during continuous stimulation. In the model, each successive secondary peak decreased in intensity. This result is often observed experimentally in individual cells, whereas in biochemical measurements on cell populations, the second phase of response ramps up slowly to a low peak level (see Box 1) (20). Consistently, when we modeled a population of cells with a distribution in network parameters, the second phase did show a more gradual rise due to averaging of different responses (Fig. 2).

The model successfully accounted for or predicted the cellular responses to compound temporal stimuli (Fig. 3). First, the model indicated that, when the response shuts off after the initial peak, the cells are not adapted. Removal and immediate reapplication of the same stimulus at this point triggers another response nearly as large as the first. However, after the series of secondary responses subside, the cells are adapted and a much longer recovery period is required before the same stimulus can trigger a full response (13). In recent experiments using a microfluidic device to rapidly apply and remove stimuli, consistent behavior was observed for the PIP₃ responses in Dictyostelium. Second, the model generated biphasic responses each time the stimulus was incremented with the integrated magnitude of each response roughly equal to the relative change in receptor occupancy as has been observed experimentally. Third, the model as implemented predicted that removal of the stimulus from adapted cells should cause a transient suppression of spontaneous activity because the LEGI module generates a below-basal response regulator. To our knowledge, such suppression of basal biochemical activity has not been reported, although we have noted that cells chemotaxing toward a micropipette “collapse” when the pipette is lifted.

Importantly, the model explained the ability of the chemoattractant to direct the migration of the cells (Fig. 4). In our simulations the extent of confinement of activity patches to the correct direction was proportional to the steepness of the gradient. A strong directional response was observed even when receptor occupancy across the cell differed by as little as 6%. Furthermore, because the LEGI module always attains the same basal level at steady state, amplification is independent of the midpoint of the gradient and depends only on the steepness, matching a feature of chemotaxing cells. What is the origin of this extraordinary sensitivity? In a gradient, the response regulator of the LEGI module deflects above or below the baseline level toward the side of the cell facing the higher or lower chemoattractant concentration, respectively. However, the difference between the two ends is not amplified compared with the external gradient (see Box 2, Fig. 4, and ref. 27). Remarkably, when the excitable network is coupled to the LEGI module, the extreme amplification of the gradient falls out naturally. Because the response regulator serves as an input to an excitable network, the slight deflections above or below the basal level strongly enhance or suppress the spontaneous activity of the excitable network toward or away from the gradient, respectively (Fig. 4 B and D). The relationship between the response regulator and the activity of the LEGI-biased excitable network can also be seen by plotting both against the external gradient on the same graph (Fig. S1). Below-basal levels of response regulator suppress spontaneous activity, whereas above-basal levels that cross a threshold enhance the frequency of events.

Our model relies on noise to select the sites where the excitable network is spontaneously triggered. It is reasonable to assume that such noise can arise from the intrinsic and extrinsic fluctuations inherent in biochemical reactions (35). This implementation sets the model apart from that of Hecht et al. where foci are fixed in space but can be triggered at random times (32). Our model does not require that we select foci locations; instead, foci arise naturally from the localized fluctuations of the system. This feature makes it possible for chemoattractants to steer the spontaneous activity without further components or assumptions.

We have speculated on the correspondence of elements in the LEGI-biased excitable network model with components in the cellular signaling pathways. First, because actin waves propagate in cells lacking the Gβ-subunit (36), it appears that the chemoattractant receptor and associated G proteins are upstream and not part of excitable network. We assign these components, along with an unknown inhibitor that brings about adaptation, to the upstream LEGI module. Second, we suggest that Ras and PI3K activations are part of the downstream excitable network because they occur spontaneously in patches in unstimulated cells and display biphasic responses to increments in chemoattractant. Furthermore, we propose that all of the front and “back” events triggered by chemoattractants are part of the excitable network (see Box 1). It is expected that the front and back events will fluctuate 180° out of phase. Indeed, wave-like association of PTEN with the membrane, in opposition to PIP₃ accumulation, has been observed (37). Further assignment of the components of the excitable system awaits the development of biosensors to observe these events in cells. Two recent studies, carried out in growth stage Dictyostelium cells, demonstrated that PIP₃ accumulation displayed wave-like behavior (33, 34). Surprisingly, in these studies the PIP₃ and actin waves appeared to be out of phase. As reported, most often we observe these front events to be colocalized on expanding waves at the edge of the cell, although we have noted a displacement of the two markers associated with unusual structures.

Perturbations to the parameters of the LEGI-biased excitable network model led to important insights into the phenotypes of known classes of mutants (Fig. 5). Reducing the output of the LEGI module decreased both the response to uniform stimuli and impaired directional sensing of spatial gradients. Numerous cell lines carrying point mutations in chemoattractant receptors or G-protein subunits show weakened biochemical responses and poor chemotaxis and likely correspond to this case (38). The dramatic increases in the secondary oscillatory responses of the excitable network and delayed appearance of directional sensing obtained by slowing the LEGI inhibitor are reminiscent of the behavior of cells such as fibroblasts which adapt slowly, display prolonged responses to growth factors, and sense the absolute, rather than the relative, concentration of the gradient (39). To our knowledge, no variants of Dictyostelium or neutrophils have been isolated that display such nonadaptive behavior that would correspond to a slowing of inhibition.

Turning to the downstream excitable network, decreasing the negative feedback loop greatly enhanced the sizes and durations of the activity patches and the secondary responses, and strongly interfered with gradient sensing. This behavior mimicked that of cells lacking NF1, a GTPase activating protein for RasG, as well as cells expressing the constitutively active RasC_Q62L which display excessive phosphorylation of PKB substrates (40–42). These mutants extend multiple extraneous pseudopodia simultaneously in the absence and presence of chemoattractant and are extremely defective in chemotaxis. Thus, the negative feedback loop may act to curtail the activation of the Ras proteins. Cells lacking PTEN, a negative regulator of PIP₃, also display a similar phenotype, which may indicate that PIP₃ is part of the positive feedback loop. Indeed, multiple reports in neutrophils indicate that PIP₃ is part of a positive feedback loop that plays a role in polarity. Increasing the negative feedback loop, or partially reducing the positive feedback, decreased the frequency and size of the spontaneous patches of activity. With a uniform stimulus, the first peak was smaller and secondary peaks were essentially absent. Interestingly, the responses to the gradient, although weaker than the “wild-type” system, were more intense and frequent than in the absence of the gradient and strongly aligned in the correct direction. This result might be expected if, as noted above, PIP₃ is part of the positive feedback loop. Cells treated with PI3K inhibitors display no random motility but are able to track toward a steep gradient (20). When the gradient is applied to cells with increased negative or reduced positive feedback, the constant input from the response regulator at the front of the cell may be sufficient to enhance directed activity. Further decreasing the positive feedback loop virtually eliminated the spontaneous activity of the system but the model still displayed directional sensing. This case is reminiscent of cells treated with Latrunculin A which largely lose spontaneous activity but retain signaling responses to uniform stimuli and direct stable crescents of front (i.e., RBD-GFP and PH-GFP) or back (i.e., PTEN membrane association) events, respectively, toward or away from gradients.

In general, perturbations to the model are consistent with the effects of genetic and pharmacological interventions observed experimentally and provide several important insights. First, partial defects that slow the inhibitor within the upstream LEGI module may not prevent the rapid shutoff of the response or eliminate directional sensing. Second, all the perturbations within the excitable network affect prestimulus activity, responses to uniform stimuli, as well as directional sensing. Thus, mutations which separately alter directional sensing without affecting motility are predicted to be rare, consistent with experience. The previously unexplained correlation among prestimulus activity, the magnitude of the secondary responses to uniform stimuli, and chemotaxis is a natural consequence of the model.

The LEGI-biased excitable network model quite accurately captures the general behavior of chemotactic cells though many challenges remain for future studies. First, it is not understood exactly how or which activity patches lead to pseudopodia. Although any patch might potentially generate a protrusion, obvious mechanical constraints on the basal surface do not completely eliminate the signaling responses, and additionally, not all cytoskeletal responses are accompanied by signaling responses of equal strength. These observations suggest that the components of the excitable network are not obligatorily linked. The excitable network may contain several parallel positive or negative feedback loops, which we have greatly simplified here. Second, our current scheme does not account for the stable polarity which causes some chemotactic cells to turn, rather than establish a new front, toward a new gradient. It is evident to us that an additional slow-acting positive feedback loop could bring polarity to our scheme; this is currently under investigation. Third, the molecular nature of the LEGI inhibitor and the mechanism by which it limits activity of the receptor/G-protein system are unknown. Nevertheless, the model allows us to understand how newly appreciated excitable behavior can be regulated by external cues and satisfactorily accounts for most of the responses of chemotactic cells to spatial and temporal stimuli. This understanding provides a framework for motivating experimentation and interpreting new observations as they emerge.

Materials and Methods

Wild-type Dictyostelium cells (AX2 background) were transformed with GFP-tagged PHCrac, Raf1-RBD, Hspc300, or LimE-RFP by electroporation and cultured axenically in HL5 medium containing G418 (20 μg∕mL) or hygromycin (50 μg∕mL) at 22 °C. TIRFM was carried out in an Olympus IX71 inverted microscope illuminated by a Kr/Ar laser source. Further details can be found in SI Text.