Microstructured elastomeric surfaces with reversible adhesion and examples of their use in deterministic assembly by transfer printing

Abstract

Reversible control of adhesion is an important feature of many desired, existing, and potential systems, including climbing robots, medical tapes, and stamps for transfer printing. We present experimental and theoretical studies of pressure modulated adhesion between flat, stiff objects and elastomeric surfaces with sharp features of surface relief in optimized geometries. Here, the strength of nonspecific adhesion can be switched by more than three orders of magnitude, from strong to weak, in a reversible fashion. Implementing these concepts in advanced stamps for transfer printing enables versatile modes for deterministic assembly of solid materials in micro/nanostructured forms. Demonstrations in printed two- and three-dimensional collections of silicon platelets and membranes illustrate some capabilities. An unusual type of transistor that incorporates a printed gate electrode, an air gap dielectric, and an aligned array of single walled carbon nanotubes provides a device example.

Modes of adhesion observed in insects and small animals such as geckos are repeatable, robust, and power efficient. In fact, certain features such as the ability to adhere to a wide variety of surfaces, to rapidly and reversibly change adhesion strength between strong and weak modes, and to self-clean contaminants significantly exceed those available in conventional pressure sensitive tapes or structural adhesives. Many of these creatures have micro and nanoscale structures with varying levels of complexity on foot or toe-pads (1). Some of these beneficial aspects can be reproduced in synthetic materials, to yield dry adhesives (2–4) that offer, for example, switchability in adhesion through changes in thermal and/or mechanical conditions (3, 4). Although most reports focus on fibrillar structures mimicking those found on the feet of gecko lizards, attachment mechanisms that emulate adhesion organs or pads of common insects might provide attractive alternatives. For example, when adhering to or releasing from a smooth surface, aphid adhesion organs (pulvilli) are everted by increased blood pressure or withdrawn by contraction of tibial muscles (5), respectively. This pressure driven mechanical sagging or retraction of the pulvillus enlarges or diminishes the contacting areas, in a reversible fashion that induces corresponding changes in adhesion strength. This and related biological strategies provide opportunities for controlled adhesion in engineered systems, with one area of possible utility in methods for deterministic assembly of micro/nanomaterials by transfer printing. Here we introduce an adhesive surface inspired by the aphid in which pressure induced sagging of a microstructured elastomeric surface provides extreme, reversible levels of switchability in nonspecific, generalized adhesion, with strong to weak adhesion ratios higher than 1,000. The designs, which we refer to as microtip surfaces, are robust, reusable, and can be easily cleaned with commercial pressure sensitive adhesives like Scotch™ tape. Experimental and theoretical studies provide insights into the basic mechanisms of adhesion. We exploit these ideas in advanced stamps for printing-based assembly of silicon nanomembranes and platelets on a variety of surfaces, in two- and three-dimensional layouts that would be difficult or impossible to accommodate using other methods. As a device example, we use printing to form an unusual type of carbon nanotube transistor that uses a nanoscale air gap as a gate dielectric.

The adhesives reported here have potential uses in many applications. Our principal motivation is for advanced capabilities in the manipulation of stiff, solid micro/nano-objects via their selective transfer from one substrate (i.e., donor substrate) to another substrate (i.e., receiver substrate) using soft, elastomeric stamps. This transfer printing process (6–9) enables massively parallel assembly of diverse materials (i.e., Si, GaN, GaAs, mica, graphene, silica, and others) in various structural forms (i.e., wires, membranes, plates, with dimensions from a few nanometers to macroscopic scales), with throughputs that correspond to millions of objects per hour. A rapidly growing number of applications in micro and nanotechnology benefit from or are enabled by this type of approach (6–8). Transfer yields depend critically on the ability to switch from strong to weak adhesion between retrieval (i.e., “inking”) and delivery (i.e., “printing”), respectively, and to maximize the versatility, control must be accomplished without specialized surface chemistries or adhesives. Kinetic approaches that exploit viscoelastic effects in the stamps (9) are useful, but the low contrast in adhesion switching (i.e., ∼3) limits their broad utility. The experimental results and associated theoretical models presented here provide alternative design strategies, with significantly enhanced capabilities for printing-based assembly, and the potential for other areas of use.

Results

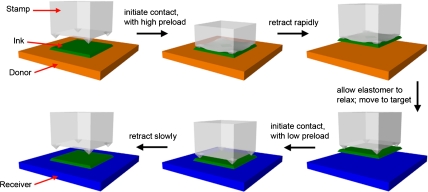
Fig. S1A illustrates a representative elastomeric microtip surface, with key dimensions labeled. The geometry consists of four features of pyramidal relief on the surfaces of square posts in a square array placed on a ∼1 mm thick backing layer of the same material, configured to allow collapse of the regions of each post between the pyramids when subjected to sufficient applied force. This design enables extremely high levels of switching in adhesion, with a physics that involves a complex interaction between the pressure-controlled contact area and aspects of soft adhesion inherent in the viscoelastic nature of the elastomer, as revealed through systematic studies presented next. We begin with a qualitative description of the process for use in transfer printing (Fig. 1), and then outline some aspects of design, supported by quantitative measurements and theory. During retrieval, downward force mechanically collapses the regions between the microtips, thereby maximizing the contact area and, as a result, the strength of generalized adhesion, typically dominated by van der Waals interactions (10), between the object to be transferred (green platelet in Fig. 1) and the stamp. For sufficiently low strengths of adhesion to the donor substrate, retracting at high speeds retrieves the platelet, in a way that maximizes adhesion to the stamp through viscoelastic effects. Immediately after retraction, elastic restoring forces bring the relief back to its original geometry, leaving contact only at the sharp points of the microtips. To affect printing, the stamp, inked in this manner, presses against a receiver surface such that the platelet comes into complete contact on its bottom surface, but the relief on the stamp does not collapse. Slow retraction minimizes the adhesion strength associated with viscoelastic effects, thereby facilitating release and completing the transfer printing assembly process.

Fig. 1.

Implementation of elastomeric, microtip adhesive surface in a stamp for deterministic assembly by transfer printing.

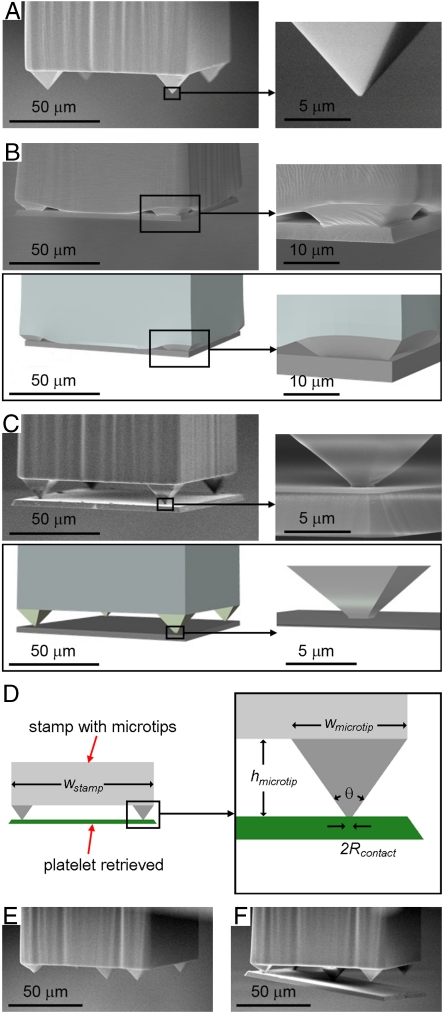
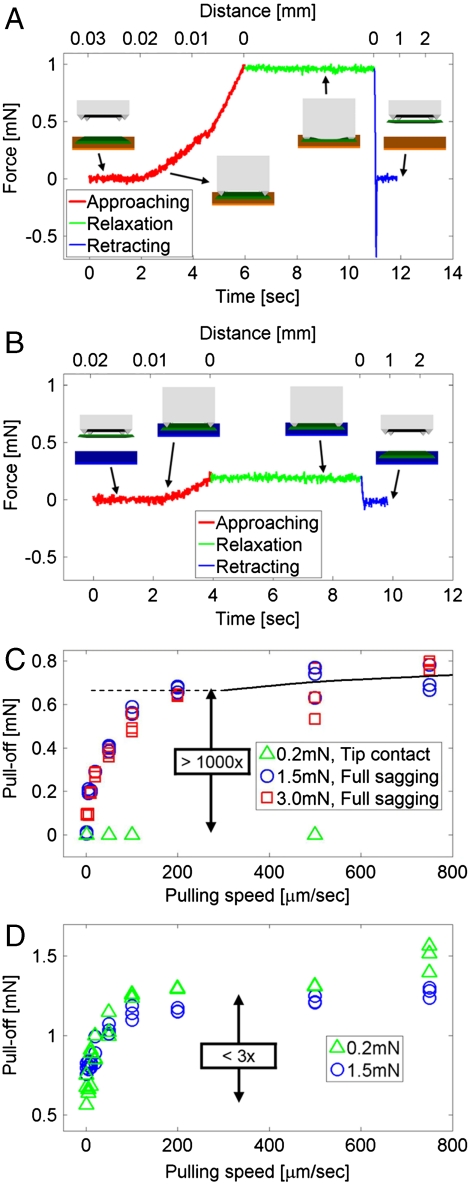
A custom measurement setup provides the ability to quantify the adhesion (Fig. S2A). The system consists of motorized x, y stages and a manual tilting stage (Newport, UTR46) that supports a precision load cell (Transducer Techniques, GSO-10). Microtip surfaces, similar to the one illustrated in Fig. 1 and Fig. S1A are mounted on an independent vertical stage (Aerotech, PRO165) that allows contact with a target substrate (i.e., silicon wafer for the results presented here) at controlled speeds and forces. For the work presented here, we formed these surfaces with the elastomer poly(dimethylsiloxane) (PDMS), using casting and curing procedures of soft lithography with appropriate templates (Fig. S1B). PDMS is a transparent elastomer with well known, attractive properties for this application, such as linear elastic response to elongations of 100% or more, high physical toughness, and excellent fatigue characteristics. Fig. 2 A–D provide SEM images of a structure in the design of Fig. 1 and Fig. S1A, without and with an adhering silicon platelet and a schematic illustration for the latter case. Fig. 2 E, F show an advanced configuration that involves the addition of a large microtip in the center, for purposes described subsequently. Fig. 3 A, B present typical force-time plots for a single post having the four-tipped design, with distance scales indicated on the top axes, collected at an approach speed of 5 μm/s, terminated at a specified load for 5 s, and then retracted at 1 mm/s. The maximum tensile force during retraction defines the strength of adhesion (i.e., pull-off). Fig. 3A shows data for a representative case of full mechanical collapse under a preload of 1 mN, with a retraction speed of 1 mm/s. Two slopes are evident in the approaching curve (red line), indicating an increase in stiffness when the region between the microtips collapses and contacts the substrate. The slope in the first region defines an effective spring constant associated with compression of the microtips, with a minor contribution from deformation of the post. The second region includes the elasticity of the post itself, and its elastomeric support. The sharp, negative feature in the curve collected during retraction (blue line) corresponds to rapid release from the contacting surface; its magnitude defines the adhesion force (i.e., pull-off). Fig. 3B summarizes the corresponding case without collapse, at 0.2 mN preload and 1 mm/s retraction. Here, the adhesion force is too small to measure with the load cell. Images collected with an inverted optical microscope and an SEM (Fig. 2 and Fig. S3A) suggest effective contact areas in the collapsed and uncollapsed states that correspond to ∼80% and ∼0.07% of the projected area of the post and the microtips, respectively. The ratio of these areas suggests an expected difference in adhesion of more than 1,000 times. This value, however, underestimates the actual difference that can be achieved because it ignores viscoelastic effects, as observed clearly in the data of Fig. 3C. In particular, with preloads sufficient to induce mechanical collapse (i.e., 1.5 mN and 3 mN), the adhesion force depends strongly on retraction speed. This functional dependence, which is evident also in data for the corresponding flat surfaces (Fig. 3D), arises from the viscoelastic nature of the PDMS, as reported previously (9). We did not observe any significant changes in these adhesion behaviors even on repeated cycling tests (Fig. S2B).

Fig. 2.

SEM and FEM images of representative elastomeric stamps in microtip designs, with and without silicon platelets (3 μm thick; 100 × 100 μm) on their surfaces. (A–C) Four-tipped layout. The right frames provide magnified views of one of the microtips and the bottom frames provide corresponding images of the results of finite element modeling (B, C). (D) Schematic illustration for notation of the stamp dimension. (E, F) Five-tipped layout. In this design, the silicon platelet remains in contact only with the largest, central microtip in the final stages of the transfer printing process.

Fig. 3.

Typical force-time (bottom axis) and force-distance (top axis) curves associated with contact of a microtip surface with the flat surface of a silicon wafer (A, B). The inset illustrations correspond to the steps of retrieval (A) and delivery (B) for use of such a surface in a transfer printing mode. Plots of force required to remove a microtip surface (C) and a corresponding flat surface (D) from the silicon, as a function of retraction speed for three different preload cases, simulating the steps of retrieval (0.2 mN) and delivery (1.5, 3 mN) in a printing process. Modeling results for the microtip surface are indicated as a black line (C).

These combined geometric and material effects offer exceptionally high levels of switching in adhesion, for unmatched capabilities in transfer printing, without the need for surface chemistries or separate adhesives to guide transfer. For purposes of demonstration, we use platelets of silicon (100 × 100 μm; thicknesses of 260 nm or 3 μm) fabricated by removing the buried oxide layer from a silicon-on-insulator (SOI) wafer, as illustrated in Fig. S1C. Fig. 4A shows such platelets printed onto an array of islands (7 × 7 μm squares, separated by 13 μm with square packing arrangement). The ability to transfer at high yields without adhesives, particularly on structured surfaces where contact areas with the receiver are much smaller than the areas of the platelets themselves, clearly illustrates the utility of the microtip design; these capabilities are unavailable to methods that just use viscoelastic effects for control (9). As a more challenging example, Fig. 4B shows results of printing onto the rough surface of a film of ultrananocrystalline diamond (2 μm thick, rms roughness > 70 nm with sharp facet edges; see inset), where we estimate the contact area to be less than 1% of the platelet area. Stamps with five microtips (Fig. 2 E, F and Fig. S3B) were needed for successful printing of 260 nm thick platelets, where adhesion in the printing mode can be quite small, due to contact only at the single, central microtip in the final stages of release. Freely suspended geometries are also possible. Fig. 4 C,D show printed platelets (3 μm and 260 nm thick) that span gaps between pairs of silicon bars on receiver substrates. The high yield and versatility of this process also enable the formation of complex, three-dimensional assemblies. Fig. 4 E, F provide images of multilayer configurations of 3 μm thick silicon platelets in single and multiple stacks with translational and rotational increments. These examples demonstrate a construction capability for three-dimensional micro/nanostructures that approaches those of macroscale fabrication methods based on assembly of building blocks, e.g., LEGO® with silicon.

Fig. 4.

SEM images of representative printing results with thick (3 μm) and thin (260 nm) silicon platelets (100 × 100 μm squares) on different surfaces and in free standing and multilayer stacked geometries. (A) Image of platelets printed on an array of square islands. (B) Image of 3 μm thick silicon platelets printed on the rough surface of a film of ultrananocrystalline diamond on a silicon wafer. Images of 3 μm (C) and 260 nm (D) thick silicon platelets printed onto two silicon bars, to yield freely suspended structures. Images of multilayer configurations of 3 μm thick silicon platelets in a single stack with small incremental rotations and translations (E) and four similar stacks, capped with a pair of platelets in the center (F), both on flat silicon wafer substrates.

Similar microtip designs can be exploited in the fabrication of active devices for applications in areas ranging from photonics and metamaterials to photovoltaics and electronics. To demonstrate an example, we built an unusual class of transistor that combines a printed gate electrode, an air gap dielectric, and a parallel array of single walled carbon nanotubes. Fabrication steps and characterization details are described in SI Text.

Discussion

The pyramid geometry a microtip has certain practical advantages: (i) it is easy to fabricate in a well controlled, lithographic manner using techniques of anisotropic etching in silicon and (ii) the radius of curvature of the tip can be extremely small, and it is decoupled from the overall height of the relief feature (i.e., the microtip). The underlying mechanics principles can be used with other shapes.

Data analysis guided by theoretical mechanics modeling reveals the underlying physics of adhesion in surfaces of the type described previously, and identifies the key parameters for optimization. We first consider the strength of the low adhesion state, where the adhesion energy per unit area in the limit of zero peel rate multiplied by the area of contact at the ends of the microtips is important. Fig. 2 A, C show a representative case, where the stamp, made of PDMS, incorporates anisotropically etched pits in silicon (100), to yield microtips with radii of curvature, R_microtip, less than ∼100 nm (Fig. S1B). Contact with the silicon causes the microtips to deform, to maintain equilibrium between attraction from surface adhesion and elastic repulsion. These deformations lead to contact areas that are considerably larger than those that might be inferred based only on the geometry of the stamp. Classical models of contact mechanics (11) can be adapted to give analytically the contact radius R_contact (Fig. 2D) (see SI Text for details)

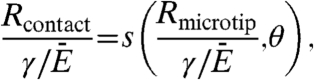[1]

where s is a nondimensional function of the microtip cone angle θ (Fig. 2D) and R_microtip (Fig. S1A) is given in SI Text. Finite element analysis yields similar results (see Fig. 2C and the SI Text). The value of R_contact scales linearly with the work of adhesion γ between the PDMS and the contacting surface, and inversely with the plane-strain modulus 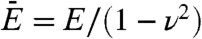of PDMS (E--Young’s modulus, ν ≈ 0.5--Poisson’s ratio). Analysis shows that R_contact decreases with R_microtip, but reaches an asymptotic value for R_microtip → 0 (Fig. S5A) given by

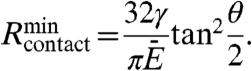[2]

We note that our analytical models assume symmetric deformations, without any bending or buckling. The SEM and finite element method (FEM) results of Fig. 2 support the validity of this assumption.

For the case of a PDMS stamp and a silicon surface, where E = 1.8 MPa (12) and γ = 155 mJ/m², (13, 14), R_contact is approximately the same as 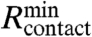when R_microtip is less than ∼100 nm (Fig. S1B). When θ = 90° between two opposite edges of pyramid ( 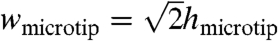in experiments, Fig. S1A), 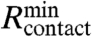is ∼680 nm, comparable to 750 nm evident from Fig. 2C, and 732 nm given by the finite element method (Fig. 2C and SI Text). The conclusion, then, is that existing methods for producing elastomer surfaces in a material like PDMS can already achieve values of R_microtip well below the value needed to realize minimal contact area. Advanced microtip layouts can, however, reduce the contact area below that provided by the four tip design. Fig. 2 E, F show examples of such reduced contact area schemes. In these designs, during release separation occurs initially at the smaller corner microtips leaving the final central microtip in contact with the platelet, thereby reducing the contact area immediately before release to the minimum possible value immediately before release (Fig. S3B), (four times lower than that associated with Fig. 2C). Further reductions might be possible by increasing E, with other silicones, or decreasing γ, with related elastomers such as perfluoropolyethers, or decreasing the microtip cone angle θ.

The heights of the microtips and their nearest neighbor separations represent other critical parameters. The designs must enable unstable collapse, with near full area contact in the compressed state. For a given separation, there exists a minimum height of the microtip, h_min, below which the elastic restoring force is too small to bring the relief back to its original geometry after pressure induced collapse. This minimum height can be determined by equating the strain energy in the compressed PDMS and microtips to the adhesion energy between the contacting surfaces, which gives (see SI Text for details), for the four tip design,

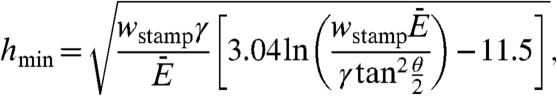[3]

where w_stamp is the width of the post of the stamp. For w_stamp = 100 μm (E = 1.8 MPa, γ = 155 mJ/m², and θ = 90°), the above expression gives h_min = 8.44 μm, which agrees well with the minimum height of ∼8.5 μm observed systematically in experiments (see Fig. S5B and SI Text for details). There also exists a maximum height, h_max, above which the elastic restoring force associated with compression of the microtips is so large that the stamp rapidly delaminates from the platelet after the pull-off force is applied, thereby preventing large contact areas for efficient removal of an object (e.g., platelet, as illustrated in Fig. 1) from a donor substrate. The value of h_max can be determined analytically by equating the energy release rate to the work of adhesion between the PDMS stamp and the silicon platelet. The result is (see SI Text for details)

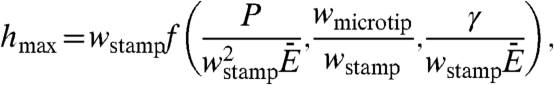[4]

where f is a nondimensional function of the applied force P, the microtip width (w_microtip, Fig. S1A), and the work of adhesion γ. For the full expression, see the SI Text. For an applied force of 1 mN and 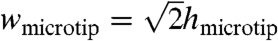(other material and geometry parameters the same as before), the maximum height is h_max = 13.3 μm, which agrees reasonably well with the maximum height of ∼12.7 μm from experiments (see Fig. S5 C,D and SI Text for details). These minimum and maximum values elucidate criteria that define three possible energy states of the stamp and the platelet: (i) platelet retrieval with relief collapsed, (ii) platelet retrieval with relief delaminated, (iii) failure in platelet retrieval. The microtip sizes were optimized to obtain the second state for representative preload forces (> 1 mN) and retrieval velocities (> 200 μm/s). Experiments with different microtips showed that when h is ∼20% smaller or larger than this optimal value, states (i) (platelet retrieval with relief collapsed) or (iii) (failure in platelet retrieval) with the same preloads and velocities could be achieved, respectively.

The rate dependence observed in the microtip structures is identical, to within experimental uncertainties, to that in flat post stamps. The latter effects were explored previously by us, in the case of transfer printing (9), and by many others in the more general context of adhesion between viscoelastic and nonviscoelastic materials (10, 13, 15).

For operation in the retrieval mode, the stamp must be retracted sufficiently quickly that the fracture of the interface between the platelets and their donor substrate occurs before the viscoelastic fracture of the stamp/platelet interface. During fast retraction the compressed microtips do not have time to relax back to their original shapes; their heights remain small and the overall contact area remains high, such that the energy release rate is lower than the work of adhesion. An analytical viscoelastic model, with creep compliance data for PDMS from the literature (16), gives a relaxation time of 0.052 s (for pulling speed 460 μm/s), at which the collapsed stamp starts to debond from the substrate (see SI Text). For fast retraction (pulling speed > 200 μm/s), this time scale is roughly consistent with experimental observation because the time for complete separation of the stamp/substrate interface is about the same as the time for initial debonding. Additionally, this viscoelastic analysis predicts a pull-off force that is in quantitative agreement with the experiments at pulling speeds > 200 μm/s, as shown in Fig. 3C. For pulling speeds < 200 μm/s, the analysis gives a larger pull-off force than the experiments because the debonding may gradually propagate along the stamp/substrate interface due to slow retraction, but the model does not account for crack propagation along the interface. Improved analysis and comparison to experiment will require accurate measurements of creep compliance in our PDMS and direct visualization of the interface using high speed imaging techniques. These topics are the focus of future work.

The force-distance curves and other behaviors of Fig. 3 can also be captured by mechanics modeling. For the case of Fig. 3A, modeling predicts two slopes, as observed in experiment: k_microtip when contact occurs only at the microtips, and k_post for contact at both the microtips and the intervening regions. In particular, analysis yields (see SI Text)

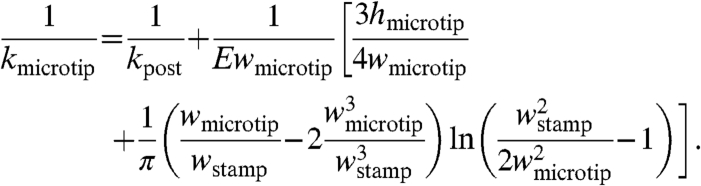[5]

For k_microtip = 30 N/m and k_post = 90 N/m extracted from Fig. 3A, and h_microtip = 10.6 μm and width 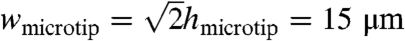from experiments, the left- and right-hand sides of Eq. 5 give 0.033 m/N and 0.036 m/N, respectively. This excellent level of agreement validates the modeling, and its further use in examining the differences between Fig. 3 C and D to gain insights into the adhesion mechanics. In the collapsed state, the microtips provide forces that add to the externally applied force needed to cause delamination. This effect can be explored through calculation. In particular, the mechanics models described previously yield analytical forms for the restoring force, F, associated with the compressed microtips. The result takes the form (see SI Text for details)

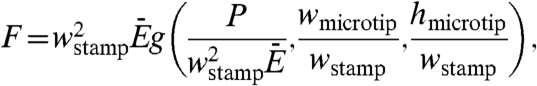[6]

where g is a nondimensional function of the applied force P, microtip width w_microtip, and height h_microtip, and is given in the SI Text. This force, as shown in Fig. S6A, is the same as the preload when only microtips contact the platelet. The sudden increase in the restoring force corresponds to the collapse of post between microtips. This force then increases linearly with the preload (post contact in Fig. S6A), but with reduced slope due the elasticity of the post. This dependence is followed by a nonlinear increase, at a reduced rate because the contact area also increases (zipping of interface in Fig. S6A). For an applied force of 1.5 mN, the total restoring force is 0.63 mN for the collective effect of four microtips with height h_microtip = 10.6 μm and width 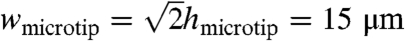(other material and geometry parameters are the same as above). Note that this restoring force is larger than the preload 0.39 mN needed to cause collapse of the regions between the microtips (i.e., position in the red curve of Fig. 3A that occurs at the point where the linear slope changes) because the microtips continue to be compressed after the intervening regions collapse (see Fig. S6A). Fig. S6B presents a master plot obtained by shifting the data of Fig. 3D downward along the y-axis by an amount equal to the total restoring force evaluated by modeling, and the plotting results together with the data of Fig. 3C. The overlap of the resulting curves, to within experimental uncertainty, supports the modeling and the associated interpretation of the underlying physics.

Conclusion

This paper reports a unique adhesive surface for deterministic assembly of solid micro/nanoscale parts into two- and three-dimensional configurations, and some theoretical foundation for understanding key design parameters. The work provides experimental data and theoretical models on pressure induced switching in adhesion strength in these systems. Theoretically guided design optimization yields high levels of control, with more than three orders of magnitude difference between the forces measured in strong and weak adhesive states. These characteristics enable transfer printing reliably and repeatedly with very high yield (almost 100%) in new modes, with important consequences for applications. Future opportunities include exploring other uses, and pursuing strategies for increasing the adhesion over the corresponding flat surface using vacuum effects or notched features on the sidewalls of the posts. These and other structural designs can be further enhanced through the introduction of new materials, using guidance from mechanical models similar to those presented here.

Materials and Methods

Fabrication of Elastomeric Surfaces with Microtips.

The fabrication (Fig. S1B) involved casting and curing the elastomer PDMS (Sylgard 184, Dow Corning; 5∶1 mixture of base to curing agent) against a Si (100) wafer (Addison Engineering) with a pattern of photodefined epoxy (SU-8 50; MicroChem Corp.; 100 μm thick) and an array of pyramidal pits (15 × 15 μm squares, 10.6 μm deep, separated by 70 μm with square packing arrangement) formed by anisotropic etching with KOH through a photolithographically patterned hard mask of SiN (100 nm thick, formed using plasma enhanced chemical vapor deposition, PECVD, PlasmaTherm). The epoxy layer provided square openings (100 × 100 μm) with corners aligned to sets of pits. Casting the prepolymer to PDMS (base oligomer and crosslinking agent) against the functionalized (trichlorosilane, United Chemical Technology) surface of this wafer, thermally curing the PDMS (70 °C for > 1 h) and then peeling it back yielded the desired elastomeric surfaces with microtips.

Fabrication of Silicon Platelets for Printing.

The printed structures consisted, in all cases, of flat plates of silicon (100) derived from SOI wafers (Shin-Etsu Chemical Co., Ltd. and Soitec), with thicknesses of 3 μm or 260 nm. These plates were defined by patterning a layer of photoresist (AZ5214, 1.5 μm thick) in a square geometry (100 × 100 μm, square packing arrangement, 300 μm separation) and then etching the exposed top Si by SF₆ reactive ion etching (PlasmaTherm). Next, wet etching with concentrated hydrofluoric acid, HF, through a mask of photoresist removed the buried oxide everywhere except for 110 × 110 μm squares cocentered with the squares of silicon. A final pattern of photoresist (AZ5214) defined mechanical anchor features (15 × 45 μm rectangles, 1.5 μm thick) to tether the silicon squares to the underlying wafer at each of their four corners. Undercut etching of the remaining oxide with HF completed the process. Fig. S1C summarizes the steps.

Transfer Printing.

Precision translation and rotational stages controlled the positions of the stamps during the various steps in printing, as illustrated in Fig. 1. After each complete sequence of printing, the structures were annealed at 200–900 °C depending of receiver substrates in air for 3 min (TMC Services, Inc., Micristar Model 828) to eliminate residual photoresist and to increase the strength of adhesion.