Towards a quantitative understanding of mitotic spindle assembly and mechanics

Abstract

The ‘simple’ view of the mitotic spindle is that it self-assembles as a result of microtubules (MTs) randomly searching for chromosomes, after which the spindle length is maintained by a balance of outward tension exerted by molecular motors on the MTs connecting centrosomes and chromosomes, and compression generated by other motors on the MTs connecting the spindle poles. This picture is being challenged now by mounting evidence indicating that spindle assembly and maintenance rely on much more complex interconnected networks of microtubules, molecular motors, chromosomes and regulatory proteins. From an engineering point of view, three design principles of this molecular machine are especially important: the spindle assembles quickly, it assembles accurately, and it is mechanically robust – yet malleable. How is this design achieved with randomly interacting and impermanent molecular parts? Here, we review recent interdisciplinary studies that have started to shed light on this question. We discuss cooperative mechanisms of spindle self-assembly, error correction and maintenance of its mechanical properties, speculate on analogy between spindle and lamellipodial dynamics, and highlight the role of quantitative approaches in understanding the mitotic spindle design.

Introduction

Recently, there has been a surge of studies that, based on accumulated knowledge of the molecular players, examined mechanisms governing the mitotic spindle – a molecular machine built by the cell to segregate chromosomes before cell division (Fig. 1). To complete this task, the spindle has to assemble quickly, with few errors, into a mechanically robust (i.e. functioning under mechanical stress) structure. Therefore, any mechanism of spindle assembly and maintenance must conform to these three design objectives. A growing amount of insight into the physical and engineering principles of the spindle design has emerged from recent interdisciplinary studies combining cell biological methods with biophysical techniques and computational modeling. Although the current understanding of the mechanisms of spindle assembly and maintenance is still confusing and incomplete, a commentary on these efforts and emerging unifying themes is in order.

Fig. 1.

A ‘simple’ spindle. (A) Two searching MTs [arrows indicate growing (up) and shrinking (down)] are shown at the left. The longer MT grows in the wrong direction, away from the KT, whereas the shorter one is about to make a capture. Monotelic attachment is the first stage in achieving the correct amphitelic attachment. The erroneous syntelic attachment usually occurs when a chromosome is close to one of the poles (centrosomes), so that sister KTs are both visible. Then, capture from another pole makes this attachment merotelic. (B) In the metaphase spindle, the correctly attached chromosomes are arranged at the equator and K-fibers are under tension (arrows show the direction in which the centrosomes are pulled). The interpolar MT antiparallel overlaps are crosslinked by kinesin-5 molecular motors that push the MTs apart.

In mitosis, microtubule (MT) asters (radial arrays of MTs that converge at the centrosome) and chromosomes are separated until after breakdown of the nuclear envelope. One of the central questions in the study of mitosis is how the spindle assembles during prometaphase. The discovery of MT dynamic instability led to the elegant ‘search-and-capture’ hypothesis (Kirschner and Mitchison, 1986): astral MTs grow and shrink rapidly and repeatedly in all directions, probing the volume of the former nuclear sphere (Fig. 1A) until they capture chromosomes by binding to their kinetochores (KTs; specialized chromosome structures that function as an interface between the chromosomes and the spindle). Such capture of a KT by a single astral MT has been visualized in newt lung cell cultures (Hayden et al., 1990). To correctly segregate sister chromatids to opposite spindle poles during anaphase, spindle assembly must be accurate. Chromosomal connections have to be correct amphitelic attachments, in which the two sister KTs on each chromosome are captured from the opposite spindle poles (Fig. 1A). Whereas syntelic or merotelic attachments also occur in early mitosis (Fig. 1A), most, but not all, of them are corrected later (Ault and Rieder, 1992; Cimini et al., 2003; Lampson et al., 2004). The canonical view of the metaphase mitotic spindle is that of a bipolar aster (Walczak and Heald, 2008): MTs from two asters extend and bend from the poles (i.e. centrosomes; also known as MT-organizing centers) and connect to the chromosomes that are aligned at the equator (Fig. 1B). To maintain spindle length, some antiparallel MTs extending from the poles have to overlap at the spindle equator and be pushed outward by molecular motors to balance inward tension in the MTs connecting the poles and KTs (Fig. 1B) (Wollman et al., 2008).

This ‘simple’ picture is challenged by recent data suggesting the following: that cooperative dynamics of MTs and chromosomes are needed to assemble the spindle (O'Connell and Khodjakov, 2007), that error correction imposes stringent constraints on these dynamics (Paul et al., 2009), that the force balance and its role in maintaining the spindle length are not that simple (Dumont and Mitchison, 2009a), and that the MT spindle architecture is complex and dynamic (Yang et al., 2007; Needleman et al., 2010). In this Commentary, we focus on the following questions. What MT and chromosome dynamics are needed for fast and error-free spindle assembly? What are the mechanical properties of the spindle and how do they depend on MT dynamics? We also emphasize the quantitative character of these questions, and discuss analogies between MT and actin dynamics. We do not review in detail many important aspects of the spindle design that have received much attention recently, such as mechanisms of spindle-length maintenance (Dumont and Mitchison, 2009a); molecular motor action (Brust-Mascher and Scholey, 2007; Gatlin and Bloom, 2010); spindle positioning (Grill and Hyman, 2005); chromosomal motility (Gardner and Odde, 2006; Walczak et al., 2010), including that in anaphase; and molecular mechanisms regulating MT dynamics within the spindle (Walczak and Heald, 2008; Goshima and Kimura, 2010).

Speed of spindle assembly

The main quantitative question about the search-and-capture process described above is whether such a random process can lead to the capture of all chromosomes within just tens of minutes. As it is difficult to experimentally resolve individual MTs and follow their dynamics, this question prompted calculations (Hill, 1985; Holy and Leibler, 1994) demonstrating that there is an optimal set of dynamic-instability parameters that results in the fastest search (Box 1), leading to capture of a KT by a MT within ~10 minutes. Computer simulations showed, however, that random delays in capturing the last of many chromosomes, some of which are located too far from the centrosomes, prolong assembly to an hour or longer (Wollman et al., 2005) (Box 1).

Box 1. Mathematical aspects of spindle assembly

MT dynamic instability is characterized by speeds of growth and shrinking (V_g~V_s~0.2 μm/second), and frequencies of rescue (f_r) and catastrophe (f_c). In the optimal search, there should be no rescue, because rescuing a polymer growing in the wrong direction (Fig. 1A) just wastes time. The catastrophe frequency has to be such that, on average, a MT grows to a length equal to the pole-KT distance (which is ~R~10 μm, where R is the radius of the nuclear sphere): if catastrophes are rare, then growth in the wrong direction is too long, but frequent catastrophes lead to possible withdrawal from the right direction before capture. One optimal growth and shrinking cycle takes ~R/V_g + R/V_s ~40 seconds. Most of the cycles are not successful: estimates show that the probability of encountering a KT is ~r²/4R² ~0.0025, where r~1 μm is the KT radius. One out of a few hundred (N_MT) MTs, however, encounters a KT with a probability of ~N_MTr²/4R²~1, so it seems that just 1 minute is needed for capture. However, because MTs search for N_KT~100 targets in parallel, the search is over only when the last KT is captured, which, owing to the stochastic nature of the search, prolongs the process ~log(N_KT)~5 times. The geometric factor – chromosomes are scattered at varying distances from the centrosomes – extends the search another order of magnitude, to about an hour, because the catastrophe rate optimized for a certain distance to the target is far from being optimal for different distances.

If spindle assembly relies on a random search only to capture a fraction of the chromosomes, after which the rest is captured rapidly by deterministic processes, then assembly can be speeded up: the average time to capture N_KT–n_KT out of N_MT objects in a random search (Ross, 1972) can be estimated as

$$\tau \sum _{j=n_{KT}}^{N_{KT}}\frac{1}{j}\approx \tau \text{log}\frac{N_{KT}}{n_{KT}},$$

where τ is the time taken to capture one KT. So, if only half of the chromosomes have to be captured randomly, the assembly time is

$$~\tau \text{log}\frac{N_{KT}}{N_{KT}∕2}~\tau \text{log}2,$$

which, at N_MT~100, is more than five times shorter than the full random search time (~τlogN_KT).

We solved differential equations describing the kinetics depicted in Fig. 2D and found the following time series for amphitelic (black), syntelic (red) and merotelic (blue) attachment numbers for stable (figure A), less stable (figure B) and unstable (figure C) MT-KT associations.

In reality, in most situations the cell does not take this long to capture all of its chromosomes; clearly, there are mechanisms to facilitate KT capture – but what are they? One possible mechanism is that the search is biased by a gradient of RanGTP (the GTP-bound state of the small GTPase Ran) that is created around the chromosomes by activation of Ran on the chromosome arms. Activated Ran diffuses into the cytoplasm and is then spontaneously deactivated (Fig. 2A, top) (Caudron et al., 2005; Athale et al., 2008). A high concentration of RanGTP can stabilize MTs, so that they would grow more frequently towards the chromosomes and catastrophe when growing away from the nuclear sphere. Computer simulations showed that indeed such a spatially biased search accelerates chromosome capture (Wollman et al., 2005), suggesting that the search and capture is not so random after all. In particular, this mechanism doubles the speed by focusing all MTs inside the nuclear sphere and accelerates the search further by allowing the MTs to scan the chromosomal crowd more uniformly. Another possibility is that MT-length-regulating motors in the spindle (Varga et al., 2006; Gardner et al., 2008) similarly bias the MT distribution (Fig. 2A).

Fig. 2.

Cooperative mechanisms of spindle assembly. (A) Right: a chromosome close to the pole (darker) screens out a distal chromosome (lighter) from the pole and hinders its capture. Hypothetical mechanisms of biasing and accelerating spindle assembly include a RanGTP ‘cloud’ around the chromosome (top) that stabilizes searching MTs and promotes the chromosomal MT bundles. Bottom: motor-driven poleward gliding brings the chromosome close to one pole, where one of the KTs is rapidly captured, whereas a MT bundle extends from the sister KT towards the equator, where it is captured by a centrosomal MT from another pole. Middle: an anti-poleward motor-driven chromosome converges on the equator, where the sister KTs are captured easily by MTs that have been nucleated on the sides of the existent MTs. Later, motors could detach the captor MT minus ends and drive them to the poles. (B) Left: MT bundles growing from the KTs of three chromosomes converge to three points that could become future multiple poles. Right: during hybrid assembly, centrosomal MTs capture the chromosomal MT bundles, ensuring spindle bipolarity. (C) Chromosomal rotation after the first capture shields the sister KT from the captor pole and prevents erroneous attachments. (D) Kinematics of pole-KT connections: each KT can be captured from either pole with the constant rate and each attachment dissolves with another constant rate. The correct amphitelic attachment (shaded box) is stabilized and does not dissolve.

However, this hypothetical spatial bias of MT growth does not help with another daunting problem: recent computer simulations (Paul et al., 2009) predict that the chromosome arms crowd the space to the extent that the chromosomes at the periphery completely shield the KTs in the interior from the MTs protruding from the spindle poles (Fig. 2A). In principle, this obstacle can be bypassed through chromosomal movements: there are multiple reports of chromosomal displacements with rates on the order of micrometers per minute (Levesque and Compton, 2001; Murata-Hori and Wang, 2002; Paul et al., 2009), which can be generated by motor (chromokinesin, dynein or CENP-E) forces. Regardless of their origin, these movements can shuffle the chromosomes, bringing each one close to a centrosome every few minutes and allowing rapid capture at these times. However, chromosomes have not been accurately tracked for long intervals and in many spindles, so this mechanism remains an untested hypothesis.

A quarter of a century ago, Nicklas and Kubai (Nicklas and Kubai, 1985) noted that “a mixed origin of KT-MTs by both capture and nucleation is a real possibility”. Recent data (reviewed in O'Connell and Khodjakov, 2007) indeed suggest that MT bundles can be organized at the chromosomes and grow outward (Fig. 2B). This led to the proposal (O'Connell and Khodjakov, 2007) that a cooperative, hybrid pathway for spindle assembly occurs, in which the centrosomal MTs search for long chromosomal MT bundles – which provide a larger target than KTs alone – and, upon capturing them, are integrated into continuous MT bundles (K-fibers) that connect the centrosomes and KTs (Fig. 2B). Molecular details of such cooperative capture are vague, but one attractive possibility is that minus-end-directed kinesin-14 and dynein motors help to crosslink the MTs, align them and transport them poleward (Goshima et al., 2005). Paul et al. (Paul et al., 2009) predicted that such a hybrid pathway would accelerate spindle assembly more than twofold because of the higher probability of capturing the long targets.

Why does the cell need centrosomal MTs at all? There are anastral spindles that assemble from MTs growing outward from the chromosomes (Sköld et al., 2005). Naively speaking, the obvious problem with this chromosome-directed spindle-assembly pathway in cells would be the emergence of multipolar spindles, because K-fibers of randomly oriented chromosomes would converge at multiple points (Fig. 2B). It was also observed that chromosomal fibers can loop and create syntelic attachments (Khodjakov et al., 2003) (Fig. 1A). Thus, one of the functions of the centrosomal MTs could be to integrate multiple chromosomal MT bundles into a common structure (Fig. 2B). However, multipolar spindles are rarely found in systems that lack centrosomes (Wadsworth and Khodjakov, 2004). This indicates that mechanisms other than centrosome-related ones must operate in these spindles. For example, motors might arrange chromosomes in parallel, so that all K-fibers project outward and parallel to each other, and then other motors focus the fiber ends. In fact, MTs have a tendency to align in parallel even in the absence of motile chromosomes (in bead spindles) and some of the motors (Hannak and Heald, 2006). One of the roles of centrosomal MTs might be to interact with the cell cortex and properly orient the spindle in the cell: acentrosomal spindles undergo anaphase, but they are often improperly oriented, resulting in abortive cytokinesis (Khodjakov and Rieder, 2001). Finally, it is worth noting that multiple centrosomes tend to cluster (Ring et al., 1982).

There are other cooperative mechanisms at play in spindle assembly. First, after attachment of the first KT to the spindle, the chromosome often moves towards the spindle pole (Rieder and Alexander, 1990). This chromosome then remains associated with this pole until its unattached KT becomes attached to a MT growing from the distal pole (McEwen et al., 1997). This phenomenon seems counterproductive, because few MTs from the distal pole reach the proximal one, but this behavior is exhibited by many chromosomes (Lampson et al., 2004). One possible rationale is that this movement brings the chromosome close to the pole, where many centrosomal MTs push on its arms and orient it so that a K-fiber associated with the opposite, unattached KT extends towards the distal pole, allowing this fiber to be captured in an errorless way (Fig. 2A, bottom). Second, there are reports that, after this initial movement towards the pole, the chromosome could glide back towards the spindle equator alongside existing K-fibers associated with other chromosomes that are already properly attached (Kapoor et al., 2006) (Fig. 2A, middle). In fact, Cai et al. (Cai et al., 2009) recently reported that CENP-E motors could be responsible for spindle-equator-directed gliding of unattached chromosomes along spindle MTs. At the equator, the chromosomes would be optimally positioned to capture the MTs from both poles. A third possibility is that MTs can form inside the spindle (Mahoney et al., 2006), nucleated from the sides of pre-existing MTs (Goshima et al., 2008), a process that is mediated by augmin. As speculated recently (Lüders and Stearns, 2007; Goshima and Kimura, 2010), the capture of these nucleated MTs can contribute cooperatively to spindle assembly. One could envision that, when a chromosome is near the equator, it is easy for nascent MTs that have been nucleated nearby to capture their KTs; of course, then the MT minus ends have to be integrated with the spindle poles, perhaps by being transported by minus-end-directed motors (Fig. 2A, middle).

From a mathematical point of view, these cooperative mechanisms could make spindle formation less stochastic, which could accelerate assembly and make it less sensitive to random variations. For example, the first few chromosomes could be captured through a random search, and then the rest could be captured deterministically using a combination of the mechanisms described above and cooperative chromosome behavior (Tanaka et al., 2005; Li et al., 2007). Indeed, according to calculations (Paul et al., 2009), the first few chromosomes during the random search are captured rapidly and then the search becomes slower as fewer chromosomes are left. Deterministic incorporation of half of the chromosomes into the spindle after the other half is captured can accelerate the process, according to the mathematical estimate in Box 1.

Accuracy of spindle assembly

The speed of spindle self-assembly is only part of the problem – it also has to be accurate. For chromosomes to be segregated correctly during cell division, the erroneous syntelic and merotelic attachments (Fig. 1A) that appear in early mitosis (Ault and Rieder, 1992; Cimini et al., 2003) must be corrected (Cimini et al., 2003; Lampson et al., 2004; Cimini et al., 2006). (Monotelic attachment is a transient stage rather than an error.) The seriousness of this task is emphasized by the fact that persistent merotelic errors are a common cause of chromosomal instability in aneuploid tumor cells (Thompson and Compton, 2008). To explain the factors contributing to erroneous attachments, Nicklas and Ward (Nicklas and Ward, 1994) suggested a simple ‘stochastic-geometric’ idea: for certain chromosomal orientations, errors are inherent to the random nature of the search-and-capture process. For example, when one KT is ‘visible’ from both spindle poles, MTs from each pole reach this KT almost simultaneously, leading to merotelic attachment. Similarly, if sister KTs are both visible from the same pole, syntelic attachment is likely (Fig. 1A). This hypothesis has been supported by recent studies (Ganem et al., 2009; Silkworth et al., 2009) showing that spindle multipolarity promotes erroneous attachments by positioning more than one centrosome, and thus multiple MT searching arrays, in front of an individual KT.

When we simulated random search-and-capture from two poles, the computations yielded the astonishing ~65% merotelic, ~20% syntelic and only ~15% amphitelic attachments (Paul et al., 2009). This is because, owing to crowding in the nuclear sphere, only the chromosomes at the periphery, close to the centrosomes, are likely to get captured. Such chromosomes often have both sister KTs visible from the centrosome, allowing syntelic attachments to be established rapidly. Subsequent attachments often turn those syntelic configurations into merotelic ones (Fig. 1A). The cell, however, makes few errors: only ~0.2 chromosomes per cell are syntelically attached in prometaphase PtK1 cells (Hauf et al., 2003) and only ~30% of prometaphase PtK1 cells possess one or two, rarely more, merotelically oriented KTs (Cimini et al., 2003).

Most likely, the cell makes fewer erroneous attachments in the first place and, in the second place, corrects the mistakes made without waiting for the search and capture to end (Nicklas, 1997). What are the respective mechanisms? One possibility is that a KT is shielded from the ‘wrong’ pole by the chromosome arms (Nicklas, 1997). This mechanism for error prevention relies on the chromosome being oriented properly, with sister KTs facing opposite poles. This is possible if, upon capture, the chromosome rotates so that the captured KT faces the pole it is captured from, whereas its sister KT faces away from that pole (Fig. 2C). When we included this mechanism in our simulations, the number of errors indeed decreased dramatically to the percentages observed in cells (Paul et al., 2009). Hypothetically, this chromosome rotation can result from torque created by motor-mediated pulling of the captured KT towards the respective pole, combined with astral MTs pushing on the chromosome arms.

Another hypothetical error-correction mechanism (Nicklas and Ward, 1994; O'Connell and Khodjakov, 2007) is that amphitelic attachments evolve in a Darwinian process of trial and error, such that syntelic attachments are initially frequent and are dissolved repeatedly (Lampson et al., 2004) until only correct stable attachments survive. In this case, correction of improper attachments is intimately tied to the rate at which KTs release MTs. We illustrate this situation in Fig. 2D, making the simplistic assumptions that each KT is captured from either pole at a rate of k_on ~1/minute and also that each MT is destabilized and the connection dissolved at a rate of k_off. In addition, we assume that all amphitelic attachments are secured from any further improper captures. We found mathematically that, if k_off = k_on, then about 10 minutes is needed for all KTs to have attachments of some kind. In this case, the numbers of syntelic and merotelic attachments peak at ~10% within a minute, and decrease to almost nothing by the end (Box 1). If the MTs are more stable – k_off just three times smaller – then the capture time accelerates very little, but at the end of the search there are still quite a few chromosomes per cell attached merotelically (Box 1). Recent experimental data support this prediction: simply increasing the half-life of MTs at KTs twofold leads to a significant increase in the number of merotelic attachments (Yang et al., 2009; Bakhoum et al., 2009a). On the other hand, calculations show that making the MTs much more unstable would prolong the process prohibitively (Box 1). Tanaka and Hirota (Tanaka and Hirota, 2009), for example, suggested that the cell could save time by dissolving only ‘wrong’ MTs in merotelic attachments. Note that this simple calculation only illustrates the point because it considers just one MT attachment per KT, whereas in reality, many more MTs associate with each KT. The calculation, however, is supported by more realistic simulations (Paul et al., 2009), suggesting that there is an inherent conflict between the speed and the accuracy of spindle assembly. Therefore, the cell must carefully regulate MT dynamics to find a compromise. It is not out of the question that, as soon as the first MT-KT attachment is established, other MTs are nucleated on the attached MTs close to the KT and further attachments are established. Note also that the chromosome-rotation mechanism discussed earlier is deterministic, whereas the trial-and-error process is stochastic; their combination would be likely to accelerate assembly without compromising its accuracy.

Relatively little is known about molecular mechanisms of error correction, despite recent advances in understanding the roles of tension and inter- and intra-KT stretching in MT-KT interaction dynamics (Maresca and Salmon, 2010). MT release from KTs is regulated by Aurora B kinase activity (Lampson et al., 2004; Pinsky and Biggins, 2005), which destabilizes syntelic attachments (Biggins and Murray, 2001; Tanaka et al., 2002; Hauf et al., 2003). Aurora B has also been shown to play a role in the correction of merotelic attachments (DeLuca et al., 2006). Specifically, Aurora B uses a tension-dependent mechanism (Liu et al., 2009) to regulate both the MT-destabilizer mitotic centromere-associated kinesin (MCAK) (Kline-Smith et al., 2004; Knowlton et al., 2006), which is implicated in the correction of both syntelic and merotelic attachments (Kline-Smith et al., 2004), and the Ndc80 complex (Cheeseman et al., 2006), which is involved in the correction of merotelic attachments (DeLuca et al., 2006). One of the models suggests that, in merotelic and syntelic chromosomes, which do not have a stretched centromere, centromere-associated Aurora B is close enough to interact with MCAK at the KT, allowing MCAK activity to dissolve the attachment. On the other hand, in correct amphitelic attachments, centromere tension prevents Aurora B from coming into contact with MCAK and these attachments are left intact (Ohi et al., 2003; Bakhoum et al., 2009b).

Finally, motor-generated tension on MTs connecting centrosomes and KTs could have a direct role in correcting merotelic connections, perhaps by just breaking the improper connections with brute force (Cimini et al., 2004). This raises the mechanical challenge for the spindle of having to be firm enough to maintain this tension without significant deformation. How is this firmness achieved?

Spindle mechanical properties

Nicklas (Nicklas, 1983) measured forces in the spindle on the order of tens of piconewtons per chromosome. If there are tens of chromosomes in animal-cell spindles, then a characteristic total internal force of ~1 nN is developed in the spindle. Theoretical estimates predict similar forces in Drosophila melanogaster spindles (Wollman et al., 2008), so it is clear that the spindle has to be firm enough to withstand internal forces of this magnitude. External forces on the spindle during mitosis from myosin-generated tension in the cell cortex are also in the nanonewton range, based on data from Raucher and Sheetz (Raucher and Sheetz, 1999).

In a recent tour-de-force study, Itabashi et al. (Itabashi et al., 2009) measured mechanical properties of meiotic spindles by compressing them with a pair of cantilevers and found that the effective spring constant of the spindle is approximately 1 nN/μm. This indicates that, if acted upon by the ~1 nN force, the spindle would be only slightly deformed – by ~1 μm or less than 10% of its length. Moreover, Itabashi et al. (Itabashi et al., 2009) showed that such deformation would be reversible: after the force is released, the spindle completely recovers its shape. Physical estimates of the strength of elastic interpolar MT bundles and K-fibers (Rubinstein et al., 2009a) agree with these measurements: one such bundle or fiber is equivalent to a spring with stiffness on the order of tens of piconewtons per micrometer. Tens of such elastic elements arranged in parallel between the poles (Fig. 1B) constitute an assembly with stiffness on the order of 1 nN/μm.

However, spindle mechanics are more complex than simply an elastic cage made of the K-fibers and interpolar MT bundles. Itabashi et al. (Itabashi et al., 2009) observed so-called ‘hysteresis’ behavior: the spindle resistance force was greater while compressed by cantilevers and smaller when the cantilevers were released, relieving the compression. This can be explained if there are dashpot elements [mechanical dampers that resist motion by way of viscous friction; for an excellent primer on cytoskeleton mechanics, see (Howard, 2001)] inside the spindle in parallel with the elastic elements (Fig. 3A): both the spring and the dashpot elements resist compression, but after compression is released, the spring force leads to expansion of the system but is partially damped out by the dashpot element. This clearly suggests that the spindle is viscoelastic rather than elastic. From the data in Itabashi et al. (Itabashi et al., 2009), one can glean the effective dashpot drag coefficient (~1 nN×second/μm), which is an order of magnitude greater than the drag estimated from simply squeezing the cytoplasm through the spindle MT mesh (Wollman et al., 2008). Qualitatively, these data also agree with two other recent mechanical studies (Dumont and Mitchison, 2009b; Gatlin et al., 2010), in which the spindle was ‘squashed down’ and microneedles were dragged through it, respectively.

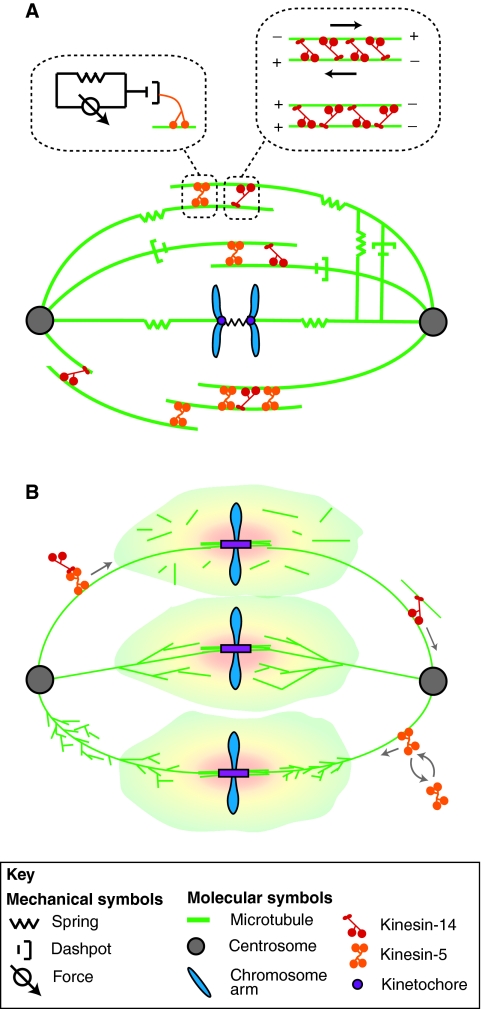
Fig. 3.

Spindle mechanics. (A) The spindle can effectively be considered to be many springs and dashpots in parallel arranged both longitudinally and laterally. Both elastic and viscous elements originate from the viscoelastic nature of molecular motors (upper left), MT elasticity and turnover, and the tiled-array architecture of the spindle. Upper right: multiple motors cooperate and slide antiparallel MTs apart, but oppose each other and lock the parallel MTs together. A large external force can lead to rapid detachment of half of the motors, breaking MT-MT crosslinking and leading to a plastic spindle response. (B) Robust spindle architecture depends on properly homogeneous ‘filling’ of the spindle interior by MTs. This cannot be achieved by random MT nucleation within the RanGTP cloud (shaded region, top) – the MTs are too spread out and disjointed. Nor can this be achieved by the autocatalytic nucleation (bottom) of short MTs, which leads to dense, disjointed clumps of MTs. The optimal regime (middle) is a combination of autocatalytic MT branching with a RanGTP-mediated enhancing effect and fast MT growth and turnover dynamics.

This highly viscous spindle behavior probably stems from two factors. First, it is becoming clear that MTs are arranged in some spindles in a ‘tiled array’ (Fig. 3A) (Yang et al., 2007): a number of shorter MTs crosslinked by multiple molecular motors and MT-associated proteins, rather than one or two long MTs spanning the spindle length (Fig. 3A). The motors can be thought of as a combination of force-generating, elastic and viscous units; the origin of the viscous units is protein friction (Bormuth et al., 2009). These effectively viscous motor elements could act together to dampen the spindle deformation rate. Another factor contributing to viscous spindle behavior could be the highly dynamic nature of individual MTs in the spindle, which turn over in around 10 seconds (Cheerambathur et al., 2007; Needleman et al., 2010), as well as the dynamic behavior of individual molecular motors, which stay on MTs for only seconds before dissociating (Cheerambathur et al., 2008). Such frequent uncoupling and/or disappearance of elastic elements lead to dissipation of the elastic stress (Howard, 2006) and further ‘fluidization’ of the spindle.

Interestingly, the spindle exhibits viscoelastic behavior regardless of whether it is deformed parallel or perpendicular to its long axis (Itabashi et al., 2009; Gatlin et al., 2010). This suggests there might be viscoelastic elements perpendicular to the pole-pole axis, in addition to the interpolar viscous elements described above (Fig. 3A). These are probably composed of numerous MTs that are nucleated in the spindle (Needleman et al., 2010) and oriented laterally (McDonald et al., 1992), and the motors crosslinking them. Viscoelastic elements perpendicular to the pole-pole axis could serve as trusses and struts (Fig. 3A), making the spindle matrix a dense gel of interconnected elements (Nicklas et al., 1982). This gel is ‘anisotropic’ – it is slightly weaker along the short axis (Itabashi et al., 2009) – and, even more interestingly, it is ‘plastic’: if the external stress exceeds a certain threshold, the spindle deforms irreversibly (Itabashi et al., 2009; Dumont and Mitchison, 2009b). The anisotropy could be explained simply by the preferred orientation of longer MTs in the spindle, whereas the plasticity could stem from the complex response of some molecular motors to external force (Dumont and Mitchison, 2009b). Another possible origin of the plastic behavior is the observation [in vitro (Fink et al., 2009) and in silico (Zemel and Mogilner, 2009)] that kinesin-14 motors that crosslink parallel MTs also ‘lock’ them together (Fig. 3A), stabilizing the spindle shape until a threshold force breaks the MT-MT connection. This could cause an avalanche-like cascade of crosslink breakage and consequent reshaping of the spindle.

Does the viscoelasticity benefit spindle behavior in any way? One possibility is that the firm elasticity protects the spindle from collapse under external deformations, whereas the large viscous drag ensures that the spindle responds to perturbations very slowly, thus filtering out environmental noise. For the interconnected gel structure to be robust and not vary its mechanical properties too much from one part of the spindle to another, the MT mesh in the spindle has to be homogeneous enough. Clausen and Ribbeck (Clausen and Ribbeck, 2007) showed that this can only be achieved if, in addition to random MT nucleation within the spindle and MT dispersion owing to dynamic instability and turnover, there is also autocatalytic nucleation of nascent MTs sprouting from the sides of existent ones (Fig. 3B). This autocatalytic nucleation can also result in amplification of asters where not needed, but the strong ability of spindles to capture MT asters (Rusan et al., 2002) might prevent these run-away processes. Vigorous transport of motors and MTs in the spindle (Janson et al., 2007; Burbank et al., 2007) is also likely to promote homogeneity (Fig. 3B). Taken together, the recent studies discussed here suggest that some spindles are anisotropic viscoelastic-plastic gels that are active (i.e. force generating), similar to the actin-myosin gel in motile cells (Joanny and Prost, 2009). Similarities between the spindle MT and actin systems extend further.

Analogy between the spindle and the motile actin treadmill

Some analogy between self-organizing spindle-like MT assemblies and actin ‘tails’ growing from beads coated with actin-nucleating proteins was pointed out a few years ago (Karsenti and Nédélec, 2004). One has to be cautious not to get carried away with overemphasizing superficial similarities, but so many features of protruding actin structures and MT-motor assemblies can be gleaned from the data that one cannot help wondering whether this analogy runs even deeper (Fig. 4). At the core of this analogy is the fundamental self-organization tendency of ensembles of polar filaments mixed with motors (Mitchison, 1992). For example, filament asters can emerge from an ensemble of polar filaments in the presence of molecular motors that can cluster together and glide to filament ends (Fig. 4A,B). In vitro, such asters were observed both in actin-myosin systems (Backouche et al., 2006) and in MT-kinesin systems (Nédélec et al., 1997) (Fig. 4).

Fig. 4.

Analogy between spindle and lamellipodial mechanisms. (A) The lamellipodial actin network consists of a dendritic branched mesh of short filaments interspersed with long filopodial bundles. At the rear of the cell, myosin motors reorganize the mesh into a muscle-like bundle and pull the lamellipodium backwards, assisted by filaments pushing at the front. In vitro, myosin motors focus the filament barbed ends together, producing asters. The membrane constrains and shapes the lamellipodium. (B) K-fibers in the spindle are interspersed with shorter MTs, probably interconnected and branched. The poleward flux is contributed to by MT polymerization against the chromosome arms and kinesin motors reeling in the MT minus ends at the poles, in addition to other mechanisms. In vitro, kinesin motors and MTs self-organize into asters. (C) Two actin comet tails assembled on a 220 nm ActA-coated bead (in the middle, not visible) in the presence of 75 nM of Arp2/3 and 42 nM of capping protein. Adapted from figure 2 in Akin and Mullins (Akin and Mullins, 2008) with permission. Scale bar: 3 μm. (D) Bipolar MT array organized around chromatin-coated beads in a Xenopus tropicalis extract in which dynein is inhibited. Image courtesy of R. Loughlin and R. Heald (University of California, Berkeley, USA). Scale bar: 20 μm.

Both MT and actin gels growing around protein-coated beads tend to break symmetry and self-organize into ‘polymer tails’ (Hannak and Heald, 2006; Akin and Mullins, 2008) (Fig. 4C,D). The morphologies and physical mechanisms are not the same: elastic stresses break the symmetry in the actin shell, usually resulting in a single actin tail (Dayel et al., 2009), whereas kinesin motors slide MTs apart from the beads into two opposing tails (Hannak and Heald, 2006). However, despite differences in the force generation on the molecular level, macroscopic spatial-temporal stresses might be similar in some circumstances. Thus, under certain concentrations of Arp2/3 and capping proteins that regulate the actin gel structure, two tails can also emerge in the actin system (Akin and Mullins, 2008) (Fig. 4C).

One of the best-understood actin motile systems is the lamellipodium – a protrusive appendage of the migrating cell (Fig. 4A) (Small et al., 2002). On relevant time scales, lamellipodial actin networks and mitotic spindles are both viscoelastic (Rubinstein et al., 2009b; Itabashi et al., 2009), with similar viscoelastic moduli (Kole et al., 2005; Itabashi et al., 2009). Furthermore, nanonewton forces significantly deform both networks (Prass et al., 2006; Itabashi et al., 2009), generating local flows on the order of tenths of micrometers per second, and the elastic response of both structures is characterized by a Young's modulus (i.e. the measure of the stiffness of an elastic material) in the kilopascal range. There are also similarities between the dynamic structures in the lamellipodium and those in the ‘half spindle’ (Fig. 4A,B): both networks are polarized, with MT plus ends oriented towards the chromosomes at the equator and actin barbed ends facing the leading edge of the cell. The actin network mainly comprises the branched dendritic network of short filaments that sprout from one another, but it is sometimes interspersed with long filament bundles called filopodia (Schaefer et al., 2008). The spindle, on the other hand, consists largely of arc-like K-fibers and interpolar MT bundles, but available EM data suggest that numerous MTs orient laterally (McDonald et al., 1992), rather than along the spindle axis. Perhaps, as speculated by Goshima and Kimura (Goshima and Kimura, 2010), these lateral MTs are nucleated at and branch from the K-fibers, interpolar MTs and each other. Augmin in the spindles could mediate MT branching (Goshima et al., 2008), similar to the Arp2/3 complex that is responsible for actin-network branching in motile cells. In fact, 40° branching angles between ‘mother’ and ‘daughter’ MTs, similar to branched Arp2/3-mediated structures, were observed in plant cells (Wasteneys and Williamson, 1989). In the lamellipodium, the length of the branched filaments is limited by the capping proteins. In the spindle, there is probably no need for this, because dynamic instability by itself limits polymer length. However, both actin and MT filaments are periodically severed by cofilin and katanin, respectively.

One of the striking dynamic similarities between mitotic spindles and lamellipodia is the flow of their cytoskeletal networks. In the spindle, there is poleward flux of MTs [reviewed recently in Kwok and Kapoor (Kwok and Kapoor, 2007)] (Fig. 4B), which is associated with MT polymerization at the spindle equator and disassembly near the poles. In lamellipodia, there is retrograde flow of the actin array, which is associated with its polymerization at the leading edge and depolymerization at the rear. Although the forces responsible for the poleward flux in the spindle are still being debated, it has been suggested that kinesin-5 slides MTs apart at the spindle equator and/or kinesin-13 ‘reels’ the MTs towards the pole (Kwok and Kapoor, 2007). Similarly, retrograde flow in the lamellipodia is mainly caused by myosin contraction at the rear of the network (Vallotton et al., 2004). Myosin action can be complemented by the polymerization force of the growing actin filaments pushing at the leading-edge membrane; likewise, growing MTs pushing on the chromosome arms can contribute to poleward flux (Kwok and Kapoor, 2007). One of the functions of these flows could also be similar: in the lamellipodia, the flow is sometimes the result of the motile machinery ‘idling’ when an adhesion clutch is disengaged; when adhesion is deployed, the flow is converted into protrusion (Hu et al., 2007). In the spindle, switching off depolymerization at the poles is part of the machinery for turning the flux into pole separation in anaphase (Brust-Mascher and Scholey, 2002). Recent findings of Matos et al. (Matos et al., 2009) indicate that the flux might synchronize chromosome segregation; it remains to be seen whether the lamellipodial flow plays some role in synchronization in motile cells.

Finally, membrane envelops the lamellipodium, and its tension globally restrains and shapes the cell in some cases (Keren et al., 2008). Membrane also surrounds some spindles (Kramer and Hawley, 2003) and it was suggested that it could play a similar restraining role there (Mitchison et al., 2005). There are, of course, significant differences between the lamellipodia and the spindle, and not only in their respective molecular players. For example, the spindle does not have a complex dynamic adhesion system, and the leading-edge protein complexes responsible for lamellipodial polarization and assembly have little in common with the motor-based organization of MTs near the chromosomes. Nevertheless, the multiple analogies between the actin- and MT-based systems could help in understanding the design principles in both cytoskeletal machines.

Perspectives

The mitotic spindle looks deceptively simple: two half-asters with centrosomes at the poles, and antiparallel overlapping MTs and chromosomes at the equator. However, the task of assembling this structure quickly, accurately and with proper mechanical features is daunting. Unlike the nearly complete molecular inventory of the spindle (Goshima et al., 2007), an understanding of the design is in its infancy, but general principles are beginning to emerge. They include a combination of stochastic and deterministic mechanisms of assembly and error correction, as well as a combination of unstable mechanical elements to maintain robust but adaptable mechanics. The devil in biology, however, is in the detail and the challenge is to understand how exactly this system – composed of moving and force-generating MTs, dynein, at least seven different kinesins and a host of essential MT- and motor-associated proteins – self-organizes in the presence of cue-providing centrosomes and chromosomes.

Most of the existing quantitative spindle models are ‘Frankenstein’ like, developed using assumptions based on data collected from different mitotic and meiotic spindles. However, because of the remarkable diversity of mitosis, there is no ‘the’ spindle. Large, slow and viscoelastic anastral spindles (Groen et al., 2008) differ significantly from mammalian spindles, in which most MTs extend the half-length between the pole and equator (McDonald et al., 1992) and for which the tiled-array model is unlikely to apply. Rapidly dynamic Drosophila embryo spindles (Brust-Mascher and Scholey, 2007) and ‘simple’ one-dimensional yeast spindles (Bouck et al., 2008) are examples of further diversity. Thus, to achieve a comprehensive understanding, mechanical perturbations have to be combined with molecular readouts. In addition, better markers and imaging systems to track the motility of individual MTs, KTs, motors and chromosomes have to be developed and used to collect spatio-temporal systems-level data rich enough to calibrate mechanistic models in each given spindle. These future models will probably move past conceptual reductionist models to those of a reverse-engineering type, employing computational search algorithms that use quantitative experimental measurements from wild-type and experimentally perturbed spindles (Wollman et al., 2008; Fernandez et al., 2009; Doncic et al., 2009). This will make it possible to eliminate thousands of possible scenarios and to calibrate models with predictive power for a given spindle system.

These future models will probably first succeed in providing a complete quantitative description of low-dimensional spindles reconstituted in cytoplasmic extracts, recent studies of which revealed important scaling laws (Gaetz et al., 2006; Dinarina et al., 2009), and ‘one-dimensional’ yeast spindles in which individual elements can be more readily observed (Bouck et al., 2008; Vizeacoumar et al., 2010). Then, to put together comprehensive models of three-dimensional and complex spindles in animal cells, besides the MT-, KT- and chromosome-tracking data, we will need to understand collective motor action (Ally et al., 2009), ways in which stochastic gradients of regulatory molecules affect MT-motor dynamics (Athale et al., 2008), and to measure force maps in the spindle (Ke et al., 2009). Similar data led to the elucidation of lamellipodial actin dynamics (Keren et al., 2008), and they will ultimately lead us to an understanding of three-dimensional spindle morphogenesis and function based on the physical properties of its components.