Abstract
This paper presents a differential geometry based model for the analysis and computation of the equilibrium property of solvation. Differential geometry theory of surfaces is utilized to define and construct smooth interfaces with good stability and differentiability for use in characterizing the solvent-solute boundaries and in generating continuous dielectric functions across the computational domain. A total free energy functional is constructed to couple polar and nonpolar contributions to the salvation process. Geometric measure theory is employed to rigorously convert a Lagrangian formulation of the surface energy into an Eulerian formulation so as to bring all energy terms into an equal footing. By minimizing the total free energy functional, we derive coupled generalized Poisson-Boltzmann equation (GPBE) and generalized geometric flow equation (GGFE) for the electrostatic potential and the construction of realistic solvent-solute boundaries, respectively. By solving the coupled GPBE and GGFE, we obtain the electrostatic potential, the solvent-solute boundary profile, and the smooth dielectric function, and thereby improve the accuracy and stability of implicit solvation calculations. We also design efficient second order numerical schemes for the solution of the GPBE and GGFE. Matrix resulted from the discretization of the GPBE is accelerated with appropriate preconditioners. An alternative direct implicit (ADI) scheme is designed to improve the stability of solving the GGFE. Two iterative approaches are designed to solve the coupled system of nonlinear partial differential equations. Extensive numerical experiments are designed to validate the present theoretical model, test computational methods, and optimize numerical algorithms. Example solvation analysis of both small compounds and proteins are carried out to further demonstrate the accuracy, stability, efficiency and robustness of the present new model and numerical approaches. Comparison is given to both experimental and theoretical results in the literature.
Keywords: Generalized Poisson-Boltzmann equation, Biomolecular surface formation and evolution, Potential driving geometric flows, Solvation free energy, Multiscale models
I Introduction
Among the various components of molecular interactions, electrostatic interactions are of special importance6,8,41,44,55,59,71,142–144,169,170 because of their long range and influence on polar or charged molecules – including water, aqueous ions, and amino or nucleic acids. Electrostatic interactions are ubiquitous for any system of charged or polar molecules, such as biomolecules (proteins, nucleic acids, lipid bilayers, sugars, etc.) in their aqueous environment. Electrostatic solute-solvent interactions, therefore, are of central importance in analyzing molecular structure and modeling the intramolecular and intermolecular interactions of macromolecules in simulations. There are two types of solvation models:131,142,143,169 explicit solvent models that represent the solvent in molecular or atomic detail, and implicit solvent models that essentially replace the explicit solvent with a dielectric continuum. Each type of methods has its strengths and weaknesses. Although explicit solvent models provide some of the highest levels of detail, they generally require extensive sampling to converge thermodynamic or kinetic properties of interest. On the other hand, implicit solvent models trade detail and some accuracy to eliminate costly sampling of solvent degrees of freedom. Because of their fewer degrees of freedom, implicit solvent methods have become popular for many applications in molecular simulation.6,8,22,44,55
Solute-solvent interactions are typically described by solvation energies (or closely related quantities): the free energy of transferring the solute from a vacuum to the solvent environment of interest (e.g., water at a certain ionic strength). Solvation energies can be decomposed into polar and nonpolar contributions. It is important to realize that this polar/nonpolar decomposition is arbitrary and, although widely used, has caveats associated with the non-unique nature of the polar and nonpolar processes102 and the intrinsic coupling between these two components of solvation.49,50
Solvation free energies can be calculated by a variety of computational methods ranging from very time-consuming quantum mechanical approaches77,102,129 to simple phenomenological modifications of Coulomb’s law. Traditionally, explicit solvent methods with classical descriptions of intermolecular interactions have been the standard approach for obtaining very detailed descriptions of solvation.125 However, such methods require extensive sampling of solvent degrees of freedom which creates a significant computational burden. Implicit solvent methods, as used in the present work, have become popular alternatives to more computationally-expensive approaches although they have a lower accuracy.7,9,41,74,131 In implicit solvent methods, an atomic-detail solute is surrounded by continuum solvent modeled by its “pre-equilibrated” effect on the solute.131
Due to the ubiquitous nature of electrostatics and the aqueous environment common to most biomolecular systems, analysis of molecular solvation and electrostatics is of significant importance to research in chemistry, biophysics, and medicine. Such analysis can be classified into two general types: quantitative analysis for thermodynamic or kinetic observables and qualitative analysis for general characteristics of biomolecular solvation. One of the primary quantitative applications of implicit solvent methods in computational biology and chemistry research has been the calculation of thermodynamic properties. Implicit solvent methods offer the advantage of “pre-equilibrating” the solvent and mobile ions, thus effectively pre-computing the solvent contribution to the configuration integral or partition function for a system.131 Such pre-equilibration is particularly evident in MM/PBSA models103, 122, 151, 156, 176 which combine implicit solvent approaches with molecular mechanics models to evaluate binding free energies from an ensemble of biomolecular structures. Another important and related application of implicit solvent computational methodology is the calculation and assignment of protein titration states.3,13,66,90–92,99,104,114,115,115,159,178 Such methods have been used to interpret experimental titration curves, decompose residue contributions to protein-protein and protein-ligand binding energetics, examine structural/functional consequences of RNA nucleotide protonation, and several other applications. Yet another application area for implicit solvent methods is in the evaluation of biomolecular kinetics where implicit solvent models are generally used to provide solvation forces for molecular Langevin dynamics, 97, 98, 126, 127, 155 Brownian dynamics,52, 61, 101, 138 or continuum diffusion 33, 34, 148, 149, 182 simulations.
A major qualitative use of implicit solvent methods in experimental work is the visualization and qualitative analysis of electrostatic potentials on and around biomolecular surfaces.6, 10, 124, 171 Visualization of electrostatic potentials was popularized by the availability of software such as Grasp124 and is now a standard procedure for the analysis of biomolecular structures with thousands of examples in the literature, including ligand-receptor binding and drug design, protein-nucleic acid complexes, protein-protein interactions, macromolecular assembly, enzymatic mechanism analysis, etc.
The polar solvation energy is generally associated with a difference in charging free energies in vacuum and solvent. A variety of implicit solvent models are available to describe the polar solvation process;8, 9, 29, 41, 64, 82, 131, 137, 141, 142, 157, 165, 169, 170 however, the most widely-used methods are currently the Generalized Born12, 29, 43, 64, 70, 82, 109, 119, 161, 162, 188 and Poisson-Boltzmann (PB)6, 41, 44, 59, 71, 84, 142 models. Generalized Born methods are very fast but are only heuristic models for estimating the polar salvation energies of biomolecular structures. These methods are often used in high-throughput applications such as molecular dynamics simulations.12, 29, 39, 43, 55, 82, 119, 143, 162 PB methods can be formally derived from more detailed theories18, 72, 112 and offer a somewhat slower, but often more accurate, method for evaluating polar solvation properties.12, 39, 118 Additionally, PB techniques are often used to parameterize and assess the accuracy/performance of Generalized Born models.39, 43, 118, 118, 161, 163 Finally, unlike most generalized Born methods, PB models provide a global solution for the electrostatic potential and field within and around a biomolecule, therefore making them suited to visualization and other analysis20, 40, 42, 52, 61, 95, 139, 149, 166 that require global information about electrostatic properties. The PB equation6, 41, 44, 59, 71, 84, 142 is a nonlinear elliptic partial differential equation (PDE) which is solved for the electrostatic potential. It can be linearized for cases where the interactions between mobile ions and the solute electrostatic potential are very weak. This assumption leads to the “linearized PB equation”. The PB theory is approximate and, as a result, has several well-known limitations which can affect its accuracy.31, 37, 44, 54, 71, 72, 112, 135, 141, 157, 158, 169 These limitations have been reviewed in previous articles and will only be briefly summarized here. First, most continuum models assume linear and local solvent response.18, 54, 141, 169 However, nonlinear solvent response (usually through dielectric saturation or electrostriction), can be important in regions of strong electric field.54, 141, 169 Biologically-relevant examples of nonlinear solvent response have been found near highly charged ions, biomolecules, and other interfaces. Nonlocal solvent response generally involves the finite non-zero size of water and its unique hydrogen bonding with solute and other solvent molecules. Such nonlocal response can be important in describing the orientation of water at biomolecular interfaces,26 differing solvation of cations and anions, and the solvation of asymmetric charge distributions. The second major limitation is the mean-field treatment of ions in PB theory.71, 72, 112 Mean field models assume that each ion experiences only the average influence of the other ions in solution. Such averaging precludes detailed ion-ion interactions involving steric repulsion of ions (or their solvation shells) and Coulombic interaction of ions, including repulsion and attractive pairing. The mean field assumption thereby eliminates correlations and fluctuations which can have important energetic and structural consequences for solutions of divalent and multivalent ions surrounding highly-charged molecules such as nucleic acids.31, 37, 135, 157, 158 As suggested by the limitations above, PB models also neglect detailed ion-solvent interactions which eliminate differences between ion species in solution and thereby prevent effects analysis of specific ion species – which can be important in biophysical modeling. However, despite these limitations, PB methods are still very important for biomolecular structural analysis, modeling, and simulation. Furthermore, these limitations are currently being addressed through new implicit solvent models5, 37, 112, 123, 157 and hybrid treatments11, 87, 110, 117, 164 which extend the applicability of PB theory while preserving some of its computational efficiency through pre-averaging solvent and ion response.
PB methods provide polar solvation energies and therefore must be complemented by nonpolar solvation models to provide a complete view of biomolecular solvent-solute interactions. Nonpolar solvation is generally associated with the insertion of the uncharged solute into solvent. There are many nonpolar solvation models available; however, recent work by Levy, Gallicchio, and others62–64,89 as well as our own research167 has demonstrated the importance of nonpolar implicit solvent models which include treatment of attractive solute-solvent dispersion terms as well as models of solvent-solvent repulsive interactions that include both area and volume contributions.167
All implicit solvent models require an interface definition to indicate the separation of solute atoms from the surrounding solvent. In the context of the PB equation the solute-solvent boundary is used to define the dielectric constant and ion accessibility coefficients. For nonpolar models the solute-solvent boundary is used to define the solvent accessible domain which, in turn, defines the area and volume. The van der Waals surface, the solvent accessible surface,86 and the molecular surface (MS)130 are often used for this purpose. All of the physical properties of interest, including electrostatic free energies, biomolecular surface areas, molecular cavitation volumes, solvation free energies, and pKa values are very sensitive to the interface definition.45, 47, 116, 152 These surface definitions have been found successful in biomolecular modeling;19, 38, 48, 79, 83, 94, 96, 150 however, these surfaces are simply ad hoc divisions of the solute and solvent regions of the problem domain; none of them takes into account minimization of interfacial free energies during equilibrium solvation.
The first partial differential equation (PDE) based molecular surface was constructed by Wei el al. in 2005.175 Unlike the commonly used PDE based surface smoothing techniques which start with a given surface, this approach embeds the atomic information, i.e., atomic coordinates and radii, instead of a given surface, in the Eulerian formulation, and generates hypersurfaces by curvature controlled PDEs. The biomolecular surface is subsequently extracted from the hypersurface by a level-set approach.175 This approach produces well defined molecular surfaces for both small molecules and large proteins. The true physical boundary of a biomolecule in solvent, as a physical concept, should be in general determined by the optimization of the free energy of the macromolecule in the aquatic environment. This issue was addressed by a variational derivation of the minimal molecular surface (MMS) that minimizes a surface free energy functional by the mean curvature flow model in 2006.15, 16 As in the classical theory of minimal surfaces, the mean curvature flow minimizes the surface area for a given constraint. For simple models of solute-solvent interactions, interfacial free energy minimization is often equivalent to surface area minimization, and gives rise to the MMS, which was the first biomolecular surface that has ever been constructed by the variational approach. Electrostatic solvation free energies of 26 proteins have been calculated by using MMSs.17 To our knowledge, our geometric PDE based models15–17, 175 are the first of their kind for biomolecular surfaces, electrostatics and solvation modeling. More recently, we have presented a general procedure for the formation and construction of biomolecular surfaces by balancing the geometric curvature effects and potential effects.14 This formalism enable the incorporation of microscopic interactions, such as van der Waals potentials, into the macroscopic curvature description. The mathematical structure of this approach was prototyped by one of the present authors in 1999.172 Most recently, differential geometry based multiscale models have been proposed to describe the dynamics and transports of chemical and biological systems, including fuel cells, ion channels, DNA packing, nanofluidic systems, and virus evolution.27, 173
Geometric flows,177 particularly mean curvature flows, have been of interest in applied mathematics for many years with an emphasis on image analysis, material design57, 68, 106, 120, 134, 136, 140, 147 and surface processing.183 Computational techniques using the level set formalism were devised by Osher and Sethian132, 140 and have been applied by many others.25, 35, 146 The impact of the level set theory is far beyond applied mathematics. An alternative approach is to minimize the mean curvature or the energy functional of the characteristic function in the framework of the Mumford-Shah variational functional,111 and the Euler-Lagrange formulation of surface variation.21, 24, 93, 121, 132, 133 In 1999, Wei introduced some of the first high-order geometric flow equations for image analysis.172 Coupled geometric flow equations were also proposed by Wei and Jia174 for image edge detection and feature extraction.
While implicit solvent models are very efficient, they are approximate treatments of the solvent environment around a solute assuming linear and local solvent response to all solute perturbations.18, 46, 131, 169 As such, they can fail to accurately describe solvent behavior in situations where nonlinear or nonlocal solvent response is important to the phenomenon of interest or where the atomic details of solute-solvent interactions are needed.1, 2, 4, 8, 23, 26, 30, 36, 49–51, 58, 60, 75, 76, 81, 85, 88, 107, 108, 128, 145, 153, 154, 160, 167 Limitations of the PB equation have been indicated above and follow directly from these assumptions of linearity and locality in solvent-solute interactions. Similar limitations are present for the nonpolar models discussed. However, despite their shortcomings, implicit solvent models have many uses in a variety of chemical, physical, and biomedical research fields and therefore continue to be an important area of computational research.
Yet, an important problem in implicit solvent models is the lack of sufficient descriptions of polar-nonpolar coupling and solvent-solute interactions.4, 23, 26, 36, 49, 58, 60 This problem has recently considered by Dzubiella et al49 who proposed an interesting free energy optimization procedure to couple polar-nonpolar interactions. Their model includes contributions from pressure, Gauss and mean curvatures, van der Waals interactions and electrostatic effects. Biomolecular surfaces were generated from this model via the level set approach32 which is similar to our earlier Eulerian geometric flow approaches of biomolecular surfaces and solvation analysis.15–17, 175
The use of the PB theory in computational biology, chemistry, and physics still faces a number of challenges – many of which are related to the definition of the solute-solvent interface. First, there is significant controversy over the choice of solute-solvent interface.45, 47 This controversy stems, in part, from the ad hoc nature of the current popular surface definitions. Second, many popular surface definitions lack the stability and differentiability for routine use in molecular simulations due to extreme sensitivity to atomic positions, radii, etc. This sensitivity often drives the use of alternative “smoothed” solvent-solute interface definitions69, 78 which can introduce additional computational artifacts.152 Finally, the wide range of surface definitions has led to confusion and misuse of parameter (radii) sets developed for implicit solvent calculations with specific surface definitions.
The objective of the present work is to introduce a differential geometry based approach for the generation of smooth surfaces with good stability and differentiability for use in both polar and nonpolar modeling, thereby addressing many of these current challenges. We propose to optimize a polar and nonpolar solvation free energy functional to drive the construction of realistic solvent-solute boundaries and thereby improve the accuracy and stability of implicit solvent calculations. The differential geometry theory of surfaces and manifolds is employed to result in new coupled geometric and potential flows for the generation of a physical solvent-solute boundary and the optimization of solvation energy. Technically, the smoothness of the resulting solute-solvent boundary is ensured by coupled geometric and potential flows of parabolic type. Computational methods and algorithms are constructed and carefully validated to ensure their accuracy, stability, and efficiency. The proposed solute-solvent boundary model and associated free energy functional are tested by their applications in several common biomolecular modeling tasks.
The rest of this paper is organized as follows. Section §II is devoted to the theoretical foundation of the present differential geometry based solvation model. A variational framework is established to couple different parts of the solvation contributions. Governing equations are derived by variational principles. The solution of the governing equations leads to physical solvent-solute boundaries and accurate solvation free energies. Numerical methods and algorithms are discussed in Section §III. Schemes of the second order numerical accuracy are designed for the construction and evolution of solute characteristic function. Appropriate preconditioners are used for solving the generalized Poisson-Boltzmann equations. The coupled equations are solved by two iterative schemes. Section §IV presents validation and analysis of the proposed numerical approaches. The accuracy and convergence of various computational schemes, including the surface area formulation based on the geometric measure theory, are carefully tested to ensure their computational reliability and efficiency. The applications of the proposed theories, methods and algorithms are considered to two sets of compounds: small molecules and proteins in Section §V. Comparison is given to results in the literature. Finally, this paper ends with concluding remarks.
II Differential geometry based solvation model
In this section, a differential geometry based model of solvation is briefly described for macromolecules and their aquatic environment that are near equilibrium. More details about the differential geometry based multiscale formalism, particularly dynamics and transport aspects, can be found elsewhere.173 For a system near equilibrium, the density of charged particles in the solvent can be approximated by the Boltzmann distribution, which considerably reduces the number of degrees of the freedom of the solvation system. Alternatively, the Nernst-Planck equations or the full set of the Navier-Stokes equations might be utilized to describe systems that are far from the equilibrium.173
II.A Solute-solvent boundary
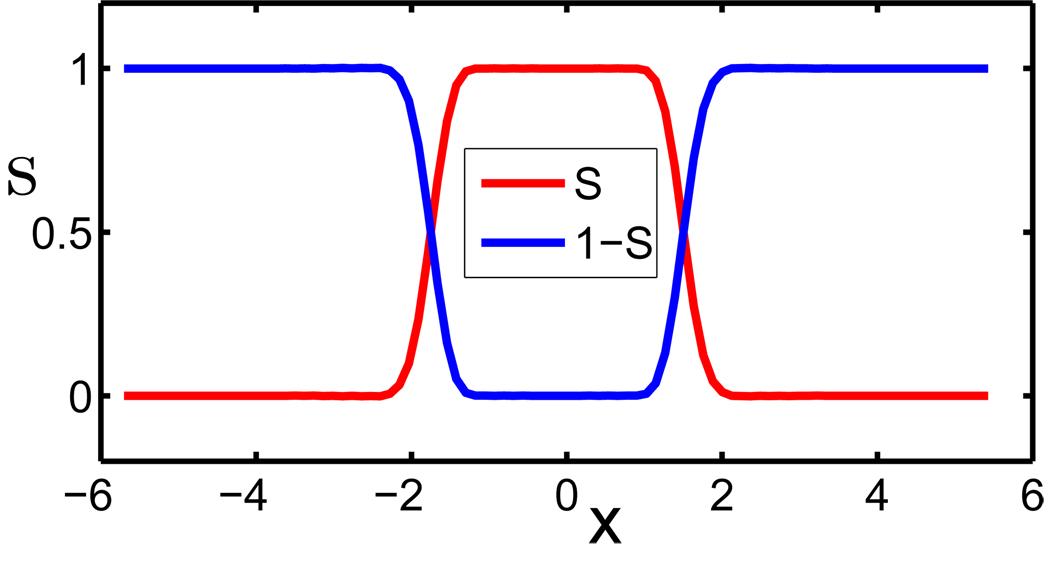
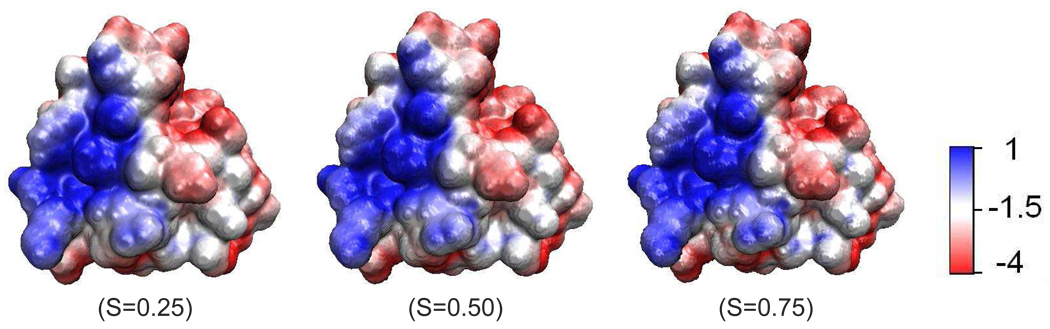
Let us consider a multi-domain setting of a macromolecule and solvent system. The macromolecule is described in discrete atomic detail, while the aqueous solvent is treated as a continuum. Therefore, the domain Ω ∈ ℝ3 is essentially divided into two (types of ) regions, i.e., aqueous solvent domain Ωs and macromolecular domain Ωm. Therefore, one has Ω = Ωs ∪ Ωm. However, because electron wavefunctions of the solvent and the solute overlap at the atomic scale, Ωs and Ωm should overlap with each other at the boundary of molecules and solvent, i.e., Ωb = Ωs ∩ Ωm ≠ ⊘, where Ωb is the region of solvent-solute boundary. Therefore, we propose a characteristic function S : ℝ3 → ℝ to characterize this overlapping solvent-solute boundary. As such, S(x) is a description function or a characteristic function of the solute domain, i.e., it is one (S = 1) inside the biomolecule and zero (S = 0) in the aquatic solvent. However, S takes a value between zero and one at the solvent-solute boundary region. Therefore, (1 − S) is a description function or a characteristic function for the solvent domain. The profiles of S and (1 − S) are depicted in Fig. 1 for a simple system. It is seen that there is a transition region at the solvent-solute boundary where the solvent and the solute regions overlap. Obviously, in our model, the evaluation of all the solvent-solute properties depends on S. Physically, S and thus the profile of solvent-solute boundary, must be determined by the energy minimization principle. Therefore, our task is to identify the energy functional that to be optimized. This task is accomplished via the differential geometry of surfaces and manifolds in the present work.
Figure 1.
The cross line of S and (1 − S) of a diatomic system described in Section IV.C
II.B Total free energy functional
The solvation process of macromolecules involves a number of interactions. As discussed in the Introduction, typically, the free energy of solvation models consists of polar and nonpolar contributions, as well as polar and nonpolar interactions.
II.B.1 Polar free energy functional
The polar part is standardly represented by electrostatic interactions, which are of special importance because of their long range and influence on polar or charged molecules including water, aqueous ions, and amino or nucleic acids. They are also some of the most important aspects that determine the physical and chemical properties of biomolecules, such as protein folding, protein-DNA binding, gene expression and regulation, etc. The widely used free energy functional of the electrostatic system was given by Sharp and Honig142 and Gilson et al.67 However, their formulation is based on a sharp interface that separates the solvent and solute domains. In our formulation, we incorporate the function S into the polar solvation free energy functional
| (1) |
where ϕ is the electrostatic potential whose domain is the whole computational domain Ω, and εs and εm are the dielectric constants of the solvent and solute, respectively. Here is the density of molecular charges, with Qj being the partial charge on an atom located at xj, qi is the charge of ion species i, Nc is the number of ion species, kB is the Boltzmann constant, T is the temperature, and ci is the bulk concentration of the ith ionic species. The term associated with S is the electrostatic free energy of the solute and that with (1 − S) is the electrostatic free energy of the solvent.
The above electrostatic free energy functional is inherently multidomain in nature and the domain is divided into the solute subdomain and the solvent subdomain as indicated by S and 1 − S, respectively. These subdomains do not have to be mutually exclusive. A discrete description of the solute and a continuum description of the solvent are also employed in Eq. (1) in the framework of the implicit solvent treatment, in which the charge density of mobile ions follows the Boltzmann distribution. Moreover, it will be demonstrated that the present electrostatic free energy functional is able to reproduce the classical Poisson-Boltzmann equation when a sharp solvent-solute interface is used and S becomes a Heaviside function. Finally, we note that the terms that are quadratic in the potential gradient in Eq. (1) have negative signs. Therefore, the free energy will be optimized instead of being minimized. In this work, we have adopted the earlier sign convention in the field.67, 142
II.B.2 Non-polar free energy functional
For the nonpolar contribution, we consider the following nonpolar solvation free energy functional proposed by Wagoner and Baker.167
| (2) |
where Area is the surface area of the macromolecule, γ is the surface tension, Vol represents the volume occupied by the molecule of interest, p is the hydrodynamic pressure, ρ0 is the solvent bulk density and Uatt(r) is the attractive portion of the van der Waals potential at point r. The first term is the surface energy. It measures the disruption of intermolecular and/or intramolecular bonds that occurs when a surface is created. The second term is the mechanical work of creating the vacuum of a biomolecular size in the solvent. The third term represents the attractive dispersion effects near the solvent-solute interface which has been shown by Wagoner and Baker167 to play a crucial role in accurate nonpolar solvation analysis.
To obtain a functional relation for S, it is necessary to rewrite nonpolar free energy formulation in terms of S(r). The enclosed volume of biomolecule can be given by
| (3) |
Similarly the attractive dispersion term can be rewritten in the form
| (4) |
where we assume that the solvent bulk density ρ0 is a constant in space.
Typically, one expresses the area of a unique surface as a surface integration over the biomolecular boundary in the Lagrangian formulation. However, this approach does not work directly in our formulation because no sharp solvent-solute boundary is assumed. In fact, the concept of the surface area cannot be defined in the same manner as in the sharp surface case. For a smooth boundary, there are infinitely many surfaces and the surface area can be defined as a weighted mean of this family of surfaces. Additionally, for practical purpose, we need an appropriate Eulerian formulation for the surface area so that we can put all energy contributions into an equal footing. Therefore, we need to convert the surface integral into a volume one. To this end, we make use of the coarea formula in the geometric measure theory.53 For a scalar field B in ℝ3, with C1 continuity condition, integrating a function f over its isolevel c in a region Ω can be done directly by a volume integral over Ω through the expression
| (5) |
where c denotes an isovalue of B, and B−1 represents the c-isosurface, i.e., the set of points {rc} such that B(rc) = c. Here, the coarea formula prescribes a relationship between the sum of area integrals and a global volume integral. In our case, we introduce the concept of mean surface area of the family of isosurfaces which are subsets of point satisfying {S(r) = y}, where 0 ≤ y ≤ 1. Therefore the mean surface area can be given by a volume integral as
| (6) |
Note that ∇S ≠ 0 only in the region of the solvent-solute boundary. Numerical test of this formulation will be presented in Section §IV.A.
Finally, the electrostatic free energy functional is complemented by the nonpolar free energy functional to give the total free energy functional of solvation for biomolecules at equilibrium
| (7) |
Note that the polar and nonpolar parts are coupled via the characteristic function S, which is determined by the total energy optimization instead of the surface free energy optimization as done in our earlier work.17 The above total free energy expression provides a basis for the evaluation of the solvation free energy and a starting point for the derivation of governing equations for the solvation analysis. A similar coupling of polar and nonpolar interactions was described previously by Dzubiella and co-workers;49, 50 however, the implementation of non-polar interactions and the representation of continuum and discrete domains differ significantly from the present work.
II.C Governing equations
The solvation free energy functional is a functional in terms of characteristic function S and potential ϕ. The integral is taken over the whole space. From the physical point of view, there should exist an optimal function S(r) and an optimal potential ϕ at the equilibrium state which optimize the total energy. Since S and ϕ can vary independently in our formulation, to optimize Gtotal, it is necessary that
| (8) |
and
| (9) |
where is a generalized Laplace-Beltrami operator, which is a generalization of the usual Laplacian operator to a smooth manifold.14, 173 In general, γ can be a function of the position γ = γ(r) to reflect surface hydrophobicity at different locations. However, it is treated as a constant in our present computation. From Eq. (8) we result in the generalized Poisson-Boltzmann equation (GPBE)
| (10) |
where the dielectric function is given by
| (11) |
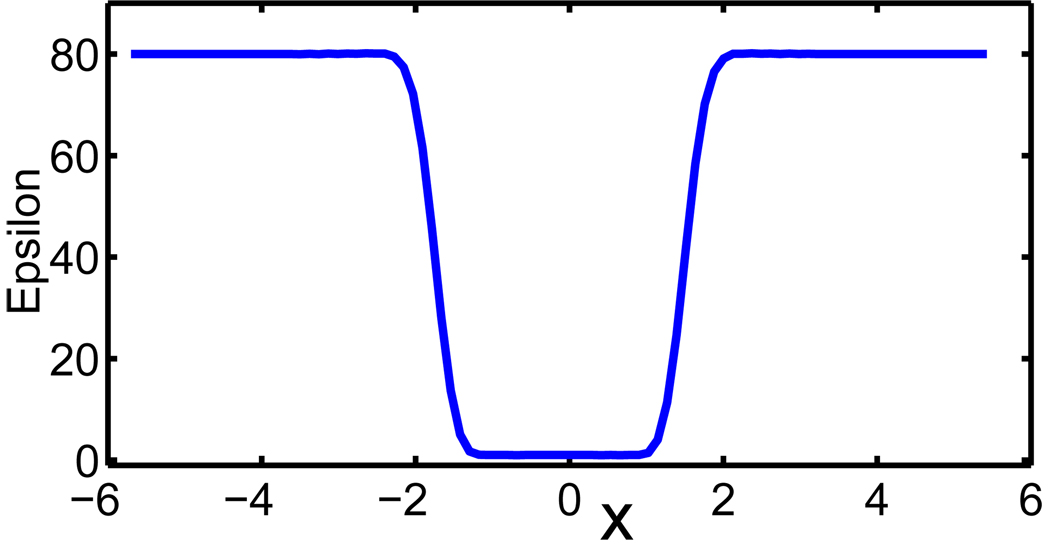
This expression provides a smooth dielectric profile. Figure 2 shows the cross line of the dielectric function ε(S) of a diatomic system. It is seen that there is a smooth transition region for the dielectric constant to change from εs to εm. The solution procedure of Eq. (10) can differ very much from that of the standard PB equation, due to the smooth dielectric function. Particularly, many mathematical difficulties of solving elliptic equations with discontinuous oefficients180, 181, 184, 186, 187 can be avoided in the present generalized Poisson-Boltzmann equation.
Figure 2.
The cross line profile of ε(S) of a diatomic system described in Section IV.C. Here, we have set εs = 80 and εm = 1.
For a weak electrostatic potential, i.e., ϕ ≪ 1, one can linearize the generalized PB equation
| (12) |
where κ̄ is a modified Debye-Hϋckel screening function describing the ion strength.73
Furthermore, the solution of Eq. (9) leads to a “physical solvent-solute boundary” (S). As discussed in earlier work,14, 17, 173 the solution of this elliptic partial differential equation can be attained via a parabolic partial differential equation
| (13) |
where the generalized “potential” V is defined as
| (14) |
Note that Eq. (13) has the same differential operator as the mean curvature flow equation,17 except for the extra external source term. Therefore, it is a special case of the potential driven geometric flow equation proposed in our earlier work.14 In Eq. (13), as t → ∞, the initial profile of S evolutes into a steady state solution, which solves the original Eq. (9).
It is interesting to see that the sharp solvent-solute interface and the standard PB equation, as well as related interface conditions, can be recovered from Eq. (10). For a sharp interface, S becomes a Heaviside function, having value 1 for the solute subdomain and 0 for the solvent subdomain. As such, the smooth transition region in the dielectric function disappears and the dielectric function becomes discontinuous. Then, Eq. (10) reduces to the classical form of the Poisson-Boltzmann equation73
with appropriate interface conditions
| (15) |
where ϕm and ϕs represent the potential in the solute domain Ωm and solvent domain Ωs, respectively, Γ denotes the sharp interface, and n is the normal vector of the solvent-solute sharp interface.
Note that the generalized Poisson-Boltzmann Eq. (10) and the potential driven geometric flow equation (13) are strongly coupled. Therefore, these two equations have to be solved by appropriate iterative procedures. This aspect will be discussed in Section III.C.
III Methods and algorithms
This section presents a variety of computational methods and algorithms for the solution of the generalized Poisson-Boltzmann equation and the generalized geometric flow equation.
III.A Discretization schemes of the governing equations
We design second order finite difference schemes for governing equation derived from the free energy optimization.
III.A.1 The generalized Poisson-Boltzmann equation
For the solution of the generalized PB equation, the finite difference scheme is utilized in this study. The continuous dielectric definition allows us to obtain accurate solution by using the standard second order center difference scheme. Let the pixel (i, j, k) represent the position (xi, yj, zk). The discretized form of Eq. (12) is
| (16) |
where h is the grid spacing, and q(i, j, k) is the fractional charge at grid point (xi, yj, zk), which is resulted from the interpolation of the charge density ρm. The second order interpolation (i.e., the trilinear mapping) is used to distribute charges. Thus, the discretized PB equation can be cast into the standard linear algebraic equation system of the form AX = B, where X is the solution of the interest, A is the discretization matrix and B is the source term associated with the continuum and discrete charges. The boundary condition is built up by the far field condition and practically obtained by the sum of potential contributions from individual atom charges with a decay factor from the continuum charge strength κ.65 Initially, we have explored the use of the biconjugate gradient method as the linear solver. Matrix acceleration is discussed in a later section. The initial guess of the solution is set to 0 and the convergence tolerance is set as 10−6. It is shown in the test section that the PB solver is able to deliver the designed second-order accuracy.
III.A.2 The potential driven geometric evolution equation
To attain the solution of geometry flow equation (13), one has to determine all of the involved physical parameters first. Some parameters in the literature,89, 113 including the CHARMM force field, can be adopted for this purpose. However, due to the nonpolar solvation energy expression in our model, not all parameters can be adopted from the literature. Some modifications are necessary. In particular, surface tension γ should vary according to the surface definition.89, 113 Therefore, it is used as a fitting parameters in our model. To this end, we write
| (17) |
where with γ as a nonzero parameter and V being defined in Eq. (14). In addition to the Lennard Jones parameters εi, σs and σi, what will be determined in the generalized geometry flow equation are p/γ, ρ0/γ, εs/γ, εp/γ and ρm/γ. Note that since ρm/γ is assigned at the center of atoms, term (ρm/γ) ϕ has nonzero value only at atomic center so that it does not have contributions to the surface evolution when S evolves only outside the van der Waals volume.
The discretization scheme used here for the solution of the generalized geometry flow equation (17) is similar to what we designed previously.14, 17 It can be rewritten in the form
| (18) |
where t′ = tγ. To obtain the discretized form, we introduce the following notations. We consider a discrete time tn := nτ where n is a non-negative integer and τ is the time stepping size. We denote to be the discretized form of S(xi, yj, zk, tn). An explicit scheme of the generalized geometry flow equation is given by
| (19) |
where
where
and
For the initial value of S, we consider
| (20) |
where we define the domain enclosed by the solvent accessible surface to be , with rp being the probe radius. Here Na denotes the total number of the atoms for a given biomolecular system. Let the atom centers be ri = (xi, yi, zi), i = 1, …, Na, and ri represents the radius of the ith atom. To protect the van der Waals surface and make the computation more efficient, we only update the values of S(x, y, z, t) at the points in between the van der Waals surface and the solvent accessible surface; i.e.,(x,y,z) ∈ . Numerically, to avoid possible zeros in the denominator of Eq. (18) we add a very small number, such as 10−7 into the square root expression, which does not affect the result at all. The forward Euler method is initially used for time integration, and the explicit second order central difference scheme is performed for the spatial discretization. Moreover, the numerical algorithms based on semi-implicit scheme can be applied to relax the step size limitation and to accelerate the geometry flow solver. This aspect is studied in the next section.
III.B Acceleration procedures
The computational efficiency of the solution process is an important issue and can be a bottleneck for further applications of the present model. Particularly, when this model is applied to molecular dynamic simulation, the generalized PB equation and geometry flow equation are to be solved up to millions of times. Therefore, any nontrivial improvement in computational efficiency will make the present model more feasible to many practical applications in chemical and biological systems.
III.B.1 Precondition of the PB solver
The linear algebraic system of the discretized PB equation can be solved by two major approaches: direct methods and iterative methods. Large memory requirement prohibits direct methods to be used in the matrix resulted from large chemical and biological systems. Widely used iterative methods, including Gauss-Seidel and successive over-relaxation (SOR), work well for the generalized PB equation, but typically converge slowly. Conjugate Gradient method is quite efficient for symmetric and positively definite matrices. However, the sparse matrix A resulted from Eq. (16) is seven-fold banded but non-symmetric because the dielectric distribution function is not a constant and varies in the transition region. The biconjugate gradient (BiCG) method can be a good choice for non-symmetric systems and has been adopted in a variety of our MIB schemes,180, 181, 184, 186, 187 but attentions are still to be paid in regard to the convergence issue. We have studied the application of pre-conditioners in two linear solver libraries, the SLATEC (http://people.sc.fsu.edu/~burkardt/f_src/slatec/slatec.html) and the PETSc (http://www.mcs.anl.gov/petsc/petsc-as/) to the solution of the PB equation.28 It turned out that combination of stabilized biconjugate gradient method (BiCG) and the blocked Jacobi preconditioner (BJAC) from the PETSc and the combination of the orthomin method (OM) and the incomplete LU factorization preconditioner (ILU) from the SLATEC performed better compared to other tested solvers, preconditoners and their combinations.28 In this study, we focus on the combination of the ILU and the OM from the SLATEC, which is easy to incorporate into the present iteration procedure and provides a stand-alone package, while the PETSc needs to be pre-installed before being used. In Section §IV, we further demonstrate the improvement by the combination of pre-conditioners and the iterative linear solvers.
III.B.2 Initial guess of the generalized PB solution
A good initial guess is always desired for the speedup of the iterative PB solver. Normally, the initial guess can be simply set to 0 because it is complicated and computationally expensive to find good ones. However, in our iteration procedure, it is found that the electrostatic potential distribution does not change dramatically from the prior calculation due to the small adjustment in dielectric from the prior step. Therefore, it is beneficial to take the prior potential as a good guess for solving the linear system. It turns out that the generalized PB solver converges faster when the electrostatic potential from the previous iteration is used as an input.
III.B.3 Convergence criteria in the generalized PB solver
The convergence criterion directly influences the accuracy and CPU cost of the solution of the generalized PB equation. The smaller convergence criterion, the more accurate the solution of linear system is. However, the smaller convergence criterion requires more iterations and longer CPU time in the iterative solution process. Therefore, it is worthwhile to find a criterion which is a good compromise between the accuracy and the efficiency. Typically, a value of 10−6 is used in many chemical and biological applications. Later on we will numerically investigate the effect of convergence criterion on the electrostatic solvation energy, mean surface area and mean volume which are used to compute the total salvation free energy. With the 10−8 as a standard, we will examine the efficiency and the accuracy for several relaxed convergence criteria, such as 10−6, 10−4, 10−3, 10−2 and 10−1.
III.B.4 Numerical schemes for the generalized geometric flow equation
The explicit scheme described in Section §III.A for the generalized geometric flow equation has the advantage of saving much memory. Nevertheless, it is not very efficient because a very small time step size i.e., time stepping, is required to guarantee the stability of the algorithm. This motivates us to find a faster semi-implicit algorithm. An alternative direction implicit (ADI) scheme reported in our earlier work14 was the fastest scheme among the tested ones under typical accuracy requirement in the mean curvature flow. One of the reasons is that the traditional ADI method, widely used in linear diffusion equations, is unconditionally stable. It allows a much larger time stepping than does the explicit scheme in guaranteeing the accuracy and avoiding the stability concern. Another reason is that the capability of applying the fast O(N) Thomas algorithm to solving the tridiagonal linear system in the ADI further speeds up the computation. Considering the similarity of the current differential operator and the mean curvature flow, we adopt the splitting algorithm based ADI scheme to speed up our generalized geometric flow solver. To this end, we modify Eq. (19) as
| (21) |
It follows that
| (22) |
where
| (23) |
Here υx, υy, υz, and are defined in Section §III.A. The following multi-step implementation can be carried out. Step 1:
| (24) |
Step 2:
| (25) |
Step 3:
| (26) |
This ADI algorithm is used to integrate our generalized geometric flow equation (10).
III.C Dynamical coupling of the generalized Poisson Boltzmann and geometry flow equations
As described in Section §II, the present differential geometry based solvation model prescribes a procedure to set up the total free energy functional of the solvation. By the variational principle, we obtain generalized coupled PB equation (10) and potential driven geometric flow equation (10). The solution of these coupled nonlinear equations provides a “physical” dielectric profile ε(S) and the electrostatic potential ϕ and thereby enables the calculation of the solvation free energy. The solution of the potential driven geometric flow equation (10) requires the knowledge of ϕ, while the solution of the generalized PB equation (10) requires the input of S and ε (S). Therefore, in principle, the geometric flow equation needs to be solved simultaneously with the generalized PB equation until a self-consistency is reached. In this study, we explore two self-consistent iteration procedures.
III.C.1 Approach I
The iteration process can be carried out by breaking up the process into an iterative sequence of two steps as follows: Starting with an initial guess of characteristic function S, one finds out the temporary electrostatic potential ϕ by solving the generalized PB equation with a given initial S. Once the electrostatic potential is obtained, the electrostatic energy can be calculated. The second step is to solve the time-dependent generalized geometric flow equation for S with a prior calculated potential ϕ. In this step, the time integration can usually reach a quasi-steady state. With the updated quasi-steady S, one can come back to the first step for the next cycle until the solvation free energy converges to within a predetermined criteria. However, in practice, simply re-inserting S into the PB solver may diverge. Because the quasi-steady S may vary dramatically during the iteration. Note that all changes in S are concentrated around the solvent-solute boundary, as the final solution of the potential driven geometric flow equation reflects the balance between the intrinsic curvature energy and the external potential terms. A large change in S near the solvent-solute boundary in turn leads to much adjustment in the electrostatic potential which differs much in the solute and solvent regions. To avoid this problem, we adopt a simple relaxation algorithm: the characteristic function S used for the PB solver is a linear combination of the previous one Sold and the newly generated one Snew
| (27) |
It turns out that the convergence of the generalized PB equation is guaranteed if α is small enough. In this work, α can be taken in the range from 0.1 to 0.7. The choice of α is explored later. Note that this approach may fail sometimes when the generalized geometric flow equation blows up due to a large variation in the temporary electrostatic potential. We therefore utilize a similar procedure for the electrostatic potential used in the evolution of the generalized geometric flow equation
| (28) |
where ϕold and ϕnew are previous and newly resolved electrostatic potentials, respectively. This treatment can avoid the blow-up of the generalized geometric flow soluation.
III.C.2 Approach II
To reduce the dramatic changes in S and ϕ, we can consider a straightforward way in which solving generalized PB equation follows each time-step integration of the generalized geometry flow equation. However, this treatment makes the whole iterative procedure computationally over expensive as many more PB solution processes are required. Additionally, it may not be necessary since the change in the S from one time step to another one is so small that the change in the corresponding potential distribution should be very small. Indeed, it is practical to update electrostatic potential after a number of time steps (i.e., 10 to 100 steps) in the generalized geometry flow equation integration rather than every time step. We call the number of time integration between two ϕ updatings the number of intermittency Nstep. This approach effectively speeds up the whole process. Additionally, the relaxation algorithm given in Eqs. (27) and (28) can also be used here to guarantee the convergence. Moreover, in this approach, one better starts the iterative process by solving the S from Eq. (13) without the electrostatic potential term. So that the later iteration procedure can focus on the impact of electrostatic potential to the generation of the solvent-solute boundary. This treatment reduces the total iteration number and save the computational time significantly.
In fact, there is a relationship between Approach I and Approach II. When the number of the time integrations becomes larger and larger, Approach II returns to Approach I. In Section IV, we systematically study the difference between these two approaches. This can be done by comparing the impacts of different approaches on the resulting total solvation free energy, surface area and volume of the solute molecule. It is found that these two approaches lead to the same results. This, to some degree, indicates the reliability and validity of the proposed iteration procedures.
III.D Evaluation of the solvation free energy
Once the electrostatic potential ϕ and the characteristic function S are obtained, the solvation free energy is given by
| (29) |
where G0 is the energy calculated from the homogeneous environment with εs = εm = 1 without the nonpolar energy part. Therefore, we have
| (30) |
The expressions of Gp and Gnp are taken from Eq. (7). Here Gp − G0 can be considered as the electrostatic solvation free energy. In all calculations presented here except for salt effect calculation, mobile ions will be set to zero corresponding to a solution without salt. Therefore we have
| (31) |
Discretizing the integral yields
| (32) |
where Q(ri) is the ith partial charge at ri in the biomolecule, and Nm is the total number of partial charges. Now the electrostatic solvation free energy can be calculated as
| (33) |
where ϕ and ϕ0 are electrostatic potentials in the presence of the solvent and the vacuum, respectively. Here ϕ is computed from the generalized Poisson equation (10) using the continuous dielectric distribution
| (34) |
where ε(S) and ρm are the same as the ones in Eq. (10). The homogeneous solution ϕ0 is computed with ε(S) = εm in the whole domain. The nonpolar part, Gnp, is computed exactly by Eq. (2).
IV Numerical test and validation
This section provides systematic validations for the computational algorithms and schemes proposed in the last two sections. We first examine the behavior of the coarea formula, then continue testing through various equation solvers, and finally check the impact of the potential term in our generalized geometric flow equation.
IV.A The behavior of the coarea formula
As described earlier, the coarea formula plays an important role in describing the mean surface area of an infinite family of smooth solvent-solute boundaries by a volume integral. This Eulerian formulation puts the free energy of the surface area and other free energies in an equal footing. Usually, the isovalue of the surface area in the coarea formula can be any positive real number. But for the present derivation, it is limited to be between 0 and 1 because S is defined as a characteristic function of the solute. Here, we numerically explore the behavior of the coarea formula in a bounded open set. To this end, we design some test cases as follows: Let B be a smooth function with a specific expression according to the geometry in the coarea formula, we set
| (35) |
where Ω is a bounded open set. Therefore, the mean surface area has the same value as the volume of open set Ω∩{x|0 < B(x) < 1}. Computationally, integrating over the norm of the gradient of B gives rise to the corresponding mean surface area. The volume integral of a density function f is just simply approximated by
| (36) |
where the summation is over J, the set of points inside Ω, and (xi, yj, zk) is the coordinates of grid points (i, j, k). Table (1) lists the numerical results and exact values of the surface areas for the following cases
A unit sphere: and .
A cylinder: and .
A ellipsoid: and , where a = 20/7, b = 25/14, and c = 25/14.
Table 1.
Areas computed from the coarea formula for bounded open sets
| grid spacing |
||||||
|---|---|---|---|---|---|---|
| case | 0.5 | 0.25 | 0.1 | 0.05 | 0.025 | exact value |
| Sphere | 4.00 | 4.00 | 4.15 | 4.17 | 4.18 | 4.189 |
| Cylinder | 22.50 | 23.25 | 24.49 | 24.84 | 25.01 | 25.133 |
| Ellipsoid | 37.75 | 37.97 | 38.10 | 38.17 | 38.16 | 38.163 |
It is evident that the numerical result converges to the exact value. The errors from the cylinder are slightly larger than those from the sphere and ellipsoid because the cylinder has non-smooth edges. However, the errors are small for all cases. Therefore, we conclude that the mean value of the areas of the family of smooth solvent-solute surfaces indeed converges to the area of the corresponding sharp surface. Thus, the present definition of the mean surface area of an infinite family of smooth surfaces is an important generalization of the classic concept of the area of a sharp surface.
IV.B Accuracy of the generalized PB solver
In this section, we investigate the accuracy of the proposed numerical solvers. The generalized geometric flow equation (19) has the same differential operator as the mean curvature flow17 except for the extra source terms. Previously, we have numerically proved that the explicit Euler algorithm delivers the reliability and convergence of the solution of geometric flow equations, and the finite central different scheme is of second order convergence in space.14 Here, we focus on the test of the accuracy of the generalized PB solver with the proposed dielectric function ε(S). Although the discretization form of the second-order finite difference PB expression has been used for other continuous dielectric definitions,78 the accuracy of this approach has not been examined. Moreover, it is worthwhile to validate the generalized PB solver due to its different settings of dielectric function, i.e., the ε(S) profiles generated by the geometric flow equation. For this purpose, we construct a benchmark test of a simple one-ball system. We examine the convergence order and the accuracy of the finite difference scheme in solving the generalized PB equation. In particular, we consider a modified Poisson equation with a designed dielectric definition given by
| (37) |
where r = (x, y, z), ε1 and ε2 are two constants to be determined, and
| (38) |
where a < b. Note that through the definition of ε and Su(r), this designed case has the same features of the dielectric definition as that in our model. The exact solution is designed to be
| (39) |
Then the modified equation becomes
| (40) |
where
and
For ε, if , we have
and
Otherwise, εx = εy = εz = 0. Table (2) lists the computed errors under different mesh sizes with a = 1 and b = 3. The standard absolute norm error measurement L∞ is employed. Here ε1 is fixed to be 1 and ε2 is taken to be 80 or 10. The second order convergence in space is observed for the scheme. Furthermore, it is found that a large ε2 may slightly deteriorate the convergence.
Table 2.
Errors and convergence orders for the generalized PB solver (ε1 = 1)
| ε2 = 80 |
ε2 = 10 |
|||
|---|---|---|---|---|
| spacing | L∞ | order | L∞ | order |
| 1 | 0.22 | 0.13 | ||
| 0.5 | 8.13*10-2 | 1.65 | 3.18*10-2 | 2.02 |
| 0.25 | 2.06*10-2 | 1.99 | 7.97*10-3 | 2.00 |
| 0.125 | 5.44*10-3 | 1.94 | 1.98*10-3 | 2.01 |
IV.C Convergence of boundary profile and dielectric function
In the present model, the characteristic function S defines the solvent-solute boundary. Consequently, it can significantly affect the solution of the generalized Poisson-Boltzmann equation, the surface area and volume, and thus, plays a key role in the solvation free energy calculation. To illustrate the evolution and the convergence of the generalized geometric flow equation and corresponding S function, we solve Eq. (13) without the electrostatic potential term in this test. However, the electrostatic solvation free energy at a given time can still be calculated. The expression of attractive interaction needs to be given explicitly in order to solve the geometric flow equation. Here we consider the following 6–12 Lennard-Jones (L-J) pair potential to model :
| (41) |
where εi is the well-depth parameter, and σi and σs are solute atomic and solvent radii, respectively. Here r and ri are positions. The L-J potential can be divided into attractive Uatt and repulsive Urep in different ways. It can be a “6–12” decomposition as follows:
| (42) |
Or it can also be a “WCA” decomposition based on the original WCA theory89
| (43) |
| (44) |
All the calculations in this work are carried out by using the WCA decomposition.
To illustrate the S profile and evolution, we consider a diatomic system with the van der Waals radius 2.2Å and coordinates (x, y, z) = (−3, 0, 0) and (1.4, 0, 0). The spacing and time stepping are chosen as h = 0.25Å and τ = h2/4.5, respectively. The solvent probe radius is set to 2Å, which is used for the initial value setting and constraint construction. In fact a much small solvent probe radius can ensure the correct surface topology.17 The computational domain is set to [−8.70, 7.05] × [−5.7, 5.55] × [−5.7, 5.55]. Thus, the size of computational system is 64 × 46 × 46. The L-J parameters are set as follows: σi is taken from atomic radius and σs is chosen to be 0.65Å. We set well depth εi = 0.039 kcal/mol and bulk density coefficient ρ0/γ = 2, where, γ = 1/15kcal/(molÅ2). To compute the electrostatic solvation free energy during the evolution of solvent-solute boundary, 1 unit charge is set on the center of each atom. We choose the dielectric constants εm = 1 and εs = 80, respectively. We set pressure coefficient p/γ = 0.2. A different γ is used for real systems.
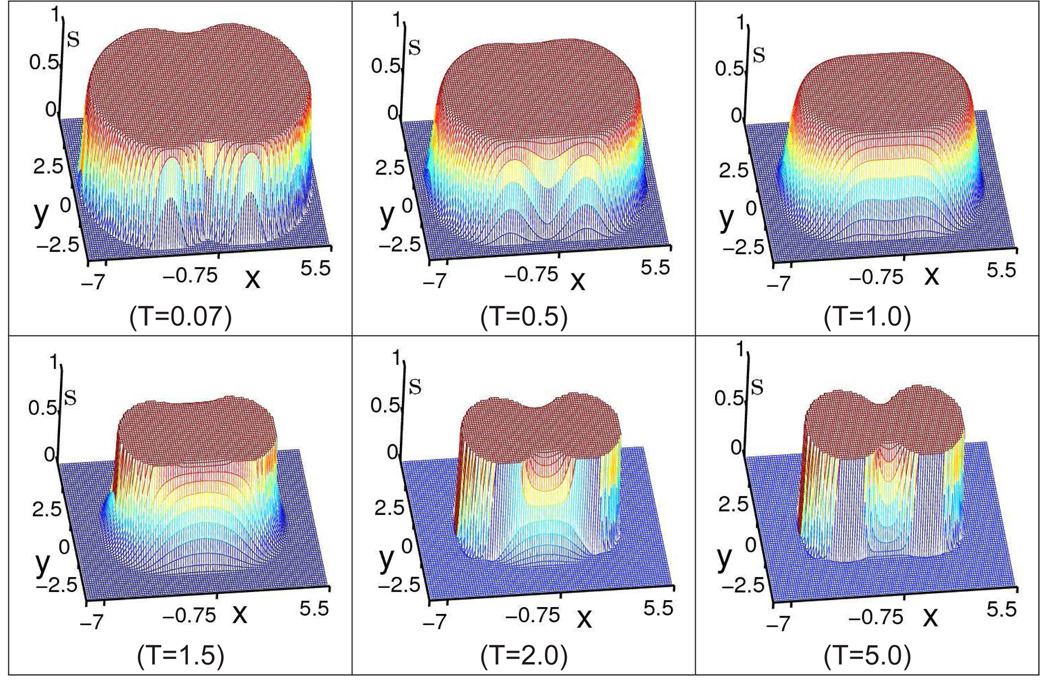
The evolution process of diatomic solvent-solute boundary is depicted through a group of cross section profiles of the S function in Fig. 3 where the values of S from a set of points of (x, y, 0.05) are described. The cross sections start with a relatively fat-shaped interface which reflects the solvent accessible density. Here, S = 1 inside the molecular domain and S = 0 in the solvent domain. Then the solvent-solute boundary is driven inward by intrinsic geometric curvature effect and external potential. At the same time, there appears a transition region between the solvent and the solute. Finally a convergence is reached with a balance among intrinsic geometric curvature effect, different potentials and enforced constraints. To have a clear idea about the distribution feature of the S function, we draw a cross line from the cross section graph at T = 5 along x = −0.75 which are shown in Fig. 1, where the functions of S and 1 − S are described together. It can be seen that the S function in the transition region is rather smooth. Once the S function is determined, the dielectric function ε(S) is calculated according to Eq. (11). Here the dielectric function ε(S) corresponding to the S function in Fig (1) is also exhibited in Fig. 2. It has a pattern similar to 1 − S but with different values. It is important to note that the dielectric function ε(S) is also very smooth at the solute-solvent boundary. That is why the classical finite difference scheme can be applied to solve the generalized PB equation without reducing the accuracy of the solution.
Figure 3.
The evolutionary profiles of the S function at cross section (x, y, 0.05) in a diatomic system plotted from six intermediate states.
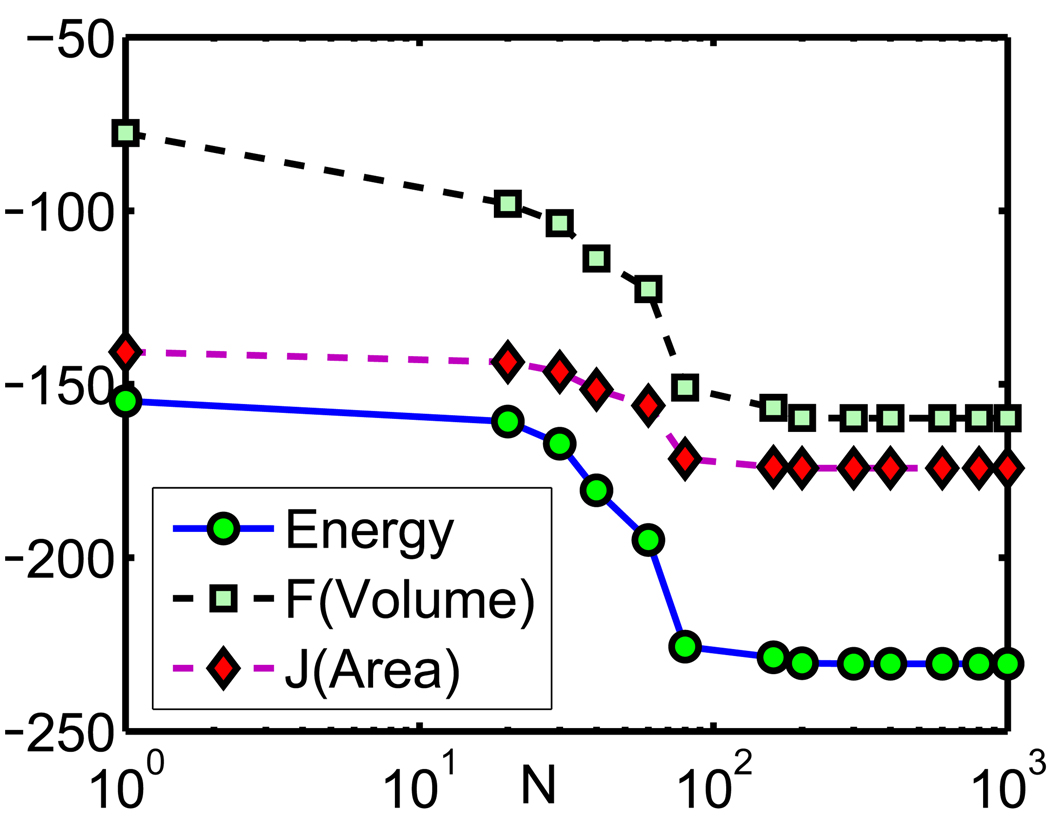
Once the solution of the generalized PB equation is computed, the electrostatic solvation free energy can be calculated. Therefore, the time history of the free energy along with the evolution of solvent-solute boundary can be recorded. To illustrate the convergence pattern of the solvation free energy, we compute the electrostatic solvation free energies in intermediate states during the time evolution. The results are shown in Fig. 4. In order to show evolution histories of the surface area, volume and solvation free energy together in one plot, we plot two linear functions F(Volume) and J(Area) which have the same time dependence as the volume and the surface area, respectively. Here T denotes the time span and represents the number of computational steps in the generalized geometric flow solver. It is found that the solvation free energy decreases with respect to the time evolution, which is consistent with our theoretical formulation. It is observed that the solution of our model converges to a steady state in terms of volume (Å3), area (Å2) and electrostatic solvation free energy (kcal/mol). Moreover, to obtain the results at the steady state, N = 200 or T = 3.5 is large enough to be taken as the stopping time in our geometry flow solver for this system. Normally, it takes a longer evolution time for a large system to set down to the steady state. The total integration time could be considerably shortened had a small probe radius been used.17
Figure 4.
The time evolution histories of the electrostatic solvation free energy, F(Volume) and J(Area), where F(Volume) = volume/5 – 180 and J(Area) = (surface area)/5 – 200.
IV.D Consistency of iteration procedures
If the electrostatic potential effect is taken into account during the solvent-solute boundary evolution, the iteration procedure has to be used to update the electrostatic potential repeatedly. As described earlier, there are two possible iterative approaches which can be explored to solve the coupling system, in which the simple relaxation algorithm guarantees the convergence of the algorithm. The question is whether these two approaches lead to the same outcome.
To study the consistency between these two approaches, the above mentioned diatomic system is employed as well as a small molecule called glycerol triacetate (Gly) from a set of 17 test compounds whose detailed information is given in Section §V. The self-consistent iteration is performed until the electrostatic solvation free energy converges to within 0.01 kcal/mol. The electrostatic solvation free energy(kcal/mol), surface area (Å2) and volume
(Å3) resulted from these two different methods are compared. The results are shown in Table 3. Here we take α = 0.5 for both methods. The electrostatic potential ϕ is updated in every 15 steps of the generalized geometric flow integrations in Approach II. It is evident that the results from these two approaches are almost the same. Therefore, they can be alternatives for each other at least in small molecular systems. But for large protein systems, as we mentioned, it is better to use the second approach to avoid the possible blowup in the generalized geometry flow caused by unpredictable large changes in the temporary electrostatic potential. Thus, in the following tests and applications, the second method is applied except specified.
Table 3.
Comparison between two iteration approaches
| 2 atoms |
Gly |
|||
|---|---|---|---|---|
| Approach I | Approach II | Approach I | Approach II | |
| Energy | −231.18 | −231.18 | −12.44 | −12.44 |
| Surface area | 128.67 | 128.67 | 271.91 | 272.02 |
| Volume | 100.72 | 100.83 | 287.85 | 287.93 |
In Approach II, the relaxation factor α and the number of intermittency Nstep need to be determined. We are interested in knowing whether the relaxation factor α plays a role in the final result. Similarly, it is important to know whether the Nstep makes a difference in the converged result. We address these issues by examining the effects of α and Nstep on the electrostatic solvation free energy, surface area and enclosed volume. The above mentioned diatomic system is used here again.
It is known that a stable α value is between 0 and 1 but can not be very close to 1. We consider a number of α values in the diatomic system while keeping other settings fixed. Table 4 shows the electrostatic solvation free energy, surface area and volume for α = 0.1, 0.2, 0.5 and 0.7. It is found that the procedure diverges when α ≥ 0.8. However, convergence is achieved as long as the relaxation factor α is small enough. Once the convergence is achieved there is no much difference in the final outcome. We therefore take α = 0.5 in the following tests and applications.
Table 4.
Effect of relaxation factor α on final results
| α | 0.1 | 0.2 | 0.5 | 0.7 | 0.8 |
|---|---|---|---|---|---|
| Energy | −231.26 | −231.18 | −231.18 | −231.18 | divergence |
| Surface area | 100.73 | 100.94 | 100.83 | 100.71 | |
| Volume | 128.65 | 128.62 | 128.67 | 128.71 |
To study the effect of the number of intermittency, we take Nstep = 5, 10, 15, 40 and 100, while fixing α = 0.5 and other settings. The results are listed in Table 5. It is seen that all values obtained from different number of intermittency are very close to each other. However, a numerically too large or too small Nstep is not preferable. If Nstep is too large, Approach II goes back to the first one. If Nstep is too small, the iterative process may stop too early because the perturbation in each iteration is so weak that the convergence criteria is satisfied unexpectedly sometimes. In addition, small step number makes the whole process computationally expensive.
Table 5.
Effect of the number of intermittency in Approach II
| Nstep | 100 | 40 | 15 | 10 | 5 |
|---|---|---|---|---|---|
| Energy | −231.18 | −231.19 | −231.18 | −231.17 | −231.11 |
| Surface area | 100.83 | 100.83 | 100.83 | 100.89 | 101.07 |
| Volume | 128.63 | 128.63 | 128.67 | 128.48 | 128.63 |
IV.E Efficiency of the accelerated iteration procedure
We study the efficiency of the accelerated self-consistent iteration in this section. At the beginning we analyze the CPU time usage based on an original combination of methods: Biconjugate Gradient (BiCG) method for the generalized PB solver and a widely used explicit scheme for the generalized geometric flow (GGF) solver. In addition, as commonly used in the linear system of the PB equation, we take 10−6 as the initial convergence criteria and set the first guess of the electrostatic potential in each generalized PB run to be 0. The above mentioned diatomic and Gly systems will be utilized through this efficiency test. Table 6 lists the breakup of time spending in the different parts of the self-consistent iteration procedure. It is seen that for these two systems the major computation cost lies in the routines of the generalized PB solver and the generalized geometric flow solver (more than 90%). Therefore, the total time will be dramatically reduced when efficient accelerations are achieved in the generalized PB solver and generalized geometric flow solver. Note that all of the computations are performed on a SGI Altix 350 workstation with a 1.4 GHz Itanium processor and 4 GB memory. Additionally, we explore the improvement made to the generalized PB solver, the generalized geometric flow solver, and consequently to the total time cost. First, we combine an appropriate preconditioner with the iterative solver of the linear system. Additionally, we make use of the prior electrostatic potential as a first guess for the next PB run. Moreover, we obtain the approximations through the relaxation of the convergence criteria of the linear solver. Finally, we employ the ADI scheme to integrate the generalized geometric flow equation.
Table 6.
CPU time analysis from original schemes
| 2 atoms |
Gly |
|||
|---|---|---|---|---|
| Time(s) | % | Time(s) | % | |
| Total | 23.95 | 58.4 | ||
| GF | 4.95 | 21 | 11.31 | 19 |
| PB | 18.25 | 76 | 45.24 | 77 |
| Other | 0.75 | 3 | 2.03 | 4 |
First of all, we do the following improvement: Take the prior potential solution as the first guess of each run of the linear solver, then replace BiCG scheme with a combination of the preconditioner and the iterative solver (ILU/OM), while keeping other settings unchanged.
Table 7 gives the total computational costs of the generalized PB solver in the diatomic system as well as the total iteration numbers which are inside the parenthesis. The third column lists the time spending for original schemes, the fourth one makes use of prior potential as a first guess and the fifth one records the time spending from the usage of the preconditioner and the new first guess setting. It is seen that the gain of speedup is related to the size of system: The larger size is the system, the more acceleration is achieved. For a 127× 92× 92 system, combination of the above two implementations can obtain a speedup up to a factor of 4, while a single adjustment does not give much impressive improvement. It is also found that although the total iteration number reduces dramatically by adding the preconditioner, the total computational cost is reduced with a much smaller factor. The reason is that the PB solver with a preconditioner takes more time in each step.
Table 7.
Speedup from adjustment of initial guess and preconditioner in PB solver
| h | size | BiCG | BiCGi | ILU/OM | Speedup |
|---|---|---|---|---|---|
| 1 | 17× 12× 12 | 0.0557(252) | 0.0322(152) | 0.0371(50) | 1.50 |
| 0.5 | 32× 23× 23 | 0.775(419) | 0.467(248) | 0.420(82) | 1.85 |
| 0.25 | 64× 46× 46 | 17.676(841) | 10.410(490) | 6.947 (166) | 2.54 |
| 0.125 | 127× 92× 92 | 525.74(2771) | 263.11(1371) | 130.76 (410) | 4.02 |
Next, we study the impact of the convergence criteria to the electrostatic solvation free energy of the diatomic system. Table 8 summarizes the calculated electrostatic solvation free energies and total time cost of the PB solver under different convergence criteria. It indicates that 10−4 is good enough to deliver accurate results. In fact, 10−2 is still fine but 10−1 is clearly unacceptable. In this study, we take 10−4 as the convergence criteria of the linear system in the following calculations except specified. Because it is able to save much time compared to 10−6 while at the same time maintains the accuracy to a satisfied level. In practical application, one might use 10−2. A further reduction in computational time is possible if one sets the probe radius to rp = 0.25rvdW, where rvdW is the van der Waals radius.17
Table 8.
Influence of convergence criteria on electrostatic solvation free energy and computational time for the diatomic system
| Criteria | 10−8 | 10−6 | 10−4 | 10−3 | 10−2 | 10−1 |
|---|---|---|---|---|---|---|
| Energy (kcal/mol) | −231.17 | −231.17 | −231.19 | −231.28 | −231.07 | −239.80 |
| PB Time (s) | 10.44 | 6.95 | 4.17 | 3.09 | 2.05 | 0.90 |
Finally, we implement the ADI scheme in the generalized geometric flow solver. Thus we can use a much larger time increment than that used in an explicit scheme without the stability concern. For example, if grid spacing is h = 0.25, the time step size can be taken as large as 0.2 for the ADI scheme to be a good balance between accuracy and efficiency, while it has to be less than 0.02 in the explicit scheme. The acceleration of the generalized geometric flow solver can be found in Table 9, which is obtained by applying all of the speedup strategies we have discussed to the diatomic and Gly systems. This table shows all the time spending for major routines in the iterative process before and after the acceleration. It indicates that speedup in the PB solver can reach a factor of 4 or 5. However, the speedup in the total time is not as impressive as in the PB solver. It is about a factor of 3 in the Gly system and about a factor of 2 in the diatomic system. The reason is that the acceleration in the generalized geometric flow equation through the ADI can not have the same speedup factor as that of the PB solver. The electrostatic solvation free energies are also given in the table for a comparison before and after the speedup. Little difference in energies is observed due to varying schemes and the approximation.
Table 9.
Comparison of CPU time (s) in the iteration procedures with and without accelerations
| 2 atoms |
Gly |
|||||
|---|---|---|---|---|---|---|
| without accel. | with accel. | Speedup | without accel. | with accel. | Speedup | |
| Total | 23.95 | 8.87 | 2.70 | 58.40 | 16.28 | 3.59 |
| GF | 4.95 | 3.67 | 1.35 | 11.13 | 5.57 | 2.00 |
| PB | 18.25 | 4.45 | 4.10 | 45.24 | 8.71 | 5.19 |
| Other | 0.75 | 0.75 | 2.03 | 2.00 | ||
| Energy | −231.17 | −231.18 | −12.44 | −12.44 | ||
IV.F Impact of potentials in the geometric flow equation
The potential source terms in the generalized geometric flow equation include pressure, long-ranged attractive dispersion interaction and electrostatic potential. The solution (S) of the generalized geometric flow reflects a balance between the intrinsic geometric curvature effect and several external potentials at the equilibrium. In this section, we illustrate the impact of involved potentials to the characteristic function S, and consequently to the solvation free energy. Although in our model there is no explicit surface definition to be demonstrated, the impacts of these potentials can be reflected by volume, area and the electrostatic solvation free energy. In particular, if the flow is driven inward by a potential, the volume should become smaller, and an outward driving makes the volume larger. These are true at least during the early stage of the solvent-solute boundary evolution. In fact, they are not true for the system near the equilibrium. The present study is carried out through two proteins (PDB ID 1ajj and 1fca) from protein data bank (PDB). Their detailed coordinates and parameters are given in the application section of 22 proteins. Without any potential term, the mean curvature flow equation is driven purely by intrinsic geometric curvature effect, which leads to the minimal molecular surface (MMS).17 With the MMS as a reference, each time we use one additional potential term in Eq. (17) to produce a new characteristic function S which will be used in the PB solver to calculate the electrostatic potential. In other words, starting with the MMS, we attain the different characteristic functions S with either pressure, attractive non-polar potential, or electrostatic potential separately. Only when electrostatic potential term is taken into account, is it needed to run the self-consistent iteration process for the solution of the coupled system. Table 10 gives the calculated volume and electrostatic solvation free energy under each potential term. We also calculate the solvation free energy when all the potentials are turned on. It is seen that all the potentials involved here drive the flow inward so that there are more solvent components between or around two spherical solutes when just an individual potential is turned on. This is consistent with the experimental observations168 and our previous studies.14
Table 10.
Effects of potentials on the solvent-solute boundary
| 1ajj |
1fca |
|||
|---|---|---|---|---|
| Volume | Energy | Volume | Energy | |
| MMS | 6601.9 | −975.6 | 9345.7 | −1082.2 |
| Pressure | 6195.1 | −1032.1 | 8866.6 | −1123.2 |
| Attractive | 5533.8 | −1139.3 | 8107.2 | −1192.8 |
| Electrostatic | 6585.8 | −1061.4 | 9329.3 | −1112.4 |
| Total potential | 5381.6 | −1165.6 | 7886.8 | −1211.9 |
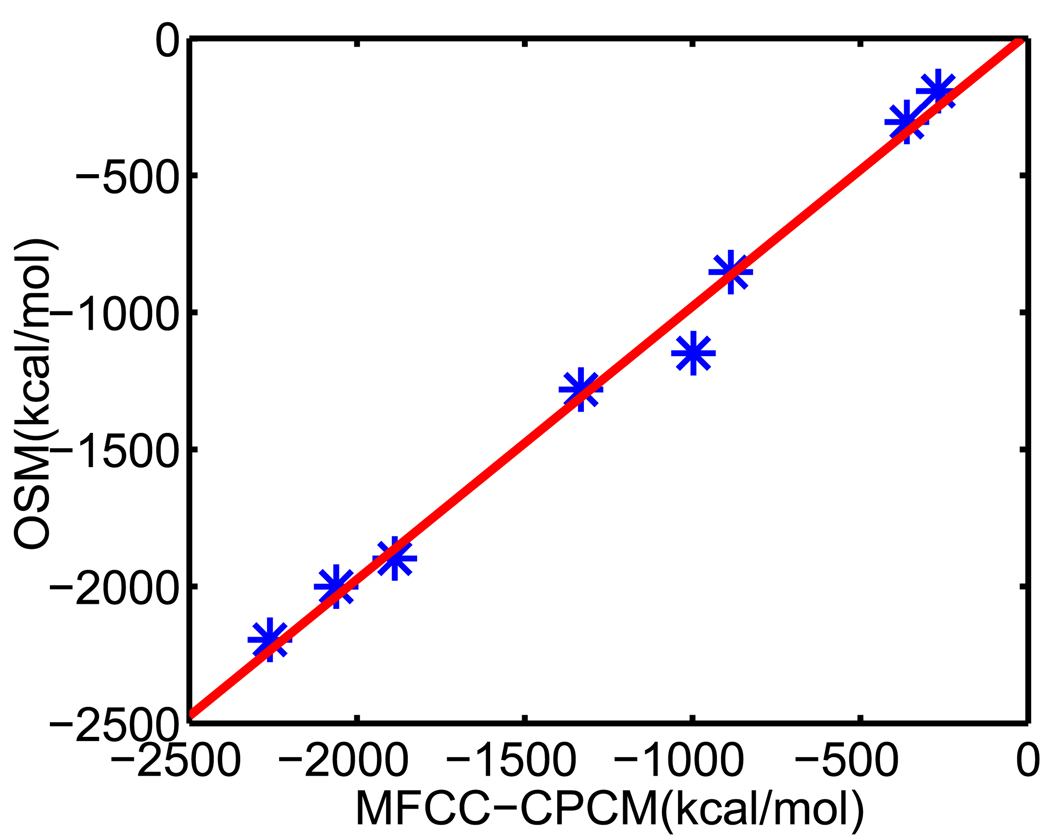
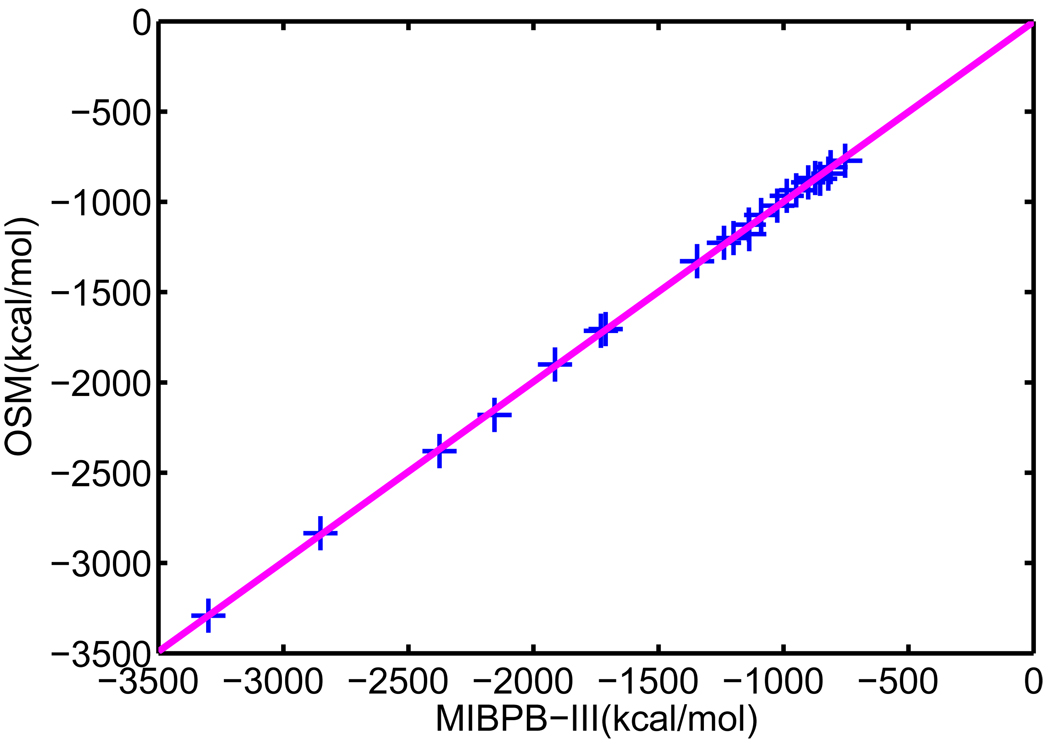
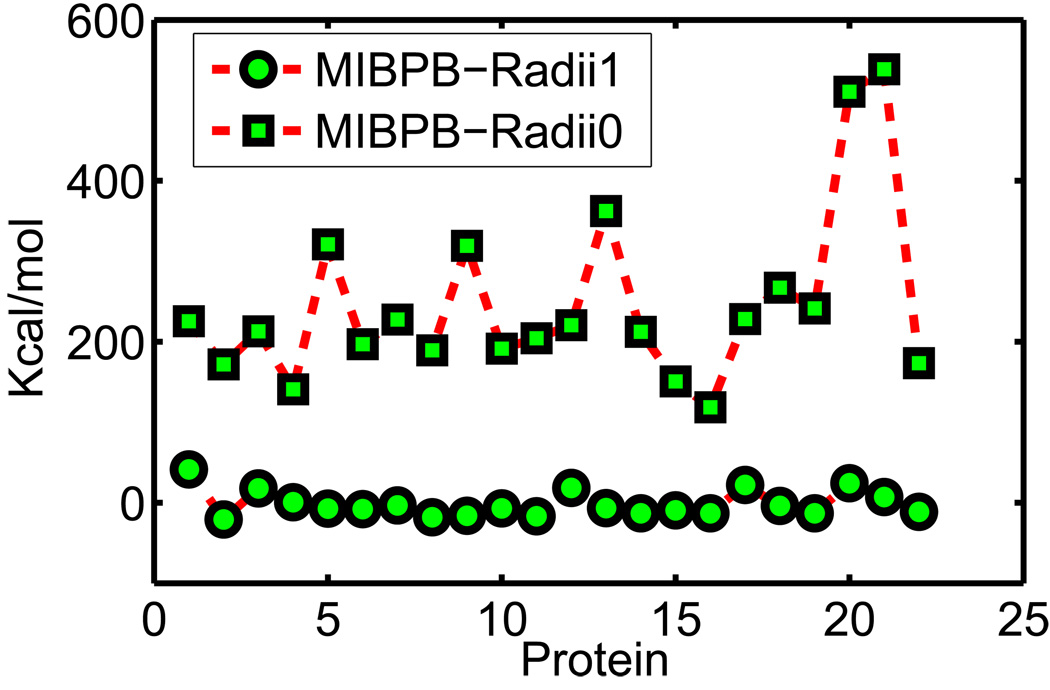
V Applications
We consider two types of problems in this section. First, we apply our new approach to a set of 17 small molecules. Then, some protein examples are studied. The Dirichlet boundary condition is used for both the generalized Poisson-Boltzmann equation and the generalized geometric flow equation as in our previous calculations17, 65, 179, 185
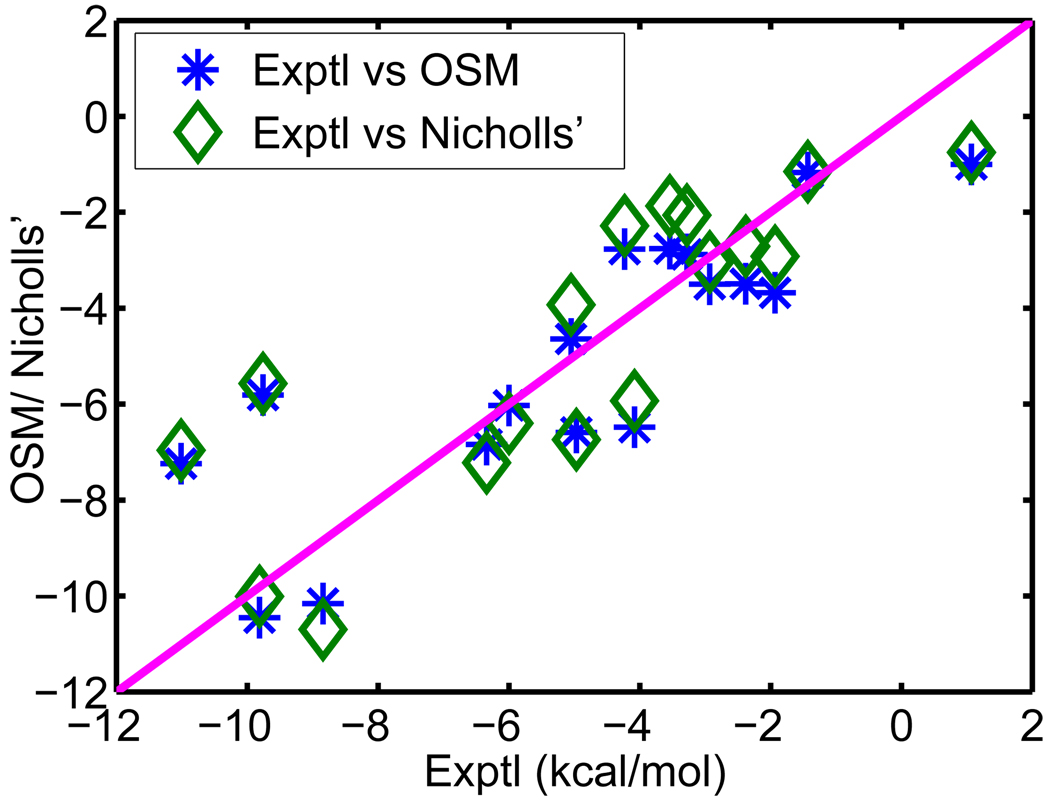
V.A Set of 17 test molecules
We apply our optimized surface model (OSM) of solvation to compute the solvation free energies of a set of 17 small compounds. This test set was studied by Nicholls et al113 using a number of approaches, including quantum mechanics, PB theory etc. An important aspect about this test set is that experimental data are available. Therefore, solvation free energies predicted from our new model can be compared with both experimental values and other numerical results. Moreover, these compounds are considered as a challenging test set for computational methods because the existence of polyfunctional or interacting polar groups, which lead to strong solvent-solute interactions.
In our calculation, we set the dielectric constants εm = 1 and εs = 80. We use γ as fitting parameter, and its initial value is set to γ = 1/15 kcal/(molÅ2) to compute other γ-dependent parameters, see Eq. (17). We choose ρ0/γ = 2 by comparing the bulk density 0.033Å−3 and the possible γ value. For micro-molecular systems, pressure p can be very small and sometimes is neglected in the calculation.32 But here we still take it into account and set p/γ to 0.2. Note that in the numerical simulation, all ratio parameters here are treated as dimensionless. For L-J parameters, σs is chosen to be 0.65Å as a good fitting solvent radius and σi is the solute atomic radii.167 Note that due to the continuum representation of solvent in our model, the 6–12 Lennard Jones potential formula (41) differs from the standard version — the distance used in our formula is no longer the distance between the centers of solute atoms and the centers of solvent atoms but the distance between a specific position in the solvent area and the centers of solute atoms. This should make the setting of well depth εi different from the ones taken from AMBER or OPLS force fields. However, the performance of the L-J potential should be similar, i.e, the value of the L-J potential in the solvent caused by a solute atom only depends on the distance from the center of the atom. It implies that the value of L-J potential caused by a solute atom should be a constant on the van der Waals surface of the atom. In other words, if r is on the vdW surface of the atom. Here the constant Di should have different values for various types of atoms. For simplicity we use a uniform constant D to determine the value of εi given σs and σi. In the present calculation, we pick 1.0 for D and the WCA expression is chosen as the attractive van der Waals potential. We choose grid spacing h = 0.25Å and time stepping τ = h2/4.5. Here, γ (kcal/(molÅ2)) serves as a fitting parameter, and its final value is 0.0065 kcal/(molÅ2).
Structure and charge information of the 17 compounds are adopted from those of Nicholls et al113 and can be obtained from the supporting information of their paper. In particular, charges are taken from the OpenEye-AM1-BCC v1 parameters.80 Atomic coordinates and radii are based on their new parametrization called ZAP-9 in which certain types of radii are adjusted by them from Bondi radii to improve the agreement with experimental free energy. With these structures and charges parameters, the root mean square error (RMS) obtained in their paper is 1.71± 0.05 kcal/mol via the explicit solvent model. And the smallest RMS error of their single - conformer Poisson-Boltzmann approach is 1.87±0.03 kcal/mol.113 Such a large RMS error indicates the challenge of this test set. Usually, different surface definitions in implicit solvent models should have their own optimal radii set. In particular, a continuous dielectric definition based model is supposed to have radii set with larger values than those of a discontinuous dielectric model. Otherwise, the calculated free energy does not give a good fitting to experimental data.152 This also occurs in the present model. Therefore, we multiply the radii from ZAP-9 by a common factor 1.1. It turns out this treatment leads to a good agreement with experimental data in terms of electrostatic solvation free energies and total solvation free energies. The results are summarized in Table 11, which gives a comparison between calculated and experimental values of solvation free energies of 17 compounds. RMS error of the present model is 1.76 kcal/mol which is similar to that of Nicholls et. al, i.e., 1.87 kcal/mol. This RMS error is competitive to that of the explicit solvent approach (1.71±0.05 kcal/mol) under the same charge and structure parameters set.113 This may be credited to the more satisfactory nonpolar terms and the enforcement of the potential driven geometric flow. Here, as expected, major errors are from the calculation of benzamides which are between 3.5 and 4.0 kcal/mol, see Fig. 5. Without these benzamide compounds, the RMS error drops from 1.76 kcal/mol to 1.24 kcal/mol. This problem with benzamides is likely due to radius adjustment for the carbonyl oxygens and tertiary nitrogens in ZAP 9 under the OpenEye-AM1-BCC v1 charges.113 In other words, these large errors from benzamides can not be avoided if both OpenEye-AM1-BCC v1 charge and corresponding optimized ZAP 9 radii are used in PB approaches. Based on these considerations, one possible approach for improvement is to create a new charge set more appropriate for the PB approach with the same ZAP radii. It may be realized by introducing quantum mechanical corrections to our model to take care of charge density. However, this aspect is out of the scope of the present paper and will be investigated in our future work.
Table 11.
Comparison of free energies (kcal/mol) for 17 compounds
| Compound | Gnp | ΔGp | ΔG | Exptl | Error |
|---|---|---|---|---|---|
| glycerol triacetate | 2.27 | −12.44 | −10.16 | −8.84 | −1.32 |
| benzyl bromide | 1.40 | −4.89 | −3.49 | −2.38 | −1.11 |
| benzyl chloride | 1.35 | −5.02 | −3.68 | −1.93 | −1.75 |
| m-bis(trifluoromethyl)benzene | 2.22 | −3.22 | −1.00 | 1.07 | −2.07 |
| N,N-dimethyl-p-methoxybenzamide | 1.96 | −9.20 | −7.24 | −11.01 | 3.77 |
| N,N-4-trimethylbenzamide | 1.86 | −7.67 | −5.81 | −9.76 | 3.95 |
| bis-2-chloroethyl ether | 1.45 | −4.22 | −2.77 | −4.23 | 1.46 |
| 1,1-diacetoxyethane | 1.65 | −8.24 | −6.59 | −4.97 | −1.62 |
| 1,1-diethoxyethane | 1.52 | −4.40 | −2.88 | −3.28 | 0.40 |
| 1,4-dioxane | 1.01 | −5.65 | −4.64 | −5.05 | 0.41 |
| diethyl propanedioate | 1.82 | −7.85 | −6.03 | −6.00 | −0.03 |
| dimethoxymethane | 1.03 | −4.52 | −3.50 | −2.93 | −0.57 |
| ethylene glycol diacetate | 1.59 | −8.43 | −6.84 | −6.34 | 0.50 |
| 1,2-diethoxyethane | 1.55 | −4.31 | −2.76 | −3.54 | 0.78 |
| diethyl sulfide | 1.22 | −2.39 | −1.17 | −1.43 | 0.26 |
| phenyl formate | 1.37 | −7.84 | −6.48 | −4.08 | −2.40 |
| imidazole | 0.82 | −11.27 | −10.45 | −9.81 | −0.64 |
Figure 5.
Correlation between experimental data and the present optimized surface model (OSM)(also results from Nicholls’) in electrostatic solvation free energies of 17 compounds.
V.B Solvation free energy of proteins
Validation by using a set of 17 molecules has shown that proposed differential geometry based solvation model works well for the energy prediction of small compounds. Since small molecules are accessible to more accurate computational means, such as quantum mechanical calculations, one of the main purposes of developing the present optimized surface model (OSM) is to attack relatively large macromolecules. To this end, we consider a test set of proteins employed by Mei et al.105 For this set, the total number of residues ranges from 21 to 275. The initial structures of all proteins are taken from the protein data bank (PDB). The hydrogen atoms, which are typically missing from the X-ray data, are added to the structures to obtain full all-atom models with optimized hydrogen bondings. Partial charges at atomic sites and atomic van der Waals radii in angstroms are assigned from the CHARMM27 force field.100 All of these operations, i.e, the transformation from PDB files to PQR files, can be easily done with a software PDB2PQR. Parameters of the present calculation are set in the same way as those for 17 compounds except for Nstep = 2. Similar to the treatment of the 17-compound set, the radii from the CHARMM force field need to be multiplied by a common factor of 1.1. Our results are summarized in Table 12.
Table 12.
Comparison of electrostatic solvation free energies (kcal/mol) obtained from the MFCC-CPCM, the present model (OSM) and MIBPB.
| ΔGp(kcal/mol) |
|||||
|---|---|---|---|---|---|
| Protein | PDBID | No.of residues | MIBPB-III | MFCC-CPCM105 | OSM |
| RP71955 | 1RPB | 21 | −184.68 | −267.60 | −192.23 |
| Amyloid | 1AMC | 28 | −861.65 | −886.01(−798.72) | −852.68 |
| Crambin | 1CBN | 46 | −303.80 | −361.52 | −304.84 |
| BPTI | 1BPI | 58 | −1301.9 | −1332.71(−1263.52) | −1281.19 |
| Calbindin | 1CDN | 75 | −2188.96 | −2259.62 | −2195.42 |
| Ubiquitin | 1UBQ | 76 | −1170.61 | −997.02 | −1148.81 |
| Lysozyme | 2BLX | 129 | −1913.40 | −1887.71 | −1898.07 |
| Subtilisin | 1SBT | 275 | −1896.5 | −2062.2 | −2001.4 |
For a comparison, The results of Mei et al are listed in Table 12 as well. Their results obtained from the molecular fractionation with conjugate caps and conductor-like polarizable continuum model (MFCC-CPCM). This is an approximate quantum approach that divides the macromolecule into fragments, such that the quantum calculations at HF/6-31 G level and B3LYP/6-31 G level can be applied. The solvation effect is estimated vis the polarizable continuum method with the classic molecular surface.105 It is seen from the table that there are relatively large deviations, up to 28%, between results obtained by the present OSM and those of the MFCC-CPCM. These derivations might due to the different methodologies, computational environments and structures. In fact, the results from two different quantum basis sets have up to 10% deviation for protein Amyloid. Another deviation between results of two quantum basis sets is about 5% for the protein BPTI.
As the largest deviation between the results from the proposed OSM and that of the MFCC-CPCM is quite large as shown in Fig. 6, we consider another independent approach, the MIBPB,65, 179, 185 to evaluate the present method. A specific MIBPB code, the MIBPB-III which has the treatment of geometric and charge singularities,65 is employed in our calculations. MIBPB-III has been intensively calibrated in the past and is the only known second accurate method for solving the Poisson-Boltzmann equation with both molecular surfaces and partial charges represented by the Dirac delta functions. To deliver such an accuracy, the MIBPB-III has built in the MIB scheme181, 187 and Dirichlet to Neumann mapping.65 Similar to the present approach, the structural data of MIBPB-III is also prepared with the PDB2PQR software. As such, we can eliminate the difference due to the different treatment of initial data. However, the MIPPB utilizes the classic PB equation and the molecular surface, while the present method has a generalized PB equation, and an optimized smooth surface. It is seen from Table 12 that solvation energy results from the present OSM and from the MIBPB have an excellent agreement on most proteins except for Subtilisin. For this protein, the difference of energies from two methods is about 5%.
Figure 6.
Correlation between the MFCC-CPSM105 and the present optimized surface model (OSM) in electrostatic solvation free energies of 8 proteins.
V.C Twenty two proteins
Encouraged by the good consistency of the proposed method and the MIBPB-III, we further compare these approaches by a larger set of protein molecules — twenty two proteins that have been frequently used in previous studies.14, 56, 65, 179 The implementation of these two methods is the same as that described in the last section.
Table 13 shows the results from the present continuous dielectric model, denoted as “Radii1” in the table, and those by MIBPB-III. It turns out that electrostatic solvation energies obtained via our minimization process are very close to those based on the MIBPB-III. This can also be seen through Fig. 7 which shows that the results between them are quite linearly correlated. The correlation coefficient is 0.999.
Table 13.
Electrostatic solvation free energies for 22 proteins
| ΔGp(kcal/mol) |
||||
|---|---|---|---|---|
| PDB-ID | No.of atoms | MIBPB-III | Radii1 | Radii0 |
| 1ajj | 519 | −1137.2 | −1178.5 | −1362.6 |
| 1bbl | 576 | −986.8 | −965.94 | −1158.7 |
| 1bor | 832 | −853.7 | −871.4 | −1066.5 |
| 1fca | 729 | −1200.1 | −1200.6 | −1340.9 |
| 1frd | 1478 | −2852.2 | −2844.8 | −3173.4 |
| 1fxd | 824 | −3299.8 | −3291.9 | −3496.9 |
| 1hpt | 858 | −811.6 | −808.2 | −1039.1 |
| 1mbg | 903 | −1346.1 | −1328.2 | −1535.4 |
| 1neq | 1187 | −1730.1 | −1713.9 | −2049.3 |
| 1ptq | 795 | −873.1 | −866.2 | −1064.5 |
| 1r69 | 997 | −1089.5 | −1072.7 | −1294.0 |
| 1sh1 | 702 | −753.3 | −771.8 | −973.8 |
| 1svr | 1435 | −1711.2 | −1704.6 | −2073.7 |
| 1uxc | 809 | −1138.7 | −1125.7 | −1350.9 |
| 1vii | 596 | −901.5 | −892.0 | −1052.1 |
| 2erl | 573 | −948.8 | −935.8 | −1067.3 |
| 2pde | 667 | −820.9 | −843.0 | −1049.3 |
| 451c | 1216 | −1024.6 | −1020.6 | −1291.8 |
| 1a2s | 1272 | −1913.5 | −1900.3 | −2155.0 |
| 1a7m | 2809 | −2155.5 | −2179.8 | −2666.1 |
| 1a63 | 2065 | −2373.5 | −2380.5 | −2912.0 |
| 1vjw | 828 | −1237.9 | −1226.6 | −1411.4 |
Figure 7.
Correlation between MIBPB-III and the present model (OSM) in electrostatic solvation free energies of 22 proteins
It is still interesting to understand how important it is to use a slightly enlarged radius in smooth surface models.152 To this end, we carry out the present calculations by using the original CHARMM22 van der Waals radii, denoted as “Radii0”. This result is also listed in Table 13. It is seen that results from the original CHARMM22 van der Waals radii can have over 20% deviations from those of “Radii1”. This helps to come to a conclusion that for continuous dielectric models, it is necessary to enlarge atomic radii obtained from widely used force fields. Otherwise, the results will be inconsistent with those of other analysis. This is in agreement with the observation in the literature.152 The necessity of using larger radii is also shown clearly in Fig 8 by the differences of electrostatic solvation free energies obtained from the MIBPB-III and the present calculations with original radii (Radii0) or enlarged radii (Radii1).
Figure 8.
Differences between electrostatic solvation free energies obtained from the MIBPB and the present model with original radii (Radii0) or enlarged radii (Radii1).
Additionally, it is useful to demonstrate that the electrostatic potential function computed in the present OSM can be illustrated at arbitrary isosurface of the characteristic function S. This is done by first computing a sharp surface at a given S value, then projecting the ϕ value on the isosurface of a given S value. Figure 9 shows three plots of the electrostatic potentials at S = 0.25, 0.5 and 0.75. A comparison of these potentials indicates the fast/slow electrostatic potential changing regions in the solvent-solute boundary. These regions are also interactive regions in the protein-protein or protein-ligand interactions.
Figure 9.
Surface potential display of one protein(PDBID: 1frd) at different isosurfaces
Finally, it remains an important issue to further improve the computational efficiency, although systematical efforts have been made in this work to reduce CPU cost. Since the coupled generalized PB and geometry flow equations are needed to evolve self-consistently to reach the steady state, it takes more CPU time for the present method to calculate the total free energy than some existing approaches that compute the polar and nonpolar energies separately.
VI Concluding remarks
This paper presents a novel differential geometry based solvation model. A crucial concept in the present model is the characteristic function or the description function of solute molecules which is one inside the solute domain and zero inside the solvent. Near the solvent-solute boundary, the characteristic function gradually changes from one to zero over a region of transition. The exact position and width of the transition region are determined by a variational framework, which is formulated based on the total solvation free energy. As a key ingredient of the present framework, the total energy encompasses coupled polar and nonpolar contributions. The polar solvation free energy functional is described by the electrostatic theory at equilibrium, while the nonpolar solvation free energy functional consists of surface energy, mechanical work and attractive solvent-solute interactions. Both the polar and nonpolar solvation free energies are coupled through the characteristic function S. This approach is similar in spirit to the works of Sharp and Honig,142 Gilson et al.,67 Dzubiella et al.49, 50 and some of our own work;15, 17 however, the present work is unique in its implementation of non-polar interactions and differential geometry based representation of continuum and discrete domains. The differential geometry aspects are built upon our geometric flow formulations and variational minimization of surface free energy.14, 15, 17, 172, 174, 175 In the present work, the characteristic function of the solute is naturally described by differential geometry theory of surfaces and manifolds. Geometric measure theory is utilized to convert the Lagrangian formulation of the surface into appropriate Eulerian formulation. By variation of the total solvation free energy functional with respect to the characteristic function and electrostatic potential, a generalized geometric flow equation for the electrostatic potential and a generalized Poisson-Boltzmann equation for the characteristic function are obtained. Unlike the standard Poisson-Boltzmann equation, the generalized Poisson-Boltzmann admits a smooth dielectric profile governed by the generalized geometric flow equation, which provides a physical description of the true solvent-solute dielectric boundary, according to the variational principle. The generalized geometric flow equation balances the intrinsic geometric curvature effect and external potential due to mechanical work, solvent-solute interactions, and the electrostatic potential. The solution of the generalized geometric flow equation and the generalized Poisson-Boltzmann equation leads to quantities for the direct evaluation of the solvation free energy.
Computational methods and algorithms are designed and developed for the solution of the generalized Poisson-Boltzmann equation and generalized geometric flow equations. Specifically, a second-order finite difference scheme is designed to solve the generalized Poisson-Boltzmann equation. The effect of the appropriate preconditioner to the basic Poisson-Boltzmann solver is explored. Both a simple-minded Euler method and an appropriate alternative direction implicit (ADI) scheme are constructed to solve the nonlinear generalized geometric flow equation. The ADI scheme allows a relatively large time stepping and provides better efficiency. Finally, two iterative approaches are designed and tested for the solution of the coupled Poisson-Boltzmann equation and the generalized geometric flow equation. All computational methods have been extensively validated.
Numerical applications of the present differential geometry based solvation paradigm are considered to a set of 17 small compounds and a set of proteins. The 17 small compounds consist of very different types of molecules, ranging from polar to nonpolar. The strong solvent-solute interactions are presented in many of these compounds. The present model takes a blind approach to these compounds, i.e., the same set of parameters are used for all the compounds without parameter fitting or adjustment according to an individual molecule. Our new model outperforms the standard Poisson-Boltzmann method and is compared well with the quantum mechanical method employed by Nicholls et al.113 To further demonstrate the utility and usefulness of the present differential geometry based solvation model, we considered a group of protein molecules in our study. Similar to the treatment of 17 small compounds, the same set parameters are applied to all the proteins to compute electrostatic free energies and/or solvation free energies. Results from present model compare well with those of quantum mechanical calculations based on the polarizable continuum method.105 The present predictions have also been compared with those obtained with the standard Poisson-Boltzmann theory utilizing sharp interfaces.65 Results from these two theories shown a very good consistency. However, our study on small compounds, particularly on the benzamide derivatives, indicates the need to refine the charge assignment for certain conjugated polar groups. Therefore, the incorporation of quantum mechanical description in the present theory is necessary. A differential geometry based multiscale solvation paradigm including continuum, discrete and quantum descriptions is under our consideration.
Acknowledgments
The authors thank Weitao Yang for useful discussions of solvation modeling. This work was supported in part by NSF grants DMS-0616704 and CCF-0936830, and NIH grants CA-127189 and R01 GM-090208. The work of Baker was supported by NIH R01 GM069702-01.
Literature cited
- 1.Abrams JB, Rosso L, Tuckerman ME. Efficient and precise solvation free energies via alchemical adiabatic molecular dynamics. The Journal of Chemical Physics. 2006;125(7):074115. doi: 10.1063/1.2232082. [DOI] [PubMed] [Google Scholar]
- 2.Amovilli C, Mennucci B. Self-consistent-field calculation of Pauli repulsion and dispersion contributions to the solvation free energy in the polarizable continuum model. Journal of Physical Chemistry B. 1997;101(6):1051–1057. [Google Scholar]
- 3.Antosiewicz J, McCammon JA, Gilson MK. The determinants of pKas in proteins. Biochemistry. 1996;35(24):7819–7833. doi: 10.1021/bi9601565. [DOI] [PubMed] [Google Scholar]
- 4.Ashbaugh HS. Convergence of molecular and macroscopic continuum descriptions of ion hydration. Journal of Physical Chemistry B. 2000;104(31):7235–7238. [Google Scholar]
- 5.Azuara C, Lindahl E, Koehl P, Orland H, Delarue M. PDB_Hydro: incorporating dipolar solvents with variable density in the Poisson-Boltzmann treatment of macromolecule electrostatics. Nucleic Acids Research. 2006;34:W38–W42. doi: 10.1093/nar/gkl072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Baker NA. Poisson-Boltzmann methods for biomolecular electrostatics. Methods in Enzymology. 2004;383:94–118. doi: 10.1016/S0076-6879(04)83005-2. [DOI] [PubMed] [Google Scholar]
- 7.Baker NA. Biomolecular applications of Poisson-Boltzmann methods. In: Lipkowitz KB, Larter R, Cundari TR, editors. Reviews in Computational Chemistry. volume 21. John Wiley and Sons: Hoboken, NJ; 2005. [Google Scholar]
- 8.Baker NA. Improving implicit solvent simulations: a Poisson-centric view. Current Opinion in Structural Biology. 2005;15(2):137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 9.Baker NA, Bashford D, Case DA. Implicit solvent electrostatics in biomolecular simulation. In: Leimkuhler B, Chipot C, Elber R, Laaksonen A, Mark A, Schlick T, Schutte C, Skeel R, editors. New Algorithms for Macromolecular Simulation. Springer: 2006. [Google Scholar]
- 10.Baker NA, McCammon JA. Electrostatic interactions. In: Bourne P, Weissig H, editors. Structural Bioinformatics. New York: John Wiley & Sons, Inc.; 2003. pp. 427–440. [Google Scholar]
- 11.Banavali NK, Im W, Roux B. Electrostatic free energy calculations using the generalized solvent boundary potential method. Journal of Chemical Physics. 2002;117(15):7381–7388. [Google Scholar]
- 12.Bashford D, Case DA. Generalized Born models of macromolecular solvation effects. Annual Review of Physical Chemistry. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 13.Bashford D, Karplus M. pKa’s of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 1990;29(44):10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 14.Bates PW, Chen Z, Sun YH, Wei GW, Zhao S. Geometric and potential driving formation and evolution of biomolecular surfaces. J. Math. Biol. 2009;59:193231. doi: 10.1007/s00285-008-0226-7. [DOI] [PubMed] [Google Scholar]
- 15.Bates PW, Wei GW, Zhao S. The minimal molecular surface. arXiv:q-bio/0610038v1. 2006 [q-bio.BM] [Google Scholar]
- 16.Bates PW, Wei GW, Zhao S. The minimal molecular surface. Midwest Quantitative Biology Conference; September 29 – October 1, 2006; Mission Point Resort, Mackinac Island, MI. [Google Scholar]
- 17.Bates PW, Wei GW, Zhao S. Minimal molecular surfaces and their applications. Journal of Computational Chemistry. 2008;29(3):380–391. doi: 10.1002/jcc.20796. [DOI] [PubMed] [Google Scholar]
- 18.Beglov D, Roux B. Solvation of complex molecules in a polar liquid: an integral equation theory. Journal of Chemical Physics. 1996;104(21):8678–8689. [Google Scholar]
- 19.Bergstrom CAS, Strafford M, Lazorova L, Avdeef A, Luthman K, Artursson P. Absorption classification of oral drugs based on molecular surface properties. Journal of Medicinal Chemistry. 2003;46(4):558–570. doi: 10.1021/jm020986i. [DOI] [PubMed] [Google Scholar]
- 20.Blomberg N, Gabdoulline RR, Nilges M, Wade RC. Classification of protein sequences by homology modeling and quantitative analysis of electrostatic similarity. Proteins. 1999;37(3):379–387. doi: 10.1002/(sici)1097-0134(19991115)37:3<379::aid-prot6>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
- 21.Blomgren P, Chan T. Color TV: total variation methods for restoration of vector-valued images. Image Processing, IEEE Transactions on. 1998;7(3):304–309. doi: 10.1109/83.661180. [DOI] [PubMed] [Google Scholar]
- 22.Boschitsch AH, Fenley MO. Hybrid boundary element and finite difference method for solving the nonlinear Poisson-Boltzmann equation. Journal of Computational Chemistry. 2004;25(7):935–955. doi: 10.1002/jcc.20000. [DOI] [PubMed] [Google Scholar]
- 23.Bostrom M, Tavares FW, Bratko D, Ninham BW. Specific ion effects in solutions of globular proteins: Comparison between analytical models and simulation. Journal of Physical Chemistry B. 2005;109(51):24489–24494. doi: 10.1021/jp0551869. [DOI] [PubMed] [Google Scholar]
- 24.Carstensen V, Kimmel R, Sapiro G. Geodesic active contours. International Journal of Computer Vision. 1997;22:61–79. [Google Scholar]
- 25.Cecil T. A numerical method for computing minimal surfaces in arbitrary dimension. Journal of Computational Physics. 2005;206(2):650–660. [Google Scholar]
- 26.Cerutti DS, Baker NA, McCammon JA. Solvent reaction field potential inside an uncharged globular protein: A bridge between implicit and explicit solvent models? The Journal of Chemical Physics. 2007;127(15):155101+. doi: 10.1063/1.2771171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen CJ, Saxena R, Wei GW. Differential geometry based multiscale models for virus formation and evolution. Int. J. Biomed. Imaging. 2009 in press. [Google Scholar]
- 28.Chen D, Chen Z, Geng WH, Wei GW. Mibpb: Asoftware package for electrostatic analysis. J. Comput. Chem. 2009 doi: 10.1002/jcc.21646. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen D, Wei GW, Cong X, Wang G. Computational methods for optical molecular imaging. Communications in Numerical Methods in Engineering. doi: 10.1002/cnm.1164. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen J, Brooks CL., III Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. Physical Chemistry Chemical Physics. 2008;10:471–481. doi: 10.1039/b714141f. [DOI] [PubMed] [Google Scholar]
- 31.Chen YG, Weeks JD. Local molecular field theory for effective attractions between like charged objects in systems with strong Coulomb interactions. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(20):7560–7565. doi: 10.1073/pnas.0600282103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cheng LT, Dzubiella J, McCammon AJ, Li B. Application of the level-set method to the implicit solvation of nonpolar molecules. Journal of Chemical Physics. 2007;127(8) doi: 10.1063/1.2757169. [DOI] [PubMed] [Google Scholar]
- 33.Cheng Y, Suen JK, Radi Z, Bond SD, Holst MJ, McCammon JA. Continuum simulations of acetylcholine diffusion with reaction-determined boundaries in neuromuscular junction models. Biophysical Chemistry. 2007;127(3):129–139. doi: 10.1016/j.bpc.2007.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cheng Y, Suen JK, Zhang D, Bond SD, Zhang Y, Song Y, Baker NA, Bajaj CL, Holst MJ, McCammon JA. Finite element analysis of the time-dependent Smoluchowski equation for acetylcholinesterase reaction rate calculations. Biophysical Journal. 2007;92(10):3397–3406. doi: 10.1529/biophysj.106.102533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chopp DL. Computing minimal surfaces via level set curvature flow. Journal of Computational Physics. 1993;106(1):77–91. [Google Scholar]
- 36.Chorny I, Dill KA, Jacobson MP. Surfaces affect ion pairing. Journal of Physical Chemistry B. 2005;109(50):24056–24060. doi: 10.1021/jp055043m. [DOI] [PubMed] [Google Scholar]
- 37.Chu VB, Bai Y, Lipfert J, Herschlag D, Doniach S. Evaluation of ion binding to DNA duplexes using a size-modified Poisson-Boltzmann theory. Biophysical Journal. 2007;93(9):3202–3209. doi: 10.1529/biophysj.106.099168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Crowley PB, Golovin A. Cation-pi interactions in protein-protein interfaces. Proteins: Structure, Function, and Bioinformatics. 2005;59(2):231–239. doi: 10.1002/prot.20417. [DOI] [PubMed] [Google Scholar]
- 39.David L, Luo R, Gilson MK. Comparison of generalized Born and Poisson models: Energetics and dynamics of HIV protease. Journal of Computational Chemistry. 2000;21(4):295–309. [Google Scholar]
- 40.Davis ME, Madura JD, Sines J, Luty BA, Allison SA, McCammon JA. Diffusion-controlled enzymatic reactions. Methods in Enzymology. 1991;202:473–497. doi: 10.1016/0076-6879(91)02024-4. [DOI] [PubMed] [Google Scholar]
- 41.Davis ME, McCammon JA. Electrostatics in biomolecular structure and dynamics. Chemical Reviews. 1990;94:509–521. [Google Scholar]
- 42.De Rienzo F, Gabdoulline RR, Menziani MC, De Benedetti PG, Wade RC. Electrostatic analysis and Brownian dynamics simulation of the association of plastocyanin and cytochrome F. Biophysical Journal. 2001;81(6):3090–3104. doi: 10.1016/S0006-3495(01)75947-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dominy BN, Brooks CL., III Development of a generalized Born model parameterization for proteins and nucleic acids. Journal of Physical Chemistry B. 1999;103(18):3765–3773. [Google Scholar]
- 44.Dong F, Olsen B, Baker NA. Computational methods for biomolecular electrostatics. Methods in Cell Biology. 2008;84:843–870. doi: 10.1016/S0091-679X(07)84026-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dong F, Vijaykumar M, Zhou HX. Comparison of calculation and experiment implicates significant electrostatic contributions to the binding stability of barnase and barstar. Biophysical Journal. 2003;85(1):49–60. doi: 10.1016/S0006-3495(03)74453-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dong F, Wagoner JA, Baker NA. Assessing the performance of implicit solvation models at a nucleic acid surface. Physical Chemistry Chemical Physics. 2008;10:4889–4902. doi: 10.1039/b807384h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dong F, Zhou HX. Electrostatic contribution to the binding stability of protein-protein complexes. Proteins. 2006;65(1):87–102. doi: 10.1002/prot.21070. [DOI] [PubMed] [Google Scholar]
- 48.Dragan AI, Read CM, Makeyeva EN, Milgotina EI, Churchill ME, Crane-Robinson C, Privalov PL. DNA binding and bending by HMG boxes: Energetic determinants of specificity. Journal of Molecular Biology. 2004;343(2):371–393. doi: 10.1016/j.jmb.2004.08.035. [DOI] [PubMed] [Google Scholar]
- 49.Dzubiella J, Swanson JMJ, McCammon JA. Coupling hydrophobicity, dispersion, and electrostatics in continuum solvent models. Physical Review Letters. 2006;96:087802. doi: 10.1103/PhysRevLett.96.087802. [DOI] [PubMed] [Google Scholar]
- 50.Dzubiella J, Swanson JMJ, McCammon JA. Coupling nonpolar and polar solvation free energies in implicit solvent models. Journal of Chemical Physics. 2006;124:084905. doi: 10.1063/1.2171192. [DOI] [PubMed] [Google Scholar]
- 51.Edinger SR, Cortis C, Shenkin PS, Friesner RA. Solvation free energies of peptides: Comparison of approximate continuum solvation models with accurate solution of the Poisson-Boltzmann equation. Journal of Physical Chemistry B. 1997;101(7):1190–1197. [Google Scholar]
- 52.Elcock AH, Gabdoulline RR, Wade RC, McCammon JA. Computer simulation of protein-protein association kinetics: Acetylcholinesterase-fasciculin. Journal of Molecular Biology. 1999;291(1):149–162. doi: 10.1006/jmbi.1999.2919. [DOI] [PubMed] [Google Scholar]
- 53.Federer H. Curvature Measures. Trans. Amer. Math. Soc. 1959;93:418–491. [Google Scholar]
- 54.Fedorov MV, Kornyshev AA. Unravelling the solvent response to neutral and charged solutes. Molecular Physics. 2007;105(1):1–16. [Google Scholar]
- 55.Feig M, I. Brooks CL. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr Opin Struct Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 56.Feig M, Onufriev A, Lee MS, Im W, Case DA, I. Brooks CL. Performance comparison of generalized Born and Poisson methods in the calculation of electrostatic solvation energies for protein structures. Journal of Computational Chemistry. 2004;25(2):265–284. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 57.Feng X, Prohl A. Analysis of a fully discrete finite element method for the phase field model and approximation of its sharp interface limits. Mathematics of Computation. 2004;73:541–567. [Google Scholar]
- 58.Fixman M. The Poisson-Boltzmann equation and its application to polyelectrolytes. Journal of Chemical Physics. 1979;70(11):4995–5005. [Google Scholar]
- 59.Fogolari F, Brigo A, Molinari H. The Poisson-Boltzmann equation for biomolecular electrostatics: a tool for structural biology. Journal of Molecular Recognition. 2002;15(6):377–392. doi: 10.1002/jmr.577. [DOI] [PubMed] [Google Scholar]
- 60.Forsman J. A simple correlation-corrected Poisson-Boltzmann theory. Journal of Physical Chemistry B. 2004;108(26):9236–9245. [Google Scholar]
- 61.Gabdoulline RR, Wade RC. Brownian dynamics simulation of protein-protein diffusional encounter. Methods-a Companion to Methods in Enzymology. 1998;14(3):329–341. doi: 10.1006/meth.1998.0588. [DOI] [PubMed] [Google Scholar]
- 62.Gallicchio E, Kubo MM, Levy RM. Enthalpy-entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation. Journal of Physical Chemistry B. 2000;104(26):6271–6285. [Google Scholar]
- 63.Gallicchio E, Levy RM. AGBNP: An analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. Journal of Computational Chemistry. 2004;25(4):479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 64.Gallicchio E, Zhang LY, Levy RM. The SGB/NP hydration free energy model based on the surface generalized Born solvent reaction field and novel nonpolar hydration free energy estimators. Journal of Computational Chemistry. 2002;23(5):517–529. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 65.Geng W, Yu S, Wei GW. Treatment of charge singularities in implicit solvent models. Journal of Physical Chemistry. 2007;127:114106. doi: 10.1063/1.2768064. [DOI] [PubMed] [Google Scholar]
- 66.Georgescu RE, Alexov EG, Gunner MR. Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins. Biophysical Journal. 2002;83(4):1731–1748. doi: 10.1016/S0006-3495(02)73940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gilson MK, Davis ME, Luty BA, McCammon JA. Computation of electrostatic forces on solvated molecules using the poisson-boltzmann equation. Journal of Physical Chemistry. 1993;97(14):3591–3600. [Google Scholar]
- 68.Gomes J, Faugeras OD. Using the vector distance functions to evolve manifolds of arbitrary codimension. Lecture Notes in Computer Science. 2001;2106:1–13. [Google Scholar]
- 69.Grant JA, Pickup BT, Nicholls A. A smooth permittivity function for Poisson-Boltzmann solvation methods. Journal of Computational Chemistry. 2001;22(6):608–640. [Google Scholar]
- 70.Grant JA, Pickup BT, Sykes MT, Kitchen CA, Nicholls A. The Gaussian Generalized Born model: application to small molecules. Physical Chemistry Chemical Physics. 2007;9:4913–4922. doi: 10.1039/b707574j. [DOI] [PubMed] [Google Scholar]
- 71.Grochowski P, Trylska J. Continuum molecular electrostatics, salt effects and counterion binding a review of the Poisson-Boltzmann theory and its modifications. Biopolymers. 2007;89(2):93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 72.Holm C, Kekicheff P, Podgornik R. Electrostatic effects in soft matter and biophysics; NATO Science Series. Boston: Kluwer Academic Publishers; 2001. [Google Scholar]
- 73.Holst MJ. Multilevel Methods for the Poisson-Boltzmann Equation. Urbana-Champaign: University of Illinois at Urbana-Champaign, Numerical Computing Group; 1993. [Google Scholar]
- 74.Honig B, Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268(5214):1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 75.Hori T, Takahashi H, Nakano M, Nitta T, Yang W. A qm/mm study combined with the theory of energy representation: Solvation free energies for anti/syn acetic acids in aqueous solution. Chemical Physics Letters. 2006;419(1–3):240–244. [Google Scholar]
- 76.Huang DM, Geissler PL, Chandler D. Scaling of hydrophobic solvation free energies. Journal of Physical Chemistry B. 2001;105(28):6704–6709. [Google Scholar]
- 77.Husowitz B, Talanquer V. Solvent density inhomogeneities and solvation free energies in supercritical diatomic fluids: A density functional approach. The Journal of Chemical Physics. 2007;126(5):054508. doi: 10.1063/1.2432327. [DOI] [PubMed] [Google Scholar]
- 78.Im W, Beglov D, Roux B. Continuum solvation model: electrostatic forces from numerical solutions to the Poisson-Boltzmann equation. Computer Physics Communications. 1998;111(1–3):59–75. [Google Scholar]
- 79.Jackson RM, Sternberg MJ. A continuum model for protein-protein interactions: Application to the docking problem. Journal of Molecular Biology. 1995;250(2):258–275. doi: 10.1006/jmbi.1995.0375. [DOI] [PubMed] [Google Scholar]
- 80.Jakalian A, Bush BL, Jack DB, Bayly CI. Fast, efficient generation of high-quality atomic charges. am1-bcc model: I. method. Journal of Computational Chemistry. 2000;21(2):132–146. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- 81.Jayaram B, Sprous D, Beveridge DL. Solvation free energy of biomacromolecules: Parameters for a modified generalized Born model consistent with the AMBER force field. Journal of Physical Chemistry B. 1998;102(47):9571–9576. [Google Scholar]
- 82.Koehl P. Electrostatics calculations: latest methodological advances. Current Opinion in Structural Biology. 2006;16(2):142–151. doi: 10.1016/j.sbi.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 83.Kuhn LA, Siani MA, Pique ME, Fisher CL, Getzoff ED, Tainer JA. The interdependence of protein surface topography and bound water molecules revealed by surface accessibility and fractal density measures. Journal of Molecular Biology. 1992;228(1):13–22. doi: 10.1016/0022-2836(92)90487-5. [DOI] [PubMed] [Google Scholar]
- 84.Lamm G. The Poisson-Boltzmann equation. In: Lipkowitz KB, Larter R, Cundari TR, editors. Reviews in Computational Chemistry. Hoboken, N.J.: John Wiley and Sons, Inc; 2003. pp. 147–366. [Google Scholar]
- 85.Lebard DN, Matyushov DV. Redox entropy of plastocyanin: Developing a microscopic view of mesoscopic polar solvation. The Journal of Chemical Physics. 2008;128(15):155106. doi: 10.1063/1.2904879. [DOI] [PubMed] [Google Scholar]
- 86.Lee B, Richards FM. The interpretation of protein structures: estimation of static accessibility. J Mol Biol. 1971;55(3):379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 87.Lee MS, Salsbury J, F. R., Olson MA. An efficient hybrid explicit/implicit solvent method for biomolecular simulations. Journal of Computational Chemistry. 2004;25(16):1967–1978. doi: 10.1002/jcc.20119. [DOI] [PubMed] [Google Scholar]
- 88.Lee TS, York DM, Yang W. The Journal of Chemical Physics. 1996;105(7):2744–2750. [Google Scholar]
- 89.Levy RM, Zhang LY, Gallicchio E, Felts AK. On the nonpolar hydration free energy of proteins: surface area and continuum solvent models for the solute-solvent interaction energy. Journal of the American Chemical Society. 2003;125(31):9523–9530. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 90.Li H, Robertson AD, Jensen JH. The determinants of carboxyl pKa values in turkey ovomucoid third domain. Proteins. 2004;55(3):689–704. doi: 10.1002/prot.20032. [DOI] [PubMed] [Google Scholar]
- 91.Li H, Robertson AD, Jensen JH. Very fast empirical prediction and rationalization of protein pka values. Proteins. 2005;61(4):704–721. doi: 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
- 92.Li J, Fisher CL, Chen JL, Bashford D, Noodleman L. Calculation of redox potentials and pKa values of hydrated transition metal cations by a combined density functional and continuum dielectric theory. Inorganic Chemistry. 1996;35(16):4694–4702. [Google Scholar]
- 93.Li Y, Santosa F. A computational algorithm for minimizing total variation in image restoration. IEEE Transactions on Image Processing. 1996;5(6):987–995. doi: 10.1109/83.503914. [DOI] [PubMed] [Google Scholar]
- 94.Licata VJ, Allewell NM. Functionally linked hydration changes in escherichia coli aspartate transcarbamylase and its catalytic subunit. Biochemistry. 1997;36(33):10161–10167. doi: 10.1021/bi970669r. [DOI] [PubMed] [Google Scholar]
- 95.Livesay DR, Jambeck P, Rojnuckarin A, Subramaniam S. Conservation of electrostatic properties within enzyme families and superfamilies. Biochemistry. 2003;42(12):3464–3473. doi: 10.1021/bi026918f. [DOI] [PubMed] [Google Scholar]
- 96.Livingstone JR, Spolar RS, J. Record MT. Contribution to the thermodynamics of protein folding from the reduction in water-accessible nonpolar surface area. Biochemistry. 1991;30(17):4237–4244. doi: 10.1021/bi00231a019. [DOI] [PubMed] [Google Scholar]
- 97.Lu Q, Luo R. A Poisson-Boltzmann dynamics method with nonperiodic boundary condition. Journal of Chemical Physics. 2003;119(21):11035–11047. [Google Scholar]
- 98.Luo R, David L, Gilson MK. Accelerated Poisson-Boltzmann calculations for static and dynamic systems. Journal of Computational Chemistry. 2002;23(13):1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 99.MacDermaid CM, Kaminski GA. Electrostatic polarization is crucial for reproducing pKa shifts of carboxylic residues in turkey ovomucoid third domain. Journal of Physical Chemistry B. 2007;111(30):9036–9044. doi: 10.1021/jp071284d. [DOI] [PubMed] [Google Scholar]
- 100.J. MacKerell AD, Bashford D, Bellot M, J Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, I. Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. Journal of Physical Chemistry B. 1998;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 101.Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz J, Gilson MK, Bagheri B, Scott LR, McCammon JA. Electrostatics and diffusion of molecules in solution - simulations with the University of Houston Brownian Dynamics program. Computer Physics Communications. 1995;91(1–3):57–95. [Google Scholar]
- 102.Marenich AV, Cramer CJ, Truhlar DG. Perspective on foundations of solvation modeling: The electrostatic contribution to the free energy of solvation. Journal of Chemical Theory and Computation. 2008;4(6):877–887. doi: 10.1021/ct800029c. [DOI] [PubMed] [Google Scholar]
- 103.Massova I, Kollman PA. Computational alanine scanning to probe protein-protein interactions: A novel approach to evaluate binding free energies. Journal of the American Chemical Society. 1999;121(36):8133–8143. [Google Scholar]
- 104.Matousek WM, Ciani B, Fitch CA, Garcia-Moreno BE, Kammerer RA, Alexandrescu AT. Electrostatic contributions to the stability of the GCN4 leucine zipper structure. Journal of Molecular Biology. 2007;374(1):206–219. doi: 10.1016/j.jmb.2007.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Mei Y, Ji CG, Zhang JZH. A new quantum method for electrostatic solvation energy of protein. J. Chem. Phys. 2006 doi: 10.1063/1.2345201. 094906. [DOI] [PubMed] [Google Scholar]
- 106.Mikula K, Sevcovic D. A direct method for solving an anisotropic mean curvature flow of plane curves with an external force. Mathematical Methods in the Applied Sciences. 2004;27(13):1545–1565. [Google Scholar]
- 107.Miller JL, Kollman PA. Solvation free energies of the nucleic acid bases. Journal of Physical Chemistry. 1996;100(20):8587–8594. [Google Scholar]
- 108.Mohan V, Davis ME, McCammon JA, Pettitt BM. Continuum model calculations of solvation free energies: accurate evaluation of electrostatic contributions. Journal of Physical Chemistry. 1992;96(15):6428–6431. [Google Scholar]
- 109.Mongan J, Simmerling C, McCammon JA, Case DA, Onufriev A. Generalized Born model with a simple, robust molecular volume correction. Journal of Chemical Theory and Computation. 2007;3(1):159–169. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Mu Y, Yang Y, Xu W. Hybrid hamiltonian replica exchange molecular dynamics simulation method employing the Poisson-Boltzmann model. Journal of Chemical Physics. 2007;127(8) doi: 10.1063/1.2772264. [DOI] [PubMed] [Google Scholar]
- 111.Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems. Communications on Pure and Applied Mathematics. 1989;42(5):577–685. [Google Scholar]
- 112.Netz RR, Orland H. Beyond Poisson-Boltzmann: Fluctuation effects and correlation functions. European Physical Journal E. 2000;1(2–3):203–214. [Google Scholar]
- 113.Nicholls A, Mobley DL, Guthrie PJ, Chodera JD, Pande VS. Predicting small-molecule solvation free energies: An informal blind test for computational chemistry. Journal of Medicinal Chemistry. 2008;51(4):769–779. doi: 10.1021/jm070549+. [DOI] [PubMed] [Google Scholar]
- 114.Nielsen JE, Andersen KV, Honig B, Hooft RWW, Klebe G, Vriend G, Wade RC. Improving macromolecular electrostatics calculations. Protein Engineering. 1999;12(8):657–662. doi: 10.1093/protein/12.8.657. [DOI] [PubMed] [Google Scholar]
- 115.Nielsen JE, Vriend G. Optimizing the hydrogen-bond network in Poisson-Boltzmann equation-based pK(a) calculations. Proteins. 2001;43(4):403–412. doi: 10.1002/prot.1053. [DOI] [PubMed] [Google Scholar]
- 116.Nina M, Im W, Roux B. Optimized atomic radii for protein continuum electrostatics solvation forces. Biophysical Chemistry. 1999;78(1–2):89–96. doi: 10.1016/s0301-4622(98)00236-1. [DOI] [PubMed] [Google Scholar]
- 117.Okur A, Wickstrom L, Layten M, Geney R, Song K, Hornak V, Simmerling C. Improved efficiency of replica exchange simulations through use of a hybrid explicit/implicit solvation model. Journal of Chemical Theory and Computation. 2006;2(2):420–433. doi: 10.1021/ct050196z. [DOI] [PubMed] [Google Scholar]
- 118.Onufriev A, Bashford D, Case DA. Modification of the generalized Born model suitable for macromolecules. Journal of Physical Chemistry B. 2000;104(15):3712–3720. [Google Scholar]
- 119.Onufriev A, Case DA, Bashford D. Effective Born radii in the generalized Born approximation: the importance of being perfect. Journal of Computational Chemistry. 2002;23(14):1297–1304. doi: 10.1002/jcc.10126. [DOI] [PubMed] [Google Scholar]
- 120.Osher S, Fedkiw RP. Level set methods: An overview and some recent results. Journal of Computational Physics. 2001;169(2):463–502. [Google Scholar]
- 121.Osher S, Rudin LI. Feature-oriented image enhancement using shock filters. SIAM Journal on Numerical Analysis. 1990;27(4):919–940. [Google Scholar]
- 122.Page CS, Bates PA. Can MM-PBSA calculations predict the specificities of protein kinase inhibitors? Journal of Computational Chemistry. 2006;27(16):1990–2007. doi: 10.1002/jcc.20534. [DOI] [PubMed] [Google Scholar]
- 123.Penfold R, Nordholm S, Jnsson B, Woodward CE. A simple analysis of ion-ion correlation in polyelectrolyte solutions. Journal of Chemical Physics. 1990;92(3):1915–1922. [Google Scholar]
- 124.Petrey D, Honig B. GRASP2: Visualization, surface properties, and electrostatics of macromolecular structures and sequences. Methods in Enzymology. 2003;374:492–509. doi: 10.1016/S0076-6879(03)74021-X. [DOI] [PubMed] [Google Scholar]
- 125.Ponder JW, Case DA. Force fields for protein simulations. Advances in Protein Chemistry. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- 126.Prabhu NV, Panda M, Yang QY, Sharp KA. Explicit ion, implicit water solvation for molecular dynamics of nucleic acids and highly charged molecules. J. Comput. Chem. 2008;29:1113–1130. doi: 10.1002/jcc.20874. [DOI] [PubMed] [Google Scholar]
- 127.Prabhu NV, Zhu P, Sharp KA. Implementation and testing of stable, fast implicit solvation in molecular dynamics using the smooth-permittivity finite difference Poisson-Boltzmann method. Journal of Computational Chemistry. 2004;25(16):2049–2064. doi: 10.1002/jcc.20138. [DOI] [PubMed] [Google Scholar]
- 128.Quina FH, Alonso EO, Farah JPS. Incorporation of nonionic solutes into aqueous micelles: a linear solvation free energy relationship analysis. Journal of Physical Chemistry. 1995;99:11708–11714. [Google Scholar]
- 129.Reddy MR, Singh UC, Erion MD. Ab initio quantum mechanics-based free energy perturbation method for calculating relative solvation free energies. Journal of Computational Chemistry. 2007;28(2):491–494. doi: 10.1002/jcc.20510. [DOI] [PubMed] [Google Scholar]
- 130.Richards FM. Areas, volumes, packing, and protein structure. Annual Review of Biophysics and Bioengineering. 1977;6(1):151–176. doi: 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
- 131.Roux B, Simonson T. Implicit solvent models. Biophysical Chemistry. 1999;78(1–2):1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 132.Rudin LI, Osher S, Fatemi E. Proceedings of the eleventh annual international conference of the Center for Nonlinear Studies on Experimental mathematics : computational issues in nonlinear science. Amsterdam, The Netherlands, The Netherlands: Elsevier North-Holland, Inc; 1992. Nonlinear total variation based noise removal algorithms; pp. 259–268. [Google Scholar]
- 133.Sapiro G, Ringach DL. Anisotropic diffusion of multivalued images with applications to color filtering. Image Processing, IEEE Transactions on. 1996;5(11):1582–1586. doi: 10.1109/83.541429. [DOI] [PubMed] [Google Scholar]
- 134.Sarti A, Malladi R, Sethian JA. Subjective surfaces: A geometric model for boundary completion. International Journal of Computer Vision. 2002;46(3):201–221. [Google Scholar]
- 135.Savelyev A, Papoian GA. Inter-DNA electrostatics from explicit solvent molecular dynamics simulations. Journal of the American Chemical Society. 2007;129(19):6060–6061. doi: 10.1021/ja070207t. [DOI] [PubMed] [Google Scholar]
- 136.Sbert C, Solé AF. 3d curves reconstruction based on deformable models. Journal of Mathematical Imaging and Vision. 2003;18(3):211–223. [Google Scholar]
- 137.Schaefer M, Karplus M. A comprehensive analytical treatment of continuum electrostatics. Journal of Physical Chemistry. 1996;100(5):1578–1599. [Google Scholar]
- 138.Sept D, Elcock AH, McCammon JA. Computer simulations of actin polymerization can explain the barbed-pointed end asymmetry. Journal of Molecular Biology. 1999;294(5):1181–1189. doi: 10.1006/jmbi.1999.3332. [DOI] [PubMed] [Google Scholar]
- 139.Sept D, McCammon JA. Thermodynamics and kinetics of actin filament nucleation. Biophysical Journal. 2001;81(2):667–674. doi: 10.1016/S0006-3495(01)75731-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Sethian JA. Evolution, implementation, and application of level set and fast marching methods for advancing fronts. Journal of Computational Physics. 2001;169(2):503–555. [Google Scholar]
- 141.Sham YY, Muegge I, Warshel A. The effect of protein relaxation on charge-charge interactions and dielectric constants of proteins. Biophysical Journal. 1998;74(4):1744–1753. doi: 10.1016/S0006-3495(98)77885-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Sharp KA, Honig B. Calculating total electrostatic energies with the nonlinear poisson-bottzmann equation. Journal of Physical Chemistry. 1990 [Google Scholar]
- 143.Simonson T. Macromolecular electrostatics: continuum models and their growing pains. Current Opinion in Structural Biology. 2001;11(2):243–252. doi: 10.1016/s0959-440x(00)00197-4. [DOI] [PubMed] [Google Scholar]
- 144.Simonson T. Electrostatics and dynamics of proteins. Reports on Progress in Physics. 2003;66(5):737–787. [Google Scholar]
- 145.Simonson T, Brunger AT. Solvation free energies estimated from macroscopic continuum theory: an accuracy assessment. Journal of Physical Chemistry. 1994;98(17):4683–4694. [Google Scholar]
- 146.Smereka P. Semi-implicit level set methods for curvature and surface diffusion motion. Journal of Scientific Computing. 2003;19(1):439–456. [Google Scholar]
- 147.Sochen N, Kimmel R, Malladi R. A general framework for low level vision. Image Processing, IEEE Transactions on. 1998;7(3):310–318. doi: 10.1109/83.661181. [DOI] [PubMed] [Google Scholar]
- 148.Song Y, Zhang Y, Bajaj CL, Baker NA. Continuum diffusion reaction rate calculations of wild-type and mutant mouse acetylcholinesterase: Adaptive finite element analysis. Biophysical Journal. 2004;87(3):1558–1566. doi: 10.1529/biophysj.104.041517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Song Y, Zhang Y, Shen T, Bajaj CL, McCammon JA, Baker NA. Finite element solution of the steady-state Smoluchowksi equation for rate constant calculations. Biophysical Journal. 2004;86(4):2017–2029. doi: 10.1016/S0006-3495(04)74263-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Spolar RS, Ha JH, J Record MT. Hydrophobic effect in protein folding and other noncovalent processes involving proteins. Proceedings of the National Academy of Sciences of the United States of America. 1989;86(21) doi: 10.1073/pnas.86.21.8382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Swanson JMJ, Henchman RH, McCammon JA. Revisiting free energy calculations: A theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophysical Journal. 2004;86(1):67–74. doi: 10.1016/S0006-3495(04)74084-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Swanson JMJ, Mongan J, McCammon JA. Limitations of atom-centered dielectric functions in implicit solvent models. Journal of Physical Chemistry B. 2005;109(31):14769–14772. doi: 10.1021/jp052883s. [DOI] [PubMed] [Google Scholar]
- 153.Takano Y, Houk KN. Benchmarking the conductor-like polarizable continuum model (cpcm) for aqueous solvation free energies of neutral and ionic organic molecules. Journal of Chemical Theory and Computation. 2005;1(1):70–77. doi: 10.1021/ct049977a. [DOI] [PubMed] [Google Scholar]
- 154.Tan C, Tan YH, Luo R. Implicit nonpolar solvent models. Journal of Physical Chemistry B. 2007 doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- 155.Tan C, Yang L, Luo R. How well does Poisson-Boltzmann implicit solvent agree with explicit solvent? A quantitative analysis. Journal of Physical Chemistry B. 2006;110(37):18680–18687. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 156.Tan JJ, Chen WZ, Wang CX. Investigating interactions between HIV-1 gp41 and inhibitors by molecular dynamics simulation and MM-PBSA/GBSA calculations. Journal of Molecular Structure: THEOCHEM. 2006;766(2–3):77–82. [Google Scholar]
- Tan ZJ, Chen SJ. Electrostatic correlations and fluctuations for ion binding to a finite length polyelectrolyte. Journal of Chemical Physics. 2005;122:044903. doi: 10.1063/1.1842059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Tanaka M, Grosberg AY. Giant charge inversion of a macroion due to multivalent counterions and monovalent coions: Molecular dynamics study. Journal of Chemical Physics. 2001;115(1):567–574. [Google Scholar]
- 159.Tang CL, Alexov E, Pyle AM, Honig B. Calculation of pKas in RNA: On the structural origins and functional roles of protonated nucleotides. Journal of Molecular Biology. 2007;366(5):1475–1496. doi: 10.1016/j.jmb.2006.12.001. [DOI] [PubMed] [Google Scholar]
- 160.Tawa GJ, Topol IA, Burt SK, Caldwell RA, Rashin AA. Calculation of the aqueous solvation free energy of the proton. The Journal of Chemical Physics. 1998;109(12):4852–4863. [Google Scholar]
- 161.Tjong H, Zhou HX. GBr6NL: A generalized Born method for accurately reproducing solvation energy of the nonlinear Poisson-Boltzmann equation. Journal of Chemical Physics. 2007;126:195102. doi: 10.1063/1.2735322. [DOI] [PubMed] [Google Scholar]
- 162.Tsui V, Case DA. Molecular dynamics simulations of nucleic acids with a generalized Born solvation model. Journal of the American Chemical Society. 2000;122(11):2489–2498. [Google Scholar]
- 163.Tsui V, Case DA. Calculations of the absolute free energies of binding between RNA and metal ions using molecular dynamics simulations and continuum electrostatics. Journal of Physical Chemistry B. 2001;105(45):11314–11325. [Google Scholar]
- 164.Vitalis A, Baker NA, McCammon JA. ISIM: A program for grand canonical Monte Carlo simulations of the ionic environment of biomolecules. Molecular Simulation. 2004;30(1):45–61. [Google Scholar]
- 165.Vitalis A, Pappu RV. ABSINTH: a new continuum solvation model for simulations of polypeptides in aqueous solutions. Journal of Computational Chemistry. doi: 10.1002/jcc.21005. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Wade RC, Gabdoulline RR, De Rienzo F. Protein interaction property similarity analysis. International Journal of Quantum Chemistry. 2001;83(3–4):122–127. [Google Scholar]
- 167.Wagoner JA, Baker NA. Assessing implicit models for nonpolar mean solvation forces: the importance of dispersion and volume terms. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(22):8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Wallquist A, Berne BJ. Computer-simulation of hydrophobic hydration forces stacked plates at short-range. Journal of Physical Chemistry. 1995;99:2893–2899. [Google Scholar]
- 169.Warshel A, Papazyan A. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Current Opinion in Structural Biology. 1998;8(2):211–217. doi: 10.1016/s0959-440x(98)80041-9. [DOI] [PubMed] [Google Scholar]
- 170.Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. Biochimica et Biophysica Acta (BBA) - Proteins & Proteomics. 2006;1764(11):1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]
- 171.Warwicker J, Watson HC. Calculation of the electric potential in the active site cleft due to alpha-helix dipoles. Journal of Molecular Biology. 1982;157(4):671–679. doi: 10.1016/0022-2836(82)90505-8. [DOI] [PubMed] [Google Scholar]
- 172.Wei GW. Generalized Perona-Malik equation for image restoration. IEEE Signal Processing Letters. 1999;6(7):165–167. [Google Scholar]
- 173.Wei GW. Differential geometry based multiscale models. Bulletin of Mathematical Biology. 2009:1–61. doi: 10.1007/s11538-010-9511-x. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Wei GW, Jia YQ. Synchronization-based image edge detection. Europhysics Letters. 2002;59(6):814. [Google Scholar]
- 175.Wei GW, Sun YH, Zhou YC, Feig M. Molecular multiresolution surfaces. arXiv:mathph/0511001v1. 2005:1–11. [Google Scholar]
- 176.Weinzinger P, Hannongbua S, Wolschann P. Molecular mechanics PBSA ligand binding energy and interaction of efavirenz derivatives with HIV-1 reverse transcriptase. Journal of Enzyme Inhibition and Medicinal Chemistry. 2005;20(2):129–134. doi: 10.1080/14756360400020520. [DOI] [PubMed] [Google Scholar]
- 177.Willmore TJ. Riemannian Geometry. Oxford University Press: USA; 1997. [Google Scholar]
- 178.Yang AS, Gunner MR, Sampogna R, Sharp K, Honig B. On the calculation of pK(a)s in proteins. Proteins-Structure Function and Genetics. 1993;15(3):252–265. doi: 10.1002/prot.340150304. [DOI] [PubMed] [Google Scholar]
- 179.Yu S, Geng W, Wei GW. Treatment of geometric singularities in implicit solvent models. Journal of Chemical Physics. 2007;126:244108. doi: 10.1063/1.2743020. [DOI] [PubMed] [Google Scholar]
- 180.Yu S, Wei GW. Three-dimensional matched interface and boundary (MIB) method for treating geometric singularities. Journal of Computational Physics. 2007;227:602–632. [Google Scholar]
- 181.Yu S, Zhou Y, Wei GW. Matched interface and boundary (MIB) method for elliptic problems with sharp-edged interfaces. Journal of Computational Physics. 2007;224(2):729–756. [Google Scholar]
- 182.Zhang D, Suen J, Zhang Y, Radic Z, Taylor P, Holst M, Bajaj C, Baker NA, McCammon JA. Tetrameric mouse acetylcholinesterase: Continuum diffusion rate calculations by solving the steady-state Smoluchowski equation using finite element methods. Biophysical Journal. 2005;88(3):1659–1665. doi: 10.1529/biophysj.104.053850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Zhang Y, Xu G, Bajaj C. Quality meshing of implicit solvation models of biomolecular structures. Computer Aided Geometric Design. 2006;23(6):510–530. doi: 10.1016/j.cagd.2006.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Zhao S, Wei GW. High-order FDTD methods via derivative matching for maxwell’s equations with material interfaces. Journal of Computational Physics. 2004;200(1):60–103. [Google Scholar]
- 185.Zhou YC, Feig M, Wei GW. Highly accurate biomolecular electrostatics in continuum dielectric environments. Journal of Computational Chemistry. 2008;29:87–97. doi: 10.1002/jcc.20769. [DOI] [PubMed] [Google Scholar]
- 186.Zhou YC, Wei GW. On the fictitious-domain and interpolation formulations of the matched interface and boundary (MIB) method. Journal of Computational Physics. 2006;219(1):228–246. [Google Scholar]
- 187.Zhou YC, Zhao S, Feig M, Wei GW. High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources. Journal of Computational Physics. 2006;213(1):1–30. [Google Scholar]
- 188.Zhu J, Alexov E, Honig B. Comparative study of generalized Born models: Born radii and peptide folding. Journal of Physical Chemistry B. 2005;109(7):3008–3022. doi: 10.1021/jp046307s. [DOI] [PubMed] [Google Scholar]