Radial Sampling for Fast NMR: Concepts and Practices over Three Decades

1. INTRODUCTION

For almost as long as three- and four-dimensional NMR experiments have been used, NMR spectroscopists have been devising ways to speed them up. Indeed, the publication that is often cited as the very first to demonstrate a 3-D NMR experiment commented, “it has been thought that…high-resolution 3-D NMR experiments are impracticable because of huge data matrices and long measurement times,” but went on to “suggest a technique for reduction of data matrices” using selective excitation pulses [1]. Although both spectrometers and computers have advanced considerably since this 1987 publication, somewhat changing the definitions of huge and long, the fundamental problem of measurement time continues to limit the experiments that can be carried out in practice using conventional multidimensional NMR methodology, and significant effort is still devoted to alleviating this restriction.

The problem arises from the very nature of Fourier transform (FT) NMR, which involves the systematic sampling of a signal over time followed by the calculation of the spectrum using the FT [2, 3]. Traditionally, an n-dimensional (n-D) experiment is obtained through the sampling of the time domain on a complete n-D Cartesian grid; since the number of points in an n-D grid grows exponentially with the number of dimensions n, the measurement time needed to record the experiment becomes considerable even for small n. Yet NMR spectra are generally only sparsely populated with signals, suggesting that there is no statistical need for so many observations (other than signal accumulation for sensitivity in some cases), and that a suitable alternative approach to sampling and/or processing might significantly reduce the time requirement, while generating the same or more spectral information. Two trends in biomolecular NMR research have given particular impetus to these efforts: the drive for increased throughput in studies of small proteins—for example in structural genomics—which requires running today’s routine experiments more quickly, and the increasing attention given to large and challenging systems, which require more dimensions and higher resolution than conventional experiments can offer.

A variety of methods have been introduced in these efforts to reduce the amount of data needed for multidimensional NMR, but a surprising number of them share in common that they sample the indirect dimensions of the time domain along radial spokes. The measurement of a radial spoke simply means collecting data samples along a line in the time domain that passes through the origin. If multiple radial spokes are sampled, the resulting dataset is equivalent to recording the NMR experiment in cylindrical coordinates or their higher-dimensional equivalent (cylindrical rather than spherical because the directly observed dimension is always sampled conventionally). The potential advantage of this arises from the fact that one can arrange the radial sampling points so as to obtain higher resolution information than with conventional Cartesian sampling, for the same or a smaller number of samples. Depending on the processing method used to extract spectral information from the data, this approach may lead to artifacts or ambiguities—but it also has the potential to provide complete spectral information in considerably less time than required for conventional NMR.

The purpose of this article is to review the long history of radial sampling in NMR, from its initial introduction in the “accordion spectroscopy” experiments, through reduced-dimensionality and G-matrix Fourier Transform (GFT) spectroscopy, and on to the projection spectroscopy and projection-reconstruction techniques. Because all of these methods share a common mathematical foundation—despite their sometimes differing vocabularies—we first explain these underlying concepts. We then continue with a chronological survey of the different approaches, describing how they were developed, how they work and how they have been put to use. Particular attention is given to how these methods can be used to reduce the measurement time of the experiment, including the theoretical basis for the time savings and the practical tradeoffs that can result.

It is important to note that while this review describes a number of techniques for reducing NMR measurement time, it does not attempt to describe the many methods that have been introduced recently for that purpose which do not use radial sampling. These include random sampling [4–11], concentric ring or shell sampling [12, 13] and other unconventional sampling approaches (e.g. spiral [14]); filter diagonalization analysis to extract high-resolution information from low-resolution conventionally sampled data [15–17]; the measurement of a spectrum in a single scan through the encoding of the spectroscopic frequency information spatially within the sample [18, 19]; Hadamard encoding to measure signal intensities at a small number of directly excited frequencies [20–22]; covariance spectroscopy, which enhances the resolution in the indirect dimensions through a statistical symmetrization with the directly observed dimension [23–26]; and the “minimal sampling” procedure, which involves calculating the possible correlations between the signals on the “first planes” of a multidimensional experiment and resolving any ambiguities by measuring a single additional sampling point [27, 28]. We touch on processing methods such as multidimensional decomposition [7, 29] and maximum entropy reconstruction [30] only to the limited extent that they have been applied to radial sampling experiments. Additionally, we do not discuss methods for reducing experiment time by optimizing the longitudinal relaxation rate to allow a much shorter interscan delay, which could be applicable to any type of sampling [31–34].

2. FUNDAMENTAL CONCEPTS

2.1. Signals and Sampling

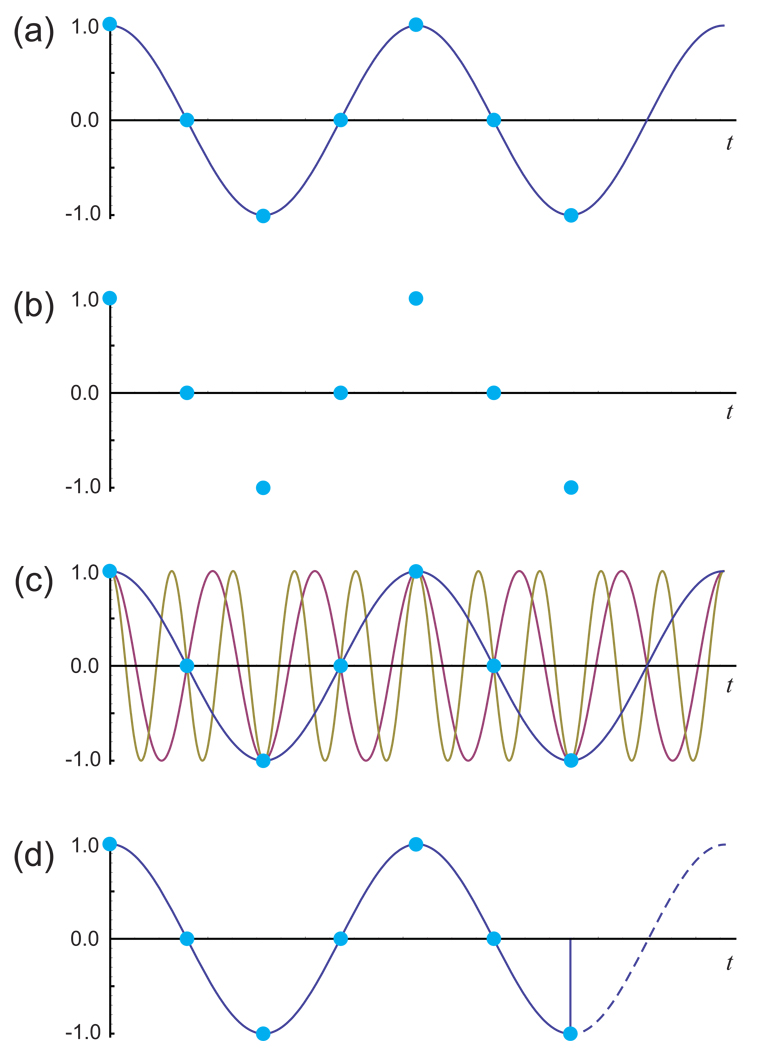
NMR signals are continuous, but they are known only through discrete sampling, meaning observation at specific times. Since the purpose of an NMR experiment is almost always to discover the frequencies, lineshapes and relative intensities of the signals as normally presented in the frequency domain spectrum, it is useful to consider how accurately and unambiguously this information can be obtained through the discrete sampling of a continuous signal. As a general rule, taking a limited number of measurements of an analog signal results in a loss of information [35]. For example, the most common approach to sampling, in NMR or otherwise, is to record a set of evenly spaced measurements during a finite period of time (Fig. 1a). One consequence of this is the loss of all information about what the signal does during the intervals between the samples. Given the sampling points alone (Fig. 1b) and no a priori information about the signal, one could infer an infinite number of signals at a variety of frequencies that would be equally consistent with the data (Fig. 1c); indeed, one cannot even definitively say that there is only one signal contributing to the data¹. The sampling process has introduced ambiguity about the signal frequencies. A second consequence of discrete sampling is the loss of all information about what happens to the signal after the end of the sampling period. It is unclear from the data whether the signal ends abruptly, decays slowly or continues forever (Fig. 1d), and one could infer infinitely many different frequency domain lineshapes for the signal that would be equally consistent with the known information. Again, the sampling process has introduced ambiguity, in this case about the lineshape.

Figure 1. Ambiguity from Discrete Sampling of a Continuous Signal.

(a) In NMR, a continuous sinusoidal signal (solid line) is normally measured as discrete samples (points). (b) The actual information available about the original signal after sampling is limited to the values at the sampling points, introducing two forms of ambiguity. (c) One form of ambiguity is the lack of information about what happens between sampling points. In the case of regularly spaced samples, as plotted here, an infinite number of sinusoidal signals of various frequencies can be considered to fit the data equally well. (d) The second form of ambiguity concerns what happens after the end of the sampling period. The data do not allow one to distinguish between a signal that stops abruptly and a signal that continues infinitely.

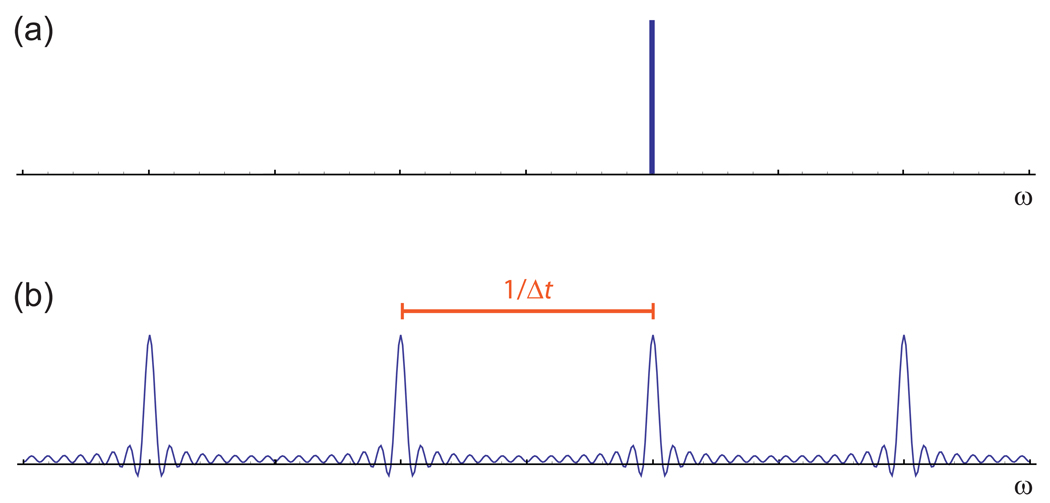
These ambiguities can be seen clearly in a comparison between the spectrum of the original continuous signal (Fig. 2a) and the spectrum of the samples alone² (Fig. 2b) [35, 36]. Two major effects are apparent when uniform discrete sampling is used. The first is a duplication of the continuous signal’s single peak at many different frequencies. The second is an alteration in the shape of the peak and its duplicates, such that each appears much broader than the line obtained from the continuous data and is accompanied by a series of small wiggles that disturb the neighboring baseline. The duplications of the peak at regular intervals in the spectrum can be interpreted as reflecting the set of infinitely many signals that fit the data equally well, owing to the gaps between samples; these aliases are prevented by sampling at a rate that equals or exceeds the Nyquist rate. The changes in the shape of the peaks reflect the truncation of the signal at the end of the sampling period. The broadening of the peak arises because of the inverse relationship between the duration of a signal and its linewidth, a fundamental form of mathematical uncertainty [35]. The wiggles represent the sharp discontinuity at the end of the sampling, which introduces low-level artifacts at many frequencies. These truncation artifacts are customarily eliminated through apodization [30].

Figure 2. Comparison of Spectra for Continuous and Sampled Signals.

(a) The spectrum of a continuous signal contains a single, infinitely sharp peak at the signal frequency. (b) The spectrum of the same signal sampled at regular intervals over a finite period of time shows both aliasing and truncation artifacts, reflecting the ambiguities of the sampling.

The phenomena of aliasing and truncation are thoroughly familiar to NMR spectroscopists, but we revisit them to point out an interpretation that will be useful in understanding the advantages and disadvantages of radial sampling. We describe them as ambiguities introduced by sampling because they can be shown to depend entirely on the sampling pattern, and on its ability to capture information about the continuous signals that may be present—and not on the signals themselves, or the Fourier transform calculation [3, 35, 37]. Most importantly, other sampling patterns would have different kinds of ambiguity, and would show different artifacts, and one can imagine that it might be possible to find patterns that collect the same information more efficiently.

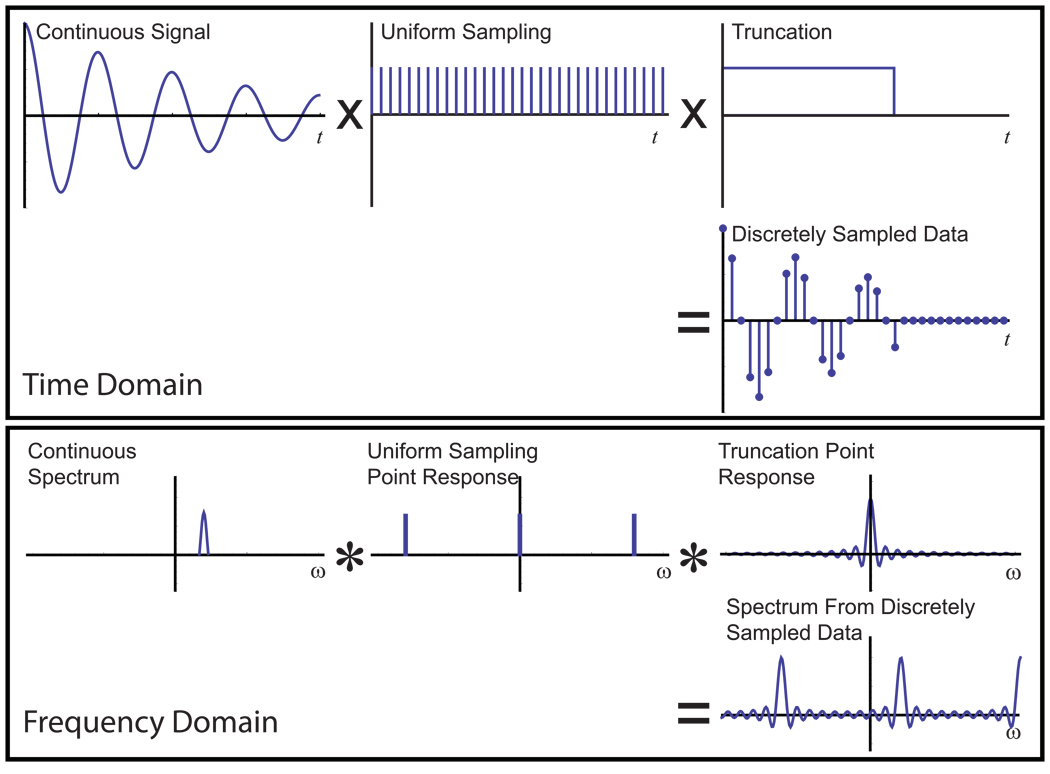
The consequences of sampling by any pattern can be found by calculating the spectrum of the sampling pattern alone, which is commonly called the point response [3, 35]. The point response can be determined by treating the sampling pattern as a function with a value of unity at each position measured, and zero otherwise, and computing the Fourier transform of this function. The term point response arises because it shows the frequency domain response that would be obtained if the sampling process were applied to the time domain signal corresponding to a single infinitely sharp peak, a point in the frequency domain; it is also called the point spread function, since discrete sampling has the inevitable consequence of spreading the energy of the point signal elsewhere in the spectrum. The convolution theorem explains how the point response can be applied to understand the effects of sampling in a particular case. If two functions are multiplied together in the time domain, the result in the frequency domain is their convolution, the intermingling of their lineshapes. Since sampling is equivalent to multiplying the continuous signal by the sampling function in order to obtain discrete data, the spectrum determined from a discretely sampled dataset is simply the convolution of the true spectrum with the point response. For conventional NMR sampling, one can decompose the process into the product of two sampling functions, one representing the even spacing (and in particular the gaps between points), and the other representing the finite duration of the data collection (Fig. 3). Since the final observed data is equivalent to multiplying the continuous signal with these two sampling functions in turn, the final observed spectrum will be simply the convolution of the true spectrum with the two point responses. The final spectrum shows both types of artifacts mixed together, but it is analytically equivalent to applying two separate sampling functions, each with independent artifact behavior, sequentially.

Figure 3. Point Responses, Convolution and Discrete Sampling.

The consequences of discretely sampling a continuous signal can be understood through the convolution theorem of the Fourier transform. In the time domain, the sampling process can be written mathematically as a multiplication of the continuous signal with functions describing the sampling—in this case, one function specifying evenly distributed samples, and a second function specifying the limited duration of the sampling interval. Each of these sampling functions has a Fourier transform, shown below, which is called its point response. According to the convolution theorem, the effects of sampling in the frequency domain are described by convolving (in the commonly-accepted convention of Bracewell, indicated by the operator “*”) the continuous spectrum with the point responses from the two sampling functions, yielding the discrete spectrum, with its aliasing and truncation artifacts.

The decomposition of discrete sampling and its effects into two separate processes, one pertaining to the arrangement of the sampling points and the other pertaining to the finite duration of the signals, highlights the fact that the two main types of sampling artifacts are very different in origin and implications, even though both reflect ambiguity about the signal frequencies due to a loss of information. Truncation and peak broadening will occur in exactly the same manner for any arrangement of sampling points that covers the same finite time period, and as long as the duration of the sampling is shorter than the duration of the signal³. Thus the only way to improve the resolution of a spectrum is to increase the portion of the time domain that is sampled, providing additional information that will reduce the uncertainty of the frequency estimation. By contrast, it is the particular arrangement of the points within the sampling window that leads to the generation of aliasing artifacts. For evenly spaced samples, there is an infinite set of equally possible frequencies for each signal, reflected in the complete duplication of the peak at regular intervals. A different sampling pattern, however, with a different principle for arranging the sampling points, would lead to a different kind of aliasing.

2.2. Radial NMR Sampling

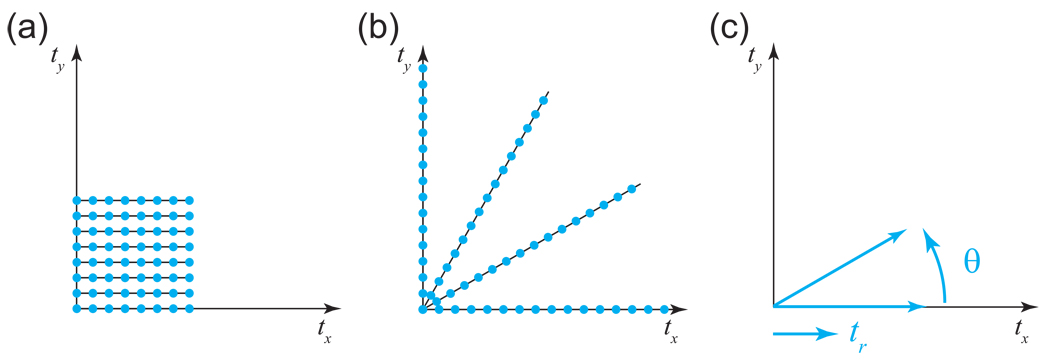
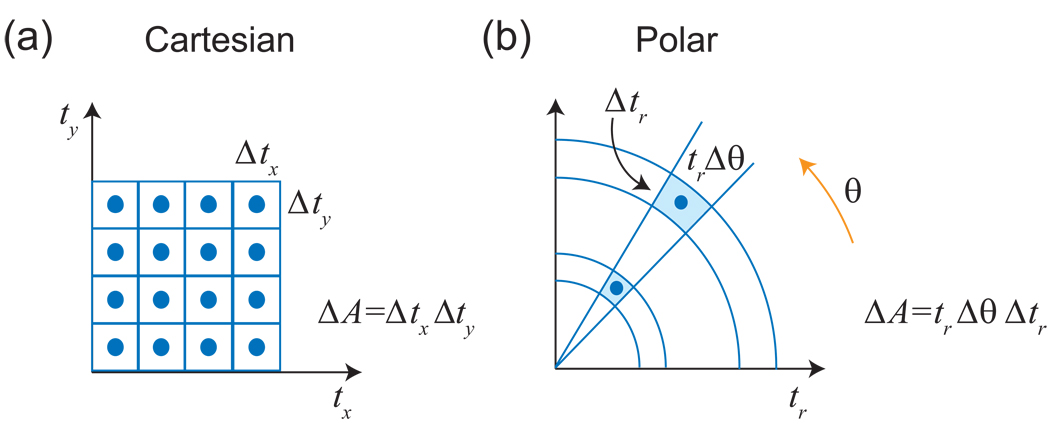
Since the evolution times for the indirect dimensions of a multidimensional NMR experiment can be set arbitrarily, it is possible to measure the multidimensional time domain signal at any point desired. Conventionally, however, the sampling times for multidimensional NMR experiments have been chosen such that the data points fall on an evenly spaced time domain grid (Fig. 4a) [3, 38]. The same principles apply to multidimensional grid sampling as for the uniform 1-D sampling just described; namely, one can see aliasing artifacts if the sampling rate in any dimension is too low, and one can see truncation artifacts if the finite sampling period in any dimension is shorter than the duration of the signal. These phenomena occur independently for each dimension, since the multidimensional grid pattern can be decomposed as the product of orthogonal 1-D uniform sampling patterns. The independence of the dimensions means, however, that the number of sampling points on a grid pattern grows exponentially as the resolution or dimensionality of the spectrum is increased. Unfortunately, many experiments that would be helpful or essential for particular projects are impractical due to such sampling requirements.

Figure 4. Comparison of Conventional and Radial Sampling.

(a) Conventionally, multidimensional NMR experiments have been sampled on regular grids. In this example, we depict an experiment with 8 × 8 = 64 sampling points. (b) In radial sampling, data are collected at evolution times falling on radial spokes. Because it is often possible to determine spectral information from a small number of radial spokes, each of those spokes can be measured to longer evolution times than for a conventional experiment of the same duration. Here, we show a radial experiment with four spokes each of 16 points; the number of samples and resulting measurement time are the same as in (a), but the resolution has been doubled. (c) Radial sampling is in fact a sampling in polar coordinates.

The alternative that we describe in this review is to sample the multidimensional time domain along radial spokes (Fig. 4b), or in other words, in polar coordinates (Fig. 4c). Collecting such data is straightforward: the same pulse sequence can be used, but with a different set of evolution times for the indirect dimensions⁴. As will be demonstrated below, the potential advantage of radial sampling is that it is possible in many cases to determine the signal properties accurately from a small number of radial spokes in a small number of directions. If such sampling is sufficient, one can afford to include more data points on each spoke for the same total measurement time. This means that a larger area of the time domain is covered by the sampling pattern, and the longer evolution times result in a higher resolution spectrum than one would obtain from conventional sampling with the same number of samples (Fig. 4a/b).

In the sections below, we analyze radial sampling in detail. We begin by examining the information content of a single radial spoke, and go on to consider the information in sets of radial spokes taken together, and the issues that arise in trying to determine signal properties from radial data. Of particular importance in addressing these topics is the connection between radial spokes and projections, which we develop in the next section. As we go along, we will pay particular attention to ambiguity caused by sampling, building up an understanding of how aliasing manifests itself in a radial context. Lastly, we present the point response of the radial sampling pattern, and consider how it can illuminate the differences between radial and conventional sampling, and how it can explain when and why radial sampling can be useful.

2.3. Slices and Projections

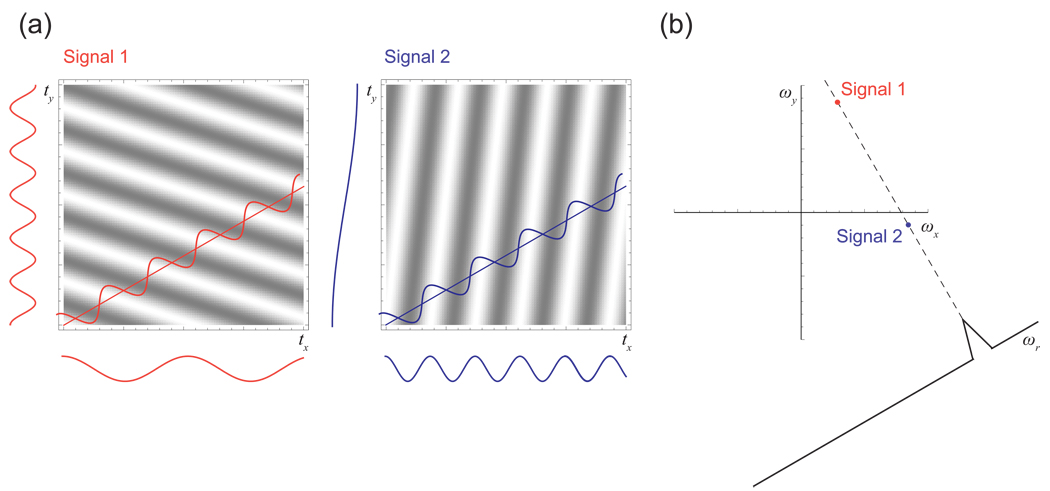
Consider a 2-D experiment containing several signals. If we let x and y refer to the two dimensions⁵, each signal consists of a 2-D wave formed as the product of a 1-D wave along the x time axis and a 1-D wave along the y time axis; the full time domain is the sum of these 2-D waves. Conventional 2-D grid sampling and a conventional fast Fourier transform (FFT) would yield a 2-D spectrum containing peaks positioned according to the frequencies of the 2-D waves with respect to the two axes.

Now consider a line of evenly spaced sampling points measured along the t_x axis of the 2-D time domain. These sampling points would capture information about the x components of all the 2-D signals, but would fail to capture information about the y components, since they cannot “see” any effect from the y modulation. If a 1-D spectrum were computed from this line of samples, it would contain a peak for each of the signals, and the peak positions would be dependent only on the x frequencies. This 1-D spectrum would be a projection of the full 2-D spectrum, effectively collapsing the y dimension to a single line. One might be inclined to make a visual analogy and think of this projection as the silhouette of the 2-D spectrum when sighted down the y axis—but this would not be quite correct, since the projection is actually the integral along the y direction. If two of the 2-D signals shared the same x frequency but different y frequencies and were in phase, from the standpoint of the line of x samples they would appear as a single x wave with a magnitude equal to the sum of the intensities of the two signals. Thus in the spectrum they would appear as a single peak with an intensity equal to the sum of the intensities of the two peaks in the 2-D spectrum—and this is, in fact, the integral with respect to the y dimension.

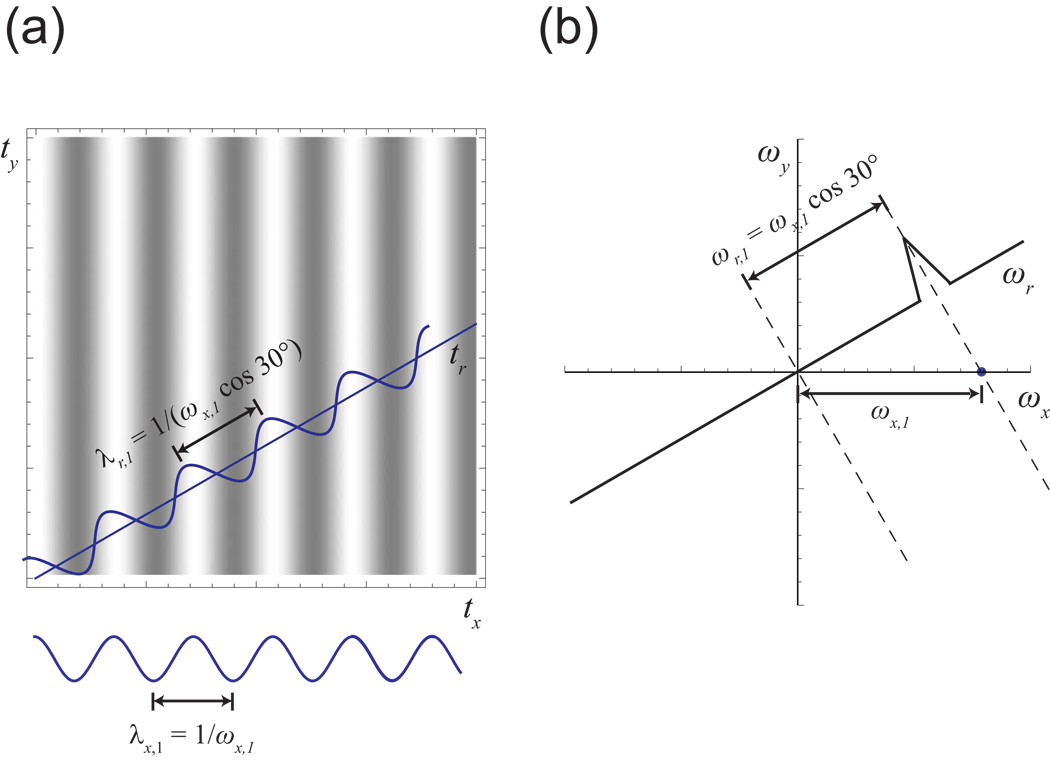
NMR spectroscopists are familiar with this principle from recording the “first planes” of a multidimensional experiment, but what may be less obvious is that the same principle applies to any straight line of sampling points, regardless of their direction. Consider, for example, a line of sampling points crossing the 2-D time domain at a 30° angle with respect to x (Fig. 5). This is effectively a 1-D experiment at a 30° angle with respect to x and a 150° angle with respect to y. It is sensitive to the component of the 2-D signal along the 30° vector (a linear combination of the x and y modulations), and it is insensitive to the component of the 2-D signal along the orthogonal vector with angle 30° + 90° = 120° (a different linear combination of the x and y modulations). From the perspective of this 1-D tilted experiment, signals with identical modulation along the 30° vector cannot be distinguished and would overlap, regardless of their modulation with respect to the 120° vector. Upon computation of the FT, the result is the projection of the signals onto the 30° vector, collapsing the unsampled 120° modulation.

Figure 5. The Projection-Slice Theorem.

The projection-slice theorem of the Fourier transform states that a slice through the time domain yields, upon Fourier transformation, a projection in the frequency domain. (a) Measuring slices at a 30° angle through two different multidimensional sinusoidal signals. The frequency observed on such a slice is a linear combination of the signal’s original x and y frequencies, with coefficients depending on the angle of the slice. Note that two signals with very different x and y frequencies can happen to appear identically on a slice, as shown here. (b) The Fourier transform of such a slice shows a projection of the original spectrum. In this example, the two signals coproject at the chosen angle.

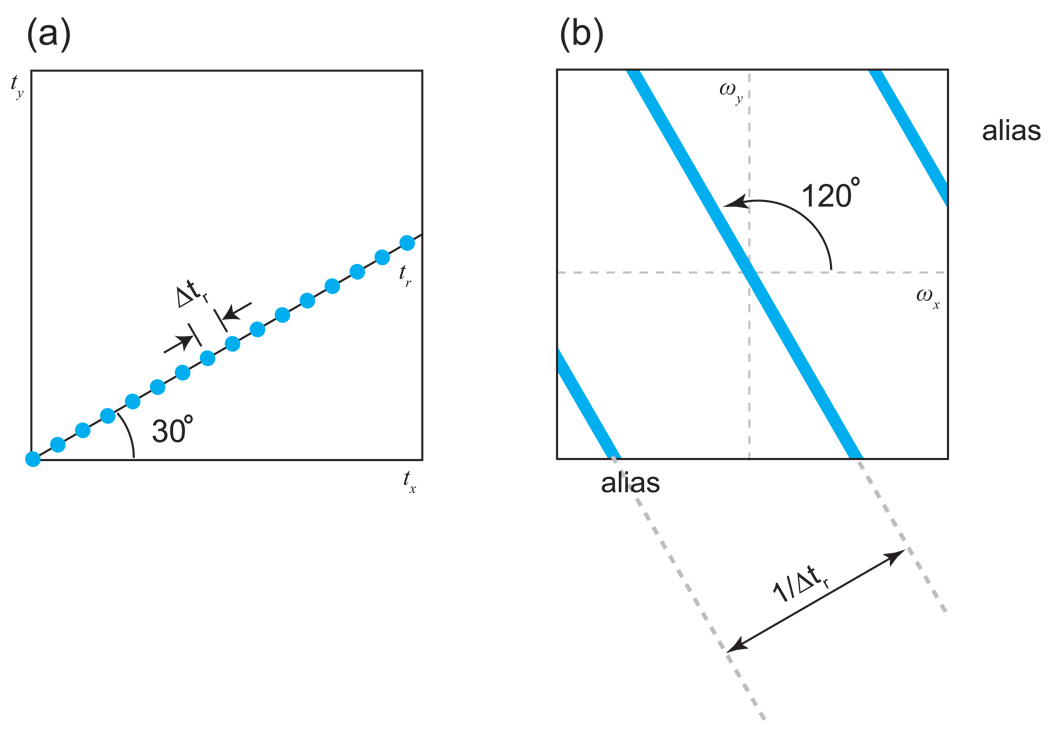
This result, which is well known from many fields and was first described in NMR by Nagayama et al. [39], is commonly referred to as the projection-slice theorem, and can be stated succinctly: The Fourier transform of a cross-section through the time domain yields a projection at the same angle in the frequency domain. The measurement of a projection reduces the dimensionality of an experiment, eliminating all information about the behavior of the signals in the direction perpendicular to the line of sampling. While a tilted projection can capture some information about multiple dimensions simultaneously, it cannot capture complete information about them, since it is insensitive to orthogonal modulation⁶. The ambiguity inherent in the sampling of a multidimensional time domain by a single spoke can be appreciated from the point response of the spoke, shown in Fig. 6 for the 2-D case described above [37]. The main feature of the point response is a ridge running perpendicular to the line of the sampling, reflecting the total lack of information about the signals for this particular direction.

Figure 6. The Point Response of a Single Radial Spoke.

(a) A radial spoke at an angle of 30°, sampled uniformly at an interval of Δt_r. (b) The point response for the radial spoke. A ridge of intensity is observed in the frequency domain passing through the origin and running perpendicular to the direction of the radial spoke, reflecting the complete lack of information about the modulation of the signal in the 120° direction. Additional ridges are observed with a spacing of 1/Δt_r; these are aliases, resulting from the discrete sampling of the spoke.

The projection coordinate for each peak on a projection is a linear combination of its ω_x and ω_y coordinates, since the frequency of the modulation in the projection direction is a linear combination of the x and y frequencies of each signal. To be explicit for the example above, a peak at (ω_x, ω_y) would appear on the 30° projection at a position ω_r = ω_x cos 30° + ω_y sin 30°. An alternative way to write this that generalizes readily to higher dimensions is to use direction cosines, the cosines of the angles between the projection vector and each of the coordinate axes. Thus the formula in the example becomes ω_r = ω_x cos 30° + ω_y cos 60°, and the general formula is ω_r = Σ ω_i cos θ_i, where ω_i is the frequency in dimension i and θ_i is the angle between the projection and axis i.

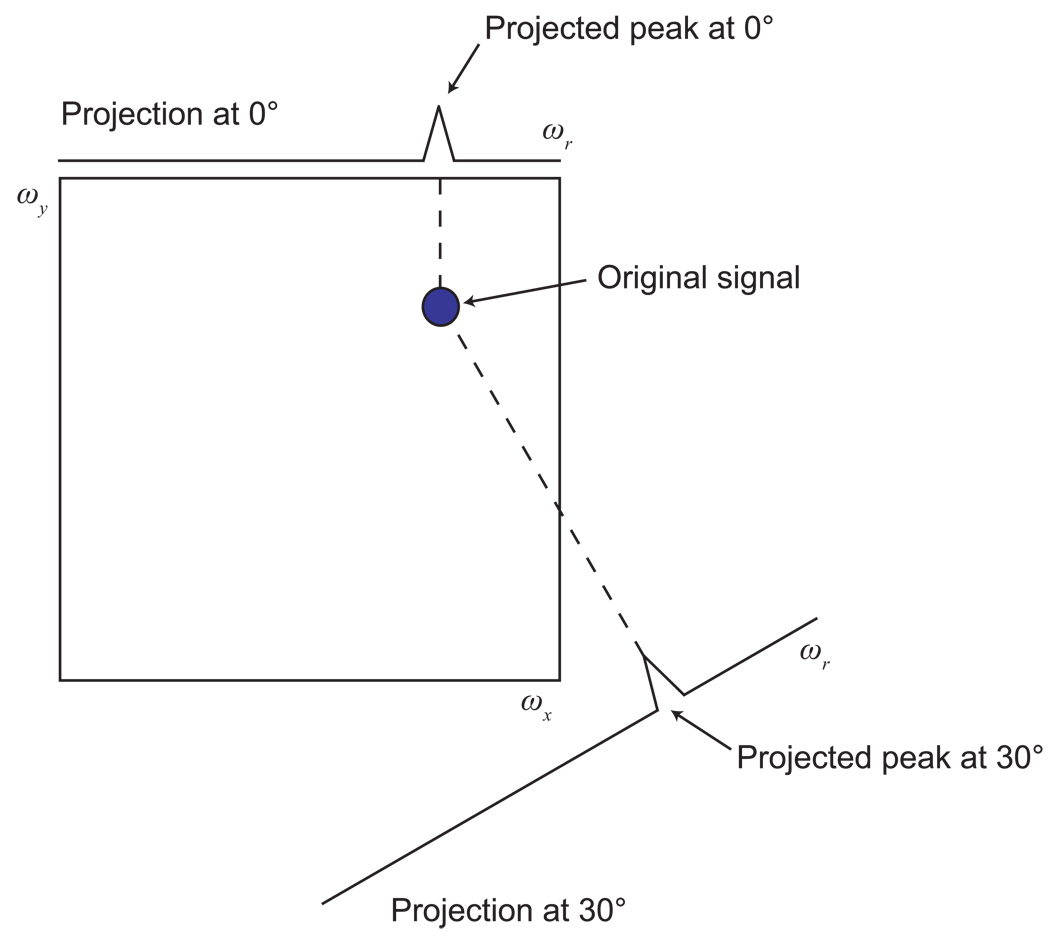
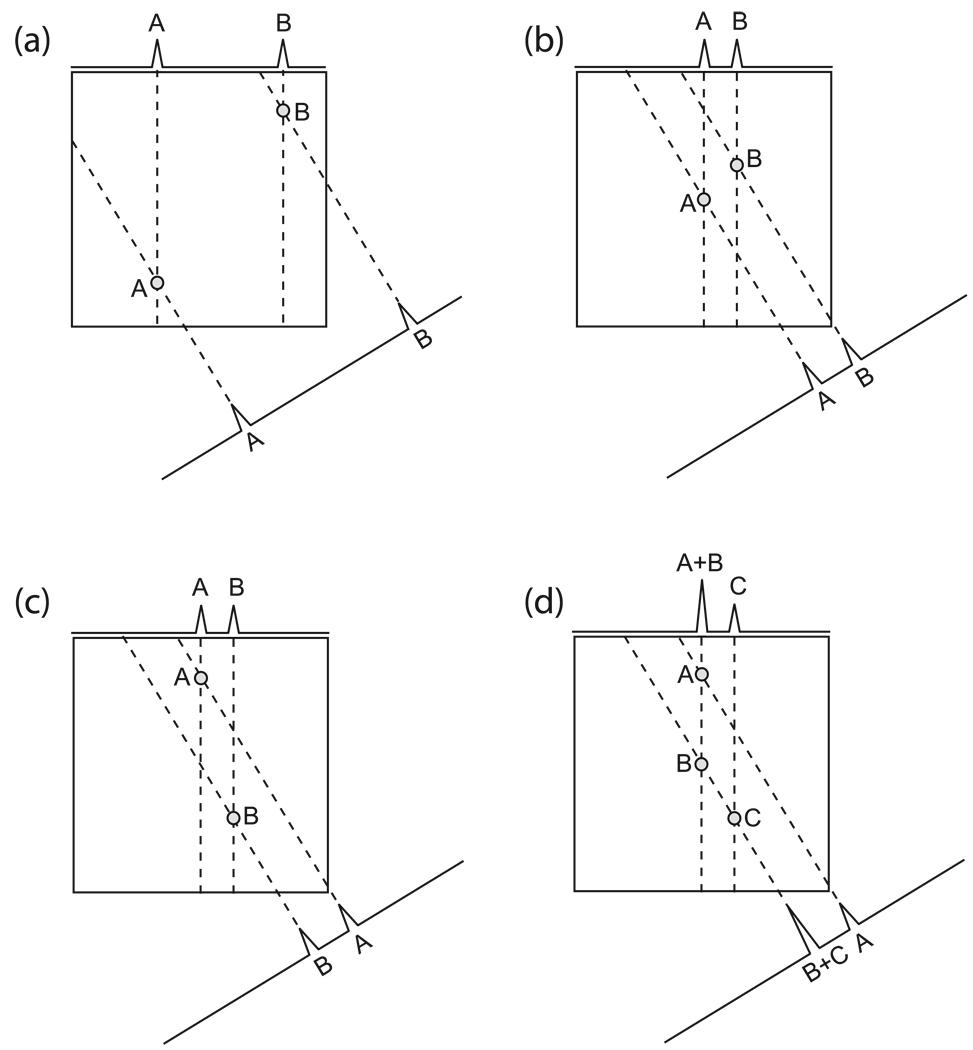
The potential benefit of measuring projections comes not from measuring a single projection, but rather from measuring sets of projections in different directions. While each projection has limited information, projections in different directions provide different information about the multidimensional experiment, which one might imagine could be combined to deduce the full spectral information. In fact, in the most favorable cases, only a very small number of projections is needed for such a deduction—for a single peak in a 2-D spectrum, for example, only two projections are needed to position the peak correctly in the 2-D space by visual inspection alone (Fig. 7). As for radial sampling more generally, the advantage in measurement time for projection experiments versus complete grid sampling arises because a small number of projections can be collected at very high resolution with considerably fewer total sampling points than would be needed for conventional sampling at the same resolution (cf. Fig. 4). Unfortunately, the problem of deriving peak information from projections is not consistently so trivial as in Fig. 7, but we shall see that there are a variety of methods that are able to accomplish it, depending on the situation.

Figure 7. Identification of a Multidimensional Signal Position from Projections.

Given a set of projections of a multidimensional signal, it is often possible to determine the position of the signal in the full spectrum. In this example, by extending lines back from each projected peak, one finds a single intersection point, which must be the location of the original signal. This geometric logic has been exploited in a number of approaches: explicitly for reconstruction, as well as implicitly in calculations done directly from projected peak positions.

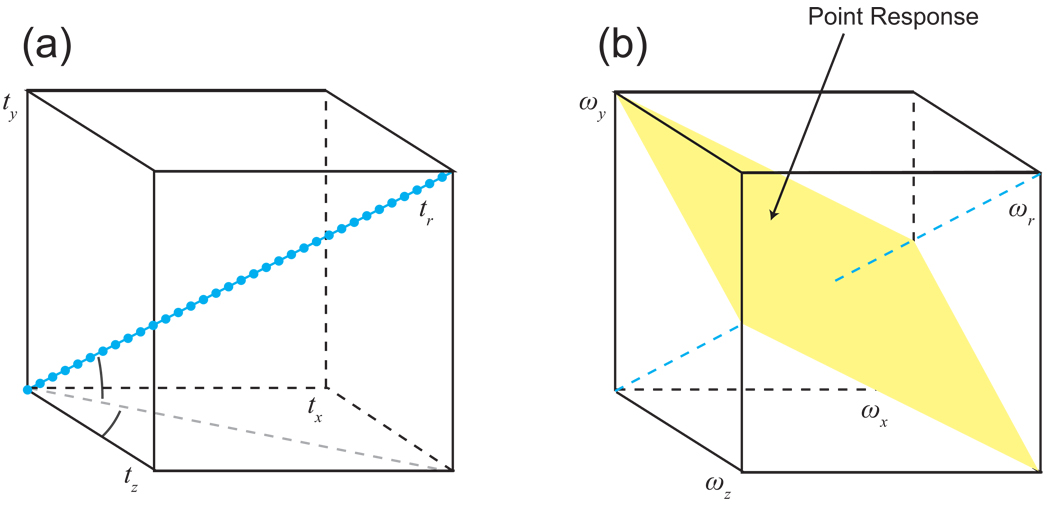
Although the example was given for a 1-D projection of a 2-D spectrum, the same basic principle applies for higher dimensionalities. Thus a line of sampling points passing through a 3-D time domain yields a two-fold reduction in dimensionality for that specific projection, projecting the 3-D spectrum down to a 1-D vector. As reflected in the point response (Fig. 8), the sampling is sensitive to modulation in the same direction as the sampling vector, and insensitive to modulation in the directions defined by a plane perpendicular to that vector. By comparison, a 2-D plane of samples from a 3-D space will be sensitive to modulation parallel to that plane, and insensitive to modulation that is perpendicular; its point response is thus a line. Note finally that in practice, NMR experiments always have a directly observed dimension, meaning that a projection will always have at least two dimensions, one directly observed conventional axis and one indirectly observed projection axis. Likewise, the parent multidimensional experiment will always have at least three dimensions, one directly observed and at least two that are coevolved to produce the radial sampling. Thus the sampling is best described as cylindrical or hypercylindrical rather than polar.

Figure 8. Radial Spokes and Projections in a 3-D Space.

(a) A radial spoke t_r can be measured in a time domain with three indirect dimensions t_x, t_y and t_z. (b) The resulting point response shows a plane of intensity, perpendicular to the sampling direction, reflecting the complete lack of information about the location of the signal within this planar region.

A multidimensional function and its complete set of projections in all directions are related by an integral transform called the Radon transform [40–42]. Since each point on a projection is nothing more than an integral of a region of the multidimensional function, the forward Radon transform generates projections from the starting function by simple integration in all directions. The inversion of the Radon transform is called tomography, and is mathematically more complicated, as discussed below. The forward Radon transform literally describes how projections are obtained in a number of other fields that work with projections, such as CT scanning in medical imaging, where the imaging process involves physical integration (absorption of X-rays in the patient) to yield a projection [42]. In NMR there is no physical Radon transform, as the projections are obtained from radial sampling in the time domain and Fourier transformation—but the result is equivalent, and the same considerations apply for inversion. The inverse Radon transform will thus be our starting point for addressing reconstruction from projections.

Note that in the direction(s) sampled by a radial spoke, the use of evenly spaced points behaves like any other sampling by evenly spaced points, introducing the same kinds of ambiguity and therefore the same aliasing and truncation artifacts (cf. Fig. 6). To prevent aliasing, the sampling rate along the spoke must be set to meet the Nyquist criterion for the component of the signals in the sampling direction; since this is a linear combination of the frequencies on the orthogonal axes, the required spectral width of the spoke may be greater than for the independently acquired orthogonals, corresponding to a closer spacing of the time domain samples [43–45]. As always in NMR, the resolution of the projection is determined by the maximum evolution time, and truncation artifacts may result if the signals are cut off abruptly.

2.4. Comodulation and Splitting: An Alternative Interpretation of Radial Sampling

There is a second common interpretation for what appears in the Fourier transform of a radial spoke, besides that it is a projection at a specific angle. This second interpretation is built on an explicit consideration of how the orthogonal 1-D signals (for example, the x and y signals above) combine to form the sampled data values. Since the multidimensional signal is a product of these 1-D signals, the result in the frequency domain is a convolution. One can thus understand the contents of a projection in terms of the convolution of the original signals. This interpretation is of great importance, as it formed the basis for the development of the reduced dimensionality and GFT experimental approaches (see Sections 3.2 and 3.3).

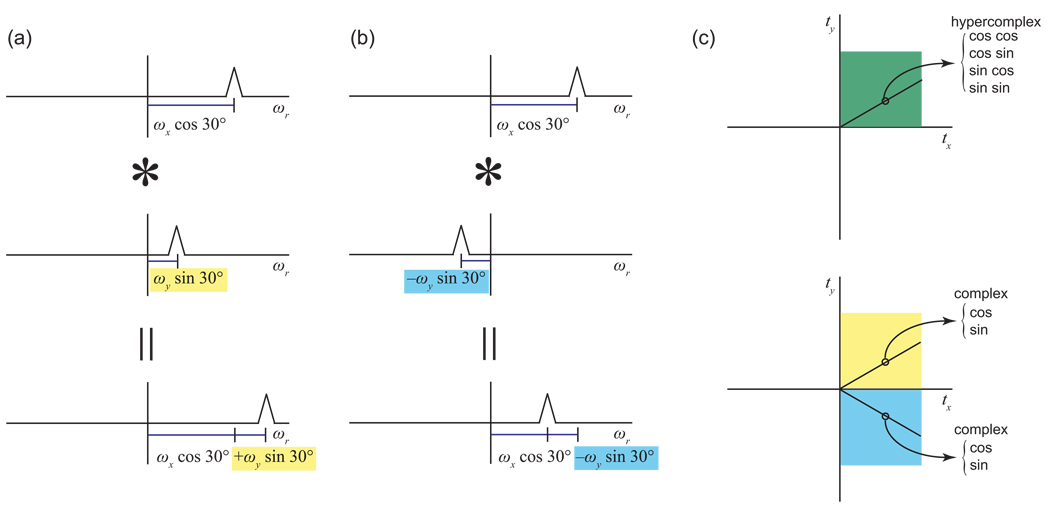
Consider again the example of a 2-D time domain, and a vector of samples from that time domain taken at a 30° angle from the x axis. As illustrated in Fig. 9a, from the perspective of these samples, the x modulation would appear to be expanded by the factor of 1/(cos 30°). The Fourier transform of this expanded modulation would show the same peak as for the original x signal, except with the frequency scaled by the factor cos 30° (Fig. 9b). Likewise, in these samples the y modulation would appear as if it were expanded by the factor 1/(sin 30°), and the Fourier transform would show the y peak with its frequency scaled by sin 30°. The actual observed data are the product of the scaled x signal and the scaled y signal; by the convolution theorem, the result in the frequency domain is the convolution of the scaled x peak and the scaled y peak (Fig. 10a). This spectrum would contain a single peak at the position ω_x cos 30° + ω_y sin 30°, with a lineshape that blends the lineshapes of the x and y signals. Note that this is precisely the peak position that would be predicted from the projection argument, as we described above.

Figure 9. Scaled Wavelengths in the Time Domain Determine Projected Peak Positions in the Frequency Domain.

(a) Consider a signal with modulation only in the x dimension, at a frequency of ω_x,1. In the time domain, this signal would appear as a plane wave with a wavelength λ_x,1 of 1/ω_x,1. The wavelength λ_r,1 that would be observed by a slice at a 30° angle would be 1/(ω_x,1 cos 30°). The wave therefore appears to be scaled by a factor of 1/(cos 30°) when measured by the slice. (b) In the 2-D frequency domain, the peak from the signal would be located along the ω_x axis at position ω_x,1. The Fourier transform of the 30° slice would show a projection of this peak, appearing at ω_x,1 cos 30°.

Figure 10. Convolution Interpretation of Radial Spoke Peak Positions, and Conversion of Hypercomplex to Complex Data.

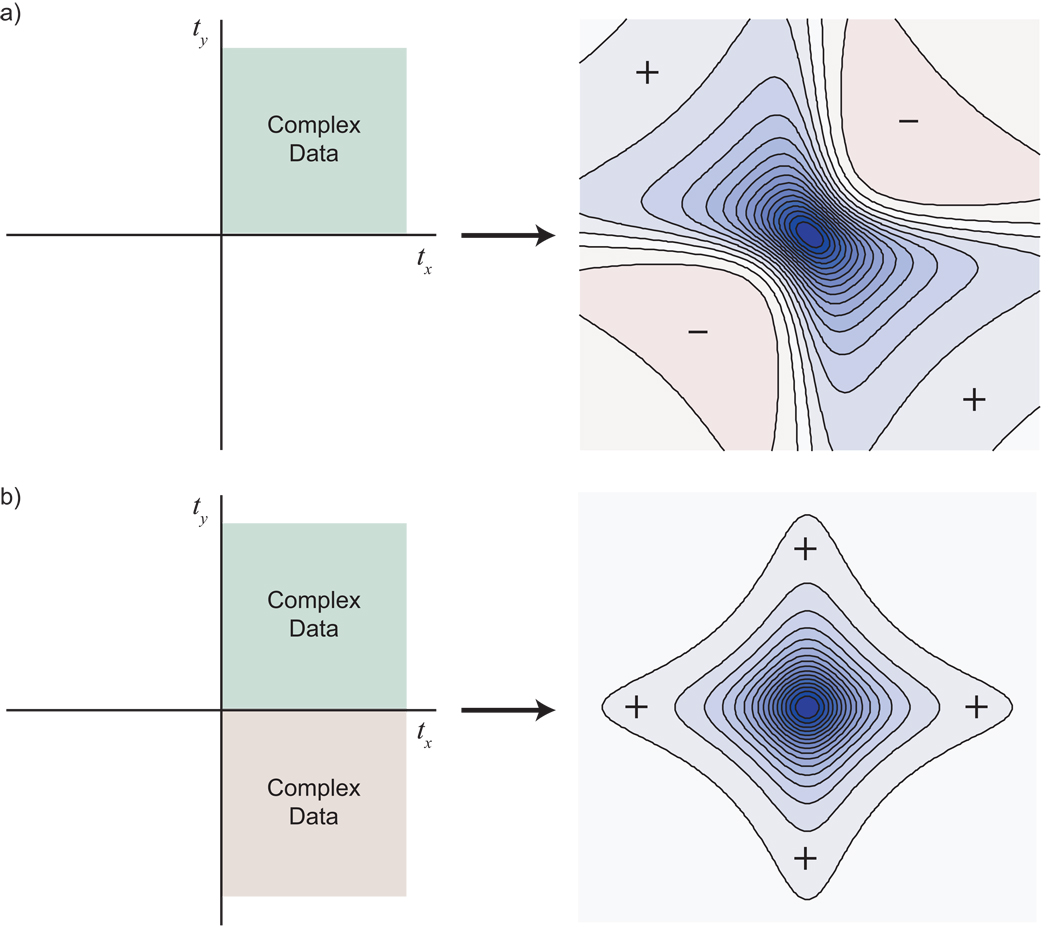
(a) The frequency domain result of measuring a radial spoke can be understood geometrically as taking a projection; it can also be understood, however, as a convolution (denoted by *). In this example, a spoke is measured at an angle of 30° in a 2-D time domain. From the perspective of the spoke, the x signal would appear scaled by a factor of cos 30°. The y signal would likewise appear scaled by a factor of sin 30°. The actual time domain observation is the product of these two scaled signals, meaning that the resulting frequency domain signal is their convolution, a single peak at the position ω_x cos 30° + ω_y sin 30°. (b) If one measured a slice at an angle of −30°, the direction of the y modulation in the time domain would appear reversed. In the frequency domain, the y signal would appear at the position −ω_y sin 30° instead of ω_y sin 30°, and the result after convolution would be ω_x cos 30° − ω_y sin 30°. Measuring a slice at a negative angle would mean recording data at negative evolution times, which is not physically meaningful. However, equivalent data can be obtained by taking linear combinations of hypercomplex components. (c) NMR data collection is normally hypercomplex, and can only be carried out for positive evolution times. Once collected, however, that hypercomplex data can be converted to complex data, to produce slices at both positive and negative angles. The conversion process preserves all of the information in the data; in this example, four independent hypercomplex measurements become two complex data values in the +t_x +t_y quadrant, and two complex data values in the +t_x −t_y quadrant.

2.5. Quadrature Detection and Projections

The complete description of a 1-D NMR signal requires complex data rather than real data, meaning that two measurements of the signal with a phase relationship of 90° must be acquired simultaneously for each sampling position [3, 38]. The reason for this is that the magnetization vector of an NMR coherence behaves as a phasor, precessing about an axis, the external magnetic field, over time. With only a single intensity measurement for each time point, it is not possible to determine the direction of rotation of the phasor, and the resulting Fourier transform reflects this ambiguity by splitting the peak into a doublet. With two intensity measurements taken 90° apart—in other words, a sampling in complex numbers—it becomes possible to determine the sign of the frequency of the signal. The measurement of an NMR signal as complex values is referred to as quadrature detection.

When multiple dimensions are involved, quadrature detection becomes more complicated. A multidimensional signal is formed as the product of complex 1-D signals for each dimension. One might imagine that this would occur as a traditional product of complex numbers, producing a new complex number—for example, (x_r + ix_i)(y_r + iy_i) = (x_ry_r − x_iy_i) + i(x_ry_i + x_iy_r) for two dimensions x and y, with real and imaginary components designated via subscripts r and i, respectively—but in fact the typical pulse sequence techniques used in NMR do not capture the quadrature information in this form⁷. Instead, data collection in NMR is said to be hypercomplex, measuring 2ⁿ components for n dimensions, which in the 2-D example would be x_ry_r, x_ry_i, x_iy_r and x_iy_i. With a conventional multidimensional NMR experiment sampled on a rectangular grid, the standard approach to data processing involves computing the Fourier transform for each dimension independently, holding the other dimensions constant during the calculation [46]. Each of these transforms is over complex data, using pairs of hypercomplex components; after a dimension is transformed, its imaginary components are discarded, as the information in the frequency domain imaginary components is redundant and will lead to phase-twist lineshapes (see Section 2.9) if retained.

This conventional approach of independent, sequential transforms for each of the nuclei in the experiment cannot be applied in processing radial spokes to produce projections. A radial spoke captures information from multiple nuclei simultaneously as a slice through the time domain, and the projection-slice theorem calls for taking the Fourier transform along the slice in order to generate a projection. Such a slice will have a reduced dimensionality from the original time domain, and computing the transform of the slice will require some method of reducing the number of hypercomplex components. The two main approaches that have been taken are either measuring fewer components to begin with, such that one has the correct number of components for the transform of the slice, or measuring the full set of hypercomplex components, but rearranging the components so that the correct number is supplied to the Fourier transform.

The first solution is to limit the experimental sampling to the correct number of hypercomplex components for the dimensionality of the slice; for the typical experiment combining two or more indirect dimensions into a single radial dimension, this means measuring only two components, so as to present complex data to the 1-D Fourier transform [47, 48]. In practice, one simply limits the quadrature detection in the pulse sequence to one of the indirectly observed dimensions. Thus for the 2-D example, one could record the experiment with quadrature in x and not in y by measuring the two components x_ry_r and x_iy_r at each of the sampling points on the tilted vector, and use them as the complex input for the 1-D FT with respect to the radial dimension.

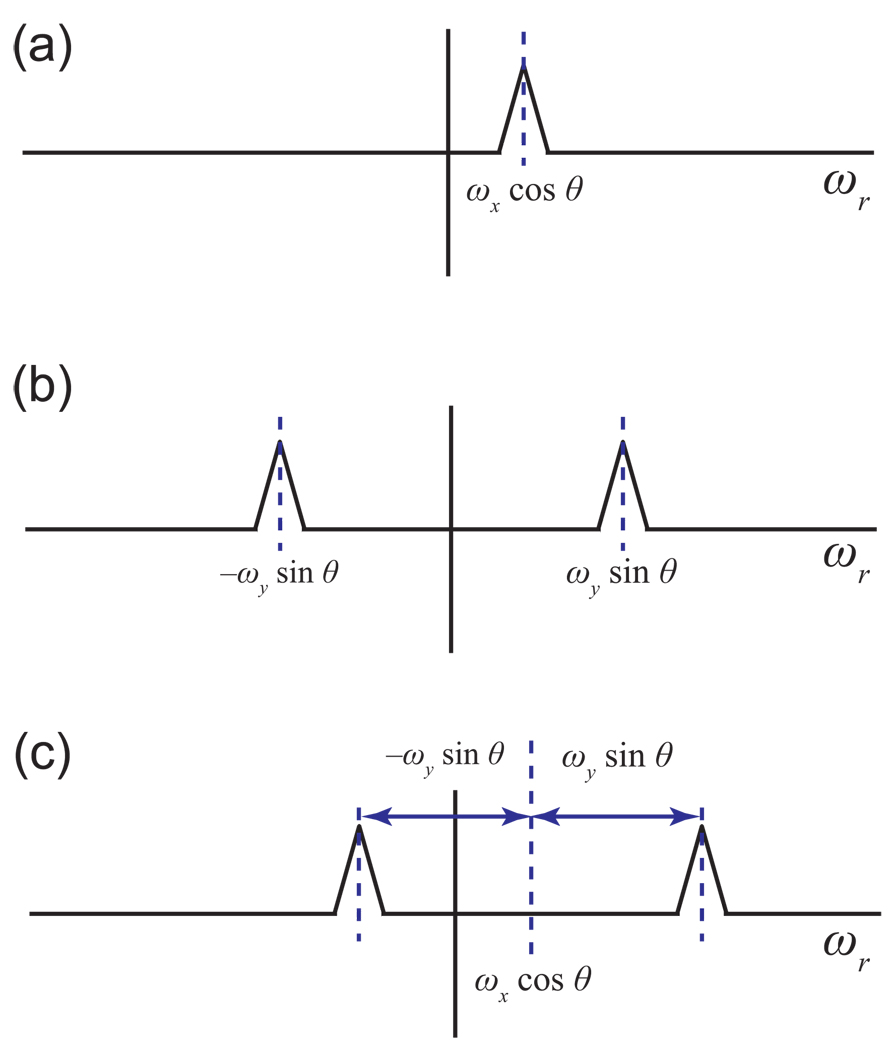
One might expect that collecting less data will result in increased ambiguity somewhere, and this ambiguity in fact appears as a duplication of each signal. This result can be deduced using the convolution argument presented in the preceding section, as worked out graphically in Fig. 11. We shall look at the contributions from x and y independently, and then examine their convolution. Since the sampling of x is in quadrature, the transform of the x contribution alone would give the projection of the x peak onto the tilted axis (Fig. 11a). The contribution from y, however, is purely real, and its spectrum would have two peaks, one of positive frequency and the other of negative frequency (Fig. 11b). The observed time domain data are the product of the x and y contributions. Since the effect of multiplying two functions in the time domain is to convolve their spectra in the frequency domain, the final spectrum is the convolution of the x signal’s spectrum with the spectrum of the y signal. The split y signal causes the final result to be a doublet, with the pair centered on the scaled x frequency and separated by the scaled y frequency (Fig. 11c).

Figure 11. Radial Spoke Peak Positions in the Absence of Full Quadrature Detection.

Fourier transformation of a radial spoke measured with quadrature information for only one dimension leads to a frequency domain multiplet. That can be understood by the convolution argument, shown here for the example of a slice at angle θ through a 2-D time domain, with quadrature detection in x and real detection in y. (a) Because complex data are available for x, a radial slice of the x signal alone would show as a single peak at the position ω_x cos θ. (b) Since imaginary components are not available for the y signal, the Fourier transform of a slice of it alone would show a doublet. (c) The actual time domain observation is the product of the x and y signals, yielding a convolution of (a) and (b) in the frequency domain. The result is a doublet centered on the scaled x frequency, with a splitting equal to twice the scaled y frequency.

The same procedure could be applied for other dimensionalities, using quadrature detection in one dimension and measuring real data for the others. The result would be a more complicated splitting pattern, with an additional splitting for each cosine-modulated indirect dimension.

The second solution is to record the full set of hypercomplex components for all indirect dimensions, and then to rearrange the components before computing the Fourier transform [49–53]. In practice, this normally means converting hypercomplex data to complex data. We have already seen that complex and hypercomplex components are related in the case of two dimensions by the simple rule (x_r + ix_i)(y_r + iy_i) = (x_ry_r − (x_iy_i) + i(x_ry_i + x_iy_r), indicating that we can convert hypercomplex data to complex data by taking a linear combination of the hypercomplex components. Equivalent rules can be deduced for any other dimensionality by finding the analogous product. The result of computing the transform of the converted complex data is the expected projection of the 2-D peak onto the tilted axis, with no duplication of the signal, since all dimensions are sampled in quadrature.

Interestingly, it is possible to form more than one linear combination from a set of hypercomplex components. In the case of two coevolved indirect dimensions, for example, it is possible to form a second linear combination, (x_ry_r + x_iy_i) + i(x_iy_r − x_ry_i This combination would appear to generate the time domain data corresponding to the product (x_r + ix_i)(y_r − iy_i). Since (y_r − iy_i) is the complex conjugate of the y signal, the product (x_r + ix_i)(y_r − iy_i) would be a mirror image of the 2-D signal but with the direction of precession reversed, thus extending the complex time domain into the +t_x −t_y quadrant [37]. In the context of 1-D radial spokes, the data values generated from this alternative linear combination of the sampled hypercomplex components thus trace a spoke in a new direction −θ mirroring the original sampling angle θ [53]. The transform of this new spoke would yield the projection in this new direction, with a single projected peak for each 2-D signal.

An alternative interpretation, by the modulation and convolution argument, is shown in Fig. 10b.

Note that it does not matter whether the second linear combination is computed as a mirror image of the data in the x dimension [(x_r − ix_i)(y_r + iy_i) = (x_ry_r + x_iy_i) + i(x_ry_i − x_iy_r)] or as a mirror image of the data in the y dimension [(x_r + ix_i)(y_r − iy_i) = (x_ry_r + x_iy_i) + i(x_iy_r − x_ry_i)] —but only one of these can be used productively at a time, as they provide access to the same mirror image projection.

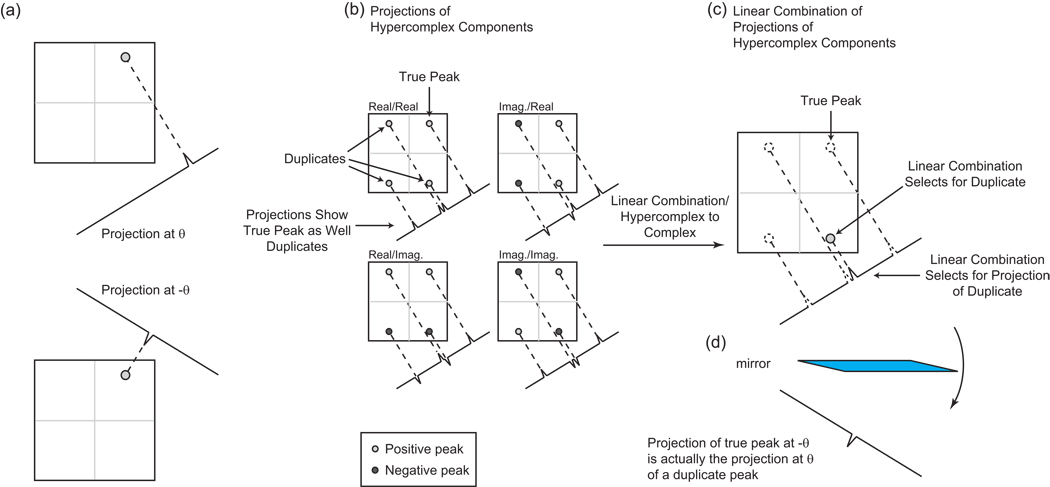
The hypercomplex sampling of a radial spoke thus provides access not just to the projection in the direction of the spoke, but also to projections in mirror image directions, a phenomenon that arises because of the inability of any single hypercomplex component to distinguish between positive and negative frequencies (Fig. 12). The Fourier transform of a single hypercomplex component shows both the true peak and a set of mirror-image duplicates in the other quadrants (Fig. 12b). Taking a linear combination of these hypercomplex components results in a spectrum showing a single peak, either the true peak or one of the duplicates (Fig. 12c). The same principles apply to radial spokes, as shown in Fig. 12b/c. One finds that the “extra” projections arising from linear combinations of hypercomplex components are in fact projections of these duplicate, mirror-image peaks (Fig. 12d).

Figure 12. Geometric Explanation for Why Multiple Projections are Obtained from a Single Hypercomplex Spoke.

(a) In this example, a 2-D spectrum contains a single peak, in the upper right corner. If hypercomplex components are measured for a radial spoke at angle θ, after conversion to complex components and Fourier transformation one obtains both the projection at angle θ (top) and a second projection at angle −θ (bottom). This can be explained by convolution, as in Fig. 10b. It can also be explained geometrically as follows. (b) An individual hypercomplex component cannot distinguish which quadrant contains the true peak, showing a mirror image duplicate in each quadrant. Projections of hypercomplex components at angle θ likewise show the true peak as well as its duplicates, each projection containing a quartet. (c) Taking a linear combination of the hypercomplex components selects for one of the four peaks. Depending on the particular linear combination, this may or may not be the true peak. Here, the duplicate peak in the lower right was selected. After taking a linear combination of the projections at angle θ of the hypercomplex components, one obtains a projection at angle θ with a single peak. In this case, the linear combination has selected for the projection of the lower-right duplicate peak. (d) The projection of the true peak at angle −θ obtained in panel (a) is in fact the projection at angle θ of the lower-right duplicate peak.

Note that if one takes into account the full set of linear combinations, the process of converting hypercomplex to complex data does not reduce the number of data values, but rather changes their form. In the 2-D example, conversion takes us from having four hypercomplex components defined over the +t_x + t_y quadrant to having two complex components defined over both the +t_x + t_y and + t_x − t_y quadrants (Fig. 10c). A set of four data values sampled at a time domain position (t_x, t_y) becomes two components at (t_x, t_y) and two components at (t_x, −t_y). Because there is no reduction in the amount of information, there is also no introduction of ambiguity.

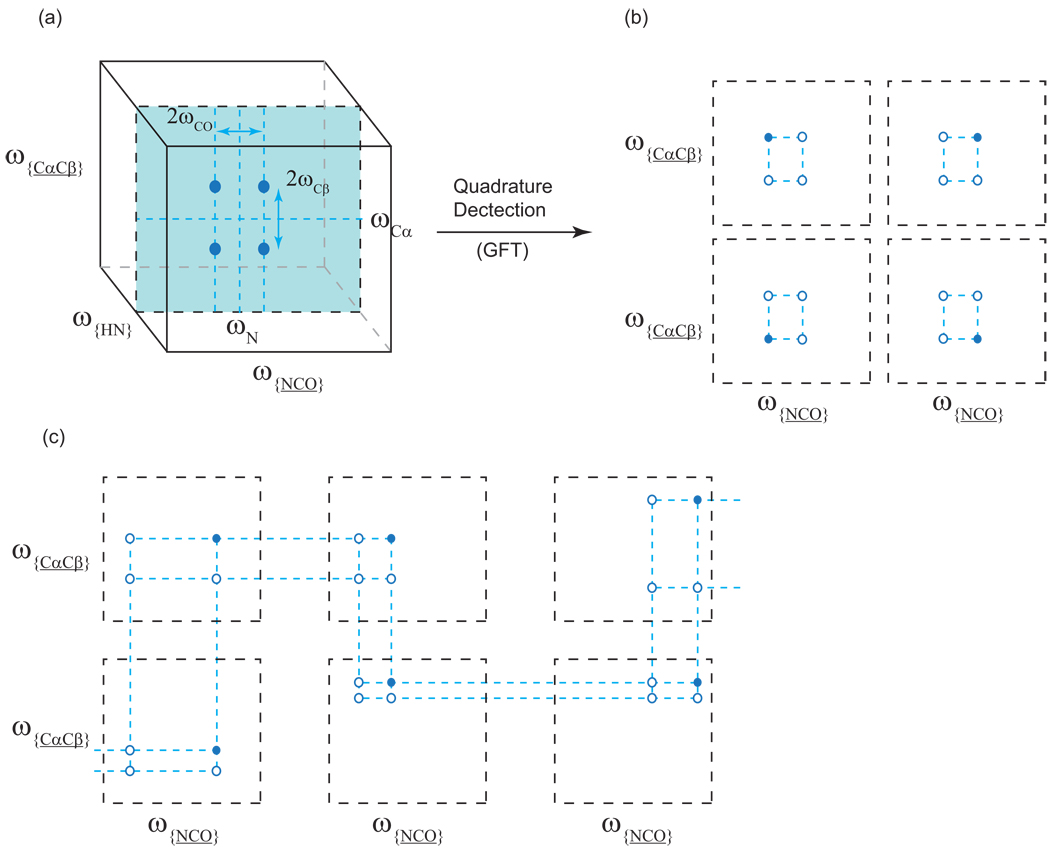
The linear combinations that can be used for any particular dimensionality in order to obtain independent mirror image projections from hypercomplex data can be calculated conveniently using tensor product formalisms introduced by Kim and Szyperski [52]. The “G matrix” for a given dimensionality provides the appropriate coefficients for each of the possible independent combinations of the time domain data.

Note that it is possible to arrive at the same result by taking linear combinations in the frequency domain, where one may note a strong resemblance to the IPAP (In-Phase/Anti-Phase) technique used in the measurement of couplings (cf. [54]). Kozminski and Zhukov demonstrated this by computing 1-D transforms over pairs of hypercomplex components, i.e. using x_ry_r and x_iy_r for one transform and x_ry_i and x_iy_i for the other [55]. The former transform would produce an in-phase doublet split by the y frequency, while the latter would produce an antiphase doublet. By taking linear combinations of these doublets, one can separate the two mirror-image projections. Kim and Szyperski supplied an “F matrix” formalism giving the appropriate coefficients to carry out this kind of frequency domain processing for any dimensionality [52].

The connection between multiplet components and mirror-image projections is important for understanding one technique that was used with reduced dimensionality experiments without full quadrature detection [48, 56]. Consider a 2-D case where the chemical shifts in y are significantly larger than those in x. If one measures x with quadrature and y without quadrature, the splittings will be so large that the upfield doublet components for all the signals will tend to cluster together in an upfield region of the spectrum, while the downfield components will tend to cluster together in a downfield region of the spectrum, with a gap between the clusters. Furthermore, by adjusting the angle of the sampling, one can calibrate the size of the splitting and thus the gap between the clusters. This phenomenon makes the data easier to analyze, and was often considered in the design of reduced dimensionality experiments. In fact, the two clusters are the two mirror-image projections, and this method therefore provides a way to separate them without using full quadrature detection. Ding and Gronenborn later showed that TPPI could be used to introduce very large artificial frequency offsets in the cosine-modulated dimensions, allowing them to produce a (4,2)-D experiment with the four mirror-image projections placed in an equispaced row within the same spectrum (see Section 3.2 for a more detailed discussion and illustrations) [57].

To summarize this section, we have seen that measuring pairs of hypercomplex components along radial spokes causes the peaks to be split into multiplets, which is what one analyzes in the classic reduced dimensionality experiments. One can take linear combinations of the hypercomplex components in order to select out particular multiplet members. The individual multiplet members correspond to the projections in certain directions that are related by mirror-image symmetry, and thus taking linear combinations allows one to separate out the projections in these directions. One can also say that the linear combinations of hypercomplex components generate complex data corresponding to different regions of the time domain. When we move on to polar Fourier transforms of radial data, we shall see a few additional considerations involving quadrature detection, but the principles described in this section allow one to explain all of the different approaches to data collection and manipulation that have been used for quadrature detection in reduced dimensionality and projection experiments.

2.6. Using Projections: Directly Interpreting Projected Peak Positions

Having described radial sampling and the conversion of radial time domain data to frequency domain projections, we shall now consider how information about the signals can be obtained from such data. As we saw above, it is possible in simple cases to examine projections directly to determine the position of an original peak in the multidimensional space. Under the most favorable circumstances only two projections are needed to position a peak correctly (Fig. 7); as we shall see, it is unfortunately not always so straightforward. This general idea, however, has inspired a number of approaches for using radial data, both manual and automated, that seek to determine the frequencies of the signals in the multidimensional spectrum by examining the positions of the peaks on projections⁸. The specific approaches will be addressed in detail when we consider the history of radial sampling in NMR, but for the moment we wish to consider some general aspects of the problem.

The primary difficulty with interpreting projected peak positions is in determining which projected peaks originate from the same multidimensional signal. With a single peak this is never a problem. Depending on the directions of the projections and positioning of the peaks, the assignment may also be unambiguous for multiple peaks (Fig. 13a). However, it is not hard to imagine pathological cases. Given the two projections in Fig. 13b/c, the spectrum in Fig. 13c is just as likely as that in Fig. 13b— indeed, one cannot say whether two, three or even four of these possible peaks exist (Fig. 13d). One can extend a vector from each projected peak across the multidimensional spectrum, and wherever such vectors cross is a possible peak; if there are multiple crossings for the same vectors, one is faced with the question of how many and which ones are real. One criterion is that a real peak should appear on all of the projections, and any intersection that does not feature a vector from every projection can generally be disregarded⁹. In addition to this, another clue available for resolving any uncertainty is the relative intensities of peaks on the projections: if there is no peak overlap on the projections, one should be able to assign the projected peaks of matching intensities to the same source signal; naturally, assignment by comparing intensities presumes that the signals have substantially different intensities, which is not always true. If there is overlap, the pattern can still potentially be resolved by analyzing the intensities of the projected peaks, which should be sums of the original signal intensities (Fig. 13d).

Figure 13. Identification of Multidimensional Signal Positions from Projections When Multiple Signals are Present.

(a) Two peaks are present on each of these two projections (one projection parallel to x, and the other at an angle of 30° to x). By extending lines back across the 2-D space of interest from the projected peaks, one can determine the locations of the original signals, which are found where the backprojection lines intersect. In this case, there are only two possible intersection points for the backprojection vectors within the spectral region, meaning that the original positions of the two peaks can be identified unambiguously. (b and c) In a less favorable case, there are two possible interpretations for the projection data, both equally likely. The original peaks could be located as in (b) or they could be located as in (c); these two configurations give identical projection data, and one needs additional information to resolve the ambiguity. Note that this ambiguity would plague any method trying to interpret this data, regardless of whether it is automatic or manual, and regardless of whether it attempts to reconstruct a spectrum or merely attempts to calculate frequencies from the projected peak positions. (d) The relative intensities of the projected peaks might provide a means for resolving ambiguities. In this case, one possible answer is that there are three peaks of equal height, A, B and C, positioned as shown. However, without additional information one could not exclude another possibility, namely a configuration like that of (b), but with a peak A twice as strong as B.

If one can correctly match which projected peaks belong to which signal, the determination of the multidimensional signal frequencies is straightforward. The calculation can be neatly formed as a system of linear equations relating the unknown signal frequencies to the known projected peak positions, with the projection angles supplying the coefficients. An argument has been made that if there are enough projections the problem becomes overdetermined, allowing the signal frequencies to be calculated by a least-squares fit with greater precision than for conventional NMR [52]. Whether this in fact applies depends on a number of variables specific to the case at hand.

The classic reduced dimensionality experiments use the limited quadrature detection approach, where each signal is split into a multiplet (almost always a doublet, from coevolving two indirect dimensions—but as described below, other cases involving more dimensions and more complicated multiplets have also been demonstrated) [47, 48]. Such data can easily be analyzed by hand, provided that the intensities and/or lineshapes of the signals are different enough to allow each doublet to be identified unambiguously, and that there is minimal overlap of the split peaks. In cases where the pairing of peaks into doublets is ambiguous, and for automated processing, a knowledge of the center point of each doublet can be very helpful [56, 58, 59].

If full quadrature detection is used, the overlap problems can be reduced significantly (since the ω_x + ω_y and ω_x − ω_y peaks are separated onto independent spectra), but at the expense of making the visual identification of multiplets, as well as the bookkeeping, more difficult for the spectroscopist to perform by hand. At the extreme, one can coevolve several dimensions, leading to multiplets of four or even eight components, which are separated onto independent spectra [52]. These would constitute a set of projections of the multidimensional spectrum: one in the direction of the spectrum’s diagonal, and the others in mirror image directions. Kim and Szyperski’s key insight into this problem is that it can be analyzed as a hierarchical series of splittings [52]. The splitting patterns can be discerned with the aid of additional sets of projections that coevolve fewer dimensions and show the center point at each level of splitting (cf. Fig. 24b). This analysis can be carried out by hand, or it can be automated [60]. Customarily, it has been used only with the diagonal projections, but with automation it should be easier to incorporate projections other than the diagonal to resolve overlap problems.

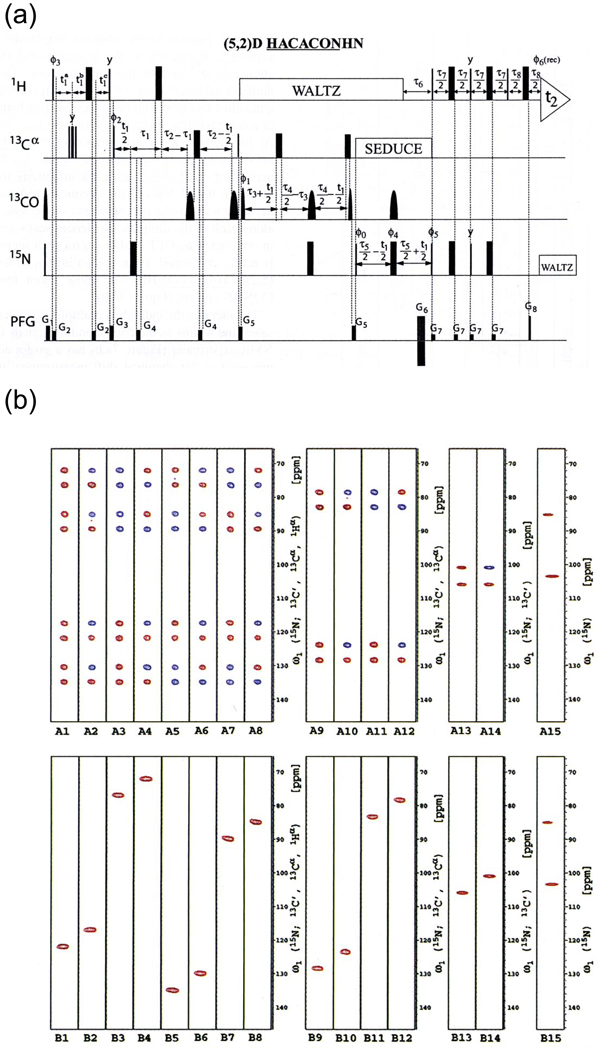
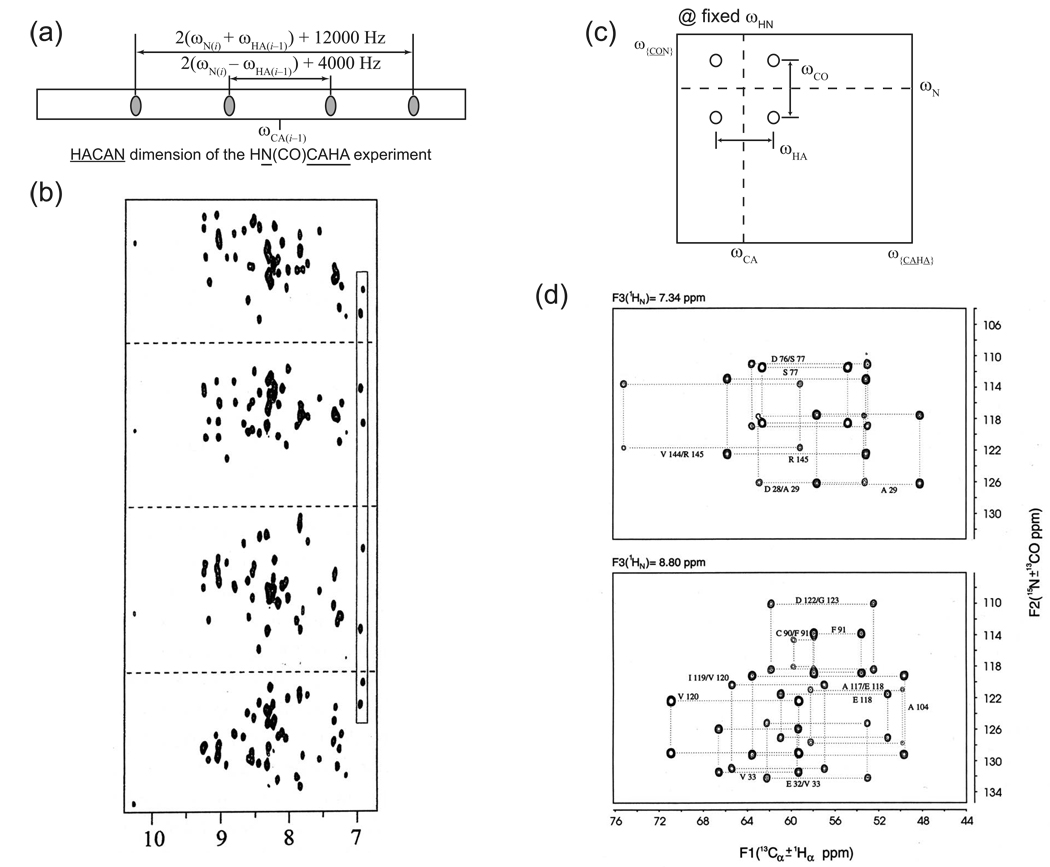
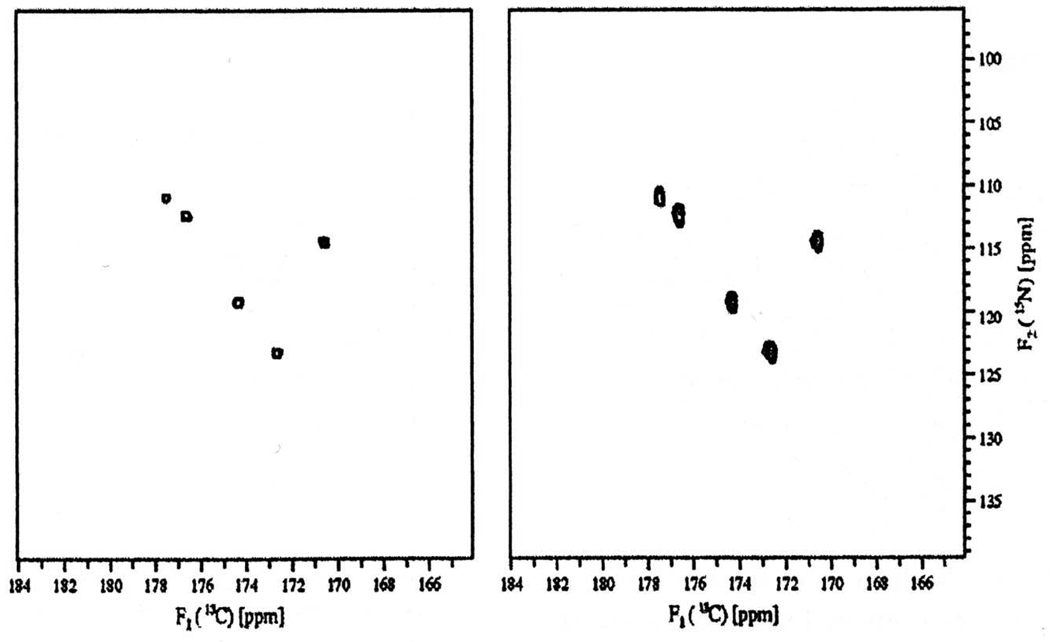
Figure 24. (5,2)-D GFT. The first GFT experiment was the (5,2)-D HACACONH of ubiquitin.

(a) The pulse sequence. (b) Data for residue S20, showing the full hierarchical splitting pattern and the separation of multiplet components onto subspectra. At left are the strips for the 8 basic spectra, followed by the four first-order central peak spectra, the two second-order central peak spectra, and finally the one third-order central peak spectrum. In each case, the top half of the panel shows the transforms of the hypercomplex components prior to application of the G matrix, showing the full multiplet patterns, while the bottom half shows the result after application of the G matrix, with multiplet components separated onto independent subspectra. Reprinted, with permission, from [52] (© 2003 American Chemical Society).

The other kind of reasoning one could use to sort out which projected peaks belong to the same originating signal is the geometric approach illustrated in Fig. 13, where the potential locations for the peaks are determined by finding the intersection points of vectors extended from each projected peak. This has formed the basis for several automated procedures (such as APSY), which are discussed below, and can also be the starting point for the development of nonlinear reconstruction algorithms.

2.7. Reconstruction from Projections

A second option for utilizing projection data is to attempt to reconstruct the spectrum in full. There are several motivations for seeking a full reconstruction rather than calculating a list of signal frequencies. Provided it is a complete and faithful reconstruction of the information that would be found in the equivalent conventional spectrum, a full spectrum (1) would contain more information about the experiment—for example, pulse sequence and instrumental artifacts, unusual lineshapes, the full structures of overlapped peaks, and the like—which are captured by the projections, and which may be of use to an experienced spectroscopist; (2) it would present the signal information in the format that spectroscopists are used to, allowing the use of conventional methods for resonance assignment; (3) it would implicitly solve the problem of matching together the projected peaks belonging to the same signal, which makes the direct analysis of projected peaks difficult; (4) depending on the reconstruction method, it might be possible to improve the sensitivity of the experiment via signal averaging across the projections. Some would argue that points (1) and (2) are insignificant or a matter of preference, but it is clear that (3) and (4) would be genuine advantages of full reconstruction. The key qualification, however, is that the reconstruction must be complete and faithful for these advantages to accrue. Much hinges on how accurately a reconstruction can be obtained and the amount of data required.

From a theoretical standpoint, reconstruction from a set of uniformly distributed projections, also known as tomography, can be accomplished by inversion of the Radon transform. How to do this was first worked out by Johann Radon in 1917, who was investigating the properties of integral transforms in a purely theoretical context [61]. It has since been rediscovered on several occasions [62–67], as the same problem has appeared in many scientific fields, including radioastronomy, electron microscopy and medical imaging. Several formulations have been given, but the most straightforward is known as filtered backprojection (FBP) [42, 63, 68].

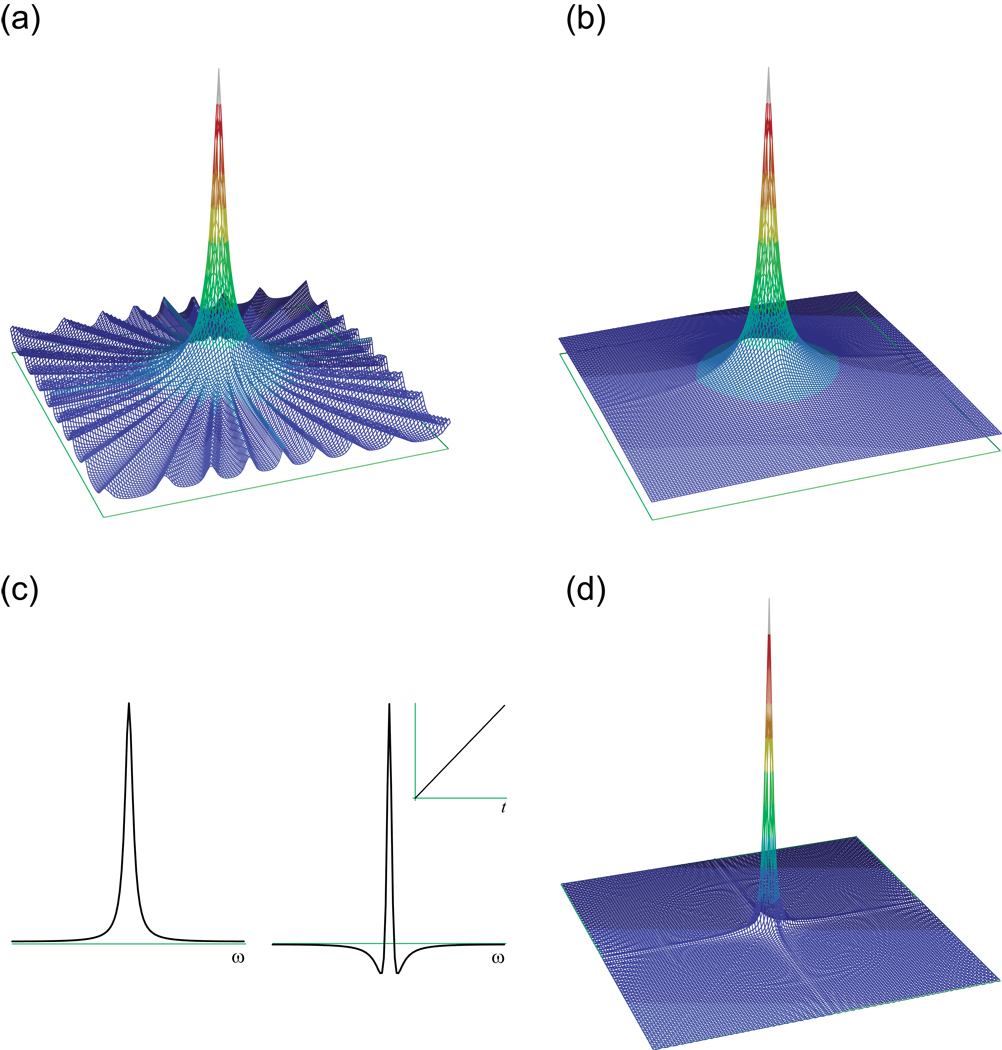
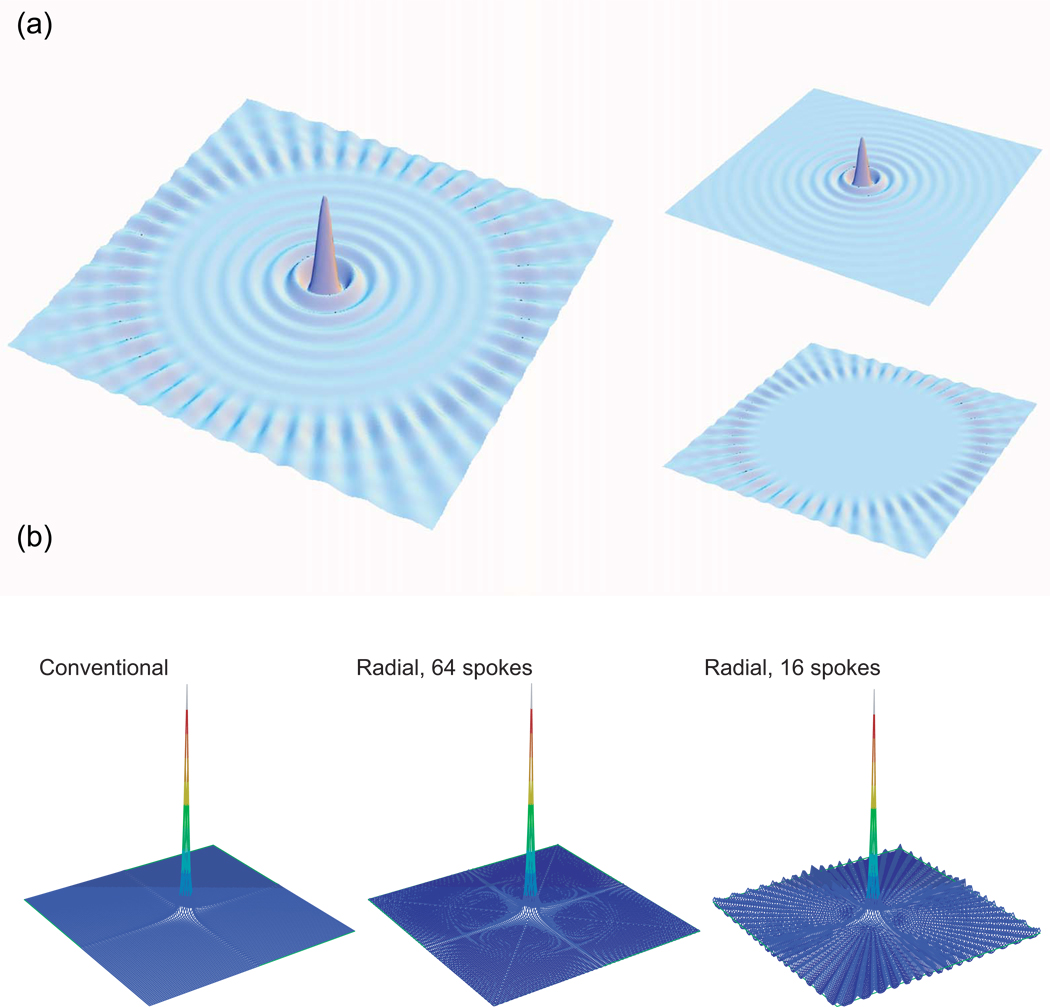
Backprojection means to extend each projection backwards over the reconstruction space—such that each peak generates a ridge of intensity, as in the point response of a single projection shown in Fig. 6—and then to take the sum or superposition of these ridges [63, 67, 69]. The result for a small number of projections is a set of ridges for each signal, intersecting at the locations of the peaks of the signals (Fig. 14a). For a large number of projections, the ridges merge to form a mountain of intensity at each peak position, with each peak broadened, and the baseline elevated (Fig. 14b) [67, 69]¹⁰.

Figure 14. Backprojection and Filtered Backprojection Reconstructions.

(a) The backprojection reconstruction of a Lorentzian signal from 16 simulated projections. One observes ridges perpendicular to the projection directions; where these ridges intersect, the peak is formed, albeit broadened. The merging of the ridges also leads to an elevated baseline. (b) The backprojection reconstruction of a signal from 128 projections. Here, the ridges have completely merged. The peak is still broadened, however, and the baseline is still elevated. (c) By applying the filter function shown in the inset to each time domain radial spoke, the lineshapes on the projections are altered from the Lorentzian shape at left to the modified shape at right. (d) The filtered backprojection reconstruction of the same signal, from 128 projections. The peak is of the correct width, and the baseline is not elevated. Panel (c) is adapted, with permission, from [44]. © 2006 Springer.

Filtering can be thought of as a way of correcting for this broadening, although it is not an ad hoc correction but rather an integral part of the theory. In signal processing, a filter originally meant a device that could filter out specific frequencies from a collection of signals, but it has additionally come to refer to any processing procedure that alters the signals via convolution, or equivalently by multiplication in the Fourier domain. FBP calls for a very specific filter to be applied to each of the projections, as derived from a theoretical analysis of backprojection, altering the shapes of the projected peaks (Fig. 14c) [42, 63, 68, 69]. This can be carried out either by convolution of the projections with a new lineshape function in the NMR frequency domain, or more practically by multiplication of the time domain data with a specific window function [68]. The result is that each backprojection ridge is bordered by troughs on each side; these troughs serve to cancel out the ridges when there is overlap, and in the limit of infinitely many projections a completely faithful reconstruction of the original signal—a true inversion of the Radon transform—is obtained (Fig. 14d).

Filtered backprojection is linear and gives completely predictable quantitative results, and it is widely used in medical imaging and other fields that require tomography (e.g. cf. [42]). Both it and its unfiltered cousin, pure backprojection, have been described and used for NMR [70, 71]. Because these methods involve the summation of contributions from each of the projections, they effectively carry out signal averaging over the full set of projections. As a result, the sensitivity in backprojection and FBP reconstruction is proportional to the total measurement time used to collect all of the projections— although one should note that filtering causes a loss of sensitivity from what would be obtained by pure backprojection, as it tends to emphasize data at longer evolution times, when the signals have decayed [12]. In cases of poor sensitivity, the gain from using backprojection or filtered backprojection, even accounting for a loss due to the filter function, may provide a very significant advantage over directly analyzing projections. Backprojection and filtered backprojection are simple to implement, and fast to calculate. The filtering requires a single multiplication in the time domain, and after Fourier transformation with respect to the tilted axis (performed quickly using the FFT) one need only sum the contribution from each projection.

We have just seen that backprojection-based reconstructions form peaks at the intersections of ridges of intensity. This no doubt will seem similar to the geometric analysis described in the previous section and illustrated in Fig. 13, where peaks are located at the intersections of projection vectors. Despite their very different origins—the one from intuition and the other from the analytical inversion of an integral transform— these methods seem to embody the same logic. We shall see, in fact, that all methods for utilizing radial data can be related to this same logic. This also means that these methods can suffer from the same problems. In Fig. 13, we show how geometic analysis of peak positions can be ambiguous when multiple peaks are present. If the same data were used in a backprojection or filtered backprojection reconstruction, one would see this same ambiguity, manifesting itself in the form of spurious peaks appearing wherever ridges from different signals intersect (Fig. 15b). The only solution to this in a backprojection or FBP reconstruction is to measure more projections, reducing the intensities of spurious intersections relative to the real peaks, eventually reaching the perfection of Fig. 14d (or Fig. 29d).

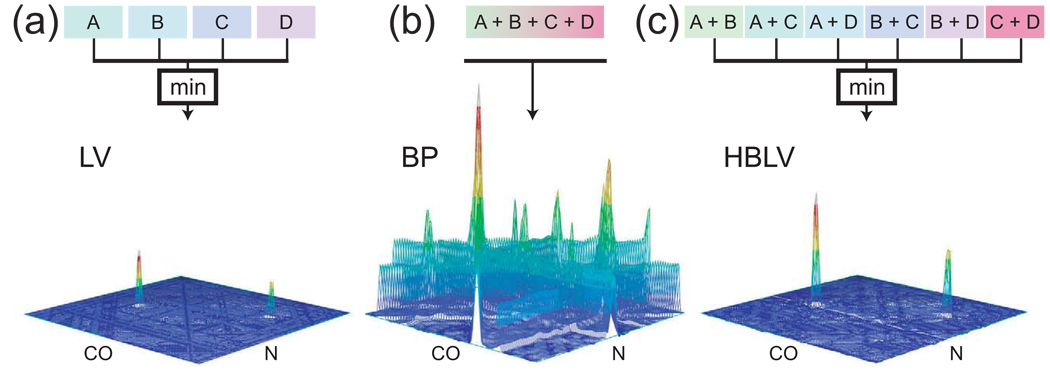
Figure 15. The Lower-Value, Backprojection and Hybrid Backprojection/Lower-Value Reconstruction Algorithms.

In these three panels, the stacked plots show reconstructions by the three methods of a plane extracted from the (3,2)-D HNCO of GB1. Four projections were used, at the angles 0°, 45°, 90° and 135°. The reconstructions have been normalized to allow for the comparison of signal and noise levels. The diagrams at top illustrate how each method calculates an output given the four inputs A, B, C and D, representing the four projections. (a) In the lower-value (LV) algorithm, the value assigned to a point in the spectrum is the minimum of the corresponding values found on the projections. The resulting reconstruction shows the two peaks found on this plane. (b) In backprojection (BP) reconstruction, the value assigned to a point in the spectrum is the sum of the corresponding values found on all of the projections. This produces reconstructions with backprojection ridges. The two true peaks are formed in locations where the ridges intersect; there are additional intersection points between ridges, however, which lead to spurious peaks of various heights. The signal level is eight times higher in this reconstruction than in the lower-value reconstruction, because of the additive nature of the backprojection process. (c) The hybrid (HBLV) method involves computing the sums of all possible combinations of k projections, and then assigning to the reconstruction point the smallest value encountered from among the set of sums. For four projections and a bin size k = 2, there are six combinations to be compared, which are shown in the diagram at top. The resulting spectrum shows stronger signals than in lower-value reconstruction, reflecting the partially additive nature of the process, without introducing artifacts. Reprinted, with permission, from [72]. © 2005 American Chemical Society.

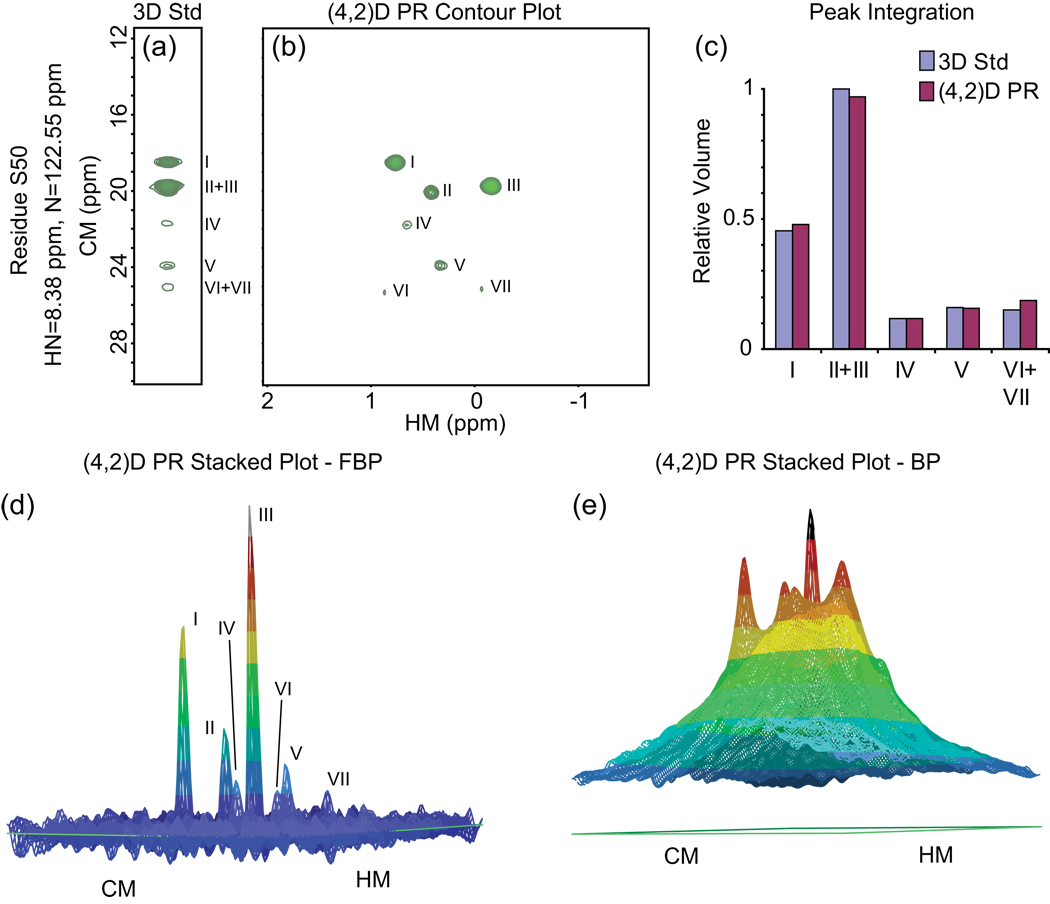
Figure 29. Projection-Reconstruction Methyl/Amide NOESY of HCA II.

Data are shown for residue S50. (a) Strip from the 3-D conventional experiment at the (HN,N) coordinates of residue S50. (b) Contour plot of the equivalent HM/CM plane from the (4,2)-D reconstruction, computed from 100 projections using FBP. (c) Comparison of peak volumes between the conventional 3-D experiment and the (4,2)-D reconstruction. (d) Stacked plot. (e) Stacked plot from a BP reconstruction. The comparison with (d) shows the advantages of using the filter function. Panels (a)–(d) reprinted, with permission, from [71] (© 2005 American Chemical Society).

In cases where one wishes to determine reconstructions from a small number of projections, one must find some other approach, not subject to this limitation. The most significant idea described to date is the lower-value method (now sometimes called lowest-value or minimum-value) [53]. One way to describe this method is by analogy to backprojection. Assume that the process of forming ridges by extending projections is carried out in independent spaces for the different projections. The backprojection reconstruction would be the sum or superposition of these spaces. As in Fig. 15b, this can lead to spurious peaks as well as substantial ridge artifacts. In contrast, with the lower-value method one assigns to a point in the reconstruction the smallest value encountered in any of these spaces at the corresponding position (Fig. 15a). Thus, as in backprojection reconstruction, peaks are found at positions where ridges from all projections intersect, since these are the only positions where every projection contributes intensity. Unlike in backprojection, one would not encounter spurious peaks when a smaller number of ridges intersect, since the smallest value found in the comparison would be a noise value from one of the other projections. Thus in a lower-value reconstruction, a peak is produced at a given location only if every one of the projections of that location also contains a peak.

While the lower-value method reduces the likelihood of encountering false peaks, it unfortunately cannot guarantee that they will not occur. Situations like that of Fig. 13b/c, where there are as many or more peaks as there are projections, will always pose a risk of generating a false peak, depending on the geometry of peak positions and projection angles. If one knows a priori from other experiments how many real signals to expect, one can protect against this by collecting more projections than the number of signals [72]. Even this does not provide absolute protection, however, as it is built on the assumption of infinitely sharp peaks; in practice, with a large number of peaks and/or overlapping peaks, lower-value reconstructions can generate false peaks even if there are more projections than signals.

Besides this issue, lower-value reconstructions differ from the true spectra in several other ways. First, the lineshapes are not reproduced accurately, although this can be corrected artificially by convolving with lineshapes extracted from the projections [70]. Second, overlap on the projections may lead to peaks with incorrect relative intensities. Third, the apparent noise level in a lower-value reconstruction will always be substantially lower than the true noise level, since the lower-value comparison for noise points will always choose the lowest of the random noise values [72]. This may mislead an unaware spectroscopist regarding the sensitivity of the experiment. Fourth, the sensitivity of a lower-value reconstruction is no better than the sensitivity of an individual projection [70, 72]. Finally, lower-value reconstructions are likely to fail if negative peaks are present [72, 73].

Another approach for a relatively small number of projections is to combine the lower-value and backprojection methods in a hybrid method (named the hybrid backprojection/lower-value or HBLV algorithm), which offers some of the benefits of each [72]. The original formulation was equivalent to calculating independent backprojection reconstructions for all possible groupings¹¹ of projections into groups of a specified size k, and then taking the lowest value from among the groups (Fig. 15c). The backprojection provides a sensitivity boost, while the lowest-value comparison eliminates ridge artifacts—since any given ridge cannot appear consistently in all of the groups—and reduces the broadening effect (cf. Fig. 28f–h). False peaks are generally eliminated, although it is still possible to produce one in some particularly unfavorable circumstances. The choice of group size k determines whether the method behaves more like LV or more like backprojection. The hybrid algorithm is effective, but the combinatorics involved in forming and evaluating the groups of k projections is a major computational burden. It was recently shown by Ridge and Mandelshtam that one can obtain almost the same result instantaneously by taking the absolute values of the projections, and adding together the k lowest projection intensities [73]. This simplification substantially improves the practical feasibility of the HBLV method.

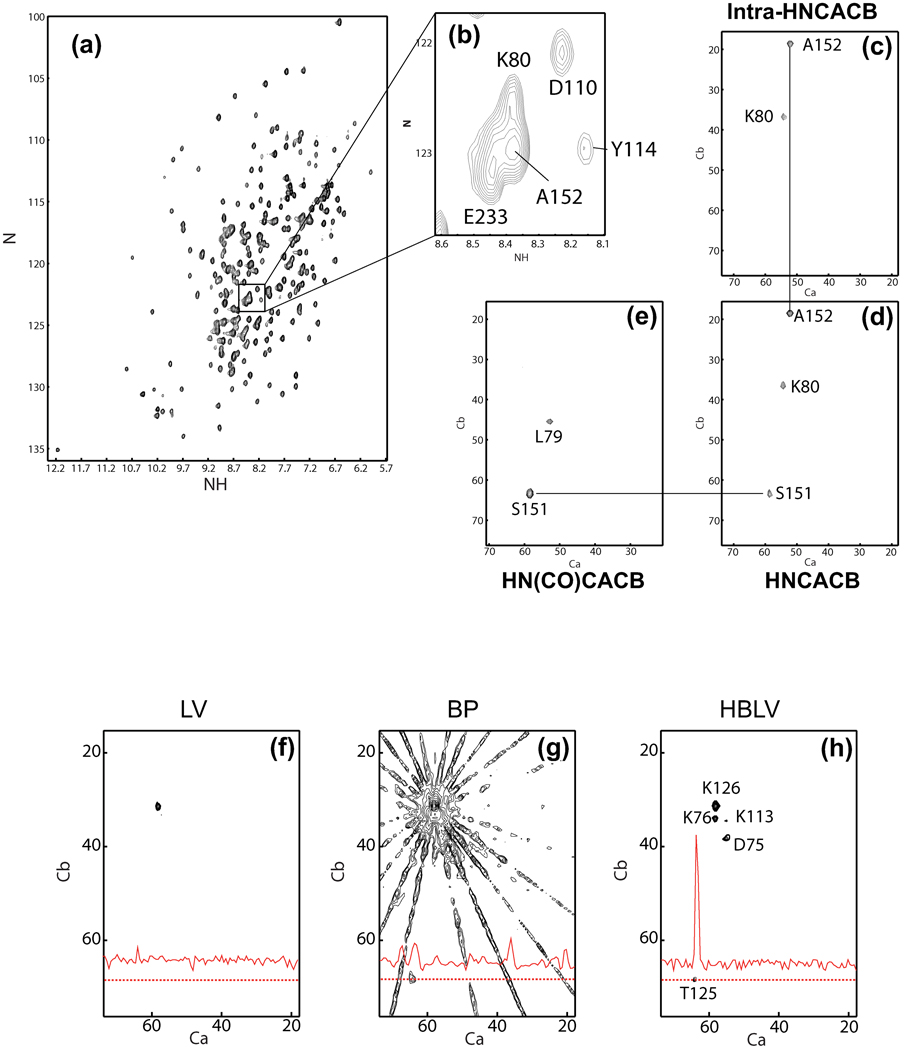
Figure 28. (4,2)-D PR Sequential Assignment Experiments on the 29 kDa HCA II.

(a) The TROSY HN/N correlation spectrum of HCA II, recorded at 800 MHz. (b) Enlargement of the region containing residues K80, D110, A152 and E233. (c,d,e) C_α/C_β planes at the (HN,N) position of A152 for the intra-HNCACB, HNCACB and HN(CO)CACB experiments, respectively. Each spectrum was measured as eight radial spokes, becoming 23 projections after conversion from hypercomplex to complex data, and then reconstructed using the HBLV algorithm with a bin size of eight projections. (f,g,h) Comparison of lower-value, backprojection and HBLV (k=8) reconstructions of the C_α/C_β plane of the HNCACB experiment for residue K126. The lower-value reconstruction is free from artifacts, but shows only the strong intra-residue correlation. The backprojection reconstruction detects the inter-residue correlation to T125 as well, but its intensity is equal to that of the backprojection ridges. Additionally, all nearby crosspeaks are obscured through the broadening of the intraresidue peak. The HBLV reconstruction shows the K126 intra- and interresidue correlations, as well as all nearby crosspeaks, clearly, with no visible artifacts and no line broadening. Reprinted, with permission, from [72] (© 2005 American Chemical Society).

Ridge and Mandelshtam have also very recently proposed a “Histogram Method,” which calculates the value at each point in the spectrum by considering a histogram of the projected values [73]. Instead of assigning the lowest value or a sum of the lowest values, the histogram method in essence assigns the mode, the most frequent value. Of course, the literal mode is meaningless for projection intensities, which constitute a continuous variate. Instead, an intensity distribution function is computed by adding together Gaussian functions centered at each projection intensity value, and the intensity value corresponding to the maximum of this distribution is assigned to the projected point. As with the lower-value algorithm, the sensitivity of the histogram approach is no better than the sensitivity of the weakest projection, and it does not preserve lineshapes.

Thus there are several choices for how one can reconstruct a spectrum from projections, with trade-offs in each case. The theoretically derived method, filtered backprojection, offers the most accurate reconstructions, albeit at the expense of requiring a relatively large number of projections if one is to avoid ridge artifacts. It is also able to offer nearly maximum sensitivity by accumulating signal intensity from all the projections. Backprojection without a filter can achieve truly maximum sensitivity, but produces significantly broadened peaks. By contrast, the lower-value and related methods are able in many cases to produce cosmetically artifact-free spectra from a small number of projections, but at the same time suffer from limited sensitivity and altered lineshapes, and a danger of introducing false peaks. Note that in any event, the accuracy of all reconstruction methods is limited by the ambiguity of the data, as determined by the sampling. With an extremely small number of projections, a situation such as that of Fig. 13b/c can cause any of these methods to produce false peaks.

Regardless of the particular reconstruction algorithm used, there are a small number of practical problems that arise in any computer implementation of reconstruction from projections. Most significant is the issue that the projection data are collected in polar coordinates, while the reconstruction is generated in rectangular coordinates. Thus the projection of a particular discrete location in the reconstruction onto a projection will almost always lie between two discrete sampling points, requiring interpolation. The choice of interpolation method can have a significant impact on the quality of the reconstruction, and it has been a major topic of debate in other fields using tomography (for example, see [66] and [74]). The second major issue with multidimensional NMR spectra is the data storage requirement of the reconstructed spectrum, especially for spectra with more than four dimensions: in many cases it is extremely difficult to reconstruct the full spectrum at the desired resolution without exceeeding operating system limitations on file sizes. If one knows the expected locations of peaks a priori (for example, from other, lower-dimensional experiments) one can selectively reconstruct the particular planes or regions of interest [44]. An alternative idea that has not yet been used widely in practice is to compute reconstructions of spectral regions as needed in real time within an interactive spectral viewing program [44].

2.8. Fitting Signal Models to Radially Sampled Data

A third strategy for deriving signal information from radially sampled data is to fit a model of the signals to the data. In a sense, every method that derives signal properties from spectral data is a kind of modeling, but here we refer specifically to methods that iteratively optimize the parameters of a model while comparing backcalculated data from the model to the experimental data. These approaches have a long history in NMR, and have attracted particular interest in recent years in the context of their application to various sparse sampling methods. The model in such a procedure could mean a spectrum, with the intensity at each position adjusted iteratively, or a list of signals of an explicit functional form and their intensities, frequencies and linewidths. The search algorithm is the particular mathematical method used to carry out the optimization. The model is evaluated by backcalculating either time domain or frequency domain radial data and comparing to the experimental values. Since the scenarios contemplated for radial sampling of NMR involve deliberate undersampling to reduce the measurement time, one expects that in some cases there could be multiple possible models that would be consistent with the data, requiring a regularization procedure to choose between them.

The full catalog of specific algorithms that have been applied to NMR will be considered below.

2.9. Multidimensional Fourier Transformation of Radially Sampled Data

After considering radially sampled data as a source for projections—which we have seen can be used in a variety of ways—and as the reference data for the fitting of models, a final possibility remains: to determine the higher-dimensional spectrum by directly computing the multidimensional Fourier transform of the full set of radially sampled data. The Fourier transform has the advantage of being a stable and predictable linear method, well understood by NMR spectroscopists. At the same time, it must be remembered that Fourier transformation always reveals the ambiguities of discrete sampling, in the form of artifacts.

One way to calculate the Fourier transform of radial data is to substitute the data values (after first multiplying them by a weighting factor) and sampling point coordinates directly into the equation of the discrete Fourier transform. For input data consisting of n radial spokes of m points each, producing an output spectrum of d indirect dimensions with m points per dimension, a total of O(nm^d+1) operations are required¹². Working with radially sampled radioastronomy data in 1974, Thompson and Bracewell noted that there is a faster way to carry out this transform: first reweight and transform each radial spoke independently, then calculate the value at each output position by summing the transforms of the spokes [74]. This method requires only O(nm^d) operations¹³, saving a factor of m in calculation time.

If the faster method of Thompson and Bracewell sounds familiar, it is because of the simple fact that it is the same as FBP. It is possible because of the linearity of the Fourier transform: if a time domain input can be written as the sum of multiple functions, then the frequency domain output can be written as the sum of the transforms of those multiple functions. Since a time domain radial dataset can be expressed as the sum or superposition of its radial spokes, its Fourier transform can be obtained by transforming each spoke individually and summing together those transforms. Properly speaking, we are concerned with the multidimensional transforms of each of the spokes; however, as the point response in Fig. 6 suggests, this is the same as computing the 1-D transform of each spoke, with respect to radius, and then backprojecting these. Thus the overall process of computing a polar FT for radial data can be carried out most quickly by employing FBP.

There are extensive connections between the Radon, Fourier, inverse Radon and inverse Fourier transforms, which have proven important in many fields. Bracewell [62] has several useful figures illustrating these connections. The formal distinction in the mathematical literature between the polar Fourier transform and FBP is their starting point, the polar Fourier transform converting time domain radial spokes to a frequency domain spectrum, and FBP instead converting frequency domain projections to a frequency domain spectrum. Since the latter process can be accomplished for NMR data only if the data are first converted to projections, the net process for NMR is always a polar Fourier transform, regardless of whether the data are temporarily placed into the form of projections during the processing [37]. Indeed, even when nonlinear methods are used for reconstruction from projections, the net process can still best be thought of as achieving the equivalent of a multidimensional Fourier transform by means of a 1-D Fourier transform and a subsequent inverse Radon transform¹⁴.

A weighting factor—or as it is known in FBP, a filter function—is required because the sampling points in a radial pattern are not evenly distributed throughout the plane, but rather are concentrated with increasing density towards the zero time point, the “hub” where the spokes converge [37, 75]. This must be accounted for in the Fourier transform calculation, or the excessive emphasis on the low-resolution information found close to the origin of the time domain will lead to broadening of the signals. The specific correction can be derived by considering how the change from rectangular to polar coordinates affects the infinitesimal area element in the Fourier transform equation¹⁵ (dt_x dt_y for the 2-D transform, which can be written more generally as dA) [37, 75]. For rectangular grid sampling, each point occupies the same area, and the dA factor can be ignored (Fig. 16a). In polar coordinates, however, the points do not occupy the same area. In 2-D, dA = dt_x dt_y must become dA = t_r dt_r dθ (Fig. 16b), where the linear function t_r, the distance from the origin, is the relevant correction that must be applied in the calculation.

Figure 16. Weighting of Data Points in the Polar Fourier Transform.

(a) With conventional grid sampling, the area occupied by each sampling point, ΔA, is the same, and no special weighting is required during the Fourier transform. (b) In polar coordinates, sampling points that are closer to the origin are spaced more closely together. To correct for this, one must weight the points during the Fourier transform according to their area, ΔA. The appropriate weighting factor for 2-D is t_r, the distance from the origin. Note that this weighting factor is identical to the filter function used in filtered backprojection.

The final matter that remains to be considered with respect to computing Fourier transforms of radially sampled data is quadrature detection. In Section 2.5, we explained how NMR data are collected as hypercomplex rather than complex components, and how the conventional data processing procedure is able to use this hypercomplex information for frequency discrimination, by computing independent Fourier transforms for each dimension. We also explained why this procedure cannot be applied to radially sampled data when calculating projections from spokes, and the alternatives that one has: either to measure a subset of the hypercomplex components, as in some reduced dimensionality experiments, or to collect the complete set of hypercomplex components and convert the data to a complex form.

With full Fourier transformation of radial data, the same difficulties prevent the use of the conventional procedure, and once again alternatives are needed. The option of using quadrature detection in only one dimension could be used, and indeed was used in the early days of multidimensional NMR for conventionally sampled data, with the help of techniques such as TPPI [3, 38]. The disadvantages of this type of data collection are well-known, however, and it has not been used for polar Fourier transforms.

The other option that was described for projections—conversion of the data from hypercomplex to complex—is indeed a useful method in this context [37]. Using the relationships given above, each measured hypercomplex data point can be converted into a complex value. In addition, the complex value at one or more (depending on the dimensionality) mirror-image positions can also be calculated. These complex data can then be used as the input for a complex Fourier transform in polar coordinates.

It is very important that the mirror-image reflections in the time domain be included in the calculation of the Fourier transform from complex data, as the failure to include them will result in a mixed-phase lineshape, an overlay of absorptive and dispersive lineshapes [3]. To show why this occurs, we return to the 2-D example. Looking at the x dimension alone, if the 1-D Fourier transform is calculated using the x data corresponding to positive evolution times, the resulting complex 1-D spectrum has an absorptive real component and a dispersive imaginary component, which can be expressed as A_x + iD_x, where A and D are the absorptive and dispersive lineshapes. The y signal behaves identically, with a spectrum A_y + iD_y. Since the 2-D data are the product of the x and y signals, the 2-D spectrum is the product of the 1-D x and y lineshapes, (A_x + iD_x)(A_y + iD_y), giving a final lineshape A_xA_y − D_xD_y that blends the absorptive and dispersive shapes (Fig. 17a). Adding data for an extra quadrant resolves this problem: the transform for another quadrant will also have a mixed-phase shape, but with the sign of the dispersive contribution reversed (A_xA_y + D_xD_y); when data for both quadrants are combined, the dispersive contributions cancel to leave only the absorptive lineshape (Fig. 17b).

Figure 17. Data Reflection and Lineshapes.

(a) When complex data are available for only one quadrant, the result is a mixed-phase lineshape, as shown here in a contour plot (positive values are blue contours; negative values are pale red contours). (b) By reflecting the time domain data into a second quadrant, the dispersive terms are made to cancel, producing a purely absorptive lineshape.

The problem of phase-twist lineshapes and the concept of time reversal with complex data are not, in fact, new. Early 2-D NMR experiments frequently recorded complex data, and the resulting spectra suffered from phase-twist lineshapes. One solution was to collect additional FIDs with the direction of precession for the indirect dimension reversed, and include this information in the computation of the spectrum¹⁶ [77].

There is an additional way to arrive at the full Fourier transform of a hypercomplex data set that was not discussed in the context of projections, which is to compute an explicitly hypercomplex Fourier transform. The idea of a hypercomplex Fourier transform was introduced in NMR by Ernst some years ago [3, 77], and has recently been reintroduced by the Marion and Zhukov groups [9, 14]. A hypercomplex Fourier transform can be derived by using multiple imaginary units instead of the single imaginary unit i; for 2-D, these could be designated i and j. The hypercomplex transform with hypercomplex data produces the same spectrum as the complex transform using mirror-image reflected data—the difference is the formalism that describes the operation, and the ordering of the numerical manipulations to arrive at the final result. The connections between the hypercomplex transform and the approach of using reflected data and a complex transform were nicely illustrated in a recent paper from Gledhill and Wand [78].

2.10. The Radial Sampling Point Response and the Information Content of Radial Sampling

As discussed above, the forms of ambiguity introduced by any kind of sampling are revealed in the point response of the sampling pattern. The point response for radial sampling can be derived easily thanks to the linearity of the Fourier transform: one need only add together the point responses contributed by each of the radial spokes [37]. Considering a 2-D case for the moment, since the point response of a single radial spoke is a ridge in the perpendicular direction (Fig. 6), the point response for the full pattern is a set of ridges. Accounting for the interference between the ridges, and including the weighting factor discussed in the previous section, we obtain the pattern shown in Fig. 18a. The ridges are found throughout the point response, except in a central “clear zone” where they interfere destructively. The result of applying this point response to a Lorenztian peak of finite linewidth is compared to the result from a conventional experiment in Fig. 18b. With sufficient radial spokes, the clear zone covers the entire spectrum, and the radial result is identical to the conventional one. With fewer spokes, one observes an identical peak, but surrounded by low-level ridge artifacts. This result is, of course, identical to what was observed above for filtered backprojection.

Figure 18. The Radial Sampling Point Response, and Polar Fourier Transform Results.

(a) The point response for radial sampling, plotted here for 25 radial spokes, can be separated into a ripple pattern and a ridge pattern. The ripples are the result of truncation from the finite duration of the sampling, and can be smoothed out by apodization. The ridges, which do not begin right at the peak but rather some distance from it, are the result of the radial configuration of the sampling points and are essentially a form of aliasing. The size of the “clear zone” that is free of ridge artifacts has been found to depend on the maximum evolution time in the time domain and the number of radial spokes. (b) Polar Fourier transforms from simulated radial data with 16 and 64 spokes is compared to the Fourier transform of simulated conventional data. With 16 spokes, the clear zone extends only just beyond the peak, and the ridges are seen over most of the spectrum. With 64 spokes, the clear zone extends beyond the edge of the spectrum, and thus no artifacts are seen. Reprinted from [37].

An alternative analytical derivation of the radial sampling point response can be made based on synthesizing the sampling pattern as a collection of rings rather than a collection of spokes, adding together the point responses generated by each of the rings [37, 69]. The point response for a single ring of sampling points is a Bessel function with respect to radius and a cosine function with respect to azimuth, with the order of the Bessel function determined by the number of sampling points on the ring (Fig. 19) [79]. By adding together these Bessel functions for rings of sampling points at different radii, one arrives at an expression of the radial sampling point response that is equivalent to the one derived by adding together the point responses of the individual spokes (see ref. [37], based on historical derivations for helical diffraction described in references [80, 81]). The value of this mathematical form is that it allows one to determine the parameters of the artifact pattern around each peak analytically [37]. The size of the artifact-free clear zone, the region in which the ridge artifacts cancel one another, is found to be N/πt_{r, max}, where N is the number of projections and t_r,max is the maximum evolution time for the collected data in the time domain. Further parameters of the point response can be determined1 directly from the analytical form; as a general rule, both the magnitude and coverage area of the ridge artifacts are inversely proportional to the number of projections available, and directly proportional to the resolution of the data.

Figure 19. Bessel Functions and the Radial Sampling Point Response.

The radial sampling point response can be derived analytically as the sum of a set of terms generated by the individual rings of sampling points. (a) A plot of the Bessel functions of orders zero to four, traditionally designated J₀ to J₄. (b) The Fourier transform of a single ring of sampling points is a Bessel function with respect to radius, and a sinusoid with respect to angle. This case corresponds to 10 radial spokes. (c) The case of a ring of sampling points corresponding to 16 radial spokes. Increasing the number of sampling points increases the frequency of the sinusoidal oscillation with respect to angle, and increases the order of Bessel function with respect to radius. (d) The case of a ring of sampling points corresponding to 16 radial spokes, but with a larger radius in the time domain. The result in the frequency domain is the same as (c), except scaled to have a smaller radius in the frequency domain, and therefore a smaller clear zone. Since each concentric ring of sampling points in a radial pattern has the same number of points, the terms they generate are of the same order but with different scaling, as in (c) and (d). The sum of terms like (c) and (d) for many radii generates the point response shown in Fig. 17.

The radial sampling point response illustrates how radial sampling is able to determine peak positions from a small number of radial samples. Measuring the components of a signal in various directions provides specific constraints on where the signal might be located. A single radial spoke is sensitive to modulation in the direction of the spoke, and insensitive to modulation that is perpendicular to it; the data from one spoke is thus able to constrain the position of the signal to a line perpendicular to the spoke. The way this information constrains the possible solutions is made manifest in the point response as a ridge of intensity, showing the possible positions for the peak. The actual location of the peak must be at a point that would be consistent with all of the available radial data—at a point where the ridges generated by the various spokes intersect, as in triangulation. The data on the various spokes thus collectively imply the location of the signal.

One can also view the point response as representing the ambiguity inherent in the sampling method—demonstrating that the ambiguity of radial sampling is very different from that of conventional grid sampling. Unlike grid sampling, radial sampling does not produce full-intensity aliases of each peak at regularly spaced intervals; instead, it produces low level ridges in numerous directions. The aliases in conventional sampling reflect a total inability to distinguish between a set of multiple evenly-spaced frequencies for each signal. With radial sampling, the ambiguities are observed directly as the spokes; as more spokes are added, the uncertainty from each spoke becomes less significant to the overall result, and the ridges become correspondingly less intense relative to the intensity of the peak.

The false peaks seen in FT/FBP spectra arise when the particular frequencies of the signals are such that there are multiple possible interpretations for the available data, appearing in the FT spectrum as additional points where the ridges intersect besides those corresponding to real peaks. This uncertainty is inherent in the data, and is not a function of the FT/FBP procedure. It is the same uncertainty that plagues the direct analysis of projection data by a spectroscopist in methods such as GFT—making it difficult to identify which projected peaks originate from the same signals—and that also plagues the various nonlinear reconstruction methods. It is the principal danger with any attempt to determine signal frequencies from a very small number of projections. Of course, these issues apply specifically in the context of radial sampling with a very small number of projections; when a larger number of projections are used, false peaks are no longer a problem, and the main issue with the ridge artifact pattern is that it may obscure weak peaks.

Thus the key principle underlying all radial approaches is that measuring the time domain in polar coordinates provides access to different information than measuring it in rectangular coordinates. For the highly compact peaks that comprise NMR spectra, a knowledge of the signal components in a small number of directions is in fact usually sufficient to resolve the peak positions, and indeed even the lineshapes and relative intensities. There are a great variety of processing and analysis methods for extracting this information, but the idea behind all of them is that the signal components for a small number of directions can collectively imply the locations of the peaks. Since relatively few spokes are measured, each of them can be sampled out to very long evolution times to provide high resolution information about the signals, while still reducing the overall measurement time from that of a high resolution conventional experiment. The weakness of radial sampling is that aliasing may occur when multiple signals are present, for particular combinations of sampling directions and signal frequencies, in those unfortunate cases where the signal components imply more possible peaks than there are real signals. Such ambiguity can be addressed by specialized procedures, as discussed below for GFT or projection spectroscopy, or by employing nonlinear reconstruction algorithms. It is also easily resolved by collecting more radial spokes, since it only occurs with the most extreme undersampling. For a large amount of data, all that remains of the ambiguity is a residue, in the form of the very low level ridge artifacts that appear upon the FT or inverse Radon transform.

3. THE DEVELOPMENT AND USE OF RADIAL SAMPLING IN NMR

Having described the fundamental concepts underlying radial sampling, we now turn to the story of its application in biomolecular NMR, and the development of the radial sampling techniques used today. We shall address them here in the order of their introduction, beginning with the very unusual class of experiments that marked the first use of a kind of radial sampling.

3.1. Accordion Spectroscopy

In 1981, Bodenhausen and Ernst introduced an experiment in which a chemical shift evolution period and a mixing period were incremented simultaneously from one FID to the next [82]. Because this “concerted ‘stretching’ of the pulse sequence” resembled the stretching of an accordion’s bellows (Fig. 20a), they named the method “the accordion experiment.” The context for this experiment was 2-D exchange spectroscopy, which observed processes such as chemical exchange, spin diffusion and NOE transfer by showing crosspeaks at the chemical shifts of the resonances participating in the process, as well as diagonal peaks representing magnetization that does not exchange or cross-relax [3]. Prior to the introduction of the accordion experiment, quantitatively measuring the exchange rates for such processes using exchange spectroscopy required the time-consuming collection of a series of 2-D spectra with different mixing times—in other words a 3-D experiment.

Figure 20. Accordion Spectroscopy.

(a) In an accordion experiment, the evolution time, t₁, and the mixing time, τ_m, are increased simultaneously. The expanding pulse sequence can be likened to the bellows of an accordion. (b) The sampling points in an accordion experiment trace out a radial spoke, but unlike most radial experiments, one of the two dimensions is a mixing time rather than a chemical shift. The proportionality constant relating the simultaneous increases in the two experimental parameters is κ, which determines the slope (and therefore the angle) of the radial spoke. (c) A schematic representation of the data that would result from the accordion experiment. The lineshapes of the diagonal and cross-peaks reflect the dynamics of the exchange process observed during the experiment. (d) The peaks in an accordion spectrum can be inverse-Fourier-transformed to reveal the buildup curves. Shown here are the transforms of one diagonal peak (top) and one crosspeak (bottom) from cis-decalin, measured at 240 K in a Bruker 300 MHz spectrometer. Panels (c) and (d) are reprinted from [82].

The accordion experiment made it possible to reduce three dimensions to two by measuring a tilted 2-D slice through the 3-D time domain formed by the two chemical shift dimensions and the one mixing dimension (Fig. 20b). Because the signal along the slice is the product of the sinusoidal chemical shift evolution and the envelope produced by the exchange process during the mixing period, the result after Fourier transformation is the convolution of these two effects. Thus the peaks are positioned on the tilted axis according to their chemical shifts prior to exchange, but the lineshapes are altered to reflect the dynamic process (Fig. 20c). Although the lineshapes can be analyzed directly, the authors found it more convenient to extract each peak from the projection and compute reverse Fourier transforms to recover the build-up and decay curves for the peaks (Fig. 20d). The method was first applied to study exchange rates in cis-decalin.

From the very beginning, the accordion experiment was understood to be a reduction of dimensionality (and hence data collection time) by measuring a tilted or “skew” projection of a higher-dimensional space. The mixing time dimension is significantly different from chemical shift dimensions: because it is real rather than complex, there is no issue of quadrature detection to address; and because it is not oscillatory, it affects only the lineshapes of the signals in the tilted dimensions, and not their frequencies. Thus accordion experiments do not suffer from the same issues of ambiguity as experiments that simultaneously evolve multiple chemical shift dimensions.

Since its introduction, the accordion concept has been applied to a host of similar situations, primarily for studies of small molecules, involving the repeated sampling of a 2-D spectrum as a function of some third variable (other than chemical shift). These are summarized in Table 1 [57, 82–100]. A few accordion studies date back to the early 1980s, but the technique was revived again in the second half of the 1990s. Besides exchange rates, accordion spectroscopy has been used to measure relaxation times, coupling constants, diffusion coefficients—and in a particularly elaborate case, the number of coherence transfers occuring for each crosspeak of a TOCSY experiment [88].

Table 1.

Accordion Experiments

Measurement	Sample	Experiment	Ref.
Ring inversion rate	cis-decalin	derived from EXSY	[82]
Ring inversion rate	cis-decalin	derived from EXSY	[83]
Enzyme-catalyzed exchange	phosphocreatine and ATP	derived from EXSY	[84]
Spin-lattice (T1) relaxation	N-myristyl-F-alanine	DQF-COSY	[85]
Multisite chemical exchange	4-germa-3a,4,4a,8-tetrahydro-4,4,8,8- tetramethyl-S-indacene	derived from EXSY	[86]
15N spin-lattice relaxation	Ca2+-loaded calbindin D9k	derived from EXSY	[87]
Number of successive couplings	gramicidin S	Taylored TOCSY	[88]
1H/15N scalar coupling constants	acyl carrier protein	CE-HSQC SCE-HSQC	[89]
Heternuclear coupling constants	Sucrose	HECADE	[90]
1H/13C coupling constants	sucrose and strychnine	ACCORD-HMBC	[91]
15N/13CO T1 relaxation rates	fibronectin type III domain of human tenascin	derived from 3-D HNCO	[92]
Translational diffusion coefficients	BOC-resorcinarene tetraurea and peptide T	GAUDI	[93]
Heteronuclear coupling constants	various small molecules	IMPEACH-MBC Cigar-HMBC 2J,3J-HMBC ACCORD-HMBC	[94–97]
1H/13C coupling constants	Cefuroxime	INEPT	[57]
Heteronuclear coupling constants	15N urea, Cd-EDTA and mouse (Cd7] metallothionein-1	ACCORD-HMBC	[98]
J(H,H) and J(X,H) couplings	ethyl trans-cinnamate	XLOC ACCORD J- HMBC	[99]
13C/13C couplings	ethyl trans-crotonate and jamaicamide A	ACCORD- ADEQUATE	[100]

3.2. Reduced Dimensionality

Almost as soon as the first 4-D triple-resonance experiments for backbone assignment were introduced, Szyperski and coworkers recognized two important points: that 4-D correlation information would be valuable even for small proteins, but that spreading the signals into four dimensions would be unnecessary and wasteful of measurement time when there are only a small number of signals present [47]. They proposed obtaining the same correlation information more quickly by evolving two of the nuclei as a function of a single evolution time. Because this is equivalent to multiplying the two time domain signals together, the result in the frequency domain would be a convolution, with the information from both resonances encoded in a single dimension as a split peak. As an example, they presented a (4,3)-D HACANH experiment, where the underline indicates that the C^α and N dimensions are sampled simultaneously, and where (4,3)-D indicates that the experiment measures four chemical shift dimensions using three independently incremented evolution times, with the two coevolved dimensions sharing one of the three evolution times¹⁷. The coevolution was achieved using a two-spin heteronuclear multiple-quantum coherence, with quadrature detection on the N, resulting in a final spectrum containing split peaks in the jointly sampled dimension, centered on the N chemical shift and separated by twice the C^α chemical shift (Fig. 21). The magnetization transfer pathway can be written as H^α (t₁) C^α ± N (t₂) H (t₃), with “C^α ± N” reflecting the fact that both nuclei are evolving simultaneously on the transverse plane during the evolution time t₂. The experiment was called reduced dimensionality because it collected 4-D correlation information with only three conventionally sampled evolution periods.

Figure 21. Reduced Dimensionality NMR.

Contour plot of a plane from the first reduced dimensionality experiment, the multiple quantum (3,2)-D HACANH of the mixed disulfide of E coli glutaredoxin (C14S) and glutathione, recorded on a 600 MHz spectrometer. The plane is taken at an H_α chemical shift of 4.28 ppm. Reprinted, with permission, from [47] (© 1993 ESCOM Science Publishers B.V.).

Shortly thereafter, the same authors presented a second version of this pulse sequence that did not use multiple-quantum coherences, but instead featured separate evolution periods for single-quantum C^α and N coherences, like a traditional 4-D pulse sequence [48]. Unlike in a traditional 4-D experiment, however, the pulse sequence was programmed such that the same evolution time was always used for C^α and for N; this magnetization transfer pathway can be written H^α (t₁) C^α (t₂) N (t₂) H (t₃), where the same quantity of time t₂ is used for two different nuclei evolving at two different positions in the pulse sequence. This method also gives the product of the C^α and N signals in the time domain, and their convolution in the frequency domain. Because quadrature detection is used with respect to one of the two dimensions, but not the other, the resulting spectrum shows a split peak. In this case, only the C^α chemical shift was detected in a phase-sensitive manner, so that crosspeaks were obtained at C^α ± N. This approach was demonstrated using a 2.5 mM sample of the ¹³C- and ¹⁵N-labeled mixed disulfide between glutaredoxin and glutathione. As with the multiple-quantum version, four dimensions of information were obtained while only sampling three evolution times.

These experiments were the first of what became a very large category, known by the name reduced dimensionality, that can be described as jointly sampling two (or in some cases, more) indirect dimensions with the same (or in some cases, a proportionally scaled) evolution time. If the sampling positions in the time domain are plotted, one finds that using the same evolution time in multiple dimensions results in the sampling points tracing out a radial spoke, running along the diagonal of the time domain. For the common case of two jointly sampled dimensions, the angle of this spoke is 45°. If two dimensions are incremented simultaneously by proportional but not identical amounts, the result is a radial spoke at an angle other than 45°. As described above, computing the Fourier transform along such a spoke yields what can be interpreted most easily as a convolution of the two coevolved signals¹⁸, appearing as a split peak due to the lack of quadrature detection in one of the dimensions. The center of the doublet and the size of the splitting provide the two chemical shifts. The information from two dimensions is thereby compressed into one. Because the splittings are symmetric and the doublet components appear together in the same spectrum, the data are particularly easy to analyze by hand, at least for smaller proteins with minimal spectral crowding.

The two main experimental strategies for achieving coevolution in reduced dimensionality experiments are exactly those introduced by Szyperski and coworkers in the first and second reduced dimensionality papers: (1) using multiple-quantum coherences, which physically evolve multiple nuclei simultaneously during a single evolution period (with a magnetization transfer element that we shall write as x ± y [t_coevolution]); and (2) using more conventional pulse sequences, where individual evolution periods for each of the resonances are programmed to use the same delay (with magnetization transfer elements that we shall write as x [t_coevolution] y [t_coevolution]). A number of experiments were developed using the multiple-quantum approach, which constitutes a very special case of radial sampling, where the natural properties of the coherence provide for the measurement of a 45° radial spoke¹⁹. The second strategy is more versatile, however, allowing one to vary the angle of the spoke by setting the evolution time of one dimension to be proportional to, but not equal to, that of the other. Reduced dimensionality experiments using standard evolution periods are very similar to the conventional pulse sequences from which they have been derived²⁰.

With only one exception that we are aware of, described in the next section, for their first ten years reduced dimensionality experiments were always conducted with quadrature detection on only one of the coevolved nuclei. Regardless of which experimental strategy is used, quadrature detection is accomplished in the same way, by applying one of the standard techniques to the pulses affecting the selected nucleus. Note that the splitting reduces the intensity of the peaks by half, although this is partly counterbalanced by the fact that a splitting pattern can be detected with higher confidence at lower signal-to-noise ratios than a single peak [56]. In addition, the lack of quadrature detection for any given nucleus removes the sign information about this frequency dimension, leading to the requirement that the frequency offset be set outside of the region of interest and that the spectral window be increased. The choice of which resonance to measure in quadrature can generally be made based on the preference of the spectroscopist, noting that whichever resonance is measured in quadrature will define the center points of the observed doublets, with the chemical shifts for the other resonance determining the size of the splitting [48, 56]. When one nucleus has much larger chemical shifts (as measured in Hz) than the other, it is often convenient to use the one with smaller shifts (in Hz) as the center points and the one with larger shifts (in Hz) as the splitting, since the larger splitting factors will divide the upfield and downfield components of the doublets into separate regions of the spectrum for more convenient analysis [48].

It was recognized early on that a knowledge of the center points of the doublets could be a useful aid in interpreting reduced dimensionality spectra. In the first publication to address the question of protein backbone assignment strategy using reduced dimensionality, Simorre and coworkers pointed out the advantage of using the N nucleus as the center point in (3,2)-D HNCA and HNCO experiments, allowing one to identify doublets from the N chemical shifts on the ¹H/¹⁵N-HSQC [56]. The first program for automated sequential assignment from reduced dimensionality data, introduced by the same group, required this information for its analysis [58].

An important advance was made by Szyperski and coworkers when they found a way to obtain extra peaks marking the center points, which they termed central peaks, simultaneously with the doublets themselves [59, 101]. This was achieved by taking advantage of the fact that magnetization transfer steps in pulse sequences are often incomplete. Because the residual magnetization terms left behind after each transfer step do not carry the full complement of frequency modulations, they would produce artifactural axial peaks if they were not normally suppressed by phase cycling or other techniques. However, in the particular case of the residual magnetization remaining after transfer from the first of the two coevolved nuclei, the failure to pick up the frequency labeling from the second coevolved nucleus does not result in axial peaks but rather central peaks²¹. Since this magnetization would have been wasted otherwise, there is no loss of sensitivity for the doublets when central peaks are measured. This technique was first demonstrated for a (4,3)-D HN<CO,CA> experiment²². [101], where negative central peaks and positive doublets were produced simultaneously, and was later generalized to a number of other experiments [59], with a modification allowing the doublets and central peaks to be separated onto independent subspectra during post-processing to reduce spectral crowding. The generation of central peaks became a standard feature found in many of the sequential assignment sequences developed by Szyperski, Wüthrich and coworkers [102, 103].

Reduced dimensionality can also be used to measure scalar coupling constants. An example where multiple chemical shifts are coevolved at the same time as multiple scalar couplings is the unusual experiment by Rexroth and coworkers, which they called DQ/ZQ+SQ-HNCA [104]. The coevolution of multiple chemical shifts leads to chemical shift multiplets, as in other reduced dimensionality experiments; the additional coevolution of scalar couplings results in scalar coupling multiplets overlaid on top of the chemical shift multiplets. Note that there are also many experiments in which a single chemical shift is coevolved with one or more scalar couplings (for example, [105–107]). Because the chemical shifts are evolved separately from one another, these experiments do not achieve a reduction in dimensionality, but they could be considered a kind of accordion experiment.

In most cases, reduced dimensionality without full quadrature detection was used to coevolve two dimensions—reducing 3-D experiments to 2-D, or 4-D to 3-D—but the two exceptions that coevolved more than two dimensions are each worthy of comment. Ding and Gronenborn developed a set of sequential assignment experiments that include the (4,2)-D HN(CO)CAHA and the intraresidue-only HN(COCA)CAHA, each of which coevolves three nuclei as a function of a single evolution time [51]. This results in the signal being split twice, into a quartet, which naturally raises concerns about spectral crowding. Their solution was to extend an idea that dates back to the very beginning of the method—namely the use of large chemical shifts to separate the components of chemical shift multiplets [48, 56]—in this case introducing large artificial frequency offsets via TPPI. As a result, the multiplet components appear in four different regions of the spectrum (Fig. 22a/b). Besides being the first to coevolve three nuclei as the function of a single evolution time, and besides the clever use of TPPI, their work is also interesting for including the development of exclusively intraresidue transfer sequences, and for introducing (3,2)-D HN(CO)C^α/β and intra-HN(COCA)C^α/β experiments employing TPPI for peak separation and offering central peak detection²³.

Figure 22. Reduced Dimensionality Beyond Three Dimensions.

(a) Coevolving three dimensions in a (4,2)-D reduced dimensionality experiment would produce quartets. To reduce spectral crowding, Ding and Gronenborn used TPPI to introduce large frequency offsets between the multiplet components. (b) These offsets result in a spectrum in which the multiplet components appear grouped together as four subspectra. This example is from their HN(CO)CAHA of GB1, recorded on a 500 MHz spectrometer. (Note that these are the same as the four subspectra one would obtain if one used a full quadrature radial sampling approach.) (c) For a (5,3)-D experiment, Löhr and Rüterjans grouped the indirect dimensions into pairs, with each pair separately coevolved. This produces rectangular 2-D quartets. (d) Representative planes from their experiment on the protein flavodoxin, recorded on a 500 MHz spectrometer. Panel (b) is reprinted from [51]. Panel (d) is reprinted, with permission, from [108] (© 1995 ESCOM Scientific Publishers B.V. ).

The other experiment that coevolved more than two nuclei was a (5,3)-D experiment by Löhr and Rüterjans, in which four nuclei were coevolved, but as two separate groups of two nuclei each [108]. We shall call this experiment {HACA}{CON}H, with the curly braces indicating the two groups of coevolved nuclei, according to the nomenclature later introduced by Atreya and coworkers [109]²⁴. By evolving H^α and C^α as a function of one evolution time, and CO and N as a function of a second evolution time, a 3-D spectrum is produced with the signals split into doublets on each of the indirect axes, resulting in a rectangular quartet overall (Fig. 22c/d).

The host of reduced dimensionality protein and nucleic acid assignment experiments that have been reported are summarized in Table 2 [47, 48, 56, 59, 101–104, 108, 110–118]. The “Type” column indicates for each experiment whether it uses the multiple-quantum (MQ) or individual evolution period (IEP) strategy. A point to be noted is that a number of the papers in Table 2 describe coevolving two nuclei at different rates—that is, collecting a projection at an angle other than 45°—to scale the size of the splitting to account for different relaxation rates and/or chemical shift ranges. This is especially true of experiments coevolving H^α/β and C^α/β. Many of these experiments record central peaks, as noted in the table. Several papers describe assignment strategies combining multiple experiments, beginning with the (3,2)-D experiments introduced by Marion’s group in 1995 [56, 111], and culminating in the suite of six new experiments and three previously reported experiments presented by Szyperski and coworkers in 2002 [103]. For backbone assignment with smaller proteins—as well as several other purposes—reduced dimensionality experiments provide higher-dimensional information with decreased instrument time usage, increased digital resolution and smaller data sets, in a format that can be analyzed easily by hand. With larger systems, the increased spectral crowding can lead to problems from overlap unless the doublet components are separated into different regions of the spectrum using TPPI.

Table 2.

Reduced Dimensionality Experiments without Full Quadrature Detection

Measurement	Sample	Experiment(s)†	Type‡	Ref.
Backbone assignment	mixed disulfide of E. coli glutaredoxin- (C14S) and glutathione	(4,3)-D HACANH	MQ	[47]
Backbone assignment	mixed disulfide of E. coli glutaredoxin- (C14S) and glutathione	(4,3)-D HACANH, (3,2)-D HNCA	IEPs	[48]
Backbone assignment	DnaJ, residues 2-108	(4,3)-D Hα/βCα/β(CO)NH	IEPs	[110]
Backbone assignment	Rhodobacter capsulatus cytochrome c2	(3,2)-D HNCA, HNCO	MQ	[56]
Backbone assignment	Rhodobacter capsulatus ferrocytochrome c2	(3,2)-D HNCO, HN(CO)CA, H(N)COCA, HN(COCA)H, HNCA, HN(CA)CO and HN(CA)H	both	[111]
Backbone assignment	Desulfovibrio vulgaris flavodoxin	(5,3)-{HACA}{CON}H	IEPs	[108]
Backbone assignment	Rhodobacter capsulatus cytochrome c′	(4,3)-D HNCOCA	IEPs	[112]
Backbone assignment	P14A	(4,3)-D HN<CO,CA> with central peaks, originally named COHNNCA	IEPs	[101]
Uridine HN/H6 assignment Cytidine H2N/H6 assignment	leadzyme	(4,3)-D H(NCC)CH	IEPs	[113]
Backbone assignment	N-terminal 63-residue polypeptide fragment of the 434 repressor	(4,3)-D Hα/βCα/β(CO)NH with central peaks	IEPs	[59]
Scalar coupling constants	rhodniin	(3,2)-D DQ/ZQ+SQ-HNCA	both	[104]
Backbone assignment	ubiquitin	(4,3)-D HN(COCA)NH	MQ	[114]
Sidechain carboxylate assignment and titration	N-terminal 63-residue polypeptide fragment of the 434 repressor	(3,2)-D HCCCO2	IEPs	[115]
1H/13C assignments	cyclosporin A	(3,2)-D HC(C)H-COSY with central peaks	IEPs	[116]
Backbone assignment	N-terminal 63-residue polypeptide fragment of the 434 repressor	HNCAHA, plus previously described (4,3)-D HN<CO,CA> and (4,3)-D Hα/βCα/β(CO)NH), with central peaks	IEPs	[102]
Solid state backbone assignments	N-acetyl-Valine-Leucine	(3,2)-D CONCA; (3,2)-D CANCOCA (simultaneous direct acquisition of CO and CA)	IEPs	[117]
Backbone assignments	TM1112	(4,3)-D HNCOCA and HNCACO, as a suite with time-shared 3-D HN[CA/HA] and HN(CO)[CA/HA]	IEPs	[118]
Backbone assignment	GB1	(4,2)-D HN(CO)CAHA, HN(COCA)CAHA; (3,2)-D HN(CO)Cα/β, intra- HN(COCA)Cα/β	both	[57]
Backbone, aliphatic sidechain and aromatic sidechain assignments	Z-domain of Staphylococcal protein A	(4,3)-D HACA(CO)NH and Hα/βCα/βCOHA with central peaks, HCCH-COSY, HCCH-TOCSY; (3,2)-D HBCB(CGCD)HD, TOCSY-relayed-HCH- COSY, plus previously described (4,3)-D Hα/βCα/β(CO)NH, HNCAHA, HN<CO,CA>	IEPs	[103]

^†(n,m)-D indicates that n dimensions of correlations are collected with m independent evolution times. Underlining indicates coevolved nuclei; underlined nuclei grouped in {curly braces} indicate independent sets of coevolved nuclei. (Parentheses) indicate nuclei through which magnetization is passed, without evolving chemical shifts. <Angled brackets> indicate nuclei involved in bifurcated magnetization transfer. C^CO2 represents sidechain carboxylate carbon nuclei. [Square brackets] indicate time-shared evolution of two nuclei, with diagonal slashes separating the nuclei or sets of nuclei that evolve independently. For the meaning of DQ/ZQ+SQ, please see the text. The names for some experiments have been adjusted from the original publications to maintain consistency in nomenclature.

^‡MQ indicates that the coevolution is accomplished by evolving a multiple-quantum coherence; IEPs indicates that the coevolution is accomplished with individual evolution periods.

3.3. Reduced Dimensionality with Full Quadrature Detection: GFT and Friends

An important advancement came with the introduction of reduced dimensionality experiments that employ quadrature detection in all of the coevolved indirect dimensions. As described above, with full quadrature detection several different procedures can be used to separate the multiplets of reduced dimensionality experiments into independent spectra. This has the major advantage of eliminating the spectral crowding problem of reduced dimensionality, allowing the idea of coevolving multiple nuclei to be applied to larger proteins, and allowing a larger number of dimensions to be coevolved. Also, since more FIDs are collected when compared with the single quadrature detection data, and since the data sets are summed prior to Fourier transformation, the overall signal-to-noise ratio is increased. At the same time, however, separating the multiplet components makes interpretation of the spectra more difficult, since one must identify which peaks belong to which multiplet across the spectra.

The first such experiments to be described were the full quadrature (4,3)-D doubly filtered (¹³C/¹⁵N and ¹³C/¹³C) NOESY experiments from Brutscher and coworkers, reported in 1995 [119]. These offer equal sensitivity and higher resolution when compared with their 4-D conventional counterparts, as shown in data collected on a 2 mM sample of ¹³C/¹⁵N-labeled Rhodobacter capsulatus ferrocytochrome c₂. Additionally, the added chemical shift information allowed for significantly more unambiguous assignments to be determined compared to the traditional 3-D singly filtered NOESY experiments.

There were no further reports of full quadrature detection with reduced dimensionality until 2003, when three groups independently reintroduced the idea over the period of a few months. Kim and Szyperski’s paper was published online in January of 2003 [52]; Kozminski and Zhukov submitted their paper [55] a few days later, and Bersch and coworkers [50] a few weeks after that.

Bersch and coworkers presented the (3,2)-D backbone assignment experiments HNCA, HN(CO)CA, HN(CA)CB, HN(COCA)CB, HN(CA)HA and HN(COCA)HA using a ¹³C,¹⁵N-labeled sample of the 68 N-terminal residues of the cytosolic mercuric reductase merA from Ralstonia metallidurans CH34 [50]. For each of these experiments, the full set of quadrature components is collected, and the data are then processed in the time domain by taking linear combinations of these components, as described in Section 2.5.

Kozminski and Zhukov began by demonstrating (3,2)-D HNCA, HN(CO)CA and (4,2)-D HACANH experiments on a 1.5mM ¹³C,¹⁵N-labeled ubiquitin sample at pH 6.0 [55], separating the multiplet components in the frequency domain as described in Section 2.5 above (Fig. 23). They subsequently introduced two sets of unusual and interesting experiments that combine full quadrature reduced dimensionality with multiple quantum evolution for backbone assignment. Their purposes for using multiple-quantum coherences were to improve the resolution, by eliminating peak broadening from active carbon-carbon scalar coupling, and to shorten the pulse sequence, thus improving the sensitivity. The first set consisted of HNCACB and HN(CO)CACB experiments that use two evolution periods, one for N and the second for simultaneous multiple-quantum evolution of C^α and C^β [120]²⁵. The phase cycle was designed so that this second period produces only the double-quantum term, C^α + C^β. The experiments can be run in a (4,3)-D mode with N evolved conventionally, to produce crosspeaks at (HN, N, C^α + C^β) positions, or they can be run in a (4,2)-D mode with the N evolution time set to match the carbon double-quantum evolution. The resulting two subspectra contain crosspeaks at the positions (HN, C^α + C^β + N) and (HN, C^α + C^β − N).

Figure 23. Full Quadrature Reduced Dimensionality.

When quadrature detection is used in all dimensions, it is possible to separate the multiplet components onto independent subspectra. (a) Data from the first full quadrature reduced dimensionality experiment, a (4,3)-D ¹³C/¹⁵N-filtered NOESY experiment recorded on a 600 MHz spectrometer, reported in 1995 by Brutscher and coworkers for the Rhodobacter capsulatus ferrocytochrome c₂. Crosspeaks are produced at coordinates (HC, C + N, HN) and (HC, C − N, HN), with the former appearing in the subspectrum at left and the latter in the subspectrum at right. Data are shown for HC = 4.44 ppm. (b) An example of spectra obtained by Kozminski and Zhukov from (3,2)-D HN(CO)CA (top) and HNCA (bottom) of ubiquitin, the slices showing the sequential connectivity between residues I36 and G35. The spectra were recorded on a 500 MHz spectrometer. Panel (a) is reprinted from [49]. Panel (b) is reprinted, with permission, from [55] (© 2003 Kluwer Academic Publishers).

The second set of experiments are (3,2)-D and (4,2)-D full quadrature reduced dimensionality experiments that accomplish all chemical shift evolution via a single multiple-quantum evolution period at the center of the pulse sequence, set within nested HMQC transfers to prepare and reverse the magnetization state [121]. The (4,2)-D HNCOCA thus uses a three-spin coherence to coevolve all three nuclei simultaneously, according to the transfer pathway

$$\text{HN}\mathrm{N}\text{CO}\mathbf{N}+\mathbf{\text{CO}}+{\mathbf{C}}^{\mathbf{\alpha }}({\mathit{t}}_{\mathbf{1}})\text{CO}\mathrm{N}\text{HN}(t_2),$$

where the multiple quantum evolution is indicated in bold, while the (3,2)-D HNCO, HNCA, HN(CO)CA and H(N)COCA evolve two-spin coherences. An additional element can be inserted into those sequences that evolve N that provides additional single-quantum N evolution, allowing the N chemical shifts to be scaled²⁶. These experiments are considerably shorter and use considerably fewer pulses than traditional experiments with individual evolution periods.

It has been Szyperski’s group, however, that has taken the full quadrature detection concept the farthest. Kim and Szyperski developed a formalism that they called the G-matrix, which concisely describes the time domain manipulations needed to separate the multiplet components onto different spectra [52]. If the full set of hypercomplex components are collected, applying the G-matrix gives 2ⁿ⁻¹ projections separating out the 2ⁿ⁻¹ multiplet components²⁷, where n is the number of coevolved dimensions. At the same time, they also outlined a method for analyzing the data, especially suited for experiments with many coevolved dimensions, based on a generalization of the central peak concept that Szyperski, Wüthrich and co-workers had introduced for reduced dimensionality [59, 101]. The new procedure involves recording spectra with progressively fewer coevolved dimensions (n−1, n−2, n−3, etc.); each time a dimension is removed from the coevolution, the central peak for that level of splitting is revealed. In this manner, the full splitting pattern can be resolved, and the multiplet components can be matched together. The 2ⁿ⁻¹ projections produced from the original data with all dimensions coevolved are called basic spectra, while the projections generated with fewer coevolved dimensions are called central peak spectra. Central peak spectra with n−1 coevolved dimensions are termed first-order, those with n−2 are termed second-order, and so forth. Note that central peak spectra can be obtained in three different ways: (1) in one experiment, detected simultaneously with the basic spectra using axial peak magnetization, as described above for reduced dimensionality; (2) in a separate experiment with the same pulse sequence as for the basic spectra, but with one or more of the evolution periods disabled; or (3) through independent experiments with different pulse sequences. All of these methods have been employed, with strategy (1) typically used for first-order central peaks, and either (2) or (3) for the higher orders (cf. [52, 122]).

Kim and Szyperski called their complete approach G-matrix Fourier Transform spectroscopy or GFT (later amending this to “GFT projection spectroscopy”), and they initially demonstrated it by collecting (5,2)-D HACACONH data on a 2 mM sample of the 76 residue protein ubiquitin [52]. The diagonal radial spoke was measured using the pulse sequence in Fig. 24a, incrementing all of the indirect evolution dimensions at the same rate, with the spectral width of each dimension set to the same value. Systematic phase modulation of ϕ₁, ϕ₂, ϕ₃ and ϕ₄ between 0° and 90° allows for collection of the cosine- and sine-modulated data for each evolution time (full quadrature detection). Eight basic spectra were generated by applying the G-matrix to these data (Fig. 24b). Seven additional central peak spectra were measured (Fig. 24b): four first-order in which C^α, CO and N were coevolved; two second-order in which CO and N were coevolved; and one third-order in which only N was evolved. In practice, Kim and Szyperski used a (3,2)-D HNCO for the second-order central peak spectrum and a 2-D ¹⁵N/¹H-HSQC for the third-order, while the first order were detected simultaneously with the basic spectra. The results were compared with the 2-D orthogonal projections of a conventional 5-D spectrum. Total data collection for the GFT-NMR experiment was only 138 minutes on a 600 MHz spectrometer—saving several orders of magnitude in measurement time.

An important enhancement used in a number of GFT experiments is the idea of having two independent sets of coevolved dimensions. As discussed above, there was a precedent for this in the reduced dimensionality work of Löhr and Rüterjans [108], but it was not seen again until ten years later, when it was reintroduced by Szyperski’s group under the name G²FT [109]. As in the previous work, this results in splittings in two different coevolution dimensions (Fig. 25a), which now can be divided among subspectra by quadrature detection and GFT processing (Fig. 25b). The purpose of using two independent coevolution processes in the GFT sequential assignment strategy is to divide the dimensions used to separate and index spin systems from those used for matching sequential connectivities. For example, with larger proteins it may be advantageous to use the three dimensions HN, N and CO as the “fingerprint” of the protein, rather than just HN and N. By coevolving the N and CO together in all of the sequential assignment experiments, the same signature can be observed for each spin system in each experiment. The C^α and C^β connectivities can then be coevolved as a separate grouping, with the splitting in a different dimension, allowing forward and reverse connectivities to be identified easily.²⁸. The result is a straightforward walk-through of the sequence. Fig. 26c shows how the data for this assignment strategy would appear.

Figure 25. G²FT.

(a) Echoing the previous work of Löhr and Rüterjans, Atreya and coworkers introduced GFT experiments with multiple groups of coevolved dimensions. (b) Because they use full quadrature detection, however, Atreya and coworkers were able to separate the multiplet components onto independent subspectra. Any individual subspectrum will show only one of the muiltiplet components (filled circle) and omit the others (unfilled circles). (c) Atreya and coworkers designed their experiments to facilitate sequential assignment, grouping together the N and CO dimensions as one coevolved group, to produce a reduced dimensionality “fingerprint” for each residue, and grouping together C_α and C_β as a second group, giving each connectivity its own unique signature.

Figure 26. Geometric Relationship Between Projections and the Full Spectrum.

A 3-D contour plot of the lower-value reconstruction of the (3,2)-D HNCO of GB1 is shown here, along with three of the projections used in its reconstruction. Residue F52 is highlighted.

For measuring couplings—in particular residual dipolar couplings—Atreya and coworkers introduced an interesting variant on these concepts [123]. Instead of coevolving multiple chemical shifts, they coevolve multiple couplings. In order to be able to separate the multiplet components into independent subspectra, each coupling evolution must be measured in quadrature—but the natural evolution of spin-spin couplings produces only sine modulation. To obtain cosine-modulated coupling evolution they introduced a delay, sized to shift the phase of the signals by 90° on average. Because the delay cannot be correct for all of the spins, it is necessary either to introduce a phase correction or to use a mirror image processing technique, where a second spectrum is collected with the direction of coupling evolution reversed. One of the most important elements in this work is the presentation of a general approach to phase correction in radially sampled data, which for this application was used as part of an iterative method for correcting the phase errors introduced by the use of an average delay for the synthetic cosine channel²⁹. Using these techniques, a (6,2)-D experiment was implemented where only the N and HN chemical shifts are evolved, while the sum of the scalar and residual dipolar couplings (denoted as K) are measured for the pairs of nuclei C^α–H^α, C^α–CO, N–CO and N–HN. The peaks in the resulting basic spectra are thus found at the positions N ± ½K_N–H ± ½K_N–CO ± ½K_Cα–CO ± ½K_Cα–Hα; four orders of central peak spectra are used to untangle the encoding.

Given that many other methods for accelerating NMR have been introduced in recent years, it should perhaps come as no surprise that several groups have combined full-quadrature reduced dimensionality with other, complementary techniques for reducing measurement time. Szyperski’s group has introduced a number of GFT experiments that feature optimization of the proton longitudinal relaxation (designated by a prefix “L-”), so as to reduce substantially the delay needed between NMR transients [124]. In addition, Szyperski’s group has introduced a (4,3)-D GFT-NOESY experiment that uses the time-shared technique to combine an N/N, a C^aliphatic/N and a C^aliphatic/C^aliphatic NOESY into a single experiment [125]; a similar experiment was later published by a different group [126]. Finally, Sun and coworkers have shown that reduced dimensionality can be combined with nonuniform sampling and maximum entropy reconstruction to obtain an additional reduction in measurement time [127]. In their HC(CO)NH-TOCSY experiment, they used random sparse sampling and MaxEnt reconstruction in both the N dimension and the jointly-sampled HC dimension.

Full-quadrature reduced dimensionality has been applied extensively in structural genomics, primarily for backbone and sidechain assignment, as well as to a number of other purposes—including even a solid state experiment [128]. Table 3 summarizes the many experiments that have been reported, listing both the introduction of new pulse sequences as well as a few cases where previously reported pulse sequences were applied to novel problems [49, 50, 52, 55, 109, 120–134].

Table 3.

Full Quadrature Reduced Dimensionality Experiments

Measurement	Sample	Experiment(s)†	Time‡ (hrs.)	Ref.
NOE-derived distance restraints	Rhodobacter capsulatus ferrocytochrome c2	(4,3)-D 13C/15N-NOESY (4,3)-D 15N/15N-NOESY	not given	[119]
Backbone assignment	residues 1-68 of merA from Ralstonia metallidurans CH34	(3,2)-D HNCA, HN(CO)CA, HN(CA)CB, HN(COCA)CB, HN(CA)HA, HN(COCA)HA	14	[50]
Backbone assignment	1.5 mM ubiquitin	(3,2)-D HNCA, HN(CO)CA (4,2)-D HACANH	not given	[55]
Solid-state backbone assignment	histidine	(3,2)-D MAS NCC	not given	[128]
Backbone assignment	2 mM ubiquitin	(5,2)-D HACACONH	2.3	[52]
Backbone assignments	1.5 mM ubiquitin 1.1 mM 21 kDa bovine S100A1	(4,2)-D HNCACB and HN(CO)CACB, with Cα and Cβcoevolved as an MQ coherence producing only the DQ (Cα+Cβ) peak	Not given	[120]
Backbone assignments	1.5 mM ubiquitin	(3,2)-D HNCO, HNCA, HN(CO)CA, H(N)COCA; (4,2)-D HNCOCA (all MQ)	not given	[121]
Backbone and sidechain assignments	1.4 mM ubiquitin	(3,2)-D HNCO, HNCACB, HN(CO)CACB, HN(CA)CO, HNCA, HN(CO)CA, CBCANH, CBCA(CO)NH, C(CCO)NH, H(CCCO)NH	18	[129]
Backbone and Cβ assignment	2 mM ubiquitin, 1 mM TT212	(5,2)-D intra-HACACONN and HACACONH; (5,3)-D intra-<HACA,CO>NH and HACACONH; (4,3)-D intra-<CBCA,CO>NH and CBCACONH	42.6, 62.6	[122]
Backbone and sidechain assignments	1 mM 17 kDa ER75, 1 mM 13 kDa PfR13, 2 mM ubiquitin	(4,2)-D HCCH; (4,3)-D Cα/βCα(CO)NH, L- HN(CO)Cα/βCα, HNCα/βCα and L-HNCα/βCα; (5,3)-D Hα/βCα/βCα(CO)NH and HCCCH; (6,3)-D Hα/βCα/βCαCONH	224, 32, 68.8	[124]
Backbone and sidechain assignments [also reported structures using non-GFT time-shared NOESY]	8 targets from the NESH consortium, at ~1 mM each	(4,3)-D Hα/βCα/β(CO)NH and HCCH [plus previously published (4,3)-D Cα/βCα(CO)NH, L- HN(CO)Cα/βCα; and (5,2)-D HACACONH]	26 to 214	[130]
Structure determination: backbone assignments by previously published protocols; distance constraints from GFT NOESY	1 mM 14 kDa YqfB	(4,3)-D [HCali/HN]- NOESY-[CHali/NH], which is a time-shared NOESY experiment detecting HCali HCali, HN HCali HCali HN and HN HN [assignment by previously published experiments]	16.9+, 39	[125]
Dynamics of aromatic rings	21 kDa HR41, 13 kDa MAR11	(4,3)-D L-HCCH and L- TROSY-HCCH	24, 0.42	[131]
Backbone assignments	0.8 mM 17 kDa yqbG, 13.5 kDa rps24e, 8 kDa protein Z-domain, ubiquitin, 13.5 kDa rps24e	various combinations of (5,3)-D HN{NCO} {Cα/βCα}, intra-HN{<N,CO>} {Cα/βCα}, intra-HN{<N,CO>} {Cα/βHα}, {HαCα}{CON}NH HN{NCα}{Cα/βCα}, HN{N(CO)Cα}{Cα/βCα} and (6,3)-D {Hα/βCα/βCα}{CON}NH, with and without L-optimization and/or TROSY	7 to 44	[109]
Residual dipolar couplings	8 kDa protein Z- domain	(6,2)-D (HA-CA-CO)-N- HN	24	[123]
Sidechain assignments	Nck Sh3-1	(4,3)-D HC(CO)NH- TOCSY, with nonuniform sampling and MaxEnt reconstruction in both the combined HC dimension and the conventional N dimension	48	[127]
Membrane protein backbone And sidechain assignments	Subunit c of F1F0 ATP synthase in micelles	previously published (3,2)- D HNNCO; (4,3)-D L- HNCα/βCα, L-HN(CO)Cα/βCα HCCH; (4,2)-D HACA(CO)NH; (5,3)-D intra-HN{<N,CO>}{Cα/βCα} and {Cα/βCα}{CON}NH	118	[132]
Scalar coupling constants	9.5 kDa M-crystallin 16.2 kDa Eh-CaBP	(3,2)-D quantitative-J HNHA, HNHB	1.5 to 18	[133]
Pseudocontact shifts	8.5 kDa calbindin	previously published (3,2)- D HNCO, HN(CO)CA, HN(COCA)CB, HNHA	7.5	[134]
NOE-derived distance restraints	1.4 mM ubiquitin	(4,3)-D time-shared NOESY detecting HN CH and HN NH	48	[126]

^†(n,m)-D indicates that n dimensions of correlations are collected with m independent evolution times. Underlining indicates coevolved nuclei; underlined nuclei grouped in {curly braces} indicate independen sets of coevolved nuclei. (Parentheses) indicate nuclei through which magnetization is passed, without evolving chemical shifts. <Angled brackets> indicate nuclei involved in bifurcated magnetization transfer. intra- indicates that only the intraresidue peaks are detected. [Square brackets] indicate time-shared evolution of two nuclei, with diagonal slashes separating the nuclei or sets of nuclei that evolve independently. L- indicates that longitudinal relaxation optimization is used. Hyphens between nuclei indicate that the coupling between the nuclei are evolved. The names for some experiments have been adjusted from the original publications to maintain consistency in nomenclature.

^‡The measurement times represent the time reported for running the set of experiments on the sample, or a range of times for multiple samples. Where multiple individual times are listed on separate lines, they correspond to the samples listed in the sample column, and are in the same order. For the YqfB structure determination, a+b indicates a hours for the assignment experiments and b hours for the NOESY.

3.4. Projection-Reconstruction NMR

Projection-reconstruction NMR (PR-NMR) was originally proposed by Kupče and Freeman in 2003 [53, 135]. As with the methods in the preceding section, PR-NMR involves collecting data by phase-sensitive joint sampling of multiple indirect dimensions; unlike with these other methods, in PR-NMR one measures multiple projections (multiple radial spokes) at varying angles, instead of just the diagonal, and one uses these to reconstruct the full multidimensional spectrum, rather than analyzing them directly. While the need to reconstruct images from projections is a common problem in many scientific fields, in most of these the image to be reconstructed is a continuously varying density, necessitating the collection of large numbers of projections. In contrast to this, PR-NMR involves the reconstruction of relatively sparsely populated spectra comprised of sharp, compact peaks, and only a handful of projections are needed for high-quality reconstruction in favorable cases, such as backbone assignment. For higher-dimensional spectra (4-D and beyond), the time savings for PR-NMR, as with RD and GFT experiments, can be orders of magnitude.

The projection-slice theorem [35, 39], discussed earlier, provides the basis for obtaining projections from radial slices taken at varying angles through the time domain [53]. Along a single slice, the evolution times for the indirect dimensions are incremented simultaneously at a fixed ratio that defines the projection angle. With two indirect dimensions the calculation of the evolution times is straightforward [53]; for more dimensions, it can be helpful to use direction cosines [43]. It is necessary to adjust the spectral width to avoid the aliasing of projected peaks [43]. The hypercomplex data for each slice must be converted to complex data prior to computing the Fourier transform, which yields projections at mirror-image angles as described previously [43, 53, 136]. The geometric relationship between the projections and the full spectrum is illustrated for a simple case with two indirect dimensions in Fig. 26.

The first demonstration of PR-NMR was a (3,2)-D HNCO experiment on ubiquitin conducted by Kupče and Freeman [53]. They measured projections at 0°, 30° and 90° from the CO axis, over a total data acquisition time of 29 min 11 s. The 30° projection was recorded in full quadrature, as four hypercomplex components, which were then converted into complex data for the mirror-image projections at 30° and 150°. As a control, they recorded a conventional 3-D HNCO at the same resolution in 18 h 54 min of acquisition time. The two versions were described as “indistinguishable,” except that the reconstruction was carried out successfully at twice the digital resolution of the conventional control (Fig. 27).

Figure 27. The First Projection-Reconstruction NMR Experiment.

Comparison of the 2-D planes at HN=8.77 ppm for the projection-reconstruction (left) and conventional (right) HNCO spectra of ubiquitin. Reprinted, with permission, from [53] (© 2003 Kluwer Academic Publishers).

This first example was quickly followed by demonstrations of PR with 4-D and 5-D spectra, using the lower-value reconstruction method described above [43, 136, 137]. In an effort to make PR-NMR feasible for applications with poor intrinsic sensitivity, Kupče and Freeman proposed the use of backprojection as an alternative to the lower-value method [70]. In doing so, one vastly improves the sensitivity of the experiment, albeit while introducing some artifacts. In a later publication [138], Kupče and Freeman suggested suppressing artifacts from backprojection reconstruction using a variation on the nonlinear CLEAN algorithm from radioastronomy [139]. This involves locating the strongest peak in the reconstruction, which one can safely assume to represent a real signal. From the position of this peak, one can calculate its projected image for each of the projection directions, and subtract these images from the projection data. A subsequent reconstruction will be missing both the peak and its artifacts, and the next strongest peak can safely be assumed to be a real peak, since any artifacts from the stronger first signal have already been removed. This process is repeated iteratively to determine a list of the true signals, which are then reintroduced artificially without artifacts. This method was shown to be successful for an HNCO spectrum on a 187-residue protein.

Like reduced dimensionality, PR-NMR was originally conceived as a way to reduce the time needed to obtain higher-dimensional information for the backbone assignment of relatively small proteins. It is not limited to such applications, however. By using a slightly larger number of projections (on the order of 20–30 rather than 5–10) and a reconstruction algorithm that is able to capitalize on the combined sensitivity of multiple projections, it is possible to apply these methods to protonated and perdeuterated proteins with higher molecular weights [71, 72]. Under these circumstances, a certain amount of signal averaging and, therefore, instrument time is required in order to achieve reasonable signal intensities. Instead of aiming to reduce instrument time significantly, as is the goal with small proteins with ample signal intensity, the goal becomes the maximization of resolution and dimensionality in order to best separate the signals, using whatever instrument time is needed to meet the sensitivity requirements. Since signals from large proteins relax too quickly to allow for reasonable signal-to-noise ratios in most (5,2)-D and higher PR-NMR experiments, due to the length of the pulse sequence and the number of magnetization transfers and selections, (4,2)-D experiments offer the best compromise between resolution and sensitivity [72]. Compared to conventional 4-D experiments, the (4,2)-D PR-NMR experiments can be collected at much higher resolution while using significantly less instrument time.

Venters and coworkers introduced a suite of (4,2)-D backbone assignment pulse sequences for this purpose, and at the same time introduced the hybrid backprojection/lower-value or HBLV algorithm, described above [72]. These methods were demonstrated using human carbonic anhydrase II, a 29 kDa protein, and calbindin D_28k, a 30 kDa protein [72]. The samples were labeled with ¹³C and ¹⁵N and perdeuterated, and eight radial spokes were collected over 20–40 hours for each experiment (yielding 23 projections after reflection). By configuring the hybrid algorithm to add together groups of eight projections, sufficient signal intensity was accumulated to detect almost all expected peaks, while still suppressing artifacts effectively (Fig. 28a–e). The backprojection method was shown to be ineffective in this case due to peak broadening and the presence of artifacts, while many signals could not be detected when using the lower-value algorithm due to the lack of signal accumulation (Fig. 28f–h). The 4-D data made it possible to assign some resonances that could not be assigned from the conventional 3-D data available previously.

Nor is PR-NMR limited to backbone assignment. Shortly after the demonstration of (4,2)-D backbone assignment on HCA II, a PR-NMR (4,2)-D methyl-amide NOESY experiment on the same protein was reported (Fig. 29) [71]. This study was the first to use FBP in NMR. In this application, sensitivity was at a premium, requiring a method that would extract the maximum signal intensity possible from the input data. At the same time, the broadening of plain backprojection made that method ineffective (Fig. 29e), and the hybrid method was deemed unacceptable firstly because it could not provide the accurate peak shapes and volumes needed for quantitative interpretation of the NOESY spectrum, and secondly because of concerns about false peaks from the lower-value analysis given the number of true signals expected. A large number of projections was needed—100 radial spokes were collected, producing just under 400 projections after mirror-image reflection—but the savings in measurement time over a conventional experiment at the same resolution was still orders of magnitude. The final experiment required 88 hours but needed only 5% of the measurement time that would be required for a conventional 4-D experiment with the same resolution.

The questions of how many projections to collect and which angles to use are two of the most important arising in PR-NMR. For filtered backprojection, Fourier transform theory states that any kind of nonuniform distribution of projection directions will lead to distortion of peak shapes, and provides analytical expressions relating the distribution and size of spectral artifacts to the number of uniformly distributed projections used in the calculation. Thus a uniform distribution should be used, and the choice of how many projections to collect can be made, without regard to the number of peaks, by calculation from these formulas based on the dynamic range needed to resolve the peaks.

The nonlinear methods present the possibility of getting by with far fewer projections than FBP would require, provided that there are only a small number of peaks, and provided that accurate peak lineshapes and volumes are not needed. It would seem that in many cases there is a unique, minimal set of projections that most efficiently and effectively resolves a particular distribution of signals—for example, in Fig. 13a two projections are sufficient if the directions are chosen correctly. However, determining such a minimal set would seem to require a priori knowledge of the signals, which is not usually available. For the lower-value and HBLV algorithms, if one has an estimate of the number of signals present, an upper bound on the number of projections needed can be predicted according to a formula given by Venters and coworkers [72]. To go further requires calculating a provisional map of potential signal locations using the orthogonal “first planes” of the spectrum, and then determining the set of projections that will most effectively resolve which of these provisional signal locations actually contains a signal. Two algorithms have been suggested for this. Kupče and Freeman evaluate the “skyline projection” or silhouette of the provisional peak lattice for a number of different angles, and choose angles based on which directions show minimal overlap of provisional peak sites [70]. The second method was presented recently by Gledhill and Wand, who use a geometric analysis of a lower-value provisional signal map and the projection vectors to identify which of the provisional signals could be artifacts, and to select the angle most likely to resolve the ambiguity [140].

The reported applications of the projection-reconstruction approach are summarized in Table 4 [43, 53, 70–72, 136, 137, 141, 142]. A software package for calculating reconstructions, PR-CALC, has been released [44].

Table 4.

Projection-Reconstruction Experiments

Measurement	Sample	Experiment(s)†	Reconst. Alg.‡	Time (hrs.)	Ref
Backboneassignment	1mMubiquitin	(3,2)-D HNCO	LV	0.49	[53]
Backboneassignment	1mMubiquitin 1.7 mM HasA	(3,2)-D HNCA, HN(CO)CA,HNCO	LV	1.5 0.56	[141]
Backboneassignment	1mMubiquitin	(4,2)-D HNCOCA	LV	0.63	[136]
Backboneassignment	3mMnucleaseA inhibitor	(4,2)-D HNCOCA	LV, BP	0.58	[137]
Backboneassignment	2mMproteinGB1 domain	(5,2)D HACACONH	LV	1.45	[43]
Backboneassignment	3 mMnucleaseA inhibitor	(3,2)-D HNCA	LV, BP	1.0	[70]
Backboneassignment	0.94 mM HCA II 0.9 mMcalbindin D28K	(4,2)-D HNCACB, HN(CO)CACB, intra- HNCACB, HNCACO, HNCOCA, HNCOi-1CAi HACA(CO)NH, HACANH	LV, BP, HBLV	307.2	[72]
Backboneassignment	1.7 mM HasA	(3,2)-D HNCO	BP with CLEAN	0.83	[138]
Backboneassignment	1.7 mM HasA	(3,2)-D HNCO	LV, BP, Others	not given	[152]
Sidechainassignments	1mMproteinGB1 domain	(4,3)-D HC(CCO)NH and intra-HC(C)NH	LV	47.5	[142]
NOESY	0.9 mM HCA II	(4,2)-D methyl-amide NOESY detecting CH3 NH	FBP	88	[71]

^†(n,m)-D indicates that n dimensions of correlations are collected with m independent evolution times. Underlining indicates coevolved nuclei; underlined nuclei grouped in {curly braces} indicate independent sets of coevolved nuclei. (Parentheses) indicate nuclei through which magnetization is passed, without evolving chemical shifts. intra- indicates that only the intraresidue peaks are detected. The names for some experiments have been adjusted from the original publications to maintain consistency in nomenclature.

^‡LV = lower-value, BP = backprojection, HBLV = hybrid backprojection/lower-value, FBP = filtered backprojection. Ridge and Mandelshtam’s method [73] has not been demonstrated on experimental data. Yoon and coworkers reported several methods which we have classified as “iterative model-fitting” and which are discussed in that section.

3.5. Projection Spectroscopy

The PR-NMR ideas of collecting multiple radial spokes at varying angles, and of interpreting the Fourier transforms of these as projections, inspired a number of efforts— not all of them involving reconstruction. Several groups recognized that the information needed for sequential assignment, namely the chemical shifts of the signals, might be derived directly from the projections without going through the calculation of a reconstruction. This is, of course, a similar premise to reduced dimensionality and GFT, except that in the series of experiments loosely classed under the name projection spectroscopy, there is an explicit intention to use multiple projections at varying angles to overcome overlap problems. There is also a shift in strategy towards automated analysis of the projections, it being considerably easier for a computer to cope with varying projection angles than a human. This automated analysis could in principle follow (1) the “bottom-up” reasoning of GFT, built on the interpretation of splitting patterns via central peak spectra; (2) the geometric reasoning illustrated in Fig. 13, where the potential locations for the peaks are determined by finding the intersection points of vectors extended from each projected peak; or (3) the model-fitting approach. In practice, the latter two have received significant attention, and will be considered in this section and the next.

The challenge of the geometric approach, employed by Hiller and coworkers in their automated projection spectroscopy (APSY) method [143], is finding a robust algorithm for identifying which intersection points correspond to real peaks. Their answer to this problem is to use a kind of cross-validation. They determine candidate peak positions by taking a subset of the projections and intersecting the projection vectors, and then calculate a self-consistent assignment of the projected peaks to the intersections via a deterministic algorithm favoring the most likely possibilities. This alone is not likely to lead to a correct result in every case, but by repeating this procedure for different randomly-chosen subsets they are able to arrive at a consensus answer with the confidence of having explored the solution space rather thoroughly.

The original demonstration of APSY was done using a (4,2)-D HNCOCA experiment and a (5,2)-D HACACONH experiment [143]. For the former, a total of 27 projections were recorded on a 6.9 kDa protein, using four hours of measurement time. After computing the Fourier transform of each projection, peaks were picked with the ATNOS program, and the peak lists were input to the program GAPRO (geometric analysis of projections) which carries out the APSY analysis. The automated procedure correctly placed 59 of the 60 signals present, having missed only the weak signal from the N-terminal residue, and listed no false signals. The second experiment was applied to a 12.4 kDa protein. A total of 28 projections were recorded in 11 hours, and the final list of signals included all expected signals, and no false ones.

An impressive and important body of work followed, including the complete backbone assignments for the two proteins used in the original APSY study, utilizing data from a 6-D APSY-seq-HNCOCANH sequence [144]; assignment of unfolded proteins using 7-D APSY-seq-HNCO(CA)CBCANH experiments [145]; assignment of aliphatic sidechain resonances using the 5-D APSY-HC(CC-TOCSY)CONH experiment [146]; and the automation of the sequence-specific protein resonance assignment process using APSY data and a fragment-matching algorithm, MATCH [147]. An extremely useful and practical guide for successfully implementing the APSY approach to the protein assignment problem has recently been published providing specifics regarding experiment selection, optimization of data collection and spectral analysis recommendations [148].

Any potential set of signals determined by matching together peaks on projections originating from the same signal can be tested by backcalculating the projection peak frequencies from the proposed signals and comparing to the frequencies of the peaks on the experimental projections. This idea is the basis for the EVOCOUP algorithm from Malmodin and Billeter [149], which evaluates all possible combinations of projected peaks as to possible signals, and has also been incorporated into a recent version of APSY as a means of validating potential solutions determined in the geometric algorithm [148].

3.6. Applications of Iterative Model-Fitting to Radial Data

Several groups have reported efforts to use iterative model-fitting algorithms with radially sampled NMR data. The algebraic reconstruction technique (ART), developed in the medical imaging community in the early 1970s [150], is in many ways the prototypical iterative model-fitting method. Although this method has not actually been applied in protein NMR, it was employed in the first magnetic resonance imaging (“zeugmatography”) experiments, conducted by Paul Lauterbur and coworkers in the early 1970s [151], and its historic importance seems an appropriate justification for its inclusion here (cf. [40] and [42] for comprehensive discussions of its use in imaging).

ART is built specifically around the fact that the projection values are integrals of the spectral intensities [150]. A system of linear equations is constructed describing each sampled projection intensity as the sum of a set of voxel intensities from the spectrum (Fig. 30), which is then solved for the unknown spectral intensities given the known projection data. Traditional matrix inversion techniques could presumably be used to solve this problem, but the size of the system of equations has historically made it more feasible to do so by iterative methods. In these, the proposed spectrum is the model, and the search algorithm adjusts the proposed spectrum to obtain agreement between calculated projection values from the system of linear equations and the observed projection values. Because this problem is often underdetermined, some versions of ART incorporate a regularization procedure to bias the process towards a more likely solution out of the various ones that might be consistent with the data.

Figure 30. The Algebraic Reconstruction Technique.

ART is based on the fact that projection values are integrals of the spectrum along lines. The spectrum is divided into discrete elements, here 2-D pixels numbered S(x, y). For an individual observed projection value, such as point A at left, one can write a linear equation describing the projection intensity as the sum of weighted contributions from the pixels of the spectrum. To determine the weight for a specific pixel on a specific projection point, one extends vectors from the projection across the spectrum (dashed lines) and determines the overlap integral. For example, the weight of pixel S(2, 2) on the orange projection point is determined by the area of the region U, while that of S(3, 3) on point B is determined by the area of region V. After defining this system of linear equations, ART proceeds by adjusting the values of S iteratively until the calculated sums agree with the observed data.

A least-squares fitting procedure, conceptually similar to ART, has been applied in NMR spectroscopy by Yoon and coworkers, in which the spectrum was iteratively adjusted to find the best least-squares fit between backcalculated projection data (presumably calculated by summation along projection vectors, as in ART, although the authors do not specify) and the experimental data [152]. Maximum entropy reconstruction also involves the iterative adjustment of model data to minimize the difference between backcalculated and experimental data, but with the crucial modification that one simultaneously seeks to minimize the power spectrum of the model, which is essentially the meaning of maximizing the information-theoretical entropy [30]. This second criterion is a regularization procedure, allowing the search algorithm to choose between models that fit the experimental data equally well. Maximum entropy has been demonstrated successfully for radially sampled data by Yoon and coworkers [152] and by Mobli and coworkers [153].

The above methods all involve the optimization of a model spectrum (or a model time domain) independently of any explicit consideration of the signals. It is also possible to develop models of the spectral data that explicitly optimize parameters for individual signals. The Monte Carlo methods demonstrated by Yoon and coworkers use such models, coupled with Bayesian reasoning about the probability of different parameter values [152]. A somewhat different approach is the multiway decomposition method, which has been used extensively with random sampling, but has also been applied to projection data by Malmodin and Billeter in their program PRODECOMP [154]. The idea is to construct a frequency domain model for each signal in the spectrum, formed as the product of orthogonal 1-D “shapes” in each direction. No explicit functional form is assumed for the signals. The projection data can be backcalculated from these shapes via convolutions: the projected shape is simply the convolution of the 1-D shapes (cf. Section 2.4 above). Iterative numerical optimization is used to find the best model, as evaluated by comparing the backcalculated data to the experimentally observed projections.

Mueller has very recently explored extending the PRODECOMP approach by using deconvolution as well as convolution [155]. This suggests several possibilities for new data analysis procedures based on generating the 1-D “shapes” by deconvolution from the tilted projection data and checking them against the observed signals on the orthogonal first planes.

One of the most interesting methods to be introduced for utilizing radially sampled data is the HIFI algorithm from Eghbalnia and coworkers [156]. HIFI runs on the spectrometer itself and directs the data collection process, deciding in real time whether to collect additional projections, and in which directions. HIFI iteratively optimizes a model in which the frequency domain spectrum is divided into voxels, each of which is considered to have a certain probability of containing a signal. The initial probabilities are estimated using the conventional “first planes” of the experiment, as well as a priori information from, for example, the BioMagResBank frequency distributions for the type of resonance in question. On the basis of this probability map, HIFI calculates the projection angle that should provide the most information for determining which possible signals are real, and it directs the spectrometer to collect this projection. An updated probability is then calculated for each voxel according to Bayes’ rule, incorporating the prior probability as well as a new probability estimate derived from the projection. This process is continued until the probability model predicts that only negligible information could be obtained by measuring more projections, at which point a list of signal frequencies can be generated from the model according to the probabilities in the voxels.

In the original report introducing HIFI, the approach was tested using several proteins—brazzein (54 residues), ubiquitin (76 residues), mouse protein Mm202773 (101 residues), Anabaena variabilis flavodoxin (179 residues) and Prp24_12 (166 residues)— and several experiments, including (3,2)-D HNCO, HNCACB and CBCA(CO)NH [156]. The results were compared against peak lists generated by conventional 3-D data sets with manual peak picking. HIFI NMR was able to identify 98–100% of the correct peaks automatically when compared with manually picked conventional 3-D data, in one-tenth to one-fourth of the spectrometer time. In a subsequent publication, the same group extended HIFI NMR to the measurement of small N-CO residual dipolar couplings in proteins (HIFI-C) using a 3-D quantitative-J experiment [157].

3.7. Polar Fourier Transforms

The most recent major idea to be introduced regarding the use of radially sampled data is its processing by Fourier transforms in polar coordinates [14, 37, 75]. As we showed [37], filtered backprojection is in fact essentially identical to one implementation of the polar Fourier transform (PFT), and thus the projection-reconstruction NOESY experiment processed by FBP that was reported in 2006 [71] was arguably also the first demonstration of a radially sampled dataset being processed by PFT. Almost immediately thereafter, however, came the nearly simultaneous publication by three different groups of papers explicitly considering PFT processing. The first of these, by Kazimierczuk and coworkers [14], discussed direct computation of the Fourier transform of radial data using the traditional discrete Fourier transform equation, modified in similar fashion to Ernst and coworkers [3, 77] with quaternions to handle hypercomplex data. This equation is not specific for polar cases, but can rather be applied to any kind of sampling. One weakness of this study was that no weighting (or “filtering” in FBP parlance) was used to correct for the sampling distribution. The method was demonstrated using the (3,2)-D HNCO spectrum of ubiquitin, calculated from three radial spokes at 4.5°, 45° and 85.5°. Note that the quaternion calculation is equivalent to the reflection method derived from the projection interpretation, as illustrated by the presence of mirror-image artifact ridges in the reported spectra (Fig. 31a).

Figure 31. NMR Spectra Computed from Radial Samples with the Polar Fourier Transform.

(a) C/N plane at HN=6.28 ppm from the HNCO spectrum of ubiquitin recorded on a 500 MHz spectrometer, as calculated from radial spokes at 4.5°, 45° and 85.5° by a hypercomplex Fourier transform. Note that the hypercomplex transform supplied with data for the +t_x +t_y quadrant automatically produces the symmetric ridges one would expect using a complex transform with data for both the +t_x +t_y and +t_x −t_y quadrants. (b) C/N plane at HN=8.54 ppm from the HNCO spectrum of ubiquitin recorded at 600 MHz, calculated in subpanel (1) from 18 radial spokes with artificially added noise, in (2) from 18 radial spokes with the natural experimental noise, and in (3) from a subset of 6 out of the 18 radial spokes, in all cases by a hypercomplex transform. Panel (a) is reprinted from [14]. Panel (b) is reprinted, with permission, from [75] (© 2006 Springer).

The other two papers appeared very shortly thereafter. Marion cited the PFT as a linear alternative to the non-linear reconstruction methods being used, recognizing that the artifacts observed upon computing the Fourier transform are a type of aliasing due to undersampling or uneven sampling [75]. By applying appropriate weighting to correct for the distribution of sampling points, proper peak shapes are obtained, although ridge artifacts cannot be prevented. This weighting was derived by introducing the change in the coordinate system into the standard discrete Fourier transform equation. Marion also employed a quaternion formalism to enable the processing of hypercomplex data. Results were shown for a (3,2)-D HNCO experiment on the protein ubiquitin, using 18 radial spokes (Fig. 31b).

Coggins and Zhou covered the same subject matter as the other two, but also presented a theoretical treatment of the undersampling artifacts, by reference to linear response theory, and pointed out the connection to filtered backprojection reconstruction, and the possibility of using that method as a faster way to carry out the polar Fourier transform [37]. Unlike the others, this paper used the hypercomplex-to-complex conversion approach to handle quadrature-detected data, obtaining the same kind of result as for the quaternion methods. The approach was demonstrated using the (3,2)-D HNCO spectrum of the 19 kDa protein OTU, computed with either 12 or 48 radial spokes. As predicted by theory, 48 radial spokes provides sufficient sampling that artifacts are not produced, whereas a dataset with only 12 spokes is undersampled and produces ridge artifacts upon PFT.

These studies provided the launching point for all three groups to begin exploring sampling patterns other than radial sampling. Kazimierczuk and coworkers explicitly considered spiral sampling in the same paper with radial sampling [14], and went on in subsequent publications to focus on purely random sampling [8, 10, 158]. Marion likewise moved on to random sampling [9], whereas Coggins and Zhou proceeded to develop sampling patterns based on concentric rings and shells [12, 13]. The study of alternative sampling coupled to Fourier transform processing is ongoing.

4. CONCLUSIONS

In the nearly three decades since the first accordion spectroscopy experiment was demonstrated, radial sampling methods have proven again and again, and in numerous guises, to be of great utility as a means for accelerating NMR data collection. By evolving two or more signals simultaneously—or in the case of the accordion experiments, by coevolving a signal as well as some other experimental parameter, such as a mixing time—high resolution, high-dimensionality information can be obtained rapidly, often in orders of magnitude less time than for an equivalent conventional experiment. This has made it possible to shorten routine data collection for many systems, and has facilitated a number of experiments with four or more dimensions that were not previously practical. Although radial experiments have been used most commonly for the backbone sequential assignment of small proteins, they are by no means restricted to this one application, as their use for scalar and residual dipolar coupling, TOCSY, NOESY and many other experiments, for both small and large proteins, would indicate. While radial methods have their limitations, they have also clearly been of great value, as nearly thirty years of experience has shown. The idea of improving the efficiency of NMR data collection via coevolution has been turned to again and again—and has resulted in impressive successes, again and again. It is likely that radial sampling will continue to be an important tool for addressing challenging biomedical questions by NMR in the years to come.

GLOSSARY

accordion spectroscopy

a method whereby one or more mixing times are incremented simultaneously with the chemical shift evolution time of an indirectly observed dimension.

algebraic reconstruction technique (ART)

an algorithm for reconstruction of a function from its projections, which relies on the fact that the intensity measurements on the projections are integrals of the intensity values in the original function. This allows one to construct a system of linear equations relating the function values to the projection values, which system can be solved iteratively to yield the spectrum.

aliasing

a situation wherein artifactural intensity appears in a spectrum due to uncertainty about signal positions, as a result of insufficient sampling. The form taken by the aliasing depends on the sampling pattern.

automated projection spectroscopy (APSY)

an automated method for analyzing projection data from radial sampling experiments, based on a geometric algorithm and cross-validation.

backprojection (BP)

the process of extending a projection of a function back over the full domain of that function, along the lines over which the original function was integrated (or theoretically would have been integrated) in producing the projection. Also, a reconstruction procedure in which a spectrum is calculated as the superposition of the backprojections of all the available projections.

Cartesian sampling

the sampling of a multidimensional function at regular intervals in each dimension, so that the positions of the sampling points form a rectangular grid.

central peak

a peak which marks the center point of a chemical shift doublet. Central peaks can be obtained from the residual magnetization remaining after incomplete magnetization transfers, either simultaneously with the doublet or in a separate FID, depending on the pulse sequence.

chemical shift multiplet

a multiplet that is produced due to coevolution of two or more dimensions, centered at the chemical shift in one dimension and split by the chemical shift(s) in the other dimension(s). If quadrature detection is used in all dimensions, the multiplet members can be separated onto independent subspectra; in other experiments, quadrature detection is used only in one dimension, and the multiplet components appear together.

continuous Fourier transform

a Fourier transform computed using an integral of infinitely many samples over an infinite domain. In NMR, the notion of a continuous transform is useful primarily as a theoretical tool.

convolution

a mathematical operation that measures the degree of overlap between two functions as one is shifted along the other, the output often appearing as if the shapes of the functions were blended together.

convolution theorem

a theorem of the Fourier transform stating that if two functions are multiplied together, the Fourier transform of the product is the convolution of their individual Fourier transforms.

delta function

a function containing a single, infinitely sharp peak.

discrete Fourier transform (DFT)

a Fourier transform computed using discretely sampled data, taking the form of a summation rather than an integral. While the DFT equation can be written in a way that incorporates knowledge of Cartesian sampling, it can also be defined more generally as the sum of the available time domain measurements, regardless of the form of the sampling, after multiplication with the appropriate cosine and sine basis functions. The DFT is equivalent to computing a continuous Fourier transform of a function that is set to the measured data values at each measured evolution time, and otherwise to zero.

discrete sampling

the process of measuring the value of a continuous function at specific positions. In NMR, refers to the process of measuring a signal or set of signals at specific combinations of evolution times.

EVOCOUP

an algorithm for the automated analysis of projection data from radial experiments, which exhaustively searches the possible matchings between the peaks on the projections to determine which ones were generated by the same spin systems, and tests its matches by backcalculating the projections and comparing with the experimental data.

fast Fourier transform (FFT)

an algorithm for the computation of discrete Fourier transforms that saves a factor of log N over the traditional DFT equation, where N is the number of data points. The FFT is only applicable if the data are measured on a Cartesian grid, or can be cast onto such a grid.

filter

a process that alters the lineshape of a signal. For the purposes of this review, a filter is a function that can be multiplied with experimental data in the time domain in order to alter the lineshapes of the signals in the resulting spectrum, the alteration being governed by the convolution theorem.

filtered backprojection

a method for reconstructing a function from its projections, whereby the projections are first filtered through the application of a window function in the time domain that corrects for uneven sampling density with respect to radius, and then backprojected. It has been shown analytically that filtered backprojection is a form of the inverse Radon transform; thus with infinitely many projections distributed uniformly in all directions, filtered backprojection would yield a perfect reconstruction.

G²FT

a version of GFT spectroscopy in which the indirect dimensions are divided into multiple groups, and coevolution is carried out independently within each group, producing projections with two or more independent coevolution dimensions.

G-matrix

a formalism for calculating the coefficients to be used in time domain processing for separating the members of chemical shift multiplets. Equivalent to converting hypercomplex data defined over one quadrant (octant, etc.) of the time domain into complex data defined over multiple quadrants (octants, etc.).

G-matrix Fourier transform spectroscopy (GFT)

a method whereby the chemical shift evolution periods for two or more indirect dimensions are incremented simultaneously, with full quadrature detection in all dimensions; the resulting data are decoded from hypercomplex to complex format to separate the elements of the chemical shift multiplets (application of the “G-matrix”); and the positions of the peaks from the multiplets are analyzed to determine the frequencies of the multidimensional signals. This is equivalent to measuring a single radial spoke and decoding a set of projections in mirror-image directions.

high-resolution iterative frequency identification (HIFI)

an automated method for the collection and analysis of radially sampled data, run on the spectrometer, in which a probabilistic model of the spectrum is iteratively improved by computer-controlled measurement of additional radial spokes.

histogram method

a reconstruction method based on calculating a histogram of the intensities observed at the positions on the projections corresponding to the point being reconstructed, and taking the intensity value where the distribution is highest, roughly equivalent to the most frequent value found on the projections.

hybrid backprojection/lower-value reconstruction (HBLV)

a reconstruction method that combines backprojection and lower-value reconstruction, obtaining some of the benefits of each. In the first step, backprojection is carried out for all possible combinations of k projections, where k is specified by the user. In the second step, a lower-value comparison is made between these backprojection reconstructions.

individual evolution period reduced dimensionality

an experimental design in which the coevolution of multiple nuclei is achieved by a series of evolution periods, one for each nucleus, which are programmed to use the same or a proportionally related evolution time.

inverse Radon transform

an integral transform that computes a multidimensional function from its complete set of projections in all directions.

lower-value reconstruction (LV)

a method for reconstructing a spectrum from projections, which can be described as follows. In the first step, each projection is backprojected across an independent, empty spectrum. In the second step, a pointwise comparison is made between the spectra, taking the value that is closest to zero for each position. In practice, LV can be carried out quickly by looking up the values on the projections at the locations that correspond to the position to be reconstructed in the spectrum, and taking the one that is closest to zero.

multiple-quantum reduced dimensionality

an experimental design in which coevolution of multiple nuclei occurs by creating a multiple quantum coherence, with all of the coevolving nuclei on the transverse plane simultaneously. The resulting sampling forms a radial spoke along the diagonal of the time domain.

point response or point spread function

a function illustrating how a process such as sampling alters signals, by showing the response that is generated when the process is carried out on a signal that would constitute a point (a single infinitely sharp peak) in the frequency domain. The point response for sampling is the Fourier transform of the sampling pattern, as calculated by transforming a function that is unity at each sampling position, and zero otherwise. The pattern of intensity in a point response shows that would result were the sampling pattern to be used for data collection; it can also be thought of as a graphical representation of the sampling pattern’s uncertainty.

PR-CALC

a program for the reconstruction of spectra from projections.

PRODECOMP

a program for multiway decomposition analysis of projection data.

projection

the integral of a multidimensional function, such that it is collapsed onto a line or plane. The projection-slice theorem states that a projection of a frequency domain spectrum can be obtained by measuring a radial spoke in the time domain in the same direction as the desired projection (perpendicular to the desired direction or directions of integration).

projection-reconstruction

a method whereby radial spokes are measured in various directions and converted into projections, which are then used as input for algorithms that attempt to reconstruct the corresponding full multidimensional spectrum.

projection-slice theorem

a theorem of the Fourier transform which states that the Fourier transform of a cross-section of the time domain, computed with respect to the axis or axes of the cross-section, yields a projection of the frequency domain in the same direction as the cross-section.

projection spectroscopy

a set of methods that involve measuring multiple radial spokes, converting them to projections, and then analyzing them automatically to determine the properties of the signals.

radial spoke

a set of samples of a multidimensional time domain, arranged in a straight line passing through the origin.

Radon transform

an integral transform that computes the complete set of projections of a multidimensional function in all directions.

reduced dimensionality

a class of experiments whereby the chemical shift evolution periods for two or more indirect dimensions are incremented simultaneously with quadrature detection in only one of those dimensions, the other dimensions being measured as cosine modulation. Upon Fourier transformation, one obtains a chemical shift multiplet encoding the chemical shifts of the coevolved dimensions. The sampling is equivalent to measuring a single radial spoke.

sample

the measurement of the value of a function at a specific point in its domain. In NMR, refers to the measurement of the intensity of a signal or set of signals for a particular combination of evolution times; that is, at a particular position in the time domain.

sampling

see discrete sampling.

signal

a representation of the magnetization of a nucleus as it evolves in time, as detected directly in a receiver coil or indirectly the manipulation of quantum states in a pulse sequence. Also, a multidimensional representation of the magnetizations of multiple nuclei correlated to one another by magnetization transfers in a pulse sequence.

tomography

the process of reconstructing a function from its projections.

truncation

failure to sample a time domain signal over its full duration, leading to increased linewidth and possible baseline artifacts in the frequency domain.