Abstract
Purpose: By using Monte Carlo simulations, the authors investigated the energy and angular dependence of the response of plastic scintillation detectors (PSDs) in photon beams.
Methods: Three PSDs were modeled in this study: A plastic scintillator (BC-400) and a scintillating fiber (BCF-12), both attached by a plastic-core optical fiber stem, and a plastic scintillator (BC-400) attached by an air-core optical fiber stem with a silica tube coated with silver. The authors then calculated, with low statistical uncertainty, the energy and angular dependences of the PSDs’ responses in a water phantom. For energy dependence, the response of the detectors is calculated as the detector dose per unit water dose. The perturbation caused by the optical fiber stem connected to the PSD to guide the optical light to a photodetector was studied in simulations using different optical fiber materials.
Results: For the energy dependence of the PSDs in photon beams, the PSDs with plastic-core fiber have excellent energy independence within about 0.5% at photon energies ranging from 300 keV (monoenergetic) to 18 MV (linac beam). The PSD with an air-core optical fiber with a silica tube also has good energy independence within 1% in the same photon energy range. For the angular dependence, the relative response of all the three modeled PSDs is within 2% for all the angles in a 6 MV photon beam. This is also true in a 300 keV monoenergetic photon beam for PSDs with plastic-core fiber. For the PSD with an air-core fiber with a silica tube in the 300 keV beam, the relative response varies within 1% for most of the angles, except in the case when the fiber stem is pointing right to the radiation source in which case the PSD may over-response by more than 10%.
Conclusions: At ±1% level, no beam energy correction is necessary for the response of all three PSDs modeled in this study in the photon energy ranges from 200 keV (monoenergetic) to 18 MV (linac beam). The PSD would be even closer to water equivalent if there is a silica tube around the sensitive volume. The angular dependence of the response of the three PSDs in a 6 MV photon beam is not of concern at 2% level.
Keywords: plastic scintillation detector, energy dependence, angular dependence, Monte Carlo
INTRODUCTION
Plastic scintillation detectors (PSDs) have many advantages for ionizing radiation dosimetry,1, 2, 3, 4 e.g., water equivalence, photon beam-quality independence, dose-rate independence, linearity with dose, instantaneous readout, and high spatial resolution. All these merits make PSDs preferable to other detectors for real-time in vivo dosimetry.3, 5, 6, 7 PSDs are generally categorized as being one of two types.8 Those with cladding around the scintillating core are called scintillating fibers and those without it are called plastic scintillators. Scintillating fibers are recently developed PSDs. Their major merits are their small detector volume (roughly 1 mm3), which gives them high spatial resolution, and their cladding, which reduces the loss of optical photons. Plastic scintillators are traditional PSDs. They can be made into any size and shape and thus cladding is not used. For in-phantom dose measurements, such as percent-depth dose curves or dose profiles, the placement and orientation of PSDs are usually well controlled, thus the angular or directional dependence of PSDs are not of concern. For in vivo applications, however, since it is difficult to control and ensure the orientation of the detectors relative to the radiation source (either external beams or brachytherapy sources), the angular dependence of PSDs could be an issue and needs to be investigated. This is especially true considering the presence of an optical fiber coupled to a PSD to guide the optical light to a photodetector. Angular dependence can be axial (e.g., for typical placement, the radiation beam axis is always perpendicular to the detector axis) or azimuthal (the angle between the beam axis and the detector axis varies). Axial dependence should not exist for PSDs because of their cylindrical symmetry. In this work, therefore, we investigated only azimuthal angular dependence. Only a few studies have been published on the angular dependence of PSD responses and they considered only low-energy photon beams, a diagnostic x-ray source,9 and a brachytherapy source.5, 10 For the diagnostic x-ray source, the measurement was performed free-in-air for one revolution of a clinical computed tomography (CT) unit (operating at 120 kVp) around the detector. The signal was reduced dramatically when the radiation was incident from the back of the PSD because of the attenuation of the x ray in the optical fiber.9 It is expected that the effect would be reduced for in-phantom measurements due to scattering effect. For the brachytherapy sources, the measurement was performed in a polymethylmethacrylate (PMMA) phantom with an 192Ir high dose-rate brachytherapy source. It was found that the PSD’s sensitivity varied by about 2% in the range of angles studied.5 Unfortunately, no data are available for back-incident situations; in particular, when the optical fiber stem points directly to the radiation source.
In this study, we used EGSnrc11, 12 Monte Carlo codes to investigate the angular dependence of PSD responses in photon beams. Because it was previously demonstrated experimentally13, 14 that the light yield from a PSD is proportional to the energy deposited for the range of energies considered here (>200 keV), we scored the absorbed dose in the detector and used the detector dose per unit phantom dose as a measure of the detector’s response. In fact, a PSD’s response is also dependent on such factors as the generating efficiency of the fluorescent light in the detector and the coupling efficiency between the PSD and optical fiber.15, 16 We did not consider those factors in the current study because we were only interested in the relative dosimetry and these factors will not affect the results as long as they can be kept at a constant. Čerenkov radiation induced in the optical fiber by the incident radiation beam is an important issue with the PSD-based dosimetry.2, 16, 17 Various methods have been described to remove the Čerenkov radiation from the detector’s signal.2, 4, 18, 19, 20 An elegant method of circumventing the production of Čerenkov radiation in the optical fiber has also been proposed.21, 22 Since air has a refractive index very close to 1, those investigators used a hollow optical fiber (filled with air) instead of one with a solid fiber core to minimize the generation of Čerenkov radiation. In this work, we assumed the Čerenkov light was not present or was completely removed. As a first step, we studied the energy dependence (or beam-quality dependence) of PSDs in photon beams with low (<0.3%, 1σ) statistical uncertainties and compared the results to those obtained using the Burlin cavity theory1 and those calculated previously23 (2%–4%, 1σ) using the MCNP (Ref. 24) Monte Carlo code. Next, we studied the angular dependence of PSDs and the perturbation effect of the optical fiber of different materials (plastic, glass, or air) on detector response.
MATERIALS AND METHODS
Computational models of PSDs
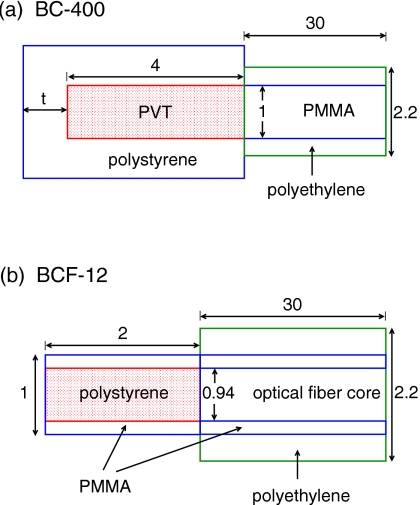
We modeled three PSDs based on the specifications of the commonly used BC-400 plastic scintillator and BCF-12 scintillating fiber (Saint-Gobain Crystals, Nemours, France). Figure 1 shows schematically the computational models for the two of the three modeled PSDs coupled to an optical fiber 3 cm long. The optical fiber modeled was the Eska Premier GH4001 (Mitsubishi Rayon Co. Ltd., Tokyo, Japan). Figure 1a shows the BC-400 plastic scintillator (model 1). The detector material is polyvinyltoluene (PVT) wrapped with polystyrene. The core of the optical fiber is PMMA which is protected by a polyethylene jacket. No cladding is used for this scintillator and so no cladding was modeled for the attached optical fiber. The thickness of the polystyrene on the tip of the PVT detector was modeled at 1 mm in this study. Figure 1b shows the BCF-12 scintillating fiber (model 2), in which the sensitive material is polystyrene doped with fluor. A PMMA cladding 30 μm thick was modeled for both the scintillating fiber and the optical fiber. Also modeled was a polyethylene jacket outside of the optical fiber. The optical fiber core of the scintillating fiber is PMMA. To see how the optical fiber core material affects, if any, the response of the PSD, we replaced the PMMA core with either silica (or glass, SiO2) or air and calculated the responses of the PSDs. With a glass-core fiber of diameter of 1 mm, we simulate the Ft-1.0-UMT quartz optical fiber made by 3M (3M Canada, London, Ontario, Canada). The glass-core fiber was used in scintillator dosimetry25 because it has high light transmission efficiency. Air has also been used as a core material for optical fibers21 to circumvent the generation of Čerenkov light. Naseri et al.22 studied experimentally and computationally the interdosimeter effect of an array of BC-400 scintillators with air-core optical fiber with a glass tube. Since a simple replacement of PMMA core by air does not correspond to the realistic air-core optical fiber, we also modeled this scintillator with air-core fiber as in Fig. 2, which is our third model (model 3), with the geometrical data taken from Naseri et al.,22 except we used polystyrene as the material for the black polymer sheath.
Figure 1.
Computational models of two PSDs for (a) BC-400, which uses PVT as the sensitive material, and (b) BCF-12, which uses polystyrene doped with fluor as the sensitive material. The sensitive region is designated by the shaded area. All measures are in millimeters. For BC-400, the polystyrene thickness at the tip of the PVT is either 3 or 1 mm.
Figure 2.
Computational model of a BC-400 scintillator, which was used by Naseri et al. (Ref. 22), with air-core optical fiber with a silica tube. The sensitive region is designated by the shaded area. All measures are in millimeters unless specified.
Energy cutoff and other Monte Carlo parameters
As there exists a very thin structure, e.g., silver layer of 0.12 μm, in the model of the air-core fiber with a silica tube (Fig. 2), the electron transport cutoff could be an issue in the Monte Carlo simulation. The generally used energy cutoff for electron (ECUT) and energy cutoff for photon (PCUT) transports in EGSnrc is 521 keV (or 10 keV kinetic energy) and 10 keV, respectively. The 10 keV electron kinetic energy corresponds to a continuous slowing down approximation range of electrons in silver of 0.56 μm, larger than the silver layer thickness in the model. To increase the spatial resolution, a lower energy cutoff should be used and this would lead to a longer simulation time. We have compared the calculated dose in the scintillator for different particle energy cutoffs for three orientations of the scintillator at 10 cm depth in a 6 MV photon beam. The results are shown in Table 1, where the dose is normalized to that calculated with ECUT=512 keV and PCUT=1 keV. The results suggest that for this particular model, the difference in detector doses by using different energy cutoffs is negligible at about 0.2% level. For this reason, we used 521 keV for electron cutoff and 10 keV for photon cutoff in this study, which takes roughly only one third of calculation time than when 512 keV and 1 keV are used. The detector dose was scored in the sensitive region of the scintillators (shaded areas in Figs. 12). The phantom dose was scored in a disk voxel with a diameter of 10 mm and thickness of 2 mm and with the disk’s end surfaces always perpendicular to the axis of incident beams. The photon splitting variance reduction technique29 was used with the splitting number varying from 10 to 100 depending on the radiation source quality.
Table 1.
Comparison of dose in the BC-400 scintillator attached by an air-core optical fiber with a silica tube (Fig. 2) for different particle energy cutoffs. Three orientations of the scintillator are calculated and for each orientation, the dose is normalized to that calculated with electron cutoff ECUT=512 keV and photon cutoff PCUT=1 keV. The orientation angles are defined as shown in Fig. 3.
| Scintillator orientation (deg) | Relative dose in scintillator | |
|---|---|---|
| ECUT=512 keV, PCUT=1 keV | ECUT=521 keV, PCUT=10 keV | |
| 0 | 1 | 0.9975±0.17%(1σ) |
| 90 | 1 | 1.0025±0.14%(1σ) |
| 180 | 1 | 0.9995±0.17%(1σ) |
Calculation of energy dependence
The energy (or beam-quality) dependence of the response of a PSD was studied by simulating the irradiation of the detector, which is located in a water phantom with its axis perpendicular to the incident beams, by a variety of photon beams. The ratio of the dose in the sensitive region of the detector to that in the phantom without the presence of the detector (i.e., the detector dose per unit phantom dose) was then calculated. Both monoenergetic and spectrum-based photon beams were used in the calculations. The energy of the monoenergetic photon beams ranged from 150 keV to 18 MeV. All spectrum-based sources were megavoltage beams: The spectrum for the 60Co beam was taken from Mora et al.26 and the spectra for 6 and 18 MV photon beams were taken from a Monte Carlo simulation of a Varian linac.27 For megavoltage beams, including spectrum-based sources and monoenergetic photon beams with energy greater than 1 MeV, the PSD was modeled at a depth of 10 cm in a cubic water phantom with 30 cm sides, with geometrical center of the detector’s sensitive region at the point of measurement. The radiation source was modeled as a point source at a 100 cm source-to-surface distance with a 10×10 cm2 field size. For medium-energy photon beams (down to 150 keV), the PSD was modeled at a depth of 2 cm in a cubic water phantom with 20 cm sides, which corresponds to conditions of reference dosimetry for medium-energy x rays as specified by AAPM TG-61.28 The radiation source was at a 20 cm source-to-surface distance with a 5×5 cm2 field size. These arrangements were also chosen for improving computational efficiency, as these medium-energy photons attenuate much faster in a phantom than megavoltage photons. To compare our findings to those from a previous study,23 we also modeled a PVT scintillator embedded in a polystyrene protective layer but without the attached 3 cm optical fiber. In this case, the thickness of the polystyrene at the head of the PVT scintillator was set at 3 mm [see Fig. 1a]. Since there is no universal way to specify the photon beam quality for energies from 150 keV to 18 MeV, we used the photon energy or nominal energy as the quality specifier for monoenergetic photon beams or spectrum-based beams, respectively, e.g., for 6 MV linac beam, we use 6 MeV as the photon energy though the average photon energy is close to 2 MeV. For the 60Co beam, we used the mean energy 1.25 MeV as the photon energy. The exact specification of beam quality is not relevant here since all high-energy data points are approximately on the same horizontal line in the graphs shown later (Figs. 45). For the realistic model of the BC-400 scintillator attached by an air-core optical fiber (Fig. 2), because of the presence of the silver layer enclosing the sensitive volume of the scintillator, we expect some impact on the response of the detector due to silver’s high atomic number. Thus we also studied the variation of the energy dependence on the thickness of the silver layer either with or without the 0.16 mm silica tube. For the latter case, the silica is replaced by polystyrene in the simulation.
Figure 4.
The energy, or beam-quality, dependence of a BC-400 scintillator [as in Fig. 1a with a polystyrene thickness of 3 mm, but without attachment to the optical fiber stem]. The ordinate is the detector dose per unit phantom dose. For linac spectrum sources, the photon energy is the nominal energy of the photon beam (i.e., 6 MV is treated as 6 MeV). For the 60Co beam, the mean photon energy 1.25 MeV is the photon energy. The statistical uncertainty is less than 0.5% (1σ). Solid circles are the results obtained by applying the Burlin cavity theory (Ref. 1). Open squares are the results from a previous Monte Carlo calculation with MCNP code (Ref. 23) (2%–4% 1σ uncertainty, error bar not shown). See Sec. 2C for detailed geometrical information.
Figure 5.
The energy dependence of the BCF-12 scintillating fiber coupled with different optical fibers [Fig. 1b] and the BC-400 scintillator coupled with the PMMA fiber [Fig. 1a with a thickness of 1 mm] and the air-core fiber with a glass tube. The optical fibers are modeled as 3 cm long. The ordinate is the detector dose per unit phantom dose. For data points with photon energy greater than 1 MeV, spectrum sources are used, with the nominal energy as the abscissa. Lower energy sources (<1 MeV) were monoenergetic photon beams. The statistical uncertainty is less than 0.3% (1σ).
Calculation of angular dependence
We studied the azimuthal angular dependence of the all three PSD models for a 6 MV spectral photon beam and a 300 keV monoenergetic photon beam in a water phantom. Figure 3 shows how the orientation angle of the PSD is defined relative to the incident radiation beam. The detector dose is normalized to that for the angle of 90° when the incident beam is perpendicular to the axis of the detector. For the 300 keV photon beam, since the PSD is modeled at a depth of 2 cm, the optical fiber length is set at 1.5 cm instead of 3 cm so that the entire fiber will be immersed in the phantom when the angle is 0° (i.e., when the optical fiber stem is pointing to the source). We also studied the angular dependence for a bare PVT scintillator, and a PVT scintillator with a polystyrene layer but not the optical fiber, in the 6 MV photon beam. In addition to the in-phantom simulations, we calculated the free-in-air angular dependence for the polystyrene scintillating fiber with PMMA optical fibers of different lengths. The radiation source modeled is a monoenergetic photon beam point source with an energy of 100 keV, a source-to-detector distance of 40 cm, and a field size of 5×5 cm2 at the detector. The space surrounding the detector and that between the source and the detector are modeled as if filled with air. The calculation results are compared to free-in-air measurements of Hyer et al.,9 which were obtained with a CT unit operating at 120 kVp.
Figure 3.
Diagram showing how the azimuthal angle is defined. The thick arrows with angular degrees indicate the direction of the incident radiation beams. For example, at 90°, the radiation beam axis is perpendicular to the axis of the scintillator.
RESULTS AND DISCUSSION
Energy dependence
Figure 4 shows the energy dependence of the PVT scintillator with a polystyrene protective layer but no optical fiber attached. This scintillator model is studied here solely for a comparison to a previous study by MCNP code on the same model.23 There is no significant difference between using spectrum sources and using monoenergetic beams at megavoltage photon energies. This finding is reasonable since the curve for energy dependence of monoenergetic beams is quite flat across photon energies of almost two orders of magnitude. The results from this study agree with those from the previous study using the MCNP code, but the current statistical uncertainties are much lower (∼0.5%). The results also agree with those obtained using the Burlin cavity theory1 except at a photon energy of 2 MeV, where the discrepancy is about 1%. This discrepancy is probably due to the limitations of the Burlin cavity theory for some of the assumptions made. The drop of the responses at lower energy end (<300 keV) is due to the ratio of the mass energy absorption coefficients of water to PVT.
Figure 5 shows the energy dependence of the BC-400 scintillator coupled with the PMMA optical fiber (model 1), the BCF-12 scintillating fiber coupled with PMMA-core, glass-core, and air-core optical fibers (model 2), and the BC-400 scintillator coupled with the air-core fiber with a silica tube (model 3). Since there is no difference between using spectrum sources and using monoenergetic photon beams, the data points for both sources are combined on a single curve for each PSD. Similar to the results for the scintillator without optical fiber shown in Fig. 4, the PSDs of the models 1 and 2, made with different scintillating materials and∕or different optical fiber cores, show excellent energy independence for photon energies ranging from 300 keV to 18 MV: The variations of the detector dose per unit water dose are within 0.5% at a statistical uncertainty of less than 0.2%. Below 300 keV the responses drop which is the behavior of the ratio of the mass energy absorption coefficients of water to polystyrene (or PVT). For the PSD of the third model, BC-400 with air-core fiber with silica tube, the detector dose per unit water dose is closer to unity. This is because the presence of the high-Z atoms (Si and Ag) around the sensitive volume enhances the energy deposition to the scintillator, thus making the whole response curve shifted upward by about 2%. The flatness of the detector response is a little bit worse than others but the variation is still within 1% in the photon energy range from 300 keV to 18 MV. For energies lower than 300 keV, the scintillator over-responses due to the presence of silver.
Figure 6 shows the effects of the silver layer thickness on the energy dependence of the PSD for the third model either (a) without or (b) with a 0.16 mm silica tube. In Fig. 6a, when there is no silver layer, the curve is basically the same as that in Fig. 5 for model 1 (BC-400, PMMA). This is what we expected since the polystyrene is close to water equivalent. A silver layer of 1 μm will have a significant effect on the detector: Increasing the response by a couple of percent in megavoltage region and dramatically for photon energies below 300 keV. A silver layer thickness of 10 μm will make the detector essentially useless because of the very large energy dependence. For the silver layer thickness of 0.3 μm or less, it has negligible effects on the response for megavoltage photon beams but still has significant effect for photon energies less than 300 keV. In Fig. 6b, due to the presence of the 0.16 mm silica tube, all the curves (for silver thickness ≤0.3 μm) are shifted upward by about 2%–3%. Figure 6 demonstrates that even for a small variation of thickness (∼0.3 μm) of the silver layer, there is a more than 5% change on the response of the detector for photon energy of 200 keV. As the purpose of the silver coating is to prevent the optical light exchange at the silica and the scintillator∕air boundary, one way to minimize the variation of the detector response at lower photon energy is to use aluminum coating instead of silver. Figure 6b also shows the result for a 10 μm aluminum coating, which is almost the same as the result for zero thickness silver layer because the atomic number of aluminum is only one less than silicon and 10 μm is negligible compared to the 0.16 mm silica.
Figure 6.
The energy dependence of a BC-400 scintillator coupled with an air-core fiber with a silica (SiO2) tube (see the model in Fig. 2) for a variety of silver thicknesses with (a) no silica present and (b) a silica thickness of 0.16 mm. The legend shows in μm the silver layer thickness except the one explicitly specified as aluminum.
Angular dependence
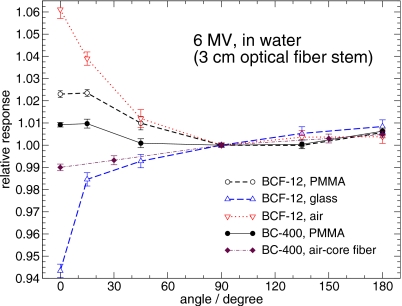
Figure 7 shows the angular dependence of the bare PVT scintillator simulated at a 10 cm depth in a water phantom irradiated by a 6 MV photon beam. The figure also shows the azimuthal angle between the detector and the incident beam. The detector dose at any azimuthal angle is normalized to that calculated at 90°. For the bare scintillator, because of the symmetry, only responses for angles from 90° to 180° are calculated. The relative response varies at most 0.8%. When the polystyrene tip thickness is 1 mm, the angular variation of the response is about the same as that of the bare scintillator. For a 3 mm polystyrene tip thickness, the angular variation of the response could be as large as 1.8%. These results suggest that minimizing the thickness of the protective layer at the head of a PSD may reduce the angular dependence of the detector’s response. Figure 8 shows the angular dependence of the three PSD models simulated at a 10 cm depth in a water phantom in the 6 MV photon beam. For simulations in which the detector head points toward the radiation source (i.e., angles greater than 90°), the response of the PSDs for all three models remains almost constant (within 1%), regardless of the optical fiber core material. When the detector head points away from the radiation source (i.e., angles less than 90°), conversely, the response of the PSDs varies depending on the optical fiber material. At 0°, with the stem pointing directly to the source, the detector’s response could be 6% higher than at 90° when it is attached to an air-core fiber (BCF-12, model 2) and 6% lower when it is attached to a glass-core fiber. (Note, however, that these values are for a fiber stem length of 3 cm.) This is mainly an attenuation issue: Air causes less attenuation on the incident photon beam than water, but glass (SiO2) causes more attenuation than water due to its higher density and effective atomic number. However, for the PMMA-core optical fiber, the effect is at most 2% for all angles for its close to water equivalent. For the BC-400 scintillator coupled with the air-core fiber with a silica tube (model 3), the variation of the response for all angles is also within 2%. This behaves differently from the other PSD with air-core fiber in model 2 because the presence of high-Z atoms (Si and Ag) in the air-core fiber in model 3 happens to compensate the effect of air.
Figure 7.
The angular dependence of a bare BC-400 scintillator [as in Fig. 1a but without attachment to the optical fiber stem] at a depth of 10 cm in water in a 6 MV photon beam. The inset shows the definition of the angle (which is the same as in Fig. 3). In the inset, the fiber stem is drawn in dashed line indicating that it is not modeled but only for identification purpose. The detector dose at any angle is normalized to that at 90°. Two tip thicknesses t=1 mm and t=3 mm are studied. The statistical uncertainty is less than 0.3% (1σ).
Figure 8.
The angular dependence of the BCF-12 scintillating fiber coupled with different optical fibers [Fig. 1b] and the BC-400 plastic scintillator coupled with the PMMA fiber [Fig. 1a with thickness at the tip of 1 mm] and the air-core fiber with a glass tube at a 10 cm depth in a water phantom in a 6 MV photon beam. Angles are defined as shown in Fig. 3. The detector dose at any angle is normalized to that at 90°. The length of the optical fibers is modeled as 3 cm. The statistical uncertainty is less than 0.3% (1σ).
Figure 9 shows the angular dependence for all of these PSD models in a water phantom irradiated by a 300 keV monoenergetic photon beam. The relative response of the detectors deviates significantly from unity only for angles very close to 0°. For angles greater than 10°, the relative response of all the detectors varies within 2% regardless of the models or the optical fiber core material used. This result is true even at 0° for the detectors attached by the PMMA-core optical fiber. For the PSD attached to an air-core optical fiber (BCF-12, model 2), the detector’s response at 0° could be about 15% higher than at 90°, and for the glass-core fiber it is about 15% lower. The apparent different behaviors of the angular dependence between Figs. 89 can be explained by the fact that the phantom scattering for the 6 MV photon beam is much higher than that for the 300 keV beam, and the effect of attenuation by the fiber stem, i.e., photoelectric absorption, is much larger in 300 keV beam than in 6 MV beam. For example, for the BC-400 PSD with air-core fiber (model 3) at 0°, the effects of air and high-Z atoms (Si and Ag) compensate mutually in the 6 MV beam where Compton effect dominates; they no longer cancel each other in the 300 keV beam where photoelectric effect becomes important.
Figure 9.
The angular dependence of the BCF-12 scintillating fiber coupled with different optical fibers [Fig. 1b] and the BC-400 plastic scintillator coupled with the PMMA fiber [Fig. 1a with a tip thickness of 1 mm] and the air-core fiber with a glass tube at a 2 cm depth in a water phantom in a 300 keV monoenergetic photon beam. The angle is defined as shown in Fig. 3. The detector dose at any angle is normalized to that at 90°. The length of the optical fibers is modeled as 1.5 cm. The relative responses for the scintillating fiber attached to optical fibers with glass and air cores at 0° are 0.83 and 1.15, respectively. The statistical uncertainty is less than 0.3% (1σ).
Figure 10 shows the free-in-air calculations of the angular dependence of the BCF-12 scintillating fiber coupled to a PMMA-core fiber stem 3 or 10 cm long in a 100 keV monoenergetic photon beam. There is essentially no scatter in this case, so the drop in signal at 0° is very steep compared to that in the phantom case (Fig. 9). The length of the optical fiber stem mainly has an effect at 0° due to attenuation by the fiber. The calculated angular dependence agrees qualitatively with the measurements as far as the large drop in response near 0° is concerned. Quantitatively, however, there is still disagreement between the calculations and the experiments since we were not able to model the exact material and geometrical data used in the experiments. The factors most responsible for the disagreement would be the length and path of the curved fiber exposed to the radiation and the material and shape of the detector holder. Using a monoenergetic x-ray beam instead of a more realistic spectrum source might also result in some differences. Another factor to be noted is that the measured data are normalized at 90° where the data point itself has an uncertainty of about 5%. So, for example, if the response at this angle happens to be overestimated by 5%, then the actual measured curve would be shifted upward by 5%, which would make the agreement better.
Figure 10.
The angular dependence of the BCF-12 scintillating fiber coupled with PMMA plastic optical fibers with lengths of 3 and 10 cm irradiated free-in-air by a 100 keV monoenergetic photon beam. The angle is defined here as shown in Fig. 3. The detector dose at any angle is normalized to that at 90°. The statistical uncertainty for the calculation is around 2% (1σ). The solid symbols represent a measurement by Hyer et al. (Ref. 9), who used a clinical CT unit operating at 120 kVp. Because of the detectors’ symmetry, only half the data (0°–180°) are taken from Fig. 8 in their paper.
CONCLUSIONS
In this study, we used Monte Carlo simulations to investigate the response of PSDs to photon beams. A plastic scintillator (BC-400) and a scintillating fiber (BCF-12), both attached by a plastic-core optical fiber stem, are modeled. Also studied is a plastic scintillator (BC-400) attached by an air-core optical fiber stem with a silica tube coated with silver. The detectors’ responses are calculated as the detector dose per unit phantom dose. For the energy dependence of the PSDs in photon beams, the calculations show that the PSDs with plastic-core fiber have excellent energy independence within about 0.5% with a low (<0.3%, 1σ) statistical uncertainty at photon energies ranging from 300 keV (monoenergetic) to 18 MV (linac beam). The PSD with an air-core optical fiber with a silica tube also has good energy independence within 1% in the same photon energy range and it is even closer to water equivalent due to the presence of silica wall around the scintillator. About the angular dependence, the relative response of all the three modeled PSDs is within 2% for all the angles in a 6 MV photon beam. This is also true in a 300 keV monoenergetic photon beam for PSDs with plastic-core fiber. For the PSD with an air-core fiber with a silica tube in the 300 keV beam, the relative response varies within 1% for most of the angles except in the case when the fiber stem is pointing right to the radiation source in which case the PSD may over-response by more than 10%. For a PSD with a glass-core fiber in either photon beams, the variation of the response is also within 2% for most of the angles except when the fiber stem is pointing to the radiation source. These results suggest that for most situations where the orientation of the detectors can be controlled, the angular dependence of PSDs is not of concern no matter what kind of material is used for the optical fiber core. For in vivo applications, especially for intensity-modulated radiation therapy or arc therapy, since the detector’s orientation cannot be guaranteed once it has been inserted into the patient’s body and since the radiation beam may come from various directions, it is probable that the optical fiber stem could point directly to the source. In this extreme condition, the response of PSDs either with plastic-core fiber or with air-core fiber with a silica tube has a maximum deviation of 2%, while a PSD with glass-core fiber would have large deviations in dose reading thus should be avoided.
ACKNOWLEDGMENTS
The authors are very thankful to the associate editor and an anonymous referee for their comments which have helped to improve this manuscript a lot. This research was supported by the National Cancer Institute (NCI) Grant No. 1R01CA120198-01A2 and NIH∕NCI Grant No. T32 CA119930-04.
References
- Beddar A. S., Mackie T. R., and Attix F. H., “Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: I. Physical characteristics and theoretical considerations,” Phys. Med. Biol. 37, 1883–1900 (1992). 10.1088/0031-9155/37/10/006 [DOI] [PubMed] [Google Scholar]
- Beddar A. S., Mackie T. R., and Attix F. H., “Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: II. Properties and measurements,” Phys. Med. Biol. 37, 1901–1913 (1992). 10.1088/0031-9155/37/10/007 [DOI] [PubMed] [Google Scholar]
- Flühs D., Heintz M., Indenkampen F., Wieczorek C., Kolanoski H., and Quast U., “Direct reading measurement of absorbed dose with plastic scintillators—The general concept and applications to ophthalmic plaque dosimetry,” Med. Phys. 23, 427–434 (1996). 10.1118/1.597736 [DOI] [PubMed] [Google Scholar]
- Archambault L., Beddar A. S., Gingras L., Roy R., and Beaulieu L., “Measurement accuracy and Čerenkov removal for high performance, high spatial resolution scintillation dosimetry,” Med. Phys. 33, 128–135 (2006). 10.1118/1.2138010 [DOI] [PubMed] [Google Scholar]
- Lambert J., McKenzie D. R., Law S., Elsey J., and Suchowerska N., “A plastic scintillation dosimeter for high dose rate brachytherapy,” Phys. Med. Biol. 51, 5505–5516 (2006). 10.1088/0031-9155/51/21/008 [DOI] [PubMed] [Google Scholar]
- Beierholm A. R., Andersen C. E., Lindvold L. R., Kjaer-Kristoffersen F., and Medin J., “A comparison of BCF-12 organic scintillators and Al2O3:C crystals for real-time medical dosimetry,” Radiat. Meas. 43, 898–903 (2008). 10.1016/j.radmeas.2007.12.032 [DOI] [Google Scholar]
- Eichmann M., Fluhs D., and Spaan B., “Development of a high precision dosimetry system for the measurement of surface dose rate distribution for eye applicators,” Med. Phys. 36, 4634–4643 (2009). 10.1118/1.3218762 [DOI] [PubMed] [Google Scholar]
- Archambault L., Polf J. C., Beaulieu L., and Beddar S., “Characterizing the response of miniature scintillation detectors when irradiated with proton beams,” Phys. Med. Biol. 53, 1865–1876 (2008). 10.1088/0031-9155/53/7/004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyer D. E., Fisher R. F., and Hintenlang D. E., “Characterization of a water equivalent fiber-optic coupled dosimeter for use in diagnostic radiology,” Med. Phys. 36, 1711–1716 (2009). 10.1118/1.3116362 [DOI] [PubMed] [Google Scholar]
- Cartwright L. E., Lambert J., McKenzie D. R., and Suchowerska N., “The angular dependence and effective point of measurement of a cylindrical scintillation dosimeter with and without a radio-opaque marker for brachytherapy,” Phys. Med. Biol. 54, 2217–2227 (2009). 10.1088/0031-9155/54/7/024 [DOI] [PubMed] [Google Scholar]
- Kawrakow I. and Rogers D. W. O., “The EGSnrc code system: Monte Carlo simulation of electron and photon transport,” Technical Report No. PIRS-701 (National Research Council of Canada, Ottawa, Canada, 2000). See also http://www.irs.inms.nrc.ca/inms/irs/EGSnrc/EGSnrc.html.
- Kawrakow I., “Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version,” Med. Phys. 27, 485–498 (2000). 10.1118/1.598917 [DOI] [PubMed] [Google Scholar]
- Brannen E. and Olde G. L., “The response of organic scintillators to electron energy deposited in them,” Radiat. Res. 16, 1–6 (1962). 10.2307/3571123 [DOI] [PubMed] [Google Scholar]
- Smith D. L., Polk R. G., and Miller T. G., “Measurement of the response scintillators to electrons, protons and deuterons,” Nucl. Instrum. Methods 64, 157–166 (1968). 10.1016/0029-554X(68)90189-4 [DOI] [Google Scholar]
- Beddar A. S., Law S., Suchowerska N., and Mackie T. R., “Plastic scintillation dosimetry: Optimization of light collection efficiency,” Phys. Med. Biol. 48, 1141–1152 (2003). 10.1088/0031-9155/48/9/305 [DOI] [PubMed] [Google Scholar]
- Beddar A. S., Suchowerska N., and Law S. H., “Plastic scintillation dosimetry for radiation therapy: Minimizing capture of Cerenkov radiation noise,” Phys. Med. Biol. 49, 783–790 (2004). 10.1088/0031-9155/49/5/009 [DOI] [PubMed] [Google Scholar]
- Beddar A. S., Mackie T. R., and Attix F. H., “Cerenkov light generated in optical fibres and other light pipes irradiated by electron beams,” Phys. Med. Biol. 37, 925–935 (1992). 10.1088/0031-9155/37/4/007 [DOI] [Google Scholar]
- de Boer S. F., Beddar A. S., and Rawlinson J. A., “Optical filtering and spectral measurements of radiation-induced light in plastic scintillation dosimetry,” Phys. Med. Biol. 38, 945–958 (1993). 10.1088/0031-9155/38/7/005 [DOI] [Google Scholar]
- Clift M. A., Johnston P. N., and Webb D. V., “A temporal method of avoiding the Cerenkov radiation generated in organic scintillator dosimeters by pulsed mega-voltage electron and photon beams,” Phys. Med. Biol. 47, 1421–1433 (2002). 10.1088/0031-9155/47/8/313 [DOI] [PubMed] [Google Scholar]
- Frelin A. -M., Fontbonne J. -M., Ban G., Colin J., Labalme M., Batalla A., Isambert A., Vela A., and Leroux T., “Spectral discrimination of Cerenkov radiation in scintillating dosimeters,” Med. Phys. 32, 3000–3006 (2005). 10.1118/1.2008487 [DOI] [PubMed] [Google Scholar]
- Lambert J., Yin Y., McKenzie D. R., Law S., and Suchowerska N., “Cerenkov-free scintillation dosimetry in external beam radiotherapy with an air core light guide,” Phys. Med. Biol. 53, 3071–3080 (2008). 10.1088/0031-9155/53/11/021 [DOI] [PubMed] [Google Scholar]
- Naseri P., Suchowerska N., and McKenzie D. R., “Scintillation dosimeter arrays using air core light guides: Simulation and experiment,” Phys. Med. Biol. 55, 3401–3415 (2010). 10.1088/0031-9155/55/12/009 [DOI] [PubMed] [Google Scholar]
- Beddar A. S., Briere T. M., Mourtada F. A., Vassiliev O. N., Liu H. H., and Mohan R., “Monte Carlo calculations of the absorbed dose and energy dependence of plastic scintillators,” Med. Phys. 32, 1265–1269 (2005). 10.1118/1.1897465 [DOI] [PubMed] [Google Scholar]
- LANL, “MCNPX user’s manual version 2.4.0,” Los Alamos National Laboratory Report No. LA-UR-02–5253, edited by Waters L. S., 2002.
- Létourneau D., Pouliot J., and Roy R., “Miniature scintillating detector for small field radiation therapy,” Med. Phys. 26, 2555–2561 (1999). 10.1118/1.598793 [DOI] [PubMed] [Google Scholar]
- Mora G., Maio A., and Rogers D. W. O., “Monte Carlo simulation of a typical 60Co therapy source,” Med. Phys. 26, 2494–2502 (1999). 10.1118/1.598770 [DOI] [PubMed] [Google Scholar]
- Sheikh-Bagheri D. and Rogers D. W. O., “Monte Carlo calculation of nine megavoltage photon beam spectra using the BEAM code,” Med. Phys. 29, 391–402 (2002). 10.1118/1.1445413 [DOI] [PubMed] [Google Scholar]
- Ma C. -M., Coffey C. W., DeWerd L. A., Nath R., Liu C., Seltzer S. M., and Seuntjens J., “AAPM protocol for 40–300 kV x-ray beam dosimetry in radiotherapy and radiobiology,” Med. Phys. 28, 868–893 (2001). 10.1118/1.1374247 [DOI] [PubMed] [Google Scholar]
- Kawrakow I., “EGSnrc C++ class library,” NRC Technical Report No. PIRS-898 (National Research Council of Canada, Ottawa, Canada, 2005). See also http://www.irs.inms.nrc.ca/EGSnrc/pirs898/.