Principles of Biomimetic Vascular Network Design Applied to a Tissue-Engineered Liver Scaffold

Abstract

Branched vascular networks are a central component of scaffold architecture for solid organ tissue engineering. In this work, seven biomimetic principles were established as the major guiding technical design considerations of a branched vascular network for a tissue-engineered scaffold. These biomimetic design principles were applied to a branched radial architecture to develop a liver-specific vascular network. Iterative design changes and computational fluid dynamic analysis were used to optimize the network before mold manufacturing. The vascular network mold was created using a new mold technique that achieves a 1:1 aspect ratio for all channels. In vitro blood flow testing confirmed the physiologic hemodynamics of the network as predicted by computational fluid dynamic analysis. These results indicate that this biomimetic liver vascular network design will provide a foundation for developing complex vascular networks for solid organ tissue engineering that achieve physiologic blood flow.

Introduction

The clinical need for tissue-engineered organs is based on the dramatic shortage of organs for transplantation. For all organs, and in particular the liver, this shortage continues to grow. The waiting list for all organs in the United States in 1989 was 19,095 patients; 20 years later the list has grown to over 100,000 patients.¹ The liver is the second most common transplanted organ, and the waiting list for livers is currently over 16,000 patients.¹

The two central components of any engineered tissue are the architecture of the scaffold and the cells to be placed within the scaffold. Solid organs are thick tissues that require an extensive branching network of blood vessels to supply oxygen and nutrients and remove waste from the organ. The effective diffusion distance of oxygen and nutrients in a tissue is on the order of hundreds of microns, but diffusion distance is influenced by many factors, including the metabolic rate of the tissue.

For state-of-the-art liver transplants, the tolerated warm ischemia time is only a few hours. A transplanted liver, either a donated graft or an engineered organ, needs to have over a liter of blood flow per minute within hours of being removed from its original nutrient supply. This blood flow must pass within a few hundred microns of every cell in the organ for the organ to survive. Many researchers have proposed angiogenesis as a means of establishing a network of blood vessels within a tissue-engineered organ.^2–5 For a solid organ such as the liver, even if an angiogenesis network could be established in a tissue in vitro, by the time the network inosculated with the host's vascular system, the majority of the parenchymal cells of the liver would be impaired or necrotic. Based on this observation Vacanti and colleagues proposed that a solid organ scaffold with a preformed vascular network would be a means of delivering needed blood flow to the tissue.^6,7 This architectural concept of a tissue scaffold results in liver cells adjacent to the channels of a vascular network separated by a semipermeable membrane.⁸ The scaffold can be scaled up by stacking layers of the vascular networks and the adjacent liver cells. This approach to liver tissue engineering has been demonstrated in vitro.⁸ Progress has also been made by using a microfluidic scaffold to engineer liver tissues in vitro for potential drug toxicity testing or a bioartificial liver device.^9,10 Microfluidic-based vascular networks have been investigated in an effort to optimize individual aspects of transport, bifurcation hydrodynamics, and hemocompatibility.^11–13

A central aim of this work was to establish a set of biomimetic design principles to achieve physiologic blood flow within a vascular network. This work outlines seven general design principles as the major technical considerations for design of any vascular network. Tissue-specific design inputs were applied to create a liver vascular network with the same radial flow architecture as the native liver lobule. These vascular network design principles and tissue-specific design inputs are shown in Table 1 and described below.

Table 1.

Biomimetic Vascular Network Design Principles to Achieve Physiologic Blood Flow in Tissue Engineering Scaffolds and Tissue-Specific Design Inputs to Tailor the Flow and Architecture to Meet the Metabolic Demands of a Particular Tissue

Biomimetic vascular network design principles	Tissue-specific vascular network design inputs
1. Defined relationship between parent and daughter diameters	1. Tissue-specific architecture
2. Physiologic branching angle	2. Inlet pressure
3. Biomimetic vessel length	3. Outlet pressure
4. 1:1 aspect ratio for all vascular channels	4. Volume flow rate
5. Venous scaling	5. Channel density
6. Uniform flow at bifurcations
7. Physiological shear stress

Previous development of vascular networks for engineered liver tissue utilized generic vascular network designs rather than focusing on the unique features of the liver architecture.^6–8 In the native liver, the vasculature is arranged in radial configuration with portal triads around the periphery of a hexagonal-shaped lobule.¹⁴ Blood flows from portal vein and hepatic artery branches in the portal triad through a liver sinusoid to the central vein. The hepatocytes within the lobule have different metabolomes depending on their radial distance from the central vein. These metabolic differences are induced by the decreasing oxygen and nutrient gradient along the sinusoid. The periportal hepatocytes are highly active in carbohydrate and lipid metabolism, and the pericentral hepatocytes contribute more to drug metabolism and detoxification.^15,16 A tissue-engineered liver will need to have a variety of hepatocyte metabolomes similar to the native liver. The vascular network developed in this study has not been tested with hepatocytes in vitro or in vivo. These studies will be part of the next phase of validating these network designs.

Radial blood flow is only one fundamental component of a tissue-engineered liver vascular network. A biomimetic liver vascular network must also account for a unique blood vessel found only in the liver: the liver sinusoid. The shear stress in a liver sinusoid is not directly known. They are approximately 30 μm in diameter, giving them a larger cross-sectional area than capillaries. Sinusoids most likely have lower velocities than arteries of similar cross-sectional area because significant transport of nutrients and oxygen occurs within them. Due to this intermediate condition, we estimated that the shear stress in liver sinusoids is in the range of high venous to low arterial shear stress.

Using the general biomimetic design principles and tissue-specific design inputs outlined below, we designed a liver-specific vascular network with physiologic flow and the same radial architecture as the native liver lobule. This network was manufactured with a 1:1 aspect ratio for all channels, and in vitro testing confirmed that the design met the original specifications.

Materials and Methods

Biomimetic design principles

Defined relationship between parent and daughter diameters

Nearly a century ago, Murray derived a relationship between parent and daughter diameters of branching networks in the body that has been shown to be valid for blood vessels as well as airway structures.^17,18 The relationship was derived based on the principle of minimum work required to achieve flow through a network. Networks that conform to this law also have uniform shear stress throughout the network. The equation of Murray's Law states that

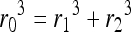(1)

where r₀ is the radius of the parent diameter of the vessel, and r₁ and r₂ are the radii of the daughter vessel diameters. This relationship holds for symmetric and asymmetric bifurcations as well as rectangular channels.^18,19 Vascular networks may be optimally designed with diameters that conform to this relationship so that shear stress can be maintained within a narrow range.

Physiologic branching angle

The bifurcation angle of vessels in the body is dictated by optimality principles.^20,21 Zamir and Brown identified trends for optimized arterial branching angles dependent on vessel diameter.²¹ These bifurcation angles are a central design feature of natural blood vessels to achieve uniform flow at the site of bifurcations while dividing the flow in simple or complex bifurcations or trifurcations. In our design all bifurcations had equal-diameter daughter vessels and bifurcation angles of 45° (angle from centerline of parent vessel to centerline of daughter vessel). Bifurcation angles for complex bifurcations or unequal daughter branches for future networks can be determined using the optimality principles defined by Zamir.^20,21

Biomimetic vessel length

Blood vessel length is related to diameter in an empirically described but mathematically undefined relationship.²² In general, smaller diameter vessels have shorter lengths. This paired diameter-to-length relationship may minimize shear stress disturbances in the flow path, thereby minimizing platelet activation and thrombus formation. In biomimetic vessel design, a principle goal is to avoid long, small-diameter channels. To achieve a biomimetic length for the channels, the vessel length data from Milnor was plotted and converted into a third order polynomial equation using Microsoft Excel (Microsoft, Redmond, WA).²² The biomimetic length was used for the smallest channels of the vascular network design and the lengths of the branches proximal and distal to the smallest channels were scaled to fit within the design space.

1:1 aspect ratio for all vascular channels

A significant limitation of previously designed vascular networks made by photolithography is the single depth of channel for the entire network. This results in smaller channels in the network having a 1:1 width-to-height aspect ratio; however, some channels in the network have a 30:1 aspect ratio.⁸ These large aspect ratios make achieving physiologic flow impossible. For vascular networks made using a microfluidic approach, a 1:1 aspect ratio for rectangular channels is paramount to achieve the most uniform circumferential shear stress in a rectangular channel. With 1:1 aspect ratio channels, more uniform flow in the bifurcations can be achieved, further minimizing flow disturbances and possible thrombosis. In this design, a novel manufacturing method was used to create 1:1 aspect ratio channels throughout the network.

Venous scaling

The venous system in the body has the same flow volume as the arterial system with a fraction of the resistance. This decrease in resistance is achieved by an increase in vascular diameter compared to the arterial system. In our design, the venous resistance was originally set at a 10% increase in diameter over the corresponding generation of channels on the arterial side. This resulted in some areas of the channels having a shear stress less than 1 dyn/cm². The diameters were then empirically adjusted, balancing the desired pressure drop of the entire network and keeping the distal or venous outflow of the network within the range of high venous shear stress.

Uniform flow at bifurcations

Bifurcations are the principal site for flow disturbances in the arterial system. Even simple 1:2 bifurcations may have a widely varying shear stress profile, flow separation, and stasis. Flow at these bifurcations must be optimized to achieve uniform flow and minimize shear stress changes. Uniform flow must be achieved within a narrow range throughout the vascular network and represents a critical design endpoint that must be met for platelet activation to be minimized. Optimization of each bifurcation was achieved through an iterative design process and verified by computational fluid dynamic (CFD) analysis (FloWorks^®; SolidWorks, Concord, MA).

Physiological shear stress

In every part of the body, blood flow is highly regulated and remains within tight physiological constraints. Any engineered vascular network must maintain physiological blood flow to minimize the formation of thrombus. Shear stress, in particular, is a very important aspect of physiologic flow. Areas of high shear stress can induce platelet activation and adherence, which may lead to the formation of thrombus.^23,24 Areas of low shear stress and flow velocity may also lead to thrombus formation.²⁴ Chronic altered shear stress induces proinflammatory and proliferative pathways; therefore, uniform shear stress must be maintained within a narrow range throughout the vascular network.²⁵ Shear stress in arteries ranges from 10 to 70 dyn/cm² and in veins ranges from 1 to 6 dyn/cm².²⁶ We estimated that sinusoidal physiologic shear stress ranges between high venous to low arterial shear stress, 5 to 25 dyn/cm². Shear stress of the network was achieved within the narrow physiologic range through an iterative design process with repeated CFD analysis.

Liver-specific vascular network design inputs and boundary conditions

According to the tissue-specific vascular network design inputs outlined in Table 1, the radial blood flow of the liver lobule was the defining architecture for this network. The central goals for this initial liver network design were focused on achieving physiological flow using the design principles. Therefore, a lower channel density was designed than will eventually be required to support hepatocytes across the area of the network. The other design inputs and boundary conditions are described below.

Inlet and outlet pressure

Using the design parameters outlined above, a radial vascular network was designed to replicate the anatomical arrangement of flow within a liver lobule. Two significant boundary conditions for the CFD evaluation of a liver-specific vascular network were the inlet and outlet pressures of the device. The device was designed as an implantable liver assist device to be placed in parallel to the native liver with portal venous inflow and outflow to the inferior vena cava. We selected 10 mmHg as the inlet pressure boundary condition as this is a minimum expected portal venous pressure for a patient with liver disease needing liver assist therapy. An outlet pressure of 3 mmHg was selected as the outlet pressure boundary condition with anticipation that the central venous pressure of these patients would be slightly elevated.

Volume flow rate

This vascular network was planned as the foundation of a liver assist device to replace the function of 30% of the liver. From the surgical literature, the minimum volume of normal liver that can be left after a surgical resection is 20%.²⁷ Using a minimal volume of 30% of normal liver mass provides a safety factor. The total volumetric flow of a normal portal system is 1000 mL/min.²⁸ CFD has a maximum accepted correlation with physical testing of 20% difference. To ensure that the flow rate was at least 30% of portal blood flow, the volumetric flow rate was increased to 350 mL/min. The vascular network was arranged in stacked layers and was designed to ultimately have 40 layers based on current manufacturing and size limitations. This equates to a target blood flow rate of 9 mL/min per single layer of the vascular network. The flow within the device was modeled and tested at a constant flow rate. The majority of blood flow to hepatocytes in the native liver is from the portal vein flow, which in humans is normally less than 10 mmHg and has minimal pulsatility compared to arterial flow.

Vascular network design

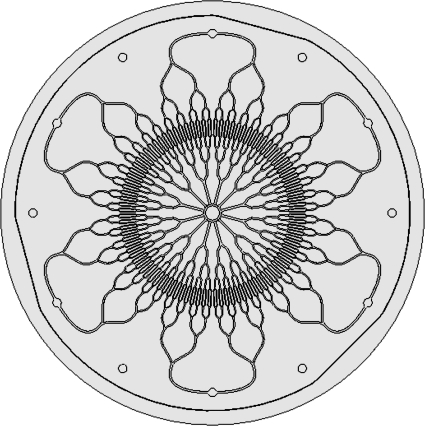
Based on the radial architecture of the liver lobule, a six radial input design with a central outlet was drafted in 3D using SolidWorks^® (SolidWorks). A top view of the design is shown in Figure 1. The network channel dimensions were originally selected based on estimates for the desired flow and pressure drop. All channel generations followed Murray's Law and were created with a 1:1 aspect ratio. A header was designed to divide inlet flow from a single inlet into the six radial inlets of the vascular network. For a 40-layer device, the header would divide the flow in the six radial inlets and flow would continue vertically through the layers to feed each inlet. The blood would flow into each layer orthogonal to the vertical inlet supply channels.

FIG. 1.

Top view of radial branching vascular network designed according to biomimetic principles. The six radial vascular inlets are shown at the periphery, and the vascular channels bifurcate into several generations of inlet channels toward the smallest channels. The channels then coalesce into 12 outlet channels and enter the central venous outlet.

CFD analysis and design optimization

CFD is a powerful tool to simulate fluid flow and optimize flow parameters before manufacturing vascular networks. CFD has been used to optimize blood flow in other microvascular networks.^8,11,13 Utilizing the 3D geometric vascular network model created in Solidworks, a computational mesh was generated using FloWorks (SolidWorks), a CFD software package integrated with SolidWorks. The radial symmetry of the design enabled the blood flow to be simulated in only one-sixth of the vascular network design. The mesh for the simulation contained 336,235 complete fluid cells and 381,529 partial fluid cells. The CFD analysis was completed using the FloWorks solver in 271 iterations. A non-Newtonian blood model was used that accounted for the suspension of red blood cells in plasma that has a viscosity that varies with strain rate. The non-Newtonian model was based on the Hurschel–Buckley model, where the viscosity μ varies according to the law

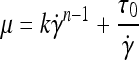(2)

where k is the liquid's consistency coefficient (Pa × sⁿ), 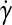is the strain rate, n is the liquid's power-law index (dimensionless), and τ_o is the liquid's yield stress (Pa). This model has been used to model the rheological behavior of blood.^29,30 The experimental values recommended by Kim were utilized as n = 0.83, τ_o = 17.5 mPa, and a density of 1049.5 kg/m³.²⁹ The consistency coefficient varies for human and bovine blood as defined by Kim. We empirically determined the value of k for sheep blood at 37°C by setting up a simple flow system using small-diameter silicone tubing and a syringe pump. The value of k was empirically varied in similar range of k as human and bovine blood²⁹ until there was excellent correlation between the inlet pressure measured in vitro and predicted by the model. From this testing, a k value of 0.0124 Pa · s was used.

Utilizing the results of the CFD analysis, the channel dimensions were adjusted until the corresponding flows were within 10% of the target flow rate for the pressure drop of the design inputs. The network was designed so that laminar flow was achieved throughout. Although turbulent flow was found to stimulate regeneration after liver resection,³¹ the risk of platelet activation with a vascular network made with a polymer outweighed any potential benefit. Further, the benefit of turbulence is mediated through a liver sinusoidal endothelial cellular response that is not appreciated in the absence of those cells. Accordingly, the fillets at each bifurcation were empirically adjusted in an iterative process using CFD analysis until uniform flow with minimal shear stress changes was achieved. The header layer flow and fillet angles were also optimized using CFD.

Mold and device manufacturing

A positive feature mold for the vascular network was made in stainless steel using electrical discharge machining (EDM) at the Ex One Company (Irwin, PA). The positive feature header mold and nozzle were made using traditional machining in stainless steel and polycarbonate, respectively.

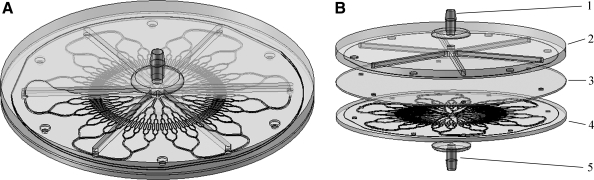
The vascular network devices were made with traditional soft lithography techniques by casting Sylgard 184 polydimethylsiloxane (PDMS) (Ellsworth Adhesives, Germantown, WI) on the molds and heat curing it according the manufacturer's specifications. A thin sheet of PDMS with holes punched at the radial inlets of the vascular layer was interposed between the header and vascular layers, as otherwise the open channels of the header layer would directly communicate with the open channels of the vascular layer. The vascular layer, flat sheet, and header layer were bonded together using oxygen plasma bonding (Model PX-250; March Plasma Systems, Concord, CA). Inlet and outlet nozzles were attached to the header layers using silicone RTV sealant 732 (Dow Corning, Midland, MI). Devices were built and tested as single layer devices. Figure 2 shows the assembled device in an isometric view and in an exploded view to demonstrate the exact configuration of the design. The vascular network had a diameter of 130 mm. This size could fit into an abdomen of a patient with moderate liver failure or could possibly be used as an extracorporeal device in an intensive care setting.

FIG. 2.

Isometric view of single-layer liver vascular network with header and nozzles (A). Exploded view of single-layer vascular network showing inlet nozzle (1), header layer (2), spacer (3), vascular layer (4), and outlet nozzle (5) (B). Flow enters the nozzle and is divided into six channels in the header layer to enter the radial inlets of the vascular layer. Blood flows through the vascular layer and collects at the central outlet and flows out of the lower nozzle.

In vitro design verification testing

Verification testing was performed on single layer devices (n = 9) using the following in vitro test apparatus. A syringe pump (PHD 2000; Harvard Apparatus, Holliston, MA) was used to pump 37°C anticoagulated sheep blood (Lampire Biologics, Pipersville, PA) through each device. The blood was collected into a reservoir that maintained the outlet pressure at 3 mmHg. The inlet pressure to the device was continuously monitored using a pressure transducer (Model PX209-30V15G5V; Omega Engineering, Stamford, CT) connected to a digital display (Model DPi8-EI; Omega Engineering). Each device was tested over a range of flow rates three times. The inlet pressure was recorded for each flow rate. The values were then averaged for each device and for all of the devices combined.

Results

Using the seven described biomimetic design principles, a radial vascular network design was developed. The iterative design process using CFD analysis achieved the design input pressure drop, flow rate, and optimized flow at the bifurcations. The resulting diameters, channel lengths, and degree of venous scaling are shown in Table 2.

Table 2.

Vascular Network Dimensions for Each Generation and the Venous Scaling Expressed as a Percent Diameter Increase from the Matching Generation Inlet Diameter

Vascular network channel	Channel diameter (μm)	Channel length (mm)	Venous scaling (%)
Inlet channels	673	10.09	n/a
2nd-generation inlet	534	5.74	n/a
3rd-generation inlet	424	4.44	n/a
4th-generation inlet	334	3.44	n/a
Smallest channel	267	6.80	n/a
1st-generation outlet	364	3.44	8.98
2nd-generation outlet	458	4.44	8.02
3rd-generation outlet	576	5.74	7.87
4th-generation outlet	727	10.09	8.02

n/a, not applicable. There was no scaling used on the inlets.

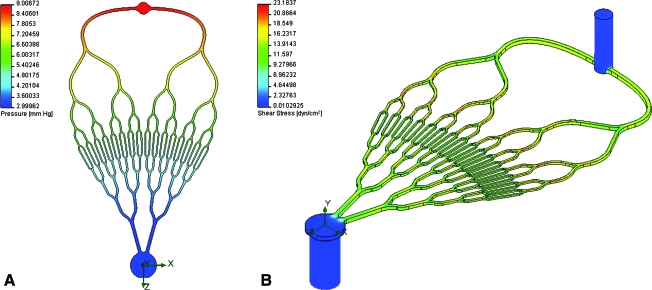
For CFD analysis, the pressure was set to 9 mmHg inlet pressure (a 1 mmHg pressure drop is present in the header layer) and 3 mmHg outlet pressure. The resulting pressure plot from the CFD analysis is shown in Figure 3A. The CFD predicted flow rate of blood for this pressure drop was 8.96 mL/min, compared to the target flow rate of 9.0 mL/min. The shear stress within the channels ranged between 11.1 and 23.2 dyn/cm², excluding the corners of the channels, where the shear stress was a minimum of 6.49 dyn/cm². This is consistent with the design goal that the targeted shear stress be between high venous and low arterial shear stress (5 to 25 dyn/cm²). An isometric plot of the shear stress is shown in Figure 3B.

FIG. 3.

Pressure drop from radial inlet to central outlet of vascular network. The pressure drop is uniform across the network; due to venous scaling, more pressure drop occurs in the inlet generations than the outlet generations (A). Isometric view of the shear stress of the vascular network. Shear stress variation was minimized by utilizing both Murray's law for channel diameter relationships and channels with 1:1 aspect ratio (B). Color images available online at www.liebertonline.com/ten.

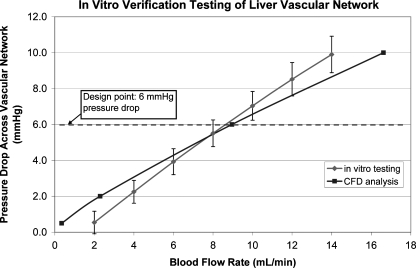
The in vitro design verification testing results were compared to the CFD analysis results over a range of flow rates from 2 to 14 mL/min, including the design point of 9 mL/min. At this design point, the difference in pressure drop between the CFD analysis and the in vitro verification testing was less than 5%. This is well within the accepted CFD rate of correlation with in vitro testing of 20%. A plot of the verification testing results compared to the CFD analysis results is shown in Figure 4.

FIG. 4.

Graph of in vitro verification testing results (error bars ± one standard deviation) for blood flow compared to the CFD analysis. The error at the design point of 6 mmHg pressure drop across the network was less than 5%. CFD, computational fluid dynamic.

Discussion

Branched vascular networks are a central component of scaffold architecture for solid organ tissue engineering. This work presents a biomimetic design methodology founded on independently investigated anatomic and physiological principles of natural blood vessels. The concept was to develop a broadly applicable set of biomimetic design principles that could be used to create both simple and complex vascular networks for tissue-engineered scaffolds. These design principles were applied to a liver scaffold design in a unique branched radial vascular network design to replicate the blood flow pattern of the liver lobule.

The presented vascular network was an application of these biomimetic design principles in a simplified vascular network with lower channel density than will eventually be required to support a large mass of hepatocytes. For the 40-layer device with 30% of the liver blood flow, it would support 30% of the hepatocytes of a normal liver. Twenty percentage of the hepatocytes of a normal liver are considered an absolute minimum volume required to provide to basic liver function with 30% of hepatocytes representing a safety factor. However, to effectively do this the channel density will need to be increased. Future networks will need a maximum distance between channels of a few hundred microns. At 130 mm, the diameter of the vascular network was much larger than that of a normal liver lobule, which is reported to be 0.8 to 1.5 mm in diameter.³² Future liver lobule designs will need to begin to approach these dimensions, probably within an order of magnitude, to begin to have a physiological effect. This will require further reduction in scale of the biomimetic length as liver sinusoids are on the order of 30 μm in diameter. The importance of strict adherence to biomimetic lengths is unknown. However, long channels with very small diameters may cause flow disturbances and possibly platelet activation.

The importance of minimizing platelet adherence, platelet activation, and ensuing thrombus formation in these vascular networks cannot be overstated. Achieving physiologic shear stress within the network is a fundamental first step in minimizing the risk of thrombus formation. It is expected that further design refinements will be required with subsequent in vitro and in vivo testing to determine the degree of thrombus formation within the device. Ideally, separate assays to measure platelet adherence and platelet activation could be preformed to understand design implications on these important parameters. The platelet activation assay developed by Jesty and Bluestein³³ has been evaluated in other systems^34,35 and may be applied to these networks. Chronic in vivo testing is the all-encompassing analysis of thrombus formation in these vascular networks. Achieving prolonged blood flow with clinically acceptable anticoagulation and antiplatelets agents is the ultimate goal.

Another feature of the design that may improve in future generations and contribute to minimized platelet activation relates to the diameter tapering approach. In this design, the diameter changes of the channels occurred at the bifurcation. In the body, the geometric tapering of the arteries is constant. The effect of both geometric tapering as well as the progressive increase in stiffness of vessels as they move away from the heart (elastic tapering) has significant impacts on the impedance of the vascular network. This has been well studied and mathematical models to predict these effects have been developed.^36–38 Although this has been well defined for the arterial circulation, a similar phenomenon may exist for the portal circulation. Future designs will include constant geometric tapering to better mimic native vessels. Elastic tapering is not able to be well controlled within the current architecture, but analysis may include the effects of pulsatile waveform reflection that may be done for portal venous pressures. Future designs with higher channel density may also have thinner PDMS walls between the channels. When the walls become very thin, the elastic deformation due to pressure may become significant, as has been demonstrated by Gervais et al., and will need to be accounted for in the design.³⁹

Iterative design is a central component of any engineering effort, and CFD analysis allows optimization of the vascular network before production of a mold. The biomimetic design principles outlined herein are flexible enough to accommodate a very wide range of general vascular network sizes and architectures. To achieve uniform flow and physiological shear stress throughout the entire network, a careful analysis by CFD is required with iterative design changes, until these parameters are optimized. Even exquisite and costly in vitro testing cannot produce the same level of data as current CFD packages. Although there is an understood error rate of CFD compared to bench top testing, CFD remains an efficient method to optimize the finer aspects of a vascular network. This was apparent at the design flow rate where the correlation between the CFD and the in vitro results was excellent, whereas at the highest and lowest flow rates the pressure difference was much greater. The difference in slope of the CFD predicted values may be a function of a number of variables. The surface finish of the EDM mold was rougher than the mirror finish of photolithography and the model, and this may have had an effect. Although empiric testing was done to slightly modify the non-Newtonian blood model for sheep blood, further optimization may be done in the future. Despite these limitations, the close correlation of the CFD analysis and the in vitro testing in this experiment validates this methodology for vascular network design and paves the way for further network design to follow a similar developmental methodology.

Photolithography is the current mainstay of mold manufacturing for microfluidics.^40,41 The precision and low cost of photolithography molds make them an ideal method for many microfluidic applications. However, the constraint of a single channel depth is a very significant limitation of this technology. Although multiple mask processing can achieve multidepth molds, this is rarely done and results in step transitions. Vascular network channels with 1:1 aspect ratios and rounded corners have a more physiological shear stress distribution and in theory can achieve more physiological axial concentration of red blood cells in laminar flow.⁴² The limitation to date has been identification of a manufacturing process that can produce 3D microfluidic molds with tapered channel depths while retaining adequate feature resolution. For this project, EDM was used to manufacture a 3D mold in stainless steel. The fundamental methodology of EDM is shown in Figure 5. Once the mold was created, the soft lithography process to create the devices was identical to what is done with photolithography molds. Although this was a step forward in that a 3D mold with 1:1 aspect ratios was achieved, the process has some inherent limitations. To produce the mold, a graphite electrode was created using traditional machining that has a positioning accuracy of 5 to 10 μm, significantly less precise than photolithography. The surface finish of the mold was much rougher than the typical mirror finish of a photolithography mold. The devices were assembled using oxygen plasma bonding but required higher clamping forces during bonding than do PDMS layers from a photolithography mold. This mold-manufacturing approach will likely be a step toward other technologies that can produce molds with 3D features but with more precision and better surface finish than EDM.

FIG. 5.

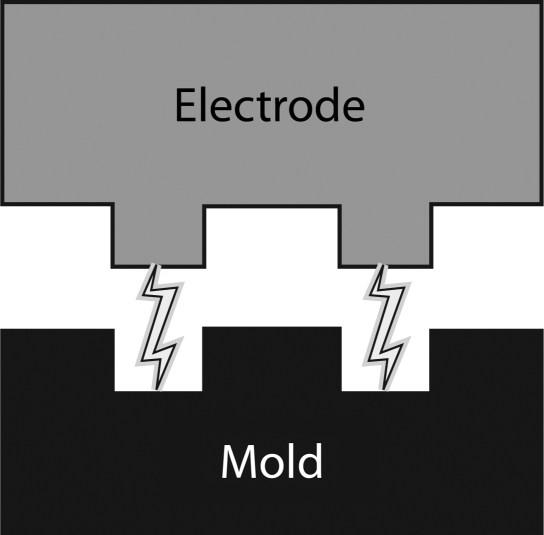
Electrical discharge machining utilizes an electrode of the desired pattern usually machined with a traditional milling machine in graphite. A high voltage is placed across the electrode and the steel mold material. As the electrode comes into proximity with the mold, a spark will arc across a dielectric fluid and remove a very small bit of the mold material. This process is repeated usually millions of times until the impression of the electrode has sunk into the mold to form the desired pattern.

Microvascular networks and other innovative approaches have been described as a solution to the vascularization of hepatocytes for in vitro or in vivo applications. Our lab has demonstrated a general vascular network design that supports hepatocytes.⁸ Another group also utilized a radial design approach but without a branched network and with direct exposure of hepatocytes to shear stress.¹⁰ Table 3 outlines the major features of several other approaches to vascularization of hepatocytes or tissue. The approach of this work is centered on a radial branched vascular network that mimics the physiologic shear stress of the liver and utilizes a more biomimetic-focused approach than previous works.

Table 3.

Different Reported Approaches of Vascularizing Hepatocytes and Microfluidic Vascular Networks for Liver Tissue Engineering are Compared

Author	Concept	Design
Biomimetic vascular network	Microfluidic vascular network with adjacent hepatocytes separated by porous membrane	Biomimetic radial design with physiologic shear stress and 1:1 aspect ratio of all channels
Carraro et al.8	Microfluidic vascular network with adjacent hepatocytes separated by porous membrane	Linear network with multiple parallel capillary like beds, variable aspect ratio
Park et al.10	Microfluidic channels with hepatocytes and fibroblasts exposed to direct flow	Radial pattern of straight channels containing hepatocytes exposed to very low shear stress
Janakiraman et al.12	Microfluidic vascular network with adjacent porous material, optimized for nutrient transport	Multiple generation bifurcation design with large width:height aspect ratio for high planar diffusion of nutrients
Gilbert et al.11	Microfluidic vascular network with interconnected channels	Open network with diamond-shaped posts with high aspect ratio (>10:1 width:height)
McGuigan and Sefton44	Modules of hepatocytes suspended in collagen gel, coated with endothelial cells	Modules suspended in tube and form interconnected network of channels that can support perfusion

Although PDMS was used for the devices in this study, medical-grade silicone such as Dow Corning 4210 silicone could be used to create an implantable device. A silicone-based vascular network scaffold may function as a bridge to liver transplant or as a short-term liver assist device with adequate anticoagulation and antiplatelet agents. The advantage of silicone is its elasticity, low reactivity, and ease of manufacturing into these complex microfluidic devices. Silicone replicates the surface finish of the mold down to the micron scale. The elasticity of silicone is not capitalized upon in this design, as the thickness of polymer between the channels is relatively large. Future designs may employ thinner walls and may take advantage of the high elasticity of silicone but balancing the burst strength to retain a high safety factor in the design.

The next phase of validation of the vascular network will be to test the capacity of the network to support adjacent hepatocytes in a tissue-engineered liver construct. For this future aim, the device will be manufactured with the vascular network adjacent to an open parenchymal chamber, separated by a porous polycarbonate membrane. Primary hepatocytes will be metabolically supported by the vascular network in an in vitro culture test with media flowing through the vascular network. The oxygen and nutrients diffuse through the porous membrane to supply the cells. These tests will assess the maintenance of synthetic and metabolic functions of hepatocytes and specifically the capacity of the liver vascular network to support these functions for an extended time. Previous in vitro support of hepatocytes has been demonstrated with an earlier generation vascular network.⁸ Further validation of these design principles will be done with revising the network to create a much higher density design using the same principles where nearly all points on the network are within a few hundred microns of a vascular channel. This high-density design vascular network may also have multiple interconnected lobules, analogous to native liver.

However, the goal remains to develop these vascular networks using resorbable polymers that can be seeded with endothelial cells in addition to the other parenchymal cells required for the tissue. This concept has been demonstrated in vitro,⁴³ but the exact polymer and manufacturing techniques are still under development. As the designs of vascular networks mature and achieve physiological flow in a high-density design, the manufacturing of the networks in resorbable polymers at an appropriate scale will become the next significant hurdle in creating a feasible vascularized scaffold for a tissue-engineered liver.

Microfluidic vascular networks can deliver oxygen and nutrients to parenchymal tissues and may be used to develop tissue-engineered organs and organ assist devices. In this work a set of biomimetic principles was outlined and a liver-specific vascular network was designed using these principles. Optimization of the vascular network was done with iterative design changes based on CFD analysis and in vitro verification testing was performed. Future work will focus on optimizing these vascular networks and validating their ability to support hepatocytes for clinical use.

Acknowledgments

The authors gratefully acknowledge support from the NIH (F32 DK076349-01 to D.M.H., and T32 DK07754-09 to H.I.P.). The authors would like to thank the Ex One Corporation for their generous contribution of machining the molds for this project. The authors would like to thank Ali Hart for her technical assistance.

Disclosure Statement

No competing financial interests exist.