Generalized Additive Models and Inflated Type I Error Rates of Smoother Significance Tests

Abstract

Generalized additive models (GAMs) have distinct advantages over generalized linear models as they allow investigators to make inferences about associations between outcomes and predictors without placing parametric restrictions on the associations. The variable of interest is often smoothed using a locally weighted regression (LOESS) and the optimal span (degree of smoothing) can be determined by minimizing the Akaike Information Criterion (AIC). A natural hypothesis when using GAMs is to test whether the smoothing term is necessary or if a simpler model would suffice. The statistic of interest is the difference in deviances between models including and excluding the smoothed term. As approximate chi-square tests of this hypothesis are known to be biased, permutation tests are a reasonable alternative. We compare the type I error rates of the chi-square test and of three permutation test methods using synthetic data generated under the null hypothesis. In each permutation method a distribution of differences in deviances is obtained from 999 permuted datasets and the null hypothesis is rejected if the observed statistic falls in the upper 5% of the distribution. One test is a conditional permutation test using the optimal span size for the observed data; this span size is held constant for all permutations. This test is shown to have an inflated type I error rate. Alternatively, the span size can be fixed a priori such that the span selection technique is not reliant on the observed data. This test is shown to be unbiased; however, the choice of span size is not clear. A third method is an unconditional permutation test where the optimal span size is selected for observed and permuted datasets. This test is unbiased though computationally intensive.

1. Introduction

The Generalized Additive Model (GAM) is a semiparametric extension of a Generalized Linear Model (GLM) that allows nonlinear functions of covariates to be included in regression equations. GAMs require an additive combination of functions of covariates but otherwise avoid stringent restrictions imposed by parametric assumptions. A general formula for a GAM is:

$$g\left(\mu \right)=\alpha +\sum _{j=1}^p{f}_j\left(X_j\right)+\epsilon ,$$

where g(μ) is a link function, α is the intercept, and f_j(·) are functions of the covariates, X_j. (Hastie and Tibshirani, 1990) A distinct advantage of GAMs is the ability to include smoothing terms taking the form of nonparametric functions of predictors in a model.

GAMs using univariate or bivariate smoothers are popular in current literature. Recent applications of GAMs have spanned may fields including public health (Hoffman et al., 2010, Vieira et al., 2005, Vieira et al., 2009), marine studies (Maravelias et al., 2000), and ecology (Guisan et al., 2002). In one example, markedly different results were observed when GAMs were compared to a logistic regression analysis when studying whether infant age and weight were associated with survival after cardiac surgery (Williams et al., July 1990). Where Williams et al. found a linear association between infant age and logodds of survival, Efron and Tibshirani display a roughly parabolic curve when a univariate smooth was applied. Lowest risk was found for subjects who were around 200 days old while substantially increased risk was found for those who were much younger or much older than that age, a trend that was missed by logistic regression. (Efron and Tibshirani, 1991) In spatial environmental epidemiology, a bivariate smoothing term is applied to the longitude of a subject's location of residence. Investigators map the study region to visually display areas of increased and decreased risk and test for spatial variation in disease risk across the region. (Webster et al., 2006) Many different smoothing techniques can be applied to covariates in a GAM (Hastie and Tibshirani, 1990); discussed here are GAMs with locally weighted regression smoothes (LOESS) (Cleveland, 1979), a popular and widely available method of smoothing.

When applying a GAM with a LOESS smooth, investigators determine the span, or neighborhood, size to apply to the model, assigning the proportion of the data given non-zero weights by the tri-cube weight function. (Hastie and Tibshirani, 1990) Often, spans are selected through the minimization of Akaike's information Criterion (AIC) (Hurvich et al., 1998), a measure of goodness of fit that can be used to balance the bias-variance trade-off.

$$AIC=\raisebox{1ex}{$(D(y;\mu )+2df)$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$$

where D(y; μ) is the deviance of the observed data from the fitted values, df are the degrees of freedom of the model, and n is the sample size. Small span sizes correspond to low bias with fitted values near observed values while large span sizes have increased bias and smaller variation across the fitted surface. (Hastie and Tibshirani, 1990) The minimal AIC statistic optimizes the fitted values to the observed data while also prioritizing less complex models. A GAM is applied to data using a series of possible span sizes. The AIC statistic for each span size is recorded and the “optimal” span corresponds to the minimal AIC statistic (Hurvich et al., 1998; Webster et al., 2006)

While often used as an exploratory data analysis method, a natural hypothesis when applying GAMs is whether the smoothing term is necessary or if a simpler model, applied with GLM techniques, would suffice. In the GLM framework, hypotheses testing nested models are evaluated with a likelihood ratio test to compare model deviances. For GLMs, the likelihood ratio statistic has an asymptotic chi-square distribution and the computation of degrees of freedom is straightforward. For GAMs, the likelihood ratio statistic does not follow a chi-square distribution and as a result, p-values are only approximate. (Hastie and Tibshirani, 1990) That said, an approximate chi-square statistic, degrees of freedom, and p-value are produced when GAMs are applied using statistical software R v2.8.0 (2008) and S-Plus v8.0 (2007). An alternative method to perform the hypothesis test is based on a permutation test applied after determining the optimal span. (Webster et al., 2006) The statistic of interest is the difference in deviance of GAMs including and excluding a smooth term. After obtaining the difference in deviance statistic from the observed data, investigators permute the values of the covariate(s) smoothed, otherwise maintaining relationships between the outcome and non-smoothed predictors. GAMs are applied to each of 999 permuted datasets, using the optimal span for the observed data. A conditional distribution of differences in deviance statistics is generated from the permuted datasets, given the selected span size. (Webster et al., 2006) Hypotheses are tested based on the rank of the observed difference in deviance statistic compared to the conditional permutation distribution. The Conditional Permutation Test is used to reduce the computational complexity required when the optimal span size is determined for each permuted dataset.

In their application of GAMs, Kelsall and Diggle selected the appropriate span size through a cross validation technique and applied a Monte Carlo test to evaluate overall departure from the null hypothesis. Using a statistic measuring the squared differences of observed probabilities of disease and probabilities under a null distribution, the authors determine the p-value as the rank of the observed statistic when compared to data under the null hypothesis, a method not unlike the Conditional Permutation Test described above. (Kelsall and Diggle, 1998)

Permutation tests are unbiased and appropriately sized, given that the observed statistic is compared to an appropriate permutation distribution. In this application, the span size is selected based on the observed dataset and a goodness of fit statistic, the AIC. The permutation distribution of differences in deviances is generated, conditioned on a now fixed span size that does not necessarily minimize the AIC for a given permuted dataset. Due to the different assumptions made during the application of the GAM to the observed and permuted datasets, the permutation distribution as described may not be an appropriate distribution to make inferences about the observed statistic.

It is unclear whether the Approximate Chi-Square and the Conditional Permutation Tests described above are of the correct size when span selection is based on the observed data. To investigate this we use synthetic data and compare the size of the Approximate Chi-Square Test, the Conditional Permutation Test, and two alternative permutations tests: a Fixed Span Permutation Test where the span size is determined a priori and an un Conditional Permutation Test where the optimal span is determined for each observed and permuted dataset. We show that the Approximate Chi-Square Test and the Conditional Permutation Test have inflated type I error rates while the fixed span and un Conditional Permutation Tests do not. We discuss mechanisms causing the inflated type I error rates and make recommendations for when each method is most appropriate.

2. Simulated Data

Data were simulated to examine the type I error rate of hypothesis tests using GAMs. Simulated data were created under the null hypothesis of no association between the outcome and predictor(s). There was no correlation between predictors of interest and the outcome and the outcome and predictors were generated independently. For each set of parameters, 1000 datasets were simulated, each with 1000 observations. The sample size was chosen to reflect the size of previous analyses that examined the Cape Cod Family Health Study data and employed GAMs as a statistical analysis technique. (Aschengrau et al., June 2008; Vieira et al., 2009; Webster et al., 2003)

2.1 Univariate Smooth under Null Hypothesis

Data were simulated to evaluate tests when a LOESS smooth was applied to a single variable. The outcome was dichotomous to reflect common outcomes of interest, such as cancer and low birth weight, examined in environmental epidemiology studies that used GAMs as a statistical analysis method. (Aschengrau et al., June 2008; Vieira et al., 2009; Webster et al., 2003) Three sets of simulations were performed with outcome probabilities equal to 0.05, 0.10, and 0.20. These probabilities were chosen to reflect data likely to be seen in epidemiologic studies with outcomes such as breast cancer (Webster et al., 2008), children living with a substance-abusing parent (SAMHSA) (2009), and age and sex-adjusted childhood obesity (Anderson and Whitaker, 2009). The predictor was uniformly distributed between ±1, representing some exposure of interest. While it is unlikely that a covariate will be uniformly distributed in practice, we simulated data under an optimal scenario where the distribution of the covariate was not expected to affect the type I error rate.

Data were also simulated with a Gaussian outcome. Results were similar to those obtained with a dichotomous outcome and are not presented here. Further information is available upon request.

2.2 Bivariate Smooth under Null Hypothesis

Data were simulated to evaluate the null hypothesis of no association between a dichotomous outcome and a bivariate smooth applied to two uniformly distributed predictor variables, perhaps representing geographic location. Again, three sets of simulations were performed with outcome probabilities equal to 0.05, 0.10, and 0.20.

3. Hypothesis Testing Methods

3.1 Approximate Chi-Square Test

The Approximate Chi-Square Test was based on the likelihood ratio test and assumed that the deviance had an asymptotic chi-square distribution, an assumption known to be approximate. (Hastie and Tibshirani, 1990) GAMs were applied to datasets using the R v2.8.0 (2008) function gam() from the gam package (Hastie, 2008) across a range of span sizes. The optimal span was selected as that which minimized the AIC statistic. For the model corresponding to the optimal span size, the approximate chi-square statistic p-value was recorded. The type I error was estimated as the proportion of data sets for which the p-value fell below 0.05.

3.2 Conditional Permutation Test

For each of the 1000 datasets, the optimal span size was selected as described for the Approximate Chi-Square Test and was subsequently held constant for the remainder of the analysis. As described in the introduction, the difference in deviance between the model including and excluding the smooth term was computed. Through permutation of the smoothed variable(s), 999 permuted datasets were created. Larger numbers of permutations were considered; however computing time became unwieldy and critical values obtained from permutation distributions were not substantially altered when reduced numbers of permutations were used. GAMs were applied using the span size previously selected for the observed data and the differences in deviance for these datasets were recorded. The differences in deviance were ranked and the null hypothesis of no association between the outcome and smoothed term was rejected if the observed difference in deviance fell in the upper 5% of the conditional permutation distribution. (Webster et al., 2006)

3.3 Fixed Span Size Permutation Test

As a general comment with respect to non-parametric methods, Hart suggests authors determine smoothing parameters prior to performing hypothesis tests to ensure appropriate test size. (Hart, 1997) We apply his suggestion to determine if there was some influence of a predetermined span size on the type I error rate, analyses were performed conditioning on a preset span size of 0.10, 0.30, 0.50, 0.70, and 0.90 in place of the optimal span. The test was otherwise performed as described for the Conditional Permutation Test.

3.4 Unconditional Permutation Test

We selected the optimal span size for the observed data as previously described. For each of the 999 permuted datasets we applied GAMs with a range of span sizes and selected the span that minimized the AIC. We computed the differences in deviance from models that used the permuted dataset optimal spans and created a permutation distribution from these statistics. The null hypothesis was rejected if the observed difference in deviance statistic fell in the upper 5% of the permutation distribution.

3.5 Applying Methods to Simulated Data

The four GAM hypothesis testing methods were applied to data simulated under the null hypothesis. Results from the Fixed Span Size Permutation Test for probabilities of success of 0.10 and 0.20 are not presented. Similar results were observed and are available upon request. The results from the Conditional Permutation Test and Unconditional Permutation Test are displayed for all three probabilities of success. All tests were performed with a nominal α of 0.05.

4. Results

4.1 Type I Error Rate

Application of the Approximate Chi-Square Test to simulated data verified that the type I error rate for this test was inflated. The results showed that for GAMs applied with both univariate and bivariate smoothes, the type I error rate exceeded three times the nominal α of 0.05. (Table 1)

Table 1.

Type I Error Rates for Approximate Chi-square, Conditional and Unconditional Permutation Tests

	Approximate X2 Method	Conditional Permutation Test	Unconditional Permutation Test
Univariate Smooth
P(Success)=0.05	0.192	0.132	0.038
P(Success)=0.10	0.178	0.141	0.050
P(Success)=0.20	0.187	0.135	0.055
Bivariate Smooth
P(Success)=0.05	0.161	0.095	0.060
P(Success)=0.10	0.161	0.095	0.042
P(Success)=0.20	0.151	0.090	0.045

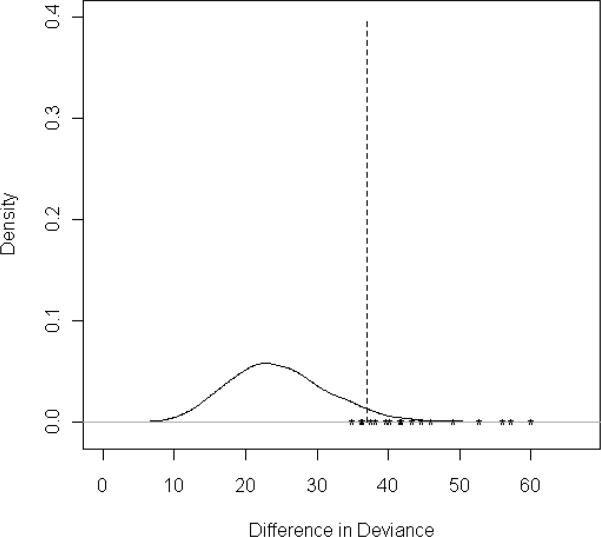
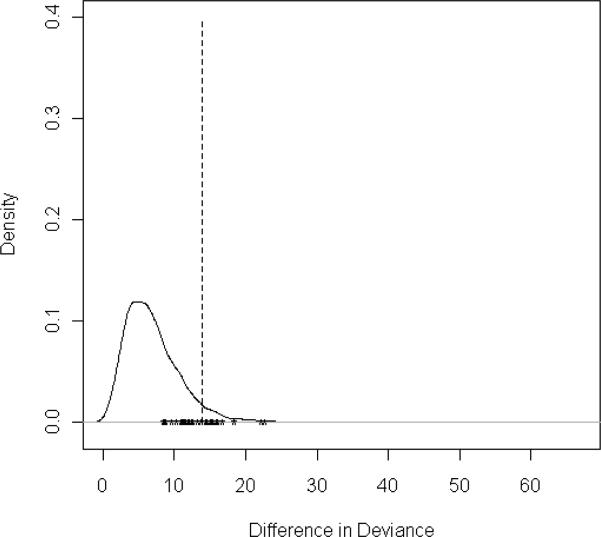
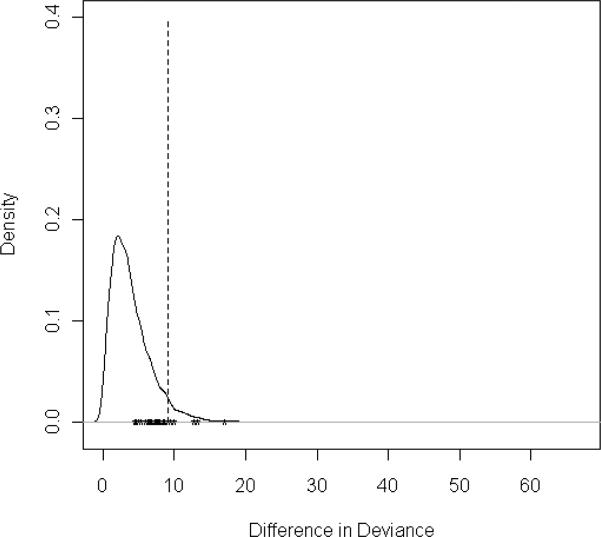
The Conditional Permutation Test displayed an inflated type I error rate when applied to simulated data including both the univariate and bivariate LOESS smoothing terms. (Table 1) Figures 1a-1e display the observed difference in deviance statistic compared to the permuted distribution of the statistics for a subset of five possible span sizes. When a small span size was selected based on the observed data, the observed difference in deviance statistic tended to be inflated when compared to the distribution of statistics from the permuted data. (Figure 1) Of note, the null hypothesis was rejected over 25% of the time when the selected span size was less than 0.90 and was rejected less than 5% of the time for spans of at least 0.90. (Table 2)

Figures 1a-e.

Difference in Deviance Distributions for Observed Statistics from CPT and Corresponding Permutation Distributions

Figure 1a: CPT Observed Statistics and Permutation Distribution for Optimal Span of 0.1

Figure 1b: CPT Observed Statistics and Permutation Distribution for Optimal Span of 0.3

Figure 1c: CPT Observed Statistics and Permutation Distribution for Optimal Span of 0.5

Figure 1d: CPT Observed Statistics and Permutation Distribution for Optimal Span of 0.7

Figure 1e: CPT Observed Statistics and Permutation Distribution for Optimal Span of 0.9

Table 2.

Type I Error and Span Selection for Conditional Permutation Test

	Span < 0.90		Span ≥ 0.90
	# Datasets	# Rejecting Ho	# Datasets	# Rejecting Ho
Univariate Smooth
P(Success)=0.05	332	101 (30.4%)	668	31 (4.6%)
P(Success)=0.10	331	111 (33.5%)	669	30 (4.5%)
P(Success)=0.20	350	116 (33.1%)	650	19 (2.9%)
Bivariate Smooth
P(Success)=0.05	255	67 (26.3%)	745	28 (3.8%)
P(Success)=0.10	241	65 (27.0%)	759	30 (4.0%)
P(Success)=0.20	244	68 (27.9%)	756	22 (2.9%)

The Fixed Span Size Permutation Test showed a type I error rate close to 0.05. When the test was conditioned on a predetermined span size, it was unbiased. (Table 3) The effect of small spans for the Conditional Permutation Test was not observed here as the span sizes were not selected based on artifacts in the data. Instead they were determined a priori and, as a result, the observed statistics were compared to appropriate permutation distributions. Investigators may use the Fixed Span Size Permutation Test to test for association using multiple spans. We suggest choosing three or five span sizes for this comparison to obtain information from the data across the range of possible spans. When examining multiple spans, investigators must adjust the nominal α level to avoid multiple testing biases. One adjustment is to divide α by the number of spans evaluated. We would reject the null hypothesis if any statistic corresponds to a p-value at or below the reduced cut-off. Only one statistically significant value would be required to reject the null hypothesis. With this adjustment the test is unbiased, if slightly conservative. (Table 4)

Table 3.

Type I Error Rates for Fixed Span Size Permutation Test

	Univariate Smooth*	Bivariate Smooth*
Span = 0.1	0.045	0.046
Span = 0.3	0.052	0.048
Span = 0.5	0.056	0.044
Span = 0.7	0.049	0.051
Span = 0.9	0.052	0.047

^*P(Success) = 0.05

Table 4.

Type I Error Rates for Testing Multiple Fixed Span Sizes with Adjusted Nominal α Level^‡

Spans Evaluated	Univariate Smooth*	Bivariate Smooth*
5 Spans	0.024	0.026
3 Spans
0.1,0.5,0.9	0.031	0.037
0.3,0.5,0.7	0.027	0.021
0.5,0.7,0.9	0.024	0.027

^‡Null hypothesis rejected if one or more statistics fall in upper $100\left(\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\#spansevaluated$}\right.\right)\%$ of permutation distribution

^*P(Success) = 0.05

When the Unconditional Permutation Test was applied, type I error rates were observed near 0.05, the correct nominal level. (Table 1)

4.2 Span Size and Difference in Deviance Distribution

The marginal distribution of selected span sizes across 1000 simulated datasets was unimodal and skewed toward smaller spans. (Figure 2) Under the null hypothesis, there is association between the outcome and predictor and the most appropriate span is equal to 1. In other words, 100% of the data are assigned non-zero weights. Our range of possible spans was between 0.05 and 0.95 with 0.95 being the most appropriate value. A “large” span, equal to 0.9 or 0.95, was selected near 65 and 75% of the time for the univariate and bivariate smooths, respectively. (Table 2)

Figure 2.

Marginal Distribution of Selected Span for GAM with a Univariate Smooth

Increasing span sizes corresponded to decreasing difference in deviance statistics. (Figure 3, Figure 4) As displayed in Table 5, the mean and median difference in deviance statistic decreases substantially as the span size increases.

Figure 3.

Joint Distribution of Selected Span and Difference in Deviance for GAM with a Univariate Smooth

Figure 4.

Difference in Deviance Distributions across Span Sizes

Table 5.

Mean and Median Difference in Deviance Statistics across 1000 Simulated Datasets

	Univariate Smooth*		Bivariate Smooth*
	Mean	Median	Mean	Median
Span = 0.1	24.51	23.81	52.33	51.91
Span = 0.3	6.91	6.35	17.01	16.71
Span = 0.5	4.00	3.50	10.28	9.89
Span = 0.7	2.80	2.34	7.14	6.65
Span = 0.9	2.06	1.47	5.30	4.86
Optimal Span	5.38	2.39	7.87	4.98

^*P(Success) = 0.05

5. Discussion

We begin by noting that the Approximate Chi-Square Test had an inflated type I error rate, a result of inappropriate assumptions regarding the asymptotic distribution of the difference in deviance statistic. The error rate was over three times the nominal 5% level. The Conditional Permutation Test also displayed an inflated type I error rate: there was approximately twice the probability of falsely rejecting the null hypothesis. In practice, when observed p-values are extreme, say in the upper 2.5%, investigators may feel confident with the study results.

A negative association was observed between span size and difference in deviance statistics. In general, smaller span sizes more accurately fit the data, at the cost of added complexity, an added penalty when computing the AIC statistic. As a result, datasets with a small optimal span size will have larger difference in deviance statistics than datasets with a large optimal span. When a small span was selected based on the minimal AIC statistic, only a very small proportion of permuted datasets would have minimal AIC statistics corresponding to this same span size. As a result, the observed difference in deviance statistic fell in the upper tail of the distribution obtained from the permuted datasets. The result was an inflated statistic and a deflated p-value, as observed in Figure 1.

The inflated type I error rate of the Approximate Chi-Square Test was due to the use of an approximate asymptotic distribution for evaluation of the statistic while the inflated rate for the Conditional Permutation Test was due to the inappropriate permutation distribution. The observed p-values for these tests should not be used as conclusive evidence of an association unless they are very small, i.e., less than $\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ for the Approximate Chi-Square Test and $\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ or $\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ for the Conditional Permutation Test with univariate and bivariate smoothes, respectively.

When we conditioned on a span size, selected a priori, and subsequently held the span constant for the observed and permuted data, the difference in deviance statistic from the observed data was compared to an inappropriate permutation distribution. The test was unbiased. In practice, if investigators have some prior knowledge of an appropriate span, this may guide the choice of span. This method has advantages as the test is unbiased and computationally inexpensive. However without prior information it is not clear how to choose an appropriate span size independent of the observed data. If investigators simply guess they may bias study result by influencing the model's ability to detect different magnitudes of variation in risk. (Hastie and Tibshirani, 1990) Furthermore, maps using a small versus large span size can visually differ greatly. (Webster et al., 2006) It may be desirable for an investigator to perform multiple tests using different span sizes. With an appropriate adjustment to the nominal α, the tests appear to be unbiased.

When we performed an Unconditional Permutation Test where the span size was selected for the observed and the permuted datasets, the permutation distribution for the difference in deviance statistic was appropriate. As a result, we observed an unbiased hypothesis test. Span sizes less than 0.9 were observed in over 25% of datasets. Despite this, the statistics were not inflated when compared to the unconditional distribution. Span selection for the 999 permuted datasets produced a permutation distribution to which the observed data was appropriately compared.

Here we considered a single span size selection technique based on minimal AIC and GAMs applied with LOESS smoothing terms. Many other methods of span size selection and smoothing techniques are available. Many span selection criteria rely on a measure of goodness of fit, such as the AIC, Bayesian Information Criteria, or Cross Validation techniques. (Hastie and Tibshirani, 1990) We hypothesize that, as these methods are based on the deviance of models, they too will lead to inflated type I error rates when the Approximate Chi-Square or Conditional Permutation Tests are applied. We leave the evaluation of this hypothesis for future research. A popular alternative to LOESS smoothing is the application of penalized splines. Here, the number of knots included in the model is selected in place of the span size. Again, selection is based on goodness of fit or Cross Validation. (Hastie and Tibshirani, 1990) We hypothesize that the Conditional Permutation Test applied with splines will also suffer from inflated type I error rates though we leave this investigation to future research. Multiple covariates were not included in this study. The impact of the inclusion of other variables in GAM models is left for future research.

The Unconditional Permutation Test is the most appropriate method mathematically but is computationally intensive. When applied using the statistical program R v2.8.0 (2008) using a desktop personal computer with 504MB RAM to a single dataset with 1000 observations, the Unconditional Permutation Test analysis computed for 3 hours with a univariate smooth. When applied with a bivariate smooth, the analysis was completed after 5.5 hours of computing time. For comparison, a GAM applied with a bivariate smoothing term, a sample size of 1000, and a fixed span size of 0.9 was completed in about 15 minutes, as was the Conditional Permutation Test for the same scenario. Increased sample size corresponds to an increase in computing time. Applying the Unconditional Permutation Test to a sample of 5000 observations with a univariate smooth, the analysis was completed after 16.5 hours of computing time, 5.5 times longer than the analysis with 1000 observations.

While the extent of this simulation study was limited in choice of span selection and smoothing techniques and the distribution of covariates, we suggest a rule of thumb when performing such hypothesis tests with GAMs. The decision of which permutation method to apply should be based on the resources and goals of the study. Investigators must consider their computing capabilities in relation to the study sample size prior to method selection. With adequate computing power, if investigators are performing an exploratory analysis to obtain a general understanding of the data, the Approximate Chi-Square Test and Conditional Permutation Test are appropriate. Investigators must be aware of inflated type I error rates for these methods. Reduced significance levels based on the results of this study could be applied for the Approximate Chi-Square and Conditional Permutation Tests using a significance level of 0.05. We have not examined type I error rates at other significance levels and other adjustments may need to be made in order to obtain appropriately sized tests. Conclusive findings cannot be made with either method unless observed p-values are extremely small. If researchers are interested in testing for variation at different levels of smoothing, the Fixed Span Size Permutation Test is most appropriate as it provides an accurate type I error rate with limited computational expense. The use of multiple span sizes requires an adjustment for multiple testing. When investigators are interested in obtaining the most accurate p-values with an appropriately sized test without preconceived notions of cluster size, the Unconditional Permutation Test should be performed.