Molecular-level tradeoffs and metabolic adaptation to simultaneous stressors

Summary

Life is a dynamic process driven by the complex interplay between physical constraints and selection pressures, ranging from nutrient limitation to inhibitory substances to predators. These stressors are not mutually exclusive; microbes have faced concurrent challenges for eons. Genome-enabled systems biology approaches are adapting economic and ecological concepts like tradeoff curves and strategic resource allocation theory to analyze metabolic adaptations to simultaneous stressors. These methodologies can accurately describe and predict metabolic adaptations to concurrent stresses by considering the tradeoff between investment of limiting resources into enzymatic machinery and the resulting cellular function. The approaches represent promising links between computational biology and well established economic and ecological methodologies for analyzing the interplay between physical constraints and microbial fitness.

Mathematical modeling of microbial responses to environment

Microbes are complex systems; mathematical expressions have been used to predict and interpret these dynamic systems for more than a century [e.g. ^1,2,3]. Microbial growth expressions were soon combined into systems of differential equations to consider a multitude of stressors including combinations of limiting substrates, competitors, predators and the presence of inhibitors [4,5]. Unfortunately, kinetic models are parameter heavy, both in terms of number and sensitivity. Literature values for enzyme kinetic parameters often vary over several orders of magnitude [6]. Full parameter evaluation for large, biologically relevant networks is currently prohibitive and limits the ability of these modeling approaches to take full advantage of the omics data revolution. However, kinetic models are still popular, and progress continues in the development of innovative parameter approximations [7–11].

Alternative mathematical modeling methods circumvent the requirement for large condition-sensitive parameter sets. One particularly successful technique is stoichiometric modeling, which extracts systemic information from molecular-level network structure and conservation relationships. Stoichiometry-based methods can utilize a variety of omics datasets and thus occupy a practical position in modern biology. Stoichiometric modeling can be divided into three major classifications: constraint based linear programming, often termed flux balance analysis (FBA); metabolic flux analysis (MFA); and metabolic pathway analysis, frequently called elementary flux mode analysis (EFMA). All three methods define a hyper-dimensional solution space containing every biologically meaningful steady-state metabolism for a defined network model. The three methods differ in how they select particular metabolic flux distributions from this space. Articles discussing the details of stoichiometric modeling approaches can be found elsewhere [e.g. ^12,13–15]. Stoichiometric models typically produce steady-state approximations of intracellular fluxes, limiting dynamic analysis. However, techniques for approximating dynamic responses by sequentially identifying flux distributions as a function of changing environments have been developed and applied [16,17].

Stoichiometric analysis of single stress adaptations

The functional properties of metabolic systems are the product of evolutionary processes and are competitive given the organism’s life history. Therefore, assumptions about competitive cellular behavior are used to select solutions to stoichiometry-based models. A widely utilized criterion presumes that microorganisms maximize biomass yield (microbe production from a fixed quantity of substrate). This criterion is convenient, simple, and successfully describes microbial behavior under certain conditions; one such circumstance is E. coli grown in glucose-limited chemostats at modest dilution rates [18]. Biomass yield maximization sometimes (e.g. batch growth [19]) produces inadequate descriptions, implying that alternative metabolic strategies can be ecologically competitive. Game-theory-based interpretations are available for a variety of such cases [20]. Numerous criteria used in stoichiometric models are compared to experimental data in [19]; a summary of kinetic metabolic modeling criteria can be found in [21].

Economic considerations and metabolic strategies

Resource availability limits growth in most environments and is an important component of animal immune systems, commonly referred to as nutritional immunity [22,23]. This has driven microbial evolution toward strategies that allocate limiting resources to different metabolic isozymes and alternative pathways in a manner that favors fitness [24]. Standard economics approaches such as resource allocation theory and tradeoff analysis can be used to quantitatively compare the huge number of potential metabolic resource investment schemes [25–29].

Stoichiometric modeling criteria which account for resource investment have identified metabolic flux distributions which accurately describe microbial behaviors not covered by a maximum biomass yield strategy. For instance, criteria involving the minimization of total cellular metabolic fluxes are proxies for minimizing resource investment into enzymes [19,30]. This consideration is also implied by the criterion of maximizing growth while constraining enzyme-occupied volume [31]. These two criteria are mathematically related, and it has been reported that both identify the same flux distribution [32]. Explicit consideration of resource investment into metabolic strategies has been performed using elementary flux mode analysis (EFMA) [25,33]. Resource requirements for enzymes were compiled from subunit compositions, protein sequences, and amino acid elemental formulae. The study enumerated resource allocations for every biologically feasible pathway through a metabolic network. These investment requirements were then concatenated with biomass yields, a metric for metabolic efficiency. This approach identified cost-benefit tradeoff curves representing metabolic flux distributions optimal for any combination of two environmental stresses. The tradeoff curves highlight a central tenet of economics: resource value changes as a function of abundance. The tradeoff curve slope represents the exchange ratio between two resources. At either extreme, optimal use of the scarce resource becomes significantly more expensive in terms of the second resource (Fig. 1). A discussion of possible relationships between relative enzyme abundance and metabolite flux can be found in [25,33].

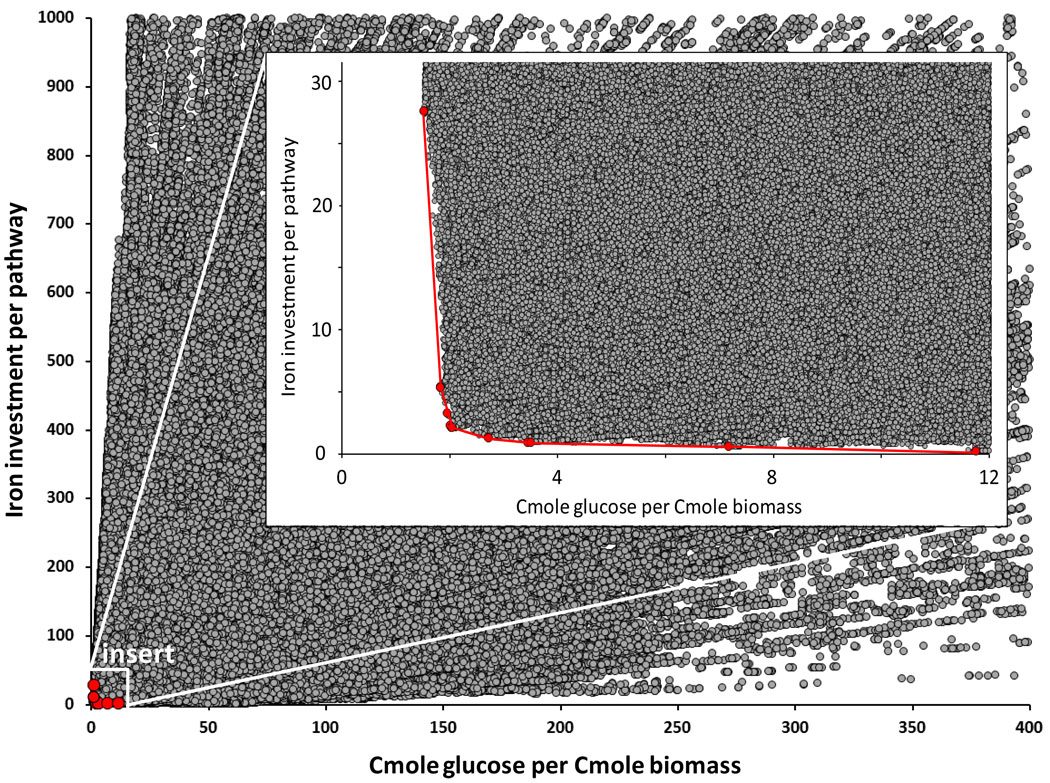
Figure 1. Illustration of a metabolic tradeoff curve.

Each circle represents a genetically independent and biologically meaningful steady-state growth metabolism (elementary flux mode) for E. coli. The position of each circle represents the metabolism’s resource investment (iron per elementary mode, y-axis) and operational efficiency (Cmoles glucose consumed per Cmole biomass produced, x-axis). The tradeoff curve, highlighted in red, represents the optimal relationship between enzymatic iron investment and the biomass production efficiency from glucose. From left to right, the slope of the tradeoff curve decreases, indicating a more severe penalty to operation costs (Cmole glucose per Cmole biomass) as limitations on iron investment increase. The large plot scale permits approximately 10.3 million of the 10.7 million possible biomass-producing pathways to be shown; the insert shows approximately 1 million pathways. Simulation data included maintenance energy requirements for a 60 minute doubling time.

A number of recent studies corroborate the concept of strategic resource investment into enzymes. An E. coli metabolomics study reported that the majority of measured metabolite concentrations exceeded half-saturation constants (K_m) for the appropriate substrate-enzyme pairs [34]. Operating enzymes near v_max maximizes flux per unit of invested resource. Substrate-enzyme pairs not falling into this category were proposed to be important for controlling flux directionality and magnitude. This control could be modulated by altering cellular investment into specific metabolite pools. Metabolites are a resource investment, although they represent only a small fraction of the total cellular contents: 5% of typical E. coli on a dry mass basis while protein represents 50–70% [35]. Results from kinetic simulations suggest network topology and kinetic parameters are sufficient to maintain cellular goals when enzyme concentrations are randomly perturbed [30], indicating that changes in metabolite pools can buffer proteomic disturbances. In addition, a recent experimental study demonstrated that changes in metabolite pools can support functional homeostasis when enzyme levels were experimentally altered in yeast central carbon metabolism [36]. Maintaining competitive flux distributions through changes in metabolite concentrations requires little or no active alteration of enzyme levels, resulting in significant resource investment savings.

Resource allocations and simultaneous stresses

Life is inherently competitive and stressors are not mutually exclusive. Microbes cope simultaneously with an assortment of constraints [37]. Economic and ecological theory provides a framework for predicting and interpreting microbial adaptations to multiple stresses [28,38,39]. When subjected to multiple pressures, cells must allocate finite resources to different subsystems in a proportion that improves fitness; the systems biology challenge is to determine how these allocations respond to different demands. While dynamic modeling methods have considered simultaneous pressures for decades [4,26], such considerations are just beginning to be addressed via genome-enabled molecular-level modeling approaches.

A stoichiometric modeling study considered metabolic adaptation to multiple stresses [33]. The study identified an ecologically relevant set of metabolic pathways that optimize tradeoffs between resource investment and functional benefit. Non-negative least squares regression assembled these pathways to describe metabolic fluxes measured under different growth conditions [from ¹⁹]. The aggregate stress response, comprised of linear combinations of 3–4 distinct pathways, represents a competitive allocation of resources, with the relative weight for each pathway theoretically proportional to the degree of corresponding stress. The approach described the fluxomic data more accurately than any reported single metabolic optimization criterion (typically based on a single stress) [19,33].

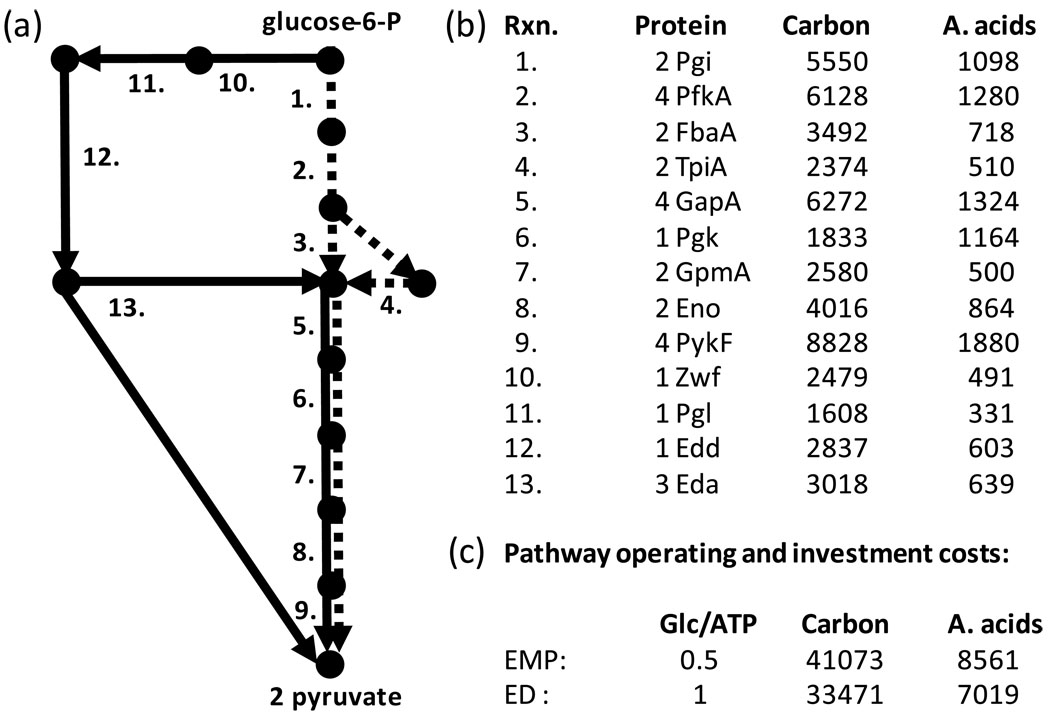
The study supported the observations that not all carbon-limited chemostat growth is equal and that carbon-limited chemostat growth does not necessarily equate to a single culturing stress. At high growth rates, oxygen transfer is known to constrain metabolic function [18], but at low growth rates there are additional slow-growth-associated stresses. For instance, it is metabolically more expensive to synthesize biomass at low growth rates because of increased cellular protein fraction and the relative increase in maintenance processes (e.g. macromolecular turnover) [40]. At slow growth rates, intracellular fluxes are best described by a combination of stress responses that reduce infrastructure investment, not by maximal biomass yield [33]. Tradeoff curves suggest that resource exchange ratios at low nutrient availability encourage microbial metabolisms to adopt cheaper-to-build but less efficient pathways. This is supported by experimental data. For instance, E. coli expresses the Entner-Doudoroff (ED) pathway under carbon and phosphorus starvation [41]. The ED pathway requires fewer resources to synthesize than the Embden-Meyerhof-Parnas (EMP) glycolysis pathway, although it produces less ATP per glucose (Fig.2). These shifts toward simpler, less resource intensive, enzymatic infrastructure can result in an overflow metabolism where partially oxidized metabolites like acetate are secreted. This partial oxidation represents a competitive strategy under nutrient scarcity, because it obviates synthesis of resource intensive citric acid cycle enzymes like α-ketoglutarate dehydrogenase.

Figure 2. Comparison of resource investment requirements and metabolic efficiency of two glycolysis pathways.

(a) Schematic diagram of biochemical pathways converting glucose-6-P to 2 pyruvate molecules. Nodes represent metabolites, dashed lines represent enzymes associated with Embden-Meyerhof-Parnas (EMP) pathway, and solid lines represent enzymes associated with Entner-Doudoroff (ED) pathway. Numbers refer to enzymes listed at right. (b) Enzyme identifier and resource investment requirements for E. coli K12. Protein column lists the subunits composing each functional enzyme. Carbon and A. acids columns list the total number of carbon atoms and amino acids required for a complete subunit set. (c) Pathway tradeoff quantification based on ATP production and resource investment. Glc/ATP is the moles of glucose required to produce a mole of ATP during the conversion of glucose to 2 pyruvate. Carbon and A. acids columns list the summed pathway resource investments in terms of carbon atoms and amino acids respectively.

Stress adaptations and opportunity costs

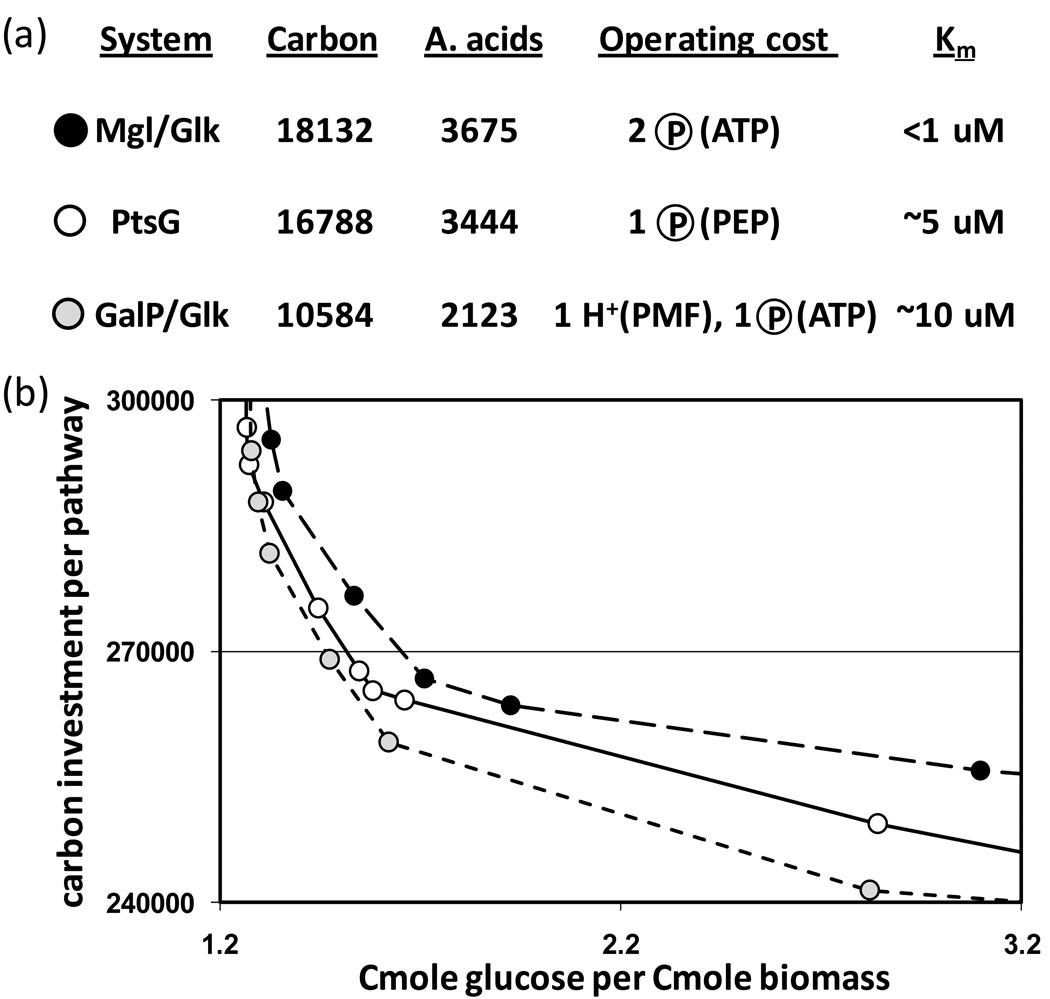
Microbial responses to a variety of stressors can be quantified using the economic concept of opportunity costs. As an example of opportunity costs, E. coli shifts from the phosphotransferase system (K_m ~5 um) to a higher affinity ABC transporter (K_m <1 um) coupled with glucose kinase under glucose-scarce conditions [42]. The high affinity system requires more resources to assemble and operate (Fig. 3), however these costs are offset by improved glucose uptake at low external concentrations. The opportunity cost associated with this benefit can be quantified from tradeoff curves [25]. This framework for understanding adaptation to multiple limiting resources easily accommodates other simultaneous stresses (e.g. osmotic, oxidative, or toxic). Investment of resources towards fitness-enhancing functions, including the production of compatible solutes, synthesis and operation of efflux pumps, or the reduction of reactive oxygen species and toxic metals, can be expressed as a loss in the production of other cellular products like biomass or ATP. The magnitude of the opportunity cost depends on the degree of stress and the current metabolic response to nutrient conditions.

Figure 3. Opportunity costs associated with three separate E. coli glucose transport and phosphorylation systems.

(a) Carbon and amino acid investment requirements and operating costs for transport and phosphorylation of glucose. The glucose affinity is reflected in the Michaelis-Menten constant (K_m); lower values correspond to higher affinities. Circled ‘P’ represents a high-energy phosphate bond, and PMF indicates proton motive force (1 H⁺ = ~0.3 ATP). (b) Tradeoff curves for growth utilizing each glucose transport system. The curves, derived from elementary flux mode analysis, account for carbon investment in central metabolism enzymes (Carbon per pathway, y-axis) and the corresponding biomass production efficiency (Cmoles of glucose consumed per Cmole biomass produced). The points on each curve are color-coded to correspond with the transport systems from (a). The opportunity costs to produce and operate higher affinity systems are shown by the vertical and horizontal distances, respectively, between the tradeoff curves. Note that opportunity costs increase with more severe investment limitation. This is a result of increased glucose intake to accommodate less efficient (but cheaper) enzymatic machinery. Diagram adapted from [25]. Data did not include maintenance energy expenditures.

Biodiversity, network robustness, and the Darwinian demon

All life faces physical, physiological, energetic, and temporal constraints. Resources allocated to one capacity cannot be allocated elsewhere. The resulting tradeoffs have been used to explain biodiversity on both an evolutionary and a dynamic basis [43,44]. Ecologists often invoke a thought experiment to test the null hypothesis of free specialization. The exercise proposes the existence of a ‘superspecies’, termed a Darwinian demon, unconstrained by tradeoffs: living long, reproducing quickly and copiously, and maximizing all aspects of fitness simultaneously [45]. An animalcule possessing such superior properties would obviously outcompete other microbes, leading to monoculture. Given extant biodiversity, physical constraints must be associated with tradeoffs between fitness strategies and ecological functions; differences in community composition across habitats further support this idea.

The Darwinian demon offers an interesting perspective on a common biochemical network property, metabolic robustness. A popular definition of metabolic robustness is phenotypic buffering against genetic mutations or environmental perturbations [46]. Two sources of robustness are gene duplication and pathway redundancy [47]. The relative importance of these two mechanisms appears to vary by species; gene duplication is less important in microbes having greater metabolic versatility [48,49]. Pathway redundancies can be systematically explored through synthetic genetic interactions, both in silico [49–52] and in vitro [e.g. ^53,54]. It has been observed that metabolic robustness facilitates evolutionary innovation, allowing mutations to accumulate without immediate consequences [55], but the strong conservation of metabolic alternatives requires further explanation. In ecology, tradeoffs are credited with ‘taming’ the Darwinian demon, permitting the coexistence of multiple species; it is proposed here that tradeoffs at a cellular scale are a guiding principle to the chromosomal coexistence of isozymes and alternative pathways.

Conclusions

Decades of economic and ecological studies have highlighted the importance of strategic resource allocation and the associated constraints on competitive functionality. These concepts are relevant at all biological scales, from individual microbes to ecosystems, and appear to play key roles in the composition, organization, and functioning of molecular-level metabolic systems. The large body of theoretical and applied work in these fields provides a firm foundation for systems approaches to understand microbial adaptations to simultaneous stressors, as well as strong hope for the development of dynamic, molecular-level predictive tools.