Computer-Aided Detection – The Effect of Training Databases on Detection of Subtle Breast Masses

Abstract

Rationale and Objective

Lesion conspicuity is typically highly correlated with visual difficulty for lesion detection and computer-aided detection (CAD) has been widely used as a “second reader” in mammography. Hence, increasing CAD sensitivity in detecting subtle cancers without increasing false-positive rates is important. This study investigates the effect of training database case selection on CAD performance in detecting low conspicuity breast masses.

Materials and Methods

A full-field digital mammography image database that includes 525 cases depicting malignant masses was randomly partitioned into three subsets. A CAD scheme was applied to detect all initially suspected mass regions and compute region conspicuity. We iteratively selected training samples from two of the subsets. Four types of training datasets, namely; (1) one including all available true-positive mass regions in the two subsets (termed here “All”); (2) one including 350 randomly selected mass regions (“diverse”); (3) one including 350 high conspicuity mass regions (“easy”); and (4) one including 350 low conspicuity mass regions (“difficult”), were assembled. In each training dataset the same number of randomly selected false-positive regions as the true-positives was also included. Two classifiers, an artificial neural network (ANN) and a k-nearest neighbor algorithm (KNN), were trained using each of the four training datasets and tested on all suspected regions in the remaining dataset. Using a 3-fold cross-validation method, we computed and compared the performance changes of the CAD schemes trained using one of the four training datasets.

Results

CAD initially detected 1025 true-positive mass regions depicted on 507 cases (97% case-based sensitivity) and 9569 false-positive regions (3.5 per image) in the entire database. Using the “All” training dataset, CAD achieved the highest overall performance on the entire testing database. However, CAD detected the highest number of low conspicuity masses when the “difficult” training dataset was used for training. Results did concord for both ANN and KNN based classifiers in all tests. Compared with the use of the “All” training dataset, sensitivity of the schemes trained using the “difficult” dataset decreased by 8.6% and 8.4% for ANN and KNN on the entire database, respectively, but the detection of low conspicuity masses increased by 7.1% and 15.1% for ANN and KNN at a false-positive rate of 0.3 per image.

Conclusion

CAD performance depends on the size, diversity, and “difficulty” level of the training database. To increase CAD sensitivity in detecting subtle cancer, one should increase the fraction of “difficult” cases in the training database rather than simply increase the training dataset size.

I. INTRODUCTION

Computer-aided detection (CAD) systems for mammography have been widely used in the clinical practice when interpreting screening breast examinations. CAD systems process digitized or digital mammograms and mark on the images detected suspected regions for masses and micro-calcification clusters. “The second reader” approach emphasizes that radiologists should first read and interpret mammograms “without CAD” followed by review of CAD results in particular as related to regions that perhaps were missed and/or underestimated in importance, prior to making a final diagnostic decision. A number of studies have assessed the impact of using CAD on radiologists’ performance but the results remained somewhat inconclusive and perhaps even controversial to date [1–6]. In general CAD detects more cancers associated with micro-calcification clusters than radiologists (i.e., 22 versus 15 [2]) but has lower sensitivity in detecting malignant masses than radiologists (i.e., 18 versus 26 [2] and 86 versus 105 [5]). Thus, reported cancer detection rates show primarily an increase in the detection of additional micro-calcification clusters [3]. When testing performance of the commercial CAD systems on different types of cases, several tendencies were reported in that CAD performance typically decreases with (1) breast tissue density increase [7] and (2) lesion size decrease [8]. As a result, CAD results were found to be relatively highly correlated with radiologists’ visual detection, namely, masses that were missed by radiologists were more likely to be also missed by CAD [9].

Regardless of the different machine learning (computerized) classifiers being used, CAD performance depends on specific selection of training and testing datasets. Several studies used computer-generated (simulated) databases to predict the effect, if any, of database selection on CAD performance and reported a substantially possible bias if CAD was trained with a small dataset and/or used a large number of features [10–12]. Other studies used actual image data to investigate the relationship between CAD performance and database selection. One study investigated the dependence of CAD performance on the “difficulty” of the testing datasets. At a false-positive rate of one per image, the sensitivity levels of a pre-optimized CAD scheme were 26%, 74%, and 100% on three testing datasets with different “difficulty” levels [13]. Two studies investigated CAD performance changes as a function of the training dataset size when applied to a fixed (independent) testing dataset. One reported a performance increase from AUC (area under receiver operating characteristic (ROC) curve) of 0.724 to 0.836 as the size of training dataset increased from 50 to 500 [14] and the other reported that CAD performance increased from AUC = 0.715 to 0.874 as the training database size increased from 630 to approximately 2000 and then reached a plateau as training database size increased to 3150 [15]. Other studies also independently trained two CAD schemes, one using masses depicted on “current” examinations on which the masses were detected by radiologists (an “easy” dataset) and one using the masses depicted on “prior” examinations on which the masses were missed (or not reported) by the radiologists during the original interpretation but were considered “visible” during a retrospective review (a “difficult” dataset). Both studies demonstrated that combining the two schemes improved overall CAD performance [16, 17].

Despite these research efforts, there are no direct studies that investigated the effect of training database selection on CAD performance in detecting specific types of masses, in particular masses that are “visually difficult” to be detected to date. As CAD has typically lower sensitivity than radiologists in detecting masses, improving CAD performance in detecting “visually difficult” masses is perhaps more important than optimizing and testing CAD performance on large and diverse databases that are dominated by relatively “easy” cases. In this study, we investigated this very issue. First, we selected one image feature of a mass namely “conspicuity” as a summary measure (index) of “visual difficulty.” Lesion conspicuity is defined as the lesion contrast divided by the local pixel value fluctuation in the surrounding background and it has been shown to be associated with detestability of lung nodules on chest images [18–20]. A similar relationship between CAD performance and conspicuity of breast masses was also demonstrated in our previous study [21]. Second, using a relatively large, diverse and fully verified full-field digital mammography (FFDM) image database, we assembled several training datasets with different “difficulty” levels as measured by region conspicuity to independently train CAD schemes and assessed changes of CAD performance in detecting masses with varying levels of “difficulty.” The primary objective of this study was to optimally select a training dataset that would improve CAD sensitivity in detecting a larger number of low conspicuity mass regions without increasing the false-positive detection rate.

II. MATERIALS AND METHODS

2.1. An image database

From previously ascertained FFDM examinations under different institutional review board approved protocols, we assembled a large and diverse image database for this study. The database included 525 cases acquired on patients who underwent FFDM examinations at our breast imaging facility between 2006 and 2008. Each of the patients was later diagnosed as having a breast cancer that had been depicted on the mammogram as a mass. In this group of 525 patients, 351 had only one (“current”) FFDM examination during the period in question, 136 had two (one “current” and one “prior”) examinations, and 38 had three (one “current” and two “prior”) examinations. The 737 available examinations included 629 with four FFDM images of craniocaudal (CC) and mediolateral oblique (MLO) view of the left and right breast, and 108 with only CC and MLO views of one breast. Thus a total of 2732 fully anonymized FFDM images were included in the database. Cancer was detected on the “current” examination of each patient while all “prior” examinations (when available) were originally interpreted as negative. Upon the retrospective review of all prior examinations, 174 breast masses were detected and marked by radiologists on 103 “prior” examinations. In summary, a total of 1265 mass regions associated with verified cancer were detected and marked by radiologists in this database. Among these, 1064 mass regions were marked on images from “current” examinations and 201 were marked on images from “prior” examinations.

The assembled FFDM database has the following characteristics. First, the density ratings by the radiologists during the original image interpretation were as following: 21 cases (4.0%) were rated as almost entirely fatty (BIRADS 1), 194 (36.9%) were rated as scattered fibro-glandular (BIRADS 2), 295 (56.2%) were rated as heterogeneously dense (BIRADS 3), and 15 (2.8%) were rated as extremely dense (BIRADS 4). Second, 464 of the 525 verified malignant masses were described by the radiologists as to their margins appearance during the clinical interpretation. Among these masses, 11 (2.4%) were described as “smooth,” 293 (63.1%) as “irregular,” 123 (26.5%) as “spiculated,” and 37 (8.0%) as “focal asymmetry.” Thus, a large fraction of women whose images were included in this database had relatively dense breasts (BIRADS 3 or 4) and the majority of mass margins were described as either “irregular” or “spiculated.”

2.2. CAD scheme

An in-house developed CAD scheme previously tested in our research group [9, 22] was applied to all 2732 images in the database. In brief, the CAD scheme used three image processing and feature analysis stages to detect and classify suspected masses depicted on mammograms. The first stage uses a difference-of-Gaussian filtering method to identify all possible suspected regions. This stage typically detects somewhere between 10 and 30 initially suspected regions per image depending on breast tissue density and pattern distribution. The second stage applies a multilayer topographic region growth algorithm to segment identified (suspected) mass regions. For each growth layer, a growth threshold is adaptively selected based on measurements of the region’s contrast and a set of simple intra- and inter-layer classification rules on size, growth ratio, contrast, and shape factor of the region in question are applied to eliminate a large fraction of the initially identified regions. This stage typically reduces the number of suspected mass regions to less than 5 per image. In this database, CAD initially detected and segmented 10,594 suspected mass regions including 1025 true-positive and 9569 false-positive identifications.

The third stage of the CAD scheme is the focus of this investigation. In this stage CAD computes a set of 36 morphological and intensity distribution based image features for each initially detected and segmented region. The scheme then applies a pre-trained multi-feature based machine learning classifier to generate a likelihood (detection) score for each suspected mass region as being positive (or depicting a malignant mass). Although several machine learning classifiers had been developed and tested in our previous studies, we re-optimized and tested two classifiers namely an artificial neural network (ANN) and a k-nearest neighbor (KNN) algorithm for the purpose of this investigation. The ANN and KNN are widely used classifiers representing two different machine learning concepts [23]. The ANN uses a global data based optimization method and it is typically trained using all samples in the dataset to build a single “global” optimization target function to cover the entire feature domain. The primary advantage of ANN is its ability to approximate any function given a sufficiently complex architecture. However, over-fitting the training data is an important issue during ANN optimization potentially resulting in poor testing performance. On the other hand, KNN uses a local instance-based learning method and it adaptively builds different local approximations to the target function depending on the “neighborhood” of the test case. KNN has an advantage when the target function is very complex as it can be generally described by a collection of less complex local approximations. A primary disadvantage of KNN is its sensitivity to the data noise (including both in selecting neighbors and features). In our studies, a genetic algorithm was applied to select an optimal set of effective features from the initial pool of 36 features and determine the structure parameters of the classifier (i.e., the number of hidden neurons in the ANN and the number of reference neighbors in the KNN) [21, 24, 25]. Both advantages and limitations of these two classifiers when they are used in CAD schemes for detecting breast masses were previously investigated [24].

In this study, we re-trained these two classifiers with the same pre-optimized model structures [24] using different training datasets to investigate the effect of training dataset selection, if any, on CAD performance when applied to the entire testing database as well as to sub-groups with different “difficulty” levels. The ANN has 14 input neurons represented by 14 image features computed for each detected suspected region, four hidden neurons, and one decision (output) neuron. The definition and detailed computational methods of these 14 features were described elsewhere [25]. A nonlinear sigmoid function, g(z) = 1/(1 + e^−z), is used as the ANN activation function and the ANN generates a detection (or classification) score from 0 to 1, which is directly associated with the likelihood of a tested region representing a true-positive mass. The KNN classifier searches for K = 15 most “similar” suspected mass regions to the test region from the training (reference) dataset. Similarity is measured by the Euclidean distance (d) between a test region (y_T) and each of the reference regions (x_i) in a multi-dimensional space that includes the same 14 image features as used in the ANN.

$$d(y_T,x_i)=\sqrt{\sum _{r=1}^{14}{(f_r(y_T)-f_r(x_i))}^2}$$

The smaller the distance, the higher is the degree of “similarity” between any two regions being compared. The KNN generated detection score is computed as following:

$$P_{TP}=\frac{{\displaystyle \sum _{i=1}^N}{w}_i^{TP}}{{\displaystyle \sum _{i=1}^N}{w}_i^{TP}+{\displaystyle \sum _{j=1}^M}{w}_j^{FP}}$$

where $w_i=\frac{1}{d{(y_T,x_i)}^2}$ (a distance weight), $w_i^{TP}$ and $w_j^{FP}$ are the distance weights for true-positive (i) and false-positive (j) regions, respectively. N is the number of verified true-positive (TP) mass regions, M is the number of CAD-generated false-positive (FP) regions, and N + M = 15.

2.3. CAD performance assessment

We used a 3-fold cross-validation method to train two classifiers (ANN and KNN based) and test CAD performance. For this purpose, we randomly partitioned the entire database of 525 cases into three subsets with an equal number of 175 in each. Each subset included approximately the same number of CAD-detected true-positive mass regions (either 341 or 342). However, since this is a case-based partition in which different cases may involve a different number of examinations (i.e. one or more) and a different number of images in each examination (either 2 or 4 images per examination), the actual number of images and CAD-generated false-positive regions were different in each subset (Table 1). In this 3-fold cross-validation approach, the classifier was trained repeatedly (three times) using a training dataset that included the regions selected from two subsets (partitions) and CAD was tested by applying it to all suspected regions in the remaining partition. Thus, each suspected region was used twice as a candidate for the training datasets and once as a test region.

Table 1.

The three data partitions (subsets) generated from the original FFDM image database.

Data subset (partition)	1	2	3
Number of cases	175	175	175
Number of images	836	836	1060
Number of true-positive mass regions	342	342	341
Number of false-positive regions	2766	2989	3814

In this study, the region conspicuity was used as a summary feature (index) representing the difficulty level of a mass region. A computerized algorithm was applied to compute conspicuity. For each segmented region, a boundary window of the surrounding background was defined as 10mm from the segmented mass boundary in all four directions. The scheme first computed region contrast as $C=\frac{1}{m}{\displaystyle \sum _{k=1}^m}{I}_k-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{I}_i$, where I represents the pixel value (intensity), n and m are the number of pixels inside a mass region and its surrounding background, respectively. The scheme also computed the average local pixel value fluctuation in the surrounding background using a 5 × 5 pixel convolution kernel that was scanned over all pixels in the surrounding background area. For each scanned pixel (i) and 24 other pixels (k) inside the kernel, the scheme computed the maximum pixel value difference, pf_i = |Max(I_i − I_k)|. The local pixel value (intensity) fluctuation was computed as the average of all maximum pixel value differences inside the surrounding background. Thus, following the original definition [18], the region conspicuity level was computed as the region contrast divided by the local C pixel value fluctuation in the surrounding background area ( $F=\frac{C}{{pf}_{\mathit{AVE}}}$). Conspicuity values for all CAD detected suspected mass regions was computed in this manner. Based on the identified minimum (F_min) and the maximum (F_max) conspicuity values, we scaled (normalized) the computed conspicuity values, F_N = (F − F_min)/(F_max − F_min), in the range between 0 and 1.

We independently trained and tested each classifier (ANN or KNN) four times using four training datasets. The first training dataset included all 683 or 684 true-positive mass regions in two of the partitions of the database (termed as the “All” training dataset). The second training dataset included only the 350 mass regions that were randomly selected from the first training dataset (termed as the “diverse” dataset). After sorting the mass regions by their normalized conspicuity values, the third training dataset included the regions with 350 higher values (termed as the “easy” dataset) and the fourth training dataset included the regions with 350 lower values (termed as the “difficult” dataset). For each training dataset, we randomly selected the same number of CAD-generated false-positive regions from the two partitions from which training regions were selected. Hence, each training dataset had an equal number of true-positive and false-positive mass regions. All true-positive and false-positive mass regions in the remaining subset (e.g., 342 true-positive mass regions and 2766 false-positive regions in partition 1) were used as a testing dataset.

After using the 3-fold validation method, the overall performance in classifying 1025 true-positive mass regions and 9569 false-positive regions in the entire database was evaluated and plotted as a free-response receiver operating characteristic (FROC) type performance curve [26]. Due to the fixed number of test regions in all tests, we computed and compared the normalized areas under the FROC curves for all CAD test results using the method we previously reported [24]. Since current commercial CAD systems operate at a marking (operating) threshold that results in generating a false-positive mass detection rate of approximately 0.3 false identifications per image [9, 27], we also compared and analyzed the change in CAD sensitivity levels in detecting mass regions in different “difficult” (conspicuity level) groups at this false-positive detection rate.

III. RESULTS

At the second stage, prior to the application of any machine learning based classifier, the CAD scheme detected 1025 true-positive mass regions depicted on 507 cases representing an upper limit of 97% (507/525) case-based sensitivity and 81% (1025/1265) region-based sensitivity, respectively. At this stage, the scheme also identified 9569 false-positive mass regions representing a maximum false-positive detection rate of 3.5 per image. Table 2 shows the distribution of true-positive and false-positive mass regions in the three conspicuity level groups. In this database, the largest fraction of detected true-positive mass regions (51.5%) was classified as having “moderate” conspicuity, while the majority of false-positive regions (70.3%) were classified as having the “low” conspicuity.

Table 2.

Distribution of normalized conspicuity levels for CAD generated true-positive (TP) and false-positive (FP) regions.

Conspicuity level	Low	Moderate	High	Total
Conspicuity values	0 ≤C < 0.33	0.33 ≤ C < 0.67	0.67 ≤ C ≤ 1.0	0 ≤ C ≤ 1.0
Number of TPs	325 (31.7%)	528 (51.5%)	172 (16.8%)	1025
Number of FPs	6734 (70.3%)	2608 (27.3%)	227 (2.4%)	9569

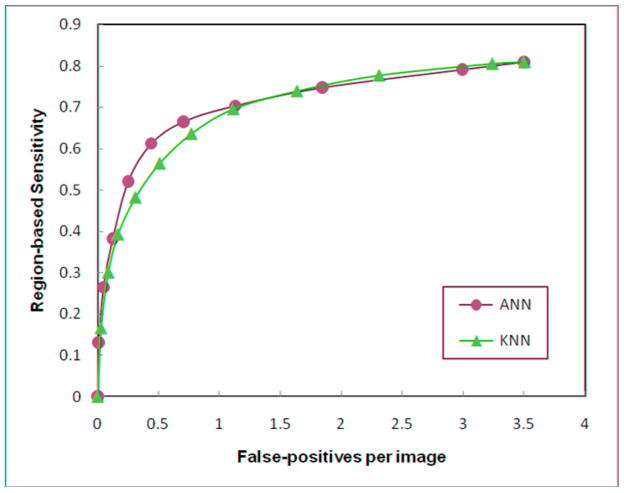
Figure 1 shows two region-based FROC-type performance curves for two CAD schemes applied to the entire testing dataset after the inclusion of either an ANN or a KNN in the respected classifiers. Both classifiers were trained using the “All” training dataset. In the region of low false-positive detection rates (<1.0 per image) the ANN based scheme yielded a higher detection sensitivity than the KNN based scheme (e.g., a 7% sensitivity increase at a false-positive rate of 0.3 per image). Table 3 summarizes the normalized areas under the FROC curves for the ANN and KNN based classifiers when the training was performed with each of the four training datasets. The results show that the overall performance levels are significantly higher (p < 0.05) for the classifiers (both ANN and KNN) trained using the “All” dataset as compared with any of the other three training datasets (“diverse,” “easy,” or “difficult”).

Figure 1.

Two region-based FROC-type performance curves generated by the ANN and KNN-based CAD schemes when trained using the “All” training dataset.

Table 3.

Region-based CAD performance levels on the entire database (normalized areas under FROC curves and standard deviations) for the ANN and KNN based classifiers that were independently trained by each of the four training datasets

Training dataset	“All”	“Diverse”	“Easy”	“Difficult”
CAD using ANN	0.864 ± 0.005	0.814 ± 0.007	0.816 ± 0.007	0.808 ± 0.007
CAD using KNN	0.854 ± 0.006	0.817 ± 0.007	0.821 ± 0.006	0.821 ± 0.006

Table 4 summarizes the true-positive detection (sensitivity) levels at a false-positive rate of 0.3 per image, for the ANN classifier when it was trained by each of the four training datasets. For the entire testing database, the scheme trained with the “All” and the “diverse” datasets yielded higher sensitivity. Although the CAD scheme trained with the “difficult” dataset had lower sensitivity when applied to the entire database, it did detect a larger number of “difficult” mass regions in the low conspicuity group. For example, comparing to the CAD scheme trained with the “All” training dataset, the overall sensitivity of the scheme trained with the “difficult” dataset on the entire testing dataset reduced 8.6% (from 66.0% to 57.4%) but its sensitivity on the low conspicuity mass group increased by 7.1% (from 37.5% to 44.6%). We also noted that the CAD scheme trained with the “easy” dataset alone had the lowest performance when applied to the entire testing database and it only detected 0.9% (3/325) of the mass regions in the low conspicuity group.

Table 4.

Number of true-positive (TP) mass regions detected by ANN-based CAD at a false-positive rate of 0.3 per image.

Conspicuity level	Low	Moderate	High	Total
Initially detected TP ROIs	325	528	172	1025
“All” training dataset	122 (37.5%)	390 (73.9%)	164 (95.3%)	676 (66.0%)
“Diverse” training dataset	109 (33.5%)	363 (68.8%)	156 (90.7%)	628 (61.3%)
“Easy” training dataset	3 (0.9%)	369 (69.9%)	161 (93.6%)	533 (52.0%)
“Difficult” training dataset	145 (44.6%)	330 (62.5%)	113 (65.7%)	588 (57.4%)

Table 5 summarizes the detection performance of the KNN based CAD scheme for the same scenarios. There were several performance differences between the results generated by the ANN and KNN based schemes. First, the KNN based CAD scheme trained using the “diverse” reference dataset yielded the highest sensitivity (i.e., 1.8% higher than the scheme using the “All” training dataset). Second, the scheme using the “easy” training dataset achieved a higher performance level than that using the “difficult” training dataset (i.e., 3.7% higher when applied to the entire testing database). Despite these differences, we noted that similar to the ANN-based scheme, the CAD scheme using the “difficult” training dataset detected the highest true-positive fraction in the low conspicuity group resulting in a 15.1% and 11.4% sensitivity level increase in detecting low conspicuity mass regions than the schemes trained with the “All” and “diverse” training datasets, respectively.

Table 5.

Number of true-positive (TP) mass regions detected by the KNN-based CAD at a false-positive rate of 0.3 per image.

Conspicuity level	Low	Moderate	High	Total
Initially detected TP ROIs	325	528	172	1025
“All” training dataset	84 (25.8%)	355 (67.2%)	163 (94.7%)	602 (58.7%)
“Diverse” training dataset	96 (29.5%)	371 (70.3%)	153 (90.0%)	620 (60.5%)
“Easy” training dataset	26 (8.0%)	363 (68.8%)	165 (95.9%)	554 (54.0%)
“Difficult” training dataset	133 (40.9%)	315 (59.7%)	68 (39.5%)	516 (50.3%)

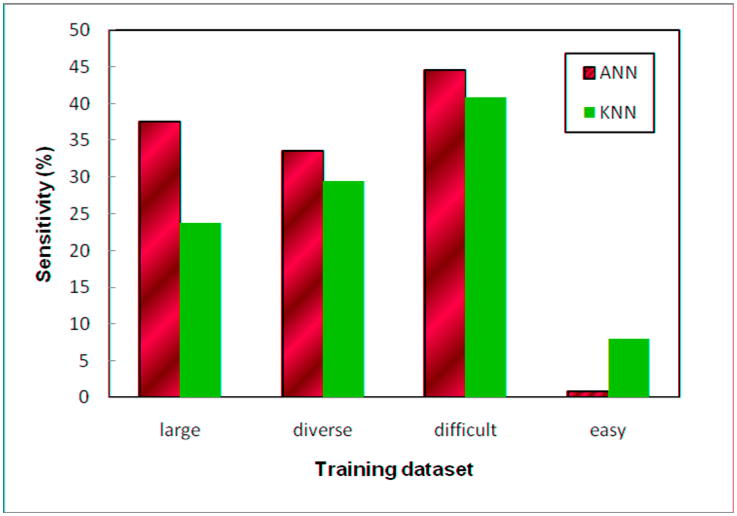
Figure 2 shows region-based sensitivity levels of all eight ANN and KNN based CAD schemes trained by four training datasets. The results show that the ANN based CAD scheme trained by the “difficult” training dataset achieved the highest true-positive detection fraction (sensitivity) for the “difficult” mass regions with lower conspicuity.

Figure 2.

Region based sensitivity levels in detecting low conspicuity mass regions at a false-positive of 0.3 per image. The eight CAD schemes include two classifiers (ANN and KNN) that were independnetly trained by each of the four training datasets.

IV. DISCUSSION

Several studies have showed that the sensitivity of CAD schemes in detecting malignant masses was substantially lower than radiologists’ visual detection [2, 5]. In the hope of aiding radiologists to detect more possibly missed subtle cancers depicted as masses when using CAD as “the second reader,” CAD should perform better in the detection and identification of “difficult” masses that are more likely to be missed or underestimated by the interpreting radiologist. A number of studies showed that current CAD schemes yielded a substantial lower true-positive detection fraction in small masses [8, 13] or alternatively, masses depicted on “prior” examination [16, 17]. This study has a number of unique characteristics. First, we recognized that “visual difficulty” remains a subjective concept. Thus, a summary measure (quantitative index) is required to reduce the inter-observer variation in assessing visual difficulty of the breast masses. As studies showed that lesion conspicuity was reasonably-correlated with visual difficulty for detection lesions depicted on chest radiographic images [18–20], we used conspicuity as a summary measure to automatically classify breast masses into three “difficulty” groups. When compared with the other subject measures of “difficulty” [16, 17], this summary measure (index) is quantitatively computed, which increases the reproducibility of the study results. Second, unlike previous studies that used either a fixed training dataset [13] or a fixed testing dataset [14], we divided both training and testing datasets into different “difficulty” groups (subsets) and investigated the effect of training database selection on CAD performance in detecting masses in several “difficulty” groups.

Although a number of different machine learning classifiers have been trained and implemented in CAD schemes developed by different research groups, these classifiers can be basically divided into two types (groups). One uses all available training data to build a single “global” optimization target function and one uses the local data to adaptively build local approximations to the target function. The selection of ANN and KNN for this work was based on the fact that these two classifiers are frequently used in imaging based CAD schemes and also represent two typical types of machine learning concepts [24]. Due to the different underlying nature of these two machine learning (optimization) approaches, the effect of training database selection on the performance of the ANN and KNN based classifiers may vary in several respects. First, the large training dataset helps in building a more accurate and robust global optimization function in the case of the ANN, but it may not be as helpful in building local instance based optimization functions for the KNN. Thus, the ANN-based CAD scheme generally yielded higher performance levels when trained with the “All” (large) training dataset and the KNN-based CAD scheme achieved a higher performance when the KNN was trained with the “diverse” dataset. Second, since a large fraction of CAD-generated false-positive regions have low conspicuity regions (70.3% in our database), reducing the number of low conspicuity true-positive mass regions in the training dataset could result in a suboptimal global function that tends to classify more low conspicuity regions as false-positives. As a result, when using the “easy” training dataset, the ANN-based scheme detected only 3 (0.9%) of the low conspicuity true-mass regions, while the KNN-based CAD scheme detected substantially higher fraction of low conspicuity mass regions (8.0%).

Despite the different effects of training database selection on CAD results when using the ANN and KNN classifiers, there were similar trends observed for both classifiers. First, performance levels increased with increasing size or diversity of the training database. Generally this resulted in better performance in detecting a higher fraction of the “easy” or “high conspicuity” masses. Second, with increasing the “difficulty” levels in the training dataset (by discarding “easy” true-positive training samples) the schemes detected a larger fraction of masses with lower conspicuity. Third, as the majority of false-positive regions have low conspicuity, even schemes trained with “difficult” true-positive masses tend to detect a substantially higher fraction of “easy” mass regions than that of “difficult” mass regions. This stems from the fact that discrimination between the typical false-positive region with its low conspicuity and an easy true-positive mass with its typical high conspicuity remains a relatively easy task for all classifiers. This suggests that weighing heavily toward the inclusion of more “difficult” cases in the training dataset is an important consideration for improving overall CAD performance and in particular as related to performance in the detection of “difficult” masses.

This study also has several limitations in an attempt to achieve the optimal CAD performance in detecting “difficult” (low conspicuity) masses. First, we only focused on analyzing CAD performance on the true-positive mass regions detected and segmented by the first two stages of our CAD schemes, which had already eliminated 3% of masses or 19% of mass regions (because a fraction of masses was only detected in one view). The majority of these eliminated mass regions are likely to be low conspicuity regions. We did not explore the possibility of changing the initial stages of the CAD scheme to improve initial image (region) based detection and increase the initial sensitivity before applying the ANN or KNN based classifier. Second, adaptive approaches, namely the segmentation of the database into mass based characterization (such as “low,” “moderate,” and “high” conspicuity suspected masses) followed by specific optimization of a separate CAD for each subset [21] was not explored. Either of these approaches or a combination of both is possible but these require a fundamental change in the underlying approach to develop an overall CAD scheme and therefore are beyond the scope of this study. Last, despite the relatively large and diverse dataset used in this study, the relatively smaller sample size in the different conspicuity subsets (as shown in Table 2) also limited the ability to assess the results with comparable confidence intervals as the overall CAD. To maximize the training dataset size and minimize the potential testing bias, we used a 3-fold cross-validation method in this study. We recognized the advantages and limitation of this cross-validation method in evaluating CAD performance [28]. Therefore, as the increase of database size, the reproducibility and generalization of the results have to be validated in the future studies.

Based on the previous studies that demonstrated the strong correlation between the lesion conspicuity and radiologists’ detection performance using chest radiographs [18–20], the primary hypothesis of this study is that the feature of conspicuity can also be used as an index to assess “visual difficulty” in detecting breast masses. We recognized the substantial difference between human vision and computer vision as well as the difference between mammograms and chest radiographs. Therefore, the actual relationship between the breast mass conspicuity and radiologists’ performance in interpreting screening mammograms ultimately needs to be tested and justified by the future observer studies. Since this study only concerned the stand-alone performance of a CAD scheme, whether and how the reported CAD performance translates to the human (radiologists) performance is unclear and it also needs to be investigated in the future observer performance studies.

In summary, as long as CAD has lower detection sensitivity than radiologists’ visual detection and it is used as “the second reader,” increasing CAD sensitivity on the “visually difficult” (i.e., low conspicuity) masses is an important objective if we wish to increase the clinical utility of CAD systems. This study demonstrated that in order to increase CAD sensitivity in detecting “difficult” breast masses an optimal training database should include a high percentage of depicted but “difficult” masses. Although building the large image databases has always been an important research task and effort in CAD development, this study suggested that because using a large training database dominated by relatively “easy” masses was not very helpful for achieving this objective and more effort should be focused on identifying “difficult” cases for this purpose rather than simply increasing the size of the image database.