Abstract
When averaged over the full yeast protein–protein interaction and transcriptional regulatory networks, protein hubs with many interaction partners or regulators tend to evolve significantly more slowly due to increased negative selection. However, genome-wide analysis of protein evolution in the subnetworks of associations involving yeast transcription factors (TFs) reveals that TF hubs do not tend to evolve significantly more slowly than TF non-hubs. This result holds for all four major types of TF hubs: interaction hubs, regulatory in-degree and out-degree hubs, as well as co-regulatory hubs that jointly regulate target genes with many TFs. Furthermore, TF regulatory in-degree hubs tend to evolve significantly more quickly than TF non-hubs. Most importantly, the correlations between evolutionary rate (KA/KS) and degrees for TFs are significantly more positive than those for generic proteins within the same global protein–protein interaction and transcriptional regulatory networks. Compared to generic protein hubs, TF hubs operate at a higher level in the hierarchical structure of cellular networks, and hence experience additional evolutionary forces (relaxed negative selection or positive selection through network rewiring). The striking difference between the evolution of TF hubs and generic protein hubs demonstrates that components within the same global network can be governed by distinct organizational and evolutionary principles.
INTRODUCTION
In recent years, the focus of genomic research has shifted from the generation of a biological ‘parts list’ to understanding how interactions among these biological parts lead to the collective behavior of the entire cellular system. Central to this research paradigm is the concerted experimental and computational efforts to accurately map the genome-wide protein networks in various organisms, and to study the relationships between structure, function and evolution at the level of networks (1). In particular, a fundamental goal of the emerging field of evolutionary systems biology is to elucidate the universal relationships between a protein’s evolutionary rate and its role in cellular networks (2,3).
A well-known example in evolutionary systems biology is the discovery that hubs in the Saccharomyces cerevisiae protein–protein interaction network tend to evolve more slowly than non-hubs (4). While this trend is generally accepted, the underlying mechanistic explanation—i.e. that more interaction partners lead to an increase in structural and/or functional constraint—has been intensely debated (5–9). This controversy stems from issues of incomplete coverage and specific biases in experimental interaction networks, as well as confounding correlates of evolutionary rate such as protein abundance (10), essentiality (11) and structure (12). More recently, sophisticated multivariate analyses have been applied to modeling the evolutionary effects of multiple genomic properties simultaneously (13–18). Protein abundance consistently appears as the dominant influencing factor in protein evolution, most likely due to selection pressure on the rate and accuracy of protein synthesis and folding (19). On the other hand, a protein’s number of interaction partners exerts some influence on its evolutionary rate that is independent of its abundance (15,17), most likely due to increased structural co-evolutionary constraints (negative selection) imposed by protein–protein interaction (20). Collectively, this work illustrates the potential power of biomolecular network analyses in revealing the large-scale organizational and evolutionary principles of a cell.
Many network-based studies focus on graph theoretical analysis of nodes and edges within a single, global biomolecular network. However, there exists a high level of chemical and functional heterogeneity within the underlying biomolecules, biomolecular interactions and interaction subnetworks (20–24). It remains an open question whether or not the global properties of the full interaction network extend to these subnetworks. In addition, subnetworks may exhibit unique, emergent properties that are absent in the conglomeration of the full interaction network.
In this article, we study evolutionary principles in the subnetworks of associations involving yeast transcription factors (TFs). TFs are important regulators of cellular processes at the transcriptional level. The interactions and coordinated actions of multiple TFs provide a primary mechanism for achieving fine-tuned transcriptional control in eukaryotes. A previous analysis of the yeast transcriptional regulatory network failed to detect significant correlations between evolutionary rate and several measures of degree (25). A more recent analysis reported a significant, positive correlation between evolutionary rate and regulatory in-degree for TFs (26). However, neither of these studies directly compared the evolutionary behavior of TFs and generic proteins within the same global protein–protein interaction/transcriptional regulatory network. Here, we present strong evidence that the interaction of TFs evolves significantly differently from the interaction of generic proteins, and that the regulation of TFs evolves significantly differently from the regulation of generic proteins. We explore theoretical explanations for these empirical observations based on relaxed negative selection as well as additional positive selection acting on TF hubs.
MATERIALS AND METHODS
Collecting datasets
Information on yeast TFs was downloaded primarily from the Yeast Search for Transcriptional Regulators And Consensus Tracking database (YEASTRACT; http://www.yeastract.com) (27). Their dataset (October 2007) contains 170 TFs, and we manually added 4 TFs annotated in the Saccharomyces Genome Database (28). In Supplementary Table S1, we list all 174 TFs by name, evolutionary rates, number of interactors (degree) in the protein–protein interaction network, number of regulators (in-degree) and number of targets (out-degree) in the transcriptional regulatory network, as well as number of co-regulatory relationships (degree) in the co-regulatory network.
Yeast physical protein–protein interaction data were downloaded from BioGRID (version 2.0.41) (29). There are a total of 4899 proteins and 37 814 interactions. Transcriptional regulatory data were assembled based on associations between TFs and target genes (TGs) as detected by large-scale ChIP-chip experiments in (30–35). In total, there are 143 TFs, 4774 TGs and 16 656 transcriptional regulations. Finally, we collected additional TF–TG associations as annotated in the YEASTRACT database.
Reconstructing the TF co-regulatory network
We constructed TF co-regulatory networks by enumerating all TF pairs where there is a significant overlap of TGs (24). Cooperative TFs tend to share more common TGs in the transcriptional regulatory network than expected by chance (36). We developed two scores, a P-value score and an enrichment score, to assess the significance of TG overlap for a pair of TFs. These two scores are further combined as a single TG overlap score for defining the co-regulatory relationship of TF pairs.
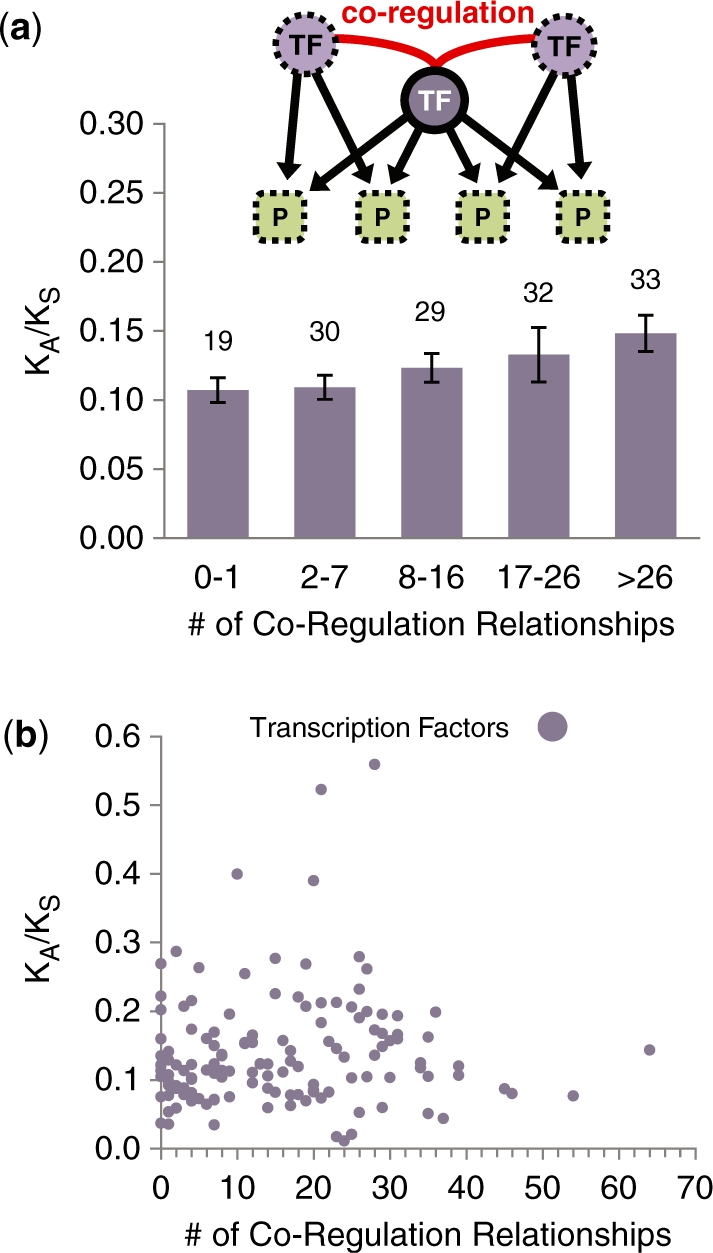
To determine whether the TG overlap is statistically significant for a given TF pair, we fix the total number of TGs in the yeast genome (N), the number of TGs regulated by the first TF (N1) and the number of TGs regulated by the second TF (N2). We then treat the number of TGs regulated by both TFs as a random variable X. Under the null hypothesis that regulation by the first TF is independent of regulation by the second TF, X follows a hypergeometric distribution:
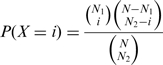 |
From here we can calculate a P-value score, which is defined as the probability that the TG overlap would assume a value greater than or equal to the observed value, m, by chance:
The TG overlap is statistically significant if the P-value score is smaller than a chosen cutoff.
The above procedure gives us all TF pairs for which the TG overlap is statistically significant. To further quantify the extent of the TG overlap, we also calculate an enrichment score, defined as the ratio of the observed TG overlap versus the expected TG overlap by chance:
A score larger than 1 indicates that there is more TG overlap than expected by chance.
We select all TF pairs for which both P-value and enrichment scores are significant (P-value < 10−3, enrichment score >2). In total, this TF co-regulatory network contains 143 TFs and 1165 co-regulatory TF pairs.
Calculating measures of protein evolution in yeast
KA/KS represents the ratio of the rate of non-synonymous substitutions (KA) to the rate of synonymous substitutions (KS), and serves as a measure of the strength of selection acting on a protein-coding gene (37). We performed local alignment (38) between each translated S. cerevisiae open reading frame (ORF) and its annotated ortholog(s) in S. paradoxus, the closest related yeast with a sequenced genome, using the orthology information defined by Wapinski et al. (39). Only the most conserved ortholog was considered for yeast ORFs with multiple annotated orthologs. These protein-level alignments were used to generate corresponding DNA codon alignments, which were then piped into the program yn00 within the PAML software package (40) to calculate KA/KS; values reported are based on the method of (41). These procedures were repeated to calculate KA/KS from two additional paired comparisons of S. cerevisiae and S. paradoxus with S. mikatae, a third closely related yeast species.
Correlating measures of protein evolution with network statistics
We used Spearman’s rank correlation coefficient (rs) to assess the correlation between measures of protein evolution, such as KA/KS, and network statistics, such as degree (for undirected networks), in-degree and out-degree (for directed networks). The rank correlation coefficient is a non-parametric technique that does not make any assumption regarding population distribution, and it is relatively insensitive to outliers through operating on the rank of the data (42).
In addition to scatter plots, we used a simple binning strategy to visualize the correlations: we partitioned TFs and generic proteins into five bins of roughly equal occupancy based on their degrees in different networks. For each bin, we calculated and plotted the median value of KA/KS; the standard errors associated with these values were calculated using bootstrap resampling.
When ranking proteins by KA/KS for correlation coefficient and median KA/KS calculation, we assigned maximum rank to yeast proteins with no ortholog in a given species comparison.
RESULTS
Significantly different evolutionary trends for TF hubs and generic protein hubs in the protein–protein interaction network
We studied protein evolution among TFs in the genome-wide protein networks of S. cerevisiae (baker’s yeast). We assembled two types of whole-genome networks: the protein–protein interaction network and the transcriptional regulatory network. We further collected 174 yeast TFs (see Supplementary Table S1) and assembled the TF subnetworks based on three types of associations: protein–protein interactions involving TFs, transcriptional regulatory relationships, as well as joint regulation of TGs among TFs (forming the TF co-regulatory network) (see ‘Materials and Methods’ section).
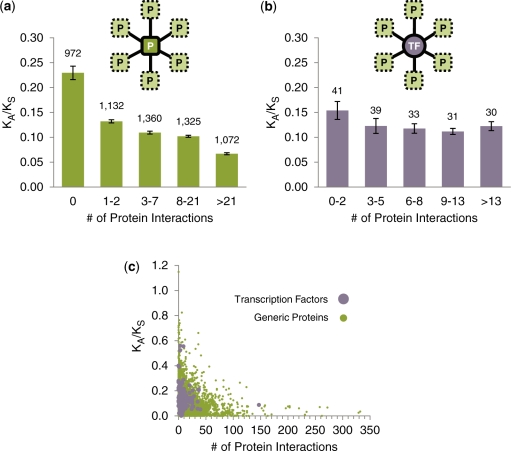
We first examined the yeast protein–protein interaction network. We quantified the relationship between number of physical interactors (degree in the protein–protein interaction network) and KA/KS over all 5861 yeast proteins (Figure 1a; see Figure 1c for a scatter plot, and Supplementary Figure S2 for an alternative binning). KA/KS is the ratio of the rate of non-synonymous DNA substitutions (KA) to the rate of synonymous DNA substitutions (KS) in a protein-coding gene; it serves as an approximate measure of the strength of evolutionary selection acting on the corresponding protein sequence (factoring out mutational background and selection on synonymous codons). Smaller KA/KS values are associated with heightened negative selection (slow evolution), while larger values are associated with neutral or adaptive evolution (fast evolution). We calculated KA/KS over alignments between the coding sequences of S. cerevisiae and their orthologs in S. paradoxus (39) (the closest related yeast with a sequenced genome). We observed a significantly negative correlation between KA/KS and degree in the protein–protein interaction network (Spearman’s rank correlation rs = –0.34, two-tailed P < 10−6, 11.6% of the variance in KA/KS ranks can be explained by interaction degree ranks). This observation is consistent with the previous findings (4).
Figure 1.
The relationship between KA/KS and interaction degree for TFs (purple) and generic proteins (green). KA/KS was calculated over alignments between S. cerevisiae ORFs and their orthologs in S. paradoxus. (a) The relationship between KA/KS and number of physical interactors for 5861 yeast proteins. (b) The relationship between KA/KS and number of physical interactors for the 174 yeast TFs. TFs and proteins were binned according to degree percentile; median KA/KS was calculated for each bin. Numbers above the bars represent the number of TFs/proteins in the bin; error bars reflect the standard error. (c) Scatter plot relating KA/KS and number of physical interactors for generic proteins and TFs.
Next, we focused on the 174 TFs in the protein–protein interaction network. We calculated the number of physical interactors for each TF (degree) and correlated this value with KA/KS. If TFs evolve similarly to generic proteins, we would expect to observe a similarly negative correlation between degree and KA/KS (4). Surprisingly, such a trend is only weakly evident over the low-degree TFs, and fails to encompass the high-degree TFs (Figure 1b; see Figure 1c for a scatter plot). The overall correlation between a TF’s number of physical interactors and KA/KS is negative but only weakly significant (rs = –0.16, permutation-based two-tailed P = 0.033, 2.6% of the variance in KA/KS ranks can be explained by interaction degree ranks). Moreover, if we define protein hubs a priori as the 20% of proteins with largest degree, and TF hubs as those TFs that are protein hubs, then the median KA/KS value for TF hubs is not significantly different from that for TF non-hubs (permutation-based two-tailed P = 0.48).
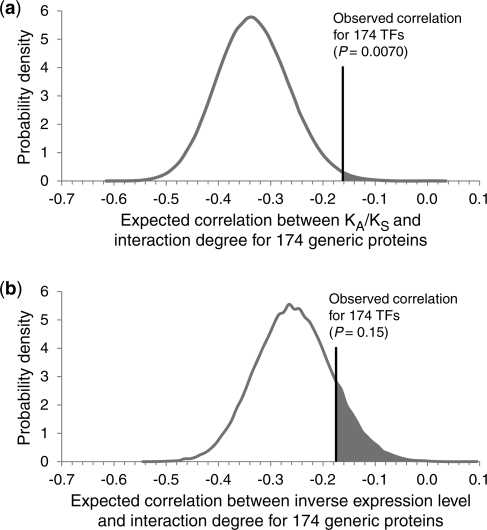
Our unexpected finding here is that the correlation between KA/KS and number of physical interactors for TFs appears to be significantly more positive than the correlation calculated over all proteins. Is such a difference in trends likely to arise by chance sampling of the proteome? To answer this, we repeatedly selected 174 proteins (the number of TFs studied) at random from the 5861 yeast proteins considered in Figure 1a, and then calculated the correlation coefficient between KA/KS and number of physical interactors for this subset of proteins. The observed correlation between KA/KS and number of physical interactors for TFs was more positive than the sampled correlation for generic proteins in 99.30% of the 105 trials (P = 0.0070, Figure 2a). We conclude that physical interactions involving TFs and those involving generic proteins evolve in very different ways: proteins hubs in the protein–protein interaction network tend to evolve significantly more slowly than non-hubs, whereas TF hubs do not tend to evolve significantly more slowly than TF non-hubs. This deviation from the generic KA/KS versus degree relationship is highly unlikely to have occurred by chance. We repeated the above analyses using KA/KS values derived from two other close yeast species comparisons: S. cerevisiae with S. mikatae, as well as S. paradoxus with S. mikatae, and found that the correlation between KA/KS and interaction degree is again significantly more positive for TFs than it is for generic proteins in both cases (P = 0.00096 and 0.00066, respectively). This suggests that our observed trend difference is not due to S. paradoxus lineage-specific effects, but rather applies to all three closely related yeast species.
Figure 2.
Evaluating the statistical significance of the differences in the correlations between measures of protein evolution and interaction degree for TFs and generic proteins. The probability distribution of the expected Spearman’s rank correlation coefficients was generated by considering 105 samples of 174 proteins randomly selected from the 5861 total yeast proteins. The position of the observed correlation coefficient for the actual 174 yeast TFs is highlighted. (a) The correlation between KA/KS and interaction degree is significantly more positive for TFs than it is for generic proteins (P = 0.0070). (b) The correlation between inverse expression level and interaction degree is not significantly more positive for TFs than it is for generic proteins (P = 0.15).
An important alternative hypothesis that we must consider relates to protein abundance (expression level), which—as mentioned in the Introduction—is a dominant determinant of protein evolutionary rate. Highly expressed proteins are subject to intense selection on the rate and accuracy of protein synthesis and folding, and hence they tend to evolve slowly. Conversely, proteins with limited expression levels tend to evolve quickly. Moreover, TFs tend to be expressed at lower levels on average than generic proteins (Supplementary Figure S1). Could the observed difference in the correlation between KA/KS and interaction degree for TFs and generic proteins be simply explained by expression level? To answer this, we used Codon Adaptation Index as a proxy for expression level (43), and used inverse expression level as a surrogate for KA/KS (due to the inverse correlation between expression level and KA/KS). If expression levels were the causal factor behind our observation that the correlation between KA/KS and interaction degree for TFs is significantly more positive than the correlation for generic proteins, then we would expect to find the correlation between inverse expression level and interaction degree for TFs to be also significantly more positive than the correlation for generic proteins. However, we found that the correlation between inverse expression level and interaction degree for TFs is not significantly more positive than the correlation for generic proteins (P = 0.15, Figure 2b). This suggests that the observed significant difference in KA/KS versus degree correlation between TFs and generic proteins cannot be explained by expression level. While expression may play a significant role in explaining the negative correlation between evolutionary rate and degree in the global protein–protein interaction network, it cannot explain the significantly different evolutionary trends that we observe here in the TF subnetwork.
While the full BioGRID data set used above minimizes the potential effects of false negatives, we must also consider the robustness of our conclusions against the potential effects of false positives. To minimize false positives, we constructed a second smaller and more reliable data set containing 10 589 physical interactions reported by at least two independent experiments in the BioGRID database, and repeated our calculations. Our conclusions remain unchanged: the correlation between KA/KS and interaction degree is significantly more positive for TFs than it is for generic proteins (P = 0.00077), and the correlation between inverse expression level and interaction degree is not significantly more positive for TFs than it is for generic proteins (P = 0.33). Our conclusions are therefore robust against false positives and false negatives in protein–protein interaction data sets.
We further repeated our calculations using KA as a measure of protein evolutionary rate at the amino acid sequence level, and found that the correlation between KA and number of physical interactors is again significantly more positive for TFs than it is for generic proteins (P = 0.00049). Lastly, we repeated our calculations using KS as a measure of protein evolutionary rate at the synonymous codon level, and found that the trend difference disappears: the correlation between KS and number of physical interactors for TFs is not significantly more positive than it is for generic proteins (P = 0.10). Our calculations demonstrate that the observed trend difference is driven by selective pressure at the level of amino acid sequence, but not at the level of synonymous codons.
Opposite evolutionary trends for TF in-degree hubs and generic protein in-degree hubs in the transcriptional regulatory network
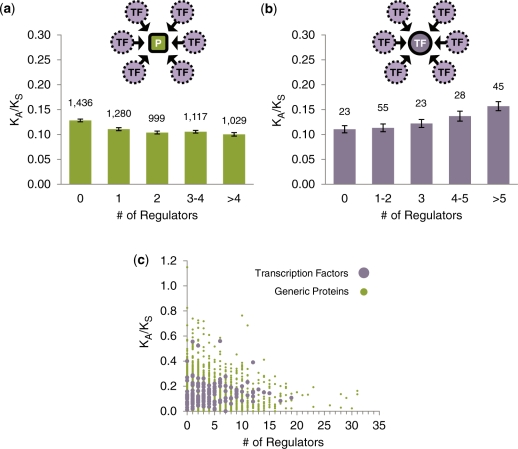
In addition to the protein–protein interaction network, another major type of protein network is the transcriptional regulatory network. Here, we demonstrate an even more significant difference between the evolutionary properties of TFs and generic proteins. We reconstructed the transcriptional regulatory relationships among TFs in S. cerevisiae based on large-scale chromatin immunoprecipitation followed by microarray identification (ChIP-chip) experiments (see ‘Materials and Methods’ section). Since the transcriptional regulatory network is a directed graph, each node has an in-degree (number of regulators) and an out-degree (number of regulated targets). Here, we consider the relationship between in-degree (number of regulators) and KA/KS, as it is applicable to both TFs and generic proteins.
First, we calculated the regulatory in-degree (number of regulators) for each protein in the whole-genome transcriptional regulatory network and correlated these values with KA/KS. When averaged over the entire genome, we find that there is a weak yet statistically significant trend for generic proteins with more regulators to evolve more slowly due to increased negative selection (Figure 3a; see Figure 3c for a scatter plot, and Supplementary Figure S3 for an alternative binning), in agreement with our previous findings (18) (rs = –0.08, two-tailed P < 10−6, 0.64% of the variance in KA/KS ranks can be explained by regulatory in-degree ranks). We repeated this calculation with additional TF–TG regulatory relationships as annotated in the YEASTRACT database, and observed the same trend (rs = –0.15, P < 10−6, 2.25% of the variance in KA/KS ranks can be explained by regulatory in-degree ranks).
Figure 3.
The relationship between KA/KS and regulatory in-degree for TFs (purple) and generic proteins (green). Arrows indicate transcriptional regulatory relationships. (a) The relationship between KA/KS and number of TF regulators for 5861 TGs. (b) The relationship between KA/KS and number of TF regulators for the 174 yeast TFs. (c) Scatter plot relating KA/KS and number of regulators for generic proteins and TFs.
Next, we focused on the relationship between regulatory in-degree (number of regulators) and KA/KS for yeast TFs (Figure 3b; see Figure 3c for a scatter plot). In agreement with the findings of previous studies (26), the correlation between KA/KS values for TFs and regulatory in-degree is significantly positive over the full range of in-degree values (rs = 0.185, permutation-based two-tailed P = 0.014, 3.42% of the variance in KA/KS ranks can be explained by regulatory in-degree ranks). This positive correlation cannot be explained by expression level, as the correlation between inverse expression level and regulatory in-degree for TFs is actually negative (rs = –0.14) and certainly not significantly positive.
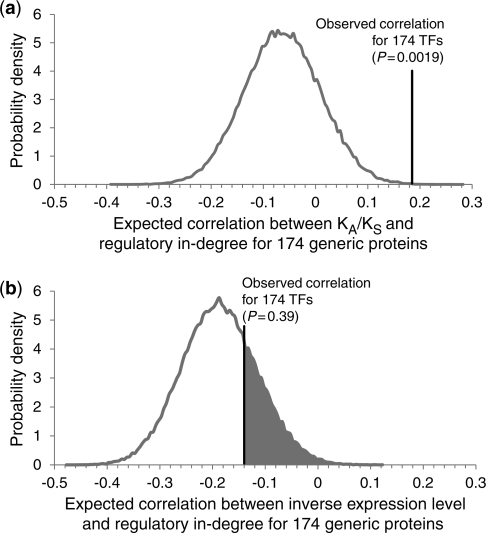
Our unexpected finding here is that, similar to number of physical interactors studied in the previous section, the correlation between number of regulators and KA/KS for TFs also appears to be significantly more positive than the correlation calculated over all proteins. Is such a difference in trends likely to arise by chance sampling of the proteome? Following the same sampling procedure used in our previous analysis of the protein–protein interaction network, we found that the difference in the KA/KS versus regulatory in-degree trends for TFs and generic proteins is highly unlikely to result from chance (P = 0.0019, Figure 4a). This trend difference remains consistent and significant in comparisons with a third closely related yeast species, S. mikatae (P = 0.0046 for S. cerevisiae versus S. mikatae comparison, and 0.00097 for S. paradoxus versus S. mikatae comparison). This difference in evolutionary trends cannot be explained by expression level: the correlation between inverse expression level and regulatory in-degree for TFs is not significantly more positive than the correlation for generic proteins (P = 0.39, Figure 4b).
Figure 4.
Evaluating the statistical significance of the differences in the correlations between measures of protein evolution and regulatory in-degree for TFs and generic proteins. The probability distribution of the expected Spearman’s rank correlation coefficients was generated by considering 105 samples of 174 proteins randomly selected from the 5861 total yeast proteins. The position of the observed correlation coefficient for the actual 174 yeast TFs is highlighted. (a) The correlation between KA/KS and regulatory in-degree is significantly more positive for TFs than it is for generic proteins (P = 0.0019). (b) The correlation between inverse expression level and regulatory in-degree is not significantly more positive for TFs than it is for generic proteins (P = 0.39).
While the full ChIP-chip data set used above minimizes the potential effects of false negatives as well as investigator bias, we must also consider the robustness of our conclusions against the potential effects of false positives. To minimize false positives, we constructed a second smaller and more reliable data set containing 4545 transcriptional regulatory interactions reported by at least two independent ChIP-chip experiments, and repeated our calculations. Our conclusions remain unchanged: the positive correlation between KA/KS and regulatory in-degree for TFs is significantly more positive than the negative correlation for generic proteins (P = 0.014), and the correlation between inverse expression level and regulatory in-degree is not significantly more positive for TFs than it is for generic proteins (P = 0.55). We further constructed a third data set containing 5758 transcriptional regulatory interactions reported by at least two independent experiments as annotated in the YEASTRACT database, and repeated our calculations. Our conclusions remain unchanged: the positive correlation between KA/KS and regulatory in-degree for TFs is significantly more positive than the negative correlation for generic proteins (P = 0.0038), and the correlation between inverse expression level and regulatory in-degree is not significantly more positive for TFs than it is for generic proteins (P = 0.22). Our conclusions are therefore robust against false positives and false negatives in transcriptional regulatory data sets.
We further repeated our calculations using KA as a measure of protein evolutionary rate at the amino acid sequence level, and found that the correlation between KA and regulatory in-degree is again significantly more positive for TFs than it is for generic proteins (P = 0.00032). Lastly, we repeated our calculations using KS as a measure of protein evolutionary rate at the synonymous codon level, and found that the trend difference disappears: the correlation between KS and regulatory in-degree for TFs is not significantly more positive than it is for generic proteins (P = 0.38). Our calculations again demonstrate that the observed trend difference is driven by selective pressure at the level of amino acid sequence, but not at the level of synonymous codons.
TF regulatory out-degree and co-regulatory hubs do not tend to evolve more slowly than TF non-hubs
Next, we considered the relationship between KA/KS and regulatory out-degree (number of regulated targets) in the transcriptional regulatory network. Note that this measure can only be defined for TFs as it has no analog among generic proteins. For each TF, we calculated two measures of regulatory out-degree: the total number of regulated TGs and the number of regulated TFs. Consistent with findings of previous studies (25,26), the correlation between number of regulated TGs and KA/KS is not significantly different from zero (rs = 0.018, two-tailed P = 0.83). We further restricted our analysis to TGs that are also TFs (Figure 5a; see Figure 5b for a scatter plot), and found that the correlation between number of regulated TFs and KA/KS is weakly positive but again not significantly different from zero (rs = 0.047, two-tailed P = 0.58). Although these positive correlations are not statistically significant, it is clear that TF regulatory out-degree hubs do not tend to evolve more slowly than TF non-hubs.
Figure 5.
The relationship between number of regulated TFs and KA/KS for TFs (purple). Arrows indicate transcriptional regulatory relationships. (a) The relationship between KA/KS and number of regulated target TF genes for 143 yeast TFs based on ChIP-chip data. (b) Scatter plot relating KA/KS and number of regulated target TF genes for TFs.
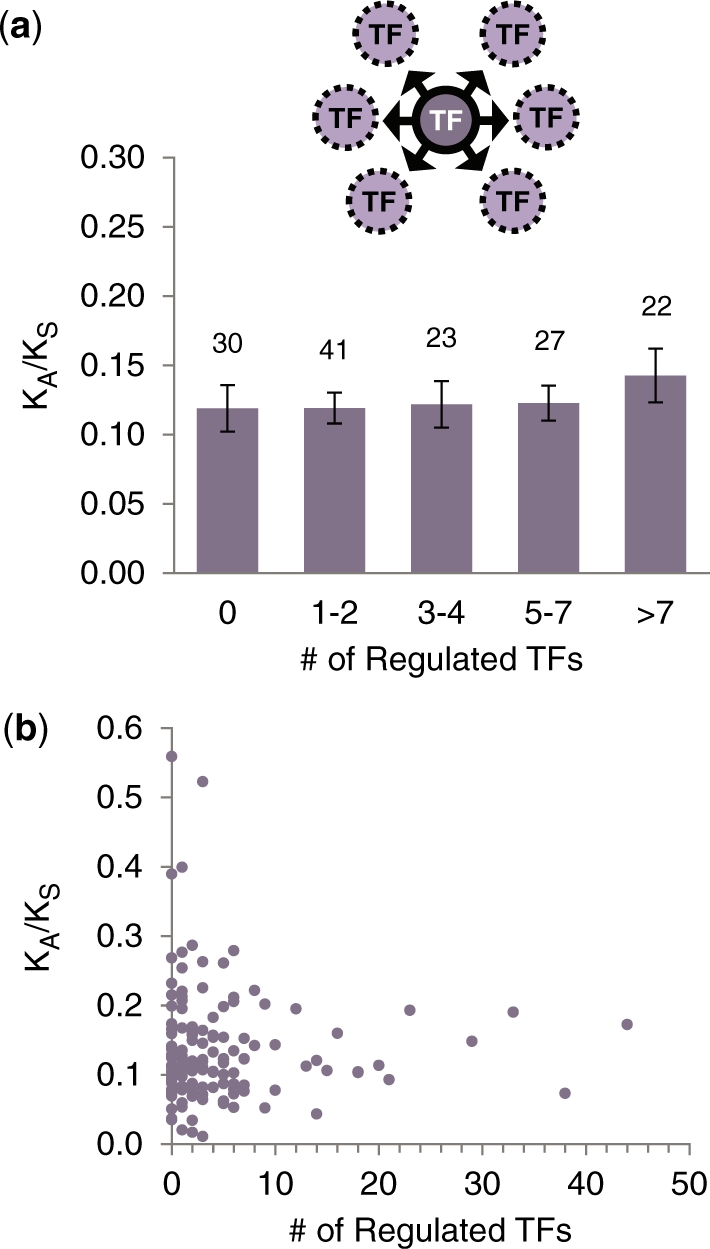
In addition to physical interactions and directed regulatory TF–TG relationships, a third major type of association in which TFs participate is the co-regulatory relationship, defined as the significant association among TFs in the joint regulation of common TGs. As is the case for out-degree, this measure can only be defined for TFs as it has no analog among generic proteins. Our reconstruction of the TF co-regulatory relationship is based on the hypothesis that cooperative TFs tend to share more common TGs than expected by chance (36); this notion has been widely applied to study the mechanisms and general principles of combinatorial regulation (44). We reconstructed the TF co-regulatory network in S. cerevisiae by enumerating all co-regulatory TF pairs based on large-scale ChIP-chip experiments (see ‘Materials and Methods’ section). For every TF, we counted the number of co-regulatory edges in the TF co-regulatory network, and correlated this degree with KA/KS (Figure 6a; see Figure 6b for a scatter plot). The correlation is positive and weakly significant (rs = 0.19, two-tailed P = 0.022, 3.6% of the variance in KA/KS ranks can be explained by co-regulatory degree ranks). This positive correlation cannot be explained by expression level, as the correlation between inverse expression level and co-regulatory degree for TFs is not significantly positive (P = 0.63). When KA is used as a measure of evolutionary rate, a positive and weakly significant correlation with co-regulatory degree is again observed (rs = 0.18, two-tailed P = 0.031, 3.24% of the variance in evolutionary rate ranks can be explained by co-regulatory degree ranks). On the contrary, when KS is used as a measure of evolutionary rate, the correlation is no longer significant (P = 0.70).
Figure 6.
The relationship between KA/KS and co-regulatory degree for TFs. A co-regulatory relationship is defined as the significant association between two TFs in the joint regulation of common TGs (see ‘Materials and Methods’ section). (a) The relationship between KA/KS and degree for the 143 yeast TFs in the TF co-regulatory network. (b) Scatter plot relating KA/KS and number of co-regulatory relationships for TFs.
We considered the possibility that the positive correlation between cooperativity and KA/KS for TFs could be a byproduct of gene duplication, as duplicated TFs may have a boosting effect on cooperativity, and duplicated genes tend to evolve quickly (45). Here, we define gene duplication for TFs as a TF–TF alignment having BLAST E value of at most 10−5 and at least 50% coverage. We found that the correlation between degree of gene duplication and KA/KS for TFs is not significantly positive (P = 0.20). We conclude that gene duplication cannot explain the positive correlation between cooperativity and KA/KS for TFs. At the same time, it is still possible that TF hubs experience a higher degree of other types of functional redundancy that remain to be characterized.
When a third closely related yeast species S. mikatae is used in comparison, the correlation between KA/KS and co-regulatory degree remains positive but the statistical significance diminishes (rs = 0.047 and two-tailed P = 0.58 for S. cerevisiae versus S. mikatae comparison; rs = 0.11 and two-tailed P = 0.18 for S. paradoxus versus S. mikatae comparison). Nevertheless, our main conclusion remains correct that TF co-regulatory hubs do not tend to evolve more slowly than TF non-hubs.
DISCUSSION
Our findings can be summarized as follows: within the global protein–protein interaction and transcriptional regulatory networks, TF hubs and protein hubs evolve in qualitatively different—and sometimes even opposite—ways. Protein hubs in the interaction and regulatory networks tend to experience strong negative selection, and thus evolve more slowly than protein non-hubs. On the contrary, four lines of evidence based on interaction degree, regulatory in-degree, regulatory out-degree and co-regulatory degree consistently and collectively demonstrate that TF hubs do not tend to evolve significantly more slowly than TF non-hubs. Most importantly, the correlations between evolutionary rate and degrees for TFs are significantly more positive than those for generic proteins within the same global protein–protein interaction and transcriptional regulatory networks. These observations cannot be explained by confounding variables such as expression level and gene duplication, and hold for three closely related yeast species.
The existence of a significant correlation, whether positive or negative, between degree and strength of selection for TFs and generic proteins in protein–protein interaction and transcriptional regulatory networks indicates that a protein’s network properties may play an important role in determining its fitness contribution and evolution. Indeed, our observations suggest that both generic protein hubs and TF hubs are important to a cell’s overall fitness, with measurable evolutionary consequences. At the same time, the observed difference in the strength and sign of these evolutionary trends suggests that there are fundamental differences in the function and evolution of generic protein hubs and TF hubs.
The evolution of generic protein hubs can be largely understood in terms of negative selection. Generic protein–protein interactions are fundamental to the basic functions of a living cell, and as such they tend to be ancient, well-conserved among species and under strong negative selection. Protein hubs with many interactors are expected to experience greater structural and functional constraint, resulting in stronger negative selection (20,46). In the absence of a competing force, generic protein interaction hubs are therefore expected to be slow evolving. Similarly, proteins under a high level of regulation tend to be important to the basic function of the cell under various conditions (such as heat shock proteins), and are therefore subject to strong negative selection. Hence, generic protein hubs with many regulators are also expected to be slow evolving.
Many of our observations regarding TF hubs can also be explained by negative selection. As a group, TFs (including TF hubs) are predominantly under negative selection, with KA/KS values much less than 1 (Figure 1b). Like other proteins, TFs experience strong sequence constraints for proper folding and for maintaining the functionality of their protein- and DNA-binding interfaces—both of which contribute to the overall fitness density of the TFs. Our observation that TF hubs in the protein–protein interaction network do not tend to evolve significantly more slowly than TF non-hubs can be explained by a relaxation of negative selection: protein–protein interactions tend to impose a reduced level of structural and functional constraint on TFs compared to generic proteins. This is potentially due to the fact that interactions involving TFs may play a regulatory role in the cell, and as a result may be more transient, more dynamic and more subtle than generic protein–protein interactions. In addition, our observation that TF regulatory out-degree hubs do not tend to evolve more slowly than non-hubs suggests that TF regulatory out-degree edges impose at most weak selective constraint on TF evolution.
At the same time, the observed trends that TF in-degree hubs in the transcriptional regulatory network tend to evolve more quickly than TF non-hubs can be best explained by the additional force of positive selection among the TF hubs (26). There are fundamental differences in the evolutionary capacity of TFs and generic proteins. Generic proteins perform specific, highly optimized biochemical activities that are fundamentally important across diverse species. An organism’s TFs regulate and organize these biochemical activities, in part fostering compatibility between the organism and its environment. As a result, TF hubs are fine-tuned in a lineage-specific manner, with great potential for adaptive variation and network rewiring. Interaction and regulation of TFs operate at a higher level than interaction and regulation of generic proteins, generating regulatory complexity and specificity in a particular organism. While changes in protein hubs are more likely to produce non-viable phenotypes, changes in TF hubs are more likely to produce innovative phenotypes. Because TF hubs have large influence over transcriptional regulation, such subtle changes may produce wide-spread reorganization of the regulatory network, ultimately facilitating adaptation to different environmental conditions. Finally, positive selection may also play a role in the elevated evolutionary rates of TF hubs in the protein–protein interaction network. These differences between TFs and generic proteins underlie the significantly different evolutionary trends of TF subnetworks and generic protein networks. Known cases of positive selection acting on yeast genes did not provide sufficient statistical support to explain our observed trends (47,48), possibly due to the inherent difficulty of detecting positive selection. In the following sections, we offer support for our hypotheses in the form of case studies on fast evolving TF hubs and network rewiring.
There are many examples of rapid and potentially adaptive evolution among TF hubs in yeast (30,49–54). The transcriptional activator GAL4 is an interaction hub (interacting with 37 proteins, including 6 TFs), regulatory in-degree hub (regulated by 6 other TFs), regulatory out-degree hub (regulating 100 genes, including 6 TFs) and co-regulatory hub (acting cooperatively with 21 other TFs) in S. cerevisiae interaction and regulatory networks. At the same time, GAL4 is among the top 20% fastest evolving TFs in paired comparison with S. paradoxus. Recent analysis of the galactose genetic pathways in Candida albicans and S. cerevisiae reveals that GAL4 plays an important role in the rewiring of the transcriptional regulations of galactose catabolism in yeasts (55). A second example is IME1, a transcriptional activator and master regulator that initiates yeast sporulation. IME1 is a regulatory in-degree hub (regulated by 11 TFs) and co-regulatory hub (acting cooperatively with 26 other TFs) in S. cerevisiae regulatory networks. At the same time, IME1 ranks among the top 20% fastest evolving TFs in paired comparison with S. paradoxus. A recent study shows that natural variation in the efficiency of sporulation between oak tree and vineyard yeast strains is due to allelic variation between four nucleotide changes in three TFs, including IME1 (54). A third and final example is ACA1, a regulatory in-degree hub (regulated by 12 TFs), which has been previously proposed as a target of positive selection by a sliding window analysis (47).
Further evidence of a role for positive selection in explaining the elevated evolutionary rates of TF hubs is found in experimental reports of the prevalence and adaptive significance of TF network rewiring. This is in stark contrast to the generic protein–protein interaction network, where network rewiring appears to be much less widespread. Genome-wide studies reveal signs of extensive transcriptional rewiring in related yeasts, indicating that even closely related organisms regulate their genes using markedly different transcriptional regulatory interactions (53,55,56). Several striking cases of TF network rewiring have been identified by comparing C. albicans and S. cerevisiae; examples include the transcriptional regulation of (i) the galactose catabolism pathway (55), (ii) the mating circuit (51,57,58), as well as (iii) the nuclear (59) and mitochondrial (60) ribosomal genes. Interactions and regulations involving TFs form high-level, dynamic network structures such as feed-forward and feed-back loops (61,62), and they are important in combinatorial regulation—a pervasive mechanism in eukaryotic organisms used to achieve increased specificity and integration of multiple signals in the control of gene expression (52). It is plausible that changes in the interaction and regulation of TFs could facilitate transcriptional regulatory circuit rewiring, and subsequently accelerate the evolution of TFs. Differences in the interaction and regulation patterns of TFs across related species may be responsible for rapid evolutionary adaption to varied ecological niches (54). Recent studies reveal that the yeast transcriptional regulatory network responds to different conditions using distinct subnetworks of TF–TF regulatory interactions with large topological differences (63). Within species, genetic interactions between TFs are a major source of phenotypic diversity, and there is evidence of positive selection for such interactions (54). Indeed, a recent gene network rewiring experiment shows that adding new links among TFs can confer a fitness advantage in Escherichia coli (62), elegantly highlighting the potential adaptive significance of network rewiring.
We recognize that TF sequence change is not the sole driving force in adaptive network evolution. In fact, we expect the majority of network rewiring to result from the creation and elimination of DNA binding sites, which are much more evolvable than their corresponding TFs and TF–DNA binding interfaces (30,64). Finally, we note that TFs in general are composed of multiple domains with modular functions such as DNA-binding, transactivation and other regulatory activities. While this work utilizes a single, averaged measure of selective strength for each TF, further examination of the patterns of amino acid substitution in these specific domains may provide additional mechanistic insight into the evolutionary trends reported here.
Biomolecular network analyses have been highly successful in revealing the large-scale organizational and evolutionary principles of a cell. Such studies tend to focus on graph theoretical analysis of nodes and edges within a single, global biomolecular network. In this article, we propose the novel concept of the TF subnetworks, which are the subnetworks of physical interaction, transcriptional regulation and co-regulatory relationships involving TFs. By carrying out a systematic analysis of protein evolution in the TF subnetworks in comparison to the global protein networks, we reached the surprising conclusion that subnetworks within the same global network can display different evolutionary trends. For example, within the global protein–protein interaction network, TF hubs and protein hubs have significantly different evolutionary trends. Similarly, within the global transcriptional regulatory network, TF in-degree hubs and protein in-degree hubs have strongly opposing evolutionary trends. Most importantly, we show that the observed differences in evolutionary trends are not due to systematic differences between protein–protein interaction networks and transcriptional regulatory networks, but rather result from the different functional roles that TFs and generic proteins play within both the protein–protein interaction and transcriptional regulatory networks. Our work suggests that biological networks in a cell are multileveled, and that high-level network components (such as TFs) are subject to additional evolutionary forces compared to low-level components (such as generic proteins). The striking difference between the evolution of TF hubs and generic protein hubs demonstrates that components within the same global network can be governed by distinct evolutionary principles, and suggests that general network organizational and evolutionary principles may not be applicable to specific subnetworks. Our work demonstrates a high degree of functional and evolutionary heterogeneity within biological networks, and highlights the rich insights that can be gained from modeling biomolecular subnetworks.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Natural Science Foundation of China (No. 10801131 to Y.W.) and (No. 10631070 to X.-S.Z.); National Science Foundation (IGERT grant DGE-0654108 to E.A.F.); Pharmaceutical Research and Manufacturers of America (PhRMA) Foundation (Research Starter Grant in Informatics to Y.X.). Y.X. gratefully acknowledges the support of K. C. Wong Education Foundation, Hong Kong. Funding for open access charge: National Science Foundation IGERT grant DGE-0654108.
Conflict of interest statement. None declared.
Supplementary Material
REFERENCES
- 1.Barabasi AL, Oltvai ZN. Network biology: understanding the cell's functional organization. Nat. Rev. Genet. 2004;5:101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- 2.Pal C, Papp B, Lercher MJ. An integrated view of protein evolution. Nat. Rev. Genet. 2006;7:337–348. doi: 10.1038/nrg1838. [DOI] [PubMed] [Google Scholar]
- 3.Koonin EV, Wolf YI. Evolutionary systems biology: links between gene evolution and function. Curr. Opin. Biotechnol. 2006;17:481–487. doi: 10.1016/j.copbio.2006.08.003. [DOI] [PubMed] [Google Scholar]
- 4.Fraser HB, Hirsh AE, Steinmetz LM, Scharfe C, Feldman MW. Evolutionary rate in the protein interaction network. Science. 2002;296:750–752. doi: 10.1126/science.1068696. [DOI] [PubMed] [Google Scholar]
- 5.Bloom JD, Adami C. Apparent dependence of protein evolutionary rate on number of interactions is linked to biases in protein-protein interactions data sets. BMC Evol. Biol. 2003;3:21. doi: 10.1186/1471-2148-3-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fraser HB, Wall DP, Hirsh AE. A simple dependence between protein evolution rate and the number of protein-protein interactions. BMC Evol. Biol. 2003;3:11. doi: 10.1186/1471-2148-3-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jordan IK, Wolf YI, Koonin EV. No simple dependence between protein evolution rate and the number of protein-protein interactions: only the most prolific interactors tend to evolve slowly. BMC Evol. Biol. 2003;3:1. doi: 10.1186/1471-2148-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bloom JD, Adami C. Evolutionary rate depends on number of protein-protein interactions independently of gene expression level: response. BMC Evol. Biol. 2004;4:14. doi: 10.1186/1471-2148-4-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fraser HB, Hirsh AE. Evolutionary rate depends on number of protein-protein interactions independently of gene expression level. BMC Evol. Biol. 2004;4:13. doi: 10.1186/1471-2148-4-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pal C, Papp B, Hurst LD. Highly expressed genes in yeast evolve slowly. Genetics. 2001;158:927–931. doi: 10.1093/genetics/158.2.927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hirsh AE, Fraser HB. Protein dispensability and rate of evolution. Nature. 2001;411:1046–1049. doi: 10.1038/35082561. [DOI] [PubMed] [Google Scholar]
- 12.Bloom JD, Drummond DA, Arnold FH, Wilke CO. Structural determinants of the rate of protein evolution in yeast. Mol. Biol. Evol. 2006;23:1751–1761. doi: 10.1093/molbev/msl040. [DOI] [PubMed] [Google Scholar]
- 13.Rocha EP, Danchin A. An analysis of determinants of amino acids substitution rates in bacterial proteins. Mol. Biol. Evol. 2004;21:108–116. doi: 10.1093/molbev/msh004. [DOI] [PubMed] [Google Scholar]
- 14.Wall DP, Hirsh AE, Fraser HB, Kumm J, Giaever G, Eisen MB, Feldman MW. Functional genomic analysis of the rates of protein evolution. Proc. Natl Acad. Sci. USA. 2005;102:5483–5488. doi: 10.1073/pnas.0501761102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Drummond DA, Raval A, Wilke CO. A single determinant dominates the rate of yeast protein evolution. Mol. Biol. Evol. 2006;23:327–337. doi: 10.1093/molbev/msj038. [DOI] [PubMed] [Google Scholar]
- 16.Kawahara Y, Imanishi T. A genome-wide survey of changes in protein evolutionary rates across four closely related species of Saccharomyces sensu stricto group. BMC Evol. Biol. 2007;7:9. doi: 10.1186/1471-2148-7-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Plotkin JB, Fraser HB. Assessing the determinants of evolutionary rates in the presence of noise. Mol. Biol. Evol. 2007;24:1113–1121. doi: 10.1093/molbev/msm044. [DOI] [PubMed] [Google Scholar]
- 18.Xia Y, Franzosa EA, Gerstein MB. Integrated assessment of genomic correlates of protein evolutionary rate. PLoS Comput. Biol. 2009;5:e1000413. doi: 10.1371/journal.pcbi.1000413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Drummond DA, Bloom JD, Adami C, Wilke CO, Arnold FH. Why highly expressed proteins evolve slowly. Proc. Natl Acad. Sci. USA. 2005;102:14338–14343. doi: 10.1073/pnas.0504070102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kim PM, Lu LJ, Xia Y, Gerstein MB. Relating three-dimensional structures to protein networks provides evolutionary insights. Science. 2006;314:1938–1941. doi: 10.1126/science.1136174. [DOI] [PubMed] [Google Scholar]
- 21.de Lichtenberg U, Jensen LJ, Brunak S, Bork P. Dynamic complex formation during the yeast cell cycle. Science. 2005;307:724–727. doi: 10.1126/science.1105103. [DOI] [PubMed] [Google Scholar]
- 22.Han JDJ, Bertin N, Hao T, Goldberg DS, Berriz GF, Zhang LV, Dupuy D, Walhout AJM, Cusick ME, Roth FP. Evidence for dynamically organized modularity in the yeast protein-protein interaction network. Nature. 2004;430:88–93. doi: 10.1038/nature02555. [DOI] [PubMed] [Google Scholar]
- 23.Papp B, Pal C, Hurst LD. Metabolic network analysis of the causes and evolution of enzyme dispensability in yeast. Nature. 2004;429:661–664. doi: 10.1038/nature02636. [DOI] [PubMed] [Google Scholar]
- 24.Wang Y, Zhang XS, Xia Y. Predicting eukaryotic transcriptional cooperativity by Bayesian network integration of genome-wide data. Nucleic Acids Res. 2009;37:5943–5958. doi: 10.1093/nar/gkp625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Evangelisti AM, Wagner A. Molecular evolution in the yeast transcriptional regulation network. J. Exp. Zoolog. B Mol. Dev. Evol. 2004;302:392–411. doi: 10.1002/jez.b.20027. [DOI] [PubMed] [Google Scholar]
- 26.Jovelin R, Phillips P. Evolutionary rates and centrality in the yeast gene regulatory network. Genome Biol. 2009;10:R35. doi: 10.1186/gb-2009-10-4-r35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Teixeira MC, Monteiro P, Jain P, Tenreiro S, Fernandes AR, Mira NP, Alenquer M, Freitas AT, Oliveira AL, Sa-Correia I, et al. The YEASTRACT database: a tool for the analysis of transcription regulatory associations in Saccharomyces cerevisiae. Nucleic Acids Res. 2006;34:D446–D451. doi: 10.1093/nar/gkj013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cherry JM, Adler C, Ball C, Chervitz SA, Dwight SS, Hester ET, Jia Y, Juvik G, Roe T, Schroeder M, et al. SGD: saccharomyces genome database. Nucleic Acids Res. 1998;26:73–79. doi: 10.1093/nar/26.1.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Stark C, Breitkreutz B.-J, Reguly T, Boucher L, Breitkreutz A, Tyers M. BioGRID: a general repository for interaction datasets. Nucleic Acids Res. 2006;34:D535–D539. doi: 10.1093/nar/gkj109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Borneman AR, Gianoulis TA, Zhang ZD, Yu H, Rozowsky J, Seringhaus MR, Wang LY, Gerstein M, Snyder M. Divergence of transcription factor binding sites across related yeast species. Science. 2007;317:815. doi: 10.1126/science.1140748. [DOI] [PubMed] [Google Scholar]
- 31.Borneman AR, Leigh-Bell JA, Yu H, Bertone P, Gerstein M, Snyder M. Target hub proteins serve as master regulators of development in yeast. Genes Dev. 2006;20:435–448. doi: 10.1101/gad.1389306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW, Hannett NM, Tagne JB, Reynolds DB, Yoo J, et al. Transcriptional regulatory code of a eukaryotic genome. Nature. 2004;431:99–104. doi: 10.1038/nature02800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Horak CE, Luscombe NM, Qian J, Bertone P, Piccirrillo S, Gerstein M, Snyder M. Complex transcriptional circuitry at the G1/S transition in Saccharomyces cerevisiae. Genes Dev. 2002;16:3017–3033. doi: 10.1101/gad.1039602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, et al. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- 35.Workman CT, Mak HC, McCuine S, Tagne J.-B, Agarwal M, Ozier O, Begley TJ, Samson LD, Ideker T. A systems approach to mapping DNA damage response pathways. Science. 2006;312:1054–1059. doi: 10.1126/science.1122088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tsai H-K, Lu HH-S, Li W-H. Statistical methods for identifying yeast cell cycle transcription factors. Proc. Natl Acad. Sci. USA. 2005;102:13532–13537. doi: 10.1073/pnas.0505874102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nei M, Kumar S. Molecular Evolution and Phylogenetics. Oxford: Oxford University Press; 2000. [Google Scholar]
- 38.Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wapinski I, Pfeffer A, Friedman N, Regev A. Natural history and evolutionary principles of gene duplication in fungi. Nature. 2007;449:54–61. doi: 10.1038/nature06107. [DOI] [PubMed] [Google Scholar]
- 40.Yang Z. PAML: a program package for phylogenetic analysis by maximum likelihood. Bioinformatics. 1997;13:555–556. doi: 10.1093/bioinformatics/13.5.555. [DOI] [PubMed] [Google Scholar]
- 41.Yang Z, Nielsen R. Estimating synonymous and nonsynonymous substitution rates under realistic evolutionary models. Mol. Biol. Evol. 2000;17:32–43. doi: 10.1093/oxfordjournals.molbev.a026236. [DOI] [PubMed] [Google Scholar]
- 42.Zar JH. Significance testing of the Spearman rank correlation coefficient. J. Am. Stat. Assoc. 1972;67:578–580. [Google Scholar]
- 43.Sharp PM, Li WH. The codon Adaptation Index–a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 1987;15:1281–1295. doi: 10.1093/nar/15.3.1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Babu MM, Luscombe NM, Aravind L, Gerstein M, Teichmann SA. Structure and evolution of transcriptional regulatory networks. Curr. Opin. Struct. Biol. 2004;14:283–291. doi: 10.1016/j.sbi.2004.05.004. [DOI] [PubMed] [Google Scholar]
- 45.Lynch M, Conery JS. The evolutionary fate and consequences of duplicate genes. Science. 2000;290:1151–1155. doi: 10.1126/science.290.5494.1151. [DOI] [PubMed] [Google Scholar]
- 46.Franzosa EA, Xia Y. Structural determinants of protein evolution are context-sensitive at the residue level. Mol. Biol. Evol. 2009;26:2387–2395. doi: 10.1093/molbev/msp146. [DOI] [PubMed] [Google Scholar]
- 47.Sawyer SL, Malik HS. Positive selection of yeast nonhomologous end-joining genes and a retrotransposon conflict hypothesis. Proc. Natl Acad. Sci. USA. 2006;103:17614–17619. doi: 10.1073/pnas.0605468103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li Y, Liang H, Gu Z, Lin Z, Guan W, Zhou L, Li Y, Li WH. Detecting positive selection in the budding yeast genome. J. Evol. Biol. 2009;22:2430–2437. doi: 10.1111/j.1420-9101.2009.01851.x. [DOI] [PubMed] [Google Scholar]
- 49.Bilu Y, Barkai N. The design of transcription-factor binding sites is affected by combinatorial regulation. Genome Biol. 2005;6:R103. doi: 10.1186/gb-2005-6-12-r103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tsong AE, Miller MG, Raisner RM, Johnson AD. Evolution of a combinatorial transcriptional circuit a case study in yeasts. Cell. 2003;115:389–399. doi: 10.1016/s0092-8674(03)00885-7. [DOI] [PubMed] [Google Scholar]
- 51.Tsong AE, Tuch BB, Li H, Johnson AD. Evolution of alternative transcriptional circuits with identical logic. Nature. 2006;443:415–420. doi: 10.1038/nature05099. [DOI] [PubMed] [Google Scholar]
- 52.Tuch BB, Galgoczy DJ, Hernday AD, Li H, Johnson AD. The evolution of combinatorial gene regulation in fungi. PLoS Biol. 2008;6:e38. doi: 10.1371/journal.pbio.0060038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tuch BB, Li H, Johnson AD. Evolution of eukaryotic transcription circuits. Science. 2008;319:1797. doi: 10.1126/science.1152398. [DOI] [PubMed] [Google Scholar]
- 54.Gerke J, Lorenz K, Cohen B. Genetic interactions between transcription factors cause natural variation in yeast. Science. 2009;323:498–501. doi: 10.1126/science.1166426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Martchenko M, Levitin A, Hogues H, Nantel A, Whiteway M. Transcriptional rewiring of fungal galactose-metabolism circuitry. Curr. Biol. 2007;17:1007–1013. doi: 10.1016/j.cub.2007.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hogues H, Lavoie H, Sellam A, Mangos M, Roemer T, Purisima E, Nantel A, Whiteway M. Transcription factor substitution during the evolution of fungal ribosome regulation. Mol. Cell. 2008;29:552–562. doi: 10.1016/j.molcel.2008.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rokas A. Evolution: different paths to the same end. Nature. 2006;443:415–420. doi: 10.1038/443401a. [DOI] [PubMed] [Google Scholar]
- 58.Scannell DR, Wolfe K. Rewiring the transcriptional regulatory circuits of cells. Genome Biol. 2004;5:206. doi: 10.1186/gb-2004-5-2-206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Tanay A, Regev A, Shamir R. Conservation and evolvability in regulatory networks: the evolution of ribosomal regulation in yeast. Proc. Natl Acad. Sci. USA. 2005;102:7203–7208. doi: 10.1073/pnas.0502521102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ihmels J, Bergmann S, Gerami-Nejad M, Yanai I, McClellan M, Berman J, Barkai N. Rewiring of the yeast transcriptional network through the evolution of motif usage. Science. 2005;309:938–940. doi: 10.1126/science.1113833. [DOI] [PubMed] [Google Scholar]
- 61.Ideker T. Forging new ties between E coli genes. Cell. 2008;133:1135–1137. doi: 10.1016/j.cell.2008.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Isalan M, Lemerle C, Michalodimitrakis K, Horn C, Beltrao P, Raineri E, Garriga-Canut M, Serrano L. Evolvability and hierarchy in rewired bacterial gene networks. Nature. 2008;452:840–845. doi: 10.1038/nature06847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Luscombe NM, Babu MM, Yu H, Snyder M, Teichmann SA, Gerstein M. Genomic analysis of regulatory network dynamics reveals large topological changes. Nature. 2004;431:308–312. doi: 10.1038/nature02782. [DOI] [PubMed] [Google Scholar]
- 64.Gasch AP, Moses AM, Chiang DY, Fraser HB, Berardini M, Eisen MB. Conservation and evolution of cis-regulatory systems in ascomycete fungi. PLoS Biol. 2004;2:e398. doi: 10.1371/journal.pbio.0020398. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.