RNAMotifScan: automatic identification of RNA structural motifs using secondary structural alignment

Abstract

Recent studies have shown that RNA structural motifs play essential roles in RNA folding and interaction with other molecules. Computational identification and analysis of RNA structural motifs remains a challenging task. Existing motif identification methods based on 3D structure may not properly compare motifs with high structural variations. Other structural motif identification methods consider only nested canonical base-pairing structures and cannot be used to identify complex RNA structural motifs that often consist of various non-canonical base pairs due to uncommon hydrogen bond interactions. In this article, we present a novel RNA structural alignment method for RNA structural motif identification, RNAMotifScan, which takes into consideration the isosteric (both canonical and non-canonical) base pairs and multi-pairings in RNA structural motifs. The utility and accuracy of RNAMotifScan is demonstrated by searching for kink-turn, C-loop, sarcin-ricin, reverse kink-turn and E-loop motifs against a 23S rRNA (PDBid: 1S72), which is well characterized for the occurrences of these motifs. Finally, we search these motifs against the RNA structures in the entire Protein Data Bank and the abundances of them are estimated. RNAMotifScan is freely available at our supplementary website (http://genome.ucf.edu/RNAMotifScan).

INTRODUCTION

Non-coding RNAs play a large variety of roles inside a cell, and recent discoveries point to many of their novel cellular functions (1,2). The variety of functionalities of non-coding RNA is determined by their complex structures. Unlike DNAs, which usually exhibit regular double helical structures due to the interactions with the complementary strands, RNAs are single strand molecules and can fold into irregular 3D structures. Among the complex structures, there exist conserved and recurrent segments whose arrangement, abundance and interaction largely determine the folding behaviors and functionalities of the structures. These segments, viewed as the `building blocks' of RNA architecture, are usually referred to as RNA structural motifs (3–5). The identification and analysis of these motifs have largely enriched our experiences in RNA studies.

The common approach for RNA structural motif identification is to represent the RNA structural motifs by different 3D properties (i.e. torsion angles or atomic distances) of the key nucleotides and then apply heuristics to searching for the topological occurrences of the motif in the 3D RNA structures [similar to the methods for 3D protein structure comparison (6)]. Computer program, such as PRIMOS (7) and COMPADRES (8), represents and searches certain backbone conformations using pseudotorsion angles. On the other hand, NASSAM encodes the 3D motif by using a graph to store pairwise atomic distances between the key nucleotides (9). To reduce the information contained in pairwise atomic distances, ARTS builds approximated anchors based on a set of seed points before detailed matching (10). Recent progress uses shape histograms, which are also computed from pairwise atomic distances, to summarize the structural motifs (11). This method has identified the occurrences of many structural motifs in ribosomal RNAs (12). Instead of considering solely torsion angles or atomic distances, FR3D, which searches for recurrent motifs considering a combination of geometric, symbolic and sequence information, achieves the most satisfying performance (13). Although the existing methods have successfully identified many occurrences of several known RNA structural motifs, most of them require the accurate 3D coordinates of the query motif, and thus are limited to structural motifs with rigid 3D topologies. However, it is known that many motifs exhibit certain structural variation, and thus cannot be well characterized by their 3D topologies (14). Therefore, the more conserved base-pairing pattern should be considered when searching for RNA structural motifs (15,16).

It was observed that many non-canonical base pairs in RNA structural motifs are isosteric and these base pairs can interchange with each other without affecting the overall RNA structure (17). Generally, a base pair should have three properties: (i) the two nucleotides interacting through hydrogen bonds; (ii) nucleotide edges participating in the interaction; and (iii) the relative orientation of the glycosidic bonds, which is either cis or trans. Each nucleotide has three edges that can interact with another nucleotide to form a base pair, namely the Watson–Crick edge (denoted as `WC' edge), Hoogsteen edge (denoted as `H' edge) and Sugar edge (denoted as `SE' edge). Given the three properties, it is sufficient to classify all base pairs into one of the isosteric groups (17). Modeling RNA structural motifs through non-canonical base pairs is theoretically sound and can largely reduce the complexity of 3D RNA motifs. First, the definition of isostericity serves as the foundation of relating tertiary structure with non-canonical base pairs. Second, some motifs are defined by their characterized non-canonical base-pairing patterns, instead of their 3D structures. Finally, modeling RNA structural motifs by their base-pairing pattern is easier to understand comparing to their atomic coordinates.

Djelloul and Denise (19) modeled the RNA structural motifs through graphical representation of these non-canonical base pairs. They extracted structural segments containing non-canonical base pairs from the annotated RNA 3D structure. By constructing clusters through the measurement of pairwise maximum isomorphic base-pairing cores, they characterized the recurrent base-pairing patterns among these structural segments. This method has led to the rediscovery of many structural motifs, which shows the potential power of utilization of non-canonical base pairs in modeling RNA structural motifs. However, this method is not optimized for structural motif identification, for the isomorphic condition is not suitable to identify the motifs that exhibit variations in non-canonical base pairs.

Therefore, well-developed algorithms for comparing the non-canonical base-pairing patterns between two RNA tertiary structural segments are in urgent demand. However, most existing methods model and compare RNA structures only through canonical base pairs. In a typical approach, free energy values are assigned to the canonical base pairs, and secondary structure with minimum free energy are computed to model the structure (20–24). Comparative genomics approaches aim at the identification of consensus canonical base pairs from a set of synthetic genomic sequences of multiple species that are previously aligned (25,26) or even unaligned (27–30). The RNA homolog search approaches attempt to find genome sequences that match a query RNA in sequence and a model secondary structure annotated with canonical base pairs (31–33). RNA canonical base pairs are also modeled into tree structures, and the edit distance between two tree structures is then computed (34,35). Recently, variants of Sankoff's algorithm (36) are also used to compare the canonical base pairs between two RNA structures (37,38).

These computational methods can be extended to comparing RNA structures with non-canonical base pairs. We need to address the following issues raised by the inclusion of non-canonical base pairs. Most importantly, the similarity between two non-canonical base pairs should be measured. The reason is that canonical base pairs can interchange with each other while maintaining the tertiary structure, but such possibility is not guaranteed for non-canonical base pairs as defined in the isosteric matrices. In addition, canonical base pairs are usually nested stacked in forming the A-form helical regions, while RNA structural motifs usually include many multi-pairings (interactions involves more than two nucleotide residues, i.e. base triples) and pseudoknots (crossing base pairs), see Figure 3. Therefore, non-canonical base pairs, multi-pairing and crossing base pairs must be handled in order to properly compare the structural motifs.

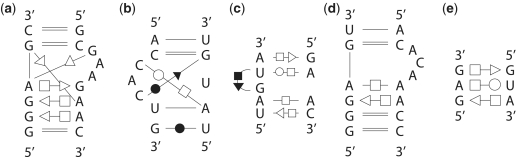
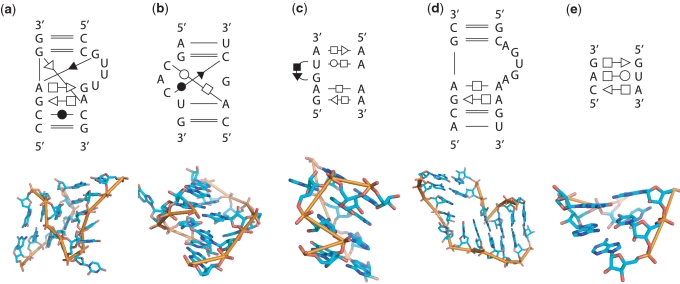
Figure 3.

Base-pairing patterns of the query motif structures in 2D diagrams. (a) kink-turn motif. (b) C-loop motif. (c) sarcin-ricin motif (d) reverse kink-turn motif. (e) E-loop motif.

In this article we describe a new computational method for RNA structural motif identification that takes into account isosteric base pairs and multi-pairings. Given a query motif (represented by base-pairing patterns, see Figure 1b), our new method, called RNAMotifScan, attempts to identify all possible similar motifs from the target 3D structures. The core algorithm of RNAMotifScan finds the maximum common isosteric base pairs between two RNA structures, which runs in the time complexity of O(m²n²), where m and n are the number of base pairs in the query and target RNA structural segment. Since RNA structure motifs usually have only a small number of base pairs, our rigorous algorithm is extremely efficient. We tested RNAMotifScan by searching for five previously known motifs in RNA 3D structures from Protein Data Bank (PDB) (39) and compared the results with related publications as well as the SCOR database (40). It is shown that RNAMotifScan can identify many new motif occurrences that are previously unknown and has better performance in terms of both its speed and accuracy. The complete search results can be found at the supplementary website (http://genome.ucf.edu/RNAMotifScan).

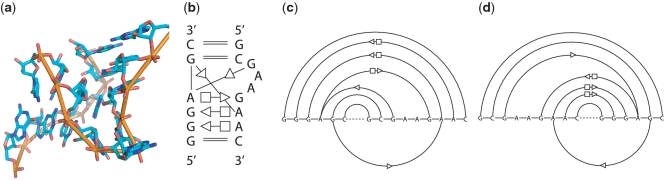
Figure 1.

Kink-turn motif. (a) 3D structure. (b) 2D diagram for base-pairing patterns (notation is the same as proposed in (18)). (c) and (d) Arc representations built by concatenating the two strands of the motif with two different orders. For (c) and (d), the arcs rest above on the horizontal line represents the base pairs that are optimally aligned in the first step, while the arcs below are processed in the second step. The motif is from a 23S rRNA in H. marismortui (1S72, chain `0', location 77-82/92-100).

MATERIALS AND METHODS

The query RNA structural motif base-pairing patterns are adopted from related publications (see ‘Data processing' Section). We concatenate two strands of the query RNA motif into one sequence for the alignment (see Figure 1c and d, there are two ways to concatenate the query and both are searched against the target). For the target RNA segments, we first use annotation software (see ‘Data processing' Section) to translate the RNA 3D coordinates into base-pairing patterns that contain sufficient information for isosteric group classification (i.e. pairing nucleotides, interacting edges, and relative glycosidic bond orientations). We then cut the annotated target RNA structure into many local (interactions within two strands, long-range interactions are ignored) RNA structural segments. Similarly, we concatenate two strands of the target RNA structural segments into one sequence. To identify RNA motif instances, we use a dynamic programming procedure to compute the similarity between the query RNA motif and all structural segments in the target RNA and report the significant hits.

The recursive functions of the alignment procedure need to address three major issues. First, the isostericity of the base pairs should be incorporated into the scoring functions such that only base pairs belong to the same isosteric group (17) can be matched to each other. Second, there are many multi-pairings occurring in the RNA structural motif and the target RNA, which is introduced by one nucleotide simultaneously paired with two or more other nucleotides. This can be observed since each nucleotide has three edges, thus the nucleotide is able to participate in at most three base pairs. We discuss the multi-pairing issue in ‘Base-pairing relations in RNA structured motifs' Section for the alignment procedure. Finally, both the query RNA motif and the target RNA segments may contain crossing base pairs.

We divide the alignment into two steps. We first align non-crossing base pairs in the query. (Crossing base pairs in query are removed temporarily and processed in the second step, while the crossing base pairs in target structure are retained.) We then try to reinsert the removed crossing base pairs based on the resulting alignment. Note that we select the minimum number of base pairs to be matched in the second step so that most of the base pairs can be aligned optimally in the first step. Because the structural motifs are likely to be well represented by its major part of nested base pairs, which are matched optimally, it should work in most practical cases. Also, users can select the base pairs to form the query motif for the first step searching.

Base-pairing relations in RNA structural motifs

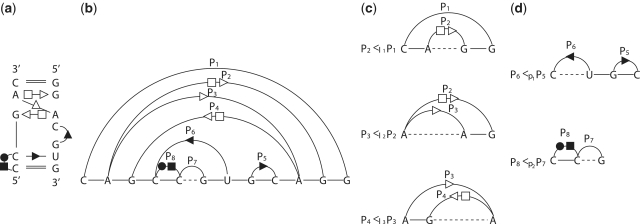
Multi-pairings are not only frequently occurred, but also important in forming the RNA structural motifs. Here, we formally define the classifications and relations of base pairs including multi-pairings. We denote the indices of the left and right nucleotides of a base pair P as P_l,P_r. Generally, two base pairs, P^A and P^A′, may have one of the following relations: (i) P^A and P^A′ are interleaving; (ii) P^A′ is enclosed with P^A (denoted by P^A′ < _IP^A); (iii) P^A′ is juxtapose to P^A and before P^A (denoted by P^A′ < _pP^A). Specifically, RNA structural motifs may contain multi-pairings. To handle these situations, we need to redefine the above definition. We extend the enclosing relation (<_I) to three subgroups (Figure 2c): P^A′ < _I1P^A (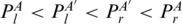), P^A′ < _I2P^A (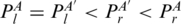) and P^A′ < _I3P^A (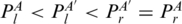). We also extend the juxtaposing relation (<_p) to two subgroups (Figure 2d): P^A′ < _p1P^A (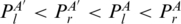) and P^A′ < _p2P^A ().

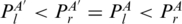Figure 2.

An artificial RNA structural motif containing all base-pairing relations including multi-pairing. (a) The base-pairing pattern of the motif. (b) The arc representation of the motif. (c) Base-pairing relation subgroups in the motif belong to enclosing relation. (d) Base-pairing relation subgroups in the motif belong to the juxtaposing relation.

Aligning two RNA structural motifs

We can use a dynamic programming algorithm to compute an optimal alignment between two RNA structural segments (27). There are three major contributions in this algorithm. First, the dynamic programming algorithm is guided by the partial order base pairs. Second, we consider non-canonical base pairs and their isostericity. Finally, we also allow non-crossing multi-pairings for the query and target structure.

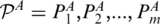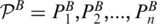Given an RNA structural motif A and a target RNA structural segment B with concatenated strands and m and n base pairs, respectively. Dummy base pairs were added between nucleotides A[0] and A[|A|+1] and between nucleotides B[0] and B[|B|+1]. Let and denote the two sets of base pairs, ordered according to increasing values of the right-most base. Define the following terms:

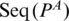• : the two nucleotides that form the base pair P^A, given by 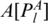and .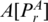

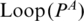• : the subsequence covered by the two nucleotides of the base pair P^A excluding the two nucleotides themselves. In other words, the sequence .

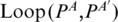• : the term is defined if and only if P^A′ is completely juxtaposing to the left of P^A, as the loop region corresponding to .

The score of the optimal alignment between two RNA sequences consists of three parts: the score of matching base pairs, the score of matching paired bases, and the score of matching unpaired subsequences (including gaps). These scores are assigned with different weights (w₁, w₂ and w₃, respectively) to distinguish the importance of them in building an RNA motif. Define the following terms:

• (P^A,P^B): the matching score between two base pairs, P^A and P^B. The score is evaluated by the isostericity between two P^A and P^B. Base pairs within the same isostericity group are considered to have similar structural contribution to the motifs, and their matching is given higher bonus score. Non-isosteric matching is also allowed, but with less bonus score.

• (A[i...j],B[k...l]): the matching score between two subsequences A[i...j] and B[k...l]. The score is evaluated through the optimal global alignment between the two subsequences.

• Gap(k): the gap penalty of inserting/deleting a sequence of length k.

• M[P^A,P^B]: the score of the optimal alignment of the regions enclosed by base pairs P^A and P^B, given that P^A and P^B are aligned to each other. Entry 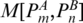records the score of the optimal alignment between two structures A and B.

All the weights and scores defined above are fixed for all searches conducted in this work.

We can compute M[P^A,P^B] for all pairs in , which would take O(m²n²) time, where m and n are the number of base pairs in A and B, respectively. While many RNA structural alignment algorithms have biquadratic time complexity in terms of sequence length, our algorithm is relatively efficient since the number of base pairs in an RNA structure is much smaller than its length in sequence. In computing M[P^A,P^B], we have two choices for matching the subsequences inside P^A and P^B, as they could either form consensus hairpin loops (the terminal case) or there are base pairs to be matched inside (nested base pairs, internal loop or multi-loop). Therefore,

(1)

Here, M_s[P^A,P^B] is the score of matching base pairs P^A and P^B based on both structure isostericity and sequence conservation, and thus can be computed by

(2)

M_h[P^A,P^B] is the score of matching the loop regions of P^A and P^B, assuming that no consensus base pair is included by P^A and P^B. (For example, these regions form matched hairpin loops.) It can be computed by

(3)

For the nested base pairs, internal-loop or multi-loop case, we need to define some additional terms. A sequence of base pairs P₁,P₂,…,P_k form a chain if 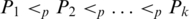. M_l[P^A,P^B] represents the matching score between P^A and P^B, given that there is a pair of chains included by P^A and P^B, which form the loop. Let 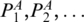(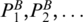, respectively) denote base pairs enclosed by P^A (P^B, respectively), and ordered according to increasing values of the last coordinate. For two base pairs P^A′, P^A that P^A′ < _IP^A, Loop(P^A) is separated into three major regions: left region, Loop(P^A′) and right region. We denote the left reg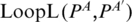ion as () and the right region as 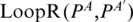(). Then, we will have

(4)

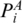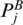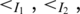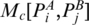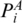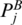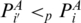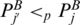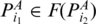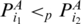To enforce the matched base pairs have the same multi-pairing pattern, we must ensure that and P^A, and P^B are in the same enclosing subgroup ( or <_I3, Figure 2). Here, is defined as the score of two chains of the optimal matching configurations that end at and , and begin at some , and . Denote if and there is no base pair 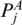such that 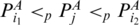. Then,

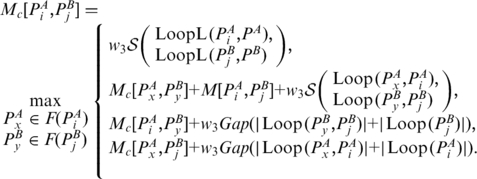(5)

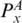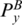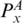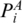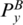The Gap means the corresponding sequences are matched to nothing (i.e. they are deleted). Similarly, to enforce the matched base pairs have the same multi-pairing constraint, we must ensure that and P^A, and P^B are in the same enclosing subgroup, and and , and 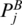are in the same juxtaposing subgroup.

P-value computation

To compute the P-value for the probability that an RNA motif hits a random substructure in the database, we used the non-parametric Chebyshev's inequality. In future research, we will optimize these parameters by fitting the distribution of the overall alignment scores between pairs of RNA structures into a Gumbel-like distribution to get more accurate P-value. To obtain the mean and variance, the query is aligned against the background segments, which are generated by randomly picking base pairs from real RNA structures while maintaining the similar GC content, as well as frequencies of the interacting edges and glycosidic bonds orientations. We applied this approach on kink-turn motif, and observed Gumbel's distribution of the alignment scores (see supplementary website, http://genome.ucf.edu/RNAMotifScan). Since each motif has its own base-pairing patterns and degree of tolerance against base-pair variations, we suggest different P-value cutoffs for different motifs based on tested results (see Table 3 for the cutoffs). Additionally, false positive rates (FPRs) are computed through simulation and available on the supplementary website (http://genome.ucf.edu/RNAMotifScan).

Table 3.

Summary of the RNAMotifScan search results against the entire PDB comparing with SCOR (40)

Motif	P-value cutoff	PDB	NR PDB	SCOR
Kink-turn	0.07	553	39	195
C-loop	0.04	167	18	–
Sarcin–ricin	0.02	633	46	107
Reverse kink-turn	0.14	56	3	–
E-loop	0.13	1356	148	37

C-loop and reverse kink-turn are not included in SCOR. Motifs characterized in SCOR were from the entire PDB released by October. 24, 2004. The non-redundant set (NR PDB) is constructed by removing entries with sequence identities >90%.

Data processing

Base-pair interactions of all RNA 3D structures from PDB (39) (released on August 2008) were first annotated by using MC-Annotate (41). RNAVIEW (42) generates similar results based on our experiments, and RNAMotifScan provides interfaces for both annotation tools. After annotation, 1445 RNA structures were generated from PDB (including incomplete RNA chains in the raw PDB file). Five RNA structural motifs were used as queries to test our method: the kink-turn, C-loop, sarcin–ricin, reverse kink-turn and E-loop motifs. Because they are well characterized, documented and important for many RNA folding behaviors or functionalities. The query base-pairing patterns for these motifs come from the following references: kink-turn (43), C-loop (14), sarcin–ricin (44), reverse kink-turn (4) and E-loop (14). The 2D diagrams for query base-pairing patterns of these motifs are shown in Figure 3. RNAMotifScan was implemented in ANSI C. All experiments were carried out on an Intel Xeon 2.66 GHz workstation. The tertiary structure figures were generated using PyMol (http://www.pymol.org).

RESULTS

To assess the performance of RNAMotifScan, we searched five RNA motifs against a 23S rRNA structure from Haloarcula marismortui (1S72, resolution 2.40 Å). We compared our results with three latest methods: FR3D (13), a de novo clustering method developed by Djelloul and Denise (19), and the shape histogram method developed by Apostolico et al. (11). Since the clustering method mainly aims at the de novo motif discovery, the method may miss some true instances. We also used RNAMotifScan to search the five motifs against the entire PDB for new motif occurrences.

Kink-turn

The kink-turn motif is an asymmetric internal loop serving as an important site for protein recognition and RNA tertiary interactions (45,46). The `kink' can be observed in the longer strand of the loop, which is stabilized by the two cross-strand stacking adenine residues. It brings together the two minor groove edges, and, consequently, produces a sharp turn of the two supporting helices (14,43).

RNAMotifScan has identified six local motifs (motifs involve two or less strands) following by one composite motif (motifs involve three or more strands) from 1S72 (Table 1). FR3D finds all these seven motifs but introducing several `related motifs' using the same query [see Table 5 of FR3D results (13)]. FR3D also retrieves two more composite motifs. (The reason is that FR3D produces target segment structure based on spacial frame instead of sequence order.) The current version of RNAMotifScan does not focus on identifying composite motifs, but this feature can be included in the future (see ‘Discussion' Section). The shape histogram method finds all the six local motifs, but missing all the composite motifs. The de novo clustering method successfully rediscovers the motif, however, it misses four out of the six local motifs and all composite motifs. The results suggest that RNAMotifScan has higher sensitivity than shape histogram method and de novo clustering method in identifying kink-turn motifs.

Table 1.

Top hits obtained by searching the five motifs against 1S72 using RNAMotifScan

Ranking	Chain	Location	Score	P-value	FR3D	de novo Clustering	Shape Histogram
Kink-turn
1	0	77-82/92-100	70.2	0.009	*	*	*
2	0	1211-1217/1146-1156	62.1	0.014	*		*
3	0	936-941/1025-1034	55.8	0.022	*	*	*
4	0	1338-1343/1311-1319	54.7	0.024	*		*
5	0	1586-1593/1601-1609	45.4	0.062	(*)		*
6	0	244-250/259-267	44.4	0.072	(*)		*
7	0	2903-2906/2845-2855	43.8	0.078	(*)
C-loop
1	0	1436-1440/1424-1430	40.9	0.033	–	*	–
2	0	2760-2764/2716-2722	39.1	0.041	–	*	–
3	0	1939-1945/1892-1898	38.4	0.044	–		–
4	0	1004-1009/957-964	34.4	0.081	–		–
Sarcin–ricin
1	0	211-215/225-228	42.8	0.007	*	*	–
2	0	1368-1372/2053-2056	42.8	0.007	*	*	–
3	0	2690-2694/2701-2704	42.8	0.007	*	*	–
4	9	76-80/102-105	42.0	0.007	*		–
5	0	461-466/475-478	37.5	0.010	*	*	–
6	0	380-383/406-408	34.4	0.013		*	–
7	0	951-955/1012-1016	33.4	0.015			–
8	0	173-177/159-162	29.8	0.022	*	*	–
9	0	2090-2094/2651-2654	26.2	0.037			–
10	0	1775-1779/1765-1768	25.5	0.042			–
11	0	1542-1545/1640-1643	21.0	0.117			–
12	0	585-590/568-572	20.8	0.126	*		–
13	0	355-360/292-296	20.8	0.126	*		–
Reverse kink-turn
1	0	1661-1666/1520-1530	48.6	0.114	–	*	–
2	0	1530-1536/1649-1661	46.8	0.145	–	*	–
E-loop
1	0	706-708/720-722	21.2	0.052	–	*
2	0	1543-1545/1640-1642	20.6	0.061	–	*
3	0	174-177/159-161	18.7	0.098	–		*
4	0	663-666/680-683	18.6	0.100	–
5	0	586-590/568-571	18.0	0.120	–		*
6	0	356-360/292-295	18.0	0.120	–		*
7	0	2691-2694/2701-2703	17.8	0.130	–		*
8	0	1369-1372/2053-2055	17.8	0.130	–		*
9	0	463-466/475-477	17.8	0.130	–		*
10	0	380-383/406-408	17.8	0.130	–		*

Symbol notations: `*' the motif occurrences are identified by the corresponding method; `(*)' motif occurrences rank below some `related motifs'; `-' the motif is not studied by the corresponding method. The bona fide motifs validated by visual inspection are indicated with bold typeface of their location. The underlined motifs are de novo found by RNAMotifScan (even they might be manually characterized before).

C-loop

The C-loop motif is an RNA–protein binding site, and characterized by the unique multi-pairings formed by its two cytosine residues (14). The two interleaving non-canonical base pairs from the two multi-pairings bring together the interacting nucleotides, leaving the unpaired adenine residue at the minor groove and fully accessible (47).

RNAMotifScan has identified three C-loop motifs in 1S72 (Table 1). The de novo clustering method can also classify the first two C-loop motifs. (FR3D and shape histogram methods were not used to search C-loop motifs. Because it is difficult for these 3D structure-based methods to identify motifs that are small and usually exhibit high structural variations, such as C-loops.) The first two C-loop motifs exhibit high conservation comparing to the query motif (isomorphic as defined in the de novo clustering method), such that they can be easily detected by the de novo clustering method. The fourth C-loop motif [supported by (43)] has one nucleotide inserted between the two multi-paired cytosine residues. Therefore, it cannot be found by the de novo clustering method but still can be detected by RNAMotifScan in which insertions (deletions) are taken into account. The results suggest that RNAMotifScan has higher sensitivity than the de novo clustering method. At the same time, we expect that our specificity can also be raised by carefully distinguishing the effects of different variations (see ‘Discussion' Section).

Sarcin–ricin

The sarcin–ricin motif in the ribosomal RNAs is involved in the interaction with elongation factors (48). This interaction can be inhibited while the motif is bounded and modified by ribotoxins such as α-sarcin (ribonuclease) and ricin (RNA N-glycosidase) (49). The base-pairing pattern is highly conserved in 23S–28S rRNA from large ribosomal subunit, producing an `S' shape bend in most of the sarcin–ricin motifs.

RNAMotifScan has identified nine known sarcin–ricin motifs, whereas eight were identified by FR3D and six were classified by the de novo clustering method. RNAMotifScan identified one new sarcin–ricin motif, which was also observed by St-Onge et al. (50). Three other motifs found by RNAMotifScan rank at low places in the results, showing a satisfactory specificity for our method (Table 1). Even though these instances show higher structural variation from the query structure, we suggest that they should be further inspected as they show interesting conservations in base-pairing pattern comparing to the known sarcin–ricin motifs.

Reverse kink-turn

The reverse kink-turn is also an asymmetric internal loop that produces sharp bend as the kink-turn motif, however, towards the opposite direction (4). Another difference is that the longer strand of the kink-turn motif makes a tight bend, while in the reverse kink-turn motif, the tight bend is observed in the shorter strand as the longer strand gradually turns to the major/deep groove (51).

The de novo clustering method suggests six reverse kink-turn occurrences. (FR3D and shape histogram method were not used to search reverse kink-turn motifs either.) We noticed that three of these six motifs given by clustering are false positives (2397–2399/2389–2391, 2307–2310/2298–2300 and 1132–1134/1228–1230), as they either come from the irregular pairing regions near hairpin loop regions instead of being the junction regions between two helical regions, or do not produce significant sharp turns. RNAMotifScan has identified two of the three true reverse kink-turn motifs (Table 1). The one motif missed is due to its higher structural variation. Even though RNAMotifScan may miss several occurrences, it has much higher specificity and thus more reliable is practical applications.

E-loop

The E-loop was originally defined as the symmetric internal loop region in the 5S rRNA that separates its helical regions IV and V (52,53). The motif can be decomposed into two isosteric submotifs, which are positioned with relative 180° rotation (44,53). The submotif is usually referred to as `bacterial E-loop', and its base-pairing pattern was summarized as a trans H/SE base pair, a trans WC/H or trans SE/H base pair, and a cis bifurcated or trans SE/H base pair by Leontis et al. (44). Since the isostericity related with bifurcated base pair is not defined, we consider only the trans SE/H as the third base pair in the query.

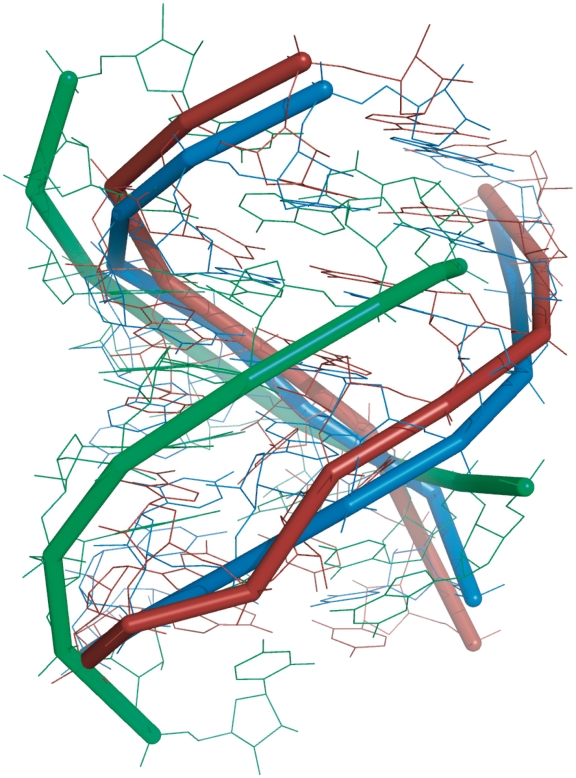
There are two E-loop motifs classified by the de novo clustering method and eight identified by the shape histogram method. The two sets of results show no overlap and the union of them gives totally 10 E-loop motifs. RNAMotifScan has successfully identified nine of them (Table 1), and one new E-loop occurrence. This new E-loop occurrence, as well as a segment of regular A-form helix, are superimposed with a well characterized E-loop motif (Figure 4). The superimposition of the new E-loop instance results much smaller RMSD than the superimposition of the A-form helix, indicating that this E-loop occurrence cannot be expected to find randomly. RNAMotifScan has missed one E-loop motif that has both high sequence and base-pairing variations. Note that E-loop motifs can tolerate higher variations comparing to other motifs. [They were clustered into three families using the de novo clustering method (19).] Therefore, the results generated by searching only one of its variants could be limited. However, RNAMotifScan outperforms both methods when given only one query, and the E-loop identification can be further optimized by including other variants of E-loop motifs as query.

Figure 4.

The superimposition of the new E-loop motif found by RNAMoitfScan (red, 1S72, chain `0', 662–669/677–684), a segment of regular A-form helix (green, 1S72, chain `0', 13–20/523–530), and a well characterized E-loop motif (blue, 1S72, chain `0', 1639–1646/1539–1546). The RMSD resulting from superimposing the new motif (red) and the model (blue) is 2.496 Å; while the RMSD for superimposing the regular A-form helix (green) and the model (blue) is 4.807 Å.

3D Resolution affects identification accuracy

We observe that the identification results of RNAMotifScan is dependent on the quality of the annotation program, which turns out to be dependent on the resolution of the 3D RNA structure. To demonstrate this, we selected three PDB entries with different resolutions for the same 16S rRNA structure from Thermus thermophilus (PDBid: 2VQE, 1J5E and 1I95), and used RNAMotifScan to identify the five motifs in them. Only hits with P-value less than the defined cutoffs (Table 3) are counted. Since the RNA structure from 2VQE contains three RNA chains, while the other two structures contain only one RNA chain, we only consider their common RNA chain (chain A in the comparison). The results are shown in Table 2. In Table 2, we can find that MC-Annotate tends to annotate fewer base pairs in the low-resolution RNA structures. Among those missed base pairs, most of them are non-canonical base pairs, which are critical for the structural motif identification. Even if the numbers of annotated base pairs are comparable for two structures with different resolutions, their qualities differ. For example, 2VQE and 1J5E have almost the same number of annotated base pairs, but one kink-turn that can be identified in 2VQE is missed in 1J5E.

Table 2.

The performance of RNAMotifScan with different resolutions of RNA structures

PDB ID	Resolution	Length	#bp	#Can. bp	#Non-can. bp	#KT	#CL	#SR	#RK	#EL
2VQE	2.50 Å	1522	766	433	333	3	0	2	0	6
1J5E	3.05 Å	1522	761	434	327	2	0	2	0	6
1I95	4.50 Å	1514	699	422	277	1	0	0	0	3

The columns in the tables represent PDB codes of the RNA structures, the resolution, the length, the number of base pairs (bp) annotated by MC-Annotate, the number of annotated canonical base pairs (Can. bp), the number of annotated non-canonical base pairs (Non-can. bp), the number of kink-turn (KT), C-loop (CL), sarcin–ricin (SR), reverse kink-turn (RK) and E-loop (EL) being identified. All structures are Thermus thermophilus 16S rRNA structures. The P-value cutoffs are the same as those shown in Table 3.

Scanning PDB

Finally, we searched the entire PDB for the five query motifs. The running time for scanning PDB is 64 m35s for kink-turn, 74 m29s for C-loop, 51m49s for sarcin–ricin, 77 m59s for reverse kink-turn and 72 m55s for E-loop motif. The results are summarized in Table 3. The motifs identified by RNAMotifScan are several times more than the current known instances (P-value cutoffs are shown in Table 3, the estimated FPR is <0.01). Still, we expect the numbers are underestimated since our cutoffs are set to be rather stringent. Although the large difference between the identified motifs and the currently known ones may due to the fast growing of RNA structures deposited in PDB, we still find new RNA motif occurrences in non-ribosomal RNAs, such as riboswitches, ribozymes and protein–mRNA complexes. The complete results can be found at the supplementary website http://genome.ucf.edu/RNAMotif Scan.

To demonstrate the advantages of RNAMotifScan, we compared five query motifs (Figure 3) with five different newly identified motifs (Figure 5). For C-loop motif, we observed that the sequence identity is 66% between the C-loop query (Figure 3b) and the new identified C-loop motif (Figure 5b), which sequence-based search methods may miss. The sarcin–ricin motif (Figure 3c) and the E-loop motif (Figure 3e) consist of all non-canonical base pairs, such that they cannot be searched by methods that are restricted to canonical base pairs. The newly identified sarcin–ricin motif and E-loop motifs also have three isosteric base-pairing changes (Figure 5c and e). The newly identified kink-turn motif (Figure 5a) shows two base-pairing variations (trans SE-H to cis SE-SE, and trans SE-H to cis WC-WC), which would be missed by the strict base-pairing graph isomorphism search. More importantly, we found that the newly identified kink-turn (Figure 5a) and reverse kink-turn motifs (Figure 5d) show structural variations comparing to the query motifs. One nucleotide is inserted at the `kink' region of the newly identified kink-turn motif, resulting an `U' shape `kink' rather than the `V' shape `kink' in the query (Figure 6a). For the newly identified reverse kink-turn motif, the structural variation is observed at the longer strand of its junction between two helices. Two nucleotides are inserted at this region, relaxing the turn significantly (Figure 5d). At the same time, a sharp bend is created at this region (Figure 6b), in order to accommodate the insertions and maintain the proper structure of the motif.

Figure 5.

The 2D diagrams and 3D structures of newly identified motifs with sequence or base-pairing variations. (a) Kink-turn motif from 23S rRNA in H. marismortui (PDBid: 1QVF, chain `0', location 936–941/1025–1034). (b) C-loop motif from 5.8S/28S rRNA in Saccharomyces cerevisiae (PDBid: 1S1I, chain `3', location 1436–1440/1424–1430). (c) Sarcin–ricin motif from 16S rRNA in Escherichia coli (PDBid: 1VS7, chain A, location 888–892/906–909). (d) Reverse kink-turn motif from 23S rRNA in H. marismortui (PDBid: 1QVF, chain `0', location 1661–1666/1520–1530). (e) E-loop motif from 23S rRNA in S. oleracea (PDBid: 3BBO, chain A, location 1392–1394/1379–1381).

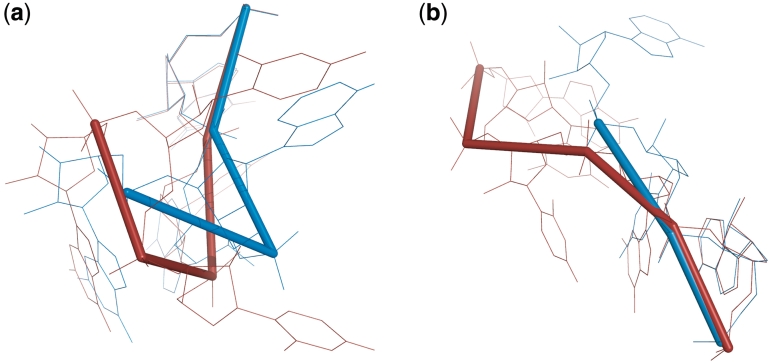
Figure 6.

The Superimposition between the newly identified motifs (red) and the queries (blue) at the regions where nucleotide insertion(s) are observed. (a) The `kink' regions in kink-turn motifs (red structure: 1QVF, chain `0', 1027–1031; blue structure: 1S72, chain `0', 94–97). (b) The longer strands at the junctions between helices in reverse kink-turn motif (red structure: 1QVF, chain `0', 1522–1526; blue structure: 1ZZN, chain B, 198–200).

DISCUSSION

The base pairs from the RNA 3D structures are extracted and classified by various annotation tools. The annotations of base pairs are produced based on the geometric constraints among atoms involving the hydrogen bond interactions. In another word, the accurate coordinates of atoms are critical for the classification of base pairs. Therefore, the quality of annotation results, and consequently the accuracy of RNAMotifScan, depends largely on the resolution of the RNA 3D structure (Table 2). We anticipate that with the advances of RNA structure determination techniques, more and more high-quality data can be produced and the RNA motif identification can be more reliable.

It is mentioned that FR3D is capable of discovering composite motifs, while RNAMotifScan mainly focuses on local motifs. However, RNAMotifScan can be easily extended to include RNA composite motifs. If the motif consists of n strands, there are in total n! combinations of orders that these strands can be concatenated. Theoretically, it is possible to include any number of strands with the compensation of running time. In practice, there is only a small number of strands in RNA structural motifs. Therefore, it is feasible to enumerate all possible strand concatenations. We plan to include this feature in the future versions of RNAMotifScan.

Currently, RNAMotifScan uses a scoring function that does not distinguish substitutions between different isosteric groups. Recently, Stombaugh et al. (54) studied the frequencies of non-canonical base pair substitution among different isosteric groups and proposed a more sophisticated scoring function. We plan to incorporate such scoring function into our method. Moreover, the scoring function should also be position dependent (similar as the position-specific scoring matrix). For example, the determination of C-loop motif relies on the two multi-paired cytosine residues. We should assign heavy penalty to the mutations on these nucleotides. Similarly, for E-loop motifs, we should give heavy weight to the conserved trans H/SE base pair according to the E-loop motif definition. With the incorporation of more sophisticated base pair substitution scoring function and position-dependent weights, we anticipate that RNAMotifScan will become much more accurate in identifying RNA structural motifs.

FUNDING

C.Z. and S.Z. are funded in part by the University of Central Florida In-House Research Grant (1048479). H.T. is funded in part by the METACyt Initiative at Indiana University (funded by Lilly Endowment, Inc.). Funding for open access charge: METACyt Initiative at Indiana University (funded by Lilly Endowment, Inc.).

Conflict of interest statement. None declared.