Abstract
Spiking in primary motor cortex (MI) exhibits a characteristic beta frequency periodicity, but the functional relevance of this rhythmic firing is controversial. We simultaneously recorded multiple single units and local field potentials in MI in two monkeys (Macaca mulatta) during continuous, self-paced movements to serially presented targets. We find that the appearance of each new target evokes precisely timed spiking in MI at a characteristic latency but that the exact timing of this response varies depending on its relationship to the phase of the ongoing beta range oscillation. As a result of this interaction between evoked spiking and endogenous beta periodicity, we find that the amount of information about target location encoded in the spiking of MI neurons is not simply a function of elapsed time but depends also on oscillatory phase. Our results suggest that periodicity may be an important feature of the early stages of sensorimotor processing in the cortical motor system.
Introduction
In primary motor cortex (MI), oscillations in the beta (10–45 Hz) frequency range are commonly observed in local field potential (LFP) recordings (Murthy and Fetz, 1992; Sanes and Donoghue, 1993). These oscillations reflect concurrent variations in the polarization of large numbers of individual neurons (Fetz et al., 2000), and as a result, the phase of the beta-LFP is often correlated with the probability of single-unit spiking. Although the existence of this phenomenon has been known for some time (Murthy and Fetz, 1992, 1996; Donoghue et al., 1998), its functional relevance has been the subject of debate. Beta range rhythmicity in spiking has been proposed to play a role in corticomuscular output (Baker et al., 1999; Schoffelen et al., 2005), proprioceptive feedback (Riddle and Baker, 2005; Baker et al., 2006; Baker, 2007), sensorimotor attention (Murthy and Fetz, 1992; Sanes and Donoghue, 1993), or no functional role at all (Pfurtscheller, 1992).
The interaction between incoming sensory information and endogenous rhythms has been extensively studied in the insect olfactory system (Stopfer et al., 1997; MacLeod et al., 1998). Fewer studies have examined the interaction between endogenous periodicity and evoked spiking in mammalian cortex. In primate visual cortex, Fries et al. (2001) found that the latency of fast cortical responses to visual cues depended on the timing of stimuli with respect to the phase of ongoing gamma oscillations. Schroeder and colleagues (Lakatos et al., 2007) have found that the phase of ongoing oscillations in primate auditory cortex are quickly reset by salient somatosensory stimuli and that, as a result, responses to simultaneously presented auditory cues are enhanced. Modulation of sensory responses by phase-locked cortical oscillations may be a more general phenomenon in the processing of early sensory information (Lakatos et al., 2008; Schroeder and Lakatos, 2009).
We recorded multiple single units and local field potentials from MI in monkeys while they generated continuous trajectories between serially presented random targets. We found that the appearance of each new target quickly reset the phase of the ongoing beta oscillation in MI and, in a subset of MI neurons, produced a volley of precisely timed spikes after the phase-resetting that were informative about the new target location. We found that the exact timing of this precise spiking response depended on the phase of the ongoing periodic activity in MI and that, by accounting for slight target-to-target differences in the time course of the phase-locked beta oscillation, the variability in evoked spike times was reduced. As a consequence of this interaction with phase, we show that the information about target direction encoded in MI single-unit spiking is not simply a function of elapsed time after a target event but also of the postevent phase progression of the beta oscillation in MI. Our results indicate that an area downstream from MI could potentially access more information if its own oscillations were coherent with the upstream oscillations and similarly reset by the target appearance, and suggest that early sensorimotor processing may occur periodically, rather than continuously, in primary motor cortex.
Materials and Methods
Behavioral task.
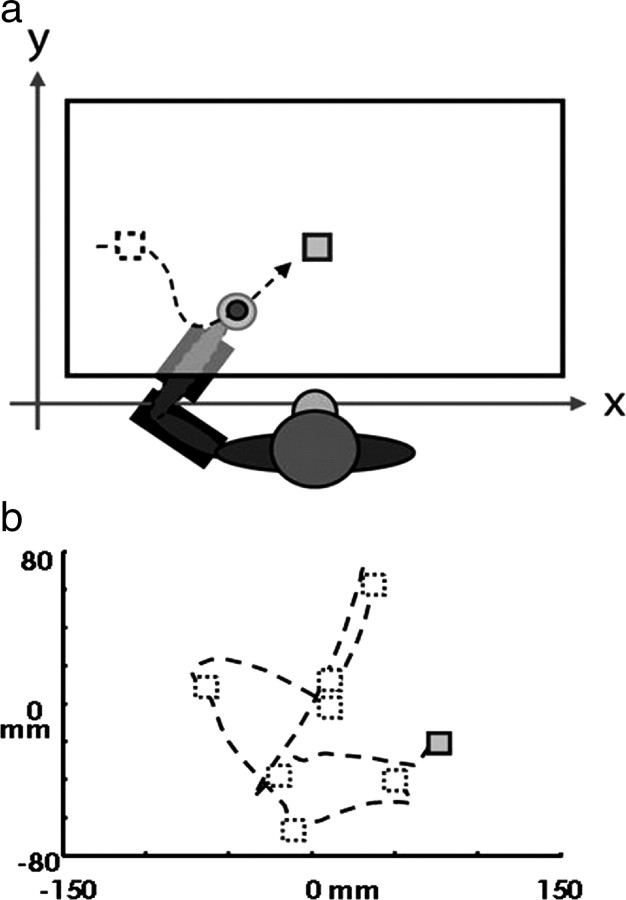
Two monkeys (Macaca mulatta) were trained to perform a visuomotor task using a two-link robotic exoskeleton (KINARM) (Scott, 1999). During the task, the monkey's arm rested in a manipulandum below a horizontal screen that displayed a target (10 mm square) and a cursor aligned to the position of the monkey's hand (5 mm diameter circle). The monkey was required to move the cursor (hand) to the position of the target (see Fig. 1a). Each successful target acquisition caused the current target to be extinguished and a new target to be immediately presented at a random location within a limited workspace; thus, we call this task random target pursuit (RTP). The monkeys received a juice reward after completing a successful trial of five to seven consecutive targets (see Fig. 1b). In general, the animals generated continuous trajectories over many minutes, acquiring hundreds or thousands of targets without pausing or removing their arm from the KINARM. Over a typical hour-long recording session, each monkey acquired several thousand targets.
Figure 1.
Behavioral task. a, The monkey's arm rests in a two-link robotic manipulandum below a horizontal screen. The task involves moving a cursor (filled circle) aligned to the position of his hand to the target (squares). Acquisition of each target results in the immediate appearance of a new target at a random location in the workspace (the previous target location and movement trajectory are shown with dotted lines in the figure but are not visible in the task). Arm movements are constrained in two dimensions by the manipulandum, and the position of the monkey's hand is sampled at 500 Hz. b, The monkey generates a continuous trajectory through sequential targets, receiving a juice reward every five to seven targets, and hitting several thousand targets in a typical recording session. [This figure was adapted from the study by Tkach et al. (2007).]
Data collection.
Neural data were collected using 100-electrode “Utah” microelectrode arrays (Blackrock Microsystems; 1 mm length, 400 μm interelectrode spacing) implanted in primary motor cortex in two monkeys contralateral to the relevant arm. Signals from up to 96 electrodes from each array were amplified (gain of 5000) and bandpass filtered between 0.3 Hz and 7.5 kHz. Neural spikes identified by threshold crossings were recorded as 1.6 ms segments sampled at 30 kHz per channel and stored digitally (14 bit) using a Cerebus acquisition system (Blackrock Microsystems). Spike waveforms were sorted off-line using a semiautomated method developed in our lab incorporating some elements of a previously published algorithm (Vargas-Irwin and Donoghue, 2007). Signal-to-noise (SNR) ratios for each unit were defined as the difference in mean peak-to-trough voltage divided by twice the mean SD over all spikes at each of the 48 sample time points of the waveform. We discarded units with <100 spikes over the entire recording session or SNR <3. A total of nine data sets (five data sets for animal Mk, and four data sets for animal Rs) were analyzed. Two of the four Rs data sets included a number of conditions in which a viscous load was applied to the arm during execution of the task. In every other respect, the task was the same, and we treated these data sets the same as the others. Although we analyzed 839 neuronal spike trains, this number may be an overestimate of the actual number of distinct neurons if any of the same neurons were recorded on different days from the same electrodes on each array. Our own analysis suggests that over a 2 week period, a little more than one-quarter of neurons can be reliably identified as the same cells (Dickey et al., 2009). The length of time between recordings for monkey Rs ranged from 1 to 5 months, and for monkey Mk, from 4 d to 3 months.
LFP signals on each channel were recorded continuously at 1 kHz, amplified using a gain of 5000, and bandpass filtered from 0.30 to 250 Hz or 0.30 to 500 Hz. The SD of the LFP signal on each channel was calculated over the entire recording session, to identify outlier channels containing significant noise. These channels were excluded from the phase-locking analysis described below. LFPs were bandpass filtered (bidirectionally to avoid phase distortion) in the beta frequency range between 10 and 45 Hz using an eighth-order Butterworth filter.
Spectra, spectrograms, and phase locking.
Preevent and postevent 1–55 Hz spectra were computed over the 400 ms periods before and after the target appearance (Hamming window) and averaged over all targets. Perievent 1–55 Hz spectrograms were computed over a 128 ms Hamming window stepped by 10 ms over the −500 to 500 ms perievent period and then averaged across all targets. The instantaneous phase of the beta-LFP was calculated using the discrete Hilbert transform (MATLAB Signal Processing Toolbox), and segments of the resulting phase series were aligned on target appearances. The result was a series of phase distributions collected across targets at each millisecond from 200 ms before to 500 ms after the target event. We calculated the percentage phase locking (PPL), which we define as follows: [1 − (H(θt)/Hmax)]*100, where H(θt) is the entropy [−Σxp(x)log(p(x))] of the binned phase distribution at peritarget time t (10 phase bins, millisecond resolution), and Hmax is the maximum possible entropy (representing a uniform distribution across all phase bins) (Rubino et al., 2006). The PPL was then averaged over channels and data sets for each monkey. The relatively larger offset evident in the monkey Mk traces (see Fig. 2h) reflects the smaller number of channels/trials contributing to this average compared with monkey Rs.
Figure 2.
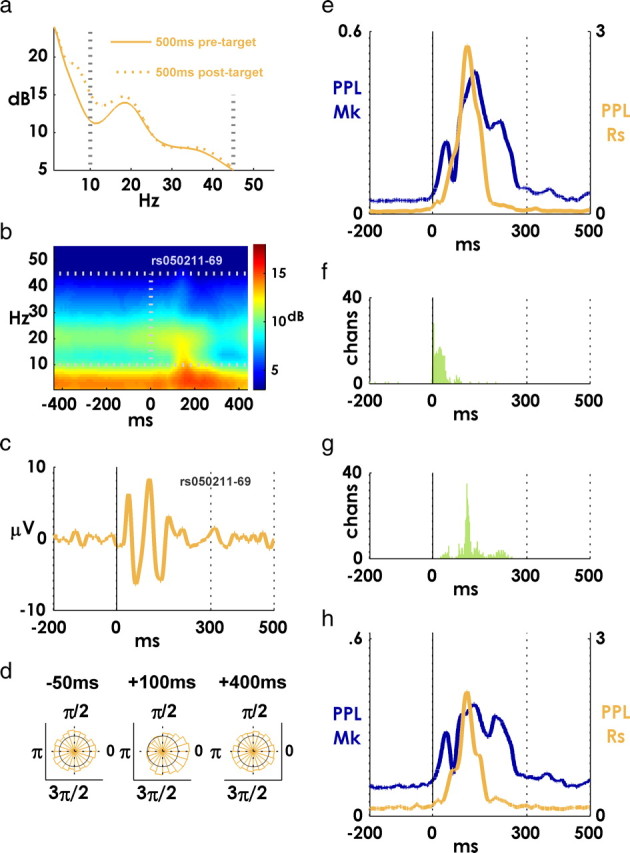
Phase-locking of beta-LFP to target appearance. a, Mean spectrum over all channels for monkey Rs. The solid line is spectrum for 400 ms preevent period, and the dotted line is the spectrum for the 400 ms postevent period. A 10–45 Hz window is indicated with vertical dotted lines. A “beta bump” in the spectrum is visible around 20 Hz. b, Perievent spectrogram for a single beta-LFP channel computed using a 128 ms Hamming window at 10 ms steps. Robust beta activity is visible throughout the perievent period. c, Mean peritarget beta-LFP for the channel in b. d, Phase distributions over all targets for the same channel in c at three perievent latencies. e, Mean PPL averaged over all channels and sessions for each monkey (blue trace and left y-axis, monkey Mk; orange trace and right y-axis, monkey Rs). The higher values indicate that the phase distribution across targets is less uniform. f, Histogram of onset latencies of phase locking (significant elevation of PPL above pretarget baseline, p < 0.001) for all channels for both monkeys. g, Histogram of PPL peak latencies for all channels for both monkeys. h, Mean PPL values over a subset of targets where the mean oscillatory amplitude stayed the same or decreased after the target appearance. The axes are the same as in e.
Precise spiking.
Perievent histograms were constructed by binning spikes in 1 ms bins from 0 to 300 ms after each target event, and averaging over all events. Perievent histograms in Figure 3a were normalized by the peak rate observed in the 0–300 ms period and smoothed with a ±4 ms boxcar filter (running mean). Example peristimulus time histograms (PSTHs) were smoothed with ±1 ms boxcar filter.
Figure 3.
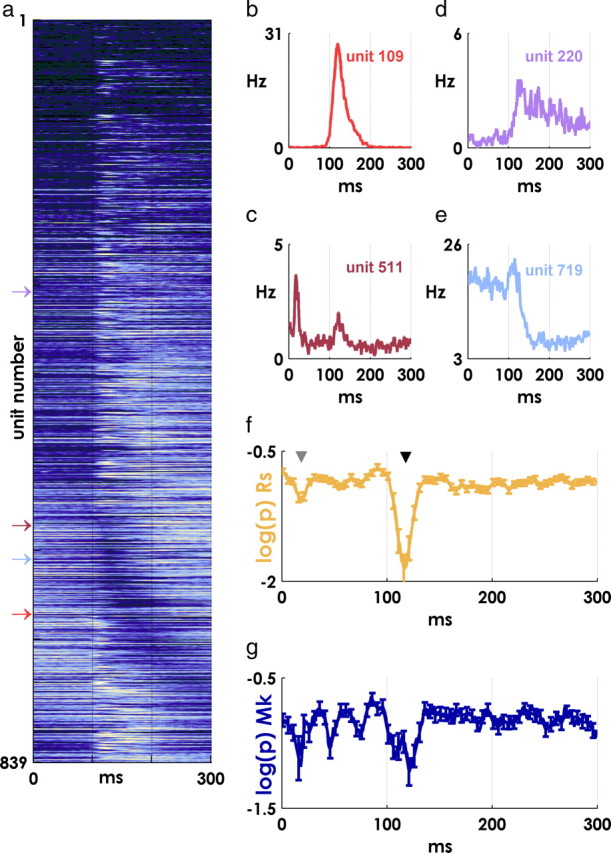
Event-related spiking. a, Mean PSTHs for all units from 0 to 300 ms after target appearance. The lighter colors indicate more activity, and the darker colors represent less firing; all PSTHs are normalized by the peak value for each unit. Units are ordered by the latency of their minimum perievent firing rate for visualization purposes. Many units display an abrupt modulation in firing at ∼100 ms after the event. b–e, Example PSTHs for four units showing the diversity of responses. The position of each unit in a is indicated by an arrow. f, Spiking precision transiently increases at characteristic latencies. Lower log(p) values at a particular latency indicate that there are more precisely timed spikes than would be expected given the background firing rate for a unit (monkey Rs; mean ± SE over all units). Two transient periods of precise spiking are visible at latencies near 15 ms (gray arrowhead) and 120 ms (black arrowhead) after the target event. g, Same result as in f for monkey Mk.
To determine the precision of neural spiking with respect to target events, we used a spike-resampling (“jitter”) method (Hatsopoulos et al., 2003; Harrison and Geman, 2009). This method provides a nonparametric test of the likelihood of observing spikes within a small window around a particular postevent latency, given the spiking within a larger surrounding window. In principle, the null distribution for this test could be constructed for each unit and latency by repeatedly jittering spike times within a larger jitter window (thus preserving the overall spike count) and assessing the number of resulting precise spikes (spikes occurring within a smaller “synchrony” window). However, we were grateful to be able to use a fast algorithm (and associated code) courtesy of Matthew Harrison (Pittsburgh, PA) (Hatsopoulos et al., 2003; Harrison and Geman, 2009) that analytically computes the expected distribution of precise spike counts after an infinite number of repetitions of the above jittering procedure. Our choice of parameters (in this case, ±5 ms precision window, 25 ms jitter window) defines a priori what we mean by a “precise” timescale. As a result, we were not strictly interested in hypothesis testing per se, but rather in the relative degree of precise firing reflected in variations in the p value of the test. Mean log(p) values in Figure 3f were smoothed with a ±1 ms boxcar filter.
Mutual information.
The mutual information between two variables represents the reduction in uncertainty in one variable, given knowledge of the other. More formally, mutual information between a neural signal S and a kinematic signal K is defined as follows: I(S;K) = H(K) − H(K|S), where H(X) is the entropy [−Σxp(x)log(p(x))] (Paninski et al., 2004; Cover et al., 2006). We calculated the mutual information between the distribution of binned spike counts and the direction of the vector between the acquired target and the simultaneously appearing new target (5 ms time bin stepped at 1 ms resolution over perievent latencies from −200 to 300 ms, 16 equally spaced direction bins). The empirical (i.e., unfitted) joint distribution of binned spike counts and direction counts was used in the calculation of conditional entropy H(K|S). All information traces were smoothed with a ±2 ms boxcar filter. We compensated for potential biases in information values caused by binning or sampling errors by subtracting the mean information calculated with respect to shuffled kinematic data (Treves and Panzeri, 1995; Paninski et al., 2004). We used the mean value calculated over 10 shuffles of the data, which we found was sufficient since the variance between shuffles was typically small compared with the mean (bias) of the result. Furthermore, in all the analyses described here, we estimated the bias separately at each time point (−200 to +300 ms), and so any errors in our estimate were independent from point to point (and from unit to unit). The extent of residual bias not eliminated by this shuffling procedure is likely attributable to sampling errors for cells with very few spikes and is visible as the small, constant elevation above zero in the preevent period in Figure 5.
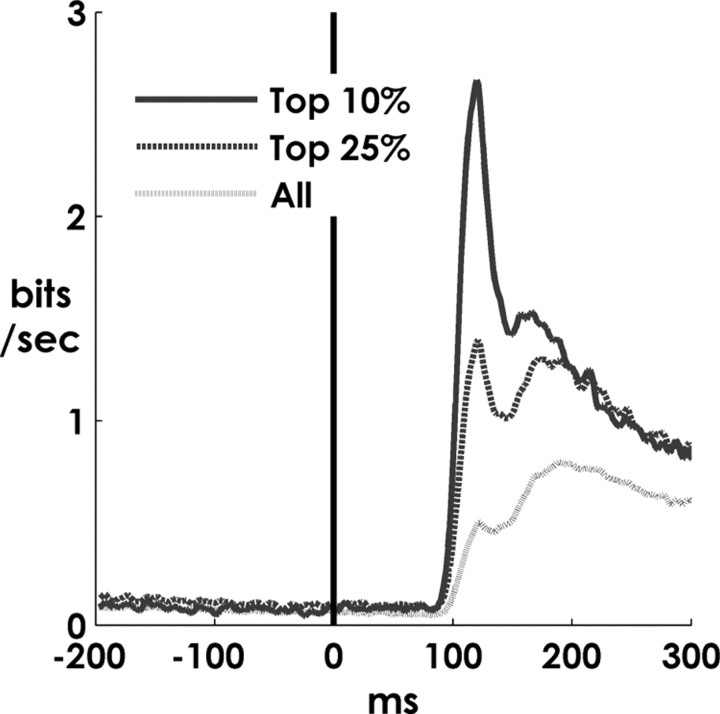
Figure 5.
Information content of perievent spiking. Mutual information between 5-ms-binned spike counts and target direction (the Cartesian direction from the location of the previous target to the location of the new target) (see Materials and Methods). The solid line is the mean information obtained from the spiking of the 10% of units that were most the precisely firing. The dashed line is mean over the 25% of units that were most precise. The gray line is mean over all units.
Oscillation and spiking latency.
The latency of the phase-locked oscillation after each target appearance on a single channel was defined by first locating the peak in the mean beta evoked potential closest to 100 ms after the event. The location of this peak defined a reference, and the latency of the beta-LFP after each target appearance was defined as the difference in the timing of the closest peak to this reference. For example, if the reference peak for a particular channel was located at 120 ms and the closest peak in the beta-LFP after a particular target occurred at 108 ms, the latency for that target would be −12 ms.
In the example in Figure 6d, the “early” and “late” perievent histograms are smoothed with a ±3 ms boxcar filter.
Figure 6.
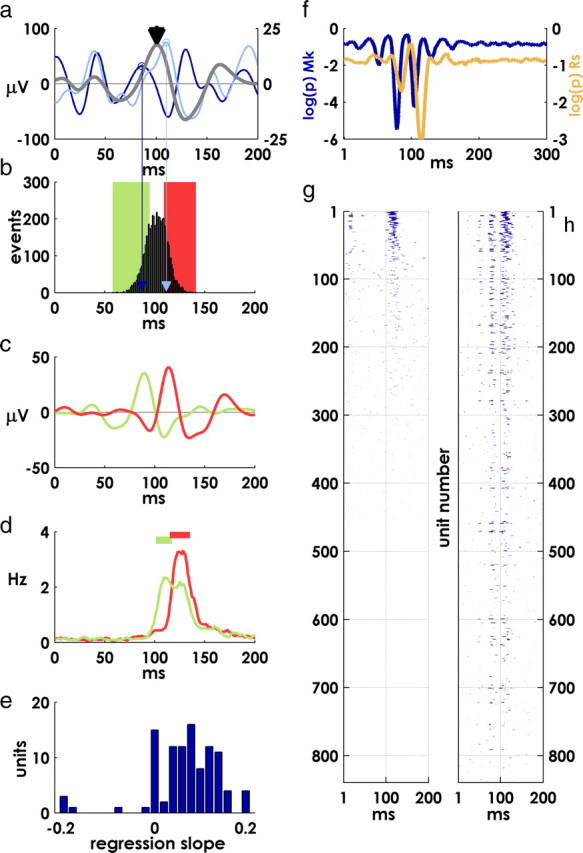
Covariation of oscillation and spike latencies and spiking precision. a, Single-channel mean beta-LFP (right y-axis, gray trace) and two examples from individual targets (left y-axis, colored traces). b, Distribution of characteristic oscillation peak times over all targets for the channel in a. Characteristic peaks are identified by proximity to the reference peak in mean LFP near 100 ms (black arrowhead in a; colored arrows indicate peak locations for single-target example traces in a). The green and red bars represent the lower and upper quartiles of the distribution. c, Averaging over the lower and upper quartiles produces an early and late mean evoked potential. d, Mean postevent firing of a unit recorded on the same electrode as the oscillation in a–c. The green and red traces are average spike rates for that unit over the lower and upper quartiles of oscillation latencies, respectively. Periods of precise spiking (p < 5 × 10−4) are indicated by horizontal lines. The latency of precise spiking mirrors the latency of the oscillation. e, Regression slopes between spike times and oscillation latencies (see Materials and Methods)—histogram of significant regression coefficients (p < 0.05). f, Subtracting LFP relative latencies from spike latencies on the same channel increases the apparent precision of postevent spiking. Log p values for each monkey after adjusting spike times by the latency of the phase-locked oscillation on the same electrode (compare with Fig. 3f,g, noting difference in scale). g, Incidence of precise spiking; mean p values for all units, thresholded at p < 0.01 before adjusting spike times. h, Thresholded mean precision of spiking as in g, after adjusting spike times as in f.
In the regression between spike and oscillation latencies (see Fig. 6e), we considered spikes between 100 and 150 ms after the target event that also fell within periods of significantly precise spiking (p < 0.05) defined by the jitter method; the median latency of these spikes defined the latency of precise spiking for each target appearance. For each unit, we then regressed these spike latencies against the latencies of the phase-locked oscillation recorded on the same electrode. We used a less stringent criteria for precise spiking (±10 ms synchrony window and a 50 ms jitter window) in this analysis. This larger window allowed more variability in spike times within still significantly precise periods. Without this increased variability, a regression analysis would have been impossible, since median precise spikes would have all been constrained within an extremely narrow temporal window (compare the brevity of periods of precise spiking identified using the 5 ms/25 ms criteria in supplemental Fig. 2, available at www.jneurosci.org as supplemental material).
For each unit, we adjusted the timing of postevent spikes by subtracting the latency of the phase-locked oscillation recorded on the same electrode from the spike latencies after each target event. We then reran the above precision analysis on the adjusted spike times.
Phase-binned spikes.
In a typical peristimulus time histogram, spikes are binned in fixed time bins at various latencies with respect to a reference event. We performed a similar procedure, but instead of aligning the histogram on the target appearance, we aligned the histograms on a characteristic peak in the phase-locked beta oscillation, and instead of binning spikes in fixed time bins, we binned spikes in phase bins defined by the phase progression of the beta-LFP (supplemental Fig. 3, available at www.jneurosci.org as supplemental material).
For each target, the location of the central “zero” bin was defined by the postevent peak located closest to the reference peak in the mean near 100 ms (the same landmark used in the calculation of oscillation latencies described above). Moving forwards along the unwrapped Hilbert phase series from this point, we binned all spikes that occurred within a π/8 radian phase advance in bin 1, all spikes between a π/8 to π/4 radian phase advance in bin 2, and so on—and the same in the reverse direction.
We calculated the mutual information between phase-binned spikes and target direction as with the information PSTH above. As a control, we also binned spikes after each target using the postevent phase series from a different, randomly chosen target appearance (10 shuffles). In Figure 7, a, b, e, and f, the unshuffled traces were smoothed with a ±1 bin boxcar filter.
Figure 7.
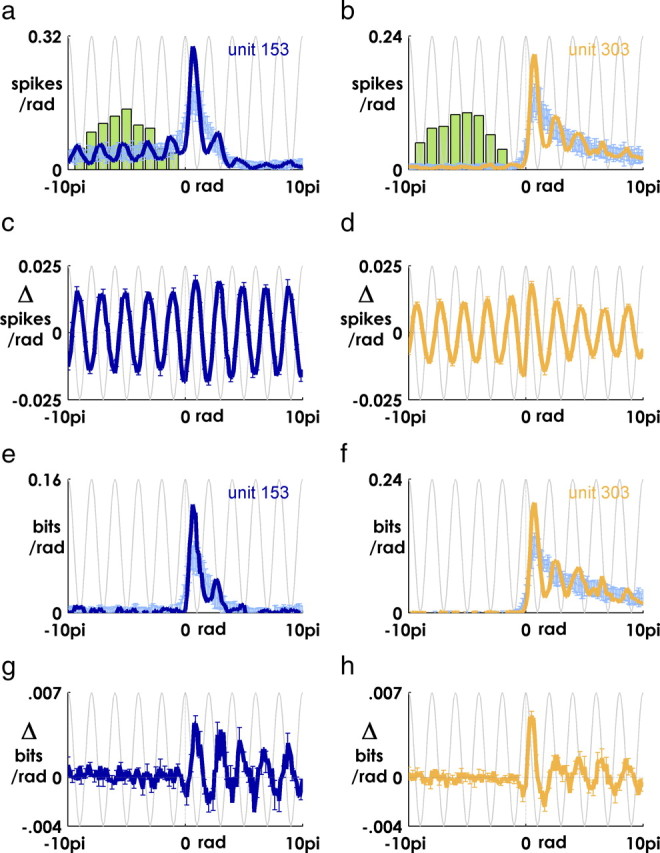
Information in phase-binned spikes is augmented at particular phases of the oscillation. a, b, Mean (over all targets) of phase-binned spike counts for one unit from monkey Mk (a, dark blue trace) and Rs (b, orange trace). Spike counts calculated from shuffled controls are in light blue (see Materials and Methods) (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). Error bars are mean ± 2SD over 10 shuffles. The green histogram is distribution of target events. The light gray sinusoidal curve is the cosine of the phase of the oscillation. c, d, Mean difference between shuffled and unshuffled spike counts for each monkey (mean ± 2SD). e, f, Same as a and b, but y-axis is mutual information with respect to target direction (see Materials and Methods). g, h, Same as c and d, but y-axis is the difference in information between phase-binned spikes and shuffled control.
Classifying cells by waveform shape and interspike interval.
We defined spike waveform width as the time between the peak and trough of the mean spike waveform for each unit. Based on the observed distribution of spike widths, we classified waveforms as “narrow” if they were ≤0.35 ms wide and “wide” otherwise. A small number of cells with waveforms <0.13 ms or >0.6 ms were discarded. We also classified cells based on their interspike interval (ISI) distribution. A cell was defined as having a bursting component based on the ratio of ISIs <9 ms to ISIs between 10 and 200 ms. If this ratio fell in the top quartile of the distribution of all units for each monkey (≥0.0897), the unit was classified as having a “bursting” component. If this ratio was in the bottom quartile (≤0.0309), a unit was classified as “nonbursting.” The remaining cells in the interquartile range were classified as “other.”
Results
The two monkeys in this study performed a random pursuit tracking task, generating continuous arm movements to acquire thousands of serially presented random targets in each recording session (Fig. 1) (see Materials and Methods). The acquisition of one target immediately triggered the presentation of the next target. There was no imposed “set” or “hold” period, and the monkeys typically initiated their reach to the new target within 250–300 ms (supplemental Fig. 4, available at www.jneurosci.org as supplemental material).
Event-locked beta oscillation
Primary motor cortex local field potentials contained a characteristic oscillatory mode within the 10–45 Hz beta range; these oscillations varied in magnitude around target events but remained prominent throughout the perievent period (Fig. 2a,b). We have shown previously that beta oscillations are phase-locked to the appearance of instructive visual targets during a stationary set period in a “center-out” task (O'Leary and Hatsopoulos, 2006; Rubino et al., 2006), and target-triggered averages revealed that MI beta oscillations were also locked to target events during the self-paced, continuous movements generated in the RTP task (mean beta-filtered LFP for a representative channel averaged across targets) (Fig. 2c).
To quantify the timing and extent of phase locking, we examined the distribution of beta-LFP phases across targets at perievent times from 200 ms before the target appearance to 500 ms after the event (phase distributions across all targets at three perievent times for the same channel in Fig. 2c,d). Within the 300 ms period after the appearance of the target, the entropy of the phase distribution was substantially reduced, indicating that the beta-LFP was more highly stereotyped across targets (Fig. 2e) [the reduction in entropy is expressed as “percentage phase-locking,” the percentage decrease from a maximally entropic uniform distribution (Tass et al., 1998; Rubino et al., 2006)] (see Materials and Methods).
The temporal profile of this effect was stereotyped across channels and occurred rapidly after the appearance of the target. With respect to the 200 ms preevent period, PPL values were significantly elevated (two-tailed t test, p < 0.001) within tens of milliseconds of the target appearance (22.1 ± 1.1 ms; mean ± SE across channels) and reached a maximum at a latency of 125.3 ± 1.8 ms (Fig. 2f,g).
We found that power in the beta band tended to increase transiently after the appearance of the target (1.2 ± 0.05% for monkey Mk and 3.9 ± 0.09% for monkey Rs; mean ± SE) (Fig. 2b), and we examined whether the reduction in phase entropy we observed was secondary to this increase in oscillatory power (perhaps reflecting the addition of a periodic driving input to MI) (Makeig et al., 2002). However, when we recalculated PPL values over a subset of targets that lacked an event-related increase in the amplitude of the oscillation, we found that, although the absolute magnitude of phase-locking was reduced, the phenomenon itself was not eliminated (Fig. 2h). This result suggests that the phase of the ongoing beta oscillation may be reset independent of any concomitant increase in power.
Event-related spiking
PSTHs aligned on target events revealed heterogeneous patterns of activity, as well as a more widespread change in firing at a latency around 100 ms [normalized PSTHs viewed “from above” for all units (Fig. 3a); PSTHs for several representative units depicting a wide range of responses (Fig. 3b–e)]. A number of units displayed an abrupt and dramatic increase in firing around ∼100 ms (Fig. 3b), and we were interested in examining these precise responses in more detail. To avoid the semantic uncertainty associated with the term “precision,” we operationalized precise spiking in terms of the null hypothesis that, given a particular unit and a particular postevent latency, the number of spikes occurring near that latency (±5 ms) was not statistically different from what would be predicted by the firing of the cell over the surrounding (25 ms) period. We used a spike-resampling method to systematically test this hypothesis for all units and latencies (Hatsopoulos et al., 2003; Harrison and Geman, 2009). In this approach, at each postevent latency t, the exact timing of spikes within a surrounding 25 ms window is randomly varied, while the total number of spikes in the window (i.e., the average firing rate of the cell over the 25 ms same period) is held constant. Repeating this procedure a large number of times, and each time counting the number of precise spikes (spikes that occur within 5 ms of t), generates the distribution of precise events that would be expected by chance. This chance distribution of precise events is compared with the actual observed distribution of precise events across repeated target appearances using a two-tailed t test, and the procedure is then repeated at each millisecond latency for each recorded unit.
When the hypothesis was rejected, we used the p value of the test as a relative measure of the precision of spiking (smaller p values reflected a statistically less likely excess of precise spikes at a particular latency). With this metric, we found we were more reliably able to identify transient periods of precise spiking than by using features of the PSTH of each unit, the shape of which varied widely from neuron to neuron. (Supplemental Figures 1 and 2, available at www.jneurosci.org as supplemental material, illustrate the ability of the method to identify moments of precise spiking for units with a variety of PSTH shapes.)
Consistent with our initial inspection of peristimulus histograms (Fig. 3a), we observed a dramatic increase in the precision of neural spiking at latencies near ∼100 ms after the target appearance (Fig. 3f,g; f, black arrowhead), as well as an earlier increase in precision around ∼15 ms (Fig. 3f, gray arrowhead) (mean ± SE is plotted in both panels).
Functionally defined cell classes
Interestingly, we found that this precise spiking was a feature of certain classes of functionally defined cortical neurons (Chen and Fetz, 2005; Mitchell et al., 2007). Following Chen et al. (2005), we sorted units into three classes: wide waveforms units (n = 300), units with narrow waveforms and a bursting component (n = 188), and units with narrow waveforms that lacked a bursting component (n = 104). In vivo intracellular recordings in motor cortex suggest that this classification scheme may capture intrinsic differences in neuronal membrane properties between different cell types (Chen and Fetz, 2005). In monkey Rs, the distribution of observed spike widths was clearly bimodal, with both narrow (Fig. 4a) and wide (Fig. 4b) waveforms, whereas in monkey Mk, the distribution was skewed toward narrow waveform units (Fig. 4c). Consistent with previous observations (Chen and Fetz, 2005), narrow-waveform cells tended to have a peak in their ISI distributions around 40–50 ms and occasionally contained a prominent bursting component (Fig. 4d) (note logarithmic scale), whereas wide waveform units displayed a more uniform distribution of ISIs (Fig. 4e).
Figure 4.
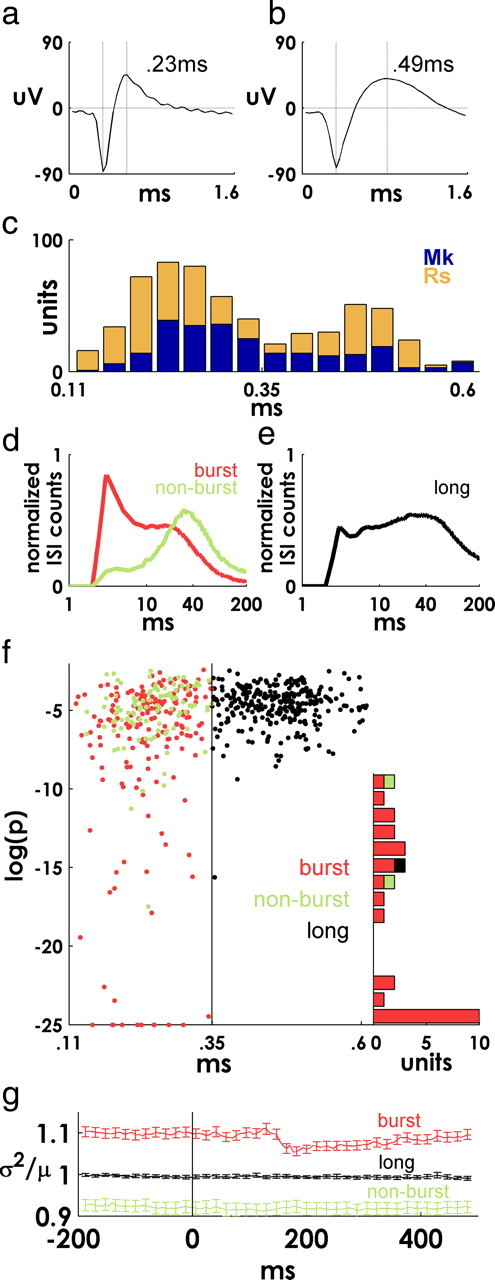
Functional cell classes. a, b, Examples of units with narrow and wide mean spike waveforms (see Materials and Methods). c, Superimposed (unstacked) histograms of spike waveform widths for each monkey. d, Mean normalized ISI distributions for two subsets of units with narrow spike waveforms that were bursting or nonbursting based on their ISI distribution (see Materials and Methods). e, Mean normalized ISI distributions for units with wide spike waveforms. Note logarithmic scale in d and e. f, Spike width (x-axis) versus spiking precision [minimum log(p) value] for all units. Narrow units are more precise than wide units, and bursting units tend to be more precise than nonbursting units. Values of log(p) less than −25 are plotted at −25 for visualization purposes. The right-side histogram shows the frequency of log(p) ≤ −10 for each class of units (note that bars are stacked—only a single wide waveform unit falls under this criteria). g, Mean ± SE fano factor computed in sliding 25 ms bins for each cell class, computed independently for each of 10 different target directions and then averaged.
This feature-based classification scheme captured functional differences in the temporal precision of event-related spiking (Fig. 4f). Narrow-waveform units tended to fire more precisely than wide-waveform units (p < 10−7, Wilcoxon's rank sum test), and bursting narrow cells tended to be more precise than nonbursting narrow cells (p < 0.005, Wilcoxon's rank sum test). Units with highly precise (log(p) ≤ −10) firing were almost entirely narrow-waveform bursting cells (Fig. 4f, histogram). The mean fano factor also varied by cell class (variance divided by mean of binned spike counts across trials, calculated independently for different target directions). Units with wide waveforms had a mean fano factor of 1.00 ± 0.004 (mean ± SE), reflective of nearly Poisson spiking. Among narrow-waveform units, units without a bursting component were more regularly spiking, with a mean value of 0.92 ± 0.01. Narrow bursting units were more irregularly spiking overall (1.09 ± 0.01) and were unique among the three classes in displaying a reduction in mean fano factor between 100 and 200 ms latency (Fig. 4g).
Information in neural spiking
We hypothesized that the widespread modulation in activity around ∼100 ms might reflect the initial arrival of information about the location of the new target in MI. To examine the time course of informative postevent spiking, we calculated the mutual information between target location and binned spike counts (5 ms sliding window stepped at 1 ms resolution) (see Materials and Methods). This analysis revealed a sharp demarcation between uninformative and informative spiking around ∼100 ms (Fig. 5), presumably reflecting the first arrival of target-related information in MI. Note that the lack of information during the immediate postevent period was not attributable to an absence of spiking activity in general; many cells were active throughout the perievent period (Fig. 3a), but the activity during that period contains no information about the direction of the new target.
When units were ranked by maximum spiking precision (minimum p value), we found that the most precise 10% of units displayed the most dramatic increase in information values (Fig. 5, solid line), suggesting that these precisely firing cells contain a substantial portion of the initial information about the new target location in MI.
Phase-locking and spike timing
We next examined the interaction between precise target-evoked responses and the intrinsic periodicity in spiking reflected in the beta-LFP (Fries, 2005; Schaefer et al., 2006). We hypothesized that some of the observed target-to-target variability in the timing of event-related spikes might be attributable to the superposition of this beta rhythmicity on the time course of evoked responses.
Note that, despite the reduction in target-to-target variability in phase during the posttarget period, the absolute PPL values we observed were still small, indicating that there is still substantial variation in phase across target events (Fig. 2e). To characterize this variability, we defined the “latency” of each postevent oscillation using the beta-LFP peak nearest to a reference peak in the mean evoked potential as a landmark (Fig. 6a,b) (see Materials and Methods). By definition, averaging over the upper and lower quartiles of the resulting distribution of latencies produced early and late event-locked beta oscillations (Fig. 6c).
As we hypothesized, the timing of evoked spiking of units recorded on the same electrode also varied with the latency of the phase-locked beta oscillation (Fig. 6d; horizontal bars indicate periods of precise spiking, p < 5 × 104). Note that the early and late periods of precise spiking are both aligned with the downward deflection of the corresponding evoked potential (Fig. 6c). Regressing median precise-spike latencies against the latencies of the beta oscillation recorded on the same electrode yielded mostly positive or nonsignificant correlations (Fig. 6e) (see Materials and Methods). For each target hit, we subtracted the relative latency of the beta oscillation from the spike times recorded on the same electrode, thus removing the variability in timing attributable to the periodic, phase-locked component. By adjusting postevent spike times by the latency of the oscillation in this way, we increased the apparent precision of event-related spiking nearly threefold (Fig. 6f) (compare with Fig. 3f,g). This effect was widespread (compare Fig. 6g before adjusting spike times with Fig. 6h after adjusting spike times; precision metric for all units sorted from most to least precise and viewed from above as in Fig. 3a; blue lines indicate epochs where p < 0.01).
Phase-binned information
We reasoned that as a result of the interaction with endogenous beta periodicity, the information available in evoked spiking might vary, not just with elapsed time from the target appearance (as in Fig. 5), but also with the phase of the phase-locked beta-LFP (which itself varied slightly from target to target).
To test this hypothesis, we calculated the information available in the spiking of each unit using the phase of the local beta oscillation after each event as a metric of postevent time. Rather than binning spikes in time bins (i.e., a 5 ms bin) with respect to the target appearance (Fig. 3a–e), we binned spikes in phase bins (π/8 radians per bin) with respect to a characteristic peak in the mean beta-LFP near 100 ms (Fig. 7a, dark blue line; b, orange line) (see also supplemental Fig. 3, available at www.jneurosci.org as supplemental material) (see Materials and Methods). By treating beta phase as a consistent frame of reference across target events, we shifted and warped spike times as the target-to-target variations in the latency and frequency of the oscillation dictated, gathering spikes from different latencies into the same bin of a canonical postevent phase progression. The warping effects of this procedure can be seen in Figure 7, a and b, where the green histogram depicts the distribution of target events across a range of phase bins. The spread in the distribution reflects the variable number of cycles traversed by the LFP between the time a target appeared and the “characteristic peak” near 100 ms latency that we used to define the location of the zero bin after each target.
As a control, we repeated this same binning procedure after shuffling target events, so that spikes were binned by the phase of the beta-LFP oscillation that occurred after a different target appearance (Fig. 7a,b, light blue lines) (supplemental Fig. 3, available at www.jneurosci.org as supplemental material) (see Materials and Methods). This shuffling procedure eliminated the relationship between firing probability and oscillatory phase, while maintaining the overall shape of the (phase-binned) PSTH. As expected, subtracting the shuffled values from the actual phase-binned spike counts revealed an underlying periodicity in MI spiking. Residual spikes tended to be concentrated near the downward, preferred phases of the oscillation (Fig. 7c,d). The mean variation in spike rate with respect to the shuffled control was relatively constant over the entire range of perievent phases.
The mutual information between phase-binned spikes and target direction also rose above the shuffled values at the descending phase of the oscillation and dipped below the shuffled information during the opposite phase (one example unit from each monkey) (Fig. 7d,e). However, the residual information obtained after subtracting the shuffled values varied significantly with phase only in the latter half of the phase series (Fig. 7g,h), reflecting the arrival of target-related information in MI around 0 radians (remember that the zero bin in the phase series is defined by the LFP near 100 ms) (Fig. 6). Thus, although the information available in MI spiking varies on a coarse scale with external time (Fig. 5), it also varies on a finer scale with the fluctuating rhythm of endogenous cortical oscillations.
Discussion
Although it may seem strange to focus on the timing of responses to sensory cues in motor cortex (rather than relationship between MI spiking and behavior), it is worth pointing out that the 19th century designation of parts of frontal cortex as “motor” areas has tended to obscure the fact that even primary motor cortex displays robust and complex responses to sensory stimuli (Lamarre et al., 1983; Riehle et al., 1997; Tkach et al., 2007). Compared with canonical sensory areas, the nature of early motor–cortical responses to sensory events has received less attention, and MI beta activity in particular has typically been studied with respect to features of movement. In one previous study examining the relationship between ongoing beta EEG activity and evoked responses in motor cortex, the ongoing beta phase was found to have no effect on the amplitude of responses to median nerve stimulation (Lalo et al., 2007). Unfortunately, the authors appear not to have examined the influence of phase on the latency of responses, which our results [and previous work in other cortical areas (Fries et al., 2001)] suggest may be the more salient effect.
Spike timing
We chose a behavioral task that involved continuous movements with very few constraints on the timing of the behavior. Paired with the ability to observe the activity of hundreds of neurons over thousands of target events, these self-paced movements offered a window onto the statistical regularities governing the intrinsic timing of sensorimotor processing in MI. We found that MI neurons generated spikes within a narrow range of latencies after the appearance of each target and that the exact timing of these event-related spikes also depended on the phase of the local beta oscillation, which was itself phase-locked to the target event. As a result of this relationship, event-related spiking appeared even more precise when the variation attributable to beta periodicity was accounted for (Fig. 8a; see also Fig. 6).
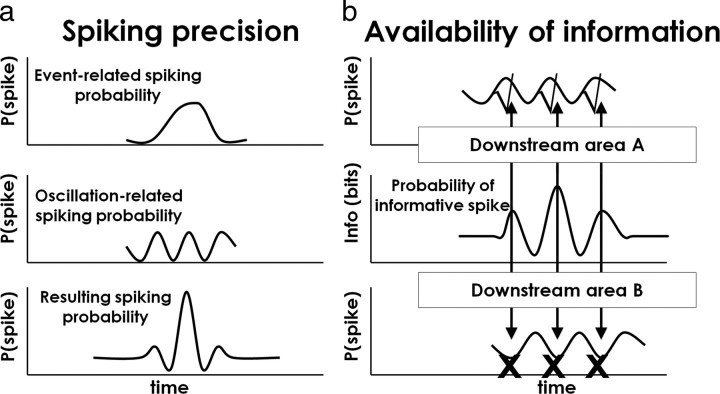
Figure 8.
Summary of the effects of MI beta oscillations on spike timing and information coding. a, The interaction between event-related spiking probability (top panel) and the intrinsic periodicity in MI spiking (middle panel) produces a quasi-periodic temporal profile (bottom panel). When the target-to-target variability in the beta-LFP is accounted for, the precision of event-related spiking is increased. b, The information available in spiking varies periodically with the oscillation (middle panel). As a consequence, a downstream area (area A) oscillating coherently with the local oscillation would potentially be more receptive (check marks) at the time of more informative spiking (arrows), whereas a population oscillating out of phase (area B) would be less receptive (“X” symbols) at the times at which informative spikes are concentrated. [This figure was adapted from the study by Fries (2005).]
Effects of phase-locking on the informative output of MI
We show that the quantity of early target information available in MI spiking varies periodically with the endogenous beta oscillation; to our knowledge, the quasi-periodic character of information encoded in MI spiking has not been previously described. A natural question is what the implications of this effect might be for cortical motor processing more generally.
As described previously, beta oscillations have been observed to occur coherently across large regions of motor and somatosensory cortex (Murthy and Fetz, 1992; Feige et al., 2000; Brovelli et al., 2004; Soteropoulos and Baker, 2006), and it is possible that these coherent oscillations may serve to automatically align the periodic variations in informative spiking that we describe here (Fig. 7), with periodic variations in the receptivity of downstream targets (Fries, 2005; Womelsdorf et al., 2007). If the phase differences and conduction times between the two areas are relatively small, the arrival of informative spiking from MI would tend to occur at the depolarized phase of the oscillation in the downstream area, periodically enhancing information transfer (Fig. 8b). Notably, beta oscillations have been shown to vary in both strength and frequency with reach direction (O'Leary and Hatsopoulos, 2006) and grasp type (Spinks et al., 2008). We speculate that these changes may reflect differences in the composition and extent of neural ensembles sharing in the temporal structure provided by coherent oscillations.
It may be worth pointing out that, in contrast with previous studies in other areas that have demonstrated “phase-of-spiking” encoding [typically for oscillations <10 Hz (Huxter et al., 2003; Montemurro et al., 2008)], these results do not support the view that the beta-LFP phase at which a neuron spikes is informative. On the contrary, we show that spike times and oscillatory phase are not independent, and by binning spikes by phase (Fig. 7) we remove any potential stimulus-related variability between spiking and phase that might exist. Also, in our analysis, there is no fixed relationship between bits per second (Fig. 5) and bits per radian (Fig. 7) because of the target-to-target variability in the frequency and latency of the phase-locked beta-LFP.
In the behavioral task described here, target, hand, and eye locations and directions are tightly correlated. In fact, we find that the temporal profiles of postevent information about hand and target directions, for example, are virtually identical (Reimer and Hatsopoulos, 2009). Thus, we are not able to make conclusions about the relative degree of encoding of spatial features of the target, hand, and eye. This is a longstanding question in motor cortical research, and one we have addressed more directly in other publications (cf. Tkach et al., 2007). In this study, we focus instead on the timing of informative event-related spiking (i.e., when it occurs, rather than what it encodes).
The origin and significance of phase-locked oscillations
Recently, a two-stage mechanism has been proposed for certain kinds of multimodal sensory processing. According to this proposal, salient stimuli quickly reset the phase of ongoing oscillations in a cortical area through fast nonspecific projections, so that when sensory information arrives, it is processed in time to the beat of that transiently event-locked oscillation (Lakatos et al., 2007, 2008; Schroeder and Lakatos, 2009).
Our results appear to be at least consistent with this proposal. We find that the onset of phase-locking occurs immediately after the target appearance and reaches a peak around 100 ms (Fig. 2e–g). We believe that the early rise in PPL values that we observe may reflect in part the monkey's ability to anticipate the time of the upcoming target appearance based on their impending acquisition of the current target (supplemental Fig. 5, available at www.jneurosci.org as supplemental material). Notably, in addition to the precise spiking around 100 ms that we have focused on here (Fig. 3f, black arrowhead), we also observe a more transient increase in precision at extremely low latencies (∼15 ms) (Fig. 3f, gray arrowhead), which might be interpreted as the arrival of an early phase-resetting “salience” signal in MI. Because it seems highly unlikely that this extremely fast response is attributable to visual stimulation—even through nonspecific thalamic afferents—we speculate that it may be attributable to the accompanying auditory cue that indicates to the monkey that a new target has appeared. This interpretation is supported by our finding that MI beta oscillations can be quickly reset by the auditory cue alone (i.e., when the tone is presented without an accompanying visual target). This auditory phase-locking occurs earlier than visual phase-locking when targets are presented without the associated tone, and the timing is consistent with previous reports of short-latency visual and auditory responses in MI (supplemental Fig. 5, available at www.jneurosci.org as supplemental material) (Lamarre et al., 1983; Ledberg et al., 2007).
Motivated by the large body of existing work on beta oscillations in motor cortex, we have limited the focus of this study to the 10–45 Hz band. An obvious additional question concerns the relationship between phase-locking in the beta frequency band, and oscillations in other bands—particularly in the delta (1–4 Hz) and theta (4–10 Hz) ranges. Consistent with our previous observations, we find that evoked responses are also present in the theta band after target appearances, and a number of studies have shown that cross-frequency interactions (m:n phase coupling, for example) are an important feature of cortical oscillations (Lakatos et al., 2008). We suspect there may be interesting relationships between the event-related activity in lower frequencies and the beta range phenomena we have described here.
Functionally defined cell classes
Narrow spike waveforms are typically associated with GABAergic interneurons (Wilson et al., 1994; Mitchell et al., 2007), which have been shown to play an important role in the generation of oscillatory activity (Cobb et al., 1995; Fetz et al., 2000; Salinas and Sejnowski, 2001; Cardin et al., 2009). Consistent with this view, the nonbursting, narrow-waveform neurons that we describe are similar to the type III inhibitory neurons described by Chen and Fetz (2005), which contain an intrinsic beta period “rebound afterhyperpolarization” that may have a role in the generation of beta activity. The identity of the narrow-waveform bursting cells that we observed is less clear. The highest information values and most precise firing were observed in this class of cells (Figs. 4f, 5), but we also found that the most precise units had low firing rates, inconsistent with the standard description of fast-spiking interneurons like parvalbumin-positive basket cells (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). This sparse, irregular spiking is characteristic of the “type II” neurons described by Chen and Fetz (2005), but to our knowledge these features have not been previously linked to event-related precision, or to the first arrival of information in MI about a behavioral cue. Interestingly, in addition to contributing to the initial peak in target-related information, we found that these units displayed an immediately subsequent characteristic reduction in spiking variance (fano factor) (Fig. 4g), a signature of the onset of stimulus processing in a wide range of cortical areas (Churchland et al., 2010). We speculate that this class of cells may play a role in the initial stages of sensorimotor processing in MI, perhaps in the selection of the networks of neurons that are subsequently active in generating the target-directed movement. More research is clearly needed to help disambiguate the functional roles of these cell classes, and in particular to determine whether these different classes of MI cells may encode behaviorally relevant information at different timescales.
Footnotes
The work was supported by funding from National Institutes of Health–National Institute of Neurological Disorders and Stroke Grants R01 NS45853 and 1F31NS060384-01A1. We thank D. Paulsen, D. Tkach, and A. Suminski for their assistance with the experiments, M. Harrison for providing the MATLAB code for the jitter analysis, M. Green, M. Carrol, J. Beshel, and K. Takahashi for useful feedback, and L. Demski, A. Beulig, and the organizers of the 2005 Neuroinformatics class at the Woods Hole Marine Biology Laboratory for additional training.
References
- Baker SN. Oscillatory interactions between sensorimotor cortex and the periphery. Curr Opin Neurobiol. 2007;17:649–655. doi: 10.1016/j.conb.2008.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker SN, Kilner JM, Pinches EM, Lemon RN. The role of synchrony and oscillations in the motor output. Exp Brain Res. 1999;128:109–117. doi: 10.1007/s002210050825. [DOI] [PubMed] [Google Scholar]
- Baker SN, Chiu M, Fetz EE. Afferent encoding of central oscillations in the monkey arm. J Neurophysiol. 2006;95:3904–3910. doi: 10.1152/jn.01106.2005. [DOI] [PubMed] [Google Scholar]
- Brovelli A, Ding M, Ledberg A, Chen Y, Nakamura R, Bressler SL. Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by Granger causality. Proc Natl Acad Sci U S A. 2004;101:9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardin JA, Carlén M, Meletis K, Knoblich U, Zhang F, Deisseroth K, Tsai LH, Moore CI. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D, Fetz EE. Characteristic membrane potential trajectories in primate sensorimotor cortex neurons recorded in vivo. J Neurophysiol. 2005;94:2713–2725. doi: 10.1152/jn.00024.2005. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Cunningham JP, Sugrue LP, Cohen RC, Corrado GS, Newsome WT, Clark AM, Hosseini P, Scott BB, Bradley DC, Smith MA, Kohn A, Movshon JA, Armstrong KM, Moore T, Chang SW, Snyder LH, Lisberger SG, et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat Neurosci. 2010;13:369–380. doi: 10.1038/nn.2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobb SR, Buhl EH, Halasy K, Paulsen O, Somogyi P. Synchronization of neuronal activity in hippocampus by individual GABAergic interneurons. Nature. 1995;378:75–78. doi: 10.1038/378075a0. [DOI] [PubMed] [Google Scholar]
- Cover TM, Thomas JA. Elements of information theory. New York: Wiley-Interscience; 2006. [Google Scholar]
- Dickey AS, Suminski A, Amit Y, Hatsopoulos NG. Single-unit stability using chronically implanted multielectrode arrays. J Neurophysiol. 2009;102:1331–1339. doi: 10.1152/jn.90920.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoghue JP, Sanes JN, Hatsopoulos NG, Gaál G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. J Neurophysiol. 1998;79:159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Feige B, Aertsen A, Kristeva-Feige R. Dynamic synchronization between multiple cortical motor areas and muscle activity in phasic voluntary movements. J Neurophysiol. 2000;84:2622–2629. doi: 10.1152/jn.2000.84.5.2622. [DOI] [PubMed] [Google Scholar]
- Fetz EE, Chen D, Murthy VN, Matsumura M. Synaptic interactions mediating synchrony and oscillations in primate sensorimotor cortex. J Physiol Paris. 2000;94:323–331. doi: 10.1016/s0928-4257(00)01089-5. [DOI] [PubMed] [Google Scholar]
- Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn Sci. 2005;9:474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- Fries P, Neuenschwander S, Engel AK, Goebel R, Singer W. Rapid feature selective neuronal synchronization through correlated latency shifting. Nat Neurosci. 2001;4:194–200. doi: 10.1038/84032. [DOI] [PubMed] [Google Scholar]
- Harrison MT, Geman S. A rate and history-preserving resampling algorithm for neural spike trains. Neural Comput. 2009;21:1244–1258. doi: 10.1162/neco.2008.03-08-730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatsopoulos N, Geman S, Amarasingham A, Bienenstock E. At what time scale does the nervous system operate. Neurocomputing. 2003;52–54:25–29. [Google Scholar]
- Huxter J, Burgess N, O'Keefe J. Independent rate and temporal coding in hippocampal pyramidal cells. Nature. 2003;425:828–832. doi: 10.1038/nature02058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P, Chen CM, O'Connell MN, Mills A, Schroeder CE. Neuronal oscillations and multisensory interaction in primary auditory cortex. Neuron. 2007;53:279–292. doi: 10.1016/j.neuron.2006.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P, Karmos G, Mehta AD, Ulbert I, Schroeder CE. Entrainment of neuronal oscillations as a mechanism of attentional selection. Science. 2008;320:110–113. doi: 10.1126/science.1154735. [DOI] [PubMed] [Google Scholar]
- Lalo E, Gilbertson T, Doyle L, Di Lazzaro V, Cioni B, Brown P. Phasic increases in cortical beta activity are associated with alterations in sensory processing in the human. Exp Brain Res. 2007;177:137–145. doi: 10.1007/s00221-006-0655-8. [DOI] [PubMed] [Google Scholar]
- Lamarre Y, Busby L, Spidalieri G. Fast ballistic arm movements triggered by visual, auditory, and somesthetic stimuli in the monkey. I. Activity of precentral cortical neurons. J Neurophysiol. 1983;50:1343–1358. doi: 10.1152/jn.1983.50.6.1343. [DOI] [PubMed] [Google Scholar]
- Ledberg A, Bressler SL, Ding M, Coppola R, Nakamura R. Large-scale visuomotor integration in the cerebral cortex. Cereb Cortex. 2007;17:44–62. doi: 10.1093/cercor/bhj123. [DOI] [PubMed] [Google Scholar]
- MacLeod K, Bäcker A, Laurent G. Who reads temporal information contained across synchronized and oscillatory spike trains? Nature. 1998;395:693–698. doi: 10.1038/27201. [DOI] [PubMed] [Google Scholar]
- Makeig S, Westerfield M, Jung TP, Enghoff S, Townsend J, Courchesne E, Sejnowski TJ. Dynamic brain sources of visual evoked responses. Science. 2002;295:690–694. doi: 10.1126/science.1066168. [DOI] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg KA, Reynolds JH. Differential attention-dependent response modulation across cell classes in macaque visual area V4. Neuron. 2007;55:131–141. doi: 10.1016/j.neuron.2007.06.018. [DOI] [PubMed] [Google Scholar]
- Montemurro MA, Rasch MJ, Murayama Y, Logothetis NK, Panzeri S. Phase-of-firing coding of natural visual stimuli in primary visual cortex. Curr Biol. 2008;18:375–380. doi: 10.1016/j.cub.2008.02.023. [DOI] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Coherent 25-to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proc Natl Acad Sci U S A. 1992;89:5670–5674. doi: 10.1073/pnas.89.12.5670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys. J Neurophysiol. 1996;76:3968–3982. doi: 10.1152/jn.1996.76.6.3968. [DOI] [PubMed] [Google Scholar]
- O'Leary JG, Hatsopoulos NG. Early visuomotor representations revealed from evoked local field potentials in motor and premotor cortical areas. J Neurophysiol. 2006;96:1492–1506. doi: 10.1152/jn.00106.2006. [DOI] [PubMed] [Google Scholar]
- Paninski L, Fellows MR, Hatsopoulos NG, Donoghue JP. Spatiotemporal tuning of motor cortical neurons for hand position and velocity. J Neurophysiol. 2004;91:515–532. doi: 10.1152/jn.00587.2002. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G. Event-related synchronization (ERS): an electrophysiological correlate of cortical areas at rest. Electroencephalogr Clin Neurophysiol. 1992;83:62–69. doi: 10.1016/0013-4694(92)90133-3. [DOI] [PubMed] [Google Scholar]
- Reimer J, Hatsopoulos NG. The problem of parametric neural coding in the motor system. Adv Exp Med Biol. 2009;629:243–259. doi: 10.1007/978-0-387-77064-2_12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddle CN, Baker SN. Manipulation of peripheral neural feedback loops alters human corticomuscular coherence. J Physiol. 2005;566:625–639. doi: 10.1113/jphysiol.2005.089607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riehle A, Kornblum S, Requin J. Neuronal correlates of sensorimotor association in stimulus-response compatibility. J Exp Psychol Hum Percept Perform. 1997;23:1708–1726. doi: 10.1037//0096-1523.23.6.1708. [DOI] [PubMed] [Google Scholar]
- Rubino D, Robbins KA, Hatsopoulos NG. Propagating waves mediate information transfer in the motor cortex. Nat Neurosci. 2006;9:1549–1557. doi: 10.1038/nn1802. [DOI] [PubMed] [Google Scholar]
- Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci. 2001;2:539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanes JN, Donoghue JP. Oscillations in local field potentials of the primate motor cortex during voluntary movement. Proc Natl Acad Sci U S A. 1993;90:4470–4474. doi: 10.1073/pnas.90.10.4470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaefer AT, Angelo K, Spors H, Margrie TW. Neuronal oscillations enhance stimulus discrimination by ensuring action potential precision. PLoS Biol. 2006;4:e163. doi: 10.1371/journal.pbio.0040163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoffelen JM, Oostenveld R, Fries P. Neuronal coherence as a mechanism of effective corticospinal interaction. Science. 2005;308:111–113. doi: 10.1126/science.1107027. [DOI] [PubMed] [Google Scholar]
- Schroeder CE, Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32:9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott SH. Apparatus for measuring and perturbing shoulder and elbow joint positions and torques during reaching. J Neurosci Methods. 1999;89:119–127. doi: 10.1016/s0165-0270(99)00053-9. [DOI] [PubMed] [Google Scholar]
- Soteropoulos DS, Baker SN. Cortico-cerebellar coherence during a precision grip task in the monkey. J Neurophysiol. 2006;95:1194–1206. doi: 10.1152/jn.00935.2005. [DOI] [PubMed] [Google Scholar]
- Spinks RL, Kraskov A, Brochier T, Umilta MA, Lemon RN. Selectivity for grasp in local field potential and single neuron activity recorded simultaneously from M1 and F5 in the awake macaque monkey. J Neurosci. 2008;28:10961–10971. doi: 10.1523/JNEUROSCI.1956-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stopfer M, Bhagavan S, Smith BH, Laurent G. Impaired odour discrimination on desynchronization of odour-encoding neural assemblies. Nature. 1997;390:70–74. doi: 10.1038/36335. [DOI] [PubMed] [Google Scholar]
- Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, Schnitzler A, Freund HJ. Detection of n:m phase locking from noisy data: application to magnetoencephalography. Phys Rev Lett. 1998;81:3291–3294. [Google Scholar]
- Tkach D, Reimer J, Hatsopoulos NG. Congruent activity during action and action observation in motor cortex. J Neurosci. 2007;27:13241–13250. doi: 10.1523/JNEUROSCI.2895-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treves A, Panzeri S. The upward bias in measures of information derived from limited data samples. Neural Comput. 1995;7:399–407. [Google Scholar]
- Vargas-Irwin C, Donoghue JP. Automated spike sorting using density grid contour clustering and subtractive waveform decomposition. J Neurosci Methods. 2007;164:1–18. doi: 10.1016/j.jneumeth.2007.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson FA, O'Scalaidhe SP, Goldman-Rakic PS. Functional synergism between putative γ-aminobutyrate-containing neurons and pyramidal neurons in prefrontal cortex. Proc Natl Acad Sci U S A. 1994;91:4009–4013. doi: 10.1073/pnas.91.9.4009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]