Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Oct 1.
Published in final edited form as: Geocarto Int. 2010 Oct 1;25(6):443–452. doi: 10.1080/10106049.2010.496496

Geomasking sensitive health data and privacy protection: an evaluation using an E911 database

William B Allshouse 1, Molly K Fitch 2, Kristen H Hampton 3, Dionne C Gesink 4, Irene A Doherty 5, Peter A Leone 6,7, Marc L Serre 8, William C Miller 9,10
PMCID: PMC2952889  NIHMSID: NIHMS219832  PMID: 20953360

Abstract

Geomasking is used to provide privacy protection for individual address information while maintaining spatial resolution for mapping purposes. Donut geomasking and other random perturbation geomasking algorithms rely on the assumption of a homogeneously distributed population to calculate displacement distances, leading to possible under-protection of individuals when this condition is not met. Using household data from 2007, we evaluated the performance of donut geomasking in Orange County, North Carolina. We calculated the estimated k-anonymity for every household based on the assumption of uniform household distribution. We then determined the actual k-anonymity by revealing household locations contained in the county E911 database. Census block groups in mixed-use areas with high population distribution heterogeneity were the most likely to have privacy protection below selected criteria. For heterogeneous populations, we suggest tripling the minimum displacement area in the donut to protect privacy with a less than 1% error rate.

Keywords: donut geomasking, confidentiality, k-anonymity, privacy protection, spatial resolution

1. Introduction

When health researchers want to georeference study participants or reported cases of various diseases, they can either geocode these persons using an address or aggregate them to a geopolitical or mail sorting area, assigning them to the centroid of that area or region (MacDorman and Gay 1999, Rushton et al. 2006). Geocoding is usually preferable for in-house use, but depending on the source and sensitivity of the subject location and nature of the study, may not be acceptable for sharing the data more broadly. Consequently, aggregation is often used to preserve confidentiality (Duncan and Pearson 1991). Assigning a person to the centroid of an area ensures that the subject is sufficiently hidden within a larger population, protecting his or her identity. Non-spatial aggregation methods such as age and race categories have also been utilized to keep individuals in the dataset from being identified (Sweeney 2002a).

Although aggregation protects confidentiality, it substantially degrades spatial resolution. The higher the level of aggregation, the less effective a map will be for identifying geographical and epidemiological trends at the local level (Boulos et al. 2006). A disease map with the highest possible spatial resolution (i.e. showing the most detail) should be the most informative and lead to the most efficient use of public health resources.(Cassa et al. 2006, Olson et al. 2006, Gutmann and Stern 2007). For example, identifying that county X has the highest incidence rate of syphilis for the year 2009 is much less helpful for allocating resources for disease control and intervention than being able to say that there appears to be a syphilis outbreak occurring on the college campus in census block group Y in county X. Similarly, the progression of an infection that crosses a geopolitical boundary of the corresponding aggregation level will be obscured by moving cases to the centroid.

The importance of privacy protection for spatial information depends on several factors. One of the most important is the disease or outcome of interest. For common diseases, such as influenza, the need for masking the location of a patient is probably small, as the risk of privacy compromise is small. In contrast, HIV infection is relatively rare, carries social stigmas, and is costly to manage and treat. It is critical to sufficiently mask the locations of these cases, because many individuals are only willing to be tested if their identity remains anonymous. Most health outcomes fall between these two extremes (Wieland et al. 2008, Brownstein et al. 2006).

Geomasking is a class of methods for changing the geographic location of an individual in an unpredictable way to protect confidentiality, while trying to preserve the relationship between geocoded locations and disease occurrence (Sherman and Fetters 2007, Wiggins 2002). Random perturbation is one example of a method to alter the geographic location of an individual without aggregating (Armstrong et al. 1999, Armstrong and Ruggles 2005, Kwan et al. 2004). We have modified the basic random perturbation method to require that an individual is moved at least a minimum distance, so that they cannot be randomly placed in their original location, creating a donut area for possible masking locations (Stinchcomb 2004). This has been shown to greatly improve privacy protection with a negligible effect on the sensitivity and specificity of detecting disease clusters (Hampton et al. 2009).

Random perturbation methods (including the donut method) use the population density to determine the distance an individual needs to be moved in order to achieve a certain level of privacy protection. Geographic information systems (GIS) are usually used to obtain population density estimates for the calculation and to match the proper census level, county, or ZIP code to the subject location. However, this methodology almost always relies on the assumption that the population density is homogeneously distributed. This condition is rarely met and can lead to under-protection of individuals when mapping sensitive health data.

With the rapid increase in the use of GIS, many United States counties have begun to create databases that list every geocoded residential address. The original intention was to give the coordinate locations of every household within the county so that dispatchers can quickly route emergency personnel to an address given during a 911 call without relying on a caller in a stressful situation to provide the information. Thus, they are commonly referred to as E911 databases. These databases also provide important information about the distribution of households across a spatial area.

We determined the estimated privacy protection obtained using donut geomasking under the assumption that households are uniformly distributed within each census block group to address potential geomasking confidentiality concerns arising when household addresses are revealed by an E911 database and then calculated the actual privacy protection based on household addresses in such a database. We provide an approximate correction factor that anticipates the loss of privacy protection that may occur when household addresses are revealed by comparing the estimated privacy protection with the actual privacy protection achieved.

2. Methods

2.1 E911 Database and GIS Data Sets

We obtained the most recent version of the Orange County, North Carolina E911 database (Orange County GIS Division 2007). This county was chosen because its E911 data were readily available and it contains census block groups with a variety of population densities. Orange County includes the city of Chapel Hill with several areas of high density student housing and apartment complexes, the small town of Hillsborough, and a significant percentage of low density rural land.

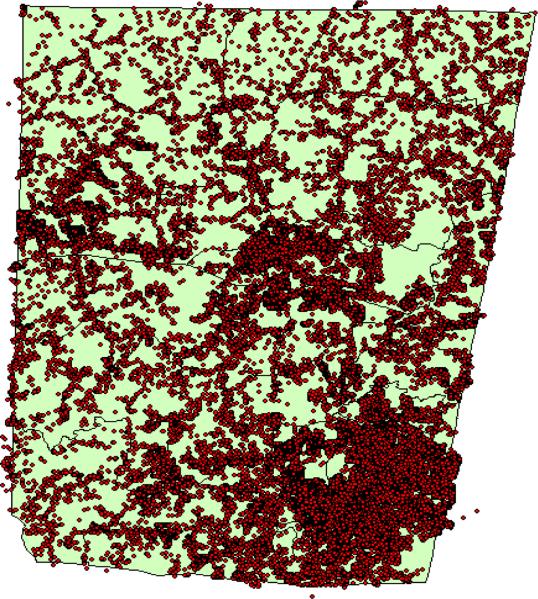
The Orange County E911 data is formatted as a GIS spatial data set that includes every identified residential unit in the county. For example, an apartment complex with 200 units would be identified as 200 points representing the centroids of the individual apartment units. Ideally, such a database would include every housing unit within the county, but new construction may not always be reflected in the database. The current database includes the coordinates of 62,675 households in the county (Figure 1). We also obtained the 2007 Orange County census block group spatial data set, which is based on the 2000 census, with demographic information projected for the year 2007. The E911 and census block group data sets were linked using ESRI's ArcMap Version 9.3.

Figure 1.

Figure 1

Open in a new tab

The locations of all households in Orange County, NC according to the 2007 E911 database.

We calculated the number of households from the E911 database within each census block group. Although in most situations, geomasking algorithms would use the population and area of the census block group, we used household density, because the E911 file has household locations (not locations of individuals). We substituted the number of households in a block group for the population of that block group in this simulation.

2.2 Donut Geomasking

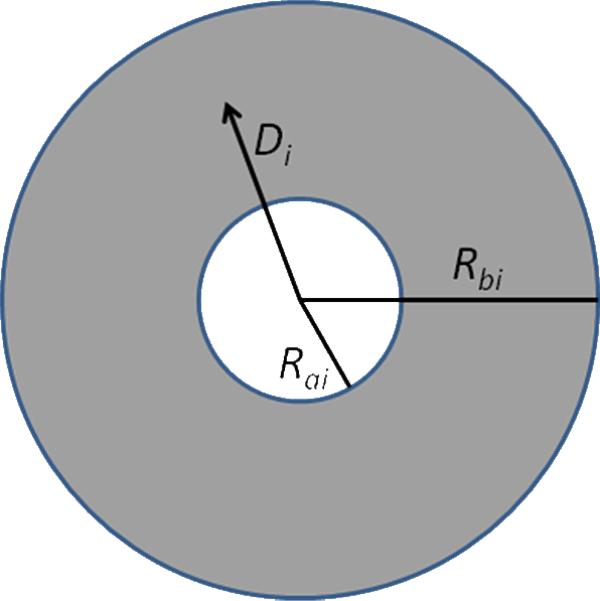
Each of the 62,675 households (i) in Orange County was donut geomasked by moving its geocoded location in a random direction by more than a specified minimum distance (Rai), but less than a maximum distance (Rbi), while remaining in its original census block group (Figure 2). This census level was chosen because we believe that it provides the optimal balance of anonymity while maintaining spatial resolution of the subject locations. Also, it is smallest geographical unit for which the detailed long-form census data are available (starting with the 2010 Census, the decennial long form data collection will be replaced bv the continuously-updated American Community Survey). The distance of displacement for a given household is randomly selected between the lower and upper bounds Rai and Rbi that are dependent on the number of households (Ni) and area (Ai) of the census block group where that household resides (Eqs 1a and 1b).

Rai=((Ai∕π)∗(ka∕Ni))1∕2 (1a)
Rbi=((Ai∕π)∗(kb∕Ni))1∕2 (1b)

The parameters ka and kb are chosen by the user so that by assuming a homogeneous household density across the census block group, the subject will be displaced by a minimum of ka households and a maximum of kb households. If the geomasked household is placed outside of its original census block group, the algorithm is rerun until the household falls into its original census block group.

Figure 2.

Figure 2

Open in a new tab

Each household is geomasked by a random direction and distance, where the distance Di must fall within the donut created by radii Rai and Rbi The geomasked household must also reside in its original census block group so that neighborhood demographic and socio-economic factors for the masked location are the same as the original location.

Multiple runs of the donut geomasking simulation were conducted varying the parameter ka for each run. The parameter kb was maintained at 10*ka. For this simulation we used ka=5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, and 75 households.

2.3 K-Anonymity

We determined the privacy protection offered by the geomask using the concept of k-anonymity as the measure of success. K-anonymity is defined as the number of households from whom a de-identified subject cannot be distinguished. Spatially, this measure is simply the number of households closer to the original location than the distance of displacement for the geomask. It can be illustrated as the number of households within a circle whose centroid is the original household location and radius is the Euclidean distance between the original and masked locations (Sweeney 2002b).

After the households were donut geomasked for a given value of ka and kb, the estimated and actual k-anonymity were determined for each of the 62,675 locations. The estimated k-anonymity for a location i was calculated as:

kest,i=π∗Di2∗(Ni∕Ai) (2)

where Di is the Euclidean distance between the original location and the masked location and Ai and Ni are the area and number of households, respectively, of the corresponding census block group. This value for k-anonymity gives an estimated measure of privacy protection based on the assumption that the census block groups' households are uniformly distributed. The actual k-anonymity for each location (kact,i) was defined as the number of households from the E911 file that were closer to the original location than the distance of displacement. As its name suggests, the actual k-anonymity measures the actual level of confidentiality achieved by the masking algorithm once the locations of households in the E911 database are revealed.

2.4 Evaluation

Often the estimated k-anonymity is used to claim a certain level of privacy protection when information regarding actual household locations is unavailable. Since we have the actual household locations for Orange County, we evaluated how well that kest, based on a uniform household distribution assumption, serves as a proxy for kact, based on the actual E911 household locations.

The analysis focuses on the percentage of households across the county that did not achieve kact,i≥Kmin in order to illustrate the overall failure of the geomasking method with parameters ka and kb to achieve the desired level of privacy protection. The decision of an acceptable value for Kmin, which is defined as the smallest value for actual k-anonymity that is acceptable, must be chosen by the user to ensure adequate privacy protection for a given study situation, taking into account things such as the disease, study area, and privacy factors.

For a given ka and kb, we made comparisons among the census block groups to assess how the method performed across areas with differing household densities. As the parameters ka and kb increase, we describe the changing geographic pattern of census block groups' percentage of households unable to meet the privacy protection criterion kact, i≥Kmin, i.e. we evaluate the relationship between ka (and kb) and the rate of kact, i<Kmin.

We used Kmin=5 as our minimum acceptable actual k-anonymity in the simulations presented here. We are not recommending this particular choice, but use it for illustration as other values of Kmin should reveal a similar relationship among ka, kb, and the percentage of households that do not meet the Kmin standard. Additional simulations with Kmin > 5 yielded similar results.

Given our use of Kmin = 5 as our standard, we initiated our simulations with ka = 5 (kb = 50). In theory, with ka = 5, all census block groups would meet our minimum privacy protection standard under the assumption of homogeneous household distribution. Households with kact,i < 5 would indicate a failure of that assumption. Increasing ka should be associated with fewer failures given the use of a constant Kmin.

3. Results

The first run of the geomasking simulation used the parameters ka=5 and kb=50, so that if the assumption of a homogeneous distribution of households is correct, every household should be displaced by at least 5 additional households. Across the census block groups, the percentage of households with an actual k-anonymity less than 5 varied from 1.5% to 7.5%. The 5 block groups in the highest quintile (worst-performing) were all close to the city of Chapel Hill with 4 of the 5 located in the northern section of the city. This particular section of town is the location of several large apartment complexes intermingled with single-family houses and forested land, creating substantial heterogeneity in the household distribution.

When the parameters ka and kb were changed to 10 and 100 respectively, the proportion of households with violations of Kmin < 5 decreases. All census block groups had less than 2.5% of their households violating the standard of actual k-anonymity less than 5. Furthermore, the relative privacy protection for census groups varied substantially, as compared to the initial set of parameters. None of the five worst-performing block groups that were located around Chapel Hill remained in the worst quintile during the second run. The worst performing areas moved to western Hillsborough (in the central part of the county) and southwestern Chapel Hill.

The user-defined minimum and maximum parameters, ka and kb, were increased to 15 and 150 for the third simulation. Using this masking procedure, the majority of census block groups had less than 1% of their households with an actual k-anonymity less than 5, with only 340 households (0.54%) across Orange County not achieving the standard. The census block groups in the highest quintiles tend to appear around the outskirts of Hillsborough and Chapel Hill. These block groups often appear to have widely varying household densities from one area of the block group to another.

As the ka parameter increases to greater than 3*Kmin, a pattern for block groups violating Kmin becomes less discernable. All but 15 of the county's block groups had every household adequately protected with ka=20 and kb=200. The geographical pattern of the mapped quintiles shows only small changes from the previous run with the notable exception that a block group in southeastern Chapel Hill switched from the highest quintile of violation percentage when masking with ka=15 and kb=150 to having zero violations using the largest parameters. Overall, the worst performing blocks groups still tended to be those situated between a city and rural land.

Evaluating a map to find where cases are not adequately protected can help inform a researcher with a strong knowledge of the study area as to why the assumption that households are distributed homogeneously is inadequate. However, often the researcher does not know how households or people are distributed across a various study area and simply needs to correct for the assumption of homogeneity.

As we varied the minimum acceptable k-anonymity so that Kmin=10, 15, 20, and 25, a pattern in the percentage of violations across the county begins to take shape. In each instance, approximately 99.5% of the households achieve the privacy standard when ka=3*Kmin. Further increases in ka make fairly minimal gains in privacy protection at a continued (nearly linear) loss of spatial resolution (Table 1). Multiplying by a factor of three can help to correct for the homogeneity assumption when the actual locations of households are unavailable.

Table 1.

The percentage of households unable to achieve an actual level of k-anonymity (kact) for various values of the user-defined parameters for the inner (ka) and outer (kb) geomasking donut, which assumes that households are distributed homogeneously in space.

ka kb % kact < 5 % kact < 10 % kact < 15 % kact < 20 % kact < 25
5 50 3.96% 13.00% 22.59% 31.40% 39.18%
10 100 1.14% 4.83% 9.70% 15.03% 20.37%
15 150 0.54% 2.23% 5.19% 8.64% 12.23%
20 200 0.30% 1.21% 3.02% 5.36% 8.04%
25 250 0.20% 0.79% 1.99% 3.59% 5.63%
30 300 0.13% 0.56% 1.37% 2.57% 3.96%
35 350 0.10% 0.35% 0.93% 1.81% 3.00%
40 400 0.07% 0.29% 0.64% 1.31% 2.28%
45 450 0.07% 0.25% 0.54% 1.04% 1.79%
50 500 0.05% 0.15% 0.41% 0.75% 1.33%
60 600 0.03% 0.11% 0.26% 0.52% 0.93%
75 750 0.03% 0.08% 0.16% 0.30% 0.50%
Open in a new tab

4. Discussion

As the use of GIS has become more available to a variety of users, research involving health and disease mapping has risen as well. When the data are available at the address level, balancing individual privacy protection versus the spatial resolution of the map is an important initial consideration that should depend on several factors including the disease or infection being mapped.

Aggregating data has often been used to protect the individual in a database, but this method substantially reduces the resolution of the data available to the researcher. Random perturbation geomasks are desirable because the random component prevents one from back-transforming the process to find the original location. We prefer to use the donut method of random perturbation because it provides additional privacy protection for the individual with a negligible loss in sensitivity and specificity for detecting disease clusters (Hampton et al. 2009). Also, due to the minimum distance requirement, a subject cannot be randomly placed in its original location. This can be especially helpful in an area of the census block group where the household density is less than the mean. Finally, by assuring that the subject stays in its original census block group, the neighborhood demographic and socio-economic information assigned to the masked subject is relevant to the unknown original location.

Our geomasking simulation utilized households in place of persons for determining the distance of displacement and to calculate the estimated and actual k-anonymity. In the majority of real world situations, individual persons would be the basis of these calculations because individuals (not households) contract disease and the most readily available census statistics are produced for individuals. Across the United States, the average of 2.0 persons per household is fairly consistent. Therefore, we believe that using households as a proxy for individuals is a reasonable thing to do. However, using individuals should create even more heterogeneity in the population distribution because they are confined to the locations of the households. In other words, the people cannot be more evenly distributed than the households if you make the assumption that a person must live in an available household (discounting the fact that people could be homeless, etc.). Therefore, one might want to increase the displacement parameters to account for using individuals instead of households.

We used the census block group level to enhance the likelihood of adequate privacy protection. The average population of a block for census year 2000 in the state of North Carolina was only 34.5, making it insufficient for hiding cases. The census block group level, which had a mean population greater than 5,000, offered a large enough population to mask the subject and can always be upscaled to the census tract and county level. Using the smallest feasible unit (block group) is also desirable because the population density estimate used for calculating the distance of displacement should be more accurate on average since it is based on a smaller geographical area. ZIP codes do not necessarily correspond to census or county boundaries, reducing their desirability for geomasking algorithms.

We elected to keep the ratio of kb=10*ka constant simply to reduce the possible combinations of parameters to evaluate. In an actual spatial epidemiological application, the value for the inner radius of the donut should be carefully considered as the choice for the minimum amount of protection that is acceptable. The value for the outer donut should be viewed with regards to the maximum amount of spatial distortion acceptable. While the lower limit of ka is debatable with regards to how much protection is enough, the upper limit of kb is bounded by the fact that too much distortion approaches aggregation in mapping resolution, negating the benefits of the donut geomasking method. Additionally, while the upper bound for kb can be made infinite, the number of people contained in a census block group places its own bound on this parameter. For example, if kb is set to 10,000 and there are only 1,000 in the block group, the largest kact achievable is 1,000, due to the constraint that a subject must be geomasked within the same census block group.

Using a factor less than 10 should mean that a larger adjustment needs to be made to correct for population heterogeneity. A factor greater than 10 should need less of a correction because as the size of the area in the donut grows, the population density within the donut area should approach that of the respective census block group. For the same reason, our constraint that the subject must be masked within their census block group increases the need to correct for heterogeneity because the donut area is effectively reduced.

K-anonymity was chosen as the measure of privacy protection because it has been defined and referenced in other peer-reviewed research articles. However, it is a little misleading because one must know the original and masked location to calculate it. Under normal circumstances, only the masked location will be available. Given that the randomly generated distance and direction are unknown, and typically the masking parameters are unknown as well, the overall protection provided by our method is greater than the number calculated as the k-anonymity.

The donut geomasking method described in this paper makes the assumption that the masked coordinates of subjects is the only information available. Typically, health databases will also include other variables for the subjects such as sex, age, and race. The donut method can easily be adapted to account for these other factors. Since demographic information is available in the block group spatial data sets from the census, the number of people (or households in this simulation) in the distance of displacement calculation can simply be replaced by the number of people in the same age/sex/race category of the subject's respective census block group.

The tradeoff between the degree of protection and level of spatial detail depends on factors including the disease and concerns for patient confidentiality. Therefore, we provide a table showing the results for different levels of privacy protection for a given ka and kb, so that one can choose the level of confidentiality that works for their particular situation. As a general guideline, we suggest tripling the parameters ka and kb to help account for the heterogeneity in the population distribution across a given census block group. Our simulation consistently showed that 3*ka led to >99% of households having kact ≥ka.

If one is geomasking within the census block group, a rough measure of population heterogeneity can easily be obtained by calculating the variance of population density in the blocks that make up a block group. A low variance means that kest will more closely approximate kact. A high variance should lead one to choose more conservative parameters for the donut geomasking.

One of the limitations of this research is the fact that we only geomasked households in Orange County, North Carolina. We believe that this county was a reasonable choice because it contains a variety of population densities across its 56 census block groups that range from 40–17,000 persons/mi2, with heterogeneity in population distribution among and within block groups. Also, since this is the location for the University of North Carolina at Chapel Hill, our familiarity with the area helped inform conclusions regarding the simulation.

Orange County does not contain any large cities and it's possible that results could be different for a large urban area. For example, a census block group in a major urban area could contain high density residential units close to business or industrial areas with very few residential units, causing an even greater contrast in population heterogeneity than what we found. However, since large cities are often planned in a grid-like fashion, there is a high likelihood that they would more closely approximate a uniform population distribution than Orange County.

There has recently been a large increase in demand for mapping health outcomes in order to distinguish spatial patterns, correlate with environmental factors, and control outbreaks. As more GIS databases are created and made available to the public, it is critical to ensure that data from those patients in sensitive health databases remain protected and confidential throughout the research process.

References

  1. Armstrong MP, Rushton G, Zimmerman DL. Geographically masking health data to preserve confidentiality. Statist Med. 1999;18:497–525. doi: 10.1002/(sici)1097-0258(19990315)18:5<497::aid-sim45>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
  2. Armstrong MP, Ruggles AJ. Geographic information technologies and personal privacy. Cartographica. 2005;40(4):63–73. [Google Scholar]
  3. Boulos MNK, Cai Q, Padget JA, Rushton G. Using software agents to preserve individual health data confidentiality in micro-scale geographical analyses. Journal of Biomedical Informatics. 2006;39:160–170. doi: 10.1016/j.jbi.2005.06.003. [DOI] [PubMed] [Google Scholar]
  4. Brownstein JS, Cassa CA, Mandl KD. No place to hide-reverse identification of patients from published maps. N Engl J Med. 2006;355(16):1741–1742. doi: 10.1056/NEJMc061891. [DOI] [PubMed] [Google Scholar]
  5. Cassa CA, Grannis SJ, Overhage JM, Mandl KD. A context-sensitive approach to anonymizing spatial surveillance data: impact on outbreak detection. Journal of the American Medical Informatics Association. 2006;13(2):160–165. doi: 10.1197/jamia.M1920. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Duncan GT, Pearson RW. Enhancing access to microdata while protecting confidentiality: prospects for the future. Statistical Science. 1991;6(3):219–232. [Google Scholar]
  7. Gutmann MP, Stern PC, editors. Putting People on the Map: Protecting Confidentiality with Linked Social-Spatial Data. The National Academies Press; Washington, DC: 2007. [Google Scholar]
  8. Hampton KH, Fitch MK, Allshouse WB, Law DCG, Doherty IA, Leone PA, Serre ML, Miller WC. Mapping individual STD case data: geomasking events to protect patient privacy. 18th ISSTDR Meeting; London. June–July 2009.2009. [Google Scholar]
  9. Kwan M, Casas I, Schmitz BC. Protection of geoprivacy and accuracy of spatial information: how effective are geographical masks? Cartographica. 2004;39(2):15–28. [Google Scholar]
  10. MacDorman MF, Gay GA. State initiatives in geocoding vital statistics data. J Public Health Manage Pract. 1999;5:91–93. [PubMed] [Google Scholar]
  11. Olson KL, Grannis SJ, Mandl KD. Privacy protection versus cluster detection in spatial epidemiology. American Journal of Public Health. 2006;96(11):2002–2008. doi: 10.2105/AJPH.2005.069526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Orange County GIS Division [Accessed 28 February 2008];Orange County E911 Database. 2007 [online]. Available from: http://gis.co.orange.nc.us/land/search.asp.
  13. Rushton G, Armstrong MP, Gittler J, Greene BR, Pavlik CE, West MM, Zimmerman DL. Geocoding in cancer research. Am J Prev Med. 2006;30(2S):S16–S24. doi: 10.1016/j.amepre.2005.09.011. [DOI] [PubMed] [Google Scholar]
  14. Sherman JE, Fetters TL. Confidentiality concerns with mapping survey data in reproductive health research. Studies in Family Planning. 2007;38(4):309–321. doi: 10.1111/j.1728-4465.2007.00143.x. [DOI] [PubMed] [Google Scholar]
  15. Stinchcomb D. Procedures for geomasking to protect patient confidentiality. ESRI International Health GIS Conference; Washington, DC. 17–20 October 2004.2004. [Google Scholar]
  16. Sweeney L. Achieving k-anonymity privacy protection using generalization and suppression. International Journal on Uncertainty, Fuzziness and Knowledge-based Systems. 2002a;10(5):571–588. [Google Scholar]
  17. Sweeney L. K-anonymity: a model for protecting privacy. International Journal on Uncertainty, Fuzziness and Knowledge-based Systems. 2002b;10(5):557–570. [Google Scholar]
  18. Wieland SC, Cassa CA, Mandl KD, Berger B. Revealing the spatial distribution of a disease while preserving privacy. PNAS. 2008;105(46):17608–17613. doi: 10.1073/pnas.0801021105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wiggins L, editor. Using Geographic Information Systems Technology in the Collection, Analysis, and Presentation of Cancer Registry Data: A Handbook of Basic Practices. North American Association of Central Cancer Registries; Springfield, IL: 2002. [Google Scholar]

RESOURCES