Finite Element Algorithm for Frictionless Contact of Porous Permeable Media Under Finite Deformation and Sliding

Abstract

Background

This study formulates and implements a finite element contact algorithm for solid-fluid (biphasic) mixtures, accommodating both finite deformation and sliding. The finite element source code is made available to the general public.

Methods

The algorithm uses a penalty method regularized with an augmented Lagrangian method to enforce the continuity of contact traction and normal component of fluid flux across the contact interface. The formulation addresses the need to automatically enforce free-draining conditions outside of the contact interface. The formulation addresses the need to automatically enforce free-draining conditions outside of the contact interface.

Results

The accuracy of the implementation is verified using contact problems for which exact solutions are obtained by alternative analyses. Illustrations are also provided that demonstrate large deformations and sliding under configurations relevant to biomechanical applications such as articular contact.

Conclusions

This study addresses an important computational need in the biomechanics of porous-permeable soft tissues. Placing the source code in the public domain provides a useful resource to the biomechanics community.

Introduction

Porous media theories are widely applicable to the analysis of hydrated biological tissues, where they can describe the deformation of the solid matrix and flow of interstitial fluid. In the study of soft tissues in particular, large deformations are often encountered, which can be suitably investigated with the finite element method. Contact problems are fundamental to the study of biological tissues, especially in the area of diarthrodial joint biomechanics. Finite element formulations and implementations of the contact mechanics of porous media remain challenging, and only a limited number of studies have proposed solution schemes for these types of problems.

Donzelli and Spilker [1] have implemented a Lagrange multiplier method for examining the contact of biphasic cartilage layers [2] in two dimensions under small strains, whereas Yang and Spilker [3] have provided a similar method for three-dimensional problems. Chen et al. [4] have provided an implementation valid for large deformations and sliding, also using the method of Lagrange multipliers, formulated in a material frame. These implementations have provided a valuable description of alternative methods for enforcing contact conditions in porous media analyses. Unfortunately, finite element codes using these formulations are not generally available to the public.

A commonly used commercial finite element implementation of porous media contact is provided by Abaqus FEA (www.simulia.com), which has been used for studying articular contact mechanics [5-7]. This implementation is also able to analyze large sliding and finite deformations. However, to the best of our knowledge, the details of the implementation have not been published in the peer-reviewed literature. The Abaqus implementation allows the application of a ‘drainage-only-flow’ boundary condition that is inconsistent with the equation of conservation of mass across the contact interface, a limitation that needs to be corrected by a user-defined routine [5]. Furthermore, the Abaqus implementation does not automatically enforce free-draining conditions outside of the contact region while enforcing continuity of the contact traction and fluid flux across the contact interface.

The objective of the current study is to formulate a finite element contact implementation for solid-fluid mixtures (biphasic materials) in the spatial frame, that can accommodate finite deformation and large sliding, using a penalty method regularized with augmented Lagrangian to enforce the continuity of contact traction and normal component of fluid flux across the contact interface [8, 9]. This formulation explicitly addresses the need to automatically enforce free-draining conditions outside of the contact interface. Furthermore, the implementation of this contact algorithm is incorporated into a free, open source finite element code (FEBio, http://mrl.sci.utah.edu/software.php?menu=Software). Several examples are provided that verify the accuracy of this code.

Methods

Governing Equations for Solid-Fluid Mixtures

Consider a mixture consisting of a solid constituent and a fluid constituent. Both constituents are considered to be intrinsically incompressible, but the mixture can change volume when fluid enters or leaves the porous solid matrix [2, 10]. According to the kinematics of the continuum [11], each constituent α of a mixture (α = s for the solid and α = w for the fluid) has a separate motion χ^α (X^α,t) which places particles of each mixture constituent, originally located at X^α, in the current configuration x according to

$$\mathbf{x}={\mathbf{\chi }}^{\alpha }\left({\mathbf{X}}^{\alpha },t\right).$$ (1)

For the purpose of finite element analyses, the motion of the solid matrix, α = s, is of particular interest.

The governing equations that enter into the statement of virtual work are the conservation of linear momentum and the conservation of mass, for the mixture as a whole. Under quasi-static conditions, in the absence of external body forces, the conservation of momentum reduces to

$$\text{div}\mathbf{T}=0,$$ (2)

where T is the Cauchy stress for the mixture. Since the mixture is porous, this stress may also be written as

$$\mathbf{T}=-p\mathbf{I}+{\mathbf{T}}^e,$$ (3)

where p is the fluid pressure and T^e is the effective or extra stress, resulting from the deformation of the solid matrix. Conservation of mass for the mixture requires that

$$\text{div}\left({\mathbf{v}}^s+\mathbf{w}\right)=0,$$ (4)

where v^s = ∂χ^s/∂t is the solid matrix velocity and w is the flux of the fluid relative to the solid matrix. Let the solid matrix displacement be denoted by u, then v^s = u̇.

To relate the relative fluid flux w to the fluid pressure and solid deformation, it is necessary to employ the equation of conservation of linear momentum for the fluid,

$$-{\phi }^w\text{grad}p+{\widehat{\mathbf{p}}}_d^w=0$$ (5)

where φ^w is the solid matrix porosity, and ${\widehat{\mathbf{p}}}_d^w$ is the momentum exchange between the solid and fluid constituents, typically representing the frictional interaction between these constituents. This equation neglects the viscous stress of the fluid in comparison to ${\widehat{\mathbf{p}}}_d^w$. The most common constitutive relation is ${\widehat{\mathbf{p}}}_d^w=-{\phi }^w{\mathbf{K}}^{-1}\cdot \mathbf{w}$, where the second order, symmetric tensor K is the hydraulic permeability of the mixture. When combined with Eq.(5), it produces

$$\mathbf{w}=-\mathbf{K}\cdot \text{grad}p,$$ (6)

which is equivalent to Darcy's law. In general, K may be a function of the deformation.

Principle of Virtual Work

A weak form of the statement conservation of linear momemtum for the quasi-static case is obtained by using Eqs.(2) and (4):

$${\int }_b\left[\delta {\mathbf{v}}^s\cdot \text{div}\mathbf{T}+\delta p\text{div}\left({\mathbf{v}}^s+\mathbf{w}\right)\right]dv=0,$$ (7)

where b is the domain of interest defined on the solid matrix, δv^s is a virtual velocity of the solid, and δp is a virtual pressure of the fluid [12]; dv is an elemental volume of b. Using the divergence theorem, this expression may be rearranged as

$$\delta W={\int }_b\mathbf{T}:\delta {\mathbf{D}}^{s}dv-{\int }_{\partial b}\delta {\mathbf{v}}^s\cdot \mathbf{t}da+{\int }_b\left(\mathbf{w}\cdot \text{grad}\delta p-\delta p\text{div}{\mathbf{v}}^s\right)dv-{\int }_{\partial b}\delta p{w}_{n}da=0,$$ (8)

where δD^s = (gradδv^s + grad^T δv^s)/2 is the virtual rate of deformation tensor, t = T · n is the total traction on the surface ∂b, and w_n = w · n is the component of the fluid flux normal to ∂b, with n representing the unit outward normal to ∂b ; da represents an elemental area of ∂b. In this type of problem, essential boundary conditions are prescribed on u and p, and natural boundary conditions on t and w_n. In the expression of Eq.(8), δW (χ^s, p,δv^s,δ p) represents the virtual work.

Since the system of equations in Eq.(8) is highly nonlinear, its solution requires an iterative scheme such as Newton's method. This requires the linearization of δW at some trial solution $\left({\mathbf{\chi }}_k^s,p_k\right)$, along an increment Δu in χ^s and an increment Δp in p,

$$\delta W+D\delta W\left[\Delta \mathbf{u}\right]+D\delta W\left[\Delta p\right]=0,$$ (9)

where Df [Δq] represents the directional derivative of f along Δq. For convenience, the virtual work may be separated into its internal and external parts,

$$\delta W=\delta W_{\text{int}}-\delta W_{\text{ext}},$$ (10)

where

$$\delta W_{\text{int}}={\int }_b\mathbf{T}:\delta {\mathbf{D}}^{s}dv+{\int }_b\left(\mathbf{w}\cdot \text{grad}\delta p-\delta p\text{div}{\mathbf{v}}^s\right)dv,$$ (11)

and

$$\delta W_{\text{ext}}={\int }_{\partial b}\delta {\mathbf{v}}^s\cdot \mathbf{t}da+{\int }_{\partial b}\delta p{w}_{n}da.$$ (12)

The evaluation of the directional derivatives can be performed following a standard approach [13]. For the internal part of the virtual work, the directional derivative along Δu yields

$$D\delta W_{\text{int}}\left[\Delta \mathbf{u}\right]={\int }_b\delta {\mathbf{D}}^s:\mathcal{C}:\Delta \epsilon dv+{\int }_b\mathbf{T}:\left({\text{grad}}^T\Delta \mathbf{u}\cdot \text{grad}\delta {\mathbf{v}}^s\right)dv-{\int }_b\delta p\left(\left[\left(\text{div}\Delta \mathbf{u}\right)\mathbf{I}-{\text{grad}}^T\Delta \mathbf{u}\right]:\text{grad}{\mathbf{v}}^s+\text{div}\stackrel{.}{\stackrel{‒}{\Delta \mathbf{u}}}\right)dv,-{\int }_b\text{grad}\delta p\cdot \left(\mathcal{K}:\Delta \epsilon \right)\cdot \text{grad}pdv$$ (13)

where $\mathcal{C}$ is the fourth-order spatial elasticity tensor for the mixture and Δε = (grad Δu + grad^T Δu)/2. Based on the relation of Eq.(3), the spatial elasticity tensor may also be expanded as

$$\mathcal{C}={\mathcal{C}}^e+p\left(-\mathbf{I}\otimes \mathbf{I}+2\mathbf{I}\underset{‒}{\stackrel{‒}{\otimes }}\mathbf{I}\right),$$ (14)

where ${\mathcal{C}}^e$ is the spatial elasticity tensor for the solid matrix.¹ It is related to the material elasticity tensor ${\mathbb{C}}^e$ via

$${\mathcal{C}}^e=J^{-1}\left(\mathbf{F}\underset{‒}{\otimes }\mathbf{F}\right):{\mathbb{C}}^e:\left({\mathbf{F}}^T\underset{‒}{\otimes }{\mathbf{F}}^T\right),$$ (15)

where F = Gradχ^s is the deformation gradient of the solid matrix. As usual in hyperelasticity, ${\mathbb{C}}^e=\partial {\mathbf{S}}^e∕\partial \mathbf{E}$ where E is the Lagrangian strain tensor and S^e is the second Piola-Kirchhoff stress tensor, related to the Cauchy stress tensor via T^e = J^-1F·S^e · F^T. Since S^e may be obtained from a strain energy density function Ψ according to S^e = ∂Ψ/∂E, it follows that the material and spatial elasticity tensors exhibit two minor symmetries and one major symmetry.

Similarly, $\mathcal{K}$ is a fourth-order tensor that represents the spatial measure of the rate of change of permeability with strain. It is related to its material frame equivalent $\mathbb{K}$ via

$$\mathcal{K}=J^{-1}\left(\mathbf{F}\underset{‒}{\otimes }\mathbf{F}\right):\mathbb{K}:\left({\mathbf{F}}^T\underset{‒}{\otimes }{\mathbf{F}}^T\right),$$ (16)

where $\mathbb{K}=\partial {\mathbf{K}}_0∕\partial \mathbf{E}$ and K₀ is the permeability tensor in the material frame, such that K = J^-1F · K₀ · F^T. Since K₀ and E are symmetric tensors, it follows that $\mathbb{K}$ and $\mathcal{K}$ exhibit two minor symmetries (e.g., ${\mathcal{K}}_{jikl}={\mathcal{K}}_{ijkl}$ and ${\mathcal{K}}_{ijlk}={\mathcal{K}}_{ijkl}$); however, unlike the elasticity tensor, it is not necessary that these tensors exhibit major symmetry (e.g., ${\mathcal{K}}_{klij}\ne {\mathcal{K}}_{ijkl}$ in general).

The directional derivative of δW_int along Δp is given by

$$D\delta W_{\text{int}}\left[\Delta p\right]=-{\int }_b\text{grad}\delta p\cdot \mathbf{K}\cdot \text{grad}\Delta pdv-{\int }_b\Delta p\text{div}\delta {\mathbf{v}}^{s}dv.$$ (17)

Note that letting p = 0 and δp = 0 in the above equations recovers the virtual work relations for nonlinear elasticity of compressible solids. The resulting simplified equation emerging from Eq.(13) is symmetric to interchanges of Δu and δv^s, producing a symmetric stiffness matrix in the finite element formulation [13]. However, the general relations of Eqs.(13) and (17) do not exhibit symmetry to interchanges of (Δu, Δp) and (δv^s,δ p), implying that the finite element stiffness matrix for a solid-fluid mixture is not symmetric under general conditions.

The directional derivatives of the external virtual work δW_ext depend on the type of boundary conditions being considered. Conditions relevant to contact analyses are addressed below.

Contact Integral

Consider that the domain b consists of two bodies b⁽¹⁾ and b⁽²⁾ with respective boundaries ∂b⁽¹⁾ and ∂b⁽²⁾. The two bodies are in contact over portions of ∂b⁽¹⁾ and ∂b⁽²⁾, respectively denoted by γ⁽¹⁾ and γ⁽²⁾. According to Eq.(12), the part of the external virtual work arising from the contact may be written as

$$\delta G_c=\sum _{i=1}^2{\int }_{{\gamma }^{\left(i\right)}}\left(\delta {\mathbf{v}}^{\left(i\right)}\cdot {\mathbf{t}}^{\left(i\right)}+\delta p^{\left(i\right)}{w}_n^{\left(i\right)}\right)d{a}^{\left(i\right)},$$ (18)

where δv⁽ⁱ⁾ is a virtual solid velocity and δ p⁽ⁱ⁾ a virtual fluid pressure on γ⁽ⁱ⁾, and da⁽ⁱ⁾ is an elemental area of γ⁽ⁱ⁾. Similarly, t⁽ⁱ⁾ and $w_n^{\left(i\right)}$ represent the total mixture traction and outward normal relative fluid flux on γ⁽ⁱ⁾. According to basic jump conditions on the linear momentum and conservation of mass [15, 16], the total traction and the outward normal component of the fluid flux at the contact interface of solid-fluid mixtures must satisfy

$${\mathbf{t}}^{\left(1\right)}+{\mathbf{t}}^{\left(2\right)}=0,w_n^{\left(1\right)}+w_n^{\left(2\right)}=0.$$ (19)

Similarly, continuity of force and flow rate across the interface requires that t⁽¹⁾da⁽¹⁾ + t⁽²⁾da⁽²⁾ = 0 and $w_n^{\left(1\right)}d{a}^{\left(1\right)}+w_n^{\left(2\right)}d{a}^{\left(2\right)}=0$, respectively. Therefore, the virtual work arising from contact may be rewritten as an integral over γ⁽¹⁾ only:

$$\delta G_c={\int }_{{\gamma }^{\left(1\right)}}\left[\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot {\mathbf{t}}^{\left(1\right)}+\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)w_n^{\left(1\right)}\right]d{a}^{\left(1\right)}.$$ (20)

Eq.(20) is commonly referred to as the contact integral.

Frictionless Contact

The formulation of frictional contact of porous media requires special consideration with regard to interstitial fluid pressurization [17]; this topic is beyond the scope of the present study. Therefore, this presentation focuses on the special case of frictionless contact. To evaluate the directional derivatives of δG_c along Δu⁽ⁱ⁾ and Δp⁽ⁱ⁾, it is necessary to formulate the integration over an invariant domain, so that the directional derivative may be brought inside the integral without concern for variations in the domain of integration. In our approach, we extend the method adopted by Bonet and Wood for evaluating the directional derivative of the external virtual work integral in the case of a uniform pressure acting normal to the surface [13]. The method is extended by accounting for frictionless contact conditions, whereby

$${\mathbf{t}}^{\left(i\right)}=t_n{\mathbf{n}}^{\left(i\right)}$$ (21)

and t_n is the normal component of the contact traction, which is unknown a priori. Note that it is possible to model frictionless contact in this solid-fluid mixture framework because the viscous stress in the fluid is neglected.

On each surface γ⁽ⁱ⁾ (i = 1,2), covariant basis vectors are denoted by

$${\mathbf{g}}_{\alpha }^{\left(i\right)}=\frac{\partial {\mathbf{x}}^{\left(i\right)}}{\partial {\eta }_{\left(i\right)}^{\alpha }}\alpha =1,2.$$ (22)

Here, x⁽ⁱ⁾ is the current position of point X⁽ⁱ⁾ on γ⁽ⁱ⁾, ${\eta }_{\left(i\right)}^{\alpha }$ are the contravariant parametric surface coordinates of that point, and Greek subscripts and superscripts vary implicitly from 1 to 2. These covariant basis vectors are tangent to γ⁽ⁱ⁾ and it follows that

$${\mathbf{n}}^{\left(i\right)}=\frac{{\mathbf{g}}_1^{\left(i\right)}\times {\mathbf{g}}_2^{\left(i\right)}}{\mid {\mathbf{g}}_1^{\left(i\right)}\times {\mathbf{g}}_2^{\left(i\right)}\mid },$$ (23)

and

$$d{a}^{\left(i\right)}=J_{\eta }^{\left(i\right)}d{\eta }_{\left(i\right)}^{1}d{\eta }_{\left(i\right)}^2,J_{\eta }^{\left(i\right)}=\mid {\mathbf{g}}_1^{\left(i\right)}\times {\mathbf{g}}_2^{\left(i\right)}\mid .$$ (24)

Therefore, in the case of frictionless contact, the contact integral of Eq.(20) may be rewritten in terms of the covariant base vectors as

$$\delta G_c={\int }_{{\Gamma }_{\eta }^{\left(1\right)}}{t}_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right)d{\eta }_{\left(1\right)}^{1}d{\eta }_{\left(1\right)}^2+{\int }_{{\Gamma }_{\eta }^{\left(1\right)}}{w}_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid d{\eta }_{\left(1\right)}^{1}d{\eta }_{\left(1\right)}^2,$$ (25)

where $w_n=w_n^{\left(1\right)}$, and ${\Gamma }_{\eta }^{\left(1\right)}$ represents the invariant parametric space of surface γ⁽¹⁾.

Due to the invariance of ${\Gamma }_{\eta }^{\left(1\right)}$, it is possible to linearize δG_c by applying the directional derivative operator directly to the integrand:

$$D\delta G_c={\int }_{{\Gamma }_{\eta }^{\left(1\right)}}D\left(t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right)\right)d{\eta }_{\left(1\right)}^{1}d{\eta }_{\left(1\right)}^2+{\int }_{{\Gamma }_{\eta }^{\left(1\right)}}D\left(w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid \right)d{\eta }_{\left(1\right)}^{1}d{\eta }_{\left(1\right)}^2.$$ (26)

In particular,

$$D\left(t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right)\right)=D{t}_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right)+t_n\left(D\delta {\mathbf{v}}^{\left(1\right)}-D\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right),+t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot D\left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right)$$ (27)

and

$$D\left(w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid \right)=D{w}_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid +w_n\left(D\delta p^{\left(1\right)}-D\delta p^{\left(2\right)}\right)\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid ,+w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)D\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid$$ (28)

where it is understood that for any function f,

$$Df\equiv \sum _{i=1}^{2}Df\left[\Delta {\mathbf{u}}^{\left(i\right)}\right]+Df\left[\Delta p^{\left(i\right)}\right].$$ (29)

To evaluate these directional derivatives, it is necessary to define a relation between contacting points on γ⁽¹⁾ and γ⁽²⁾.

Gap Function

The definition of the gap function employed in this study differs slightly from the conventional approach that leads to the definition of contacting surfaces as ‘slave’ and ‘master’ surfaces [8, 9, 18]. Therefore that nomenclature is not employed here, and the contact surfaces are simply called ‘primary’ and ‘secondary’. Let the gap function g be defined as the distance from the primary surface to the secondary surface, along the unit outward normal to the primary surface,

$${\mathbf{x}}^{\left(2\right)}={\mathbf{x}}^{\left(1\right)}+g{\mathbf{n}}^{\left(1\right)},g=\left({\mathbf{x}}^{\left(2\right)}-{\mathbf{x}}^{\left(1\right)}\right)\cdot {\mathbf{n}}^{\left(1\right)}$$ (30)

In this definition, g is positive when the surfaces α⁽¹⁾ and α⁽²⁾ are separated, and negative when the surfaces penetrate. In a strict geometrical sense, x⁽¹⁾ is the location on γ⁽¹⁾ closest to x⁽²⁾. (In the conventional approach, g is defined along the normal to the secondary surface, n⁽²⁾, and is usually positive when surfaces penetrate, g = (x⁽²⁾ – x⁽¹⁾)· n⁽²⁾ [8]; then, geometrically, x⁽²⁾ is the location on γ⁽²⁾ closest to x⁽¹⁾. In the limit of true contact, when the surfaces are perfectly mating, n⁽²⁾ → –n⁽¹⁾ and the positions of x⁽¹⁾ and x⁽²⁾ coincide, so that the distinction between the current and conventional definitions of the gap function reduces only to the sign of g.)

The contact integral over γ⁽¹⁾ is performed over points X⁽¹⁾ of prescribed parametric coordinates ${\eta }_{\left(1\right)}^{\alpha }$. However, the point X⁽²⁾ on γ⁽²⁾ that is in contact with X⁽¹⁾ has parametric coordinates ${\eta }_{\left(2\right)}^{\alpha }$ that vary according to changes in x⁽¹⁾, x⁽²⁾ and n⁽¹⁾. Accordingly, directional derivatives of x⁽ⁱ⁾, p⁽ⁱ⁾, δv⁽ⁱ⁾ and δ p⁽ⁱ⁾ are given by

$$\begin{array}{cc}\hfill D{\mathbf{x}}^{\left(1\right)}& =\Delta {\mathbf{u}}^{\left(1\right)}D{\mathbf{x}}^{\left(2\right)}=\Delta {\mathbf{u}}^{\left(2\right)}+{\mathbf{g}}_{\alpha }^{\left(2\right)}\Delta {\eta }_{\left(2\right)}^{\alpha }\hfill \\ \hfill D{p}^{\left(1\right)}& =\Delta p^{\left(1\right)}D{p}^{\left(2\right)}=\Delta p^{\left(2\right)}+\frac{\partial p^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\Delta {\eta }_{\left(2\right)}^{\alpha }\hfill \\ \hfill D\delta {\mathbf{v}}^{\left(1\right)}& =0D\delta {\mathbf{v}}^{\left(2\right)}=\frac{\partial \delta {\mathbf{v}}^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\Delta {\eta }_{\left(2\right)}^{\alpha }\hfill \\ \hfill D\delta p^{\left(1\right)}& =0D\delta p^{\left(2\right)}=\frac{\partial \delta p^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\Delta {\eta }_{\left(2\right)}^{\alpha }.\hfill \end{array}$$ (31)

To evaluate $\Delta {\eta }_{\left(2\right)}^{\alpha }$ in terms of increments in solid displacements on the contacting surfaces, we use a method similar to that proposed by Laursen and Simo [8]: Recognizing that $\left({\mathbf{x}}^{\left(2\right)}-{\mathbf{x}}^{\left(1\right)}\right)\cdot {\mathbf{g}}_{\alpha }^{\left(1\right)}=0$, the directional derivative of this expression is evaluated and the resulting system of linear equations in two unknowns is inverted to yield

$$\Delta {\eta }_{\left(2\right)}^{\alpha }=\left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)\cdot a^{\alpha \beta }{\mathbf{g}}_{\beta }^{\left(1\right)}-a^{\alpha \beta }g{\mathbf{n}}^{\left(1\right)}\cdot \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\beta }},$$ (32)

where a^αα = (A_αβ)^-1 and $A_{\alpha \beta }={\mathbf{g}}_{\alpha }^{\left(1\right)}\cdot {\mathbf{g}}_{\beta }^{\left(2\right)}$.

Penalty Method

To enforce the contact constraint based on the penalty method, let the normal component of the contact traction be given by

$$t_n=\{\begin{array}{cc}{\epsilon }_{n}g\hfill & g<0\hfill \\ 0\hfill & g\ge 0\hfill \end{array}\phantom{\}},$$ (33)

where ε_n is a penalty factor with units of force per volume. In the notation of this study, the contact traction t_n is negative in compression and we avoid using the term ‘contact pressure’ which might cause confusion with the fluid pressure p⁽ⁱ⁾ on the contact interface. For a sufficiently large penalty factor, the penalty method ensures that the contact surfaces overlap by an acceptably negligible amount g. Note that by letting t_n = 0 outside of the contact interface, it is implicitly assumed that the ambient fluid pressure is zero in the bath surrounding the contacting bodies, since t_n is a traction component derived from the mixture stress T in Eq.(3).

In mixtures of solids and fluids, an additional constraint on continuity must be satisfied at a porous-permeable contact interface. The constraint is derived from jump conditions on the mechano-chemical potential on a non-dissipative interface [15, 16, 19]:

$$p^{\left(1\right)}=p^{\left(2\right)},$$ (34)

where p⁽ⁱ⁾ represents the fluid pressure on γ⁽ⁱ⁾. The penalty method may be used to enforce this condition, using

$$\{\begin{array}{cc}{w}_n={\epsilon }_p\pi \hfill & t_n<0\hfill \\ p^{\left(i\right)}=0\hfill & t_n=0\hfill \end{array}\phantom{\}},$$ (35)

where

$$\pi =p^{\left(1\right)}-p^{\left(2\right)}.$$ (36)

ε_p is a penalty factor with units of membrane permeability (length cubed per force·time), and the pressures p⁽ⁱ⁾ are understood to represent gauge pressures. When ε_p is sufficiently large, the penalty method ensures that the fluid pressure difference π is acceptably negligible. The condition w_n = ε_pπ appearing in Eq.(35), valid inside the contact region, is similar to the condition enforced by Federico et al. [5] in their Abaqus finite element contact analysis. In the special case when one of the contacting bodies is a non-porous solid, then w_n = 0 should be used instead, inside the contact interface. In all cases, outside of the contact region, the normal traction and fluid pressure must reduce to zero.

The penalty method may also be regularized using an augmented Lagrangian framework to overcome the numerical ill-conditioning resulting from large penalty factors and to allow enforcement of the constraints based on user-defined tolerances. The scheme outlined by Simo and Laursen [9] was adapted to the current porous media contact framework (Table 1).

Table 1.

Augmented Lagrangian algorithm for frictionless contact of porous media

Initialization of contact iterations:

Set r = 0

$\text{Set}{\lambda }_n^{\left(r\right)}={\lambda }_n\text{from last time step}$

$\text{Set}{\lambda }_p^{\left(r\right)}={\lambda }_p\text{from last time step}$

Solution Step:

Do while contact iterations have not converged

Do while nonlinear iterations have not converged

Evaluate g(X(1)) and π(X(1)) for all X(1) ∊ ∂v(1)

$\text{Set}{t}_n=\{\begin{array}{cc}{\lambda }_n^{\left(r\right)}+{\epsilon }_{n}g\hfill & {\lambda }_n^{\left(r\right)}+{\epsilon }_{n}g<0\hfill \\ 0\hfill & {\lambda }_n^{\left(r\right)}+{\epsilon }_{n}g\ge 0\hfill \end{array}\phantom{\}}$

$\text{Set}\{\begin{array}{cc}{w}_n={\lambda }_p^{\left(r\right)}+{\epsilon }_p\pi \hfill & t_n<0\hfill \\ p^{\left(i\right)}=0\hfill & t_n=0\hfill \end{array}\phantom{\}}$

Solve for Δu and Δp

Check convergence of nonlinear iterations

End Do

If |g(X(1))|>GTOL or |π(X(1))|>PTOL for any X(1) ∊ γ(1)

Augment:

$\text{Set}{\lambda }_n^{(r+1)}=\{\begin{array}{cc}{\lambda }_n^{\left(r\right)}+{\epsilon }_{n}g\hfill & {\lambda }_n^{\left(r\right)}+{\epsilon }_{n}g<0\hfill \\ 0\hfill & {\lambda }_n^{\left(r\right)}+{\epsilon }_{n}g\ge 0\hfill \end{array}\phantom{\}}$

$\text{Set}{\lambda }_p^{(r+1)}=\{\begin{array}{cc}{\lambda }_p^{\left(r\right)}+{\epsilon }_p\pi \hfill & {\lambda }_n^{(r+1)}<0\hfill \\ 0\hfill & {\lambda }_n^{(r+1)}=0\hfill \end{array}\phantom{\}}$

r ← r + 1

Else contact has converged

End Do

Given the relations of Eqs.(33) and (35) inside the contact interface (t_n < 0), the directional derivatives of t_n and w_n reduce to Dt_n = ε_nDg and Dw_n = ε_pDπ. Using the definitions of Eqs.(30) and (36) and the relations of Eq.(31), it follows that

$$D{t}_n={\epsilon }_n\left(\Delta {\mathbf{u}}^{\left(2\right)}-\Delta {\mathbf{u}}^{\left(1\right)}+{\mathbf{g}}_{\alpha }^{\left(2\right)}\Delta {\eta }_{\left(2\right)}^{\alpha }\right)\cdot {\mathbf{n}}^{\left(1\right)},$$ (37)

$$D{w}_n={\epsilon }_p\left(\Delta p^{\left(1\right)}-\Delta p^{\left(2\right)}-\frac{\partial p^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\Delta {\eta }_{\left(2\right)}^{\alpha }\right).$$ (38)

These expressions can be substituted into Eqs.(27)-(28), and using Eqs.(31)-(32), the resulting expressions become

$$D\left(t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right)\right)=-J_{\eta }^{\left(1\right)}{\epsilon }_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{n}}^{\left(1\right)}\otimes {\mathbf{n}}^{\left(1\right)}\right)\cdot \left(\mathbf{I}-a^{\alpha \beta }{\mathbf{g}}_{\alpha }^{\left(2\right)}\otimes {\mathbf{g}}_{\beta }^{\left(1\right)}\right)\cdot \left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)-J_{\eta }^{\left(1\right)}{t}_n\left(a^{\alpha \beta }{\mathbf{g}}_{\alpha }^{\left(2\right)}\cdot {\mathbf{n}}^{\left(1\right)}\right)\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{n}}^{\left(1\right)}\otimes {\mathbf{n}}^{\left(1\right)}\right)\cdot \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\beta }}-J_{\eta }^{\left(1\right)}{t}_n\frac{\partial \delta {\mathbf{v}}^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\cdot \left({\mathbf{n}}^{\left(1\right)}\otimes a^{\alpha \beta }{\mathbf{g}}_{\beta }^{\left(1\right)}\right)\cdot \left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)+g{J}_{\eta }^{\left(1\right)}{t}_n{a}^{\alpha \beta }\frac{\partial \delta {\mathbf{v}}^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\cdot \left({\mathbf{n}}^{\left(1\right)}\otimes {\mathbf{n}}^{\left(1\right)}\right)\cdot \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\beta }}+t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left(\frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^1}\times {\mathbf{g}}_2^{\left(1\right)}+{\mathbf{g}}_1^{\left(1\right)}\times \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^2}\right),$$ (39)

$$D\left(w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid \right)=J_{\eta }^{\left(1\right)}{\epsilon }_p\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\left(\Delta p^{\left(1\right)}-\Delta p^{\left(2\right)}\right)-J_{\eta }^{\left(1\right)}{\epsilon }_p\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\frac{\partial p^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\left(\left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)\cdot a^{\alpha \beta }{\mathbf{g}}_{\beta }^{\left(1\right)}-a^{\alpha \beta }g{\mathbf{n}}^{\left(1\right)}\cdot \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\beta }}\right)-J_{\eta }^{\left(1\right)}{w}_n\frac{\partial \delta p^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\left(\left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)\cdot a^{\alpha \beta }{\mathbf{g}}_{\beta }^{\left(1\right)}-a^{\alpha \beta }g{\mathbf{n}}^{\left(1\right)}\cdot \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\beta }}\right)+w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right){\mathbf{n}}^{\left(1\right)}\cdot \left(\frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^1}\times {\mathbf{g}}_2^{\left(1\right)}+{\mathbf{g}}_1^{\left(1\right)}\times \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^2}\right).$$ (40)

Note that instances of ε_ng and ε_pπ were respectively substituted with t_n and w_n in the above expressions.

Now these expressions can be evaluated in the limit of true contact when γ⁽¹⁾ and γ⁽²⁾ become perfectly mating surfaces, from which a number of relations emerge, such as g → 0, n⁽²⁾ → –n⁽¹⁾ and $a^{\alpha \beta }\to {\mathbf{g}}_{\left(2\right)}^{\alpha }\cdot {\mathbf{g}}_{\left(1\right)}^{\beta }$, where ${\mathbf{g}}_{\left(i\right)}^{\alpha }$ are contravariant basis vectors on γ⁽ⁱ⁾. Thus, in this limit, $a^{\alpha \beta }{\mathbf{g}}_{\beta }^{\left(1\right)}={\mathbf{g}}_{\left(2\right)}^{\alpha }$, $a^{\alpha \beta }{\mathbf{g}}_{\alpha }^{\left(2\right)}={\mathbf{g}}_{\left(1\right)}^{\beta }$ and $\mathbf{I}-a^{\alpha \beta }{\mathbf{g}}_{\alpha }^{\left(2\right)}\otimes {\mathbf{g}}_{\beta }^{\left(1\right)}=\mathbf{I}-{\mathbf{g}}_{\left(1\right)}^{\beta }\otimes {\mathbf{g}}_{\beta }^{\left(1\right)}={\mathbf{n}}^{\left(1\right)}\otimes {\mathbf{n}}^{\left(1\right)}$. Furthermore, since p⁽²⁾ = p⁽¹⁾ on the contact interface according to Eq.(34), the projections of the gradient of the fluid pressure on γ⁽¹⁾ and γ⁽²⁾ must be the same, $\frac{\partial p^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}{\mathbf{g}}_{\left(2\right)}^{\alpha }=\frac{\partial p^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\alpha }}{\mathbf{g}}_{\left(1\right)}^{\alpha }$; this substitution is particularly useful when analyzing contact with a rigid impermeable or semi-permeable wall (see below). Given these identities, Eqs.(39)-(40) further simplify to

$$D\left(t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\right)\right)=-J_{\eta }^{\left(1\right)}{\epsilon }_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left({\mathbf{n}}^{\left(1\right)}\otimes {\mathbf{n}}^{\left(1\right)}\right)\cdot \left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)+J_{\eta }^{\left(1\right)}{t}_n\frac{\partial \delta {\mathbf{v}}^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}\cdot \left({\mathbf{n}}^{\left(2\right)}\otimes {\mathbf{g}}_{\left(2\right)}^{\alpha }\right)\cdot \left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)+t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot \left(\frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^1}\times {\mathbf{g}}_2^{\left(1\right)}+{\mathbf{g}}_1^{\left(1\right)}\times \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^2}\right),$$ (41)

$$D\left(w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\mid {\mathbf{g}}_1^{\left(1\right)}\times {\mathbf{g}}_2^{\left(1\right)}\mid \right)=J_{\eta }^{\left(1\right)}{\epsilon }_p\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\left(\Delta p^{\left(1\right)}-\Delta p^{\left(2\right)}\right)-J_{\eta }^{\left(1\right)}\left[{\epsilon }_p\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\frac{\partial p^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\alpha }}{\mathbf{g}}_{\left(1\right)}^{\alpha }+w_n\frac{\partial \delta p^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}{\mathbf{g}}_{\left(2\right)}^{\alpha }\right]\cdot \left(\Delta {\mathbf{u}}^{\left(1\right)}-\Delta {\mathbf{u}}^{\left(2\right)}\right)+w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right){\mathbf{n}}^{\left(1\right)}\cdot \left(\frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^1}\times {\mathbf{g}}_2^{\left(1\right)}+{\mathbf{g}}_1^{\left(1\right)}\times \frac{\partial \Delta {\mathbf{u}}^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^2}\right).$$ (42)

and these relations may now be used to evaluate DδG_c from Eq.(26).

Discretization of Contact Virtual Work

The contact integral of Eq.(25) may be discretized as

$$\delta G_c=\sum _{e=1}^{n_e^{\left(1\right)}}\sum _{k=1}^{n_{\text{int}}^{\left(e\right)}}{W}_k{J}_{\eta }^{\left(1\right)}\left[t_n\left(\delta {\mathbf{v}}^{\left(1\right)}-\delta {\mathbf{v}}^{\left(2\right)}\right)\cdot {\mathbf{n}}^{\left(1\right)}+w_n\left(\delta p^{\left(1\right)}-\delta p^{\left(2\right)}\right)\right],$$ (43)

where $n_e^{\left(1\right)}$ is the number of element faces on γ⁽¹⁾, $n_{\text{int}}^{\left(e\right)}$ is the number of integration points on the e – th element face of γ⁽¹⁾, W_k is the weight associated with the k – th integration point, and where it should be understood that terms associated with γ⁽¹⁾ (such as $J_{\eta }^{\left(1\right)}$, δv⁽¹⁾, t_n, etc.) are evaluated at the parametric coordinates ${\eta }_{\left(1\right)}^{\alpha }$ of X⁽¹⁾ representing the k – th integration point, and terms associated with γ⁽²⁾ (such as δv⁽²⁾ and δ p⁽²⁾) are evaluated at the parametric coordinates ${\eta }_{\left(2\right)}^{\alpha }$ of the point X⁽²⁾ closest to X⁽¹⁾ according to Eq.(30).

The continuous variables on the primary and secondary surface may be interpolated over each element face according to

$$\begin{array}{cc}\hfill \delta {\mathbf{v}}^{\left(1\right)}& =\sum _{a=1}^{m^{\left(1\right)}}{N}_a^{\left(1\right)}\delta {\mathbf{v}}_a^{\left(1\right)}\delta {\mathbf{v}}^{\left(2\right)}=\sum _{b=1}^{m^{\left(2\right)}}{N}_b^{\left(2\right)}\delta {\mathbf{v}}_b^{\left(2\right)}\hfill \\ \hfill \Delta {\mathbf{u}}^{\left(1\right)}& =\sum _{c=1}^{m^{\left(1\right)}}{N}_c^{\left(1\right)}\Delta {\mathbf{u}}_c^{\left(1\right)}\Delta {\mathbf{u}}^{\left(2\right)}=\sum _{d=1}^{m^{\left(2\right)}}{N}_d^{\left(2\right)}\Delta {\mathbf{u}}_d^{\left(2\right)}\hfill \\ \hfill \delta p^{\left(1\right)}& =\sum _{a=1}^{m^{\left(1\right)}}{N}_a^{\left(1\right)}\delta p_a^{\left(1\right)}\delta p^{\left(2\right)}=\sum _{b=1}^{m^{\left(2\right)}}{N}_b^{\left(2\right)}\delta p_b^{\left(2\right)}\hfill \\ \hfill \Delta p^{\left(1\right)}& =\sum _{c=1}^{m^{\left(1\right)}}{N}_c^{\left(1\right)}\Delta p_c^{\left(1\right)}\Delta p^{\left(2\right)}=\sum _{d=1}^{m^{\left(2\right)}}{N}_d^{\left(2\right)}\Delta p_d^{\left(2\right)},\hfill \end{array}$$ (44)

where $N_a^{\left(i\right)}$ represent interpolation functions on the element faces of γ⁽ⁱ⁾, m⁽ⁱ⁾ is the number of nodes and interpolation functions on each element face, and $\delta {\mathbf{v}}_a^{\left(i\right)}$,$\delta p_a^{\left(i\right)}$,$\Delta {\mathbf{u}}_a^{\left(i\right)}$,$\Delta p_a^{\left(i\right)}$ represent respective nodal values of δv⁽ⁱ⁾,δ p⁽ⁱ⁾, Δu⁽ⁱ⁾, Δp⁽ⁱ⁾. In this approach, it is assumed from the outset that displacements and fluid pressures use the same nodal interpolation scheme. Using Eq.(44), the contact integral of Eq.(43) may be rewritten as

$$\delta G_c=\sum _{e=1}^{n_e^{\left(1\right)}}\sum _{k=1}^{n_{\text{int}}^{\left(e\right)}}{W}_k{J}_{\eta }^{\left(1\right)}\left(\sum _{a=1}^{m^{\left(1\right)}}\left[\delta {\mathbf{v}}_a^{\left(1\right)}\delta p_a^{\left(1\right)}\right]\cdot \left[\begin{array}{c}\hfill {\mathbf{f}}_a^{\left(1\right)}\hfill \\ \hfill f_a^{\left(1\right)}\hfill \end{array}\right]+\sum _{b=1}^{m_k^{\left(2\right)}}\left[\delta {\mathbf{v}}_{b,k}^{\left(2\right)}\delta p_{b,k}^{\left(2\right)}\right]\cdot \left[\begin{array}{c}\hfill {\mathbf{f}}_{b,k}^{\left(2\right)}\hfill \\ \hfill f_{b,k}^{\left(2\right)}\hfill \end{array}\right]\right),$$ (45)

where

$$\begin{array}{cc}\hfill {\mathbf{f}}_a^{\left(1\right)}& =N_a^{\left(1\right)}{t}_n{\mathbf{n}}^{\left(1\right)}{f}_a^{\left(1\right)}=N_a^{\left(1\right)}{w}_n\hfill \\ \hfill {\mathbf{f}}_{b,k}^{\left(2\right)}& =-N_b^{\left(2\right)}{t}_n{\mathbf{n}}^{\left(1\right)}{f}_{b,k}^{\left(2\right)}=-N_b^{\left(2\right)}{w}_n.\hfill \end{array}$$ (46)

The subscript k appearing in the terms associated with γ⁽²⁾ emphasizes that there may be up to $n_{\text{int}}^{\left(e\right)}$ distinct element faces on γ⁽²⁾ associated with all the integration points X⁽¹⁾ on the e – th element face of γ⁽¹⁾, based on the location of X⁽²⁾ obtained from Eq.(30).

Similarly, substituting the interpolations of Eq.(44) into Eqs.(41)-(42), and the resulting expressions into Eq.(26), the directional derivative DδG_c may be discretized as

$$\begin{array}{cc}\hfill & -D\delta G_c=\sum _{e=1}^{n_e^{\left(1\right)}}\sum _{k=1}^{n_{\text{int}}^{\left(e\right)}}{W}_k{J}_{\eta }^{\left(1\right)}\hfill \\ \hfill & (\sum _{a=1}^{m^{\left(1\right)}}\left[\delta {\mathbf{v}}_a^{\left(1\right)}\delta p_a^{\left(1\right)}\right]\cdot \left(\sum _{c=1}^{m^{\left(1\right)}}\left[\begin{array}{cc}\hfill {\mathbf{K}}_{ac}^{(1,1)}\hfill & \hfill 0\hfill \\ \hfill {\mathbf{k}}_{ac}^{(1,1)}\hfill & \hfill k_{ac}^{(1,1)}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill \Delta {\mathbf{u}}_c^{\left(1\right)}\hfill \\ \hfill \Delta p_c^{\left(1\right)}\hfill \end{array}\right]+\sum _{d=1}^{m_k^{\left(2\right)}}\left[\begin{array}{cc}\hfill {\mathbf{K}}_{ad,k}^{(1,2)}\hfill & \hfill 0\hfill \\ \hfill {\mathbf{k}}_{ad,k}^{(1,2)}\hfill & \hfill k_{ad,k}^{(1,2)}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill \Delta {\mathbf{u}}_{d,k}^{\left(2\right)}\hfill \\ \hfill \Delta p_{d,k}^{\left(2\right)}\hfill \end{array}\right]\right)\phantom{)}\hfill \\ \hfill & \phantom{(}+\sum _{b=1}^{m_k^{\left(2\right)}}\left[\delta {\mathbf{v}}_{b,k}^{\left(2\right)}\delta p_{b,k}^{\left(2\right)}\right]\cdot \left(\sum _{c=1}^{m^{\left(1\right)}}\left[\begin{array}{cc}\hfill {\mathbf{K}}_{bc,k}^{(2,1)}\hfill & \hfill 0\hfill \\ \hfill {\mathbf{k}}_{bc,k}^{(2,1)}\hfill & \hfill k_{bc,k}^{(2,1)}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill \Delta {\mathbf{u}}_c^{\left(1\right)}\hfill \\ \hfill \Delta p_c^{\left(1\right)}\hfill \end{array}\right]+\sum _{d=1}^{m_k^{\left(2\right)}}\left[\begin{array}{cc}\hfill {\mathbf{K}}_{bd,k}^{(2,2)}\hfill & \hfill 0\hfill \\ \hfill {\mathbf{k}}_{bd,k}^{(2,2)}\hfill & \hfill k_{bd,k}^{(2,2)}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill \Delta {\mathbf{u}}_{d,k}^{\left(2\right)}\hfill \\ \hfill \Delta p_{d,k}^{\left(2\right)}\hfill \end{array}\right]\right)),\hfill \end{array}$$ (47)

where

$$\begin{array}{cc}\hfill {\mathbf{K}}_{ac}^{(1,1)}& =N_a^{\left(1\right)}\left({\epsilon }_n{N}_c^{\left(1\right)}{\mathbf{N}}^{\left(1\right)}+t_n{\mathbf{A}}_c^{\left(1\right)}\right)\hfill \\ \hfill {\mathbf{K}}_{ad,k}^{(1,2)}& =-{\epsilon }_n{N}_a^{\left(1\right)}{N}_d^{\left(2\right)}{\mathbf{N}}^{\left(1\right)}\hfill \\ \hfill {\mathbf{K}}_{bc,k}^{(2,1)}& =-N_c^{\left(1\right)}\left({\epsilon }_n{N}_b^{\left(2\right)}{\mathbf{N}}^{\left(1\right)}+t_n{\mathbf{M}}_b^{\left(2\right)}\right)-t_n{N}_b^{\left(2\right)}{\mathbf{A}}_c^{\left(1\right)}\hfill \\ \hfill {\mathbf{K}}_{bd,k}^{(2,2)}& =N_d^{\left(2\right)}\left({\epsilon }_n{N}_b^{\left(2\right)}{\mathbf{N}}^{\left(1\right)}+t_n{\mathbf{M}}_b^{\left(2\right)}\right),\hfill \end{array}$$ (48)

$$\begin{array}{cc}\hfill {\mathbf{k}}_{ac}^{(1,1)}& =N_a^{\left(1\right)}\left({\epsilon }_p{N}_c^{\left(1\right)}{\mathbf{q}}^{\left(1\right)}-w_n{\mathbf{A}}_c^{\left(1\right)}\cdot {\mathbf{n}}^{\left(1\right)}\right)\hfill \\ \hfill {\mathbf{k}}_{ad,k}^{(1,2)}& =-{\epsilon }_p{N}_a^{\left(1\right)}{N}_d^{\left(2\right)}{\mathbf{q}}^{\left(1\right)}\hfill \\ \hfill {\mathbf{k}}_{bc,k}^{(2,1)}& =N_c^{\left(1\right)}\left(-{\epsilon }_p{N}_b^{\left(2\right)}{\mathbf{q}}^{\left(1\right)}+w_n{\mathbf{m}}_b^{\left(2\right)}\right)+w_n{N}_b^{\left(2\right)}{\mathbf{A}}_c^{\left(1\right)}\cdot {\mathbf{n}}^{\left(1\right)}\hfill \\ \hfill {\mathbf{k}}_{bd,k}^{(2,2)}& =N_d^{\left(2\right)}\left({\epsilon }_p{N}_b^{\left(2\right)}{\mathbf{q}}^{\left(1\right)}-w_n{\mathbf{m}}_b^{\left(2\right)}\right),\hfill \end{array}$$ (49)

$$\begin{array}{cc}\hfill k_{ac}^{(1,1)}& =-{\epsilon }_p{N}_a^{\left(1\right)}{N}_c^{\left(1\right)}\hfill \\ \hfill k_{ad,k}^{(1,2)}& ={\epsilon }_p{N}_a^{\left(1\right)}{N}_d^{\left(2\right)}\hfill \\ \hfill k_{bc,k}^{(2,1)}& ={\epsilon }_p{N}_b^{\left(2\right)}{N}_c^{\left(1\right)}\hfill \\ \hfill k_{bd,k}^{(2,2)}& =-{\epsilon }_p{N}_b^{\left(2\right)}{N}_d^{\left(2\right)},\hfill \end{array}$$ (50)

and

$$\begin{array}{cc}\hfill {\mathbf{N}}^{\left(1\right)}& ={\mathbf{n}}^{\left(1\right)}\otimes {\mathbf{n}}^{\left(1\right)}\hfill \\ \hfill {\mathbf{A}}_c^{\left(1\right)}& =\frac{1}{J_{\eta }^{\left(1\right)}}\mathcal{A}\left\{\frac{\partial N_c^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^1}{\mathbf{g}}_2^{\left(1\right)}-\frac{\partial N_c^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^2}{\mathbf{g}}_1^{\left(1\right)}\right\}\hfill \\ \hfill {\mathbf{M}}_b^{\left(2\right)}& ={\mathbf{n}}^{\left(2\right)}\otimes {\mathbf{m}}_b^{\left(2\right)}\hfill \\ \hfill {\mathbf{m}}_b^{\left(2\right)}& =\frac{\partial N_b^{\left(2\right)}}{\partial {\eta }_{\left(2\right)}^{\alpha }}{\mathbf{g}}_{\left(2\right)}^{\alpha }\hfill \\ \hfill {\mathbf{q}}^{\left(1\right)}& =\frac{\partial p^{\left(1\right)}}{\partial {\eta }_{\left(1\right)}^{\alpha }}{\mathbf{g}}_{\left(1\right)}^{\alpha }.\hfill \end{array}$$ (51)

In the above expression, the operator $\mathcal{A}\left\{\mathbf{v}\right\}$ represents the skew-symmetric tensor whose dual vector is v ; thus $\mathcal{A}\left\{\mathbf{v}\right\}=-\mathcal{E}\cdot \mathbf{v}$, where $\mathcal{E}$ is the third-order permutation pseudo-tensor. In Eq.(47), ${\left[\Delta {\mathbf{u}}_c^{\left(1\right)}\Delta p_c^{\left(1\right)}\right]}^T$ is the vector of incremental changes in the degrees of freedom of the c – th node of the e – th element face on γ⁽¹⁾. Similarly, ${\left[\Delta {\mathbf{u}}_{d,k}^{\left(2\right)}\Delta p_{d,k}^{\left(2\right)}\right]}^T$ represents the incremental changes in the degrees of freedom of the d – th node of the element face on γ⁽²⁾ which contains the point X⁽²⁾ closest to the k – th integration point X⁽¹⁾ on the e – th element face of γ⁽¹⁾.

An examination of Eqs.(47)-(51) shows that the stiffness matrix associated with this contact formulation is not symmetric. Even in the special case of contact between two non-porous solids (where the degrees of freedom for the fluid pressure and all associated terms are eliminated, leaving only the terms appearing in Eq.(48)), the resulting stiffness matrix remains non-symmetric. This outcome was also noted by Bonet and Wood [13] for the case of a prescribed uniform ‘pressure’ (or prescribed normal traction t_n in the current notation); however, they demonstrated that such a boundary condition produces a symmetric system when the footprint over which the normal traction is prescribed remains invariant. In contact problems, this specialization is rarely applicable since the boundary of the contact region generally varies with loading.

Integration Scheme for Contact Integral

In principle, any desired integration scheme may be implemented in the evaluation of Eqs.(45) and (47), such as Gaussian quadrature. When dealing with porous-permeable media, there would appear to be a specific benefit of using a nodal integration scheme as explained here. In porous-permeable media, traction-free surfaces are normally free draining, allowing the interstitial fluid to flow freely across such boundaries (other conditions, such as semi-permeable² or impermeable boundaries, represent special cases, as they restrict the fluid flow). In the u – p formulation adopted here, the free-draining condition must be enforced as an essential boundary condition (p = 0).

Thus, in a contact problem, p⁽ⁱ⁾ = 0 must be prescribed on the traction-free regions of ∂b⁽ⁱ⁾, as also indicated in Eq.(35). Since the definition of the contact regions evolves dynamically in a contact analysis, the nodes at which this essential boundary condition needs to be applied must be identified automatically at each contact iteration. The determination of whether a node of ∂b⁽¹⁾ is in contact is achieved by examining whether t_n is negative or zero at that node, at the current iteration. This determination is most convenient when the integration scheme adopted for the contact integral is nodal, in which case the integration points X⁽¹⁾ coincide with the nodes of element faces on ∂b⁽¹⁾, yielding nodal values of t_n.

While t_n is readily available at the nodes of the primary surface ∂b⁽¹⁾ in a nodal integration scheme, the same is not true for the nodes of the secondary surface ∂b⁽²⁾, which also require the application of the essential boundary condition p⁽²⁾ = 0 outside of the contact region. Therefore, for each node of ∂b⁽²⁾, it is necessary to search for the closest point X⁽¹⁾ on ∂b⁽¹⁾ using Eq.(30), and evaluate t_n by interpolating over the nodal values of the element face of ∂b⁽¹⁾ to which X⁽¹⁾ belongs. If this interpolated t_n is equal to zero, then p⁽²⁾ = 0 must be prescribed for the corresponding node of ∂b⁽²⁾. In this case as well, knowledge of t_n at the nodes of ∂b⁽¹⁾ represents a major advantage of a nodal integration scheme. Note that this type of contact algorithm is of the node-to-segment type.

Alternatively, a contact algorithm may use a Gaussian quadrature rule that yields a contact algorithm of the segment-to-segment type. In this case, for the reasons explained above, it is still necessary to evaluate t_n at the nodes of each element face on ∂b⁽ⁱ⁾ to determine whether p⁽ⁱ⁾ = 0 should be enforced at those nodes. Consequently, a method must be provided to recover nodal values of the contact traction t_n, when its value at quadrature points is known. A nodal interpolation of the contact traction on element faces of ∂b⁽¹⁾ is given by

$$t_n=\sum _{b=1}^{m^{\left(1\right)}}{N}_b^{\left(1\right)}{t}_b^{\left(1\right)},$$ (52)

where the nodal values of the contact traction, $t_b^{\left(1\right)}$, need to be determined. Normally, the number of quadrature points $n_{\text{int}}^{\left(e\right)}$ at which t_n is evaluated during the solution scheme outlined in the previous sections, equals or exceeds the number of nodes m⁽¹⁾ on the corresponding face. Therefore there are $n_{\text{int}}^{\left(e\right)}\ge m^{\left(1\right)}$ equations of the form given in Eq.(52), evaluated at the parametric coordinates of each quadrature point, and this overdetermined system of linear equations may be solved for the unknown $t_b^{\left(1\right)}$ values using a least-squares scheme.

A careful numerical comparison of these two alternative schemes, nodal integration versus Gaussian quadrature, has led us to adopt the latter approach for two principal reasons: (1) Segment-to-segment contact consistently provided more robust convergence of the nonlinear and contact iteration schemes; and (2) it satisfied the patch test more consistently [18].

Contact with a Rigid Wall

Contact of a porous medium with a rigid wall represents a special case of sufficient interest to be addressed here. In the notation adopted in this study, the rigid wall must be represented by γ⁽²⁾, and since rigid walls are either stationary or have prescribed motions, the only unknowns are related to γ⁽¹⁾. Therefore the expressions of Eqs.(45) and (47) reduce to

$$\delta G_c=\sum _{e=1}^{n_e^{\left(1\right)}}\sum _{k=1}^{n_{\text{int}}^{\left(e\right)}}{W}_k{J}_{\eta }^{\left(1\right)}\sum _{a=1}^{m^{\left(1\right)}}\left[\delta {\mathbf{v}}_a^{\left(1\right)}\delta p_a^{\left(1\right)}\right]\cdot \left[\begin{array}{c}\hfill {\mathbf{f}}_a^{\left(1\right)}\hfill \\ \hfill f_a^{\left(1\right)}\hfill \end{array}\right],$$ (53)

$$-D\delta G_c=\sum _{e=1}^{n_e^{\left(1\right)}}\sum _{k=1}^{n_{\text{int}}^{\left(e\right)}}{W}_k{J}_{\eta }^{\left(1\right)}\sum _{a=1}^{m^{\left(1\right)}}\left[\delta {\mathbf{v}}_a^{\left(1\right)}\delta p_a^{\left(1\right)}\right]\cdot \sum _{c=1}^{m^{\left(1\right)}}\left[\begin{array}{cc}\hfill {\mathbf{K}}_{ac}^{(1,1)}\hfill & \hfill 0\hfill \\ \hfill {\mathbf{k}}_{ac}^{(1,1)}\hfill & \hfill k_{ac}^{(1,1)}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill \Delta {\mathbf{u}}_c^{\left(1\right)}\hfill \\ \hfill \Delta p_c^{\left(1\right)}\hfill \end{array}\right].$$ (54)

There are three possible types of rigid walls: impermeable, semi-permeable, and free draining. The corresponding boundary conditions on γ⁽¹⁾ are

$$\begin{array}{cc}\hfill w_n& =0\text{impermeable}\hfill \\ \hfill w_n& =L_p{p}^{\left(1\right)}\text{semi-permeable}\hfill \\ \hfill p^{\left(1\right)}& =0\text{free draining}.\hfill \end{array}$$ (55)

In the case of a semi-permeable rigid porous wall, L_p represents the effective hydraulic permeability of the wall, and it is assumed that the fluid pressure on the other side of the wall (the side not contacting γ⁽¹⁾) is ambient. In the case of a free draining wall, it is similarly assumed that the fluid pressure inside the porous wall is ambient.

The impermeable and semi-permeable walls can be modeled with Eqs.(53)-(54), using the corresponding expressions for w_n in Eq.(55), and substituting ε_p = 0 (impermeable) or ε_p = L_p (semi-permeable), in the expressions for ${\mathbf{k}}_{ac}^{(1,1)}$ and $k_{ac}^{(1,1)}$ appearing in Eqs.(49)-(50). In the case of the free draining wall, the essential boundary condition p⁽¹⁾ = 0 must be prescribed on γ⁽¹⁾, and Eqs.(53)-(54) may be further simplified with $\delta p_a^{\left(1\right)}=0$.

Examples and Verifications

Examples of Constitutive Relations

Several examples of porous media contact are illustrated below, some of which are used to directly verify the accuracy of the implementation. For all these examples, the constitutive relations proposed by Holmes and Mow [20] are used to describe the solid matrix elasticity and permeability under finite deformation. For the solid matrix, modeled as isotropic and hyperelastic, the Cauchy stress tensor and spatial elasticity tensor are given respectively by

$${\mathbf{T}}^e=\frac{1}{2J}{e}^Q\left(\left[2{\mu }_s+{\lambda }_s\left(I_1-1\right)\right]\mathbf{B}-{\lambda }_s{\mathbf{B}}^2-\left({\lambda }_s+2{\mu }_s\right)\mathbf{I}\right),$$ (56)

and

$${\mathcal{C}}^e=\frac{4\beta }{{\lambda }_s+2{\mu }_s}J{e}^{-Q}{\mathbf{T}}_e\otimes {\mathbf{T}}_e+J^{-1}{e}^Q\left[{\lambda }_s\left(\mathbf{B}\otimes \mathbf{B}-\mathbf{B}\underset{‒}{\stackrel{‒}{\otimes }}\mathbf{B}\right)+\left({\lambda }_s+2{\mu }_s\right)\mathbf{I}\underset{‒}{\stackrel{‒}{\otimes }}\mathbf{I}\right],$$ (57)

where

$$Q=\frac{\beta }{{\lambda }_s+2{\mu }_s}\left[\left(2{\mu }_s-{\lambda }_s\right)\left(I_1-3\right)+{\lambda }_s\left(I_2-3\right)-\left({\lambda }_s+2{\mu }_s\right)\ln I_3\right].$$ (58)

In these expressions, B = F · F^T is the left Cauchy-Green tensor, I₁, I₂, I₃ are its invariants, and J = detF. The material coefficients are the Lamé-like coefficients λ_s,μ_s, and the dimensionless nonlinear stiffening coefficient β. Stability constraints require that μ_s ≥ 0, λ_s ≥2μ_s / 3, and β ≥ 0.

In the spatial frame, the permeability tensor and rate of change of permeability with strain are given respectively by

$$\mathbf{K}=k\left(J\right)\mathbf{I},$$ (59)

and

$$\mathcal{K}=k\left(J\right)\left[\left(1+\frac{\alpha J}{J-{\phi }_0^s}+M{J}^2\right)\mathbf{I}\otimes \mathbf{I}-2\mathbf{I}\underset{‒}{\stackrel{‒}{\otimes }}\mathbf{I}\right],$$ (60)

where

$$k\left(J\right)=k_0{\left(\frac{J-{\phi }_0^s}{1-{\phi }_0^s}\right)}^{\alpha }\text{exp}\left[\frac{M}{2}\left(J^2-1\right)\right].$$ (61)

In these expressions, the material properties are k₀ (the permeability in the limit of no change in volume, J = 1) and the non-dimensional parameters α and M. All of these parameters should be positive. ${\phi }_0^s$ represents the volume fraction of the porous solid matrix when J = 1 ($0<{\phi }_0^s<1$ for a porous solid).

Representative values of these material properties were obtained from our earlier study [21]: λ_s = 0 MPa, μ_s = 0.2 MPa, β = 0.35, k₀ = 2.7×10^-3 mm⁴/N·s, M = 2.2, α = 2, and ${\phi }_0^s=0.2$.

Finite Element Implementation

A custom, open source finite element code available to the general public (FEBio, http://mrl.sci.utah.edu/software.php?menu=Software) was modified to test the proposed contact algorithm. All finite element analyses were performed using three-dimensional models and 8-node hexahedral isoparametric elements. Thus contact surfaces consisted of 4-node quadrilateral isoparametric element faces. The calculation of the gap distance g was obtained by projecting a ray from each integration point on an element face of γ⁽¹⁾, along n⁽¹⁾, searching for valid intersections with all the element faces of γ⁽²⁾, and keeping the solution corresponding to the smallest algebraic value of g (i.e., the most negative value when surfaces overlapped at that integration point, or the smallest positive value when they did not). For each element face of α⁽²⁾ examined in this manner, if an intersection was not found using a ray along n⁽¹⁾, then a solution was sought using a ray directed along n⁽²⁾. The use of both algorithms avoided the pitfalls associated with each approach alone.

Unless specified otherwise, a two-pass algorithm was used in the contact analyses of deformable bodies by enforcing the contact constraints twice, swapping the primary and secondary surface definitions the second time and applying the same procedure. A ‘contact point locking’ scheme was also employed during nonlinear Newton iterations, whereby the identification of the element faces of γ⁽²⁾ intersected by rays issued from integration points on γ⁽¹⁾ was fixed after a prescribed number of iterations; this locking scheme avoided back-and-forth bouncing when the intersection point on γ⁽²⁾ fell on (or very close to) the shared edge of two adjoining element faces.

For each contact pair, the penalty factors ε_n and ε_p were computed using

$${\epsilon }_n={\alpha }_n\frac{1}{N}\sum _{i=1}^N\frac{E_i{A}_i}{V_i},$$ (62)

$${\epsilon }_p={\alpha }_p\frac{1}{N}\sum _{i=1}^N\frac{k_i{A}_i}{V_i},$$ (63)

where the summation is taken over all the element faces representing the contact surfaces in the contact pair, V_i is the volume of each element, A_i is the area of the element face on the contact surface, E_i is a measure of the average Young's modulus and k_i is the mean hydraulic permeability of the element in the reference configuration. α_n and α_p are user-defined, non-dimensional scale factors.

Patch Tests and Verification in Confined and Unconfined Compression

Two specialized plane strain analyses were performed to verify that the contact algorithm functioned as expected and passed the patch test. In each analysis, two models were created, one where two bodies come into contact, and the other where a single body of the same overall geometry was loaded under the same conditions.

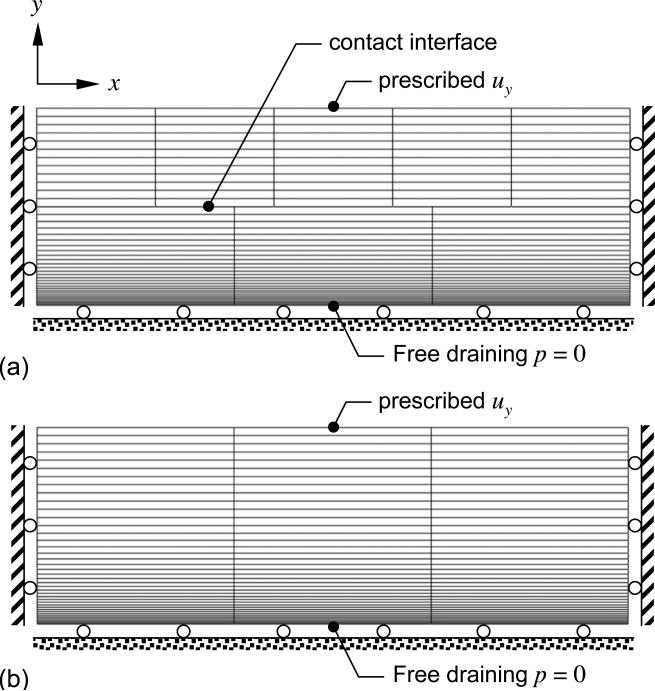
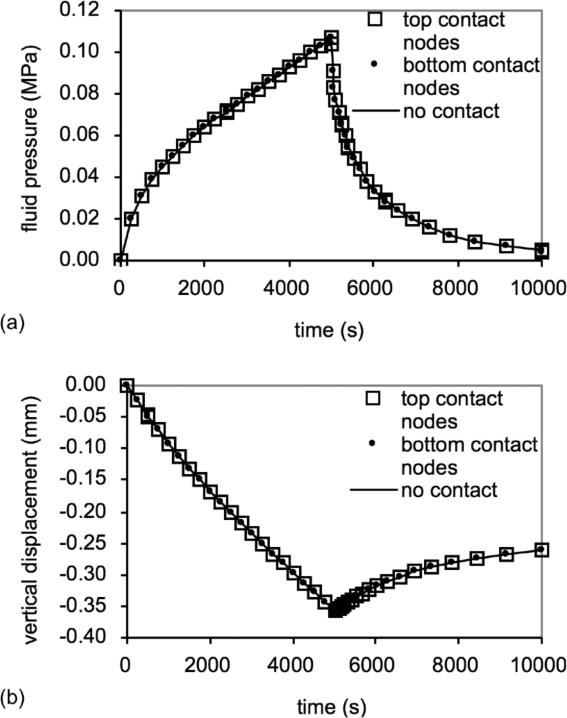
In the first case, a confined compression analysis was performed (Fig. 1). Two rectangular slabs of porous material, having identical material properties, were loaded in contact under a prescribed displacement profile on the upper body, to produce a stress-relaxation response. The time-dependent variation in the vertical displacement and fluid pressure at the nodes belonging to either contact surface were compared (Fig. 2). Results demonstrated that the nodal displacements and fluid pressures were identical over the entire width of the contact interface, and across contacting surfaces, over the entire time course of the analysis. Thus the patch test was satisfied in this analysis. Furthermore, a single rectangular slab having the same overall dimensions as the combined slabs of the contact analysis, and the same mesh distribution along the vertical direction, was analyzed under the same boundary conditions. The vertical displacement and fluid pressure at the nodes coinciding with the contact interface of the corresponding contact model were plotted (Fig. 2). Results demonstrated the contact analysis response was identical to the equivalent solution for a single slab (no contact), thus verifying the contact algorithm for this one-dimensional problem.

Fig. 1.

Confined compression stress relaxation analysis in plane strain. The prescribed displacement u_y on the top surface has a ramp-and-hold profile, with a ramp rate of -10^-4 mm/s and a final displacement of -0.5 mm. (a) The contact model consists of two slabs constrained as shown (slab width = 12 mm, height = 2 mm). The top slab has 5×12 uniformly spaced elements; the bottom slab has 3×28 elements, with a mesh bias in the vertical direction to accommodate the boundary layer anticipated at the free-draining bottom surface. (b) The no-contact model consists of a single slab (width = 12 mm, height = 4 mm) with 3×40 elements and a mesh bias in the vertical direction in the bottom half, replicating the mesh distribution of the contact model in (a) along the vertical direction.

Fig. 2.

Transient response of the confined compression analysis of Fig. 1, at all the nodes of the contact surfaces in the contact model, and the corresponding nodes (same y coordinate) of the no-contact model: (a) nodal fluid pressure p ; (b) nodal displacement u_y. Symbols are displayed for all the nodes on each contact surface, but since the results are nearly identical on each surface, the graph appears to show only one symbol at each time point.

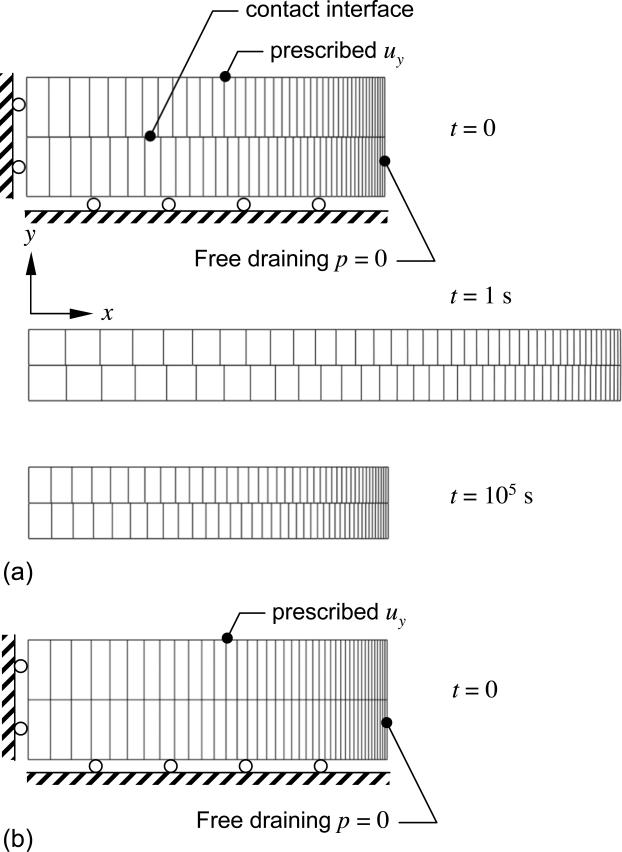
In the second analysis, two rectangular slabs of porous media were loaded in unconfined compression (Fig. 3a). Due to symmetry about the y – z plane, only one-half of the geometry was modeled. To evaluate the patch test, a different number of elements was used in the top and bottom slabs, guaranteeing that nodes on opposing contact surfaces did not face each other directly. The deformed mesh was displayed at the end of the displacement ramp (t = 1 s) and after reaching equilibrium (steady deformation, zero fluid pressure and flux, t = 10⁵ s) (Fig. 3a). At all times, the lateral edges of the two slabs lined up together to within numerical exactness, despite the difference between the finite element meshes of the two slabs. A plot of the nodal fluid pressures at the contact interface similarly showed that the pressure distribution is identical on γ⁽¹⁾ and γ⁽²⁾ (Fig. 4a) in agreement with the requirement of Eq.(34), and a plot of the element normal stress component $T_{yy}^e$ (averaged over all integration points in each element) in the elements of each slab also showed an identical distribution at all time points (Fig. 4b). These results demonstrate that the contact algorithm successfully enforces the contact conditions for porous media, while also passing the patch test.

Fig. 3.

Unconfined compression stress-relaxation analysis in plane strain. The prescribed displacement u_y on the top surface has a ramp-and-hold profile, with a ramp rate of -0.4 mm/s and a final displacement of -0.4 mm. The models are symmetric about the y – z plane. (a) The contact model consists of two slabs constrained as shown (slab width = 3 mm, height = 0.5 mm). The top slab has 1×41 elements with a mesh bias in the horizontal direction to accommodate the boundary layer anticipated at the free-draining right surface; the bottom slab has 1×40 elements, with a similar mesh bias. The deformed mesh is also shown at the end of the prescribed ramp displacement (t = 1 s) and after the response has nearly reached equilibrium (t = 10⁵ s). (b) The no-contact model consists of a single slab (width = 3 mm, height = 2 mm) with 2×41 elements and a similar mesh bias in the horizontal direction, replicating the mesh distribution of the top slab of the contact model in (a) along the horizontal direction.

Fig. 4.

Spatio-temporal response of the unconfined compression analysis of Fig. 3, across the nodes of the contact surfaces in the contact model, and the corresponding nodes (same y coordinate) of the no-contact model: (a) nodal fluid pressure p ; (b) nodal extrapolation of element effective stress component $T_{yy}^e$. The spatial distribution for these variables is shown at three select time points.

The equivalent model using a single slab with the same overall dimensions, and subjected to the same boundary conditions, was also analyzed (Fig. 3b). The fluid pressure and normal stress component at nodes coinciding with the contact interface of the corresponding contact model were plotted (Fig. 4), demonstrating excellent agreement with the contact analysis and verifying the contact algorithm for this unconfined compression configuration.

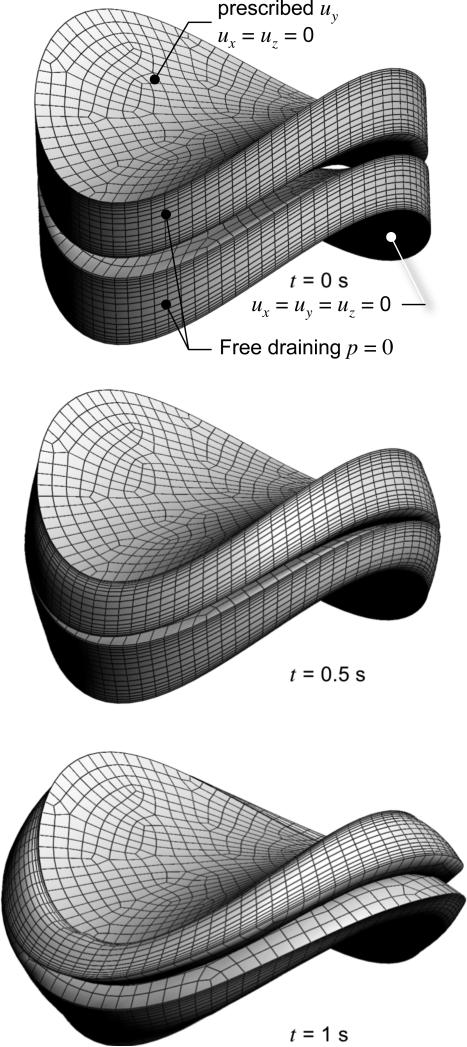
Normal Contact of Saddle-Shaped Layers

Two identical saddle-shaped layers, reminiscent of articular layers of diarthrodial joints, were loaded in contact (Fig. 5). The principal radii of curvature of the opposing contact surfaces were initially different, so that the surfaces did not mate perfectly in the reference configuration. Both layers were bonded to rigid impermeable foundations; the foundation of the bottom layer was stationary and that of the top layer was displaced along a direction normal to the surfaces at the initial point of contact. Each layer had a thickness of 0.4 mm; a total displacement of 0.3 mm was prescribed to the foundation of the top layer, increased linearly over 20 uniform time increments from 0 to 1 s.

Fig. 5.

Normal contact of saddle-shaped layers. The layers are identical but rotated by 90 degrees about the axis passing through the center of, and normal to, the contact surfaces (the y – axis). The contact surfaces were generated from the inner rim of the surface of a torus; their principal radii of curvature at the center point are -3.5 mm and +2.5 mm; their rim projects onto the x – z plane as a circle with a diameter of 3 mm. Each layer has a thickness of 0.4 mm and is supported on a rigid substrate; the bottom layer's substrate is stationary and the top layer's substrate has a prescribed ramp displacement u_y at a ramp rate of -0.3 mm/s, with a final value of -0.3 mm. The model has a total of 21420 nodes and 18784 elements. Each layer's mesh has a dual bias along the layer thickness (20 elements). The mesh is shown at three select time points.

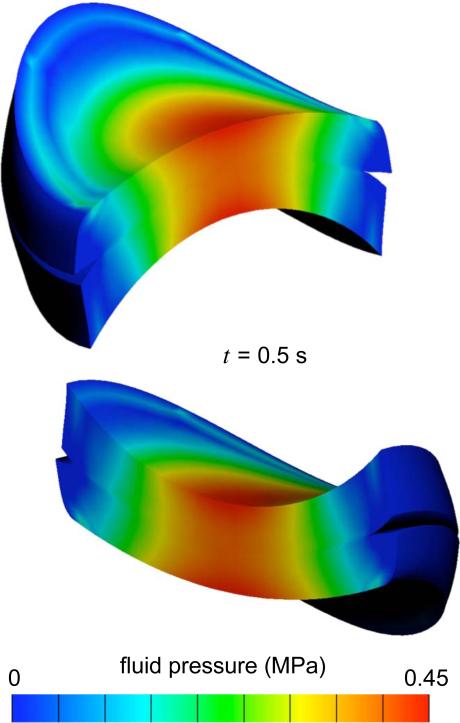
As noted in the deformed meshes (Fig. 5) and color contours for the fluid pressure (Fig. 6), the layers were subjected to large deformations, bulging away from the contact region due to the nearly isochoric response of the porous medium under rapid loading conditions [22, 23]. The successful completion of this analysis demonstrates the effectiveness of the proposed contact algorithm for performing analyses relevant to articular contact under large deformation.

Fig. 6.

Fluid pressure distribution for the contact model of Fig. 5, at t = 0.5 s. Two sectioned views are presented, using the x – y plane (top) and the y – z plane.

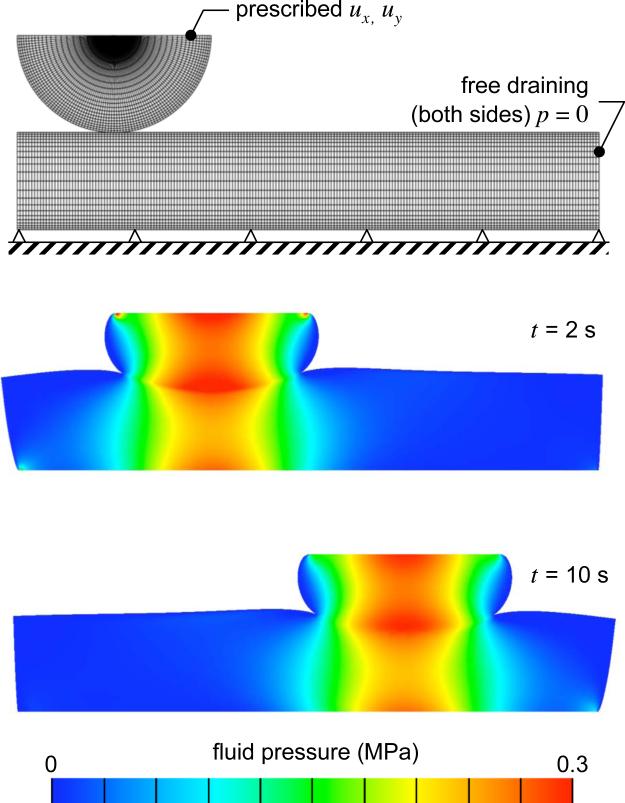
Sliding Contact With Large Deformation

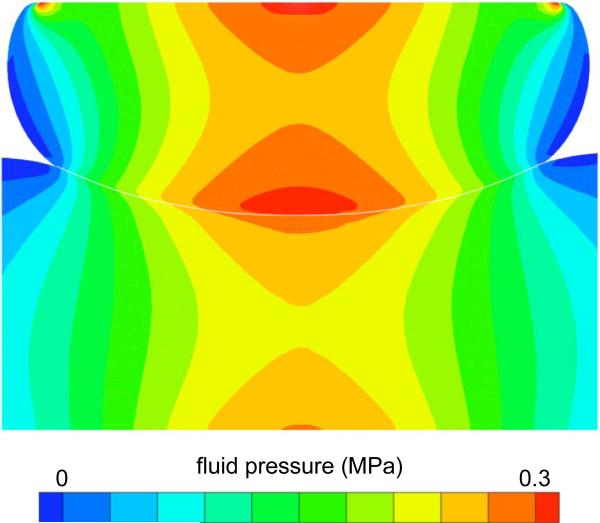
To demonstrate sliding contact under large deformations, a semi-cylindrical slab was loaded against a rectangular slab, in a plane strain analysis (Fig. 7). The rectangular block was bonded to a rigid impermeable foundation. The motion of the top surface of the semi-cylinder was prescribed to produce a downward motion by 0.75 mm (in 10 uniform time steps of 0.2 s), followed by rightward sliding at a velocity of 0.5 mm/s (in 40 uniform time steps of 0.2 s). Results demonstrate that the large deformations remains nearly isochoric throughout most of the two bodies, over the time scale of this analysis, as also suggested from the bulging on either side of the cylinder (Fig. 7). Fringe plots of the fluid pressure distribution across the interface demonstrated continuity across the contact interface (Fig. 8). This analysis demonstrates the ability of the contact algorithm to handle finite sliding and large deformations.

Fig. 7.

Finite deformation and sliding contact of a semi-cylindrical slab (radius = 2 mm) and a rectangular slab (width = 12 mm, height = 2 mm) in a plane strain analysis. The cylinder is initially prescribed a displacement profile of u_x = 2 mm and u_y = (–0.375 mm/s)×t for 0 ≤ t ≤ 2s, followed by sliding with a profile of u_x = 2 + (0.5 mm/s)× t for 2s ≤ t ≤ 10s. The cylinder has 20×100 elements along the radius and circumference, with a biased mesh along the radius to produce a finer mesh at the contact surface. The rectangular slab has 20×200 elements, with a dual bias mesh along the height. The deformed mesh and fluid pressure distribution are shown at two select time points.

Fig. 8.

A close-up of the model of Fig. 7 at t = 2 s, using discrete color contours, demonstrates clearly the continuity of fluid pressure across the contact interface (emphasized with a white line trace).

Verification of Sliding Contact with Rigid Impermeable Cylinder

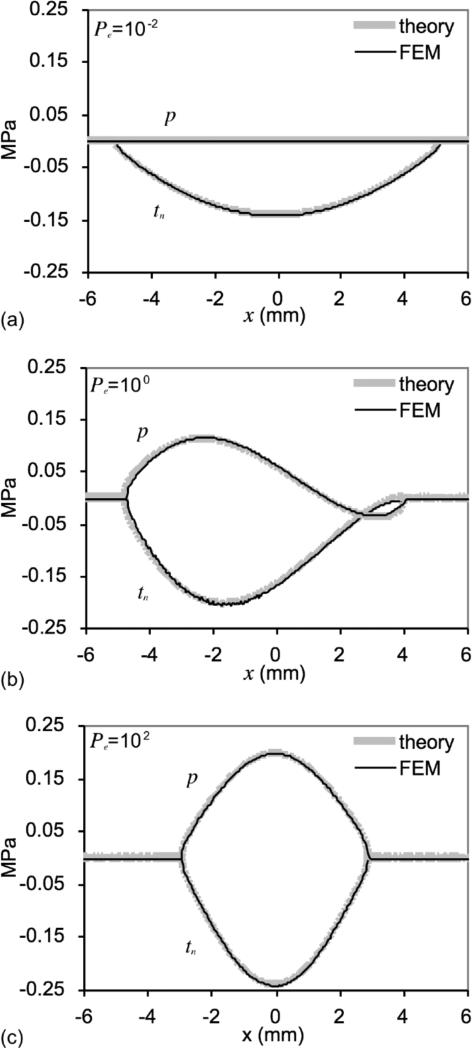
Few analytical solutions are available for biphasic contact problems. In an earlier study [24], we solved the problem of steady-state rolling or sliding contact of frictionless cylindrical biphasic layers using semi-analytical methods, for the case of infinitesimal strain and linear isotropic elastic solid matrix. When the radii of curvature of identical cylindrical biphasic layers are large compared to the contact width, the solution is also equivalent to sliding of a rigid impermeable cylinder (which can be closely approximated by a parabola) on a flat biphasic layer. For this problem, the plane strain solution was obtained analytically in Fourier transform space, and the inverse transform was evaluated numerically using Fast Fourier Transform methods. It was shown that the solution exhibited distinct characteristic traits depending on the Peclet number for the problem, where the Peclet number represents the ratio of convective velocity (the sliding velocity) to diffusive velocity (the characteristic velocity at which interstitial fluid diffuses through the porous solid matrix).

To verify the solution of the finite element biphasic contact method presented here for large sliding, a contact analysis was performed between a rigid impermeable cylindrical indenter of radius R, and a flat biphasic layer, of thickness h, supported on a rigid impermeable foundation. The solid matrix of the biphasic layer was modeled as linear isotropic, with aggregate modulus H_A = λ_s + 2μ_s and Poisson's ratio ν, and constant (isotropic) hydraulic permeability k. The rigid indenter was imparted a sliding velocity V. The Peclet number for this problem is given by P_e = V h/ H_Ak. The applied load intensity (load per unit depth in the out-of-plane direction) is W. The three-dimensional analysis was specialized to the plane strain case by constraining out-of-plane normal displacements and fluid flux.

For this specific analysis the selected parameters were h = 1 mm, R = 100 mm, H_A = 1 MPa, ν = 0, k = 1 mm⁴/N·s, and V = 0.01, 1 or 100 mm/s, to produce P_e = 0.01, 1 or 100. The load intensity was W = 1 N/mm to maintain deformation in the range of small strains. The extent of the biphasic layer was 40 mm. The mesh consisted of 1024 8-node hexahedral elements along the width and 20 elements through the height of the layer, for a total of 20480 elements; the mesh had a dual bias along the height, with a finer mesh at the top and bottom of the layer (similar to that shown in Fig. 7). The gap tolerance for the augmented Lagrangian scheme (Table 1) was set to a tight value of 0.0005 mm and the pressure tolerance was set to a loose value of 0.1 MPa.

To achieve steady-state conditions, for comparison to the semi-analytical solution, multiple time increments were analyzed until no further change in the solution was observed over time; large sliding occurred over these time increments. The contact traction and fluid pressure from the finite element contact analysis were compared to the theoretical solution (Fig. 9). For all three Peclet numbers, very good agreement was observed between the two methods, thus verifying the finite element solution. As discussed in the original contact study [24], the profiles for t_n are nearly symmetric when P_e << 1 and P_e >> 1 (Fig. 9a & c), since the biphasic material behaves as an elastic incompressible and elastic compressible material, respectively, in these two limiting cases. When P_e ~ 1, the interstitial fluid flow and resulting dissipative drag against the solid matrix are significant, and the biphasic material behaves viscoelastically; therefore, as the rigid cylinder slides past a particular region, there is a significant delay in the rebounding of the material, yielding an asymmetric traction distribution (Fig. 9b).

Fig. 9.

Steady-state response of the contact traction t_n and contact interface fluid pressure p for sliding of a rigid impermeable cylinder over a rectangular slab of biphasic material, in a plane strain analysis. The slab (width = 40 mm, height = 1 mm) is bonded to a rigid impermeable substrate. The model (not shown) has 20×1024 elements, with a dual bias mesh along the height. The applied load intensity is 1 N/mm. Results are shown for three different Peclet numbers (representing the ratio of sliding velocity to characteristic diffusive velocity of interstitial fluid flow): (a) P_e = 10^-2; (b) P_e = 10 ⁰; (c) P_e = 10².

Discussion

The objective of this study was to formulate, implement and verify a finite element contact algorithm for solid-fluid mixtures that can accommodate large deformation and sliding. There is a significant need for this type of implementation in the field of biomechanics of hydrated tissues, yet few alternatives are available to the biomechanics community.

Arguably, the most widespread finite element contact implementation used in biomechanics to date is provided by the commercial finite element code, Abaqus (www.simulia.com) [6, 7, 25-29]. Though this code offers many powerful features, it is apparently unable to automatically enforce free-draining conditions outside the contact region. In the study of Federico et al. [5], this limitation was circumvented by constraining the fluid flux component in the non-contacting region to w_n = L_pp⁽ⁱ⁾ when p⁽ⁱ⁾ ≥ 0, and w_n = 0 when p⁽ⁱ⁾ < 0. This approximation may have yielded reasonable results for the problem tested in their study, but it does not strictly represent the correct set of free-draining boundary conditions (p⁽ⁱ⁾ = 0) for contact problems. Furthermore, it restricts the fluid flux to the outward direction, whereas sliding contact problems generally produce a mix of inward and outward flux in the vicinity of the contact region (see figure 4 of [24]). Therefore, while providing a valuable analysis tool for biomechanics, the Abaqus finite element implementation of poroelastic contact exhibits a significant limitation, and the details of its code implementation are not available to the public.

Among the biphasic contact algorithms described in the biomechanics literature, those presented by Spilker and co-workers have been formulated either as true contact algorithms for small deformations [1, 3], or approximate penetration-based algorithms for small [30] or large deformations [12, 31]. The true contact algorithms [1, 3] used the method of Lagrange multipliers to enforce the contact conditions of Eq.(19), rather than the penalty method employed in Eqs.(33) and (35), but otherwise enforce the same governing equations and constraints. Since the algorithms in these references are limited to small deformations, they are less general than the current formulation. The penetration-based algorithms [30, 31] represent simplified approaches intended to provide more efficient computations, since the solution is obtained separately for each body in a contact pair. In general, the examples presented in these studies have not included large sliding.

The biphasic contact algorithm of Chen et al. [4] was formulated to account for handling large deformations and sliding. Thus, in principle, the current study replicates the capabilities of this earlier formulation. Some differences exist in the implementation: Their formulation was based on the material frame of reference, while the current study used the spatial frame; their dependent variables (nodal degrees of freedom) included u, w and p, whereas this study used only u and p ; and they used Lagrange multipliers to enforce the contact constraints, whereas this study used the penalty method. These authors provided examples for normal contact, including a validation against a test problem from the earlier work of Donzelli et al. [1], as well as large sliding. However, their illustrations are limited to small deformations.

In the current study, an original algorithm for frictionless contact of solid-fluid mixtures undergoing large deformations and sliding has been proposed. While this algorithm produces a non-symmetric contribution to the stiffness matrix of the finite element formulation, as shown in Eqs.(47)-(51), this is no more restrictive than the formulation of the general stiffness matrix for biphasic finite element problems, which is also strictly non-symmetric, Eqs.(A4)-(A5). The algorithm and its implementation were verified in a number of test problems, including confined and unconfined compression patch tests under large deformations, that have equivalent solutions not requiring a contact analysis (Fig. 2 & Fig. 4); as well as large sliding contact with a rigid impermeable cylinder, under small deformations, for which semi-analytical solutions exist (Fig. 9). Additional examples illustrated large deformations under normal contact (Fig. 5) and large sliding contact (Fig. 8). In general, this algorithm and its implementation have proven to be robust, able to handle some of the more challenging problems that arise in the biomechanics of soft tissues. They are also applicable to large deformation and sliding contact of non-porous materials, subject to the appropriate reduction of the governing equations. Although not illustrated here, this algorithm has produced convergence for elastic saddle-shaped layers (similar to Fig. 5) at higher deformations than could be achieved with the contact algorithm of Laursen and Simo [8], as implemented in NIKE3D [32].

In summary, this study addresses an important computational need in the biomechanics of porous-permeable soft tissues. It provides a robust contact algorithm that can accommodate large deformations and sliding. Several illustrations are provided that validate and demonstrate the capabilities of its implementation. Importantly, an open source finite element code that implements this algorithm is made available to the general public, providing a valuable tool and common computational platform to the biomechanics community.

Appendix

Discretization of Internal Virtual Work

Let

$$\begin{array}{cc}\hfill \delta {\mathbf{v}}^s& =\sum _{a=1}^m{N}_a\delta {\mathbf{v}}_a\delta p=\sum _{a=1}^m{N}_a\delta p_a\hfill \\ \hfill \Delta \mathbf{u}& =\sum _{b=1}^m{N}_b\Delta {\mathbf{u}}_b\Delta p=\sum _{b=1}^m{N}_b\Delta p_b\hfill \end{array}$$ (A1)

where N_a represents the interpolation functions over an element, δv_a,δ p_a, Δu_b,Δp_b respectively represent nodal values of δv^s,δ p, Δu, Δp, and m is the number of nodes in an element. Then the discretized form of δW_int in Eq.(11) may be written as

$$\delta W_{\text{int}}=\sum _{e=1}^{n_e}\sum _{k=1}^{n_{\text{int}}^{\left(e\right)}}{W}_k{J}_{\eta }\sum _{a=1}^m\left[\delta {\mathbf{v}}_a\delta p_a\right]\cdot \left[\begin{array}{c}\hfill {\mathbf{r}}_a^u\hfill \\ \hfill r_a^p\hfill \end{array}\right]$$ (A2)

where n_e is the number of elements in v, $n_{\text{int}}^{\left(e\right)}$ is the number of integration points in the e – th element, W_k is the quadrature weight associated with the k – th integration point, and J_η is the Jacobian of the transformation from the spatial frame to the parametric space of the element. In the above expression,

$${\mathbf{r}}_a^u=\mathbf{T}\cdot \nabla N_a{r}_a^p=\mathbf{w}\cdot \nabla N_a-N_a\text{div}{\mathbf{v}}^s$$ (A3)

and it is understood that J_η, ${\mathbf{r}}_a^u$ and $r_a^p$ are evaluated at the parametric coordinates of the k – th integration point.

Similarly, the discretized form of DδW_int in Eq.(13) may be written as

$$D\delta W_{\text{int}}=\sum _{e=1}^{n_e}\sum _{k=1}^{n_{\text{int}}^{\left(e\right)}}{W}_k{J}_{\eta }\sum _{a=1}^m\left[\delta {\mathbf{v}}_a\delta p_a\right]\cdot \sum _{b=1}^m\left[\begin{array}{cc}\hfill {\mathbf{K}}_{ab}^{uu}\hfill & \hfill {\mathbf{k}}_{ab}^{up}\hfill \\ \hfill {\mathbf{k}}_{ab}^{pu}\hfill & \hfill k_{ab}^{pp}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill \Delta {\mathbf{u}}_b\hfill \\ \hfill \Delta p_b\hfill \end{array}\right]$$ (A4)

where

$$\begin{array}{cc}\hfill {\mathbf{K}}_{ab}^{uu}& =\nabla N_a\cdot \mathcal{C}\cdot \nabla N_b+\left(\nabla N_a\cdot \mathbf{T}\cdot \nabla N_b\right)\mathbf{I}\hfill \\ \hfill {\mathbf{k}}_{ab}^{up}& =-N_b\nabla N_a\hfill \\ \hfill {\mathbf{k}}_{ab}^{pu}& =-\left(\nabla N_a\cdot \mathcal{K}\cdot \nabla N_b\right)\cdot \text{grad}p-N_a\left[\left(\text{div}{\mathbf{v}}^s+\frac{1}{\Delta t}\right)\mathbf{I}-{\text{grad}}^T{\mathbf{v}}^s\right]\cdot \nabla N_b\hfill \\ \hfill k_{ab}^{pp}& =-\nabla N_a\cdot \mathbf{K}\cdot \nabla N_b\hfill \end{array}$$ (A5)

and Δt is a discrete increment in time. In a numerical implementation, it has been found that evaluating divv^s from J̇/J, where J = detF, yields more accurate solutions than evaluating it from the trace of grad v^s [23].