Contributions of modern measurement theory to measuring executive function in early childhood: An empirical demonstration

Executive functions refer to cognitive abilities involved in the control and coordination of information in the service of goal-directed actions (Fuster, 1997; Miller & Cohen, 2001). As such, executive function can be defined as a supervisory system that is important for planning, reasoning ability, and the integration of thought and action (Shallice & Burgess, 1996). At a more fine grained level, however, executive function, as studied in the cognitive development literature, has frequently been characterized in terms of specific interrelated information processing abilities that enable the resolution of conflicting information; namely, working memory, defined as the holding in mind and updating of information while performing some operation on it; inhibitory control, defined as the inhibition of prepotent or automatized responding when engaged in task completion; and mental flexibility, defined as the ability to shift attentional or cognitive set among distinct but related dimensions or aspects of a given task (Davidson et al., 2006; Garon, Bryson, & Smith, 2008; Zelazo & Müller, 2002).

Carlson (2005) summarized numerous tasks that have been developed to measure executive function in early childhood. These tasks reflect the creative efforts of investigators to develop game-like tasks that are engaging to children and present novel challenges designed to elicit individual differences in working memory, inhibitory control, and attention shifting processes. Observed age differences in children’s performance, primarily in cross sectional samples, on many of these tasks has provided an initial empirical basis for documenting improvement in executive functions during the early childhood period. The majority of tasks designed to measure executive function in young children, however, have not undergone formal psychometric evaluations and few are appropriate for longitudinal use beyond a relatively narrow age range. The absence of psychometrically validated measures appropriate for longitudinal use vitiates our ability to test theoretical questions related to the developmental course, as well as the criterion and predictive validity, of executive functions. The primary goal of the current study is to use an extended empirical example to delineate the benefits of using modern measurement theory (Item Response Theory; IRT) for evaluating the psychometric properties of executive function tasks commonly used in early childhood. To be clear, we intend to provide a nontechnical description of IRT, which is accessible to a broad readership. Readers interested in a more technically rigorous treatment of IRT are referred to one of many outstanding book length treatments (Thissen & Wainer, 2001; Hambelton & Swaminathan, 1985; Embretson & Reise, 2000).

Common Approaches to Measuring Children’s Executive Function & Their Assumptions

Children’s performance on executive function tasks is typically summarized either dichotomously or continuously. For dichotomously scored tasks, investigators typically define an ad hoc criterion which is used to define the presence of some underlying ability state. Children whose score meets or exceeds this criterion are said to “pass” a task, while children whose score does not are said to “fail” the task. Dichotomously scored tasks are often used to demonstrate, in a rather coarse way, age-based progression of executive functions. More often, children’s performance on executive function tasks is defined with respect to the percentage (or simple count) of test items that were answered correctly.

Regardless of whether a task is scored dichotomously or continuously, most studies that involve executive function tasks with young children share a core set of implicit assumptions. First, children are given a score on a task which is presumed to reflect an estimate of their true ability level. While this is not an unreasonable assumption, it is important to remember that, as defined by classical test theory (CTT), the score derived from a given executive function task is only representative of a child’s ability as measured by that specific task (i.e., the score is task specific). Any changes to the task (even a skipped item on the task) changes the definition of the score on that task. Second, reliability measures (e.g., coefficient alpha) for CTT-based scores assume that all scores are equally reliable (see, for example, Cronbach, 1951). That is, it is assumed that the precision of measurement (for either pass/fail or percentage correct scores) of a given executive function task is constant for all children, regardless of their ability level. Third, assigning children scores on executive function tasks based on the number of items correctly answered, implicitly treats all of the items on a given executive function task as inter-changeable. That is, each item is given equal “weight” when computing a score (Lord & Novick, 1968). While this assumption of CTT scores is testable, it is rarely evaluated in practice (see, for example, Edwards & Wirth, 2009). Fourth, it is assumed that executive function task scores “work” equally well for specific subgroups of youth. That is, the measurement characteristics of a task (i.e., item difficulty level, as well as the strength of association between individual test items and the underlying ability being measured) are assumed to be invariant across children being tested. However, even small changes in the measurement properties of a scale, if not modeled correctly, can result in the apparent group differences that are actually an artifact of the differential measurement properties of a given instrument for the groups being compared (Meredith, 1993).

There are several reasons to be concerned about the appropriateness of CTT assumptions as applied to measures of EF. For one, the assumption that the precision of measurement is constant across the range of ability level may not be justified for many measures of EF. Given that scores tend to cluster at the high and low end of certain measures, it is likely that information about the range of ability is not captured by these measures. For another, the assumption that items are interchangeable or of equal weight is also difficult to justify. For example, on measures such as peg tapping (Diamond & Taylor, 1996) or the Head-Toes-Knees-Shoulders (McClelland et al., 2007), many children are able to successfully complete the first several items, and it is later rather than earlier items that discriminate ability on these measures. Similarly in measures that involve switching between congruent and incongruent responding, such as the flanker, it may be that items on which switches occur are more informative than other items (Mayr, Awh, & Laurey, 2003)

Modern Measurement Theory Applied to Measures of Children’s Executive Function

Adopting a modern measurement theory approach, such as using IRT, provides a framework for evaluating and, in some cases, disavowing the aforementioned assumptions. From the perspective of IRT, all children have an underlying latent ability with respect to performance on executive function tasks. This ability level is latent because it is never directly observed (it is only inferred based on performance on specific executive function tasks) and, unlike in classic test theory, is independent of the items used to measure its level. In IRT parlance, the parameter that describes individual differences in true executive function ability is “theta” (θ). Children’s performance (not their “true-score”) on any executive function task is a joint function of their ability (theta) and characteristics of test items. Test items are characterized with respect to their difficulty level (e.g., how likely it is that a child of a specific ability level will pass an item) and discrimination (e.g., how informative passing an item is with respect to gauging a child’s latent ability).

Item Evaluation

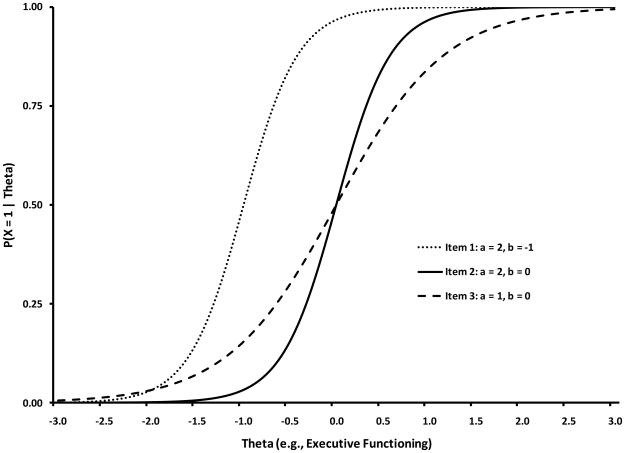
Three exemplar items from a prototypic executive function task (where individual items are coded as correct/incorrect) are depicted in Figure 1. Latent executive function ability (theta) is plotted along the X axis while the probability of getting an item correct is plotted along the Y axis. Each of three prototypic items is represented by what is known as an item characteristic curve (ICC). ICCs describe the probabilistic relationship between underlying (latent) ability level and performance on any given item. In Figure 1, items 1 and 2 have the same discrimination parameter (typically denoted ‘a’) values but different difficulty parameter (typically denoted ‘b’) values. In other words, while items 1 and 2 are equally informative indicators of a child’s latent ability level, item 1 is easier (a relatively better indicator of lower ability level) than item 2 (a relatively better indicator of higher ability level). In contrast, item 3 has the same difficulty value as item 2 (a child of average executive function ability would have a 50% chance of endorsing both items 2 and 3) but is less discriminating. That is, correctly answering Item 3 provides less information about a child’s underlying ability level relative to correctly answering items 1 or 2 (i.e., item 3 has a “weaker signal” relative to items 1 and 2).

Figure 1.

Item characteristic curves for three hypothetical dichotomous items varying in item slope (a) and difficulty (b).

ICCs provide item-level information about executive function tasks. That is, inspection of ICCs facilitates an improved understanding of which items of a task are the most reliable indicators of ability level (i.e., the “steeper” the ICC the more strongly related an item is to an underlying construct), as well as the relative difficulty of items (i.e., the midpoint of any dichotomous item’s ICC defines the point on theta that corresponds to a 50% probability of passing an item such that the more ICCs are shifted to the “left” or “right” of theta, the less or more difficult they are, respectively). Discrimination and difficulty parameters have a direct correspondence to factor loading and intercept parameters in factor analytic models (see e.g., Wirth & Edwards, 2007). Regardless of the item factor model being used (IRT or categorical factor analysis) the methods differentially weight the response to each item based on the item’s difficulty and discrimination thereby increasing the precision of measurement.

Test Information

The information conveyed by item characteristic curves can be aggregated to compose a test information curve. Test information curves convey the precision of measurement of a task as a function of theta. The relative “height” of a test information curve informs the measurement precision of a task. IRT allows the precision of measurement to vary as a function of ability level (theta). Hence, inspection of test information curves can help clarify what range of ability a task is optimally suited to measure. Under ideal circumstances, investigators would base their selection of executive function tasks in part by comparing test information curves of individual tasks given an understanding of the sample to be studied. For example, investigators interested in studying executive function in young (e.g., 2–3 year old) children or children with disabilities (e.g., Autism), might select tasks that have test information curves that are peaked along the low end of ability level (e.g., theta values < 0). In contrast, investigators interested in studying whether executive functions in early childhood are predictive of subsequent eligibility for Academically Gifted services at school entry would select tasks that have test information curves that are peaked along the high end of ability level (e.g., theta values > 0). Test information curves provide researchers an empirical description and comparison of available tasks. The higher the test information curve over a given range of theta, the more reliable a score corresponding to a theta value with in that range will be. The point here is not to devalue CTT but rather to highlight how an IRT-based conceptualization of reliability can facilitate researchers in the selection of measures.

Scoring

IRT-based scoring of executive function tasks provides an estimate of a child’s true ability that is free of measurement error and that makes maximal use of the item-level information provided in the item characteristic curves (ICCs). Characterizing a child’s performance on an executive function task by the percentage of correctly answered items implicitly treats all items as equal. As noted above, however, it is very likely given the nature of EF and the inherent difficulty of switching between congruent and incongruent items on a given task, that items involving switches rather than repetitions are more informative than items that maintain a pattern of responding, whether congruent or incongruent (Mayr et al., 2003). This is a testable but typically unrealistic situation—one that implies that all items are equally difficult and discriminating. In terms of IRT parameters, all items would have the same a and b values (or the same factor loadings and thresholds in categorical factor analysis). IRT-based scores represent an estimate of true ability which differentially weight the contribution of each item to the total score as a function of their difficulty and discrimination parameters (i.e., their ICC). Not only does the proper weighting of items with regard to their relationship to theta (e.g., executive function ability) provide greater precision in score estimation, it also removes the item-score dependency found with Classic Test Theory (CTT) methods (where a score is items set dependent). That is, in latent variable models like those found within the IRT framework, an individual’s score will remain unchanged (assuming proper item calibration) regardless of which items, from the universe of possible items, that individual answers.

Differential Item Functioning

Because modern methods like IRT focus on items in terms of item quality (discrimination and difficulty) to inform score estimation, it is important to consider whether items function equivalently (i.e., are invariant) across all subpopulations that are included in a given study. Item characteristic curves (ICCs) provide a useful framework for evaluating whether the measurement characteristics of items (and collectively a task) work equally well for defined subgroups. For example, to the extent that the ICCs for a task are equivalent across males and females, an investigator has increased confidence that any between group differences in performance are attributable to sex differences in true ability level. Testing for such differences is broadly known in the psychometric literature as testing for measurement invariance (Meredith, 1993). Within IRT, the formal comparison of item parameters across mutually exclusive groups is known as testing for Differential Item Functioning (DIF). DIF is used to ensure that a given item is providing the same information across groups or time. An item may differ across groups with respect to its difficulty parameter(s). This is known as b-DIF (where ‘b’ refers to difficulty parameters described above). An item that exhibits b-DIF would be “harder” to endorse for one group of participants than the other. An item may also differ across groups with respect to its discrimination parameter. This is known as a-DIF (where ‘a’ refers to discrimination parameters described above). An item that exhibits a-DIF would be more discriminating (i.e., would be a stronger indicator of underlying ability level, theta, for one group of participants than the other). Failure to test whether items are equally informative across subgroups may lead researchers to erroneous conclusions regarding the presence (or absence) of expected group differences. It is important to note that DIF refers to differences in the probability of getting a particular item correct given the same level of theta, it does not refer to group mean differences.

To illustrate the foregoing, we make use of data collected on a battery that we have been developing to measure executive function longitudinally in children from 3–5 years of age in the context of large scale studies. Specifically, we created and/or adapted six tasks that putatively measured three dimensions of executive function in early childhood: working memory, inhibitory control, and attention shifting. For expository purposes, we will demonstrate the application of IRT-based evaluation of three tasks—one each for putative dimensions of working memory, inhibitory control, and attention shifting at child age of approximately 48 months. The battery was included as part of an ongoing prospective longitudinal study (N= 1292) of families who were recruited from central PA and eastern NC, with over-sampling for low-income and in NC, African American families. The specific goals of the current study include estimating and describing item characteristic curves, formally evaluating whether the measurement characteristics of each executive function task are equivalent for children residing in low versus not low income households, estimating and describing test information curves for each task, and demonstrating the difference between percent correct versus IRT-based scores. The overall goal of this effort is to provide an accessible, non-technical description of the types of questions that can be addressed using IRT methods, with specific attention to the ways in which this information can enhance the development of new tasks, the evaluation of extant tasks, and the selection of tasks for use in future studies that are optimized to the specific research questions under investigation.

Method

Participants

The Family Life Project was designed to study young children and their families who lived in two of the four major geographical areas of the United States with high poverty rates (Dill, 2001). Specifically, three counties in Eastern North Carolina and three counties in Central Pennsylvania were selected to be indicative of the Black South and Appalachia, respectively. The Family Life Project adopted a developmental epidemiological design in which sampling procedures were employed to recruit a representative sample of 1292 children whose mothers resided in one of the six counties at the time of the child’s birth. In addition, low-income families in both states and African American families in NC were over-sampled to ensure adequate power for dynamic and longitudinal analyses of families at elevated psychosocial risk (African American families were not over-sampled in PA because the target communities were at least 95% non-African American).

At both sites, recruitment occurred seven days per week over the 12-month recruitment period spanning September 15, 2003 through September 14, 2004 using a standardized script and screening protocol. The coverage rate was over 90% for all births that occurred to women in these counties in that one year period. In PA, families were recruited in person from three hospitals. These three hospitals represented a weighted probability sample (hospitals were sampled proportional to size within county) of seven total hospitals that delivered babies in the three target PA counties. PA hospitals were sampled because the number of babies born in all seven target hospitals far exceeded the number needed for purposes of the design. In NC, families were recruited in person and by phone. In-person recruitment occurred in all three of the hospitals that delivered babies in the target counties. Phone recruitment occurred for families who resided in target counties but delivered in non-target county hospitals. These families were located through systematic searches of the birth records located in the county courthouses of nearby counties.

Family Life Project recruiters identified 5471 (59% NC, 41% PA) women who gave birth to a child in the 12-month period. A total of 1515 (28%) of all identified families were determined to be ineligible for participation for three primary reasons: not speaking English as the primary language in the home, residence in a non-target county, and intent to move within three years. Of the 2691 eligible families who agreed to the randomization process, 1571 (58%) families were selected to participate using the sampling fractions that were continually updated from our data center. Of those families selected to participate in the study, 1292 (82%) families completed a home visit at 2 months of child age, at which point they were formally enrolled in the study.

The current study focused on children’s performance on a newly developed battery of Executive Function tasks that were administered at the 48-month home visit. Compared to those who did not participate in the 48-month visit (N = 226), families who participated in the 48-month visit (N = 1066) were not more poor (77% vs. 81% poor at the time of recruitment into the study, p = .18), to have had a male child (51% vs. 52%, p = .65), or to have had an African American child (42% vs. 46%, p = .30). However, compared to those who did not participate in the 48-month visit, families who participated in the 48-month visit were more likely to reside in PA (34% vs. 42%, p = .03).

Procedures

Families participated in one home visit when children were approximately 48 months of age. Among other things, children were administered 6 newly developed tasks that were designed to measure their executive function ability. Children were seated across from the experimenter at a convenient location in the home. All tasks were administered in a standard order. Cumulatively, these tasks took about 30–40 minutes to complete (the entire visit took approximately 90–120 minutes to complete).

Measures

Executive function

The set of executive function tasks shared a number of features. Each task was presented in an open spiral bound flipbook format (pages measured 8” × 14”) which allowed the examiner to easily turn pages that present stimuli on one page and highly scripted instructions for administration on the other. For each of the tasks, examiners first administered training trials and up to three practice trials if needed. If children failed to demonstrate an understanding of the goals of the task following the practice trials, the examiner discontinued testing on that task. Each task was administered by two research assistants(, one who was responsible for administering tasks to the child and the other who was responsible for recording child responses. By disassembling administration and response recording roles, and not requiring either research assistant to evaluate the accuracy of child responses (accuracy was evaluated using computerized scoring), we minimized the cognitive load on research assistants, making the tasks more amenable to administration by lay staff who did not have specialized training or expertise in task content.

Pick the Picture Game (Working Memory)

This is a Self-Ordered Pointing task (Petrides & Milner, 1982; Cragg & Nation, 2007). Children are presented with a set of pictures. For each set, they are instructed to pick each picture so that all of the pictures “get a turn”. For example, in the 2-picture condition, they might see a page of an apple and dog. For the first page, they pick (touch) either of the two pictures. For the second page they are requested to pick a different picture. There are two each of 2-, 3-, 4-, and 6-picture sets for a total of 8 items. The arrangement of pictures within each set is randomly changed across trials so that spatial location is not informative. This task requires working memory because children have to remember which pictures in each item set they have already touched. The person scoring the task only records which picture the child touched on each trial. Due to the dependence of responses within each picture set, each picture set is scored as a single ordinal item that reflects the number of consecutive correct responses beginning at the second picture of any given set (because the first picture in any set serves as a reference picture against which all responses are judged). This item scoring method results in two dichotomous items (picture sets 1 and 2), two trichotomous items (picture sets 3 and 4), two four-category items (picture sets 5 and 6), and two 6-category items (picture sets 7 and 8).

Silly Sounds Stroop (Inhibitory Control)

This task was derived from the Day-Night task developed by Gerstadt, Hong, and Diamond (1994). Children are presented with pictures of a cat and dog. The experimenter asks the child to make the sounds of a dog and then a cat. The experimenter then introduces the idea that, in the Silly Sounds game, dogs make the sounds of cats and vice versa. Scripted coaching and elaboration is provided. Then pages of a flip book are presented that contain side-by-side pictures of cats and dogs (in random order). The experimenter points to first picture and asks what sound this animal makes in the Silly Sounds game and then points to the adjacent picture and asks the same question. A total of 36 items are presented (18 flip book pages). In terms of administration, verbal prompts are discontinued after the first 8 items (the experimenter just flips a page and points to pictures). For purposes of this paper, we only focus on the first animal on each page (due to high levels of item dependence for pictures on the same page). We also excluded 4 items that were identified as problematic during preliminary analyses. The 14 remaining items were all dichotomous (correct/incorrect).

Something’s the Same Game (Attention Shifting)

This task was derived from Jacques and Zelazo’s (2001) flexible item selection task. In this task, children are shown a page containing two pictures that are similar along one dimension (content, color, or size). The experimenter then explicitly states the dimension of similarity. The next page would present the same two pictures, plus a new third picture. The third picture is similar to one of the first two pictures either along a dimension that is different from that of the first two cards (e.g., if the first two pictures were similar along the dimension of shape, the third card would be similar to one of the first two along the dimension of color or size.) Children are asked to choose which of the two original pictures are the same as the new picture. This requires the child to shift his/her attention from the initial dimension of similarity to a new dimension of similarity. The person scoring the task only records which picture the child touched on each trial. This task is preceded by a pretest in which children demonstrate knowledge of color, shape, and size. For purposes of this paper, we exclude 3 items that were identified as problematic during preliminary analyses, as well as the first item, which is un-scored because it is used for teaching the task. The 16 remaining items were all dichotomous (correct/incorrect).

Analytic Strategy

Tasks were evaluated using modern measurement theory, item-factor models found within both the structural equation and IRT frameworks. As recommended by Wirth and Edwards (2009), categorical confirmatory factor analysis (CFA) methods were used to examine the dimensionality of tasks while IRT methods were used to better understand item and score characteristics (also see Mislevy, 1986, and Takane & de Leeuw, 1987, for information regarding the relationship between item-factor models). More specifically, analyses proceeded in four phases. First, CFAs were used to evaluate the dimensionality of each executive function task. Each task was developed to be uni-dimensional. However, when the fit of uni-dimensional models was poor, bi-factor models were considered. Bi-factor models are defined by a single “general” factor that accounts for the common variance among all items (much like the unidimensional model). However, bi-factor models also include method factors that can be used to take into account additional systematic variability such as the residual correlations that remain between like-types of items after accounting for overall shared variance with the general factor. A series of exact and approximate fit indices were used to evaluate the fit of each model as per the guidelines outlined by Hu and Bentler (1999). All CFA models were estimated using Mplus version 5 (Muthén & Muthén, 2007).

Second, differential item functioning (DIF), as defined within the IRT literature, was examined for all items across all dimensions. This study used the non-anchor (also commonly referred to constrain-all/test-all) approach for testing for (see Edwards & Edelen, 2009, for a recent review of DIF methods). More specifically, each set of item parameters (all a’s and b’s for a given item) was compared across groups (children residing in low vs. non-low income homes at study entry) by first constraining all item parameters to be equal across groups (mean and variance differences are estimated between groups) to obtain the log-likelihood value (i.e., the base model) and then, while constraining the mean and variance estimates to the values obtained in the first model, the model parameters are re-estimated freeing each set of item parameters though independent runs to obtain a new log-likelihood for each freed item (i.e., a comparison model). The difference between the base model’s log-likelihood and the comparison model’s log-likelihood is chi-square distributed with degrees of freedom equal to the number of additional parameter estimates in the comparison model. For example, testing for differential item functioning (DIF) for a dichotomous item would require two additional item parameters in the comparison model, an additional a- and b-parameter for the comparison group. Due to the number of comparisons within each DIF analysis, Benjamini-Hochberg (1995) false discovery rate adjustments were made to maintain a false discovery rate of .05.

Third, final IRT model parameters were estimated using methods outlined by Gibbons and Hedeker (1992, see also, Gibbons et. al. 2007). Finally, expected a posteriori scale scores were estimated for each of the tasks. All IRT models were evaluated using the IRTPro (Cai, du Toit, & Thissen, forthcoming) software developed as part of SBIR# HHSN-2612007-00013C.

Results

Sample Description & Rates of Executive Function Task Completion

Descriptive characteristics of the families and children who participated in the 48-month visit are provided in Table 1. Of the 1066 children and families who participated in the 48-month visit, N=41 (4%) of children did not have the opportunity to complete the executive function battery. This was due primarily to families moving out of the geographic area and having interviews conducted by phone (no opportunity for child testing). With three exceptions, children who did not have an opportunity to complete executive function tasks were demographically similar to children who completed one or more tasks (see Table 1). Specifically, compared to children who completed one or more tasks, children who did not have an opportunity to complete tasks were less likely to reside in PA (10% vs. 42%, p < .0001), were more likely to have a primary caregiver who was married (78% vs. 57%, p = .007), and to be slightly older (M = 49.0 vs. M = 48.3 months, p = .001). These differences likely reflect greater residential mobility of NC relative to PA families and 2 versus 1 parent families. The slight age difference is likely an artifact of the extended time necessary to locate families who relocated from the study area.

Table 1.

Sample Description at 48-Month Visit

		EF Task Summary
Descriptor		Total (N=1066)	Completed (N=1008)	No-Opp (N=41)	Not-Comp (N=17)
		%	%	%	%
State Residence	PA	42	42	10	65
Race	PC (AA)	41	41	34	24
	TC (AA)	42	42	37	24
Gender	PC (Female)	98	98	100	100
	TC (Female)	49	50	46	41
PC Marital status	Married	57	57	78	29
		M (SD)	M	M	M
Age	PC (Years)	30.6 (7.2)	30.6	31.8	28.5
	TC (Months)	48.3 (1.6)	48.3	49.0	48.1
PC	Education (years)	13.1 (2.0)	13.1	13.6	12.6
Household	Income/Needs	1.6 (1.4)	1.6	1.9	1.2

Note: Completed = Children who completed one or more of the executive function tasks; Not-Comp = Children who were unable or unwilling to complete one or more executive function tasks; No-Opp = Children who were not given an opportunity to complete an executive function task; M = Mean; SD = Standard Deviation;

Of the remaining N=1025 children, N=17 (1.6% of all children; 1.7% of those given opportunity) children were unable to complete any of the executive function tasks while N=1008 (95% of all children; 98% of those given opportunity) children completed one or more tasks. Children who were unable to complete any executive function tasks differed along numerous dimensions from children who completed one or more tasks (see Table 1), though given the small number of non-completers most comparisons were not statistically significant (under-powered). Compared to children who completed one or more executive function tasks, child who were unable to completed any tasks were more likely to reside in PA (65% vs. 42%, p = .07), less likely to be African American (24% vs. 42%, p = .12), less likely to have a primary caregiver who was married (29% vs. 57%, p = .03), and lived in lower income households (M = 1.2 vs. M = 1.6 income/needs ratio, p = .25).

Among the N=1008 children who completed at least one executive function task, the rates of task completion for the three tasks that are the focus of this manuscript were uniformly high (i.e., Something’s the Same/Attention Flexibility = 96% completion; Pick the Picture/Working Memory = 93% completion; Silly Sounds Stroop/Inhibitory Control = 89% completion). These tasks were selected because they represent the range of abilities subsumed under the broader construct of executive function and because preliminary analyses indicated that they differ in their difficulty levels and measurement precision—making them good candidates for demonstrating the merits of an IRT-based approach.

Dimensionality of Individual Executive Function Tasks

Modern measurement theory generally assumes that task scores are a reflection of individuals’ standing on a single underlying construct. That is, children’s performance on the set of items being evaluated is presumed to be characterized by a single latent factor (theta). Hence, initially, a 1-factor categorical confirmatory factor analysis (CFA) model was fit to each executive function task. If model fit was poor (i.e., CFA < .90, TLI < .90, & RMSEA > .08), modification indices, standardized residuals (see, for example, Hill et al., 2007), and discussions among the authors about possible item dependencies were used to inform the fitting of bi-factor models, which take into account plausible patterns of residual item correlations thus maintaining a general unidimensional executive function construct.

Pick the Picture

A one factor model fit the 8 item scale well (χ²₍₁₉₎ = 44.32, p < .0009, CFI = .99, TLI = .99, RMSEA = .04, N = 934). Recall that the 8 items reflect ordinal scores indicating the number of consecutive correct responses, beginning with the second picture, within each picture set (i.e., ordinal scores for each of the two 2-, 3-, 4-, and 6-picture sets).

Silly Sounds Stroop

A one factor model fit the 14 item scale poorly (χ²₍₂₇₎ = 1203.98, p < .0001, CFI = .77, TLI = .79, RMSEA = .22, N = 894). However, a bi-factor model that included two orthogonal method (or stimulus) factors fit the data well (χ²₍₃₄₎ = 271.89, p < .0001, CFI = .95, TLI = .96, RMSEA = .09, N = 894). These two method factors accounted for the fact that there was systematic variation in children’s responses to cat and dog items that was not adequately captured by a common ability factor. By introducing method factors, the general factor only accounted for the variability in responses that was common across dog and cat items (i.e., executive function ability).

Something’s the Same

Mixed results were found for a one factor model fit to the 16 item scale (χ²₍₇₅₎ = 527.79, p < .0001, CFI = .66, TLI = .73, RMSEA = .08, N = 971). While the RMSEA appeared to provide moderate support for a one factor model, both the CFI and TLI suggested a very poor fit to the data. Due to these inconsistencies, a bi-factor model comprised of a general executive function factor and two orthogonal method factors was explored. These method factors were defined by “color” items (i.e., the type of item used during the training stage of the scale) and “other” items with similarities (in size or object type) that were new to the children. This may reflect the fact that the first item of the task matched on color; hence, color matches on subsequent trials were more salient to children than were matches involving size or object type. This bi-factor model was found to fit the data well (χ²₍₇₁₎ = 201.23, p < .0001, CFI = .90, TLI = .92, RMSEA = .04, N = 971).

Item Parameter Estimation

With the dimensionality of each task established, we next focused on item parameter estimation in the context of IRT. The Silly Sound Stroop and Something’s the Same tasks, whether uni-dimensional or bi-factor, were parameterized using the 2-parameter logistic model because the tasks under consideration involved dichotomous responses (i.e., each response was either correct or incorrect). We have been describing the 2-parameter logistic model (including the example items in Figure 1) throughout this paper. That is, we have been discussing a model that accommodates tasks in which items can be scored dichotomously (correct/incorrect). However, the Pick the Picture task involved 8 ordinal items. Ordinal scored (Likert type) items cannot be accommodated by the 2-parameter logistic model; hence the Pick the Picture task was fit using an alternative model—Samejima’s (1969) graded response model.

The graded response model is closely related to the 2-parameter logistic model. In fact, the graded response model reduces to the 2-parameter logistic model when an item only has two response options. The parameters of the graded response model and 2-parameter logistic model are interpreted in a very similar fashion. The graded response model has a single discrimination parameter (commonly referred to as the a-parameter, just as in the 2-parameter logistic model). The interpretation of the discrimination parameter remains unchanged; the larger the discrimination value, the more related that particular item is to theta (our latent construct). An a = 2.00 from a 2-parameter logistic model and an a = 2.00 from a graded response model would be said to be equally related to the construct. The discrimination parameter ranges from 0 to infinity, but values greater than approximately 4 for a uni-dimensional model are generally considered problematic (Wirth & Edwards, 2007). For bi-factor models, the values can be larger before suggesting anything problematic is occurring with estimationⁱ.

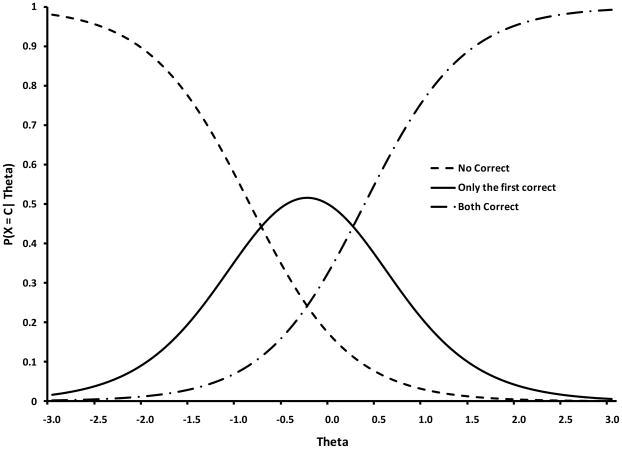
Just as the 2-parameter logistic model has a difficulty parameter (the b-parameter), so does the graded response model. In both cases, the parameters are in a z-metric (i.e., can be interpreted just as a z-score is interpreted). Also like the 2-parameter logistic model, the graded response model has one fewer difficulty parameters than the number of categories for a given item. For example, a graded response model for an item with three possible response categories would have two difficulty parameters. An item with four possible response categories would have three difficulty parameters and so on. This idea can often be best understood visually. Figure 2 provides the item characteristic curves for a trichotomous item. The three possible responses for this item were “no correct pictures”, “only the first picture correct”, and “both pictures correct.” The dashed line represents the probability of getting no pictures correct given an individual’s level of theta (executive function ability). The solid line “traces” the probability of a child getting only the first picture correct given the child’s level on theta. The dash-dot-dash line shows the probability of getting both pictures correct given an individual’s level of theta. The steepness of all three lines is defined by the a-parameter (a = 1.86 in Figure 2). The b-parameters (b₁ = −0.88 and b₂ = 0.35) denote the point on theta where an individual with that level of theta has a 50-50 chance of getting, say for example, no pictures correct or 1 or more pictures correct (i.e., the “cut-point” on theta between the first two response categories). In Figure 2, the first difficulty parameter (b₁) has a value of −0.88. This means that a child who is 0.88 SD below the mean in executive function ability has a 50-50 chance of getting no pictures correct and getting one or more pictures correct. In the case of the Pick the Picture task, the number of difficulty parameters for any given item ranged from one (for the 2-picture sets) to five (for the 6-picture sets).

Figure 2.

Item characteristic curves for a single three-category graded response item set from the Pick-the-Picture (PTP) task.

Pick the Picture

As can be seen in Table 2, all Pick the Picture items were related to theta (i.e., executive function ability underlying Pick the Picture performance). The item slopes (i.e., ‘a’ parameters) varied slightly (range: 1.04 to 1.86) suggesting that there was differential information (and reliability) across the various items. The difficulties varied widely both across and within items (e.g., −1.18 to 3.73 for item 8, a 6-picture set) suggesting that at least the more difficult items on the Pick the Picture scale measured a wide range of ability level.

Table 2.

Item difficulty (b), discrimination (a), and their standard errors (s.e.) for the Pick-the-Picture (Working Memory) task.

Item	Pictures	a	(se)	b1	(se)	b2	(se)	b3	(se)	b4	(se)	b5	(se)
1	2	1.08	(0.12)	−1.32	(0.14)
2	2	1.38	(0.14)	−1.29	(0.11)
3	3	1.86	(0.15)	−0.88	(0.07)	0.35	(0.06)
4	3	1.48	(0.12)	−1.27	(0.10)	−0.23	(0.06)
5	4	1.65	(0.13)	−0.91	(0.08)	0.28	(0.06)	1.35	(0.10)
6	4	1.28	(0.11)	−1.13	(0.10)	0.20	(0.07)	1.59	(0.13)
7	5	1.04	(0.09)	−1.49	(0.13)	0.21	(0.08)	1.11	(0.12)	2.32	(0.20)	4.18	(0.39)
8	6	1.18	(0.10)	−1.18	(0.11)	0.37	(0.08)	1.13	(0.11)	2.10	(0.17)	3.73	(0.33)

Silly Sounds Stroop

The Silly Sounds Stroop items from the bi-factor model were found to vary in their strength of relationship to theta (a’s ranging from 0.54 to 5.10; see Table 3). Unlike the Pick the Picture scale, the range of item difficulties for the Silly Sounds Stroop was narrow (ranging from −0.99 to 0.18 across all items) suggesting that an individual more than 1 SD below the mean would likely get all of the items incorrect while an individual more than .18 SD above the mean would likely get all of the items correct. However, having 14 items focused within that range suggests that the Silly Sounds Stroop scale is very good at differentiating individuals right around the mean executive function ability and that the scale is good at classifying individuals as either falling above or below the mean level executive function ability.

Table 3.

Item difficulty (b), discrimination (a), and the discrimination parameter’s standard errors (s.e.) for the Silly Sounds Stroop (Inhibitory Control) task.

Item	a	(s.e.)	Cat		Dog		b
			a	(s.e.)	a	(s.e.)
3	1.40	(0.16)	0.38	(0.14)	----	----	−0.96
5	1.38	(0.16)	----	----	0.65	(0.12)	−0.99
7	1.86	(0.20)	----	----	0.72	(0.13)	−0.78
9	1.69	(0.17)	0.69	(0.14)	----	----	−0.20
11	4.42	(0.64)	1.58	(0.29)	----	----	−0.38
13	5.10	(0.82)	2.20	(0.43)	----	----	−0.31
17	0.92	(0.13)	----	----	1.16	(0.14)	−0.43
19	0.54	(0.15)	1.79	(0.22)	----	----	0.04
21	0.96	(0.14)	----	----	1.44	(0.16)	−0.22
23	1.20	(0.33)	3.86	(0.88)	----	----	0.18
25	1.46	(0.23)	2.49	(0.31)	----	----	−0.09
29	1.31	(0.21)	----	----	2.98	(0.31)	0.00
31	1.77	(0.39)	----	----	5.33	(0.93)	−0.13
33	1.45	(0.26)	----	----	3.69	(0.44)	−0.04

Note: This model was originally parameterized using an intercept parameter instead of the traditional b-parameter. The b-parameter value was obtained from the intercept value post hoc. No standard error for the b-parameter is available for this model.

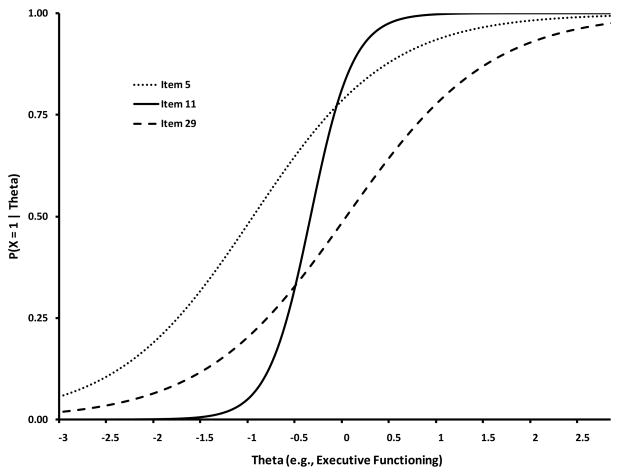
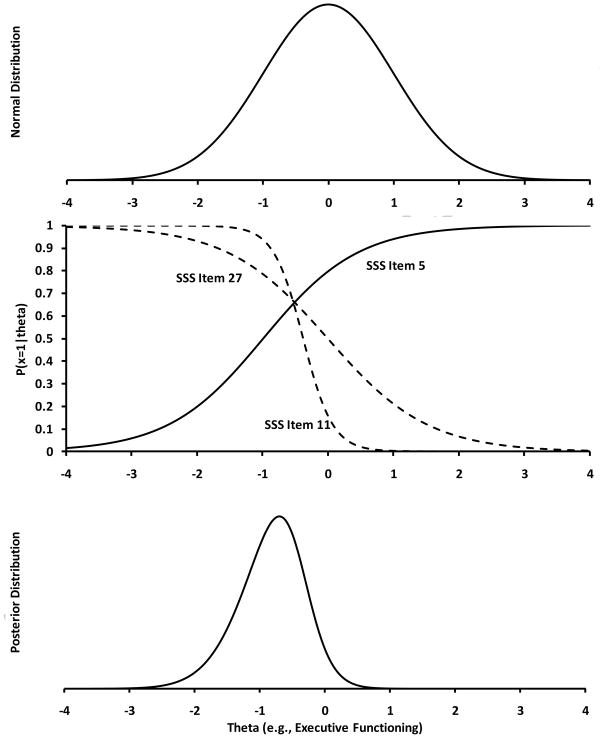
Figure 3 provides three exemplar items from the Silly Sounds Stroop scale. Item 5 has a moderate slope (a = 1.38) and is relatively easy (b = −0.99). This suggests that the item is informative but an individual who is fairly low in executive function, approximately 1 SD below the mean, still has a 50-50 chance of getting this item correct. Thus, if an individual gets this item incorrect, we can have some degree of certainty that the individual is likely less than 1 SD below the mean level of executive function. Item 29 is also shown in Figure 3. This item was also found to be informative (a = 1.31) but is more difficult (b = 0) than Item 5. In the case of Item 29, if an individual answered this item correctly, we have some certainty that the individual is above average in executive function ability. The last item presented in Figure 3 is item 11. Item 11 was found to be extremely discriminating (a = 4.42), but again it was fairly easy (b = −0.38). Indeed, the model suggested that we could have a high degree of certainty that an individual who got this item correct was above .38 SD below the mean.

Figure 3.

Item characteristic curves for three exemplar Silly-Sound-Stroop (SSS) items.

Something the Same

As seen in Table 4, Something’s the Same items were all found to be related to theta with slopes ranging from 0.42 to 1.67. The item difficulties, while suggesting that all Something’s the Same items were easy, also varied widely (ranging from −2.44 to 0.17). Taken together, the Something’s the Same scale will provide more reliable scores below the mean executive function ability than above the mean.

Table 4.

Item difficulty (b), discrimination (a), and the discrimination parameter’s standard errors (s.e.) for the Something’s-the-Same (Attention Shifting) task.

Item	a	(s.e.)	Color		Other		b
			a	(s.e.)	a	(s.e.)
2	1.52	(0.23)	0.02	(3.64)	----	----	−2.44
3	0.42	(0.10)	----	----	0.61	(0.12)	−0.02
4	0.89	(0.14)	----	----	1.00	(0.16)	−0.71
5	0.88	(0.12)	0.02	(3.64)			−0.65
6	1.67	(0.28)	----	----	−0.81	(0.24)	−1.89
7	1.00	(0.14)	----	----	0.92	(0.15)	−0.45
8	0.78	(0.11)	0.02	(3.64)	----	----	−0.55
9	1.37	(0.19)	0.02	(3.64)	----	----	−1.82
11	0.89	(0.13)	----	----	−0.40	(0.13)	−0.13
12	1.42	(0.23)	----	----	−0.96	(0.23)	−1.55
13	1.31	(0.18)	----	----	1.13	(0.20)	−0.43
14	0.98	(0.14)	----	----	0.72	(0.15)	−0.54
16	0.61	(0.12)	----	----	0.79	(0.14)	−0.87
17	0.84	(0.13)	----	----	−0.53	(0.14)	0.17
18	0.73	(0.12)	----	----	−0.29	(0.12)	−0.14
19	0.94	(0.14)	----	----	0.65	(0.13)	−0.65

Note: This model was originally parameterized using an intercept parameter instead of the traditional b-parameter. The b-parameter value was obtained from the intercept value post hoc. No standard error for the b-parameter is available for this model.

Testing for Differential Item Functioning

The item parameters described above were computed for the total sample. In this section, we test whether the item parameters are equivalent for distinct subpopulations of interest. Specifically, we tested for differential item functioning (DIF) of tasks for children who resided in low (N = 779) versus not low (N = 229) income homes at the time of their birth (and recruitment into the study). In the Family Life Project, solely for purposes of hospital-based recruitment, low income status was defined as household headed by adults with less than a high school education, a household income to needs ratio (INR) of less than or equal to 2.0, or household receipt of services that require an INR less than or equal to 2.0 (e.g., free lunch status for siblings at school, food stamps).

Only three items were found to exhibit possible DIF. These three items were Silly Sounds Stroop item 13 (χ²₍₃₎ = 12.2, p < .001), Something’s the Same item 18 (χ²₍₃₎ = 9.0, p < .029), and Something’s the Same item 19 (χ²₍₃₎ = 8.7, p < .034). However, when controlling for the number of DIF tests within each scale (14 and 16 for the Silly Sound Stroop and Something’s the Same scales, respectively), using the Benjamini-Hochberg (1995) false discovery rate adjustment, no significant DIF was foundⁱⁱ. Therefore, a single set of item parameters were deemed appropriate to describe both subpopulations of interest. That is, we found no evidence that the tasks “worked differently” for children residing in low versus not low income households.

Test Information Curves

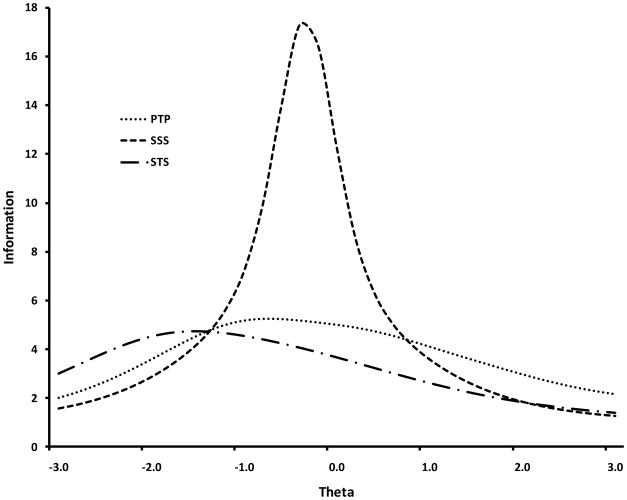
A byproduct of Item Parameter estimation is the ability to compute test information curves. Test information in its original metric is difficult to interpret directly. However, it can still provide important insights into how well a given test measures particular ranges of the construct it was designed to measure. For a given number of items, the height of a test information curve at any given level of theta reflects the strength of the items (the slopes) making up that test. Where (along the dimension of theta) the test information curve peaks is in large part defined by the difficulty parameters of the items that make up the test. Given that all three of the scales presented in this paper measure executive function ability, we overlaid all three test information curves in a single figureⁱⁱⁱ. As can be seen in Figure 4, different scales are higher or lower at different points along theta (as a reminder, theta refers to latent ability level and can be interpreted on a Z-score metric). This means that the different scales provide more or less information about an individual’s level of executive function ability depending on that individual’s true level of ability. While the Silly Sound Stroop scale proves to be the most informative scale (highest curve), the Something’s the Same scale actually provides more information about individuals who are extremely low in executive function ability (note that the Something’s the Same curve is higher than the Silly Sound Stroop curve for theta values less than approximately -1 SD below the mean). The Pick the Picture scale, on the other hand, provides more information that the Silly Sound Stroop or the Something’s the Same scale for children 1 SD above the mean level of executive function ability.

Figure 4.

Overlay of the Pick-the-Picture (PTP), Silly-Sound-Stroop (SSS), and Something’s-the-Same (STS) test information curves +/− 3 SD around the mean level of EF ability

Test information curves can be very useful when planning a study by allowing researchers to choose scales that maximize the information over the range of theta being studied. As was previously mentioned, information itself is hard to interpret directly, as the metric is contingent on the number of items in a score. Fortunately, information can be converted into score reliabilities. Unlike in classic test theory (CTT) where a scale is assumed to provide a constant score reliability regardless of who is being measured, modern approaches such as IRT first need to know who is being measured. Table 5 provides the reliability estimates for each of the three scales using Cronbach’s alpha (α; the reliability of CTT-based scores) and a score-specific IRT method presented over the range of theta in 1 SD increments. As can be seen in Table 5, the Pick the Picture scale has score reliabilities greater than .6 (on average) from −/+ 3 SD around the mean level of executive function ability. Moreover, for some intervals of ability (i.e., theta ranging from −2 to 1), IRT reliability exceeds coefficient alpha, which is .73 for this scale, while for other intervals IRT reliability is less than coefficient alpha (i.e., theta ranging from −3 to −2; 1 to 3). Consistent with Figure 4, the IRT reliability of the Silly Sound Stroop scale is very good (.84–.91) for children whose ability level is within 1 SD of the average ability level, but becomes much worse for children whose true ability level is markedly better or worse. Finally, although the Something’s the Same scale never provides score with very high reliability (> .8), it provides fairly consistent reliability, on average, ranging from approximately .72 at −3 SD below the mean to approximately .69 at 1 SD above the mean. If only a single scale was going to be used, the best scale for the job would depend on the individuals intended to be measured. The Something’s the Same scale provides the best reliability for 4 year old children who are low to very low in executive function. The Silly Sound Stroop scale provides good reliability for4 year olds who are in the mid-range of executive function and the Pick the Picture scale provides the most reliable measure for 4 year old children extremely high in executive function ability. The choice of the appropriate scale depends on who you are interested in scoring and the intended use of those scores.

Table 5.

Average IRT reliability estimates in 1 standard deviation (S.D.) unit increments from −3 to 3 standard deviations around the mean level of EF as well as coefficient alpha (α) estimates for the Pick the Picture, Silly Sounds Stroop and Something’s the Same scales.

Scale	Range of Theta						α
	−3 to −2	−2 to −1	−1 to 0	0 to 1	1 to 2	2 to 3
Pick the Picture	0.60	0.77	0.81	0.79	0.72	0.60	0.73
Silly Sounds Stroop	0.48	0.74	0.91	0.84	0.62	0.33	0.83
Something the Same	0.72	0.79	0.76	0.69	0.56	0.37	0.68

IRT Versus Percentage Correct Scores

Once a measure(s) has been selected and data collected, scores are needed. Using Classic Test Theory (CTT) methods, one would generally estimate a sum or mean (proportion) score. Doing so assumes that all items are equally related to the construct (all slopes are equal) and that all items are equally difficult (all difficulty parameters are equal). Failing to take into account differences in how each item behaves results in under- or over-weighting particular items. Incorrectly weighting items can lead to scale scores that are biased and thereby less accurate when comparing individuals (or groups) within or over time (Edwards & Wirth, 2009; Wirth 2008).

IRT, as do other modern measurement theory methods, take into account the specific qualities of each item used and weights each item appropriately. In general terms, the b-parameters are used to provide scoring information about where a person is on theta while the a-parameter provides information about how heavily the item should be weighted when estimating the overall score. How this weighting occurs becomes clearer when we examine the IRT scoring process visually. Figure 5 contains 3 panels. The top panel contains the normal distribution—this represents the population of executive function ability^iv. The middle panel represents three item characteristic curves (ICCs) for items 5, 11, and 27 from the Silly Sound Stroop scale. It shows the ICCs for an individual who correctly responded to item 5 but incorrectly responded to items 11 and 27 (for 2PL models, ICCs for incorrect items are simply one minus the probability of a correct response). The bottom panel presents the posterior distribution that is obtained by multiplying the normal distribution (i.e., top panel) by each of the ICCs over each point of theta. The posterior distribution is the score distribution for anyone who answered item 5 correctly and items 11 and 27 incorrectly (ignoring all other items). Using the posterior distribution allows us to assign a single score to that response pattern in a number of ways. Two common scores are modal a posteriori and expected a posteriori scores. Modal a posteriori scores are estimated by finding the mode of the posterior distribution while expected a posteriori scores are estimated by finding the mean of the posterior distribution. The standard error of the score (regardless of the scoring method) is found by estimating the spread of the posterior distribution. To be clear, we are using three items here to facilitate an understanding of how IRT-based scoring worked. In practice, all items a child answered for a task were used in scoring.

Figure 5.

Three panels outlining the IRT-based scoring methodology.

IRT-based scoring requires more effort than does CTT scoring (e.g., taking the proportion correct). However, it does offer many benefits. For example, an expected a posteriori (or modal a posteriori) score estimated from only these three Silly Sounds Stroop items is an estimate of the same score that would be estimated using all of the Silly Sounds Stroop items. Fewer items will lead to a less reliable score estimate, but the scores are in the same metric (i.e., z-scores) as scores based on all of the Silly Sound Stroop items (also z-scores) and can be directly compared regardless of the number of Silly Sound Stroop items completed. Thus, if a child only answered three of the 14 item items, his IRT-based score could still be estimated and this score would “mean” the same thing as a score based on all 14 items (however there would be greater uncertainty in the score that was based on 3 items and this would be represented by the standard error of the score). Using CTT, a proportion score based on only three items is not on the same scale as a proportion score based on all 14 Silly Sound Stroop items. These two proportion score estimates (three vs. all items) are no longer estimating the same “thing” and particular care should be taken when attempting to compare to one the other.

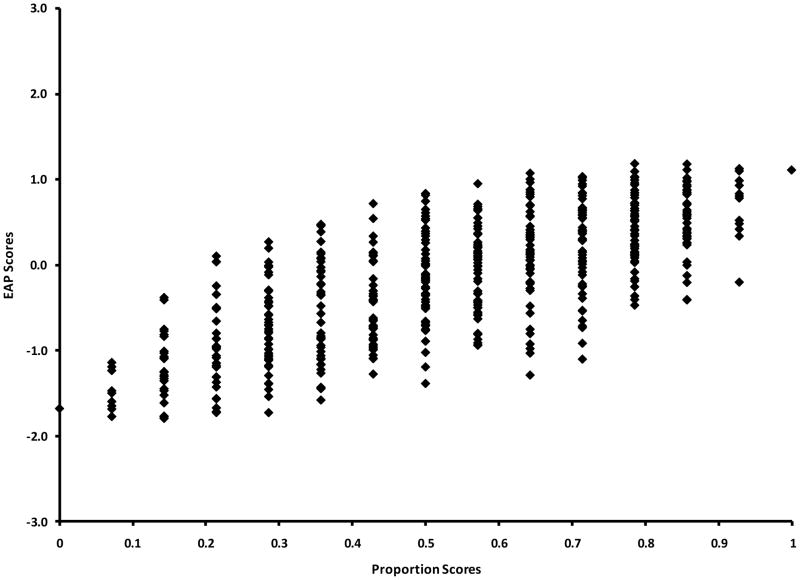
Another very important benefit offered by IRT-based scoring is their increased precision. Greater differentiation among individuals is achieved by accounting for individual item characteristics in the scoring process. Figure 6 shows a scatter plot between individual Silly Sound Stroop expected a posteriori scores and the corresponding percent correct scores. As would be expected, the scores are highly correlated (r = .84) because the general rank order of individuals has changed little (Curran et al., 2007). However, notice that for every proportion score there are a range of expected a posteriori scores. More specifically, the 92 children in this sample who received a proportion score of 0.5 (suggesting they are all equal in executive function ability) had expected a posteriori scores suggesting the children different by as much as 2.22 SDs in executive function ability (expected a posteriori scores ranged from −1.38 to 0.84 for children with proportion scores of 0.5). The reason for this variation is that although children may answer the same proportion of items correctly, distinguishing which specific items that they answered correctly (with respect to difficulty and discrimination), provides additional information regarding their latent ability level. In general, Figure 5 highlights the level of individual differentiation that is lost when relying on CTT methods. To be clear, if the difficulty and discrimination parameters for items on a task were all similar, IRT-based scores would not yield much additional information beyond a proportion or sum score.

Figure 6.

Scatter plot of the Silly-Sound-Stroop (SSS) expected a posteriori (EAP) scores by proportion scores for 894 children.

Discussion

Given the relation of executive functions to a number of aspects of child development—including self-regulation, mental development, and risk for psychopathology—research on the measurement of executive function in young children is a scientific priority. Increased precision in the measurement of early executive function will facilitate an improved understanding of the developmental course of executive function in early childhood, including the identification of naturally occurring experiences, as well as experimental interventions, that promote competence and resilience in children at risk for school failure and early developing psychopathology (Blair, Zelazo, & Greenberg, 2005). With these goals in mind, this study demonstrated, by way of an extended empirical example, how IRT may be used to evaluate the psychometric properties of executive function tasks designed for use with young children.

It is probably not too far of an exaggeration to suggest that there exists a “cottage industry” around the development of Executive Function tasks for use with young children (see e.g., Carlson, 2005). Collectively, these tasks represent the ingenuity of researchers for developing tasks that are engaging to young children and that present novel challenges that (purportedly) engage executive function abilities. Nonetheless, the majority of newly developed tasks have never undergone formal psychometric evaluations. Uncertainty regarding the measurement properties of most executive function tasks that are used with young children potentially undermines researchers’ ability to rigorously test scientific questions related to executive function abilities in early childhood. Moreover, this dearth of knowledge complicates efforts to select executive function tasks that are optimally useful for the specific populations of children and research questions being tested.

Modern measurement methods provide a comprehensive framework for evaluating executive function tasks. As demonstrated in this study, standard applications of IRT can facilitate an evaluation of item characteristics, including the identification of items that work poorly, as well as informing how items might be modified to make the task more or less difficult. The focus on item level characteristics is consistent with an iterative-approach to task development. That is, like all test development, creating executive function tasks for use with young children is best accomplished using an iterative approach, in which items are generated, pilot tested, administered to large samples, empirically evaluated, and then further modified based on analysis. Although this process is time intensive and potentially costly, the result is improved measurement of executive function, which ensures that substantive results (or lack thereof) are not an artifact of poor measurement.

Consideration of item parameters also provides a formal strategy for testing whether items function equivalently for distinct subpopulations of participants. This is broadly known as testing for measurement invariance. Within IRT, this involves testing for differential item functioning. In this study, we demonstrated that the item characteristics for each of the three executive function tasks under consideration were equivalent for children residing in low and not low income households, at least in this sample. Of particular importance for studies of executive function in early childhood is testing for differential item functioning across time. Investigators routinely compare performance of children of distinct age groups to demonstrate developmental changes in executive function ability. However, these comparisons are only valid to the extent that the measurement characteristics of a given executive function task are modeled properly across time. Failing to adjust for any changes in the measurement structure of a task (whether over time or across groups) results in items being under or over weighted during score estimation. Inaccurate item weighting (including the use of mean/percentile scores where all items are weighted equally) can result in biased mean differences, biased variance estimates, and incorrect interpretations of the function of change over time (Edwards & Wirth, 2009; Wirth 2008).

In addition to item evaluation, IRT methods provide test information. Test information indicates how the precision of measurement of a task varies as a function of child ability level. The three tasks considered in this study differed markedly with respect to task information. Whereas the Something’s the Same and Pick the Picture tasks provided moderately good reliability over broad ranges of executive function ability level, the Silly Sounds Stroop task provided very good reliability over a more narrowly defined range of executive function ability level. The routine presentation of test information curves for measures of executive function in early childhood would facilitate the selection of tasks that match the characteristics of children under study.

A final advantage of IRT methods for evaluating executive function tasks in early childhood is the provision of scores which are purged of measurement error and that make most use of item information. Although the creation of percent correct (or simple sum) scores is easy, and such scores will be highly correlated with IRT-based scores, they can conflate true score and error variation if the CTT assumptions that all of the items on a task are equally difficult and discriminating are not met. As shown in this study, IRT-based scores can “squeeze” additional information about individual differences in ability level from children who have identical proportion correct scores. The amount of additional information that is available to be “squeezed” out of proportion scores is directly related to variation in item difficultly and discrimination parameters (the more similar items on a task are, the more similar proportion correct and IRT scores will be).

Using IRT methods to evaluate executive function tasks in early childhood has many advantages but also involves some tradeoffs. The estimation and appropriate interpretation of IRT models requires specialized knowledge and software. Moreover, given the use of marginal maximum likelihood estimation procedures, IRT models should ideally involve much larger samples than have typically be used in previous studies that developed executive function tasks for use in early childhood. Although representative samples are not needed, it is important that the sample include children who represent the full range of ability level.

In addition to these “costs”, the unique characteristics of assessing executive function abilities in early childhood may present some challenges to traditional applications of IRT. For example, unlike achievement tests, where every item is unique, many executive function tasks repeatedly present the same identical item to a child. In our Silly Sounds Stroop task, children are repeatedly asked to either bark or meow to cats or dogs, respectively. This may lead to questions about why we would expect items to be differentially difficult or discriminating as indicators of underlying ability. It may also introduce problems of local dependence that require creative modeling approaches. Similarly, the idiosyncratic ways in which young children respond to some executive function tasks may introduce item dependencies that are not anticipated. In this study, we estimated bi-factor models in order to take into account residual correlations between items that remained even after modeling item inter-relations due to a shared common factor. Finally, the limited attention spans of many young children impose natural constraints on the length of tasks. Hence, although the results of IRT models may suggest ways to expand tasks to improve their measurement (e.g., inclusion of additional items that cover a broader range of ability level), it may be more appropriate to develop shorter, more discrete tasks that target specific ability levels, rather than developing longer tasks that attempt to measure the full range of ability well. Anyone who has administered measures of cognitive ability to young children knows that it is often preferable, if given the choice, to administer two, 7-minute tasks than a single 15-minute task, as the former provide a natural opportunity for breaks.

Beyond the technical contributions of using an IRT-based approach for evaluating executive function measures, the results of this study inform two issues in the substantive literature. First, there is uncertainty about the dimensionality of executive function in early childhood. Although executive function is conceptualized as a multi-dimensional construct in older samples, it may be better conceptualized as an undifferentiated, uni-dimensional construct in early childhood (Miyake et al, 2000; Wiebe et al, 2008). Correlation matrices representing children’s performance on multiple executive function tasks form the basis of most of this work. To the extent that the tasks used in any given study are optimized to measure different ability levels, the magnitude of correlations between tasks will be attenuated, which may undermine the ability to delineate the true latent structure. Future studies of the dimensionality of executive function in early childhood will be well served by ensuring that tasks that putatively measure inhibitory control, working memory, and attention shifting have comparable levels of reliability. Second, an emerging body of work has demonstrated that poverty is predictive of executive functions in early childhood (Blair et al, submitted; Noble et al, 2007). If the results of this study were replicated, there would be increased confidence that these group differences are not artifacts related to the differential measurement properties of tasks across low and not low income groups.

In sum, despite an explosion of research on children’s self regulation in early childhood, the field continues to be dependent on tasks that have not been subjected to rigorous psychometric evaluation. Moreover, given a central assumption that early childhood is characterized by rapid developmental onset of executive function abilities, it will be imperative to develop scalable instruments that facilitate inferences about inter-individual differences in intra-individual change in executive function across ages 3–5 years. The methods used in the current study have the potential to facilitate these efforts. The development of psychometrically sound, scalable measurement tools, that both facilitate the study of inter-individual differences in executive function ability and that can be used in the context of large scale studies, will dramatically improve the scientific study of executive function in early childhood.