Restriction-modification systems and bacteriophage invasion: who wins?

Abstract

The success of a phage that infects a bacterial cell possessing a restriction-modification (R-M) system depends on the activities of the host methyltransferase and restriction endonuclease, and the number of susceptible sites in the phage genome. However, there is no model describing this dependency and linking it to observable parameters such as the fraction of surviving cells under excess phage, or probability of plating at low amount of phages. We model the phage infection of a cell with a R-M system as a pure birth process with a killing state. We calculate the transitional probabilities and the stationary distribution for this process. We generalize the model developed for a single cell to the case of multiple identical cells invaded by a Poisson-distributed number of phages. The R-M enzyme activities are assumed to be constant, time-dependent, or random. The obtained results are used to estimate the ratio of the methyltransferase and endonuclease activities from the observed fraction of surviving cells.

1. Introduction

The phenomenon of restriction-modification (R-M) was discovered in the 1950s during experiments in which different strains of the same bacterial species were infected with bacterial viruses (bacteriophages or phages for short) (Luria and Human, 1952; Bertani and Weigle, 1953). It was observed that while the efficiency of plating (calculated as the proportion of phage particles capable of productively infecting the host bacterium and ultimately leading to plaques, i.e., observable foci of infection on host bacterium lawns) on permissive, non-restricting strains was close to one, efficiency of plating on non-permissive, restricting strains was about five orders of magnitude lower. However, phage progeny that recovered from rare productive infections of restricting hosts were able to plate with equally high efficiency on both restricting and non-restricting strains. Furthermore, the progeny of “modified” phages lost the ability to productively infect the restricting strain after a single passage on the non-restricting strain. Thus, phages recovered from the restricting-strain infections do not contain a heritable change; they are said to be “modified” by the restricting host.

In experiments that ultimately led to the development of molecular cloning and genetic engineering, the molecular basis of R-M phenomena were uncovered. It was shown that restricting hosts encode two enzymatic activities that are absent in non-restricting bacteria (reviewed in Arber (1978)).

The endonuclease molecules can cut DNA at recognition sites. Consequently, they can destroy both the foreign DNA and the genomic DNA itself.

The cell uses methyltransferase to protect its genome from being killed by its own endonuclease, as a methylated site is not recognized by the endonyclease. Moreover, even a hemimethylated site is not recognized and cut, retaining protection of a newly replicated genomic DNA molecule. These sites are then fully methylated by the methyltransferase, and thus the methylated state is stably maintained in multiple rounds of replication.

On the other hand, if the phage DNA becomes methylated in the bacterial cell, it also cannot be cut by the endonuclease. The progeny phages are methylated as well, and further rounds of the infection proceed without interference from the R-M system. This means that the fate of the cell and the phage largely depends on the competition between the methyltransferase and the endonuclease for the sites in the invading phage genome: if all sites in the phage genome are methylated before endonuclease recognizes any one of them, the phage survives, leading to successful infection.

Over the years, many R-M enzyme pairs (R-M systems) have been isolated from diverse bacteria, the search has been mostly driven by the constant need of restriction endonucleases with novel specificities to be used for molecular cloning (REBASE, http://rebase.neb.com). Cells possessing an R-M system by definition are more resistant to certain phages, obviously an advantageous trait. Analysis of various phages reveals that their genomic DNA contains little or no recognition sequences for restriction endonucleases commonly found in their hosts, or that they use special mechanisms such as heavy methylation of their DNA or specialized antirestriction proteins that bind to and inactivate restriction endonucleases of the host (Tock and Dryden, 2005). Clearly, phages have evolved these mechanisms to avoid the action of the R-M systems of the host.

The protection afforded by the R-M systems against the infecting phage is not absolute, and a cell that is productively infected ends up serving as a source of modified phage progeny that can effectively wipe out the rest of the population. The efficiency of restriction appears to be genetically determined and is both host strain and phage specific. The physiology of the host also appears to play a role. However, the actual mechanisms that lead to and determine the frequency of overcoming the host restriction by phages are unknown. Here, we model the process of phage infection of a bacterial cell harboring an R-M system. The model makes specific predictions about the efficiency of the phage restriction at varying multiplicity of infection for phage containing different numbers of R-M system recognition sites. We specifically take into account the fluctuations in the amount of restriction endonuclease, methyltransferase, and phage infecting a cell. The results set the stage for discriminative experiments that will allow to confirm or refute the mechanism of phage restriction implicitly assumed in the model and thus increase our understanding of the mechanism of restriction of foreign DNA by cells harbouring R-M systems.

2. Model

We model a culture of bacterial cells that harbors an R-M system and is invaded by a phage. The number of restriction sites N in the phage genome is known, the total number of bacteria in the culture is K, and the total number of phages equals V. The bacterial cells are assumed to be identical up to the effective activities (see below) of restriction endonuclease and methyltransferase denoted by ρ and μ, respectively. The effective activity of an enzyme is the product of the number of molecules of the enzyme and its single-molecule activity. The effective activities ρ and μ can be time-dependent, constant, or randomly depending on the number of enzyme molecules per cell. In the next section we provide details on the concept of effective activity. We assume that the phage is restricted (or modified) before the replication commences. Our first goal is to obtain probabilities of survival or death for a single bacterium, and, simultaneously, the probabilities of productive or abortive infection for a single phage. We start by modelling our system for the case of a single bacterium invaded by a single phage assuming time-dependent activities ρ(t) and μ(t). Then we generalize our results to the case of a bacterial culture invaded by multiple identical phages. We assume that the number of phages infecting a single cell is Poisson-distributed. The distribution of the number of R and M molecules per cell is assumed to be Poisson and the single-molecule activities are assumed to be constant. We do not consider conversion to the lysogenic state that is modeled, e.g. in (Avlund et al., 2009). We also do not model the spatial distribution of susceptible and restricting colonies, or colonies possessing different R-M systems (Gregory et al., 2010).

2.1. Mathematical Model

The process of infection of a bacterial cell is modelled by a pure birth process with killing (see, for example, Karlin and Tavaré (1982); van Doorn and Zeifman (2005); Coolen-Schrijner et al. (2006) for some general results on this type of processes). We calculate the stationary distribution for the process for a general situation of time-dependent enzyme activities.

Let R(t) be a continuous time Markov process with N + 1 states i = 0, … , N and a so-called ”killing state” −1. The system is at the state i if exactly i restriction sites of the phage DNA are methylated. Assume that effective activities of the methyltransferase and the restriction endonuclease in a bacterial cell are time-dependent functions μ(t) and ρ(t), respectively.

We suppose that at any state i the methyltransferase and the endonuclease select a site to be processed (methylated or cut) with probability 1 − i/N. Thus, at the state 0 the next site will be methylated/cut with the probability 1. In fact, the enzyme molecules select an unmethylated site with probability 1 − i/N if i sites are already methylated. We assume that the enzyme molecules cannot select the same site simultaneously. We also assume that a methylated site cannot be selected by the methyltransferase again.

If all N sites are methylated, the phage survives and the bacterium dies. In this case the Markov chain hits the absorbing state N. If the restriction endonuclease encounters an unmethylated site, the phage dies and the Markov chain hits the “no-phage state” −1 meaning that the bacterium has survived the phage invasion.

Let μ_i(t) = (1 − i/N)μ(t), ρ_i(t) = (1 − i/N)ρ(t). In fact, µ_i(t) is the transition rate from the state i to the state i + 1 at the time t; ρ_i(t) is the transition rate to the state −1 from the state i at the time t. Roughly speaking, µ_i(t)h is the probability of methylating a site in the phage genome during an infinitely small time interval h → 0 if exactly i sites are methylated at the time t, and ρ_i(t)h is the probability of cutting a site during an infinitely small time interval h → 0 if exactly i sites of the phage are methylated at the time t.

Let P_k(t) = P{R(t) = k} be the probability that k sites are methylated at the time t. Applying the theory of birth-and-death processes (Karlin and McGregor, 1957; Feller, 1968) we obtain the following system of differential equations

$$\begin{array}{l}{\mathbf{P}}_0^{\prime }(t)=-({\mu }_0(t)+{\rho }_0(t)){\mathbf{P}}_0(t),\hfill \\ \begin{array}{l}{\mathbf{P}}_k^{\prime }(t)=-({\mu }_k(t)+{\rho }_k(t)){\mathbf{P}}_k(t)+{\mu }_{k-1}(t){\mathbf{P}}_{k-1}(t),k=1,\dots ,N-1\end{array}\hfill \end{array}$$ (1)

with the equations for the absorbing states

$${\mathbf{P}}_N^{\prime }(t)={\mu }_{N-1}(t){\mathbf{P}}_{N-1}(t),{\mathbf{P}}_{-1}^{\prime }(t)={\displaystyle \sum _{i=0}^{N-1}{\rho }_i(t){\mathbf{P}}_i(t),}$$

where the initial conditions are P₀(0) = 1, P_k(0) = 0, k ≠ 0.

2.2. Stationary Distribution

Solving the system of the differential equations (see Appendix), we get the stationary distribution of the process R(t),

$$\underset{t\to \infty }{\text{lim}}{\mathbf{P}}_k(t)=\{\begin{array}{l}{\left(\frac{1}{N}{\displaystyle \underset{0}{\overset{\infty }{\int }}\mu }(u)G(u)du\right)}^N,k=N,\hfill \\ 1-{\left(\frac{1}{N}{\displaystyle \underset{0}{\overset{\infty }{\int }}\mu }(u)G(u)du\right)}^N,k=-1,\hfill \\ 0,k=0,\dots ,N-1,\hfill \end{array}$$

where $G(u)=\text{exp}\{-\frac{1}{N}{\displaystyle \underset{0}{\overset{u}{\int }}\mu (\upsilon )+\rho (\upsilon ))d\upsilon \}}$.

3. Estimating the ratio of R-M enzyme activities

Recall that the effective activity is defined as a product of a single enzyme molecule activity and the number of enzyme molecules per cell. Denote by N_M and N_R the number of molecules of methyltransferase and restriction endonuclease in a cell, respectively. Let a_M and a_R be single-molecule activities of methyltransferase and restriction endonuclease, correspondingly. Then the corresponding effective activities are given by μ = a_MN_M and ρ = a_RN_R. In this section we consider the cases of constant or random effective activities. First, we consider a situation when a single cell with constant effective activities is infected by a single phage. Then we generalize it to the case of multiple cells with constant activities that are infected by a Poisson-distributed number of phages. Finally, we consider the case in which the number of phages is Poisson-random as before, but the numbers of enzyme molecules are not constant but Poisson-random. Our goal is to estimate the ratio of single-molecule activities τ = a_R/a_M and the ratio of effective activities ρ/μ.

3.1. Constant activities

Consider first an imaginary scenario of a single cell being infected by a single phage. Assume that the R-M enzyme effective activities μ and ρ are constant, µ(t) ≡ μ and ρ(t) ≡ ρ. This means that the number of the enzyme molecules in a cell does not depend on time. We have $G(u)=\text{exp}\{-\frac{1}{N}(\mu +\rho )u\}$. The probabilities to hit absorbing states given that R(0) = 0 are

$$\underset{t\to \infty }{\text{lim}}{\mathbf{P}}_N(t)={\left(\frac{\mu }{\mu +\rho }\right)}^N,\underset{t\to \infty }{\text{lim}}{\mathbf{P}}_{-1}(t)=1-{\left(\frac{\mu }{\mu +\rho }\right)}^N.$$

This result has a clear intuitive explanation. The situation with constant effective activities can be modelled by a series of Bernoulli experiments. The outcome of each experiment is either methylating or cutting with probabilities μ/(μ + ρ) and ρ/(μ + ρ), respectively. Thus, the probability of the phage survival is equal to the probability of methylating exactly N sites, (μ/(μ + ρ))^N. This implies the first formula. The second formula follows from the first one as its complement with respect to one. The general result for time-dependent activities can be also explained in such a way if we take into account that the probability of exactly one site to be methylated during time t equals $\frac{1}{N}{\displaystyle \underset{0}{\overset{t}{\int }}\mu (u)G(u)du}$.

Imagine that we repeat our experiment of single-cell infection by a single phage n times. Denote by ϕ the probability of phage survival, $\varphi =\underset{t\to \infty }{\text{lim}}{\mathbf{P}}_N(t)$. Denote by $Z_n^{(N)}$ the number of infected bacteria that are killed by a phage with N restriction sites in a series of n experiments. In fact, in the case of an infection of a single bacteria by a single phage this number is exactly the same as the number of surviving phages. From the observed average number of surviving phages (killed cells) ${\overline{Z}}_n^{(N)}=Z_n^{(N)}/n$ we can estimate the ratio of R-M enzyme activities τ = a_R/a_M. Indeed, by the law of large numbers, for large n, $Z_n^{(N)}/n$ tends to ϕ. Recall the definitions of effective activities, μ = a_MN_M and ρ = a_RN_R. Then the probability of phage survival is given by

$$\varphi ={\left(\frac{\mu }{\mu +\rho }\right)}^N={\left(\frac{a_M{N}_M}{a_M{N}_M+a_R{N}_R}\right)}^N={\left(1+\tau \frac{N_R}{N_M}\right)}^{-N}.$$

Using this formula it is easy to obtain an estimator of the ratio of activities τ̂,

$$\widehat{\tau }=\frac{N_M}{N_R}\left[{({\overline{Z}}_n^{(N)})}^{-1/N}-1\right].$$

Similarly, the ratio of the effective activities ρ/μ is estimated as

$$\widehat{\rho /\mu }={({\overline{Z}}_n^{(N)})}^{-1/N}-1.$$

Further we will always denote an estimate of a parameter by a hat.

3.2. Random number of phages in a cell

Consider now the situation of K bacterial cells infected by V phages. The numbers of cells and phages are large, K, V → ∞, and V/K → Λ as K, V → ∞, where Λ is the average number of phages per cell. All phages and all cells, respectively, are assumed to be identical in a sense that the phages have the same number of restriction sites N and the enzymes have the same constant effective activities. We assume that the activities of the methyltransferase, μ = a_MN_M, and the restriction endonuclease, ρ = a_RN_R, are constant, and the effective activities depend on the numbers of molecules of each enzyme, N_M and N_R, respectively, in the cells. Denote by ψ the probability of phage death, $\psi =\underset{t\to \infty }{\text{lim}}{P}_{-1}(t)$, obviously, ψ = 1 − ϕ.

The distribution of phages between the cells satisfies the Bose-Einstein statistics with the number of possible variants $\left(\begin{array}{c}K+V-1\\ V\end{array}\right)$. Let q_j be the probability that there are exactly j phages in a bacterium. Then

$$q_j=\frac{\left(\begin{array}{c}K+V-j-2\\ V-j\end{array}\right)}{\left(\begin{array}{c}K+V-1\\ V\end{array}\right)}.$$

It is known (Feller, 1968) that for V/K → Λ, K → ∞, V → ∞, this probability converges to the geometric distribution,

$$q_j\to \frac{{\Lambda }^j}{{(1+\Lambda )}^{j+1}}.$$

Note that for a sufficiently small Λ this distribution can be approximated by the Poisson distribution with the mean Λ.

In practice, not every phage may manage to infect. In this case the real value of Λ will differ from the simple ratio V/K. To estimate the effective number of phages per cell Λ_e, we can calculate the fraction of survived cells q͂₀ for a phage with zero restriction sites. Of course, in this case only uninfected cells will survive. Assuming that q͂₀ converges to (Λ_e + 1)⁻¹ as V, K → ∞ we can estimate the effective number of phages per cell Λ_e. Inverting the approximate formula for q͂₀, we obtain Λ_e = 1/q͂₀ − 1. Hereinafter we assume that the number of phages is geometrically distributed between the cells with mean Λ_e.

We assume that the restriction events in a cell are independent. Thus, the probability of survival of a single cell infected by j phages is ψ^j (all j phages must be restricted, i.e., their DNA cut at least once). Then the probability that a single bacterial cell survives equals $S_V={\displaystyle \sum _{j=0}^V{q}_j{\psi }^j}$. Thus, as K, V → ∞, we have

$$S_V\to {\displaystyle \sum _{j=0}^{\infty }\frac{{\Lambda }_e^j}{{(1+{\Lambda }_e)}^{j+1}}{\psi }^j}=\frac{1}{1+{\Lambda }_e(1-\psi )}.$$

Let ν ≡ ν_K be the observed fraction of survived bacterial cells over K cells. Using the obtained formula for the probability of single cell survival S, we can estimate the ratio of activities τ. Indeed, since $\psi =1-{\left(\frac{a_M{N}_M}{a_M{N}_M+a_R{N}_R}\right)}^N$, we can write

$$S_V\to {\left[1+{\Lambda }_e{\left(\frac{a_M{N}_M}{a_M{N}_M+a_R{N}_R}\right)}^N\right]}^{-1}\equiv {\left[1+{\Lambda }_e{\left(\frac{N_M}{N_M+\tau N_R}\right)}^N\right]}^{-1},K,V\to \infty .$$

By the law of large numbers the fraction of survived bacteria ν ≡ ν_K converges to S_V as K → ∞. Using the above limit for S_V we can estimate τ as

$$\tilde{\tau }=\frac{N_M}{N_R}\left[{\left({\Lambda }_e\frac{\nu }{1-\nu }\right)}^{1/N}-1\right].$$

Note that τ̂ is negative for ν < (Λ_e + 1)⁻¹ and is undefined for ν = 1. The probability that ν < (Λ_e + 1)⁻¹ tends to zero as K → ∞, since the probability q₀ that a cell is not infected by any phage converges to (Λ_e + 1)⁻¹ as V,K → ∞. Thus, the fraction of survived bacteria will be greater than (Λ_e + 1)⁻¹ with probability tending to 1. The case ν = 1 corresponds to the situation when the restriction endonuclease is much more active that the methyltransferase, so that τ → ∞.

Thus, we can rewrite the estimate as

$$\widehat{\tau }=\frac{N_M}{N_R}\left[{\left({\Lambda }_e\frac{\nu }{1-\nu }\mathrm{I}\left\{\frac{1}{{\Lambda }_e+1}<\nu <1\right\}\right)}^{1/N}-1\right].$$ (2)

Here I{a ≤ X ≤ b} denotes the indicator of the set {a ≤ X ≤ b} such that I{a ≤ X ≤ b} = 1, if a ≤ X ≤ b and I{a ≤ X ≤ b} = 0, otherwise. It yields an estimate for the ratio of effective activities,

$$\widehat{\rho /\mu }={\left({\Lambda }_e\frac{\nu }{1-\nu }\mathrm{I}\left\{\frac{1}{{\Lambda }_e+1}<\nu <1\right\}\right)}^{1/N}-1.$$

Let us comment about the performance of τ̂. The estimator τ̂ is asymptotically normal as K → ∞ with the asymptotic mean-square risk

$$K\cdot {\mathbf{E}}_{\tau }{(\widehat{\tau }-\tau )}^2~\frac{1}{N^2{\Lambda }_e}\frac{N_M^2}{N_R^2}\frac{{({\Lambda }_e+{(1+\tau )}^N)}^2}{{(1+\tau )}^{N-2}},K\to \infty .$$

It is not difficult to obtain this result using standard techniques of the estimation theory (see, for example, Borovkov (1998)). Thus, the performance of our estimate depends on N, Λ_e and τ. In particular, for large τ, τ → ∞,

$${\mathbf{E}}_{\tau }{(\widehat{\tau }-\tau )}^2~\frac{1}{K}\frac{N_M^2}{N_R^2}\frac{{(1+\tau )}^{N+2}}{N^2{\Lambda }_e}.$$

Obviously, in this case the estimator performs worse for larger values of N. On the other hand, for small values of τ, τ → 0, we have

$${\mathbf{E}}_{\tau }{(\widehat{\tau }-\tau )}^2~\frac{1}{K}\frac{N_M^2}{N_R^2}\frac{{({\Lambda }_e+1)}^2}{N^2{\Lambda }_e}.$$

In this case the accuracy of estimation increases for larger N.

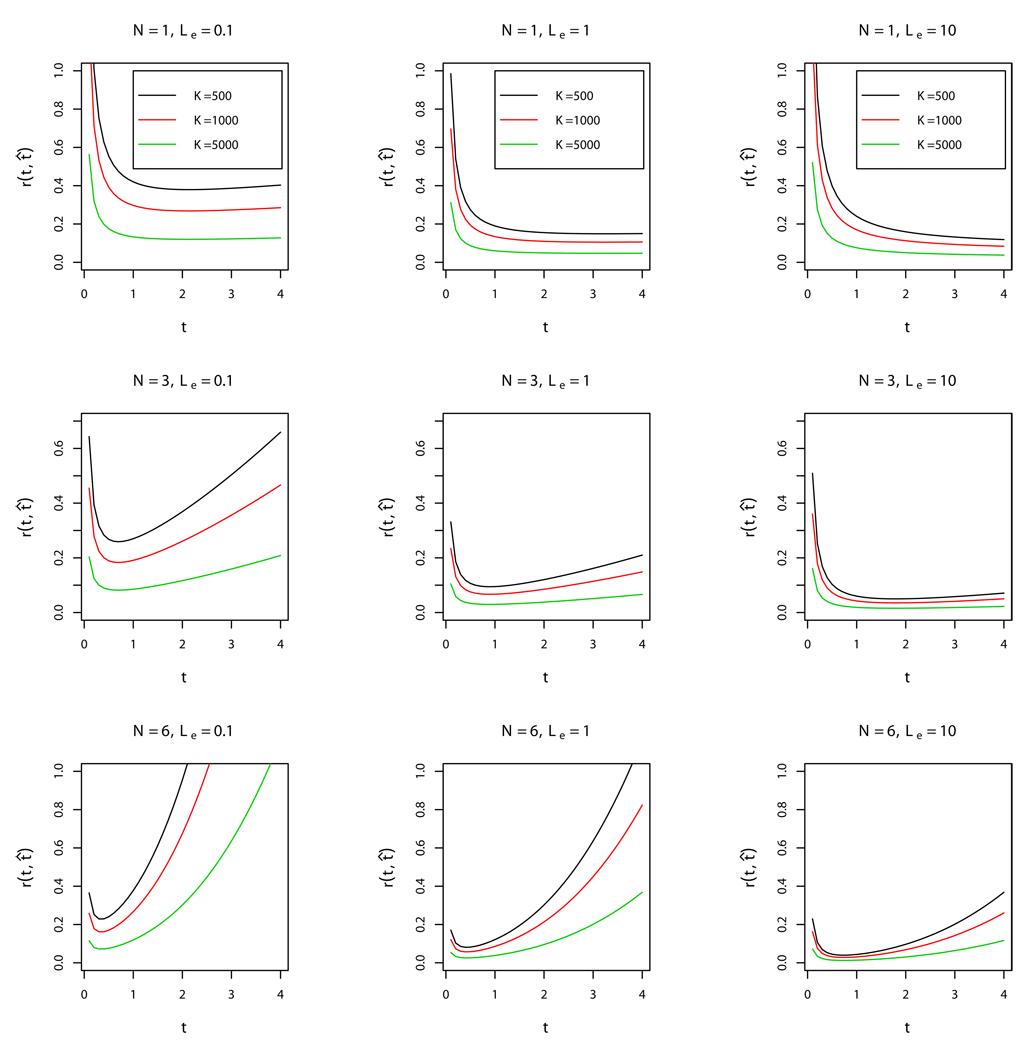
Figure 1 presents the plots of the dependence of relative mean-square error on τ,

$$r(\widehat{\tau },\tau )=\frac{1}{\tau }{({\mathbf{E}}_{\tau }{(\widehat{\tau }-\tau )}^2)}^{1/2},$$

for different values of N, Λ_e, and K. We see that if 0 < τ < 1, τ̂ is more efficient for larger values of N. On the other hand, if τ is large, τ̂ is more efficient for smaller values of N. Efficiency of τ̂ increases as Λ_e and K increase. We should note that on practice the numbers of phages and infected bacterial cells are of order 10⁵ and larger. Simulations show that the approximation by geometric distribution works fine for K, V ≥ 10³ and that the theoretical risk of estimation is very close to the empirical risk. In any case, on practice, we are interested in a large number of bacteria K (of order 10⁵ and above) infected by a relatively large number of phages.

Figure 1.

Dependence of the relative mean-square error r(τ̂, τ) = τ⁻¹E_τ(τ̂, τ) on the ratio of single molecule activities, τ. The graphs are presented for different values of Λ_e = 0.1, 1, 10 and for the number of sites N = 1, 3, 6. Each subfigure contains three graphs of the relative mean-square error for the number of cells K = 500 (black line), K = 1000 (red line), and K = 5000 (green line).

3.3. Random activities and random number of phages

Let a bacterial culture be infected so that the number of phages V is much smaller than the number of bacteria K in the culture, V ≪ K. Then we may assume that each bacterial cell will be infected by a small number of phages (zero, one or two) such that the probability of infecting a cell with k phages p_k is the Poisson distribution with mean Λ_e,

$$p_k=e^{-{\Lambda }_e}\frac{{\Lambda }_e^k}{k!}.$$

Here Λ_e < Λ ≡ V/K.

A cell is not infected with the probability p₀ = e^−Λe, this is due to the possibility for a phage to get into the intercellular space. Observing the number of killed bacterial cells which is equivalent to the number of colonies formed by surviving phages, we would like to estimate the ratio of R-M enzymes activities τ = a_R/a_M, where the numbers of molecules of both enzymes are supposed to be random as well as the number of phages in a cell. Denote by $Z_K^{(N)}$ the total number of bacterial cells killed by phage with N restriction sites that infected K bacterial cells.

Note that in the case of infection by a phage without restriction sites (N = 0) all phages survive. Thus, in this case the average number of killed bacterial cells (survived phage) is equal to 1 − p₀. It means that we can estimate the value of Λ_e by making an experiment with a phage without restriction sites. We have

$$\mathbf{E}{Z}_K^{(0)}=K(1-p_0)=K(1-e^{-{\Lambda }_e})$$

and, consequently, we can estimate Λ_e by $\text{log}\frac{K}{K-Z_K^{(0)}}$.

Let the numbers of molecules of methyltransferase and endonuclease in the i-th cell, $N_M^i$ and $N_R^i$, respectively, be Poisson-distributed (Golding et al., 2005). We assume that all cells are identical in a sense that the number of enzyme molecules per cell has the same Poisson distribution for each cell. Denote for brevity $N_M^i$ by N_M ~ Π(λ_M) and $N_R^i$ by N_R ~ Π(λ_R), where λ_M and λ_R are the average numbers of molecules of methyltransferase and restriction endonuclease per cell, respectively. Then the probability of a phage survival ϕ(N_M, N_R) given N_M and N_R molecules of enzymes in a cell is given by

$$\varphi \equiv \varphi (N_{M,}{N}_R)=\{\begin{array}{lll}{\left(1+\tau \frac{N_R}{N_M}\right)}^{-N}\hfill & ,\hfill & N_M,N_R\ne 0\hfill \\ \hfill & 1,\hfill & N_R=0\hfill \\ \hfill & 0,\hfill & N_M=0,N_R\ne 0.\hfill \end{array}$$

Note that for N_R = 0 we have ϕ = 1, since in this case a cell does not contain molecules of restriction endonuclease and all phages infecting this cell obviously survive. By the same reason we set ϕ = 1 for N_M = 0, N_R = 0.

Let us now calculate the expected value $\mathbf{E}{Z}_K^{(N)}$ of the number of killed bacterial cells $Z_K^{(N)}$, where N stands for the number of restriction sites in a phage and K is the total number of infected cells. A cell survives if all phages infected the cell die. It means that a cell dies if at least one phage infected this cell survives. Therefore, if a cell is infected by k phages, the probability of killing the cell is equal to 1 − (1 − ϕ)^k. Here the probability of phage survival ϕ depends on the (random Poisson) number of enzyme molecules in this cell. Next, we have to average this probability with respect to the number of enzyme molecules per cell and with respect to the Poisson number of phages per cell and obtain the following average probability of a cell death,

$${\displaystyle \sum _{k=1}^{\infty }{p}_k}{\mathbf{E}}_{M,R}(1-{(1-\varphi )}^k).$$

Here E_M,R denotes the mean over all possible values of N_M and N_R and p_k is the probability that there are exactly k phage in a cell. Since we have K cells, we have to multiply the above average probability by K to obtain the average number of killed bacterial cells,

$$\mathbf{E}{Z}_K^{(N)}=K{\displaystyle \sum _{k=1}^{\infty }{p}_k}{\mathbf{E}}_{M,R}(1-{(1-\varphi )}^k).$$

The precise formula for $\mathbf{E}{Z}_K^{(N)}$ in terms of λ_M and λ_R is rather complicated (see Appendix). To make our computations easier we assume that a cell can be infected by at most two phages (p_k=0 for k > 2). This assumption makes sence if, for example, Λ_e ≤ 0.1. We have

$$\begin{array}{ll}\mathbf{E}{Z}_K^{(N)}\hfill & =K{p}_1{\mathbf{E}}_{M,R}(1-(1-\varphi ))+K{p}_2{\mathbf{E}}_{M,R}(1-{(1-\varphi )}^2)\hfill \\ \hfill & =K(p_1+2p_2)\mathbf{E}\varphi -2p_2\mathbf{E}{\varphi }^2,\hfill \end{array}$$

where

$$\mathbf{E}\varphi \equiv {\mathbf{E}}_{M,R}\varphi =\mathbf{E}\left[{\left(1+\tau \frac{N_R}{N_M}\right)}^{-N}|N_M\ne 0\right]$$

is the average fraction of survived phages given the number of molecules of methyltransferase N_M is not equal to zero. Further details on the approximation of Eϕ and $\mathbf{E}{Z}_K^{(N)}$ are given in Appendix.

Let us introduce the ratio of the average numbers of enzyme molecules per cell,

$$\alpha =\frac{{\lambda }_R}{{\lambda }_M}.$$

Obviously, the behavior of $\mathbf{E}{Z}_K^{(N)}$ will be different for different values of the average activities with the same ratio α.

Consider two important cases. In the first case, λ_M and λ_R are large such that λ_M, λ_R ≥ 10. In this case we can use the approximate formula for $\mathbf{E}{Z}_K^{(N)}$ (see Appendix),

$$\mathbf{E}{Z}_K^{(N)}\approx {\tilde{Z}}_K^{(N)}=(p_1+2p_2){(1+\tau \alpha )}^{-N}\equiv K{\Lambda }_e({\Lambda }_e+1)e^{-{\Lambda }_e}{\left(1+\tau \frac{{\lambda }_R}{{\lambda }_M}\right)}^{-N}.$$ (3)

The second case is when λ_M and λ_R are small, λ_M, λ_R → 0 as K → ∞, for example, λ_M, λ_R < 1. In this case the behavior of $\mathbf{E}{Z}_K^{(N)}$ is controlled by the behavior of the term 1 − p₀, since

$$\mathbf{P}\{{\xi }_i=1\}\to (p_1+p_2)\approx 1-p_0,{\lambda }_R,{\lambda }_M\to 0.$$ (4)

In the case of moderate values of λ_M, λ_R as 1 ≤ λ_M, λ_R ≤ 5 the approximate formula for $\mathbf{E}{Z}_K^{(N)}$ will depend not only on the ratio α = λ_R/λ_M but also on λ_M,

$$\mathbf{E}{Z}_K^{(N)}\approx {\tilde{Z}}_K^{(N)}=K{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)e^{-{\mathrm{\Lambda }}_e}\times {\left[1+\tau \frac{{\lambda }_R}{{\lambda }_M}\left(1+\frac{1}{{\lambda }_M}\right){(1-e^{-{\lambda }_M})}^2\right]}^{-N}.$$

Using approximation (3) we can estimate the parameter τ for λ_R, λ_M > 5. Indeed, if $Z_K^{(N)}$ is the observed number of killed bacterial cells invaded by phages with N restriction sites, then

$$\widehat{\tau }=\frac{{\lambda }_M}{{\lambda }_R}[(\frac{e^{{\mathrm{\Lambda }}_e}}{{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)}\times \frac{Z_K^{(N)}}{K}\mathrm{I}{\{0<\frac{Z_K^{(N)}}{K}<\frac{{\mathrm{\Lambda }}_e}{{\mathrm{\Lambda }}_e+1}\})}^{-1/N}-1]$$ (5)

and the ratio of average effective activities can be estimated as

$$\widehat{\rho /\mu }={\left(\frac{Z_K^{(N)}}{K}\frac{e^{{\mathrm{\Lambda }}_e}}{{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)}\mathrm{I}\{0<\frac{Z_K^{(N)}}{K}<\frac{{\mathrm{\Lambda }}_e}{{\mathrm{\Lambda }}_e+1}\}\right)}^{-1/N}-1.$$

The condition $\mathrm{I}\left\{0<\frac{Z_K^{(N)}}{K}<\frac{{\mathrm{\Lambda }}_e}{{\mathrm{\Lambda }}_e+1}\right\}$ is obtained by the same reasoning as in Section 3.2. Indeed, for $Z_K^{(N)}=0$ the estimate (5) is undefined (it approaches infinity as $Z_K^{(N)}\to 0$). For $\frac{Z_K^{(N)}}{K}\ge \frac{{\mathrm{\Lambda }}_e}{{\mathrm{\Lambda }}_e+1}$ the estimate is negative which can happen with a very small probability for sufficiently large K.

If we know λ_M, we can estimate τ for moderate values 1 < λ_R, λ_M ≤ 5 as

$$\widehat{\tau }=\frac{{\lambda }_M}{{\lambda }_R}{(1-e^{-{\lambda }_M})}^{-2}{\left(1+\frac{1}{{\lambda }_M}\right)}^{-1}\times \left[{\left(\frac{Z_K^{(N)}}{K}\frac{e^{{\mathrm{\Lambda }}_e}}{{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)}\mathrm{I}\{0<\frac{Z_K^{(N)}}{K}<\frac{{\mathrm{\Lambda }}_e}{{\mathrm{\Lambda }}_e+1}\}\right)}^{-1/N}-1\right].$$ (6)

Estimate (5) can be compared with the estimate obtained in Section 3.2 for the case of cells with constant activities invaded by a random number of phages. Indeed, we can rewrite the estimate from (2) in terms of the number of killed bacterial cells $Z_K^{(N)}$. We have

$${\widehat{\tau }}_C=\frac{N_M}{N_R}\left[{\left(\frac{1}{{\mathrm{\Lambda }}_e}\frac{Z_K^{(N)}/K}{1-Z_K^{(N)}/K}\mathrm{I}\{0<\frac{Z_K^{(N)}}{K}<\frac{{\mathrm{\Lambda }}_e}{{\mathrm{\Lambda }}_e+1}\}\right)}^{-1/N}-1\right].$$

Subscript C in τ_C stands for the case of constant activities. This estimate and the one from (5) are very similar. Indeed, for small Λ_e we have $\frac{e^{{\mathrm{\Lambda }}_e}}{{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)}\approx \frac{1}{{\mathrm{\Lambda }}_e}$. Also, for small Λ_e the average number of killed cells is very small which explains $\frac{Z_K^{(N)}}{K}\approx \frac{Z_K^{(N)}}{K}{\left(1-\frac{Z_K^{(N)}}{K}\right)}^{-1}$.

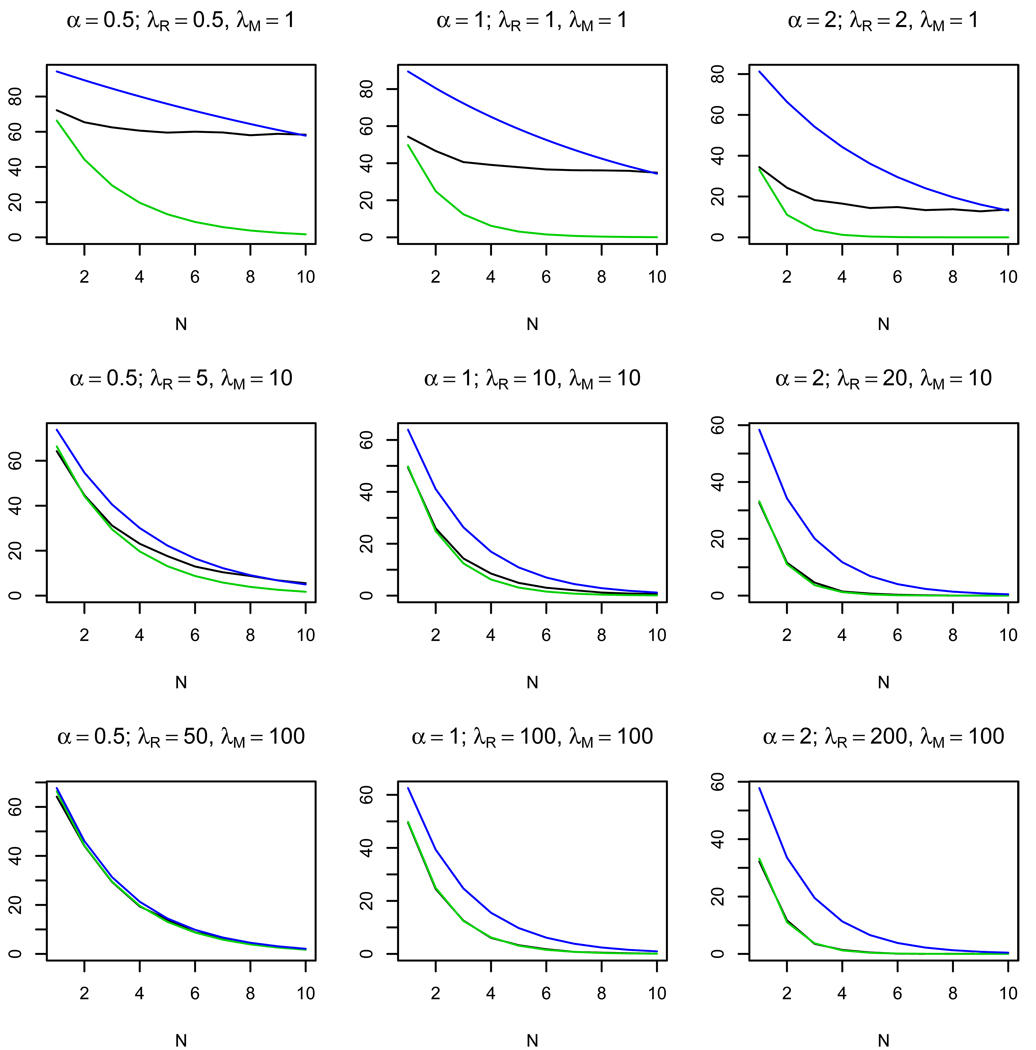
Figures 2–4 show the results of 1000 simulations for K = 10³ bacterial cells with the average number of phages per cell Λ_e = 0.1 and the ratio of activities τ = 1, 0.5, 0.1, respectively. The plots show how the number of restriction sites N influences the observed average number of killed bacteria ${\overline{Z}}_K^{(N)}$ and of the approximate value ${\tilde{Z}}_K^{(N)}$ of $\mathbf{E}{Z}_K^{(N)}$ given by formula (3). We also present an estimate ${\widehat{Z}}_K^{(N)}$ of $\mathbf{E}{Z}_K^{(N)}$ given by the following formula

$${\widehat{Z}}_K^{(N)}=K{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)e^{-{\mathrm{\Lambda }}_e}{(1+\widehat{\tau }\alpha )}^{-N}\equiv K{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)e^{-{\mathrm{\Lambda }}_e}{\left(\frac{Z_K^{(N)}}{K}\frac{e^{{\mathrm{\Lambda }}_e}}{{\mathrm{\Lambda }}_e({\mathrm{\Lambda }}_e+1)}\right)}^{-1/N}.$$

Figure 2.

Plots of the observed average number of killed cells ${\overline{Z}}_K^{(N)}$ (black line), the approximate average number of killed cells ${\tilde{Z}}_K^{(N)}$ (green line), and the estimate of the average number of killed cells ${\widehat{Z}}_K^{(N)}$ (blue line) depending on the number of restriction sites N. 10³ simulations were made for τ = 1 for K = 10³ bacterial cells. The approximate formula (3) works well for large λ_M and λ_R and small values of α = λ_R/λ_M.

Figure 4.

Plots of the observed average number of killed cells ${\overline{Z}}_K^{(N)}$ (black line), the approximate average number of killed cells ${\tilde{Z}}_K^{(N)}$ (green line), and the estimate of the average number of killed cells ${\widehat{Z}}_K^{(N)}$ (blue line) depending on the number of restriction sites N. 10³ simulations were made for τ = 0.1 for K = 10³ bacterial cells. The approximate formula (3) works well for λ_M, λ_R ≥ 5.

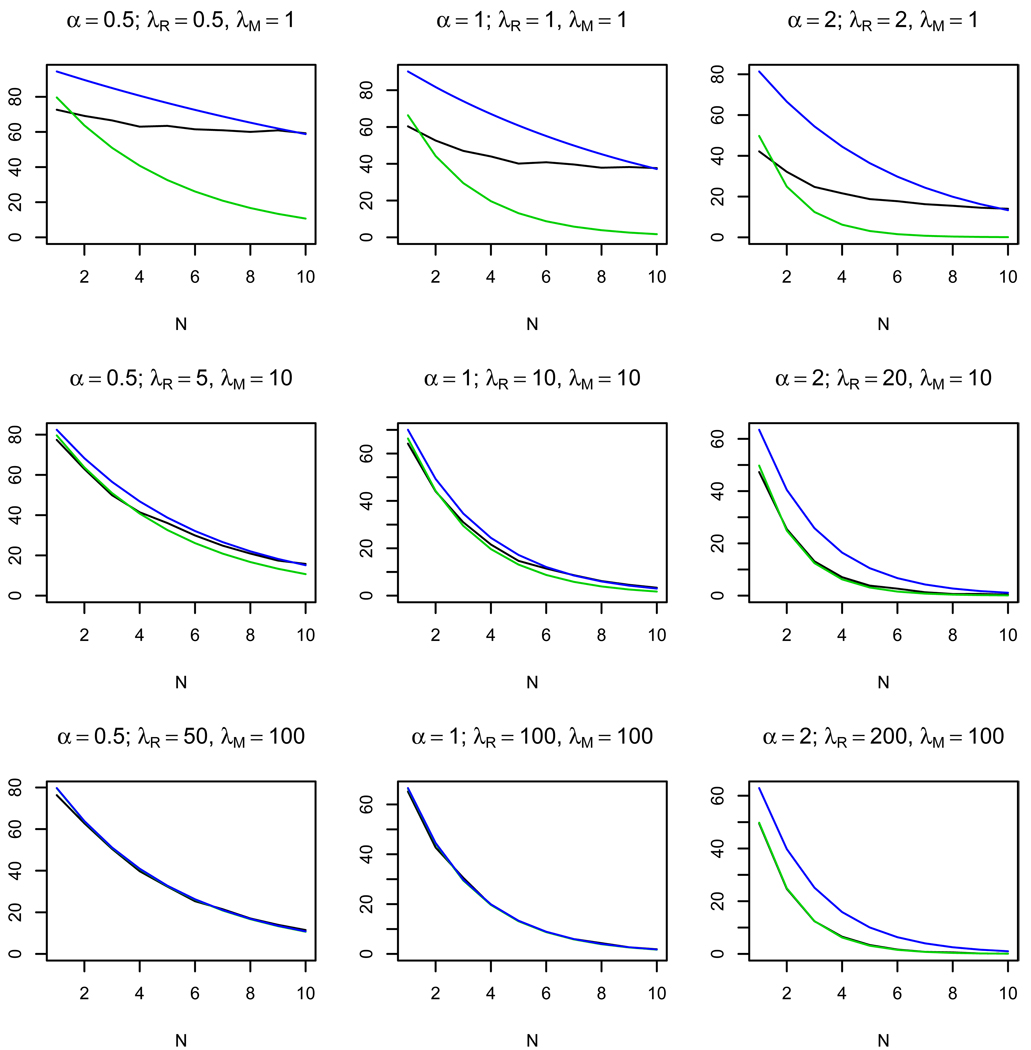
This formula is obtained by substituting the estimate τ̂ (5) into (3). The plots show that for the same ratio of the average number of enzyme molecules α the approximate formula works well for λ_M, λ_R > 5. The quality of the approximation increases as τ decreases (see Fig. 3, 4). On the other hand, for small λ_R, λ_M the approximation is bad for all values of τ, which allows us to distinguish between the cases of small and large average numbers of enzyme molecules per cell.

Figure 3.

Plots of the observed average number of killed cells ${\overline{Z}}_K^{(N)}$ (black line), the approximate average number of killed cells ${\tilde{Z}}_K^{(N)}$ (green line), and the estimate of the average number of killed cells ${\widehat{Z}}_K^{(N)}$ (blue line) depending on the number of restriction sites N. 10³ simulations were made for τ = 0.5 for K = 10³ bacterial cells. The approximate formula (3) works well for λ_M, λ_R ≥ 5 and α = λ_R/λ_M ≤ 1.

4. Discussion

In this work, we proposed a mathematical model for the process of infection of a bacterial cell harboring an R-M system with a phage. The model provides an estimate for the ratio of average effective activities τ · (λ_R/λ_M) of the methyltransferase and the restriction endonuclease, based on the number of killed bacterial cells observed in experiments.

Numerical simulations (Fig. 2–4) show that the quality of approximation is essentially better for small values of the ratio of single-molecule activities τ and also that the approximation is very bad for small average number of enzyme molecules per cell λ_M and λ_R. It allows us to distinguish between the case of the large number of enzymes per cell and the case of the small number of enzymes per cell (see Figures 2–4, the plots for the same ratio α = λ_R/λ_M and different values of λ_R and λ_M).

To validate the model, a series of experiments should be done with identical phages having different numbers of restriction sites N = 0, 1, 2, … , 10. The experiment with N = 0 allows one to estimate the effective mean number of phages per cell Λ_e. For N = 1, 2, … one needs to measure the average number of killed bacterial cells ${\overline{Z}}_K^{(N)}$ in each series and to check whether this number depends exponentially on the number of sites N according to the obtained formula ${\widehat{Z}}_K^{(N)}$. If the graphs ${\overline{Z}}_K^{(N)}$ and ${\widehat{Z}}_K^{(N)}$ are close to each other, it means that the approximation works well and the average numbers of enzymes per cell λ_M, λ_R are large. In this case we can estimate τ̂ using formula (5) and, correspondingly, obtain an estimate $\widehat{\rho /\mu }$. On the other hand, if the graphs are far from each other, we have the case of small λ_R and λ_M. In this case we cannot estimate τ well using estimate (5). To construct a good estimate we have to use formula (6), where λ_M is unknown. Hence in this case, in the absence of additional data, we cannot say anything except that λ_M and λ_R are small.

The efficiency of plating of phage lambda containing two or three recognition EcoRI sites on a restricting host was estimated in Rambach and Tiollais (1974). By design, this experiment was conducted at conditions of large excess of cells over the phage (Λ_e in our notation). The results indicated that an extra site increased the plating efficiency by an order of magnitude (from 4×10⁻² to 5×10⁻³). This is roughly consistent with the predicted dependence of the probability of successful infection on the number of sites, assuming the plating efficiency close to 1 for a phage with no sites.

One can imagine at least two possible non-overlapping mechanisms of overcoming the protection afforded by an R-M system by an infecting phage (we assume that the phage lacks specific antirestriction mechanisms of the type described in Tock and Dryden (2005)). First, it is possible that a small proportion of cells has no restriction endonuclease (or, conversely, a very large amount of methyl-tranferase) at the time of infection (Mruk and Blumenthal, 2008). The variation in the amount of restriction-modification enzymes in the cell can be the result of a stochastic noise in the levels of R-M gene expression, unequal partitioning of the R-M gene products to daughter cells etc. In this scenario, the proportion of cells that are susceptible to infection should remain constant and should not depend on the multiplicity of infection (i.e., the average number of phage particle infecting each cell).

An alternative scenario may involve fluctuations in the number of phages infecting bacterial cells at a particular multiplicity of infection. One can imagine that restriction endonuclease in cells receiving more than the average number of phage becomes “overwhelmed” allowing productive infection to occur. In this scenario, the proportion of cells that become productively infected should increase together with multiplicity of infection. The second scenario is suggested by the fact that the number of productive infections of restricting cells with a non-modified phage lambda increases when the cells are “preinfected” at high multiplicity with another non-modified phage immediately prior to infection with the first phage (Heip et al., 1974). Since our model explicitly involves different Poisson distributions for the activities of the methyltransferase and endonuclease, and for the number of phage invading a cell, it allows one in principle to distinguish between these scenarios, which may be different for different R-M systems and, possibly, phages.

Our analysis and numerical simulations show that both the best power to discriminate between the continuous model (assuming large amounts of the endonuclease and methyltransferase) and the discrete model (few molecules), and the more robust estimates of the ratio of activities is provided by the systems when the phage has a small number of sites for the R-M system. To compare the models and to estimate the ratio, different types of experiments may be suggested, including changing the number of sites by point mutagenesis, changing the expression rate of the R-M operon (retaining the ratio of activities, but changing the number of molecules), changing the activity of the endonuclease by point mutagenesis, changing the expression rate of either endonuclease or methyltransferase by inroducing additional gene copies in separate operons, etc. Having calculated the number of successful infections, and knowing the number of sites, one can then estimate the degree of fit to either model, and obtain an estimate for the ratio of activities of the endonuclease and the methyltransferase.

6. Appendix

6.1. Transitional probabilities

The first equation of system (1) can be easily solved, ${\mathbf{P}}_0(t)=\text{exp}\{-{\displaystyle \underset{0}{\overset{t}{\int }}(\mu (u)+\rho (u))du\}}$. Solving recursively the next N equations gives the solutions for k = 0, … , N,

$${\mathbf{P}}_k(t)=\left(\begin{array}{c}N\\ k\end{array}\right){\left[\frac{1}{N}{\displaystyle \underset{0}{\overset{t}{\int }}\mu (u)G(u)du}\right]}^k{G}^{N-k}(t),$$

where $G(u)=\text{exp}\{-\frac{1}{N}{\displaystyle \underset{0}{\overset{u}{\int }}(\mu (\upsilon )+\rho (\upsilon ))d\upsilon \}}$. The function 1 − G is the distribution of time between two consequent states of R(t). Now, the probability of the phage death can be calculated,

$${\mathbf{P}}_{-1}(t)=1-{\displaystyle \sum _{k=0}^N{\mathbf{P}}_k(t)=1-{\left(\frac{1}{N}{\displaystyle \underset{0}{\overset{t}{\int }}\mu (u)G(u)du+G(u)}\right)}^N.}$$

The stationary distribution of the process X(t) is given by

$$\underset{\mathrm{t}\to \infty }{\text{lim}}{\mathbf{P}}_k(t)=\{\begin{array}{l}{\left(\frac{1}{N}{\displaystyle \underset{0}{\overset{\infty }{\int }}\mu (u)G(u)du}\right)}^N,k=N\hfill \\ 1-{\left(\frac{1}{N}{\displaystyle \underset{0}{\overset{\infty }{\int }}\mu (u)G(u)du}\right)}^N,k=-1\hfill \\ 0,k=0,\dots ,N-1.\hfill \end{array}$$

Note that for constant effective activities µ(t) ≡ µ and ρ(t) ≡ ρ we have $G(u)=\text{exp}\{-\frac{1}{N}(\mu +\rho )u\}$ and the solution to the system for k = 0, … , N is given by

$${\mathbf{P}}_k(t)=\left(\begin{array}{c}N\\ k\end{array}\right){\left(\frac{\mu }{\mu +\rho }\right)}^k{(1-G(t))}^k{G}^{N-k}(t).$$

For k = −1 we have

$${\mathbf{P}}_{-1}(t)=1-{\displaystyle \sum _{k=0}^N{\mathbf{P}}_k(t)=1-{\left(\frac{\mu }{\mu +\rho }+\frac{\rho }{\mu +\rho }G(t)\right)}^N.}$$

6.2. Average number of killed bacterial cells for random activities

In this section we will estimate the average number of killed bacterial cells

$$\mathbf{E}{Z}_K^{(N)}=K{\displaystyle \sum _{k=1}^{\infty }{p}_k{\mathbf{E}}_{M,R}(1-{(1-\varphi )}^k).}$$

Here $p_k=e^{-{\mathrm{\Lambda }}_e}\frac{{\mathrm{\Lambda }}_e^k}{k!}$ are the Poisson probabilities of the number of phages in a cell. Since N_M and N_R are Poisson distributed Π(λ_m), Π(λ_r), respectively, we have the following precise formula

$$\mathbf{E}{Z}_K^{(N)}=K(1-p_0)e^{-{\lambda }_R}+K{\displaystyle \sum _{k=1}^{\infty }{p}_k[e^{-({\lambda }_R+{\lambda }_M)}}\times {\displaystyle \sum _{u=1}^{\infty }{\displaystyle \sum _{\upsilon =1}^{\infty }\left(1-{\left(1-{(1+\tau \frac{u}{\upsilon })}^{-N}\right)}^k\right)\frac{{\lambda }_R^u}{u!}\frac{{\lambda }_M^{\upsilon }}{\upsilon !}}}].$$

This distribution is non-lattice, which is considerably more difficult to handle than a lattice distribution. Our goal is to obtain an approximate formula for $\mathbf{E}{Z}_K^{(N)}$.

We first consider the behavior of the above formula for two boundary cases, τ → 0 and τ → ∞.

In the first case, when τ is small and a_R ≪ a_M, the restriction endonuclease has much smaller activity, than the methyltransferase. The formula for the average number of killed bacterial cells turns to

$$\mathbf{E}{Z}_K^{(N)}=K\mathbf{P}\{{\xi }_i=1\}=(1-p_0)K[1-e^{-{\lambda }_M}(1-e^{-{\lambda }_R})].$$

We can easily interpret this formula. Here e^−λ_M is the probability that there are no molecules of methyltransferase in a cell and 1−e^−λ_R is the probability that the cell contains molecules of restriction endonuclease. Roughly speaking, in the case of small τ, phages survive if the average number of molecules of methyltransferase λ_M is large or the average number of molecules of restriction endonuclease λ_R is small. In fact, a cell survives only if there is no methyltransferase and there is at least one molecule of restriction endonuclease.

In the second case, when τ is very large and a_R ≫ a_M, the formula for the average number of surviving phages becomes

$$\mathbf{E}{Z}_K^{(N)}=K\mathbf{P}\{{\xi }_i=1\}=(1-p_0)K{e}^{-{\lambda }_R}.$$

It means that for the large ratio of activities τ the phages survive only if the amount of restriction endonuclease is small independently of the amount of methyltransferase.

Let us now find the approximate formula for $\mathbf{E}{Z}_K^{(N)}$. For simplicity we will consider only the case when the probabilities p_k, k ≥ 3 that there are more than two phages in a cell are very small. For example, for Λ_e = 0.1 the probability that there are 3 phages in a cell is p₃ = 0.0001508062. We assume p_k = 0, k ≥ 3. Then our formula transforms into

$$\mathbf{E}{Z}_K^{(N)}=K\{p_1+2p_2\}\mathbf{E}\varphi -2p_2\mathbf{E}{\varphi }^2,$$ (7)

where

$$\mathbf{E}\varphi =\mathbf{E}\left[{\left(1+\tau \frac{N_R}{N_M}\right)}^{-N}|N_M\ne 0\right].$$

Here N_R ~ Π(λ_R), N_M ~ Π(λ_M). We can find the approximation for Eϕ using the method of propagation of error. Define the following random variable

$$X=\left\{\frac{N_R}{N_M}|N_M\ne 0\right\}.$$

We have

$$\mathbf{P}\{N_M=k|N_M\ne 0\}=\frac{e^{-{\lambda }_M}}{1-e^{-{\lambda }_M}}\frac{{\lambda }_M^k}{k!}.$$

The approximation for $\mathbf{E}\left(\frac{1}{N_M}|N_M\ne 0\right)$ is calculated using the method of propagation of error,

$$\mathbf{E}\left[\frac{1}{N_M}|N_M\ne 0\right]\approx {\lambda }_M^{-1}{(1-e^{-{\lambda }_M})}^2\left(1+\frac{1}{{\lambda }_M}\right).$$

Next, we can find the approximation for the mean EX,

$$\mathbf{E}X=\mathbf{E}{N}_R\cdot \mathbf{E}\left[\frac{1}{N_M}|N_M\ne 0\right]\approx \frac{{\lambda }_R}{{\lambda }_M}\left(1+\frac{1}{{\lambda }_M}\right){(1-e^{-{\lambda }_M})}^2$$

Using the same method again we obtain the following approximate formula for Eϕ:

$$\begin{array}{lll}\mathbf{E}\varphi \hfill & =\hfill & \mathbf{E}{(1+\tau X)}^{-N}\approx {(1+\tau \mathbf{E}X)}^{-N}\hfill \\ \hfill & =\hfill & {\left[1+\tau \frac{{\lambda }_R}{{\lambda }_M}\left(1+\frac{1}{{\lambda }_M}\right){(1-e^{-{\lambda }_M})}^2\right]}^{-N}.\hfill \end{array}$$

Here we use just the first two terms of the Taylor series expansion around EX to approximate Eϕ. The quality of approximation would be better if we used the terms of second and higher orders, but in this case it would be harder to derive an estimator for τ. The approximation works well for 0 < τ < 1. Since the second order term depends on τ², the formula will work worse for large τ, however, in the vicinity of τ = 1 it is sufficiently precise.

Finally, we have the following approximate formula

$$\mathbf{E}{Z}_K^{(N)}\approx K(p_1+2p_2){\left[1+\tau \frac{{\lambda }_R}{{\lambda }_M}\left(1+\frac{1}{{\lambda }_M}\right){(1-e^{-{\lambda }_M})}^2\right]}^{-N}.$$

We omit the term 2p₂Eϕ² in formula (7), since its contribution to the total value of $\mathbf{E}{Z}_K^{(N)}$ is very small compared to the contribution of the first two terms.