Partial volume correction of PET-imaged tumor heterogeneity using expectation maximization with a spatially varying point spread function

Abstract

Tumor heterogeneities observed in positron emission tomography (PET) imaging are frequently compromised of partial volume effects which may affect treatment prognosis, assessment, or future implementations such as biologically optimized treatment planning (dose painting). This paper presents a method for partial volume correction of PET-imaged heterogeneous tumors. A point source was scanned on a GE Discover LS at positions of increasing radii from the scanner’s center to obtain the spatially varying point spread function (PSF). PSF images were fit in three dimensions to Gaussian distributions using least squares optimization. Continuous expressions were devised for each Gaussian width as a function of radial distance, allowing for generation of the system PSF at any position in space. A spatially varying partial volume correction (SV-PVC) technique was developed using expectation maximization (EM) and a stopping criterion based on the method’s correction matrix generated for each iteration. The SV-PVC was validated using a standard tumor phantom and a tumor heterogeneity phantom, and was applied to a heterogeneous patient tumor. SV-PVC results were compared to results obtained from spatially invariant partial volume correction (SINV-PVC), which used directionally uniform three dimensional kernels. SV-PVC of the standard tumor phantom increased the maximum observed sphere activity by 55 and 40% for 10 and 13 mm diameter spheres, respectively. Tumor heterogeneity phantom results demonstrated that as net changes in the EM correction matrix decreased below 35%, further iterations improved overall quantitative accuracy by less than 1%. SV-PVC of clinically observed tumors frequently exhibited changes of ±30% in regions of heterogeneity. The SV-PVC method implemented spatially varying kernel widths and automatically determined the number of iterations for optimal restoration, parameters which are arbitrarily chosen in SINV-PVC. Comparing SV-PVC to SINV-PVC demonstrated that similar results could be reached using both methods, but large differences result for the arbitrary selection of SINV-PVC parameters. The presented SV-PVC method was performed without user intervention, requiring only a tumor mask as input. Research involving PET-imaged tumor heterogeneity should include correcting for partial volume effects to improve the quantitative accuracy of results.

1. Introduction

Positron emission tomography (PET) is a functional imaging modality that is currently being used in oncologic studies to obtain information pertaining to tumor glucose metabolism, proliferation, hypoxia, as well as other biological processes (Denoyer et al 2006, Kumar et al 2007). PET-imaged tumors frequently exhibit non-uniform tracer uptake, indicating the presence of so-called tumor heterogeneities (Heppner and Miller 1983, Heppner 1984, Sutherland et al 1996, Hanahan and Weinberg 2000), where tumor subvolumes exhibit increased uptake relative to the uptake of the remaining tumor volume. The field of radiation therapy is interested in heterogeneous tumors, as regions of increased biological function may be used for increasing tumor control in radiation therapy (Ling et al 2000, Tomé and Fowler 2000, Chao et al 2001), treatment assessment (O'Sullivan et al 2003, Eary et al 2008a), or as prognostic indicators (Eary et al 2008b, Kidd and Grigsby 2008).

However, heterogeneities imaged using PET frequently suffer from partial volume effects (PVE) due to the poor resolution associated with PET imaging (Hoffman et al 1979, Soret et al 2007). PVE decrease the observed uptake of tumor heterogeneities depending on heterogeneity size (Hoffman et al 1979) and contrast (Kessler et al 1984, Bendriem et al 1991). The small size of tumor heterogeneities and often close proximity to larger tissue regions with differing tracer uptakes such as muscle, homogeneous tumor, bone, or necrosis make them susceptible to being blurred-out by PVE (Kessler et al 1984, Bendriem et al 1991, Soret et al 2002). The magnitude of PVE is strongly dependent on the system resolution (Hoffman et al 1979, Soret et al 2007).

Scanner resolution is systematically limited by detector geometry and the physics of positron decay and detection during acquisition (Tarantola et al 2003), and is further degraded by image reconstruction methods. Statistical reconstruction methods such as ordered-subset expectation maximization (Hudson and Larkin 1994) (OSEM) or maximum a posteriori (Levitan and Herman 1987) (MAP) are frequently used in oncological PET imaging due to their successful mitigation of artifacts and noise typically seen in analytical reconstruction techniques (filtered-backprojection) (Barrett et al 1994, Qi and Leahy 2000). However, these iterative reconstruction techniques frequently complicate PVE by modifying scanner resolution. Current OSEM implementations terminate the iterative process prior to full convergence in order to reduce variance, creating a strongly object-dependent resolution that fails to resolve small objects and introduces bias (Veklerov and Llacer 1987). Furthermore, uniform penalty terms (Fessler and Rogers 1996) and smoothing performed between successive iterations (Mustafovic et al 2001, Mustafovic and Thielemans 2004) result in spatially variant, object dependent system resolution. Reconstruction choices are typically made to optimize image quality for qualitative assessment (reduced variance and reconstruction time), without consideration of bias or PVE.

Partial volume correction (PVC) methods undo the image blurring associated with the system resolution, either during or after image reconstruction. Several groups and manufacturers have incorporated system response functions into the reconstruction algorithms in an effort to improve resolution (Reader et al 2003, Alessio et al 2004, Alessio and Kinahan 2006, Panin et al 2006, Tohme and Qi 2009). However, clinical implementation of these methods is difficult due to limited access to proprietary software and reconstruction algorithms, the variety of PET scanner models and manufacturers available, and the variety in acquisition modes and reconstruction algorithms available. Post-reconstruction PVC avoids these pitfalls, enabling PVC to be performed on images obtained from any scanner or reconstruction algorithm, given that the scanner resolution, referred to as the point spread function (PSF), is properly characterized for each scanner and reconstruction.

Post-reconstruction PVC is typically performed using one of two methods, the first consisting of local deconvolution using anatomical segmentation (Rousset et al 1998, Aston et al 2002). This method is frequently used in brain studies, where functional PET imaging is assumed to follow anatomical structure defined by co-registered magnetic resonance images (Meltzer et al 1990). This method requires accurate co-registration of PET images to an anatomical image set, strong correlation between tracer uptake and anatomical boundaries, and an estimate of the PSF. The second method is applied when the tracer uptake fails to coincide with any observed patient anatomy, which is frequently the case in oncology where contrast is insufficient to determine tumor boundaries from healthy tissue. In cases of tumor heterogeneity, standard anatomical imaging techniques fail to distinguish differences in tumor sub-region functions. Therefore, clinical PVC of tumor heterogeneity can not rely upon anatomical imaging.

Post-reconstruction PVC is referred to as deconvolution, deblurring, or image restoration of a linear imaging system, which sharpens the input image using an iterative algorithm with the imaging system’s blurring kernel (PSF). Expectation maximization (Dempster et al 1977) is usually the most frequently used algorithm for deconvolution (Snyder et al 1992, Vardi and Lee 1993), particularly those frequently encountered in nuclear medicine imaging (El Naqa et al 2006, Gantet et al 2006); however, numerous other algorithms have also been used (Byrne 1998, Teo et al 2007). Two decisions must be made when performing post-reconstruction PVC: determining the size of the kernel for deconvolution, and determining when to cease iterating. This first decision is typically addressed by determining the most suitable kernel for the entire image based on a priori knowledge or measurement. As there is no single kernel representative of the system’s resolution, this method requires an arbitrary choice in kernel width. The second decision is complicated by an increase in image variance as the number of iterations increases. This is frequently addressed by regularization via local smoothing, which essentially reblurs the image with a smaller kernel. This increases the number of iterations required for bias improvement as well as introducing further position and object dependence of the resolution.

Recently, several groups have introduced anatomically independent post-reconstruction techniques for PVC in oncologic PET using iterative methods. Teo et al. developed a forward based method testing locally invariant PSFs of various sizes while implementing Van Cittert’s iterative method (Teo et al 2007). They reported errors to within approximately 10% as long as Gaussian kernels with widths within 1 mm of the true value were used. Kirov et al. used an iterative maximum likelihood expectation maximization approach with user-defined kernels, while focusing on limiting variance increases via topology-adaptive regularization (Kirov et al 2008). However, despite the fact that tumors exhibit non-uniform uptake, which affects standard quantitative PET measures (Soret et al 2002), no study has yet focused on the impact of PVC on tumor heterogeneity.

This work introduces an iterative partial volume correction method using expectation maximization with a spatially varying point spread function. Rather than arbitrarily selecting a single deblurring kernel, the method uses a spatially variant PSF based on experimental non-collimated point object measurements. The method avoids significant increases in image variance by applying PVC to only the tumor region and terminating the iterative process prematurely. The number of iterations is determined by a stopping criterion, derived from the convergence of the expectation maximization correction matrix to a matrix of ones, which is validated using an experimental tumor heterogeneity phantom. The proposed spatially variant PVC (SV-PVC) method is compared to spatially-invariant PVC (SINV-PVC) using the tumor heterogeneity phantom and a Gammex ACR PET/CT phantom (Gammex RMI, Middleton, WI) as well as image data from a prospective dose painting candidate whose regional node exhibits hypoxic tumor heterogeneities.

2. Materials and Methods

2.1. General Theory

The partial volume correction (PVC) scheme treats PET as a linear imaging system that can be modeled as a system that obtains images, g(r⃑), from the convolution of a radioactive distribution, f(r⃑), with the imaging system’s PSF, h(r⃑),

$$g(\stackrel{\rightharpoonup }{r})={\displaystyle \int f(\stackrel{\rightharpoonup }{r\prime })h(\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{r\prime })d\stackrel{\rightharpoonup }{r\prime },}$$ (1)

where r⃑ and r⃑′ are vectors of the same image domain. When solving for f(r⃑), given that both g(r⃑) and h(r⃑) are known with non-negativity constraints, equation 1 is a special case of a Fredholm integral of the first kind, where the system PSF is assumed spatially invariant. Due to the presence of noise this linear inverse problem is ill-posed in the sense that there is no precise solution and subtle variation in g(r⃑) or h(r⃑) leads to drastically different solutions. Such problems are frequently approached using iterative methods which avoid increasing variance resultant from the amplification of high frequency noise. Numerous iterative algorithms exist, however the expectation maximization algorithm (Dempster et al 1977) (EM) has been used for numerous inverse problems (Vardi and Lee 1993), particularly in nuclear medicine image reconstruction (Shepp and Vardi 1982, Hudson and Larkin 1994) and deconvolution (Gantet et al 2006). In the interative EM technique, the estimate for the original image activity distribution f_n(r⃑) is updated by a multiplicative correction matrix c_n(r⃑):

$$f_{n+1}(\stackrel{\rightharpoonup }{r})=f_n(\stackrel{\rightharpoonup }{r})c_n(\stackrel{\rightharpoonup }{r}),$$ (2)

where c_n(r⃑) is obtained through application of the EM algorithm:

$$c_n(\stackrel{\rightharpoonup }{r})=\left[\left(\frac{g(\stackrel{\rightharpoonup }{r})}{f_n(\stackrel{\rightharpoonup }{r})\otimes h(\stackrel{\rightharpoonup }{r})}\right)\otimes h(\stackrel{\rightharpoonup }{r})\right],$$ (3)

where ⊗ denotes the convolution operator. When used for image deconvolution, the EM correction matrix is generated by first convolving the test object with the system’s PSF, then taking the quotient of the reconstructed image to the convolved PSF and test object. This ratio is then convolved with the PSF, serving to normalize and locally weight each element of the quotient product using the PSF. Equation 3 is referred to as spatially invariant partial volume correction (SINV-PVC) because a spatially uniform kernel is used. In SINV-PVC three dimensional convolutions may be performed using Fourier transforms, taking only seconds per iteration.

2.2. Spatially Variant Modification

When the PSF of a PET imaging system is known to exhibit spatial dependencies, the linear inverse problem of equation 1 is rewritten as:

$$g(\stackrel{\rightharpoonup }{r})={\displaystyle \int f(\stackrel{\rightharpoonup }{r})H(\stackrel{\rightharpoonup }{r},\stackrel{\rightharpoonup }{r}\prime )d\stackrel{\rightharpoonup }{r}\prime ,}$$ (4)

where H(r⃑, r⃑′) represents the spatially varying PSF, and now represents the general case of a Fredholm integral of the first kind. The iterative EM algorithm expressed in equation 2 can no longer be performed using frequency space convolutions, but must use image space superpositions. In such cases, computation time of equation 4 is increased by several orders of magnitude when calculation is performed on a voxel-by-voxel basis for every voxel in the image. This spatially-variant PVC (SV-PVC) is expressed:

$$f_{n+1}(\stackrel{\rightharpoonup }{r})=f_n(\stackrel{\rightharpoonup }{r})\left[{\displaystyle \sum _{\stackrel{\rightharpoonup }{r\prime }}\left(\frac{g(r\prime )}{{\displaystyle \sum _{\stackrel{\rightharpoonup }{r}}{f}_n(\stackrel{\rightharpoonup }{r})H(\stackrel{\rightharpoonup }{r},\stackrel{\rightharpoonup }{r}\prime )}}\right)H(\stackrel{\rightharpoonup }{r},\stackrel{\rightharpoonup }{r}\prime )}\right],$$ (5)

where the summations now represent the pixel-by-pixel superposition required by the EM algorithm when using a spatially varying PSF.

To combat the increase in computation time encountered with superposition convolution techniques, our method implements a binary mask delineating the region to undergo PVC (frequently using the oncologist defined gross tumor volume), thereby decreasing the number of calculations performed. However, due to the masking process overestimation in the EM step occurs at the edges of the mask because each spatially variant PSF kernel is normalized with a volume of unity. The method alleviates this error by expanding the original mask by several voxels, creating a shell surrounding the original mask. At the conclusion of PVC, this shell experiencing overestimation due to cropping is removed from the corrected image and replaced by the original image’s shell.

2.3. Establishing a Stopping Criterion

Iterative restoration algorithms are frequently associated with an increase in variance as the number of iterations is increased. As with image reconstruction, this effect is mitigated by regularization or early termination of the iterative process before a significant increase in variance is reached. Because regularization requires an increased number of iterations and can further degrade image resolution, we have chosen to terminate PVC early according to the local rate of change within the image’s contoured tumor region.

In order to determine a proper stopping criterion, the PVC scheme compares the correction matrix that updates the model at every iteration to a matrix of ones. Because the EM algorithm will eventually converge to a final solution, the correction matrix will converge to a matrix of ones, which implies that the normalized sum squared difference between the correction matrix and a ones matrix should be a monotonically decreasing function:

$$C_n=\frac{1}{N}{\displaystyle \sum _i^N{\left(c_i-1\right)}^2,}$$ (6)

yielding a single value corresponding to the difference from perfect convergence for that particular iteration, where c_i refers to the correction matrix after iteration n while summing over every voxel i in the tumor mask containing N total voxels. However, of greater interest is the rate at which C_n approaches zero:

$$\mathrm{\Delta }{C}_n=\frac{C_n-C_{n-1}}{C_n}.$$ (7)

Because the correction matrix is calculated over only the tumor mask, this method focuses on the changes experienced only in the tumor region as a result of PVC. Equation 7 indicates the rate at which changes are made to subsequent PVC iterations and can be used as a stopping criterion by determining when improvement has sufficiently slowed.

The stopping criterion in equation 7 was validated using a tumor heterogeneity phantom (discussed below) to determine how the correction matrix’s rate of change correlates to the agreement between the PVC phantom image after each iteration and the phantom’s true activity distribution. PVC is performed on the heterogeneity phantom for the stated contrasts and agreement between PVC images and the true activity is then described by the normalized sum squared difference of both:

$$PV{C}_{\mathit{\text{error}},n}=\frac{1}{N}{\displaystyle \sum _i^N{\left(f_{n,i}-R_i\right)}^2,}$$ (8)

where f_n,i refers to the PVC image after iteration n, R refers to the reference image, and i indexes every voxel in the tumor mask containing N total voxels. Because the PVC method converges, this error will also be a decreasing function of PVC iteration. Similarly to the change in correction matrix, we determine when the change in PVC_error,n from subsequent iterations has sufficiently slowed, which will then determine the stopping tolerance of the correction matrix:

$$\mathrm{\Delta }PV{C}_{\mathit{\text{error}},n}=\frac{PV{C}_{\mathit{\text{error}},n}-PV{C}_{\mathit{\text{error}},n-1}}{PV{C}_{\mathit{\text{error}},n}}.$$ (9)

2.4. Image Acquisition and Reconstruction

All PET images in this work were obtained on a GE Discovery LS PET/CT scanner (GE, Waukesha, WI) scanning in high resolution 2D mode (septa in place) with real time subtraction of randoms. Sinograms were corrected for normalization, decay, and CT-based attenuation prior to reconstruction. Images were reconstructed on a 256 × 256 × 35 grid over a 50 cm field of view using OSEM with 2 iterations and 28 subsets, 5.3 mm Gaussian loop (inter-iteration) filtering, and 3.0 mm Gaussian post filtering.

2.5. Acquiring the Spatially Variant PSF

The spatially varying point spread function (PSF) was determined by scanning a cylindrical trap and release filter initially containing 85 MBq of F-18 concentrated into a source measuring 1 mm in diameter and 2 mm in length. This point source was scanned twice in centrally located, direct planes (planes 17 and 19) moving radially outwards from the center of the bore in horizontal and vertical directions. The point source was moved using a 1D table-mounted controller arm from a Standard Imaging (Standard Imaging, Middleton, WI) scanning tank. Nineteen horizontal scans were performed at radial distances of: 0, 1, 2, 3, 4, 5, 7.5, 10, 12.5, 20, 30, 40, 50, 75, 100, 125, 150, 175, and 200 mm. Vertical scanning to 20 cm occurred at radial distances of: 5, 10, 25, 50, 75 100, 125, 150, 175, and 200 mm. Scanning at each position lasted between 60–180 s accumulating at least 10⁷ acquired prompts. The PSF was not scanned over every detector slice because the 2D high resolution mode accepts coincidences from only direct and cross planes. Because each detector plane (excluding the first and last) sees the same acceptance angles, the transaxial resolution can be treated as approximately equivalent for each detector plane.

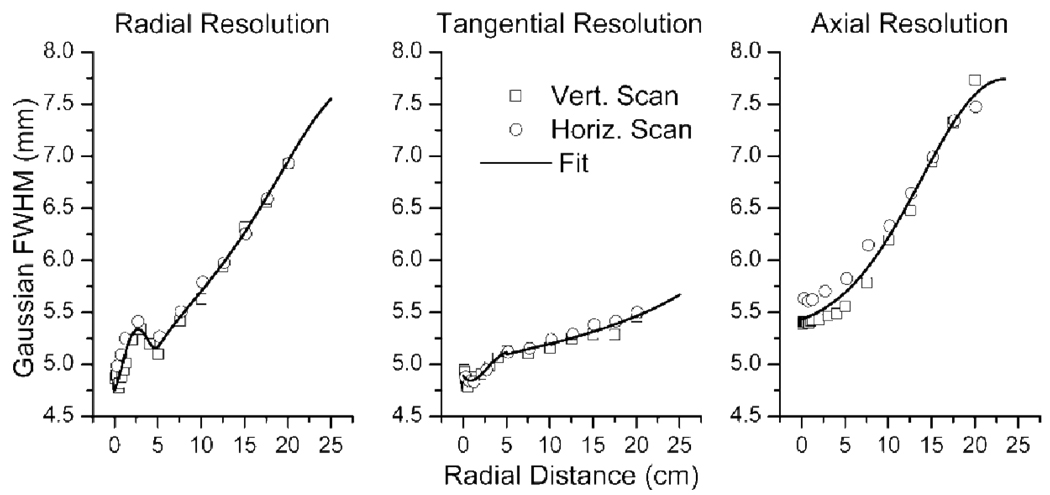
Three dimensional Gaussian distributions were fit to resultant images of each point source position using a least squares method. The associated tangential, radial, and axial resolutions were determined as a function of radial distance from the center of the bore for each scanned position. The resultant Gaussian width parameters were fit piecewise to fifth order polynomials with a discontinuity at 5 cm, while the axial resolution was fit to a Gaussian distribution. These functions were chosen due to their fit of the data (see figure 2). With the Gaussian width parameters described as functions of continuous variables, the point spread function could now be described as a finite three dimensional Gaussian at any point in image space according to:

$$H\left(\stackrel{\rightharpoonup }{r},\stackrel{\rightharpoonup }{r}\text{'}\right)=\frac{1}{b_t\left(\stackrel{\rightharpoonup }{r}\text{'}\right)b_r\left(\stackrel{\rightharpoonup }{r}\text{'}\right)b_a\left(\stackrel{\rightharpoonup }{r}\text{'}\right)}\text{exp}\left[-\pi \left[{\left(\frac{\left(\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{r}\text{'}\right)\cdot \widehat{x}{\text{'}}_{\theta }}{b_t\left(\stackrel{\rightharpoonup }{r}\text{'}\right)}\right)}^2+{\left(\frac{\left(\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{r}\text{'}\right)\cdot \widehat{y}{\text{'}}_{\theta }}{b_r\left(\stackrel{\rightharpoonup }{r}\text{'}\right)}\right)}^2+{\left(\frac{\left(\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{r}\text{'}\right)\cdot \widehat{z}}{b_a\left(\stackrel{\rightharpoonup }{r}\text{'}\right)}\right)}^2\right]\right],$$ (10)

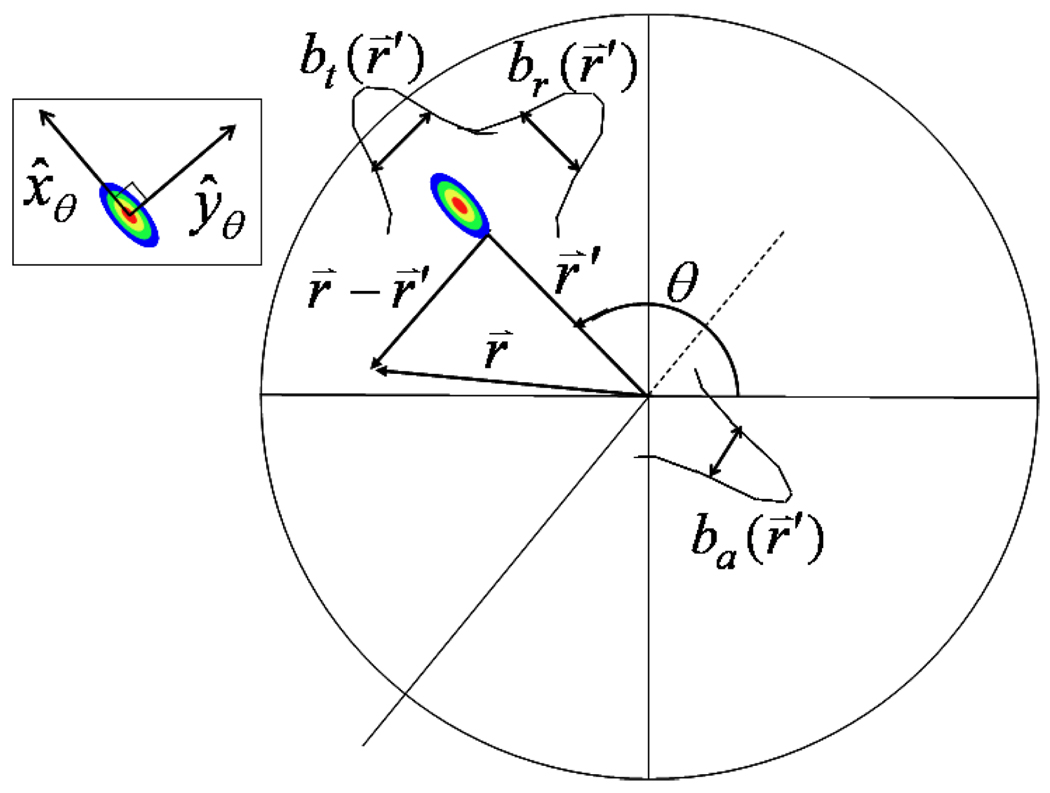
where x̂_θ and ŷ_θ are unit vectors indicating the tangential and radial directions, respectively, and the axial unit vector ẑ = x̂_θ × ŷ_θ is parallel to the direction of table travel. The radial, axial, and tangential resolutions are given as: b_r(r⃑), b_a(r⃑′), and b_t(r⃑′), respectively (see figure 1), where b represents the Gaussian half-width at approximately 4% the maximum value and is related to the full-width at half maximum (FWHM) by: $b=\frac{\mathit{\text{FWHM}}}{2}\sqrt{\frac{\pi }{\text{ln}(2)}}$. Note that the Gaussian distribution has dependence on radial position, only in the widths parameter. SV-PVC was performed using the spatially variant PSFs of equation 10.

Figure 2.

Radial, tangential, and axial measurements of the scanner’s resolution as a function of radial distance. Point source positions were varied both vertically and horizontally from the center of the scanner bore to radial distances of 20 cm. The radial and tangential data were fit piece-wise, with the discontinuity at a radial distance of 5cm, to fifth order polynomials, while the axial resolution was fit to a Gaussian distribution.

Figure 1.

A diagram depicting the geometric dependencies of the variables used in equation 10. Inset is a depiction of the radial and tangential unit vectors, where the axial unit vector points into the page. In this diagram the PSF has been elongated in the radial direction.

2.6. Phantom Studies

Two phantoms were used to test SV-PVC and SINV-PVC. The first phantom was a Gammex (Gammex RMI, Middleton, WI) ACR phantom with an additional PET research module affixed to one end. The PET research module consisted of a 25 cm diameter by 8 cm depth solid water cylinder with 5 cylindrical cutouts, into which 5 acrylic cylinders were placed. Each acrylic cylinder contained a spherical chamber with diameters of: 25, 20, 16, 13, and 10 mm. These spherical regions were filled with approximately 1 MBq/ml of Cu-64 (t_1/2 = 12.7 h) and the phantom was scanned for 45 minutes as a Cu-64 acquisition. SV-PVC was performed on each sphere to ensure the presented method appropriately restored quantitative accuracy of uniform spheres of various dimension. Multiple SINV-PVC images were generated using uniform kernel widths of 5 and 6 mm Gaussian FWHM and by varying the number of iterations from 4–7 iterations. These values were chosen based upon the experimentally generated spatially varying PSF and number of iterations determined during SV-PVC.

The second phantom studied was a tumor heterogeneity phantom developed in-house. The tumor heterogeneity phantom consisted of hollow spheres (Data Spectrum, Hillsborough, NC), mounted in close proximity into a 5 cm wide, 15 cm long acrylic cylinder, such that spheres were aligned within the phantom in the same axial plane. Spheres were filled with either water (15 and 10 mm diameter) or Cu-64 (15, 10, and 5 mm diameter). Cu-64 spheres were filled with 1 MBq/ml of Cu-64, while the phantom space surrounding the spheres was filled with approximately 1.5 MBq/ml of F-18 (t_1/2 = 110 m), achieving Cu-64:F-18 contrasts varying from 0.15:1 – 4:1 over an 11 hour period. Five contrasts were chosen for study (0.15, 0.5, 2.0, 3.0, and 4.0) using 20 minute acquisitions for each. Contrasts took into account the positron branching ratios of each isotope rather than their actual activity and were in the range of clinically observed tumor heterogeneity contrasts.

The heterogeneity phantom was placed in a 20 cm diameter NEMA PET phantom (Data Spectrum) and filled with water for additional scatter. This phantom therefore simulated PET images of non-uniform tracer uptake for a circular 5 cm tumor for a variety of different heterogeneity contrasts relative to the surrounding tumor. SV-PVC was applied to the tumor region containing heterogeneity spheres. SV-PVC was applied for 25 iterations to determine the stopping criterion, after which it was determined that only 7–8 iterations were necessary. Multiple images were obtained from SINV-PVC using uniform kernel widths of 4, 5, and 6 mm Gaussian FWHM for 6–9 iterations, again based on the observed PSF and number of iterations determined in SV-PVC.

Quantitative accuracy of SV-PVC and SINV-PVC was determined for both phantoms using the recovery coefficient (RC), defined as the ratio of imaged activity to true activity. Recovery coefficients were generated using the maximum imaged activity of the Gammex ACR phantom. The mean value of the imaged spheres was used for recovery coefficients of the tumor heterogeneity phantom due to varying contrasts.

2.7. Patient Study

Spatially variant and invariant PVC was performed on a head and neck squamous cell carcinoma patient injected with 170 MBq of ⁶¹Cu-ATSM (Cu(II)-diacetyl-bis(N(4)-methylthiosemicarbazone) a surrogate for hypoxia) and dynamically scanned for 30 m, 3 h post-injection. The patient exhibited fairly uniform tracer uptake in the primary tumor region, but severe tumor heterogeneity in a regional lymph node (∼65 ml) twice the size of the primary tumor. SINV-PVC was also applied using 4–8 iterations and uniform kernels of 4–8 mm Gaussian FWHM, in 0.5 mm increments.

3. Results

3.1. Spatially variant PSF

Figure 2 presents the fitted Gaussian full-width half maximum (FWHM) values for the scanned point spread function. The observed trends and values are consistent with previously published reports for the Discovery LS scanner (DeGrado et al 1994, Bolard et al 2007). The observed degradation in radial resolution at approximately 2.5 mm occurs as a result of the detector geometry. This distance is approximately half the size of an individual detector’s width. Because the scanner’s lines of response are centered about the transaxial center, fewer lines of response sample points at radial distance of half the detector width, relative to the transaxial center. This causes degradation in the radial and transaxial resolution relative to the transaxial center. A similar bump in radial resolution at this distance was also observed by DeGrado, despite the fact that images were reconstructed using filtered backprojection in their study.

3.2. Establishing a Stopping Criterion

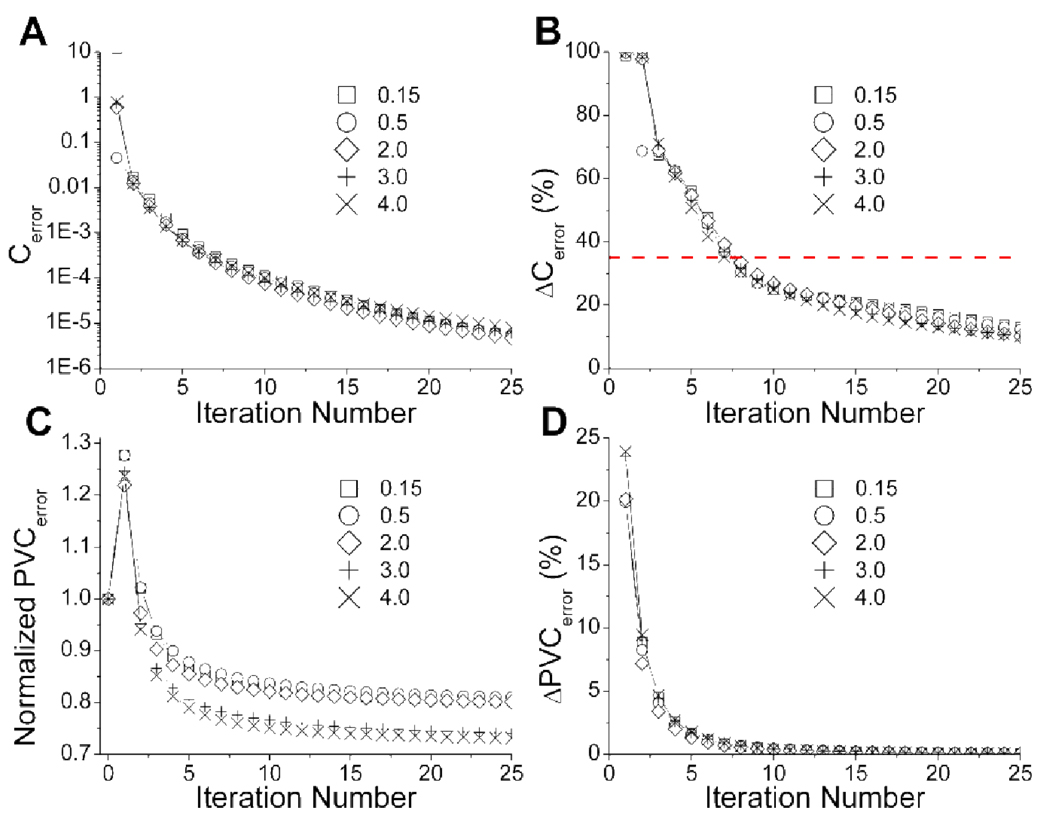
SV-PVC was performed on five different contrasts of the tumor heterogeneity phantom for 25 iterations. For each iteration the metrics of equation 6–equation 9 are plotted in figure 3. This figure demonstrates that similar values are observed regardless of the specific heterogeneity distribution studied for subplots A, B, and D, however, subplot C shows that SV-PVC has increased quantitative accuracy as the heterogeneity uptake increases relative to uniform tumor uptake. Figure 3A demonstrates the monotonic decrease of the difference between the correction matrix and ones matrix as SV-PVC continues. Ideally, convergence is reached when C_error is represented by a horizontal line at a value of zero, but it is important to note that this plot is logarithmic and therefore very nearly converged.

Figure 3.

Plots pertaining to the development and validation of a stopping criterion using the heterogeneity phantom for contrasts of 0.15, 0.5, 2.0, 3.0, and 4.0. The decrease in the correction matrix from a ones matrix is displayed in (A), while the percentage rate of change in this value used for the stopping criterion is shown in (B). The normalized least square error between the PVC phantom images and their associated true reference image are shown in plot (C). Plot (D) depicts the change in PVC_error used to determine when improvement to PVC images had sufficiently slowed with increasing iteration number.

The PVC_error shown in figure 3C is normalized by the difference between the original image and the reference image. Initially, SV-PVC performs much worse than standard PET imaging, but improvements of at least 10% are made after the fourth iteration. In figure 3C contrasts of 4.0 and 3.0 receive improvements of greater than 25% relative to the original images, while other contrasts are improved by approximately 15%. Figure 3D shows that the change in PVC_error is a quickly decreasing function, where changes <1% occur after seven to eight iterations.

SV-PVC was determined to be sufficiently converged when the change in PVC_error was <1%, which occurred after seven to eight iterations. At this point, the reduction in PVC_error was at least 95% of the reduction after 25 iterations, meaning continued iterations would reap minimal bias improvements while variance would certainly increase. These results corresponded to a reduction in the EM correction matrix of approximately 35%, which was therefore chosen to be the stopping criterion and is indicated by a horizontal line in figure 3B. A distinctive crux is apparent at this threshold, signaling large changes to the correction matrix leading up to this point and significantly slower change afterwards.

3.3. Phantom Studies

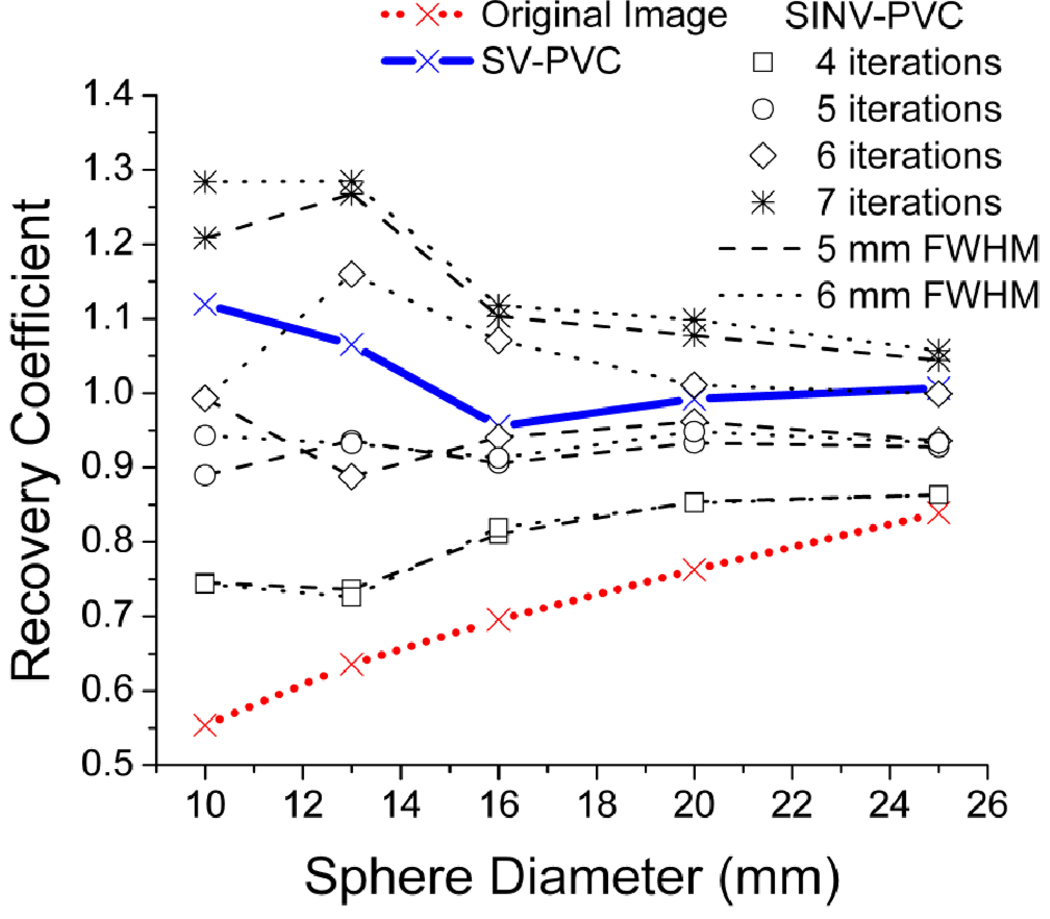
The magnitude of PVE and subsequent PVC was quantified using the recovery coefficient, defined as the ratio of imaged activity to true activity. In both phantom studies SV-PVC generated one image using the analytical generated PSF kernels of figure 2, while SINV-PVC generated several images with varying numbers of PVC iterations and dimensions of the uniform kernel. The Gammex ACR phantom’s recovery coefficients for the maximum pixel intensity are displayed in figure 4 for the original image, SV-PVC with stopping criterion, and SINV-PVC for a range of kernel widths and iterations. The SV-PVC method increased recovery coefficients by: 55, 40, 25, 20, and 15% for spheres of 10, 13, 16, 20, and 25 mm diameter, respectively. Furthermore, figure 4 demonstrates the difficulty involved with choosing parameters for SINV-PVC, where too few/many iterations result in under/over estimations by nearly 30% for spheres of 10 and 13 mm diameter. Conversely, SV-PVC improves recovery coefficients to nearly uniform levels of unity by automatically implementing the proper Gaussian kernel width at each image position and determining the number of iterations (6–7) based on a user input region of interest. SV-PVC recovery coefficients are slightly higher for 10 and 13 mm diameter due to the smaller contour sizes, which required an extra iteration before meeting the stopping threshold. This emphasizes that the SV-PVC method is most ideally suited for larger tumors experiencing non-uniform activity distributions.

Figure 4.

Measured recovery coefficients for the original Gammex phantom PET image with comparisons between the proposed SV-PVC and traditional SINV-PVC for a variety of SINV-PVC iterations and kernel widths. SV-PVC required six to seven iterations for each sphere.

Images of the tumor heterogeneity phantom are shown in figure 5 before and after SV-PVC for contrasts of 0.15 and 4.0. After SV-PVC spheres containing activity above and below the surrounding F-18 activity are much better delineated as PVC altered activity distributions by up to 35% in many cases. However, the 5 mm sphere was never recovered in this study due to insufficient contrast and the excessive smoothing used in reconstruction, essentially smoothing out its signal completely.

Figure 5.

Fused PET/CT images of the heterogeneity phantom before and after the spatially variant partial volume correction (SV-PVC) for contrasts of 4:1 and 0.15:1. The rightmost column displays the percent change relative to the original PET image. Arrows indicate water-filled spheres containing no radioactivity, while the three remaining spheres (15, 10, 5 mm diameter) contain Cu-64. Note that activity for the 5 mm sphere (indicated by white arrow) is unobserved in either the original PET or SV-PVC images due to severe PVE created by the adjacent 15 mm water-filled sphere.

Recovery coefficients of the heterogeneity phantom using the mean value of the inner sphere volume are displayed in figure 6 for the 15 and 10 mm diameter Cu-64 filled spheres. Immediately recognizable is the fact that at a contrast ratio of 1 the recovery coefficients do not also intersect at 1, the value expected because PVE should not occur under such conditions. This apparent activity underestimation can be explained by PVE caused by the zero activity contribution of the 1 mm thick sphere walls (Turkington et al 2001, Hamill et al 2005, Bazañez-Borgert et al 2008). Due to the close proximity of spheres, zero activity regions from neighboring spheres also contribute to PVE. Therefore, the ideal response of this phantom to PVC is a constant recovery coefficient value over all contrast ratios.

Figure 6.

Recovery coefficients for the mean value of 15 and 10 mm spheres in the tumor heterogeneity phantom. Recovery coefficients are presented for the original PET image and the SV-PVC image, indicated by a dotted and solid lines with no symbols, respectively. SINV-PVC is shown using a range of kernel widths and number of iterations indicated by line type and symbol type, respectively. Contrasts between the Cu-64 filled spheres and F-18 background ranged from 0.15 to 4.0. A flat recovery coefficient response to changing contrast is ideal for this phantom, as opposed to a value of 1 due to the zero activity of the 1 mm thick sphere wall.

SV-PVC required seven to eight iterations and created a flat response for both the 10 and 15 mm spheres for all contrasts, with exception to the 10 mm sphere in the 0.15 contrast ratio, which showed improvement but remained nearly twice the true activity. SINV-PVC is shown for kernels of 4–6 mm FWHM and 6 and 9 iterations, where line type indicates the uniform kernel width of SINV-PVC and symbol type indicates the number of SINV-PVC iterations used. For the case of the 15 mm sphere, SINV-PVC using a 5 mm kernel provided results most similar to SV-PVC, with six iterations outperforming nine iterations. SINV-PVC using a 4 mm kernel failed to provide sufficient correction, while a 6 mm kernel overcorrected the images for both 6 and 9 iterations. Differences of approximately 5–30% were observed for the various contrasts when kernel dimensions varied by only 1 mm. Increasing the number of SINV-PVC iterations from 6 to 9 resulted in RC differences of less than 10% for the 15 and 10 mm diameter spheres, with the exception of the 10 mm sphere at low contrasts and with a 6 mm FWHM Gaussian kernel. For the 10 mm sphere, both the SV-PVC and SINV-PVC methods provided similar recovery coefficients. Again, 6 mm kernels slightly overcorrected and 4 mm kernels undercorrected, with similar 5–30% differences observed with SINV-PVC kernels varying by 1 mm.

3.4. Patient Study

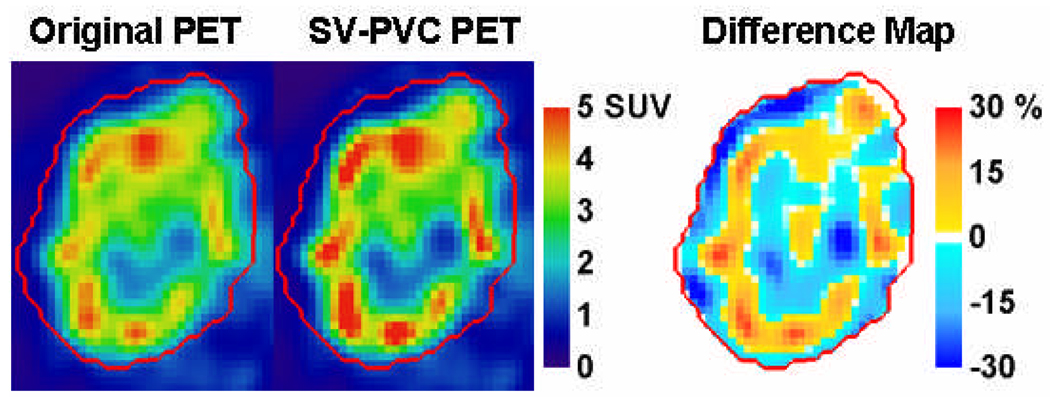
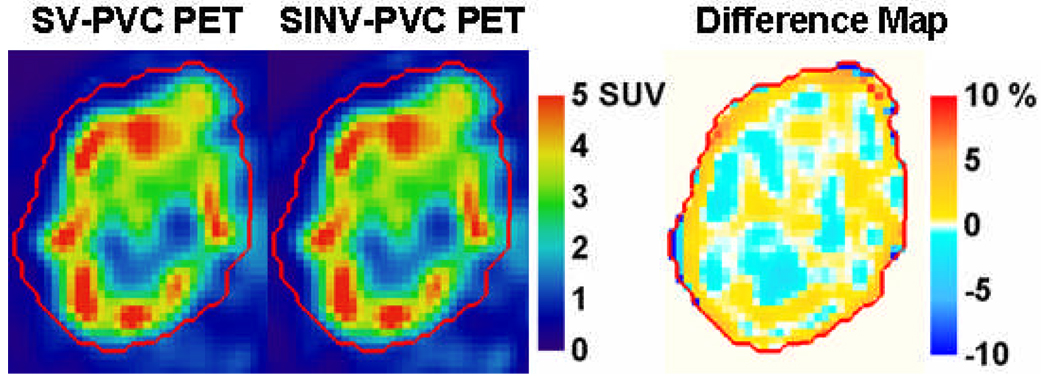
Figure 7 shows a transaxial PET image of the regional node with tumor heterogeneity, and the resultant tumor slice after SV-PVC. Differences of ±30% are observed relative to the original image for many of the target heterogeneities. Additionally, SV-PVC is compared to SINV-PVC where differences of approximately ±3% relative to the SV-PVC image are observed. The regional node displaying heterogeneous uptake was located between radial distances of 2.5 and 8.5 cm, which roughly correspond to resolution FWHM changes of 0.75, 0.25, and 0.5 mm in the radial, tangential, and axial resolution, respectively. From this a 5.5 mm kernel was chosen for SINV-PVC using the same number of iterations as SV-PVC. Therefore, the SINV-PVC presented represents the ideal scenario for comparison against SV-PVC because the number of necessary iterations and kernel dimensions are provided, which would not typically be the case. SINV-PVC with Gaussian kernel widths of 5.0 and 6.0 mm differed from SV-PVC by up to 10% on opposing tumor boundaries due to the changing PSF used by SV-PVC.

Figure 7.

⁶¹Cu-ATSM images of a patient’s node before and after spatially variant PVC (top row) and a comparison between spatially variant and spatially invariant PVC (bottom row). The right column displays the percentage difference of the middle column relative to the left column image. The CT delineated tumor mask is defined by the red contour.

4. Discussion

Partial volume effects corrupt the quantitative accuracy of PET-imaged tumor heterogeneities. The PVC method proposed in this work sets out to specifically correct tumor heterogeneity in an autonomous manner while preventing excessive noise enhancement. The strength of this particular method is in using the EM correction matrix to define when the bias of the non-uniform distribution has been sufficiently improved. The technique is adaptable to any scanner and most reconstruction types as long as the PSF is properly modeled for both. Additionally, calculation is sufficiently fast (∼70 s per iteration for 7000+ voxels on a 3.2 GHz CPU) for clinical implementation, despite requiring superposition convolution calculations.

In comparison to the application of other iterative deconvolution techniques, our method requires the input of only a user defined region of interest. This essentially mitigates the subjective decisions required for SINV-PVC, where users define deconvolution kernel dimensions, the number of iterations, and other parameters for a particular tumor and location. However, as a result of local deconvolution, the potential quantitative improvement in imaged activity concentration is limited to only the defined region of interest. Because the presented method is applied only to the input region of interest, an increase in variance does not occur throughout the image. In PET tumor imaging, tumors frequently exhibit higher radiotracer uptake resulting in decreased noise. Therefore, a significant increase in variance does not occur when applying this method to tumor images. The only form of regularization the method uses is the early termination of the iterative process. Further regularization applied using filtration or smoothing would affect image resolution, which is a vital component to the spatially varying PVC method.

Using approximately equivalent kernels and number of iterations, the difference between images obtained with SV-PVC and SINV-PVC is dependent on the spatial uniformity of the point spread function. In regions where the PSF width varied by less than 0.5 mm, the differences between SV-PVC and SINV-PVC were less than ±5%. However, differences between SV-PVC and SINV-PVC of greater than ±10% were observed when SINV-PVC kernel widths differed by more than 1 mm or when SINV-PVC used a different number of iterations. This fact highlights that the two methods are capable of producing similar results; however, significant differences occur when the arbitrary selection of SINV-PVC parameters differ from those used in SV-PVC. Such differences were observed in the maximum uptake recovery coefficients of the ACR phantom (figure 4), and the mean uptake recovery coefficients of the tumor heterogeneity phantom (figure 6).

The continuous PSF function expressions developed for PVC were derived from measurements made in air, representing the best possible resolution attainable for the scanner. Additional scatter and activity further degrade the resolution meaning that true resolution is actually worse than the measured point sources. In such experiments we saw increases of approximately 1 mm to tangential resolution with the introduction of scatter and activity at 10 cm from the central axis (results not presented). Using a smaller PSF in these cases results in underestimated PVC, however, quantitative accuracy is still significantly improved despite the PSF’s size. Because the PSF is analytically modeled, further improvement can be made to SV-PVC by modeling the PSF for scatter and object dependence similar to the approach published by Chen (Chen et al 1998).

5. Conclusion

A post reconstruction partial volume correction method has been developed for PET-imaged tumor heterogeneities. The method employs expectation maximization using a spatially varying point spread function and utilizes a tumor mask and the iterative correction matrix as a stopping criterion. The stopping criterion was validated using a traditional sphere phantom as well as a tumor heterogeneity phantom. Improvements as large as 30% were observed in corrected phantom studies, while changes as great as 30% were seen in a patient study. The method autonomously corrected phantom images to optimal levels regardless of object size, position, and contrast, whereas other methods require that kernel dimensions and the number of iterations be defined specific to each application. Such a method should be implemented prior to performing quantitative measures or diagnoses on heterogeneous tumors.