Abstract
A new 3D model is developed to simulate the self-oscillation of the elongated vocal folds. This model allows for large deformation and longitudinal displacement. The displacement boundary condition is applied on the posterior side to represent the elongation of vocal fold length by the cricothyroid or the thyroarytenoid muscles. After this model is verified by comparing its outputs using modal analysis and principle component analysis with those of previous models and experimental studies, it is applied to simulate the vibration of elongated vocal fold. Numerical simulation showed that longitudinal elongation increases the y-direction normal stress, decreases the lateral maximum displacement, and increases the fundamental frequency. These results agree with experimental measurements from an excised larynx setup, which suggests that the proposed elongation vocal fold model could be a useful tool to investigate voice production and the control of vocal fold vibration.
Keywords: Vocal folds, vocal fold elongation, finite-element model, phonation
1. Introduction
Elongation of the vocal folds is an important factor in controlling voice production. During phonation, the interarytenoid muscles adduct the arytenoid cartilages in the midline and the cricoid-arytenoid muscles immobilize the posterior ends of the vocal folds. Then, the cricothyroid (CT) or thyroarytenoid (TA) muscles contract leading to an increase or decrease, respectively, in vocal fold length. The elongation of the vocal folds could alter the stress distribution in vocal folds, which is believed to be one important reason for vocal lesions [1–3]. Moreover, the regulation of stress in the vocal folds with elongation is the primary means of controlling pitch [4]. Therefore, modeling the elongated vocal folds has significance for studying voice production, vocal fold trauma and vocal fold disease.
The early lumped-mass models increase the spring stiffness to represent the increase of tension in an elongated vocal fold [5]. However, elongation may potentially change several vocal fold characteristics, including longitudinal fiber tension, vocal fold length, shape, and even glottal shape. The lumped-mass model cannot effectively represent these effects. Finite element models provide a closer approximation of the vocal fold due to their ability to deal with complex boundaries [1, 6–11]. Many phenomena have been studied using these finite-element models, including vocal fold collision [3], energy transform in voice production systems [10], vocal fold bulging effects [7], vocal lesion-related mechanical stress [2, 11], and the normal vibration frequencies of the vocal ligament [12].
However, to the best of our knowledge, the self-oscillating model of elongated vocal fold has seldom been reported. Two limitations of the early models prevent them from simulating the vibration of the elongated vocal fold. Firstly, many are two dimensional or quasi-three-dimensional [6, 10, 11], where vocal fold movement in the anterior-posterior direction is ignored. Secondly, most assume a small deformation [1, 6, 8, 11]. This assumption is not suitable for depicting the large deformation of tissue in an elongated vocal fold. Therefore, the vibration of the elongated vocal folds has not been well studied.
In this study, a new vocal fold model is developed to simulate the vibration of the elongated vocal fold. In this three-dimensional vocal fold model, longitudinal displacement is allowed, and the large deformation of vocal tissue is considered. The displacement boundary condition is applied on the posterior side of the vocal fold to represent the elongation of vocal fold length by the CT and TA muscles. These characteristics allow the new model to portray vocal fold elongation. Moreover, this model can generate a self-oscillating solution by coupling the glottal aerodynamics. The detailed development of this model will be proposed in section II. Then, we simulate the vibration of elongated vocal folds using this model and compare the results with previous experimental measurements.
2. Model Development
2.1 Model Structure
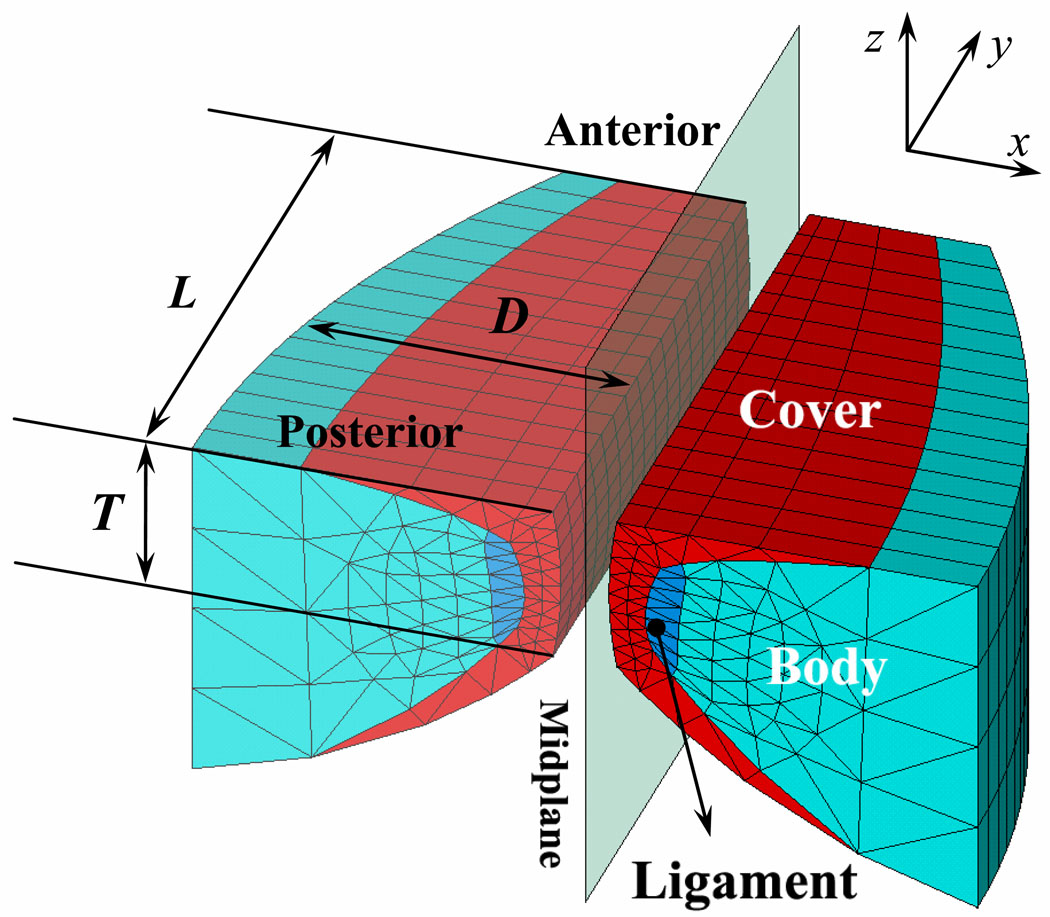
Figure 1 gives a 3-dimensional view of our finite-element model. The model is defined in Cartesian coordinates. The x and z dimensions define the vocal fold movement in the lateral and vertical directions, respectively. The y dimension represents the anterior-posterior direction in which the vocal folds are elongated. The length (L) and thickness (T) of the vocal folds are 1.6 cm and 0.45 cm, respectively (Alipour et al., 2000). The depth (D) of the vocal folds decreases from 1.0 cm on the posterior side (y = 0) to 0.5 cm on the anterior side (y = L) by following the formula D(y) = 1.0 – 0.5(y/L)2 [13]. The tissues in the vocal folds, including the vocal fold cover, body and ligament (see Fig.1), are assumed to be transversely isotropic [6]. To simplify our model, linear elastic constants and linear damping were used to describe the tissue properties of each layer. The transverse Young’s modulus of the body, cover, and ligament are 4 kPa, 2 kPa and 12 kPa, respectively. The longitudinal shear moduli of the body, cover, and ligament are 12 kPa, 10 kPa and 40 kPa, respectively. The longitudinal Young’s modulus for the body, cover, and ligament is 40 kPa. The viscosity of each layer is 0.5 Pa·s. The linear elastic constants used in this model were measured for various vocal fold tissues [14–18].
Figure 1.
A 3-dimensional view of the finite-element vocal fold model.
In addition, we assumed that the left and right folds are symmetric to simplify the model and reduce computational cost. Therefore, only the right vocal fold is solved to represent symmetric vocal fold vibration. The collision between the left and right vocal folds is modeled by the interaction between the right fold and a rigid mid-plane [1, 2] using the augmented Lagrangian method [19].
The 3D vocal-fold model is meshed by a first-order prism-shaped element. This element is defined by six nodes with three degrees of freedom at each node: translations in the nodal x, y, and z directions. The whole vocal fold finite-element model contains 2272 elements with 1411 nodes. In this model, movement of the nodes in the anterior-posterior direction is allowed; moreover, a large deformation can be predicted. Therefore, this finite-element vocal fold model has the potential to simulate the elongation of vocal folds.
2.2 Elongation and self-oscillation of the vocal fold model
By applying appropriate boundary conditions, the self-oscillation of the elongated vocal fold is modeled in two steps. The boundary conditions of the vocal fold model are implemented by defining the displacements, velocities and pressures of the nodes on the vocal fold surface.
In the first step, the static displacement and stress of the vocal folds are predicted under a given elongation length Le. A fixed boundary condition (the displacement is fixed at zero) is applied on the anterior side of the vocal fold. The displacement boundary condition is applied on the posterior surface nodes: The displacements in the x and z directions are fixed at zero, which represents the adduction and immobilization of the posterior side in the midline done by the interarytenoid muscles and the cricoid arytenoid muscle [4], while the displacement in the y direction (the anterior-posterior direction) is specified as the elongated length Le of the vocal fold. A free boundary condition is applied on the medial surface, superior surface and subglottal surface. For the nodes on the lateral surface, the movement in the anterior-posterior direction is allowed in this stage, but the movements in the medial-lateral direction and the inferior-superior direction are forbidden. In this step, the static displacement and the stress distribution of the vocal folds under a given elongated length Le can be solved using these boundary conditions.
In the second step, the self-oscillating solution is generated by coupling the glottal airflow with the elongated vocal fold model solved in the first step. In this step, the displacements of the nodes on the anterior surface are continuously fixed at zero, according to the fixed boundary condition. The nodes on the posterior surface are fixed at the same displacements as in the first step. The nodes on the lateral surface are fixed at their corresponding static displacement solved in the first step. The airflow-tissue interaction occurred on the medial, superior and inferior surfaces. The glottal airflow pressure was applied on these surfaces as the driving force.
The glottal aerodynamics is predicted using the FLOTRAN CFD analysis of the finite-element software ANSYS. In this study, the airflow in the glottis is assumed to be a single phase incompressible Newtonian laminar fluid governed by the Navier-Stokes (NS) equations. The airflow is symmetric about the mid-plane line. The density of the fluid is 1.2 kg/m3 and the viscosity of the fluid is 1.8×10−5 N-s/m2, similar to the properties of air at 37 °C. In order to simulate the fluid-tissue interaction, the moving wall condition [3] is applied on the airflow boundary which contacts the vocal fold surfaces. One subglottal tube (1-cm length, 1-cm radius) and one supraglottal tube (2-cm length, 1-cm radius) are attached to simulate the upstream flow and the downstream flow. The symmetry condition was applied on the midline plane, and the no-slip condition was applied to both the tracheal wall and the vocal tract wall. The model is driven by lung pressure (PL) input at the inlet of the subglottal tube. A zero pressure boundary condition is set at the outlet of the supraglottal tube. More details of the glottal airflow can be found in Tao et al., 2006 [3]. Using the given boundary condition, airflow is predicted, and the calculated airflow pressure is applied on the surface of the vocal fold. Simultaneously, the movement of the vocal fold under the airflow pressure drive is solved, and this solved vocal fold displacement is used to adjust the airflow region. Alternatively solving the NS equations and the elongated vocal fold model with a step length of 50 µs in time domain [6], a self-oscillating solution is obtained from the iterative process. The finite element analysis software ANSYS is used to build and solve the elongated vocal fold model and the glottal aerodynamics. This study’s main focus was vocal fold vibration. The acoustic loading and flitting effect of the vocal tract are ignored, which is one limitation of the current model.
3. Results and Discussion
3.1 Model Validation
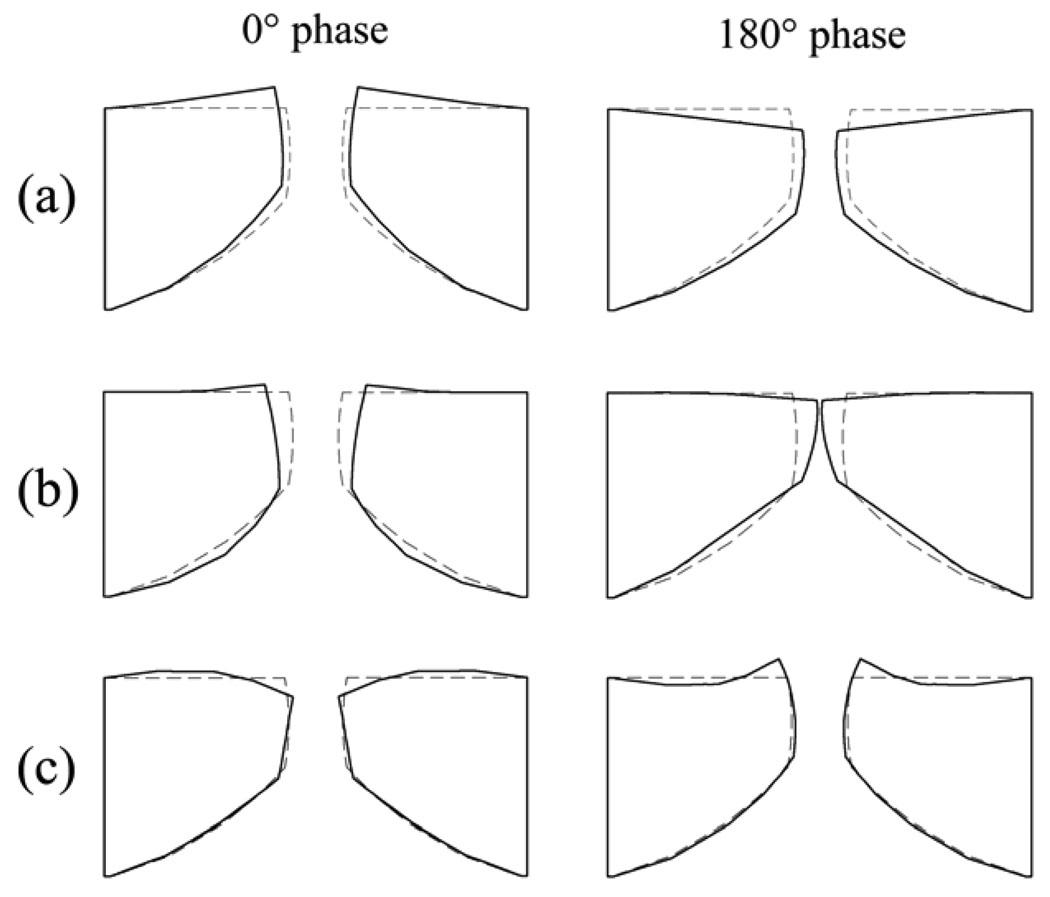
To verify the current model, some general outputs are given and compared with the previous model and experimental studies. A modal analysis is used to calculate the eigenmodes and eigenfrequencies of the unelongated vocal fold model. Figure 2 illustrates three eigenmodes, where their corresponding eigenfrequencies are 97 Hz, 113 Hz, 143 Hz, respectively. The modes 1 and 2 are analogous to the z-10 mode and the x-10 mode [20]. Recently, using electromagnetic excitation and laser optoreflectometry for response monitoring, Garrel et al. measured the resonance properties of a vocal fold and calculated that the resonance frequency of the porcine vocal fold is about 71.8 Hz [21]. This resonance frequency generated by a vertical excitation could respond to the low modes of a modal analysis. The eigenfrequencies of the modes 1 and 2 of the current model are close to the experimentally measured resonance frequency [21]. However, the eigenfrequencies obtained from the human-sized model, which will be used in this study, is still higher than the experimental results in the porcine vocal fold [21]. We proportionally increase the size of the vocal fold model by 20% (L = 1.92 cm, T = 0.54 cm, D = 1.20 cm) and rerun the modal analysis. The eigenfrequencies of the first two eigenmodes decrease to 81 Hz and 94 Hz respectively, which are closer to the resonance frequency of the porcine vocal fold than the eigenfrequencies obtained from the human sized model. Therefore, the difference between the eigenfrequencies obtained from the human sized model and the experimental results could be due to the differences in the vocal fold size.
Figure 2.
The three eigenmodes extracted from the finite-element model of vocal fold using a modal analysis. (a) eigenmode 1, analogous to the z-10 mode; (b) eigenmode 2, analogous to the x-10 mode; (c) eigenmode 3, analogous to the x-11 mode.
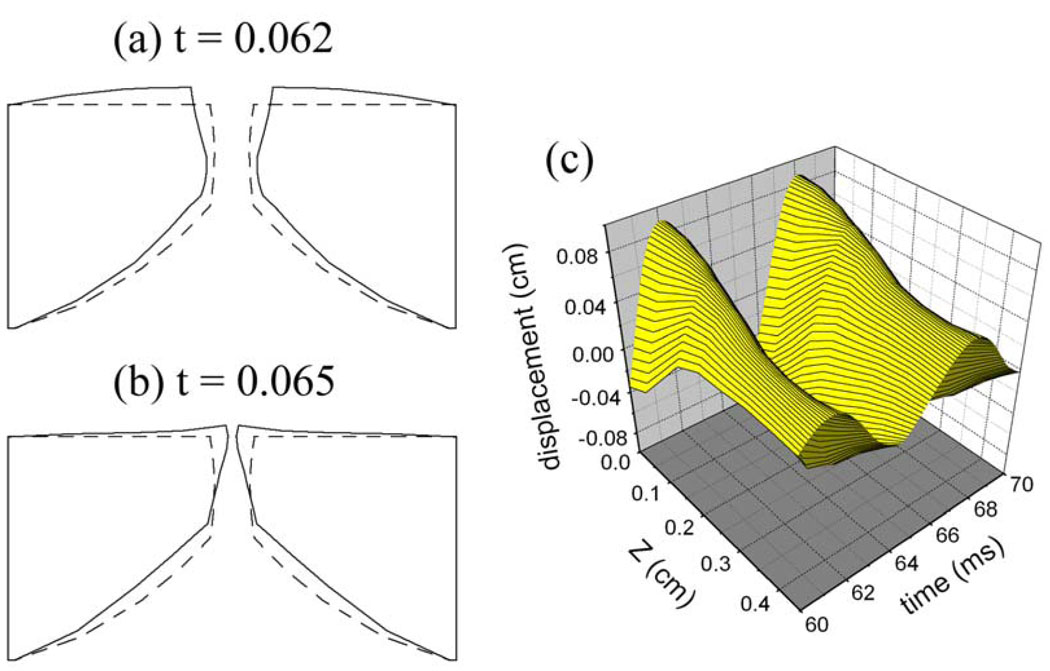
Figure 3 presents the surface dynamics of the self-oscillating solution of the finite-element model, where (a–b) illustrate the vocal fold deformation at t = 0.062s and 0.065s respectively, and (c) presents the medial surface displacement as a function of time. It can be seen that the deformation of the self-oscillating vocal fold model is analogous to the x-11 mode. It has long been asserted that x-11-like eigenmode is essential for self-oscillation, and it has already been shown to produce alternating divergent and convergent shapes in the glottis during oscillation [22]. The fundamental frequency (162 Hz) of the self-oscillating simulation is close to the eigenfrequency (143 Hz) of the x-11-like eigenmode obtained by modal analysis [see Fig.2 (c)].
Figure 3.
the surface dynamics of the vocal folds simulated by the self-oscillating finite-element model. (a) the vocal fold deformation at t = 0.062s; (b) the vocal fold deformation at t = 0.065s; (c) the medial surface displacement of the self-oscillating models as a function of time.
Applying the principle component analysis [23] on the medial surface displacement series [Fig.3 (c)], it is found that the largest empirical eigenfunctions (EEF) captured 78.6% of the energy, and the second largest EEF captured 20.8% of the energy. Using an excised hemilarynx setup, Döllinger et al. have measured the medial surface dynamics of a canine vocal fold during phonation [24–25]. Their experiments show that for one vibration sequence, the largest EEF captured 69.5% of the energy and the second largest EEF captured 23.6% of the energy; for another vibration sequence, the largest EEF captured 60.2% of the energy and the second largest EEF captured 33.1% of the energy. In addition, using a finite-element model, it has been found that the first and second EEF explain about 72% and 26% of the variance of the nodal trajectories, respectively [23], where the first two EEF explain approximately 98% of the variance of normal phonation [6, 23]. Our EEF analysis results are close to these. These agreements between our general outputs and those found in previous studies validate the current model.
3.2 Simulation of vocal fold elongation
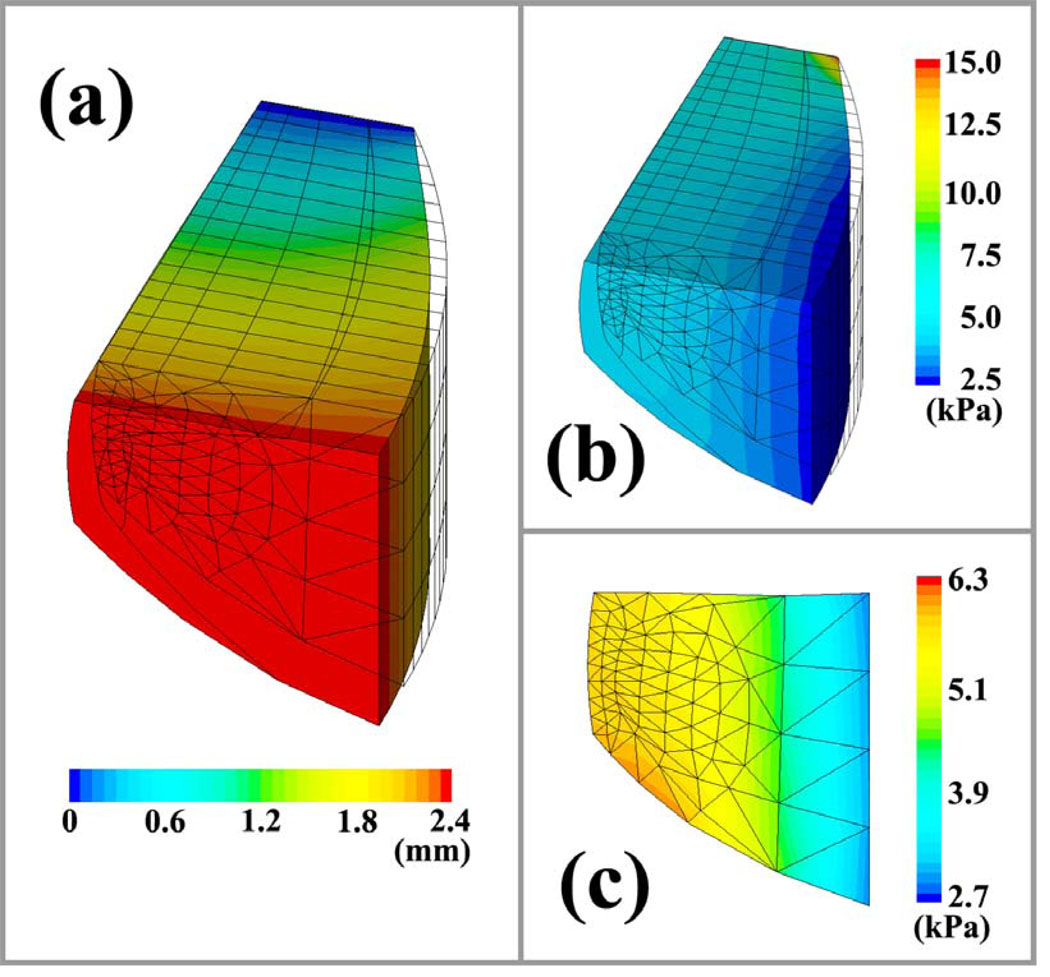
In this section, the vibration of the elongated vocal fold is simulated using the proposed model. First, the static status of the elongated vocal fold is solved. Because the oscillatory motion mainly takes place in the coronal plane [24–26], the longitudinal movement of the vocal fold is usually ignored in early quasi-3D models [3, 6]. However, for elongated vocal folds, the longitudinal displacement is large and cannot be ignored. Moreover, large deformation may be induced by elongation. The model proposed in this study allows the longitudinal movement and large deformation. Therefore, it can be used to simulate vocal fold elongation. Figure 4 (a) presents the y displacement in the vocal fold model, where the anterior side of the model is fixed and the posterior side is extended 2.4 mm in the y direction. The y displacement of the nodes in the vocal fold gradually decreases from the posterior side to the anterior side. The geometrical outline of the vocal fold model is elongated in the anterior-posterior direction.
Figure 4.
The longitudinal displacement and stress distribution in the vocal fold with an elongation of Le = 2.4 mm. (a) the longitudinal displacement distribution. (b) the stress distribution in vocal fold. (c) the y-directional normal stress in the cross-section at the anterior-posterior midpoint of vocal fold.
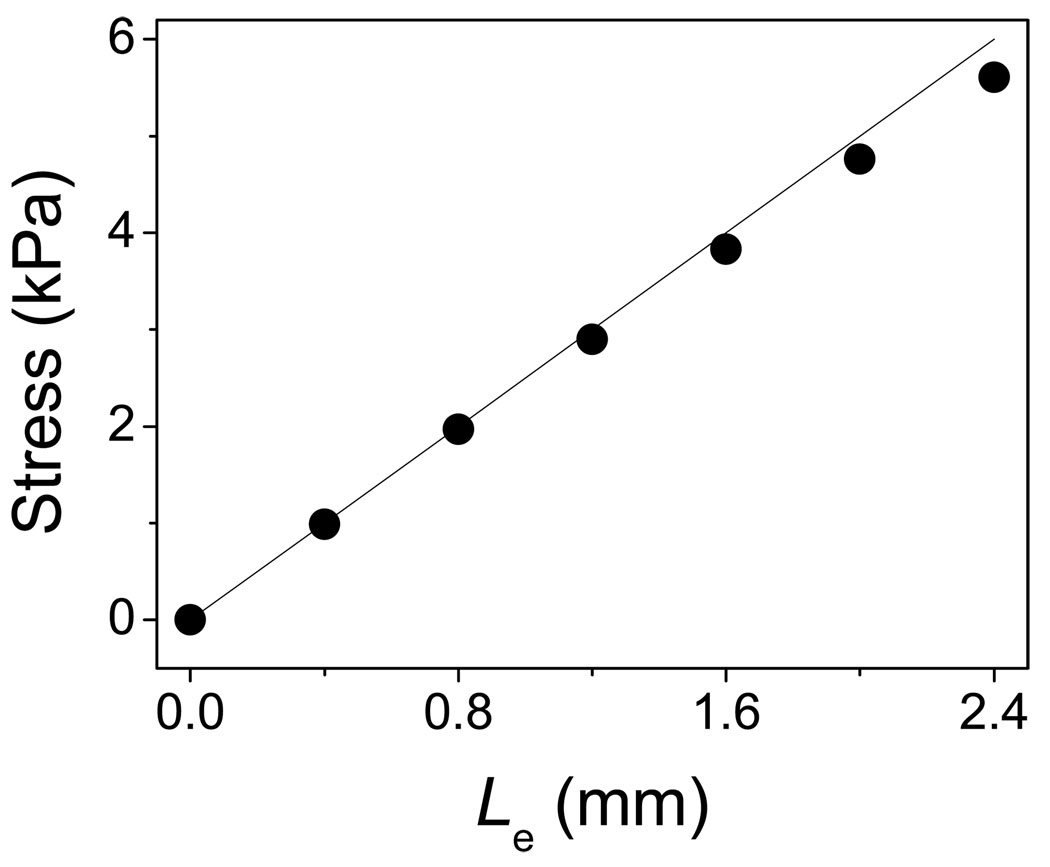
Elongation not only changes vocal fold shape, but it also alters the tension distribution in the vocal folds. Figure 4 (b) presents the distribution of y-directional normal stress in the model. Longitudinal elongation significantly increases the y-direction normal stress in the vocal fold. The maximum value occurs at the anterior side because there has the minimum cross-sectional area. The y-direction normal stress in the cover layer and ligament is about 6.0 kPa – 7.0 kPa under 2.4 mm elongation. Figure 4 (c) presents the stress distribution in the cross-section at the anterior-posterior midpoint of the vocal fold. The high stress occurs at the cover and ligament layers. The average normal stress in y-direction is about 5.61 kPa at the midpoint of the ligament. The normal stress value is associated with the elongated length of the vocal folds, as shown in Fig. 5. It is evident that stress increase with elongation (Le = 0 mm ~ 2.4 mm). The relationship between longitudinal stress and elongation is roughly linear due to the linear elastic assumption. In comparison to the neutral vocal fold length of 1.6 cm, the elongation length Le of 2.4 mm represents a 15% longitudinal strain. According to Alipour and Titze’s measurements [14], the stress-strain relationship of vocal fold tissue is fairly linear at low strains (<15%). Therefore, a linear tissue stress–strain approximation is valid within the elongation range (0 mm ~ 2.4 mm) used in this study.
Figure 5.
the longitudinal stress in vocal fold ligament as a function of elongation length Le.
The proposed model can provide a self-oscillating solution by coupling it with the airflow model, which makes it an important tool for understanding the effects of elongation on vocal fold vibration and voice production.
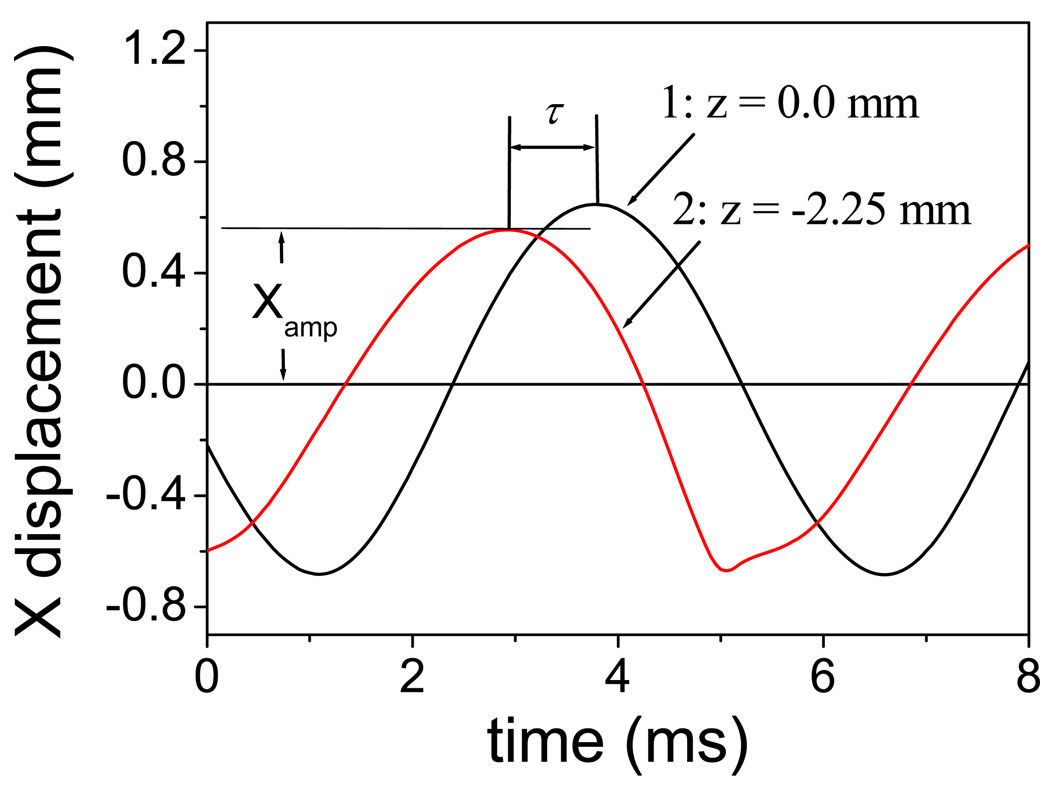
The phase delay (φ) between the vocal folds’ upper and lower margins due to mucosal wave propagation is one important factor that facilitates self-oscillation of the vocal folds [22]. Therefore, the mucosal wave that propagates vertically along the medial surface of the vocal fold mucosa has important clinical significance in voice production [27]. Because the finite-element model can provide rich spatiotemporal information, the propagation of the mucosal wave can be represented with the proposed model. Figure 6 illustrates the waveform of the displacement of two nodes on the vocal fold surface, where curve 1 corresponds to the node on the upper margin of the vocal fold and curve 2 corresponds to the node 2.25 mm below the upper lip. The phase of the upper lip (curve 1) is late with respect to the lower node (curve 2). The time interval (τ) between the peaks of the two curves is 0.85 ms (see Figure 6). The mucosal wave velocity c can be estimated by 2.25 mm / 0.85 ms = 2.68 m/s. The phase delay per millimeter (φ/z) is about 24.8 degrees/mm, which is estimated by φ/z = 360 F0/c. F0 = 179 Hz is the fundamental frequency. These results are close to the range (0.6 m/s – 2.2 m/s for mucosal wave velocity; 24.5 degree/mm – 61 degree/mm for the phase delay per millimeter; 100 Hz – 180 Hz for fundamental frequency) measured previously using an excised larynx setup [28].
Figure 6.
The vertical propagation of mucosal wave along the medial surface of the vocal fold, where curve 1 corresponds to the node on the upper margin of vocal fold, curve 2 corresponds to the node 2.25 mm below the upper lip, the lung pressure is 1 kPa, and the elongation length Le is 2.4 mm.
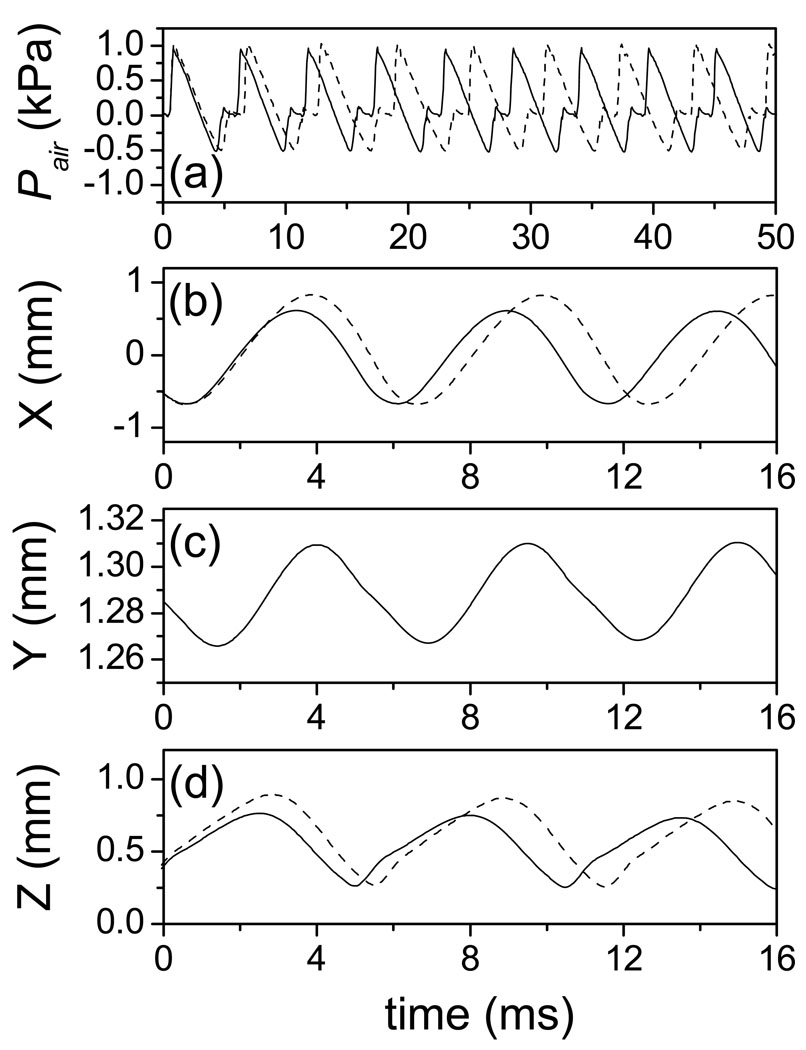
The driving force provided by glottal airflow is another important factor in vocal fold vibration. Figure 7 presents the waveform of intraglottal air pressure (a) and the node displacement in the x, y, and z directions (b–d) with solid lines, where the lung pressure is 1.0 kPa and the elongated length Le is 2.4 mm. The figure (a) shows the waveform of the intraglottal airflow pressure (Pair) and the figures (b–d) illustrate waveforms of the x, y, and z displacements for the third node from the top left edge in the anterior-posterior mid-plane of the vocal fold. During phonation, high lung pressure pushes the vocal folds apart and the glottis open. Air is accelerated and escapes through the glottis. Consequently, Pair is decreased due to Bernoulli’s effect generated by the high velocity glottal airflow [Fig. 7 (a)]. This aerodynamic force and the elastic recoil of the deformed tissue cause the vocal fold to close, and a new cycle begins. The interaction between the vocal fold model and the glottal airflow generates the oscillating solution. The vibratory amplitude (about 1.3 mm) in the lateral direction (x-direction) is larger than that (about 0.5 mm) in the vertical direction (z-direction). In the anterior-posterior direction (y-direction), the mean value of the displacement is large (about 1.28 mm) due to the longitudinal elongation. However, the vibratory amplitude in the y direction (only about 0.0425 mm) is much smaller than that in the x and z directions. All of these waveforms are reasonable when compared with other computer models [6]. Also, they agree with previous measurements of vocal fold surface dynamics [24] and glottal aerodynamics [29].
Figure 7.
The air pressure in glottis and the node displacements on vocal fold surface with the lung pressure of PL = 1.0 kPa, where the solid lines and the dashed lines correspond to the elongation length Le = 2.4 mm and Le = 0.0 mm respectively. (a) the waveform of intralglottal air pressure. (b, c, d) the node displacement in x, y, and z direction for the 3rd node from the top left edge in the anterior-posterior mid-plane of vocal fold.
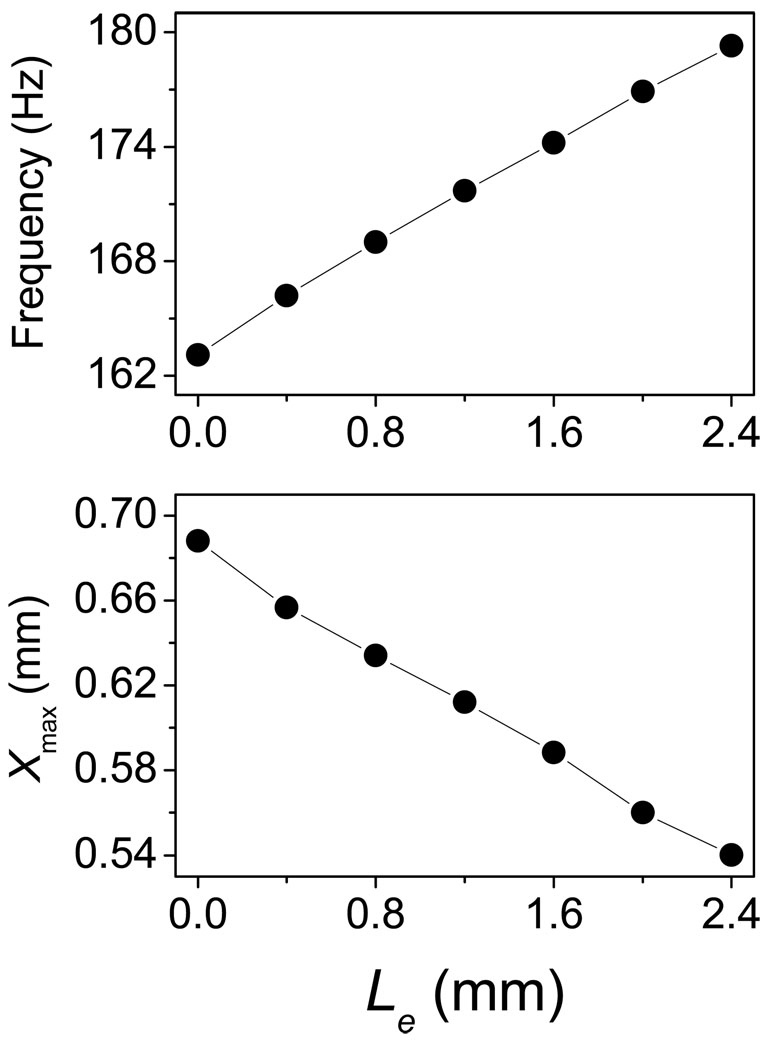
For the sake of comparison, the model outputs with PL = 1.0 kPa and Le = 0.0 mm are depicted in Figure 7 with dashed lines. Because the elongation significantly increases longitudinal tension in vocal folds (see Figure 4 and [12]), the waveforms of the vocal fold differ when elongation length changes. The amplitudes of the x and z displacements, corresponding to Le = 2.4 mm, are smaller than those corresponding to Le = 0.0 mm. Elongation increases the longitudinal length of the vocal fold, whereas it also increases the longitudinal tension, which decreases the lateral and vertical vibratory amplitudes of the vocal fold. Furthermore, fundamental frequency increases when the vocal fold is elongated. Therefore, there exists a phase difference between the waveforms of elongated (solid line) and un-elongated (dashed line) vocal folds. Moreover, this phase difference increases each cycle. Figure 8 (a) and (b) shows that the fundamental frequency roughly linearly increases with elongation, whereas, the lateral maximum displacement approximately decreases with elongation. Here, the fundamental frequencies are determined according to the average cycle-to-cycle period. When Le = 0.0 mm, the fundamental frequency and the maximum lateral displacement are 163 Hz and 0.69 mm, respectively. When the vocal fold is elongated, Le = 2.4 mm (15% elongation), the fundamental frequency and the maximum lateral displacement are 179 Hz and 0.54 mm, respectively. The fundamental frequency increases about 10.0% and the maximum lateral displacement decreases about 21.6% in comparison to the situation of Le = 0.0 mm. In a previous excised larynx study, Jiang et al. found that elongation increases the fundamental frequency of vocal fold [30]. Titze and Hunter predicted that the frequency of the ligament’s normal mode increases with elongation [12]. The above simulations confirm these experimental and theoretical results. Furthermore, Jiang et al. found that elongation decreased the amplitude of the mucosal waves in most of the canine larynges [30]. It is known that the amplitude of the mucosal wave depends mainly on the lateral maximum displacement of the node on the vocal fold surface. In this simulation, we find that the lateral displacement of the vocal fold surface node is decreased with elongation. Therefore, this result is in accordance with the measurements of Jiang et al. [30].
Figure 8.
the fundamental frequency and the laterally vibratory amplitude as a function of the longitudinal elongation. (a) the fundamental frequency. (b) the maximum lateral displacement.
4. Conclusion
In this study, a three-dimensional finite-element vocal fold model is proposed to simulate the vibration of the elongated vocal fold. The longitudinal movement and large deformation of vocal tissue are considered in this model. Moreover, instead of the fixed boundary condition, the displacement boundary condition is applied on the posterior side of vocal fold, which represents the elongation of vocal fold length done by the CT and TA muscles. These improvements of this model allow the simulation of vocal fold elongation.
Using this model, we studied the vibration of the elongated vocal fold. It was found that longitudinal elongation not only changes the vocal fold shape, but it also alters the tension distribution in the vocal fold tissue. The longitudinal elongation significantly increases the y-direction normal stress. This stress approximately linearly increases with longitudinal elongation (0% – 15%). The longitudinal tension due to elongation significantly changes the vibratory characteristics of vocal folds. It was found that elongation decreases the lateral maximum displacement of the vocal folds but increases the fundamental frequency. The fundamental frequency increases about 10.0% and the maximum lateral displacement decreases about 21.6% when the vocal fold is elongated from 0% to 15%. These results explain observations in the previous excised larynx experiment very well. The agreement between our model simulation and the experimental measurements suggests that the proposed elongation vocal fold model could be a useful tool for investigating the control of vocal fold vibration and voice production.
ACKNOWLEDGMENTS
This study was supported by NIH Grant (No. 1-RO1DC006019 and No. 1-RO1DC05522) from the National Institute of Deafness and other Communication Disorders.
Reference
- 1.Gunter HE. A mechanical model of vocal-fold collision with high spatial and temporal resolution. J. Acoust. Soc. Am. 2003;113:994–1000. doi: 10.1121/1.1534100. [DOI] [PubMed] [Google Scholar]
- 2.Gunter HE. Modeling mechanical stresses as a factor in the etiology of benign vocal fold lesions. Journal of Biomechanics. 2004;37:1119–1124. doi: 10.1016/j.jbiomech.2003.11.007. [DOI] [PubMed] [Google Scholar]
- 3.Tao C, Jiang JJ, Zhang Y. Simulation of vocal fold impact pressures with a self-oscillating finite-element model. J. Acous. Soc. Am. 2006;119(6):3987–3994. doi: 10.1121/1.2197798. [DOI] [PubMed] [Google Scholar]
- 4.Fink BR, Demarets RJ. Laryngeal Biomechanics. Harvard Univ Pr.; 1978. [Google Scholar]
- 5.Ishizaka K, Flanagan JL. Synthesis of voiced sounds from a two mass model of the vocal cords. Bell Syst. Tech. J. 1972;51:1233–1268. [Google Scholar]
- 6.Alipour F, Berry FDA, Titze IR. A finite-element model of vocal-fold vibration. J. Acoust. Soc. Am. 2000;108(6):3003–3012. doi: 10.1121/1.1324678. [DOI] [PubMed] [Google Scholar]
- 7.Alipour F, Scherer RC. Vocal fold bulging effects on phonation using a biophysical computer model. J. Voice. 2000;14:470–483. doi: 10.1016/s0892-1997(00)80004-1. [DOI] [PubMed] [Google Scholar]
- 8.de O. Rosa M, Pereira JC, Grellet M, Alwan A. A contribution to simulating a three-dimensional larynx model using the finite-element method. J. Acoust. Soc. Am. 2003;114:2893–2905. doi: 10.1121/1.1619981. [DOI] [PubMed] [Google Scholar]
- 9.Hunter EJ, Titze IR, Alipour F. A three-dimensional model of vocal fold abduction/adduction. J. Acoust. Soc. Am. 2003;115(4):1747–1759. doi: 10.1121/1.1652033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thomson SL, Mongeau L, Frankel SH. Aerodynamic transfer of energy to the vocal folds. J. Acous. Soc. Am. 2005;118(3):1689–1700. doi: 10.1121/1.2000787. [DOI] [PubMed] [Google Scholar]
- 11.Tao C, Jiang JJ. Mechanical stress during phonation in a self-oscillating finite-element vocal fold model. Journal of Biomechanics. 2007;41:2191–2198. doi: 10.1016/j.jbiomech.2006.10.030. [DOI] [PubMed] [Google Scholar]
- 12.Titze IR, Hunter EJ. Normal vibration frequencies of the vocal ligament. J. Acoust. Soc. Am. 2004;115(5):2264–2269. doi: 10.1121/1.1698832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Titze IR, Talkin TD. A theoretical study of the effects of various laryngeal configurations on the acoustics of phonation. J. Acoust. Soc. Am. 1979;66:60–74. doi: 10.1121/1.382973. [DOI] [PubMed] [Google Scholar]
- 14.Alipour F, Titze IR. Elastic models of vocal fold tissues. J. Acoust. Soc. Am. 1991;90(3):1326–1331. doi: 10.1121/1.401924. [DOI] [PubMed] [Google Scholar]
- 15.Alipour F, Titze IR. Active and passive characteristics of cricothyroid muscles. J. Voice. 1999;13(1):1–10. doi: 10.1016/s0892-1997(99)80056-3. [DOI] [PubMed] [Google Scholar]
- 16.Hirano M, Kakita Y, Ohmaru K, Kurita S. Structure and mechanical properties of the vocal fold. Speech Language. 1982;7:271–297. [Google Scholar]
- 17.Min YB, Titze IR, Alipour F. Stress-strain response of the human vocal ligament. Ann Otol Rhinol Laryngol. 1995;104(7):563–569. doi: 10.1177/000348949510400711. [DOI] [PubMed] [Google Scholar]
- 18.Chan RW, Titze IR. Viscoelastic shear properties of human vocal fold mucosa: Measurement methodology and empirical results. J. Acoust. Soc. Am. 1999;106:2008–2021. doi: 10.1121/1.427947. [DOI] [PubMed] [Google Scholar]
- 19.Simo JC, Laursen TA. An Augmented Lagrangian Treatment of Contact Problems Involving Friction. Computers and Structures. 1992;42:97–116. [Google Scholar]
- 20.Berry DA, Titze IR. Normal modes in a continuum model of vocal fold tissues. J. Acoust. Soc. Am. 1996;100:3345–3354. doi: 10.1121/1.416975. [DOI] [PubMed] [Google Scholar]
- 21.Garrel R, Nicollas R, Giovanni A, Ouaknine M. Optoreflectometry Determination of the Resonance Properties of a Vocal Fold. Journal of Voice. 2007;21(5):517–521. doi: 10.1016/j.jvoice.2006.05.002. [DOI] [PubMed] [Google Scholar]
- 22.Titze IR. The physics of small-amplitude oscillation of the vocal folds. J. Acoust. Soc. Am. 1988;83(4):1536–1552. doi: 10.1121/1.395910. [DOI] [PubMed] [Google Scholar]
- 23.Berry DA, Herzel H, Titze IR, Krischer K. Interpretation of biomechanical simulations of normal and chaotic vocal fold oscillations with empirical eigenfunctions. J. Acoust. Soc. Am. 95(6):3595–3604. doi: 10.1121/1.409875. [DOI] [PubMed] [Google Scholar]
- 24.Döllinger M, Berry DA, Berke GS. Medial surface dynamics of an in vivo canine vocal fold during phonation. J. Acoust. Soc. Am. 2005;117(5):3174–3183. doi: 10.1121/1.1871772. [DOI] [PubMed] [Google Scholar]
- 25.Döllinger M, Berry DA. Computation of the three-dimensional medial surface dynamics of the vocal folds. 2006;39(2):369–374. doi: 10.1016/j.jbiomech.2004.11.026. [DOI] [PubMed] [Google Scholar]
- 26.Saito S, Fukuda H, Kitahara S, Isogai Y, Tsuzuki T, Muta H, Takayama E, Fujioka T, Kokawa N, Makino K. In: Vocal Fold Physiology: Biomechanics, Acoustics, and Phonatory Control. Titze IR, Scherer RC, editors. Denver: Denver Center for the Performing Arts; 1985. pp. 169–182. [Google Scholar]
- 27.Bless D, Hirano M, Feder R. Videostroboscopic evaluation of the larynx. Ear Nose Throat J. 1987;66:289–296. [PubMed] [Google Scholar]
- 28.Titze IR, Jiang JJ, Hsiao T-Y. Measurement of mucosal wave propagation and vertical phase difference in vocal fold vibration. Annals of Otology, Rhinology & Laryngology. 1993;102:58–63. doi: 10.1177/000348949310200111. [DOI] [PubMed] [Google Scholar]
- 29.Jiang JJ, Titze IR. Measurement of Vocal Fold Intraglottal Pressure and Impact Stress. J. Voice. 1994;8:132–144. doi: 10.1016/s0892-1997(05)80305-4. [DOI] [PubMed] [Google Scholar]
- 30.Jiang JJ, Chang C-IB, Raviv JR, Gupta S, Banzali FM, Hanson DG. Quantitative Study of Mucosal Wave Via Videokymography in Canine Larynges. The Laryngoscope. 2000;110:1567–1573. doi: 10.1097/00005537-200009000-00032. [DOI] [PubMed] [Google Scholar]