Survival analysis in infectious disease research: Describing events in time

Abstract

Survival analysis methods can be used in infectious disease research to describe the occurrence and timing of clinical or other events subject to censoring and truncation. Here, the survival, hazard and cumulative hazard functions are defined and simple nonparametric estimators are provided using an illustrative example of survival after AIDS diagnosis. An understanding of these foundational measures is central for an informed use of the survival analysis methods common in infectious disease research.

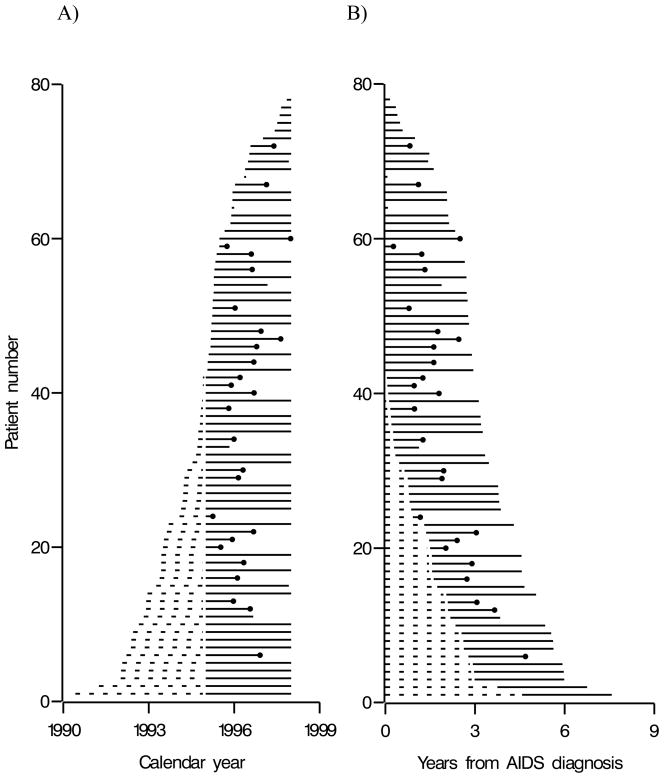
Survival analysis is a set of methods that can be used to describe the occurrence and timing of clinical or other events [1–4]. The target of inference for survival analysis is the time between an origin and event. For instance, in the example below we are interested in the survival time from AIDS diagnosis until death. Survival analysis is crucial when observed data are censored or truncated. Censoring and truncation are common in infectious disease research. Censoring occurs when we do not know the exact time of an event, but we do know the event occurred before or after a known time, or within a given interval. Here we consider only censoring after a known time (i.e., right censoring), which is the most common form of censoring in biomedical research. Such censoring may be due to completing the study free of the event (i.e., administrative censoring) or loss to follow up free of the event but before completing the study (i.e., drop out). Truncation occurs when we do not observe individuals with event times that are smaller or larger than certain values. Here we consider only left truncation (i.e., not observing individuals with small event times), which is the most common form of truncation in biomedical research. Such truncation occurs when we begin observation after some or all individuals have already been at risk for the event of interest. For example, in Figure 1 we present left truncated and right censored data for 78 men followed from the later of AIDS diagnosis or 1995 through the earliest of death, drop out, or 1998.

Figure 1.

Time line plots with (A) calendar time and (B) years from AIDS diagnosis as the time scale for 78 men enrolled in the Multicenter AIDS Cohort Study, alive on 1 January 1995 and diagnosed with AIDS before 1 January 1998. Dashed lines represent time between AIDS diagnosis and study entry, solid lines represent time after study entry, and dots represent deaths.

Existing introductions to survival analysis (e.g., [5–6]) typically ignore truncation, move quickly to group comparisons, and do not concentrate on infectious diseases. The intent of this paper is to clarify foundations for survival analysis that are standard in modern statistics but not universally understood by clinicians and (non-statistician) scientists working in infectious diseases. We concentrate on clarifying foundations of survival analysis, a prerequisite for group comparisons. First we provide a motivating example.

Motivating Example: Survival after AIDS

Say we are interested in describing survival after AIDS. In this example, the origin is AIDS diagnosis and the event is all-cause mortality. The time between the origin and event is AIDS duration. We conduct a cohort study and enroll 42 men alive on 1 January 1995 with a prior clinical AIDS diagnosis. These 42 men comprise a “prevalent” or left-truncated cohort, because the 42 men began observation after their origin (i.e., AIDS diagnosis) for the event death after AIDS. The median (quartiles) AIDS duration at study enrollment for these 42 men is 1.42 (0.34, 2.18) years.

We then prospectively enroll 36 additional men beginning at their clinical AIDS diagnosis between 1 January 1995 and 1 January 1998. We follow all 78 (= 42 + 36) men for all-cause mortality through 1 January 1998, the date of study completion. Typically a minimum amount of time between study enrollment and the date of study completion is required, but here we make no such requirement. The 36 additional men comprise an “incident” cohort, because each of the 36 additional men was observed from their origin (i.e., AIDS diagnosis) for the event death after AIDS. Here “prevalent” and “incident” are used in conjunction with the origin of the time at risk, rather than their typical use in conjunction with the event.

To carefully describe survival analysis methodology, we use the following mathematical notation. A symbol key is presented in Table 1. In general, uppercase letters denote random variables and lowercase letters denote possible realizations of random variables, or constants. Let W denote the years from AIDS diagnosis to study enrollment. For incident AIDS cases, who are enrolled at AIDS diagnosis, W = 0. Let T denote the years from AIDS diagnosis to death, and let C denote the years from AIDS diagnosis to right censoring. In practice, we only get to observe the minimum of T and C, which we denote by T* = min(T,C). Let D = 1 if death occurred before censoring and D = 0 otherwise. Finally, let the subscript i = 1 to N index the N = 78 men. For instance, D_i = 1 if individual i died during follow up (i.e., T*_i = T_i).

Table 1.

Symbol Key

Symbol:	Definition:
N	Sample size
W	Years from AIDS to study enrollment
T	Years from AIDS to death
C	Years from AIDS to right censoring
T*	Minimum of T and C
D	Indicator of death before right censoring
Rk	Time of kth ranked event
Yk	Number of deaths at time Rk
Nk	Number at risk at time Rk
Δk	Time interval between ranked death times
S(t)	Probability of survival to time t
h(t), hk	Hazard at time t, or Rk
H(t)	Cumulative hazard to time t

Data for these 78 men are provided in Table 2. Reading from Table 2, individual 1 was diagnosed with AIDS on 1990.425, enrolled in the study W₁ = 4.575 years after AIDS diagnosis, and remained alive (D₁ = 0) at study completion on 1998.0 at T*₁ = 7.575 years after AIDS diagnosis. These data were obtained from version 11 of the Multicenter AIDS Cohort Study [7] public use data set. Dates in the public use data are given by month and year, so we randomly selected the day of the month to obtain exact dates. Randomly assigning dates in practice is not recommended in general. The intention here is to illustrate methods using data in the typical form, while both allowing public consumption of the example data and protecting anonymity. Dates will be available in most infectious disease research settings and are available in the non-public Multicenter AIDS Cohort Study data.

Table 2.

Individual identifier (i), decimal calendar date of AIDS diagnosis (AIDSY_i), years from AIDS diagnosis to study entry (W_i), years from AIDS diagnosis to minimum of death or censoring (T*_i), and indicator of death during follow up (D_i) for 78 men enrolled in the Multicenter AIDS Cohort Study, alive on 1 January 1995 and diagnosed with AIDS before 1 January 1998 ^a

i	AIDSYi	Wi	T*i	Di
1	1990.425	4.575	7.575	0
2	1991.250	3.750	6.750	0
3	1992.014	2.986	5.986	0
4	1992.030	2.970	5.970	0
5	1992.072	2.928	5.928	0
6	1992.220	2.780	4.688	1
7	1992.374	2.626	5.626	0
8	1992.389	2.611	5.611	0
9	1992.450	2.550	5.550	0
10	1992.653	2.347	5.347	0
11	1992.825	2.175	3.842	0
12	1992.906	2.094	3.655	1
13	1992.911	2.089	3.062	1
14	1992.958	2.042	5.042	0
15	1993.264	1.736	4.653	0
16	1993.384	1.616	2.729	1
17	1993.436	1.564	4.564	0
18	1993.439	1.561	2.897	1
19	1993.444	1.556	4.556	0
20	1993.503	1.497	2.024	1
21	1993.533	1.467	2.400	1
22	1993.637	1.363	3.043	1
23	1993.700	1.300	4.300	0
24	1994.081	0.919	1.169	1
25	1994.137	0.863	3.863	0
26	1994.189	0.811	3.811	0
27	1994.212	0.788	3.788	0
28	1994.228	0.772	3.772	0
29	1994.253	0.747	1.894	1
30	1994.358	0.642	1.951	1
31	1994.538	0.462	3.462	0
32	1994.664	0.336	3.336	0
33	1994.708	0.292	1.125	0
34	1994.734	0.266	1.258	1
35	1994.742	0.258	3.258	0
36	1994.798	0.202	3.202	0
37	1994.814	0.186	3.186	0
38	1994.836	0.164	0.973	1
39	1994.872	0.128	3.128	0
40	1994.903	0.097	1.794	1
41	1994.933	0.067	0.962	1
42	1994.950	0.050	1.255	1
43	1995.059	0.000	2.941	0
44	1995.070	0.000	1.619	1
45	1995.103	0.000	2.897	0
46	1995.169	0.000	1.619	1
47	1995.178	0.000	2.456	1
48	1995.189	0.000	1.752	1
49	1995.202	0.000	2.798	0
50	1995.231	0.000	2.769	0
51	1995.239	0.000	0.791	1
52	1995.247	0.000	2.753	0
53	1995.280	0.000	2.720	0
54	1995.286	0.000	1.881	0
55	1995.286	0.000	2.714	0
56	1995.309	0.000	1.322	1
57	1995.342	0.000	2.658	0
58	1995.384	0.000	1.216	1
59	1995.478	0.000	0.269	1
60	1995.481	0.000	2.500	1
61	1995.664	0.000	2.336	0
62	1995.869	0.000	2.131	0
63	1995.897	0.000	2.103	0
64	1995.914	0.000	0.086	0
65	1995.936	0.000	2.064	0
66	1995.941	0.000	2.059	0
67	1996.027	0.000	1.107	1
68	1996.350	0.000	0.067	0
69	1996.384	0.000	1.616	0
70	1996.486	0.000	1.431	0
71	1996.530	0.000	1.470	0
72	1996.572	0.000	0.820	1
73	1997.011	0.000	0.989	0
74	1997.422	0.000	0.578	0
75	1997.511	0.000	0.489	0
76	1997.597	0.000	0.403	0
77	1997.650	0.000	0.350	0
78	1997.847	0.000	0.153	0

^aDates are provided in decimal format so that each increment of 0.001 corresponds to about 8 hours. While data were collected to the day (not in 8-hour intervals), rounding the data to the more coarse hundredths place would entail that each 0.01 increment corresponds to about 3 days and would be overly imprecise.

Each man’s time on study is the difference between study entry and exit, i.e., T*_i– W_i years. Person-years at risk are defined as the sum of each man’s time on study, or ${\sum }_{\text{i}=1}^{\text{N}}({{\text{T}}^{\ast }}_{\text{i}}-{\text{W}}_{\text{i}})$. Immortal person-time in a study occurs when the individual contributing that person time could not, by study criteria, have died or been censored: immune person-time is similar, except it pertains to outcomes other than death [8–9]. In our example, there were ${\sum }_{\text{i}=1}^{78}({{\text{T}}^{\ast }}_{\text{i}}-{\text{W}}_{\text{i}})=150.679$ person-years at risk for death under observation and ${\sum }_{\text{i}=1}^{78}{\text{W}}_{\text{i}}=60.233$ immortal or immune person-years contributed by the 42 men in the prevalent cohort.

Figure 1 presents a pair of time line diagrams for the 78 men, where the vertical axis is an individual identifier which ranges from 1 to 78. In Figure 1 panel (A), the horizontal axis is calendar year. A man’s time line begins at the date of AIDS diagnosis. If this date is before 1 January 1995, the line is dashed, denoting immortal/immune time as the number of years between AIDS diagnosis and study entry (W); after 1 January 1995 the line is solid, denoting time at-risk for death after AIDS during the study. The 27 deaths are denoted by time lines that end with dots. The 7 drop outs are denoted by time lines that end before the administrative censoring date of 1 January 1998. For instance, reading from Table 2, individual 11 was diagnosed with AIDS on 1992.825, enrolled in the study W₁ = 2.175 years after AIDS diagnosis, and remained alive (D₁ = 0) when lost to follow up on 1996.667 at T*₁ = 3.842 years after AIDS diagnosis. In Figure 1 panel (B), the horizontal axis is years from AIDS diagnosis. Time line plots like those in Figure 1 provide an important role in the exploratory analysis of survival data. Data quality is easily assessed using such simple data displays that convey a single visualization of pertinent aspects of the entire data set. Next we review standard survival analysis methods that can be used to draw inferences from survival data such as our AIDS example.

The Survival, Hazard and Cumulative Hazard Functions

Survival is a function of time and is typically denoted by S(t). Survival is the probability that the random variable T is greater than some specified time t. A formal definition is provided in Appendix A. In the AIDS example, survival at time t is the probability of not dying within t years of AIDS diagnosis.

The hazard is the instantaneous rate of events at time t and is typically denoted h(t). The hazard at time t is a ratio of the probability of an event to the survival both at time t. In discrete time, the hazard at time t is the conditional probability of an event at, given survival to, time t. Returning to the AIDS example, the hazard is the rate at which men in the population die t years after AIDS diagnosis.

The cumulative hazard function is defined as a sum (formally, an integral) of the hazard function over time, and should not be confused with the complement of the survival function (see Appendix A). Plots of the log of the cumulative hazard function are useful in choosing among candidate parametric survival regression models [10], as well as for assessing the proportional hazards assumption when using Cox regression models [11]. Next we describe how to obtain estimates of the survival, hazard and cumulative hazard functions using the example AIDS data.

Estimators of the Survival, Hazard, and Cumulative Hazard Functions

We concentrate on nonparametric estimators, which do not posit a parametric form for the survival function (more detail is provided in the Discussion). Again, formal definitions are provided in Appendix A. To define nonparametric estimators we rank-order and number the distinct (untied) observed event times T_i as shown in Table 3 in the leftmost columns. Therefore, R_k is the kth ranked event time. In our example, we have one tied event time T₄₄ = T₄₆ = 1.619 years from AIDS diagnosis, so while there are 27 events there are only 26 rows in Table 3 (plus one row for k = 0). Let Y_k be the number of individuals who died at the kth ranked event time. In Table 3, the number of events, Y_k, is equal to 1, except for the 12th event time, where there are two deaths (i.e., Y₁₂ = 2).

Table 3.

Ranked (k) observed event times (R_k), number of events (Y_k), risk-set sizes (N_k), time between events (Δ_k), hazard (h_k) and Kaplan-Meier survival (S^KM(t)) estimates for 78 men enrolled in the Multicenter AIDS Cohort Study, alive on 1 January 1995 and diagnosed with AIDS before 1 January 1998

Rank	Event Time	No. Events	No. at Risk	Time Interval	Hazard	Survival
k	Rk	Yk	Nk	Δk	hk	SKM(t = Rk)
0	0.000	0	36	NA	NA	1.000
1	0.269	1	42	0.269	0.0885	0.976
2	0.791	1	44	0.522	0.0435	0.954
3	0.820	1	44	0.029	0.7837	0.932
4	0.962	1	45	0.142	0.1565	0.912
5	0.973	1	44	0.011	2.0661	0.891
6	1.107	1	42	0.134	0.1777	0.870
7	1.169	1	40	0.062	0.4032	0.848
8	1.216	1	39	0.047	0.5456	0.826
9	1.255	1	38	0.039	0.6747	0.804
10	1.258	1	37	0.003	9.0090	0.783
11	1.322	1	37	0.064	0.4223	0.762
12	1.619	2	40	0.297	0.1684	0.723
13	1.752	1	38	0.133	0.1928	0.705
14	1.794	1	38	0.042	0.6266	0.686
15	1.894	1	36	0.100	0.2278	0.667
16	1.951	1	35	0.057	0.5013	0.648
17	2.024	1	34	0.073	0.4029	0.629
18	2.400	1	33	0.376	0.0806	0.610
19	2.456	1	32	0.056	0.5580	0.591
20	2.500	1	31	0.044	0.7331	0.572
21	2.729	1	30	0.229	0.1456	0.553
22	2.897	1	27	0.168	0.2205	0.532
23	3.043	1	27	0.146	0.2537	0.513
24	3.062	1	26	0.019	2.0243	0.493
25	3.655	1	19	0.593	0.0888	0.467
26	4.688	1	11	1.033	0.0880	0.425

Let N_k be the number of individuals at-risk for mortality while under observation at the kth ranked event time. N_k is the size of the “risk set” at the kth ranked event time. Note an individual is immortal for any event between the origin at time 0 and study entry at time W_i and is therefore not included in the risk set until they enter the study. However, individuals who are censored exactly coincident with an event at time R_k are considered to be at risk at that time, and therefore are included in the risk set N_k. In Table 3, N_k ranges from 45 individuals at-risk at 0.962 years from AIDS diagnosis to 11 individuals at-risk at 4.688 years from AIDS diagnosis.

A nonparametric estimator of the survival function is the product-limit or Kaplan-Meier estimator [13], which is defined as a cumulative product of the estimated probability of not incurring an event (see Appendix A). Note because the size of the risk sets N_k account for late entries (i.e., W_i ≥ 0), this is sometimes called the extended Kaplan-Meier estimator [14]. This Kaplan-Meier estimator implicitly imputes unseen truncated events due to some individuals entering follow up after the origin and imputes event times for individuals who are censored from follow up without the event [15–16]. The Kaplan-Meier estimator steps at event times, and is flat elsewhere. There are other nonparametric estimators of the survival function (see Appendix A), but the Kaplan-Meier estimator is most commonly used in the biomedical literature. A variance estimator for the survival function is given in Appendix B.

In Table 3, the Kaplan-Meier survival estimate ranges from 1 at AIDS diagnosis down to 0.425 at 4.688 years from AIDS diagnosis. For example, the survival at R₂ = 0.791 years after AIDS, is 0.954 and is obtained as:

$${\text{S}}^{\text{KM}}(\text{t}={\text{R}}_2)=\left(1-\frac{{\text{Y}}_0}{{\text{N}}_0}\right)\times \left(1-\frac{{\text{Y}}_1}{{\text{N}}_1}\right)\times \left(1-\frac{{\text{Y}}_2}{{\text{N}}_2}\right)=\left(1-\frac{0}{36}\right)\times \left(1-\frac{1}{42}\right)\times \left(1-\frac{1}{44}\right)=0.954$$

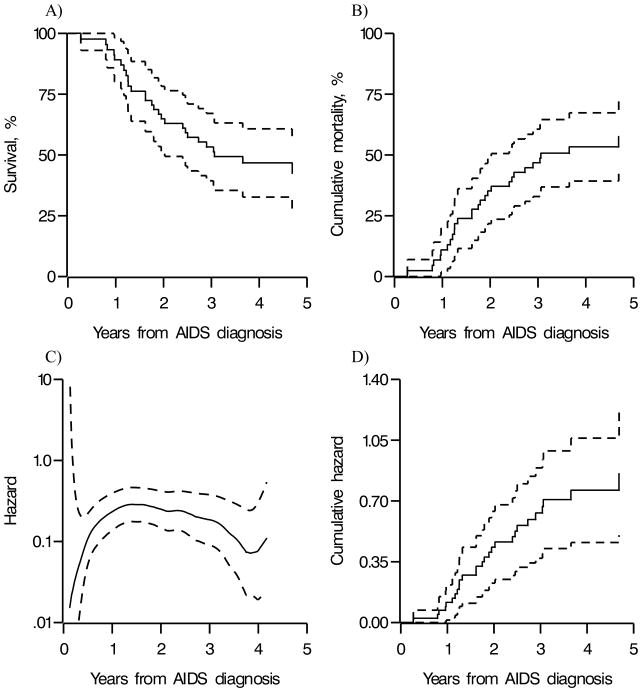
In Figure 2 panel (A), we plot the Kaplan-Meier survival function estimates and point-wise 95% confidence limits. Reading from Table 3 or Figure 2 panel (A), the first quartile and median times from AIDS diagnosis to death were about 1.6 and 3 years, respectively. The estimated first quartile of mortality of 1.6 years is similar to the 1.78 years (95% confidence limits: 1.29, 2.44) reported by Schneider and colleagues [17] for a similar time period using data from the Multicenter AIDS Cohort Study. Figure 2 panel (B) is the estimated cumulative probability of death (i.e., the complement of the estimated survival function), which is often presented in place of panel (A). Looking at Figure 2 panel (B), the estimated probability of death at 2 years from AIDS diagnosis is about 37%.

Figure 2.

Estimates of (A) the survival function, (B) the cumulative probability of death (i.e., complement of the survival function), (C) a kernel smoothed hazard function, and (D) the cumulative hazard function, with approximate point-wise 95% confidence limits (dashed) for 78 men enrolled in the Multicenter AIDS Cohort Study, alive on 1 January 1995 and diagnosed with AIDS before 1 January 1998

The hazard h(t) at the kth ranked event time can be estimated by a ratio of the number of deaths to the product of the number at risk and the time interval since the prior event. In Table 3, the hazard estimates range from 0.0435 at 0.791 years from AIDS diagnosis to 9.009 at 1.258 years from AIDS diagnosis. For example, the hazard at R₂ = 0.791 years after AIDS, was obtained as:

$${\text{h}}_2=\frac{{\text{Y}}_2}{{\text{N}}_2\times {\mathrm{\Delta }}_2}=\frac{1}{44\times 0.522}=0.0435$$

A smooth function of the hazard is often preferred, because the individual hazard estimates tend to be unstable. In Figure 2 panel (C), we plot a kernel smooth estimate of the hazard [3–4, 12]. The smoothed hazard appears to decrease between 1.5 and 4 years after AIDS diagnosis. Finally, in Figure 2 panel (D), we plot the estimator of the cumulative hazard and point-wise 95% confidence limits.

Discussion

In this paper we discussed standard methods for description of survival data with particular attention to right censoring and left truncation. A series of important caveats are discussed below.

First, in randomized trials, all individuals begin observation at a natural origin, namely randomization. In observational cohort studies there often exist multiple possible origins. Some examples include study entry, birth, and disease onset or diagnosis. In such settings time on study does not carry biologic meaning, unless study enrollment coincides with the origin of interest. Fortunately, the nonparametric estimators described above easily handle left truncation due to late entries. Note that when the data consist of a combination of incident (i.e., W = 0) and prevalent (i.e., W > 0) individuals one might ignore the prevalent individuals and still obtain consistent estimates of the survival function. However, discarding data from the prevalent cohort may lead to a loss of precision because of the reduced sample size and a potential shortening of the time period over which the survival function can be estimated because prevalent individuals typically have longer survival times.

Second, selection bias may arise whenever we select a subset of individuals for analysis. In our example, we restrict to men alive 1 January 1995 and our results may or may not generalize to men alive in other calendar periods. In a substantive analysis, this and any other restriction would have to be scrutinized before drawing inference about a particular population. Selection bias may also arise if individuals who enter follow up W years after AIDS diagnosis do so in an informative manner. For example, late entry is informative if the hazard of the event is associated with the entry time [18]. In our example of 36 incident (i.e., W = 0) and 42 prevalent (i.e., W > 0) individuals, one simple way to assess selection bias due to informative late entry is to restrict the analysis to the 36 incident individuals. If we do so in our example, the time to the first quartile of mortality (i.e., 25% dead) is about 1.47 years, which is similar to the 1.6 years in the complete sample (we cannot compare median survival times because by 1 January 1998 less than half of the 36 incident individuals had died). Therefore, the late entry does not appear to be informative in these data. Finally, selection bias may also arise whenever individuals are selected out of the study over time. In our example, 44 individuals are administratively censored on 1 January 1998 and 7 individuals are censored at drop out. Administrative censoring may be unrelated to the hazard of death here and in many other examples, but drop out may be informative. For example, in the AIDS example if men who were ill and more likely to die were also more likely to drop out then we would obtain an upwardly biased estimate of the survival function. One simple way to assess the possible effects of informative drop out is to calculate bounds [19]. For instance, in the AIDS example we can estimate the survival function if all 7 individuals who dropped out were immediate events, as well as if all 7 were still alive at the date of administrative censoring. In our example, the median survival was about 3 years in the observed data, would have been about 2.5 years had all 7 drop outs been immediately died, and about 3 years had all 7 been alive on 1 January 1998. Therefore, there is some sensitivity to drop out in these data. In the presence of substantial (e.g., >20%) drop out, bounds may become uninformative due to their width and a formal sensitivity analysis [20] may be required.

Third, when the origin or event dates are known only up to an interval and the length of a typical interval is sizable compared with the typical time from the origin to event, then survival analysis methods that allow for interval censoring should be employed [21–22]. However, when intervals are small compared to the typical time from the origin to event, simply taking the midpoint of the interval may suffice [23].

Fourth, there may be events not of central interest that compete with the event of interest. Competing risks are events other than the event of interest that remove an individual from the risk set and preclude the event of interest from occurring. This is distinct from preclusion of the event being observed due to censoring. In our motivating example, the event of interest was all-cause mortality and there were no competing risks. However, if the event of interest had been AIDS-related mortality then any non-AIDS deaths would have been competing risks. To obtain a valid estimate of the survival function in the presence of competing risks, methods that explicitly allow for competing risks should be employed [24–26]. Failure to use methods tailored to competing risks will typically overestimate the probability of the event of interest occurring. Such overestimation results because standard methods, such as those presented here, would treat competing risks as censored events of interest.

Fifth, we did not present parametric estimators of the hazard or survival function. Parametric estimators assume that the survival time T follows a distribution that is defined using a finite number of parameters. Examples of common parametric survival distributions include the lognormal and Weibull. The widely used nonparametric estimators described here do not assume that the survival time T follows a particular specified distribution. To that end, the nonparametric estimators are robust, in that they allow the distribution to be general. However, when the data do cohere with the shape of a parametric distribution, nonparametric estimators may be less precise than parametric estimators.

Sixth, the assumption that individuals are independent is needed to obtain valid estimates of the variance as given in Appendix B. In the infectious disease setting, the assumption that individuals are independent may not hold. For example, when studying the incidence of a respiratory virus close contact with infected individuals is likely to increase the hazard of infection. Therefore, in such settings clusters of individuals must be identified and methods that account for clusters should be used [28], and are akin to methods for repeated events within an individual, albeit repeated events have a natural time ordering [19], while infectious disease data often have a natural geographical space ordering in addition to time ordering.

Here we have presented an example of survival data pertinent to infectious disease research and illustrated how to describe event times using time lines and nonparametric estimators of the survival function, the hazard function and cumulative hazard function. The methods presented have broad applicability in infectious disease research. For instance, plots of estimates of these functions are helpful tools when attempting to describe the occurrence and timing of events. But the analysis presented begs the question does survival differ by measured factors?

The methods to answer important questions about differences in the survival or hazard function while continuing to account for censoring and truncation typically build upon the methods presented here. For instance, the log rank test [13] compares the survival function for two or more groups, while the Cox proportional hazards regression model [11] compares the hazard function for two or more groups with or without adjustment for concomitant variables. In conclusion, knowledge of the methods presented is central to an understanding of the survival analysis methods used in clinical research generally, and infectious disease research in particular.

Appendix A: Formal definitions

The survival function is defined as S(t) = P(T > t), where P(•) is the probability of •. Because the survival function is a probability, it has bounds of S(0) = 1 and S(∞) = 0. S(t) is the complement of the cumulative distribution function F(t), which is the probability that T is less than or equal t, i.e. F(t) = P(T ≤ t) = 1–S(t).

The hazard is defined as h(t) = f(t)/S(t), where f(t) is the probability density function, or the slope of the cumulative distribution function F(t) at time t, f(t) = d F(t)/d t. The cumulative hazard function is defined as $\text{H}(\text{t})={\int }_0^{\text{t}}\text{h}(\text{u})\text{du}=-log[\text{S}(\text{t})]$, where the definite integral is taken from 0 to t.

Observed event times T_i are ranked as R₁ < R₂ < … < R_D′, where D′ is the number of distinct (untied) event times. In our HIV example, ${\text{D}}^{\prime }={\sum }_{\text{i}=1}^{78}{\text{D}}_{\text{i}}=27$ if there are no tied event times, otherwise ${\text{D}}^{\prime }<{\sum }_{\text{i}=1}^{78}{\text{D}}_{\text{i}}=27$. For k = 1,…,D′, let Y_k be the number of individuals who died at each of the ranked times R_k, or formally ${\text{Y}}_{\text{k}}={\sum }_{\text{i}=1}^{\text{N}}{\text{D}}_{\text{i}}\times 1({\text{T}}_{\text{i}}={\text{R}}_{\text{k}})$, where 1(•) is the indicator function, such that it equals 1 if • is true and 0 otherwise.

Let N_k be the number of individuals at-risk for mortality while under observation at distinct ranked event time R_k, for k=1,…,D′. N_k is the size of the “risk set” at time R_k and is defined as ${\text{N}}_{\text{k}}={\sum }_{\text{i}=1}^{\text{N}}1({\text{W}}_{\text{i}}<{\text{R}}_{\text{k}}\le {\text{T}}_{\text{i}})$. Note individuals are immortal for any events between the origin at time 0 and entry at time W_i and are therefore not included in the risk set R_k if R_{k ≤} W_i. However, individuals who are censored exactly coincident with the event at time R_k (i.e., T_i = R_k and D_i = 0) are considered to be at risk at time R_k, and therefore are included in the risk set N_k.

A nonparametric estimator of S(t) is the product-limit or Kaplan-Meier estimator [13], which is defined as

$${\text{S}}^{\text{KM}}(\text{t})=\prod _{\{\text{k}:{\text{R}}_{\text{k}}\le \text{t}\}}(1-{\text{Y}}_{\text{k}}/{\text{N}}_{\text{k}}),$$

where at time t the product is taken over all ordered events up to time t, or {k:R_k ≤ t}. The hazard h(t) at the distinct event time t = R_k can be estimated by h_k = Y_k/(N_kΔ_k), where Δk = R_k –R_k–1 and R₀ = 0. Finally, the cumulative hazard is estimated simply as H^KM(t) = −log[S^KM(t)].

An alternative nonparametric estimator of the survival function was given independently by Nelson [32] and Aalen [33] as S^NA(t) = exp[−H^NA(t)], where H^NA(t) = Σ_{Rk ≤t} Y_k/N_k is the Nelson-Aalen estimator of the cumulative hazard function. Both the Kaplan-Meier and Nelson-Aalen estimators of the survival and cumulative hazard functions are nonparametric, consistent (i.e., converge in probability to the true value as the sample size tends to infinity), asymptotically normal and asymptotically equivalent [34]. These two approaches may differ in small sample sizes or when there are many ties. The Kaplan-Meier estimator is more commonly used in the biomedical literature.

Appendix B: Variance estimators

The most commonly used estimator of the variance for S^KM(t) is ${\text{V}[\text{S}}^{\text{KM}}(\text{t})]={\text{S}}^{\text{KM}}{(\text{t})}^2\times {\displaystyle \sum _{\{\text{k}:{\text{R}}_{\text{k}}\le \text{t}\}}}{\text{Y}}_{\text{k}}/[{\text{N}}_{\text{k}}({\text{N}}_{\text{k}}-{\text{Y}}_{\text{k}})]$, which is attributed to Greenwood [3, 35]. Approximate point-wise 95% confidence limits can be calculated by ${\text{S}}^{\text{KM}}(\text{t})\pm 1.96\times \sqrt{\text{V}[{\text{S}}^{\text{KM}}(\text{t})]}$. A formula for the variance for S^NA(t) is ${\sum }_{\{\text{k}:{\text{R}}_{\text{k}}\le \text{t}\}}{\text{Y}}_{\text{k}}/{\text{N}}_{\text{k}}^2$, which was given by Aalen [33]. A formula for the variance for H^KM(t) is ${\text{V}[\text{H}}^{\text{KM}}(\text{t})]={\displaystyle \sum _{\{\text{k}:{\text{R}}_{\text{k}}\le \text{t}\}}}{\text{Y}}_{\text{k}}/[{\text{N}}_{\text{k}}({\text{N}}_{\text{k}}-{\text{Y}}_{\text{k}})]$, which is obtained by the delta method. Alternative variance estimators exist [3].