Transitions Between Male and Female Heterogamety Caused by Sex-Antagonistic Selection

Abstract

Many animal taxa show frequent and rapid transitions between male heterogamety (XY) and female heterogamety (ZW). We develop a model showing how these transitions can be driven by sex-antagonistic selection. Sex-antagonistic selection acting on loci linked to a new sex-determination mutation can cause it to invade, but when acting on loci linked to the ancestral sex-determination gene will inhibit an invasion. The strengths of the consequent indirect selection on the old and new sex-determination loci are mediated by the strengths of sex-antagonistic selection, linkage between the sex-antagonistic and sex-determination genes, and the amount of genetic variation. Sex-antagonistic loci that are tightly linked to a sex-determining gene have a vastly stronger influence on the balance of selection than more distant loci. As a result, changes in linkage, caused, for example, by an inversion that captures a sex-determination mutation and a gene under sex-antagonistic selection, can trigger transitions between XY and ZW systems. Sex-antagonistic alleles can become more strongly associated with pleiotropically dominant sex-determining factors, which may help to explain biases in the rates of transitions between male and female heterogamety. Deleterious recessive mutations completely linked to the ancestral Y chromosome can prevent invasion of a neo-W chromosome or result in a stable equilibrium at which XY and ZW systems segregate simultaneously at two linkage groups.

AMONG species with genetic sex determination, sex is determined in the vast majority by a single locus or chromosome (Bull 1983). In taxa such as mammals, males are heterogametic (XY) and females homogametic (XX), while in groups such as birds, females are heterogametic (ZW) and males homogametic (ZZ). In contrast to the stability of the ancient sex-determination systems of groups like mammals and birds, some animal taxa show evidence of recent and rapid transitions between male and female heterogamety (Ezaz et al. 2006). For example, a phylogenetic analysis of genetic sex determination in teleost fishes found that 8 of 26 families include both species with XY and species with ZW sex determination (Mank et al. 2006). A similar survey in amphibians provides further examples of switches between XY and ZW systems (Hillis and Green 1990). Studies focused on several genera reveal details on finer evolutionary scales. In the cichlid genus Tilapia and its close relatives, sex is determined by two pairs of chromosomes, one of which functions as an XY system and the other as ZW. Sex is determined by the XY pair in some species and by the ZW pair in others, while in at least two species both pairs contribute to sex determination (Cnaani et al. 2008). In the genus Oryzias (the medaka and its relatives), there has been a transition from an ancestral XY system to a ZW sex system on a different pair of chromosomes (Takehana et al. 2008) and among the poeciliid fish (the guppy and its relatives) are species with XY and ZW sex determination (Volff and Schartl 2001).

At the chromosomal level, changes between female and male heterogamety can be grouped into two cases. The first we refer to as a nonhomologous transition. This occurs when the XY locus and the ZW locus are on different linkage groups. In this case, a transition between XY and ZW systems converts a linkage group that was the ancestral pair of sex chromosomes into autosomes and a linkage group that was autosomal into the new sex chromosomes. This situation is exemplified by Tilapia and Oryzias. The second case we term a homologous transition. An example occurs when a linkage group that already determines sex changes from an X chromosome (whose sex-determining function is recessive to that of the Y) to a W chromosome with a dominant feminizing effect over Y. A transition between male and female heterogamety then occurs as one homologous chromosome displaces another, for example, with the loss of the ancestral X and the establishment of the new W. An example of a homologous system in which X, Y, and W chromosomes all segregate at the same linkage group is known in the platyfish, Xiphophorus maculatus (Kallman 1984).

The evolutionary forces responsible for transitions between male and female heterogamety are not well understood. Three types of hypotheses have been previously proposed. If there are no fitness differences between the genotypes, there is a set of neutrally stable equilibria (Scudo 1964, 1967). The equilibria fall along a curve in the space of genotype frequencies that connects the XY and ZW endpoints, and the sex ratio at all points along the curve is 1:1. Drift along this neutral curve can produce a switch between XY and ZW (Bull and Charnov 1977).

A second kind of mechanism operates if a new sex-determining mutation enjoys a fitness advantage. It can then spread as the result of simple natural selection, resulting in a heterogamety transition when it is established (Kallman 1973; Bull and Charnov 1977; Lande et al. 2001). Alternatively, a stable polymorphism that maintains X, Y, and W chromosomes results under some fitness conditions (Orzack et al. 1980). Similarly, a transition can be driven by a novel sex chromosome that has a meiotic drive advantage (Bull and Charnov 1977; Werren and Beukeboom 1998; Jaenike 2001).

A third type of hypothesis to explain transitions between male and female heterogamety depends on the ability of some sex-determining mutations to alter the sex ratio. Sex ratios deviating from 1:1 can be favored under some circumstances, for example, when siblings compete for resources or when there is interdemic selection (Charnov 1982; West et al. 2000). Alternatively, forces such as meiotic drive can generate skewed sex ratios in a situation where selection favors equal numbers of males and females (Jaenike 2001). A new sex-determining mutation can respond to these types of selection and cause a shift between male and female heterogamety (Werren and Beukeboom 1998; Lande et al. 2001; Kocher 2004; Vuilleumier et al. 2007; Kozielska et al. 2010). This process is likely to have occurred in several mammalian species with unusual sex-determining mechanisms: the wood lemming, Myopus schisticolor (Lau et al. 1992); the Spanish mole, Talpa occidentalis (McVean and Hurst 1996); and the creeping vole, Microtus oregoni (Charlesworth and Dempsey 2001).

This article proposes a fourth hypothesis. We develop a model showing how evolutionary transitions between XY and ZW sex-determination systems can be driven by sexually antagonistic selection. This term refers to the situation where alleles advantageous in one sex are deleterious in the other sex (Rice 1984). We show that a mutation that changes the sex-determining properties of an existing sex chromosome will naturally and automatically become associated with alleles at sex-antagonistic loci nearby on the chromosome. For example, a mutation that changes an X chromosome (recessive to Y) to a W chromosome (dominant and feminizing over Y) will become correlated with alleles that enhance female fitness. Under some conditions, this new type of sex chromosome will spread by selection, causing a shift between XY and ZW sex determination. This idea extends the classical theory for the origin of sex chromosomes in a population that originally lacks them (Bull 1983; Rice 1987; Charlesworth 1991) and our recent model showing how sex-antagonistic selection can cause a new Y chromosome to supplant sex determination by an ancestral Y chromosome at a different linkage group (van Doorn and Kirkpatrick 2007).

Our hypothesis is motivated by a substantial body of evidence that suggests that sex-antagonistic selection is frequent (reviewed in van Doorn 2009). The observation that a large fraction (perhaps even the majority) of the transcriptome is expressed differently in males and females (Oliver and Parisi 2004; Gnad and Parsch 2006; Yang et al. 2006) suggests ample opportunity for sex-specific selection. Innocenti and Morrow (2010) recently estimated that 8% of genes in Drosophila melanogaster are under sex-antagonistic selection in a laboratory environment. Another line of evidence that is consistent with a role of sex-antagonistic selection in sex chromosome evolution is the growing number of examples of recently derived sex chromosomes that carry sexually selected loci. Cases are known from several groups of fishes: sticklebacks (Kitano et al. 2009), medaka (Wada et al. 1998), poeciliids (Kallman 1973; Lindholm and Breden 2002; Fernandez and Morris 2008), and cichlids (Lande et al. 2001; Streelman et al. 2003; Roberts et al. 2009).

This article develops models showing how and when sex-antagonistic selection will drive transitions between XY and ZW sex determination. We first consider the nonhomologous case. The model allows for any number of sex-antagonistic loci on the ancestral and new sex chromosomes and either loose or tight linkage between the sex-antagonistic genes and the sex-determining loci. Analytic approximations are derived for conditions that will cause invasion of a new sex chromosome that results in a transition between male and female heterogamety. We find that invasion will lead to a complete transition in the absence of other factors. We go on to consider the role of deleterious recessive mutations linked to the ancestral sex chromosomes. These tend to stabilize the ancestral sex-determination system, making it more difficult for a transition to occur and more likely that a stable polymorphic equilibrium will be attained if a new sex chromosome does begin to invade. Finally, we analyze the case of a homologous transition, in which invasion of a new chromosome at the ancestral sex-determining linkage group causes a transition between XY and ZW systems.

MODEL

The genetic model that we consider consists of two sex-determination loci and a set of loci that segregate for sexually antagonistic alleles. Sex-determining locus s, with alleles X and Y, carries the ancestral master sex-determining gene. Locus s′ represents the invading sex-determining system. This locus is initially fixed for allele Z, and we are interested in conditions that allow a dominant feminizing allele W to invade. As reflected by our notation, we suppose that male heterogamety is the ancestral state. By consistently switching the roles of males and females, the results can be made to apply to the case that the ancestral state is female heterogamety.

Assumptions and notation:

The sex-antagonistic loci, denoted a, b, c, …, are linked to one or the other of the sex-determining loci (in the case of a nonhomologous transition) or linked to both (if the sex-determining loci are on the same linkage group). Each one segregates for two alleles, denoted 0 and 1. These loci are partially sex linked; because we are interested in the evolution of evolutionarily young sex chromosomes that have not yet become heteromorphic, we allow for recombination between loci on the sex-determining chromosomes. To emphasize this fact, we use x, y, z, or w to refer to specific chromosomes, depending on the allele at the relevant sex-determining locus; uppercase X, Y, Z, and W are reserved for nonrecombining, well-differentiated sex chromosomes as in mammals and birds. The model allows for the polymorphism at sex-antagonistic loci to be maintained by sex-antagonistic selection, mutation, or a combination of the two. Mutation between the two alleles at the sex-antagonistic loci occurs at a rate μ. (The analysis in supporting information, File S1, and some of our simulations relax the assumption that the rate be symmetric.)

Selection on the sex-antagonistic loci occurs in the juvenile stage. We make no restrictions on the fitness relations between the genotypes at a locus (that is, any kind of dominance is allowed) or on the relative fitness effects on males vs. females. The loci are assumed to have independent (multiplicative) effects on viability or fecundity, however, meaning that there is no epistasis between them. We assume that mating is random. File S1 shows how the relative fitnesses of the genotypes at a sex-antagonistic locus can be used to calculate the average fitness effect of a sex-antagonistic locus. This quantity, which governs the amount of indirect selection that it generates on the sex-determining genes, is equal to the average change in fitness that would result from substituting a 1 allele for a 0 allele (see Table A1 in the appendix for a definition). We use 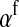to denote the average fitness effect at locus a in females and 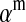for that in males.

TABLE A1.

List of definitions

Symbol	Definition
Sex-determination coefficients
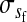	−1
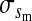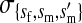
,,	−2
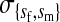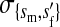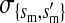
,,	2
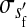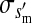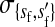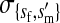
,,,	1
Transmission coefficientsa
,
,
,
,
,
,
,
,
,
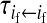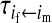
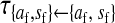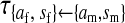
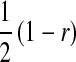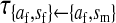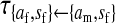
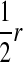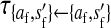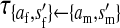
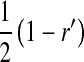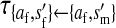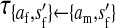
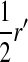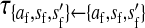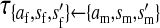
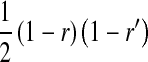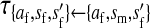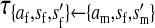
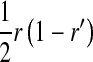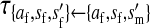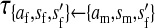
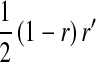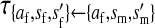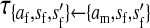
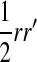Genetic associations
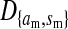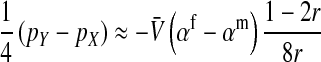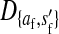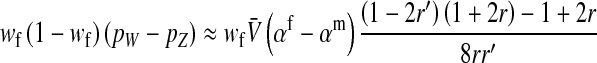Average fitness effects
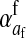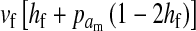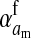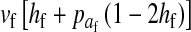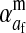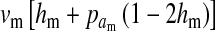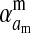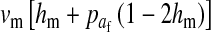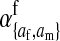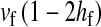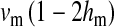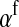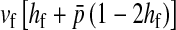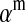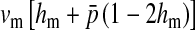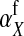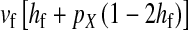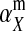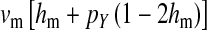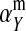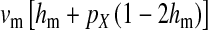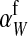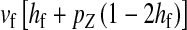Additive (co)variance for fitness

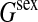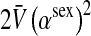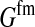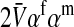^aTransmission coefficients depend on the order of the genes on the chromosome; these values assume that the sex-antagonistic locus is located between the sex-determination loci. Transmission coefficients in males (not shown) have the same values as those in females.

If the fitness effects of the sex-antagonistic loci are small, then their contributions to the evolution at the sex-determining loci are additive to leading order in the fitness effects. (This follows because departures from additivity depend on three-way linkage disequilibria between pairs of sex-antagonistic loci and either one of the sex-determination factors, and these higher-order associations do not exist under our assumption of no epistasis.) This allows us to decompose our model into submodels that each consider a single sex-antagonistic locus in isolation. We then add together their effects to find the collective impact on the sex-determination loci.

Even with this decomposition, a full description of the evolutionary dynamics would require us to keep track of 15 dynamic variables for each submodel (e.g., 2³ − 1 gamete frequencies for each sex plus the sex ratio), which change from one generation to the next in a complex manner due to sex determination, sex-specific selection, and Mendelian transmission. To deal with this complexity, we use an approximation based on the framework for multilocus systems developed by Barton and Turelli (1991) and its generalization by Kirkpatrick et al. (2002) (details are provided in the appendix). This framework distinguishes between the different positions that a gene at a given locus can occupy. A gene can be carried by either a male or a female, which we call the gene's sex-of-carrier, and can have been inherited from either a male (the father) or a female (the mother), which we call the gene's sex-of-origin. We use subscripts m (for male) and f (for female) to denote the sex-of-origin. For example, at the zygote stage, s_f refers to a gene at locus s (the ancestral sex-determination locus) inherited from a female (the zygote's mother). Since sex determination has not yet occurred, genes at the zygote stage do not have a sex-of-carrier. Likewise, positions in gametes can be distinguished only by a subscript (f if it is in an egg, m if in a sperm), reflecting the sex of the individual who produced the gamete or, equivalently, the gene's sex-of-origin in the next generation. At the juvenile and adult stages, however, we need also to specify the gene's sex-of-carrier, which we do with a superscript. For example, 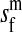refers to the gene at locus s inherited from a female and carried by a male. The sex-of-origin and sex-of-carrier (when present) are together called the gene's context. We denote a gene in a specific context using a chalkboard letter; for example, we can write s = 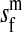. The set of all positions that contribute to sex determination in zygotes is written S = {s_f, s_m, s_f′, s_m′}. Likewise, we write A^sex = {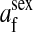, , 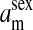, 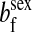…} for the set of all positions affecting fitness in juveniles, where sex equals m or f for male or female juveniles, respectively.

The genetic state of the population can be completely described in terms of the allele frequencies at each position for all of the loci and the statistical associations between the alleles at all sets of these positions (that is, linkage and Hardy–Weinberg disequilibria). The genetic association between alleles at the set of positions J, as defined by Equation A1 in the appendix, is denoted as D_J. While the number of genetic associations grows rapidly with the number of loci in the model, we show that the large majority of them are either zero or negligibly small, which leads to tremendous simplifications in the analysis.

The frequencies of the Y allele in zygotes are written y, the frequencies of the W allele are written w, and the frequencies of allele 1 at the sex-antagonistic locus a are written p_a. These frequencies are subscripted to distinguish between the positions. Thus y_m is the frequency of the Y allele in zygotes among genes inherited from a male (the father), w_f is the frequency of the W allele among genes inherited from a female (the mother), and 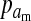is the frequency of allele 1 at locus a among genes inherited from a male. We use an asterisk to denote a frequency at the start of the following generation, e.g., .

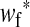RESULTS

We begin this section by developing general results for the invasion of a new w chromosome. Next are four sections that consider cases in which the ancestral and novel sex-determination loci are loosely linked. These apply to nonhomologous transitions and to homologous transitions if the loci are sufficiently far apart on the same chromosome. In the first case, the sex-antagonistic locus is loosely linked to both sex-determination loci. In the second, it is tightly linked to one of them (the distinction between loose and tight linkage depends on the magnitude of the rate of recombination relative to that of the sex-antagonistic selection coefficients; see below). In the third case, ZW sex determination is near fixation, and we use its behavior there to determine if a protected polymorphism can be established with both XY and ZW sex-determination systems segregating. The fourth case considers the effect of deleterious recessive alleles that have accumulated on the ancestral sex chromosomes. The final section of results examines homologous transitions in which the two sex-determining loci are tightly linked to each other.

General results:

As long as the W allele is rare, its frequency changes at an exponential rate 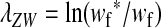that is approximately independent of the allele frequency w_f (Figure 1). This rate predicts whether the allele can increase in frequency when it is rare (W spreads only if 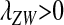). Accordingly, we refer to 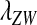as the invasion fitness of the novel sex-determining allele, conforming to the usage of this term in the adaptive dynamics literature (Metz et al. 1992); 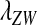can be interpreted as a net selection coefficient for the W allele at the time of invasion. Working our way back through the life cycle, and omitting associations that evaluate to zero, we find

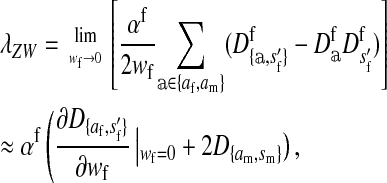(1)

where 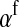is the average fitness effect of an allele substitution at the sex-antagonistic locus in females (see Table A1 in the appendix). The associations appearing in the intermediate result in Equation 1 refer to the juvenile stage. The strength of indirect selection on the W allele scales with the magnitude of its nonrandom association (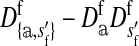) with maternally (a = a_f) and paternally (a = a_m) derived alleles at the sex-antagonistic locus a in females. In the final result, the associations are rewritten in terms of associations at the zygote stage and linearized with respect to w_f. Here we see that invasion of the new w chromosome is affected by its association with allele 1 at sex-antagonistic locus a in female gametes and by the association between allele 1 at a and the y chromosome in male gametes. These two associations have opposite signs if alleles at locus a have sexually antagonistic fitness effects. Female beneficial alleles naturally become associated with the feminizing W allele, whereas male-beneficial alleles automatically become associated with the masculinizing factor Y. The first association promotes invasion of the novel w chromosome, since it has the same sign as 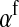, but the second stabilizes the ancestral sex-determination system (its sign is opposite to that of 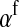, leading to a negative contribution to the fitness of W). Figure 1 shows an example with 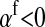; i.e., allele 1 at the sex-antagonistic locus a is a male-beneficial allele that is positively associated with the y chromosome in sperm (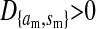) and negatively associated with the W allele in eggs ().

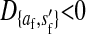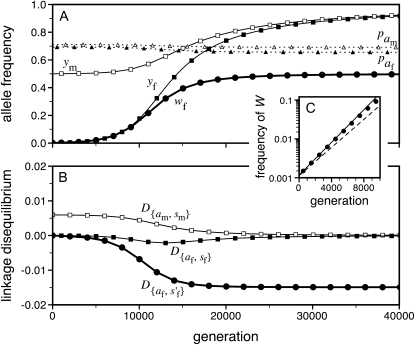
Figure 1.—

A homologous transition from male to female heterogamety. (A) A feminizing allele segregating at a novel sex-determination locus on the ancestral sex chromosomes increases in frequency (solid circles) if it is more tightly linked to a sex-antagonistic locus than the ancestral master sex-determining gene (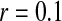 and 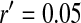in this simulation). The spread of the novel W allele is accompanied by an increase in the frequency of the ancestral masculinizing Y allele in both male and female gametes (open and solid squares, respectively) and slight changes in the allele frequencies at the sex-antagonistic locus (open and solid triangles/dashed lines). (B) The homologous heterogamety transition is driven by sex-antagonistic selection, which acts indirectly on the sex-determination loci through their nonrandom genetic association with sex-antagonistic alleles. (C) Initially, the W allele spreads at a nearly constant exponential rate and simulated frequencies (solid circles) fall along a straight line when plotted on a logarithmic scale. Analytical expressions for the invasion fitness of the W allele (dashed line, loose-linkage result; solid line, tight-linkage result) predict the slope of this line (i.e., the exponential rate of increase) during the initial phase of the simulations. 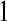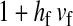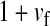Fitness values for the genotypes 00, 01, and 11 in females were given by , , and , respectively, with 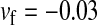and 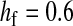. Analogous expressions define fitness in males, with 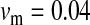and . 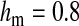Mutations between sex-antagonistic alleles occurred at rate .

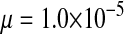The associations that appear in Equation 1 are related to sex-antagonistic allele-frequency differences between different types of gametes. The precise relationships (Table A1 in the appendix) can be derived from definition (A1) in the appendix and substituted into Equation 1 to produce an expression for the invasion fitness with a simple interpretation:

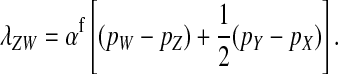(2)

Here, p_W and p_Z are the average frequencies of the sex-antagonistic allele in eggs that carry a W or a Z allele at the novel sex-determination locus s′. Likewise, p_Y and p_X are the frequencies in sperm carrying a Y or an X allele at the ancestral sex-determination locus s.

A simple argument verifies that the right-hand side of Equation 2 quantifies the fitness difference between a mutant (ZW) and a wild-type (XX) female. A mutant female has inherited a W allele from her mother instead of a Z allele. In addition, she may have inherited a Y allele from her father instead of an X. This occurs in half of the cases, whereas wild-type females always inherit an X allele from their father. Accordingly, the expected difference in allele frequency at the sex-antagonistic locus between a mutant and a wild-type female is given by 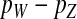for the maternally inherited half of the genome plus 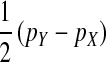for the paternally inherited part, which corresponds exactly to the term between brackets in (2). The multiplication with 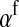, the average effect of an allele substitution, converts the sex-antagonistic allele-frequency difference into a fitness effect.

The next four sections apply these general results to cases in which the ancestral sex-determination locus and the new sex-determination loci are loosely linked to one another, as occurs in nonhomologous transitions. In a final section, we consider homologous transitions in which the two sex-determining loci are tightly linked.

Loose linkage:

Consider the situation in which the three loci (s, s′, and a) are loosely linked to one another. This is the case in nonhomologous transitions when the strength of sex-antagonistic selection is weak relative to the rates of recombination. Expressions for the allele frequency differences p_W − p_Z and p_Y − p_X can be then obtained by solving for the quasi-linkage-equilibrium (QLE) values of the associations 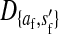and 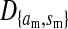that appear in our earlier result (1) using the methods of Kirkpatrick et al. (2002) (see File S1 for details). Substituting the QLE values into the expression for the invasion fitness yields our final result for loose linkage:

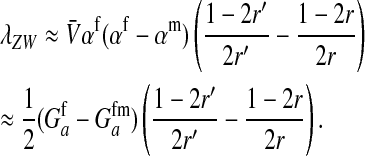(3)

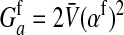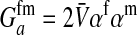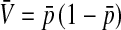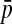Here is the additive genetic variance for fitness at locus a in females, is the genetic covariance between fitness in females and males, , and is the mean allele frequency at locus a in zygotes. Finally, r and r′ are, respectively, the recombination rates between a and s (the ancestral sex-determination locus) and between a and s′ (the new locus). These and later results based on the QLE approximation are accurate to leading order in the fitness effects (the 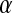) when selection is weak relative to recombination ( 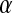≪ r, r′).

This expression verifies the intuition that a feminizing mutation can spread in a population with XY sex determination under the influence of sexually antagonistic selection (Figure 1). Indirect selection on the feminizing W allele results from 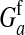, the additive genetic variance for fitness in females at locus a. That force is diminished if 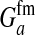, the genetic covariance between male and female fitness, is positive; on the other hand, the force is augmented if the covariance is negative. The strength of indirect selection is modulated by the relative strength of linkage between a and s and between a and s′. The sex-antagonistic locus favors invasion of W if it is more closely linked to the new sex-determination locus s′ than to the ancestral locus s (that is, r′ < r; Figure 2).

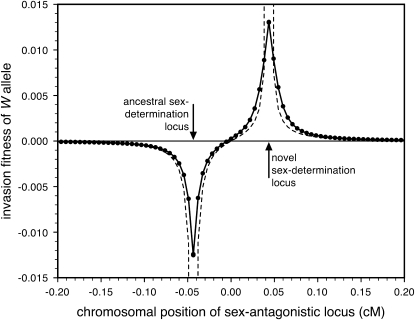
Figure 2.—

Validity of the analytical approximations. A homologous transition is modeled with a fixed distance between the ancestral and novel sex-determining loci (the rate of recombination between these loci is 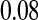), while the position of the sex-antagonistic locus (parameters: 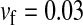, , 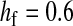, , 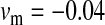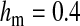and 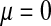) is varied (horizontal axis). The vertical axis gives the invasion fitness of the W allele on the basis of numerical iterations of the exact population-genetic recursions of the model (solid circles), the tight-linkage approximation (solid curve), and the loose-linkage approximation (dashed curve). The latter performs well as long as recombination is a stronger force than selection (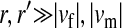), while the tight-linkage approximation is accurate over the entire range of recombination rates (noticeable differences with the simulation results appear only when linkage between the sex-determination loci is very tight). We assumed Haldane's (1919) mapping function.

These models show that a transition in the sex-determination system can occur under conditions that are more general than those typically considered in discussions of sex-antagonistic selection. It suffices for the relative fitness effects of the selected locus to be different in males and females; it is not necessary that the allele favored in males is detrimental to females (or vice versa). The latter condition is more strict; it implies that 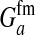has to be negative, whereas indirect selection on the sex-determination locus is already generated if 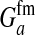is positive but smaller than 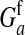. The stricter condition is necessary for selection to maintain polymorphism at the sex-antagonistic locus, but our results apply equally if the polymorphism is maintained by other evolutionary forces or is transient.

In fact, Equation 3 holds irrespective of whether selection, mutation, or a combination of both maintains variation at the sex-antagonistic locus (since for this case μ ≪ r, r′). The loose-linkage result also applies to homologous (e.g., Figure 1) as well as nonhomologous transitions, provided that the sex-antagonistic locus is not tightly linked to either one of the sex-determination loci (Figure 2). Under this condition, the results match with numerical solutions of the exact population genetic recursions for our model, providing confidence in the accuracy of the QLE approximation. The deviation between the loose-linkage prediction and the exact simulations for tightly linked sex-antagonistic loci is explained by the fact that, so far, our methods overestimate the genetic variance at such loci. Alternative sex-antagonistic alleles tend to go to fixation on different types of sex chromosomes if the rate of recombination is low, reducing the average sex-antagonistic genetic variation to less than one would expect on the basis of the average allele frequency. Accounting for this fact (see the results for tight linkage below) provides analytical fitness estimates that match very closely to the exact numerical results (Figures 1C and 2).

The effects of indirect selection generated by different sex-antagonistic loci have additive effects on the evolution at the sex-determining loci (Table S1 and Table S2). A general result for an arbitrary number of sex-antagonistic loci can therefore be obtained by calculating 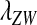for each locus in isolation and then adding together those contributions to find the net exponential rate of increase of the W allele. Sex-antagonistic loci that are linked equally to the old and new sex-determination loci will have no effect (see Equation 3 with ). At the other extreme, sex-antagonistic loci that are tightly linked to s or to s′ have a very strong effect.

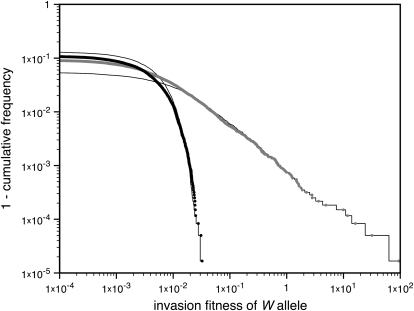
The biological implication is that the few sex-antagonistic genes that are in the immediate vicinity of the sex-determination loci have a deciding impact on the outcome of evolution. Sexually antagonistic polymorphisms tend to accumulate on the sex chromosomes and recombination between the sex chromosome homologs is often reduced (Charlesworth and Charlesworth 1978; Bull 1983; Rice 1984, 1987; Charlesworth 1991). Those factors will tend to stabilize the ancestral sex-determination system. It is possible, however, that a single sex-antagonistic gene linked to a novel sex-determining locus will tip the balance in favor of invasion of the new sex-determination system. Simulations for a large number of random genetic systems with many sex-antagonistic loci do indeed show that only a small subset of the sex-antagonistic genes effectively contribute to heterogamety transitions (Figure 3). Each dot in Figure 3 represents an invasion fitness estimate for a nonhomologous transition with two linkage groups that contain unequal fractions of the total number of sex-antagonistic loci. At the start of each simulation, two-thirds of the sex-antagonistic loci were randomly positioned on the ancestral sex chromosomes; the remaining loci were randomly distributed over the other linkage group with the novel W allele. Only positive invasion fitness values (corresponding to successful invasion of the W allele) are shown. The results for the loose-linkage approximation (Figure 3, shaded dots) emphasize the overwhelming effect of tight linkage on the invasion fitness of the W allele. When the results are corrected for the reduced variance (within sex chromosomes) at sex-antagonistic loci in the vicinity of sex-determination genes (tight-linkage approximation; Figure 3, solid dots), the tail of the distribution of fitness values is truncated at a maximal value that is of the same order of magnitude as the sex-antagonistic selection coefficients. Nevertheless, even with that correction taken into consideration, the fitness contribution of tightly linked loci is orders of magnitude larger than that of loosely linked ones. To illustrate this point, we also calculated for each replicate simulation the fitness contribution of the single sex-antagonistic locus that is most closely linked to a sex-determination gene (shown by solid lines in Figure 3). The close match between the distributions of the total invasion fitness (i.e., the net effect of all loci; Figure 3, dots) and the fitness contribution of the most tightly linked sex-antagonistic locus shows that this single locus has a deciding impact on the evolutionary fate of the W allele, even if the overall distribution of sex-antagonistic fitness variation is concentrated on the ancestral sex chromosomes. Tightly linked combinations of a novel sex-determination factor and a sex-antagonistic gene could, for example, arise when both are captured by an inversion. Such an event would immediately increase linkage between the two and could trigger a heterogamety transition.

Figure 3.—

Heterogamety transitions are governed by a small subset of the sex-antagonistic genes. The invasion fitness of the W allele was calculated for 300,000 random genetic systems, each with 200 sex-antagonistic loci. In each simulation the sex-antagonistic loci were distributed over two linkage groups; two-thirds of the loci were randomly positioned on the ancestral sex chromosomes and the remaining one-third of the loci were randomly positioned on an autosome pair with the novel sex-determination gene. The size of both linkage groups was 100 cM. Despite the twofold bias favoring the ancestral sex-determination system and the large number of loci, we observed positive values of the invasion fitness in ∼10% of the cases. The right tail of the observed distribution of fitness values is shown, with dots indicating invasion fitness estimates from individual simulations (shaded dots, loose-linkage approximation; solid dots, tight-linkage approximation). In both cases, the right-tail behavior is well approximated by the fitness contribution of the single sex-antagonistic locus that is most tightly linked to the novel sex-determination gene (thin solid lines), indicating that the sex-antagonistic variation responsible for transitions between sex-determination systems may segregate at a very small subset of the sex-antagonistic loci. The selection coefficients for individual loci were drawn from a bivariate normal distribution with mean (0, 0) and a covariance matrix with common variance 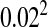and correlation coefficient −0.8. The dominance coefficients were also drawn from a bivariate normal distribution [mean (0.5, 0.5), common variance 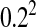, and correlation coefficient 0.7] with the additional constraint 0 ≤ h ≤ 1.

Tight linkage between a and one sex-determining locus:

This section considers the case in which a sex-antagonistic locus a is tightly linked to one of the sex-determination loci. Those loci, in turn, are again assumed to be loosely linked (e.g., on different chromosomes, as in a nonhomologous transition, or far apart on the same chromosome). The starting point for the analysis is Equation 2, which relates the invasion fitness of the W allele to average differences in allele frequencies between different types of gametes. Two separate cases need to be considered, depending on whether the sex-antagonistic allele is tightly linked to the ancestral or to the novel sex-determination locus.

In the case of tight linkage with the novel sex-determination locus s′, there is no difference between the sex-antagonistic allele frequencies in male gametes that carry an x or a y chromosome. This follows from the assumption that the sex-antagonistic locus is on a different linkage group from the ancestral sex-determination factor. Simple population genetic recursions describe the per-generation change of the allele frequencies on the ancestral autosome z, 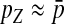, and on the new w chromosome, p_W. The recursions for the frequencies in gametes are given by

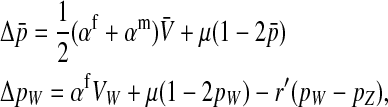(4)

where 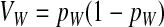is the genetic variation at locus a in gametes that carry the W allele and 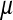is the rate of mutations between sex-antagonistic alleles. (See File S1, which also allows for biased mutation rates.) It is necessary to take mutation into explicit consideration since its effect on gene frequency change can no longer be ignored relative to that of recombination if linkage is very tight.

Combining Equation 2 and the stable equilibrium solutions of the recursions (4) provides the first of two intermediate results for the invasion fitness for nonhomologous transitions:

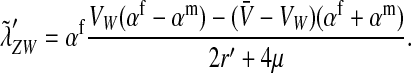(5)

The second intermediate result applies to the case that the sex-antagonistic allele is tightly linked to the ancestral sex-determination locus s. This scenario is slightly more complicated, because tight linkage with the ancestral sex-determination locus can result in significant differences in the frequencies of sex-antagonistic alleles between the x and the y chromosome, which already segregate at high frequencies in the ancestral population. The population genetic recursions for the sex-antagonistic allele frequencies on the x and the y chromosome feature sex-chromosome-specific variances (V_X and V_Y) and effects of allele substitution (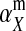 and 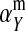in males and 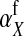in females; Table A1). The recursions are best expressed in terms of the average allele frequency 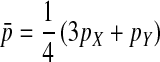and the allele frequency difference in sperm at the sex-antagonistic locus:

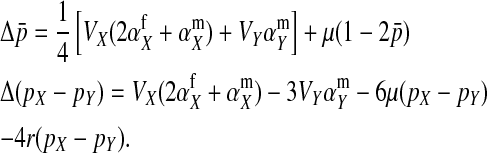(6)

To obtain an expression for the invasion fitness, it is necessary to relate these results to the allele frequencies in eggs (p_Z and p_W) that appear in Equation 2. This is relatively straightforward: mutant females can inherit a y chromosome from their father, which they may then pass on to their female offspring. This occurs with a probability of one-half. It follows that the marginal sex-antagonistic allele frequency in W gametes is given by 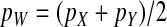. By contrast, female gametes that carry a Z allele must always carry an x chromosome, such that 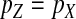. These expressions for p_W and p_Z are substituted into Equation 2 together with the equilibrium solution of the recursion for (Equation 6) to give the second intermediate result,

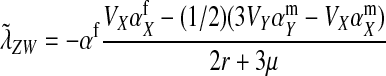(7)

We can combine our results for loose and tight linkage into a single expression. A comparison of Equations 3, 5, and 7 suggests the following linear combination as an expression for the invasion fitness:

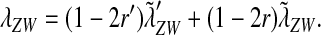(8)

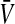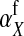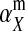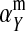Under loose linkage, the sex-chromosome-specific variances V_X, V_Y, and V_W approach the mean variance . Similarly, the effects of allele substitution , , and converge to 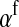and 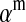. With these substitutions and for 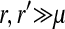, it is easily verified that (8) does indeed converge to the loose-linkage result. Equation 8 matches closely with numerical calculations based on exact population genetic recursions for the full range of recombination rates r and r′ (Figure 2). The accuracy of the predictions of Equation 8 extends to homologous transitions (Figures 1C and 2), except in cases where all three loci are tightly linked together. We separately consider this scenario in the section on homologous transitions below.

Fixation of ZW sex determination:

A successful invasion of the W allele does not necessarily imply that the ancestral XY sex-determination system will be completely replaced by the novel ZW system. In principle, the w chromosome might spread until it reaches an intermediate frequency, establishing a stable polymorphism of sex-determination factors. We can determine if that is possible by asking whether the ancestral x chromosome will increase when it is rare and so produce a protected polymorphism.

To calculate the invasion fitness of the ancestral sex-determination system, it is necessary to specify the sex of individuals that are homozygous for the ancestral Y. We assume that W is epistatically dominant over YY such that the genotype YYZW induces female development. In addition, we assume that YYZZ individuals develop as males. The X allele can be thought of as a feminizing allele that is recessive to W and the ancestral Y allele. These assumptions are motivated by the dominance relations of x, y, and z chromosomes found in fish (Kallman 1984; Ser et al. 2010), amphibians (Ogata et al. 2008), and house flies (Rubini et al. 1972).

We find that the invasion fitness of X is

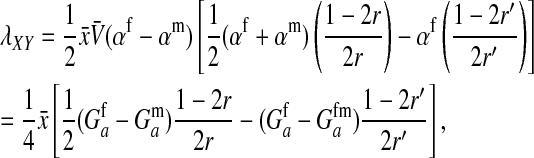(9)

where 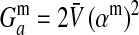is the additive genetic variance at locus a in males. A key difference between this and the previous results is that here the rate of increase of X is proportional to its frequency. Consequently, the force of indirect selection on X becomes vanishingly weak as its frequency declines to zero. That is because X is recessive and so has only a phenotypic effect on sex determination when homozygotes are formed.

A comparison of this result with Equation 3 highlights an asymmetry between the ancestral and the novel sex-determination system. Sex-antagonistic genes linked to sex-determination locus s′ contribute to the loss of the ancestral X allele to the same extent that such genes favor invasion of the W allele. However, sex-antagonistic loci on the ancestral sex chromosomes do not have exactly opposite effects on the invasion of X and W. The recessive X allele attains approximately equal frequencies in males and females when it is rare. Consequently, its invasion fitness depends on X-linked genetic variation in fitness in both males and females. The invasion of the W allele, however, is opposed only by variation in female fitness. This is an important asymmetry, since one would expect the difference in genetic variation in fitness between the sexes to be smaller (perhaps much smaller) than genetic variation in female fitness alone. Theory predicts that selection will nearly deplete genetic variation at loci that are concordantly selected between the two sexes (Fisher 1958), but considerable genetic variance in female fitness can be maintained if there is sex-antagonistic selection (Chippindale et al. 2001; Foerster et al. 2007). However, in that case the genetic covariance in fitness between males and females is negative and fitness variation among males is of a comparable magnitude to variation among females, implying that .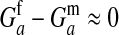

This argument leads to the conclusion that a successful invasion of a dominant feminizing allele must eventually lead to the loss of the ancestral sex-determination system. A rearrangement of the terms in Equation 9 illustrates formally that the W allele will spread to its maximum frequency in female gametes, if it is able to invade. Using Equation 3, we obtain

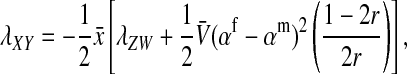(10)

which is negative if 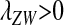. Thus if W invades, it will fully replace the ancestral sex-determination system. A protected polymorphism is not possible with loose linkage.

We can also exclude the possibility of a protected polymorphism when linkage is tight, and the argument is similar: the sex-antagonistic component of fitness variation does not contribute to selection on the X allele when it has become rare, since the allele then spends equal amounts of time in males and females. As a consequence, selection on the ancestral sex-determination system is governed by a small component of additive fitness variation that is not shared between the two sexes.

The conditions for protected polymorphism are less restrictive for sex-determination systems with partial dominance, e.g., male heterogamety with incomplete dominance of the Y allele over X (results not shown), but we are not aware of any biological examples that would motivate a detailed analysis for such cases. The analysis in File S1 could, however, be extended to examine arbitrary types of sex determination. Interestingly, there are conditions in which W cannot invade when rare (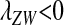), but it will spread if it becomes sufficiently common (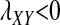). This situation (Figure S1) could lead to the maintenance of different evolutionarily stable sex-determination systems in different populations depending on their evolutionary history, as could result from drift during population bottlenecks.

Deleterious alleles on the ancestral y:

One of the striking general patterns of sex chromosome evolution is that the nonrecombining region of the Y degenerates in species with male heterogamety and well-differentiated sex chromosomes (Charlesworth and Charlesworth 2000). The degeneration of Y chromosomes is thought to result from an accumulation of deleterious recessive mutations in the vicinity of the sex-determining region. We anticipate that these will interfere with heterogamety transitions because females carrying a W allele will produce YY offspring that suffer the deleterious effects of these mutations.

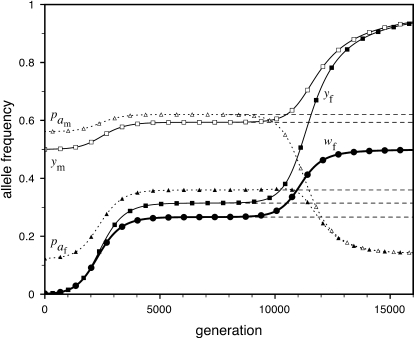
Half of the offspring produced by a W female receive a y chromosome from the father. Under weak sex-antagonistic selection, the ancestral y chromosome will therefore quickly attain a frequency of approximately one-half within the mutant population, such that close to one-quarter of the ZW females will be homozygous for the y chromosome when W first invades. This fraction grows as the W allele increases in frequency. The fitness reduction in the mutant population due to the expression of recessive deleterious alleles is directly proportional to the frequency of YYZW females if the deleterious alleles have become fixed on the y chromosome. This is particularly likely to be the case for deleterious alleles that are expressed only in the homogametic sex. Such alleles can easily become fixed by drift at loci that do not recombine with the ancestral sex-determination locus, since the associated deleterious effects are sheltered from expression in the ancestral population (Muller 1918). In addition, alleles with deleterious effects in the heterogametic sex can accumulate on the nonrecombining region of the y chromosome, under the influence of Muller's ratchet, background selection, and other processes (Charlesworth and Charlesworth 2000). When the novel sex-determination system arises, spread of the W allele causes YY individuals to be generated and these individuals are homozygous for the deleterious recessives. As W becomes more common, the force opposing spread of the W allele increases in proportion to the frequency of YY individuals. By contrast, the strength of sex-antagonistic selection promoting spread of the novel sex-determination locus remains fairly constant. If the two components of selection are of comparable magnitudes, a stable equilibrium between them can be reached at intermediate frequencies of the W and X alleles, such that a protected polymorphism of XY and ZW sex determination is maintained (Figure 4). The polymorphism is lost when genetic variation at the y chromosome is restored. The introduction of a wild-type allele (by mutation or a rare recombination event with the x) allows the y chromosome to be purged from its deleterious alleles as it is being exposed to purifying selection in ZW individuals. Once the y chromosome has lost its deleterious alleles, W can continue to spread, until genetic variation at the ancestral sex-determination locus is lost (Figure 4).

Figure 4.—

Protected polymorphism of two sex-determination factors on different linkage groups. Recessive deleterious alleles on the ancestral y chromosome can prevent the W allele from spreading to fixation, leading to a permanent state of multifactorial sex determination (equilibrium frequencies indicated by the dashed lines) if the deleterious alleles have fixed on the y chromosome and recombination with the x has been fully repressed. Even a tiny amount of recombination (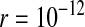 here), however, introduces genetic variation on the y chromosome and purges its deleterious alleles. When this happens, W ultimately fixes and the ancestral XY system is lost. In this simulation, a locus segregating for deleterious alleles (parameters: 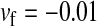, , 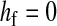, 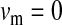and deleterious mutation rate 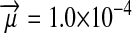; allele frequencies in male and female gametes are shown by dotted lines with open and solid triangles, respectively) is linked to Y and an autosomal sex-antagonistic locus (parameters: 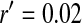, , 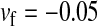, , 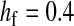, 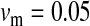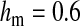and 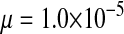; allele frequencies are not shown) is linked to W.

Most of the processes thought to be responsible for Y chromosome degeneration rely on a lack of recombination between the sex chromosomes, but some can also operate in young sex chromosomes that still recombine. Specifically, partially sex-linked alleles with deleterious effects predominantly in the homogametic sex can reach high frequencies on a recombining y chromosome where they are partially sheltered from expression (Muller 1918). The frequencies of deleterious alleles on recombining sex chromosomes depend on a balance of mutation, recombination, and selection in the homo- and heterogametic sex (see File S1). A recessive deleterious allele that is expressed only in females can reach frequency 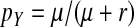on the y chromosome, under the assumption that the rate of deleterious mutations, 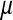is small relative to v, the fitness reduction in homozygous females caused by the deleterious alleles. Under the same condition, the inhibitory effect on the spread of ZW sex determination is given by

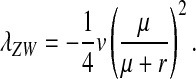(11)

This expression matches our earlier verbal argument: one-quarter of the mutant females are homozygous for Y and a fraction 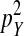of these females are homozygous for the recessive deleterious mutations. These females, finally, suffer a fitness reduction of magnitude v. Equation 11 represents a maximum estimate of the negative effect on the spread of W of recessive y-linked alleles on recombining sex chromosomes. The frequency of deleterious alleles on the y chromosome is < 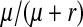if these alleles are also expressed in males, leading to a much weaker force opposing the spread of W (see Figure S2).

In short, deleterious recessive mutations with predominant fitness effects in the homogametic sex can reach higher frequencies on the ancestral y chromosome where they are partially sheltered from expression. A consequence is that they inhibit invasion of a new w chromosome because females that carry it will produce homozygous YY offspring that express the deleterious effects. If the y chromosome carries deleterious recessives at several loci, their effects are (approximately) additive, and together they could generate strong selection favoring the ancestral sex-determining system. This effect can entirely prevent a new w chromosome from invading, or it may slow down the spread of W as the y chromosome increases in frequency. Depending on the relative strengths of selection at work, the W may not be able to increase beyond an intermediate frequency, resulting in a stable polymorphic equilibrium at which the old XY system and the new ZW system are both segregating. Such a polymorphism will, however, typically be vulnerable to the introduction of genetic variation on the y (Figure 4). As the y chromosome is exposed to selection in females, it is purged from the deleterious recessives that have not reached fixation, eventually eroding the force that prevents further spread of the W allele.

Homologous transitions:

Several results for homologous transitions have already been introduced in previous sections. Specifically, if the ancestral and novel sex-determination factors segregate at two recombining loci on the same linkage group, then Equation 8 provides an expression for the invasion fitness of the novel sex-determination allele. This result makes no assumptions on the rates of recombination between sex-antagonistic loci and the ancestral or novel sex-determination locus, but it does assume loose linkage between the two sex-determination loci. A result that allows for tight linkage between the sex-determination loci can be obtained using the techniques presented in File S1, but the expressions are complicated and difficult to interpret in detail. Rather than presenting general results for this scenario, we therefore concentrate on a limiting case that is biologically relevant to homologous transitions involving a mutation at the ancestral sex-determination locus. To examine such transitions we set the rate of recombination between s and s' equal to zero and then compute the frequency of sex-antagonistic alleles in gametes with an x, a y, or a w chromosome.

For feminizing mutations at the ancestral sex-determination locus, invasion fitness is given by

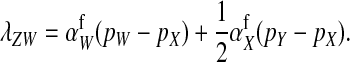(12)

An intuitive explanation of this result is again obtained by comparing mutant females with wild-type XX females. The first difference between the two is that the mutant female may have inherited a y chromosome from her father. This leads to an expected fitness difference of 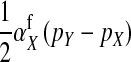, since transmission of the paternal y chromosome occurs in only half of the cases. The second difference is that the mutant female carries a w chromosome, instead of an x chromosome. This results in a fitness effect of magnitude 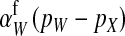, where 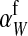is the additive effect of allele substitution for sex-antagonistic alleles on the w chromosome. This coefficient differs slightly from 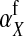due to the dissimilarity between mutant and wild-type females in the paternally inherited part of the genome (Table A1 in the appendix).

As before, a final result is obtained by solving for the sex-antagonistic allele frequencies on the different types of sex chromosomes. The recursions for these frequencies are similar to Equations 6 and 4 (see File S1). If mutation is weak relative to selection and recombination, we find

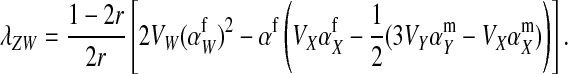(13)

This result is identical to our general result for nonhomologous transitions (Equation 8) in the limit of small mutation rate if 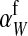is replaced by 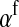, suggesting that the only effect of linkage between the sex-determination factors is that it subtly affects the sex-antagonistic allele frequency on the homolog of the w chromosome.

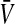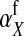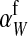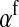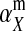If linkage between the sex-determination factor and the sex-antagonistic locus is weak, V_X, V_Y, and V_W approach the mean variance , and converge to , and and 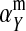converge to 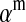. The right-hand side of (13) then evaluates to zero, in accordance with our general result for loose linkage (Equation 3), which also predicts 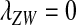for mutations at the ancestral sex-determination locus (this can be seen by substituting ). The conclusion is that a novel feminizing allele at the ancestral sex-determining locus is affected by sex-antagonistic selection only if tightly linked sexually antagonistic variation is available. Whether such variation favors the novel sex-determining allele over the ancestral one depends on the combination of selection and dominance coefficients at nearby sex-antagonistic loci. The W allele can become more strongly associated than the Y allele with sex-antagonistic alleles that are dominant and beneficial to females or recessive and beneficial to males. Such alleles therefore favor the invasion of W, whereas alleles with the other combinations of selection and dominance coefficients oppose its spread (see Figure S3). As for nonhomologous transitions, a protected polymorphism of sex-determination alleles cannot be supported by sex-antagonistic selection alone, although X, Y, and W can be maintained at the ancestral sex-determination locus if the Y carries deleterious alleles.

DISCUSSION

Genetic sex determination in some groups of animals appears to make frequent shifts between male heterogamety (XY) and female heterogamety (ZW) systems (Ezaz et al. 2006). Several mechanisms can cause these transitions, including selection on pleiotropic effects of the sex-determination genes, selection on sex ratio, and meiotic drive. Our results add to this list of possibilities. We find that sexually antagonistic selection on loci linked to the sex-determination genes can trigger a heterogamety transition. Sex-antagonistic selection is thought to be key to the evolution of other aspects of sex chromosomes (Charlesworth 1991), and so it seems plausible that it may commonly be involved in these transitions as well.

The way that sex-antagonistic selection drives a transition can be understood in simple terms. Selection naturally and automatically builds up positive associations (linkage disequilibria) between sex-determination genes that make individuals become male and genes that increase male fitness. Symmetrically, genes that make individuals develop into females become correlated with genes that enhance female fitness. These associations generate indirect fitness effects on the sex-determination genes. The effects increase with the strength of sex-antagonistic selection, the amount of genetic variation at the sex-antagonistic loci, and the strength of linkage between the sex-antagonistic and sex-determination genes. When the combined effects of indirect selection on a new feminizing W allele outweigh that experienced by the Y allele at the ancestral sex-determination locus, the W will invade. This process can operate in two modes: with the invading sex-determining locus on the same linkage group as the ancestral sex chromosomes (a homologous transition, as in X. maculatus) and with it on a different linkage group (a nonhomologous transition, as in cichlids).

The presence of sexually antagonistic genetic variation is a prerequisite for heterogamety transitions in our model. Polymorphism at sex-antagonistic loci can be maintained by constant selection pressures, but only for a restricted range of parameters. The conditions are more stringent for autosomal loci than for sex-linked loci (Rice 1984), and one would therefore predict sexually antagonistic variation to be concentrated on the sex chromosomes (Gibson et al. 2002; Mank 2009; van Doorn 2009). Nevertheless, changes in sex determination do not rely on constant selection to maintain sex-antagonistic variation. Frequency dependence, migration, and mutation can provide variation at autosomal loci and transient polymorphisms are also capable of triggering heterogamety switches. Once a sexually antagonistic allele has become associated with a novel sex-determining allele, even a considerable overall bias in the genomic distribution of sexually antagonistic variation may not be able to prevent a change in sex determination. This is because linkage strongly mediates the strength of indirect selection on a sex-determination locus that results from selection on a sex-antagonistic locus. In quantitative terms, the strength grows as the inverse of the rate of recombination between the two loci, up to a maximum that is set by the strength of sex-antagonistic selection.

As a result, sex-antagonistic loci that are tightly linked to a sex-determination locus can have a vastly stronger influence on the outcome than more distant loci. There are two implications. First, this effect can introduce a strong stochastic component into the determination of which chromosomes decide sex (even if, on average, sex-antagonistic variation is concentrated on the ancestral sex chromosomes). When reduced recombination has not yet evolved at the ancestral sex chromosomes, invasion of a new system can be triggered when a sex-determination mutant happens by chance to arise at locus that is tightly linked to another locus that is under sex-antagonistic selection. Conversely, the effect of tight linkage can stabilize an ancestral sex-determination system. If the ancestral sex chromosomes evolve reduced recombination (Charlesworth and Charlesworth 1978; Rice 1987; Charlesworth 1991), then they can bind sex-antagonistic alleles to the sex-determining region (Rice 1984). That will greatly stabilize the system against the invasion of a new sex-determining region.

This latter effect is one factor that can explain why the sex chromosomes are conserved over long periods of evolutionary time in some taxa, such as mammals. A second one is the accumulation of deleterious recessive mutations on the ancestral y chromosome. Our results show that the deleterious effects are expressed in the offspring of females carrying a new w chromosome, which can inhibit it from invading. A third factor that can stabilize the ancestral sex-determination chromosomes is when they carry genes essential for the development of one sex. For example, if x chromosomes carry a gene essential for female development, then a W allele cannot invade unless that gene is simultaneously duplicated in tight linkage to the new sex-determining region.

Sex-determination alleles at different loci typically show epistatic dominance, in which an allele at one locus determines the phenotype regardless of the genotype at a second (epistatically recessive) locus (e.g., Rubini et al. 1972; Kallman 1984; Ogata et al. 2008; Ser et al. 2010). Our results show that sex-antagonistic selection can cause an epistatically dominant allele to invade, but not an epistatically recessive allele. Thus when W trumps Y, sex antagonism can cause a transition from an XY to a ZW sex-determination system, but not the reverse. The explanation for this asymmetry is simple: if an epistatically recessive Y allele is introduced to a population with ZW sex determination, it will initially appear in XY/ZZ and in XY/ZW genotypes. The first genotype develops as male even without the Y, while the second develops as female despite its Y. Consequently, Y has no phenotypic effect and so cannot build up the associations with sex-antagonistic loci needed to drive a heterogamety transition.

This asymmetry leads to the prediction that the novel sex-determination system is dominant over the ancestral one in taxa that underwent a heterogametic transition (a similar bias would not necessarily be expected if mechanisms other than sex-antagonistic selection would drive the change in sex determination). The appropriate experiments to establish the dominance relationships between sex-determination alleles have been done in fish (Kallman 1984; Ser et al. 2010), house flies (Rubini et al. 1972), and amphibians (Ogata et al. 2008). In all of these cases W is epistatically dominant over Y and the ancestral state is either male heterogamety or unknown. We were unable to find studies that report the dominance relationship between Y and W in species that recently underwent a transition from ZW to XY sex determination. This leaves open the possibility that W sex-determination alleles are dominant over Y alleles irrespective of the ancestral state. If such a bias were indeed present, we would expect it to strongly favor transitions from XY to ZW sex determination over the reverse.

Interestingly, amphibians, the only group for which data are now available, show no evidence of this pattern: Hillis and Green (1990) estimated there have been seven independent shifts from ZW to XY and only one from XY to ZW. They propose a two-locus model of sex determination that makes the origin of a novel XY system more likely than that of a novel ZW system and suggest that it may bias amphibians toward transitions from ZW to XY. As they note, however, since female heterogamety seems to be the ancestral condition in amphibians, the larger number of transitions from ZW to XY could be a simple consequence of more evolutionary opportunity for shifts in that direction. In any event, the overall pattern of transitions in amphibians and other taxa is expected to result from the joint action of biases in the rates of origin of male and female heterogamety and biases in the rates of their fixation caused by sex antagonism.

While species that have XY and ZW sex-determination systems segregating simultaneously are rare, examples are known [e.g., in cichlids (Cnaani et al. 2008) and platyfish (Kallman 1984)]. These might be transient states in which a new system is replacing an ancestral one. Multilocus sex determination can also be stabilized by deleterious recessive alleles linked to the ancestral locus. Consider a species that has XY sex determination and suppose that the Y chromosome has started to degenerate (Charlesworth and Charlesworth 2000). If now a W invades on an autosome, YY/ZW females will be produced, causing a fitness loss from the expression of the deleterious alleles. This can halt the invasion of the W and result in a stable equilibrium with two pairs of sex chromosomes. This outcome occurs only when linkage between the ancestral sex-determination locus and the loci with deleterious alleles is complete. That situation is quite common, however, since recombination between X and Y chromosomes is often reduced or entirely shut down (Rice 1987; Charlesworth 1991). Orzack et al. (1980) found the conditions for maintenance of X, Y, and W at a single group when there is no recombination. Our results complement theirs and show how they extend to the nonhomologous transitions in which the XY and ZW sex-determination systems are segregating at different linkage groups.

We noted in the Introduction that several recently derived sex chromosomes are known with genes that appear to be targets of sex-antagonistic selection (Kallman 1973; Wada et al. 1998; Lande et al. 2001; Lindholm and Breden 2002; Streelman et al. 2003; Fernandez and Morris 2008; Kitano et al. 2009; Roberts et al. 2009). These observations are certainly consistent with the hypothesis that sex-antagonistic selection was responsible for the establishment of a new sex-determining system, but a proper test of our hypothesis would require data to rule out the plausible alternative that the sex-antagonistic alleles accumulated secondarily, after the new sex chromosomes invaded. Indeed, linkage to sex chromosomes is favorable to the maintenance of sex-antagonistic variation (Rice 1987). The required data may soon become available through comparative genomic studies on species that recently underwent a heterogamety transition and their close relatives. The presence of sex-antagonistic variation at the same genomic location in closely related species that have the ancestral sex-determining system would support the view that sex-antagonistic variation predated the origin of the derived sex chromosomes and caused the invasion of a new sex-determination system.

APPENDIX

This appendix develops the recursions for the changes in allele frequencies and associations (linkage disequilibria). Our approach is based on the framework developed by Barton and Turelli (1991) and its generalization by Kirkpatrick et al. (2002). In the following, we use conventions based on the latter and write “KJB (i)” to refer to equation (i) in that article.

To describe the associations between positions, we introduce the indicator variable I. It takes the value 1 for the Y allele at sex-determination locus s, the W allele at sex-determination locus s′, and the 1 allele at the sex-antagonistic locus a. We then define the associations between a set of positions J in zygotes as

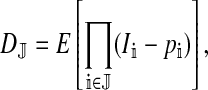(A1)

where the expectation is taken over the distribution of genotype frequencies [see KJB (3)]. The 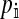that appear in (A1) are reference values that can be chosen arbitrarily, but once chosen, the same values must be used to express associations at later points of the life cycle. To calculate such associations, the expectation in (A1) has to be taken over genotype frequencies at the life history stage under consideration, but the reference values must still be the same as for associations in zygotes.

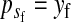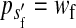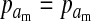We choose the reference values equal to the allele frequencies in gametes at the start of the generation (i.e., , , , , , and finally ), such that the associations in zygotes represent central moments of the distribution of genotype frequencies. Accordingly, D_i = 0 for all positions i at the zygote stage. This leads to another useful fact about associations involving only a single position: at any stage in the life cycle, D_i equals the change in the frequency of allele 1 at position i from the start of the generation to that stage.

As the genotype distribution changes in response to the evolutionary forces that act on it, so will the allele frequencies and associations. Kirkpatrick et al. (2002) provide expressions for these changes. Using those results, we now step through the life cycle to detail how the associations are affected by sex determination, viability selection, and sexual reproduction. Results for the individual steps in the life cycle can then be combined, yielding recurrence relations for the change of associations from one generation to the next.

Sex determination:

At the start of the life cycle, zygotes develop into male or female juveniles. Zygotes with genotype XXZZ develop as females, and those with genotype XYZZ develop as males. A mutant zygote that carries the dominant sex-determination allele W at locus s' develops as a female, regardless of her genotype at the ancestral sex-determination locus s. (The complete epistatic dominance of W over Y assumed here follows the pattern found in the majority of systems that have been studied. The model could be generalized to allow for other schemes, for example, partial penetrance of the sex-determining genes, at the expense of additional parameters.)

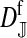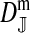Following sex determination, the genetic associations between positions in set J are denoted by and , respectively, for male and female juveniles. Associations for female juveniles are

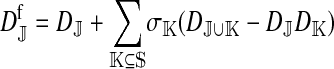(A2)

[see KJB (9)], where denotes the union of the sets J and K [if some positions appear more than once in , then we apply simplification rules for associations with repeated positions; see KJB (5)]. Associations for male juveniles are given by replacing the + by a −. The summation is over all subsets of S, the set of positions that determine sex. The 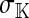are sex-determination coefficients that describe how the set of positions K affects the sex of a zygote. These coefficients are uniquely determined by the effects of the sex-determination alleles and their frequencies in gametes. Their values are calculated in File S1 and their values are shown in Table A1.

Selection:

The sex-antagonistic loci affect the probability that a juvenile survives and mates. The relative fitnesses of genotypes at sex-antagonistic locus i are written 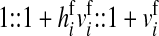, for females with the genotypes 00, 01, and 11, respectively. The corresponding parameters for male viabilities substitute m for f. Throughout, we assume that selection is weak, i.e., that the maximum of the absolute values of v is ≪1.

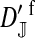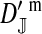Selection acts at the transition between the juvenile and the adult stages. The associations in male and female adults, denoted as and , respectively, are given by

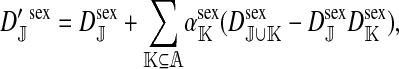(A3)

where sex equals m or f [see KJB (9)]. The summation is over all subsets of A, the set of positions that affect fitness in juveniles. The 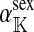are fitness effects that quantify the impact of selection on the set of positions K in the given sex. Their values are determined by the coefficients v and h as well as by the allele frequencies. Table A1 shows the values of the coefficients 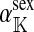as calculated in File S1.

Meiosis:

Gametes result from meiosis, which causes allele frequencies and associations in the gametes to be admixtures of those quantities in the adults. The mixing of genes from different positions complicates the expressions for associations in gametes somewhat, since associations are defined with respect to the allele frequencies at the positions concerned. Accounting for these factors gives an expression for the association in gametes

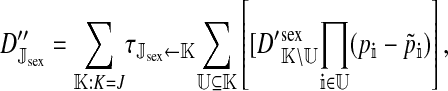(A4)

where sex equals m or f, and J_sex is a set of positions with a single sex-of-origin sex. The first summation is over all positions K from which genes in set J_sex can be inherited by meiosis (the notation 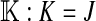means that K and J_sex must be equal when the context information is stripped from them; that is, K and J_sex must contain the same loci). The 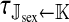are transmission coefficients, defined as the probability that genes in positions J_sex were inherited from genes in positions K. Table A1 gives the values for these coefficients. The second summation adjusts the association 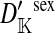for the mixing of genes from different positions [see KJB (16)]. The set K\U represents those positions in K that are not found in U, and the allele frequency is the frequency in zygotes at the position in set J_sex that corresponds to i in set U.

Mutation and completion of the life cycle:

The next generation begins with the fusion of gametes to produce zygotes. The allele frequencies in zygotes, before mutation, are given by

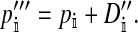(A5)

At the start of the new generation, after mutation has occurred, the allele frequencies are given by

(A6)

where is the mutation rate at position i from allele 0 to 1, and is the reverse mutation rate. Expressions for the associations in the new generation are complicated by the fact that they are defined relative to allele frequencies of the new generation, while the expressions we have derived up to this point are defined with respect to those in the previous generation. The association among a set of positions J_sex that have only the single sex-of-origin sex is

(A7)

[see KJB (15) and KJB (28)]. The resulting associations are defined relative to the postmutation allele frequencies in zygotes.

We assume that mating is random. Consequently, associations in zygotes that involve positions with both sexes-of-origin are equal to a product of associations that involve only positions with a single sex-of-origin. Writing a set of positions in zygotes as 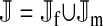, where J_f is the subset of J with the positions that were maternally inherited and J_m is the subset that was paternally inherited,

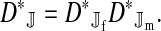(A8)

These equations give an exact set of recursions for how the genetic state of the population changes over the course of a single generation. The analysis presented in File S1 uses these recursions to find when a new w chromosome will invade a population and develops various approximations to the exact solutions.