Association Rule Discovery Has the Ability to Model Complex Genetic Effects

Abstract

Dramatic advances in genotyping technology have established a need for fast, flexible analysis methods for genetic association studies. Common complex diseases, such as Parkinson’s disease or multiple sclerosis, are thought to involve an interplay of multiple genes working either independently or together to influence disease risk. Also, multiple underlying traits, each its own genetic basis may be defined together as a single disease. These effects – trait heterogeneity, locus heterogeneity, and gene-gene interactions (epistasis) – contribute to the complex architecture of common genetic diseases. Association Rule Discovery (ARD) searches for frequent itemsets to identify rule-based patterns in large scale data. In this study, we apply Apriori (an ARD algorithm) to simulated genetic data with varying degrees of complexity. Apriori using information difference to prior as a rule measure shows good power to detect functional effects in simulated cases of simple trait heterogeneity, trait heterogeneity and epistasis, and moderate power in cases of trait heterogeneity and locus heterogeneity. Also, we illustrate that bootstrapping the rule induction process does not considerably improve the power to detect these effects. These results show that ARD is a framework with sufficient flexibility to characterize complex genetic effects.

Introduction

Over the past five years, advances in scientific technology have dramatically increased the rate and quantity of information produced from genetic studies. Like many other disciplines, this change is prompting a shift from traditional data analysis techniques to data mining methodologies. In the field of genetic epidemiology, the goal of an association study is to identify genetic variations that contribute to disease risk. Some platforms for genotyping these variants now produce 300,000 to 500,000 variables for each individual in the study, with 1 million variables possible per individual in the near future.

At the same time, there is a growing belief in the genetics community that the common diseases these platforms were developed to study are very complex, with tens or hundreds of genetic variants working independently or interacting to influence disease risk [1]. Also, complex disease phenotypes may be characterized with insufficient specificity, allowing multiple distinct traits or diseases (each with their own genetic risk factors) to be classified clinically as a single disorder. In this vein, ideal tools for analysis in genetic association studies should not only scale well to the enormous amounts of data being produced, but should also be flexible enough to model the complex genetic effects anticipated to occur in common diseases, such as Parkinson’s disease or multiple sclerosis.

In recent years, a number of computational and statistical techniques have been developed for or applied to the identification of gene-gene interactions, also known as epistasis. Automated Detection of Informative Combined Effects (DICE)[2], Patterning and Recursive Partitioning (PRP)[3], set association[4], penalized logistic regression[5], logic regression[6], and multifactor dimensionality reduction (MDR)[7] have been used to find combinations of genetic variants that influence disease risk. Much less attention has been devoted to methods that can detect trait or locus heterogeneity, where two or more genes independently contribute to disease risk. Current statistical approaches to heterogeneity, such as the admixture test[8], are not very powerful and aim only to identify the existence of heterogeneity rather than characterize it. Bayesian clustering was recently applied to trait heterogeneity with moderate success[9], but this method appears less useful when these traits have increased genetic complexity. True models of common disease risk may involve combinations of trait and locus heterogeneity and epistasis, resulting in a complex genetic architecture. Methods are needed that can address this level of complexity.

Association rule discovery (ARD) was developed to identify patterns in extremely large datasets. In a seminal work, Agrawal et al. presented the apriori algorithm for fast induction of association rules[10]. Apriori searches for frequently occurring variable combinations (called frequent itemsets). There may be many frequent itemsets – many millions or more depending on the dataset size. A minimum support threshold is specified by the user to limit the number of itemsets generated and increase computational efficiency. The support of a rule is the percentage of transactions (or data entries) that the rule can be applied to. Once rules are generated, they are scored by a rule measure, sometimes called rule interestingness. Traditionally, rule confidence is used, which is the number of transactions where the rule is true relative to the number of transactions where it can be applied.

Association rule discovery has been applied to gene expression data, searching for patterns of differential expression across tens of thousands of genes [12, 13, 14]. To the authors’ knowledge however, association rule discovery techniques have not yet been applied to genetic association studies.

ARD is an attractive platform for conducting large scale genetic analysis. The scalability and optimization of ARD algorithms is a well-studied problem in the data mining community[14], and several implementations (including parallel versions) are available. It has yet to be shown, however, if rule discovery methods can identify the complex effects inherent to genetic diseases.

Therefore, the focus of this paper is to test the ability of an association rule discovery method to detect complex genetic effects in simulated data, and to assess rule measures and algorithm considerations as a starting point for further study.

Data Simulations

To characterize the ability of association rule discovery methods to identify complex genetic effects, datasets that contain a known genetic model were needed. As real datasets with well-characterized and replicated complex effects are not available, we simulated data. ARD is most amenable to case-control data, consisting of individuals characterized by discrete genetic variables or loci (typically with three states AA, AB, and BB) and a binary disease status. We simulated a set of functional genetic variables related to disease status through four probabilistic models, defined with increasing degrees of complexity (Fig. 1). 50 non-functional variables were simulated to add random noise typical of real genetic data[9].

Fig. 1.

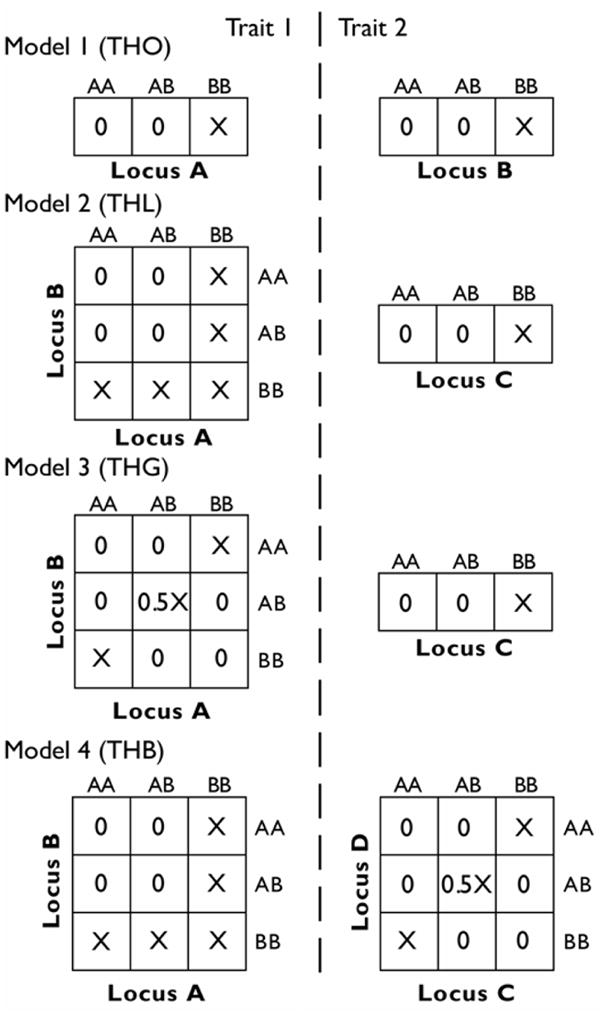
Penetrance tables for simulated genetic models. Cell values indicate the penetrance, or the probability of having the trait, for each genotype combination. The penetrance (X) is constrained by the population prevalence, set to 5%.

Model 1 is simple trait heterogeneity only (THO), where there is one genetic factor for each of the two traits. Each factor acts recessively, so affected individuals have both copies of the high risk allele (BB). For model 2, trait heterogeneity and locus heterogeneity (THL) was simulated for one of the two traits using a recessive model as described by Li and Reich[15]. The other trait has a single recessive genetic factor. Model 3 contains trait heterogeneity and a gene-gene interaction (THG). One trait has a non-linear, non-additive gene-gene interaction model described by Frankel and Schork[16]. The second trait of this model has a single recessive locus. Model 4 contains trait heterogeneity with both a gene-gene interaction and locus heterogeneity (THB). It uses the genetic heterogeneity model for the first trait and the gene-gene interaction model for the second trait (both as described above). For all models, each trait accounts for roughly half of affected individuals. A natural overlap between traits can also occur, with some affected individuals having high-risk consistent with both traits.

All four models simulate a disease with 5% population prevalence, typical of a disease such as prostate cancer[17]. 200 cases and 200 controls were used, a sample size similar to real world association studies. All genetic variables were simulated to have biallelic frequencies of 0.5. 100 datasets, each with different randomly seeded variables, were simulated for each genetic model, creating 400 datasets total. The end result of each data simulation is an input file containing nominally encoded disease status (affected/unaffected), and a set of genotype variables with three nominally encoded states (AA, AB, BB).

Data was simulated using a method developed by Thornton-Wells et al. (refer to figure 10 of [9] for details). Briefly, penetrance functions are translated into two probability arrays – one for unaffecteds containing the joint probability of being unaffected and having the multi-locus genotype, and one for affecteds containing (1- joint probability of being unaffected) and having the multi-locus genotype. Essentially, each affected multi-locus genotype is allotted a space on a number line proportional to its probability. Random uniform numbers between 0 and 1 are generated for each unaffected individual to assign that individual’s multi-locus genotype. The sum of the joint probabilities of being unaffected across all multi-locus genotypes is equal to (1 – P), the population prevalence, in this case set to 5%, and the sum of affected joint probabilities is equal to P. These cell values were then normalized to fall between 0 and 1.

Methods

An implementation of the apriori algorithm[10] by Borgelt and Kruse was used to generate association rules[18]. We chose apriori with the idea that future studies might exploit information about relationships between genetic variables that are independent of disease status. This implementation was chosen because it offers a variety of options for execution, including alternate rule interestingness measures and itemset generation algorithms. Apriori was used with a minimum support threshold from 5 to 30%. Confidence was used for rule ranking at varying thresholds. Information difference to prior (IDP) was also used as a rule ranking measure. IDP was implemented by Borgelt and Kruse and is used by decision tree learners like C4.5 to select split attributes[19]. All itemset generation was performed with a minimum of 2 and a maximum of 3 items per itemset. Unless noted, all implementation defaults were used.

To adjust for potential over-fitting, the rule induction process was bootstrapped to produce a mean rule score. The bootstrap is a re-sampling method used to estimate the standard error of a parameter[20]. It has also been used to provide stability to an induction process through a technique called bagging[21]. Specifically, bootstrapping rule induction may improve rule stability and quality[22]. In this study, bootstrapping was performed using 10 replicates.

Thousands of rules were produced for some configurations of apriori. To reduce the number of rules to an interpretable set, we reduce the ruleset to rules containing disease status and used rule ranking to select the top rule or top 5 rules. Rules were ranked by either the rule measure or bootstrap estimates thereof.

Performance was assessed in several ways. For this study, power is defined as the number of times a variable was identified as functional out of 100 datasets. The false positive rate is the proportion of non-functional variables to the total number of variables averaged over all datasets. A false positive rate of 25% means on average one of four variables in the reduced ruleset is spurious. The number of functional variables identified by each ruleset was recorded also. An ideal method, for example, would identify all four variables in the THB model, but some rulesets may identify three, two, one, or none of the functional variables.

Results

Rule Induction

We began analyzing the simulated datasets using default support and confidence thresholds (>10% support, >80% confidence) (Table 1A). Keeping the highest ranked rule only, functional variables from model 1 (THO) had 100% power, and in model 3 (THG), variables involved in the gene-gene interaction had 95% power. Model 4 (THB) showed very poor performance, with two interacting variables around 30% power, and model 2 (THL) detected almost no functional variables. Using the top 5 rules did not change the power results appreciably.

TABLE 1.

Apriori Results

Each evaluation was performed on 100 datasets of each genetic model (THB, THG, THL, and THO), keeping the best rule only or the top 5 rules in the ruleset. For each set of 100 datasets, the frequency of observing 0, 1, 2, 3, and 4 functional variables per ruleset was recorded. The frequency of detecting each individual locus A, B, C, and D is also listed as power by variables. FPR is the false positive rate, defined as the proportion of non-functional variables to total variables. Blank cells indicate a frequency is not applicable, for example the THO model contains only two functional variables A and B, so no more than 2 functional variables will ever be observed, and variables C and D are not included. Evaluations A and B use confidence as a rule metric. All others use IDP. Support and confidence cutoffs are denoted with S and C, and the use of bootstrapping is also noted.

A
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
S10 C80	Best Rule	THB	68	0	32	0	0	0	0	32	32	0.11
		THG	5	0	94	1		95	95	1		0.01
		THL	95	3	2	0		2	1	4		0.16
		THO	0	0	100			100	100			0.01
	Top 5	THB	68	0	32	0	0	0	0	32	32	0.12
		THG	4	0	95	1		96	96	1		0.08
		THL	96	2	2	0		2	1	3		0.15
		THO	0	0	100			100	100			0.23

B
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
S10 C50	Best Rule	THB	31	3	66	0	0	0	1	66	68	0.32
		THG	32	68	0	0		0	0	68		0.32
		THL	3	97	0	0		18	14	65		0.04
		THO	0	100	0			50	50			0.01
	Top 5	THB	2	2	86	10	0	4	7	69	97	0.72
		THG	22	72	6	0		8	3	73		0.81
		THL	1	22	48	29		61	61	83		0.50
		THO	0	4	96			99	97			0.45

C
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
IDP S5 C5	Best Rule	THB	0	1	99	0	0	1	2	98	98	0.00
		THG	0	0	99	1		100	100	1		0.00
		THL	1	47	52	0		52	50	49		0.01
		THO	0	5	95			98	97			0.00
	Top 5	THB	0	0	90	4	6	11	9	98	98	0.01
		THG	0	0	94	6		100	100	6		0.00
		THL	1	6	42	51		81	84	78		0.23
		THO	0	0	100			100	100			0.05

D
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
B-strap IDP S5 C5	Best Rule	THB	0	1	98	1	0	3	3	97	97	0.01
		THG	0	0	99	1		100	100	1		0.01
		THL	0	60	39	1		39	47	55		0.02
		THO	0	4	96			98	98			0.01
	Top 5	THB	0	0	83	5	12	15	16	99	99	0.02
		THG	0	0	86	14		100	100	14		0.00
		THL	0	4	38	58		84	89	81		0.22
		THO	0	0	100			100	100			0.02

E
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
IDP S10 C5	Best Rule	THB	1	1	98	0	0	1	2	97	97	0.00
		THG	0	0	100	0		100	100	0		0.00
		THL	2	47	51	0		51	49	49		0.01
		THO	0	6	94			97	97			0.01
	Top 5	THB	0	0	90	4	6	11	9	98	93	0.01
		THG	0	0	93	7		100	100	7		0.00
		THL	2	7	42	49		79	82	77		0.24
		THO	0	0	100			100	100			0.10

F
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
B-strap IDP S10 C5	Best Rule	THB	1	1	98	0	0	2	3	96	96	0.00
		THG	0	1	99	0		99	99	1		0.00
		THL	0	60	40	0		39	46	55		0.02
		THO	0	0	100			100	100			0.02
	Top 5	THB	0	0	83	5	12	15	16	99	99	0.02
		THG	0	0	85	15		100	100	15		0.00
		THL	0	4	38	58	0	84	88	82		0.23
		THO	0	0	100			100	100			0.04

G
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
IDP S20 C5	Best Rule	THB	6	2	92	0	0	3	3	90	90	0.00
		THG	0	1	99	0		99	99	1		0.00
		THL	9	73	17	1		25	28	57		0.05
		THO	0	100	0			53	47			0.01
	Top 5	THB	5	1	79	8	7	16	11	92	92	0.02
		THG	0	0	39	61		100	100	61		0.08
		THL	9	40	29	22		45	45	74		0.35
		THO	0	0	100			100	100			0.05

H
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
B-strap IDP S20 C5	Best Rule	THB	1	6	93	0	0	7	9	88	88	0.01
		THG	0	11	89	0		89	89	11		0.01
		THL	0	95	4	1		19	24	63		0.03
		THO	0	100	0			56	44			0.01
	Top 5	THB	0	2	29	46	23	45	49	98	98	0.24
		THG	0	0	20	80		100	100	80		0.09
		THL	0	20	56	24		65	57	82		0.41
		THO	0	11	89			97	92			0.26

I
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
IDP S30 C5	Best Rule	THB	93	7	0	0	0	4	3	0	0	0.00
		THG	44	56	0	0		0	0	56		0.00
		THL	13	87	0			12	15	60		0.00
		THO	0	100	0			54	46			0.00
	Top 5	THB	93	7	0	0	0	4	3	0	0	0.00
		THG	43	57	0	0		0	0	57		0.01
		THL	13	55	32			26	22	71		0.02
		THO	0	2	98			100	98			0.05

J
			# Functional Variables					Power by Variables
			0	1	2	3	4	A	B	C	D	FPR
B-strap IDP S30 C5	Best Rule	THB	24	52	24	0	0	22	30	24	24	0.24
		THG	6	79	15	0		15	15	79		0.05
		THL	0	100	0	0		17	20	63		0.01
		THO	0	99	1			97	92			0.26
	Top 5	THB	16	33	25	24	2	38	48	39	38	0.52
		THG	3	57	9	31		37	37	94		0.49
		THL	0	9	69	22		58	62	93		0.20
		THO	0	1	99			100	99			0.03

Next, we tried lowering thresholds (Table 1B). Changing the confidence threshold to >50% improved the power of all models except model 1 (THO). The power for model 1 recovered and power improved significantly for other models when keeping the top 5 rules.

The false positive rate for confidence-based ranking was rather high, especially when using the top five rules. The method did not consistently report a functional variable in the best rule, and seemed to promote noise variables into the top five rules. To help alleviate this problem, we evaluated other rule measures.

After testing on a subset of models (data not shown), the most promising measure for rule ranking in the Borgelt implementation of apriori was information difference to prior (IDP)[19]. The minimum cutoff for this statistic was set arbitrarily to 5 for all analyses to reduce the number of rules reported to a manageable number.

Using this measure, apriori is still dependent on support and confidence thresholds for itemset generation. To establish a baseline level of performance, we used extremely low cutoffs for support (>5%) and confidence (>5%) to evaluate the ranking ability of the IDP measure (Table 1C). Compared to confidence ranking, the power generally improved and more functional variables from model 2 (THL) were identified, using the best rule. The interacting variables were identified for model 3 (THG) (100% of datasets) and model 4 (THB) (98% of datasets). Also, for model 2 (THL), each of the 3 functional variables were identified with equal frequency (50%), with only one variable identified in 47% of datasets and two variables identified in 52%. Using the top 5 rules, power improved for model 2 (THL), with all three variables identified in 51% of the datasets. The overall increase in power was accompanied by a decrease in false positive rate. Power improvement for other models was marginal. A functional variable was included in the top rule consistently, and using the top five rules increased power without a dramatic increase in false positive rate (model 2 was an exception, increasing to 23% false positive rate). Information difference to prior seems to rank rules better than confidence.

Given that IDP showed improved power, we were curious how sensitive the power results were to different support thresholds (Table 1E, 1G, 1I). Using a higher support threshold of >10%, no appreciable power reduction was noted. At >20%, power for model 3 (THG) was unaffected, and there was a slight reduction in power for model 4 (THB). Model 1 (THO) showed dramatic power loss, with only one of the two variables identified, each at about equal frequency. Model 2 (THL) also had a power reduction, with only 18% of datasets reporting two or more of the functional variables. Increasing the rules kept to the top 5 improved power for all models. At >30%, there was a greater power loss for all models, almost completely for model 4 (THB). Using the top 5 rules recovers power completely for model 1 (THO) and marginally for model 2 (THL), but has no effect for models 3 and 4.

Bootstrapping

The rules discovered for the more complex models (3 and 4) tend to focus on one trait of the model, and show very little power to find the other trait. Also, rules for model 2 do not consistently find all 3 variables. We thought that instability in the induction process or inconsistency in scoring and ranking rules could influence our ability to detect these variables. To correct these issues, we applied a simple bootstrapping procedure (Table 1D, 1F, 1H, 1J).

Using 10 bootstrap replicates with a baseline support threshold (>5%), the power did not improve selecting either the top rule or the top 5 rules (based on bootstrap estimates of IDP), respectively. Increasing bootstrap replicates to 100 also did not improve power at this threshold (data not shown). Continuing with 10 bootstrap replicates, we evaluated the other three support thresholds, >10%, >20%, and >30%. For 10%, bootstrapping made no discernable improvement over a standard analysis with equivalent thresholds. At 20%, power improved for some effects when keeping the top 5 rules. For the 30% cutoff however, there was a general improvement over standard in models 3 (THG) and 4 (THB), power for model 2 (THL) improved slightly, and power for model 1 (THO) was largely unchanged. Most notably, using the single best rule, all functional variables were identified in at least 15% of the datasets. The false positive rate for model 4 (THB) increased noticeably as well, however. Increasing the number of bootstrap replicates to 100 slightly drops the false positive rate in both the top rule and top 5 rule sets, but does not impact power (data not shown).

Rule Quality

The generated rules are readily interpretable, in that each rule designates a single cell of a multi-locus penetrance table. For model 1 (THO), the most common top rule illustrates that affected individuals who are heterozygous at one locus are very likely to be recessive at the other locus. The top five rules contain variations of this idea, but occasionally include noise variables. For model 2 (THL), a similar pattern is observed between the two variables with locus heterogeneity. The recessive allele for the other trait is usually identified alone as being related to disease. Rules generated for model 3 (THG) capture the interaction effect, with the best rule typically describing how affected individuals with an AA for one locus have BB for the other. The other trait is occasionally identified as recessive. For model 4 (THB), the interaction effects are detected as in model 3, and occasionally the locus heterogeneity is detected as in model 2.

Discussion

Rule Measures

Rule confidence shows appreciable power to highly rank rules including functional variables for the case of simple heterogeneity (model 1) and gene-gene interaction effects (model 3). The IDP measure maintains the detection ability of confidence and greatly improves power to detect the remaining functional variables. In this regard, information difference to prior is a superior measure for rule ranking. Increasing the minimal support threshold from 5% to 10% had a negligible impact on power using IDP as a rule measure.

Increasing to 20% diminished power to detect heterogeneity effects in models 1 and 2, but interaction effects maintained high power. Increasing the threshold to 30% abolished power to detect the interaction effects in models 3 and 4, and further reduced power to detect heterogeneity effects. This illustrates the minimum support levels may be needed to capture specific effects in the data.

Bootstrapping

Bootstrapping rule induction surprisingly had little effect in most cases. When the support threshold is set to a low level (5–20%), bootstrapping does not improve power or reduce false positive rates. In some cases, it increased the appearance of spurious variables in the rule set. At 30% minimum support however, bootstrapping improves power broadly, fostering detection (at some level) of all functional variables in each dataset. In this circumstance, bootstrapping appears to help move weaker true signals higher in the rule ranking so they are more likely to be detected. The false positive rate also increased as noisy rules or rules containing one functional and one noise variable were promoted in some datasets. Here, increasing the number of bootstrap replicates from 10 to 100 helps to reduce these spurious results.

It is interesting to note that while the bootstrap does not improve power at low support thresholds, it can improve power at higher levels. This poses an interesting computational question; is there an efficiency benefit to bootstrapping rule induction at higher support thresholds versus general induction at lower thresholds? While the results of this study indicate that bootstrapping does not completely recover power, other parameterizations may prove otherwise. Further study is needed to fully determine the utility of bootstrapping in this area.

Application

In general, association rule discovery works well for the complex genetic models simulated (Fig. 2). Using a single best rule essentially identifies a single highly penetrant allele combination. Using the top five rules allows multiple penetrant allele combinations to be highlighted. These may be contained to a single locus or may include multiple influential loci. In general, a high ranking subset does not include additional spurious variables. Keeping a larger number of rules, however likely increases the number of noisy rules taken as true results. Ideally, a rule measure cutoff would be established rather than selecting top ranked rules. Identifying this cutoff is non-trivial, however, as rule measure values are data dependent. The threshold required for adequate power in one dataset would be different for another dataset. Assigning statistical significance to a rule poses similar problems. Permutation testing could provide p-values for a set of rules, and bootstrapping may also prove useful here, helping to normalize data specific effects so that a defined cutoff is useful. These approaches may prove computationally prohibitive for larger datasets.

Fig. 2.

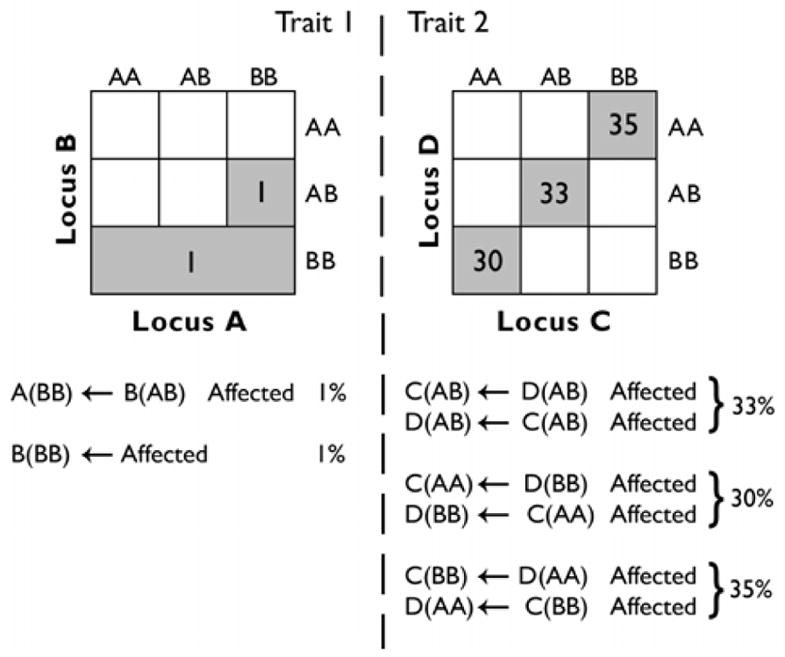
Best rules generated over 100 THB datasets using IDP with minimal confidence and support > 5% (evaluation C). Using the best rule from each apriori run consistently finds functional variable combinations

Another option for reducing rule noise is to parse the rule list to identify similar rules. Numerous rule comparison measures are available[23] which could help eliminate rules containing one functional and one spurious variable. Also, including rules that do not relate to disease status may be useful in this regard, especially in the case of gene-gene interactions. Variables that are related independent of disease status may generate high ranking rules that help confirm another effect. This approach would also come at the cost of some increase in noise, however.

While these results are promising, it is important to recognize the limitations of this study design. Real data from genetic studies can be characterized by several issues that are not addressed in our simulated data. Missing data, correlations between variables (called linkage disequilibrium), variable allele frequencies, and small sample sizes are all potential limitations. Also, the number of variables simulated in this study was small compared to the numbers possible in a large scale genetic study. Nevertheless, it is important to demonstrate that this method has utility in smaller scale studies, as techniques for characterizing the complex effects simulated are scarce.

Conclusion

This preliminary study demonstrates that association rule discovery using the apriori algorithm is an effective method for identifying variables involved in trait heterogeneity, locus heterogeneity, and gene-gene interactions, and shows moderate success with complex combinations of these effects. To date, there are very few approaches in the genetics community that can discover genetic effects with this degree of complexity. We also highlight that bootstrapping the rule induction process may not improve the stability of rule ranking with low support thresholds, but may have utility in cases where computational limitations prevent itemset generation with very low support.