Translational benchmark risk analysis

Abstract

Translational development – in the sense of translating a mature methodology from one area of application to another, evolving area – is discussed for the use of benchmark doses in quantitative risk assessment. Illustrations are presented with traditional applications of the benchmark paradigm in biology and toxicology, and also with risk endpoints that differ from traditional toxicological archetypes. It is seen that the benchmark approach can apply to a diverse spectrum of risk management settings. This suggests a promising future for this important risk-analytic tool. Extensions of the method to a wider variety of applications represent a significant opportunity for enhancing environmental, biomedical, industrial, and socio-economic risk assessments.

1. Introduction

Developed in the mid-1980s – but with roots going back much farther and deeper –benchmark analysis for estimating exposure risks to hazardous agents has become a widely accepted technology in quantitative risk assessment. As described by Crump (1984), the method relates an adverse outcome to a quantified dose or exposure, d ≥ 0, of a hazardous agent via some functional model. It then manipulates components of this model to yield a benchmark dose (BMD) of the agent at which a specified benchmark risk or benchmark response (BMR) is attained. If the exposure is measured as a concentration, one refers to the exposure point as a benchmark concentration (BMC). The BMD or BMC is used to arrive at a level of acceptable human or ecological exposure to the agent or to otherwise establish low-exposure guidelines. Risk analysts increasingly use benchmark quantities as the basis for setting occupational exposure limits (OELs) or other ‘points of departure’ when assessing hazardous stimuli/exposures (Kodell 2005; Kobayashi et al. 2006; Nielsen and Øvrebø 2008). Indeed, both the USA and the Organisation for Economic Cooperation and Development (OECD) provide guidance on BMDs in carcinogen risk assessment (US EPA 2005; OECD 2008), and the use of BMDs or BMCs is growing for quantifying and managing risk with a variety of toxicological endpoints (US General Accounting Office 2001; European Union 2003; OECD 2006). One critical modification is the use of statistical lower confidence limits on the BMD – called benchmark dose (lower) limits or simply BMDLs (Crump 1995) – in order to account for statistical variability of the BMD point estimate.

The benchmark paradigm integrates mathematical modeling into the low-dose risk-assessment process, moving away from the so-called no-observed-adverse-effect level (NOAEL) technologies for estimating low exposure doses. (The NOAEL is an older method for estimating virtually safe/low-dose exposure levels, and substantial statistical instabilities have been identified with its use. Most contemporary analysts now recommend against this dated technology [Chapman, Caldwell, and Chapman 1996; Crump 2002a; Kodell 2009].) Critical to the calculation of a BMD is the construction of a mathematical risk function, R(d), to describe how risk changes with increasing levels of dose. In many public health and environmental scenarios, R(d) is further refined into a form of excess risk, such as the additional risk R_A(d) = R(d) − R(0) or the extra risk R_E(d) = R_A(d)/{1 − R(0)}. This adjusts for background or spontaneous effects out of the control of the risk regulator (Piegorsch and Bailer 2005, §4.2). Either form may be seen in practice, depending on context.

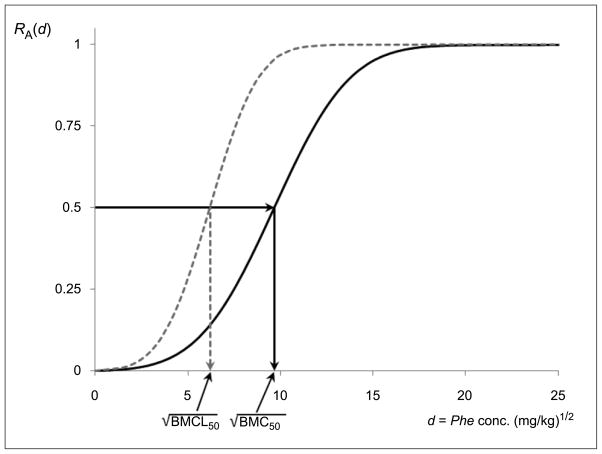
Under this mathematical modeling approach, the BMD is determined by setting R(d), R_A(d), or R_E(d), as appropriate, equal to the BMR and solving for d. Statistically, this is a form of inverse nonlinear regression, similar to the estimation of an ‘effective dose’ such as the familiar median effective dose, ED₅₀, in toxicity testing (Piegorsch and Bailer 2005, §4.1). Taken from the unit interval, the BMR is specified in advance of any data acquisition. Calculation of the BMDL can proceed similarly, using, e.g., an upper confidence band on the risk or excess risk from which to base the statistical inversion on to the dose scale (Al-Saidy et al. 2003). Figure 1 from Example 2 illustrates the operations graphically.

Figure 1.

${\text{BMC}}_{50}^{1/2}$ and 95% ${\text{BMCL}}_{50}^{1/2}$ (at BMR = 0.50) for the soil ecotoxicity data.

Note: Dark curve is estimated additional risk function R̂_A(d); dashed curve is 95% upper confidence band on the extra risk; cf. Appendix 2.

The model construction also requires specification of the data’s statistical features, which depends on their basic form, e.g., proportions versus continuous measurements. While this is a necessary and critical step in the modeling process, the benchmark paradigm’s oft-unrecognized value is its applicability to a variety of statistical models. The method can be applied to any form of outcome and/or dose–response model from which a valid risk function can be defined, estimated from the data, and inverted to calculate BMDs and BMDLs. The goal herein is to highlight the flexibility available under the benchmark approach and illustrate its widening application. It is not intended as a comprehensive review, however, since a number of excellent examples for such already exist (Crump 2002a; Falk Filipsson et al. 2003; Parham and Portier 2005; Sand, Victorin, and Falk Filipsson 2008). Nonetheless, by exploring different forms in which the benchmark paradigm can be applied, readers may discover new and effectual ways to choreograph benchmark analyses for use in quantitative risk assessments.

2. Traditional benchmark analysis with quantal data

The benchmark method is often employed with data in the form of proportions. Therein, the numerators are taken as binomial variates Y_i ~ Bin(N_i, R[d_i]) at each exposure or dose index i, where the proportion denominator N_i is the number of subjects tested, and R(d_i) is used to model the unknown probability that an individual subject will respond at dose d_i ≥ 0; i = 1, …, n. This is called the quantal response data setting in dose–response analysis. For such cases, the excess risk function is usually taken to be the extra risk R_E(d) = {R(d) − R(0)}/{1 − R(0)}.

Typically, R(d) is assigned a parametric specification, e.g., the ubiquitous logistic dose–response model R(d) = 1/(1 + exp{−β₀ − β₁d}), or the similar probit model R(d) = Φ(β₀ + β₁d), where Φ(·) is the standard normal cumulative distribution function. The unknown β-parameters are estimated from the data; maximum likelihood is a favored estimation approach (Piegorsch and Bailer 2005, §A.4.3). The maximum likelihood estimate (MLE) for the BMD is found by setting the estimated extra risk function, R̂_E (d), equal to the chosen BMR and solving for d. Denote this as BM̂D. Where needed for clarity, the notation imitates the well-known ED₅₀ and subscripts the BMR level at which each quantity is calculated: BMD_100BMR, BM̂D_100BMR, etc.

Corresponding BMDL(s) are determined using the statistical properties of BM̂D; this can involve simple, one-sided Wald confidence limits employing the large-sample characteristics of the MLE, bootstrap confidence bounds, or inversion of simultaneous confidence bands on R_E(d) (cf. Crump and Howe 1985 or Moerbeek, Piersma, and Slob 2004, among many others). In the latter case, the BMDLs inherit the simultaneous confidence features of the bands and can therefore be applied when multiple BMRs are under study (Al-Saidy et al. 2003); see Example 3.

The earliest uses of BMDs and BMDLs for studying low-dose risk with quantal data occurred with laboratory animal toxicity experiments. For example, Crump’s original 1984 article described a variety of toxicological applications, involving outcomes such as bacteriological toxicity, developmental anomalies, and in utero mortality. Since then, the approach has been applied to many other adverse quantal endpoints, including the important area of mammalian carcinogenesis (Van Landingham et al. 2001; Butterworth, Aylward, and Hays 2007). To illustrate using a contemporary dataset, consider the following example.

2.1. Example 1. Kidney carcinogenesis

The chemical 3-monochloropropane-1,2-diol (3-MCPD) is a contaminant by-product in a variety of foodstuffs, including soy sauces, processed sausages, and breakfast cereals; it can also appear in drinking water after certain types of water treatment. Unfortunately, the chemical is a mammalian nephrotoxin, and ingestion of the agent via such a variety of food and drinking water sources can lead to low-level, chronic population exposures. From a risk-analytic perspective, clearer quantification is required of its potential for producing long-term kidney damage and/or cancer. Towards this end, data were recorded on numbers of female laboratory rats developing renal tumors (adenomas and carcinomas) after exposure to 3-MCPD at a series of increasing doses (reported as mg/kg body weight) in drinking water. Table 1 presents the quantal data, taken from Hwang et al. (2009).

Table 1.

Kidney adenomas and carcinomas in female laboratory rats after exposure to the food/water contaminant 3-MCPD.

Dose, d (mg/kg)	Number with cancer, Y	Number exposed, N
0	1	50
2.68	0	50
10.34	2	50
37.03	9	50

Note: Kidney carcinogenesis data from Hwang et al. (2009).

To fit the dose–response data in Table 1, Hwang et al. (2009) chose a probit model, which produced a reasonable fit. The corresponding MLEs for the data in Table 1 yield an estimated risk function of R̂(d) = Φ(−2.252 + 0.036d). Converting to extra risk and setting BMR to, say, 0.10 – a standard level in toxicology testing – gives BM̂D₁₀ = 28.391 mg/kg. A 95% Wald lower confidence limit is BMDL₁₀ = 21.305 mg/kg. (Particulars for the BMDL calculation are detailed in Appendix 1.) Risk regulators can use these values to determine acceptable exposure limits for ingestion of 3-MCPD in any food/drinking water sources contaminated by the chemical.

It is important to note that Hwang et al. (2009) also considered a variety of other dose–response models for their data, many of which operated about as adequately as the probit model featured here. Still, cases can occur where different dose–response models fit a set of quantal data with essentially equivalent quality over the range of observed responses, but may produce substantively different BMDL(s) at very small BMR(s) (Allen et al. 1994; Faustman and Bartell 1997). Contemporary analysts caution against such extreme low-risk/low-dose extrapolations, and often choose BMR(s) in a range that meets or proximates the corresponding lower response rates in the data. In practice, levels of BMR at or between 0.01 and 0.10 are typical (US EPA 2000, §II.B; Kodell 2005). The larger issue of how to adjust or correct for problems of model selection bias/adequacy when the correct form for R(d) is unknown remains an area of active research. Recent work in this direction has led to some intriguing advances, including manipulation of information measures, such as the Akaike Information Criterion (Sand, Falk Filipsson, and Victorin 2002; Moon et al. 2005), and averaging techniques, such as Bayesian model averaging (Bailer, Noble, and Wheeler 2005; Morales et al. 2006), or its frequentist (non-Bayesian) analogs (Faes et al. 2007; Wheeler and Bailer 2007). Much of this research is still emergent, however, and the statistical science underlying this avenue of BMD estimation remains open for further development.

Increasingly, BMDs are called upon as starting points for toxicological and biomedical risk assessments across a wide variety of endpoints, carcinogenic or otherwise (Gaylor et al. 1999; Kodell 2005). Successful applications with quantal data include adverse developmental endpoints (Krewski, Zhu, and Fung 1999; Zhu, Wang, and Jelsovsky 2007), genetic toxicity (Allen et al. 2005), inhalation toxicity (Fowles, Alexeeff, and Dodge 1999; Gift et al. 2008), and extensions to human epidemiological studies (Yeh, Lee, and Chen 2006). In all the cases, the risk-analytic context may change with the differing endpoint(s), but the fundamentals of the benchmark concept remain essentially unchanged.

3. Benchmark analysis with nonquantal data

In his seminal article, Crump (1984) also described how the BMD could be constructed with nonquantal data, i.e., data not in the form of a proportion Y/N. In this case, a variety of possible outcomes becomes possible, corresponding to many discrete and continuous statistical distributions (See and Bailer 1998; Banga, Patil, and Taillie 2002; Morales and Ryan 2005). Most common in mammalian toxicological studies is the normal or ‘Gaussian’ distribution; traditional endpoints, such as weight change and hematological measurements (Slob 2002; Piegorsch et al. 2005b), developmental damage (Razzaghi and Kodell 2004), and neurological outcomes (Kodell, Chen, and Gaylor 1995) often generate normally distributed data, either directly or after logarithmic transformation. Within this context, assume the nonquantal data under study are normal with Y_i ~ N(μ[d_i], σ²) at each exposure, concentration, or dose index i, where the mean response varies over dose d_i and the variances σ² are homogenous but unknown; i = 1, …, n. Extensions for heterogeneous variances are also possible (cf. West and Kodell 1993).

Different dose–response models can be chosen to represent μ(d), depending on the endpoint under study; most common is the linear form μ(d) = β₀ + β₁d, or possibly curvilinear extensions such as the parabola μ(d) = β₀ + β₁d + β₂d² or the general power model μ(d) = β₀ + β₁d^k. Modifications that allow for possible threshold effects are easily incorporated into these constructions (Crump 1984).

The use of normal distributions and linear dose–response functions leads to questions on how to define the BMD (Crump 2002b). A formal conceptualization of exposure risk with nonquantal data was given by Gaylor and Slikker (1990) by focusing on the difference between response at exposure dose d and response at the background level d = 0. Often called the ‘hybrid’ benchmark concept, Kodell and West (1993) expanded on this and defined the risk function as:

$$\text{R}(d)=\text{P}[\text{Y}\le \mu (0)-\kappa \sigma ]$$

where κ > 0 is a constant used to tune R(d) for specific applications. In this form, a response more than κ standard deviations below the control mean is considered adverse. Suggested values include κ = 2 or κ = 3. (This formulation assumes that increasing exposure leads to decreases in the response. The risk function is easily modified if the reverse is true.) The fundamental viewpoint embodied in Equation (1) is that BMDs or BMCs for continuous responses should be defined on a probability footing, in similar fashion as that taken with quantal data.

The Kodell–West definition of risk in Equation (1) is often employed in conjunction with an additional risk function, R_A(d) = R(d) − R(0). Under the assumption Y_i ~ N(μ[d_i], σ²) and taking, say, a simple linear response function, μ(d_i) = β₀ + β₁d_i, the additional risk becomes R_A(d) = Φ(−γ₁d − κ) − Φ(−κ), where γ₁ = β₁/σ. If the mean response is quadratic, μ(d_i) = β₀ + β₁d_i + β₂d_i², the additional risk extends to R_A(d) = Φ(−γ₁d − γ₂d² − κ) − Φ(−κ), where γ_j = β_j/σ (j = 1, 2).

To estimate the BMD for any given BMR, set R̂_A(d) = BMR and solve for d. For the linear model with μ(d) = β₀ + β₁d, this yields BM̂D_100BMR = −C_BMR/g₁, where g₁ is an unbiased estimate of γ₁ and C_BMR = κ + Φ⁻¹{BMR + Φ(−κ)} (Piegorsch et al. 2005b). Corresponding BMDLs can be constructed using methods similar to those employed for quantal data; see Appendix 2 for technical details. Extensions to the quadratic case are also possible (Piegorsch et al. 2005a).

The next example illustrates this approach. To emphasize the translational potential of the benchmark paradigm, however, it employs data that differ from the traditional mammalian toxicology setting discussed in Section 2.

3.1. Example 2. Soil ecotoxicity

A growing concern in ecological risk assessment is the need to identify damage to ecosystems and to the organisms that populate them. For example, characterization and management of potential ecotoxicological risks to soil (micro)organisms from chemical pollutants is critical for protecting habitat and ecosystem function. Regulators must monitor for contaminants that trigger adverse responses in the soil-inhabiting organisms, and where possible correct for pollutant burdens that drive the risk to unacceptable levels.

For instance, in an environmental biomonitoring study of polycyclic aromatic hydrocarbon (PAH) contamination, Maliszewska-Kordybach et al. (2007) collected samples to study PAH effects on nitrifying bacteria in various soils. Consider their data on light loamy sand contamination, taken in an agricultural region within the south-eastern Polish voivodeship of Lubelskie: measured were reductions in nitrification potential of the soil over varying concentrations of the three-ring PAH phenanthrene (Phe), in mg/kg. A decreasing trend in nitrification potential was observed as Phe concentrations increased (Maliszewska-Kordybach et al. 2007, Table 3), and the authors found that a simple linear regression model for the mean response provided an adequate fit to their data if they operated with square roots of the Phe concentrations, i.e., $d=\sqrt{\mathit{Phe}\text{conc}}$. (Final results were then squared for reporting back on the original concentration scale.) The goal was to investigate and summarize the adverse effects of Phe soil contamination. To do so Maliszewska-Kordybach et al. employed the well-established median effective concentration, EC₅₀, as their summary toxicity parameter. For a more formal risk assessment of how soil nitrification potential can be affected by Phe contamination, however, one can also apply the Kodell–West benchmarking operation described above.

Using the regression estimates reported by Maliszewska-Kordybach et al. (2007), the unbiased point estimate of γ₁ from Appendix 2 calculates as g₁ = −0.311. At κ = 3 the resulting estimator of the additional risk is R̂_A (d) = Φ(0.311d − 3.0) − 0.0013. Setting this equal to any chosen BMR and solving for d, yields the benchmark point estimate. (Since the d-scale here is {Phe conc.}^1/2, one should be careful and for purposes of the technical analysis write BMC^1/2, although this is admittedly somewhat cumbersome notation.) Following the example of the original study, set BMR = ¹/₂. This yields ${\text{B}\widehat{\text{M}}\text{C}}_{50}^{1/2}=9.672{(\text{mg}/\text{kg})}^{1/2}$, with 95% lower confidence limit ${\text{BMCL}}_{50}^{1/2}=6.196{(\text{mg}/\text{kg})}^{1/2}$; Figure 1 illustrates the operation. Translating back to the original Phe scale, one finds BM̂D₅₀ = 93.543 mg/kg and BMCL₅₀ = 38.396 mg/kg.

These benchmark values allow for ecotoxicological monitoring of Phe soil contamination and for evaluation of the ecological status of the affected soil. Measured concentrations found at or above these limits indicate substantive adverse effects of the chemical on nitrification potential. This can motivate soil quality managers or environmental regulators to institute quarantines, avoid larger environmental contamination, and/or encourage remediation efforts in support of the affected ecosystem.

As Example 2 highlights, while the biological and toxicological context for construction of BMDs, BMCs, etc. may vary, the fundamental benchmarking concept remains unchanged. Indeed, ecotoxicological benchmark analyses with nonquantal data are growing (Wu et al. 2006; Suski et al. 2008), and barely keep pace with applications in more traditional, nonquantal, toxicity studies (Slob 2002) or with epidemiological investigations on nonquantal human endpoints (Bailer et al. 1997; Budtz-Jørgensen, Keiding, and Grandjean 2001; Morales and Ryan 2005). Expansion has even progressed into rapidly developing areas of biological research such as genomics/gene-expression analysis (Yang, Allen, and Thomas 2007). Opportunities therefore exist for much greater use of the benchmark paradigm, limited only by the creativity of the risk analyst. The next section describes a more divergent possibility, with an eye towards giving benchmark analysis greater translational standing in risk management and practice.

4. Other forms of translational benchmark analysis

As suggested above, an under-recognized feature of the benchmark approach is its applicability to a variety of risk-analytic scenarios. The previous examples illustrate how broadly the method can be applied within biology and toxicology, but it takes surprisingly little effort to extend it into distinctly separate areas of risk assessment.

At its core, the mathematical models that support the method can be manipulated across an assortment of data scenarios. Certainly, when the context of a particular risk analysis changes – say, from crude lethality to mammalian carcinogenesis, to ecotoxicity – the observed data can move from proportions to continuous measurements, etc. The conceptual features are essentially unaffected, however, since the basic statistical methodology remains fungible across different definitions of the adverse event. This facilitates transfer of the benchmark technology to any applicable form of adverse outcome and/or dose–response model, translating the BMDs and BMDLs to many wide-ranging problems in quantitative risk assessment.

To illustrate, the following example highlights the method in a setting far afield from the traditional toxicological arena: socio-geographic hazard analysis.

4.1 Example 3. Place-based terrorism vulnerability

Hazard/vulnerability indexing for populations, localities, ecosystems, and other entities at risk to adverse events is an emergent endeavor in twenty-first-century risk assessment, which has only recently seen substantial development (Peng, Schoenberg, and Woods 2005; Tsuzuki 2006; Mazzorana et al. 2009). For instance, a recent study on urban risk/vulnerability to terrorist attacks (Piegorsch, Cutter, and Hardisty 2007) employed a quantitative index to characterize how terrorism vulnerability changes across different urban locations. The vulnerability data indicated whether any of the 132 largest cities in the USA experienced a terrorist attack over the 35-year period 1970–2004 in which casualties (human deaths or injuries) occurred. Thus, the observed response was a simple binary indicator: Y_i = 1 if casualties had been recorded in that locale during this time period, or 0 if not. This was compared to an index – called the place vulnerability index (PVI) – that combined the locality’s spectrum of socio-economic, geo-physical, and built-environment vulnerability to hazardous events. (The study also considered other aspects of terrorism vulnerability; see the 2007 article for details and also for the complete 132 location dataset.) The PVI had no units, and was standardized to range between roughly −4 and 4. Its scale was uniquely defined, however, and as such the index could be viewed as a ‘dose’ metric for urban vulnerability: as the PVI increased, urban vulnerability to terrorism casualties also appeared to increase.

In fact, the association between urban terrorism causalities and the PVI can be modeled effectively using common dose–response functions. It was seen that a form of quantal response relationship known as the complementary log–log (CLL) model could describe the terrorism ‘dose response’: if d_i = PVI for the ith locality, then the probability of observing Y_i = 1 (i.e., terrorist casualties) at that locality was taken as R(d_i) = 1 − exp{−exp[β₀ + β₁d_i]}.

Using the urban casualty data, the goal was to identify values of PVI past which a locality’s vulnerability to terrorism casualties exceeded reasonable levels. This could be addressed via application of the benchmark approach. The risk assessor defines one or more BMR(s) as the distinguishing points for an unacceptable level of risk, sets the risk function equal to the BMR, and solves for the vulnerability index d = PVI. This produces a benchmark index, BMI, at which the risk exceeds the chosen level of BMR. Note that, because the PVI is a unitless measure, no adjustment is needed for background or spontaneous effects. Thus, one operates directly on the risk function: set R(d) = BMR and solve for d. Under the CLL model this produces BMI_100BMR = (log{−log[1 − BMR]} − β₀)/β₁.

Since these terrorism casualty data are binary, a simplified binomial model, Y_i ~ Bin(1, R[d_i]), is valid, and MLEs for the unknown β-parameters can be determined using similar techniques as those in Appendix 1; see Piegorsch, Cutter, and Hardisty (2007) for details. Doing so for the casualty vulnerability data yields an estimated risk function of R̂(d) = 1 − exp{−exp[−1.255 + 0.474d]}. Inverting the risk produces BM̂I_100BMR = (log{−log[1 − BMR]} + 1.255)/0.474. For example, the standard quartiles ¹/₄, ¹/₂, ³/₄ represent symmetric BMR cut-points that characterize levels of increasing vulnerability. For the 132 cities data, this gives BM̂I₂₅ = 0.018, BM̂I₅₀ = 1.873, and BM̂I₇₅ = 3.335.

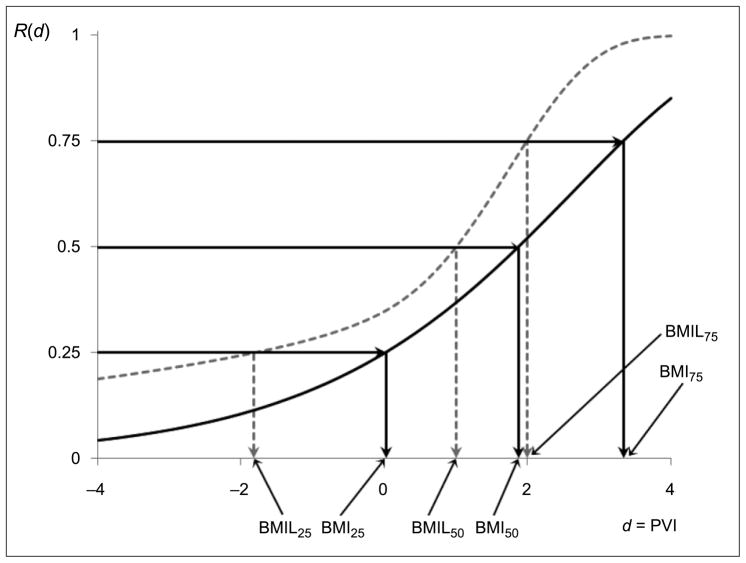
For the corresponding benchmark index (lower) limits (BMILs), adjustment is necessary here for the use of multiple BMRs, which can be achieved by inverting a 95% simultaneous upper confidence band on the extra risk (Al-Saidy et al. 2003). This yields BMIL₂₅ = −1.820, BMIL₅₀ = 1.001, and BMIL₇₅ = 1.986. Figure 2 illustrates the operations, where the similarities to Figure 1 are evident.

Figure 2.

BMIs and simultaneous 95% BMILs (at BMR = 0.25, 0.50, 0.75) for the terrorism vulnerability data. Note: Dark curve is estimated risk function R̂(d); dashed curve is 95% simultaneous upper band on the extra risk.

Further mimicking the analysis in the original article, one could return to these data and ask which of the 132 cities lie above, say, the upper risk quartile’s BMIL₇₅ of 1.986? Doing so identifies 5 of the 132 urban centers with extreme-level PVIs: New York, NY–Newark, NJ (PVI = 2.154), Norfolk–Chesapeake–Newport News–Virginia Beach, VA (PVI = 2.326), Charleston, SC (PVI = 2.543), Baton Rouge, LA (PVI = 3.016), and New Orleans, LA (PVI = 3.119). Intriguingly, all are port cities, hinting at an important marker for increased vulnerability to terrorist events. (Admittedly, a number of other port cities in the list, e.g., San Diego, CA, scored much lower PVIs. Nonetheless, these results give suggestions into the roots of urban vulnerability to terrorism.)

This untraditional application of benchmark analysis helps focus attention on those urban centers whose PVIs exceed defined benchmarks such as BMIL₇₅. From it, city officials in, e.g., Charleston, SC or Norfolk, VA may wish to consider new or updated forms of coastal anti-terrorist protection. The analysis may also prompt increases in funding allocation(s) or other heightened efforts to connect urban risk management programs with terrorism vulnerability assessments (Kunreuther 2002).

5. Discussion

As these various examples demonstrate, the benchmark paradigm’s ability to extend past its roots in toxicity testing and its potential for further implementation are quite rich. One message has pervaded throughout: even when the particular risk-analytic context changes – in the nature of the subject matter problem and/or the specifics of the statistical model – the ability of the benchmark approach to accommodate these differences is unaffected. While the context changes, the concept retains its flexibility. This was recognized by many of the authors cited herein as they employed the method to find BMDs, BMCs, BMIs, etc. More can be done, however, and as Barnes et al. (1995) concluded in a report from a 1994 Benchmark Dose Workshop, ‘to achieve general acceptance of the BMD approach, it will have to be applied to a variety of endpoints’. A marked impact on risk assessment practice will then ensue. As is true in many areas of scientific endeavor, by studying familiar processes in unfamiliar settings we gain a better grasp of both the familiar processes and the new settings.

Appendix 1. Calculating BMDs and BMDLs under a probit dose–response assumption

Suppose data are taken as binomial variates, Y_i ~ Bin(N_i, R[d_i]), at each exposure or dose index i, where the proportion denominator N_i is the number of subjects tested and R(d_i) is the unknown risk function; i = 1, …, n. Set fixed dose levels d_i ≥ 0, and assume the risk satisfies a simple probit dose response: R(d) = Φ(β₀ + β₁d), where Φ (·) is the standard normal cumulative distribution function. Estimation of the parameter vector $\beta =\left[\begin{array}{l}{\beta }_0\hfill \\ {\beta }_1\hfill \end{array}\right]$ proceeds via maximum likelihood: maximize the log-likelihood function $\ell (b)={\mathrm{\Omega }}_i+{\sum }_{i=1}^n{Y}_{i}log\left\{\mathrm{\Phi }({\beta }_0+{\beta }_1{d}_i)/\left[1-\mathrm{\Phi }({\beta }_0+{\beta }_1{d}_i)\right]\right\}+{\sum }_{i=1}^n{N}_{i}log\left\{1-\mathrm{\Phi }({\beta }_0+{\beta }_1{d}_i)\right\}$, where Ω_i is a constant not dependent upon β. Unfortunately, a closed-form solution is not possible in this case and hence calculation proceeds via computer iteration. A number of computer packages can perform the operations, producing MLEs b₀ for β₀ and b₁ for β₁; herein, the R statistical language was used (R Development Core Team 2009). The resulting MLE for the risk function is R̂(d) = Φ(b₀ + b₁d).

To estimate the BMD, find the extra risk as R_E(d) = {R(d) − R(0)}/{1 − R(0)} = {Φ(β₀+ β₁d) − Φ(β₀)}/{1 − Φ(β₀)}. The corresponding MLE is R̂_E(d) = {Φ(b₀ + b₁d) − Φ(b₀)}/{1− Φ(b₀)}. Set this equal to the pre-specified value(s) of BMR and solve for d:

$$\frac{\mathrm{\Phi }({\text{b}}_0+{\text{b}}_1\text{d})-\mathrm{\Phi }({\text{b}}_0)}{1-\mathrm{\Phi }({\text{b}}_0)}=\text{BMR}\Rightarrow {\text{B}\widehat{\text{M}}\text{D}}_{100\text{BMR}}=\frac{{\text{Q}}_{\text{BMR}}-{\text{b}}_0}{{\text{b}}_1}$$

where Q_BMR = Φ⁻¹{BMR[1 − Φ(b₀)]+Φ(b₀)}.

To compute a BMDL, a number of possible formulations exist. The simplest, and the one employed above in Example 1, is the so-called Wald 100(1 − α)% lower limit

$${\text{BMDL}}_{100\text{BMR}}={\text{B}\widehat{\text{M}}\text{D}}_{100\text{BMR}}-{\text{z}}_{\alpha }\text{se}[{\text{B}\widehat{\text{M}}\text{D}}_{100\text{BMR}}]$$

where z_α = Φ⁻¹(1 − α), and se[BM̂D_100BMR] is the standard error of BM̂D_100BMR. The standard error can be approximated via the large-sample features of the ML approach (Piegorsch and Bailer 2005, §A.5). For the probit model assumed here, the squared standard error is

$${se}^2\left[{\text{B}\widehat{\text{M}}\text{D}}_{100\text{BMR}}\right]\approx \frac{1}{{\text{b}}_1^2}{\left[(1-\text{BMR})exp\left\{\left({\text{Q}}_{\text{BMR}}^2-{\text{b}}_0^2\right)/2\right\}-1\right]}^2{se}^2[{\text{b}}_0]-\frac{2{\text{B}\widehat{\text{M}}\text{D}}_{100\text{BMR}}}{{\text{b}}_1^2}\left[(1-\text{BMR})exp\left\{\left({\text{Q}}_{\text{BMR}}^2-{\text{b}}_0^2\right)/2\right\}-1\right]\mathit{cov}[{\text{b}}_0,{\text{b}}_1]+\frac{1}{{\text{b}}_1^2}{\left[{\text{B}\widehat{\text{M}}\text{D}}_{100\text{BMR}}\right]}^2{se}^2[{\text{b}}_1]$$

where se[b_j] are the standard errors of b_j (j = 0, 1), and cov[b₀,b₁] is their estimated covariance. These latter quantities are readily available from most software routines for performing a probit regression fit.

Appendix 2. Calculating BMDs and BMDLs under a simple linear model assumption

Suppose data are taken as normal or ‘Gaussian’ variates, Y_i ~ N(μ[d_i], σ²), at each exposure, concentration, or dose d_i ≥ 0, where the mean function is the simple linear form μ(d_i) = β₀ + β₁d_i and σ² is a constant, unknown variance term; i = 1, …, n. Estimation of the β-parameters and σ² proceeds via standard least-squares (LS) techniques (Kutner, Nachtsheim, and Neter 2004). Also, let $S_{dd}={\sum }_{i=1}^n(d_i-\overline{d})$.

Under the Kodell–West construction in Equation (1), the estimated additional risk is R̂_A(d) = Φ(−g₁d − κ) − Φ(−κ), where κ > 0 is a pre-specified tuning parameter and g₁ is an unbiased estimator of the ratio γ₁ = β₁/σ. The latter term is shown to be $g_1={\xi }_{\text{n}}{\text{b}}_1/\sqrt{\text{MSE}}$, with

$${\xi }_{\text{n}}=\frac{\mathrm{\Gamma }\left(\frac{\text{n}-2}{2}\right)}{\mathrm{\Gamma }\left(\frac{\text{n}-3}{2}\right)}\sqrt{\frac{2}{\text{n}-2}}$$

and where b₁ is the LS estimator of β₁, $\sqrt{\text{MSE}}$ is the root mean squared error, and Γ(·) is the gamma function. Notice that this requires n ≥ 4.

To estimate the BMD for any given BMR, set Φ(− g₁d −κ) − Φ(−κ) = BMR and solve for d. This yields BM̂D_100BMR =−C_BMR/g₁, where C_BMR = κ+Φ⁻¹{BMR + Φ(−κ)}. To compute a BMDL, find any 100(1 − α)% lower bound G_α that satisfies P[G_α < γ₁] = 1 − α. Then, a 100(1 − α)% lower bound on the BMD_100BMR is BMDL_100BMR = −C_BMR/G_α.

Piegorsch et al. (2005b) studied different lower bounds for G_α, and favored a choice based on a Cornish–Fisher expansion for the random variable $T_1=g_1{S}_{dd}^{1/2}/{\xi }_n$ given by Akahira (1995). This led to:

$${\text{G}}_{\alpha }=\frac{{\lambda }_{\text{n}}{T}_1-z_{\alpha }\sqrt{1+T_1^2\left(1-{\lambda }_{\text{n}}^2\right)}+\frac{T_1^3\left(z_{\alpha }^2-1\right)}{24{(n-2)}^2\left\{1+T_1^2\left(1-{\lambda }_{\text{n}}^2\right)\right\}}\left\{1+\frac{1}{4(n-2)}\right\}}{\sqrt{S_{dd}}}$$

where

$${\lambda }_{\text{n}}=\frac{\mathrm{\Gamma }\left(\frac{\text{n}-1}{2}\right)}{\mathrm{\Gamma }\left(\frac{\text{n}-2}{2}\right)}\sqrt{\frac{2}{\text{n}-2}}$$

Piegorsch et al. (2005b) also showed that for positive doses d > 0, the BMDL can be extended into simultaneous 100(1 − α)% lower bounds on BMD for any BMR: one first uses G_α to construct a simultaneous upper confidence band on R_A(d) satisfying P[R_A(d) < Φ (− G_α d − κ) − Φ(−κ),∀ d >0] = 1 − α, and then inverts the band to find the BMDL at the chosen BMR. Figure 1 in Example 2, above, illustrates the operation.