On the energetics of translocon-assisted insertion of charged transmembrane helices into membranes

Abstract

The understanding of the mechanism of insertion of transmembrane (TM) helixes through the translocon presents a major open challenge. Although the experimental information about the partition of the inserted helices between the membrane and the solution contains crucial information about this process, it is not clear how to extract this information. In particular, it is not clear how to rationalize the small apparent insertion energy, ΔG_app, of an ionized residue in the center of a TM helix. Here we explore the nature of the insertion energies, asking what should be the value of these parameters if their measurements represent equilibrium conditions. This is done using a coarse-grained model with advanced electrostatic treatment. Estimating the energetics of ionized arginine of a TM helix in the presence of neighboring helixes or the translocon provides a rationale for the observed ΔG_app of ionized residues. It is concluded that the apparent insertion free energy of TM with charged residues reflects probably more than just the free energy of moving the isolate single helix from water into the membrane. The present approach should be effective not only in exploring the mechanism of the operation of the translocon but also for studies of other membrane proteins.

The insertion of transmembrane (TM) proteins into membranes is a subject of great current interest (1–6). It is known that the recognition of proteins is performed by the translocon complex that ensures both the translocation of globular proteins across membranes and the integration of membrane proteins into membranes (7). Biochemical studies have provided major information about the insertion process, and structural studies have provided key hints about the actual insertion mechanism (1, 8–10). Furthermore, clever experiments by von Heijne, White, and their coworkers (5) have determined a scale that reflects the apparent energetic of the inserting a TM helix into a membrane in biological conditions. These workers took the sequence of the double-spanning protein (bacterial leader peptidase) and added to two TM helixes of this protein (TM1 and TM2) an additional helix (the H helix), which was flanked by two acceptor sites for N-linked glycosylation (5). The degree of membrane integration of the H helix was then analyzed by the number of glycosylated sites, and the apparent equilibrium constants, K_app = f_1g/f_2g (where f_1g and f_2g were determined by the fractions of singly and doubly glycosylated proteins, respectively), were calculated. These values were then converted to the relevant apparent free energies, ΔG_app = -RT ln K_app. Decomposing ΔG_app to the contribution from different amino acids provided the insertion scale for the H helices, with each of the 20 naturally occurring amino acids placed in the middle of the 19-residue hydrophobic stretch (see ref. 5 and Results for more details).

The experimental determination of the “biological” hydrophobic scale (5) challenges one to rationalize the origin of this important scale. In particular, one would like to understand the reason for the small values of the free energy associated with the insertion of charged residues. This presents a significant problem, as the free energy of placing a charge in a nonpolar environment is expected to be very large (11), and because some attempts to simulate the relevant free energy penalty lead in most cases to a significantly larger estimate of the ΔG_app (by more than 10 kcal/mol) (12, 13) than the observed one (2–4 kcal/mol) (5). Different justifications have been given to the observed values, including the effect of water penetration, the effects of the lipid head groups, position of the charge in the membrane, and even membrane distortion (13). However, these justifications cannot fully account for the energetics of ionized groups in the center of a TM helix at the center of the membrane. Thus, this issue remains a major open problem, where it seems that the observed scale may reflect more than just the free energy of moving different residues to the center of the membrane environment, even with possible effects that can account for a part of the discrepancy.

It must also be mentioned that the experimental analysis that led to the ΔG_app scale is extremely complex, and it is not entirely clear if we are dealing with rigorous quasiequilibrium conditions (this issue is analyzed in SI Text and Discussion).

Very recent all atom simulation (14) indicated that the energetics of ionized residues can change in a drastic way if such residues are in a membrane with some protein content rather than in a pure membrane environment. Furthermore, the calculated solvation free energy profile for the Arg close to the translocon and 20 Å away from it indicated that the desolvation penalty for a charged residue close to the lateral gate is quite low (3–5 kcal/mol) and thus comparable to the experimental value. The increase in stabilization of the ionized Arg near the translocon or near membrane protein segments has been found to be partially due to water molecules in the protein interior. These results provided an interesting possible rationale for the value of ΔG_app, although the likelihood that the system would be near the translocon or in any specific insertion step was not explored, and the effect of the relationship to the actual system used for deducing ΔG_app was not modeled. Finally, it was also suggested that helix–helix interaction can account for the low apparent energy (15), but no estimate of this effect was given.

At present it seems to us that the elucidation of the nature of insertion free energies by direct all atom simulations is extremely challenging, because the structural characteristics of the TM/translocon system are not completely clear and because a converging sampling of such a complex system is extremely challenging. Thus one of the most promising options may be opened by the use of coarse-grained (CG) models of the type introduced in ref. 16 for general folding problems and subsequently for folding studies of helical proteins (17). Advances in CG simulations of membrane proteins and some examples of such simulations are summarized in a recent review (18), whereas the general development of CG models in simulation of different biological systems are reviewed in ref. 19.

The augmentation of our early CG models with more recent electrostatic modifications (20) makes them particularly suitable for studying the above fundamental problem. Thus we explore here the origin of ΔG_app of ionized residues by using a CG model for the TM insertion process. This model allows us to analyze the energetics of different configurations, where the insertion of the H helix with a charged Arg residue is assisted by contacts with other helixes and/or the translocon. Our analysis accounts for the trend in the observed ΔG_app (assuming that it follows a quasiequilibrium relationship) and indicates that this quantity probably reflects stabilization by other helixes and perhaps by the translocon.

I. Systems

As stated above, the uncertainty about the structural changes of the translocon and the complexity of the insertion process suggest that the use of a fully explicit model is not an optimal strategy. Thus it is tempting to exploit CG models of the types considered in refs. 16 and 17 and others reviewed in refs. 18 and 19, and to focus on electrostatic effects (20).

The type of structural models considered in the present work are depicted schematically in Fig. 1, where we followed tentatively the sequence of events proposed by Rapoport and coworkers (6). This description is relevant to the insertion process used in establishing ΔG_app (5). Namely, the three TM helices used in our simulations correspond to the integral membrane protein leader peptidase (Lep) with an engineered third H segment (the corresponding sequence is given in SI Text).

Fig. 1.

A schematic description of a feasible insertion process [based on a proposal by Heinrich et al. (6)].

In examining the energetics of possible insertion steps and the corresponding states of the system, we faced the problem of limited structural information. Thus we generated the relevant structures (see below) starting from the X- ray structure of the heterotrimeric membrane protein complex SecY (PDB ID code 3DIN) (10) and using molecular dynamics with the CG model to generate tentative models for the required relaxed structures. A typical structure that will be considered in this work is given as an example in Fig. 2. It should be noted, in this respect, that the considered structures will not represent the sequence of insertion events, but rather possible quasiequilibrium configurations in this process. In fact, the overall competition between translocation and insertion is very complex and unresolved (see details in SI Text). The considered configurations are consistent with the relevant experiments (6, 21), indicating that (i) two TMs can be presented in the channel—one in the pore and one intercalated into the lateral gate; (ii) during the synthesis of a multispanning membrane protein, the TMs could leave the translocon one by one or in pairs; (iii) one TM can facilitate the exit of another TM by returning to the channel to associate with the second TM.

Fig. 2.

A hypothetical structural model generated for the open translocon and three TM helixes. The positioning of the helices corresponds to model 11 on Fig. 4. The translocon is shown in orange, TM1 in yellow, TM2 in blue, H in red, and membrane in gray. Part of the membrane is removed in order to make the proteins visible.

We also like to clarify that there are other works that attempted to model the translocon structure and its opening (e.g., refs. 14, 22, and 23), but the exact structure is not known and the effect of the possible ionization states presents an additional challenge; thus the use of the CG model is probably the best current strategy for addressing energy issues.

Our strategy of exploring the energetics of the different feasible states is demonstrated in Fig. 3 for a system of two helixes embedded in the membrane. In this case we considered the energy of the CG model for different rotational angles of the helixes with a helix–helix distance of 14 Å (this distance was necessary in order to prevent the clashing of the Arg side chain with the second helix during the rotation of the H helix). The corresponding free energy surface is described in Fig. 3, where we take the lowest free energy values as our estimate of the free energy of the given system. The same approach has been used for the different constructs we examined. All the calculations were performed with the program package MOLARIS (24), using the simplified folding module.

Fig. 3.

The system free energy of the two helices, TM1 and H, in the membrane as a function of helices rotation. TM1 has polar regions and H has positively charged Arg. As can be seen from the graph, the energy goes down when the charged Arg points toward the TM1 helix, so that the exposure of charge to the membrane is reduced. The minimum of the system free energy is 0.19 kcal/mol at (240°, 180°) when the Arg is stabilized by the interaction with hydrophilic residues of TM1.

II. Results

In the first stage we explored in a very tentative way the general issue of the mechanism of insertion of TM helixes through the translocon. This was done by following the insertion sequence featured in Fig. 1. The energetic of each step was examined using the CG model, considering only the energetics of inserting the helixes in the relaxed protein. These calculations did not attempt to fully optimize the protein structure or to explore its deformation free energy and was mainly needed for estimating the energetics of states where the H helix touches the translocon. In general, the missing deformation energy will make the total energy of states where the helixes are out of the translocon more stable.

A much more detailed analysis was done in examining the nature of the energetics of the H helix and the corresponding ΔG_app (under the conditional assumption of quasiequilibrium), focusing on the case where Arg residue is in the center of the H helix. More specifically, in order to estimate ΔG_app we examined the change in free energy, ΔΔG_wat→sys(H), of transferring the H helix from water to different likely configurations (states) that can be generated during the insertion process. For each of the possible options we evaluated the lowest energy obtained by keeping the helixes rigid and mapping the energy of the system as a function of the relative orientation of the helixes involved. This was done while not allowing the helixes to move in the z direction (see SI Text). The corresponding procedure is illustrated in Fig. 3. In each case we evaluated the total free energy of the full system (translocon and helices in the membrane), ΔG_tot = ΔG_sys(all), at the lowest energy configuration. We repeated this calculation for the same system without the H helix, ΔG_sys(all-H), and for the isolated H helix in water, ΔG_wat(H). Using these values we expressed the apparent free energy of inserting the H helix as

[1]

We then calculated the ΔG_app(H) for the H helix with central Arg and with central Ala and obtained the corresponding difference:

[2]

where H/Arg and H/Ala designate an H helix with a central Arg and Ala, respectively. This treatment allowed us to conveniently evaluate the apparent free energy of Arg residue relative to that of Ala and to compare the calculated results to the corresponding experimental value (5). The resulting ΔG_app are given in Fig. 4, Table 1, and Table S1. Fig. 4 also provides the total energy of each system, and thus we can focus only on those systems with the lowest ΔG_tot. In the present case only systems 17 and 19 contribute because these are the only system with low total energy and nonnegligible probability (see, however, below).

Fig. 4.

The energetics of different feasible steps for the insertion of helices into the membrane—translocon system and the ΔΔG_app = ΔΔG_app(Ala → Arg) associated with the contribution of Arg (relative to that of Ala) to the insertion of the H-helix to the system at the given configuration. Also provided is the total free energy of each system ΔG_tot (relative to that of the system in state 1).

Table 1.

Estimating ΔG_app^*

#	ΔG(1)	ΔG(2)	ΔG(3)	ΔGapp	ΔΔGapp
10a	−39.5	−31.1	−8.8	0.4	3.6
10b	−35.5	−31.1	−1.2	−3.2
11a	−35.8	−21.8	−8.8	−5.2	4.8
11b	−33.0	−21.8	−1.2	−10.0
12a	−39.7	−31.0	−8.8	0.1	3.9
12b	−36.0	−31.0	−1.2	−3.8
13a	−49.5	−38.7	−8.8	−2.0	3.5
13b	−45.4	−38.7	−1.2	−5.5
14a	−48.3	−38.3	−8.8	−1.1	3.9
14b	−44.5	−38.3	−1.2	−5.0
15a	−47.3	−38.4	−8.8	−0.1	4.4
15b	−44.1	−38.4	−1.2	−4.6
16a	−59.0	−38.7	−8.8	−11.5	4.2
16b	−55.6	−38.7	−1.2	−15.7
17a	−62.0	−41.8	−8.8	−11.4	4.0
17b	−58.4	−41.8	−1.2	−15.5
18a	−47.7	−37.1	−8.8	−1.8	16.0
18b	−56.1	−37.1	−1.2	−17.8
19a	−61.6	−40.9	−8.8	−12.0	0.8
19b	−54.8	−40.9	−1.2	−12.8
20a	−55.0	−44.4	−8.8	−1.8	16.0
20b	−63.4	−44.4	−1.2	−17.8

^*All the energies are given in kcal/mol. The table includes only the results for models 10–20, whereas the rest of the results are given in Table S1. The models with the letter “a” and “b” have, respectively, Arg and Ala on the H helix. ΔG⁽¹⁾ = ΔG_sys(all) = ΔG_tot is the free energy of the full model (translocon and helices in the membrane) relative to our model 1. is the free energy of the full model without the H helix. ΔG⁽³⁾ = ΔG_wat(H) is the free energy of the H helix in water. ΔG_app = ΔΔG_wat→sys(H) = ΔG_sys(all) - ΔG_sys(all-H) - ΔG_wat(H) is the apparent free energy of the H helix. ΔΔG_app = ΔΔG_app(Ala → Arg) = ΔG_app(H/Arg) - ΔG_app(H/Ala) is the difference between the apparent free energies for Arg and Ala (which can be compared to experimental value). The free energy values highlighted in bold are used in Fig. 4. Glu on TM2 was found to be protonated inside the membrane at pH = 7.

As seen from Fig. 4 and Table 1 the lowest free energies correspond to the case where the insertion is assisted by the polar parts of either the translocon or the other helixes. In particular, the lowest energy configuration (state 17) gives ΔG_app = 4.01 kcal/mol in a reasonable agreement with the observed value of 2.47 kcal/mol. In principle, we have to consider the free energy weighted average of configuration 17, 19. and 16, and this will reduce the calculated ΔG_app. Although the results are quite stable and do not change significantly with a small change of the parameters used, the agreement might be coincidental and the validity of our finding requires further verification. However, the results seem to indicate that the biological insertion scale reflects a more complex situation than just the energetic of helices in solution (see also SI Text).

III. Discussion

Understanding the molecular determinants of protein insertion through membrane is a problem of major current interest. Experimental estimates of the relevant energetics provided a valuable insight about the contributions of different residues. However, the complexity of the insertion process and the uncertainty about the exact nature of the structural changes makes it very challenging to generate a detailed molecular picture of the insertion mechanism and the origin of ΔG_app.

Here the use of a simplified CG model seems to provide an excellent compromise, allowing one to explore a large range of the configurational changes and to obtain reasonable conclusions in the case of relatively “fuzzy” structural information. Furthermore, the CG model can be used when we gain more information as an optimal reference potential for studies of the energetics of explicit models (19, 20). Another potentially promising aspect of the present approach is its ability to help in refining the molecular picture of ΔG_app. This can include more exploratory studies of the paths considered in Fig. S1.

A recent interesting study (23) explored the contributions of hydrophobic residues to the energetic of the lateral gating of the translocon and has attempted to address the partition of helixes between the membrane and the translocon issue, and in some respects the origin of ΔG_app. However, ref. 23 has not explored the partition between the membrane and water or alternative measures of the relationship between translocation and insertion in addressing the nature of ΔG_app, but instead looked at the partition of the helix between the translocon and the membrane. This approach may be related to the possibility that ΔG_app (or other insertion parameters) reflects somehow kinetic effects when, for example, the assumed equilibrium is not reached during the glycosylation experiments. However, the kinetic proposal has not been formulated by workers in the field in a physical (energy-based) consideration, and our analysis pointed to the following options (see SI Text): (i) We have a quasiequilibrium condition that justifies the definition of ΔG_app as the partition between water and the membrane. (ii) ΔG_app is related to the ratio between the activation barriers for insertion and translocation (this was not explored in ref. 23). (iii)ΔG_app reflects a very complex situation in the translocon gateway.

Our analysis tends to favor a mechanism where the calculated ΔG_app of Arg⁺ reflects helix–helix interaction in the membrane more than the stabilization of this ionized group by the translocon. Nevertheless, at present the difference between the total energy of configurations 17 (or 19) and 13 may need more careful assessment (as we deal with a significantly different situation). Furthermore, it may be beneficial to quantify the CG findings by using our approach of evaluating the free energies for transformation from the CG to the explicit model (20), and such studies will be conducted in the future. In this respect we note that Johansson and Lindahl (14) considered the general effect of having an Arg near the translocon and in the membranes with different concentration of helixes, but have not explored the corresponding relative probability or the relationship to the insertion experiment.

An exciting recent experimental study of Spiess and coworkers (25) indicated quite clearly that mutations of the translocon change ΔG_app for hydrophobic residues. This finding was assumed to lend some support to the kinetic control proposal, suggesting that catalytic contribution should not affect equilibrium. However, it is more likely that the interaction between the translocon and the H helix reaches a quasiequilibrium at the different stages of insertion (e.g., some contribution of state 13 in Fig. 4) and that this determined the fraction of the H helix in the membrane. Such an effect has no relationship to the forward and backward barriers for the insertion and translocation unless some of these barriers are more than 20 kcal/mol, where it would become (according to transition state theory) rate limiting with a rate constant of about 1 min^-1. If the glycosylation experiment takes more than an hour, then the only way that we have a kinetic mechanism is the vectorial mechanism considered in Fig. S2. Thus it is more likely that the finding of different ΔG_app for different systems is not correlated with a kinetic model but with a possible complex with the translocon.

Mutational studies of the type described by Spiess and coworkers (25) and by von Heijne, White, and coworkers (26) can be very instrumental in validating or improving the present finding. They can clearly tell us if the H helix still touches the translocon during the partition between the membrane and solution. More specifically, modifying the other two helices with a “belt” of nonpolar residues in their center can be used to find out whether the H helix, with an ionized group in its center, is in contact with the other helixes. In this respect we note that the current experiments (26) are not conclusive enough.

Recent attempts to derive an implicit model for membrane proteins (27) and to explore the insertion energy by CG simulations (28) have provided some interesting insights. However, such an approach suffers from major problems when it is applied to charged residues, as it does not explore the effect of stabilization by polar groups considered here. The problem is that the CG models considered do not seem to reproduce explicit simulations (and other estimates) of oil water transfer free energy of ionized residues. What is missing are more consistent attempts to model the energetics of the insertion process, where possible protein–protein or helix–helix interactions are explored (as was done here), or full atomistic calibration of the CG electrostatic parameters. Thus it is significant to note that our model reproduced an explicit simulation of charge insertion in a membrane (Fig. S3).

Regardless of the exact explanation of the origin of ΔG_app of charged residues, it seems to us that CG models offer a powerful way to progress in analyzing the key experimental information and eventually in progressing in the detailed understanding of the complex insertion process. That is, one of the most promising directions of the current approach is its potential in providing information about the sequence of event in the insertion of membrane proteins, because we can evaluate the energetic of different steps (e.g., the steps presented in Fig. 1) and even explore the barriers for alternative paths. Combining such simulations with experimental studies is expected to be quite useful.

IV. Methods

The present work uses a CG model that describes the main chain by an explicit model and represents the side chain as a simplified united atom model. This CG model provides a more advanced treatment of electrostatic effect than most current CG models (see SI Text). More specifically, the present mode, which is a modified version of our recent work (19), expresses the overall free energy as

[3]

The main chain is treated explicitly with implicit solvent corrections, and the main-side treatment involves van der Waals and screened electrostatic terms (20). The major and most relevant part of our treatment comes from the ΔG_side, which is given by

[4]

The first term describes the effective van der Waals interactions between simplified side chains, which described in ref. 20. The second term represents the electrostatic interaction between ionizable residues (see below), and the last term represents the hydrophobic contributions that are not included implicitly in the first term (see below). The term is given by

[5]

where i runs over the protein ionized residues, is the pK_a of the ith residue in water, and Q_i is the charge of the ith residue in the given ionization state. ΔG_QQ is the charge–charge interaction free energy, which is given by

[6]

where the energy is given in kcal/mol and the distances in Å. ε_eff is the effective dielectric for charge–charge interaction, which reflects the idea established in many of our works (e.g., refs. 20, 29, and 30), that the optimal value is large even in protein interiors (namely, ε_eff > 20). This type of dielectric has been found recently to provide very powerful insight in studies of protein stability (see refs. 29 and 31), and thus it is expected to be very useful in modeling the electrostatic contribution to the stability of the simplified model. The ionization state of the protein residues was determined by the Monte Carlo approach of ref. 20 for the assumed pH.

A key element in our approach is the treatment of the self-energy, ΔG_self, associated with charging each ionized group in its specific environment. This term is given by

[7]

where i runs over all ionized residues and , , and are, respectively, the number of nonpolar residues, polar residues, and membrane atoms in the neighborhood of the ith residue. The functions and are given by

[8]

and

[9]

whereas is given by Eq. 8 with replacing . The values of , , and are taken as 4, -2, and 15, respectively. However, realizing that, in the case of the membrane, this treatment considers only the self-energy at the center of the membrane, we modified the membrane self-energy term to include the distance from the surface. The corresponding treatment is implemented in Eq. S1.

The number of nonpolar residues neighboring the ith ionized residue is expressed by the analytical function

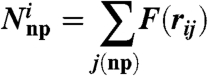[10]

with

[11]

where r_np is the nonpolar radius defining the cutoff range of nonpolar neighboring residues (typically r_np = 6 Å), and r_ij is the separation between the ionized residue i and nonpolar residue j. The same expression is used for neighboring polar residues (N_p), where r_p = 6 Å. This treatment is aimed at capturing the fact that an ionized group has to pay large energy for moving from water to a nonpolar environment (11, 32) and is usually surrounded by polar residues or water molecules (11, 30). The validation of this treatment in proteins is reported in ref. 20, and the validation in membrane is reported in SI Text.

The membrane is represented by a grid of unified atoms [as we have done in previous studies since 1989 (e.g., see ref. 33)], and this grid is used in evaluating N_mem by the equivalent of Eq. 11, with r_mem = 6 Å, when the membrane spacing is 4.0 Å. It should be noted that a large membrane spacing (DM) (which provides a useful option for regions far from the protein) leads to instability in the calculated results and requires a significant averaging on the grid position. Thus after testing the effect of different DM on the self-energy, we found that DM = 4.0 Å is the optimal value, and calibrated N_mem by using

In considering the hydrophobic effect, we noted that the hydrophobic interaction between the protein residues is reflected implicitly in the van der Waals parameters used. However, the corresponding calibration has not been done in a very systematic way in the protein and was not done at all for the membrane model. Thus we considered here a simplified treatment of the hydrophobic effect in the membrane and in the protein, adopting the same model used in the self-energy calculations, using now

[12]

where i runs over all nonpolar residues and and are the number of nonpolar residues and membrane atoms in the neighborhood of the ith residue. The functions and are given by Eq. 8, where the coefficients, and , are, respectively, -1.22 and -1. In order to avoid double counting the implicit hydrophobic effect of the protein–protein van der Walls interaction we did not include the van der Walls energy of Eq. 4 in our current determination of the total free energy.

All the above electrostatic treatment involves a self-consistent treatment of the interdependent self-energy, charge–charge interaction, and the external pH (where the ionization state is determined by a Monte Carlo treatment of the energetics of Eq. 5).

The total energy of inserting helixes into the membrane might be too negative as it does not reflect a careful calibration of the solvation of the helix hydrogen bonds in water. The assessment of this contribution and the corresponding improvement of our model are left to subsequent studies because the corresponding contribution is very similar for the systems considered here (and thus would not change the difference between the total energies).

The present study estimated the CG free energy from the total effective potential rather than by free energy perturbation calculations. This approximation is justified at the present stage as the calibration involves the same approximation.

We are aware of the great advances in recent extensions of the CG idea to studies of membranes (e.g., ref. 34), but do not think that such models will provide the optimal strategy in the present stage, where we focus on the electrostatic free energy rather than on the membrane properties or on the insertion of hydrophobic residues (see ref. 35 and the references in SI Text).