Dispersal of fungal spores on a cooperatively generated wind

Abstract

Because of their microscopic size, the forcibly ejected spores of ascomycete fungi are quickly brought to rest by drag. Nonetheless some apothecial species, including the pathogen Sclerotinia sclerotiorum, disperse with astonishing rapidity between ephemeral habitats. Here we show that by synchronizing the ejection of thousands of spores, these fungi create a flow of air that carries spores through the nearly still air surrounding the apothecium, around intervening obstacles, and to atmospheric currents and new infection sites. High-speed imaging shows that synchronization is self-organized and likely triggered by mechanical stresses. Although many spores are sacrificed to produce the favorable airflow, creating the potential for conflict among spores, the geometry of the spore jet physically targets benefits of the airflow to spores that cooperate maximally in its production. The ability to manipulate a local fluid environment to enhance spore dispersal is a previously overlooked feature of the biology of fungal pathogens, and almost certainly shapes the virulence of species including S. sclerotiorum. Synchronous spore ejection may also provide a model for the evolution of stable, self-organized behaviors.

The forcible launch of sexual spores into dispersive air flows enables ascomycete fungi to propagate between physically distant patches of habitat; for example, the pathogen Sclerotinia sclerotiorum disperses from apothecia in the ground to infect the flowers of crop plants (1), and dung fungi in the genus Ascobolus must escape from their dung piles to be ingested by animals (2, 3). Although their microscopic size enables spores to be transported by even slow flows of air, it also severely limits the distance that they may travel ballistically. Launched at a speed of 8.4 m·s^-1, the 12 μm long spores of S. sclerotiorum would be decelerated to rest after traveling less than 3 mm (4, 5). In response to this constraint, fungi have evolved multiple adaptations to maximize spore range. For example, spores that cohere during launch benefit from increased inertia (6), while individually ejected spores may be shaped in order to minimize drag (5).

Here we demonstrate the remarkable ability of apothecial fungi to manipulate their own fluid environment and negate the range constraints imposed by fluid drag. It has long been known (7, 8) that in many species spore discharge is almost synchronous between the asci of an individual apothecium, so that hundreds, thousands, or tens of thousands of spores can be discharged in a single puff, lasting a fraction of a second (Fig. 1 A, B). Discharge may be initiated spontaneously, or by changes in air pressure, or when an apothecium is touched. Buller (9) first connected spore coejection with the creation of a flow of air. In this work we adapt algorithms originally developed to simulate hundreds of thousands of droplets in clouds to prove that the hydrodynamic cooperation of spores creates a flow of air. Our simulations, analytic models, and experiments: (i) quantify the dispersal advantage provided by simultaneous ejection, (ii) elucidate the biomechanical parameters under the control of the fungus, and (iii) demonstrate a previously unreported benefit of synchronized launch; the dispersal of spores around obstacles. We also use high-speed imaging to probe how the ejection of spores from different asci is synchronized.

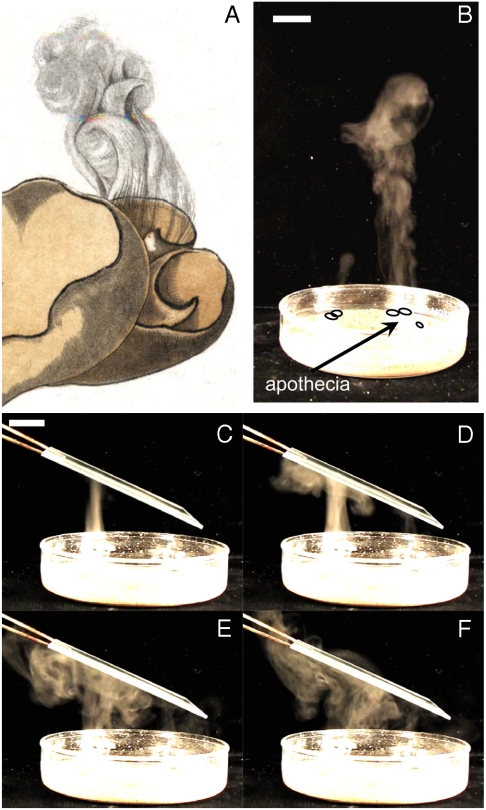
Fig. 1.

Synchronized ejection creates a coherent jet of air, enhancing dispersal in open and crowded environments. (A) Early documentation of synchronous spore release in a 1791 drawing of Otidea cochleata (8).[Reproduced with permission from Histoire des champignons de la France by J.B. Bulliard, Plate number 154, courtesy of the Farlow Library of Cryptogamic Botany]. (B) Spore jets originating from S. sclerotiorum apothecia travel much farther than individually ejected spores. (C–F) If the jet impacts upon an obstacle, such as a glass slide, then pressure gradients within the jet displace spores out and around the obstacle. Images are taken at t = 0, 0.11, 0.32, and 0.55 s after initial impact. (Scale bar: 2 cm).

Results and Discussion

Simultaneously ejected spores cooperate to create a macroscopic flow of air. To demonstrate this, we simulate the trajectory of each ejected spore, including the acceleration of the surrounding air, by direct numerical simulation (DNS) of the full Navier-Stokes equations (Fig. 2A and SI Appendix). In these simulations, spores are assumed to be randomly ejected from points uniformly covering the entire apothecium. Our simulations show that within a short (∼cm thick) basal region of the jet, rapidly moving spores mobilize the surrounding air. In crossing the basal region spores decelerate while air accelerates until they reach the same speed U uniformly across the width of the jet (Fig. 2A). Beyond the basal region spores are transported by the air flow that they have initiated. In addition to increasing spore range, the transition from ballistic to passive dispersal allows spores to avoid impact with obstacles. We saw experimentally that the pressure gradients created within the jet displace spores sideways and around obstacles (Fig. 1 C–F), enabling spores to reach flowers that are blocked e.g., by leaves*.

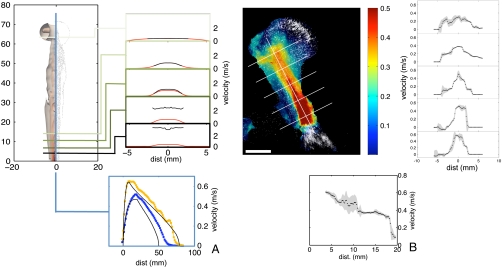
Fig. 2.

Simulations (A) and flow visualization in real fungi (B) reveal the initiation and propagation of a jet of coherent air by synchronously ejected spores. (A) Simulated jet profile for synchronous, random ejection (D = 4 mm, v_s = 4 m·s^-1). Top left: isosurfaces of the azimuthal vorticity (left half) and particle locations on a vertical cross section (right half). Top right: average spore (black curves) and air (red curves) speeds on cross sections of the jet show initiation of air flow in the basal region of the jet (where spores are faster than air), and transport of spores by the decelerating and broadening jet. Bottom shows the air speed at the center of the jet for two different simulated apothecia: D = 4 mm, v_s = 4 m·s^-1 (orange squares), D = 3.4 mm, v_s = 2 m·s^-1, (blue triangles), which is correctly described by an asymptotic theory based on Eq. 1 (black curves). (B) Real spore velocities within a jet originating from a S. sclerotiorum apothecium. Top left shows spore velocities, averaged over 3 ms, across the center-plane of the jet (Scale bar: 5 mm) and top right shows velocities sampled at different heights within the jet. Spore speed at the end of the acceleration region agrees quantitatively with model. Bottom: velocity on the center line of the broadening and decelerating jet agrees qualitatively with simulations shown in section A.

The range of cooperating spores can be 20 times greater than the ranges of individually ejected spores. In experiments we observed spore jets more than 10 cm in length (Fig. 1B, 3B) compared to the 3 mm range of singly ejected spores. Similar range enhancements were seen in simulations (Fig. 2A, 3A). We can quantify how range enhancement depends upon parameters that may vary between individual apothecia; namely the flux (rate of spore ejection), q_s, per unit area of apothecium, the jet diameter D, the mass of each spore, m_s, and the spore launch speed v_s. Since spores follow streamlines except in the basal region, and are therefore constrained by the incompressibility of the surrounding air flow, the density of spores is constant through the jet, and from conservation of mass in the basal region, is equal to ρ_s ≡ q_s/U. The speed, U, of the jet at the end of the basal region can then be calculated by equating the momentum flux of the spores and of the mobilized air at the end of the basal region with the momentum of the spores at ejection, i.e., ρU² + m_sq_sU = m_sq_sv_s, where ρ is the density of air (see SI Appendix). Viscous and gravitational stresses then limit the maximum length of the spore jet: we separately estimate the size of these forces. The weight of unit length of jet ∼m_sq_sgD²/U, where g is the gravitational deceleration. Meanwhile the viscous stress resultant on a unit length of the jet is ∼ηu_j, where η is the viscosity of the surrounding air and u_j the speed of the jet. The relative magnitude of the two resistive forces is given by the dimensionless ratio Gy ≡ m_sq_sgD²/ηUu_j. Taking parameters from real fungi (see SI Appendix) we estimate that Gy ≳ 5 at the foot of the jet and increases with height as the jet decelerates and broadens, implying that the range of the jet is limited mainly by gravity: a slug of spore laden air created in the basal region decelerates like a frictionless projectile. To predict the steady range of the jet, we balance the inertia of a horizontal slice of the steady jet against gravity and viscous forces:

[1]

Neglecting the viscous force F_visc[u_j] we integrate this equation over the length of the jet 0 < z < z_max, obtaining an expression for the steady jet range: . For S. sclerotiorum, spore weight limits the range of the jet to 90 mm (Fig. 3B). However jets created by smaller apothecia have smaller values of Gy so are stopped short of this maximum, weight-limited, height by viscous resistance. To quantify the additional resistance, we developed an asymptotic model that includes the viscous drag from shear layers around the circumference of the jet (see SI Appendix). Both this analytic model and our DNS show that, even when viscous effects are properly accounted for, spores reach more than 67% of the maximum possible height (Fig. 2A, 3A and SI Appendix). Remarkably, although the ranges of individual spores are severely limited by drag, cooperating spores behave like almost frictionless projectiles.

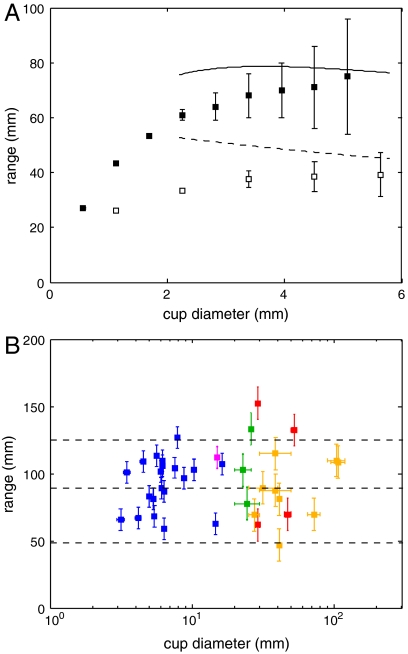
Fig. 3.

Asymptotic methods quantitatively predict the range of spores for simulated and real apothecia. (A) DNS shows that range for small- and intermediate- sized apothecia (D ≲ 5 mm) is limited by drag. For intermediate apothecium diameters (2 < D < 5 mm), jet reaches a steady state and range can be predicted by our asymptotic model (SI Appendix) (solid symbols and solid curve, v_s = 4 m·s^-1, open symbols and dashed curve, v_s = 2 m·s^-1) (B) Spore ranges of real macroscopic fungi with larger apothecia (data points) are within bounds imposed by the weight of the jet (dashed lines) (magenta: Sarcoscypha protracta (9), blue: S. sclerotiorum, green: Geopyxis vulcanalis, red: Caloscypha fulgens, and orange: Sarcosphaera crassa). To calculate these bounds, we use the spore size and speed data for S. sclerotiorum (a = 3 μm, v_s = 8.4 m·s^-1, see SI Appendix) in Eq. 1. The three dashed lines correspond to spore fluxes q_s = 1, 3.5 or 7 × 10⁴ spores/mm²·s.

Direct Particle Imaging Velocimetry (PIV) measurements of the spore velocities within real S. sclerotiorum spore jets (see Materials and Methods) quantitatively confirm our numerical and analytical models for jet initiation and propagation (see Fig. 2 and Movie S1). We directly measured the spore launch speed to be 8.4 m·s^-1 (see SI Appendix and Movie S2), but over the first few millimeters of the jet, spores decelerated to speeds between 0.4 and 0.8 m·s^-1 (Fig. 2B). These speeds are consistent with theoretical values for U, for spore fluxes q_s = 1.3 × 10⁴–5.3 × 10⁴ spores/mm²·s^-1, very close to the directly measured value of 3.5 × 10⁴ spores/mm². Above this basal region, spore speeds decrease more slowly with height and the jet broadens, also as predicted by our theory (Fig. 2 A, B).

Cooperative benefits are shared unequally among spores. If spores are ejected randomly across the apothecium over the duration of the puff, creating a uniform and homogenous spore jet, then the first spores to be ejected—between 25% and 85% of spores according to our simulations of randomly ejected spores—set the air into motion but travel less far than later ejected spores (SI Appendix). It is generally accepted (4, 10) that shorter ranges decrease spore fitness by increasing the probability of either falling back onto the parent fungus or onto already exploited resources. In this sense the first spores to be ejected are sacrificed to benefit the ensemble of spores. Because of the sensitivity of a spore’s range to the timing of its ejection within the puff, it is natural to ask what local cues or signals trigger the ejection of individual spores, and therefore control their placement within the puff. We used high-speed imaging to determine how ejection is coordinated among asci.

The synchronized ejection of spores is self-organized. Imaging of wild isolates of Ascobolus cf. furfuraceus at 1,000 fps (frames per second) shows that ejection begins when a small group of nearby asci discharge at nearly the same time, and proceeds in a wave that expands across the apothecium (Fig. 4 A–D) at a speed v_w ≈ 1.5 cm·s^-1. All spores are ejected after a time t_puff ∼ D/v_w. In fact we measured this signature scaling of puff duration with apothecium size for many different genera and these data suggest that ejection is self-organized in many apothecial fungi (Materials and Methods and SI Appendix). It is likely that after a small group of asci are triggered, e.g., by a localized change in air pressure, neighboring asci are triggered by elastic stresses within the apothecium. We documented apothecia shrinking proportionately to the number of spores ejected (Fig. 4E), strongly suggesting that apothecia are prestrained. Asci are separated by a bed of paraphyses, which become turgid as the fruit body ripens (11, 12). Although their function has been hitherto mysterious (12–14), we saw paraphyses reorganizing following nearby spore discharges, suggesting that turgid paraphyses provide the requisite elastic prestress. Simulations of spatially coordinated spore ejection, where we mimic the self-organized ejection process by releasing spores on the arrival of a wave that crosses the apothecium, rather than uniformly and randomly over the apothecium, confirm an unequal distribution of cooperative benefits between the first and last spores to be ejected (see SI Appendix).

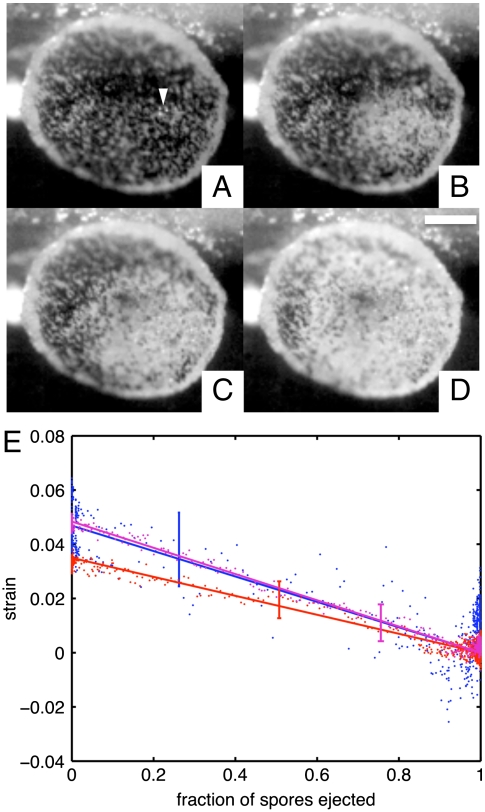
Fig. 4.

Synchronous ejection of spores is self-organized and triggered by mechanical stresses. (A–D) High-speed imaging shows a wave of ejections propagating over the apothecium of A. cf. furfuraceus. Apothecium is shown at times t = 7, 47, 87, and 127 ms following ejection of the first ascospore. The puff begins with the spontaneous ejection of a small group of asci (white arrow). (Scale bar: 0.5 mm). (E) Relaxation of strain with time (measured by fraction of spores ejected) for three A. cf. furfuraceus apothecia. Representative error bars are shown.

Nuclei of different asci across a single apothecium may be genetically different, and it is probable that the timing of ascus discharge is controlled by the nuclei contained in the ascus. Nuclei outside of the asci do not participate in ascus development, as shown by heterokaryon studies (15, 16) and by the existence of ascus dominant mutations. For example mutants such as Neurospora crassa Pk-1 and Pk-4 produce abnormal asci in crosses with wild type strains, even when the mutant is used as the male parent and does not contribute any maternal tissue (17, 18). Different asci will contain genetically different sets of nuclei if the female parent mates with multiple male partners (19) or if either parent contains genetically different nuclei (20, 21), because each ascus is produced by karygamy of a different pair of parental nuclei (22).

Experiments with A. cf. furfuraceus show that asci do not eject precisely with the arrival of the triggering wave, but may lag or lead it by up to ± 54 ms. The dispersion of response times is independent of the size of the apothecium and density of asci (see SI Appendix), and is consistent across experimental replicates, suggesting it has a genetic rather than environmental origin. In fact it is likely that the time lag between arrival of the triggering wave and actual spore ejection is determined by ascus properties known to be controlled by the ascus nuclei (12), including elasticity and initial overpressure. The potential ability of genetically different nuclei to bias their own ejection times may create conflicts across the apothecium: if a spore’s range were systematically increased by ejecting later or earlier than its neighbors then, in game theoretic terms, “cheating” spores would be advantaged over “cooperators” (23–27).

To understand how policing against cheating (28) might be provided by the geometric organization of the spore jet, we performed DNS of spores ejecting in a self-organized wave. We found that the spores create a two-dimensional sheet of air that moves across the apothecium, changing little in shape (Fig. 5A). As spores rise they mobilize a thin layer of adjacent air. We analyze how the thickness, δ_j, and speed, u_j, of this air layer increase with height, z. Balancing viscous and inertial stresses gives the familiar boundary layer scaling (29). Traction on the air layer comes from the viscous drag upon the spores. Since spores travel much faster than the air at the base of the sheet, this viscous drag is equal to Q_sζ per unit area of sheet, where Q_s is the flux of spores per unit width of sheet, and ζ is the Stokes drag coefficient for a single spore. Equating the spore drag with the viscous stress within the entrained layer of air, ∼μu_j/δ_j, we obtain 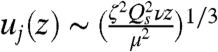and 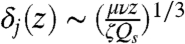. A similarity analysis based on these scalings (see Materials and Methods) reproduces the entire velocity profile across the sheet (Fig. 5B).

Fig. 5.

Hydrodynamics target dispersal benefits to cooperating spores, and penalize spores that delay their ejection. (A) Self-organized ejection produces a sheet of spores that wraps up into a jet several centimeters above the fruiting body (figure shows the simulated vorticity [colors] and spore locations on a vertical slice of the jet: puffing starts from the right end of the apothecium). (B) The spore jet entrains a thin layer of air, whose simulated velocity profile (colors; profiles evaluated at different time points at height z = 0.2v_sτ) match our asymptotic theory (SI Appendix, black curve). (C) Cheating spores that eject behind the advancing sheet are entrained only if delayed by less than δ_j(z_s)/v_w (≈50 ms). Gray scale shows the vertical position of all cooperating spores in time, blue curve the trajectory of a single spore, green curves, the change in trajectory due to delaying ejection by less than 50 ms and red curves reduced ranges from longer delays. (D) Decrease in average spore range for cheating spores at v_s = 2 m·s^-1 (blue—SI Appendix: simulation C2) and 4 m·s^-1 (orange—SI Appendix: simulation C4). Arrows show the predicted width of the entrained air layer.

To benefit from cooperative ejection a spore must be entrained by the other spores before it can be brought to rest by drag. To be entrained, a spore must eject either ahead of the sheet, which requires anticipating the arrival of the triggering signal, or less than δ_j(z_s) behind the sheet, where z_s is the range of a singly ejected spore in still air. On setting z_s ∼ τv_s, where τ is the Stokes time scale for a spore (see SI Appendix), this corresponds to a critical distance δ_j(z_s) of 0.7–0.8 mm. In other words, to benefit from the launch of other spores, each spore must eject within 45–55 ms of the arrival of the triggering wave, which accords with the measured dispersion of ejection times in A. cf. furfuraceus (SI Appendix). To confirm that hydrodynamic targeting is sufficient to prevent cheating, we directly simulated the effect of changing the ejection time of a single spore (SI Appendix: simulations C2, C4) and repeated the simulation changing both the position and ejection time of the hypothetical cheating spore. Spores that delayed their ejection by more than δ_j(z_s)/v_w were not entrained and were dispersed less far (Fig. 5 C and D). Although our simulations suggest that spores with shorter delays do travel slightly further than cooperators, in nature, these small gains may be washed out by fluctuations in air velocity. The necessity of ejecting into the thin layer of air entrained by the other spores prevents spores from cheating by delaying their ejection until the sheet has reached its maximum height, penalizing spores that do not eject in their correct sequence.

Materials and Methods

Fungal Strains and Imaging.

Apothecia were derived from three sources:

1. A. cf. furfuraceus fruit bodies (diameter: 0.5–2.5 mm) were isolated by placing cotton wool balls in trays of freshly collected horse dung fit with tight lids. The dung was moistened daily with deionized water. Fruit bodies started to appear on the cotton balls three weeks after collection, whereon individual apothecia were transferred into 50 mm petri dishes for high-speed filming.

2. S. sclerotiorum fruit bodies (diameter: 3.5–10 mm) were generated using the protocols described in ref. (30).

3. Wild isolates of Helvella, Peziza, Geopyxis, Caloscypha, Sarcosphaera, and Gyromitra species (diameter: 20–120 mm) were collected opportunistically by E. Vellinga.

To measure the flux of spores from real fungal fruit bodies we measured the fruit body area, total number of spores ejected, and the duration of the puff. The rate of spore ejection per unit area of apothecium was directly measured for A. cf. furfuraceus by filming puffs from above under a dissection scope at 2.5×, at 1,000 fps, using a Photron Fastcam high-speed camera. For macroscopic fruiting bodies the different parameters had to be measured separately. Spore range and puff duration were measured by illuminating the spore cloud from the side with bright spot lamps (9) and filming the jet using a Casio EX-ILM F1 HD digital camera. The number of spores was separately measured by holding glass microscope slides above a puffing fruiting body to collect the spores. For smaller fungi, spores were counted using a combination of hand-counts and automatic image analysis of dry spore prints. For larger fungi, spore numbers were estimated by wetting slides, pipetting spore laden fluid off the slide and measuring spore densities using a haemocytometer.

Our data, taken from multiple individual fruit bodies of eight different species, support a broadly conserved mechanism for synchronizing the ejections of spores from different asci. We find that the number of spores increases proportionately to the area of the cup, and that the duration of the puff increases proportionately to diameter (SI Appendix). Although direct imaging of the spatial coordination of spore launch is only possible for small apothecia, such as A. cf. furfuraceus, in other species, the linear increase of puff duration with apothecium diameter suggests that spore launch is also coordinated into waves of ejection that cross the apothecium at speeds of , just as was directly measured for A. cf. furfuraceus. We assume, when comparing real and predicted spore ranges in Fig. 3B, a conserved flux q_s = 3.5 × 10⁴ spores/mm²·s for all species in our study. This local value for the spore flux is obtained by dividing the density of spores per unit area of the apothecium by the time for the wave of ejection to advance 1.5 mm, which is the thickness of the air layer over which spores interact hydrodynamically (see SI Appendix).

To directly measure the air flows within the spore jets PIV was performed on several S. sclerotiorum apothecia. A laser beam (528 nm wavelength at 2.2 W output power) was passed through a cylindrical lens to generate a laser sheet of 1 mm thickness. A petri dish containing a single apothecium was placed on a stage with an apothecium pointing upwards and the laser sheet (oriented vertically) cut across the apothecium’s midsection. Spore ejection was triggered by removing the top lid. Light scattered by the spores moving along the two-dimensional sheet was recorded with a high-speed camera (Phantom v7) at frame rates between 3,000 and 7,207 frames per second and exposure times between 135 and 295 μs. Even at the highest frame rates, runs spanned at least 0.82 s, capturing both the initiation of spore ejection and the propagation of the steady-state jet. MatPIV (31) was used to construct the spore velocity fields from consecutive images. Owing to extremely high launch velocities, particles are recorded as streaks in the basal region. Although this precludes use of PIV in these regions, we were able to estimate the launch speed by dividing the streak length by the exposure time (see SI Appendix and Movie S2). Light scattering from sources other than the spores was identified through the presence of persistent streaks and removed from the statistics.

Simulation of Synchronous Spore Ejection.

Since spore mass loading is large (∼10% in typical simulations) but volume loading is very small (∼10^-4) excluded volume effects can be neglected and spores can be modeled as point forces (32). The Reynolds number based on spore velocity and diameter may exceed 1 after spore ejection (4) but decreases below 1 a few milliseconds after ejection. In this regime spores are independent Stokes particles:

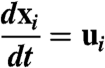[2]

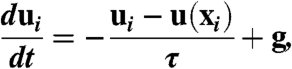[3]

where u_i and x_i are velocity and position of the i-th spore and u(x_i) is the air velocity interpolated from the gridpoints to the particle position. It can be shown that the errors from neglecting finite Reynolds number effects during the first few milliseconds of spore flight lead to small overprediction of the length of the 0.3–2 cm region in which drag from the spores accelerates the surrounding air, but does not alter quantitatively or qualitatively the dynamics of the spore jet above this region (see SI Appendix).

Due to the large Reynolds number of the jet (Re ≈ 200), the dynamics of the surrounding air are solved for by numerical integration of the full Navier-Stokes equations under point forcing:

[4]

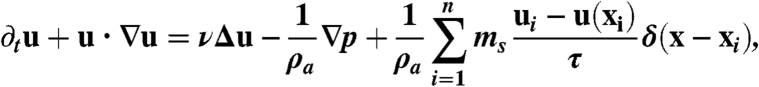[5]

where u is the air velocity field and ν and p are viscosity and pressure. The Lagrangian trajectories of the spores are integrated in time using a second-order Runge-Kutta algorithm. We rewrite the equations in vector potential form (33) and discretize using a pseudospectral method on a 256³ cubic lattice with second-order Runge-Kutta scheme for time marching, periodic boundary conditions, and 8/9 dealiasing. We show that the point force scheme represents adequately the flow field when the grid cell is properly tuned. We test that our numerical results are insensitive to the domain size and to the interpolation and coarsening schemes used to compute the fluid velocity at particle position and to distribute the point force across mesh points (see SI Appendix). We perform four series of simulations to examine: (i) the hydrodynamics of spore/air interaction; (ii) the dependence of the range of the spores on the size of the apothecium; and (iii) the range modification due to delayed launch time of a possible cheater (see SI Appendix).

Dynamics of Air Layer Entrainment by a Sheet of Upward Moving Spores.

To demonstrate that spores cannot improve their ranges by biasing the times at which they are ejected, we analyzed numerically and asymptotically the dynamics of air entrainment close to the fruit body. For small fruit bodies—i.e., precisely those for which a high fraction of ejected spores are sacrificed to initiate the air flows that ultimately enhance spore range—our simulations show that the spores form a single thin sheet that wraps up into a jet outside of the basal region. To determine how close a spore must be to the sheet in order to be entrained with the other spores, we calculate analytically the boundary layer flow induced by the spores. Neglecting variations in the sheet span wise direction, we can describe the sheet dynamics using a single variable z for variation in the direction of spore travel, and one-dimensional fields c_s, u_s, and u_j for, respectively, the number of spores per unit area of sheet, the speed of these spores, and the speed of the air in the sheet. Conservation of mass and momentum within the sheet then give:

[6]

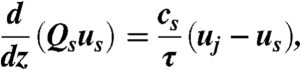[7]

where Q_s is the flux of spores per unit width of sheet, and τ is the Stokes time scale. Through the quantity u_j the dynamics of the spores in the sheet are coupled to the dynamics of the surrounding air. Air within the sheet resists being accelerated by the spores, because a finite thickness of air on either side of the sheet must also be accelerated with the air in the sheet. Quantitatively, the viscous stress from this layer of air balances the drag from the spores:

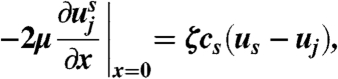[8]

where we have written 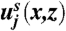for the velocity of the surrounding air, x for the distance from the sheet, μ for the viscosity of the air, and ζ for the Stokes drag coefficient for a single spore. On the sheet: .

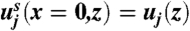In the main text we derive scaling relations for the thickness and speed of the layer of entrained air. These scalings are well supported by our DNS (SI Appendix). For quantitative comparison with the range differences that we compute for cheating and cooperating spores, we determine the full profile of the jet, and thereby the prefactors in our expressions for the thickness and speed of the entrained air layer by introducing scaled variables first proposed by Görtler (see SI Appendix for expanded discussion). If 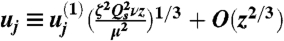for some constant 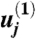, to be determined, then natural variables for analyzing dynamics of velocity variation parallel and perpendicular to the sheet are (respectively):

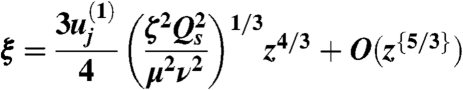[9]

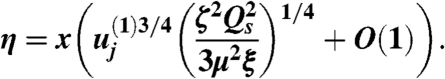[10]

Similarly to our analysis of the circular jet (see SI Appendix), we define a stream function using the ansatz: 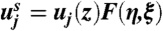, and expand the function F as a power series in powers of ξ^1/4. Keeping only the first term of the expansion F(η,ξ) = ξ^1/4f₁(η) + O(ξ^1/2), and substituting into the steady boundary layer equations ((29), SI Appendix), we see that f₁ must solve the Falkner-Skan equation:

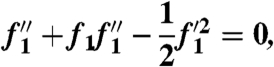[11]

subject to boundary conditions f₁(0) = 0, 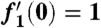, and 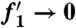as η → ∞. We solve this third order ordinary differential equation by integrating from η = 0, and numerical shooting on the unknown initial condition 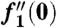(34). We find 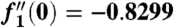and obtain the value of the constant 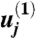, by substituting the similarity form of the velocity gradient into Eq. 8:

[12]

Finally we determine the coefficient for the boundary layer thickness from the asymptotic behavior of f₁ as η → ∞. From our integration of Eq. 11 we find f₁ → 1.0628, 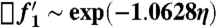, so that for x ≳ δ: 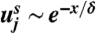with 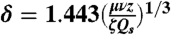. On taking these values for the thickness and center line speed the self-similar profile of the jet agrees almost exactly with the results of our DNS (Fig. 5B).