Distributed representation of spectral and temporal information in rat primary auditory cortex

Abstract

Modulations of amplitude and frequency are common features of natural sounds, and are prominent in behaviorally important communication sounds. The mammalian auditory cortex is known to contain representations of these important stimulus parameters. This study describes the distributed representations of tone frequency and modulation rate in the rat primary auditory cortex (A1). Detailed maps of auditory cortex responses to single tones and tone trains were constructed from recordings from 50–60 microelectrode penetrations introduced into each hemisphere. Recorded data demonstrated that the cortex uses a distributed coding strategy to represent both spectral and temporal information in the rat, as in other species. Just as spectral information is encoded in the firing patterns of neurons tuned to different frequencies, temporal information appears to be encoded using a set of filters covering a range of behaviorally important repetition rates. Although the average A1 repetition rate transfer function (RRTF) was low-pass with a sharp drop-off in evoked spikes per tone above 9 pulses per second (pps), individual RRTFs exhibited significant structure between 4 and 10 pps, including substantial facilitation or depression to tones presented at specific rates. No organized topography of these temporal filters could be determined.

1. Introduction

Cortical neurons are often precisely tuned for relevant features of sensory stimuli. This strategy of analyzing sensory information with neural filters distributed across the cortical surface results in the representation of individual stimuli by patterns of activity in large populations of neurons. In many sensory systems, neurons with varying filter properties are organized into ‘maps’ (Pubols and Pubols, 1971; Hubel and Wiesel, 1968; Merzenich and Brugge, 1973). Receptor surfaces, for example, are commonly systematically mapped in the cortex (Schreiner, 1992).

The auditory sensory epithelium, the cochlea, has a one-dimensional surface representing sound frequency. In every mammalian species investigated to date, the topography of the cochlea is maintained in its representation within the primary auditory cortex (Merzenich and Brugge, 1973; Merzenich et al., 1975, 1976; McMullen and Glaser, 1982; Aitkin et al., 1986; Kelly et al., 1986; Sally and Kelly, 1988; Dear et al., 1993; Thomas et al., 1993; Stiebler et al., 1997; Batzri-Izraeli et al., 1990; Suga and Jen, 1976; Tunturi, 1950; Imig et al., 1977; Reale and Imig, 1980; Hellweg et al., 1977; Romani et al., 1982; Jen et al., 1989). Neurons tuned to particular sound frequencies are organized from low to high across the cortex. Because the cortex is a two-dimensional structure with a columnar organization, stimulus features can be mapped along the other (‘iso-frequency’) representational dimension (Imig and Brugge, 1978; Middlebrooks et al., 1980; Scheich, 1991; Schreiner, 1992; Ehret, 1997). In the cat, for example, tuning curves are narrower at the center of the isofrequency contour and broader near the ends. In this study we examined the topography of both spectral and temporal filters in the rat auditory cortex.

The rat auditory system has been used in a number of neuroanatomical studies that have indicated that the thalamocortical system is similar to that of other mammals (Roger and Arnault, 1989; Clerici and Coleman, 1990; Winer and Larue, 1987; Arnault and Roger, 1990; Shi and Cassell, 1997). Despite detailed descriptions of cytoarchitecture and connectivity in the rat, few detailed electrophysiological studies have been conducted in the rat auditory cortex. Sally and Kelly (1988) investigated the organization of the frequency map in rat primary auditory cortex (A1) and demonstrated that high to low frequencies are represented from anterior to posterior. This organization parallels that defined in detailed mapping studies conducted in A1 of the gray squirrel (Merzenich et al., 1976). Rat A1 neurons were found to respond to tones with phasic short latency responses. Unlike cats and monkeys, rat A1 neurons exhibit little non-monotonicity (Sally and Kelly, 1988).

Rat vocalizations exhibit modulations in the 2–20 Hz range (Kaltwasser, 1990). Gaese and Ostwald (1995) used sinusoidal amplitude modulated (SAM) stimuli to investigate temporal coding in rat auditory cortex. The majority of responses had band-pass transfer functions for modulation rate, preferring rates between 8 and 12 Hz. The sinusoidal nature of the stimuli used makes it difficult to determine whether the cortex is band-pass for repetition rates of other simple stimuli because amplitude slope and repetition rate cannot be varied independently with SAM stimuli (Eggermont, 1991). The auditory cortex responds briskly to transients (Heil, 1997a,b). It is likely that the band-pass modulation transfer functions (MTFs) observed resulted because the rise time at low modulation rates was too slow to be detected by auditory cortex neurons (Eggermont, 1998).

In this study, the neural responses to single and repeated tones were investigated in detail to define the fundamental aspects of the distributed representations of basic spectral and temporal information in rat auditory cortex.

2. Methods

This study is based on neural responses collected from 440 microelectrode penetrations into the right primary auditory cortex in nine adult female Sprague-Dawley rats. Surgical anesthesia was induced with sodium pentobarbital (50 mg/kg). Throughout the surgical procedures and during the recording session, a state of areflexia was maintained with supplemental doses of dilute i.p. pentobarbital (8 mg/ml). The trachea was cannulated to ensure adequate ventilation and to minimize breathing-related noises. The skull was supported in a head holder. The cisterna magna was drained of CSF to minimize cerebral edema. After reflecting the temporalis muscle, auditory cortex was exposed via a wide craniotomy and the dura mater was resected. The cortex was maintained under a thin layer of viscous silicone oil to prevent desiccation. The location of each penetration was reproduced on a 40× digitized image of the cortical surface and sited with reference to the surface microvasculature.

The primary auditory cortex was defined on the basis of its short latency (8–20 ms) responses and its continuous topography of ‘best frequency’ (BF, frequency to which neurons respond at lowest intensity). Responsive sites that exhibited clearly discontinuous best frequencies and either long latency responses, unusually high thresholds, or very broad tuning were considered to be non-A1 sites. Penetration sites were chosen to avoid damaging blood vessels while generating a detailed and evenly spaced map. The boundaries of the map were functionally determined using non-responsive and non-A1 sites.

Recordings were made in a shielded, double-walled sound chamber (IAC). Action potentials were recorded simultaneously from two Parylene-coated tungsten mi-croelectrodes (FHC, 250 μm separation, 2 MΩ at 1 kHz) that were lowered orthogonally into the cortex to a depth of ~550 μm (layers IV/V). The electrodes were oriented such that they were usually within the same isofrequency contour. The neural signal was filtered (0.3–8 kHz) and amplified (1000×). Action potential waveforms were recorded whenever a set threshold was exceeded, allowing off-line spike sorting using Autocut software. Although most responses in this study represented the spike activity of several neurons, single units were separated when possible, confirming that single units exhibited tuning that was qualitatively similar to multi-unit response samples.

Monaural stimuli were delivered to the left ear via a calibrated ear phone (STAX 54) positioned just inside the pinna. Frequencies and intensities were calibrated using a B&K sound level meter and a Ubiquitous spectrum analyzer. Two types of stimuli were generated using Brainwave (Datawave). Auditory frequency response tuning curves were determined by presenting 45 frequencies spanning 3–4.5 octaves centered on the approximate best frequency of the site. Each frequency was presented at 15 intensities ranging between 0 and 75 dB (675 total stimuli). Tuning curve tones were randomly interleaved and separated by 500 ms. In four animals, repetition rate transfer functions (RRTFs) were derived at all recording sites by randomly interleaving 12 repetitions of 16 different tone repetition rates (3–25 pulses per second (pps)). A 2 s silent period separated the tone trains. The frequency of the RRTF tones was set to the frequency that resulted in consistent vigorous responses at both of the recording sites. In a few cases, tuning curves did not overlap and trains of two different tone frequencies were used. RRTF stimuli were presented at 70 dB SPL. All tonal stimuli used in this study were 25 ms long, including 3 ms rise and fall times.

Tuning curve parameters were defined by an experienced blind observer using custom software that displayed raw spike data without reference to the frequencies and intensities that generated the responses. For each tuning curve, best frequency, threshold, and bandwidth (10, 20, 30 and 40 dB above threshold) measurements were made. The minimum latency was defined as the time from stimulus onset to the earliest consistent response for all 15 intensities, for the three frequencies that were nearest the BF (45 stimuli). The signal to noise ratio is the number of spikes evoked by a 70 dB tone near the best frequency within a 35 ms window divided by the number of spikes expected due to spontaneous activity.

RRTF data were quantified by determining the number of spikes that arrived within a fixed window (4–39 ms) after tone onset. In this study the RRTF is the average number of spikes for each of the last five tones of the six tone train plotted as a function of repetition rate. To allow for comparisons across sites, normalized spike rates were generated by dividing the number of spikes per tone by the number of spikes in response to a single tone presented in isolation (first tone). Normalized spike rates above one indicate facilitation, while rates less than one indicate adaptation of the neural response relative to the response to an isolated tone. The highest repetition rate that generates a consistent multi-unit response (4–39 ms after tone onset) of one spike per tone (above background activity) is defined as the maximum following rate.

Voronoi tessellation (Matlab, MathWorks, Inc.) was used to generate polygons from a set of non-uniformly spaced points such that every point in the polygon was nearer to the sampled point than to any other (Kayser and Stute, 1989). These polygons served two purposes. (1) They provided an easy method of visualizing the cortical topography. (2) They allowed area information to be estimated from discretely sampled penetrations, by assigning each point on the cortical surface the qualities of the closest sampled point. For example, this simple measure generates reliable estimates of the percent of the cortex that responds to a given frequency-intensity combination. The percent of A1 neurons responding to a given stimulus was estimated by adding all of the areas of the penetrations that responded, divided by the total area of A1. This measure allows higher sampling of cortical regions of particular interest without introducing bias into group data because densely sampled regions result in smaller polygons that contribute less to this measure. By contrast, the percentage of sites exhibiting a particular response characteristic can be easily biased by non-uniform sampling densities. As it was often not possible to perfectly circumscribe A1 with penetrations that were either non-responsive or clearly non-A1, in some these cases borders were estimated by connecting non-A1 sites to approximate the most likely A1 shape based on other maps.

3. Results

3.1. Size and location of A1

Auditory cortex in the rat can be reliably located using the lateral suture and underlying blood vessels as landmarks (Sally and Kelly, 1988). A1 is located ~1 mm dorsal to the horizontal portion of the suture and ~1.5 mm posterior to the vertical portion of the suture. The widest anterior-posterior extent was 1.9 ± 0.2 mm (mean ± S.E.M.). The widest dorsal-ventral extent was 1.5 ± 0.2 mm. The average A1 area was 1.92 ± 0.16 mm².

3.2. Tuning curves

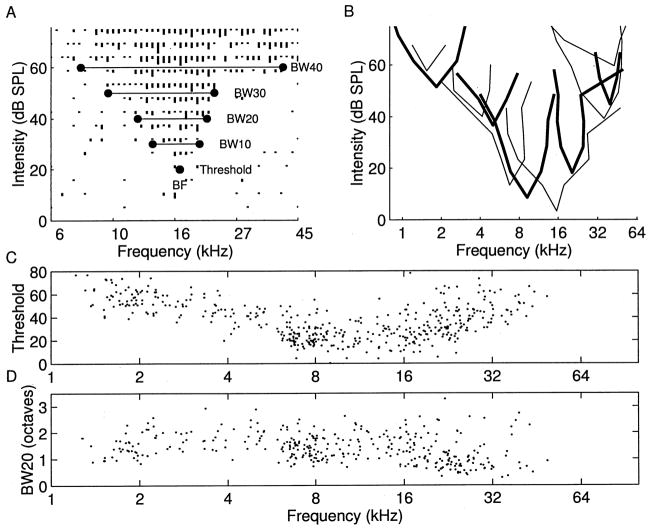
Rat A1 frequency-intensity tuning curves derived for almost all neuronal samples were V-shaped, like most tuning curves recorded in rodents (Sally and Kelly, 1988). Fig. 1A illustrates a representative tuning curve and the parameters derived from it, including threshold and bandwidth. A range of tuning curve shapes were observed, although the basic V-shape predominated (Fig. 1B). The ‘best frequency’ is the frequency that evokes a consistent neural response at the lowest tone intensity. We recorded from units at 440 sites in nine animals with best frequencies ranging from 0.8 to 60 kHz. Both behavioral thresholds and neural thresholds were higher near the extremes of the hearing range (Kelly and Masterton, 1977). The distribution of best frequencies was observed to be fairly regular across the entire rat hearing range (Fig. 1C). The average bandwidths were 0.92 ± 0.41, 1.42 ± 0.54, 1.73 ± 0.62, and 2.08 ± 0.68 octaves (mean ± S.D.) at 10, 20, 30 and 40 dB above threshold, respectively. Although there was substantial variability in the degree of spectral selectivity across the frequency map, tuning curves with high BFs tended to be more sharply tuned, compared to lower frequency tuning curves (Fig. 1D). For example, the average bandwidth 20 dB above threshold for sites above 20 kHz was 1.09 octaves, compared to 1.53 for sites below 20 kHz (t-test, P <0.00001).

Fig. 1.

A: Tuning curve for representative rat A1 penetration. BF is the frequency that elicits a consistent neural response at the lowest intensity, threshold. BW is the range of frequencies the neurons are responsive to at the specified intensity above threshold. B: Eleven tuning curve outlines from A1 in a single animal. C: Thresholds to elicit excitatory responses at BF, for neurons sampled from nine animals. D: Bandwidths at 20 dB above threshold as a function of BF.

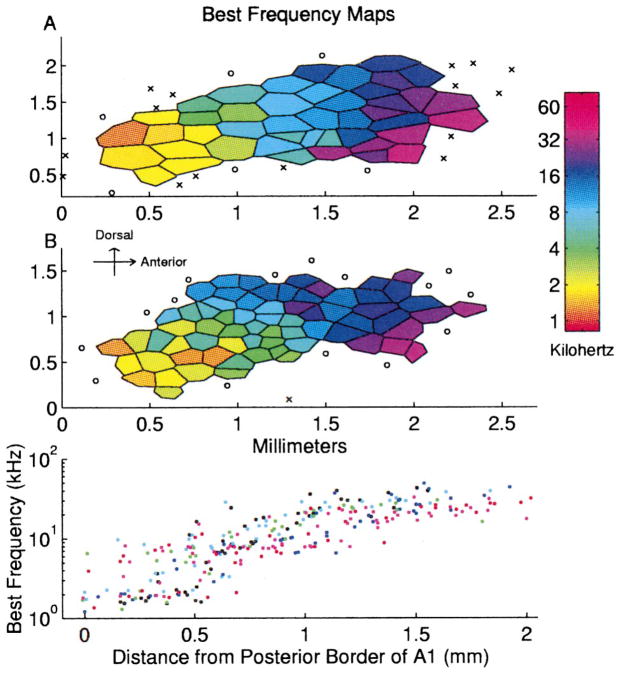
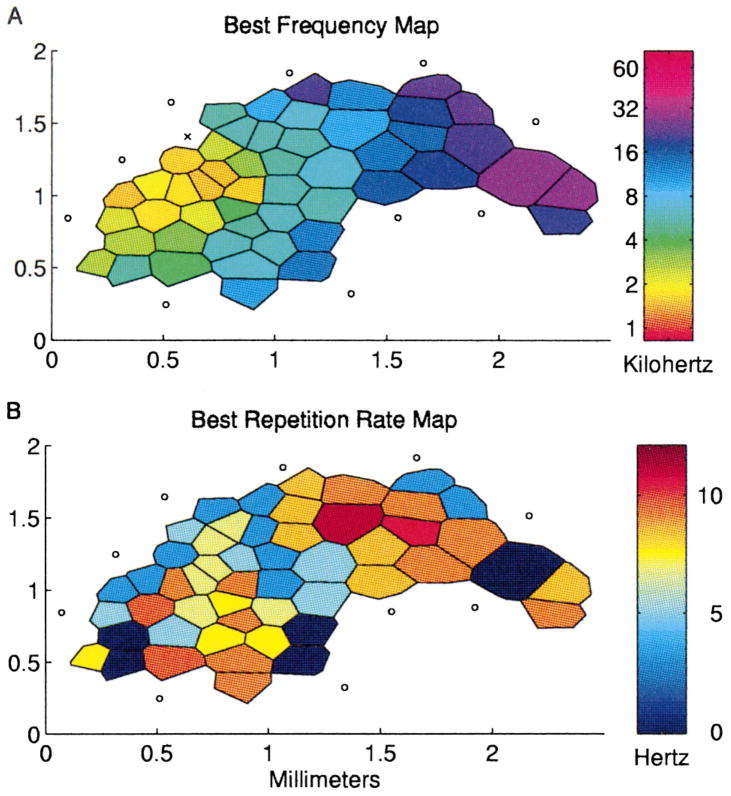
The best frequencies of A1 neurons increased from posterior to anterior, as illustrated in maps from two representative rats (Fig. 2A,B). Each polygon in a map represents one penetration; the color indicates the best frequency of neurons sampled at that site. Continuous topography of frequency tuning was observed in every animal. The bottom part of Fig. 2 illustrates the relationship between the distance from the posterior border of A1 and the best frequency of each penetration from six animals. Fig. 3A shows all of the tuning curve tips from the map shown in Fig. 2B. The reproducibility of these maps and the relatively even distribution of frequency tuning make the rat a useful species for studying the effects that behavioral training and other plasticity paradigms have on cortical representations of sound frequency.

Fig. 2.

A, B: Representative BF maps of primary rat auditory cortex from two adult rats. Each polygon represents one penetration. Color represents each site’s best frequency. Non-responsive and auditory responding non-A1 sites are marked ○ and ×, respectively. Bottom panel: Best frequency as a function of distance from the posterior border of A1. Each color represents data from an individual animal.

Fig. 3.

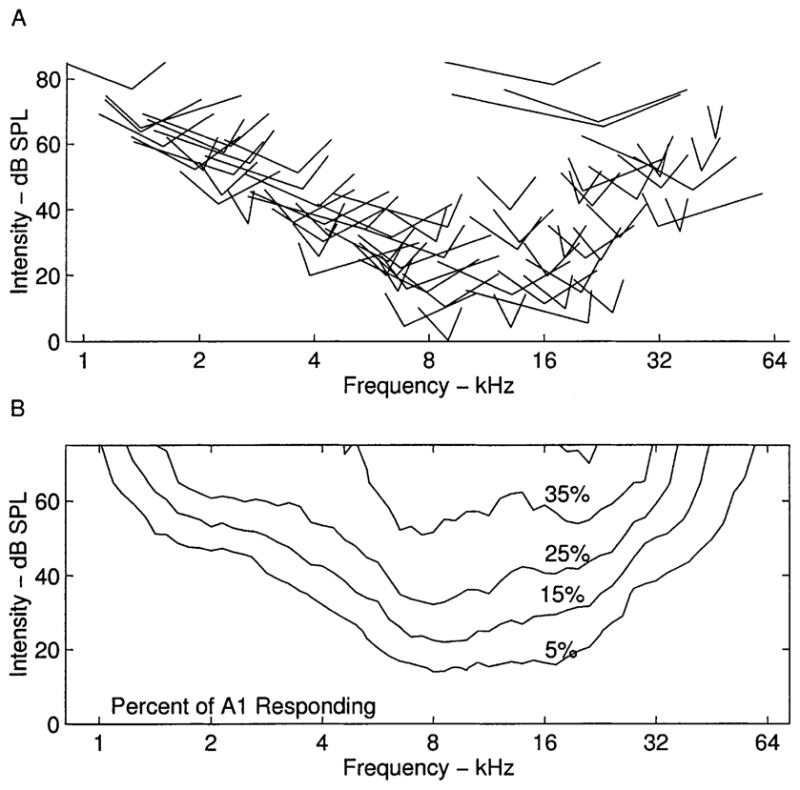
A: Tuning curve tips for all of the penetrations from one rat (Fig. 2B). The tip of each V depicts the minimum threshold for each site. Width of the V represents tuning curve width 10 dB above threshold. B: Mean percent of the cortical surface that responds to a tone of any frequency/intensity combination.

Although A1 topography is well ordered for tones presented near threshold, highly overlapping populations of neurons respond to loud tones. For example, more than one-fourth of the cortical surface is activated by a 40 dB 8 kHz tone. The average percent of the cortex responding to any frequency-intensity combination was derived by overlaying each of the tuning curve outlines weighted by the area of the polygons (Fig. 3B). This measure is useful in plasticity studies because it can be used to quantify changes in the percent of the cortex representing stimulus features (Kilgard and Merzenich, 1998).

3.3. Topography

The only recorded response property that varied systematically across the isofrequency contour was the response strength, quantified as the signal to noise ratio. Although this tendency was not obvious in every map, it was clear in the group data. The median (10–90 percentile) signal to noise ratio within 0.25 mm of the A1 midline running anterior to posterior was 18 (8–59), compared to 12 (5–42) for sites greater than 0.25 mm from the midline. No consistent mapping of response latency, stimulus threshold, or frequency tuning bandwidth was observed.

3.4. Repetition rate transfer functions

RRTFs were derived at 142 sites from responses to trains of six short tone pips presented at repetition rates ranging from 3 to 25 pps. The carrier frequency of the RRTF tones was selected to be near the best frequency of each site. On average, 1.9 ± 0.9 (mean ± S.D.) spikes were evoked by a tone in isolation within the sampling window. The spontaneous rates over this interval ranged from about 0.025 to 0.25 spikes/s. The minimum latency of driven responses was 15 ± 5 ms.

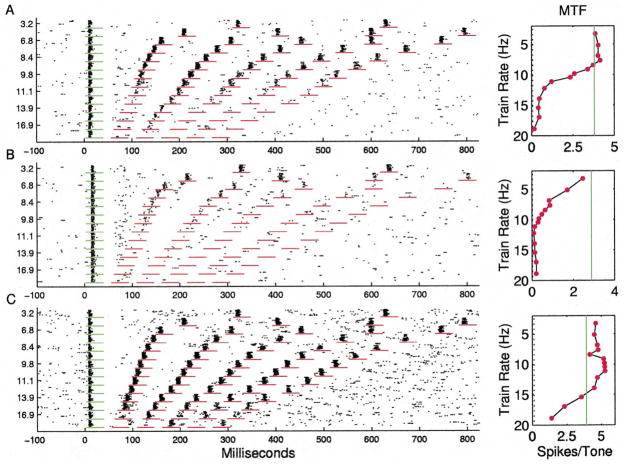
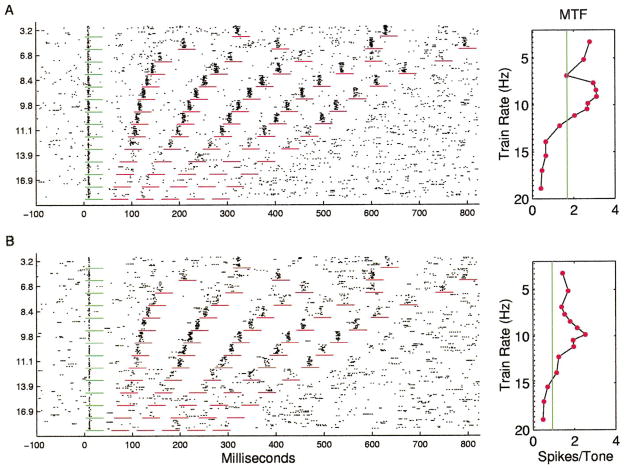
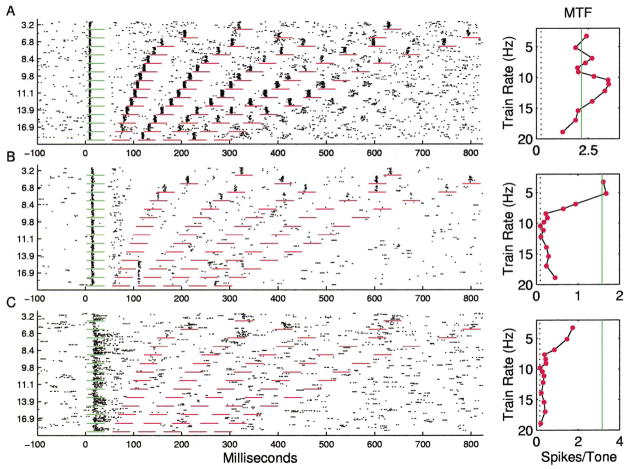
Many sites responded with approximately the same number of spikes per tone at repetition rates less than 8 pps, with sharply decreasing number of spikes per tone from 10 to 14 pps, and few spikes to tones presented at rates of more than 15 pps (Fig. 4A). The RRTF was quantified by measuring the number of spikes occurring in a fixed window (35 ms) after each stimulus. The plot next to the dot rasters shows the average number of spikes for each of the five tone pips after the first (60 stimulus presentations/symbol). The solid line shows the average number of spikes for the first stimulus in the train (168 presentations), and the dotted line shows the number of spikes expected in a 35 ms sampling window due to spontaneous activity. The average RRTFs from different sites were normalized by dividing the number of spikes for each tone by the number of spikes in response to the first tone. The mean response of the 142 A1 RRTFs derived in this study clearly shows that the average normalized response of the cortex to repeated stimuli was a low pass function that fell off rapidly above 10 pps (Fig. 5A).

Fig. 4.

A: Dot raster and repetition rate transfer function for an A1 site representative of the median response. Short horizontal lines mark time windows used for RRTF quantification. Vertical solid lines in panels to the right mark the average response to first tone. Vertical dotted line marks spontaneous rate. B: A1 RRTF with an unusually low (7 pps) cutoff. C: A1 RRTF with unusually fast (high repetition rate) following.

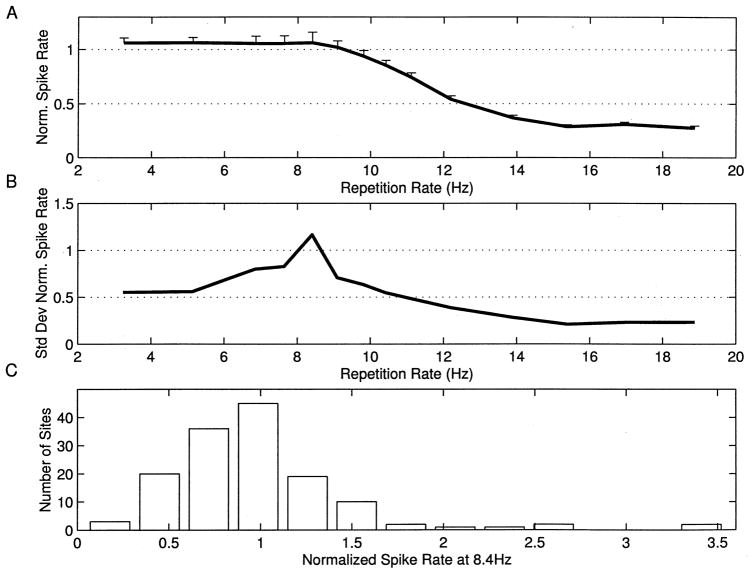
Fig. 5.

A: Mean normalized spike rate as a function of repetition rate with standard errors of the mean. B: Standard deviation of normalized spike rate as a function of repetition rate. C: Distribution of normalized spike rates at 8.4 pps. Examples shown in Figs. 4 and 7 have ratios of 0.97, 0.22, 1.07, 1.83, and 1.9 at 8.4 pps, respectively.

Although simple low-pass RRTFs were common, it is important to note that a substantial diversity of temporal response properties was observed across sites. In general, cortical RRTFs had a significant amount of structure from 2 to 9 pps, but reliably fell off above about 10 pps. The standard deviation of the normalized spike rate for repetition rates near 8 pps was as large as the mean, indicating that a range of temporal filter functions are used to represent time-varying inputs within A1 (Fig. 5B). Responses to 8.4 pps trains, for example, ranged from substantial adaptation to strong facilitation (more than twice as many spikes for each tone in the train compared to single tones in isolation (Fig. 5C). Some sites were simply slow and followed poorly at repetition rates faster than 8 pps (Fig. 4B), while other sites could respond to each event at 15 pps and followed every other stimulus at 20 pps (Fig. 4C). In addition to these examples, which represent simple shifts in the maximum following rate of cortical neurons, many sites had temporal response properties that included strong adaptation or facilitation at specific repetition rates (Fig. 6). In a few cases, the number of spikes per tone was changed two-fold by increasing the interval between tone pips by as little as 10 ms.

Fig. 6.

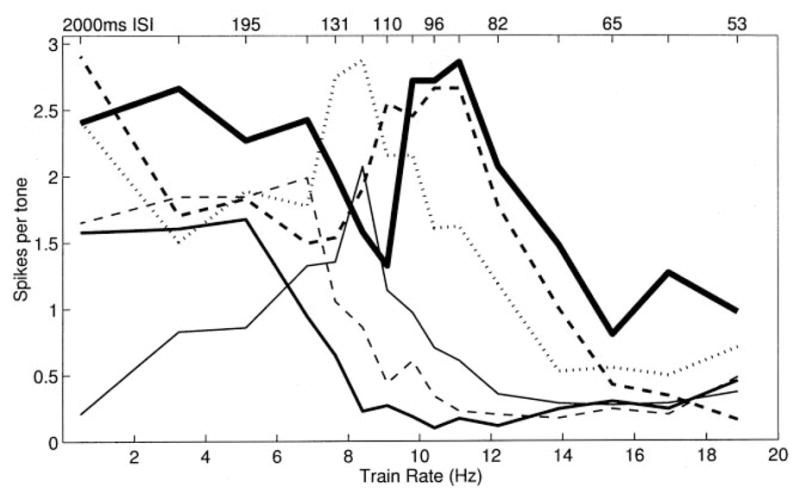
RRTFs for six penetrations with strong tuning for specific repetition rates. Note that the sum of these RRTFs has a low-pass shape.

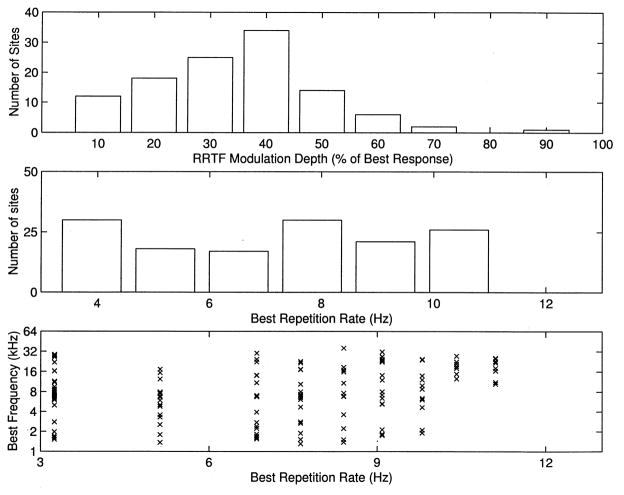
Both notched and band-pass RRTFs were observed in rat A1 (Fig. 7A,B). In the example of a notched RRTF, only half as many spikes were evoked per tone at 7 pps compared to 9 pps. Such temporal filters transform information about repetition rate into modulation of the number of evoked spikes per tone. Thus temporal information is expressed in both the timing of neural discharges and the number of action potentials evoked by each stimulus event. In approximately 60% of A1 sites, the response to some range of repetition rates slower than the best rate resulted in more than a 30% decrease in the number of spikes per tone compared to the best rate (Fig. 8A). Thus, although the mean RRTF had no peaks, most individual sites preferred particular repetition rates.

Fig. 7.

A: Example of a notched RRTF. B: Example of a band-pass RRTF.

Fig. 8.

A: Distribution of RRTF modulation depth, expressed as the minimum response for repetition rates less than the best rate divided by the response to the best rate. The examples in Figs. 4 and 7 have depths of 8, –, 26, 47 and 63%, respectively. Note that only sites with best repetition rates greater than 4 pps are shown. B: Distribution of best repetition rates (rate that evokes the most spikes per tone). C: Best repetition rate as a function of BF.

The distribution of best rates (rates that evoke the maximum number of spikes per tone pip) was fairly even; there were approximately equal numbers of sites preferring repetition rates ranging from about 12 pps to less than 3 pps (Fig. 8B). It is interesting to note that best repetition rates also appeared to be roughly evenly distributed when plotted as a function of best frequency, suggesting that any band of cortex representing a significant range of frequencies contained neurons that ‘represented’ all rates less than 12 pps (Fig. 8C). Fig. 9 illustrates the ‘topography’ of best repetition rate in relation to best tone frequency. Although similar repetition rates were sometimes clustered together in individual animals, there were no consistent patterns of such clustering across animals.

Fig. 9.

Representative map of A1 from one animal with the best tone frequency and best repetition rate labeled for each penetration. Reliable RRTFs could not be generated from sites labeled zero.

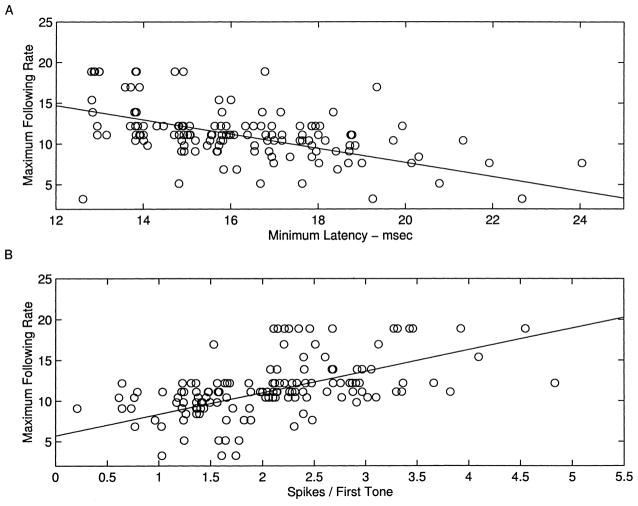
Maximum following rate was correlated with both minimum latency and number of spikes in response to an isolated tone (Fig. 10). The average minimum latency for sites that were able to follow tones presented at rates above 11 pps was 15.3 ± 0.2 ms, compared to 17.3 ± 0.3 ms for the sites with maximum rates less than 11 pps (P <0.00001). The mean driven response to an isolated tone was 2.3 ± 0.1 spikes for the fast sites compared to 1.6 ± 0. 1 for the slower sites (P <0.00001). Thus, as reported in cat A1, vigorous, short latency responses tended to be able to follow repeated stimuli at faster rates (Schreiner et al., 1997; Raggio and Schreiner, 1994; Brosch and Schreiner, 1997).

Fig. 10.

A, B: Scatter plots of maximum following rate as a function of minimum latency and spikes evoked per tone, with best linear fits.

Some sites exhibited multiple cycles of repetitive spiking following stimulus trains of 10–15 pps (Fig. 11A), consistent with these stimuli evoking oscillations in cortical excitability. At the same time, the diversity of temporal responses indicates that A1 neurons can exhibit more complicated dynamics than simple oscillations. As an extreme example, two sites responded with a burst of spikes at a fixed latency relative to the first tone when the first tone was followed closely by a second tone (Fig. 11B).

Fig. 11.

A: An RRTF that exhibits oscillatory responses after trains of greater than 10 pps. B: Unusual A1 RRTF. Note the fixed-latency response following the second tone presented at greater than 14 pps. C: Representative RRTF for the posterior auditory field. Note sustained discharge and strong adaptation to repeated stimuli.

3.5. Non-A1 responses

Several auditory fields surrounding A1 have been shown to receive projections from regions of the medial geniculate other than the ventral division (Arnault and Roger, 1990; Romanski and LeDoux, 1993; Winer and Larue, 1987). The posterior field was the easiest to identify because neurons in that region responded fairly well to tones. Additionally, this field appeared to have a tonotopic organization that was a mirror image of A1. Neurons in this field had longer latencies and adapted to repeated stimuli even at low stimulus repetition rates (Fig. 11C). Responses were more sustained compared to A1, where neurons usually responded with only a short burst of spikes at tonal onsets. As observed in several other rodent species, tuning curves in the other non-primary fields generally responded poorly to tones and had high thresholds, long latencies, and/or broad tuning (Redies et al., 1989; Stiebler et al., 1997; Thomas et al., 1993; Sally and Kelly, 1988). No clear representational topography of these peri-A1 zones could be determined from our data sampling which was focused on A1.

4. Discussion

The aim of this study was to elaborate how the primary auditory cortex in the rat represents spectral and temporal features of auditory stimuli. Detailed maps were constructed with data collected from nine adult animals. Tuning curves were derived for neurons sampled at every penetration to investigate the organization of tuned responses for tone frequency. Trains of short tone pips presented at various rates were used to investigate the nature of the distributed representations of repetition rate.

Rat A1 neurons have V-shaped tuning curves and respond to tones with phasic, short latency responses. Minimum thresholds were consistent with published behavioral thresholds (Kelly and Masterton, 1977). Bandwidths at 20 dB above threshold ranged from 0.4 to 2.5 octaves. Rat A1 exhibited an orderly map of increasing tone frequency from posterior to anterior (Sally and Kelly, 1988). In cat A1, most response characteristics (including latency, monotonicity, threshold, dynamic range, and tuning curve width) exhibit systematic variations across the isofrequency contour (for review, see Ehret, 1997). Response strength was the only response characteristic that varied systematically across the dorsal-ventral extent of A1 in the rat. It may not be surprising that no other topographies were observed, given the variability of response topographies observed in the cat and the size of rat A1 (2 mm² compared to 12 mm² in a cat).

The majority of rat A1 neurons responded well to trains of tone pips presented at rates below 10 pps. However, substantial variability exists in temporal response properties. A few sites did not follow well at rates above 5 pps, while others responded well to each tone presented at 15 pps. Some sites exhibit response profiles that manifested oscillatory processes. As others have suggested, this variability in RRTFs may represent an important coding strategy for temporal information (Dinse et al., 1997; Schreiner and Langer, 1986; Schreiner et al., 1997; Eggermont, 1991; Buonomano and Merzenich, 1995). These results are consistent with a distributed representation of repetition rate such that any frequency band of substantial width contains neurons that selectively prefer stimulus rates ranging from about 2 to 15 pps. In the mynah bird analogue of the mammalian auditory cortex, an orderly representation of repetition rate tuning was recorded orthogonal to the frequency map (Hose et al., 1987). Although nearby cortical penetrations often exhibited similar RRTFs in our study, the resolution of this data sample makes it impossible to definitively demonstrate whether or not repetition rate is systematically mapped in rat auditory cortex.

If individual neurons expressed the same degree of variability locally as was observed from penetration to penetration across A1, individual multi-unit RRTFs should exhibit the low-pass property observed in the population RRTF. The high degree of structure in the RRTFs recorded in this study provides evidence that local groups of neurons have similar temporal response properties, although it remains unclear whether this is due to local similarity of intrinsic cellular properties, local network interactions, or both. Strong local similarities of response characteristics have been documented in cats by comparing the responses of single units sorted from the same electrode (Imig et al., 1990; Schreiner and Sutter, 1992; Shamma et al., 1993).

The low-pass nature of the RRTFs described in this study is different from the predominately band-pass MTFs observed by Gaese and Ostwald (1995). It appears that differences in the stimuli presented and analysis performed account for the apparent discrepancy. The most important is that SAM tones were used in the previous study, while tones with a constant amplitude ramp were used in the present study. Primary auditory cortex responds well to intensity transients, while it responds poorly to stimuli with slowly increasing amplitude. Thus, A1 neurons may be tuned for 10 Hz SAM stimuli not because they cannot follow slower rates but because they prefer steeper-amplitude ramps. Consistent with similar findings in cat A1 (Eggermont, 1998), we observed that the mean RRTF for A1 neurons was clearly low-pass when a fixed amplitude ramp was used.

Additionally, Gaese and Ostwald (1995) quantified MTFs using either a synchronization measure or a spike rate measure that was not normalized to the number of stimulus cycles. The shallow amplitude ramps of slow SAMs provide the cortex with an impoverished time mark for stimulus onset and result in a wider distribution of spike latencies that leads to lowered synchronization scores (Eggermont, 1991). The spike rate measure used in the previous study was normalized to stimulus power and not to number of stimulus cycles. Thus, in addition to having a steeper amplitude ramp, the 10 Hz SAM stimulus had twice as many onsets as the 5 Hz stimulus. Our stimuli allowed spikes per tone onset to be measured as a function of repetition rate, while maintaining constant stimulus power. Both studies clearly demonstrate that most rat A1 neurons do not respond well to stimuli above about 15 pps.

Phillips et al. (1989) recorded the responses of cat A1 neurons to trains of short tone pips, and observed exclusively low-pass responses. Interestingly, they did not observe any facilitation of spike rate to tones during a train compared to isolated tones. In one-fourth of the sites in our study, stimulus repetition resulted in a more than 30% increase in spikes per tone compared to a single tone in isolation. Phillips adjusted the frequency at each site precisely to that site’s best frequency, while in the current study, frequencies were selected that evoked the strongest responses in the two simultaneously recorded penetrations. Phillips suggested that facilitation may only occur when off-BF frequencies are used. Systematic studies are needed to determine whether tones delivered to different regions of the tuning curve can have different RRTFs.

An important parameter that was not varied in our study was stimulus duration. It will be interesting to determine the contribution of stimulus off-time in cortical RRTFs by increasing stimulus duration.

The reduction in the ability of cortical neurons to follow repetitive stimuli compared to subcortical auditory nuclei can be explained by strong inhibition following excitatory input. Inhibitory influences would create a refractory period and generate a low-pass temporal response profile. The richness of RRTFs observed in this study likely results from interactions between a number of factors shaping cortical processing of temporal information (Buonomano et al., 1997; Buonomano and Merzenich, 1995). Paired pulse facilitation and depression clearly play a role. Rebound from inhibition could provide facilitation over a specific range of repetition rates. Intrinsic properties have also been implicated in shaping the timing of cortical responses (Langner, 1992).

Oscillatory responses have been observed in auditory cortex in a number of studies in rats, cats, and monkeys (Schreiner and Urbas, 1986; Eggermont and Smith, 1995; Sally and Kelly, 1988; Dinse et al., 1997). These oscillations appear to influence cortical responses for up to several hundred milliseconds after an initial excitatory input. Oscillations are commonly observed in the auto-correlations of spontaneous activity, and can be reset by single tone pips. Two studies have shown that best modulation frequencies are correlated with intrinsic oscillation rates (Kenmochi and Eggermont, 1997; Dinse et al., 1997). A presence of notched RRTFs in our data may be further evidence that oscillatory processes shape temporal information processing. This relationship warrants further study, including correlating intrinsic and spontaneous oscillatory response properties with RRTF notch location and width.

Rats have been used in a wide range of learning paradigms using auditory stimuli. To infer neural mechanisms involved in this learning, it is important to better understand the representation of auditory stimuli in normal animals. This study demonstrates that rat auditory cortex has a distributed representation of both spectral and temporal information. Regions of A1 representing a sufficient range of carrier frequencies contain neurons that can act as temporal filters that respond well to rates ranging from two to 15 pps. This is consistent with the progressive reduction in the maximum following rate of temporal modulations from auditory nerve to higher stations of the auditory pathway (Langner, 1992). Bilateral lesions of rat auditory cortex have been shown to abolish differentiation between unmodulated and 5 Hz AM modulated tonal stimuli in a simple classical conditioning paradigm, leaving differentiation of 50 and 500 Hz modulations intact (Grigor’eva and Vasil’ev, 1981). These results indicate that the relatively long integration time of cortical neurons is useful for extracting temporal stimulus features below 20 Hz.

In the present study, we have shown that rat primary auditory cortex is similar to other mammalian species. Spatial and temporal information is encoded in the firing patterns of neurons exhibiting a wide range of response tuning profiles. These results suggest that the representation of stimulus parameters of complex auditory signals are likely to involve spike rate, place and temporal coding strategies.