A Novel Framework for Predicting In Vivo Toxicities from In Vitro Data Using Optimal Methods for Dense and Sparse Matrix Reordering and Logistic Regression

Abstract

In this work, we combine the strengths of mixed-integer linear optimization (MILP) and logistic regression for predicting the in vivo toxicity of chemicals using only their measured in vitro assay data. The proposed approach utilizes a biclustering method based on iterative optimal reordering (DiMaggio, P. A., McAllister, S. R., Floudas, C. A., Feng, X. J., Rabinowitz, J. D., and Rabitz, H. A. (2008). Biclustering via optimal re-ordering of data matrices in systems biology: rigorous methods and comparative studies. BMC Bioinformatics 9, 458–474.; DiMaggio, P. A., McAllister, S. R., Floudas, C. A., Feng, X. J., Rabinowitz, J. D., and Rabitz, H. A. (2010b). A network flow model for biclustering via optimal re-ordering of data matrices. J. Global. Optim. 47, 343–354.) to identify biclusters corresponding to subsets of chemicals that have similar responses over distinct subsets of the in vitro assays. The biclustering of the in vitro assays is shown to result in significant clustering based on assay target (e.g., cytochrome P450 [CYP] and nuclear receptors) and type (e.g., downregulated BioMAP and biochemical high-throughput screening protein kinase activity assays). An optimal method based on mixed-integer linear optimization for reordering sparse data matrices (DiMaggio, P. A., McAllister, S. R., Floudas, C. A., Feng, X. J., Li, G. Y., Rabinowitz, J. D., and Rabitz, H. A. (2010a). Enhancing molecular discovery using descriptor-free rearrangement clustering techniques for sparse data sets. AIChE J. 56, 405–418.; McAllister, S. R., DiMaggio, P. A., and Floudas, C. A. (2009). Mathematical modeling and efficient optimization methods for the distance-dependent rearrangement clustering problem. J. Global. Optim. 45, 111–129) is then applied to the in vivo data set (21.7% sparse) in order to cluster end points that have similar lowest effect level (LEL) values, where it is observed that the end points are effectively clustered according to (1) animal species (i.e., the chronic mouse and chronic rat end points were clearly separated) and (2) similar physiological attributes (i.e., liver- and reproductive-related end points were found to separately cluster together). As the liver and reproductive end points exhibited the largest degree of correlation, we further analyzed them using regularized logistic regression in a rank-and-drop framework to identify which subset of in vitro features could be utilized for in vivo toxicity prediction. It was observed that the in vivo end points that had similar LEL responses over the 309 chemicals (as determined by the sparse clustering results) also shared a significant subset of selected in vitro descriptors. Comparing the significant descriptors between the two different categories of end points revealed a specificity of the CYP assays for the liver end points and preferential selection of the estrogen/androgen nuclear receptors by the reproductive end points.

A major initiative in predictive toxicology is the development of methods that can rapidly screen thousands of industrial and environmental chemicals of potential concern for which minimal toxicity data currently exit (Judson et al., 2009). Current toxicology data are relatively limited in the pharmaceutical field because if a chemical is found to be toxic during testing, then further development is not pursued. Within the environmental field, toxicity data are limited because of the large number of chemicals and much smaller set of available resources for testing purposes. Furthermore, existing publicly available data sets for toxicology modeling are biased toward toxic chemicals.

Several efforts are attempting to address this vast information gap by developing methods that can utilize relatively inexpensive, high-throughput screening (HTS) assays for the prediction of biological in vivo effects. Because our current understanding of the biological mechanisms which govern toxicity is incomplete, we cannot a priori determine which particular bioassays are relevant for a given toxicity phenotype (Judson et al., 2008).

The EPA has organized the ToxCast program to foster the development of methods that can predict the potential toxicity of environmental chemicals using a large set of in vitro and in silico data (Dix et al., 2007). An initial chemical library of 309 unique chemicals was created to represent a diverse chemical space and consisted primarily of food-use pesticide-active ingredients. The latest in vitro data set contains 615 biochemical and cell-based assays in the form of AC₅₀ (half-maximal activity concentration) and lowest effective concentration (LEC) values for this library of 309 chemicals. A subset of measured in vivo toxicity data was also provided for these 309 chemicals for 76 quantitative (in lowest effect level [LEL] values) and 348 chronic binary end points in rats, mice, and rabbits. For this set of 424 in vivo end points, only 78.3% of the values were measured over all the chemicals, hence creating sparse sets of data. The term “sparse” here refers to the fact that not all values of the data matrix are observed or measurable. This large amount of in vivo data serves as an invaluable set of key end points that can be used to develop predictive modeling techniques based on HTS in vitro bioassay data.

A multitude of technical issues arise when addressing this problem. These issues include: determining the optimal number of features or assays for prediction, handling of the imbalanced data sets resulting from the uneven distribution of positive and negative toxicological end points, and determining what classification approaches are effective for this problem.

In this article, we introduce an integrated approach which can be used for predicting in vivo toxicity from in vitro data. A biclustering method based on iterative optimal reordering (DiMaggio et al., 2008, 2010b) will be used to identify subsets of the in vitro assays that exhibit correlated activity over the chemicals. This clustering will enable us to assess the biological relevance of the assays for this set of chemicals and cross-check the results of the feature selection approach to ensure that redundant features are not being included. The sparse in vivo data sets corresponding to the quantitative and chronic binary end points for the 309 chemicals will be clustered using an optimal method based on mixed-integer linear optimization (MILP) for reordering sparse data matrices (McAllister et al., 2009, 2010a). A cluster of end points over all chemicals reflects the fact that these end points are observed at similar LEL concentrations for the majority of the chemicals examined. The end points therefore will most likely share common molecular pathways responsible for their observation, which in turn implies that they should share common significant in vitro descriptors. Instead of using univariate statistics to perform feature selection, we will determine the significant descriptors through a multivariate approach known as ridge regression, which is a form of logistic regression. We then analyze the specificity of the selected descriptors for particular end points, assess the biological relevance of the descriptors with supporting studies from the literature, and examine the subsets of descriptors shared among correlated end points, as determined by the sparse clustering.

MATERIALS AND METHODS

In this section, we present the mathematical models that will be used to analyze the ToxCast data set. In particular, we will utilize (1) optimal methods for the biclustering of dense data matrices that were motivated by systems biology applications, (2) optimal methods for the clustering of sparse data matrices that arise in drug discovery and chemical screening applications, and (3) logistic regression for feature selection and classification.

Optimal Methods for the Biclustering of Dense Data Matrices

In systems biology, microarray experiments are commonly used for simultaneously measuring the transcription levels of thousands of genes. Given this vast amount of dense data, the primary goal is to elucidate genes that are coregulated by identifying genes that are coexpressed in the experiment based upon similar changes in their expression levels over the various environment conditions. If a gene is involved in more than one biological process or belongs to a group of genes that are coexpressed under limited conditions, then traditional clustering techniques, such as hierarchical and partitioning clustering, fail to uncover coregulated genes (Turner et al., 2005). The structures of interest are known as “biclusters,” which are submatrices that span a certain subset of genes (rows) and conditions (columns).

Motivated by the need to address these problems, a biclustering method based on optimal iterative reordering was developed (DiMaggio et al., 2008, 2010b). Binary 0-1 variables to represent the placement of rows i and i′ adjacent to one another in the final ordering:

Given this definition, we can then define the “cost” associated with placing elements next to each other in the final ordering. A general form of this objective function is presented in Equation 1, where an index pair (i, j) corresponds to a specific row i and column j of a matrix whose value is a_i,j.

(1)

One should note that ϕ(a_i,j,a_i^′,j) can be any function of the matrix values, a_i,j. A metric commonly used is the squared difference between terms, as presented in Equation 2.

(2)

We are interested in determining the final ordering of the rows which minimizes the summation of all these costs or the total cost associated with placing the elements in a specified ordering (an analogous derivation follows for reordering the columns). Alternatively, one could interpret this as finding the ordering which maximizes the similarity of the elements that are placed next to one another. The actual physical permutations of the rows and columns can be accomplished using either (a) a network flow model (DiMaggio et al., 2010b) or (b) a traveling salesman (TSP) model (DiMaggio et al., 2008). Given the optimal reordering by solving either of these models, it is then necessary to define cluster boundaries between the reordered elements.

Determining cluster boundaries.

We propose an integer linear programming (ILP) model to determine the cluster boundaries for a given optimal ordering. First, we identify a set of “cluster seeds” by the set Seeds, which consists of neighboring elements in the final ordering that are locally most similar. We also denote the set of elements that are outliers, or elements that are not cluster seeds, by the set Outliers. The following notation is introduced: denotes the global average of c(i, i + 1) over all i, 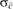is the corresponding SD of c(i, i + 1) over all i, and denotes the local average of c(i^′,i^′ + 1) for all i^′ within a neighborhood of ± X around element i. The sets Seeds and Outliers and are constructed using the following algorithm:

• Set Seeds = Ø and Outliers = Ø.

• Find the i∉Outliers∪Seeds with the minimum c(i, i + 1) in the optimal reordering.

• If 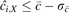, then add i to Seeds and all other elements i′ to Outliers within the range of ± X elements of i. Else add i to Outliers.

• Return to step 2 and repeat until all elements i are examined.

Given the set of cluster seeds, Seeds, we will formulate an ILP model to assign all other elements to one of these initial clusters. We introduce binary variables z_i which are equal to 1 if the element is assigned to the cluster immediately preceding it in the final ordering and 0 if it is assigned to the cluster immediately after it in the final ordering.

We define the sets Behind (i) and InFront (i) to denote the cluster seeds, represented by the index k, that are behind and in front of the element i, respectively. Finally, for every cluster k, we denote the set of elements that are fixed to belong to this cluster seed a priori by the set Fixed (k). For instance, if the first cluster seed contains the elements 2, 3, and 4, then Fixed (1) = 2, 3, 4.

The cost associated with the assignment of any element i into the cluster preceding or following it can be dissected into several terms:

• The fixed cost associated with assigning element i to the cluster preceding it, which are the distances between element i and all elements initially belonging to this cluster.

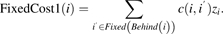
  (3)
• If element i is assigned to cluster k∈Behind(i) and element i^′ < i is assigned to the same cluster k∈InFront(i^′), then we need to include the cost associated with placing these two elements in the same cluster.

  (4)
• We also need to consider the contributions between element i and elements i^′ < i if they are assigned to the same cluster k, which precedes these elements.

  (5)
• Analogous expressions are derived for assigning elements to the clusters succeeding them in the final ordering. The fixed cost associated with assigning element i to the cluster after it is given by:

  (6)
• Lastly, we need to include the cost associated with placing elements i and i^′ > i in the same cluster k that is after these elements in the final ordering.

  (7)

  The objective function is then given by minimizing the summation of these individual contributions:

  (8)

  Note that we must constrain the feasible cluster assignments to prevent the cross-assignment of elements. In other words, if element i + 1 is assigned to the cluster before it, then element i cannot be assigned to the cluster after it. The following constraint enforces this restriction:

  (9)

  The nonlinearity associated with bilinear terms in the objective function can be alleviated by defining the following binary variable:

  (10)

  and incorporating the following constraints (Floudas, 1995) into the model:

  (11)

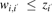
  (12)

  (13)

Minimizing Equation 8 subject to constraint Equations 9 and 11–13 provides the resulting cluster assignments for a given optimal ordering and set of cluster seeds (Seeds). The initial membership of the set Seeds is a function of the exclusion window X. We vary the value of X and select the one which results in the minimum total cluster error, which is the sum of the intra- and inter-cluster errors (Tan et al., 2007, 2008).

This biclustering model will be applied in an iterative framework to analyze the dense in vitro assay data. The chemicals and assays will be optimally reordered, and then outlier in vitro assays, whose average distance (as measured by Equation 2) to all other assays in the data is less than the distance to its nearest neighbor, will be identified and removed from the matrix. After removing the outliers, the chemical and assays are again optimally reordered and biclusters are defined using the aforementioned MILP model for determining cluster boundaries.

Optimal Methods for the Clustering of Sparse Data Matrices

A related problem is the optimal reordering of sparse data matrices, which arise in applications such as drug discovery, where an element of a data matrix corresponds to a unique molecular compound and the value of this element is some measure of drug efficacy for the compound. These data matrices are very sparse in practice as the experiments associated with synthesizing and measuring even a fraction of the total compounds are cost prohibitive. Thus, a clustering method would be desirable for guiding future compound synthesis toward target molecules that have the highest likelihood of being successful drug candidates.

It should be noted that the optimal biclustering approach presented in the previous section, as well as all other traditional clustering methods based on nearest neighbor objective functions (such as hierarchical clustering), cannot address these sparse data matrices as they consider elements with missing values to be “similar.” To address this problem, a novel clustering algorithm was developed based on integer linear optimization to optimally reorder sparse drug inhibition data matrices (DiMaggio et al., 2010a; McAllister et al., 2008, 2009). In particular, we modified Equation 1 to extend the pairwise interactions into global comparisons that are a function of the distance between two elements in the final ordering, which we denote as d_i,i^′. The modified cost expression is presented in Equation 14.

(14)

where ϕ(a_i,j,a_i^′,j) is the same as in Equation 1 and θ(d_i,i^′) is some function of the distance between the two elements i and i′ in the final ordering. For instance, we can take ϕ(a_i,j,a_i^′,j) to be the squared difference between elements and θ(d_i,i^′) to be a linear function that decreases with increasing d_i,i^′:

(15)

In this equation, θ(d_i,i^′) achieves a maximum value of 1 when d_i,i^′ = 1 and a minimum value of 1/(|I| − 1) when d_i,i^′ = |I| − 1. The term θ(d_i,i^′) is a weighting factor between two elements that gives a larger contribution to the elements that are nearby and smaller contributions to the elements that are distant from one another in the final ordering. The only restriction on θ(d_i,i^′) is that it is a linear function in d_i,i^′.

Because for sparse data matrices the physical permutations of the rows and columns cannot be accomplished using the network flow or TSP models described in the previous section, an assignment-like model based upon MILP was developed to determine the optimal ordering of the rows and columns according to the objective function in Equation 14. The derivation of this reordering model is presented in detail elsewhere (DiMaggio et al., 2010a; McAllister et al., 2009) along with computational studies that demonstrate the utility of the approach for reordering molecular compound libraries to direct the synthesis of additional compounds toward molecules with high efficacy. This sparse clustering algorithm will be used to analyze the in vivo data set, which is 21.7% sparse.

Classification via Logistic Regression

In this work, we will utilize the supervised classification method known as logistic regression to identify the smallest set of in vitro descriptors that are required for accurately classifying the 309 chemicals as either innocuous or hazardous. In essence, the logistic regression model determines the probabilistic hyperplane that separates the toxic from nontoxic chemicals in the in vitro descriptor space. Because the classifications are computed in a probabilistic manner, confidence measures can be provided when classifying new chemicals. A quadratic regularizer is included in the model to remove the redundant in vitro descriptors that are not supported by the data (Bishop, 2007). The detailed description of the logistic regression model implemented in this article is provided in the Supplementary material.

RESULTS

In Vitro ToxCast Data

All the data described in this article is available from the EPA ToxCast Web site: http://www.epa.gov/ncct/toxcast. The complete sets of AC50/LEC values are contained in a series of nine files packaged into a zip file with an accompanying README describing the contents. The in vitro data set consists of 615 assays (including a set of biochemical receptor and enzyme assays, as well as 8 cell-based assays measuring RNA and protein, cytotoxicity, cell growth, and morphology changes) in the form of AC50 and LEC values for a library of 309 chemicals. Inactive assays were given a default value of 1E6. These assays were derived from the following nine technologies:

1. Real-time cell electronic sensing (7 assays)

2. Multiplex transcription reporter (73 assays)

3. Biologically multiplexed activity profiling (BioMAP) (174 assays)

4. High-content cell imaging (57 assays)

5. Quantitative nuclease protection (42 assays)

6. HTS genotoxicity (1 assay)

7. Cell-free or biochemical HTS (239 assays)

8. Phase I and II xenobiotic-metabolizing enzymes (XME) cytotoxicity (4 assays)

9. Cell-based HTS (18 assays)

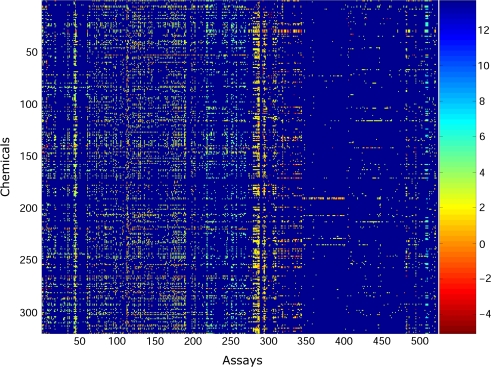
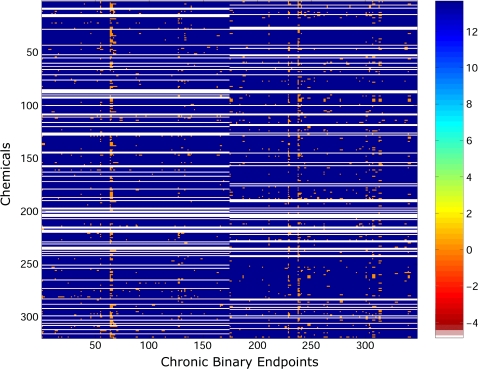
Out of the 615 assays, 91 of them showed no effect for any of the 309 chemicals, and so these assays were removed. Specifically, each of these assays had a value of 1E6 for all the 309 chemicals in this data set and therefore possess no capacity for discriminating between these chemicals. A heatmap of the logarithmic responses for the remaining 524 assays over the 309 chemicals is provided in Figure 1. The orderings for the chemicals and assays are as originally provided in the ToxCast Web site. To our knowledge, the chemicals and assays are randomized, with the exception that we have grouped the assays by their technologies listed above (e.g., in Fig. 1: columns 1 through 7 correspond to the “Real-time cell electronic sensing” assays in arbitrary order, columns 8 through 88 correspond to the “Multiplex transcription reporter” assays in arbitrary order, and so forth). One should note the scale of the heatmap, which ranges from red (denoting chemicals that have a low concentration values for the particular assay) to blue (corresponding to chemicals that did not exhibit a response for a given assay).

FIG. 1.

Original ordering for chemicals and assays for the in vitro data matrix. The color of each entry in the matrix reflects the lowest effect concentration observed for a chemical in an assay. These concentrations are color coded, and the key for the range of concentrations is given in the color bar on the right-hand side of the figure, where the numbers represent the log concentration.

Given this in vitro data set, it is of interest to determine whether or not there are correlative changes in the chemicals over particular subsets of assays. To assess this, we utilized the biclustering method based upon the optimal reordering of rows and columns (DiMaggio et al., 2008, 2010b) that was presented in the “Materials and Methods” section to cluster the data. We performed three iterations where the data was optimally reordered, and the assays identified as outliers were removed. The heatmap of the optimally reordered chemicals and assays is presented in Figure 2, where one can see the existence of several correlative assay responses over particular subsets of chemicals.

FIG. 2.

Reordered chemicals and assays for the in vitro data matrix. The color of each entry in the matrix reflects the lowest effect concentration observed for a chemical in an assay. These concentrations are color coded, and the key for the range of concentrations is given in the color bar on the right-hand side of the figure, where the numbers represent the log concentration.

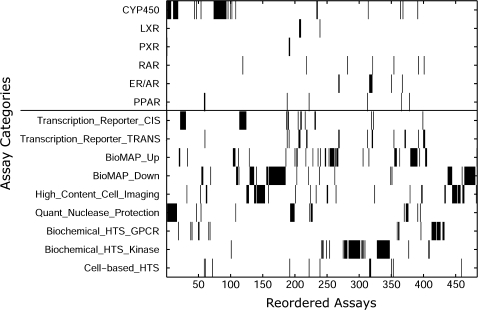
It is observed that the biclustering algorithm groups together the assays according to the assay technology as well as assay target. Figure 3 provides a birds eye view of the assay clustering for selected types and targets within the reordered assay dimension. In Figure 3, we see that the cytochrome P450 assays collapse primarily into two dense clusters: (1) the first cluster in assay positions 1 through 18 contains 14 cytochrome P450 (CYP) assays from the quantitative nuclease protection set (12 assays) and the cell-free HTS set (2 assays) and consists primarily of families 1 and 3 and subfamily “A” (i.e., CYP1A and CYP3A) and (2) the second cluster in assay positions 74 to 93 contains 20 cell-free HTS CYP450 assays corresponding primarily to the second CYP family (i.e., CYP2A, CYP2B, CYP2C, and CYP2D). It is interesting to note that the two clusters of CYP450 assays exhibit very different responses over the 309 chemicals, which can be seen by comparing the chemical responses within columns 1 to 18 and 74 to 93 in Figure 2. This contrast reveals a more consistent response from the CYP1A and CYP3A assays for these 309 chemicals.

FIG. 3.

Relative clustering of related assays. Black elements indicate the existence of a particular assay in the given position on the x-axis after optimal reordering of the assays, as shown in Figure 2. The existence of a cluster of assays is indicative that they share correlative responses over the 309 chemicals. Significant clustering is observed with respect to assay target (top-portion of the matrix) and type (bottom portion of the matrix).

There is also a significant grouping of various nuclear receptors in the reordered in vitro assays. For instance, out of the four liver X receptors (LXRs) in the 483 assays, three of them are clustered consecutively together in assay positions 207–209, as shown in Figure 3. The four pregnane X receptor (PXR) nuclear receptors are placed together in assay positions 191 and 192, corresponding to the multiplex transcription reporter and cell-based HTS PXR assays. With regards to the endocrine disrupting targets, it is seen in Figure 3 that four estrogen-related receptors are placed consecutively in positions 317–320, an androgen receptor is adjacent to this cluster in position 316, and two estrogen receptor (ER) assays are clustered together in positions 268 and 269.

The specific assay technologies were also found to cluster together in the reordered assay axis in Figure 2. For instance, two multiplex transcription reporter cis assay clusters, which correspond to the up/downregulation of endogenous transcription factor activity, were found consecutively together in assay positions 22 through 30 and 114 through 124 for a variety of different transcription factors. One should note that the nonspecific response observed within this cluster might be in part because of a general cytoxicity response. Conversely, as seen in Figure 3, the multiplex transcription reporter trans assays were observed to form several smaller clusters corresponding primarily to the aforementioned nuclear receptors (e.g., LXR, ER/AR, PXR), perhaps indicative of a more biologically relevant response.

The BioMAP assays measure lowest effect concentrations for a variety of systems, cell types, and environments (Berg et al., 2006; Houck et al., 2009). These assays also inherently distinguish between up and downregulation (annotated as “up” and “down,” respectively). In Figure 3, we observe several clusters of up and downregulated BioMAP readouts, and the systems targeted by these assays are mixed in this cluster (e.g., different cell types and environments are clustered together for small subsets of readouts). It is interesting that the larger clusters of the downregulated BioMAP assays are flanked by smaller clusters of high-content cell-imaging assays, which measure cellular toxicity phenotypes using fluorescent microscopy. The two largest high-content cell-imaging clusters correspond to: (1) two assays each measuring stress kinase, cell loss, DNA damage, nuclear size, apoptosis, and DNA texture in assays positions 137 through 153, and (2) two assays each that measure microtubuleCSK, micotubuleCSK destabilizer, p53 activation, cell loss, mitotic arrest, and mitomass in assay positions 445–457.

The quantitative nuclease protection assays target genes corresponding to XME and transporters. As previously mentioned, the first cluster of these assays in positions 1 through 18 corresponds primarily to the first and third family and “A” subfamily for CYP. There is another cluster of consecutive quantitative nuclease protection assays in positions 193 through 199 that corresponds to adenosine-5′-triphosphate (ATP)-binding cassette transporters, which are a family of membrane proteins that have ATPase activity and mediate ATP-dependent transport of various molecules, including drugs and metabolites.

The cell-free biochemical HTS assays provide a variety of measures for ligand-binding and enzyme activity. In assay positions 411 through 432, there is an almost consecutive grouping of these assays related to G protein–coupled receptors (GPCRs), which comprise a large protein family of transmembrane receptors that sense molecules outside the cell and activate signal transduction pathways. Lastly, in assay positions 275 through 309 and 328 through 347 is an almost consecutive ordering of cell-free HTS assays corresponding to various protein kinase activities (labeled as “ENZ” in Fig. 3), which often control the activities of effector proteins and then subsequent gene expression.

The clustering of the technologies is important because it identifies which descriptors from the same technology are highly correlated and therefore should not be redundantly selected as features for in vivo prediction. For instance, if two descriptors from the same technology belong to the same cluster and are highly correlated, then both should not be selected as significant descriptors as they convey redundant information and are almost linearly dependent.

In Vivo ToxRefDB Data

In vivo guideline toxicity testing data were also provided for the 309 ToxCast chemicals. These data are referred to as the Toxicity Reference Database (ToxRefDB), which consists of animal-based in vivo toxicity data from chronic/cancer rat and cancer mouse studies (Martin et al., 2009a), multigeneration reproduction rat studies (Martin et al., 2009b), and prenatal developmental toxicity studies in rats and rabbits (Knudsen et al., 2009), all of which has been curated from a variety of high-quality data sources collected since 1970. The resulting ToxRefDB in vivo data consists of (1) 76 quantitative end points in LEL values and (2) 348 chronic binary end points measured in rats, mice, and rabbits. For these 424 binary and continuous end points, only 78.3% of the possible values were measured over the 309 chemicals, thereby creating a sparse data matrix because 21.7% of the data is not known. An optimal method based on MILP for reordering sparse data matrices (DiMaggio et al., 2010a; McAllister et al., 2009) was used to cluster the (a) 76 continuous end points and the (b) 348 binary chronic end points.

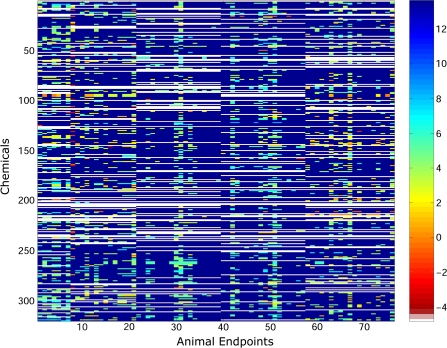
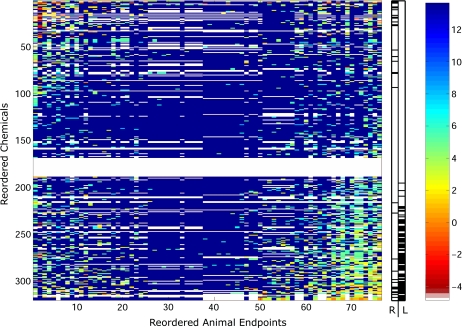
The original in vivo data matrix for the 76 quantitative chronic, developmental, and multigenerational end points is presented in Figure 4, where the original orderings for the chemicals and end points are as provided in the ToxCast Web site, and the resulting matrix after optimally reordering over both the chemicals and end points is shown in Figure 5. From visual inspection of Figure 5, it is seen that the most hazardous chemicals (i.e., chemicals with the lowest LEL values, as shown by the orange and red colors) group primarily into two areas: the upper-left and the bottom-right portions of the matrix.

FIG. 4.

Original ordering for chemicals and 76 quantitative in vivo end points. The color of each entry in the matrix reflects the LEL concentration observed for a chemical for a particular end point. These concentrations are color coded, and the key for the range of concentrations is given in the color bar on the right-hand side of the figure, where the numbers represent the log concentration. It should be noted in that lower LEL values are considered to be more harmful and white elements denote missing values in the matrix.

FIG. 5.

Reordered chemicals and quantitative end points for the in vivo data matrix. The color of each entry in the matrix reflects the LEL concentration observed for a chemical for a particular end point. These concentrations are color coded, and the key for the range of concentrations is given in the color bar on the far right of the figure, where the numbers represent the log concentration. It should be noted in that lower LEL values are considered to be more harmful and white elements denote missing values in the matrix. The most hazardous chemicals within the reproductive (R)- and liver (“L”)-related end point clusters (as defined in the text) are denoted in the central bar graph, where for a given cluster (i.e., “R” or “L”) a black element denotes that the chemical in this position is hazardous and a white element signifies a nonhazardous chemical.

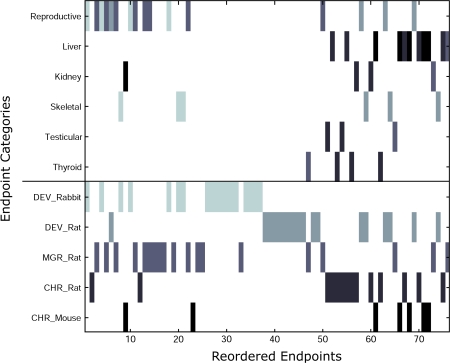
We further examined the relationships between reordered end points to determine if there was any underlying clustering with regard to end point identity. Figure 6 provides a binary description of the reordered end points, where along the x-axis are the reordered end points, along the y-axis are several possible descriptors corresponding to the end points, and the existence of a color denotes that the given end point is consistent with a given descriptor. Interestingly, we primarily observed two physiologic clusters: one where the end points classified as reproductive (i.e., these end points contained descriptors such as “maternal,” “pregnancy,” “lactation,” “litter,” “fetal,” “fertility,” “ovary,” “mating,” or “uterus”) on the left side of the matrix and the other with end points denoted as “liver” on the right-hand side of the matrix. The end points within the reproductive-related cluster mostly consist of developmental rabbit and multigenerational rat end points. The liver-related cluster of end points is dominantly made up of chronic mouse and rat end points but also contains a multigenerational rat end point. As this cluster of liver-related end points is primarily made up of cancer mouse and rat end points, it could also be considered to be a “cancer” cluster that is enriched in liver-associated end points. For reference to other physiological categories, we also show the resulting placement of end points associated with kidney, skeletal, testicular, and thyroid descriptors, which are observed to exhibit a lesser degree of clustering.

FIG. 6.

Relative clustering of related end points. The shaded elements indicate the existence of a particular end point in the given position on the x-axis after optimal reordering of the end points, as shown in Figure 5. The existence of a cluster of end points is indicative that they share correlative responses over the 309 chemicals. Significant clustering is observed with respect to physiological category (i.e., liver and reproduction) and animal species. The distinct animal end points are differentiated by shades of gray in the bottom half of the figure (e.g., DEV_Rabbit is the lightest shade of gray and CHR_Mouse is black) to reflect the heterogeneity of the physiological clusters in the top half of the figure with respect to animal species.

From Figure 5, we can also inspect the proportion of hazardous chemicals present within the liver- and reproductive-related clusters. Here we define a hazardous chemical to have an average LEL value of less than 8000 mg/kg/day within a given cluster of end points. In the liver (“L” in Fig. 5)-related cluster on the right-hand side of the reordered matrix, it is seen that the majority of hazardous chemicals (25%) do indeed cluster in the lower half of the matrix. The hazardous chemicals within the reproductive (“R” in Fig. 5)-related cluster on the left-hand side of the reordered matrix are only shown to comprise 10% of the chemicals and occupy both the upper-left and lower-left portions of the reordered matrix. Interestingly, 11% of the chemicals determined to be hazardous in the liver-related end point cluster are also hazardous in the reproductive-related end point cluster (this is shown by the overlap in the bottom half of the central bar graph in Fig. 5). This overall trend suggests that the sparse clustering is primarily guided by the majority of pesticides that were found to be hazardous to the liver-related end points and secondarily by the chemicals hazardous to the reproductive end point cluster.

In addition to the physiological clustering of the reproductive- and liver-related end points, there is also a secondary clustering observed within the different animal studies. For instance, we observe an anticorrelative response between the developmental rat and rabbit end points, which occupy the right- and left-hand side of the matrix, respectively. All the end points containing “skeletal” descriptors are associated with the developmental rat and rabbit end points, but interspecies clusters are not formed as they are with the reproductive- and liver-related end points. The developmental rabbit and rat end points also form two very dense clusters adjacently located positions 26 through 37 and positions 38 through 49, respectively. These mostly correspond to end points that have very few positive chemical responses (i.e., two “trunk,” “orofacial,” “cardiovascular,” “neurosensory”-related end points, for both the rat and rabbit studies).

The multigenerational rat end points are mostly correlated with the reproductive end point cluster and dominantly occupy the left side of the matrix with the developmental rabbit end points. In addition, they form a dense cluster between positions 11 and 18, directly adjacent to the reproductive cluster. The chronic rat end points are observed to form a dense cluster occupying positions 51–62 in Figure 6, which contains a variety of physiological groups, including two testicular, two kidney, two liver, and three thyroid-related end points. As five out of the seven chronic mouse end points are liver related, they are primarily found on the right-hand side of the matrix within the liver cluster.

The separate clustering of animal species in Figure 6 is interesting as it highlights the fact that different animal species do indeed have distinct and specific physiological responses to chemical exposure. This is a well-known, but often understated (or oversimplified), limitation in conducting animal studies with the intent of extrapolating an anticipated response in humans. In Figure 6, we even see that rats and mice, which are often times assumed to be closely related based on phenotype, are observed to show significant in vivo differences for this set of 309 pesticides (as seen by the formation of the distinct chronic rat cluster in end points 51 through 57).

We also clustered the set of 348 binary chronic end points corresponding to in vivo mouse and rat studies. The original matrix is presented in Figure 7, and the optimally reordered rows and columns are shown in Figure 8. As observed for the clustering of the 76 quantitative end points, the optimal reordering groups the most hazardous chemicals into the upper-left and lower-right regions of the matrix.

FIG. 7.

Original ordering for chemicals and 348 chronic binary end points. The values correspond to whether the end point was observed (1) or not (0) and are color coded, where the key corresponding to these values is given in the color bar on the far right of the figure (the numbers represent log values). White elements denote missing or unmeasured values in the matrix.

FIG. 8.

Reordered chemicals and 348 chronic binary end points. Note that the chemicals found to activate the chronic end points have again grouped into the corners of the matrix. The values correspond to whether the end point was observed (1) or not (0) and are color coded, where the key corresponding to these values is given in the color bar on the far right of the figure (the numbers represent log values). White elements denote missing or unmeasured values in the matrix.

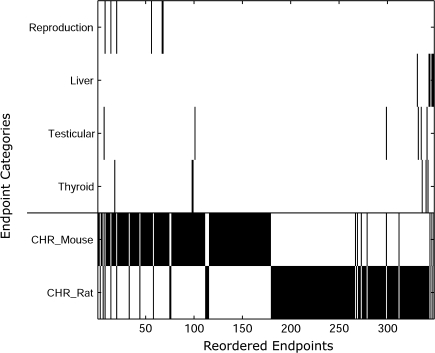
Interestingly, when examining the clustering of the different end point categories (i.e., liver, reproductive, thyroid, etc.) as presented in Figure 9, we clearly see that two major animal clusters are formed: the chronic mouse end points in positions 1 through 179 and the chronic rat end points in positions 180 through 348. There is also a significant physiological clustering of the chronic binary end points containing the “liver” descriptor, where three of the chronic mouse end points placed in the chronic rat-rich region are associated with these end points. Within the large cluster of chronic rat end points, there is also a noticeable clustering of the end points containing “thyroid” (in positions 336, 340, and 342) and “testicular” (in positions 332, 335, and 341) descriptors.

FIG. 9.

Relative clustering of the related chronic binary end points. The black elements indicate the existence of a particular end point in the given position. The complementarity pattern in the bottom portion of the figure is the result of all end points being either mouse or rat. Significant clustering is observed with respect to physiological category (i.e., liver and reproduction) and animal species.

It should be noted here that unsupervised hierarchical clustering was previously applied, on a much smaller scale, to independently cluster 16 rat and 9 mouse chronic/cancer end points (Martin et al., 2009a). For the 16 rat end points, it was observed that 3 liver- and thyroid-related end points formed separate clusters, respectively, and 2 testicular end points were also clustered together. For the nine mouse end points, the four liver-related end points were observed to split into two separate clusters. Although this study reported a clustering of chronic end points primarily by target organ within distinct animal species, our results demonstrated a simultaneous and separate clustering of the liver and reproductive end points across the rat, mouse, and rabbit animal species as well as a secondary interspecies separation between the chronic mouse and rat end points.

Feature Selection Using Logistic Regression

Logistic regression was utilized to determine the minimal set of in vitro descriptors required to perfectly separate the liver and reproductive in vivo end points analyzed in the previous section. For each end point, we begin with the set of 400 in vitro descriptors of highest variance and lowest average value because lower values are indicative of assays with greater sensitivity. A rank-and-drop strategy was adopted, where for a given in vivo end point, we performed logistic regression initially using these 400 in vitro descriptors. The model is solved by maximizing the log likelihood of the data given the model parameters and a quadratic regularization term is included to reduce overfitting and contract those weights not supported by the data to zero (see Supplementary material for model details).

After each iteration, the standard error (SE) of each feature is computed by inverting the Hessian matrix of the log likelihood function and we eliminate the 10 features with the lowest parameter value to SE ratios. This procedure is repeated until the classification is no longer perfect, and we consider the features that were not eliminated to be the most significant descriptors for the particular in vivo end point. We applied this iterative approach to the end points found within the clusters associated with “liver” and “reproductive” descriptors (as shown in Fig. 6), which consisted of 8 and 10 end points, respectively. Thus, a total of 18 sets of significant in vitro descriptors were generated for the 18 selected in vivo liver- and reproductive-related end points and are presented in Table 1 for reference. The complete list of 400 starting in vitro descriptors, corresponding subsets of selected descriptors, and their weighting coefficients are provided in the Supplementary material.

TABLE 1.

The 8 Liver and 10 Reproductive In Vivo End Points Which Were Found to Cluster Separately

Liver in vivo end points

CHR_Mouse_Liver Hypertrophy

CHR_Rat_LiverProliferativeLesions

CHR_Rat_LiverHypertrophy

CHR_Mouse_LiverProliferativeLesions

CHR_Mouse_LiverTumors

CHR_Mouse_Tumorigen

CHR_Rat_Tumorigen

MGR_Rat_Liver

Reproductive in vivo end points

DEV_Rabbit_General_FetalWeightReduction

DEV_Rabbit_PregnancyRelated_EmbryoFetalLoss

DEV_Rabbit_PregnancyRelated_MaternalPregLoss

MGR_Rat_ViabilityPND4

MGR_Rat_Ovary

MGR_Rat_LiveBirthPND1

MGR_Rat_LitterSize

MGR_Rat_LactationPND21

MGR_Rat_Fertility

DEV_Rat_PregnancyRelated_MaternalPregLoss

DISCUSSION

Recent work related to the analysis of this ToxCast data set includes a study based on eight BioMAP cell systems, consisting of a total of 87 in vitro readouts (Houck et al., 2009). These BioMAP cellular systems measure protein expression in a panel of assays for a variety of cell types (i.e., endothelial, epithelial, fibroblasts, etc.) and stimulation environments (i.e., cytokines, activators, growth factors, etc.) related to vascular inflammation and immune activation. A function similarity map was used to project the “proximity” of related profiles from several dimensions into two dimensions based on Pearson correlations and Tanimoto scores (Houck et al., 2009). Lines denoting relationships were then drawn between compounds for pairwise distance metrics below some specified threshold, and the resulting clusters were annotated with a mechanism of action (such as mitochondrial dysfunction, induction of endoplasmic reticulum stress, nuclear factor kappa-light-chain-enhancer of activated B cells (NFκB) inhibitors, elevators of cyclic adenosine monophosphate (cAMP), and microtubule function and estrogen receptor signaling) based on the BioMAP profiles for known reference compounds.

Another study focused on analyzing the GreenScreen, Cellumen, and CellSensor genotoxicity assays (Knight et al., 2009), which represent two gene targets and their end points (p53 and GADD45a in a p53 competent cell line). It is well known that p53 can act in a variety of different ways in the cell in response to genotoxic stress. For instance, when DNA is damaged p53 can: (1) activate DNA repair proteins, (2) hold the cell cycle at the G₁/S regulation checkpoint until repair is effected, and/or (3) initiate apoptosis if the DNA damage cannot be repaired. The authors state that although carcinogenesis is a complex multistage and multipathway process, it is hoped that high-throughput screening assays can serve as surrogates for the various dimensions of this process and be useful in combination. The assays were evaluated for the 309 chemicals and compared with the published Ames test data and the in vivo chronic rodent end points from the ToxRefDB database. It was concluded that positive data from these assays, which had limited overlap (perhaps because of variable sensitivities to different chemical classes), cannot be used alone for predicting animal tumorigenicity.

In this section, we will utilize the clustering results for the in vitro and in vivo data to assess the quality of the descriptors selected via logistic regression. Because the liver and reproductive clusters of end points were observed to exhibit anticorrelative behavior (see Fig. 6), one should expect that the selected in vitro descriptors are not only consistent within the liver or reproductive clusters but also significantly different between liver and reproductive clusters.

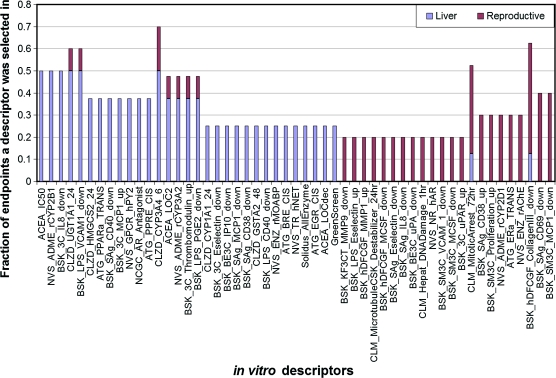
To highlight the differences in the type of descriptors selected between the liver and reproductive in vivo clusters, we computed two fractions corresponding to the relative number of times a particular in vitro assay was determined to be significant in the set of liver and reproductive end points, respectively. These two fractions were then sorted based on their absolute differences (i.e., the absolute difference between the relative number of times an in vitro descriptor is selected as significant for a liver-associated end point and the relative number of times it is selected as significant for a reproductive end point) because a larger absolute difference implies an in vitro descriptor has a specificity for either the liver or reproductive end points. The most significant differences are presented in Figure 10.

FIG. 10.

Difference between descriptors selected for the liver- versus reproductive-related end points.

It is interesting to note in Figure 10 that the liver end points are shown to preferably select CYP assays corresponding to subfamily “A” (i.e., one CYP1A and two CYP3A) when compared with the reproductive end points. This makes biological sense as CYP1A is found in the liver and is induced by a number of xenobiotics (Denison and Whitlock, 1995) and CYP3A enzymes are very active in steroid and bile acid 6β-hydroxylation and the oxidation of many xenobiotics (Honkakoski and Negishi, 2000). Interestingly, CYP3A has a wide substrate specificity, is prominently expressed in the liver, and is among the most important group of enzymes involved in drug metabolism (Thummel and Wilkinson, 1998). CYP2B, which is also preferably selected by the liver end points as seen on the left side of Figure 10, is a large gene family and the regulation of some isoforms is strongly induced by a structurally diverse array of xenobiotics, including pesticides (Honkakoski and Negishi, 2000). Many of the nuclear receptors are known to be affected by the CYP2B substrate/product. As shown in Figure 10, three out of the seven total real-time cell electronic sensing assays, which measure general cytotoxicity in terms of changes in cell growth kinetics, are also determined to be significant descriptors for the liver end points. It should be noted that these assays are found in different biclusters, so their responses over the chemicals are fairly distinct. Lastly, we observe in Figure 10 that certain nuclear receptors that are well-known regulators of CYP genes are selected as specific to the liver cluster of end points. These in vitro descriptors include peroxisome proliferator–activated receptor (PPAR) α, AR agonist, and PPRE. It should be noted here that a recent study screened a set of 200 pesticides for PPAR activity (which is expressed in the liver, heart, muscle, and kidney) interferon-gamma (INF-γ) by specifically targeting the receptor activities of PPARα and PPARγ (Takeuchi et al., 2008). The agonistic activities of the pesticides were measured in relative effective concentrations (RECs) to some standard. In this study, it was found that the chemicals diclofop-methyl and imazalil (which notably have very different chemical structures) showed PPARα-mediated transcriptional activities, and the in vivo effects of diclofop-methyl and imazalil were then measured by examining the induction of CYP4A gene expression. It was found that diclofop-methyl also induced high levels of CYP4A10 and CYP4A14 mRNA. These findings are consistent with the selection of PPARα as a significant in vitro descriptor for the liver cluster because diclofop-methyl and imazalil are among the chemicals with lowest LEL values for these in vivo end points. Furthermore, the chemical diethylhexyl phthalate also triggers low LEL responses and has also been reported to induce PPAR activity (Huber et al., 1996).

An expected, yet assuring, observation for the reproductive cluster of end points is that both the estrogen-alpha receptor (e.g., ERα) and an androgen receptor are selected as significant in vitro reproductive descriptors, relative to the liver end points. Several agricultural chemicals contain endocrine disrupting properties through interactions with the ER, and an earlier study identified 80 out of 200 chemicals as having ER receptor activity (Kojima et al., 2004). Our results are consistent with these previous findings, which reported 34 pesticides displaying both ER and anti-AR activity (Kojima et al., 2004).

Within both the liver and reproductive end points, it was observed that several clusters of differentiations, including CD38, CD40, CD69, and CD141 (thrombomodulin), were selected as significant descriptors. These clusters of differentiations are known to be important factors in immune response. Consistent with these assays are the selection of descriptors associated with chemokines, which attract leukocytes to infection sites. They are assigned into four different groups based upon their conserved cysteine residues: C-C, C-X-C, C, and CX3C. In Figure 10, it is seen that three CC motif (MCP-1) and a C-X-C motif (IP-10, which is secreted in response to INF-γ) chemokines are selected by the reproductive and liver end points.

It is interesting to note that some descriptors anticipated to be significant were not selected by the logistic regression algorithm. In particular, we noticed that the retinoic acid receptor (RAR), retinoid X receptor (RXR), and farnesoid X receptor (FXR) were not selected for any of the liver end points. These nuclear receptors are known to bind to the LXRs to form dimers. In addition, the descriptor associated with sterol regulatory element-binding protein, which is a target gene for the LXR was also not selected. For the reproductive end points, it was seen that descriptors associated with cell loss and apoptosis, which are associated with side effects of overexpression of the estrogen receptors, were missing. For a number of nuclear receptors, similar descriptors associated with different technologies were a part of the original data. In these cases, only one of the technologies was selected. This is an important indicator as it shows that the selected descriptors are linearly independent and nonredundant.

Our proposed approach can be utilized for the prediction of liver- and reproductive-related in vivo end points for a new chemical in a number of ways. If the end point of interest corresponds to one of the 18 liver and reproductive end points reported in Table 1, then one can simply measure the significant in vitro descriptors that were determined for that end point (provided in the Supplementary material). These measured in vitro assay values in combination with their determined weighting coefficients can be used to predict whether the in vivo response will be either toxic or nontoxic via the logistic regression model. Alternatively, one can apply other machine learning algorithms using the in vitro descriptors determined to be significant by our analysis for the end point of interest to predict the in vivo toxicity of the new chemical.

If the end point of interest does not correspond to one of the 18 liver and reproductive end points reported in Table 1, then a different route for prediction can be followed. Given the available existing in vivo toxicity data for the new end point, the sparse clustering algorithm should be applied to determine the known end points with which it is most similar (as determined by the resulting clusters). The corresponding in vivo predictions of the nearest neighbor end points can be utilized to derive a consensus prediction for the in vivo toxicity of the new end point, where the known end points of highest correlation to the new end point are given larger weights in their predictive contribution. Alternatively, the union of the set of significant descriptors determined for the nearest neighbor known end points can be used to build a classifier for the new end point (using the existing toxicity data for this end point). In our opinion, it will be a combination of these complementary approaches that will yield the most predictive utility.

CONCLUSIONS

In this article, we presented a novel approach which can be used for predicting the in vivo toxicities of chemicals using in vitro assay data. A biclustering method based on iterative optimal reordering (DiMaggio et al., 2008, 2010b) was utilized to bicluster the in vitro assays to determine correlative responses of the chemicals over the various assays. The biclustering of the in vitro assays revealed significant clustering of: (1) the CYP assays (split into a CYP1A/CYP3A cluster and CYP2-dominant cluster), (2) the various nuclear receptors (i.e., LXR, PXR, ER/AR), (3) the multiplex transcription reporter cis assays associated with the up/downregulation of endogenous transcription factor activity, (4) the downregulated BioMAP assays, (5) the high-content cell-imaging assays for measuring cellular toxicity phenotypes, and (6) the GPCR and protein kinase activity (ENZ) biochemical HTS assays. The quantitative and binary in vivo data were analyzed using an optimal method based on MILP (DiMaggio et al., 2010a; McAllister et al., 2009) for the clustering of sparse data matrices, and we observed a clustering of the end points with respect to physiological and animal groups. Specifically, the end points associated with liver and reproductive descriptors were observed to cluster separately on opposite ends of the optimally reordered in vivo data matrix, and secondary clustering was observed among the rat, rabbit, and mouse species. As the liver- and reproductive-related end points showed the most physiological correlation, we further analyzed them using logistic regression in a rank-and-drop framework to determine which in vitro features could be utilized for in vivo prediction. When comparing the significant in vitro descriptors selected for the liver and reproductive end point clusters, it was revealed that the CYP assays and several related nuclear receptors (in particular, PPARα, AR agonist, and PPRE) exhibited a specificity for the liver end points, and the estrogen/androgen nuclear receptor assays exhibited a specificity for the reproductive end points. These findings were consistent with earlier studies that screened a library of pesticides for PPARα, estrogen, and androgen receptor activities. The descriptors selected for the in vivo liver end point will be evaluated in a blind prediction for unknown chemicals in the future.

SUPPLEMENTARY DATA

Supplementary data are available online at http://toxsci.oxfordjournals.org/.

FUNDING

National Institutes of Health (R01LM009338 to C.A.F.); U.S. Environmental Protection Agency, EPA (R 832721-010 to C.A.F.).