Monte Carlo Simulations of Tau Proteins: Effect of Phosphorylation

Abstract

We perform Monte Carlo simulations of tau proteins bound to a cylinder that mimics a microtubule (MT), and then study them in solution. Tau protein binds to a highly anionic MT surface to stabilize the cylindrical structure of MT. The negatively charged tail domain floats away from the anionic MT surface while positively charged tau segments localize near the MT surface. Monte Carlo simulations demonstrate that, in 3RS tau isoform (which has three imperfect repeats (R) short (S) isoform), amino acids are more condensed near a highly charged interface compared to 4RL isoform (which has four imperfect repeats (R) long (L) isoform). In 4RL isoform, amino acids in tail domain stay mostly apart from the MT surface. In the bulk solution, dephosphorylated taus are separated due to Coulomb repulsion between similarly charged isoforms. Moderate phosphorylation of 3RS isoform decreases average intermolecular distance between dephosphorylated and phosphorylated taus and lead to their overlap. Further phosphorylation does not change noticeably the intermolecular distances.

Introduction

Microtubules (MTs) are stiff, highly charged hollow cylinders assembled of tubulin dimers (1). MTs are particularly abundant in neurons where they are involved in maintaining the cell shape and serve as tracks for axonal traffic. Microtubule-associated proteins are known to regulate the MT structure and to mediate the interactions between MTs and other cytoskeletal elements (such as, e.g., neurofilaments and actin). Tau protein is one of the major representatives of microtubule-associated proteins expressed in neuronal tissues.

Human tau proteins constitute a family of six isoforms that differ from each other by the number of repetitive regions in the C-terminal part of the protein and the length of the N-terminal part (referred to as the projection domain). The total number of amino-acid (aa) residues in tau proteins varies from 352 for the shortest 3RS isoform to 441 for the longest 4RL version, and chemical aa sequences in all isoforms are established. All of the tau proteins are weakly charged polyampholytes with a gradient in charge distribution along the chain. It is known that tau isoforms are flexible macromolecules with only transient elements of the secondary structure. They exhibit a random coil behavior in the solution, and are classified as naturally unfolded proteins (2).

It is established that tau proteins promote tubulin polymerization and mediate spacing between MTs in axons and dendrites (3). The phosphorylation of the serines and threonines regulates the affinity of taus to microtubules. Hyperphosphorylation can lead to detachment of tau proteins from the MT surface and coassembly of protein molecules in a neurofibrillary tangle. Such intracellular inclusions are characteristic for a number of neurodegenerative disorders such as Alzheimer's disease, amyotrophic lateral sclerosis, etc. It is not well understood yet, to our knowledge, how tau proteins modulate the structure of MTs, and why the phosphorylation of tau molecules could lead to their aggregation. Understanding the conformations of tau proteins bound at the MT surface and in the solution could provide valuable insights to rationalize such behavior.

The presence of numerous charges on MT and tau proteins suggests that the Coulomb force is among the most important interactions that govern the behavior of these protein molecules. To highlight the role of the electrostatic interactions, we focus on low salt conditions when the effect of tau phosphorylation is at its most prominent. Because the surface charge density on MT is so high, and the charge-charge correlations become an important factor (4–8), a mean-field theory is hardly applicable here. To the best of our knowledge, there is no analytical theory to describe an asymmetric flexible polyampholyte near a strongly charged interface (i.e., tau protein near MT surface). In such a system, the conformations of a polyampholyte molecule may strongly depend on actual aa sequence within the polymer chain. At this stage, only numerical simulation methods could be used to model the structure of tau proteins in the solution and the tau-MT interactions.

In this work, we use the Monte Carlo (MC) simulation method to investigate the conformations of tau proteins that are 1), bound to the MT surface, or 2), dissolved in the solution. This approach permits to account explicitly for charge-charge correlations in both bound and free states of tau isoforms, and provides information on the protein spatial organization (e.g., polymer density profile, radius of gyration, average end-to-end distance, etc.). We choose the shortest and the longest of tau isoforms (3RS and 4RL) as representatives of the tau family. We demonstrate that MC modeling allows for a comparative analysis of the conformations of different tau isoforms bound to the MT surface and of the interactions between tau molecules in the solution. The primary result of this study is demonstration that the site-specific phosphorylation of tau molecule makes the protein-MT interaction significantly weaker than expected from a mean-field theory, and promotes aggregation of tau isoforms in the solution. We focus on a first stage of the tau association when protein molecules remain essentially unfolded. Remarkably, the initial approach and overlap of two tau proteins in the solution occurs when net charge on both macromolecules is still of the same sign.

The rest of the article is organized as follows. We describe the model in System Description and justify the assumption of uniform charge distribution on the MT surface in Appendix 1. In Results, we first examine the conformations of projection domains of 3RS and 4RL isoforms tethered at the MT surface and explore the conformational rearrangements caused by the protein phosphorylation. The results of MC simulations are compared to the predictions of an analytical self-consistent-field (SCF) model of polyelectrolyte brushes summarized in Appendix 2. Finally, the interactions between unbound 3RS and 4RL isoforms in the solution are considered. Here, we analyze the phosphorylation-induced association of two similar (3RS-3RS) or two different (3RS-4RL) isoforms. We then present our Conclusions.

System Description

Microtubules constitute hollow cylindrical aggregates composed of α/β tubulin dimers. The molecular coordinates of tubulin dimers are available from the Protein DataBank (9). According to these data, most of the tubulin charges are located under the MT surface at >1 nm depth. The latter is larger than the Bjerrum length l_B, whose value is ∼7 Å in water. Due to such microtubule architecture, the counterions and added salt ions are disposed to feel the MT electric field as that of a uniformly charged surface. We demonstrate in Appendix 1 that this assumption is justified for both planar and cylindrical surface geometries in the so-called strong coupling regime.

In the MC simulation cell, a single MT is modeled as a hollow uniformly charged cylinder with radius R = 12.5 nm and surface charge density −0.87 e/nm². Its axis coincides with the axis of the cylindrical simulation cell. The latter has a radius D = 80 nm and length L = 15 nm. Periodic boundary conditions are used both along the axis of the cylinder and in the angular direction. In the angular direction, only one-quarter of the circle is taken into account and the other three quarters are treated periodically.

A bead-spring model is used to simulate tau protein molecule. The chemical sequences in 3RS and 4RL isoforms are collected in Tables 1 and 2. Ionized aa residues have a pointlike charge in the bead center. The van der Waals interactions between amino acids (beads) are incorporated in two ways: 1), through the hard sphere (HS) potential; and 2), the shifted Lennard-Jones (LJK) potential. In the latter case, the parameters of a unified interbead potential are similar to these in Liwo et al. (10). The hard-sphere model mimics good solvent conditions with respect to the nonelectrostatic interactions, whereas the shifted Lennard-Jones model allows for different solubilities of aa residues. We use both hard-sphere and shifted Lennard-Jones models to probe the effect of hydrophobic/hydrophilic interactions on the conformations of tau protein. We emphasize that in the frames of the shifted Lennard-Jones model, a protein chemical sequence is fully conserved, and that interbead interaction parameters are specified for all types of aa residues present. The phosphorylation of protein (enzymatic attachment of the phosphate group to serines and threonines) is modeled by assigning charge −2e to S and T residues without modification of the corresponding Lennard-Jones interaction parameters.

Table 1.

Chemical sequence of amino acids in 3RS tau in one-letter code, and coarse-grained sequence

MAEPRQEFEV	MEDHAGTYGL	GDRKDQGGYT	MHQDQEGDTD
AGLKAEEAGI	GDTPSLEDEA	AGHVTQARMV	SKSKDGTGSD
DKKAKGADGK	TKIATPRGAA	PPGQKGQANA	TRIPAKTPPA
PKTPPSSGEP	PKSGDRSGYS	SPGSPGTPGS	RSRTPSLPTP
PTREPKKVAV	VRTPPKSPSS	AKSRLQTAPV	PMPDLKNVKS
KIGSTENLKH	QPGGGKVQIV	YKPVDLSKVT	SKCGSLGNIH
HKPGGGQVEV	KSEKLDFKDR	VQSKIGSLDN	ITHVPGGGNK
KIETHKLTFR	ENAKAKTDHG	AEIVYKSPVV	SGDTSPRHLS
NVSSTGSIDM	VDSPQLATLA	DEVSASLAKQ	GL
NNMNPNMNMN	NMMHNNNNNN	NMPPMNNNNN	NHNMNMNMNM
NNNPNMMNNN	NMNNNNMMMN	NNHNNNNPNN	NPNPMNNNNM
MPPNPNNMNP	NPNNNNPNNN	NNNNPNNNNN	NPNNNPNNNN
NPNNNNNNMN	NPNNMPNNNN	NNNNNNNNNN	PNPNNNNNNN
NNPMNPPNNN	NPNNNPNNNN	NPNPNNNNNN	NNNMNPNNPN
PNNNNMNNPH	NNNNNPNNNN	NPNNMNNPNN	NPNNNNNNNH
HPNNNNNNMN	PNMPNMNPMP	NNNPNNNNMN	NNHNNNNNNP
PNMNHPNNNP	MNNPNPNMHN	NMNNNPNNNN	NNMNNNPHNN
NNNNNNNNMN	NMNNNNNNNN	MMNNNNNNPN	NN

The latter comprises four types of monomers: {Y, Q, H, F, W, G, P, C, M, A, L, V, I, S, T} ∈ N for neutral amino acids, {E, D} ∈ M for negatively charged amino acids, {K, R} ∈ P for positively charged amino acids, and {H} ∈ H. The projection domains are indicated in italics.

Table 2.

Chemical and coarse-grained aa sequences in 4RL isoform

MAEPRQEFEV	MFDHAGTYGL	GDRKDQGGYT	MHQDQEGDTD
AGLKESPLQT	PTEDGSEEPG	SETSDAKSTP	TAEDVTAPLV
DEGAPGKQAA	AQPHTEIPEG	TTAEEAGIGD	TPSLEDEAAG
HVTQARMVSK	SKDGTGSDDK	KAKGADGKTK	IATPRGAAPP
GQKGQANATR	IPAKTPPAPK	TPPSSGEPPK	SGDRSGYSSP
GSPGTPGSRS	RTPSLPTPPT	REPKKVAVVR	TPPKSPSSAK
SRLQTAPVPM	PDLKNVKSKI	GSTENLKHQP	GGGKVQIINK
KLDLSNVQSK	CGSKDNIKHV	PGGGSVQIVY	KPVDLSKVTS
KCGSLGNIHH	KPGGGQVEVK	SEKLDFKDRV	QSKIGSLDNI
THVPGGGNKK	IETHKLTFRE	NAKAKTDHGA	EIVYKSPVVS
GDTSPRHLSN	VSSTGSIDMV	DSPQLATLAD	EVSASLAKQG L
NNMNPNMNMN	NNMHNNNNNN	NMPPMNNNNN	NHNMNMNMNM
NNNPMNNNNN	NNMMNNMMNN	NMNNMNPNNN	NNMMNNNNNN
MMNNNNPNNN	NNNHNMNNMN	NNNMMNNNNM	NNNNMMMNNN
HNNNNPNNNP	NPMNNNNMMP	PNPNNMNPNP	NNNNPNNNNN
NNPNNNNNNP	NNNPNNNNNP	NNNNNNMNNP	NNMPNNNNNN
NNNNNNNNPN	PNNNNNNNNN	PMNPPNNNNP	NNNPNNNNNP
NPNNNNNNNN	NMNPNNPNPN	NNNMNNPHNN	NNNPNNNNNP
PNMNNNNNNP	NNNPMNNPHN	NNNNNNNNNN	PNNMNNPNNN
PNNNNNNNHH	PNNNNNNMNP	NMPNMNPMPN	NNPNNNNMNN
NHNNNNNNPP	NMNHPNNNPM	NNPNPNMHNN	MNNNPNNNNN
NMNNNPHNNN	NNNNNNNMNN	MNNNNNNNNM	MNNNNNNPNN N

Notations are the same as in Table 1. Projection domains are indicated in italics.

In the hard-sphere model, the protein chemical sequence is coarse-grained. Because the van der Waals interaction between monomers is specified by the same (hard-sphere) potential, one needs to introduce only four types of beads (P, H, M, and N) to preserve the charge sequence in a protein. Positively charged aa residues (K and R) are identified as P monomers, whereas negatively charged aa residues (E and D) are treated as M monomers. All uncharged aa residues are unified in group N. The charge is, therefore, zero for a neutral (N) bead, and is +1e or −1e for a positively charged (P) or a negatively charged (M) bead, respectively. Histidine (H), whose charge is +0.5e, is identified as an H bead. In the hard-sphere model, radius of the bead is r_b = 3.6 Å. The phosphorylation is modeled by transformation of the corresponding serines and threonines (from group N) in M monomers with assigned charge −2e. Coarse-grained aa sequences with preserved charge distributions in 3RS and 4RL isoforms are presented in Tables 1 and 2.

The beads are connected by springs whose spring constant ensures the change in the bond length to be within 5%. The counterions and salt ions provide overall electroneutrality of the simulation cell. They are modeled as spherical beads of radius 2 Å. We assume that the dielectric constant is uniform over the cell and is assigned to be ɛ = 79.

Because tau protein is a long ampholytic macromolecule which contains at least 352 amino acids (the shortest 3RS isoform), the timescale of its global rearrangement is very different from the timescale of the local configurational changes. It is therefore important to consider properly not only the fast local chain movements but the slow global scale movement as well. Specifically, two methods are employed for this purpose: 1), a pivot rotation algorithm (11), and 2), a configuration-biased Monte Carlo method (12).

Another relevant computational issue for a polyampholyte system is quasiergodic sampling. In the case when the size of a charged particle is smaller than the Bjerrum length, the energy of interaction between two such particles or between a particle and a highly anionic surface can exceed the average thermal energy. This might trap the corresponding configuration in a local energy well. To overcome this difficulty, a parallel tempering is applied (13). That is, 8–16 replicated sets are used and the corresponding temperatures of the sets are varied from 300 K to 600–900 K. A geometric progression is used to select the temperatures, and the system configurations are redistributed at every 10⁴ steps. In a cylindrical geometry, small mobile ions are less attracted (and thereby less confined) by the charged (MT) surface than in a planar geometry. As a result, a larger radial size D of the simulation cell is necessary to avoid finite size effects. To focus on the electrostatic interactions, the salt concentration is kept low, ≥1 mM, in all the MC simulations. The grand canonical ensemble is implemented to keep constant the chemical potentials of mobile ions.

A total of 10⁵ MC steps were used for the system equilibration, and 5 × 10⁵ MC steps for the data production. Each step contained three directional trial steps in x, y, and z directions, to give overall 1.8 × 10⁶ steps. For every 500–1000 steps, the pivot and configuration-biased Monte Carlo algorithms were applied for the global system rearrangement.

Results

Tau on cylindrical charged MT surface

We start with analyzing the conformations of tau protein bound to the MT surface. The simulation cell comprises a single MT, a bound tau protein (treated periodically in angular and lateral directions), and mobile ions. The latter preserve the system electroneutrality, and their total number varies upon the phosphorylation of tau protein.

It is known that the binding sites in the C-terminal domain of tau protein are entangled on the MT surface, whereas the remaining amino acids in the N-terminal projection domain float in the solvent (14). We assume that the net charge of binding domains is smeared over the MT surface, and focus on the conformations of tau projection domain. The aa residues in the projection domains of 3RS and 4RL isoforms are indicated in italics in Tables 1 and 2. Due to imposed periodic boundaries, these projection domains constitute a cylindrical polyampholyte brush tethered to the surface of microtubule.

Fig. 1 a shows the distributions of positively (P) and negatively (M) charged amino acids in the projection domain of dephosphorylated 3RS isoform as a function of distance z from the MT surface. The distributions were calculated using a shifted Lennard-Jones model, which accounts for different solubilities of aa residues. The projection domain of 3RS isoform contains N = 196 aa residues and has net charge qe = +5.5e (see Table 1). The MT surface charge density σ = −0.87e/nm² is close to the value of −0.9e/nm² for the DNA double helix. However, in contrast to DNA molecule, the MT diameter ≈25 nm is large enough to envision the electrostatic field near MT surface as planarlike. According to the strong coupling theory (4,15), in the case of a highly charged surface, the electrostatic attraction between counterion and the surface is much stronger than the thermal energy. The Gouy-Chapman length μ ∼ (l_Bσ)⁻¹ which determines the decay length of ion distribution, is ∼2.5 Å, i.e., close to ion size, 2 Å. Therefore, the majority of positively charged ions (counterions) are condensed on the MT surface in accordance with the concept of Manning condensation (16). Because tau protein is an ampholytic macromolecule, distribution of amino acids in the tail domain differs from that of counterions. The positively charged (P) beads are more frequent near the anionic MT surface while the negatively charged (M) beads are depleted here. However, at distances z >10 nm from the MT surface, the concentration of M monomers exceeds that of P monomers, indicating a net negative charge of a distal domain of 3RS tail. Overall, the projection domain of 3RS tau is weakly adsorbed on the MT surface (the snapshot of the tail typical configuration is presented in Fig. 1 b). The association of 3RS projection domain with the MT surface occurs through the tail proximal segment (adjacent to the tau binding domain) that is overall positively charged. Due to its ampholytic nature, the proximal segment adopts a fencelike configuration indicated by a maximum in the total density distribution and by local separation of positively (P) and negatively (M) charged amino acids near the MT surface (Fig. 1 a). An overall negatively charged distal segment of the projection domain is shifted away from the MT surface (Fig. 1 b).

Figure 1.

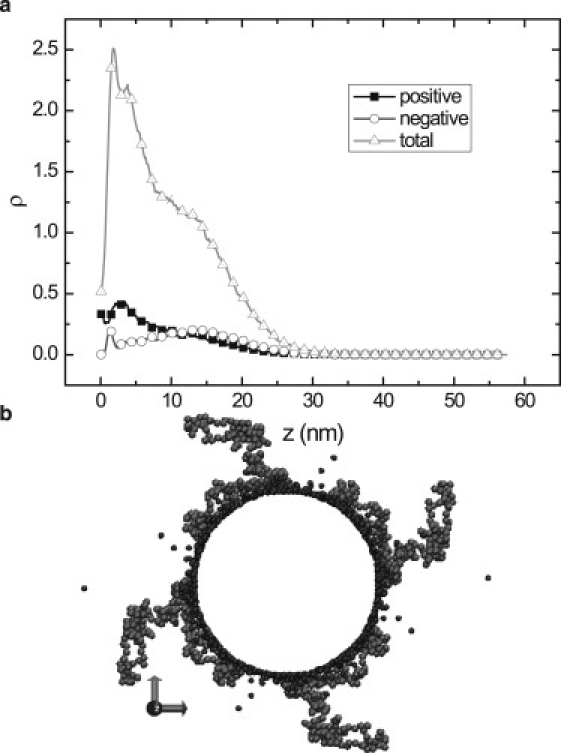
Number density distributions ρ of amino acids in 3RS tau projection domain as a function of distance z from MT surface (a), and MC snapshot of instant system configuration (b). The distributions of positively charged (P) and negatively charged (M) monomers (squares and circles, respectively). Total number density of all amino acids (triangles). (Arrows in b) System of coordinates implemented in MC simulations.

We emphasize that the conformations of 3RS tail domain are rather different from these of a uniformly charged polyelectrolyte/polyampholyte macromolecule near a weakly charged macroion. Within a mean field (the Poisson-Boltzmann) framework of the electrostatic interactions, the density profile in a polyelectrolyte (PE) brush has the Gaussian shape with a maximum at the grafting surface (17,18). To highlight the effect of charge-charge correlations in tau projections, we simulated a brush of 3RS tails near a weakly charged cylindrical surface.

In Fig. 2 a we plot the number density of aa residues ρ(z) as a function of distance z for strongly (σ = −0.87e/nm²) and weakly (σ = −0.004e/nm²) charged surfaces. To compare the polymer distribution obtained from MC simulation with the analytical mean-field theory, we use the value of σ = −0.004e/nm². In this case, the contribution from a charged surface is expected to be negligible with respect to the electrostatic interactions between the projection domains. We consider the (polyampholytic) projection domain of 3RS isoform as a positively charged polyelectrolyte, with an average degree of ionization, α = q/N ≈ 0.028. Under low salt conditions, a PE brush is found in the so-called osmotic regime, where the majority of counterions are condensed in the brush. However, in contrast to the Manning condensation, counterions retain the translational mobility within the brush volume due to weak ionization of the chains (α << 1). An analytical SCF theory of planar PE brushes (17,18) identifies the characteristic length scale of the polymer (and counterion) distribution as

$$H_0/a=\sqrt{8\alpha /\left(3{\pi }^2\right)}N\text{,}$$

where a is the monomer size (see Appendix 2 and Eq. 11). By equating a³ = 4πr_b³/3, where r_b = 3.6 Å is the bead radius, one finds a ≈ 0.58 nm, which is close to the value of a = 0.6 nm, used in self-consistent field modeling of protein brushes (19). By substituting a = 0.6 nm, N = 196, and α = 0.028 in Eq. 11, we estimate H₀ ≈ 10 nm. The polymer density distribution ϕ(z) and the distribution g(z) of free chain ends are then approximated by Eqs. 14 and 16.

Figure 2.

Number density distributions ρ of amino acids in the projection domain of 3RS isoform as a function of distance z at different values of surface charge density σ (a), and the distribution function of the free ends of projections (b). Values of σ are shown in the figures. (Solid lines) Theoretical predictions according to Eqs. 14 and 16 in the Appendix 2, shifted by δz ≈ 0.2H₀.

According to Eq. 14, polymer density ϕ(z) is maximal near the grafting surface, z = 0. The MC data in Fig. 2 a for σ = −0.004e/nm² indicate, however, that maximum in polymer density of 3RS isoform is located at z ≈ 10 nm, i.e., shifted away from the surface. Therefore, the brush of 3RS tails is noticeably more extended than expected from a self-consistent field model which treats 3RS tails as uniformly charged polyelectrolytes. Remarkably, the MC data are well described by the theoretical distributions ϕ(z) and g(z) that are shifted by distance δz ≈ 0.2H₀ (shown by solid lines in Fig. 2, a and b). The width and the decay length of the MC distributions for 3RS projection domains are close to the theoretical expectations for PE brushes.

Comparison between polymer density distributions for weakly and strongly charged surfaces in Fig. 2 a points at a larger amount of aa residues near the surface (at distance z ≃ μ) whereas the distal part of the distribution (z > 15 nm) is virtually unaffected. Therefore, for high surface charge density (σ = −0.87e/nm²), 3RS tails are also expected to be more extended than anticipated from a self-consistent field theory.

In human tau, there are at least 30 candidate amino acids that might be phosphorylated (20). Under pathological conditions, ∼7 aa among them (on average) are actually phosphorylated (21,22). Therefore, net electrostatic attraction between an anionic MT and a phosphorylated tau reduces significantly. Eventually, it turns repulsive. When the phosphorylation-induced repulsion exceeds the tau-MT binding energy, the protein could dissociate in the solution. Hyperphosphorylated tau proteins are known to desorb from the MT surfaces (23–25) and to destabilize microtubules.

In Fig. 3, we present the distributions of aa residues in projection domain of the phosphorylated and dephosphorylated 4RL tau. In the latter case, net charge on 4RL tail is −4e. The candidate sites for the phosphorylation of 4RL tau are specified in Augustinack et al. (26). We select 10 sites in the projection domain, indicated in Augustinack et al. (26), to be phosphorylated (i.e., to acquire charge −2e each). The sequence of amino acid of 4RL tau is similar to that of 3RS isoform except for the distal tail segment, which contains two inserts with excess negative charges. Due to inserts, the conformation of the 4RL tail is different from that of the 3RS tail (see Fig. 3). Positively charged residues localize close to the surface whereas the distal tail domain of the 4RL isoform is repelled further from the MT surface than the 3RS tail. Compared to mean-field expectation, the brush of 4RL tails is also more extended. This tendency is enhanced with the phosphorylation, which makes net tail charge more negative. Fig. 3 demonstrates that the site-specific phosphorylation makes the polymer density profile of bound 4RL isoform more nearly uniform and leads to a more extended tail conformation.

Figure 3.

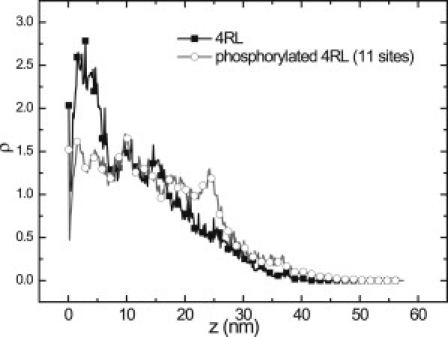
Number density distribution ρ of amino acids as a function of distance z in the projection domain of 4RL isoform. Density profiles for the dephosphorylated and phosphorylated projection domains (squares and circles, respectively).

Interaction between taus in the bulk solution

Tau proteins are commonly recognized as naturally unfolded, or unstructured proteins. Under close to physiological conditions, they are envisioned as random coil polymers with a radius of gyration of R_g ≃ 5 nm (2). The conformations of tau isoforms can be affected by variations in the solution salinity and the phosphorylation.

Although isolated tau proteins are essentially unstructured, they might form extended β-sheets when aggregated in paired helical filaments (2). The specifics of fiber formation involving tau folding and complexation are beyond the scope of this article. Here, we analyze only an initial stage of the phosphorylation-induced association of tau molecules. That is, we explore how the tau proteins interact under the conditions when they are either relatively far from each other or weakly overlap. In both cases, the protein molecules experience the hydrophobic/hydrophilic interactions (specified by shifted Lennard-Jones interaction potentials), and the Coulomb forces. The Coulomb interaction mediated by the protein phosphorylation is of specific importance at large intermolecular distances. We start with exploring the conformations of a single tau protein in bulk solution, and then consider a pair of interacting tau molecules. In this simulation, full amino-acid sequences in tau proteins, including the binding domains and head domains at C termini, are conserved. The system simulation cell has dimensions (L_x, L_y, L_z) = (50 nm, 50 nm, 50 nm), and it is periodic in all three dimensions to account for the finite number density of tau molecules.

In Fig. 4, a and b, we present radial distributions ρ(z) of amino acids from the center of mass in isolated 3RS and 4RL isoforms. Although the content of hydrophobic amino acids in each of the isoforms is rather low, comparison of the distributions obtained in hard-sphere and shifted Lennard-Jones models (shown by triangles and squares in Fig. 4, a and b) indicates that the hydrophobic attraction plays a noticeable role even when the Coulomb interactions are essentially unscreened. Comparison of the average radii of gyration, R_g, and average end-to-end distances, R_e (collected in Table 3), indicates a noticeable decrease in both parameters due to the hydrophobic interactions. For the shortest 3RS isoform, R_g decreases by ∼40% (from 8.21 nm to 5.43 nm), whereas R_e changes by ∼50% (from 16.6 nm to 8.39 nm). A similar trend is found for the longest 4RL isoform. Here, R_g decreases from 8.43 nm to 4.83 nm, whereas R_e changes from 18.6 nm to 9.48 nm.

Figure 4.

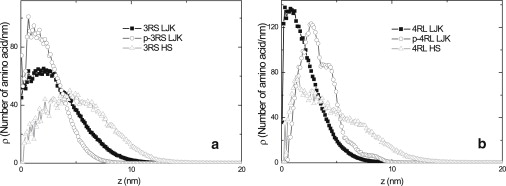
Number density distribution ρ as a function of distance z from the center-of-mass in (a) isolated 3RS tau and (b) isolated 4RL tau in the solution. The results of the hard-sphere model for dephosphorylated isoforms (triangles). Results of shifted Lennard-Jones model (spheres and circles for dephosphorylated and phosphorylated states, respectively).

Table 3.

MC data for average radius of gyration R_g and average end-to-end distance R_e (in nm) for 3RS and 4RL tau isoforms in solution obtained in hard sphere (HS) and shifted Lennard-Jones (LJK) models

	3RS		p-3RS	4RL		p-4RL
	HS	LJK	LJK	HS	LJK	LJK
Rg (nm)	8.21	5.43	3.20	8.43	4.83	5.34
Re (nm)	16.6	8.39	8.13	18.6	9.48	9.05
Rg/Re	0.49	0.65	0.39	0.45	0.51	0.59

The phosphorylation of 3RS and 4RL isoforms leads to different conformational rearrangements in the two macromolecules. Note that dephosphorylated 3RS and 4RL isoforms have different net charges (+15e and +9e, respectively). The charged amino acids in these tau isoforms are localized mostly in the head and the tail domains close to the C- and N-termini. Due to the gradient in charge distribution, the head and the tail tau domains can associate locally.

The phosphorylation of the S and T residues in 3RS tail domain leads to further decrease in average radius of gyration, R_g = 3.20 nm, at almost unchanged average end-to-end distance, R_e = 8.13 nm. In contrast, the phosphorylation of 4RL isoform leads to a moderate increase in R_g up to 5.34 nm, and a slight decrease in average end-to-end distance, R_e = 9.05 nm. We note that the calculated radius of gyration R_g ≃ 5 nm is in good agreement with the experimental values reported in von Bergen et al. (2). The average end-to-end distance R_e ≃ 8–9 nm obtained from the MC simulation is smaller than expected for a random coil model, wherein

$$R_e=R_g\sqrt{6}\approx 12\text{nm}\text{.}$$

However, R_e ≃ 8 nm is still noticeably larger than the reported experimental distance ≃2.3 nm between terminal segments of tau proteins (2). This discrepancy might be attributed to the low salt conditions imposed in the MC simulations.

To study the long-range interaction between tau proteins, two tau isoforms were placed simultaneously in the simulation cell. We used a shifted Lennard-Jones model that accounts for hydrophobic/hydrophilic interactions and considered very dilute conditions to highlight the effect of the electrostatic forces. Fig. 5 displays the average distance d_c between centers-of-mass of 3RS and p-3RS isoforms (abbreviated as the 3RS/p-3RS pair) and of 3RS and p-4RL isoforms (abbreviated as the 3RS/p-4RL pair) as a function of number n of phosphate groups in the phosphorylated (p) molecule. When both isoforms in each pair are dephosphorylated, the average intermolecular distance is ∼70 nm. This distance is much larger than the spreading width of the proteins, which is estimated as 2R_e ≃ 17 nm (shown by a dotted line in Fig. 5). An increase in number n of phosphorylated sites in one of the isoforms leads to the decrease in the average tau-tau distance d_c. Interestingly, d_c(n) decreases while both tau proteins still have net charge of the same (positive) sign. When net charge on the phosphorylated isoform is close to zero (n = 7–8 for p-3RS and n = 4–5 for p-4RL), tau molecules approach the overlap threshold. Further increase in n leads to net charge inversion in the phosphorylated isoform. However, despite increasing net electrostatic attraction between the two molecules, further phosphorylation leads to only mild changes in d_c. That is, the average intermolecular separation d_c remains close to 2R_e ≃ 17 nm.

Figure 5.

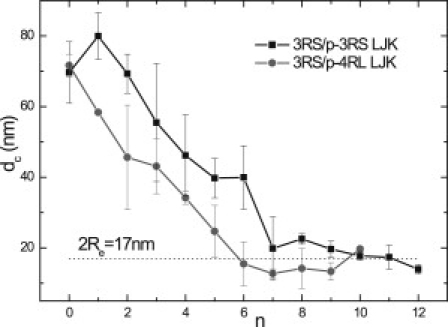
Average distance d_c between centers-of-mass of two tau molecules in the solution as a function of number n of phosphorylated sites in one of the isoforms. The data for 3RS/p-3RS and 3RS/p-4RL pairs (squares and circles, respectively). (Dotted line) The doubled average end-to-end distance (2R_e). The phosphorylation sites in 3RS tau are selected between S and T in the terminal part of projection domain. The phosphorylated sites in 4RL tau are selected as specified in Lovestone and Reynolds (20). The other conditions are the same as in Fig. 4.

The MC data therefore demonstrates that the selective phosphorylation promotes association between dephosphorylated 3RS with the phosphorylated 3RS and 4RL isoforms in the solution. The tau molecules start to approach each other even when net charge on both isoforms is positive. However, more phosphorylated sites are required to reach the same interprotein distance d_c in 3RS/p-3RS pair than in 3RS/p-4RL pair. A similar trend was observed in MC simulations using the hard-sphere model (not shown). The findings indicate that the electrostatic interaction is a significant driving force that brings taus closer—at least within a long-distance range. The oppositely charged tau isoforms exhibit weak association: the intermolecular distance d_c stays close to the overlap threshold despite increasing net Coulomb attraction between molecules. Such behavior might be attributed to a delicate balance between the electrostatic and hydrophilic/hydrophobic interactions in a forming complex.

Conclusions

By using MC simulations, we have analyzed the conformations of 3RS and 4RL tau isoforms near the highly anionic MT surface and in the bulk solution. The MT was modeled as a hollow uniformly charged cylinder. Under low salt conditions, the charged amino acids in a naturally unfolded tau protein interact with the MT surface via unscreened Coulomb force. Due to the strong electrostatic interactions, the distribution of aa residues in a bound polyampholyte (tau protein) noticeably deviates from the predictions of a mean-field theory. In a mean-field regime, the polymer conformation is independent of the actual sequence of aa residues, and only net charge is relevant. However, near a highly charged MT surface, the sequence of aa residues also become important.

The projection domains of 3RS and 4RL taus have a net charge of opposite sign and demonstrate thereby different behavior near the MT surface. In a dephosphorylated 3RS projection, whose net charge is positive, more amino acids are observed near the surface than in a 4RL projection. However, the tails are less attracted to the MT surface than predicted by a mean-field theory. In the case of 4RL tau, which is the longest tau in human body and has a net negative projection domain, fewer amino acids are found near the MT surface. In the phosphorylated taus, the net electrostatic interaction between tau and MT becomes repulsive, and more aa residues are repelled from the surface. The phosphorylation destroys the fencelike conformation of proximal domain in the 3RS tail. The density distribution profiles become more nearly uniform for both isoforms. To highlight the role of the electrostatic interactions in MT-bound and free tau proteins, we focused on low salt concentrations (≥1 mM). Under physiological conditions, the salt concentration is ∼100 mM, and the electrostatic (Debye) screening length decreases to 1 nm. Therefore, in MT-bound tau, the charge-charge correlations in the tail domain would loosen. The strong association between tau and MT would still hold, but the protein would exhibit longer tail distribution above the surface.

Hyperphosphorylated taus are known to dissociate from MTs and aggregate in intracellular inclusions that prevent normal functioning of a neuron (27). In this article, we focused on initial stages of the phosphorylation-induced association of taus by analyzing the conformations of a pair of tau isoforms in the solution. The major result of this study is a demonstration that the electrostatic interaction is an important factor which governs the behavior of taus at large intermolecular distances. A moderate phosphorylation of one isoform in a pair enhances the electrostatic attraction between the proteins. As a result, the taus get closer and start to overlap. Further phosphorylation does not noticeably affect the average tau-tau separation, and the two isoforms stay close to the overlap threshold. The short-range hydrophobic/hydrophilic interactions might be the essential stabilizing factor in this regime.

In summary, the conformations of the shortest (3RS) and the longest (4RL) human tau isoforms were investigated near the highly charged MT surface and in the bulk solution. Monte Carlo simulations demonstrated that the phosphorylation of taus plays an important role in establishing the intermolecular distance at early stages of the protein association. In addition to the long-range electrostatic attraction between the domains of tau molecules, the short-range hydrophobic/hydrophilic interactions lead to more compact protein structures, and thereby affect the tau association.

Appendix 1

Consider a cylinder of radius R with discrete charges q located on a one-dimensional (linear) lattice beneath the cylindrical surface at depth D. We assume, for simplicity, that there is only one line with a discretized charge. The generalization for the case of multiple charged lines is straightforward. The equidistance between charges on the line is Δ. In the cylindrical coordinate system, the normalized electrostatic potential between two charges separated by (r, z), where r is the radial distance and z is the lateral distance, is (28,29)

$$\varphi \left(r,z\right)=\frac{4}{\Delta }\sum _{p>0}{K}_0\left(\omega r\right)\cos \left(\omega z\right)-\frac{2}{\Delta }\log \left(\frac{r}{2L_z}\right)\text{.}$$

Here, ω = 2πp/Δ where p ≥ 0 is an integer, K₀ is the modified Bessel function, and L_z is the lateral size of simulation box wherein the periodic boundary condition is imposed. The linear charge density q/Δ determines the average surface charge density σ as

$$\frac{q}{\Delta }=2\pi R\sigma \text{.}$$

Introducing the Bjerrum length l_B ≡ e²/4πɛ₀ɛ₂ k_BT ≈ 7.0 Å and the Gouy-Chapman length μ,

$$\mu =\frac{1}{2\pi q{l}_{\text{B}}\sigma }\text{,}$$

one finds

$$\Delta =\frac{q^2\mu l_{\text{B}}}{R}\text{,}$$

and therefore,

$$\omega r=2\pi p\frac{Rr}{q^2\mu l_{\text{B}}}\text{.}$$

The coupling parameter for an MT system with monovalent charges is l_B/μ = 2.73. Because D ∼1 nm, μ < l_B < D < r, and l_B << R. Therefore ωr > > 1, and the modified Bessel function term has to be much smaller than 1 . The remaining term is just a constant plus the electrostatic potential due to a uniformly charged line. Therefore, it is reasonable to consider the MT charge as spread uniformly over the MT surface. A similar demonstration is possible for the planar geometry as well.

Appendix 2

We consider polyelectrolyte chains with the degree of ionization α and the degree of polymerization N >> 1 tethered to the surface of an uncharged cylinder with radius R. The chains are tethered with a linear density 1/L where L is the distance between neighboring chains along the axis of cylinder, and a is the size of a monomer. In the strong stretching approximation (30), the free energy functional is formulated as

$$F/kT=\frac{3}{2a^2}\underset{0}{\overset{H}{\int }}g\left(x^{\prime }\right)d{x}^{\prime }\underset{0}{\overset{x^{\prime }}{\int }}E\left(x^{\prime },x\right)dx+\underset{0}{\overset{H}{\int }}f\left[\varphi \left(x\right)\right]s\left(x\right)dx\text{,}$$ (1)

where the first term is the free energy of elastic stretching (F_elastic), and the second term (F_int) is due to the interactions between monomers. Here, g(x′) is the distribution function of the free chain end,

$$\underset{0}{\overset{H}{\int }}g\left(x^{\prime }\right)d{x}^{\prime }=1\text{,}$$ (2)

and function E(x′, x) = dx/dn determines local chain stretching at distance x from the surface for a chain with its free end located at distance x′ from the surface, and ϕ(x) is the density profile (volume fraction) whereas f[ϕ(x)] is the density of the free energy of monomer-monomer interactions. The value s(x) = s(1 + x/R) is area per chain at distance x from the surface, and H is the brush thickness. Function of local chain stretching is normalized as

$$\underset{0}{\overset{x^{\prime }}{\int }}\frac{dx}{E\left(x^{\prime },x\right)}=N\text{for any value of}0\le x^{\prime }\le H\text{,}$$ (3)

whereas polymer density profile ϕ(x) is related to g(x′) and E(x′, x) as

$$\varphi \left(x\right)s\left(x\right)=a^3\underset{0}{\overset{x}{\int }}\frac{g\left(x^{\prime }\right)d{x}^{\prime }}{E\left(x^{\prime },x\right)}\text{,}$$ (4)

and is normalized as

$$\underset{0}{\overset{H}{\int }}\varphi \left(x\right)s\left(x\right)dx=N{a}^3\text{.}$$

Variation of functional F with the account of additional constraints reduces to the unconditional minimization of functional as

$$F^{\prime }=F+\underset{0}{\overset{H}{\int }}{\lambda }_1\left(x^{\prime }\right)d{x}^{\prime }\underset{0}{\overset{x^{\prime }}{\int }}\frac{dx}{E\left(x^{\prime },x\right)}+{\lambda }_2\underset{0}{\overset{H}{\int }}\varphi \left(x\right)s\left(x\right)dx\text{,}$$

where λ₁(x′) and λ₂ are the indefinite Lagrange multipliers. Variation of F′ yields

$$\delta F^{\prime }/kT=\frac{3}{2a^2}\underset{0}{\overset{H}{\int }}\delta g\left(x^{\prime }\right)d{x}^{\prime }\underset{0}{\overset{x^{\prime }}{\int }}E\left(x^{\prime },x\right)dx+\frac{3}{2a^2}\underset{0}{\overset{H}{\int }}g\left(x^{\prime }\right)d{x}^{\prime }\underset{0}{\overset{x^{\prime }}{\int }}\delta E\left(x^{\prime },x\right)dx+\underset{0}{\overset{H}{\int }}\frac{\delta f\left[\varphi \left(x\right)\right]}{\mathit{\delta }\varphi \left(x\right)}\delta \varphi \left(x\right)s\left(x\right)dx-\underset{0}{\overset{H}{\int }}{\lambda }_1\left(x^{\prime }\right)d{x}^{\prime }\underset{0}{\overset{x^{\prime }}{\int }}\frac{\mathit{\delta }E\left(x^{\prime },x\right)dx}{E{\left(x^{\prime },x\right)}^2}+{\lambda }_2\underset{0}{\overset{H}{\int }}\delta \varphi \left(x\right)s\left(x\right)dx\text{.}$$ (5)

By using Eq. 4, one finds that combination δϕ(x)s(x) that is present in the third and the last terms in Eq. 5 is related to functions g(x′) and E(x′, x) in the same way as in the case of a planar brush. That is,

$$\delta \varphi \left(x\right)s\left(x\right)=a^3\underset{0}{\overset{x}{\int }}\left[\frac{\delta g\left(x^{\prime }\right)d{x}^{\prime }}{E\left(x^{\prime },x\right)}-\frac{g\left(x^{\prime }\right)d{x}^{\prime }}{E{\left(x^{\prime },x\right)}^2}\delta E\left(x^{\prime },x\right)\right]\text{.}$$ (6)

Therefore, the solution of this problem is formally similar to the planar case considered previously. Namely,

$$\begin{array}{l}E\left(x^{\prime },x\right)=\frac{\pi }{2N}\sqrt{{\left(x^{\prime }\right)}^2-x^2},\\ \frac{\delta f\left[\varphi \left(x\right)\right]}{\mathit{\delta }\varphi \left(x\right)}=\Lambda -\frac{3{\pi }^2{x}^2}{8N^2{a}^2},\end{array}$$ (7)

where Λ is a constant to be determined from the normalization of polymer density profile ϕ(x).

At low salt concentrations in the bulk solution, density of the free energy of the interactions f[ϕ(x)] within the brush is governed by the translational entropy of counterions (modeled as an ideal gas of pointlike elementary charges with concentration c_ion). In the framework of the local electroneutrality approximation, c_ion ≈ αϕ(x), and

$$f\left[\varphi \left(x\right)\right]=c_{\text{ion}}\text{ln}\left[{\mathit{c}}_{\text{ion}}/e\right]\approx \alpha \varphi \left(x\right)\text{ln}\left[\alpha \varphi \left(\mathit{x}\right)/e\right]\text{,}$$ (8)

to give

$$\ln \left[\alpha \varphi \left(x\right)\right]=\Lambda -\frac{3{\pi }^2{x}^2}{8N^2{a}^2}$$ (9)

or, equivalently,

$$\varphi \left(x\right)=\Lambda \exp \left(-x^2/H_0^2\right)\text{,}$$ (10)

where Λ₁ is the constant proportional to average polymer volume fraction in the brush, and

$$H_0=\sqrt{\frac{8}{3{\pi }^2}}a{\alpha }^{1/2}N$$ (11)

is the characteristic electrostatic length. We therefore obtain the same x-dependence for the polymer density profile ϕ(x) as in a planar case. (Note that here x is the distance from the grafting surface.) The difference between cylindrical and planar geometries manifests itself in the value of constant Λ_1. In a cylindrical brush, Λ₁ depends on the radius of the cylinder R. Normalization of the polymer density profile,

$$N{a}^3=\underset{0}{\overset{H}{\int }}\varphi \left(x\right)s\left(x\right)dx\approx {\Lambda }_1\underset{0}{\overset{\infty }{\int }}\exp \left(-x^2/H_0^2\right)2\pi \left(R+x\right)hdx\approx 2\pi {\Lambda }_{1}h{H}_0\left[R\frac{1}{2}\sqrt{\pi }+\frac{1}{2}{H}_0\right]\text{,}$$ (12)

where brush thickness H = ∞, gives

$${\Lambda }_1=\frac{N{a}^3}{\pi h{H}_{0}R\left(\sqrt{\pi }+H_0/R\right)}={\varphi }_0\frac{2}{\sqrt{\pi }+\omega }\text{.}$$ (13)

Here,

$$\omega =\frac{H_0}{R}\text{and}{\varphi }_0=\frac{N{a}^3}{s{H}_0}$$

are the reduced radius of the cylinder and average polymer concentration where s = 2πLR is the grafting area per chain. Overall, the polymer density profile reads

$$\varphi \left(x\right)={\varphi }_0\frac{2}{\sqrt{\pi }+\omega }\exp \left(-x^2/H_0^2\right)\text{.}$$ (14)

It reduces to a planar case when R → ∞ (ω = 0).

It is, however, known that in the parabolic potential, distribution function g(x) in convex brushes demonstrates the so-called exclusion zone (30). This zone of width x_∗ located near the grafting surface is depleted from the chain ends. An advanced SCF model (31,32) imposes an additional constraint g(x) = 0, when 0 < x < x_∗ predicts an exponential decay in x_∗ as surface curvature ω → 0. In the first approximation, x_∗ can be estimated from the condition g(x) = 0 where g(x) is obtained by inverting Eq. 4. This equation is reduced to the Abel integral equation by introducing new variables

$$\xi =H^2-x^2,\eta =H^2-{\left(x^{\prime }\right)}^2\text{,}$$

and the new function

$$\upsilon \left(\eta \right)=g\left(x^{\prime }/2x^{\prime }\right)\text{,}$$

$$\underset{0}{\overset{\xi }{\int }}\frac{\upsilon \left(\eta \right)d\eta }{\sqrt{\xi -\eta }}=\varphi \left(\sqrt{H^2-\xi }\right)s\left(\sqrt{H^2-\xi }\right)=2\pi h\left(R+\sqrt{H^2-\xi }\right){\Lambda }_1\exp (\xi -H^2)/H_0^2\text{.}$$

The solution of the Abel equation gives

$$\frac{g\left(x^{\prime }\right)}{2x^{\prime }}=\frac{1}{2N{a}^3}\left\{\frac{\varphi \left(H\right)s\left(H\right)}{\sqrt{H^2-{\left(x^{\prime }\right)}^2}}-\underset{x^{\prime }}{\overset{H}{\int }}\frac{d}{dx}\left[\varphi \left(x\right)s\left(x\right)\right]\frac{dx}{\sqrt{x^2-{\left(x^{\prime }\right)}^2}}\right\}\text{,}$$ (15)

where H is the thickness of the brush. For PE brushes in local electroneutrality approximation, H = ∞ and ϕ(H) = 0. By substituting Eq. 14 in Eq. 15, and using expression s(x) = s(1 + x/R) = s(1 + ωt) where t = x/H₀ is the reduced distance from the surface, one obtains

$$g\left(t\right)H_0=\frac{2t\exp \left(-t^2\right)}{\sqrt{\pi }+\omega }\left\{\omega \underset{0}{\overset{\infty }{\int }}\frac{\left(t^2+z-1/2\right)}{\sqrt{\left(t^2+z\right)z}}\exp \left(-z\right)dz+\sqrt{\pi }\right\}\text{.}$$ (16)

When R ≃ H₀, the width of dead zone x_∗/H ≃ 10%, and Eqs. 14 and 16 can be used as only rough approximations for polymer density profile ϕ(x) and distribution of free end g(x).