Residue-Specific Side-Chain Packing Determines the Backbone Dynamics of Transmembrane Model Helices

Abstract

The transmembrane domains (TMDs) of membrane-fusogenic proteins contain an overabundance of β-branched residues. In a previous effort to systematically study the relation among valine content, fusogenicity, and helix dynamics, we developed model TMDs that we termed LV-peptides. The content and position of valine in LV-peptides determine their fusogenicity and backbone dynamics, as shown experimentally. Here, we analyze their conformational dynamics and the underlying molecular forces using molecular-dynamics simulations. Our study reveals that backbone dynamics is correlated with the efficiency of side-chain to side-chain van der Waals packing between consecutive turns of the helix. Leu side chains rapidly interconvert between two rotameric states, thus favoring contacts to its i±3 and i±4 neighbors. Stereochemical restraints acting on valine side chains in the α-helix force both β-substituents into an orientation where i,i±3 interactions are less favorable than i,i±4 interactions, thus inducing a local packing deficiency at VV3 motifs. We provide a quantitative molecular model to explain the relationship among chain connectivity, side-chain mobility, and backbone flexibility. We expect that this mechanism also defines the backbone flexibility of natural TMDs.

Introduction

The stability and conformational dynamics of proteins and their constituent secondary structure elements depend on their primary structure. For example, a previous statistical analysis showed that β-branched amino acids such as Val and Ile, the helix breaker Pro, and the flexible Gly are underrepresented in the helices of globular proteins (1). However, exactly how different side-chain structures affect helices is still a matter of controversy. To be precise, one must distinguish between the equilibrium between the unfolded and folded states of a helix and the dynamics of the folded structure. The extent of folding was previously related to helix-promoting enthalpic factors such as side-chain packing and burial of apolar surface (2,3), and to loss of side-chain entropy due to restricted rotational degrees of freedom after folding (1,4–6). The contributions of these factors to conformational backbone dynamics, in terms of local and transient unfolding of an α-helix, are unclear.

Little is known about the conformational dynamics of helical transmembrane domains (TMDs) that make up the membrane-spanning part of most integral membrane proteins. TMD helices may undergo bending at hinge regions (7) and small-scale conformational fluctuations of their backbones (8–10), and exhibit side-chain rotations (11,12). The conformational dynamics of TMD helices has been proposed to enhance the function of membrane fusogenic proteins. This hypothesis was originally based on the finding that the helix-destabilizing Ile and Val residues account for ∼40% of the TMD residues of soluble (N-ethylmaleimide-sensitive factor) attachment protein receptor (SNARE) proteins, but only ∼25% of TMD residues of unrelated membrane proteins (13). SNAREs drive membrane fusion along the eukaryotic secretory pathway, as exemplified by fusion of synaptic vesicles with the presynaptic plasma membrane (14). Complete bilayer mixing induced by SNAREs depends on the presence of TMDs (14–19). Moreover, synthetic peptides modeling the hydrophobic core of SNARE TMDs drive liposome fusion in vitro and thus mimic basic aspects of the fusogenic function of full-length SNAREs (13,19). Because these TMD peptides are devoid of soluble domains that can mediate membrane apposition, it appears that isolated TMDs increase the likelihood of randomly colliding liposomes entering into fusion. The backbone dynamics of SNARE TMD helices was experimentally studied by recording deuterium/proton exchange (DHX) kinetics of amide deuterons in isotropic solution. The DHX kinetics of SNARE TMDs vastly exceeded that of an oligo-Leu helix, whereas multiple substitutions to Leu reduced exchange kinetics (9). To systematically investigate the contribution of Val to fusogenicity and helix dynamics, a set of low-complexity, membrane-fusogenic TMD peptides, termed LV-peptides, was designed de novo (20). Their hydrophobic core sequences are composed of helix-promoting Leu and helix-destabilizing Val residues at different ratios and different positions, as well as Gly and Pro residues in some variants. Indeed, the fusogenicity and DHX rates of LV-peptides increase with Val content and the presence of a central Gly/Pro pair, corroborating the link between backbone dynamics and lipid mixing (10). In the original design (20) the Leu/Val ratio was varied over the entire hydrophobic domain (here termed A-peptides; Table 1). Later, Val residues were concentrated at peripheral or central domains of the hydrophobic core while maintaining the Leu/Val ratio of LLV16 (B-peptides; Table 1). The results of fusion assays and DHX suggest that the increased dynamics close to the helix termini are more relevant for fusion than the central domains (21).

Table 1.

Primary structures of LV-peptides

Peptide	Sequence
A-peptides: Increasing content of helix-breaking residues
L16	KKKWLLLLLLLLLLLLLLLLKKK
LLV16	KKKWLLVLLVLLVLLVLLVLKKK
LV16	KKKWLVLVLVLVLVLVLVLVKKK
VVL16	KKKWVVLVVLVVLVVLVVLVKKK
LV16-G8P9	KKKWLVLVLVLGPVLVLVLVKKK
B-peptides: 11 Leu / 5 Val unevenly distributedParental compound: LLV16
LVL	KKKWLLLLLVVVVVLLLLLLKKK
VLV	KKKWVVLLLLLLLLLLLVVVKKK
L-LV-L	KKKWLLLVLVLVLVLVLLLLKKK
LV-L-LV	KKKWLVLVLLLLLLLVLVLVKKK

In this work, we analyzed the sequence- and position-dependent backbone and side-chain dynamics of LV-peptide helices in 80% 2,2,2-trifluoroethanol (TFE)/water (v/v) solvent (i.e., the same conditions used for the DHX experiments) using molecular-dynamics (MD) simulations. From the fractional occupancy of the amide hydrogen (H)-bonds observed in the simulations we calculated the DHX rates to validate the description of the atomistic backbone fluctuations. Here, we address the molecular mechanism by which Val enhances TMD-helix dynamics. In particular, we discuss the relationship among interaction topology, local packing density, side-chain mobility, and backbone dynamics. We conclude that rotamer-dependent van der Waals (VDW) interactions between side chains at consecutive turns of a helix are the main determinants of backbone dynamics and H-bond stability in LV-peptides. The larger dynamical volume available for Leu side chains provides favorable packing and stabilizes the backbone, whereas the constrained flexibility of Val induces packing deficiencies and promotes backbone flexibility. Understanding the molecular mechanism by which Val and Leu determine helix dynamics will make it possible to design transmembrane helices with specific local dynamical properties.

Materials and Methods

All-atom MD simulations

Simulations were carried out using the CHARMM22 force field for the peptide (22) with CMAP correction (23), TIP3 water (24), and TFE (25). The water/TFE solvent was constructed as described previously (26). The trajectories started from an ideal α-helical backbone (ϕ = −57°, ψ = −47°) with termini and lysine charged as at the experimental pH = 6.5. Side-chain rotamers were built in trans conformation (χ_1,2 = 180°). Peptide and solvent were equilibrated with gradually released constraints on the peptide for a total of 5 ns in a rectangular box of side length 74 Å × 56 Å × 56 Å (1472 water, 1472 TFE molecules) containing six neutralizing chloride counterions placed at random. The free dynamics at constant temperature and pressure (p = 0.1 MPa, T = 298 K) was recorded for 100 ns with the use of extended system algorithms (27,26), periodic boundary conditions, particle mesh Ewald electrostatics (128 × 64 × 64 grid, direct interaction cutoff 12 Å, Ewald parameter 0.36, fourth-order B-spline interpolation), a 12 Å shifted force cutoff for Lennard-Jones interactions, SHAKE constraints on the bond lengths to hydrogen atoms (28), and a time step of 2 fs for numerical integration with the Nosé-Hoover algorithm (29,30). All simulations were performed with the program CHARMMv33 (31) running on the Linux Cluster (32 processors, Itanium2 Madison, 1.6 GHz, 6.4 Gflops/s) of the Leibniz Computing Center, Munich, Germany.

Analysis

Analysis of the H-bond populations, dihedral angular correlation functions, secondary structure, and root mean-square deviations (RMSDs) was carried out with routines provided with the CHARMM software (31). To calculate pairwise rotamer-dependent interactions, Val and Leu were incorporated with spacings 3 and 4 in the center of a (Gly)₂₃ helix constrained to ideal α-helical geometry. The χ₁ and χ₂ dihedrals were adjusted to −60°, +60°, or 180°, respectively, and the side chains were relaxed with 250 steps steepest-descent minimization in vacuum. To quantify the relationships between structural and dynamical properties, we calculated Spearman's rank order correlation coefficients, ρ, and their statistical significance, p (32). The full correlation matrix is given in Table S1 of the Supporting Material.

Calculation of DHX rates from MD simulations

Under the experimental conditions (10) the exchange rate k_DX was determined by the equilibrium constant K_op for backbone fluctuations opening the structure around an amide (33): k_DX = K_op/(1 + K_op) k_int. The rate k_int for base-catalyzed exchange from an unstructured peptide was calculated using published residue-specific values (33) for hydrogen/deuterium exchange in H₂O (no salt), experimental pH, and the autoprotolysis constant of H₂O at 293 K. We applied the description of exchange competence as previously developed (34,35) for helical peptides in nonaqueous solvent. The closed state is defined by the presence of α-helical and nonregular 3₁₀- and π-helical H-bond accepting carbonyl oxygens within a cutoff distance d_HO. In the original work (34), the best correspondence between MD-derived exchange rates and those from NMR experiments was found with d_HO = 3 Å. Since separations larger than 3 A are discussed (35–37), we varied d_HO between 2.6 Å and 4.0 Å. In addition, a minimum residence time of 1 ps in a state prevents transient behavior from being considered as H-bond breakage or formation (38). For each cutoff d_HO, the fraction f_cl of the closed state, the equilibrium constant K_op = (1 − f_cl)/f_cl, and the corresponding exchange rate k_DX = (1 − f_cl) k_int were calculated for the amide protons of residues 5–23. Using these rates (Fig. S1), we modeled the time-dependent deuteron population for each of the aliphatic A-peptides and the B-peptides as the sum of 19 monoexponential decays. The quality of the models was assessed by χ²_red (39), the variance of residuals between experimental (10) and calculated deuteron populations. All χ²_red-values are given in Table S2. We conclude that an overall χ²_red < 0.5, as obtained with the cutoff d_HO = 3 Å used in the original work (34), also provides a reliable description of exchange competence for our LV-peptides. In addition, we classified the residues according to their rates into the experimentally determined four kinetic regimes (10) and evaluated the linear correlations of the class populations obtained from MD simulations and DHX experiments (Fig. S2).

Results

To delineate the mechanism by which Val enhances helix backbone dynamics, we determined several measures of local unfolding and correlated them with structural and dynamical features of Val and Leu side chains.

Conformational dynamics of LV helices

Convergence of conformational sampling

To assess the convergence of sampling of backbone conformations we analyzed the per-residue mean difference, δ, between structures averaged over nonoverlapping time windows of different lengths (40). For a fully converged simulation, the average structures taken from different sufficiently long simulation fragments are similar, with δ approaching 0 Å. For the core regions (residues 5–20) of the LV-peptides, the δ-values become independent of the window size for an averaging time of ∼10 ns and are generally <0.5 Å. The results for 10 ns and 20 ns windows are compared in Fig. S3. Only VVL16, LVL, and LV16-G8P9 show ∼1 Å differences between average structures. Thus, 10 ns sampling provides reliable conformational information about the cores. The larger structural drift (δ > 1 Å), as well as the dependence on the length of the sampling window for N-terminal (residues 1–4) and C-terminal (residues 21–23) regions and around the Gly/Pro pair in LV16-G8P9, indicate that a larger conformational space may be available there.

To assess the convergence of sampling of side-chain rotamers, we analyzed the autocorrelation functions of the dihedral fluctuations. In addition, we subjected the backbone dihedral fluctuations to the same analysis. The results are detailed in Table S3, and examples of dihedral fluctuations and autocorrelation functions are shown in Fig. S4. The autocorrelation functions decay monoexponentially to zero with relaxation times τ between ∼1/150 (Leu side chains and most of the backbone dihedrals) and ∼1/30 (Val side chains and the slowest backbone fluctuations of VVL16) of the total simulation time T_sim. With M frames stored, the statistical insignificance s = (2 τ/T_sim) M (41) can be estimated to vary between s = M/75 for the fastest fluctuations and s = M/15 for the slowest fluctuations. We conclude that reorientations are sampled frequently enough to lead to representative distributions of side-chain rotamers. The relaxation times for the slowest backbone dihedral fluctuations are on the same order as the minimum window size of ∼10 ns necessary to provide a converged mean distance between average structures for core residues (compare Fig. S3).

Global structural and dynamical properties

We monitored the global structural features of the peptide helices by computing the average helicity and the RMSD of C_α positions (C_α-RMSD) from an ideal α-helix (Table 2). First, the average α-helix contents as calculated from MD closely reproduce the helicities of the peptides as previously determined by circular dichroism (CD) spectroscopy (10). Second, both the average C_α-RMSD and the standard deviations show a pronounced increase with the content of Val or the presence of the Gly/Pro pair. The increase in RMSD parallels reduced α-helicity with increased Val content or the presence of a Gyl/Pro pair (A-peptides). B-peptides show RMSDs comparable to those of the parental LLV16. Third, the large difference between the RMSD calculated over the complete sequence in comparison to the RMSD of the core regions (residues 5–20) shows that the large deviations from an idealized α-helix are mainly due to helix fraying in the terminal regions. The largest differences in C_α-RMSD for the core region are seen with the peptides with extended Val stretches (VVL16 and LVL) or the Gly/Pro pair (LV16-G8P9). We conclude that the peptides remain α-helical and exhibit substantial structural dynamics. The dynamics in the core is particularly sensitive to primary structure, in that it increases systematically with the concentration of Val residues or the presence of a Gly/Pro pair.

Table 2.

Global structural properties of LV-peptides in 80% TFE/water (v/v) (for sequences see Table 1)

Peptide	fαCD [%]∗	fαMD [%]†	Cα-RMSD (all) [Å]‡	Cα-RMSD (core) [Å]‡
A: Increased content of helix-breaking residues
L16	83.0 ± 3.2	80.3 ± 7.5	1.7 ± 0.6	0.7 ± 0.1
LLV16	84.0 ± 3.7	79.1 ± 8.8	1.9 ± 0.5	0.9 ± 0.2
LV16	78.0 ± 4.4	76.2 ± 9.3	1.9 ± 0.5	1.0 ± 0.3
VVL16	67.0 ± 5.5	66.1 ± 12.7	2.7 ± 0.7	1.4 ± 0.4
LV16-G8P9	71.0 ± 6.2	71.4 ± 11.9	3.7 ± 1.2	2.6 ± 0.9
B: 11 Leu / 5 Val unevenly distributed
LVL	62.0 ± 8.8	79.2 ± 7.9	1.9 ± 0.5	1.1 ± 0.3
VLV	62.0 ± 5.9	77.2 ± 6.2	2.3 ± 0.4	0.9 ± 0.2
L-LV-L	75.0 ± 5.2	78.1 ± 8.7	2.3 ± 0.3	0.9 ± 0.2
LV-L-LV	67.0 ± 6.1	80.1 ± 7.2	1.6 ± 0.4	0.8 ± 0.2

Given are averages and standard errors taken over nonoverlapping 10 ns time windows.

^∗α-Helix content from CD experiment (10).

^†Average α-helix content from DSSP analysis (72) of the MD trajectories.

^‡RMSD of the C_α atoms relative to an ideal α-helix (all: average over the complete sequence, core: average over C_α atoms from residues 5–20). Rigid-body translations and rotations have been removed via a least-square fitting of the backbone to the reference helix (42,43).

Position-specific structure and dynamics

To characterize the local variations of backbone structure and dynamics, we analyzed the site-resolved C_α-RMSD and the population of intramolecular H-bonds (Fig. 1 and Fig. S5). C_α-RMSD values > 1.5 Å confirm helix fraying in the terminal regions, in particular at the N-termini. An increased Val content and the Gly/Pro pair cause larger local deviations as well as larger fluctuations (VVL16, LV16-G8P9, and LVL). The H-bond pattern confirms reduced helicity at the termini. Locally reduced α-helicity strongly depends on residue position and sequence context, and is partially compensated for by the formation of intramolecular 3₁₀–H-bonds. Specifically, oligo-Leu stretches (L16, central part of VLV, and LV-L-LV, terminal region of LVL) show contiguous α-helical H-bonding. The presence of two (VVL16) or more (LVL) sequential Val residues leads to a drastic reduction in local H-bond stability. The central Gly/Pro strongly destabilizes the helix. We conclude that the conformational dynamics of the LV cores is extremely sensitive to side-chain structure.

Figure 1.

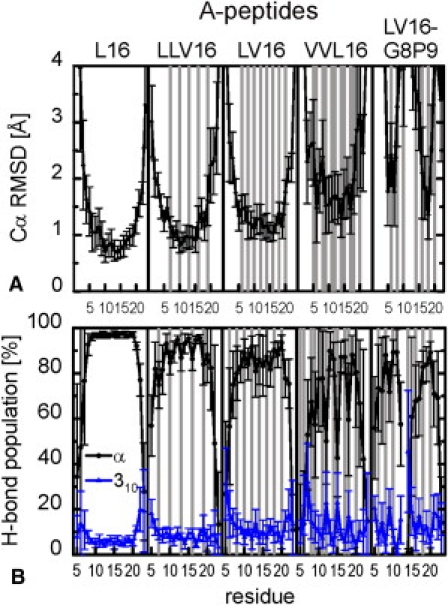
Sequence- and residue-specific structural and dynamical variations of LV-peptides of type A. The results for the B-peptides are shown in Fig. S5. Error bars indicate standard errors calculated from 10 ns block averages. Val positions are shaded in gray. (A) C_α-RMSD from an ideal α-helix. Overall rotations and translations were eliminated by a rigid-body fit to the reference structure. (B) Population of α-helical and 3₁₀-helical H-bonds. In <5% of the trajectories, the amide protons form bifurcated H-bonds.

Fig. 2 gives a graphical overview of the backbone dynamics. For each peptide, 20 structures taken every 5 ns are superimposed with a rigid-body fit (42,43) to an ideal α-helix. The structures are color-coded according to local α-H-bond stability (compare Fig. 1 and Fig. S5). For the A-peptides, both an increased deviation from helical conformation and an increase in the fluctuations with increased content of Val or the Gly/Pro pair can be clearly seen.

Figure 2.

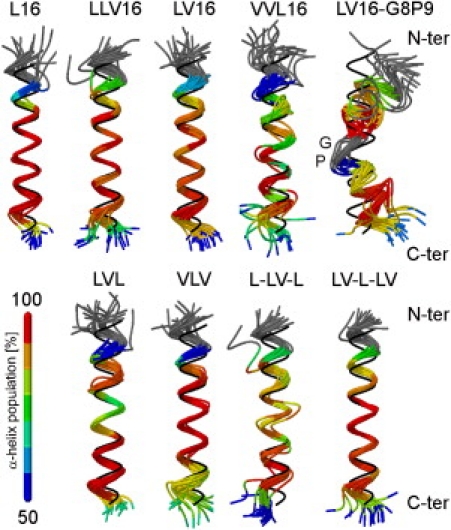
Graphical representation of LV-peptide dynamics. For each peptide 20 exemplary structures taken every 5 ns are superimposed. The C_α atoms of residues 5–20 are oriented with a rigid body to an ideal α-helix shown in black. The color code indicates the average population of α-helical H-bonds (compare Fig. 1B and Fig. S5B). For peptides in the upper row (class A) the content of Val increases from left to right. Peptides in the lower row (class B) maintain the Leu/Val ratio of the parental LLV16, but Val is concentrated at peripheral or central parts of the sequence. The sequences are given in Table 1.

Close agreement between calculated and experimental exchange kinetics validates the simulations

We aimed to validate our MD simulations by comparing predicted DHX exchange rates with previously determined experimental values (10). Experimental exchange kinetics is composed of individual site-specific exchange rate constants whose exact values depend on the extent of local helix dynamics and steric accessibility of the amide deuteron. From the fractional population of intramolecular H-bonds as observed in the simulations, we calculated sequence- and position-dependent exchange rates k_DX (Fig. S1), the numbers of deuterons as a function of reaction time, and the kinetically distinct deuteron populations (Fig. S2) (see Materials and Methods). The variance of residuals χ²_red (39) between calculated and experimental deuteron populations was <1 for most peptides (Table S2), with the exceptions of the slowly exchanging L16 and LLV16 (χ²_red = 1.6 and 2.4, respectively). The overall correlation between the populations of the four kinetic subclasses as derived from MD and DHX has a slope of ∼1 and a linear correlation coefficient of r = 0.89 (Fig. S2 B and C). We conclude that the DHX rate constants derived from our MD simulations describe exchange kinetics of the LV-peptides in close agreement with experiment, which validates the simulations.

The calculated exchange rates k_DX (Fig. S1) cover 4 orders of magnitude, corresponding to the experimental variation 10⁻¹ h⁻¹ < k_DX < 10³ h⁻¹ (10). The very fast exchanging amide deuterons at the terminal regions show rates approaching those by which random coils will exchange, which is consistent with their highly water-exposed and mostly unstructured conformations. Toward the core regions, exchange generally slows down in a manner depending on the type of peptide. The slowest deuterons are located within the oligo-Leu core of L16, whereas increasing the Val content shifts slow deuterons into faster populations. A correlation coefficient of −0.92 (Table S1) indicates that the exchange rates are mainly determined by the dynamics of the α-helical H-bonds.

What is the mechanism by which Val enhances backbone dynamics?

The context-dependent variation of helix dynamics will be inherent in the structural and dynamical differences of side chains, which determine intramolecular as well as peptide-solvent interactions. For the nonpolar LV cores, hydrophobic and VDW interactions of the side chains dominate, and both can be quantified by means of the local packing densities (44,45). To develop a mechanistic explanation for the relationship of LV-helix dynamics and primary structure, we analyzed local packing densities and related them to interaction topology and the distribution of the side-chain rotamers that form these contacts.

Backbone dynamics is determined by side-chain packing

Fig. 3 A and Fig. S6 A summarize the numbers of noncovalent heavy atom neighbors, n_P, in a 7 Å sphere around the amide protons. A radius of 7 Å was previously reported to define the desolvation sphere for an H-bond in the presence of hydrophobic side chains (44,45). The coordination numbers of water and TFE molecules in the same volume are shown in Fig. S7. Efficient packing is generally correlated with a lower accessibility to solvent (ρ = −0.75). The core regions are tightly packed and solvent is excluded, whereas the terminal regions are loosely packed and solvent-exposed. The large contact peak at position 8 in some sequences is due to interaction with Trp at position 4. Specifically, Leu positions display more contacts with peptide atoms compared to Val positions, such that sequences or sequence segments with elevated Val contents exhibit less efficient packing. The differences (up to 4 heavy atoms) exceed the 1-atom difference resulting from the different side-chain structures. A strong dependence on context superimposes these general trends; for example, Val and Leu in LV16 exhibit similiar packing density, whereas adjacent Val residues in VVL16 exhibit distinct density differences. The local packing density n_P is highly correlated with the inverse of the C_α-RMSF (ρ = −0.72) and with the α-H-bond stability, f_α (ρ = 0.75). Therefore, we conclude that local packing density is the main determinant of backbone dynamics.

Figure 3.

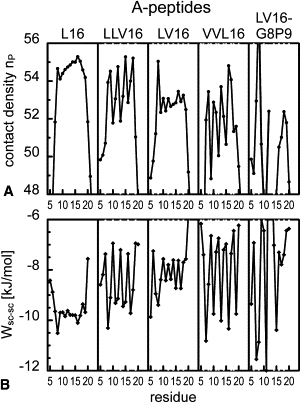
Sequence- and residue-specific side-chain packing of LV-peptides of type A. Val positions are shaded in gray. The results for the B-peptides are shown in Fig. S6. (A) Contact densities n_P defined by the number of noncovalent heavy peptide atoms in a spherical region with radius 7 Å around the amide protons. The solvent coordination numbers in the same volume are given in Fig. S7. (B) VDW interaction W_sc-sc between the side chain as position i and all other side chains. The side-chain to backbone VDW interactions are shown in Fig. S8.

Packing correlates best with side-chain to side-chain VDW interactions

For apolar side chains, close contacts will be mediated by VDW interactions. We observe a pronounced sequence and position specificity of the average interactions between side chains (Fig. 3 B and Fig. S6 B), whereas interactions of the side chains with the backbone (Fig. S8) depend primarily on residue type. Leu side chains enter into stronger average interactions with other side chains and the backbone than do Val side chains. Since the local packing density n_P correlates much better with the VDW attraction between side chains (ρ = 0.73) than with backbone to side-chain interactions (ρ = 0.41), we conclude that packing along the helix is mainly determined by VDW attraction between side chains. In an α-helix, a residue at position i contacts residues at positions i±1, i±3, and i±4, but not at position i±2, which is located on the opposite face of the helix. Attractive interactions at spacings 3 and 4 can form a stabilizing scaffold around the backbone, and may therefore define helix stability (1,46–50) as well as helix dynamics.

Side-chain interactions correlate with the rotameric state

The longer Leu side chain exhibits more rotational degrees of freedom and thus has a greater potential for contacts spaced i±3 and i±4. Fig. 4, A and B, display exemplary rotamer populations and contacts for Val and Leu side chains as observed for two LV-peptides. The preferred t-rotamer of Val (χ₁ ∼180°, population 76 ± 13% averaged over all LV-peptides; Fig. 4 A; for site-specific populations see Table S3) makes preferential contacts with side chains at position i±4 neighbors. The two rotamers populated by Leu adopt the tg⁺-state (χ₁ ∼180°, χ₂ ∼60°, 59 ± 10%; Fig. 4 B, left panel) and the g⁻t-state (χ₁ ∼ −60°, χ₂ ∼180°, 39 ± 9%; Fig. 4 B, right panel), which differ by a correlated rotation of the χ₁ and χ₂ dihedrals (Fig. S4 A). Hopping between tg⁺ and g⁻t swaps the δ-methyl groups of Leu from preferred i+4 contacts to i-4 contacts, whereas i±3 contacts are maintained in each rotameric state. We note that the δ-methyls of Leu occupy a larger dynamical volume than the Val γ-methyls.

Figure 4.

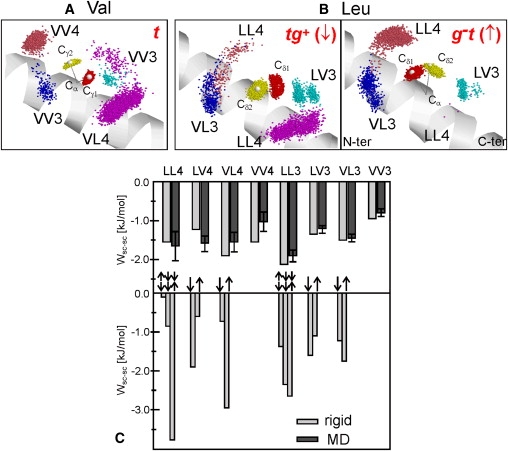
Side-chain rotamers and VDW contacts. (A and B) Exemplary contacts for Leu and Val side chains. (A) Val at position 12 in VVL16 populates mainly the trans rotamer (∼85%). (B) Leu at position 13 in LV16 swaps between tg⁺ (∼60%, left panel) and g⁻t (∼40%, right panel). Frames were taken every 20 ps and oriented with a rigid-body fit to optimize overlay of the N-C^α-C plane of the residue with an ideal α-helix (drawn as ribbon). Positions of the methyl carbons are drawn as dark (C_δ1 and C_γ1) and light-colored (C_δ2 and C_γ2) dots distributed around their ideal positions (larger white spheres). Side-chain contacts within 5 Å to methyl carbons at spacing i±3 and i±4 are labeled by the residue types involved. XYk denotes the interaction of residue X at position i with residue Y at position i+k. (C) VDW interactions of side-chain pairs in aliphatic A-peptides at different spacing. Upper panel: Averages from the MD trajectories (black) are compared with those calculated for an ideal α-helix (gray) using the rotamer populations observed in the simulations. Error bars indicate standard deviations as a result of the spread of the data for different peptides and the fluctuations within one trajectory. Lower panel: The dependence of pairwise interaction energies on Leu rotamer orientations is symbolized by arrows (↑ = g⁻t; ↓ = tg⁺). For LLk pairs, the upper arrow indicates the orientation of Leu at position i. The less favorable side-chain to backbone interaction of g⁻t as compared to tg⁺ disfavors the simultaneous population of g⁻t at positions i and i+k. For Val, only results for the trans rotamer are included.

To obtain an overall quantification of contacts, we analyzed the VDW interactions between side chains in the aliphatic A-peptides with respect to the occurrence and strength of pairwise interactions, and the relation of interaction strength to the different rotameric states. Fig. 4 C displays the VDW interactions between Leu and Val pairs at spacings 3 and 4 as calculated from the MD trajectories, and compares them with the rotamer-dependent values in a rigid ideal α-helix without interference from other residues (see Materials and Methods). Both approaches reveal that the strongest interaction occurs between two Leu forming an i,i±3 pair (LL3), whereas the VV3 interaction is the weakest among the pairs with spacing 3 or 4 (and even weaker than i,i±1 interactions; not shown). The results from rigid helix modeling show that the interaction strengths involving Leu may strongly depend on the side-chain rotamers involved. For example, close contact between the two Leu side chains at spacing 4 provided by the g⁻t(i)/tg⁺(i-4) combination is ∼3.5 kJ/mol more attractive than the orientation tg⁺ (i)/ g⁻t (i-4) with the largest side-chain separation. The interactions seen from the MD simulations are reproduced by the rotamer-averaged interactions in the rigid helix.

The analysis reveals that the longer Leu side chains explore more conformations and also show a higher amplitude of motion within a given rotameric state. We conclude that this mainly governs the strength of pairwise interactions and thus defines the helix dynamics of our LV-peptides. The sum of the pairwise interactions is composed of different increments depending on the sequence of each peptide, as detailed in Fig. S9.

Discussion

Our results characterize the backbone dynamics of LV-peptide helices and reveal the molecular mechanism by which Val residues enhance dynamics. In general, LV-helices display the following characteristics: 1), helices fray at the termini; 2), the N-termini are more disordered than the C-termini; 3), Val induces local deviations from α-helical structure and enhances the flexibility of the core; and 4), a Gly/Pro pair induces helix bending. Thus, our results support the previous putative interpretation of DHX experiments in which the observed exchange rates appeared to decrease from the terminal toward the central helix regions (10). On the other hand, they provide a much more detailed view in that they reveal site-specific backbone dynamics. The MD simulations relate helix dynamics to packing density and additive pairwise VDW interactions between nonpolar side chains in consecutive turns of the helix. Torsional flexibility and geometric specificity of the interacting side chains are important for packing. Accordingly, Val induces packing defects and enhances backbone dynamics because its side chain is locked in an orientation that minimizes i,i±3 contacts. The larger Leu undergoes frequent transitions between rotamers whose average interaction with other side chains exceeds those of Val.

Reliability of the simulations

Several observations suggest that the ∼100 ns simulations of the LV helices provide an appropriate description of their backbone and side-chain dynamics. First, the sampling of the backbone fluctuations of the hydrophobic cores converges on the 10 ns timescale, as revealed by the <1 Å RMSD between averaged structures from different time windows. Only the invariant terminal regions show sampling deficiencies, which are not relevant for the conclusions drawn here. Second, relaxation times of dihedral fluctuations on the order of 1/150 to 1/30 of the total simulation time indicate that the distributions of side-chain rotamers are representative. Furthermore, the rotamer populations observed for Leu and Val in LV helices correspond to the backbone-dependent rotamer libraries (51,52) for soluble α-helices. Nanosecond rotamer averaging was also observed for Leu side chains in hydrophobic cores of soluble proteins (53–59) and in lipid-solubilized TMD structures (11). The similarity of Leu-methyl NMR order parameters determined with picosecond to nanosecond resolution to those averaged over milliseconds to microseconds suggests that each side chain samples its conformers on a nanosecond timescale (59). Third, there is close agreement between calculated and experimental DHX kinetics (10), as documented by the comparison of the exchange kinetics and the sizes of derived kinetically distinct deuteron subpopulations. The threshold distance d_HO = 3 Å defining the transition between the closed and open states of the amide H-bonds is in accordance with values used in related work (34,60,61) and indicates that relatively small fluctuations can provide access to the catalyst. Our finding is in line with previous results indicating that the intrinsic conformational properties of isolated helical peptides can be determined by MD simulations in the 100 ns range with an accuracy comparable to that obtained from NMR structural analysis and HDX kinetics, since much of the deviation from regular structure results from localized influence of the side chains (34,60–62).

Local packing density is the main determinant of backbone dynamics

A link between packing density and backbone flexibility is indicated by a correlation coefficient ρ = 0.72. A similar link was previously shown for soluble proteins (63). Contact density measures all kinds of intramolecular and peptide-solvent interactions (63) that may involve electrostatic interactions, H-bonds, and VDW interactions. Hydrophobic interactions are likely to be of little importance in organic solvents like TFE or in a lipid membrane. Thus, we focus on VDW interactions that were previously inferred to be a dominant force in stabilizing membrane proteins (64,65). We find that the VDW attraction between side chains correlates much better with side-chain packing (ρ = 0.73) than side-chain to backbone interactions (ρ = 0.41). This strongly suggests that VDW attraction between side chains dominates local packing and backbone flexibility in aliphatic LV helices. Side-chain to side-chain interactions are confined to consecutive turns of the helix, such that a residue at position i contacts residues at positions i±3 and i±4. VDW interaction is therefore the major factor that renders backbone dynamics dependent on primary structure. Our ranking of the calculated i,i±3 and i,i±4 side-chain interactions for Leu and Val corresponds well with published values, such as those used in the program AGADIR (49) for the analysis of helix stability (ρ = 0.70; significance p = 0.25 10⁻²⁵). The low VV3 attraction is also in accordance with low contact propensities reported for globular helical proteins (66) and TMDs (67). Although the positions of the γ-methyl groups of Val are sterically restricted by helical backbone geometries, the δ-methyl groups of Leu do not experience these restrictions (5,66,67). The general implication for natural TMD helices may be that residues with interconverting rotamers, such as Leu, make efficient contacts with spatial neighbors at the i±3 and i±4 positions and thus enhance the rigidity of the backbone. Side chains that tend to be locked in a preferred orientation, such as Val, make inefficient contacts and thus favor flexibility.

Conformational dynamics of LV-peptides and relation to membrane fusion

LV-peptides were originally designed to investigate the relationship among TMD primary structure, helix dynamics, and membrane fusogenicity. Although this study provides detailed insights into the nature and cause of helix dynamics, at present we can only speculate on the mechanism by which a highly dynamic helix affects membrane structure. In the membrane environment, helix flexibility may influence the interaction of the helices with the bilayer and thus promote fusion. Previous MD studies of other bilayer-incorporated TMD helices suggested that the peptide-lipid interaction depends on H-bonding between main- and side-chain groups of the peptide and lipid atoms (68,69). Indeed, solid-state NMR experiments have demonstrated the membrane-perturbing activity of LV16 and LV16-G8P9 (70,71). MD simulations of membrane-incorporated LV TMDs are expected to provide deeper insight into this proposed mechanism.