Abstract
Gene regulation involves a hierarchy of events that extend from specific protein-DNA interactions to the combinatorial assembly of nucleoprotein complexes. The effects of DNA sequence on these processes have typically been studied based either on its quantitative connection with single-domain binding free energies or on empirical rules that combine different DNA motifs to predict gene expression trends on a genomic scale. The middle-point approach that quantitatively bridges these two extremes, however, remains largely unexplored. Here, we provide an integrated approach to accurately predict gene expression from statistical sequence information in combination with detailed biophysical modeling of transcription regulation by multidomain binding on multiple DNA sites. For the regulation of the prototypical lac operon, this approach predicts within 0.3-fold accuracy transcriptional activity over a 10,000-fold range from DNA sequence statistics for different intracellular conditions.
Introduction
In a now classic article proposing the lac operon model, Jacob and Monod put forward the very basic principles of gene regulation (1). They reasoned that there are molecules that bind to specific sites in nucleic acids to control whether or not genes are expressed. Since then, a major challenge in biology has been to understand how site-specific regulatory factors function and the effects that they have on gene regulation. Thus, over the last decades, there has been a large effort to produce reliable and efficient computer algorithms for the analysis and prediction of DNA binding sites (2).
These algorithms now have an extraordinary ability to predict with high accuracy how proteins bind single sites (3,4). At the same time, use of these highly accurate models to predict where additional binding sites might occur typically finds a wealth of sites that are not physiologically relevant (2). A rule of thumb to predict actual binding is that relevant sites often are positioned close to each other to act cooperatively (5). Clever refinement of this idea has led to heuristic approaches that have proved very successful at predicting the main gene expression trends on a genomic scale (6–12). The middle ground between detailed single-site and broad genomic predictions, however, still remains largely unexplored.
Here, we develop a quantitative framework that accurately integrates sequence statistics with a biophysical model for multidomain binding on nonadjacent DNA sites using as a prototype system the lac operon. This choice is motivated by two key features of the lac operon.
First, the very simple, yet extremely powerful, original idea of the lac repressor preventing transcription upon binding to the operator DNA in the promoter region has continued to evolve over the years to uncover a highly sophisticated mechanism that goes beyond simple binding events (13). It now incorporates an activator and two additional binding sites for the repressor outside the promoter region. These two additional sites are orders of magnitude weaker than the main site and by themselves do not affect transcription substantially. In combination with the main site, however, they can increase repression of transcription by a factor of ∼100 (14,15).
Second, there is extremely detailed information about the lac operon that offers the possibility of considering the actual mode of binding. This point is important, because the precise sequence has been shaped by evolution through the actual biophysical mechanism. The available information includes detailed quantitative models of how the lac repressor binds to two sites simultaneously (16,17) and to the three sites for the repressor together with the effects of the catabolite activator protein (CAP) (18,19). The molecular and cellular parameter values needed by the models are also available, including the in vivo free energy of binding, the energetic costs of bending and twisting DNA upon two-site binding, and the effective transcription rate as a function of the binding state of the repressor (13,20).
Therefore, the lac operon provides an efficient platform to accurately test multisite models. In this classical example, without considering the two additional sites, no matter how good the single site model is, it would be off by a factor of ∼100.
The focus here is to provide an avenue to extend traditional biophysical single-domain-binding models (21–23) to incorporate the details of multidomain binding, which are inherently different from those of single-domain binding of multiple transcription factors. The traditional approach considers the interaction of a transcription factor (TF) with a DNA site (S1) as a binding reaction of the type . The strength of the binding is typically assessed through position weight matrix (PWM) scores, which are directly related to the binding energy of the DNA-protein interaction (3,24). The extension to multidomain transcription factors in the presence of additional binding sites, denoted S2 and S3, has to consider also reactions of the type and . These more complex reactions account for binding of one domain of the TF while its other domain is still bound to DNA, and they usually involve looping the DNA between each pair of simultaneously bound sites.
The multisite approach is explicitly implemented by first considering the three lac operators as DNA signals. They are used to construct a probabilistic model that provides PWM scores for binding of a lac repressor domain to these and similar mutated sequences. The scores are subsequently linked parametrically to binding free energies and incorporated directly into a detailed biophysical model of transcription regulation that takes into account multidomain binding to multiple binding sites. The model considers a decomposition of the free energy of the protein-DNA complex into different modular contributions. The link between scores and free energies is calibrated by fitting the model to a subset of experimental transcription data. The calibrated model is then tested with different sets of data (Fig. 1).
Figure 1.
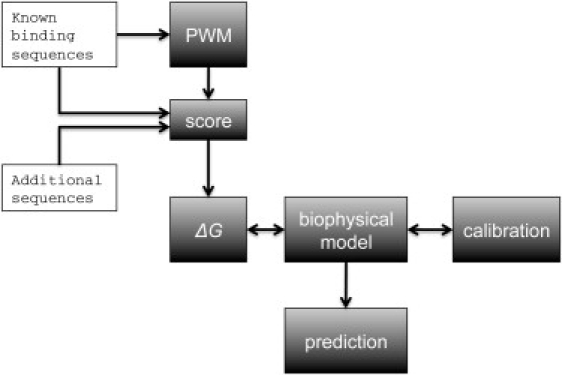
Integration of sequence statistics into predictive biophysical multidomain models. The approach is implemented by first considering the three operators as DNA signals. They are used to construct a probabilistic model that provides binding scores for these and similar mutated sequences. The scores are subsequently linked parametrically to binding free energies and incorporated directly into a detailed biophysical model of transcription regulation. The link between scores and free energies is calibrated by fitting the model to a subset of experimental data. The calibrated model is then tested with different sets of data.
Methods
From sequence to score
The PWM method is used to describe repressor-operator binding (3,24). It assigns a score, S, to the sequence according to
| (1) |
where is the estimated probability of having the nucleotide x at position i of the binding site and is the background frequency of that nucleotide. Taking into account small sample size, is estimated from the observed positional frequency as
| (2) |
where is the number of sites having a nucleotide x at position i and N is the total number of sites in the training set. In our case, we have only three sequences in the training set corresponding to the three operators.
From score to free energy
We assume a linear relationship to transform the score, S, of each sequence into the interaction free energies, e, between the lac repressor domain and the DNA site:
| (3) |
where a and b are constants to be inferred from experiments. With this linear assumption, a selects the energy units and b the reference zero of energy.
Multidomain binding
The lac repressor is a tetramer consisting of two dimeric DNA binding domains. Multidomain binding is taken into account by decomposing the free energy of the protein-DNA complex into different modular contributions, including positional, interaction, and conformational free energies (19,25).
The positional free energy, p, accounts for the cost of bringing the lac repressor to its DNA binding site. Its dependence on the repressor concentration, n, is given by p = p° − RTlnn, where p° is the positional free energy at 1M. Interaction free energies, e, arise from the physical contact between a binding domain and DNA site. Thus, when only a single domain is involved, the free energy of binding is given by ΔG = e + p. For two domains, denoted by subscripts 1 and 2, the free energy of binding is given by ΔG = e1 + e2 + c + p. Conformational free energies, c, account for changes in DNA and repressor conformation, which are needed to accommodate multiple simultaneous interactions (Fig. 2).
Figure 2.
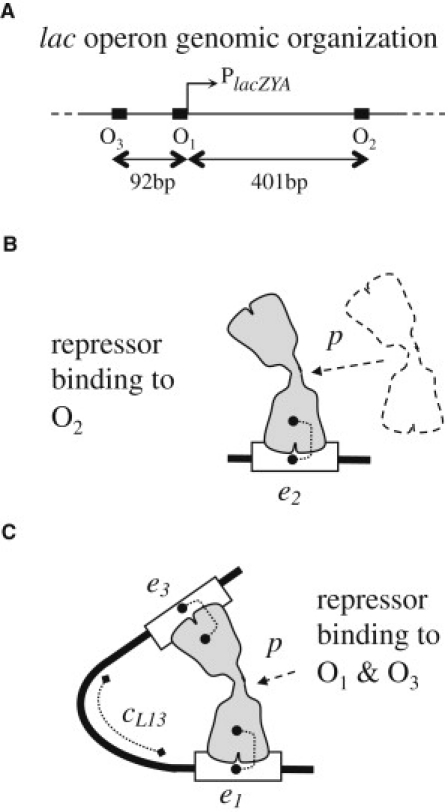
Operator locations on DNA and binding of the lac repressor. (A) The main (O1) and two auxiliary (O2 and O3) operators are shown as black rectangles on the black line representing DNA. Binding of the lac repressor to O1 prevents transcription of the three lacZYA genes. (B) A repressor is shown bound to O2. The free energy of binding is ΔG = e2 + p. (C) A repressor is shown looping DNA by binding simultaneously to O1 and O3. The free energy of this binding configuration is ΔG = e1 + e3 + cL13 + p.
All these contributions to the free energy, taking into account the three operators for specific binding of the lac repressor, can be expressed in mathematical terms as
| (4) |
where , , and are state variables that can take the values 0 and 1 to indicate whether (= 1) or not (= 0) the repressor is bound to the operators O1, O2, and O3, respectively; and , , and are variables that indicate whether (= 1) or not (= 0) DNA forms the loops O1-O2, O1-O3, and O2-O3, respectively. The subscripts of the different contributions to the free energy have the same meaning as those of the corresponding binary variables. The infinity in the last term of the free energy implements that two loops that share one operator cannot be present simultaneously by assigning an infinite free energy to those states (18).
The set of six state variables, denoted by s = (s1, s2, s3, sL12, sL13, sL23), describes the specific binding configuration of the repressor-DNA complex. For instance, a repressor bound to O2 is specified by s = (0, 1, 0, 0, 0, 0); a repressor bound to O1 and O3 looping the intervening DNA, by s = (1, 0, 1, 0, 1, 0); and three repressors bound, one to each operator, by s = (1, 1, 1, 0, 0, 0). The specific value of the free energy is obtained by substituting the values of the state variables in the expression of the free energy. This description in terms of state variables can be visualized as a factor graph (Fig. 3).
Figure 3.
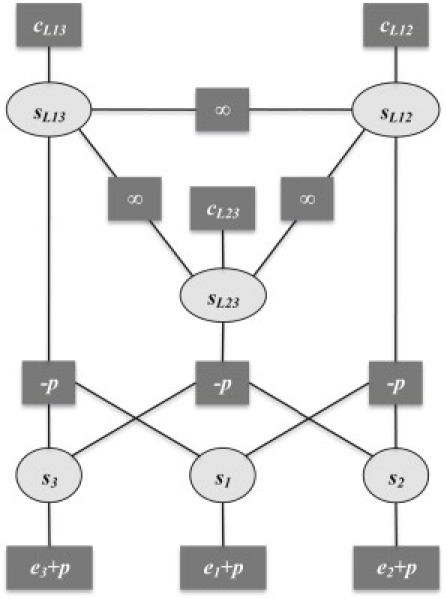
Factor graph for the free-energy components of the multisite lac repressor-operator binding. The free energy of the system, ΔG(s), as a function of the state variables, s = (s1, s2, s3, sL12, sL13, sL23), has a graphical representation in the form of a factor graph. The round nodes represent state variables and the rectangular nodes represent contributions to the free energy. The quantity in the rectangular node is present in the free energy when all its connecting state variables are equal to 1. The experimental values for wild-type parameters are e1 = −27.8 kcal/mol, e2 = −26.3 kcal/mol, e3 = −24.1 kcal/mol, cL12 = 23.35 kcal/mol, cL13 = 22.05 kcal/mol, and cL23 = 23.50 kcal/mol. The dependence on the lac repressor concentration, n, is given by the positional free energy, p = p° − RTlnn, with p° = 15 kcal/mol.
The probability of any of these states depends exponentially on its free energy and is obtained from statistical thermodynamics as
| (5) |
where RT is the gas constant times the absolute temperature. The partition function, , is used as a normalization factor.
Transcriptional control
Gene expression in the lac operon is completely abolished when the repressor is bound to O1; otherwise, transcription takes place either at an activated maximum rate, Γmax, when O3 is free or at a basal reduced rate, χΓmax, when O3 is occupied. This reduction by a factor χ arises because binding of the repressor to O3 prevents CAP from activating transcription (13,18).
The transcription rate Γ(s) can be expressed in terms of state variables as
| (6) |
With this approach, the effective transcription rate,
| (7) |
is obtained by computing the thermodynamic average over all the representative states, namely, by performing the sum above over all possible combinations of values of s.
Model calibration
The overall model has only two free parameters: the constants a and b that relate scores to free energies of binding. Their values are inferred by minimizing the square logarithmic error between measured and model normalized transcription (). The values of the other four parameters, three conformational free energies and CAP activation, are taken from the experimental data. Explicitly, the value χ = 0.03 was reported by Oehler et al. (26); the value cL12 = 23.35 kcal/mol was obtained by Saiz and Vilar (20) from experimental data in the Oehler et al. study (26); the values cL13 = 22.05 kcal/mol and cL23 = 23.50 kcal/mol were obtained from the value of cL12 by taking into account the dependence of the conformational free energy on the distance between operators (20,27,28) and the stabilization of the O1-O3 loop by CAP (29,30).
Results and Discussion
We applied the multisite approach to classic experiments on the lac operon that considered gene expression for different repressor concentrations in E. coli strains covering all eight possible combinations of operator deletions (14). The sequences of the three wild-type (WT) operators O1, O2, and O3 were used to compute the PWM from which we obtained the scores for these three operators and their respective deletions, O1M, O2M, and O3M (see Table 1). The scores correctly ranked the three WT operators according to their measured strength and consistently ranked all the deletions below all the WT operators.
Table 1.
Operator sequences and their statistical and binding properties
| Name | Sequence | S | aS + b (kcal/mol) | e (kcal/mol) | (nM) | (nM) |
|---|---|---|---|---|---|---|
| O1 | AATTGTGAGCGGATAACAATT | −13.38 | −27.62 | −27.8 | 0.728 | 0.54 |
| O2 | AAATGTGAGCGAGTAACAACC | −12.17 | −25.94 | −26.3 | 12.1 | 6.62 |
| O3 | GGCAGTGAGCGCAACGCAATT | −10.95 | −24.25 | −24.1 | 201 | 259 |
| O1M | AATTGTTAGCGGAGAAGAATT | −9.51 | −22.26 | N/A | 5600 | N/A |
| O2M | GAAGGTTAATGAATAGCACCC | −5.12 | −16.16 | N/A | 1.44 × 108 | N/A |
| O3M | TCGATCGAGCTCAACGCAATT | −4.71 | −15.60 | N/A | 3.37 × 108 | N/A |
The PWM score, S, for a given operator sequence is used to estimate its interaction free energy with the lac repressor as aS + b, with a = 1.387 kcal/mol and b = −9.064 kcal/mol. The experimental values of these free energies, e, are from Saiz and Vilar (18). Dissociation constants are computed as for the predictions from PWM scores and as for the experimental data. N/A stands for data not available.
The values of parameters a and b were obtained by fitting the model to the experimental transcription data using
| (8) |
as the free energy of the system. This expression is obtained after substitution of the relation e = aS + b in Eq. 4. In this way, the binding is described by the PWM scores, S1, S2, and S3, for each site together with the conformational contributions to the free energy from DNA looping (28).
The model, with just a and b as free parameters, is able to fit the experimental data (14) within 0.29-fold accuracy over a 10,000-fold range of transcriptional activity (Fig. 4 A). In total, there are 22 experimental points, accounting for eight operator configurations, three different repressor concentrations, and different functional forms of the transcription curves. The value FA that quantifies the ability of the model to capture the experimental data within FA-fold accuracy is explicitly defined for a set of N experimental, Γex, and computed, Γcp, transcription rates through the expression , and it indicates that typically measured and computed values differ from each other by a factor of 1 + FA.
Figure 4.
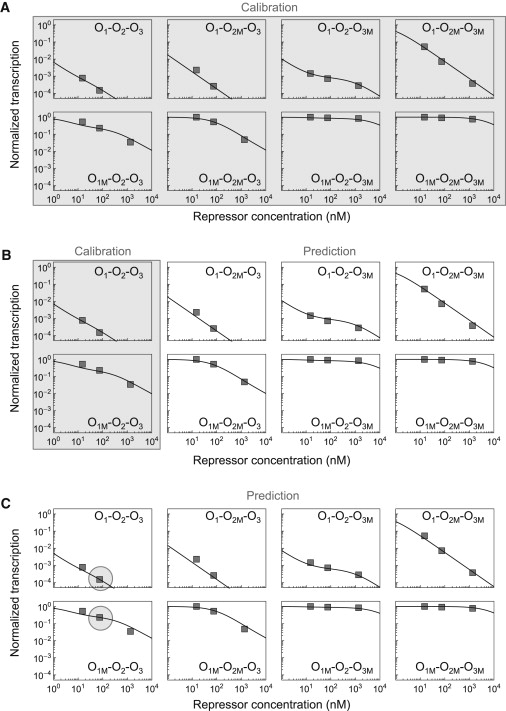
Model calibration and prediction of the transcriptional activity as a function of the repressor concentration. The normalized transcription () was obtained for WT and seven mutants accounting for all the combinations of deletions of the three operators. For each of the eight cases, the results of the model (solid lines) as a function of the repressor concentration are compared with the experimental data from Oehler et al. (14) (squares). The particular set of WT or deleted operators is indicated for each curve; for instance, O1-O2-O3 corresponds to the WT lac operon and O1M-O2M-O3M to the mutant with all three operators deleted. The values of the experimental parameters used are cL12 = 23.35 kcal/mol, cL13 = 22.05 kcal/mol, cL23 = 23.50 kcal/mol, and χ = 0.03. The PWM scores, S, for each site are as shown in Table 1. (A) Parameter values a = 1.387 kcal/mol and b = −9.064 kcal/mol, which connect interaction free energies with scores, e = aS + b, were obtained by fitting the model to all the experimental transcription data. (B) Parameter values a = 1.348 kcal/mol and b = −9.531 kcal/mol were obtained by fitting the model to the experimental data for operator configurations O1-O2-O3 and O1M-O2-O3. The model accurately predicts the normalized transcription for the other six operator configurations. (C) Only two experimental points (large gray circles) are used to obtain the parameter values a = 1.462 kcal/mol and b = −8.208 kcal/mol. The model is still able to accurately predict the normalized transcription for the remaining 20 experimental points.
The interaction free energies obtained from the model for the best-fit a and b parameters and the corresponding experimental in vivo values (18) are shown in Table 1. The results of the model exhibit good agreement with the available experimental data. In terms of dissociation constants, the differences between the predicted and observed values are within the twofold range (Table 1). An advantage of the approach we have followed is that the in vivo free energies, and the corresponding dissociation constants, take into account implicitly the effects of nonspecific binding. The reason is that their values are measured with respect to the reference state with no repressor bound to the operators, which includes the repressors in solution in the cytosol as well as the repressors bound nonspecifically to DNA (for a detailed quantitative discussion, see Appendix II of Vilar and Leibler (16)).
To test the predictive potential of the multisite model, we used experimental data sets for two operator configurations to infer the values of parameters a and b and then used the calibrated model to predict the transcriptional activity for the other six configurations (Fig. 4 B). The accuracy of the model at predicting new data decreases only slightly with respect to the all-fit accuracy. In principle, only two experimental data points would be needed to calibrate the model, because there are only two free parameters. Indeed, just two experimental points can be used to calibrate the model with just a slight additional decease in global accuracy (Fig. 4 C). Therefore, without using any free energy of binding, the multisite model is able to accurately predict gene expression curves over a 10,000-fold range for eight different E. coli strains covering all possible combinations of operator deletions from just two experimental calibration data points and the sequences of the six DNA sites involved.
There is an important prediction that goes beyond the experimentally observed free energies of binding. The deletion O1M of the main operator O1 involved the mutation of just three DNA basepairs. As a consequence, the model predicts for O1M an increase in free energy of 5.4 kcal/mol with respect to O1, or, equivalently, an ∼8000-fold increase of the dissociation constant, which is substantial but still remains relatively close to the free energy of binding to O3, the weakest WT operator (Table 1). We found that such a decrease has transcriptional consequences that make it distinguishable from a complete deletion (Fig. 5). Thus, the multisite approach is able not only to both accurately predict gene expression and recover known free energies but also to obtain precise affinity estimates for very weak sites that were assumed not to bind the lac repressor.
Figure 5.
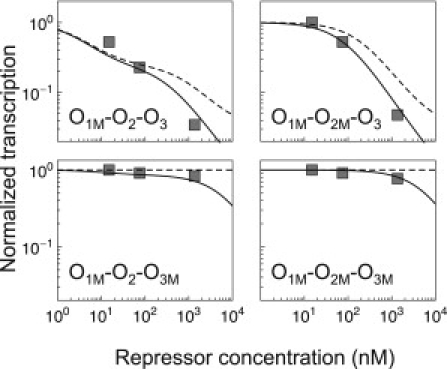
Complete deletions versus weak binding. The normalized transcription () for the four configurations with O1M is shown for the model as in Fig. 4A (solid line); for the model assuming that the free energy of binding to O1M is infinite, as in a complete deletion (dashed line); and for the experimental data from Oehler et al. (14) (squares).
Typically, the effects of a given sequence depend on the context. This dependence has been noted explicitly as one of the main limiting factors for identifying physiologically relevant sites and for linking statistical sequence information, such as PWM scores, to transcriptional activity (31). This fundamental problem in gene regulation is believed to result from the interplay among multiple DNA sites in orchestrating the binding patterns of transcription factors that control gene expression (2). The approach presented here overcomes this limitation by using detailed biophysical modeling of multidomain binding to directly connect statistical sequence information with transcriptional activity. We have shown that for the prototypical lac operon, which relies on a cluster of three nonadjacent sites over a 0.5-kb DNA region to control transcription, this multisite approach accurately recapitulates the observed transcriptional activity over a 10,000-fold range for all the possible combinations of operator deletions.
Acknowledgments
This work was supported by the Ministerio de Ciencia e Innovación under grant FIS2009-10352.
References
- 1.Jacob F., Monod J. Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 1961;3:318–356. doi: 10.1016/s0022-2836(61)80072-7. [DOI] [PubMed] [Google Scholar]
- 2.Wasserman W.W., Sandelin A. Applied bioinformatics for the identification of regulatory elements. Nat. Rev. Genet. 2004;5:276–287. doi: 10.1038/nrg1315. [DOI] [PubMed] [Google Scholar]
- 3.Stormo G.D. DNA binding sites: representation and discovery. Bioinformatics. 2000;16:16–23. doi: 10.1093/bioinformatics/16.1.16. [DOI] [PubMed] [Google Scholar]
- 4.Zhao Y., Granas D., Stormo G.D. Inferring binding energies from selected binding sites. PLOS Comput. Biol. 2009;5:e1000590. doi: 10.1371/journal.pcbi.1000590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tronche F., Ringeisen F., Pontoglio M. Analysis of the distribution of binding sites for a tissue-specific transcription factor in the vertebrate genome. J. Mol. Biol. 1997;266:231–245. doi: 10.1006/jmbi.1996.0760. [DOI] [PubMed] [Google Scholar]
- 6.Liu R., McEachin R.C., States D.J. Computationally identifying novel NF-kappa B-regulated immune genes in the human genome. Genome Res. 2003;13:654–661. doi: 10.1101/gr.911803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.van Batenburg M.F., Li H., Meijer O.C. Paired hormone response elements predict caveolin-1 as a glucocorticoid target gene. PLoS ONE. 2010;5:e8839. doi: 10.1371/journal.pone.0008839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bussemaker H.J., Foat B.C., Ward L.D. Predictive modeling of genome-wide mRNA expression: from modules to molecules. Annu. Rev. Biophys. Biomol. Struct. 2007;36:329–347. doi: 10.1146/annurev.biophys.36.040306.132725. [DOI] [PubMed] [Google Scholar]
- 9.Tavazoie S., Church G.M. Quantitative whole-genome analysis of DNA-protein interactions by in vivo methylase protection in E. coli. Nat. Biotechnol. 1998;16:566–571. doi: 10.1038/nbt0698-566. [DOI] [PubMed] [Google Scholar]
- 10.Bussemaker H.J., Li H., Siggia E.D. Regulatory element detection using correlation with expression. Nat. Genet. 2001;27:167–171. doi: 10.1038/84792. [DOI] [PubMed] [Google Scholar]
- 11.Markstein M., Zinzen R., Levine M. A regulatory code for neurogenic gene expression in the Drosophila embryo. Development. 2004;131:2387–2394. doi: 10.1242/dev.01124. [DOI] [PubMed] [Google Scholar]
- 12.van Nimwegen E. Finding regulatory elements and regulatory motifs: a general probabilistic framework. BMC Bioinformatics. 2007;8(Suppl 6):S4. doi: 10.1186/1471-2105-8-S6-S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Müller-Hill B. Walter de Gruyter; Berlin; New York: 1996. The lac Operon: A Short History of a Genetic Paradigm. [Google Scholar]
- 14.Oehler S., Eismann E.R., Müller-Hill B. The three operators of the lac operon cooperate in repression. EMBO J. 1990;9:973–979. doi: 10.1002/j.1460-2075.1990.tb08199.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mossing M.C., Record M.T., Jr. Upstream operators enhance repression of the lac promoter. Science. 1986;233:889–892. doi: 10.1126/science.3090685. [DOI] [PubMed] [Google Scholar]
- 16.Vilar J.M.G., Leibler S. DNA looping and physical constraints on transcription regulation. J. Mol. Biol. 2003;331:981–989. doi: 10.1016/s0022-2836(03)00764-2. [DOI] [PubMed] [Google Scholar]
- 17.Alberts B., Johnson A., Walter P. Garland Science; New York: 2008. Molecular Biology of the Cell. [Google Scholar]
- 18.Saiz L., Vilar J.M.G. Ab initio thermodynamic modeling of distal multisite transcription regulation. Nucleic Acids Res. 2008;36:726–731. doi: 10.1093/nar/gkm1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vilar J.M.G., Saiz L. DNA looping in gene regulation: from the assembly of macromolecular complexes to the control of transcriptional noise. Curr. Opin. Genet. Dev. 2005;15:136–144. doi: 10.1016/j.gde.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 20.Saiz L., Vilar J.M.G. DNA looping: the consequences and its control. Curr. Opin. Struct. Biol. 2006;16:344–350. doi: 10.1016/j.sbi.2006.05.008. [DOI] [PubMed] [Google Scholar]
- 21.Djordjevic M., Sengupta A.M., Shraiman B.I. A biophysical approach to transcription factor binding site discovery. Genome Res. 2003;13:2381–2390. doi: 10.1101/gr.1271603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu X., Clarke N.D. Rationalization of gene regulation by a eukaryotic transcription factor: calculation of regulatory region occupancy from predicted binding affinities. J. Mol. Biol. 2002;323:1–8. doi: 10.1016/s0022-2836(02)00894-x. [DOI] [PubMed] [Google Scholar]
- 23.Roider H.G., Kanhere A., Vingron M. Predicting transcription factor affinities to DNA from a biophysical model. Bioinformatics. 2007;23:134–141. doi: 10.1093/bioinformatics/btl565. [DOI] [PubMed] [Google Scholar]
- 24.Berg O.G., von Hippel P.H. Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters. J. Mol. Biol. 1987;193:723–750. doi: 10.1016/0022-2836(87)90354-8. [DOI] [PubMed] [Google Scholar]
- 25.Saiz L., Vilar J.M.G. Stochastic dynamics of macromolecular-assembly networks. Mol. Syst. Biol. 2006;2 doi: 10.1038/msb4100061. 2006.0024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Oehler S., Amouyal M., Müller-Hill B. Quality and position of the three lac operators of E. coli define efficiency of repression. EMBO J. 1994;13:3348–3355. doi: 10.1002/j.1460-2075.1994.tb06637.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Müller J., Oehler S., Müller-Hill B. Repression of lac promoter as a function of distance, phase and quality of an auxiliary lac operator. J. Mol. Biol. 1996;257:21–29. doi: 10.1006/jmbi.1996.0143. [DOI] [PubMed] [Google Scholar]
- 28.Saiz L., Rubi J.M., Vilar J.M.G. Inferring the in vivo looping properties of DNA. Proc. Natl. Acad. Sci. USA. 2005;102:17642–17645. doi: 10.1073/pnas.0505693102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hudson J.M., Fried M.G. Co-operative interactions between the catabolite gene activator protein and the lac repressor at the lactose promoter. J. Mol. Biol. 1990;214:381–396. doi: 10.1016/0022-2836(90)90188-R. [DOI] [PubMed] [Google Scholar]
- 30.Saiz L., Vilar J.M.G. Multilevel deconstruction of the in vivo behavior of looped DNA-protein complexes. PLoS ONE. 2007;2:e355. doi: 10.1371/journal.pone.0000355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Veprintsev D.B., Fersht A.R. Algorithm for prediction of tumour suppressor p53 affinity for binding sites in DNA. Nucleic Acids Res. 2008;36:1589–1598. doi: 10.1093/nar/gkm1040. [DOI] [PMC free article] [PubMed] [Google Scholar]


