Solution Structure of the 128 kDa Enzyme I Dimer from Escherichia coli and its 146 kDa Complex With HPr Using Residual Dipolar Couplings and Small and Wide Angle X-Ray Scattering

Abstract

The solution structures of free Enzyme I (EI, ∼128 kDa, 575×2 residues), the first enzyme in the bacterial phosphotransferse system and its complex with HPr (∼146 kDa) have been solved using novel methodology that makes use of prior structural knowledge (namely, the structures of the dimeric EIC domain and the isolated EIN domain both free and complexed to HPr), combined with residual dipolar coupling (RDC), small (SAXS) and wide (WAXS) angle X-ray scattering and small angle neutron scattering (SANS) data. The calculational strategy employs conjoined rigid body/torsion/Cartesian simulated annealing, and incorporates improvements in calculating and refining against SAXS/WAXS data that take into account complex molecular shapes in the description of the solvent layer resulting in a better representation of the SAXS/WAXS data. The RDC data orient the symmetrically related EIN domains relative to the C₂ symmetry axis of the EIC dimer, while translational, shape and size information is provided by SAXS/WAXS. The resulting structures are independently validated by SANS. Comparison of the structures of the free EI and the EI-HPr complex with that of the crystal structure of a trapped phosphorylated EI intermediate reveals large (∼70-90°) hinge body rotations of the two subdomains comprising the EIN domain, as well as of the EIN domain relative to the dimeric EIC domain. These large-scale interdomain motions shed light on the structural transitions that accompany the catalytic cycle of EI.

The phosphoenolpyruvate:sugar phosphotransferase system (PTS) is a key signal transduction pathway in bacteria whereby active sugar transport across the cell membrane is coupled to a sequential phosphorylation cascade via a series of bimolecular protein-protein complexes.^1-4 The initial two steps of the PTS are common to all branches of the pathway, and involve the autophosphorylation of enzyme I (EI) by phosphoenolpyruvate (PEP) in the presence of Mg²⁺, followed by phosphoryl transfer from His189 of EI to His15 of the histidine phosphocarrier protein HPr.^5,6 Thereafter, the phosphoryl group is transferred from HPr to the sugar specific enzymes II, and ultimately onto the incoming sugar molecule.

EI is a ∼128 kDa dimer that consists of two domains: an N-terminal phosphoryl transfer domain (EIN, residues 1-254) and a C-terminal dimerization domain (EIC, residues 261-575) that contains the PEP binding site.⁷ Isolated EIN can reversibly transfer a phosphoryl group to HPr (∼9.5 kDa) but cannot be autophosphorylated by PEP.^7-9

The EIN domain (residues 1-254) is subdivided into two subdomains: the α/β domain (EIN^α/β) contains the active site histidine (His189) while the α domain (EIN^α) provides the interaction surface for HPr.¹⁰ The structure of isolated E. coli EIN has been solved by both crystallography¹¹ and NMR,¹² and the structure of the EIN-HPr complex has been solved by NMR.¹³ In all three cases, the structure of EIN is the same within coordinate errors, and we refer to this conformation as the A state of EIN (Fig. 1A, left panel).¹⁴ Phosphorylation of EIN does not affect the backbone conformation of EIN but results in a change in the χ₂ side chain conformation of His189 from the g⁺ to g^- rotameric state that breaks a hydrogen bond between the Nε2 atom of His189 and the hydroxyl group of Thr168, thereby rendering the Nε2 atom accessible to the incoming phosphoryl group.^14,15 In this conformation of His189, a pentacoordinate phosphoryl transition state intermediate that bridges His189 of EIN and His15 of HPr can readily be modeled from the coordinates of the EIN-HPr complex without necessitating any change in backbone conformation.¹³

Figure 1. Summary of available structure information on EI.

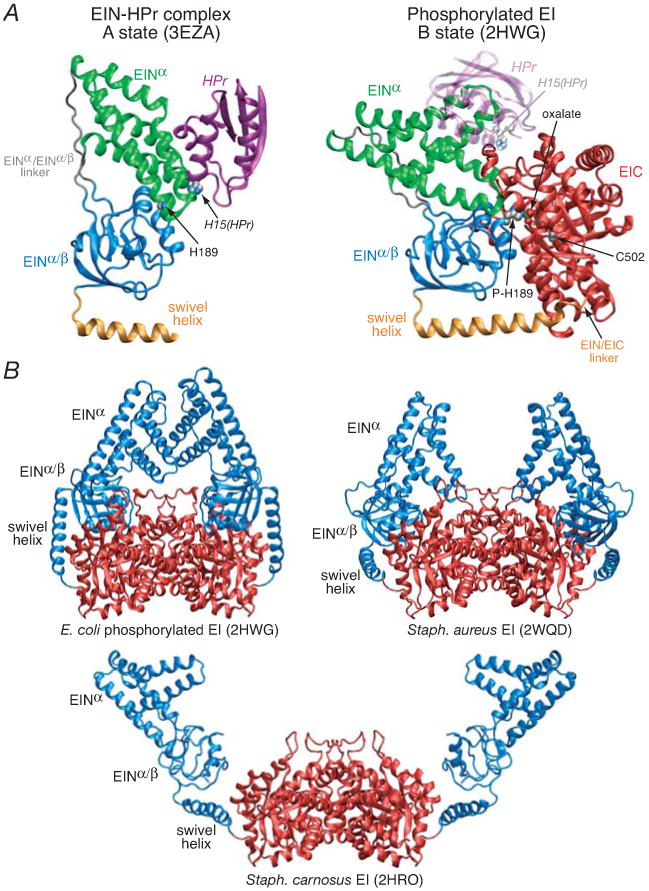
(A) Comparison of the solution NMR structure of the isolated E. coli EIN domain complexed to HPr (3EZA)¹³ which we refer to as the A state of the EIN domain (left panel) with that observed in the crystal structure of the phosphorylated EI intermediate from E. coli (2HWG)¹⁸ which we refer to as the B state of the EIN domain (right panel), displayed in the same orientation of the EIN^α/β subdomain. Only a single subunit of the phosphorylated EI dimer is shown. The structures are depicted as ribbon diagrams with the EIN^α and EIN ^α/β subdomains shown in green and blue, respectively, the swivel helix connecting the EIN and EIC domains in orange, the EIC domain in red, and HPr in purple (left panel) and transparent purple (right panel). His189 (located in the EIN^α/β subdomain; left panel), phospho-His189 (right panel), Cys502 (right panel), the oxalate anion (right panel) and His15 of HPr are shown as space-filling models color-coded according to atom type. HPr bound to the EIN^α subdomain in the same orientation as in the EIN-HPr complex is shown as a transparent ribbon in the right panel to demonstrate that the HPr binding site is available in the phosporylated EI intermediate (B state) and that there are no steric clashes between HPr and the EIC domain in this conformation of EI. (B) Comparison of the crystal structures of the phosphorylated EI intermediate from E. coli (2HWG)¹⁸ and free EI from Staph. aureus (2WQD)¹⁷ and Staph. carnosus (2HRO),¹⁶ with the EIN and EIC domains shown in blue and red, respectively. Note that the orientation of the EIN^α and EIN^α/β subdomains in isolated EIN (both in solution¹²,¹³ and in the crystal state¹¹) is the same as that seen in the crystal structure of free EI from Staph. aureus (2WQD¹⁷). The EIN^α/β subdomain in Staph. carnosus EI¹⁶ is partially disordered with some regions not visible in the electron density map. The structure of the EIC dimerization domain in all three EI crystal structures is essentially the same (Cα rms differences of less than 1 Å).

Three crystal structures of intact EI have been solved: two of free EI from Staph. carnosus¹⁶ and Staph. aureus,¹⁷ and one of intact phosphorylated EI from E. coli crystallized from a solution from a solution of PEP, Mg²⁺ and EI in which the autophosphorylation reaction was quenched by the inhibitor oxalate.¹⁸ The structure of the EIC dimerization domain is the same in all three EI crystal structures as well as in the crystal structure of the isolated EIC domain from Thermoanaerobacter tegcongensis.¹⁹ In the crystal structure of phosphorylated EI, the PEP binding site in the EIC domain is occupied by oxalate and Mg²⁺ which bridge the catalytic cysteine, Cys502, in the EIC domain, and phosphorylated His189 in the EIN^α/β subdomain.¹⁸ Compared to the structure of isolated EIN,^11-13 there is a large, ∼70°, reorientation of the EIN^α subdomain relative to the EIN^α/β subdomain which we refer to as the B state (Fig. 1A, right panel).¹⁴ As a consequence, the Cα-Cα distance between His15 of HPr bound to the EIN^α subdomain and His189 in the EIN^α/β subdomain would be increased from ∼12 Å in the EIN-HPr complex¹³ to ∼30 Å in the conformation observed in the crystal structure of phosphorylated EI.¹⁸ Thus the X-ray structure of intact phosphorylated EI represents an intermediate captured immediately subsequent to phosphotransfer from PEP, but prior to the conformational transition that brings phosphorylated His189 of EI in close proximity to His15 of HPr. In the context of the crystal structure of the phosphorylated EI intermediate,¹⁸ reorientation of the EIN^α subdomain relative to the EIN^α/β subdomain, leaving the position of the EIN^α/β subdomain relative to the EIC domain unchanged results in steric clash between the EIN^α subdomain and the EIC domain with extensive atomic overlap and interpenetration (Fig. 1B). Thus, a reorientation of the EIN^α/β subdomain relative to the EIC domain must also occur. In the structure of free EI from Staph. aureus,¹⁷ the conformation of EIN is the same as that in isolated EIN, the EIN^α/β domain undergoes a reorientation of ∼40° relative to that seen in the phosphorylated EI intermediate,¹⁸ and the tip of the EIN^α subdomain makes contact with the EIC domain. Although the conformation of the EIN domain in Staph. aureus EI is in the correct conformation to allow for in-line phosphoryl transfer to HPr, the EIN domain is packed too closely to the EIC domain to allow HPr to bind in the absence of steric clash.¹⁷ In the structure of free EI from Staph. carnosus,¹⁶ the EIN^α/β subdomain undergoes a reorientation of ∼95° relative to that in the structure of phosphorylated EI, and the conformation of the EIN domain is intermediate between that seen in free EIN and phosphorylated EI, with the orientation of the EIN^α and EIN^α/β subdomains differing from that in free EIN by ∼40°. There are minimal contacts between the EIN^α and EIN^α/β subdomains, and no interdomain contacts between the EIN and EIC domains are observed in the Staph. carnosus EI structure,¹⁶ suggesting that the conformation observed in this structure is heavily influenced by crystal packing forces, specifically between the EIN^α subdomain of one molecule and the EIN^α/β subdomain of another molecule in the crystal lattice. Crystal packing contacts likely also heavily influence the exact position of the EIN^α subdomain in the structure of E. coli phosphorylated EI: while the EIC domains and EIN^α/β subdomains are symmetrically located about the C₂ axis of the dimer, the EIN^α subdomains are not, presumably due to the small number of intramolecular contacts between the EIN^α and EIN^α/β subdomains in this structure.

In this paper we address the solution conformation of intact EI from E. coli both free (∼128 kDa) and complexed to HPr (∼146 kDa) using novel methodology that makes use of conjoined rigid body/torsion angle/Cartesian simulated annealing against residual dipolar coupling (RDC) and small (SAXS) and wide (WAXS) angle X-ray scattering data, in conjunction with knowledge of the solution structures of the isolated EIN domain and EIN-HPr complex^12,13 and the crystal structure of the dimeric EIC domain in the phosphorylated EI intermediate.¹⁸ Sparse RDCs on domains of known structure are sufficient to yield relative domain orientations,^20-22 while SAXS/WAXS provides information on the size and shape of a macromolecule.²³ Neither SAXS/WAXS nor small angle neutron scattering (SANS) data recorded on free EI are in agreement with the crystal structure of phosphorylated EI from E. coli¹⁸ or the crystal structures of free EI from Staph. aureus¹⁷ and Staph. carnosus.¹⁶ We show that the relative orientation of the EIN^α and EIN^α/β subdomains in intact EI (both free and bound to HPr) is the same as that in isolated EIN (i.e. the A state),^12,15 and that the conformational transition between free EI and the phosphorylated intermediate of EI captured by crystallography,¹⁸ involves a ∼70° reorientation of the EIN^α/β subdomain relative to the EIC domain. Binding of HPr to the EIN^α subdomain results in a further small ∼7-20° reorientation and ∼12-15 Å displacement of the EIN domain relative to the EIC domain, in order to accommodate HPr which is sandwiched between the EIN^α subdomain and the EIC domain.

In the context of an NMR structure determination of a system the size of EI (∼128 kDa) and the EI-HPr complex (∼146 kDa), there are two strategies that can be employed. The first approach involves a very time consuming and measurement intensive conventional NMR structure determination requiring close to complete assignment and extensive analysis of nuclear Overhauser enhancement (NOE) data.²⁴ However, the probability of success of such an approach, even with current start-of-the-art NMR methodology,^25-27 is extremely low, and even if a structure could be obtained in this manner it would likely be of low accuracy. The second approach employed here employs a much simpler and more streamlined strategy that makes use of prior available structural information combined with limited RDC data and SAXS/WAXS. First, backbone N-H RDCs are used to demonstrate that the structures of the EIN^α and EIN^α/β subdomains and their relative orientations in the context of the full length EI (both free and bound to HPr) remain unchanged compared to isolated EIN. Then, assuming that the overall structure of the EIC dimerization domain remains unperturbed from that observed in all three crystal structures of EI,^16-18 the orientation of the symmetrically related EIN domains relative to the EIC dimer domain can be determined by RDCs measured for residues located only in the EIN domain, since the C₂ symmetry axis of the dimer must coincide with one of the principal axes of the alignment tensor. While the RDCs alone would provide multiple solutions for the orientation of the symmetry-related EIN domains relative to the EIC dimer (owing to the equivalence of 180° rotations about the three axes of the alignment tensor), the constraints imposed by stereochemistry and covalent geometry within the linker connecting the EIN and EIC domains together with the shape and translational information afforded by the SAXS/WAXS data are consistent with only a single solution. The hybrid strategy employed here presents a general method for making optimal use of structural data from multiple sources to probe rigid body conformational transitions in large multidomain, multimeric proteins.

Experimental

Cloning, Expression, and Purification of EI

Full length EI (residues 1–575) from E. coli was cloned into a pET11 vector (Novagen) without tags. The plasmid was introduced into E. coli strain BL21 Star^TM (DE3) (Invitrogen) cells for expression. Cells were grown in either Luria Bertani medium or minimal medium in D₂O with ¹⁵NH₄Cl and ²H₇-D-glucose as the sole nitrogen and carbon sources, respectively, induced with 1 mM isopropyl-D-thiogalactopyranoside at an A₆₀₀ of 0.8, and harvested by centrifugation after 4 h of induction. The cell pellet was resuspended in 50 ml (per liter of culture) of 50 mM Tris, pH 8.0, 2 mM dithiothreitol (DTT), 1 mM phenylmethylsulfonyl fluoride and a table of protease inhibitor cocktail (Sigma S8820). The suspension was lysed by three passages through a microfluidizer and centrifuged at 70,000×g for 20 min. The supernatant fraction was filtered and loaded onto a DEAE anion exchange column (20 ml; GE Healthcare), and the protein was eluted with a 400-ml gradient of 1 M NaCl. The fractions containing the protein were confirmed by SDS-polyacrylamide gel electrophoresis and purified by gel filtration on a Superdex 200-PG column (GE Healthcare) equilibrated with 20 mM Tris, pH 7.4, 200 mM NaCl, and 0.01% (w/v) sodium azide. Relevant fractions were dialyzed against 20 mM Tris, pH 7.4, and finally purified on a monoQ anion exchange column (GE Healthcare).

¹⁵N/²H-EIN, ²H-HPr and HPr at natural isotopic abundance were expressed and purified as described previously.¹⁴

NMR Spectroscopy

NMR samples comprised ∼0.15 mM ¹⁵N/²H-EI dimer in 20 mM Tris buffer, pH 7.4, 100 mM NaCl, 10 mM DTT, 4 mM MgCl₂, 1 mM EDTA, 1 tablet of protease inhibitor cocktail (SigmaFAST S8830) and 10% D₂O (v/v). The protease inhibitor cocktail was required to maintain stability of the sample since, in the absence of protease inhibitors, EI degraded noticeably at 37°C owing to the protease-sensitive nature of the EIC domain. In addition to free EI, samples complexed to HPr (0.5 mM) at natutal isotopic abundance were also prepared.

NMR spectra were recorded at 37°C on a Bruker 800 MHz DRX spectrometer equipped with a z-shielded gradient triple resonance cryoprobe. Spectra were processed and analyzed using the programs NMRPipe²⁸ and PIPP.²⁹ Assignment of the EIN domain in the context of full-length EI and the EI-HPr complex was carried out only for well-resolved cross-peaks in the 2D ¹H-¹⁵N TROSY spectra that overlayed directly onto well-resolved cross-peaks in the previously assigned spectrum of isolated EIN and the EIN-HPr complex, respectively.^{12,13 1}D_NH RDCs for the EIN domain of full EI and the EI-HPr complex were measured by taking the difference in the one-bond ¹H-¹⁵N splittings (¹J_NH + ¹D_NH) in aligned (∼11 mg/ml phage pf1^30,31) and isotropic media^21,32,33 using transverse relaxation optimized (TROSY)-based ¹H-¹⁵N correlation spectroscopy.³⁴ During the t₁ evolution period, ¹⁵N transverse magnetization evolved either with or without a ¹H refocusing pulse, and hence ¹⁵N magnetization was recorded as the TROSY component or a mixture of TROSY and anti-TROSY components, while ¹H magnetization maintained favorable TROSY relaxation throughout. The two data sets were collected in an interleaved manner, and the separation between the TROSY and anti-TROSY ¹⁵N components is half of the ¹⁵N-¹H splitting, (¹J_NH + ¹D_NH)/2 Hz. Singular value decomposition (SVD) analysis of RDCs^21,32 was carried out using Xplor-NIH.³⁵ Note that for the EI-HPr complex, RDCs for the EIN domain were obtained using a sample of ²H/¹⁵N-EI complexed to HPr at natural isotopic abundance with HPr in excess to ensure complete occupancy of the two HPr binding sites on EI; RDCs for bound HPr, however, could not be obtained using a sample of ²H/¹⁵N-HPr bound to EI at natural isotopic abundance, as free HPr (in contrast to complexed HPr) interacts with the alignment medium, making accurate subtraction of the contribution from free HPr not feasible.

Isothermal titration calorimetry

ITC (isothermal titration calorimetry) was performed using a MicroCal iTC 200 Microcalorimeter. 0.1 mM EIN or EI was placed in the cell and titrated with 1 mM HPr in the syringe at 25 and 37°C. Proteins were dissolved in the same buffer used for NMR and SAXS studies (20 mM Tris, pH 7.4, 100 mM NaCl, 10 mM DTT, 4 mM MgCl₂, 1 mM EDTA and protease inhibitor cocktail (SigmaFAST S8830). Analysis of the data, using a single site binding model, was performed using the Origin (version 7) software provided with the instrument.

Sedimentation velocity

A 100 mg/ml (1.6 mM) stock solution of EI was diluted to a final concentration of 200 μM in buffer comprising 20 mM Tris, pH 7.4, 100 mM NaCl, 10 mM DTT, 4 mM MgCl₂, 1 mM EDTA. This solution was subsequently diluted into the same buffer to prepare a series of approximately 1.0 to 70 μM solutions for sedimentation velocity. Samples containing less than 50 μM of protein were loaded into 12 mm 2-channel epon centerpiece cells (400 μL); whereas higher concentrations were loaded into 3 mm 2-channel epon centerpiece cells (100 μL). Sedimentation velocity experiments were conducted at 20.0° C and 40 krpm on a Beckman Coulter ProteomeLab XL-I analytical ultracentrifuge with 80-100 Rayleigh interference scans collected at ∼ 6.9 minute intervals. Data were analyzed in SEDFIT 11.71³⁶ in terms a continuous c(s) distribution covering an s range of 0.05 – 12.0 S with a resolution of 150 and a confidence level (F-ratio) of 0.68. Good fits were obtained with rmsd values ranging from 0.0024 – 0.011 fringes. SEDNTERP 1.09 (Hayes DB, Laue T and Philo J, http://www.jphilo.mailway.com) was used to determine the solution density (ρ), the solution viscosity (η) and the partial specific volume of EI. Experimental sedimentation coefficients were obtained from an average of the measured monomer and dimer sedimentation coefficients determined at the lower sample concentrations.

EI monomer and dimer populations, obtained from the integral of the c(s) distributions, were used to construct partial concentration isotherms. Data were analyzed in SEDPHAT 6.21³⁷ in terms of monomer-dimer self-association to obtain equilibrium constants; errors were determined using the method of F-statistics with a confidence level of 68.3%.

Sedimentation coefficients for the EI dimer were calculated from their atomic level structures in HYDROPRO 7c³⁸ and compared to the experimental value.

SAXS/WAXS Data Collection

Solution X-ray scattering data were collected on a samples of EI (5 mg/ml corresponding to ∼40 μM dimer), EI-HPr complex (5 mg/ml EI and 4.4 mg/ml HPr, corresponding to ∼40 μM EI dimer and 0.49 mM HPr) and HPr (4.4. mg/ml) in 20 mM Tris buffer, pH 7.4, 100 mM NaCl, 10 mM DTT, 4 mM MgCl₂, 1 mM EDTA, and 1 tablet of protease inhibitor cocktail (SigmaFAST S8830). Solution X-ray scattering data were acquired at the Beam Line 12-IDC at the Advanced Light Source (Argonne National Laboratory, Argonne, IL). Data collection was done using a Gold CCD detector positioned at two distances, 4 m and 36 cm, from the sample capillary. Incident radiation with an energy of 20 keV was used resulting in observable q-ranges of 0.014 - 0.23 A^-1 (SAXS) for the 4 m sample-detector distance and 0.10 - 2.5 A^-1 (WAXS) for the 36 cm distance. Q-axis mapping for both geometries was done using scattering from a silver behenate standard sample. A total of 20 sequential data frames with exposure times of 0.25 seconds was recorded with the samples kept at 25°C throughout the measurement. To prevent radiation damage, volumes of 150 μL of samples and buffers were oscillated during data collection using a flow-though setup. Individual data frames were masked, corrected for the detector sensitivity, radially integrated and normalized by the corresponding incident beam intensities. The final 1D scattering profiles and their uncertainties were calculated as means and standard deviations over the 20 individual frames. The buffer data were then subtracted from the scattering profiles. In the case of the SAXS profile obtained for the EI/HPr sample, the contribution from unbound HPr (present in the sample in excess) was also subtracted, based on the experimental SAXS/WAXS profile of free HPr and the concentration of unbound HPr in the EI/HPr sample calculated from the K_diss determined by isothermal titration calorimetry. To evaluate the magnitude of a possible structure factor, data were collected at protein concentrations of 5.0 and 2.5 mg/ml for EI and HPr samples. The data at these concentrations were indistinguishable at q > 0.015 A^-1.

SANS Data Collection

SANS data for free EI were collected on a sample of fully deuterated EI (5 mg/ml; ∼40 μM dimer) in 20 mM Tris buffer, pH 7.4, 100 mM NaCl, 10 mM DTT, 4 mM MgCl₂, 1 mM EDTA, 1 tablet of protease inhibitor cocktail (SigmaFAST S8820), and 40.4% D₂O (v/v). SANS data for the EI-HPr complex (same buffer as for free EI) were collected on fully deuterated EI (5 mg/ml ∼40 μM dimer) and protonated HPr (4.4 mg/ml; ∼470 μM). (Although data were also collected on a sample comprising protonated EI and fully deuterated HPr in excess, the data were not useful, as the large excess of HPr required to ensure full saturation of the two symmetric binding sites on the EI dimer made subtraction to obtain the SANS curve for bound HPr unfeasible.) Small-angle neutron scattering data were collected on the 30 m NG3 SANS instrument at the National Institute for Standards and Technology (NIST) Center for Neutron Research (NCNR) using a neutron wavelength of 6.19 Å with Δλ/λ = 0.123 and a sample to detector distance of 2 m with the detector offset by 5 cm, corresponding to an observable q -range of 0.028-0.240 Å^-1. The mean incident neutron wavelength was determined using scattering from a standard silver behenate sample. Data collection times were 2 hrs. The sample data were corrected for the scattering of the buffer, empty cell and detector background using standard procedures for the NG3 instrument.³⁹ Samples were maintained at 25°C during data acquisition.

Theory and computation

In this work we make improvements in the calculation of SAXS/WAXS curves from known molecular structures and in comparing these structures to those obtained from experiment. These have been implemented in the molecular structure determination package Xplor-NIH³⁵ and are available in the v2.25 release.

Including the SAXS contribution from bound solvent for molecules of general shape

To achieve optimal agreement with observed SAXS/WAXS curves it is necessary to properly include the scattering contribution of bound solvent that takes into account complex molecular shapes. The relevant theory and method used here are described below.

The scattering intensity is calculated by numerically computing the average (over solid angle) of the square of the scattering amplitude A(q):⁴⁰

$$A(\mathbf{\text{q}})=\sum _j{f}_j^{\text{eff}}(\mathit{\text{q}})e^{i\mathbf{\text{q}}·{\mathbf{\text{x}}}_j}+{\sum _{k}f}^{\text{sph}}(q;r_k)e^{i\mathbf{\text{q}}·{\mathbf{\text{y}}}_k}$$ [1]

where q is the reciprocal space scattering vector with magnitude q, j sums over all atoms, $f_j^{\text{eff}}(q)$ is the effective atomic scattering form factor, x_j is the position of atom j, k sums over points representing boundary-associated solvent, y_k are the positions of these points, and r_k are radii described below. The effective atomic scattering amplitude is:⁴⁰

$$f_j^{\text{eff}}(q)=f_j(q)-{\rho }_s{g}_j(q)$$ [2]

where f_j(q) is the vacuum atomic scattering amplitude, ρ_s is the bulk solvent electron density, and g_j is the scattering amplitude due to excluded solvent,^41,42 which can be expressed as:

$$g_j(q)=s_V{V}_j\text{exp}(-\pi q^2{V}_j^{2/3})\text{exp}[-\pi {(q{r}_m)}^2{(4\pi /3)}^{2/3}(s_r^2-1)]$$ [3]

where V_j is the volume of atom j, r_m is the radius corresponding to the average atomic volume, and s_V and s_r are scale factors which take values close to 1, and whose values are typically determined using a fit to experimental data as in Svergun et al.⁴²

Each boundary point scatters with an effective form factor

$$f^{\text{sph}}(q;r_k)={\rho }_b(4\pi /q^2)[\text{sin}({\mathit{\text{qr}}}_k)/q-r_k\text{cos}({\mathit{\text{qr}}}_k)]$$ [4]

corresponding to a sphere of radius r_k with uniform density ρ_b. The positions and radii of the boundary points are computed as described below.

We use the method of Varshney et al.⁴³ to compute a molecular surface description defined as a triangular mesh and computed outward-pointing surface normals. In our approximate description of the boundary region, we use the Varshney algorithm to generate the outer surface described by rolling a solvent molecule of radius r_w over atoms of radius (r_i + r_b), where r_i is the atomic radius as specified in Svergun et al.⁴² and r_b is the boundary layer thickness. The inner surface of the boundary region is generated from the outer triangular mesh surface by extending, for each vertex, a line segment of length r_b in the direction opposite the surface normal. In this work we use r_w = 1.44 Å and r_b = 3 Å.

Each triangle on the outer surface and its complement on the inner surface bound an irregular triangular prism as depicted in Fig. 2. In our boundary layer description the contribution of each prism is represented as a sphere of uniform density such that each region contributes to the second sum in Eq. [1]: y_k is taken to be the center of the prism, and r_k the radius corresponding to a sphere whose volume is that of the prism.

Figure 2. Visualization of a portion of the boundary layer scatterers.

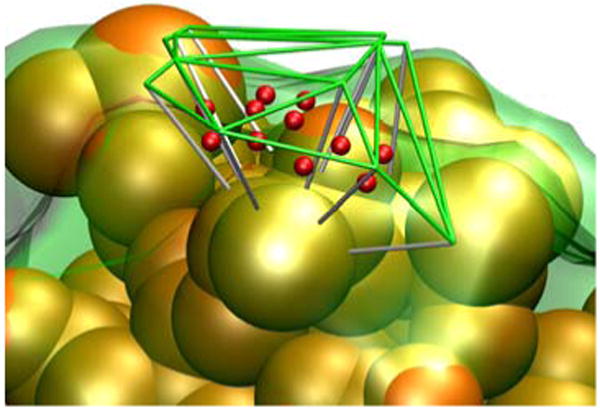
The green lines depict a portion of the tessellated surface generated using atomic radii (+3 Å). An inner surface (transparent green surface) was generated by dropping line segments (white lines) 3 Å in the direction opposite the surface normals at each vertex. A scattering center (red) was located at the center of each voxel at y_k defined by the outer and inner triangular patches. The orange spheres correspond to heavy atoms of the molecule. The scattering from each voxel is represented as a sphere of uniform density and radius r_k, corresponding to the voxel's volume.

While approximate, such a surface description has the advantage of describing surfaces with complex shapes, including concave regions. In contrast, the surface description used by Svergun et al.⁴² and implemented in CRYSOL fails to capture the bound solvent contribution in such cases. This is especially important in the case of EI.

As in Svergun et al.,⁴² the three parameters s_V, s_r and ρ_b describing the solvent scattering contribution are fit using a grid search procedure. These parameters are recomputed periodically throughout the structure determination. The boundary layer contribution to the scattering intensity is not calculated at each dynamics or minimization step. Rather, it is combined with the globic correction^40,44 in the correction factor c(q) such that

$$I(q)=c(q)I^{\text{apporox}}(q)$$ [5]

where I^approx(q) is the scattering intensity calculated without the boundary layer by combining the contribution of multiple atoms into globs and by computing the A(q) at a relatively small number of solid angle grid points. The correction c(q) is periodically recomputed from I(q) calculated including the boundary layer, individual atoms and a much finer grid of solid angle points.

Comparison with experimental solution scattering curves

The energy associated with the SAXS/WAXS term is given by:

$$E_{\mathit{\text{scat}}}=(k_{\mathit{\text{scat}}}/N)\sum _{i=1}^N{\left((I_i^{\mathit{\text{calc}}}-I_i^{\mathit{\text{obs}}})/\Delta I_i\right)}^2$$ [6]

where $I_i^{\mathit{\text{obs}}}$ is the value of the observed scattering curve at q = q_i, ΔI_i is the experimental error at this point, and N is the number of datapoints used for comparison. $I_i^{\mathit{\text{calc}}}=\mathit{\text{nI}}(q_i)$ where n is a normalization factor. In previous work n was obtained by setting $\mathit{\text{nI}}(q_j)=I_j^{\mathit{\text{obs}}}$ for a special point j, where typically q_j = 0.^27,44 In the current work, we instead determine n by minimizing E_scat, such that no single point is treated specially in Eq. [6].

Additionally, previous applications in the literature extrapolated I_obs to q = 0, and fit this extrapolated region in Eq. [6].⁴⁴ We have found this to be a dangerous and unnecessary practice, particularly when there are too few points at low q for a proper Guinier analysis. Therefore, in this work we instead include $I_i^{\mathit{\text{obs}}}$ only for regions of q for which we have actual experimental measurements.

Small angle neutron scattering (SANS) measurements were used for independent validation of calculated structures. The computation of a SANS curve from a molecular structure is identical to that for X-ray scattering except that different values are used for atomic and solvent scattering amplitudes, and in that an incoherent background scattering parameter determined in the fit-to-experiment procedure is required in addition to the three parameters determined for a SAXS/WAXS fit.⁴⁵ Due to the large difference in neutron scattering length of the proton and deuteron, the solvent contribution to SANS can be tuned over a much larger range than that of SAXS. It therefore becomes essential to have the ability to handle arbitrary proton isotopic compositions of the solvent and of different components of a complex. This capability is now present in Xplor-NIH v2.25,³⁵ and full SANS-fitting capability is now available in the calcSAXS helper program when the -sans flag is used.

Structure determination procedure

In this section we present an overview of the calculational strategy used to compute the structures of EI and the EI-HPr complex based on SAXS/WAXS and RDC data. All calculations were carried out using the molecular structure determination package Xplor-NIH (v2.25)³⁵ and visualized using VMD-XPLOR.⁴⁶

The initial structure of the EI dimer was constructed as a hybrid of the 2.7 Å resolution crystal structure of phosphorylated EI intermediate captured by the inhibitor oxalate (PDB code 2HWG)¹⁸ and the NMR structure of EIN in the EIN-HPr complex (PDB code 3EZA).¹³ The rational for making use of the NMR coordinates of EIN is that the solution RDC data fit the NMR coordinates of the two subdomains of EIN, EIN^α (residues 33-143) and EIN^α/β (residues 1-21 and 147-230), significantly better than the corresponding subdomains of the X-ray structure of either phosphorylated EI (2HWG)¹⁸ or free EIN (1ZYM).¹¹ This reflects the intermediate resolution (2.7 and 2.5 Å, respectively) of the X-ray structures. In the crystal structure of the phosphorylated EI intermediate (2HWG),¹⁸ the region connecting the EIN^α/β subdomain to the EIC domain (residues 231 to 261) comprises a long α-helix (residues 233-254), known as the linker helix, and a short loop (residues 255-261); in both the NMR (1EZA¹² and 3EZA¹³) and crystal (1ZYM)¹¹ coordinates of an isolated EIN construct comprising residues 1-259, only part of the linker helix is present (extending to residue 248 in the case of the NMR structure and 244 for the X-ray structure), and it is somewhat irregular and, in the case of the NMR structure, not particularly well packed against the EIN^α/β subdomain. Therefore the linker helix bridging the EIN^α/β subdomain to the EIC domain was taken from the crystal structure of phosphorylated EI. The NMR coordinates were used for residues 1-230, and were attached to the 2HWG crystal coordinates by best-fitting the protein backbone atoms of the EIN^α/β subdomain to the crystal coordinates of each subunit. Because the crystal structure of the phosphorylated EI dimer (2HWG)¹⁸ is not perfectly symmetric, the X-ray coordinates for residues 231-573 of subunit A were best fit onto the corresponding coordinates of subunit B, to generate a perfectly symmetric dimer. (Note that residues 574-575 are not visible in the crystal structure.) The covalent connections and overall symmetry of both EIN domains were then optimized. It should be noted that this hybrid starting structure contains significant atomic overlap between the EIN and EIC domains.

Throughout the structure determination, the atomic coordinates of each EIN domain (residues 1-254) were treated as rigid bodies, with the two symmetry related EIC domains (residues 262-573) held fixed in space. Coordinates in the linker region (residues 255-261) were allowed varying degrees of freedom (torsion or Cartesian) during the calculation through the use of the internal variable module (IVM)⁴⁷ of Xplor-NIH.^35,48

The structure of free EI was determined using a three step procedure involving the application of conjoined rigid body/torsion angle/Cartesian simulated annealing^47,49,50 under the influence of the experimental RDC and SAXS/WAXS data. (i) The first step consists of a conjoined rigid body/Cartesian dynamics simulated annealing protocol in which the linker region is given Cartesian degrees of freedom. (ii) The second step involves a simulated annealing docking protocol to ensure optimal sampling of conformational space and to exclude any possible alternative solutions. At the start of the docking calculations, the positions and orientations of the two EIN subunits are separately randomized by breaking the peptide bond between residues 261 and 262 that connects each EIC domain to the EIN/EIC linker region. Likewise, the backbone ϕ/ψ torsion angles within the linker are randomized as well. The EIN domains are then allowed to rotate and translate as rigid bodies under the influence of the RDCs and C₂ symmetry restraints, while the linker region (residues 255-261) is given torsional degrees of freedom to permit the 261/262 peptide bond to be reformed under the influence of covalent geometry restraints. Only structures that fully satisfy the RDC data (i.e. with RDC R-factors within a threshold set to 0.1% above the value obtained using SVD against a single EIN domain) are retained. The EIN domains are then allowed to translate but not rotate with torsion angle degrees of freedom for the linker region to optimize agreement with the SAXS/WAXS data. (iii) The third and final step of the calculation consists of a conjoined rigid body/torsion/Cartesian dynamics simulated annealing refinement protocol in which the backbone atoms within the linker are given Cartesian degrees of freedom and interfacial side chains between the EIN and EIC domains are given torsion angle degrees of freedom. Residues at the interface of the EIC and EIN domains were identified from the structures generated after step 2 as all residues containing an atom within 14.5 Å of a linker atom or of an EIN or EIC atom, respectively. Full details of the complete protocol are provided in Supplementary.

Potential energy terms used in the structure determination comprise the following: terms for the experimental RDC^51,52 and SAXS/WAXS (the current work) data; a restraint for the overall radius of gyration, R_gyr,⁵³ with a target value deduced from the SAXS curve by Guinier analysis (used in the docking phase only); terms for covalent geometry (bonds, angles and improper torsions) and non-bonded interactions (in the form of a quartic van der Waals repulsion term, E_repel⁵⁴); a multidimensional torsion angle database potential of mean force(E_DB)⁵⁵; torsion angle restraints for residues in the linker to restrain ϕ to a range from -175° to -40° and ψ from -60° to 180°, thereby excluding disfavored and positive ϕ regions of the Ramachandran map); and two terms to enforce C₂ symmetry of the dimer (namely, a non-crystallographic symmetry restraint and distance symmetry restraints⁵⁶). Note that the R_gyr term contains much less information than the SAXS/WAXS term but since the R_gyr term is computationally much simpler, it is used in the docking phase only to quickly converge the structure calculation to the approximately correct region of configuration space, and is omitted in the simulated annealing refinement protocols.

120 structures were generated in the first conjoined rigid body/Cartesian simulated annealing step starting from the hybrid NMR/X-ray initial coordinates described above. All 120 structures converged to a single cluster (using Xplor-NIH's findCluster helper program⁵⁷ with a clustering tolerance of 3 Å) with a Cα backbone precision for the EIN domain of 1.4±1.0 Å (i.e. the average Cα rms displacement relative to the mean coordinates), and good agreement with the RDC (R-factor = 18.09±0.07%) and SAXS/WAXS (χ² = 1.24±0.30) data. (The RDC R-factor is defined as R_inf = [<(D_obs-D_calc)²>/(2<D_obs²>)]^1/2 where D_obs and D_calc are the observed and calculated RDC values.⁵⁸) The Cα rms displacement and rotation of the EIN domain relative to the starting coordinates are ∼39 Å and 65°, respectively. 120 structures were generated in the second docking step starting from the minimum energy structure after step 1. (Note there is no need to start the docking protocol from different starting structures as the positions of the EIN domain are randomized at the start of the docking calculations). In the third and final step, all 120 docked structures were subjected to rigid body/torsion angle/Cartesian simulated annealing refinement, and the top 100 of these (sorted on the basis of agreement with first the RDC data, then the SAXS/WAXS data, and finally total energy) were retained for analysis. It is worth noting that the Cα rms displacement and rotation of the EIN domain for the restrained regularized mean structure generated from the final 100 simulated annealing structures relative to the lowest energy structure after step 1 are only 4.3 Å and 13°, respectively. We also carried out some calculations omitting either the first rigid body/Cartesian simulated annealing step or the second docking step, and the same end results were obtained.

The initial coordinates for the EI-HPr calculations were generated by taking the 120 simulated annealing structures calculated for free EI and adding two molecules of HPr, one to each EI subunit, in exactly the same position as that found in the NMR structure of the EIN-HPr complex (3EZA).¹³ This was done by simply superimposing EIN in the EIN-HPr complex on to each EIN domain of free EI. All 120 starting structures were subjected to two rounds of simulated annealing using the same protocols as that used for free EI. In this instance, the EIN-HPr moieties were treated as single rigid bodies. In the first round of simulated annealing refinement the EIN/EIC linker was given Cartesian degrees of freedom. In the second round of simulated annealing torsional degrees of freedom for side chains at the interface of HPr and EIC were included in addition to Cartesian degrees of freedom for the linker. Residues at the interface of HPr and EIC were identified as all residues containing an atom within 16.5 Å of linker atom or of an EIC or HPr atom, respectively, in the structures generated after the first round of simulated annealing. The top 100 simulated annealing structures (sorted on the basis of agreement with first the RDC data, then the SAXS/WAXS data and finally total energy) were retained for analysis.

Additional ensemble refinement calculations using a mixture of equally weighted structures (with N_e = 2 and 8) were also carried out using the ensemble calculation facility in Xplor-NIH.³⁵ In the current work, ensemble energies were calculated slightly differently than previously:^51,52,59 the RDC and SAXS/WAXS terms were multiplied by the ensemble size, while the contribution of all other terms was simply the sum of that term for each ensemble member.

Results and Discussion

Sedimentation analysis and monomer-dimer equilibrium for EI

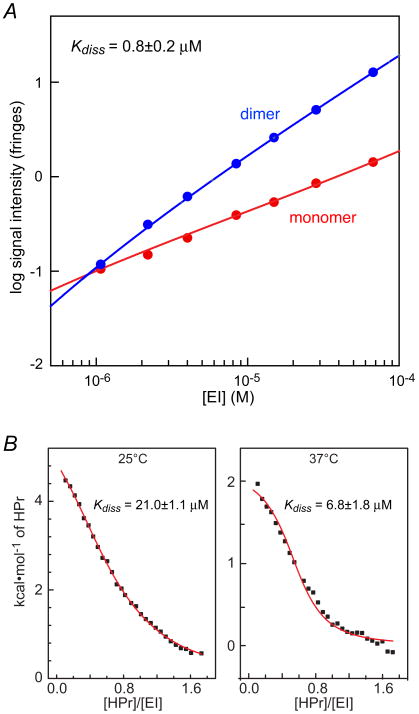
The equilibrium constant for monomer-dimer association of EI is known to be highly sensitive to solution conditions such as salt concentration and the presence or absence of Mg²⁺.⁶⁰ To this end we carried out sedimentation velocity studies on EI in the presence of 100 mM NaCl and 4 mM MgCl₂ at pH 7.4, conditions where the dimer has been reported to be most stable.⁶⁰ Both monomer and dimer species are observed with proportions dependent on the sample loading typical of a monomer- dimer reversible system (see Supplementary Fig. S1). At low concentrations, the best-fit frictional ratio returns a mass of ∼62 kDa for the slow sedimenting species, indicating that this indeed represents the EI monomer (M_calc = 63,562 Da). Similarly, at the higher concentrations the best-fit frictional ratio returns a mass of ∼135 kDa for the faster sedimenting dimer species. To obtain an estimate of the equilibrium dissociation constant (K_diss), signal intensities, calculated by integration of the c(s) monomer and dimer peaks, were fit to a simple binding isotherm describing a monomer-dimer association. Data were well fit with a K_diss of 0.8±0.2 μM (Fig. 3A), consistent with previously reported values in the literature.⁶⁰ Thus, at the concentrations employed for the NMR (0.3 mM in subunits) and SAXS/WAXS and SANS (0.08 mM in subunits) measurements, the predominant form of EI is a dimer (96.4 and 93.2%, respectively). Model calculations indicate that the contribution of monomeric EI to the RDC, SAXS/WAXS and SANS data is negligible (<5%) and can be ignored. (Note that for a given concentration the scattering intensity for the monomer will be half that of the dimer).

Figure 3. Self-association of EI and binding of HPr to EI.

(A) Determination of the EI monomer-dimer self-association constant by sedimentation velocity. Population isotherms based on sedimentation velocity data showing the contributions of the EI monomer (red) and dimer (blue). All signals were normalized to a cell path length of 12 mm. The best-fit analysis in terms of a reversible monomer-dimer equilibrium is depicted by the solid lines. (B) ITC data for the binding of HPr to EI at 25 and 37°C. The solid lines represent best-fits to the data using a simple binding isotherm. The concentration of EI is expressed in monomer units.

Equilibrium binding of HPr to EI

ITC experiments were conducted at 25°C and 37°C corresponding to the temperatures used in the SAXS/WAXS/SANS and NMR experiments, respectively (Fig. 3B). The K_diss values obtained were 21.0±1.1 μM at 25°C and 6.8±1.8 μM at 37°C. The populations of the different states are readily obtained using a model where EI = A and HPr = B such that (A + A) + B + B form complexes AA, AB, (AA)B and B(AA)B with the self-association of A and two symmetric sites for the binding of B. Taking into account the statistical factor of 2 for the binding of B to AA relative to AB, and the statistical factor of 0.25 for the binding of the second molecule of B to the AA dimer (i.e. no positive or negative cooperativity), we obtain the following results assuming a dimerization constant of 0.8 μM (determined by sedimentation velocity at 20°C) at both 25 and 37°C. In the SAXS/WAXS and SANS experiments (EI, 0.08 mM in subunits; HPr, 0.47 mM) at 25°C, the percentages of EI with two molecules of HPr bound (BAAB), one molecule of HPr bound (AAB and AB) and no HPr bound (i.e. free AA and A) are 84.0, 15.4 and 0.6%, respectively; the percentages of doubly bound HPr (BAAB), singly bound HPr (AAB and AB) and free HPr are 14.3, 1.9 and 83.8%, respectively. In the NMR experiments (EI, 0.3 mM in subunits; HPr 0.5 mM) at 37°C, the percentages of EI with two molecules of HPr bound, one molecule of HPr bound and no HPr bound are 90.5 (BAAB), 9.3 (AAB and AB) and 0.2% (A and A2), respectively. Model calculations indicate that the contributions of free EI and EI with one molecule of HPr bound to the RDC and SAXS/WAXS data are negligible (≤10%) and can for all intents and purposes be ignored.

Analysis of RDCs

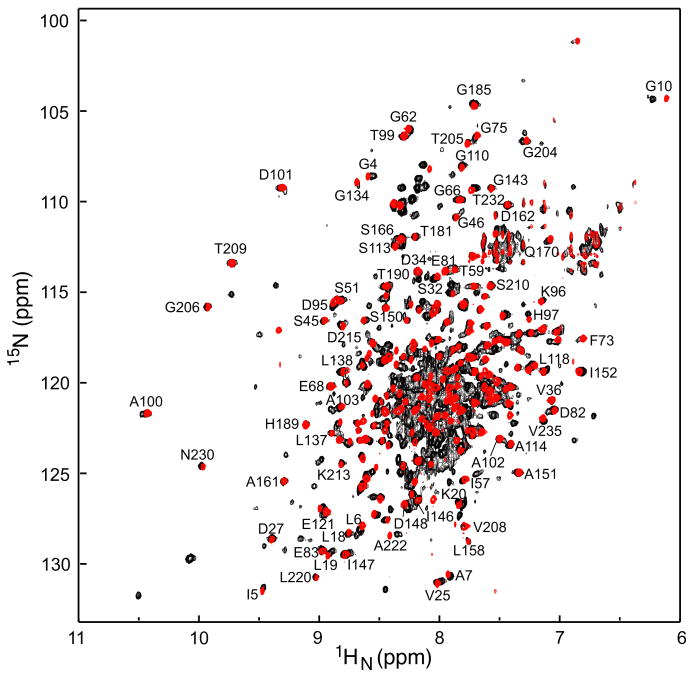
A comparison of the ¹H-¹⁵N TROSY correlation spectrum of intact dimeric EI (residues 1-575, 128 kDa) and monomeric EIN (residues 1-249, ∼29 kDa) is shown in Fig. 4. A large number of EI cross-peaks match those in the EIN spectrum (where complete assignments are available),¹² thereby enabling the assignments of ∼90 cross-peaks of the EIN domain to be readily transferred from isolated EIN to intact EI. Binding of HPr to EIN results in only small chemical shift perturbations¹⁰ and since complete assignments are also available for the EIN-HPr complex,¹³ assignments of cross-peaks within the EIN domain can also be easily transferred from the EIN-HPr complex to the EI-HPr complex.

Figure 4. Comparison of ¹H-¹⁵N correlation specta E. coli EI and EIN.

The 2D ¹⁵N-¹H TROSY-correlation spectrum of the intact 128 kDa E. coli EI dimer (black, residues 1-573) is superimposed on the spectrum of the isolated monomeric EIN domain (red, residues 1-249) recorded at 800 MHz and 37°C. Clearly resolved cross-peaks in the EIN spectrum¹² that are either not shifted or minimally shifted in intact EI are labeled, thereby permitting direct transfer of assignments of these cross-peaks from the EIN to the EI spectrum.

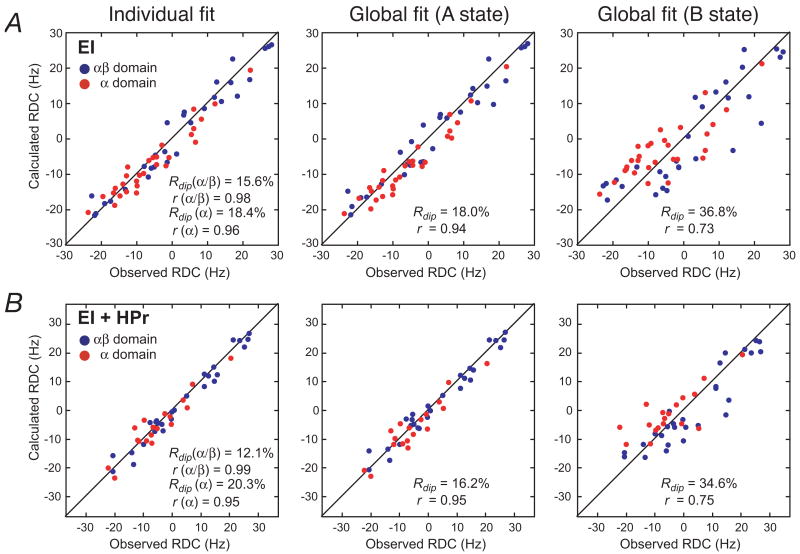
RDCs, measured in weak alignment media, provide orientational information of bond vectors relative to an external alignment tensor.^21,32,33 In systems involving rigid body reorientations, only a relatively small number of backbone ¹D_NH RDCs are required to define the orientation of one domain to another.^50,61 Backbone ¹D_NH RDCs of well-resolved cross-peaks were measured for intact EI and the EI-HPr complex in a liquid crystalline medium of phage pf1, and the results are summarized in Fig. 5 and Table 1. When the RDCs measured on EI and the EI-HPr complex are fit against the NMR coordinates of the individual EIN^α (residues 33-143) and EIN^α/β (residues 2-21 and 147-230) subdomains, excellent agreement is found between observed and calculated values with RDC R-factors ≤20% (Fig. 5, left panels). These values indicate that the accuracy of the coordinates, in terms of the orientations of the measured backbone N-H bond vectors, is comparable to that of ∼2 Å resolution crystal structures.^21,62,63 (Note that although the EIN-HPr complex refined with RDCs, the shape, size and surface composition of EIN-HPr is obviously different from that of EI or EI-HPr, and the normalized scalar product for the two alignment tensors measured for the EIN-HPr complex and free EI is 0.72.) The RDC R-factors obtained using the X-ray coordinates of the individual EIN^α and EIN^α/β subdomains from either phosphorylated EI (2HWG)¹⁸ and free EIN (1ZYM)¹¹ are significantly worse (30-40%) reflecting the intermediate resolution of the crystal structures (2.7 and 2.5 Å, respectively). Thus the NMR coordinates of the EIN^α and EIN^α/β subdomains were used for all further analysis.

Figure 5. RDC analysis of (A) EI and (B) the EI-HPr complex.

Panels provide a comparison of the observed and calculated RDCs obtained by SVD fits to the individual EIN^α and EIN^α/β subdomains (left panel), and global fits to the EIN domain in the A (middle panels) and B (right panels) states. The coordinates of the A state are taken from the NMR coordinates of the EIN-HPr complex (3EZA)¹³; for the B state, the NMR coordinates of the two subdomains, EIN^α and EIN^α/β, were best-fitted onto the X-ray coordinates of phosphorylated EI (2HWG)¹⁸. The RDC data for the EIN^α and EIN^α/β subdomains are displayed in red and blue, respectively. R_dip and r are the RDC R-factor and Pierson correlation coefficient, respectively.

Table 1.

SVD analysis of ¹D_NH RDCs measured for residues of the EIN domain in intact EI and the EI-HPr complex.^a

	Number of RDCs	Euler angles (°)b			DaNH (Hz)	η	RDC R-factorc
		ϕ	θ	ψ
A. Free EI
Fits to A state (free EIN conformation)d
EINα/β	29	231	13	139	13.9	0.56	15.6
EINα	29	249 (230)	10 (8)	113 (136)	14.7	0.49	18.4
EIN global	58	242 (235)	10 (10)	122 (132)	14.6 (14.6)	0.49 (0.50)	18.0 (17.5)
Fits to B state (orientation in crystal structure of phosphorylated EI from E. coli)
EINα/β	29	231	13	139	13.9	0.56	15.6
EINα	29	279	33	149	14.7	0.49	18.4
EIN global	58	250	28	147	13.0	0.32	36.8
Fits to orientation in crystal structure of EI from Staph. carnosus
EINα/β	29	231	13	139	13.9	0.56	15.6
EINα	29	288	15	114	14.7	0.49	18.4
EIN global	58	243	11	141	14.4	0.31	25.5
B. EI-HPr complex
Fits to A state (free EIN conformation)d
EINα/β	25	242	11	121	13.7	0.63	12.1
EINα	18	244 (216)	12 (8)	118 (144)	14.0	0.65	20.3
EIN global	43	243 (238)	10 (10)	118 (122)	13.9 (13.9)	0.63 (0.64)	16.2 (15.5)
Fits to B state (orientation in crystal structure of phosphorylated EI from E. coli)
EINα/β	25	242	11	121	13.7	0.63	12.1
EINα	18	275	32	146	14.0	0.65	20.3
EIN global	43	257	30	120	12.3	0.36	34.6
Fits to orientation in crystal structure of EI from Staph. carnosus
EINα/β	25	242	11	121	13.5	0.62	12.4
EINα	18	284	13	112	14.0	0.65	20.4
EIN global	43	242	12	132	13.3	0.40	23.7

^aThe coordinates used for SVD analysis are those of EIN in the EIN-HPr complex (3EZA).¹³ The EIN^α and EIN^α/β subdomains are then fitted onto the X-ray coordinates of E. coli phosphorylated EI (2HWG)¹⁸ and Staph carnosus (2HRO)¹⁶ EI. Thus the comparisons reflect only the relative orientation of the EIN^α and EIN^α/β subdomains and are not influenced by variations in the atomic coordinates for the different structures. SVD analysis was carried out in Xplor-NIH.³⁵

^bFor ease of comparison, the EIN^α/β subdomain is positioned in the same molecular frame throughout. The convention used for the Euler angles is the x convention of Goldstein et al.⁶⁴ ϕ describes the rotation about the z axis, θ the rotation about the resulting x axis, and ψ the rotation about the resulting z axis.

^cThe RDC R-factor⁵⁸ is defined as R_inf = [<(D_obs-D_calc)²>/(2<D_obs²>)]^1/2 where D_obs and D_calc are the observed and calculated RDC values.

^dThe values in parentheses refer to the values obtained using the NMR EIN^α and EIN^α/β coordinates in the relative orientation found in the crystal structure of free EIN (1ZYM).¹¹ (i.e. these hybrid coordinates were generated by best-fitting the EIN^α and EIN^α/β subdomains of the 3EZA NMR structure individually on to the corresponding subdomains of 1ZYM. The overall Cα rms difference for EIN^α + EIN^α/β between the 3EZA and 1ZYM orientations of the two subdomains is 0.7 Å, and the rotation and Cα rms displacement between the EIN^α subdomains when the coordinates are best-fitted to the EIN^α/β subdomains are 5.7° and 1.8 Å, respectively. These differences are within the experimental error of the current data.

When the RDCs for both EI and the EI-HPr complex are fitted against the coordinates of the EIN domain in the A state orientation (corresponding to the NMR structure of EIN, 3EZA),¹³ excellent agreement is observed (Fig. 5, middle panels) with RDC R-factors of 18.0 and 16.2%, respectively (Table 1). These values are minimally larger than the weighted means obtained from the fits to the individual subdomains (17.0 and 15.5%, respectively). However, when the B state orientation is used (corresponding to the orientation found in the crystal structure of the phosphorylated EI intermediate¹⁸), agreement is much worse (Fig. 5, right panels) with RDC R-factors of 36.8 and 34.6%, respectively (Table 1). Similarly, when the orientation of the EIN^α and EIN^α/β subdomains observed in the structure of EI from Staph. carnosus (2HRO)¹⁶ is used, agreement is also poorer, with RDC R-factors of 25.5 and 23.7%, respectively. In addition, to the RDC R-factors, comparison of the values of the Euler angles obtained by SVD fitting against the structures of the individual EIN^α and EIN^α/β subdomains in the orientations observed in isolated EIN, phosphorylated EI and Staph. carnosus EI are also informative. If the orientation of two domains is fixed in space, the axes of the alignment tensor obtained from SVD fits to the individual domains will coincide. This is reflected in the values of the three Euler angles which provide the orientation of the axis of the alignment tensor relative to the molecular frame. In the case of the individual fits to the EIN^α and EIN^α/β subdomains, the Euler angles obtained with the orientation found in isolated EIN are similar (within experimental error), while those using the orientations observed in the structure of phosphorylated EI or Staph. carnosus EI are clearly different. One can therefore conclude unambiguously that in both EI and the EI-HPr complex, the relative orientation of the EIN^α and EIN^α/β subdomains is the same as that observed in isolated EIN. (This is further confirmed by SVD analysis with the EIN^α and EIN^α/β subdomains in the orientation found in the 1ZYM crystal structure of free EIN,¹¹ which differs by 6° from that found in the 3EZA NMR structure,¹³ a difference that is within the experimental error of the NMR coordinates given that the C^α rms difference between the two slightly different orientations is only 0.7 Å; cf. Table 1).

The RDC analysis also permits one to draw the following qualitative conclusions. First, the parameters describing the alignment tensors (Euler angles, magnitude of the principal component of the alignment tensor, D_a^NH, and rhombicity η) for free EI and the EI-HPr complex are very similar. Indeed, the normalized scalar product of the two alignment tensors is 0.99. Second, since EI is a dimer, one of the axes of the alignment tensor must coincide with the C₂ axis of the dimer. Since the alignment tensor is determined by molecular shape and charge, one can deduce that (a) the overall surface envelopes of free EI and the EI-HPr complex are similar, and (b) the orientation of EIN relative to the C₂ axis of the EIC dimerization domain, and therefore relative to the EIC domain dimer is similar for EI and the EI-HPr complex. Since the RDC data indicate that the surface envelopes of EI and the EI-HPr complex are similar one can infer that HPr must be sandwiched between the EIN and EIC domains in such a manner as to minimally perturb the overall molecular shape and surface charge distribution. In addition, since ¹H_N/¹⁵N chemical shift perturbation observed upon binding HPr is the same for the assigned residues within the EIN domain of EI as for isolated EIN, one can conclude that HPr binds to intact EI in the same mode as that observed in the EIN-HPr complex.

Comparison of SAXS/WAXS and SANS data with the crystal structures of EI

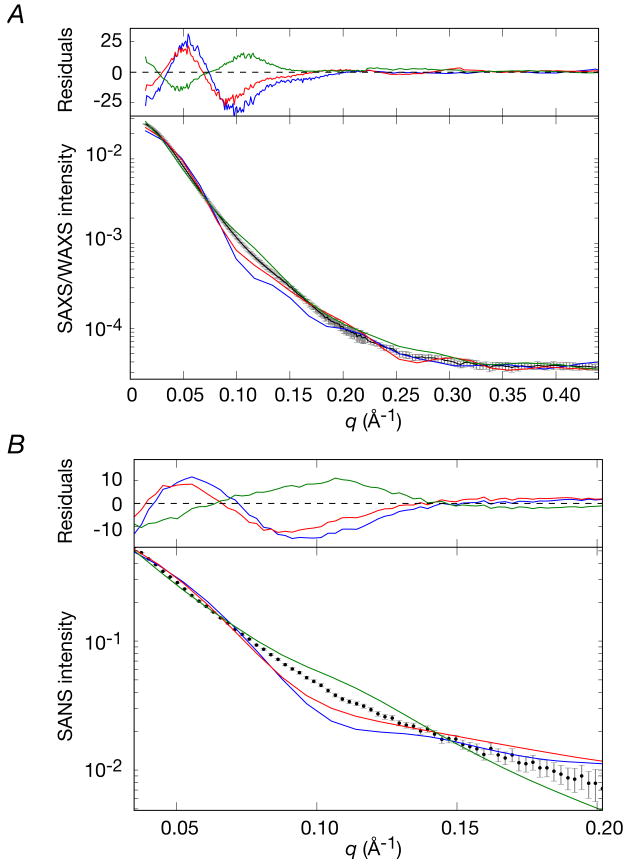
SAXS/WAXS and SANS are highly sensitive to the overall shape and size of a molecule. A comparison of the observed SAXS/WAXS (up to q = 0.44 Å^-1) and SANS (up to q ∼ 0.2 Å^-1) data obtained for free E. coli EI in solution with the best-fit calculated curves using the crystal structures of phosphorylated EI from E. coli (2HWG),¹⁸ and free EI from Staph. aureus (2WQD)¹⁷ and Staph. carnosus (2HRO)¹⁶ are shown in Fig. 6, and a summary of the χ² values is provided in Table 2. From this data it is clear that none of the three X-ray structures represent adequately the conformation of free EI in solution, and the agreement between observed and calculated scattering data is very poor. It is interesting to note that the local inflection in the region between q = 0.1 and 0.12 Å^-1 lies below the experimental data in the case of E. coli phosphorylated EI and Staph. aureus EI, but above the experimental data for Staph. carnosus EI. This feature of the SAXS and SANS data can be qualitatively attributed to the interdomain separation between the two EIN domains of the dimer, resulting in varying degrees of scattering interference. For E. coli phosphorylated EI and Staph aureus EI, the two EIN domains are too close to one another, while for Staph. carnosus EI they are too far apart.

Figure 6. Comparison of the experimental SAXS/WAXS and SANS curves measured for free E. coli EI with the best-fit SAXS/WAXS and SANS curves calculated for the three X-ray structures of EI.

(A) SAXS and (B) SANS. Black, experimental SAXS/WAXS and SANS curves (grey vertical error bars, 1 s.d.); phosphorylated EI from E. coli (2HWG,¹⁸ blue) and free EI from Staph aureus (2WQD,¹⁷ red) and Staph carnosus (2HRO,¹⁶ green). The abrupt change in the magnitude of the error bars in the SAXS/WAXS curve at q = 0.22 Å^-1 represents the change in geometry of the instrument from the SAXS (4 m detector distance) to WAXS (36 cm detector distance) regimes. The χ₂ of the fits are provided in Table 2. The residuals, given by $(I_i^{\mathit{\text{calc}}}-I_i^{\mathit{\text{obs}}})/{\mathit{\text{err}}}_i$, are plotted above each panel.

Table 2.

Comparison of observed SAXS/WAXS and SANS data with the best-fit calculated curves derived from the crystal structures of phosphorylated EI from E. coli (2HWG),¹⁸ and free EI from Staph. aureus (2WQD)¹⁷ and Staph. carnosus (2HRO).¹⁶

	χ2		Calculated hydrodynamic parametersa
	SAXS/WAXS q = 0.014→0.44 Å-1	SANS q = 0.035→0.20 Å-1	$R_{\mathit{\text{gyr}}}^{\mathit{\text{calc}}}$ (Å)	$D_{\text{max}}^{\mathit{\text{calc}}}$ (Å)	Scalc
2HWG	128.2	62.0	32.6	107.4	6.74
2WQD	56.0	34.0	35.4	124.7	6.45
2HRO	30.0	30.3	48.0	182.6	5.55

^a ${\mathit{\text{R}}}_{\mathit{\text{gyr}}}^{\mathit{\text{calc}}}$, ${\mathit{\text{D}}}_{\text{max}}^{\mathit{\text{calc}}}$ and S^calc were calculated from the atomic coordinates using HYDROPRO. ³⁸ The experimental values of R_gyr and D_max determined directly from P(r) analysis of the experimental SAXS data for free EI using GNOM⁶⁵ are 42.0±0.2 and 145-150 Å, respectively. The experimental value for the Svedberg sedimentation coefficient S for free EI determined by sedimentation velocity is 5.68±0.02 (see Supplementary Fig. S1).

The values of R_gyr and D_max determined directly from P(r) analysis⁶⁵ of the SAXS/WAXS curve for free EI are 42.0±0.2 and 145-150 Å, respectively. The R_gyr value determined from Guinier analysis of the SAXS curve is 41.0±0.6 Å. Hydrodynamic modeling³⁸ of the dimeric X-ray structures of E. coli phosphorylated EI (2HWG)¹⁸ and Staph. aureus free EI (2WQD)¹⁷ yields calculated values of R_gyr and D_max that are much smaller than the corresponding experimental values, while for the X-ray structure of Staph. carnosus free EI (2HRO)¹⁶ the calculated values are much larger (Table 2). These observations are corroborated by sedimentation velocity (Supplementary Fig. S1) where hydrodynamic modeling³⁸ of the E. coli phosphorylated EI¹⁸ and Staph. aureus free EI¹⁷ X-ray structure dimers leads to sedimentation coefficients (Table 2) that are much larger than the experimental value of 5.68 S (Supplementary Fig. S1). Even though the value of 5.55 S calculated for the Staph. carnosus EI dimer (2HRO)¹⁶ is closer to the experimental value, this only reflects the contribution from its extended EIN domains (cf. Fig. 1B).

Joint RDC and SAXS/WAXS structure determination of free EI

The calculational strategy employed to determine the solution structure of free EI involves a three step procedure driven by the experimental RDC and SAXS/WAXS data. Only the SAXS/WAXS data up to q = 0.44 Å^-1 are used in the primary calculations presented here as these reflect on overall shape and long-range interatomic interactions; the data from 0.44 < q ≤ 0.9 Å^-1 report on shorter range interatomic interactions between ∼14 and ∼7 Å and are used only for validation. The computational protocol consists of an initial conjoined rigid body/Cartesian simulated annealing step, a docking phase and a final conjoined rigid body/torsion angle/Cartesian simulated annealing refinement step (as described in the Theory and Computation Section and in Supplementary). Throughout the calculations, the two EIN domains (residues 1-254) are treated as rigid bodies, the two symmetry related EIC domains (residues 262-573) are held fixed in space, and the linker region (residues 255-261) is given torsional or Cartesian degrees of freedom. The purpose of the intermediate docking phase is to ensure extensive sampling of conformational space. A total of 120 structures were calculated and all converged to the same solution.

The rational behind this structure determination approach is that the RDCs serve to orient the two EIN domains relative to each other and to the C₂ axis of the EIC dimer (as one of the axes of the alignment tensor has to coincide with the C₂ symmetry axis). This assumes that the coordinates of the EIC dimer remain unchanged from those in the X-ray structure which seems perfectly reasonable since the structure of the EIC dimer is the same in the crystal structures of phosphorylated EI from E. coli,¹⁸ free EI from Staph. aureus¹⁷ and Staph. carnosus,¹⁶ and the isolated EIC dimer from T. tegcongensis.¹⁹ Given only a single alignment tensor, the RDCs alone are consistent with multiple solutions for the orientation of the symmetry-related EIN domains relative to the EIC dimer due to the equivalence of 180° rotations about each of the three axes of the alignment tensor.^21,33 However, when the RDC data are combined with the shape and translational information afforded by the SAXS/WAXS data, the stereochemical constraints imposed by covalent geometry within the linker connecting the EIN and EIC domains, and the physical requirement of no atomic overlap either between the domains or between the linker and one or more domains, only a single solution emerges.

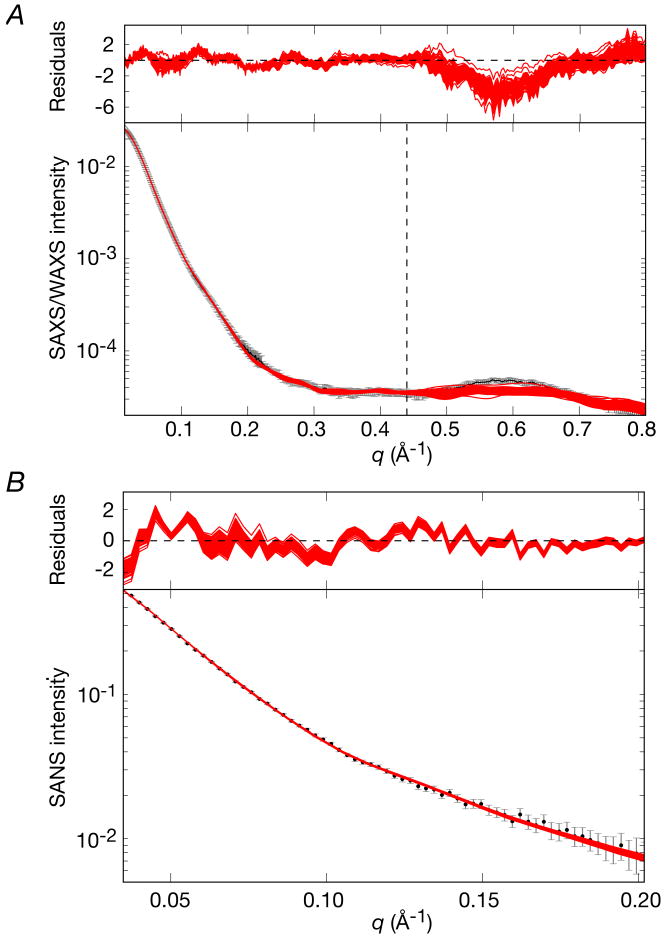
Comparisons of calculated and observed small angle scattering curves and best-fit (to the EIC domain) superpositions for the final refined EI structures are shown in Figs. 7 and 8A, respectively. A summary of the agreement with the SAXS/WAXS, SANS and RDC data is provided in Table 3. Only a single structure representation is required to account for the experimental SAXS/WAXS and RDC data within experimental error, and the precision of the coordinates is reasonably good (Table 3 and Fig. 8A). No significant improvement in agreement with the SAXS/WAXS data is observed for larger ensemble calculations. Thus, the χ² for the SAXS/WAXS curve up to q = 0.44 Å^-1 included in the calculations is only 0.30±0.05, the overall RDC R-factor (18.07±0.02%) is only minimally higher than the target value obtained by SVD analysis of a single EIN domain (18.02%), and the Cα atomic rms displacement and rotation of the EIN domain about its mean coordinate positions are reasonably small with values of 1.3±0.7 Å and 4.2±2.9°, respectively. The profile of the SAXS/WAXS curve at higher q values extending from 0.44 < q ≤ 0.8 Å-1, which were not included in the structure calculations, is reasonably well reproduced although the amplitude between q = 0.5 and 0.68 Å-1 is slightly underestimated (Fig. 7A). This is discussed in the next section.

Figure 7. Comparison of experimental SAXS/WAXS and SANS curves for free EI with the calculated curves for the simulated annealing structures obtained by refinement against the SAXS/WAXS and RDC data.

(A) SAXS/WAXS and (B) SANS. The experimental data is shown in black with gray vertical bars equal to 1 s.d.; the calculated curves for the final 100 simulated annealing structures are shown in red. The residuals, given by $(I_i^{\mathit{\text{calc}}}-I_i^{\mathit{\text{obs}}})/{\mathit{\text{err}}}_i$, are plotted above each panel. The structures were determined by fitting the SAXS/WAXS curve in the range q ≤ 0.44 Å^-1, and the upper end of this range is indicated by the vertical dashed black line in panel A.

Figure 8. The structure of free EI determined from RDC and SAXS data.

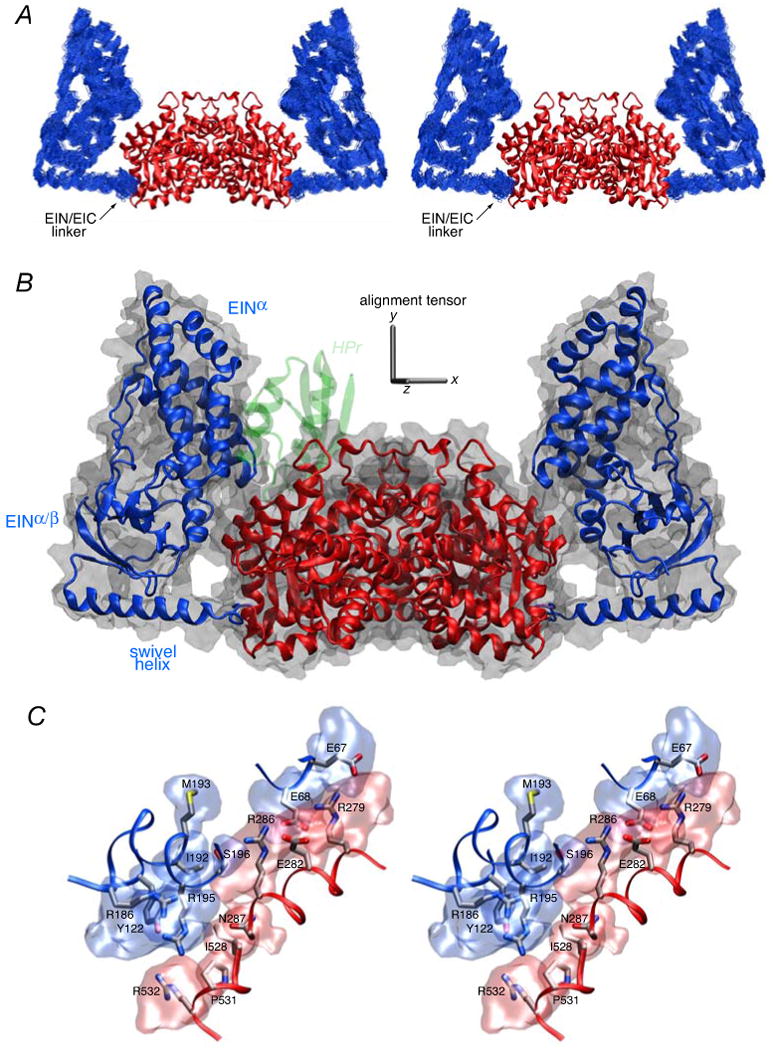
(A) Stereoview of a best-fit superposition (to the EIC dimer which remains fixed) of the 100 finals simulated annealing structures. The backbone (N, Cα, C′) atoms of the EIN domain are shown in blue, and the EIC domain is depicted as a ribbon diagram in red. (B) Ribbon diagram of the restrained regularized mean coordinates with the same color coding for the EIN and EIC domains as in panel A. The molecular surface of EI is shown in transparent gray, and the location of HPr docked to the EIN domain is depicted in transparent green to show that in this configuration there would be steric clash between HPr and the EIC domain. The axis of the alignment tensor is shown in gray; the y axis of the alignment tensor coincides with the C₂ symmetry axis of the symmetric dimer. (C) Stereoview of side chain interactions between the EIN and EIC domains in free EI. The backbones of the EIN and EIC domains (from the restrained regularized mean structure) are depicted as blue and red tubes, respectively; the side chains are color coded according to atom type (carbon, gray; nitrogen, blue; oxygen, red; sulfur, yellow), and reweighted atomic probability maps⁶⁶ (plotted at a threshold of 15% of maximum and calculated from the 100 final simulated annealing structures) for the side chains of the EIN and EIC domains at the EIN/EIC interface are shown as transparent bue and red surfaces, respectively. The interfacial side chains adopt a range of rotameric states within the conformational space delineated by the atomic probability map since there are no direct experimental restraints on these side chains; therefore the interfacial side chain positions shown within the probability map are representative rotameric states to guide the eye.

Table 3.

Structural statistics for refinement of EI and EI-HPr structures based on SAXS/WAXS and RDC data.^a

	free EI (100)	EI-HPr complex
		Cluster 1 (33)	Cluster 2 (67)
SAXS/WAXS χ2 b
q = 0.014/0.022→0.44 Å-1	0.30±0.05	0.63±0.11	0.76±0.07
q complete range predicted	2.25±0.62	0.45±0.06	0.48±0.06
q complete range fitted	1.34±0.27	0.45±0.07	0.48±0.06
SANS χ2 c	0.41±0.08	1.38±0.51	2.97±0.62
RDC R-factor (%)d	18.07±0.02	16.30±0.03	16.25±0.02
RDC DaNH (Hz)	14.5±0.1	13.73±0.05	13.83±0.08
RDC η	0.49±0.00	0.63±0.00	0.63±0.00
Coordinate precisione
EIN Cα rms displacement (Å)	1.3±0.7	2.2±1.2	2.2±1.3
rotation (deg.)	4.2±2.9	3.0±2.0	4.2±3.0
translation (Å)	3.5±2.3	3.0±1.8	3.9±2.8

^aThe final number of simulated annealing structures is given in parentheses. 100 final simulated annealing structures were calculated for free EI and the EI-HPr complex. Using a cutoff of 3 Å, the EI-HPr structures cluster into two groups with 33 structures in cluster 1 and 67 in cluster 2.

^bIn these structure calculations only the SAXS/WAXS data up to q = 0.44 Å^-1 are used. The lowest experimental q values collected for the EI and EI-HPr data are 0.014 and 0.022 Å^-1, respectively. Two χ² values are reported for the complete SAXS/WAXS curve up to q = 0.8 Å^-1 for free EI and 0.95 for the EI-HPr complex: The first set of values, denoted as ‘q complete range predicted’, are obtained by only fitting the data up to q = 0.44 Å^-1; these χ² values therefore report on how well the structures obtained using only data up to q = 0.44 Å^-1 predict the data from q = 0.44 to 0.8 Å^-1 for free EI and from q = 0.44 to 0.95 Å^-1 for the EI-HPr complex. The second set of values, denoted as ‘q complete range fitted’, are obtained when the complete SAXS/WAXS data are used in the fitting procedure (q = 0.014→0.8 Å^-1 for EI and 0.022→0.95 Å^-1 for EI-HPr).

^cThe SANS data were collected from q = 0.035→0.20 Å^-1 for ²H-EI and from q = 0.028→0.21 Å^-1 for ²H-EI/¹H-HPr.

^dThe target values for the RDC R-factors (i.e. the values obtained by SVD analysis using the NMR coordinates of EIN alone; cf Table 1) are 18.02 and 16.23%, respectively.

^eThe precision with which the position of the EIN domain or the EIN domain plus HPr is determined relative to the dimeric EIC domain (in the context of intact EI) is defined by three parameters: the average atomic Cα rms displacement, and the average rotation and translation (along the axis joining the center of masses of the two EIN, or EIN plus HPr, domains being compared) relative to the EIN domain (or EIN plus HPr) of the restrained regularized mean coordinates. All structures are first best-fit to the EIC domain (residues 262-573) whose coordinates are fixed and identical in all cases.

Independent validation is provided by the excellent agreement within experimental error between the calculated and observed SANS curves recorded on deuterated EI in 40.4% D₂O (Fig. 8B and Table 3). While similar to SAXS, SANS affords complementary information since the atomic and solvent scattering amplitudes are different in the two techniques.⁴⁵ In addition, hydrodynamic modeling³⁸ of the free EI structure returns a sedimentation coefficient of 5.88 S, which is in good agreement with the experimentally observed value of 5.68 S (Supplementary Fig. S1).

A ribbon diagram of the restrained regularized mean structure of EI is shown in Fig. 8B together with a molecular surface. The position of the EIN^α/β subdomain is rotated by ∼72, 54 and 42° from that found in the crystal structures of phosphorylated EI from E. coli,¹⁸ and free EI from Staph. aureus¹⁷ and Staph. Carnosus,¹⁶ respectively (Table 4). These rotations are accompanied by large atomic rms displacements and translations (Table 4) of the EIN domain, engendered solely by relatively small conformational changes in backbone torsion angles within the linker region (residues 255-261). In the configuration found in free EI, HPr would overlap with the EIC domain when bound to the EIN domain in the same position as that found in the EIN-HPr complex (Fig. 8B). Thus, binding of HPr to the EIN domain must be accompanied by additional movement of the EIN domain away from the EIC domain to make room for HPr.

Table 4.

Comparison of the positions of the EIN^α/β subdomain in the restrained regularized mean structures of free EI and the EI-HPr complex from E. coli with those in the crystal structures of phosphorylated EI from E. coli (2HWG)¹⁸ and free EI from Staph. aureus (2WQD)¹⁷ and Staph. carnosus (2HRO).¹⁶

	EINα/β Cα rms displacement (Å)a	rotation (deg)	translation (Å)
Free E. coli EI vs
2HWG	34.4	72.4	32.4
2WQD	25.2	53.9	20.0
2HRO	14.5	41.7	26.0
E. coli EI-HPr complex cluster 1 vs
2HWG	44.9	87.4	41.5
2WQD	37.5	71.6	26.7
2HRO	22.7	52.1	24.4
E. coli EI-HPr complex cluster 2 vs
2HWG	43.1	76.1	45.1
2WQD	31.8	54.8	24.3
2HRO	16.0	37.2	19.5

^aAll structures are first best-fitted to the dimeric EIC domain. The structures of free EI and the EI-HPr complex are the restrained regularized mean coordinates. Translation is computed along the axis joining the center of masses of the two EIN^α/β subdomains being compared. Structural alignment of the 2WQD and 2HRO structures to the E. coli EI structure was determined on a domain by domain basis using the program O.⁶⁷

Quite extensive interactions are observed between the EIN and EIC domains in free EI with a total of ∼360 Ų of accessible surface area (equally divided between EIN and EIC) buried at the interdomain interface. Although there were no direct restraints on the interfacial side chains, the interface is compatible with a number of potential salt bridge and electrostatic interactions (Fig. 8C): these include interactions between the guanidino group of Arg279 and the carboxylates of Glu67 and Glu68; between the guanidino and NεH groups of Arg286 and the carboxylate of Glu68 and the hydroxyl group of Ser196, respectively; between the side chain of Asn287 and the guanidino groups of Arg186 and Arg195; and between the guanidino group of Arg532 and the hydroxyl group of Tyr122. This modest set of interactions could potentially explain why only a single structure is required to account for the SAXS/WAXS, SANS and RDC data.

Refinement against the complete SAXS/WAXS curve for free EI

As mentioned above, the calculated WAXS curves for the free EI structures obtained using the SAXS/WAXS data up to q = 0.44 Å^-1 systematically underestimate the magnitude of the local peak centered at q = 0.59 Å^-1 in the experimental WAXS curve (Fig. 7A). The q range from 0.5 to 0.7 Å^-1 reports on shorter interatomic interactions between ∼9 and 12.5 Å. The simplest explanation for this result is that the SAXS/WAXS curve in the low q range (≤ 0.44 Å^-1) used in refinement is primarily determined by overall shape and, in this instance, fails to accurately predict some details relating to the precise configuration of the shorter (9-12.5 Å) range interdomain interactions at the interface of the EIN and EIC domains (cf. Fig. 8B). To assess this, we therefore carried out a series of simulated annealing calculations using the complete SAXS/WAXS curve for free EI from q = 0.014 to 0.80 Å^-1. The starting structures for these calculations are the final set of simulated annealing structures calculated using the SAXS/WAXS data up to q = 0.44 Å^-1, and the refinement protocol is identical to that used to generate the latter except that the SAXS/WAXS data extend to q = 0.8 Å^-1. The results are reported in Table 5 and Fig. 9.

Table 5.

Structural statistics for refinement of free EI based on the complete SAXS/WAXS data (q ≤ 0.8 Å^-1) and RDC data.^a

SAXS/WAXS χ2
q = 0.014 → 0.80 Å-1	0.56±0.09
q = 0.014 → 0.44 Å-1	0.44±0.08
SANS χ2 (q = 0.035 → 0.20 Å-1)	0.46±0.06
RDC R-factor (%)	18.08±0.03
RDC DaNH(Hz)	14.6±0.2
RDC η	0.48±0.01
Coordinate precision
EIN Cα rms displacement	1.8±0.8
rotation (deg.)	7.1±4.1
translation (Å)	5.4±3.0
EI (q → 0.8Å-1) vs EI (q → 0.44 Å-1)b
EIN Cα rms displacement (Å)	1.3
rotation (deg.)	6.3
translation (Å)	4.9

^aThe values are the averages over the top 100 simulated annealing structures (out of 120 calculated).

^bValues report the rigid body differences between the EIN domains of the restrained regularized mean coordinates with the EIC domains best-fitted

Figure 9. Comparison of the experimental SAXS/WAXS and SANS curves for free EI with the calculated curves for the simulated annealing structures obtained by refinement against the complete SAXS/WAXS data (q ≤ 0.8 Å^-1) and RDC data.

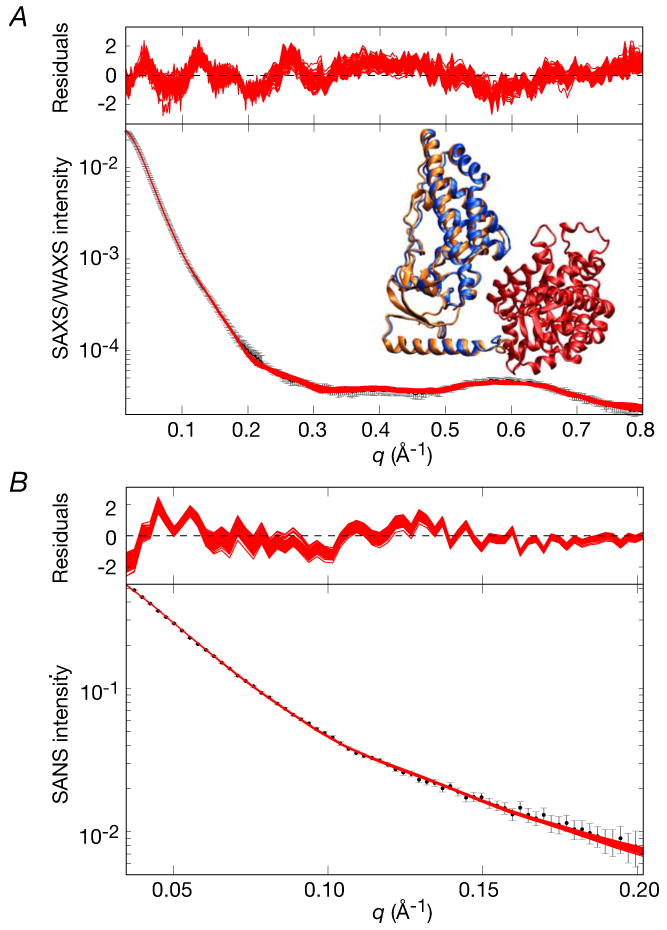
(A) SAXS/WAXS and (B) SANS. The experimental data is shown in black with gray vertical bars equal to 1 s.d.; the calculated curves for the final 100 simulated annealing structures are shown in red. The residuals, given by $(I_i^{\mathit{\text{calc}}}-I_i^{\mathit{\text{obs}}})/{\mathit{\text{err}}}_i$, are plotted above each panel. The inset in panel (A) shows a best-fit superposition (fitted to the EIC domain shown in red) of the restrained regularized mean structures obtained with q ≤ 0.8 Å^-1 and ≤ 0.44 Å^-1 with their EIN domains shown in orange and blue, respectively. Only a single subunit of EI is displayed; the view is the same as that in Figs. 8A and B.

The resulting structures exhibit excellent agreement with the complete SAXS/WAXS curve with no systematic reduction in amplitude observed at the higher q values. The amplitude of the local maximum of the WAXS curve at q = 0.59 Å^-1, which presumably arises from the short range interactions between the EIN and EIC domains, is accurately reproduced. The SAXS/WAXS χ² for the overall fit (0.56±0.09) is reduced by close to 2.5 fold relative to that of the starting structures (1.34±0.26; cf. Table 3). Although no statistically significant decrease in agreement with the low q (≤ 0.44 Å^-1) SAXS/WAXS data and SANS data (q ≤ 0.2 Å^-1) is observed, the χ² values at low q are systematically slightly worse (χ² of 0.44±0.08 Å^-1 versus 0.30±0.05 for SAXS/WAXS, and 0.46±0.06 versus 0.41±0.08 for SANS). This is as expected given that there must be a slight trade-off in the agreement with the low q SAXS data to better fit the higher q WAXS data. An important result from these calculations is that the structures obtained with q ≤ 0.8 Å^-1 overlap and occupy the same configurational space as those obtained with q ≤ 0.44 Å^-1. Thus, the differences between the two restrained regularized mean coordinates are subtle and significantly smaller than the spread of the two sets of simulated annealing structures. These differences are essentially well within the uncertainties of the current coordinates. Indeed, the Cα rms displacement of the EIN domains between the two restrained regularized mean coordinates is only 1.3 Å with a difference in orientation (relative to the EIC domain) of only 6° (see inset in Fig. 9). Also noteworthy is that the coordinate precision of the EIN domain is slightly smaller (i.e. larger spread) for the structures calculated with q ≤ 0.8 Å^-1 compared to those calculated with q ≤ 0.44 Å^-1 (cf. compare coordinate precision values reported in Tables 3 and 5). This can be attributed to the fact that inclusion of the WAXS data at higher q in the refinement calculations necessarily reduces the weight on the SAXS data at lower q, and hence the restraints imposed by the SAXS portion of the data on the overall shape are slightly weakened.

Joint RDC and SAXS determination of the structure of the EI-HPr complex

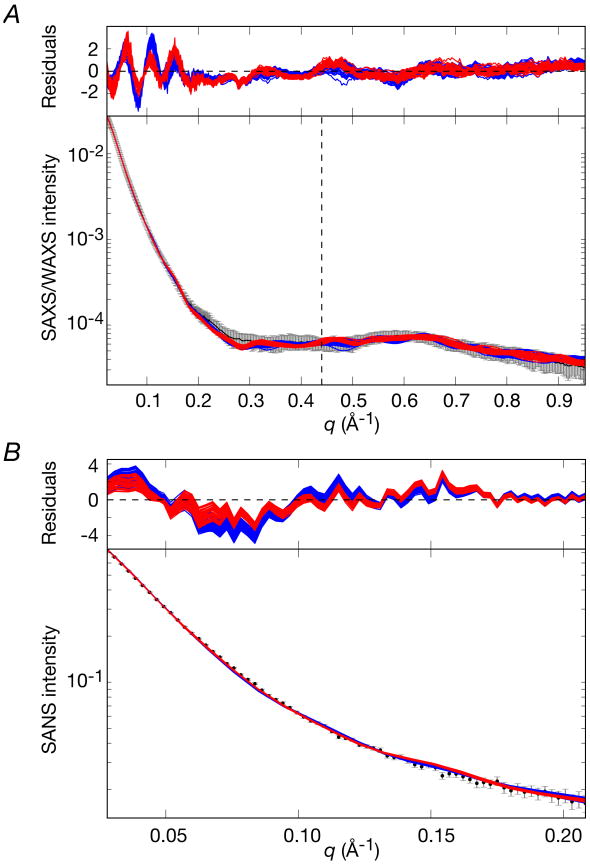
The structure of the EI-HPr complex was determined using conjoined rigid body/torsion angle/Cartesian simulated annealing as described in the Theory and Computation section. The initial coordinates for the EI-HPr calculations were generated by taking the 120 simulated annealing structures calculated for free EI and adding two molecules of HPr, one to each EI subunit, in exactly the same position as that found in the NMR structure of the EIN-HPr complex (3EZA).¹³ The two EIN-HPr moieties were then treated as rigid bodies that can move relative to the fixed EIC dimer through backbone conformational changes in the linker region (residues 255-261). A comparison of the calculated and observed SAXS/WAXS and SANS curves are displayed in Figs. 10A and B, respectively, a superposition (best-fitted to the EIC domain) of the final simulated annealing EI-HPr structures is shown in Fig. 11A, and a summary of the agreement with the SAXS/WAXS, SANS and RDC data is provided in Table 3.

Figure 10. Comparison of experimental SAXS/WAXS and SANS curves for the EI-HPr complex with the calculated curves for the simulated annealing structures obtained by refinement against the SAXS and RDC data.

(A) SAXS/WAXS and (B) Contrast-matched SANS. The SANS data were recorded on a ²H-EI/¹H-HPr sample in matched 40.4% D₂O so that the SANS curve depends only on the coordinates of the EI component of the complex. The experimental data is shown in black with grey vertical bars equal to 1 s.d.; the calculated curves for the final 100 simulated annealing structures are shown in red for cluster 1(33 structures) and blue for cluster 2 (67 structures). The residuals, given by $(I_i^{\mathit{\text{calc}}}-I_i^{\mathit{\text{obs}}})/{\mathit{\text{err}}}_i$, are plotted above each panel. The structures were determined by fitting the SAXS curve in the range q ≤ 0.44 Å^-1, and the upper end of this range is indicated by the vertical dashed black line in panel A.

Figure 11. The structure of the EI-HPr complex determined from RDC and SAXS data.

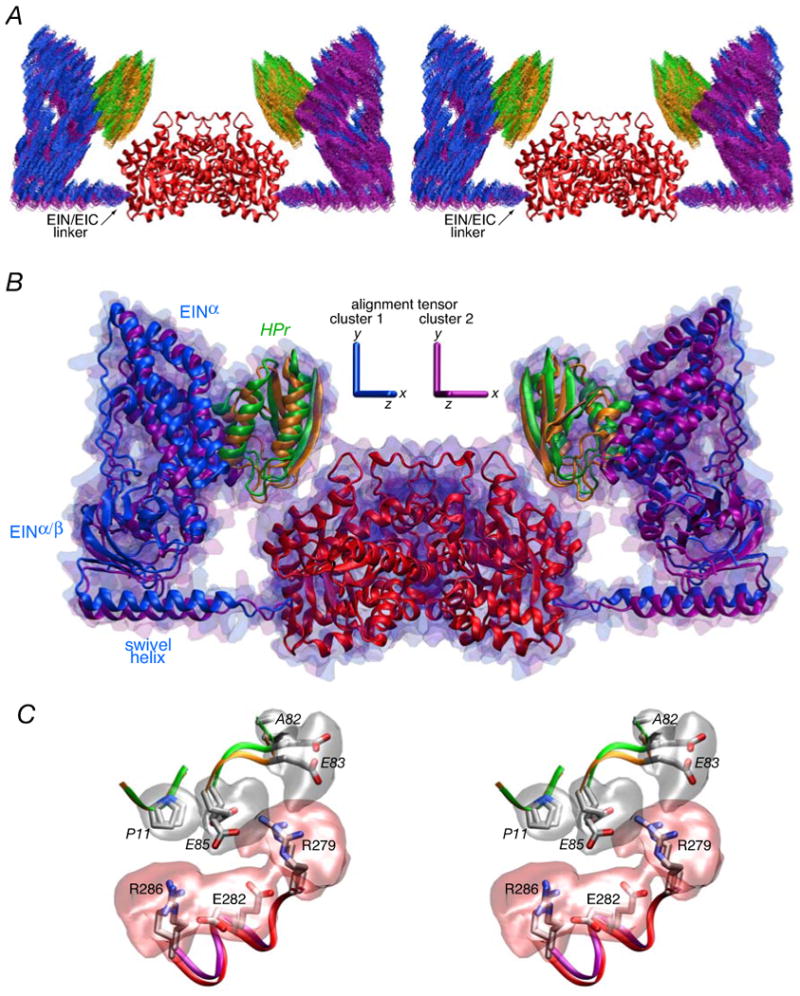
(A) Stereoview of a best-fit superposition (to the EIC domain dimer which remains fixed) of the final 100 simulated annealing structures. The backbone (N, Cα, C′) atoms of the EIN domain and HPr are shown in blue and green, respectively for cluster 1 (33 structures) and in purple and orange, respectively, for cluster 2 (67 structures). The EIC domain dimer is shown as a red ribbon. (B) Ribbon diagram of the restrained regularized mean coordinates for clusters 1 and 2 superimposed on the EIC domain. The color coding of HPr and the EIN and EIC domains is the same as in panel A. The molecular surface of the EI-HPr complex is shown in transparent blue for cluster 1 and transparent purple for cluster 2. (C) Stereoview of side chain interactions between HPr and the EIC domain in the EI-HPr complex. The backbones of HPr and the EIC domain are depicted as green and red tubes, respectively, for cluster 1, and orange and purple tubes, for cluster 2. The backbone atoms of residues 11-13 and 82-85 of HPr and residues 279-286 of EIC for the restrained regularized mean coordinates of the two clusters are best-fitted to each other. The side chains from the two clusters are color coded according to atom type (carbon, gray; nitrogen, blue; oxygen, red; sulfur, yellow), and reweighted atomic probability maps⁶⁶ (plotted at a threshold of 15% of maximum and calculated from the 100 final simulated annealing structures (clusters 1 and 2 combined) for the side chains of HPr and EIC at the HPr/EIC interface are shown as transparent gray and red surfaces, respectively. Residues of HPr are labeled in italics.

Using a tolerance of 3 Å, two clusters of solutions are found (Figs. 11A and B) using the findClusters program⁵⁷ distributed with Xplor-NIH. Cluster 1 has 33 structures while cluster 2 has 67. Both solutions satisfy the RDC and SAXS/WAXS data (Table 3 and Fig. 10A). Agreement with the SAXS/WAXS data included in the calculations (q up to 0.44 Å^-1) is within experimental error with a χ² of 0.63±0.11 and 0.76±0.07 for clusters 1 and 2, respectively, and the overall RDC R-factor (16.3%) is essentially the same as the target value obtained by SVD analysis of a single EIN domain. For both clusters, the position of EIN/HPr relative to the dimeric EIC domain and the C₂ symmetry axis is determined with good precision with values for the Cα atomic rms displacement and rotation about the respective regularized mean coordinate positions of the EIN/HPr moiety of ∼2 Å and 3-4°, respectively. In addition, the WAXS curve at higher q values (0.44 < q ≤ 0.9 Å^-1) that was not included in the calculations, is also reproduced within experimental error (Fig. 12A). Thus, the χ² for the complete SAXS/WAXS curve, using the best-fit parameters obtained from the lower q portion of the curve (up to q = 0.44 Å^-1) used in the structure calculations, is less than 0.5 for both clusters (Table 3). However, the orientations of the EIN domains between the restrained regularized mean structures for the two clusters differ by 18° (Fig. 12A). While this difference in orientation is still relatively small, it translates into Cα rms displacements between the EIN domains and between HPr of the two clusters of ∼10 and ∼3 Å, respectively, when the structures are best-fit to the dimer EIC domain (Table 6, Fig. 11B and 12A). In terms of global structure, however, these differences are small with an overall Cα rms difference for the complete dimer of 3 Å.

Fig. 12. Comparison of the restrained regularized mean coordinates of the cluster 1 and cluster 2 solutions for the EI-HPr complex to each other and to the restrained regularized mean coordinates of free EI.

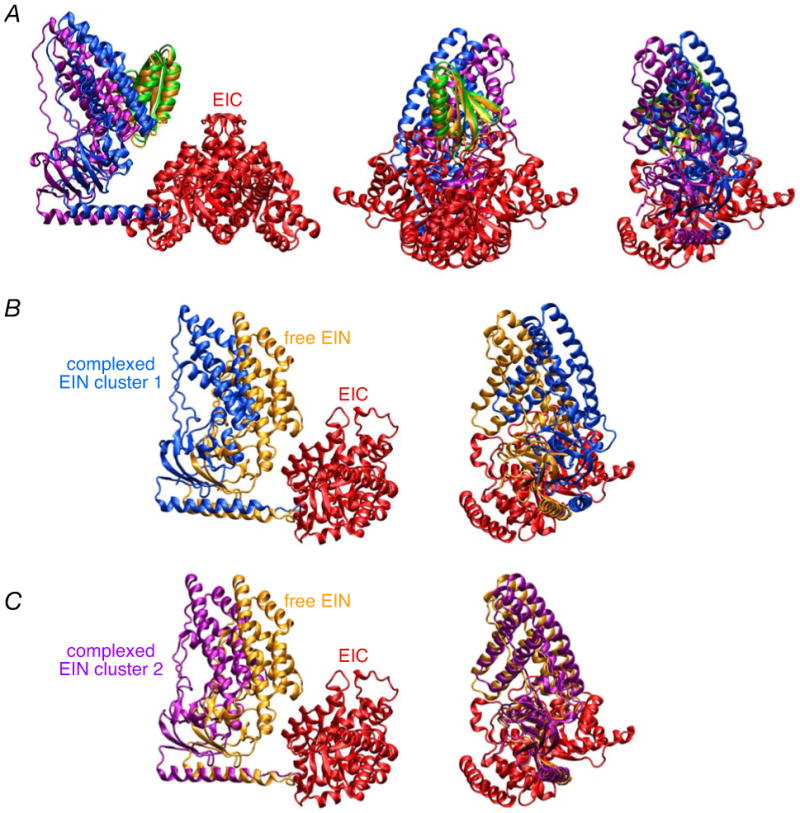
(A) Ribbon diagrams showing (A) three views of a comparison of cluster 1 and cluster 2, and two views of a comparison of (B) cluster 1 versus free EI and (C) cluster 2 versus free EI. In all cases, the EIC domain dimer is best-fitted. The color coding is as follows. EIN domain: cluster 1, blue; cluster 2, purple; free, yellow. HPr: cluster 1, green; cluster 2, orange. EIC domain, red. In the left and middle panels of A, the EIC dimer is shown; in all other panels, only one subunit of the EIC domain is displayed. The two views shown in (B) and (C) are approximately orthogonal to each other.

Table 6.

Comparison of the position of the EIN domain in the restrained regularized mean structures of free EI and the EI-HPr complex^a

	EIN Cα rms displacement (Å)	rotation (deg.)	translation (Å)
EI vs EI-HPr (cluster 1)	15.4	18.2	9.8
EI vs EI-HPr (cluster 2)	12.2	6.9	13.7
EI-HPr (cluster 1) vs (cluster 2)b	10.0 (8.8)	17.8 (17.8)	8.7 (8.7)

^aAll structures are best-fitted to the dimeric EIC domain (residues 262-573 of both subunits) whose coordinates are fixed and identical in all cases, and hence the various parameters indicate the differences in the position of the EIN domain relative to the fixed EIC domain. Translation is computed along the axis joining the center of masses of the EIN domains being compared.

^bThe values in parentheses are obtained when HPr is included in the comparison between the restrained regularized mean coordinates of cluster 1 and cluster 2.

In contrast to SAXS/WAXS which contains contributions from both EI and HPr in the EI-HPr complex, contrast-matched SANS data recorded on ²H-EI/¹H-HPr in 40.4% D₂O are only dependent on the deuterated EI component of the complex. Thus, the SANS data provide useful validation of the position of the EIN domain relative to the EIC domain in the HPr bound state. The cluster 1 structures exhibit significantly better overall agreement with the SANS data than the cluster 2 structures with χ² values of 1.4±0.5 and 3.0±0.6, respectively (Table 3). This is manifested by systematically better agreement of the cluster 1 structures with the experimental SANS curve up to q = 0.13 Å^-1 (Fig. 9B). However, between q = 0.13 and 0.17 Å^-1, the cluster 2 structures exhibit slightly better agreement with the experimental SANS data (Fig. 9B).

Ribbon diagrams of the EI-HPr complex displaying a superposition of the restrained regularized mean structures derived from two clusters are shown in Figs. 11A and 12A, and a comparison of the cluster 1 and 2 structures of the EI-HPr complex with that of free EI is provided in Table 6 and Figs. 12B and C. As expected the EIN domain moves slightly away from the EIC dimer to accommodate HPr. The key difference between the cluster 1 and 2 structures is that the transition from free to complexed EI involves a much larger rotation of the EIN domain for the cluster 1 structures (∼18°) than for the cluster 2 structures (∼7°). Thus, in the case of the cluster 2 structures, HPr is largely accommodated by a translation of the EIN domain away from the EIC domain, whereas for the cluster 1 structures, both rotation and translation of the EIN domain are involved. When compared to the crystal structures of phosphorylated EI from E. coli,¹⁸ and free EI from Staph. aureus¹⁷ and Staph. Carnosus,¹⁶ the position of the EIN domain is rotated by ∼75°, ∼55° and ∼40°, respectively, for the cluster 2 structures, comparable to the rotations seen for free EI (Table 4). For the cluster 1 structures, the rotations are 10-15° larger, ∼90°, 70° and ∼50°, respectively (Table 4).

Since HPr is sandwiched between the EIN and EIC domains, and therefore located closer to the C₂ symmetry axis than the EIN domain, the position of HPr is actually very similar in the two clusters (Fig. 11B and C and Fig. 12A), and hence the interactions between residues of EIC and HPr are maintained in both clusters (Fig. 12C). The interdomain interactions between EIN and EIC observed in free EI are replaced by a much more limited set of interactions between HPr and EIC which bury ∼110 A² of accessible surface area (equally divided between HPr and EIC). This corresponds to an approximately three-fold reduction in the buried interdomain accessible surface area relative to free EI. As in the case of free EI, the HPr/EIC interface is compatible with several salt bridge/electrostatic interactions (Fig. 12C). The guanidino group of Arg279 of EIC interacts with the carboxylates of two glutamate residues on HPr, Glu83 and Glu85 (HPr residues denoted in italics) in a configuration that is very similar to that between Arg 279 of EIC and Glu67 and Glu68 of EIN in free EI (cf. Fig. 8C). Additionally, Arg286 of EIC interacts with Glu85 of HPr in a manner that is similar to the interaction of Arg286 with Glu68 of EIN in free EI. As in free EI, the carboxylate of Glu282 may interact with the guanidino groups of Arg279 and/or Arg286, thereby stabilizing their orientations.

In contrast to the case of free EI, where refinement against the SAXS/WAXS data up to q ≤ 0.44 Å^-1 resulted in a slight underestimation of the magnitude of the calculated WAXS curve at higher q values (cf. Fig. 8A) that could only be resolved by refinement against the complete SAXS/WAXS data up to q ≤ 0.8 Å^-1 (cf. Fig. 9A), the WAXS curve from q = 0.44 to 0.95 Å^-1 for EI-HPr is well reproduced within experimental error with no systematic deviations between observed and calculated curves (Fig. 10A). As a result, refinement against the complete SAXS/WAXS curve for EI-HPR yields no significant improvement in agreement between experimental and calculated scattering curves (overall SAXS χ² = 0.44±0.06). The observation that the feature of the WAXS curve with a maximum at q ∼ 0.59 Å^-1 is reduced in magnitude for EI-HPr compared to free EI may possibly be due to attenuation arising from greater conformational heterogeneity in EI-HPr. This would be consistent with the much smaller interdomain contact surface between the EIC domain and HPr in the EI-HPr complex as compared to that between the EIC and EIN domains in free EI. Examination of the agreement with the SANS data (not included in the calculations), however, reveals a bimodal distribution with χ² = 0.97±0.29 (range 0.53 to 1.56) and 2.89±0.75 (range 0.98 to 4.79). These correspond to the same two clusters that were obtained when only the SAXS/WAXS data up to q ≤ 0.44 Å^-1 were used in refinement. The coordinate precision of the two clusters is slightly reduced when the complete SAXS/WAXS curve is employed with the result that there is some degree of overlap between the ensemble of structures representing the two clusters. The difference, however, in orientations of the EIN domains between the restrained regularized mean structures derived from the two clusters still differs by ∼20°. In addition, the difference in orientations of the EIN domains in the corresponding restrained regularized mean coordinates for each cluster is very similar for the calculations with the complete (q ≤ 0.95 Å^-1) and truncated (q ≤ 0.44 Å^-1) SAXS/WAXS curves, differing by rotations of less than 4° and Cα rms displacements for the EIN domain of <3 Å, which is within the accuracy of the current structure determination.

Further calculations were also carried out in which the SANS data were included in the refinement in addition to the SAXS/WAXS data up to q ≤ 0.44 Å^-1 and the RDC data. All resulting structures with a SANS χ² of ≤ 1 lie in the conformational space sampled by the cluster 1 structures (with a Cα rms displacement and rotation for the EIN domains between the restrained regularized mean structures of 1.3 Å and 7°, respectively). Finally we note that the use of an ensemble representation (N_e > 1) is not justified for EI-HPr since all the data are already well accounted for using a single structure representation and increasing the ensemble size above 1 does not result in any improvement in agreement with the experimental data.

Transition between the phosphorylated EI structure and the free EI and EI-HPr structures

Fig. 13 provides a molecular surface representation of the structures of free EI (I), the EI-HPr complex (V) and the oxalate-trapped phosphorylated EI intermediate (2HWG¹⁶) (II). The transition from the B state of the EIN domain in the phosphorylated EI intermediate to the A state of the EIN domain observed in free EI and the EI-HPr complex must involve two successive (or concerted) conformational transitions. In the structure of the phosphorylated EI intermediate (II), reorientation of the EIN^α subdomain relative to the EIN^α/β subdomain to generate the A state would result in steric clash between the EIN^α subdomain and EIC in the absence of concomitant reorientation of the EIN^α/β subdomain. Therefore, hinge body rotation about the EIN/EIC linker (residues 255-261) must occur first (or concomitantly) to reorient the EIN^α/β subdomain relative to the EIC domain. The resulting intermediate conformation (IV) would have the EIN^α/β subdomain oriented relative to EIC as in free EI and the EI-HPr complex with a B state conformation for the EIN domain, i.e. with the EIN^α subdomain oriented to the EIN^α/β subdomain as in the phosphorylated EI intermediate (Fig. 13). Subsequent reorientation of the EIN^α subdomain relative to the EIN^α/β subdomain about a hinge (residues 22-24 and 143-146) within the linker connecting the two EIN subdomains generates the A state conformation of the EIN domain found in free EI (I) and the EI-HPr complex (V). Since the HPr binding site on the EIN^α subdomain is fully accessible in the phosphorylated EI intermediate binding of HPr to the phosphorylated intermediate can occur (III) and induce, together with the dissociation of the product pyruvate, the concerted conformational transition to the EI-HPr configuration without going through the intermediary of free EI. With estimated intracellular concentrations of 5 and 60 μM for EI and HPr, respectively,⁶⁸ and a K_diss of ∼7 μM at 37°C (Fig. 3B), the occupancy of the HPr binding sites on EI can reach ∼90% in vivo. In the absence of HPr, the phosphorylated EI intermediate (II), upon dissociation of the product pyruvate, would relax to the free EI conformation (I) via an intermediate IV′, analogous to IV but without HPr bound.

Figure 13. Postulated catalytic cycle of EI.

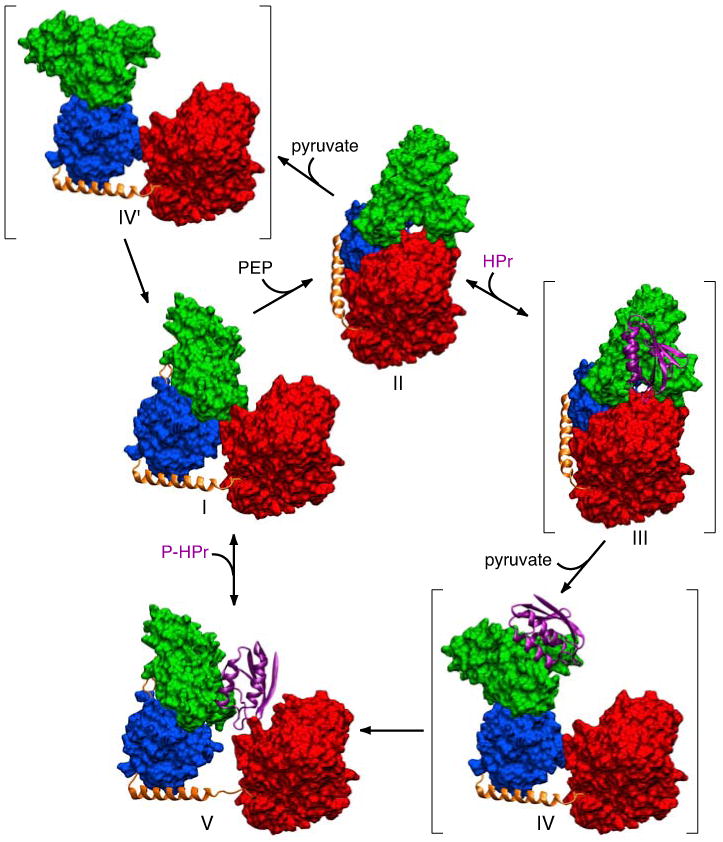
Phosphoenolpyruvate (PEP) binds to the EIC domain of free EI (I, this work) leading to a conformational change that results in the formation of the phosphorylated intermediate observed crystallographically (II¹⁶). The EIN domain is in the A state conformation in structure I and the B state conformation in structure II. The HPr binding surface on the EIN^α subdomain of II is fully accessible permitting binding of HPr (structure III). The binding of HPr, together with the dissociation of the product pyruvate, induces reorientation of the EIN^α/β subdomain through a conformational change in the EIN/EIClinker (residues 255-261) resulting in the formation of a second intermediate (IV) in which the EIN domain remains in the B state conformation but the orientation of the EIN^α/β subdomain relative to EIC is the same as that found in free EI or the EI-HPr complex. Since there are very limited contacts between the EIN^α and EIN^α/β subdomains in the B state conformation, the EIN domain in structure IV rapidly relaxes to the A state through concerted conformational changes in residues 22-24 and 143-146 located in the linker regions joining the EIN^α and EIN^α/β subdomains to generate the structure of the EI-HPr complex observed experimentally (V, this work). Subsequent dissociation of HPr results in minor inward displacement of the EIN domain to form the structure of free EI (I) in which the position of the EIN domain is stabilized by a limited set of contacts with the EIC domain. In the absence of HPr, the phosphorylated intermediate (II), upon dissociation of the product pyruvate, can relax to the free EI conformation (I) via an intermediate IV′, analogous to IV but without HPr bound. The three postulated structures, III, IV and IV′, are shown in parentheses. Only a single subunit of EI is displayed. The EIC domain and the EIN^α and EIN^α/β subdomains are displayed as red, green and blue molecular surfaces, respectively; the linker helix and linker regions (connecting EIN^α to EIN^α/β, and EIN^α/β to EIC) are shown as orange ribbons; HPr is shown as a purple ribbon.

As noted above, the EIN domain in free EI must move slightly away from the EIC dimer to permit binding of HPr. This implies that the orientation of EIN relative to EIC found in the EI-HPr complex can be sampled infrequently in free EI to permit binding of HPr to occur. Although the experimental RDC and SAXS/WAXS data for free EI can be accounted for by a single orientation of the EIN domain relative to the dimeric EIC domain, the interface between the EIN and EIC domains in free EI is sufficiently modest to readily permit such transient rigid body conformational transitions to occur.

Phosphorylation of the active site histidine of EI, located in the EIN^α/β subdomain (His189), cannot account on its own for the B state conformation of the EIN domain observed in the phosphorylated EI intermediate since phosphorylation of isolated EIN does not perturb the orientation of the EIN^α and EIN^α/β subdomains.¹⁴ The interactions stabilizing the B state conformation of the EIN domain observed in the crystal structure of the phosphorylated EI intermediate must therefore arise from bridging interactions between the EIC domain and the EIN^α/β subdomain mediated by the substrate phosphoenolpyruvate and trapped by the inhibitor oxalate that displaces phosphoenolpyruvate.

Concluding remarks

Using a combination of RDCs and SAXS/WAXS, together with prior structural data on the isolated EIN domain and its complex with HPr in solution,^12,13 and the C₂ symmetric EIC domain dimer in the context of a crystal structure of a phosphorylated intermediate state of intact EI,¹⁶ we have succeeded in determining the structures of free EI and the EI-HPr complex in solution. These structures shed light on the large-scale interdomain conformational transitions involved in the catalytic cycle whereby EI is first autophosphorylated by phosphoenolpyruvate and subsequently transfers a phosphoryl group to HPr.

The experimental RDC, SAXS/WAXS and SANS data for both free EI and the EI-HPr complex can be accounted for by a single structure representation. Representing the structures by an ensemble of states (up to N_e = 8) does not result in any improvement in agreement with the scattering or RDC data and therefore cannot be justified using Occam's Razor. These observations, however, do not imply that the structures of EIN and EI-HPr are rigid and do not exclude the presence of some interdomain motion of the EIN domain or the EIN/HPr moiety relative to the dimeric EIC domain: rather, we simply cannot quantify the extent or magnitude of any interdomain motion on the basis of the RDC and scattering data. That interdomain motion is present is evidenced by the observation that in the ¹H-¹⁵N TROSY spectrum (Fig. 4) the intensities of resolved cross-peaks arising from the EIN domain are on average a factor of 1.3-1.5 times larger than those from the EIC domain (although any detailed quantification is difficult since the shape of the molecule is highly anisotropic). Rapid interdomain motion of the EIN domain relative to the dimeric EIC domain on a time scale shorter than the overall rotational correlation time with an amplitude of ≤30° will have minimal impact on the RDCs,^21,69 but will result in substantial line narrowing for the EIN domain as observed experimentally (since the RDCs scale with the order parameter whereas linewidths scale with the square of the order parameter). Likewise SAXS/WAXS and SANS are insensitive to motions that minimally perturb the pairwise distance distribution function (cf. the almost identical SAXS/WAXS and SANS curves for the cluster 1 and 2 solutions obtained for EI-HPr seen in Fig. 10). While the experimental observables are linearly averaged in both RDC and scattering experiments, the two methods are mutually complementary since they are sensitive to different types of motion. Thus, the RDCs are affected by motion of the backbone amide bond vectors relative to the principal axes of the alignment tensor, while the scattering experiments are primarily sensitive to the overall shape and size of the molecule. Since the RDC and scattering data are mutually consistent with one another, we expect the calculated structures to be representative of the average structure in solution.⁷⁰ Probing interdomain motions as well as the existence of lowly-populated states will require the use of additional experiments, including for example, methyl relaxation dispersion,^71,72 paramagnetic relaxation enhancement,^73,74 paramagnetic pseudo-contact shifts,^75-77 and, potentially double electron-electron resonance coupled with spin labeling.⁷⁸

The improvements presented in calculating and refining against SAXS/WAXS curves now take into account complex molecular shapes in the description of the solvent layer, resulting in a better representation of the SAXS/WAXS data. The general hybrid strategy presented here for solving the structures of EI and EI-HPr is one that can be readily transferred to other structural problems involving domain reorientation in large multidomain proteins and complexes.