The Energetics of Transmembrane Helix Insertion into a Lipid Bilayer

Abstract

Free energy profiles for insertion of a hydrophobic transmembrane protein α-helix (M2 from CFTR) into a lipid bilayer have been calculated using coarse-grained molecular dynamics simulations and umbrella sampling to yield potentials of mean force along a reaction path corresponding to translation of a helix across a lipid bilayer. The calculated free energy of insertion is smaller when a bilayer with a thinner hydrophobic region is used. The free energies of insertion from the potentials of mean force are compared with those derived from a number of hydrophobicity scales and with those derived from translocon-mediated insertion. This comparison supports recent models of translocon-mediated insertion and in particular suggests that: 1), helices in an about-to-be-inserted state may be located in a hydrophobic region somewhat thinner than the core of a lipid bilayer; and/or 2), helices in a not-to-be-inserted state may experience an environment more akin (e.g., in polarity/hydrophobicity) to the bilayer/water interface than to bulk water.

Introduction

The majority of integral membrane proteins have an α-helical transmembrane (TM) region (1). The process of insertion of TM helices into a membrane is a subject of some current interest (2). In vivo helix insertion is mediated by the translocon complex, and it is thought that it is primarily driven by hydrophobic forces, although details of the mechanism remain uncertain. Thus, the mechanism of insertion, and the point of selection in the pathway encountered by the nascent peptide, remains an area of active investigation (3–5).

Measures of the free energy of insertion of amino-acid residues into a bilayer have been achieved using a number of methods, including, e.g., partition into a model membrane environment (6); via translocon-mediated insertion (7); and by a range of computational methods (e.g., (8,9)). Although the correlation between these results is generally good, the magnitude of free energy of partitioning of residues is significantly greater for the simulation-based methods than from analysis of translocon-mediated insertion (see discussion in, e.g., (10) and in (9,11)). Furthermore, there is some dependence of the range of the translocon-based scale on source (e.g., mammal versus yeast) of the translocon machinery (12). However, the hydrophobicity scale developed from the translocon-mediated data is an accurate membrane predictor of transmembrane protein topology (13). Possible explanations for the difference have focused on the lipid composition of the endoplasmic reticulum membrane (14) and on the high protein concentration in this membrane (9). Attention should also be paid to possible differences in protonation states from those generally used in simulations (8,11,15). Simulation estimates of the free energy profiles of simple model helices as a function of insertion into a lipid bilayer have also yielded free energies of insertion (16,17) that are significantly larger than the translocon-based hydrophobicity scale would predict (13).

To further investigate these differences, we have used coarse-grained molecular dynamics (CG-MD) simulations (see, e.g., (16,18–31)) to calculate the free energy profile for transfer of a complex TM helix which has been studied using the translocon-mediated method (7). The sequence of this helix is that of the second transmembrane helix of CFTR (specifically sequence TM2(-1)^CFTR and surrounding residues in (13)). The likelihood of segments adopting a transmembrane helix conformation (insertion efficiencies) of 19-residue windows from this sequence have been estimated. These may be converted into apparent free energies, which in turn may be compared indirectly with estimates of the potential of mean force (PMF) of helix insertion. Consistent with previous studies of PMFs for insertion of individual side chains (9,10), the magnitude of the helix insertion free energies from the PMF calculations is much greater than that expected from translocon-mediated insertion. Furthermore, we show that the magnitudes of the energies of insertion of helices into the hydrophobic core are lower when calculated for a bilayer with a thinner hydrophobic core, consistent with experimental and simulation evidence for model peptide sequences (4). This suggests that a hydrophobic region in the translocon thinner than the lipid bilayer core may play a role in partitioning helices into the endoplasmic reticulum membrane.

Methods

CG-MD simulations

CG-MD simulations were performed using GROMACS 3.3 (www.gromacs.org) (32) The CG force field used was a local modification of the MARTINI force field (16,25), based on a 4:1 mapping of nonhydrogen atoms to CG particles. As described in more detail in, e.g., Bond et al. (16), one CG particle is used to represent a peptide bond, and between 0 (glycine) and 2 particles to represent the side chain. The parameters for lipids and water were based on the lipid CG force field from Marrink et al. (22). Parameters for amino-acid side chains were calibrated relative to data on cyclohexane-water partitioning (16) and the model was evaluated against experimental data on membrane protein and peptide insertion into lipid bilayers (29–31). CG backbone particles in the helices were restrained to mimic secondary structure stabilizing hydrogen bonds, with a harmonic distance restraint of equilibrium length 0.6 nm and a force constant of 1000 kJ mol⁻¹ nm⁻². This restraint was absent for residues otherwise hydrogen-bonded to a proline, in order to enable the greater helix flexibility observed N-terminal to this residue (33).

Lennard-Jones interactions were shifted to zero between 9 Å and 12 Å, and electrostatic interactions were shifted to zero between 0 Å to 12 Å, with a relative dielectric constant of 20. All simulations were performed at constant temperature, pressure, and number of particles. The temperature of the protein, lipid, and solvent were each coupled separately using the Berendsen algorithm (34) at 323 K, with τ_T = 1 ps. The system pressure was semiisotropically coupled in the x/y and z directions using the Berendsen algorithm at 1 bar with τ_P = 1 ps and a compressibility of 5 × 10⁻⁶ bar⁻¹. The time step for integration was 40 fs. Coordinates were saved for subsequent analysis every 400 ps. VMD (35) was used for visualization.

PMF calculations

PMFs were calculated using helix lengths of 19, 29, and 39 residues (Fig. 1), all from a 39-residue sequence surrounding M2 of CFTR (Table 1). The 19-residue sequence was selected as the helix which best inserted experimentally (corresponding to TM2(-1)^CFTR in (13)). CG models of phosphatidyl choline bilayers had either two hydrophobic tail particles per fatty acid (CG2-PC, i.e., a CG model of DHPC), with a hydrophobic core of ∼20 Å (and a phosphate-to-phosphate width of 27 Å), or four hydrophobic tail particles per fatty acid (CG4-PC, i.e., a CG model of DPPC), with a hydrophobic core of ∼30 Å (phosphate-to-phosphate width 43 Å). We note that the phosphate-phosphate distance for a protein-depleted rat hepatocyte endoplasmic reticulum membranes is ∼39 Å and for an apical plasma membrane is ∼42 Å (36). Thus, the CG4-PC model membrane is of comparable thickness to a plasma membrane and is ∼4 Å thicker than an endoplasmic reticulum membrane.

Figure 1.

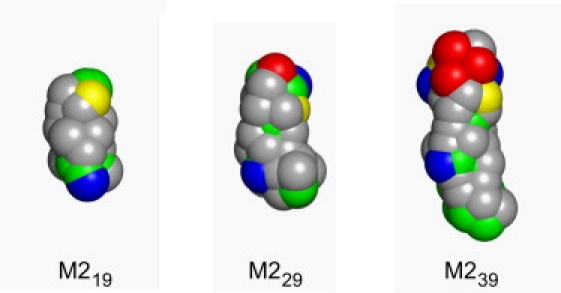
Comparison of the CG models of M2₁₉, M2₂₉, and M2₃₉. The sphere radii correspond to those used in the CG interaction potential. The N-termini are at the top. The color scheme corresponds to the particle types used in the CG model (gray, C (hydrophobic apolar), green, N (mixed polar/apolar), yellow, P (polar), red, Q− (charged, anionic), and blue, Q+ (charged, cationic)).

Table 1.

Sequences of α-helices used in the simulations

Helix	Sequence
M219	SIAIYLGIGLCLLFIVRTL
M229	ERSIAIYLGIGLCLLFIVRTLLLHPAIFG
M239	PDNKEERSIAIYLGIGLCLLFIVRTLLLHPAIFGLHHIG

PMFs were derived from umbrella sampling (CG-MD) simulations. Starting configurations were obtained by positioning the center of mass of the helix a certain distance away from the center of mass of a preformed bilayer, measured along a reaction coordinate (z) perpendicular to the bilayer. Waters were subsequently added to the system, and counterions where necessary to preserve the electroneutrality of the system. The center of mass of the helix was harmonically restrained along z for the duration of the simulations with a force constant of 1000 kJ mol⁻¹ nm⁻², leaving the helix free to rotate about its center of mass (Fig. 1). The reaction coordinate ranged from z = +75 Å to −75 Å in 1 Å increments, and each window was simulated for 40–80 ns depending on the size of the helix. PMFs were derived using WHAM (37).

Although the helix is asymmetric, the bilayer is symmetric. It is therefore reasonable to calculate a symmetrical PMF profile (which also enables comparison with other transmembrane PMF studies, e.g., (8,14,17,25)). The two halves of the profiles are therefore averaged, providing an unambiguous point from which to measure ΔG_INS (the difference between the interfacial and transmembrane states, see below). Error bars represent the difference between the halves of the profile representing the helix above and below the bilayer, and the differences between the halves of the profile as calculated over the first and second halves of equilibrated simulation time.

Results and Discussion

Helix/bilayer PMFs

The initial and final (80 ns) configurations of the M2₃₉ helix are shown in Fig. 2. This clearly shows reorientation of helix along the reaction pathway. Thus, in the aqueous phase (z = 75 to 30 Å), it is able to tumble freely. As it approaches the bilayer (z = 30 to 20 Å) it adopts an interfacial (IF) orientation, while once spanning the bilayer (z = 20 to 0 Å) it adopts a tilted, transmembrane orientation. It can also be seen that the helix is able to kink in the region of the proline residue present in M2₂₉ and M2₃₉ toward the C-terminus of the peptide.

Figure 2.

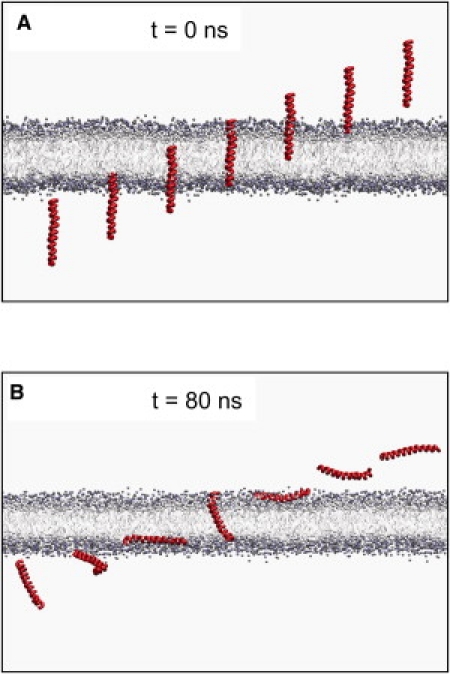
The M2₃₉ helix in its initial configuration at various points (z = +50 to −50 Å) along the z axis perpendicular to the bilayer (A), and the same helix after 80 ns of simulation (B).

To test dependence on starting conditions, a window for which M2₃₉ adopted an IF orientation was selected, and the simulations were repeated with the helix axis starting at 45°, 90°, and 180° to z axis (i.e., the reaction coordinate). In each case, the helix adopted the same IF orientation as in the original window which started with the helix axis parallel to z.

The helix tilt angle (i.e., the axis relative to z) as a function of window for the M2₁₉ CG4-PC simulation is shown in Fig. 3 A. From this it is evident that the helix tumbles within the water region on either side of the bilayer (as evidenced by the large error bars), adopts an orientation perpendicular to the bilayer-normal when at the water/bilayer interface, and an orientation parallel to the bilayer normal when the window center is within the bilayer core. This suggests that the helix was able to sample a range of possible orientations within the 80-ns duration of each window, rotating about its (restrained) center of mass. This is supported by analysis of the helix tilt angle as a function of time during selected simulations (Fig. 3 B). This shows the helix tumbles freely on a ∼5-ns timescale when in water, and adopts its preferred orientation relative to the bilayer (interfacial or transmembrane) within 5–10 ns when interacting with the lipid bilayer.

Figure 3.

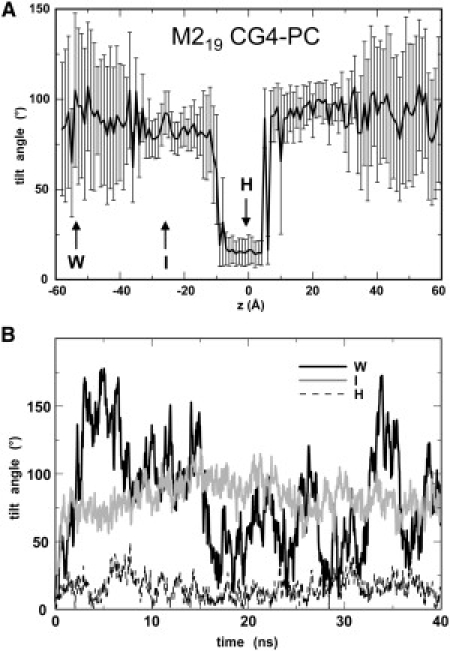
(A) Average tilt angle (relative to the bilayer perpendicular) for each windows of the M2₁₉ CG4-PC PMF simulations, shown as a function of the restrained z value for each window. Error bars correspond to standard deviations for each window. (B) Helix tilt angle versus time for three windows (as indicated by the arrows in panel A), namely in water (W), at the water/bilayer interface (I), and in the hydrophobic core (H) of the bilayer.

Calculations of PMFs from these simulations were used to demonstrate the dependence on helix length and on bilayer thickness of the PMF of M2. The PMF profiles (Fig. 4) reveal that M2 is (meta)stable in an IF location. The IF location is globally more favorable if the helix is short relative to the bilayer width. In contrast, when the helix is longer relative to the bilayer width, a TM orientation is favored. In addition, the shorter helices are observed to cause more distortion of the bilayer (see Fig. 5 and Fig. S1 in the Supporting Material) when TM inserted (as has been observed in a number of previous simulations, e.g., (4)). These effects mean that the IF state becomes more energetically favorable relative to the TM state when the helix becomes shorter relative to the bilayer width. This is in agreement with model peptide data (38,39), which indicates that negative mismatch favors a nontransmembrane helix conformation.

Figure 4.

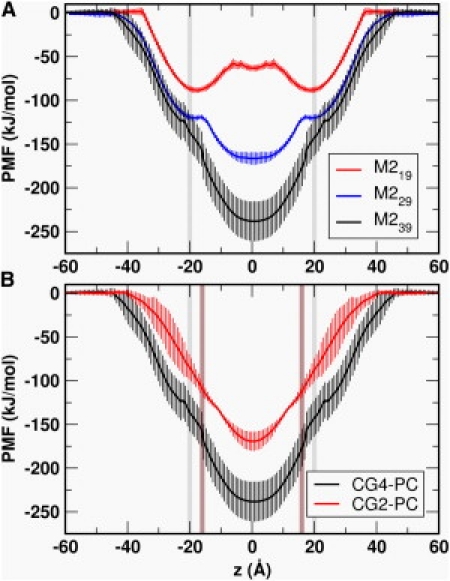
PMF profiles (A) for M2₁₉, M2₂₉, and M2₃₉ in CG4-PC bilayers and (B) for M2₃₉ in a CG2-PC versus a CG4-PC bilayer. (The edge of the lipid bilayer is marked in gray for CG4-PC and brown for CG2-PC.) Error bars were estimated by the PMFs from different 20-ns sections of the simulations.

Figure 5.

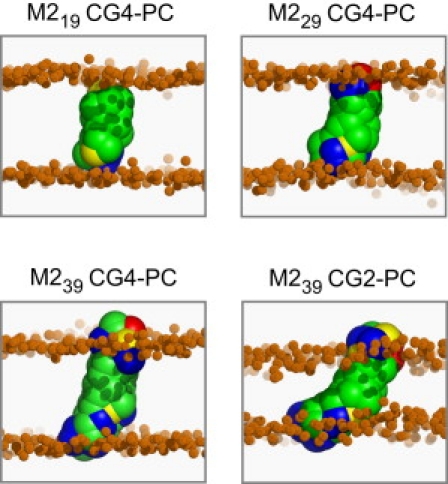
Snapshots at the end of each simulation for the central window, showing the M2 helices in bilayer-spanning orientations. (The residues are color-coded as follows: gray, hydrophobic; yellow, polar; red, anionic; and blue, cationic. The smaller brown spheres correspond to the phosphate groups of the lipids, and the N-termini of the helices are at the upper face of the bilayer.)

Comparison with hydrophobicity scales

We may usefully compare the magnitudes of the central energy well in the PMFs with a simple calculation based on summing the free energies of insertion for the central 19 hydrophobic amino acids in a lipid bilayer core as given by various hydrophobicity scales (see Table 2). It can be seen that the free energy difference between water and the global minimum for the PMFs (ranging from ∼−100 to −250 kJ/mol) corresponds well with the range predicted from simple calculations based on scales derived from: atomistic side-chain PMFs (10); CG side chain PMFs (16,25); continuum calculations (40); and from experimental partitioning data (41). In contrast, the translocon-mediated scale yields an estimate of ΔG_INS of −2 kJ/mol. This latter value should be compared with the experimental value from the translocon-mediated insertion assay of ∼−6 kJ/mol. (The differences between the experimental and calculated translocon-mediated value reflect the simplifications in the additive model, ignoring position dependency of the per residues ΔG values, etc.). However, it is clear that the magnitude of the translocon-mediated scale differs by at least a factor of 10 from the other scales.

Table 2.

Comparison of hydrophobicity scales for free energies of insertion

Scale	Free energy of insertion for 21-mer (kJ/mol)	Reference
Translocon-mediated insertion	−2	(7)
All atom side-chain PMFs	−124	(10)
Continuum electrostatics	−153	(40)
Side-chain partition coefficients	−163	(41)
CG side-chain PMFs (modified MARTINI)	−192	(16)
CG side-chain PMFs (MARTINI)	−209	(25)

These estimates are based upon an insertion model in which we simply sum the individual free energies of insertion into the hydrophobic core of a bilayer for M2₁₉ (i.e., SIAIYLGIGLCLLFIVRTL) to calculate an overall free energy of insertion. The individual free energies of insertion are taken from various residue-based scales, as listed. It should be noted that: the all-atom side-chain scale does not include values for Pro, Gly, or His; the continuum electrostatics and side-chain partition coefficients scales do not include a value for Pro; the MARTINI scale does not include values for Gly or Ala; and the modified MARTINI scale does not include values for Pro or Gly.

We may also compare our PMFs for M2 with those evaluated using CG-MD for simple model peptides, which yielded a well-depth of ∼−100 kJ/mol for LS3 (an amphipathic model helix composed of leucine and serine residues) using MARTINI (17) and ∼−175 kJ/mol for WALP23 (a hydrophobic model helix) using our local modification of MARTINI (16). Thus, there is comparability between different CG PMFs of helices, both for simple model peptides in the previous studies and for a more biological sequence in this study.

These magnitudes of the PMFs for M2 are incompatible with free energies of insertion derived from translocon-mediated insertion, which yield a ΔG of insertion of ∼−7 kJ/mol for M2₁₉ (13). However, in comparing PMFs with experimentally derived free energy differences, it is important to consider the standard state. The experimental ΔG is calculated from an apparent equilibrium constant, K_APP, for membrane insertion of a given segment which is calculated as

$$K_{\text{APP}}=f_{1\text{X}}/f_{2\text{X}},$$

where f_1x and f_2x correspond to the fractions of singly and doubly glycosylated proteins (13). If we compare

$$\Delta G_{\text{APP}}=-RT\mathit{ln}{\mathit{K}}_{\text{APP}}$$

with ΔG values for transfer from water to the hydrophobic core, we are implicitly equating the doubly glycosylated state (represented by f_2x) with the test helix in bulk aqueous solution. However, by using the PMFs calculated from our simulations, we may explore an alternative possibility, in which f_2x corresponds to a helix in an interfacial (IF) orientation. If this is so, then ΔG_APP should be compared with a free energy of insertion (ΔG_INS) derived from the PMFs as the difference between the TM and IF states (Table 3). Interestingly, a recent all-atom simulation study of the partitioning of small (4–12-mer) polyleucine peptides into a lipid bilayer (42) suggests an equilibrium between interfacial and inserted states which correlates with experimental data on related peptides (4).

Table 3.

Free energy changes from the PMF calculations for the switch from an interfacial to a TM orientation

Helix	Lipid	ΔGINS (kJ/mol)
M219	CG4-PC	+25 ± 5
M229	CG4-PC	−46 ± 7
M239	CG4-PC	−114 ± 31
M239	CG2-PC	−59 ± 14

From this comparison, it can be seen that for a stable TM helix, ΔG_INS ranges from ∼−50 to −100 kJ/mol, i.e., still between 5 and 10 times the magnitude derived from the translocon-insertion scale, despite the choice of a modified reference state (an interfacial helix).

Conclusions

We have used a CG-MD approach to estimate the PMF for insertion of a well-characterized TM helix derived from a complex, multispanning membrane protein into a lipid bilayer. Analysis of our results, bolstered by comparison with earlier single residue PMFs, indicates that the free energy of insertion of the helix is approximately an order-of-magnitude greater than that estimated from translocon-mediated insertion experiments. This in turn suggests that a reexamination of the molecular interpretation of the experimental data may be helpful. In particular, our calculations suggest that there may be a difference between the selection mechanism that the translocon uses to partition helices into the membrane and the thermodynamic stability of helices in a simple lipid bilayer. Simulations alone are unlikely to reveal the selection mechanism within the translocon. However, the results presented here enable us to formulate a hypothesis in which we suggest that:

• 1.Helices in an about-to-be-inserted state may be located in a hydrophobic region somewhat thinner than the core of a lipid bilayer; and/or
• 2.Helices in a not-to-be-inserted state may experience an environment more akin (e.g., in polarity/hydrophobicity) to the bilayer/water interface than to bulk water.

Some models for the mechanism of helix insertion via the translocon imply that the translocon enables the helix to sample both lipid and aqueous environments. The helix is envisaged to either partition into the membrane or continue within the translocon channel by a near-equilibrium process. However, recent simulations (43) suggest that the open state of the translocon is stabilized by a hydrophobic peptide in the channel, implying that the translocon plays a more active role in helix insertion. They also suggest that the escape of a helix from the translocon may be irreversible. This interpretation leads to a possible explanation for the larger ΔG_INS measured from CG PMF calculations (compared with the ΔG_APP from translocon-mediated experiments). If the translocon-mediated experiments were measuring the free energy of insertion of the helix into the translocon, with subsequent helix partitioning into the membrane-dependent on conformational changes in the translocon, rather than into the bilayer, then we would expect the ΔG_INS to be much less than if it were measured for the helix entering the bilayer directly. This is because the helix would be entering the hydrophobic region of the pore ring, ∼6 Å, compared with the thickness of the endoplasmic reticulum membrane of ∼39 Å (36).

These conclusions should be compared with a number of other more recent theoretical and experimental studies which have addressed the question of TM helix insertion. Jaud et al. (4) showed for simple model TM helices that bilayer distortion (as observed in our simulations; see Fig. S1) played an important role in the relationship between helix length and the energetics of insertion. Kauko et al. (44) have suggested that TM helices of complex membrane proteins can be repositioned relative to the membrane subsequent to insertion, and Hedin et al. (5) have indicated that nearest-neighbor TMs may aid the insertion of marginally hydrophobic helices. Thus, it is evident that further computational and experimental studies are needed to dissect the thermodynamics and mechanism of this apparently simple process.

As part of this study, we compared the magnitude of the free energy of insertion of a TM helix derived from CG-MD PMFs with estimates from a number of residue-based scales. The broad agreement suggests that CG-MD can indeed be used to study TM helix insertion into lipid bilayers. This is supported by recent combined experimental and computational studies (45) which show that CG-MD can reproduce subtle orientational effects on inserted TM helices arising from differently placed arginines within the helix sequence. Together with a number of recent studies from other groups (e.g., (46,47)), this indicates that CG-MD can capture a number of key aspects of membrane/protein structure and energetics.

These simulations allow us to compare directly the energetics of helix insertion into bilayers of different thickness. This is of interest, because a number of studies (e.g., (1)) have indicated that TM helices from proteins located in different membranes of eukaryotic cells may differ in the length of their hydrophobic core. This could be explored in more detail in CG and multiscale (2) PMF calculations.