Evaluation of Approaches to Identify Associated SNPs That Explain the Linkage Evidence in Nuclear Families with Affected Siblings

Abstract

Linkage analysis is often followed by association mapping to localize disease variants. In this paper, we evaluate approaches to determine how much of the observed linkage evidence, namely the identity-by-descent (IBD) sharing at the linkage peak, is explained by associated SNPs. We study several methods: Homozygote Sharing Tests (HST), Genotype Identity-by-Descent Sharing Test (GIST), and a permutation approach. We also propose a new approach, HSTMLB, combining HST and the Maximum Likelihood Binomial (MLB) linkage statistic. These methods can identify SNPs partially explaining the linkage peak, but only HST and HSTMLB can identify SNPs that do not fully explain the linkage evidence and be applied to multiple-SNPs. We contrast these methods with the association tests implemented in the software LAMP. In our simulations, GIST is more powerful at finding SNPs that partially explain the linkage peak, while HST and HSTMLB are equally powerful at identifying SNPs that do not fully explain the linkage peak. When applied to the North American Rheumatoid Arthritis Consortium data, HST and HSTMLB identify marker pairs that may fully explain the linkage peak on chromosome 6. In conclusion, HST and HSTMLB provide simple and flexible tools to identify SNPs that explain the IBD sharing at the linkage peak.

Introduction

There are two common statistical techniques used for gene mapping of complex human diseases: linkage analysis and association analysis. A frequently used gene mapping strategy consists of performing a genome scan to identify regions of linkage followed by association analysis to further localize the disease susceptibility loci. Once associated single nucleotide polymorphisms (SNPs) in a linkage region have been identified, it is of interest to determine if they explain none/some/all of the linkage evidence, namely the identity-by-descent (IBD) sharing at the linkage peak. In this paper, we focus on investigating methods that determine whether the IBD sharing at the linkage peak can be explained by the associated SNPs in a linked region. There are two types of such tests: the first type identifies SNPs that partially explain the linkage peak; the second type further identifies SNPs that do not fully explain the linkage peak. If none of the single associated SNPs fully explains the IBD sharing at the linkage peak, further investigation may reveal additional disease loci.

When a linkage signal is observed, one or multiple disease loci may contribute to the linkage signal. In general, complex diseases are most likely caused by multiple disease loci. For example, in Zavattari et al. [1], three loci in the human lymphocyte antigen (HLA) region were identified as risk modifiers in addition to and independent of HLA-DQB1, -DRB1 for type 1 diabetes mellitus in Sardinian population. When multiple disease loci contribute to a linkage signal, no single SNP should fully explain the IBD sharing at the linkage peak. Therefore, it is important for methods to consider multiple SNPs simultaneously.

Several researchers have developed methods to identify SNPs that explain the linkage peak for complex diseases [2,3,4,5,6,7], among others[]. Horikawa et al. [2] identified SNPs associated with the IBD sharing at the linkage peak by looking for an increase in the logarithm of odds (LOD) score in a subset of families defined by the proband carrying the risk genotypes. The significance of the change in LOD score in the subset of Ns families with the risk genotypes is assessed using a permutation approach, by randomly selecting subsets of Ns families, irrespective of proband genotypes. Sun et al. [3] defined a test statistic based on the premise that there should be no unexplained IBD oversharing in a sample of affected sibling pairs (ASPs) or nuclear families when conditioning on the affected offspring genotypes of a single causal locus. Li et al. [4] developed the Genotype Identity-by-Descent Sharing Test (GIST) to test the correlation between the family nonparametric linkage (NPL) score and a family genotype weight defined on the basis of affected offspring genotypes; the correlation should be zero when the tested SNP does not explain the IBD sharing at the linkage peak. Biernacka and Cordell [5] extended the method proposed in Sun et al. [3] by further conditioning on parental genotypes, which eliminates the need to estimate allele or haplotype frequencies.

The Homozygote Sharing Tests (HST) proposed in Dupuis and Van Eerdewegh [6] compare the IBD sharing from homozygous parents to the IBD sharing from heterozygous parents, where homozygosity status is defined at a SNP or a group of SNPs of interest. There are two test statistics: HST.P identifies SNPs that partially explain the IBD sharing at the linkage peak by looking for more IBD sharing from heterozygous parents than from homozygous parents; HST.F identifies SNPs that do not fully explain the linkage peak by looking for excess IBD sharing from homozygous parents. In this paper, we propose a novel extension combining HST and the Maximum Likelihood Binomial (MLB) statistic proposed in Abel et al. [8,9], called HSTMLB, to identify SNPs that partially explain the IBD sharing at the linkage peak (HSTMLB.P) or SNPs that do not fully explain the IBD sharing at the linkage peak (HSTMLB.F).

Our evaluation focuses on HST, HSTMLB, GIST and the method proposed in Horikawa [2], because Sun et al.'s [3] approach is sensitive to allele frequencies and no software is available for the method proposed by Biernacka and Cordell [5]. In addition, we contrast these approaches with the association tests proposed in Li et al. [10], where a likelihood function was constructed using disease-SNP haplotype frequencies and disease penetrances as parameters. Two likelihood ratio tests for association are implemented in the software ‘Linkage and Association Modeling in Pedigrees’ (LAMP). LAMP.P assesses whether the tested SNP is in linkage disequilibrium (LD) with a disease SNP, while LAMP.F assesses whether the tested SNP is in perfect LD with a disease SNP. Table 1 summarizes the characteristics of the studied methods to identify SNPs that explain the IBD sharing at the linkage peak.

Table 1.

Characteristics of the methods investigated to identify SNPs that explain the IBD sharing at the linkage peak

	GIST	Hori	HST	HSTMLB
P/F	P	P	P/F	P/F
Multiple SNPs	no	no	yes	yes
Allele freq	yes	no	no	no
Parental geno	no	no	yes	yes

P/F indicates that a method can identify SNPs that partially/do not fully explain the IBD sharing at the linkage peak. Multiple SNPs indicates whether a method can perform multiple-SNP analyses. Allele freq indicates whether known allele frequency estimates are required. Parental geno indicates whether a method requires parental genotypes.

We conduct two simulation studies: one that considers the case of a single disease SNP and that compares all approaches listed above, and one that considers two disease SNPs and offers a comparison of approaches applicable to multiple SNPs (HST and HSTMLB). In addition, we also apply these approaches to a rheumatoid arthritis (RA) real dataset provided by the North American Rheumatoid Arthritis Consortium (NARAC) in the Genetic Analysis Workshop (GAW) 15. RA is a common chronic complex disease with a genetic component that has long been recognized. Approximately 1% of the worldwide population is affected by RA (Orozco et al. [11]) which causes inflammation and destruction of the joints. Previous studies have identified linkage signals in genome-wide linkage scans [12,13,14], with the most consistent linkage evidence found around the HLA region on chromosome 6.

Methods and Results

We first review the HST method to identify SNPs explaining the IBD sharing at the linkage peak in a sample of ASPs with parental genotypes. We then introduce a new extension, HSTMLB.

Homozygote Sharing Tests

Risch [15] proposed the Maximum LOD Score (MLS) method to detect increased or higher than expected IBD sharing among ASPs. Under the null hypothesis of no linkage, the probability of an ASP sharing 0, 1 or 2 alleles IBD is 1/4, 1/2 and 1/4 respectively. A trinomial likelihood ratio can be used to test for departure from the null hypothesis. Increased sharing would indicate that the tested SNP is linked to the disease susceptibility loci. The HST uses a likelihood function that decomposes the IBD sharing in MLS by conditioning on parental genotype. Further assuming a multiplicative model of transmission, it can be shown that the parental transmissions are independent at any SNP (Appendix A). Consequently, the general likelihood function for HST can be expressed as the product of two independent binomial variables.

More formally, let X^homo and X^het be the number of alleles IBD shared by an ASP from a homozygous parent and a heterozygous parent, respectively. Under the assumption of independent parental transmissions, X^homo and X^het are two independent Bernoulli variables with means α_homo and α_het, respectively. Therefore, the log-likelihood function of N independent ASPs is

$$\begin{array}{cc}{L}_1=& N_1^{homo}log({\alpha }_{homo})+N_0^{homo}log(1-{\alpha }_{homo})\\ & +N_1^{het}log({\alpha }_{het})+N_0^{het}log(1-{\alpha }_{het}),\end{array}$$

the logarithm of the product of two independent binomial variables Bin(N^homo,α_homo) and Bin(N^het,α_het), where N_j^homo and N_j^het denote the number of ASPs sharing j allele IBD from homozygous and heterozygous parents, respectively (j = 0,1); N^homo and N^het denote the number of homozygous and heterozygous parents, respectively; and N^homo + N^het = 2N.

If a SNP is independent of the disease SNP, the IBD sharing probabilities are independent of parental genotypes. Hence, the IBD sharing probabilities from homozygous and heterozygous parents are both equal and are greater than 1/2 due to linkage. If a SNP is in LD with the disease SNP, increased IBD sharing from homozygous parents may be observed and this sharing should be less than the sharing from heterozygous parents. To determine whether a SNP partially explains the IBD sharing at the linkage peak, Dupuis and Van Eerdewegh [6] proposed HST.P, a likelihood ratio test of the hypotheses

$$H_0:1/2<{\alpha }_{homo}={\alpha }_{het}\text{vs}.H_1:1/2\le {\alpha }_{homo}<{\alpha }_{het}.$$

If a SNP is in perfect LD with the sole disease SNP in the linked region, there should be no excess IBD sharing from parents homozygous for the causal SNP, so α_homo = 1/2 (Appendix B). The fact that α_homo = 1/2 at the disease SNP was also derived in a different way in Robinson et al. [16]. Once SNPs that partially explains the linkage peak have been detected, Dupuis and Van Eerdewegh [6] proposed HST.F, a likelihood ratio test of the hypotheses H₀: α_homo = 1/2 vs. H₁: α_homo > 1/2 to further identify SNPs that do not fully explain the linkage peak. Rejection of the null hypothesis suggests the tested SNP does not fully explain the observed IBD sharing at the linkage peak.

Under the null hypotheses, both HST.P and HST.F follow a χ² mixture distribution of 0.5 χ₀² + 0.5 χ₁². A theoretical power approximation for HST.F is provided in Appendix C; a similar procedure may be used to obtain a power approximation for HST.P.

The HST.P and HST.F can be extended to multiple-SNP analysis in cases where none of the single SNPs can fully explain the observed IBD sharing at the linkage peak. The only difference between single-SNP analysis and multiple-SNP analysis in HST is the definition of parental homozygosity. For single-SNP analysis, a homozygous parent has two identical alleles at the tested SNP, while for multiple-SNP analysis, a homozygous parent has two identical haplotypes at the tested SNPs. In multiple-SNP analysis, the parental homozygosity determination does not involve haplotype reconstruction, because an individual with two identical haplotypes indicates that the individual is homozygous at all sites included in the haplotype.

When affected sibships with more than two affected siblings are present, the IBD sharing is not independent among all possible sibling pairs, violating one of the assumptions used to derive the HST asymptotic distributions. One approach to handle this issue is to multiply the likelihood of i-th nuclear family by a weight of 2/S_i, where S_idenotes the number of affected children in the family (Van Eerdewegh et al. [17]). We incorporated this correction factor in our R (R Development Core Team [18]) implementation of the HST statistics.

Homozygote Sharing Tests in Maximum Likelihood Binomial

In nuclear families, if a particular locus is unlinked to a disease of interest, the probability that an offspring inherits the maternal allele of grand maternal origin is 1/2 based on Mendelian inheritance. Therefore, the probability that k out of S offspring inherits the grand maternal allele from their mother follows a binomial distribution with probability parameter γ equal to 1/2. The same holds for the grand paternal allele transmitted from a father to his offspring. However, if the locus is linked to the disease, affected offspring will have a higher probability of inheriting the allele that is linked to the causal variant, creating a distortion from the 1/2 transmission by Mendel's first law. The MLB statistic [8,9] tests whether γ is equal to 1/2 by using a binomial likelihood ratio. Rejection of the null hypothesis γ = 1/2 indicates evidence for linkage. Because one does not know a priori which of the grand paternal or grand maternal allele segregates the disease susceptibility allele, the part of the likelihood involving γ in a nuclear family can be written as: f(γ) = γ^k(1 – γ)^{S – k} + (1 – γ)^k γ^{S – k}.

In the same spirit as the HST statistics, with parental genotypes, the likelihood can be expressed as a function of γ_het and γ_homo, where these parameters are estimated based on the transmissions from heterozygous and homozygous parents, respectively. We propose a likelihood ratio test, which we denote HSTMLB.P, to test the hypotheses H₀: 1/2 < γ_homo = γ_het vs. H₁: 1/2 ≤ γ_homo < γ_het to determine whether a SNP partially explains the observed IBD sharing at the linkage peak. Similarly, we suggest a second likelihood ratio test, HSTMLB.F, for the hypotheses H₀: γ_homo = 1/2 vs. H₁: γ_homo > 1/2 to determine if a SNP does not fully explain the observed IBD sharing at the linkage peak. Under their null hypotheses and assuming independent parental transmission, the distribution of both HSTMLB statistics asymptotically follows a χ² mixture distribution of 0.5 χ₀² + 0.5 χ₁². The software Genehunter [19] was modified to compute the HSTMLB statistics.

Simulation Study – A Single Di-Allelic Disease Locus

A simulation study using several models for complex disease was conducted to compare and contrast the HST and HSTMLB with other methods. We simulated a single disease locus consisting of risk allele D with allele frequency p and normal allele d. Table 2 characterizes the four simulated disease models. The population prevalence of disease was fixed at 5%.

Table 2.

Characteristics of simulated genetic models

Model	f0	f1	f2	p	GRR1	GRR2	ELOD
Additive	0.027	0.141	0.256	0.1	5.2	9.6	2.59
	0.016	0.101	0.187	0.2	6.3	11.7	2.59
Dominant	0.027	0.150	0.150	0.1	5.6	5.6	2.59
	0.014	0.114	0.114	0.2	8.1	8.1	2.60
Multiplicative	0.024	0.077	0.250	0.2	3.2	10.4	2.63
	0.018	0.058	0.189	0.3	3.2	10.5	2.61
Recessive	0.041	0.041	0.271	0.2	1	6.6	2.92
	0.036	0.036	0.195	0.3	1	5.4	2.84

f_i = penetrance; i = 0, 1, 2; p = risk allele frequency; GRR₁ = f₁/f₀; GRR₂ = f₂/f₀; ELOD = average LOD score.

We generated 200 nuclear families each with one ASP. For each replicate, we simulated the disease SNP, a SNP in LD (r² = 0.1, 0.2, …, 0.9) with the disease SNP, a SNP in linkage equilibrium (LE) with the disease SNP, and a fully informative microsatellite marker used to determine IBD sharing. All SNPs had identical allele frequency p, and there was no recombination between the simulated markers and hence, the observed IBD sharing is constant across the simulated markers. For every disease model in table 2, we used 9,000 replicates to assess type I error rates and 1,000 replicates to evaluate power. We compared HST.P, HSTMLB.P, GIST, and Horikawa (denoted Hori in tables and figures) for identifying SNPs that partially explain the observed IBD sharing and contrasted them with LAMP.P. When attempting to identify SNPs that do not fully explain the observed IBD sharing, HST.F and HSTMLB.F were contrasted with LAMP.F. Note that the fully informative marker was used as the flanking marker for LAMP and to determine IBD sharing for the other approaches.

Results: Identifying SNPs That Partially Explain the Linkage Peak

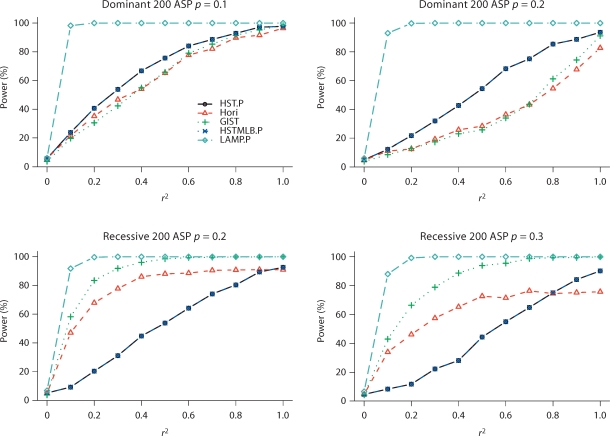
Table 3 presents the type I error rate estimates at a 5% significance level. In general, GIST has slightly conservative type I error rates, while the other methods to identify SNPs that partially explain the IBD sharing have type I error rates close to 5%. LAMP.P has slightly inflated type I error rates in testing whether there is LD between the tested SNP and the disease SNP. Figure 1 presents the power results at a 5% significance level for dominant and recessive disease models. The power increases as the LD between the disease SNP and the tested SNP increases and as the risk allele frequency decreases. GIST is more powerful than other methods to identify SNPs that partially explain the IBD sharing, except when the disease model is dominant where HST.P and HSTMLB.P have better power (results for other disease models are not shown).

Table 3.

Type I error rates (in percentage) for tests to identify SNPs that do not partially explain the IBD sharing at a 5% significance level in 9,000 replicates

Model	p	HST.P	Hori	GIST	HSTMLB.P	LAMP.P
Additive	0.1	4.8	4.6	2.3	4.9	5.8
	0.2	5.1	5.1	4.1	5.1	5.7
Dominant	0.1	5.0	5.0	2.8	5.0	5.2
	0.2	5.2	4.9	4.1	5.2	6.2
Multiplicative	0.2	5.1	4.9	3.7	5.1	6.8
	0.3	5.3	5.0	4.5	5.3	6.0
Recessive	0.2	4.5	4.9	3.8	4.5	5.6
	0.3	4.7	4.7	4.3	4.7	6.7

Results are contrasted with LAMP.P. The approximate 95% confidence intervals that do not contain 0.05 are bolded; the confidence intervals are computed by the observed type I error rate $\pm Z_{0.975}\sqrt{\frac{0.05\times 0.95}{9,000}}.$.

Fig. 1.

Power (in percentage) to identify SNPs that partially explain the linkage peak at a 5% significance level for dominant and recessive models. Results are contrasted with LAMP.P. 1,000 replicates are used in this simulation. p is the risk allele frequency. r² is the LD between the tested SNP and the disease SNP.

Results: Identifying SNPs That Do Not Fully Explain the Linkage Peak

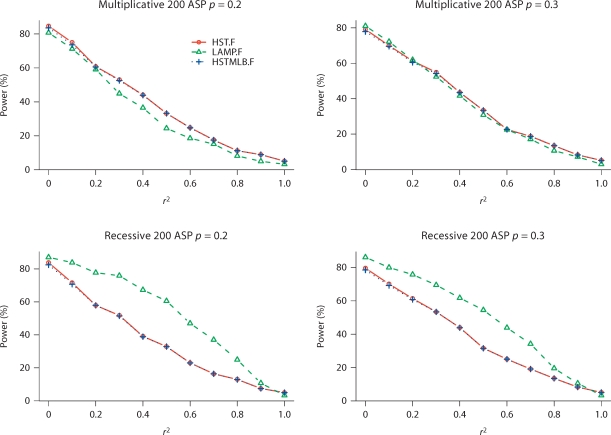
When looking for SNPs that fully explain the IBD sharing, the null hypothesis is that the tested SNP is the only disease locus or is a perfect proxy for the sole disease SNP in the linkage region and thus, fully explains the observed IBD sharing at the linkage peak. Hence, rejecting the null hypothesis indicates that the tested SNP does not fully explain the IBD sharing. Table 4 presents the type I error rates at a 5% significance level. The type I error rates are close to 5% for both HST.F and HSTMLB.F to identify SNPs that do not fully explain the IBD sharing. In contrast, LAMP.F has slightly conservative type I error rates for testing whether a SNP is in perfect LD with the disease SNP. Figure 2 presents the power results at a 5% significance level for multiplicative and recessive models (results for other disease models are not shown). As expected, the power decreases when the LD between the disease SNP and the tested SNP increases. HST.F and HSTMLB.F have similar power, and the power of HST.F was accurately estimated (within 5% difference) using the theoretical approximation (Appendix C). In contrast, LAMP.F has better power to identify SNPs not in perfect LD with the disease SNP under the recessive model.

Table 4.

Type I error rates (in percentage) for tests to identify SNPs that do not fully explain the IBD sharing at a 5% significance level in 9,000 replicates

Model	Additive		Dominant		Multiplicative		Recessive
p	0.1	0.2	0.1	0.2	0.2	0.3	0.2	0.3
HST.F	5.2	4.9	4.8	4.9	5.1	5.2	5.0	5.2
HSTMLB.F	5.2	4.9	4.8	4.9	5.1	5.2	5.0	5.2
LAMP.F	3.0	2.4	1.8	2.1	3.3	3.0	3.3	3.4

Results are contrasted with LAMP.F. The approximate 95% confidence intervals for the type I error rates that do not contain 0.05 are bolded.

Fig. 2.

Power (in percentage) to reject SNPs that do not fully explain the linkage peak at a 5% significance level for multiplicative and recessive disease models. Results are contrasted with LAMP.F. 1,000 replicates are used in this simulation. p is the risk allele frequency. r² is the LD between the tested SNP and the disease SNP.

For ASP design, our simulations show that HST (HST.P and HST.F) and HSTMLB (HSTMLB.P and HSTMLB.F) have equivalent power and type I error. Because HSTMLB does not assume independence of sibling pairs within a sibship, it may be applied to sibships with three or more siblings. However, HST uses weighted likelihood to account for the dependence of IBD sharing among sibling pairs. To compare these two approaches on larger sibships, we performed a simulation with p = 0.2 using models described in table 2 to generate 150 sibships of size three or 50 sibships of size four. We found that HST has slightly conservative type I error rates for larger sibships, while HSTMLB has type I error rates close to 5%, and that HSTMLB is slightly more powerful than HST (results not shown).

Simulation Study – Two Di-Allelic Disease Loci

When none of the single SNPs fully explain the IBD sharing at the linkage peak, one may further analyze two-SNP combinations. Among the methods investigated, only HST and HSTMLB can be extended to multiple-SNP analysis to identify SNP combinations that explain the linkage peak. We compared these two methods for single- and two-SNP analyses using simulations in which three SNPs and a fully informative marker to determine IBD sharing were simulated. All three SNPs were set to have equal allele frequencies, and there was no recombination between the simulated markers. To evaluate type I error rates of HST.P and HSTMLB.P in two-SNP analysis, one disease SNP and two mutually independent SNPs were simulated, and the two independent SNPs were used to estimate the type I error rates. The same population prevalence (5%), disease models and penetrances as in table 2 were used. A second three-SNP scenario was simulated where SNPs 1 and 3 were independent and equally contributing disease SNPs, while SNP 2 was in varying degrees of LD (r² = 0, 0.1, 0.2, …, 1.0) with SNP 1 but in LE with SNP 3. This scenario was used to assess the power of HST.P and HSTMLB.P and to evaluate the type I error rates and power of HST.F and HSTMLB.F. We used the same population prevalence (5%), disease models and penetrances as in table 2, but with penetrances conditional on the risk haplotype of the two disease SNPs. Let D₁ and D₂ be the risk alleles of the two disease SNPs, h_D = D₁D₂ be the haplotype with increased disease risk and all other haplotypes confer the same disease risk. We used subscripts to indicate which SNPs were analyzed; for example, HST.F₁₃ means that SNPs 1 and 3 were used to determine parental homozygosity status when computed the HST.F statistic. We simulated 9,000 replicates to estimate type I error rates and 1,000 replicates to estimate power at a 5% significance level for HST and HSTMLB.

Results: Identifying SNPs That Partially Explain Linkage Peak

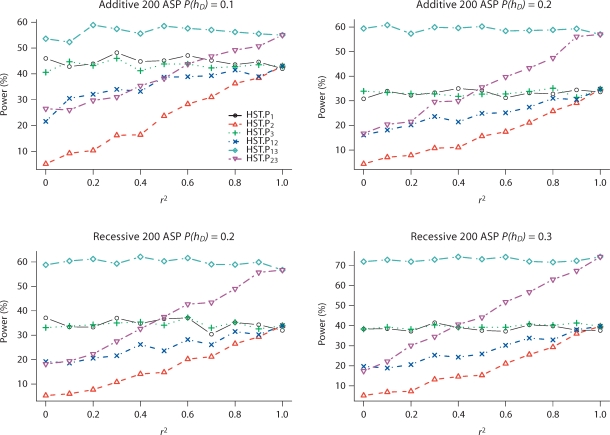
The type I error rates at a 5% significance level of two-SNP analysis for HST.P and HSTMLB.P are close to 0.05 (table 5). Figure 3 presents the power of HST.P and HSTMLB.P to identify SNPs that partially explain the observed IBD sharing at the linkage peak for single- and two-SNP analyses for additive and recessive models (results for other disease models are not shown). HST.P and HSTMLB.P have equivalent power; therefore, we only present and discuss results from HST.P in what follows. In single-SNP analysis, the simulated power of HST.P to detect the true disease loci is greater than the power to detect the SNP in LD with one of the disease loci, as expected. In two-SNP analysis, HST.P₁₃ has the best power, while the power of HST.P₂₃ increases as the LD between SNPs 2 and 1 increases.

Table 5.

Type I error rates (in percentage) for HST.P and HST-MLB.P to identify SNP pairs that partially explain the IBD sharing at the linkage peak evaluated at a 5% significance level using 9,000 replicates

Model	Additive		Dominant		Multiplicative		Recessive
P(hD)	0.1	0.2	0.1	0.2	0.2	0.3	0.2	0.3
HST.P	5.2	5.2	4.6	5.0	4.4	4.7	4.9	5.1
HSTMLB.P	5.2	5.2	4.6	5.0	4.4	4.7	4.9	5.1

P(h_D) is the risk haplotype frequency. The approximate 95% confidence intervals of the type I error rate that do not contain 0.05 are bolded.

Fig. 3.

Power (in percentage) of HST.P to identify SNP pairs that partially explain the IBD sharing at a 5% significance level for additive and recessive models. SNPs 1 and 3 are two independent and equally contributing disease SNPs; SNP 2 is in LD with SNP 1, but in LE with SNP 3. P(h_D) is the risk haplotype frequency. r² is the LD between SNPs 1 and 2. Results are based on 1,000 replicates. HSTMLB.P has similar power to HST.P and is not included. We use subscripts to indicate which SNPs were analyzed; for example, HST.P₁₃ means that SNPs 1 and 3 were used to determine parental homozygosity status when computing the HST.P statistic.

Results: Identifying SNPs That Do Not Fully Explain the Linkage Peak

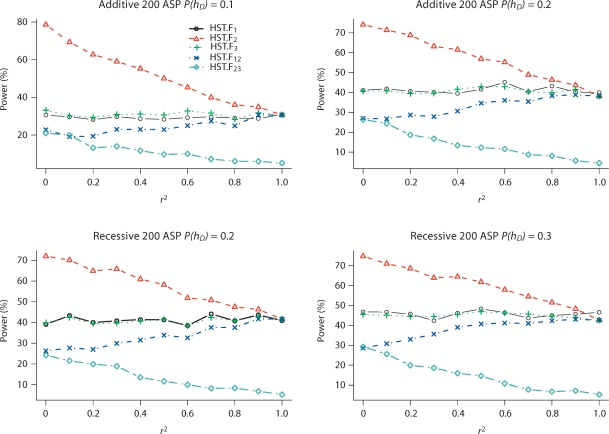
Table 6 presents the type I error rates for HST.F₁₃ and HSTMLB.F₁₃ to identify SNP pairs that may fully explain the linkage peak at a 5% significance level. HST.F₁₃ and HSTMLB.F₁₃ have type I error rates close to 5% in all scenarios. Figure 4 presents the power of HST.F and HSTMLB.F to reject SNP pairs that do not fully explain the IBD sharing for additive and recessive models (results for other disease models are not shown). Again we use HST.F to report the results because HST.F and HSTMLB.F have equivalent power. In general, single-SNP analysis has better power than two-SNP analysis to reject SNPs that do not fully explain the IBD sharing at the linkage peak due to the reduction in the number of homozygous parents.

Table 6.

Type I error rates (in percentage) for HST.F and HSTMLB.F to identify SNP pairs that do not fully explain a linkage signal evaluated at a 5% significance level using 9,000 replicates

Model	Additive		Dominant		Multiplicative		Recessive
P(hD)	0.1	0.2	0.1	0.2	0.2	0.3	0.2	0.3
HST.F	4.9	5.0	5.4	4.8	4.9	5.4	4.7	5.0
HSTMLB.F	4.9	4.9	5.4	4.8	4.9	5.3	4.7	5.0

P(h_D) is the risk haplotype frequency. All approximate 95% confidence intervals of the type I error rate contain 0.05.

Fig. 4.

Power (in percentage) of HST.F to reject SNP pairs that do not fully explain the IBD sharing at a 5% significance level for additive and recessive models. SNPs 1 and 3 are two independent and equally contributing disease SNPs; SNP 2 is in LD with SNP 1, but in LE with SNP 3. P(h_D) is the risk haplotype frequency. r² is the LD between SNPs 1 and 2. Results are based on 1,000 replicates. HSTMLB.F has similar power to HST.F and is not included. We use subscripts to indicate which SNPs were analyzed; for example, HST.F₁₂ means that SNPs 1 and 2 were used to determine parental homozygosity status when computing the HST.F statistic.

Application to GAW15 NARAC Data

We compare HST and HSTMLB with other methods included in our simulation studies for identifying SNPs that explain the observed IBD sharing at the linkage peak in the GAW15 NARAC data. The dataset contains 746 multiplex families. The full sample is used in the initial linkage and association analyses. Further analyses to identify SNPs explaining the IBD sharing at the linkage peak are restricted to 280 families with parental genotypes available so that most of the methods could be applied to the same subset of individuals for comparison purpose. Among these 280 families, there are 212 families with one genotyped parent and 68 families with two genotyped parents, and the number of affected sibships ranges from two to four. We focus our analysis on 5,407 SNPs on the 22 autosomal chromosomes.

LD among SNPs can lead to false positive linkage signals in ASP analysis when parental genotype information is incomplete [20]. Because LD exists in the set of genotyped SNPs [14], we use SNPLINK [21] to remove SNPs in LD with D′ greater than 0.5, and select a subset of 4,400 SNPs for linkage analysis. The linkage scan using Merlin [22] reveals a region of strong linkage with a maximum LOD score [23] of 15.95 at rs11908 at 32,991,663 base pairs (bp) on chromosome 6 close to major histocompatibility complex (MHC). We apply the family-based association test (FBAT) in the presence of linkage [24] to the HLA-DRB1 locus and to 14 SNPs falling within the 2-LOD score support region. The HLA-DRB1 genotype is recoded as a di-allelic marker with the highest risk alleles 0401, 0404, 0405, 0408 and 0409 forming allele 1 and the other HLA-DRB1 alleles recoded as allele 2. A total of 5,003 SNPs on chromosomes other than chromosome 6 are used to estimate type I error rates of methods for identifying SNPs that explain the IBD sharing at the linkage peak. FBAT identifies 2 associated markers (the recoded HLA-DRB1 locus and rs1003979) from the 15 markers. We apply HST, HSTMLB, Horikawa and GIST to the 2 associated markers to determine if they explain the IBD sharing at the linkage peak. The results are contrasted with LAMP. Because neither SNP can fully explain the IBD sharing at the linkage peak, we further use FBAT to identify associated marker pairs out of the 105 marker pairs formed by the 15 markers under the linkage peak and then apply two-marker HST and HSTMLB analyses to the associated marker pairs. For GIST and Horikawa, the risk allele is defined as the overtransmitted allele from heterozygous parents. After removing SNPs in LD, all SNPs residing on the same chromosome as the tested SNP are used as flanking markers in the LAMP analyses.

Single-Marker Analysis: Identifying Markers That Partially Explain the Linkage Peak

We estimate the type I error rates at a significance level of 5% for all methods except LAMP.P, using 5,003 SNPs on chromosomes other than 6 and the IBD sharing at the linkage peak on chromosome 6. For HST.P, HSTMLB.P, Horikawa and GIST, the type I error rate estimates are 4.4, 4.7, 5.2 and 5.1%, respectively. The type I error rate for LAMP.P cannot be evaluated using markers on chromosome 6 as it is not known a priori which SNPs are in LE with the disease susceptibility loci on that chromosome. Using SNPs on chromosomes other than chromosome 6 leads to an inflated positive rate of 17.9% for LAMP.P. The inflation may be due to the presence of other disease susceptibility loci in the rest of the genome and, to a smaller extent, to the inadequate modeling of familial aggregation as seen in our simulation results. Table 7 presents the results of identifying markers that partially explain the IBD sharing at the linkage peak on chromosome 6 for the two associated markers in 2-LOD score support region. Only the recoded HLA-DRB1 locus is identified as partially explaining the linkage peak by all methods but HSTMLB.P (HST.P p value = 0.046; HSTMLB.P p value = 0.14, Horikawa p value = 4 × 10^–5 and GIST p value <10^–6). Note that when using the original multi-allelic HLA-DRB1, both HST.P and HSTMLB.P detect HLA-DRB1 with p values of 0.0341 and 0.0108, respectively. By contrast, the recoded HLA-DRB1 is also identified by LAMP.P as a marker in LD with a disease locus (p value = 1.6 × 10^–24).

Table 7.

Results of testing associated markers that partially explain the IBD sharing at the linkage peak on chromosome 6 for the two associated markers located in the vicinity (2-LOD support interval) of the linkage peak

Marker	bp	LOD	HST.P	HSTMLB.P	Hori	GIST	FBAT	LAMP.P
HLA-DRB1	32654527–32665559	9.97	0.046	0.14	4 × 10−5	<10−6	8 × 10−7	1.6 × 10−24
rs1003979	33161058	15.68	1	1	0.272	0.1773	0.0244	0.17

Single-Marker Analysis: Identifying Markers That Do Not Fully Explain the Linkage Peak

On chromosomes other than chromosome 6, HST.F and HSTMLB.F have 99.96 and 100% power, respectively, to reject SNPs that cannot alone fully explain the IBD sharing at the linkage peak at a 5% significance level. In contrast, LAMP.F has 87.2% power to identify SNPs that are in partial LD but not in perfect LD with a disease SNP. The recoded HLA-DRB1 marker is rejected by HST.F (p value = 3.7 × 10^–3) and HSTMLB.F (p value = 2.8 × 10^–4) as the sole source of the observed IBD sharing at the linkage peak. Similarly, LAMP.F rejects that the recoded HLA-DRB1 marker is in perfect LD with a disease SNP on chromosome 6 with a p value of 1.8 × 10^–6. This suggests that further multiple-marker analysis is needed to determine the source of the linkage signal on chromosome 6.

Two-Marker Analysis

FBAT identifies 25 associated marker pairs from the 105 marker pairs formed by the recoded HLA-DRB1 marker and 14 SNPs in the 2-LOD score support region (results not shown). We further apply two-marker HST.P and HSTMLB.P analyses to the 25 associated marker pairs to test if they partially explain the observed IBD sharing at the linkage peak. Table 8 presents the results of 5 marker pairs that at least partially explain the linkage peak identified either by HST or HSTMLB. Both HST and HSTMLB cannot reject 3 marker pairs that may fully explain the IBD sharing at the linkage peak at a significance level of 10%: HLA-DRB1-rs169679, HLA-DRB1-rs11908 and HLA-DRB1-rs1011094. The number of homozygote parents (N^homo) for the 3 marker pairs is about 90, which might suggest that HST.F and HSTMLB.F may not have good power to reject the null hypothesis that the tested marker pair fully explains the observed IBD sharing at the linkage peak. However, the estimates of α_homo and γ_homo for HLA-DRB1-rs169679 are close to what is expected (0.5) under the null hypothesis. In addition, we assess the empirical power of HST.F to identify SNP pairs that do not fully explain the IBD sharing at the linkage peak by permuting the parental homozygosity status to form an empirical null distribution based on 10,000 replicates. The power estimates (HST.F power in table 8) are all greater than 90%, so there is good power to reject SNP pairs that do not fully explain the observed IBD sharing at the linkage peak.

Table 8.

Results for 5 marker pairs that at least partially explain the IBD sharing at the linkage peak on chromosome 6

snp1	snp2	Nhomo	Nhet	HST.P	HST.F	αhomo	HST.F power	HSTMLB.P	HSTMLB.F	γhomo
HLA-DRB1	rs169679	91	239	0.00054	0.5	0.515	0.9208	0.00012	1	0.5
HLA-DRB1	rs11908	87	243	0.0027	0.3726	0.517	0.9096	0.01329	0.1369	0.67
HLA-DRB1	rs813079	102	226	0.05558	0.0499	0.581	0.953	0.04313	0.0271	0.72
HLA-DRB1	rs1011094	90	240	0.00427	0.3123	0.526	0.9233	0.00116	0.3551	0.6
rs169679	rs1003979	91	252	0.05511	0.0902	0.571	0.9043	0.04768	0.0525	0.705

N^homo and N^het are the numbers of homozygote and heterozygote parents, respectively.

Discussion

We have investigated HST and HSTMLB and compared these methods to others to identify SNPs that explain the IBD sharing at the linkage peak. Based on our simulations, we found that examining the IBD sharing probability from homozygous parents provides a simple and powerful way to identify SNPs that do not fully explain the linkage peak (HST.F and HSTMLB.F).

In the first simulation study using an ASP sample, we simulated a single disease SNP and considered various disease models. We found that in most scenarios, GIST was the most powerful to identify SNPs that partially explain the IBD sharing at the linkage peak. On the other hand, when searching for SNPs that do not fully explain the IBD sharing at the linkage peak, HST.F and HSTMLB.F were equally powerful. In contrast, LAMP.P showed great power to detect SNPs in LD with the disease SNP, while LAMP.F showed good power to identify SNPs not in perfect LD with the disease SNP.

In the second simulation study using an ASP sample, we generated two disease SNPs with equal effect on disease susceptibility and evaluated HST and HSTMLB, the only two approaches easily generalizable to multiple-SNP analysis. Our results showed that these two methods are equivalent in terms of power and type I error.

In a sample of ASPs with parental genotypes, we derived the theoretical approximations of HST.P and HST.F, which we used to compute their noncentral χ² parameters and theoretical power. The theoretical power approximation was precise and close to the empirical power estimated from simulations with the maximum difference less than 5% among all scenarios (results not shown).

In the NARAC dataset, we applied all studied methods to attempt to identify SNPs that explained the IBD sharing at a previously reported linkage peak on chromosome 6. Among the recoded HLA-DRB1 locus and the 14 SNPs in the 2-LOD score support region, HST and HSTMLB could not reject three and four associated marker pairs that may fully explain the IBD sharing observed at the linkage peak at a 5% significance level, respectively. Most of these marker pairs are composed of the recoded HLA-DRB1 locus. We confirmed the consistent evidence that the HLA-DRB1 locus contributes to the RA susceptibility and yet, the HLA-DRB1 locus is not the sole source of the strong linkage signal.

Note that for HST.F and HSTMLB.F, the null hypothesis is H₀: markers fully explain the IBD sharing at the linkage peak. Failure to reject the null hypothesis may occur when there is insufficient power, which may be due to a low number of homozygous parents at the markers of interest. While this should be less frequent in single associated marker analysis, this is more likely to happen in multiple associated marker analysis, where it will be even rarer for parents to be homozygous at all sites tested. A more liberal significance level than the typical 5% may need to be used in order to avoid falsely identified markers as fully explaining the IBD sharing at the linkage peak.

In conclusion, the HST has the following nice properties: (1) simplicity in theory and computation; (2) ability to test whether associated SNPs explain none/some/all of the IBD sharing at the linkage peak; (3) powerful extensions such as HSTMLB.F; (4) flexibility to work with multiple-SNP combinations or multi-allelic markers. In addition, the idea of decomposing IBD sharing into sharing from heterozygous and homozygous parents can be incorporated into other linkage methods for identifying SNPs that explain the IBD sharing at the linkage peak, such as in HSTMLB and also in the application to quantitative traits. However, a limitation of the HST and HSTMLB is the requirement that parental genotypes be available. Additionally, the power of HST.F and HSTMLB.F rely on the number of homozygote parents, and the generalization to multiple-SNP analysis may reduce power because the number of parents homozygous at all markers decreases with the inclusion of additional markers. In conclusion, among the approaches investigated in this paper, we suggest using HST-based approaches to identify SNPs that explain the IBD sharing at the linkage peak when parental genotypes are available, whereas GIST is preferable when parental genotypes are missing.

Appendix A

Proof of independence of parental transmissions to ASP under a multiplicative model, assuming no imprinting in a linked region. Equivalently, for m = 0, 1 and d = 0, 1, show that

$$P(I^M=m,I^D=d|ASP)=P(I^M=m|ASP)\times P(I^D=d|ASP),$$

where IM and ID are the number of alleles shared IBD by an ASP from mother and father, respectively.

Proof: For a di-allelic disease locus with risk allele t (frequency p) and normal allele T (frequency q = 1 − p), assuming no imprinting, we define f_i as the probability that an individual is affected given that he has i copies of risk allele, i = 0, 1, 2. The genotype relative risks are denoted by

$$\gamma =\frac{f_1}{f_0}$$

and

$$\eta =\frac{f_2}{f_0}.$$

For a multiplicative model, η = γ². The population prevalence can be written as

$$K=p^2{f}_2+2pq{f}_1+q^2{f}_0=f_0(p^2\eta +2pq\gamma +q^2)=f_0{(p\gamma +q)}^2.$$

The additive (V_A) and dominant (V_D) variance components assuming no imprinting [25] can be written as:

$$\begin{array}{c}{V}_A=2pq{[p(f_2-f_1)+q(f_1-f_0)]}^2=2pq{f}_0^2{(p\gamma +q)}^2{(\gamma -1)}^2,\\ V_D=p^2{q}^2{(f_2-2f_1+f_0)}^2=p^2{q}^2{f}_0^2{(\gamma -1)}^2.\end{array}$$

Risch [26] derived the relative risk ratios, λ_M for monozygote twins, λ₁ for parent-offspring pairs, and λ_s for sibling pairs, where ${\lambda }_M-1=(1/K^2)(V_A+V_D),{\lambda }_1-1=(1/K^2)(V_A/2),{\lambda }_s-1=(1/K^2)(V_A/2+V_D/4)\text{and}{\lambda }_M=4{\lambda }_s-2{\lambda }_1-1.$. Then the IBD sharing probabilities for ASP are

$$\begin{array}{c}{z}_0=\frac{1}{4}-\frac{1}{4{\lambda }_s}\left(2\psi -1\right)\left[\left({\lambda }_s-1\right)+2\left(1-\psi \right)\left({\lambda }_s-{\lambda }_1\right)\right],\\ z_1=\frac{1}{2}-\frac{1}{2}{\left(2\psi -1\right)}^2\frac{1}{{\lambda }_s}\left({\lambda }_s-{\lambda }_1\right),\\ z_2=\frac{1}{4}+\frac{1}{4{\lambda }_s}\left(2\psi -1\right)\left[\left({\lambda }_s-1\right)+2\psi \left({\lambda }_s-{\lambda }_1\right)\right].\end{array}$$

Here, ψ = θ² + (1 θ)², and θ denotes the recombination fraction between the disease locus and the tested SNP. We rewrite the IBD sharing probabilities using λ₁ 1 = (1/K²)(V_A/2) and λs 1 = (1/K²)(V_A/2 + V_D/4).

$$\begin{array}{c}{z}_0=\frac{K^2+V_A\left(1-\psi \right)+V_D{\left(1-\psi \right)}^2}{4K^2+2V_A+V_D},\\ z_1=\frac{2K^2+V_A+2V_D\psi \left(1-\psi \right)}{4K^2+2V_A+V_D},\\ z_2=\frac{K^2+V_A\psi +V_D{\psi }^2}{4K^2+2V_A+V_D}.\end{array}$$

Assuming no imprinting, $z_1=2P(I^M=1,I^D=0|ASP)=2P(I^M=0,I^D=1|ASP)$. Therefore,

$$\begin{array}{l}P\left(I^M=1|ASP\right)=P\left(I^D=1|ASP\right)=\frac{1}{2}{z}_1+z_2\hfill \\ =\frac{2K^2+V_A\left(\psi +1/2\right)+V_D\psi }{4K^2+2V_A+V_D}.\hfill \end{array}$$

With this equation, we will prove that $P(I^M=m,I^D=d|ASP)=P(I^M=m|ASP)\times P(I^D=d|ASP)$ for m = 1 and d = 1. The cases hen m = 1 and d = 0, m = 0 and d = 1, and m = 0 and d = 0 can be proved similarly.

$$\begin{array}{l}P\left(I^M=1|ASP\right)\times P\left(I^D=|ASP\right)={\left[\frac{2K^2+V_A\left(\psi +1/2\right)+V_D\psi }{4K^2+2V_A+V_D}\right]}^2=\frac{4K^4+4\left(\psi +1/2\right)K^2{V}_A+{\left(\psi +1/2\right)}^2{V}_A^2+2\psi (\psi +1/2)V_A{V}_D+{\psi }^2{V}_D^2+4\psi K^2{V}_D}{{\left(4K^2+2V_A+V_D\right)}^2}\hfill \\ =\frac{\left(4K^2+2V_A+V_D\right)\left(K^2+\psi V_A+{\psi }^2{V}_D\right)+{\left(\psi -1/2\right)}^2{V}_A^2-{\left(2\psi -1\right)}^2{K}^2{V}_D}{{\left(4K^2+2V_A+V_D\right)}^2}=p\left(I^M=1,I^D=1|ASP\right)+\frac{{\left(\psi -1/2\right)}^2{V}_A^2-4{\left(\psi -1/2\right)}^2{K}^2{V}_D}{{\left(4K^2+2V_A+V_D\right)}^2}\hfill \\ =P\left(I^M=1,I^D=1|ASP\right)+\frac{{\left(\psi -1/2\right)}^2\left(V_A^2-4K^2{V}_D\right)}{{\left(4K^2+2V_A+V_D\right)}^2}=P\left(I^M=1,I^D=1|ASP\right)\hfill \\ \because V_A^2-4K^2{V}_D=4p^2{q}^2{f}_0^4{\left(p\gamma +q\right)}^4{\left(\gamma -1\right)}^4-4f_0^2{\left(p\gamma +q\right)}^4\times p^2{q}^2{f}_0^2{\left(\gamma -1\right)}^4=0.\hfill \end{array}$$

Therefore, parental transmissions are independent at a marker with recombination fraction θ away from the disease locus for multiplicative models. When θ = 0, this reduces to showing independence of parental transmissions at the disease locus.

Appendix B

Proof of there is no excess IBD sharing from parents homozygous at the disease locus assuming no imprinting. That is, α_homo = 1/2 at the disease locus.

Proof: We denote by m_d the parental mating type (father × mother) at the disease locus. Table B-1 presents the conditional probabilities P(I^D, I^M, ASP|m_d) for all mating types at the disease locus, assuming no imprinting [27] . At the disease locus, to prove α_homo = 1/2 is equivalent to prove P(I^D = 1|ASP) = 1/2 for a homozygous father or P(I^M = 1|ASP) = 1/2 for a homozygous mother. For a homozygous father, the parental mating type, m^d, can be tt × tt, tt × Tt, tt × TT, TT × tt, TT × Tt and TT × TT. We want to prove

Table B-1.

P(I^D,I_M, ASP|m_d) for all mating types m_d (father × mother) at the disease locus

md	ID = 1,IM = 1	ID = 1,IM = 0	ID = 0,IM = 1	ID = 0,IM = 0
tt × tt	f22 /4	f22/4	f22/4	f22/4
tt × Tt	(f22 + f12)/8	f2f1/4	(f22 + f12)/8	f2f1/4
tt × TT	f12/4	f12/4	f12/4	f12/4
Tt × tt	(f22 + f12)/8	(f22 + f12)/8	f2f1/4	f2f1/4
Tt × Tt	(f22 + 2f12 + f02)/16	(f2f1 + f1f0)/8	(f2f1 + f1f0)/8	(f2f0 + f12)/8
Tt × TT	(f12 +f02)/8	(f12 + f02)/8	f1f0/4	f1f0/4
TT × tt	f12/4	f12/4	f12/4	f12/4
TT × Tt	(f12 + f02)/8	f1f0/4	(f12 + f02)/8	f1f0/4
TT × TT	f02/4	f02/4	f02/4	f02/4

$$P\left(I^D=1|ASP,m_d\right)=\frac{P\left(I^D=1,ASP|m_d\right)}{P\left(ASP|m_d\right)}=\frac{{\sum }_{I^{M}P\left(I^D=1,I^M,ASP|m_d\right)}}{P\left(ASP|m_d\right)}=\frac{1}{2}.$$

For tt × tt, a child has the probability f₂ to be affected, therefore, $P\left(ASP|tt\times tt\right)=f_2^2.$ Thus,

$$P\left(I^D=1|ASP,tt\times tt\right)=\frac{P\left(I^D=1,I^M=1,ASP|tt\times tt\right)+P\left(I^D=1,I^M=0,ASP|tt\times tt\right)}{P\left(ASP|tt\times tt\right)}=\frac{\frac{f_2^2}{4}+\frac{f_2^2}{4}}{f_2^2}=\frac{1}{2}.$$

For tt × Tt, a child has the probability 1/2 to be either tt or Tt and thus has the probability

$\frac{f_2+f_1}{2}$ to be affected, therefore, $P\left(ASP|tt\times Tt\right)={\left(\frac{f_2+f_1}{2}\right)}^2.$

Therefore,

$$P\left(I^D=1|ASP,tt\times Tt\right)=\frac{P\left(I^D=1,I^M=1,ASP|tt\times Tt\right)+P\left(I^D=1,I^M=0,ASP|tt\times Tt\right)}{P\left(ASP|tt\times Tt\right)}=\frac{\frac{f_2^2+f_1^2}{8}+\frac{f_2{f}_1}{4}}{{\left(\frac{f_2+f_1}{2}\right)}^2}=\frac{1}{2}.$$

The case of tt × TT, TT × tt, TT × Tt, and TT × TT mating types can be proven similarly. Hence, α^homo = 1/2 at the disease locus.

Appendix C

Theoretical approximation for the expected HST.F.

$$HST.F=2\left[N_1^{homo}log\left(\frac{N_1^{homo}}{N^{homo}}\right)+N_0^{homo}log\left(\frac{N_0^{homo}}{N^{homo}}\right)-N^{homo}log\left(\frac{1}{2}\right)\right]=2\left[N_1^{homo}log{N}_1^{homo}+N_0^{homo}log{N}_0^{homo}-N^{homo}log{N}^{homo}+N^{homo}log2\right].$$

We show the approximation procedure for the expected HST.F; a similar procedure applies to HST.P. Under the alternative hypothesis that the tested SNP is in LD with the disease locus, the distribution of HST.F can be approximated by a ${\chi }_1^2,\lambda$ distribution, where λ = E(HST.F) 1 is the noncentrality parameter, provided that E(HST.F) is sufficiently large. With the approximated expected HST.F, we can compute the noncentrality parameter and then the theoretical power.

We assume that a di-allelic disease locus D has risk allele t with frequency p and normal allele T with frequency q = 1 p, and that there is no imprinting. We denote by m_D the parental mating type (paternal × maternal) at the disease locus and let I_k,m (I_k,d) be the number of alleles shared IBD by the ASP from mother (father) at the disease locus for the k-th family, I_k,m = 0,1, I_k,d = 0,1. We assume that SNP M has alleles A and a, which may or may not be in LD with the disease locus. We denote by m_M the parental mating type at SNP M and by $I_{k,m}^{homo}(I_{k,d}^{homo})$ the indicator that mother (father) is homozygous at SNP M for the k-th family. Let h_tA, h_ta, h_TA and h_TA be the haplotype frequencies for haplotypes tA, ta, TA and Ta, respectively, and P(m_M, m_D) be a product of haplotype frequencies, for example, $P\left(tt\times TT,AA\times aa\right)=h_{tA}^2{h}_{Ta}^2$. We use Taylor theorem to approximate $E\left(N_1^{homo}log{N}_1^{homo}\right),E\left(N_0^{homo}log{N}_0^{homo}\right)\text{and}E\left(N^{homo}log{N}^{homo}\right)$ in the expected HST.F to the second order, using

$$E\left(xlogx\right)\approx {\mu }_{x}log{\mu }_x+\frac{1}{2{\mu }_x}{\sigma }_x^2.$$

We only show the approximation to $E\left(N_1^{homo}log{N}_1^{homo}\right),$ the other terms can be obtained similarly.

Approximation of

$E\left(N_1^{homo}log{N}_1^{homo}\right)$

Let

$$X=N_1^{homo}=\sum _{k=1}^N{I}_{k,m}^{homo}{I}_{k,m}+I_{k,d}^{homo}{I}_{k,d}$$

with mean μ_x (1.) and variance ${\sigma }_x^2$ (2.).

1.

$${\mu }_x=E\left(\sum _{k=1}^N{I}_{k,m}^{homo}{I}_{k,m}+I_{k,d}^{homo}{I}_{k,d}\right)=2NP\left(I_{k,m}^{homo}=1,I_{k,m}=1|ASP\right).$$

When $I_{k,m}^{homo}=1,$ the possible mating types at SNP M are aa × aa, aa × AA, Aa × aa, Aa × AA, AA × aa and AA × AA. We denote by {HomoMom}_M the set of possible mating types with mom homozygous at SNP M.

$$\begin{array}{l}P\left(I_{k,m}^{homo}=1,I_{k,m}=1|ASP\right)\hfill \\ =P\left(I_{k,m}^{homo}=1,I_{k,m}=1|ASP\right)/P(ASP)\hfill \\ =\left[\sum _{mM∊{\left\{HomoMom\right\}}_M}P\left(m_M,I_{k,m}=1,ASP\right)\right]/P(ASP)\hfill \\ =\left[\sum _{mM∊{\left\{HomoMom\right\}}_M}P\left(m_M,I_{k,m}=1,I_{k,d}=0,ASP\right)+P\left(m_M,I_{k,m}=1,I_{k,d}=1,ASP\right)\right]/P(ASP),\hfill \end{array}$$

where these three probabilities are derived below:

$$\begin{array}{l}\sum _{m_M∊{\left\{HomoMon\right\}}_M}P\left(m_M,I_{k,m}=1,I_{k,d}=0,ASP\right)\hfill \\ =\sum _{m_D{m}_M}\sum _{∊{\left\{HomoMon\right\}}_M}P\left(m_M,m_D,I_{k,m}=1,I_{k,d}=0,ASP\right)\hfill \\ =\sum _{m_D{m}_M}\sum _{∊{\left\{HomoMon\right\}}_M}P\left(I_{k,m}=1,I_{k,d}=0,ASP|m_M,m_D\right)P\left(m_M,m_D\right)\hfill \\ =\sum _{m_D{m}_M}\sum _{∊{\left\{HomoMon\right\}}_M}P\left(I_{k,m}=1,I_{k,d}=0,ASP|m_D\right)P\left(m_M,m_D\right),\hfill \end{array}$$ (1)

$$\begin{array}{l}\sum _{m_M∊{\left\{HomoMon\right\}}_M}P\left(m_M,I_{k,m}=1,I_{k,d}=1,ASP\right)\hfill \\ =\sum _{m_D{m}_M}\sum _{∊{\left\{HomoMon\right\}}_M}P\left(I_{k,m}=1,I_{k,d}=1,ASP|m_M,m_D\right)P\left(m_M,m_D\right)\hfill \\ =\sum _{m_D{m}_M}\sum _{∊{\left\{HomoMon\right\}}_M}P\left(I_{k,m}=1,I_{k,d}=1,ASP|m_D\right)P\left(m_M,m_D\right),\hfill \end{array}$$ (2)

and

$$\begin{array}{l}P(ASP)=\sum _{m_D}P\left(ASP|m_D\right)P\left(m_D\right)\hfill \\ =P\left(ASP|tt\times tt\right)P\left(tt\times tt\right)+2P\left(ASP|tt\times TT\right)P\left(tt\times TT\right)+2P\left(ASP|tt\times Tt\right)P\left(tt\times Tt\right)+P\left(ASP|Tt\times Tt\right)P\left(Tt\times Tt\right)+2P\left(ASP|Tt\times TT\right)P\left(Tt\times TT\right)+P\left(ASP|TT\times TT\right)P\left(TT\times TT\right)\hfill \\ =f_2^2{p}^4+2f_1^2{p}^2{q}^2+2{\left(\frac{f_2+f_1}{2}\right)}^{2}2p^{3}q+{\left(\frac{f_2+2f_1+f0}{4}\right)}^{2}4p^2{q}^2+2{\left(\frac{f_1+f_0}{2}\right)}^{2}2p{q}^3+f_0^2{q}^4.\hfill \end{array}$$ (3)

Note that the alleles shared IBD at the disease locus is independent of the mating type at SNP M. P(I_k,m =1,I_k,d = 0,ASP|m_D) and P(I_k,m =1,I_k,d = 1,ASP|m_D) are given in table B-1. Therefore, Umu;_x can be derived by

$$2N\times \frac{(1)+(2)}{(3)}.$$

2.

$$\begin{array}{l}{\sigma }_x^2=var\left(\sum _{k=1}^N{I}_{k,m}^{homo}{I}_{k,m}+I_{k,d}^{homo}{I}_{k,d}\right)\hfill \\ ={\mu }_x-\frac{{\mu }_x^2}{N}+2NP\left(I_{k,m}^{homo}=1,I_{k,m}=1,I_{k,d}^{homo}=1,I_{k,d}=1|ASP\right)\hfill \end{array}$$

When $I_{k,m}^{homo}=1$ and $I_{k,d}^{homo}=1,$ the possible mating types at the SNP M are aa × aa, aa × AA, AA × aa and AA × AA. We denote the set of possible mating types at SNP M as {Homo × Homo}_M.

$$\begin{array}{l}p\left(I_{k,m}^{homo}=1,I_{k,m}=1,I_{k,d}^{homo}=1,I_{k,d}=1|ASP\right)=P\left(I_{k,m}^{homo}=1,I_{k,m}=1,I_{k,d}^{homo}=1,I_{k,d}=1|ASP\right)/P\left(ASP\right)\hfill \\ =\left[\sum _{m_M∊{\{Homo\times Homo\}}_M}P\left(m_M,I_{k,m}=1,I_{k,d}=1,ASP\right)\right]/p\left(ASP\right)=\left[\sum _{m_D{m}_M}\sum _{∊{\{Homo\times Homo\}}_M}P\left(m_D,m_M,I_{k,m}=1,I_{k,d}=1,ASP\right)\right]/P\left(ASP\right)\hfill \\ =\left[\sum _{m_D{m}_M}\sum _{∊{\{Homo\times Homo\}}_M}P\left(I_{k,m}=1,I_{k,d}=1,ASP|m_D,m_M\right)P\left(m_D,m_M\right)\right]/P\left(ASP\right)\hfill \\ =\left[\sum _{m_D{m}_M}\sum _{∊{\{Homo\times Homo\}}_M}P\left(I_{k,m}=1,I_{k,d}=1,ASP|m_D\right)P\left(m_D,m_M\right)\right]/P\left(ASP\right).\hfill \end{array}$$ (4)

With μx and $P\left(I_{k,m}^{homo}=1,I_{k,m}=1,I_{k,d}^{homo}=1,I_{k,d}=1|ASP\right),{\sigma }_x^2$ can be derived by ${\mu }_X-\frac{{\mu }_X^2}{N}+2N\times (4).$