RNA Polymerase II with Open and Closed Trigger Loops: Active Site Dynamics and Nucleic Acid Translocation

Abstract

RNA polymerase II is the central eukaryotic enzyme in transcription from DNA to RNA. The dynamics of RNA polymerase II is described from molecular-dynamics simulations started from two crystal structures with open and closed trigger loop (TL) forms. Dynamic transitions between neutral and forward translocated states were observed, especially for the downstream DNA duplex. Dynamic rearrangements were also seen in the active site environment, including conformations in which the active site nucleotide assumed a possibly precatalytic conformation in close proximity to the terminal 3′-hydroxyl of the nascent RNA. Because nucleic acid translocation was observed primarily in the simulations with an open TL structure, whereas close approach of the active site nucleotide to the terminal RNA ribose predominantly occurred in the closed TL structure, a modified Brownian ratchet mechanism is proposed whereby thermally driven translocation is only possible with an open TL, and fidelity control and catalysis require TL closing.

Introduction

RNA polymerase II (PolII) is the key enzyme in eukaryotic transcription that catalyzes DNA-directed synthesis of mRNA (1). PolII consists at its core of 10 subunits that bind the template DNA and nascent RNA during active transcription (2). Two additional subunits and a number of transcription factors interact with the core complex during the initiation and elongation phases (3). Much of the modern understanding of PolII has come from crystal structures of the 10- and 12-subunit PolII complexes (4). They show a clamp-like enzyme that binds an L-shaped nucleic acid complex with the active site located near the center of the enzyme (see Fig. 1).

Figure 1.

Structure and dynamics of S. cerevisiae PolII. (A) Domain organization. (B) Average structure from simulation with open TL colored according to the Cα RMSD with respect to the crystal structure (2E2J), with blue tones corresponding to RMSD values below 2 Å and red tones corresponding to RMSD values above 3 Å. (C) Average structure and RMSD from simulation with closed TL as in B. (D) Correlated motions in simulated PolII complex with open TL calculated for Cα atoms of each residue, with red indicating positive correlation above 0.5 and blue indicating negative correlation below −0.5 (domains of PolII are indicated with different colors on the sides of the correlation plot). (E) Same as D for closed TL structure.

The crystal structures have substantially advanced our understanding of PolII, but it is still unclear how nucleotides (NTPs) enter the active site, how correctly templated ribonucleotides are selected against mismatched nucleotides and deoxyribonucleotides, and how a catalytically competent active site configuration is reached. Many of the PolII crystal structures resolve nucleotides or nucleotide analogs in the active site, but in all cases except one (PDB code: 1R9S (5)) the primary phosphate of the NTP appears to be too far from the 3′-OH of the terminal RNA base for the phosphodiester bond formation reaction to proceed. At the same time, x-ray B-factors for active site nucleotide phosphates and terminal RNA O3′ atoms tend to be quite large (≥100), indicating significant dynamics and/or experimental uncertainty on the order of several angstroms.

Another key question is how the nucleic acid complex is translocated after nucleotide addition. Two competing models have been proposed for the translocation mechanism. In the Brownian ratchet model, the nucleic acid complex fluctuates stochastically between pre- and posttranslocated states until nucleotide binding locks in the posttranslocated state (6). A variant of this model, called NTP-driven translocation, proposes that not just the nucleotide entering the active site but also nucleotides templated to downstream DNA sites shift the equilibrium to the posttranslocated state (7). A Brownian ratchet mechanism is supported by experimental data (8) as well as recent molecular-dynamics (MD) simulations of T7 RNA polymerase (9). It is unclear, though, exactly how the mechanical work of unidirectional translocation is accounted for energetically. In the alternative power stroke model, external energy drives conformational change associated with translocation (10). In particular, it has been proposed that pyrophosphate release after phosphodiester bond formation may drive translocation (10), but a direct coupling of pyrophosphate release and translocation is incompatible with single-molecule studies of bacterial RNA polymerase (8).

A comparison of the large number of different crystal structures provides insight into possibly functionally relevant dynamics of key parts of the PolII structure. The so-called bridge helix (BH; rpb1 815–845), which flanks one side of the NTP-binding site and separates the DNA-RNA hybrid from the downstream DNA helix, is bent to different degrees in different crystal structures. BH bending has been suggested to be involved in translocation and/or formation of a catalytically competent active site configuration (11). Immediately above the BH is the so-called trigger loop (TL; rpb1 1070–1100), which may exist in open or closed forms (12). The open TL is partly disordered, whereas the closed TL is mostly helical and interacts extensively with the BH. NTP entry into the active site appears to require an open TL, and a transition to the closed state has been implicated in authorizing the incorporation of correctly templated NTPs (12,13). A third dynamic element in the same structural vicinity of PolII is the so-called fork loop 2 (FL2; PolII rpb2 500–515), which interacts with the single-stranded DNA template strand across from the BH and is seen in different conformations in some crystal structures (14) and disordered in other structures. FL2 has been hypothesized to be involved in unwinding of the downstream DNA, but may play a broader role in NTP binding and translocation (13,16).

Experimental studies of PolII that could provide further details regarding its functional dynamics are extremely challenging because of its size and complexity (17). Computer simulations can fill this gap and provide a dynamic perspective in atomistic detail. Previous computational studies of RNA polymerase include simulations of T7 RNA polymerase (9) and bacterial RNA polymerase (18), normal-mode studies of bacterial (19,20) and eukaryotic (20) RNA polymerases, and a restrained MD simulation that explored nucleotide entry through the main channel (21).

Recently, we reported results from a normal-mode analysis of PolII that focused on its overall dynamics (22). The key findings are that separate motions may be involved in driving downstream DNA and upstream DNA-RNA translocation. Furthermore, downstream DNA appears to be translocated primarily in a linear fashion, whereas the obligatory helix unwinding may involve a separate motion. The normal-mode study further suggests that translocation may require an open TL.

Here, we present atomistic MD simulations of the fully solvated 10-subunit PolII complex with open and closed TL conformations. These simulations explore dynamic aspects and conformational changes on timescales up to 100 ns, including forward and backward translocation of the nucleic acid, as well as active site rearrangements with possible transitions to a catalytically competent state.

Materials and Methods

Starting structures

Crystallographic structures of the 10-subunit PolII complex from Saccharomyces cerevisiae with open (PDB ID: 2E2J (12)) and closed (PDB ID: 2E2H (12)) TL conformations were used as starting structures for MD simulations. Because of their structural disorder, a number of residues were not resolved. Missing non-surface-loop residues were constructed as follows: In 2E2J, missing parts of the open TL (1082–1090 in rpb1) and the FL2 (503–508 in rpb2) were added with Modeler 9 (24). Loop modeling involved the sampling of a variety of loop conformations and subsequent selection of the best conformation according to an internal free-energy scoring function. This protocol has been shown to predict loops up to eight residues with an accuracy of <2 Å in 90% of cases (25). In 2E2H, a missing part of FL2, missing residues 315–318 and 1232–1235 in rpb1, residues 249–250 and 733–734 in rpb2, and residues 112–116 in rpb5 were rebuilt with the same protocol. Remaining unresolved residues corresponding to surface loops were not rebuilt because the modeling of large surface loops is unreliable and because those surface loops are assumed to be nonessential for the core function of PolII. The nucleic acids, the nucleotide (GTP) bound in the active site, and two Mg²⁺ and eight bound Zn²⁺ ions were retained from the crystal structures. Amino acids were protonated according to standard pKa values at pH = 7 and GTP was assumed to be fully deprotonated. Reliable pKa predictions are complicated by the low resolution of the crystal structures. However, because protonation states were assigned in the same manner for open and closed TL structures, we assume that our simulations will still provide at least qualitative insight into differences between the two states in case some of the protonation states were misassigned. The sequences of the nucleic acid are slightly different in the two crystal structures (see Supporting Material).

The complexes were fully solvated in cubic boxes of explicit water, with box sizes of ∼165 Å chosen such that at least 9 Å remained from any point of the solute to the edge of the box. To neutralize the open and closed TL complexes, we added 65 and 72 Na⁺ counterions, respectively, by randomly replacing water molecules. The different number of counterions is a result of the different number of resolved residues near surface loops and different lengths of the nucleic acid strands.

MD simulations

A total of six MD simulations (three with a closed TL and three with an open TL) were carried out. The simulations for either TL conformation differed in the assignment of initial velocities and slightly different equilibration protocols to generate independent trajectories from the same starting structures. Equilibration involved initial minimization over 500 steps with the conjugate gradient method, followed by gradual heating from 5K to 298K over the course of 200–400 ps while simultaneously reducing a weak harmonic restraint on Cα atoms with an initial force constant of 2 kcal/mol/Ų to zero. Subsequent production runs without restraints were then extended to 32–110 ns (see Supporting Material).

The CHARMM22 force field (26) including the CMAP correction (27) was used to describe the protein; the CHARMM27 force field (28) was used for the nucleic acid; explicit water was modeled with the CHARMM version of the TIP3P model (26,29); and Na⁺, Mg²⁺, and Zn²⁺ parameters were used as described previously (30,31). Modified charges were used for deprotonated cysteines involved in Zn²⁺ binding and for the 3′-OH of the terminal RNA base (−0.80 for O3′, 0.47 for H3T, 0.24 for C3′, and 0.09 for H3′) to reflect increased polarization due to interactions with a nearby Mg²⁺ ion as suggested by ab initio calculations (M. Feig, S. Seibold, R. Cukier, and Z. Burton, unpublished data). Periodic boundaries were used in conjunction with the particle-mesh Ewald summation technique (32) (168 × 168 × 168 grid) to obtain accurate electrostatic interactions. The direct sum of the electrostatic contribution and the Lennard-Jones potential were truncated at 10 Å with a switching function effective at 8.5 Å. An integration time step of 2 fs was used in conjunction with the SETTLE algorithm (33) to holonomically constrain heavy atom-hydrogen bond distances. A Langevin-type thermostat and barostat were used to maintain an NTP ensemble with a temperature of 298K and a pressure of 1 bar.

All of the simulations were run with NAMD (34), version 2.6, in conjunction with the MMTSB Tool Set (35).

Analysis

Analysis of the simulations was carried out with the MMTSB Tool Set (35) in conjunction with CHARMM (36), version c36a1. VMD (37) was used for molecular visualization.

Probability mass functions (PMFs) and averages were obtained for either open or closed TL states by simply combining the sampling from the independent simulations after discarding the initial 10 ns in each trajectory. PMFs were obtained from histograms through Boltzmann inversion to provide free energies relative to the most populated state.

Correlation matrices were calculated for Cα atoms of each residue with the matrix elements$c_{ij}=<\Delta {\widehat{\mathbf{r}}}_i\left(t\right)\cdot \Delta {\widehat{\mathbf{r}}}_j\left(t\right){>}_t$, where $\Delta {\widehat{\mathbf{r}}}_i\left(t\right)=({\mathbf{r}}_i\left(t\right)-{\mathbf{r}}_{i,avg})/\left|{\mathbf{r}}_i\left(t\right)-{\mathbf{r}}_{i,avg}\right|$ is the normalized vector of the instantaneous deviation of residue i at time t from its average position and <.>_t is the average over all frames at different times t. Hence, c_ij can assume values between −1 and 1.

Results

Relaxation of the overall PolII complex

The PolII complex remained similar to the crystallographic structures in all of the simulations (see Fig. 1), but moderate relaxation of the initial structures was observed with Cα root mean-square deviations (RMSDs) from the crystal structure of ∼3 Å with the open TL and 4–5 Å with the closed TL (see Fig. S1 in the Supporting Material). The open and closed TL crystal structures (2E2J and 2E2H, respectively) differ by only 1.1 Å Cα-RMSD from each other, and the deviations of the simulated structures were similar with respect to either crystal structure. The simulated structures with the open TL remained close to the x-ray structures, whereas the simulated closed TL structures deviated from both experimental structures. It therefore appears that the crystal structures are most representative of the open TL state, and the closed TL x-ray structure (2E2H) may be constrained as a result of the crystal environment.

A more detailed analysis of the relaxation of different parts of the complex (cf. Fig. 1 and Table S1) reveals that in simulations with the open TL, the core remained close to the crystal structure, whereas significant deviations were only seen in peripheral parts of the complex (part of the clamp domain of rpb1, rpb8, and parts of rpb10 and rpb12). In contrast, in simulations with a closed TL, structural changes were observed in a significant part of the jaw side of the complex, including large parts of rpb2 and most of the surrounding subunits. The deviations from the crystal structure and the simulated open TL structures were largest at the tip of the jaw, where rpb2, rpb9, and parts of rpb1 rearranged to varying extents in all of the closed TL simulations. There were also significant structural changes in rpb3 and rpb12 at the opposite end of the enzyme.

Correlated motions in PolII complex

The dynamic coupling between distant parts of the enzyme was analyzed in terms of correlated motions. Because the underlying simulations were limited to 100-ns timescales, the resulting correlation maps (Fig. 1, D and E) focus on nanoscale motions rather than the full dynamic spectrum that is available from normal-mode studies (19,20,22). Nevertheless, we find evidence of significant long-range correlations between distant parts of the structure consistent with our earlier normal-mode study (22). For example, almost the entire rpb2 subunit is (negatively or positively) correlated with parts of rpb1.

There are significant differences in the correlated motions between the simulations with open and closed TL. With the open TL, the rpb1 clamp domain was highly correlated with most of the rpb2 subunit, consistent with a rigid core. In the closed TL simulation, only parts of the BH/active site part of the complex and the jaw domain of rpb1 (residues 1150–1300) were correlated with rpb2 motion. At the same time, correlations within the BH/active site region were stronger with the closed TL. There were also differences in correlations with other subdomains. For example, rpb5 was almost entirely uncorrelated with the rest of the enzyme in the open TL simulations, but was correlated with parts of rpb1 and rpb2 in the closed TL simulations.

Correlated motions between the TL and the rest of the structures also appear to depend on the TL conformation (see Fig. S2). Overall, there was a stronger correlation with different parts of the structure in the simulations with the closed TL than with the open TL. The largest differences were seen for correlations between the TL and the rpb2 jaw domain, with a weak negative correlation for the open TL and a larger positive correlation for the closed TL. Other significant differences involved the coupling with rpb6 and rpb9 and with parts of rpb1. Of interest in this context is a recent experimental study that suggested that rpb9 has a critical role in ensuring transcriptional fidelity, presumably by interfering with TL closing (38).

In sum, the pattern of correlated motions suggests that an open TL favors tight coupling between large parts of rpb1 and rpb2, but maintains a comparatively loose active site environment. In contrast, TL closing seems to largely suppress correlated motions between rpb1 and rpb2 while inducing stronger coupling within the TL/BH/active site region and between the active site environment and the rpb2 jaw domain. Enhanced correlations within the active site with a closed TL can be rationalized from the additional contacts of the ordered loop with the BH and surrounding residues that would create a locally more coupled network of interactions. At the same time, the BH/active site is part of the hinge for the larger-scale, clamp-jaw motions, and a rigidification of that region due to TL closing would be expected to limit such motions.

TL conformation and BH bending

BH bending has been proposed to play a role in both the formation of a catalytically competent active site and translocation. In our simulations, we observe significant BH bending dynamics with both the open and closed TLs. By scanning the bending angle as a function of the central helix residue around which the bending angle is calculated, we find that the bending point (indicated by the maximum bending angle) is around residues 827–828 with both the open and closed TLs (see Fig. S3). Furthermore, we see an equilibrium between straight and bent helices with both the open and closed TLs. Of interest, the BH from the experimental open TL structure matches the straight conformation, whereas the BH from the closed TL structure coincides with the bent form. However, in contrast to what the crystal structures seem to suggest, the conclusion we draw from the simulations is that the bent form is more favorable with the open TL than with the closed TL (see Fig. S3), presumably because of the stabilizing interactions of the closed TL with the BH.

Effect of the TL conformation on the active site environment

The active site of PolII is located at the center of the enzyme near the BH and TL. A detailed analysis of DNA polymerase (39), whose active site and overall reaction mechanism resembles that of RNA polymerase, indicates that a catalytically competent reactant state will likely be formed when the phosphorus atom of the primary phosphate of the NTP (Pα) is within 3–3.5 Å from the O3′ atom of the terminal RNA base. In addition, proper coordination of Mg²⁺, three aspartic acid residues, and at least one water molecule is also considered to be essential based on insight from studying DNA polymerase (39). In all but one of the crystal structures of PolII, the NTP-Pα–O3′ distance is ≥4 Å, which is too far for bond formation to take place. Therefore, it appears that a conformational transition toward a precatalytic state is required from the crystal structures. Such a transition may involve coupled dynamics of the BH, the TL, and other nearby structural elements (13,40).

We observed significant differences in the average conformations of the active site environment from the simulations with open and closed TLs (Fig. 2 A). As discussed above, the helix was more bent around the central TAVKTAET (residues 827–834) motif when the TL was open than when it was closed. Furthermore, the average position of the NTP was slightly shifted and its phosphate groups were moved closer to the terminal RNA base in the simulations with the closed TL.

Figure 2.

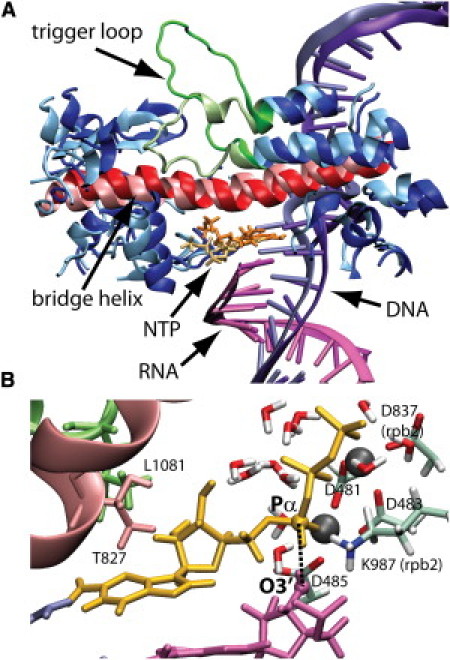
(A) Average structures from simulations of PolII with open (darker shades) and closed (lighter shades) TLs. (B) Snapshot of active site conformation with a short GTP/Pα–RNA/O3′ distance from the closed TL simulation.

To better understand the conformational dynamics that gives rise to the average structures shown in Fig. 2 A, we analyzed the sampling of the BH bending angle (around residues 827/828) versus the Pα–O3′ distance. The resulting PMFs are shown in Fig. 3 (see also the time series in Fig. S10, Fig. S11, and Fig. S12). Different states were observed for both the open and closed TL forms. Of interest, the crystal structures for the open and closed TL forms are located approximately at the center of the conformational ensembles from the simulations, indicating that they may reflect conformational averages rather than single structures. There are two main states: in the first, the BH is nearly straight and the Pα–O3′ distance is >5 Å, and in the second state the BH is more bent and the Pα–O3′ distance is shorter (3.2–4.2 Å). The first state appears to be preferred with the open TL, and the second appears to be preferred with a closed TL. In one of the closed TL simulations, very close Pα–O3′ interactions (3.2–3.5 Å) were observed.

Figure 3.

Potentials of mean force (in kcal/mol) as a function of BH bending angle (cylinder fit to Cα-atoms of rpb1 811–826 vs. 829–844) versus GTP/Pα–RNA/O3′ distance (A and B) and E529–K987 distance (between glutamic acid Oɛ1/Oɛ2 and Nζ; C and D) with open (A and C) and closed (B and D) TLs. Color-coding represents relative free energies as indicated with color bar. Values for experimental structures (2E2H and 2E2J) are indicated with a red X in each graph.

A representative conformation with the short Pα–O3′ distance is shown in Fig. 2 B. This conformation resembles the reactant state in DNA polymerase (39) and thus may be poised for catalysis under the assumption that RNA and DNA polymerase share similar catalytic mechanisms. However, it should be stressed that only quantum mechanical calculations can fully address whether the observed conformation is indeed catalytically competent. Of interest, the TL does not interact directly with the NTP in this conformation except for weak interactions between rpb1 L1081 and the NTP base. There are also no direct interactions with the BH except between rpb1 T827 and the NTP base. Instead, the NTP is well hydrated with a number of water molecules, in particular around the phosphate tail between the NTP and the BH/TL (Fig. 2 B). In addition, we observe a significant shift of the rpb1/rpb2 structure at the N-terminal end of the BH (on the left side in Fig. 2 A) away from the nucleic acid complex. This shift appears to be a consequence of direct interactions of the tip of the closed TL with rpb2, but the reduced propensity toward BH bending with the closed TL may also be a contributing factor. As a result, the short helix at rpb2 765–772, and a loop adjacent to FL2 (rpb2 528–534) near the active site NTP are shifted enough to allow the NTP to slide into what appears to be a catalytically more favorable conformation. Because we observe this transition only in the simulations with the closed TL, our results suggest that TL closing is required before catalysis can proceed; however, further studies are needed to support this point.

Previous genetic studies identified E529 and K987 as mutation-sensitive residues, and suggested that salt-bridge formation between them may be essential for catalysis (40). The rationale for such a mechanism is that K987 interacts with the phosphate tail of the NTP to position the NTP in a catalytically competent configuration. A salt bridge between K987 and E529 may stabilize such an interaction. We analyzed the E529–K987 distance versus the NTP/Pα–O3′ distance from our simulations (see Fig. 3, C and D). We find that a close GTP/Pα–RNA/O3′ distance generally requires the K987–E529 salt bridge to be present. However, we also observe close GTP/Pα–RNA/O3′ distances when the salt bridge is not formed. In fact, the closest P–O3′ distances are formed in the absence of the salt bridge. Thus, one may speculate that the transition toward a catalytically competent state initially involves the K987–E529 salt bridge to position the NTP before the salt bridge opens again to reach the catalytically active form.

Nucleic acid translocation

We will now turn to nucleic acid translocation, which is an obligatory part of the RNA elongation cycle. Translocation of the entire nucleic acid complex may proceed in a concerted fashion, but normal-mode data from our group suggest that downstream DNA and upstream DNA-RNA hybrid translocation may occur separately (22). There is also the unresolved question of whether translocation takes place spontaneously as a result of thermal fluctuations in the Brownian ratchet model or is actively driven in the so-called power-stroke model.

To analyze nucleic acid translocation in the MD simulations, we introduce two reaction coordinates: Upstream translocation is measured as translocation of the C3′ atoms along the backbone of the DNA-RNA hybrid relative to the initial crystallographic structures (cf. Fig. S4). Because the downstream DNA duplex exhibits significant lateral motions that would create artifacts with a backbone-centric measure, downstream translocation is analyzed as the distance of the projections of bases onto a helical axis through T10:N1/N5:N3 from a reference point in the RNA (R8:N1), again relative to the initial crystallographic structures (cf. Fig. S4).

Using these reaction coordinates, we analyzed downstream translocation (at base 9 of the template strand) versus upstream translocation (at base 22 of the template strand) for the simulations with open and closed TLs. The PMF shown in Fig. 4 (see Fig. S8 and Fig. S9 for individual time series) indicates substantial motion of the nucleic acid with both forward and backward translocation relative to the crystal structures. Although Fig. 4 only shows translocation of a single nucleotide, the motions in fact involve the entire downstream and upstream nucleic acid structures (Fig. S5 and Fig. S6). Downstream translocation (−3 to +9 Å) is more pronounced than upstream translocation (−2.5 to +2.5 Å). This is not surprising, because the DNA-RNA is constrained by the protein environment and the presence of an unincorporated NTP in the active site. Simulations with open and closed TLs sample a common state with slight forward translocation relative to the x-ray structures, but more significant forward translocation is only observed in simulations with an open TL. In contrast, significant backward upstream translocation is only seen with a closed TL. This suggests that an open TL may be required for forward translocation, whereas a closed TL would prevent translocation and might even lead to slight backward translocation. Neutral and forward translocated states are dynamically sampled on 10-ns timescales with an open TL (Fig. S8) but not with a closed TL. This supports a modified thermal ratchet mechanism that depends on the TL conformation.

Figure 4.

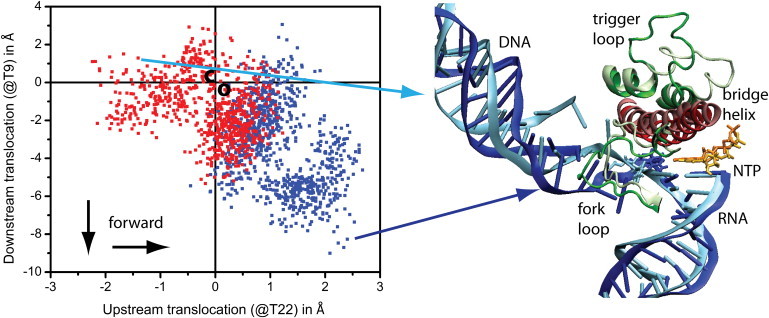
Correlation between downstream and upstream translocation for open (blue) and closed (red) TL conformations. Selected conformations at the extreme ends of the distributions are shown on the right (forward translocated structure with open TL is shown in darker shades, and closed TL structure is shown in light shades). Crystallographic structures are located near (0,0) and indicated by “o” (open TL) and “c” (closed TL).

Structures of the most extreme forward and backward translocated cases with the open and closed TLs are compared in Fig. 4. The translocation of the downstream DNA is clearly visible, whereas the upstream translocation of the DNA-RNA hybrid is more subtle. Fig. 4 includes part of the protein environment to highlight key differences. What appears to be most important for understanding the differences between the open and closed TL conformations is the FL2 conformation. When the TL is closed, the FL2 fills part of the space taken by the DNA template strand in the translocated state, thereby preventing translocation. In contrast, in the open TL structure, the FL2 is located mostly in front of the DNA in the picture, thereby allowing forward translocation. The change in FL2 is the result of both a different loop conformation and an overall shift relative to the PolII structure. The shift is part of the structural changes with the closed TL that were described earlier. It therefore appears that active site conformational changes may be coupled to downstream translocation through the dynamics of FL2 and an adjacent loop (rpb2 528–534).

Discussion and Conclusions

This study describes results from fully atomistic MD simulations of eukaryotic PolII that were conducted to explore dynamic aspects of transcription that are generally not accessible by available crystal structures. Previous normal-mode studies focused primarily on large-scale motions such as the open-closed transition of the DNA-binding cleft (19,20,22). The simulations presented here focus on more-detailed aspects, and in particular we compare simulations started with open and closed TL conformations.

In simulations with an open TL, the enzyme remained close to the crystallographic structure, but the nucleic acid sampled both neutral and forward translocated states. With a closed TL, forward translocation appeared to be inhibited, but at the same time there were subtle changes in the enzyme itself that allowed the active site nucleotide to sample states that may be catalytically more competent compared to the crystal configurations. In more detail, our simulations suggest a mechanism whereby TL closing leads to stabilizing interactions with the BH and the rpb2 subunit that cause BH straightening and a conformational shift in rpb2. The shift in rpb2 in turn appears to be coupled to FL2 closing and conformational changes in an adjacent loop. FL2 closing appears to directly inhibit downstream nucleic acid translocation, whereas the changes in the adjacent loop seem to create space for the active site NTP to slide into what appears to be a catalytically more active conformation. Consequently, we propose that TL closing promotes catalysis and that nucleic acid translocation requires an open TL.

We are asserting here that the differences observed between the simulations with the open and closed TLs are in fact due to the TL conformation. Because simulations were started from different crystal structures, it is also possible that the results reported here result from other differences unrelated to the TL. However, this seems unlikely because of the small difference (1.1 Å Cα RMSD) between the crystal structures when TL residues are excluded compared to the larger deviations from either crystal structure in the simulations. Furthermore, the key conformational changes in the vicinity of the TL described here would be difficult to explain without taking the different TL conformations into account.

Our observation of spontaneous translocation is generally consistent with previous simulations of translocation in T7 RNA polymerase (9), which support a Brownian ratchet mechanism for translocation of the DNA-RNA hybrid. In our simulations we primarily see such a mechanism for the downstream DNA duplex, whereas we observe a tendency toward forward translocation of the DNA-RNA hybrid when the TL is in the open conformation. Both our simulations and the T7 RNA polymerase simulations indicate that the downstream DNA and upstream DNA-RNA may independently translocate, although our simulations also provide evidence for at least some degree of coupling between translocation of the two nucleic acid parts. Our analysis neglects the role of the single-stranded portion of the non-template strand, of the reforming DNA duplex further upstream, and of RNA that may be actively pulled through the RNA exit channel. These parts were omitted mainly because of a lack of reliable structural information. However, the simulation studies with the truncated nucleic acid are justified by the experimental observation that transcription can proceed with a construct similar to the one studied here (41).

The BH was previously proposed to play a role in translocation. In our simulations we see substantial flexibility in the BH, with typical bending angles ranging from 150 to 175°. Consistent with previous ideas about the role of BH bending in translocation (11,42,43), we see more significant BH bending and nucleic acid translocation when the TL is open. This suggests that BH bending plays a role in translocation, but it is unclear from our simulations whether BH bending by itself drives translocation or it simply occurs as part of the translocation process to maintain close interactions with the DNA-RNA hybrid. Instead, it appears that an open conformation of the FL2 may be more critical in allowing the downstream DNA to translocate freely.

Our simulation results generally support a role of TL closing in the authorization of bond formation with a correctly templated active site NTP (12,13). In particular, the simulations support a previously proposed coupling between the TL, BH, FL2, and adjacent loop that affects the active site configuration (12,13). Of interest, the mechanism described here does not simply involve pushing of the TL or BH toward the active site NTP to result in a precatalytic state. Rather, the BH actually straightens out with the closed TL, and the key change that allows the NTP to approach the terminal RNA base more closely appears to be an altered structure in the loop adjacent to FL2 (rpb2 528–534). A critical functional role of this loop is underscored by transcriptional deficiencies of E529 mutants (40). More specifically, it appears that interactions between E529 and K987 play a key role in positioning the NTP in the active site, as previously speculated based on biochemical data (40).

The relaxation of the crystallographic starting structure with the closed TL could be a result of simulation artifacts, but may otherwise indicate that the crystallographic structure with the closed TL is more constrained by the crystal environment than the open TL form. Furthermore, it is unclear whether the TL conformation itself in the crystal structure of PolII with the closed TL represents an equilibrium state. A structure of bacterial RNA polymerase shows a more helical closed TL conformation, and one might wonder whether such a conformation could also be assumed by PolII, or these structural differences represent genuine differences between the prokaryotic and eukaryotic enzymes. In our simulations, the more disordered closed TL in the PolII crystal structure was largely maintained, but it is possible that the simulation timescales were too short to observe a transition to the more helical form seen in the bacterial enzyme.

Based on our results and previous insights into RNA polymerase function, we propose a functional mechanism as follows (Fig. 5): 1) A nucleotide enters the active site of a posttranslocated, preinsertion complex with an open TL. 2) The TL closes upon nucleotide binding. 3) The complex with the closed TL undergoes a conformational change similar to what we observe in our simulations, with the result of a tightened active site with the nucleotide positioned in a precatalytic conformation. 4) Nucleotide incorporation is catalyzed, resulting in a pretranslocated state with a closed TL. 5) The TL opens, possibly coupled to pyrophosphate release. 6) The open TL state undergoes thermal fluctuations between pre- and posttranslocated states. This functional cycle represents a modified Brownian ratchet mechanism whereby a power-stroke action may provide the energy to drive a conformational change that restores the enzyme to a translocation-capable state (with an open TL) after nucleotide incorporation rather than driving translocation itself. One might speculate that such a power-stroke action is coupled directly or indirectly to pyrophosphate release. Such a mechanism would be consistent with single-molecule data reported for bacterial RNA polymerase (8). The proposed mechanism appears also sounder from a thermodynamic perspective than the simple Brownian ratchet mechanisms proposed before, because it provides a clearer picture of how the energy gained during hydrolysis could drive the translocation process.

Figure 5.

Proposed modified Brownian ratchet mechanism for elongation by PolII based on simulation results (see text).

Our simulations directly support parts of the cycle shown in Fig. 5, but do not address the actual transition of the TL from the open to the closed state, how that transition might be involved in nucleotide entry and fidelity control, and whether pyrophosphate release is involved in driving TL reopening. These questions will be the subject of future studies.

The simulations presented here cover 100 ns timescales, which are substantial from a simulation perspective, especially for an enzyme complex of this size. The statistical significance of the reported results relies on combined results from three independent simulations for each system. However, some of the results presented here, such as the GTP/Pα–RNA/O3′ and E529–K987 distances, may not yet be fully converged (see the time series in Fig. S11 and Fig. S12), and the simulations are clearly too short to reach biological timescales of transcription, which are on the order of milliseconds to seconds. The long biological timescales are a result of significant kinetic barriers associated with bond formation (8), pyrophosphate release (8), and, presumably, TL opening and closing. To study the kinetically slower parts of the functional cycle in future studies and directly explore the transition of the TL between open and closed states, investigators will need to employ biased simulation techniques. Such simulations would also be able to more definitely establish a connection between TL dynamics, nucleic acid translocation, and conformational changes in the active site. Furthermore, quantum mechanics/molecular mechanics approaches are required to fully elucidate the chemistry of nucleotide incorporation and confirm the nature of what appears to be a catalytically competent conformation in our closed TL simulations.

It is our hope that the results reported here will encourage further experimental and computational studies that will ultimately lead to a complete understanding of the fundamental process of transcription.