Abstract
Therapies consisting of a combination of agents are an attractive proposition, especially in the context of diseases such as cancer, which can manifest with a variety of tumor types in a single case. However uncovering usable drug combinations is expensive both financially and temporally. By employing computational methods to identify candidate combinations with a greater likelihood of success we can avoid these problems, even when the amount of data is prohibitively large. Hitting Set is a combinatorial problem that has useful application across many fields, however as it is NP-complete it is traditionally considered hard to solve exactly. We introduce a more general version of the problem (α,β,d)-Hitting Set, which allows more precise control over how and what the hitting set targets. Employing the framework of Parameterized Complexity we show that despite being NP-complete, the (α,β,d)-Hitting Set problem is fixed-parameter tractable with a kernel of size O(αdkd) when we parameterize by the size k of the hitting set and the maximum number α of the minimum number of hits, and taking the maximum degree d of the target sets as a constant. We demonstrate the application of this problem to multiple drug selection for cancer therapy, showing the flexibility of the problem in tailoring such drug sets. The fixed-parameter tractability result indicates that for low values of the parameters the problem can be solved quickly using exact methods. We also demonstrate that the problem is indeed practical, with computation times on the order of 5 seconds, as compared to previous Hitting Set applications using the same dataset which exhibited times on the order of 1 day, even with relatively relaxed notions for what constitutes a low value for the parameters. Furthermore the existence of a kernelization for (α,β,d)-Hitting Set indicates that the problem is readily scalable to large datasets.
Introduction
Typically the selection of a drug therapy for a disease is limited to a single drug, however diseases such as cancer may present as a heterogeneous mix of subtypes of the general disease. In cases such as these multi-drug therapies may prove more effective than single drug therapies, and many trials have been conducted to this end [1]–[3]. Furthermore combinations of drugs may allow a more targeted approach for a selection of subtypes of a disease, while minimizing effects on unaffected cells. Unfortunately with the abundance of compounds available for the treatment of many conditions of interest, the time and expense in testing even all two drug combinations may be prohibitive. Therefore a smarter approach is needed. Vazquez [4] introduces the Hitting Set problem for this task in the context of oncological drug therapy. The Hitting Set problem is a combinatorial problem that proves extremely useful in modeling a large variety of problems in many domains including protein network discovery [5], metabolic network analysis [6], diagnostics [7]–[9], gene ontology [10] and gene expression analysis [11], [12].
The Hitting Set Problem
Hitting Set is a combinatorial problem that models the problem
of selecting a small group of elements to represent or cover a collection of
sets. Such a group that covers every set in the collection is called a hitting
set. Finding such a set without any constraint is simple, however if we required
that the size of the hitting set be relatively small, the problem becomes
computationally challenging ( -complete in a formal sense). This difficulty in obtaining
solutions with desirable qualities thus requires more thoughtful approaches.
-complete in a formal sense). This difficulty in obtaining
solutions with desirable qualities thus requires more thoughtful approaches.
We now give some technical details and formal definitions of the problems of interest.
Hitting Set is equivalent to the Set Cover
problem [13], and when otherwise unrestricted, is equivalent
to the Red/Blue Dominating Set
[14]
problem and is related to the  -Feature Set
[15]
problem.
-Feature Set
[15]
problem.
The decision version of the Hitting Set problem is defined as follows:
Hitting Set
Instance: A set
and a collection
and an integer
.
Question: Is there a set
with
such that for every
we have
?
The set  is called a hitting set for
is called a hitting set for
 , or simply a hitting set. For an element
, or simply a hitting set. For an element  and an element
and an element  if
if  we say that
we say that  hits
hits
 . This problem is
. This problem is  -complete even when the maximum size of each element of
-complete even when the maximum size of each element of  is two (by equivalence with Vertex Cover
[13])
and
is two (by equivalence with Vertex Cover
[13])
and  -complete for parameter
-complete for parameter  ; Cotta and Moscato [16] give a parameterized
proof via
; Cotta and Moscato [16] give a parameterized
proof via  -Feature Set and Paz and Moran [17] give a
proof which along with the equivalence of Hitting Set and
Set Cover leads to the same result, though predates the
parameterized complexity framework. However if we restrict the cardinality of
the elements of
-Feature Set and Paz and Moran [17] give a
proof which along with the equivalence of Hitting Set and
Set Cover leads to the same result, though predates the
parameterized complexity framework. However if we restrict the cardinality of
the elements of  to
to  the problem, while remaining
the problem, while remaining  -complete, becomes fixed-parameter tractable where
-complete, becomes fixed-parameter tractable where  is a constant and the parameter is
is a constant and the parameter is  [18]. In this case the problem is known as the
Hitting Set for Sets of Size
[18]. In this case the problem is known as the
Hitting Set for Sets of Size
 or
or  -Hitting Set problem. We note that
Hitting Set has several equivalent formulations, in
particular we choose to use the bipartite graph representation where
-Hitting Set problem. We note that
Hitting Set has several equivalent formulations, in
particular we choose to use the bipartite graph representation where  and
and  form the two partite vertex sets of the graph and an edge
form the two partite vertex sets of the graph and an edge  corresponds to the element
corresponds to the element  being an element of
being an element of  . This allows us to employ some simplifying graph theoretic
terminology and techniques. We generalize this problem to include the case where
we may want the elements of
. This allows us to employ some simplifying graph theoretic
terminology and techniques. We generalize this problem to include the case where
we may want the elements of  to be hit more than once. In particular this includes the case
where we ask if all the sets of
to be hit more than once. In particular this includes the case
where we ask if all the sets of  can be hit
can be hit  times, but extends to the case where the elements of
times, but extends to the case where the elements of  can be hit up to
can be hit up to  times. We encode this by the use of a hitting function
times. We encode this by the use of a hitting function  . Our problem then becomes the
. Our problem then becomes the  -Multiple
-Multiple
 -Hitting Set (or (
-Hitting Set (or ( )-Hitting Set):
)-Hitting Set):
-Hitting Set
Instance: A bipartite graph
where for all
we have
, a hitting function
and an integer
.
Question: Is there a set
with
such that for every
we have
?
When  for all
for all  , (
, ( )-Hitting Set can be
)-Hitting Set can be  -approximated in time
-approximated in time  [19], but cannot be approximated with a factor of
[19], but cannot be approximated with a factor of  for any
for any  unless
unless  [20].
[20].
Results and Discussion
The Fixed-Parameter Tractability of ( )-Hitting Set
)-Hitting Set
As we prove in the
Materials and Methods
section, the ( )-Hitting Set problem is fixed-parameter
tractable, and indeed a more general variant the (
)-Hitting Set problem is fixed-parameter
tractable, and indeed a more general variant the ( )-Hitting Set problem is also fixed parameter
tractable when we take the maximum degree
)-Hitting Set problem is also fixed parameter
tractable when we take the maximum degree  of the class vertices
of the class vertices  as a constant and the size
as a constant and the size  of the hitting set and the maximum desired coverage
of the hitting set and the maximum desired coverage  as a joint parameter. Though the problem is formally hard -
which would normally give the intuition that an exact solution would be too
expensive to compute - the fixed-parameter tractability indicates that it is
likely that we can obtain an exact solution efficiently. Armed with this
knowledge we proceed with the experiments of the following section, where we use
the drug response data of the NCI60 anti-tumor drug screening program to
determine a sets of drugs that hit cancerous cell lines multiple times. These
drug sets are than mathematically supportable candidates for combination
chemotherapies. Moreover we are able to tune the nature of the hitting sets via
the numbers
as a joint parameter. Though the problem is formally hard -
which would normally give the intuition that an exact solution would be too
expensive to compute - the fixed-parameter tractability indicates that it is
likely that we can obtain an exact solution efficiently. Armed with this
knowledge we proceed with the experiments of the following section, where we use
the drug response data of the NCI60 anti-tumor drug screening program to
determine a sets of drugs that hit cancerous cell lines multiple times. These
drug sets are than mathematically supportable candidates for combination
chemotherapies. Moreover we are able to tune the nature of the hitting sets via
the numbers  ,
,  and
and  , which allows us to control which cell lines are targetted
(and which are specifically not) and how much each cell line is hit in the
solution.
, which allows us to control which cell lines are targetted
(and which are specifically not) and how much each cell line is hit in the
solution.
A Comparative Application
The NCI60 human tumor anti-cancer drug screen dataset [21] was established
in the 1980s as an enabling tool for anti-cancer drug development. Included in
this dataset is response data for over  drugs against the
drugs against the  cell lines of the dataset. Vazquez [4] highlights the
utility of a hitting set approach in developing multi-drug therapies for
heterogeneous malignancies; given the plethora of available compounds, testing
multi-drug combinations exhaustively is prohibitive if not impossible. Applying
hitting set to efficacy data measured on an individual basis for each compound
allows us to determine possible drug combinations that would provide the best
chance of efficacy against many cancer types. Using the GI50 response NCI60
dataset (available from the DTP website [22]) Vazquez uncovers a
minimum hitting set with three compounds that cumulatively gives a good response
with all cell lines in the dataset, where a response is considered good if it is
more than two standard deviations above the mean of the z-transformed response
data. Vazquez uses first a greedy highest-degree-first approach to give an
estimate of the maximum size of a minimum hitting set, followed by either an
exhaustive search or simulated annealing, depending on the size of the hitting
set. Vazquez reports times for such approaches on the order of one day on a
desktop computer.
cell lines of the dataset. Vazquez [4] highlights the
utility of a hitting set approach in developing multi-drug therapies for
heterogeneous malignancies; given the plethora of available compounds, testing
multi-drug combinations exhaustively is prohibitive if not impossible. Applying
hitting set to efficacy data measured on an individual basis for each compound
allows us to determine possible drug combinations that would provide the best
chance of efficacy against many cancer types. Using the GI50 response NCI60
dataset (available from the DTP website [22]) Vazquez uncovers a
minimum hitting set with three compounds that cumulatively gives a good response
with all cell lines in the dataset, where a response is considered good if it is
more than two standard deviations above the mean of the z-transformed response
data. Vazquez uses first a greedy highest-degree-first approach to give an
estimate of the maximum size of a minimum hitting set, followed by either an
exhaustive search or simulated annealing, depending on the size of the hitting
set. Vazquez reports times for such approaches on the order of one day on a
desktop computer.
We revisit Vasquez's experiment, using data reduction (though it is not
necessary to employ the more complex rules given in the kernelization proof)
with IBM ILOG CPLEX [23] as the kernel solver by framing the problem
as a integer programming problem. We use the same threshold for the
z-transformation to identify significant response levels. Using this approach we
reduce the time to solve the instance to less than  seconds, where most of the time is spent loading and reducing
the data, with CPLEX solving the integer programming instance in approximately
seconds, where most of the time is spent loading and reducing
the data, with CPLEX solving the integer programming instance in approximately  milliseconds. Furthermore this approach guarantees optimality
in the size of the hitting set.
milliseconds. Furthermore this approach guarantees optimality
in the size of the hitting set.
From here we employ more a more recent version of the NCI60 dataset (2009 as
compared to Vazquez's 2006). At the time of writing, the latest NCI60
dataset includes 14 additional cell lines, however we remove these, as there is
insufficient response data in the dataset, leading to inflated hitting set
sizes. The latest data also includes a further  compounds. We note that employing the new GI50 response data
we are able to uncover
compounds. We note that employing the new GI50 response data
we are able to uncover  element hitting sets involving compounds not available in the
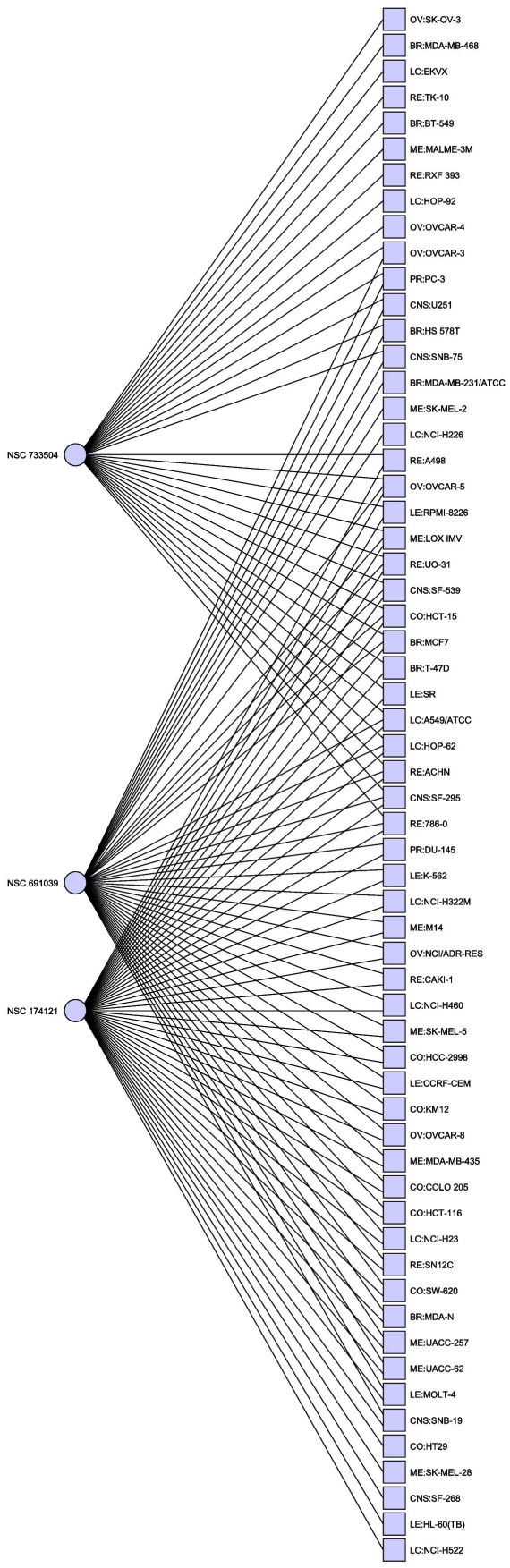
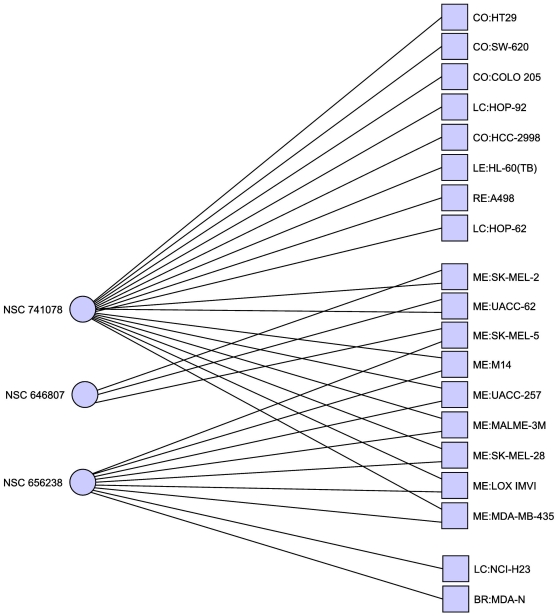
earlier dataset (an example is given in Table 1 and Figure 1), in particular Everolimus (NSC
733504) a drug now used for the treatment of advanced renal cancer which is also
giving positive results in phase II trials for metastatic melanoma [24], [25].
However there have recently been some concerns over the provenance of some of
the cell lines in the NCI60 dataset. In particular Lorenzi et al.
[26]
suggested that the MDA-N cell line, nominally a breast cancer cell line is in
fact similar the M14 and MDA-MB-435 cell lines, and thus should be is in fact a
melanoma cell line. Chambers [27] however suggests that although M14 and
MDA-MB-435 are identical cell lines, they may not in fact be melanoma cell
lines. We do not attempt to resolve this dispute, however with regard to this,
and as a indication of the flexibility of the method we employ we consider both
the case where MDA-N is a breast cancer cell line and the the case where MDA-N
is a melanoma cell line.
element hitting sets involving compounds not available in the
earlier dataset (an example is given in Table 1 and Figure 1), in particular Everolimus (NSC
733504) a drug now used for the treatment of advanced renal cancer which is also
giving positive results in phase II trials for metastatic melanoma [24], [25].
However there have recently been some concerns over the provenance of some of
the cell lines in the NCI60 dataset. In particular Lorenzi et al.
[26]
suggested that the MDA-N cell line, nominally a breast cancer cell line is in
fact similar the M14 and MDA-MB-435 cell lines, and thus should be is in fact a
melanoma cell line. Chambers [27] however suggests that although M14 and
MDA-MB-435 are identical cell lines, they may not in fact be melanoma cell
lines. We do not attempt to resolve this dispute, however with regard to this,
and as a indication of the flexibility of the method we employ we consider both
the case where MDA-N is a breast cancer cell line and the the case where MDA-N
is a melanoma cell line.
Table 1. Minimal hitting set using 2009 NCI60 data.
| NSC Number | Compound Name |
| 174121 | Methotrexate Derivative |
| 691039 | (S)-7-Hydroxy-1,2,3-trimethoxy-10-methylsulfanyl-6,7-dihydro-5H-benzo[a]heptalen-9-one |
| 733504 | Everolimus/Afinitor |
Minimal hitting set for NCI60 GI50 response data from 2009.
Figure 1. Minimal hitting set hitting for the NCI60 dataset.
This hitting set hits all cell lines at least once, but is further optimized to hit all target cell lines the maximal number of times. Of particular note are NSC 174121, a methotrexate derivative and NSC733504, Everolimus/Afinitor, both known anti-cancer agents.
Employing the ( )-Hitting Set model gives more flexibility in
what kind of therapy we would like to pursue. For instance, by choosing
)-Hitting Set model gives more flexibility in
what kind of therapy we would like to pursue. For instance, by choosing  for all vertices, we are able to find a hitting set that hits
every cell line at least twice (see Table 2). However the size of this hitting
set is
for all vertices, we are able to find a hitting set that hits
every cell line at least twice (see Table 2). However the size of this hitting
set is  , which is likely to be beyond the point where the trade off
between anti-cancer efficacy and side effects is acceptable. Fortunately we can
exploit (
, which is likely to be beyond the point where the trade off
between anti-cancer efficacy and side effects is acceptable. Fortunately we can
exploit ( )-Hitting Set more intelligently. For example
we may wish to find a hitting set that specifically targets breast cancer cell
lines – for which we set all breast cancer cell line vertices to have
)-Hitting Set more intelligently. For example
we may wish to find a hitting set that specifically targets breast cancer cell
lines – for which we set all breast cancer cell line vertices to have  and all other cell lines to have
and all other cell lines to have  . This gives a hitting set that hits only
breast cancer cell lines, which may be useful in minimizing unwanted peripheral
damage to non-breast cancer cells. This gives a hitting set with three elements.
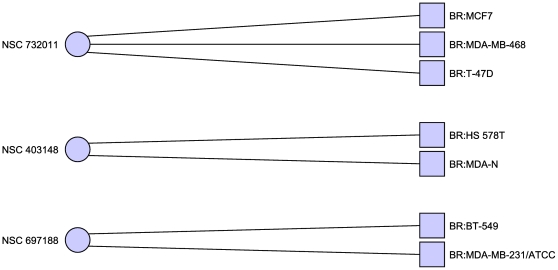
In the case where we considered MDA-N to be a breast cancer cell line (see Table 3 and Figure 2) this set includes
the compound deoxypodophyllotoxin, which is known to induce apoptosis [28]. If
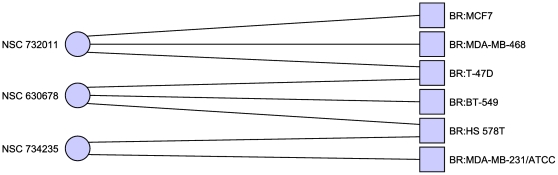
we consider MDA-N as a melanoma cell line we obtain a different hitting set (see
Table 4 and Figure 3). If we relax our
requirements an allow other cell lines to be hit at most once we can obtain a
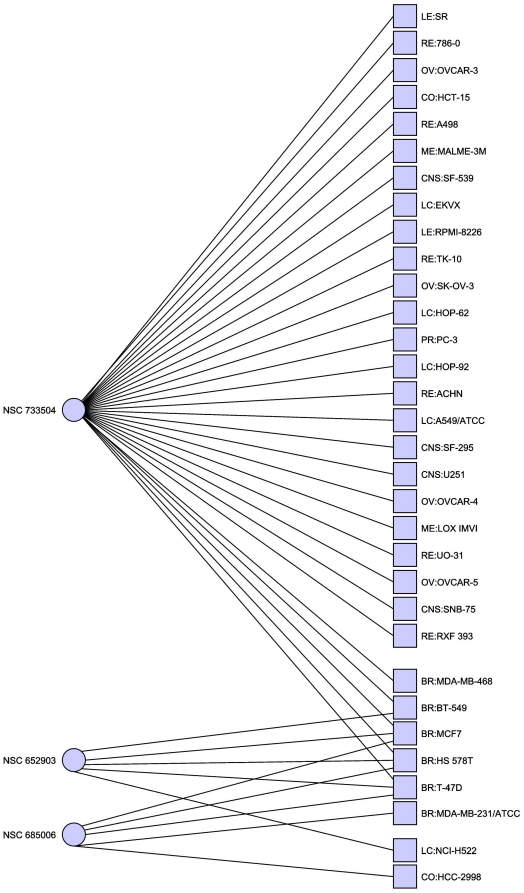
hitting set that hits the breast cancer cell lines more (Table 5 and Figure 4). The results when we set
. This gives a hitting set that hits only
breast cancer cell lines, which may be useful in minimizing unwanted peripheral
damage to non-breast cancer cells. This gives a hitting set with three elements.
In the case where we considered MDA-N to be a breast cancer cell line (see Table 3 and Figure 2) this set includes
the compound deoxypodophyllotoxin, which is known to induce apoptosis [28]. If
we consider MDA-N as a melanoma cell line we obtain a different hitting set (see
Table 4 and Figure 3). If we relax our
requirements an allow other cell lines to be hit at most once we can obtain a
hitting set that hits the breast cancer cell lines more (Table 5 and Figure 4). The results when we set  to
to  for all breast cancer lines are given in Table 6 and Figure 5 (including MDA-N) and
Table 7 and Figure 6 (excluding MDA-N). We
note particularly that in the case where MDA-N is included, the optimal hitting
set uncovered includes Docetaxel, a well known anti-cancer agent [29] for several cancer types including breast cancer.
Interestingly Docetaxel is also currently included in several clinical trials
examining its potential as part of a multi-drug therapy [30]–[34].
for all breast cancer lines are given in Table 6 and Figure 5 (including MDA-N) and
Table 7 and Figure 6 (excluding MDA-N). We
note particularly that in the case where MDA-N is included, the optimal hitting
set uncovered includes Docetaxel, a well known anti-cancer agent [29] for several cancer types including breast cancer.
Interestingly Docetaxel is also currently included in several clinical trials
examining its potential as part of a multi-drug therapy [30]–[34].
Table 2. Minimal double hitting set.
| NSC Number | Compound Name |
| 147340 | Anisomycin hydrochloride |
| 174121 | Methotrexate derivate |
| 314018 | Ansamitocin derivate TN-006 |
| 691039 | (7S)-7-hydroxy-1,2,3-trimethoxy-10-methylsulfanyl-6, 7-dihydro-5H-benzo[a]heptalen-9-one |
| 712807 | Capecitabine |
| 733504 | Everolimus/Afinitor |
Minimal hitting set hitting each cell line at least twice.
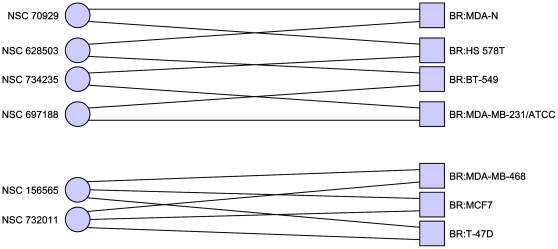
Table 3. Minimal hitting set targeting only breast cancer.
| NSC Number | Compound Name |
| 403148 | Deoxypodophyllotoxin |
| 697188 | 2-(4-methoxyphenyl)-5-[8-[5-(4-methoxyphenyl)-1,3,4-oxadiazol-2-yl]octyl]-1,3,4-oxadiazole |
| 732011 | 21-(2-N,N-Diethylaminoethyl)oxy-7.alpha.-methyl-19-norpregna-1,3,5(10)-triene-3-O-sulfamate |
Minimal hitting set hitting breast cancer cell lines at least once, and all other cell lines zero times.
Figure 2. Minimal hitting set hitting only breast cancer cell lines.
Including the disputed MDA-N cell line. This hitting set also reveals additional structure with each drug targeting a specific, disjoint subset of the breast cancer cell lines. Only cell lines with at least one adjacent compound are shown.
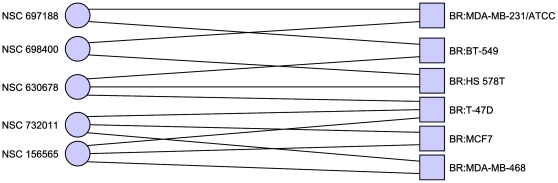
Table 4. Minimal hitting set targeting only breast cancer without MDA-N.
| NSC Number | Compound Name |
| 630678 | Streptomyces antibiotic |
| 732011 | 21-(2-N,N-Diethylaminoethyl)oxy-7.alpha.-methyl-19-norpregna-1,3,5(10)-triene-3-O-sulfamate |
| 734235 | isoindolo[1,2-a]quinoxalin-4(5H)-one |
Minimal hitting set hitting breast cancer cell lines at least once, and all other cell lines zero times.
Figure 3. Minimal hitting set hitting only breast cancer cell lines.
Excluding the disputed MDA-N cell line. In this case the hitting set is much less clearly separated, though two of the cell lines are now hit twice. Only cell lines with at least one adjacent compound are shown.
Table 5. Minimal hitting set targeting breast cancer but allowing other cell lines to be hit.
| NSC Number | Compound Name |
| 652903 | Saframycin AR1(AH2) |
| 685006 | 2-imino-8-methoxy-N-phenylchromene-3-carboxamide |
| 733504 | Everolimus/Afinitor |
Minimal hitting set hitting breast cancer cell lines at least once, and all other cell lines zero times.
Figure 4. Minimal hitting set hitting only breast cancer cell lines.
Excluding the disputed MDA-N cell line. In this case we allow non-breast cancer cell lines to be hit at most once. By relaxing the restriction on hitting non-breast cancer cell lines, we obtain a hitting set which hits more of the breast cancer cell lines repeatedly. The trade-off being that other cell lines are also affected, increasingly the likelihood that non-cancerous cells are also affected by the treatment, as the compounds are less specific to a particular genetic signature. Only cell lines with at least one adjacent compound are shown.
Table 6. Minimal hitting set hitting breast cancer twice, and no others, with MDA-N.
| 70929 | Hedamycin |
| 156565 | 1-hydroxy-4-[4-(2-hydroxyethyl)anilino]anthracene-9,10-dione |
| 628503 | Docetaxel |
| 697188 | 2-(4-methoxyphenyl)-5-[8-[5-(4-methoxyphenyl)-1,3,4-oxadiazol-2-yl]octyl]-1,3,4-oxadiazole |
| 732011 | 21-(2-N,N-Diethylaminoethyl)oxy-7.alpha.-methyl-19-norpregna-1,3,5(10)-triene-3-O-sulfamate |
| 734235 | isoindolo[1,2-a]quinoxalin-4(5H)-one |
Minimal hitting set hitting breast cancer cell lines at least once, and all other cell lines zero times.
Figure 5. Minimal hitting set hitting breast cancer cell lines twice.
Including the disputed MDA-N cell line. In this case the breast cancer cell lines separate neatly into two groups, with the first group forming a cycle and the second group forming a complete bipartite graph. Only cell lines with at least one adjacent compound are shown.
Table 7. Minimal hitting set hitting breast cancer twice, and no others, without MDA-N.
| 156565 | 1-hydroxy-4-[4-(2-hydroxyethyl)anilino]anthracene-9,10-dione |
| 630678 | Streptomyces antibiotic |
| 697188 | 2-(4-methoxyphenyl)-5-[8-[5-(4-methoxyphenyl)-1,3,4-oxadiazol-2-yl]octyl]-1,3,4-oxadiazole |
| 698400 | 5-(1,3-benzodioxol-5-yl)-1,2,3,4-tetrahydrobenzo[a]phenanthridine |
| 732011 | 21-(2-N,N-Diethylaminoethyl)oxy-7.alpha.-methyl-19-norpregna-1,3,5(10)-triene-3-O-sulfamate |
Minimal hitting set hitting breast cancer cell lines at least once, and all other cell lines zero times.
Figure 6. Minimal hitting set hitting breast cancer cell lines twice.
Excluding the disputed MDA-N cell line. Without the MDA-N cell line, the breast cancer cell lines do not separate, although the complete bipartite component is a subgraph of this graph, however we gain a greater number of hits per cell line in this case. Only cell lines with at least one adjacent compound are shown.
In another example, we may wish to target melanoma cell lines exclusively, and
furthermore, we may wish to attack each cell line with at least two drugs at
once. However in this case (where  for melanoma cell lines and
for melanoma cell lines and  for all others) the minimal hitting set size is
for all others) the minimal hitting set size is  (or
(or  if MDA-N is included as a melanoma cell line – Table 8 and Figures 7 & 8). Considering that a
therapeutic cocktail involving
if MDA-N is included as a melanoma cell line – Table 8 and Figures 7 & 8). Considering that a
therapeutic cocktail involving  compounds may have excessive side effects, we can relax the
requirements, and allow
compounds may have excessive side effects, we can relax the
requirements, and allow  for non-melanoma cell lines. In this case we find that the
smallest hitting set is of size
for non-melanoma cell lines. In this case we find that the
smallest hitting set is of size  . By altering the focus when solving the kernel by fixing the
hitting set size (
. By altering the focus when solving the kernel by fixing the
hitting set size ( ) at
) at  and maximizing the total degree of the vertices in the hitting
set, subject to the
and maximizing the total degree of the vertices in the hitting
set, subject to the  and
and  constraints, we can obtain the minimal size hitting set that
hits our targets as much as possible, within the bounds given by the
constraints. This results in the hitting sets in Tables 9 & 10 and Figures 9 & 10. Of note is AZD6244, which is currently
involved in
constraints, we can obtain the minimal size hitting set that
hits our targets as much as possible, within the bounds given by the
constraints. This results in the hitting sets in Tables 9 & 10 and Figures 9 & 10. Of note is AZD6244, which is currently
involved in  anti-cancer drug trials [35] and has
been identified as a potent kinase inhibitor [36], [37].
anti-cancer drug trials [35] and has
been identified as a potent kinase inhibitor [36], [37].
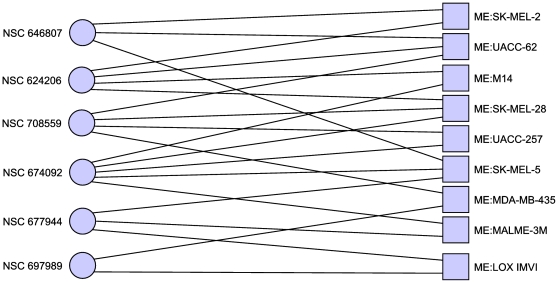
Table 8. Minimal hitting set targeting melanoma twice, without MDA-N.
| 624206 | N-[2-[(4-chlorophenyl)methyldisulfanyl]ethyl]decan-1-amine hydrochloride |
| 646807 | 2-(2-Isonicotinoylhydrazino)-N-(3-methyl-1,4-dioxo-1,4-dihydro-2-naphthalenyl)-2-oxoacetamide |
| 674092 | 2-phenyl-N-[3-[4-[3-[(2-phenylquinoline-4-carbonyl)amino]propyl]piperazin-1-yl]propyl]quinoline-4-carboxamide hydrochloride |
| 677944 | 6-[2-(4-hydroxy-3-methoxyphenyl)ethylamino]quinoline-5,8-dione |
| 697989 | dicopper 2-acetyloxy-3,5-di(propan-2-yl)benzoate |
| 708559 | 2-(3,4-dichlorophenyl)-N-methyl-N-[3-[methyl(3-pyrrolidin-1-ylpropyl)amino]propyl]acetamide |
Minimal hitting set hitting melanoma cell lines at least twice and no others. This result does not include MDA-N as a melanoma cell line.
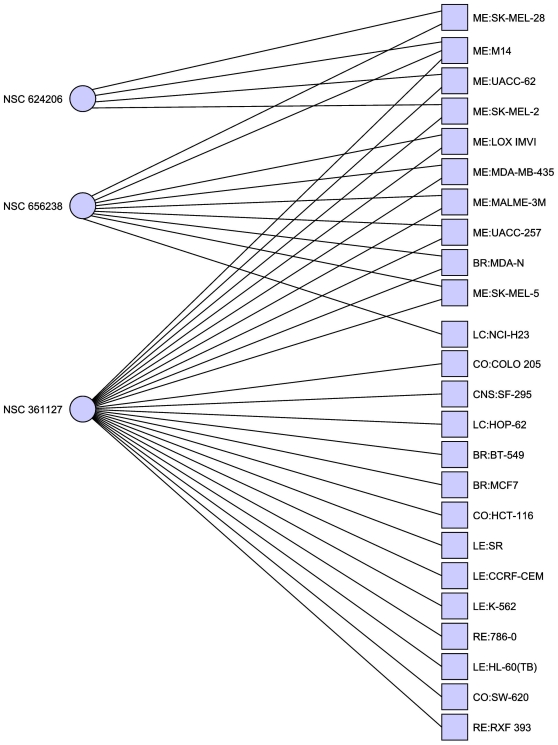
Figure 7. Minimal hitting set hitting melanoma cell lines at least 2 and no other cell lines.
This hitting set also maximizes the number of hits on the melanoma cell lines. Only cell lines with at least one adjacent compound are shown.
Figure 8. Minimal hitting set hitting melanoma cell lines at least 2 and no other cell lines.
Including the disputed MDA-N cell line. It is interesting to note that
including MDA-N as a melanoma cell line rather than a breast cancer cell
line reduces the size of the minimal hitting set from  to
to  . This hitting set also maximizes the number of hits on
the melanoma cell lines. Only cell lines with at least one adjacent
compound are shown.
. This hitting set also maximizes the number of hits on
the melanoma cell lines. Only cell lines with at least one adjacent
compound are shown.
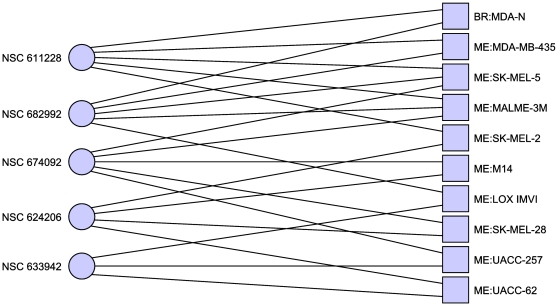
Table 9. Minimal hitting set targeting melanoma, without MDA-N.
| NSC Number | Compound Name |
| 646807 | 2-(2-Isonicotinoylhydrazino)-N-(3-methyl-1,4-dioxo-1,4-dihydro-2-naphthalenyl)-2-oxoacetamide |
| 656238 | 2-Methyl-4,8-dihydrobenzo[1,2-b:5,4-b′]dithiophene-4,8-dione |
| 741078 | AZD6244 (ARRY-142886) |
Minimal hitting set hitting melanoma cell lines at least twice, all others at most once, maximizing the degree of the melanoma cell line vertices.
Table 10. Minimal hitting set targeting melanoma, with MDA-N.
| NSC Number | Compound Name |
| 361127 | Destruxin E |
| 624206 | N-[2-[(4-chlorophenyl)methyldisulfanyl]ethyl]decan-1-amine hydrochloride |
| 656238 | 2-Methyl-4,8-dihydrobenzo[1,2-b:5,4-b′]dithiophene-4,8-dione |
Minimal hitting set hitting melanoma cell lines at least twice, all others at most once, maximizing the degree of the melanoma cell line vertices.
Figure 9. Minimal hitting set hitting melanoma cell lines at least 2 and all other cell lines at most once.
For this we consider MDA-N as a non-melanoma cell line, however it is also hit by the hitting set, though only once. This hitting set also maximizes the number of hits on the melanoma cell lines. Only cell lines with at least one adjacent compound are shown.
Figure 10. Minimal hitting set hitting melanoma cell lines at least 2 and all other cell lines at most once.
Including MDA-N as a melanoma cell line. The key difference with the case where we consider MDA-N to be a non-melanoma cell line is that in this case we obtain a hitting set that hits the melanoma cell lines slightly more. Only cell lines with at least one adjacent compound are shown.
Conclusion
Given the size of modern datasets, and the expectation that they will only get
larger, it is clear that we require efficient approaches to solving important
computational biology problems. The first phase of any such approach is simply
defining the problem at hand. Unfortunately once clearly stated, many such
problems are  -hard or worse. However this need not mean that we must resort
to inexact or approximate approaches, which could be undesirable in a field such
as drug selection. Parameterized Complexity provides a toolkit for dealing with
nominally hard problems, and identifying cases where despite super-polynomial
running times, we may still expect good performance.
-hard or worse. However this need not mean that we must resort
to inexact or approximate approaches, which could be undesirable in a field such
as drug selection. Parameterized Complexity provides a toolkit for dealing with
nominally hard problems, and identifying cases where despite super-polynomial
running times, we may still expect good performance.
The drug selection problem as examined here is one such problem. It is modeled
well by the  -Hitting Set problem, which is
fixed-parameter tractable when parameterized by the maximum size of the hitting
set. Therefore we can expect that despite being
-Hitting Set problem, which is
fixed-parameter tractable when parameterized by the maximum size of the hitting
set. Therefore we can expect that despite being  -complete, it would be relatively quick to solve when these
parameters are small. However we demonstrate that the much more flexible variant (
-complete, it would be relatively quick to solve when these
parameters are small. However we demonstrate that the much more flexible variant ( )-Hitting Set is also fixed-parameter
tractable, with only the addition of a single parameter - the maximum of the
minimum number of times any vertex should be hit. With (
)-Hitting Set is also fixed-parameter
tractable, with only the addition of a single parameter - the maximum of the
minimum number of times any vertex should be hit. With ( )-Hitting Set we are able to better control
the nature of the hitting set uncovered, and thus tailor any such hitting set to
a useful set of constraints, such as limits on which cell lines are to be hit,
the maximum any of these can be hit and of course the minimum number of times
any cell line should be hit. Moreover we can solve this problem quickly, and
guarantee optimality - without any notable restrictions on the parameters and
constants. This allows the quick generation of possible drug combinations for
testing, with guarantees of a certain baseline performance, eliminating the need
to exhaustively test all possible combinations, which would be financially and
temporally prohibitive.
)-Hitting Set we are able to better control
the nature of the hitting set uncovered, and thus tailor any such hitting set to
a useful set of constraints, such as limits on which cell lines are to be hit,
the maximum any of these can be hit and of course the minimum number of times
any cell line should be hit. Moreover we can solve this problem quickly, and
guarantee optimality - without any notable restrictions on the parameters and
constants. This allows the quick generation of possible drug combinations for
testing, with guarantees of a certain baseline performance, eliminating the need
to exhaustively test all possible combinations, which would be financially and
temporally prohibitive.
In brief this paper provides a robust and flexible methodology for multiple drug
selection, which can easily be applied to other domains that are modeled by the  -Hitting Set problem, with a sound
theoretical background as to why and how the problem can be solved efficiently,
despite its
-Hitting Set problem, with a sound
theoretical background as to why and how the problem can be solved efficiently,
despite its  -completeness. Moreover the existence of a kernelization for (
-completeness. Moreover the existence of a kernelization for ( )-Hitting Set indicates that even without
using a specialized commercial solver such as CPLEX, the problem is readily
scalable to large datasets. Given the speed at which we are able to solve
instances with on the order of
)-Hitting Set indicates that even without
using a specialized commercial solver such as CPLEX, the problem is readily
scalable to large datasets. Given the speed at which we are able to solve
instances with on the order of  vertices, we can expect that much larger datasets are also
solvable in a reasonable time.
vertices, we can expect that much larger datasets are also
solvable in a reasonable time.
A future extension that may be of interest would be to somehow encode in the problem the notion that some hitting vertices are incompatible, e.g., two compound may have severe adverse interactions, and thus can never be used together as a therapy, regardless of their individual usefulness.
Materials and Methods
Dataset and Computational Method
The dataset primarily employed is the NCI60 DTP Human Tumor Cell Line Screen, available from [22]. We use the version released in October 2009, and downloaded in April 2010. The raw dataset is presented as a series of cell line and compound pairs, along with the GI50 response measurement (the method for producing the measurements is also detailed by [22]) for that pair plus concentration information and statistical information. Where there are multiple entries for the same compound-cell line pair, we select the entry resulting from the experiment using the highest concentration of the compound. We extract this data into a matrix cross indexed by the NSC number of the compound and the name of the cell line. Where an entry does not exist for a given compound-cell line pair, we enter “NA” for that entry in the matrix.
Once the data is in this matrix format we threshold the data according to the
method used by Vazquez [4] whereby the raw data is subject to a
z-transformation over a logarithmic scale and then any value above a certain
threshold expressed in terms of the standard deviation to  , and anything below, including “NA”
values, to
, and anything below, including “NA”
values, to  . In line with Vazquez we choose two standard deviations as our
particular threshold for this paper, though this is adjustable.
. In line with Vazquez we choose two standard deviations as our
particular threshold for this paper, though this is adjustable.
We then construct a graph for the hitting set instance using the Java Universal
Network/Graph Framework (JUNG) [38] with the SetHypergraph class, representing
each compound with a vertex and each cell line with a (hyper)edge which carries
a weight indicating the number of times that edge is to be hit. This graph is
then reduced to remove vertices of zero degree, edges with no incident vertices
(which are noted as technically this would indicate a no instance unless that
edge does not require hitting) and vertices that are only adjacent to edges that
require zero hits. This basic reduction alone typically reduces the number of
vertices significantly, bringing the graph within a reasonable size for
immediate processing. From a theoretical standpoint the constant  is of importance, for the graph constructed as stated,
is of importance, for the graph constructed as stated,  (as we allow the natural value, rather than imposing an
external limit). In practice a
(as we allow the natural value, rather than imposing an
external limit). In practice a  value of this magnitude proves perfectly workable, and
returning to the theoretical viewpoint indicates that the instance is in a sense
already kernelized.
value of this magnitude proves perfectly workable, and
returning to the theoretical viewpoint indicates that the instance is in a sense
already kernelized.
Once the graph is reduced, we construct an integer programming instance
equivalent of the problem given the graph, and pass this instance to CPLEX [23]
(version 11.200) and search for an optimal solution to one of two objective
functions, given the constraints of the number of hits for each cell line (given
by the  value). The first objective function simply minimizes the size
of the hitting set (
value). The first objective function simply minimizes the size
of the hitting set ( ), for the second objective function we fix the size of the
hitting set, and maximize the number of hits on vertices where no maximum number
of hits has been set (the
), for the second objective function we fix the size of the
hitting set, and maximize the number of hits on vertices where no maximum number
of hits has been set (the  value). As part of this search CPLEX may apply some
unspecified proprietary reduction process.
value). As part of this search CPLEX may apply some
unspecified proprietary reduction process.
The figures were created using yEd Graph Editor [39].
The computer hardware employed is a Dell PowerEdge III Dual Xeon 5550 server with 32Gb of RAM, operating Red Hat Linux 64 bit EL 4 Server.
Theoretical Background and Kernelization Proof
Graph Theory and Notation
A (simple undirected) graph consists of a set  (the vertices), and a set
(the vertices), and a set  of two element subsets of
of two element subsets of  (the edges). A bipartite graph is a graph
where the vertices are partitioned into two partite sets, where all edges
have one endpoint in one set and the other endpoint in the other set, i.e.,
(the edges). A bipartite graph is a graph
where the vertices are partitioned into two partite sets, where all edges
have one endpoint in one set and the other endpoint in the other set, i.e.,  and
and  .
.
Given a graph  and two vertices
and two vertices  , we denote the edge between
, we denote the edge between  and
and  by
by  or equivalently
or equivalently  . Given two vertices
. Given two vertices  in
in  , if there is an edge
, if there is an edge  we say that
we say that  and
and  are adjacent and the
are adjacent and the  and
and  are incident on
are incident on  . Given a vertex
. Given a vertex  , the set
, the set  is the (open) neighborhood of
is the (open) neighborhood of  and consists off all vertices adjacent to
and consists off all vertices adjacent to  in
in  , we extend this notion in the natural way to sets of
vertices.
, we extend this notion in the natural way to sets of
vertices.
Parameterized Complexity
A parameterized (decision) problem is a formally defined
computational problem consisting of three components; the input, a special
part of the input called the parameter, and the question. Following Flum and
Grohe's [40] definition we may assume that the
parameter is derived from a polynomial time computable mapping from the
input to the natural numbers. A parameterized problem  is fixed-parameter tractable if there is
an algorithm
is fixed-parameter tractable if there is
an algorithm  such that for every instance
such that for every instance  where
where  is the input,
is the input,  is the parameter and
is the parameter and  ,
,  correctly answers Yes or No in time
bounded by
correctly answers Yes or No in time
bounded by  where
where  is a polynomial and
is a polynomial and  is a computable function.
is a computable function.
A polynomial time kernelization (or just
kernelization) is a polynomial time mapping that given
an instance  of a parameterized problem produces a new instance
of a parameterized problem produces a new instance  of the problem such that:
of the problem such that:
 is a Yes-instance if and only if
is a Yes-instance if and only if  is a Yes-instance,
is a Yes-instance, and
and for some computable function
for some computable function  .
.
It is easy to see that if a problem has kernelization, then it is fixed-parameter tractable. It is also easy to prove that if a problem is fixed-parameter tractable, then it has a kernelization [41].
Parameterized complexity has a fully developed theory for determining when a
problem is unlikely to be fixed-parameter tractable, but as this is not
necessary for this work, we refer the reader to the monographs of Flum and
Grohe [40] and Downey and Fellows [42] for full
discussion, and simply state that if a problem is  -hard or
-hard or  -complete for any
-complete for any  , then the problem is not fixed-parameter tractable unless
certain complexity theoretic assumptions are false, which seems
unlikely.
, then the problem is not fixed-parameter tractable unless
certain complexity theoretic assumptions are false, which seems
unlikely.
The Fixed-Parameter Tractability of ( )-Hitting Set
)-Hitting Set
Our kernelization for ( )-Hitting Set follows the basic format of
Abu-Khzam's kernelization for
)-Hitting Set follows the basic format of
Abu-Khzam's kernelization for  -Hitting Set
[18].
-Hitting Set
[18].
Let  be an instance of (
be an instance of ( )-Hitting Set which we assume to have been
preprocessed for nonsense input such as vertices
)-Hitting Set which we assume to have been
preprocessed for nonsense input such as vertices  with
with  or
or  . Therefore we may assume that for all
. Therefore we may assume that for all  we have
we have  and that for all vertices
and that for all vertices  we have
we have  .
.
We first apply Reduction Rules 1 to 3 exhaustively, before applying Rules 4 and 5.:
Reduction Rule 1: If there is a vertex  with
with  then for every vertex
then for every vertex  for every vertex
for every vertex  reduce
reduce 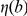 by
by  , delete
, delete  from
from  and reduce
and reduce  by
by  . Finally, delete
. Finally, delete  from
from  .
.
Lemma 1 Reduction Rule 1 is sound.
Proof. If such a vertex  exists, then all its neighbors in
exists, then all its neighbors in  must be in the hitting set, and we can remove them from the
graph after suitably noting the effect for the vertices of
must be in the hitting set, and we can remove them from the
graph after suitably noting the effect for the vertices of  .
.
Note in particular that this rule effectively allows us to assume that  is at most
is at most  . This will be used implicitly in Reduction Rule 4.
. This will be used implicitly in Reduction Rule 4.
Reduction Rule 2: If there is a vertex  with
with  , delete
, delete  from
from  .
.
Lemma 2 Reduction Rule 2 is sound.
Proof. Clearly  requires no vertices to hit it, so may be ignored.
requires no vertices to hit it, so may be ignored.
Reduction Rule 3: If there are two vertices  such that
such that  and
and  , delete
, delete  from
from  .
.
Lemma 3 Reduction Rule 3 is sound.
Proof. If two such vertices  and
and  exist, then any hitting set that hits
exist, then any hitting set that hits  at least
at least  times will hit
times will hit  at least
at least  times.
times.
Let  be a set of size
be a set of size  vertices such that
vertices such that  is the pairwise intersection of the neighborhoods of a vertex
set
is the pairwise intersection of the neighborhoods of a vertex
set  . Let
. Let  .
.
Reduction Rule 4: Let  and
and  be vertex sets as described. For each
be vertex sets as described. For each  such that
such that  add a vertex
add a vertex  to
to  with
with  and edges such that
and edges such that  and delete
and delete  from
from  .
.
Lemma 4 Reduction Rule 4 is sound.
Proof. Let  be a Yes-instance of (
be a Yes-instance of ( )-Hitting Set. Then there is a set
)-Hitting Set. Then there is a set  with
with  that hits each element
that hits each element  of
of  at least
at least  times. Assume that there are sets
times. Assume that there are sets  and
and  as described in the reduction rule and that for some
as described in the reduction rule and that for some  we have that
we have that  . Let
. Let  be the subset of
be the subset of  that hits
that hits  . Assume further that
. Assume further that  , then for each
, then for each  there is at least one other vertex in
there is at least one other vertex in  , but then
, but then  , which contradicts the assumption that
, which contradicts the assumption that  is a Yes-instance.
is a Yes-instance.
Therefore the set  must be hit by
must be hit by  , so we may restrict our search to the intersection.
, so we may restrict our search to the intersection.
Lemma 5 Reduction Rule 4 can be computed in polynomial time.
Proof. Given a set of vertices  for some
for some  with
with  , we construct an auxiliary graph
, we construct an auxiliary graph  by taking for each
by taking for each  the subgraph of
the subgraph of  induced by the vertices
induced by the vertices  . If there is a maximum matching in
. If there is a maximum matching in  of size greater than
of size greater than  , then the matched vertices from
, then the matched vertices from  form the required set with pairwise neighbohood intersection
form the required set with pairwise neighbohood intersection  .
.
As  is a constant, we can iterate over all sets of vertices of
size
is a constant, we can iterate over all sets of vertices of
size  in time
in time  . The matchings can be computed in time
. The matchings can be computed in time  .
.
Definition 6 (Weakly Related Vertices) Given two vertices  ,
,  and
and  are weakly related if
are weakly related if  , and both
, and both  and
and  .
.
Let  be a maximal set of pairwise weakly related vertices. Let
be a maximal set of pairwise weakly related vertices. Let  be a set of vertices, and denote by
be a set of vertices, and denote by  the set of vertices of
the set of vertices of  whose neighborhood is a superset of
whose neighborhood is a superset of  . Further denote by
. Further denote by  the subset of
the subset of  where for each
where for each  we have
we have  .
.
Reduction Rule 5: Compute a maximal collection  of pairwise weakly related vertices. If
of pairwise weakly related vertices. If  apply the following algorithm:
apply the following algorithm:
for
 downto
downto
 do
do
for
 downto
downto
 do
do
for each set  where
where  and
and  do
do
if
 then
then
Add a vertex  to
to  , edges such that
, edges such that  and set
and set  .
.
Delete  from
from  .
.
Lemma 7 Reduction Rule 5 is sound.
Proof. We defer the proof of the bound on the size of  until the proof of Lemma 8.
until the proof of Lemma 8.
Let  be a Yes-instance of (
be a Yes-instance of ( )-Hitting Set. Then there is a set
)-Hitting Set. Then there is a set  that hits
that hits  sufficiently. For sets of size
sufficiently. For sets of size  , Reduction Rule 4 proves the soundness of the first iteration
of the outer loop.
, Reduction Rule 4 proves the soundness of the first iteration
of the outer loop.
For each other iteration, assume that the iteration for sets of size  holds, then let
holds, then let  be set of size
be set of size  where
where  for some
for some  . If
. If  then by the pigeon hole principle there is some vertex
then by the pigeon hole principle there is some vertex  that is in at least
that is in at least  neighborhoods of vertices in
neighborhoods of vertices in  , but then
, but then  is a set that is the intersection of at least
is a set that is the intersection of at least  neighborhoods of vertices in some subset of
neighborhoods of vertices in some subset of  , contradicting the correctness of the previous iteration.
Therefore the entire set of vertices hitting each
, contradicting the correctness of the previous iteration.
Therefore the entire set of vertices hitting each  vertex is contained within
vertex is contained within  if
if  , so we may replace
, so we may replace  with a single vertex.
with a single vertex.
Note also that for each element of  there is at most
there is at most  sets
sets  , so we may iterate through all sets in time
, so we may iterate through all sets in time  , so we can perform the replacements in polynomial time.
, so we can perform the replacements in polynomial time.
Lemma 8
If
 is a Yes-instance
of (
is a Yes-instance
of ( )-Hitting Set, reduced under
Reduction Rules 1 to 5, then
)-Hitting Set, reduced under
Reduction Rules 1 to 5, then
 .
.
Proof. If  is a Yes-instance of (
is a Yes-instance of ( )-Hitting Set, then there is a set
)-Hitting Set, then there is a set  such that for every
such that for every  we have
we have  with
with  .
.
Claim 9
 .
.
By construction, every vertex in  with degree at most
with degree at most  is in
is in  . Assume there is some
. Assume there is some  with
with  and
and  , then there must be some vertex
, then there must be some vertex  such that
such that  , but then as the degree of any vertex in
, but then as the degree of any vertex in  is at most
is at most  ,
,  , and Reduction Rule 3 would apply. Therefore there are no
vertices from
, and Reduction Rule 3 would apply. Therefore there are no
vertices from  not in
not in  .
.
Claim 10
 .
.
As  hits each vertex of
hits each vertex of  at least once, by Reduction Rule 5 each element of
at least once, by Reduction Rule 5 each element of  as a singleton is in the neighborhood of at most
as a singleton is in the neighborhood of at most  vertices from
vertices from  . Therefore
. Therefore  .
.
Combining Claims 9 and 10 we have  . As each vertex of
. As each vertex of  has degree at most
has degree at most  , there are at most
, there are at most  vertices in
vertices in  , and the bound follows.
, and the bound follows.
Theorem 11 ( )-Hitting Set
is fixed-parameter tractable with parameter
)-Hitting Set
is fixed-parameter tractable with parameter
 and has a kernel of size at most
and has a kernel of size at most
 .
.
We note that although  must be a constant to obtain a polynomial time kernelization,
must be a constant to obtain a polynomial time kernelization,  may be alternatively given as an additional parameter, without
change to the kernelization.
may be alternatively given as an additional parameter, without
change to the kernelization.
This kernelization may be extended to an even more general version of the problem, where we not only specify lower bounds for the number of hits, but also upper bounds:
-Hitting Set
Instance: A bipartite graph
where for all
we have
, two hitting functions
and
and an integer
.
Question: Is there a set
with
such that for every
we have
?
Corollary 12 ( )-Hitting Set
is fixed-parameter tractable with parameter
)-Hitting Set
is fixed-parameter tractable with parameter
 and has a kernel of size at most
and has a kernel of size at most
 .
.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: The authors acknowledge the support of the Hunter Medical Research Institute, The University of Newcastle, and ARC Discovery Project DP0773279 (Application of novel exact combinatorial optimisation techniques and metaheuristic methods for problems in cancer research). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Albain KS, Crowley JJ, LeBlanc M, Livingston RB. Determinants of improved outcome in small-cell lung cancer: an analysis of the 2,580-patient southwest oncology group data base. Journal of Clinical Oncology. 1990;8:1563–1574. doi: 10.1200/JCO.1990.8.9.1563. [DOI] [PubMed] [Google Scholar]
- 2.Flamant F, Schwartz L, Delons E, Caillaud JM, Hartmann O, et al. Nonseminomatous malignant germ cell tumors in children. Multidrug therapy in stages III and IV. Cancer. 1984;54:1687–1691. doi: 10.1002/1097-0142(19841015)54:8<1687::aid-cncr2820540833>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 3.Fu KK, Silverberg IJ, Phillips TL, Friedman MA. Combined radiotherapy and multidrug chemotherapy for advanced head and neck cancer: results of a radiation therapy oncology group pilot study. Cancer Treatment Reports. 1979;63:351–357. [PubMed] [Google Scholar]
- 4.Vazquez A. Optimal drug combinations and minimal hitting sets. BMC Systems Biology. 2009;3:81–86. doi: 10.1186/1752-0509-3-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Berman P, DasGupta B, Sontag ED. Randomized approximation algorithms for set multicover problems with applications to reverse engineering of protein and gene networks. Discrete Applied Mathematics. 2007;155:733–749. [Google Scholar]
- 6.Haus UU, Klamt S, Stephen T. Computing knock-out strategies in metabolic networks. Journal of Computational Biology. 2008;15:259–268. doi: 10.1089/cmb.2007.0229. [DOI] [PubMed] [Google Scholar]
- 7.de Kleer J, Mackworth AK, Reiter R. Characterizing diagnoses and systems. Artificial Intelligence. 1992;56:197–222. [Google Scholar]
- 8.Leipins GE, Potter WD. A genetic algorithm approach to multiple-fault diagnosis. In: Davis L, editor. Handbook of Genetic Algorithms, Van Nostrand Reinhold Company; 1991. pp. 237–250. [Google Scholar]
- 9.Reiter R. A theory of diagnosis from first principles. Artificial Intelligence. 1987;32:57–95. [Google Scholar]
- 10.Hvidsten TR, Lægreid A, Komorowski HJ. Learning rule-based models of biological process from gene expression time profiles using gene ontology. Bioinformatics. 2003;19:1116–1123. doi: 10.1093/bioinformatics/btg047. [DOI] [PubMed] [Google Scholar]
- 11.Ruchkys D, Song S. A parallel approximation hitting set algorithm for gene expression analysis. 2002. pp. 75–81. In: 14th Symposium on Computer Architecture and High Performance Computing (SBAC-PAD 2002). Vitoria, Espirito Santo, Brazil.
- 12.Vinterbo SA, Kim EY, Ohno-Machado L. Small, fuzzy and interpretable gene expression based classifiers. Bioinformatics. 2005;21:1964–1970. doi: 10.1093/bioinformatics/bti287. [DOI] [PubMed] [Google Scholar]
- 13.Garey MR, Johnson DS. Computers and Intractability: A Guide to the Theory of NP-Completeness. New York: W. H. Freeman & Co; 1979. [Google Scholar]
- 14.Fernau H. Parameterized Algorithmics: A Graph-Theoretic Approach. Germany: Habilitationsschrift, Universität Tübingen; 2005. [Google Scholar]
- 15.Davies S, Russell S. NP-completeness of searches for smallest possible feature sets. In: Greiner R, Subramanian D, editors. AAAI Symposium on Intelligent Relevance. New Orleans: 1994. pp. 41–43. [Google Scholar]
- 16.Cotta C, Moscato P. The k-feature set problem is W[2]-complete. Journal of Computer and System Sciences. 2003;67:686–690. [Google Scholar]
- 17.Paz A, Moran S. Non deterministic polynomial optimization problems and their approximations. Theoretical Computer Science. 1981;15:251–277. [Google Scholar]
- 18.Abu-Khzam FN. A kernelization algorithm for d-hitting set. Journal of Computer and Systems Sciences. 2010;76:524–531. [Google Scholar]
- 19.Vazirani V. Approximation Algorithms. Berlin: Springer-Verlag; 2001. 380 [Google Scholar]
- 20.Feige U. A threshold of ln n for approximating set cover. Journal of the ACM. 1998;45:634–652. [Google Scholar]
- 21.Shoemaker RH. The NCI60 human tumour cell line anticancer drug screen. Nature Reviews Cancer. 2006;6:813–823. doi: 10.1038/nrc1951. [DOI] [PubMed] [Google Scholar]
- 22.NCI/NIH Website (Accessed 2010). Developmental Theraputics Program. http://dtp.nci.nih.gov/
- 23.IBM Website (Accessed 2010). ILOG CPLEX. http://www-01.ibm.com/software/integration/optimization/cplex/
- 24.Rao RD, Windschitl HE, Allred JB, Lowe VJ, Maples WJ, et al. Phase II trial of the mTOR inhibitor everolimus (RAD-001) in metastatic melanoma. Journal of Clinical Oncology. 2006;24:8043. [Google Scholar]
- 25.Peyton JD, Spigel DR, Burris HA, Lane C, Rubin M, et al. Phase II trial of bevacizumab and everolimus in the treatment of patients with metastatic melanoma: Preliminary results. Journal of Clinical Oncology. 2009;27:9027. [Google Scholar]
- 26.Lorenzi PL, Reinhold WC, Varma S, Hutchinson AA, Pommier Y, et al. DNA fingerprinting of the NCI-60 cell line panel. Molecular Cancer Therapeutics. 2009;8:713–724. doi: 10.1158/1535-7163.MCT-08-0921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chambers AF. MDA-MB-435 and M14 cell lines: Identical but not M14 melanoma? Cancer Research. 2009;69:5292–5293. doi: 10.1158/0008-5472.CAN-09-1528. [DOI] [PubMed] [Google Scholar]
- 28.Shin SY, Yong Y, Kim CG, Lee YH, Lim Y. Deoxypodophyllotoxin induces G2/M cell cycle arrest and apoptosis in HeLa cells. Cancer Letters. 2010;287:231–239. doi: 10.1016/j.canlet.2009.06.019. [DOI] [PubMed] [Google Scholar]
- 29.Lyseng-Williamson KA, Fenton C. Docetaxel: A review of its use in metastatic breast cancer. Drugs. 2005;65:2513–2531. doi: 10.2165/00003495-200565170-00007. [DOI] [PubMed] [Google Scholar]
- 30.Slamon D, Eiermann W, Robert N, Pienkowski T, Martin M, et al. Phase III randomized trial comparing doxorubicin and cyclophosphamide followed by docetaxel (AC-¿T) with doxorubicin and cyclophosphamide followed by docetaxel and trastuzumab (AC-¿TH) with docetaxel, carboplatin and trastuzumab (TCH) in Her2neu positive early breast cancer patients: BCIRG 006 study. Cancer Research. 2009;69:62. [Google Scholar]
- 31.Perez EA, Hillman DW, Dentchev T, Le-Lindqwister NA, Geeraerts LH, et al. North central cancer treatment group (NCCTG) N0432: phase II trial of docetaxel with capecitabine and bevacizumab as first-line chemotherapy for patients with metastatic breast cancer. Annals of Oncology. 2010;21:269–274. doi: 10.1093/annonc/mdp512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Polyzos A, Malamos N, Boukovinas I, Adamou A, Ziras N, et al. FEC versus sequential docetaxel followed by epirubicin/cyclophosphamide as adjuvant chemotherapy in women with axillary node-positive early breast cancer: a randomized study of the Hellenic Oncology Research Group (HORG). Breast Cancer Research and Treatment. 2010;119:95–104. doi: 10.1007/s10549-009-0468-0. [DOI] [PubMed] [Google Scholar]
- 33.Joensuu H, Bono P, Kataja V, Alanko T, Kokko R, et al. Fluorouracil, Epirubicin, and Cyclophosphamide With Either Docetaxel or Vinorelbine, With or Without Trastuzumab, As Adjuvant Treatments of Breast Cancer: Final Results of the FinHer Trial. Journal of Clinical Oncology. 2009;27:5685–5692. doi: 10.1200/JCO.2008.21.4577. [DOI] [PubMed] [Google Scholar]
- 34.Sparano JA, Makhson AN, Semiglazov VF, Tjulandin SA, Balashova OI, et al. Pegylated Liposomal Doxorubicin Plus Docetaxel Significantly Improves Time to Progression Without Additive Cardiotoxicity Compared With Docetaxel Monotherapy in Patients With Advanced Breast Cancer Previously Treated With Neoadjuvant-Adjuvant Anthracycline Therapy: Results From a Randomized Phase III Study. J Clin Oncol. 2009;27:4522–4529. doi: 10.1200/JCO.2008.20.5013. [DOI] [PubMed] [Google Scholar]
- 35.ClinicalTrialsgov Website (Accessed 2010). U.S. clinical trial registry. http://clinicaltrials.gov/ct2/home.
- 36.Davies B, Logie A, McKay JS, Martin P, Steele S, et al. AZD6244 (ARRY-142886), a potent inhibitor of mitogen-activated protein kinase/extracellular signal-regulated kinase kinase 1/2 kinases: mechanism of action in vivo, pharmacokinetic/pharmacodynamic relationship, and potential for combination in preclinical models. Molecular Cancer Theraputics. 2007;6:2209–2219. doi: 10.1158/1535-7163.MCT-07-0231. [DOI] [PubMed] [Google Scholar]
- 37.Yeh TC, Marsh V, Bernat BA, Ballard J, Colwell H, et al. Biological characterization of ARRY-142886 (AZD6244), a potent, highly selective mitogen-activated protein kinase kinase 1/2 inhibitor. Clinical Cancer Research. 2007;13:1576. doi: 10.1158/1078-0432.CCR-06-1150. [DOI] [PubMed] [Google Scholar]
- 38.Java Universal Network/Graph Framework Website (Accessed 2010). JUNG. http://jung.sourceforge.net/
- 39.yWorks Website (Accessed 2010). yEd. http://www.yworks.com/en/products_yed_about.html.
- 40.Flum J, Grohe M. Parameterized Complexity Theory. Berlin: Springer; 2006. 493 [Google Scholar]
- 41.Niedermeier R. Invitation to Fixed-Parameter Algorithms. Oxford: Oxford University Press; 2006. 316 [Google Scholar]
- 42.Downey RG, Fellows MR. Parameterized Complexity. Berlin: Springer; 1999. 533 [Google Scholar]