Three Roads Diverged? Routes To Phylogeographic Inference

Abstract

Phylogeographic methods enable inference of the geographical history of genetic lineages. Recent examples successfully explore the patterns of human migration and the origins and spread of viral pandemics. Nevertheless, longstanding disagreement exists over the use and validity of certain phylogeographic inference methodologies. In this paper, we highlight three distinct frameworks for phylogeographic inference to give a taste of this disagreement. Each of the three approaches presents a different viewpoint on phylogeography, most fundamentally how we view the relationship between the inferred history of the sample and the history of the population the sample is embedded in. Satisfactory resolution of this relationship between history of the tree and history of the population remains a challenge for all but the most trivial models of phylogeographic processes. Intriguingly, we believe that some recent methods that entirely side-step inference about the history of the population will eventually help the field toward this goal.

Emerging Pathways of Phylogeographic Inference

The influence of phylogeography is spreading throughout biology. Amongst other examples, phylogeographic techniques have enabled us to infer the origins of mice [1], modern humans [2; 3], and man’s “best friend”, the domesticated dog [4]. Phylogeographic analyses also allow public health officials to understand the origin and spread of emerging infectious diseases [5; 6; 7; 8]. In spite of these successes, disagreement and confusion lingers over the most effective ways to learn about phylogeographic processes from geo-spatially identified molecular sequence data. Major points of contention include: how to model the phylogeographic spread of the represented taxa under study, what statistical frameworks provide effective inference tools and how to best reconcile population frameworks with geographic information? Over the past few years, these questions have been touched upon extensively in other reviews, and we do not belabor points already made [9; 10; 11; 12]. Instead, we highlight several newer phylogeographic approaches: a Bayesian approach to nested clade phylogeographic analysis (NCPA) [13; 14], stochastic-process driven spatial diffusion models mapping viral outbreaks [15; 16], and several recent population genetic approaches to phylogeography [17; 18; 19]. After this, we draw parallels between these methods in an attempt to shed light on their similarities and differences. We hope that by exposing a general audience to a cross-section of methods, new perspectives will be shed on longstanding issues in phylogeography.

A Comparative Approach

For almost a decade, supporters of NCPA [14] and supporters of model-based phylogeographic methods [20] have argued over the merits of each respective method. Similar to previous parley in phylogenetics, this debate has generated several positive outcomes; most importantly, investigators now vigorously question assumptions when analyzing geographic, demographic, and evolutionary data [21]. Nevertheless, this long-standing discussion has introduced considerable confusion [22; 23]. Thankfully, the debate appears to be coming to an end [20]. In addition, a new model-based approach (highlighted below) overcomes many points of contention over NCPA, making the debate increasingly moot at this point. For those not familiar with the debate between NCPA and model-based approaches, we provide a synopsis in Box 1.

Box 1: NCPA Debate Background

Nested clade phylogeographic analysis (NCPA) originated in a single-locus formulation in the landmark paper by Templeton [26] where he addresses the construction of a haplotype tree [28], the nesting of the clades on the haplotype tree [31; 32], and the use of a permutation test and inference key to interpret significant results [68; 26]. The debate began when Knowles and Maddison [69] showed that single-locus NCPA has a high false-positive rate. Later, Panchal and Beaumont [27; 36] found similar high false-positive rates.

In response to these claims, Templeton [35; 70] modified his original NCPA, introduced a multi-locus “cross-validated” version, and conducted an extensive empirical validation study of single-locus NCPA. Nevertheless, supporters of NCPA and those against it soon released a flurry of papers both denouncing the method [34; 71; 72] and defending it [73; 74; 75]. Following this, both sides began to question the philosophical basis of both methods [9; 76]. Within the past six months, Templeton [77; 14] and those criticizing his method [20] continue this back-and-forth debate.

The debate has focused around two general points: i) does single-locus and multi-locus NCPA have an inherently high false-positive rate, and does this preclude its use? And ii) do model-based methods or NCPA provide a more appropriate way to analyze phylogeographic data? One decade ago, the answer to the latter question was NCPA, since model-based methods for phylogeography were not widely available and, arguably, only NCPA could explicitly incorporate geographic features. Today, however, this situation has changed. Spatial diffusion and population genetics approaches are gaining attention; the former does currently incorporate important features, like physical distance and known geographic barriers, and the latter has the potential to do so. As such, we personally believe Beaumont et al. [20] resolve both questions posed above in favor of model-based methods. Nevertheless, we encourage others to read over the relevant publications to form their own opinion.

Before discussing this newer approach, we give a short background to NCPA, a technique that, for many years, stood alone in explicitly modeling geography in an evolutionary context. The method originated in previous efforts to jointly analyze phenotypic and phylogenetic data in a comparative framework [24; 25] and follows the same general three-step scheme [26; 13; 27; 9]. First, a haplotype tree or network is constructed from molecular data using a variety of approaches [28; 29; 30]. Second, clades on the haplotype tree are nested typically following the stepwise guidelines of Templeton [31; 32]. Finally, using these nested clades, a permutation test assesses the significance of the geographical spread.

Significant ambiguity occurs in all three stages of the NCPA pipeline [9]. During the first and second stages, alternative methods can lead to different, and possibly better, haplotype tree inference and nesting structures [33; 13]. More troubling, in the third stage, determining the level of significance for a particular clade does not typically take into account multiple testing, likely leading to a high false-positive rate [34; 9] (see Box 1). Templeton [35] has introduced a multi-locus “cross-validated” remedy for the apparent high false-positive rate, although even this revision still does not provide a complete solution [20; 36]. To be fair, we note that Templeton [14] disagrees with the ambiguous label for NCPA and its apparent high false-positive rate; but, extensive research suggests otherwise (Box 1).

In addition to these issues, the pipeline nature of NCPA leads to overconfidence in the final result [13]. This phenomenon is well known in the statistics and model-based molecular evolution literature. Multiple sequence alignment provides an excellent example where conditioning on a unknown multiple sequence alignment can lead to biased conclusions and overconfidence [37; 38]. Fortunately, a joint Bayesian approach provides a formal and straightforward fix to pipelined analyses [39; 40; 41]. Recently, Brooks et al. [13] and Manolopoulou (I. Manolopoulou, PhD thesis, University of Cambridge, 2008) adopt this simultaneous paradigm to combine the three stages of NCPA. For the first stage, Manolopoulou introduces a tractable procedure to infer a haplotype tree from molecular sequence data that takes into account possible homoplasy. She then uses approximate Bayesian computation to achieve computational efficiency for this part. For the second stage of NCPA, Brooks et al. [13] describe a multivariate clustering model applicable to both phenotypic and phylogeographic data. Brooks et al. [13] do not provide an analog of the third stage of NCPA, but nevertheless suggest that posterior probabilities of various qualitative events provide a solid alternative to the inference key of NCPA. To demonstrate the model, Manolopoulou applies both methods to three empirical examples. In general, the two methods give similar conclusions, but the Bayesian approach makes formal the intuitive results from NCPA. This Bayesian framework should excite those fond of the comparative method since it maintains the spirit of the comparative method, but corrects many of the statistical issues plaguing previous efforts. We look forward to many new developments from this approach.

A Spatial Diffusion Approach

As an alternative to the comparative method and its Bayesian extensions, we now highlight recent developments towards model-based approaches that take a probabilistic perspective on spatial diffusion [15; 16]. Although much of this work is implemented as part of a comprehensive statistical inference package that witnessed fruitful advances in demographic models [42; 43], we immediately want to emphasize that, unlike spatial-coalescent approaches [44], phylogenetic diffusion models do not claim to infer population-based spatial histories. Instead, they aim to uncover the ancestral history of a particular sample of molecular sequences, namely when and where the direct ancestors relating the sample existed. Nevertheless, such models can extract important information about the processes that underlie geographic structure in genetic data. For example, the inferred movement of the direct ancestors reflects movement of or between historical populations. Noteably, limiting oneself to the ancestors, the spatial diffusion approach can accommodate geographical context more explicitly by modeling the diffusion as trait evolution on a phylogeny.

Phylogenies naturally lend themselves to exploration of population structure and to assessment of significance in various ways [45]. More challenging however is the analytical reconstruction of how this structure took shape throughout the phylogenetic history. It is almost a law of statistical inquiry that challenging problems are initially probed by heuristic approaches. Parsimony methods represent model-free heuristic approaches that achieved enormous popularity in reconstructing such ancestral histories [46], be they of nucleotides, discrete organism traits or geographical locations [47]. Probabilistic approaches to ancestral reconstruction employ continuous-time Markov chain (CTMC) models to infer discrete realizations in continuous time. Although conceptually simple, they can capture considerable complexity of the discrete transition process among many states, such as geographic locations, albeit at the expense of an increased number of instantaneous rate parameters that make up the CTMC rate matrix. An obvious criticism is that a single observation does not hold the information required to estimate all parameters in the rate matrix, since we do not observe the intermediate states of this process. Nonetheless, this should be no reason to abandon probabilistic approaches all together.

Others have reviewed ancestral reconstruction methods and highlighted the advantages of likelihood-based statistical methods [48; 49]. Maximum likelihood methods and, to a greater extent, Bayesian inference accommodate important sources of uncertainty that accompany the estimation of character evolution [49]. A recent example of a Bayesian approach to island biogeography, in which specific Canary islands represent the character state data, has recently demonstrated great potential when applied to many groups of organisms evolving on independent phylogenies [50]. For a single character, however, a probabilistic approach that diligently accounts for phylogenetic and parameter uncertainty can yield particularly high variance estimates.

Recent developments in Bayesian phylogeography have made great strides towards efficient statistical inference of spatial diffusion [15]. In general, Bayesian approaches are more robust against over-parametrization via priors and this can be exploited most efficiently in discrete phylogeography by specifying informative priors on the rate parameters. For example, prior distributions based upon distance could formalize the prior expectation of a higher organismal lineage exchange between adjacent island groups in the Canary island biogeography [50]. Such distance-informed priors have recently been explored in viral epidemiology [15]. Arguably a more important advance, presented in the same work, is the ability to reduce the set of rate parameters to a limited number that provides a parsimonious description of the spatial diffusion process. This has been achieved by a Bayesian stochastic search variable selection procedure [51], which augments the rate matrix with indicator variables and imposes a prior distribution on the total sum of non-zero rate parameters. Parametrization of the truncated Poisson prior distribution proposed in Lemey et al. [15] fulfills the wish for statistical efficiency and is motivated by the believe that most pairwise exchange rates are probably not required to explain the diffusion process along the phylogeny. As such, it has been used to construct a formal Bayes factor test to establish epidemiological linkage in viral phylogeographic histories [15], removing the need to resort to ad hoc procedures [47].

It is a basic assumption of discretized dispersal that ancestral organisms at any point along the phylogeny reside in the locations from which samples were drawn. Spatial diffusion in continuous space presents an attractive alternative for more realistic phylogeographic inference. Following Brownian motion models for quantitative traits, bivariate Brownian random walks have been used for phylogeographic analysis in a likelihood approach [52]. This basic model has recently been greatly expanded and introduced into a Bayesian statistical framework [16]. To overcome the limiting assumption of constant diffusion rate throughout the phylogeny, rate heterogeneity is accomplished by borrowing ideas from uncorrelated relaxed clock models [53]. In our opinion, this represents a much-needed extension because it might prove difficult to find any real life example of spatial diffusion that adheres to a homogeneous Brownian process. For example, mountains or valleys, bodies of water and the environmental tolerances of organisms complicate the situation.

In particular, these relaxed random walks admit several diffusion processes commonly harnessed to model animal movement in ecological contexts [54]. These include independent Cauchy- and, more generally, Student-t-distributed increments along each branch of the uncertain phylogeny. These distributions emit infinite variance and derive motivation from Lévy flight models [55; 56]. Further, the relaxed walks do not require a strict enforcement of power-law tail behavior that remains contentious in some animal movement studies [57]. Encouragingly, even for relatively simple epidemic expansions, relaxed random walks yield reconstructions with increased statistical efficiency. We believe this can add considerable credibility to spatial reconstructions in continuous space, in particular because Brownian trait estimates have often been found too variable for practical use [58].

The continuous and discrete stochastic processes furnish complementary models that expand our ability to infer phylogeographic processes. They are both implemented in the “Bayesian evolutionary analysis sampling trees” (BEAST) software package that has matured into a rich resource of stochastic evolutionary models [59]. Focusing entirely on time-measured phylogenies and offering different flavors of demographic models, such an integrated approach appears well suited for biogeographical analyses. The first phylogeographic steps with this framework were made in the field of viral epidemiology, in particular for rapidly evolving RNA viruses [8; 16]. As general tools however, these models can also prove useful in the analysis of genetic data from more slowly evolving organisms. To illustrate this, we provide a phylogeographic reconstruction in continuous space for the freshwater snail Biomphalaria glabrata, a major vector of schistosomiasis in the New World [60] (see Box 2). This box also opens a discussion on visualizing inferred evolutionary histories through both time and space.

Box 2: Visualization Tools

We revisit the phylogeography of the freshwater snail Biomphalaria glabrata that has limited dispersal abilities and occupies fragmented habitats in South America and the Caribbean islands [60]. Mavarez et al. [60] originally obtained sequence data from populations of B. glabrate sampled at the scale of the current geographic distribution of the species to study its phylogeography. As illustrated in Figure I, we apply the recently developed continuous diffusion model to 17 concatenated nuclear internal transcribed spacer-2 (484 bp) gene sequences and the partial mitochondrial large ribosomal subunit (374 bp) generated in the original study. The reconstruction confirms a clear separation into Northern (Venezuela and Lesser Antilles) and Southern clades (Brazil), in line with the Amazon river constituting an important barrier to gene flow [60]. Because the equatorial forest of the Amazon basin does not provide appropriate habitats for this species, it might therefore represent an additional barrier to gene flow [78]. The considerable divergence among the sampled haplotypes has led to the suggestion that B. glabrata constitutes a species complex [60]. As suggested by the Lesser Antilles haplotypes clustering in the same monophyletic clade [79; 80], there also appears to be significant isolation by distance at a more restricted geographic scale.

With this illustration, we also touch upon the developing visualization tools that complement the Bayesian inference. Phylogenies have previously been projected in virtual globe software [81], but we would like to argue for directing these efforts towards model-based estimates. If probabilistic approaches are able to rigorously capture the uncertainty in phylogeographic inference, it is critical that visualization tools are able to fully present this uncertainty for appropriate interpretation. For discrete ancestral reconstruction this still remains an open issue; while location probability distributions for ancestral nodes can be readily obtained, the phylogenetic uncertainty adds a level of complexity that does not easily lend itself to straightforward visual summaries. Phylogeographic estimates through time and continuous space are more naturally streamlined into rich visualization [16]. Not only does this model offer the ability to draw inference about location realizations and various summary statistics at arbitrary points in time, researchers can now explore the results in an interactive fashion (for several examples, we refer to www.phylogeography.org). Finally, more work is needed to introduce these summaries in more dedicated visualization software [82], or to accommodate them in feature-rich, multi-purpose geographic information systems software [83].

A Population Genetics Approach

By far the most popular statistical approaches to phylogeography rely on the structured-coalescent [61; 44; 62; 9]. In general, these methods assume that evolutionary trees are random draws from some underlying population-level process [9]. Essentially, population-level processes fossilize their histories as evolutionary trees that we indirectly view through molecular sequence and other data [61; 10]. These processes include selection, migration, population size changes, and recombination.

Nearly all population-level approaches embed evolutionary trees into a structured-coalescent framework to make inference [63]. Herein lies the strength and limitations of these methods. If constructed appropriately, structured-coalescent methods allow us to infer population-level information from a relatively small sample. Unfortunately, constructing these methods in an appropriate manner requires extensive time, computation, and ingenuity. The task is not trivial. Nearly a decade ago, Felsenstein et al. [64] maintained that any implementation of structured-coalescent methods, and related models, took nearly two years to develop. Nielsen and Beaumont et al. [9] suggest that things remain the same. As such, the field still does not have a way to handle even simple recombination between linked loci in a structured-coalescent framework.

Nevertheless, population genetic approaches for ancestral inference are flourishing. In the past few years, numerous highly significant contributions have appeared. As examples, Liu and Pearl [65] and Heled and Drummond [18] fully take into account gene tree uncertainty and species tree uncertainty through Bayesian statistical modeling [66; 67]. Focusing on gene-flow and migration, Hey [17] extends his previous work to incorporate migration between multiple species. Also focusing on gene-flow, Beerli and Palczewski [19] adopt thermodynamic integration to compute Bayes factors assessing panmixia and migration in a structured-coalescent framework [44]. And the list goes on. Approximate Bayesian computation allows empirical investigators to assess complex demographic histories, conditional likelihood methods allow for the approximation of the coalescent with recombination, and efficient calculation allows for full assessment of it [9].

In sum, much as in the previous two approaches, the application of population genetics to phylogeography remains a vibrant field of research. Highly significant work continues to be created, but numerous, biologically-relevant, methods need to implemented, adapted, and created. This route to phylogeography is far from a dead-end.

Three Routes To the Same Destination

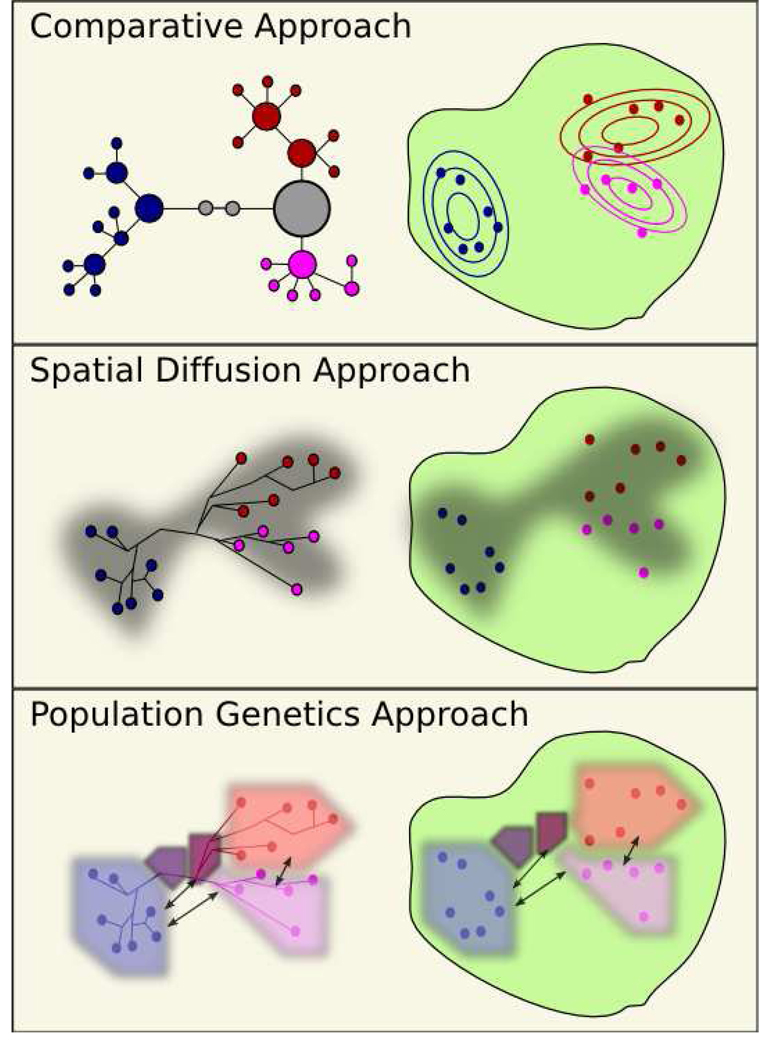
With the expansion of phylogeography in new Bayesian directions involving NCPA and spatial diffusion, the field might appear to be fragmenting. But, we believe all three approaches address the same basic question we stated at the beginning of this article: what are the most effective ways to learn about phylogeographic processes from geo-spatially identified molecular sequence data? Essentially, we believe all three frameworks produce effective answers, if one knows what questions to ask. Under the comparative approach, if one wants to assess geographical spread and molecular data, without modeling this spread explicitly, the method of Manolopoulou will be the most appropriate. If one wants to model rates of spread and take into account geographical features, the method of Lemey et al. [16] will be most appropriate. If one wants information about population size and migration, but considers population to be a coarse feature, the population genetics approach will be most appropriate. Figure 1 provides a schematic of these three phylogeographical frameworks.

Figure 1.

Three approaches to phylogeography. In all three windows, the data consist of three species (red, purple and blue) sampled across an island (green). Comparative Approach: In this window, the haplotype tree is displayed on the left; concentric circles on the island represent the geographical distribution of the three species. Spatial Diffusion Approach: In this window, the phylogenetic tree, superimposed upon the geographical location of the samples, is displayed on the left. We color the phylogenetic tree black to reinforce that we do not infer population information. The gray area behind the phylogenetic tree, and on the island, represents a high probability region contour of the locations of the ancestors of the sampled taxa. Population Genetics Approach: This window is based upon Hey (2010). The five colored polygons represent the ancestral populations and their respective population sizes. Arrows represent strong migrations between the populations. Currently, the idealized population polygons abstract away all geographic features to keep the models tractable.

One might wonder whether the advantages of all three approaches can be combined into a single framework. We hesitate to speculate on this particular question, and simply leave it as open and tractable and encourage its exploration (see Box 3 for other open issues on the verge of solution). We do note that with a shift towards likelihood-based statistical inference, ad hoc procedures are no longer the only or preferable methods available. Instead, garnering novel insight into phylogeographic processes reduces to envisioning stochastic process-driven models that incorporate the relevant aspects of the research question at hand and then developing the tools necessary to efficiently fit these models to data. The limiting aspects of this approach are chiefly creativity in modeling and effective strategies to reduce the high-dimensional model fit into a human-interpretable form.

Box 3: Some Open Issues Approaching Solution

Availability of Geo-Coded Sequence Data

The inclusion of geographical data into molecular phylogenetics increases the size and complexity of datasets. As a benefit, investigators can learn the relationships between several disparate aspects, gaining a better understanding of biological diversity and history. The downside to these complex datasets, however, is reproducibility and validity. In the past, investigators could reproduce and validate inferences since the models and datasets were readily available. In the modern climate, however, inferences are more difficult to reproduce because the geographic data is rarely provided with the molecular sequences and many modeling assumptions go unreported. One way to avoid this difficultly is to require geo-coded sequence submission and a central online repository where investigators can upload their computational scripts. Some journals have begun to require these uploads for publications, but the push needs to be stronger.

Incorporating Geographic Features and Niche Modeling

The structured-coalescent and discretized spatial diffusion approaches generate models in which researchers can inject a limited amount of information about geographic or niche features. This injection involves the definition of prior distributions on migration rates between populations or geographic locations. For these forms of discrete Markov chain models, O’Brien et al. [84] offer advice on how to make summary statistics about the diffusion process robust to some of the model misspecification that results from ignoring additional features. However, it is unclear how effective informed prior specification will remain when researchers attempt to learn from the observed data which geographic or niche features significantly affect the migration or diffusion process. In these situations, directly modeling the geographic features as hard or soft barriers in a continuous diffusion framework appears as a tenable solution. Ranking features by their barrier strength or testing which strengths do not significantly differ from zero produces a sound statistical framework. Looming over us is the modeling challenge of efficiently computing transition probabilities along the tree of migration or diffusion in the presence of multiple, possibly irregular barriers.

Next-Generation Sequencing

With the advent of next-generation sequencing technologies, biologists can now obtain de novo genomic samples from entire biological communities. Still, these metagenomic studies are in their infancy. In particular, the analysis and design of metagenomic studies is unrefined and rudimentary. For model-based methods to move into this area, advances in computational efficiency will be vital. Moreover, model-based methods will need to account for the data-collection technology, as well as the phylogeographic history of a sample under study. Currently, the lack of theoretical tools here is hindering scientific progress.

To Tree or Not To Tree

The relationship between the inferred phylogenetic tree and its embedded population has been described extensively over the past 30 years [85; 62; 9]. Nevertheless, the relationship between the two remains poorly understood, as evidenced by the three distinct approaches highlighted in this paper. Put simply, we still poorly understand whether the inferred evolutionary history remains a nuisance or fundamental entity [86]. Resolving this issue will likely require extensive work in the upcoming decade.

Figure I.

Freshwater snail phylogeny (maximum clade credibility tree) obtained using Bayesian phylogeographic inference in continuous space. The maps in the virtual globe visualization are based on satellite pictures made available in Google Earth (http://earth.google.com). A) Projection of the complete phylogeny with a red-white color (on-line) or grayscale (in print) gradient informing the relative age of the branches. The location uncertainty for each node is visualized by a polygon representing a 80% credibility contour. B) A detailed view of the Northern phylogeographic clade, as indicated by the rectangle in panel A. The orientation of the view is indicated by matching arrows in both panels. Taxa habitat (freshwater) is an important geographic feature to begin modeling directly.

Glossary

Ancestral history

any information about the direct ancestors relating a sample of molecular sequences. This term can refer, for example, to inferred sequence composition or phenotype, such as geography, and is often associated with a time-scale.

Approximate Bayesian computation (ABC)

a simulation technique used to draw statistical inference based on data summaries, often employed when the full data likelihood is impractical to compute.

Bayes factor

the ratio of marginal likelihoods of a given data set comparing two competing models that naturally incorporates uncertainty about unknown parameters in both models.

Bayesian stochastic search variable selection

a framework that estimates the posterior probability that a particular explanatory variable should be included in a model. The method is most commonly used in Bayesian inference of linear regression.

BEAST

an open-source MCMC package for the analysis of several Bayesian evolutionary models for molecular sequences and associated traits, such as geography.

Brownian diffusion

a stochastic process on the real number line or, in the work described in this article, on a geographic surface, in which increments are independent and normally-distributed with mean zero and a variance that scales linearly with duration.

Continuous-time Markov chain

a stochastic process on a discrete state-space or, in the work described in this article, a set of locations that is memoryless and whose waiting times between transitions are exponentially-distributed.

Comparative approach

a framework with which to relate observed phenotype information to an evolutionary history. Nested clade phylogeographic analysis assumes geography to be a phenotypic trait and falls under this category.

Model-based approach

a method in which a fully specified probabilistic model describes how the observed data are generated. Unknown parameters can characterize this model, and statistical inference proceeds through estimating and testing these parameters.

Nested clade phylogeographic analysis

a resampling based approach to infer geographic information from haplotype trees and networks.

Phylogeography

the interdisciplinary field that studies the evolutionary history and the geographic spread of biological populations or taxa.

Population genetics

as used in this article, a framework that uses sample molecular sequences to make statements about a population under study. The coalescent is the most widely used population genetics framework. Extensions of the coalescent to phylogeography typically focus on migration rates between multiple populations fixed in space.

Spatial diffusion model

the application of independent stochastic processes to describe changes in geographic phenotypes on a two-dimensional surface. Under the discrete framework described in this article, one divides the surface into discrete regions and models movement between regions as a continuous-time Markov chain; under the continuous diffusion framework, one subdivides these regions until they become infinitesimal and considers generalizations of Brownian diffusion.

Structured coalescent

an extension of the basic coalescent model to multiple populations. This method focuses on ancestral population sizes and migration rates between populations.