Characterization of Imaging Gradients in Diffusion Tensor Imaging

Abstract

For obtaining a complete model the diffusion tensor imaging (DTI) method is derived in a new linear algebraic framework in order to include the effect of all of the magnetic field gradients on the MRI signal. In the framework, the coefficient matrix of the estimation equations consists of the sum of three matrices corresponding to diffusion gradients, imaging gradients and the cross–terms between them. The derivations demonstrate that there exists modeling incongruities originating from the choice of phase–encoding gradient magnitude and the read–out gradient affecting the entirety of the signal sample points. These reflect on the cross–terms and the imaging gradient coefficient matrix, revealing the DTI's inadequacy for the inclusion of imaging gradients. The linear algebraic framework mitigates the inadequacy by the utilization of center–symmetric gradient schemes. The observations are verified by the experimental results obtained from an isotropic phantom using several existing diffusion gradient schemes.

1. Introduction

The Diffusion Tensor Imaging (DTI) is a widely used and important protocol that is being utilized in research and clinic to assess and diagnose the microstructural tissue changes due different conditions such as multiple sclerosis [1, 2], cancer [3], Alzheimer's disease [4] and spinal cord injury [5]. DTI has been so well established that it is now provided as a standard protocol with the clinical MR scanners. Despite its utilization as a standard, its limited capability in capturing and elucidating complicated structures has motivated several researchers to develop sophisticated models such as the diffusion spectrum imaging (DSI) [6], high angular resolution diffusion–weighted imaging (HARDI) [7], the Generalized DTI (GDTI) [8], Diffusion Orientation Transform (DOT) [9] and Q-ball imaging [10] to name a few from the comprehensive list provided in [11].

In this manuscript, the DTI model is derived in a linear algebraic framework to better discern and address the problems and the limitations of the technique. Specifically, in Section 2 the framework to include the effect of the imaging gradients is presented. Compared to the tensor algebraic approach [12, 13], the linear algebraic setup provides better capabilities in analyzing and rectifying the barriers in the DTI model (see Section 5). For example, it makes it possible to define a sample–independent norm in [14]. The norm is utilized to pose an optimization problem, which is then solved to obtain better performing diffusion gradient schemes [14].

The MR–DTI methodology is based on the work of Stejskal and Tanner [15] for the pulsed gradients spin echo (PGSE) NMR experiment. In the NMR case, the calculations in [15] show that the phase incoherence caused by the scalar diffusion coefficient is quantified by measuring the decrease in the signal peak value. The decrease is a function of the diffusion gradient pair's magnitude characterized by the so called (scalar) b–value.

The NMR formulations of [15] are translated directly to the MRI setup in [12]. There, the quantities of interest are no more scalars. The diffusion phenomenon is characterized by a rank two tensor in three dimensions, represented as a matrix D. For a given diffusion encoding gradient pair, the coefficient of D in the DTI equations is another matrix, the b–matrix, that multiplies D element by element [12]:

$$b:D.$$

In [12, 13] the measurements made with different b–matrices are utilized for estimating D via a set of linear equations.

Whether seen as tensors or matrices, mathematically both objects in b : D are elements of a vector space and the element by element multiplication is in fact their inner product. Therefore, it is beneficial to utilize a minimalist linear algebraic representation to facilitate the application of the existing mathematical methods (e.g. utilization of the appropriate norms and the corresponding matrix norms for the design of new gradient schemes [14]). Without including the imaging gradients, this setup is first exposed in [16] where D is appropriately written as a vector along with the set of corresponding linear equations. Each row of the coefficient matrix of these equations is a nonlinear function of one diffusion encoding gradient, which is now a three dimensional vector rather than a scalar. Basically, in [16] the special tensor product b : D is appropriately replaced by the product of a row vector –instead of the b–matrix– and the vector presentation of D, and the whole DTI experiment is characterized by the coefficient matrix formed by these row vectors.

A direct outcome of the vector space framework was the description of a set of necessary conditions for the choice of the diffusion gradient vectors that guarantee that the coefficient matrix has full rank [17]. Otherwise, the DTI experiment will collect redundant data leading to a set of underdetermined equations. It is shown in [18] that these conditions are also valid for the nonlinear estimation. In contrast, the tensor algebraic setup [19] fails to provide a complete description these requirements.

Physically, all of the gradients affect the signal so the imaging gradients must be included in the calculations. The rigorous derivations of [15] are obtained for PGSE without any ‘extra’ gradients, such as the imaging ones of MRI. Although it is common practice to ignore the imaging gradients in the equations, for the experiments where the field of view is small, such as in the case of animal scanners, these gradients have significantly high magnitudes.

The imaging gradients were incorporated in [13] into the tensor algebraic approach. In Sections 3.2 and 3.3, the same task is accomplished in a much less tedious fashion with the linear algebraic framework. In doing so, some modeling ambiguities are quickly unveiled. For example, each k–space line in a diffusion–weighted acquisition corresponds to one Stejskal–Tanner experiment [15] run with the addition of the imaging gradients. But the magnitude of the phase–encoding gradient changes at each k–space line. It is therefore not clear which value of the phase–encoding gradient to use in the DTI estimation equations since the intensity at each pixel of the DT images is obtained from the entirety of the k–space lines.

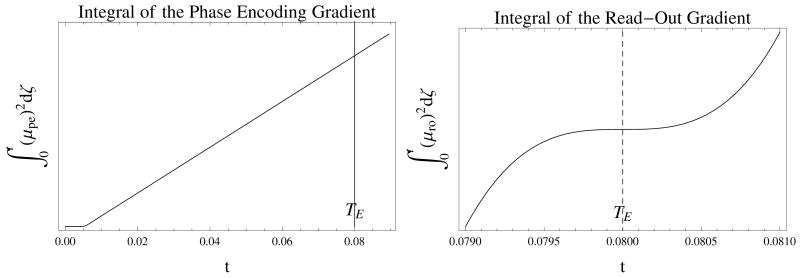
At a more fundamental level, in the Stejskal–Tanner experiment the scalar diffusion coefficient can be obtained by looking at a single point (the peak value of the signal). But for the DTI experiments, all of the data points collected during the analog to digital conversion acquisition (ACQ) periods contribute to the entirety of each image. With the read–out gradient activated and encoding the spin motion for all of the data points, all points contribute to the estimation of D. In addition, the imaging gradients do not necessarily have a null moment and their integrals do not form a plateau as in Fig. 2. Instead they possess different values at each sampling point during the ACQ period as in Fig. 3.

Figure 2.

The calculation of the time course for the entries of V_C corresponding to the read–out gradient for the PGSE pulse sequence of Fig. 1. The values are scaled and the crusher gradients are not included and the gradient offsets are exagerated for better visualization. The π–pulse occurs at $\frac{T_E}{2}$. The scalar function of time, β, is integrated to obtain μ that in turn is integrated to obtain V_D, V_C, V_I. The figures also show that by moving the read–out rewind gradient just before the read–out acquisition eliminates the diffusion effect since μ_D is zero before the echo time. However, this strategy might create artifacts, e.g. stimulated echoes, in the images. For any variation of the pulse sequence or a completely different one, the definition of h in Eq. (2) will change and accordingly these graphs will be different. In any event, as any valid model should, the DTI model should be applicable to any pulse sequence that can incorporate diffusion gradients. Therefore the usage of the current sequence of Fig. (1) is a valid procedure for testing the model.

Figure 3.

The calculation of the time course for the phase–encoding and read–out gradients for the PGSE pulse sequence of Fig. 1. Notice that the function corresponding to the phase–encoding does not plateau around T_E This creates a possible range of values to be used in the coefficient matrices, since all of the points during the acquisition period participate in image formation. The similar problem is also present for the read–out gradient for which T_E is an inflection point.

Nevertheless, keeping the phase–encoding gradient value as an unknown variable and using the single signal value at the echo time, in Section 3 the coefficient matrix of the DTI estimation equations is analytically derived as the sum of three matrices corresponding to diffusion, imaging gradients and the cross–terms between them. Although the coefficient matrix for the diffusion gradients is numerically computable, due to the unclear choice of the values mentioned above, the same is not possible for the imaging and cross term matrices. The following is concluded:

Despite the necessity to include the effect of the imaging gradients for a complete model, the DTI method is not adequate for such an inclusion.

In Section 2, the proton density related image is replaced in the estimation equations by the spin–echo image without the diffusion gradients. It is demonstrated that this theoretically eliminates the imaging gradient coefficient matrix from the equations providing a partial resolution for the issues described above. In Section 5, the linear algebraic framework offers a remedy for the cross–terms matrix. Regardless of the values of the imaging gradients used in the systems of equations, when the diffusion gradients are sign reverted (center–symmetric) the matrix corresponding to the cross–terms reverts its sign while the other matrices remain the same. Therefore, by conducting a DTI experiment with two sets of diffusion gradient vectors that are sign reverted copies of each other, the cross–terms matrix can be eliminated, at least in theory, from the estimation process with the cost of losing half of the information provided by the measurements. This method is called ‘No Cross Terms’: NoCroT. The center–symmetric strategy has been investigated in earlier diffusion–weighted imaging studies [20, 21, 22] and experimental results from Icosahedral DTI scheme have been reported [23] but it has never been theoretically and experimentally analyzed for DTI before this work. The analysis of the NoCroT method at the end of the Section 5 reveals that it is equivalent to least squares estimation by completely neglecting the imaging gradients.

The general modeling incongruity is demonstrated using the isotropic sample of Section 6.1 with the results presented in Section 6.2. The experiments were carried with center–symmetric versions of existing diffusion gradient schemes [24, 25] with the purpose of investigating the variation of the estimation results between the diffusion gradient schemes and different coefficient matrices. The same data from each scheme were used to compute the diffusion quadratic forms by two levels of image gradient incorporation: ‘all gradients’ and NoCroT. The results in Section 7 show that the computations including all of the gradients yield more inaccurate results than the ones obtained by excluding the imaging gradients, demonstrating experimentally the inadequacies in incorporating the imaging gradients into the DTI model.

In conclusion, while the analytical expressions derived in this manuscript constitute a reference for future investigations, the theoretical results build the foundation for defining optimization problems [14] to address the incongruities with more sophisticated tools as well as to improve the performance of DTI modality.

2. Estimation Equations

2.1. Coefficient Matrix V

Stejskal and Tanner's incorporation of the effect of diffusion in NMR pulsed gradient spin echo (PGSE) experiments starting from Fick's equation results in the solution of the modified Bloch equation in [15]. The solution has been generalized to MR–DTI experiments in [12, 13]. The translation of NMR model [15] to MRI in [12, Eq. (3)] is written here with an important note:

$$S(G,t)=S_{p}exp\left(-{\gamma }^2{\int }_0^{t}h(G,\zeta )D{[h(G,\zeta )]}^{T}d\zeta \right),$$ (1)

where G(·) = [G_x(·) G_y(·) G_z(·)] denotes the time course of the magnetic field gradient vector, γ is the gyromagnetic ratio, S denotes the signal intensity at each pixel. Most importantly, in this equation, S_p is different than S₀ of [12, Eq. (3)] which is the reference image obtained without diffusion gradients (see Eq. (9) below). The true nature of S_p is related to the proton density and its exact description is beyond the scope of this manuscript. The initial time, 0, is taken in this work as the time “immediately following the 90° pulse” [26]. In Fig. 1 of [13] and Fig. 2 of [27], it is shown as the time when the 90° pulse reaches its peak. The time t is chosen to be T_E, the echo time. The analytic form of the vector valued function h depends on the pulse sequence. Specifically, the one given here is for the PGSE imaging experiment with the pulse sequence diagram shown in Fig. 1 and it is derived by incorporating the unit step function for the sign change created by the π–pulse:

Figure 1.

The pulsed gradient spin echo pulse sequence and the definition of the variables used in the calculations. RO is for read out, PE for phase encode, SS is the slice select gradient with RF indicating radio frequency, ACQ stands for the acquisition and RW for rewind. The diagram is representative and is not to the scale. The offsets between the pulses are usually minimized by the MRI console. This minimum delay depends on the specifications of the magnetic field gradient hardware. The strength of the imaging gradients is also calculated by the MRI console computer to adjust for the imaging parameters e.g. the field of view.

$$h(G,\zeta )={\int }_0^{\zeta }G(\xi )d\xi -2u(\zeta -\tau ){\int }_0^{\tau }G(\xi )d\xi$$ (2)

where τ is the time of the π–pulse and u(·) denotes the unit step function. It is important to note that calculation of h involves the time course of all gradients [12, 19, 28] not just the diffusion sensitizing ones.

The diffusion tensor in Eq. (1) is of rank two and both of the arguments it operates on are always equal. By the fact that for any n × n matrix D and any x ∈ IRⁿ the following holds:

$$2x^{T}Dx=x^T(D+D^T)x,$$ (3)

it is concluded that MR-DTI can only measure the symmetric part of the diffusion tensor which, by definition, is a quadratic form represented by a symmetric matrix. The subset of symmetric n × n matrices, SM(n), is a subspace (of dimension n(n + 1)/2) of the vector space of n × n matrices. For n = 3 the image of the standard basis of IR⁶ under the map

$$d={[d_1\cdots d_6]}^T\mapsto D=\left[\begin{array}{ccc}{d}_1& d_4& d_6\\ d_4& d_2& d_5\\ d_6& d_5& d_3\end{array}\right]$$ (4)

is a basis for SM(3). By treating SM(3) as a six dimensional vector (sub)space, Eq. (1) is written as a set of linear equations between the m diffusion–weighted measurements and d. This is achieved by letting

$$h_i(\cdot )=[h_{ix}(\cdot )h_{iy}(\cdot )h_{iz}(\cdot )],i=1,\dots ,m$$

be IR³ valued functions, square integrable over the fixed finite interval [0, t] and by defining a linear map from IR⁶ to IR^m by

$$d\mapsto {\int }_0^t{[h_{1}D{h}_1^T\cdots h_{m}D{\mathit{\text{h}}}_m^T]}^{T}d\zeta ,$$ (5)

which has an m × 6 matrix representation using the basis defined by Eq. (4):

$$V=\underset{0}{\overset{t}{\int }}\left[\begin{array}{cccccc}{h}_{1x}^2& h_{1y}^2& h_{1z}^2& 2h_{1x}{h}_{1y}& 2h_{1y}{h}_{1z}& 2h_{1x}{h}_{1z}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ h_{mx}^2& h_{my}^2& h_{mz}^2& 2h_{mx}{h}_{my}& 2h_{my}{h}_{mz}& 2h_{mx}{h}_{mz}\end{array}\right]d\zeta .$$ (6)

With G_i(·) as the time course of the total magnetic field gradient vector (i.e. including imaging and diffusion) at the i^th measurement and with h defined in Eq. (2), let

$$h_i(\zeta )=h(G_i,\zeta ).$$

Using this definition, let v_i denote the i^th row of V in Eq. (6). Then

$$v_{i}d={\int }_0^{t}h(G_i,\zeta )D{[h(G_i,\zeta )]}^{T}d\zeta .$$ (7)

Now, Eq. (1) is conveniently written for the i^th acquisition by changing the arguments of S as:

$$S(v_{i}d)\doteq S_{p}exp(-{\gamma }^2{v}_{i}d)=S_i.$$ (8)

Therefore S₀ of [12, Eq. (3)] will be obtained by turning off the diffusion gradients resulting in a vector v_I that only encompasses the imaging gradients for the calculation of Eq. (7):

$$S_0=S_{p}exp(-{\gamma }^2{v}_{I}d).$$ (9)

Since S_p is not directly available, the usual approach is to replace it by writing Eq. (8) as:

$$S(v_{i}d)\doteq S_{0}exp(-{\gamma }^2(v_i-v_I)d)=S_i.$$ (10)

Applying the logarithm to this equation yields:

$${\gamma }^2(v_i-v_I)d=-ln(\frac{S_i}{S_0})=ln{S}_0-ln{S}_i,$$ (11)

where the substraction on the right is preferred to reduce the propagation of errors in numerical calculations. Finally, by defining

$$p={[ln(S_0)-ln(S_1),\dots ,ln(S_0)-ln(S_m)]}^T$$ (12)

the linear equations for the estimation of the diffusion matrix can be written as

$${\gamma }^2(V-V_I)d={\gamma }^2{V}_{DC}d=p$$ (13)

where V_I is the m × 6 matrix with rows equal to v_I (see Eq. (28)) representing the imaging gradients and V_DC, defined in Section 3, represents the diffusion sensitizing gradients and the cross–terms.

In practice, S_i is replaced in Eq. (11) by Ŝ_i, the value obtained from the experiments, to be able to estimate d from Eq. (13). Since V_DC is an m × 6 matrix, given the measurements p ∈ IR^m, for Eq. (13) to have a solution m must be at least equal to 6. In general, more than six measurements (m > 6) are made to alleviate the perturbations and the pseudoinverse matrix is used to obtain the least squares solution of Eq. (13):

$${\gamma }^2{V}_{DC}^T{V}_{DC}d=V_{DC}^{T}p.$$ (14)

In [16, 25] V_DC is replaced in Eq. (14) with V_D, the matrix corresponding to the diffusion gradients only, computed in Section 3.1. Whenever using Eq. (14) is not deemed to be satisfactory due to different kind of perturbances, nonlinear estimation methods minimizing the least squares error for Eq. (10) shown in Eq. (39) are preferred [29].

It is crucial to note that Eq. (13) or Eq. (14) pose no restrictions on the definiteness of the diffusion quadratic form D. However, according to Fick's first equation [30, p. 2] D must be positive definite. In other words, it is possible to calculate a D with a negative eigenvalue but this is physically meaningless. Therefore, it is impossible to design an experiment which would make the integral in Eq. (7) vanish in order to measure S_p directly from Eq. (8) because D > 0 implies that the integral will only be zero for h = 0 (i.e. h(ζ) = 0 for all ζ ∈ [0, t]). That means an imaging experiment without any gradients has to be realized!

S_p can be estimated by adding another (minimum 7^th) acquisition:

$$\left[\begin{array}{cc}{v}_1& -1\\ ⋮& ⋮\\ v_7& -1\end{array}\right]\left[\begin{array}{c}d\\ \frac{ln(S_p)}{{\gamma }^2}\end{array}\right]=[V-\mathrm{1I}]\left[\begin{array}{c}d\\ \frac{ln(S_p)}{{\gamma }^2}\end{array}\right]=-\frac{1}{{\gamma }^2}\left[\begin{array}{c}ln(S_1)\\ ⋮\\ ln(S_7)\end{array}\right].$$ (15)

The augmented coefficient matrix uses V of Eq. (6) rather than V_D that is used by Papadakis et al. [31] to include S₀ as a variable in the method called total fitting:

$$[V_D-\mathrm{1I}]\left[\begin{array}{c}d\\ \frac{ln(S_0)}{{\gamma }^2}\end{array}\right]=-\frac{1}{{\gamma }^2}\left[\begin{array}{c}ln(S_1)\\ ⋮\\ ln(S_7)\end{array}\right].$$ (16)

In this equation, V_D would be replaced by V_DC should the cross–terms be included for a complete model.

3. Components of V

The matrix V defined in Eq. (6) is a nonlinear function of the magnetic field gradients. In order to distinguish the contributions of the diffusion and imaging gradients in V, G can be written as a sum of its diffusion and imaging parts G = G_D + G_I since their time axis supports (gradient–on times) do not intersect. However, when the gradients are integrated to obtain h using Eq. (2), the supports intersect. So, in the calculation of V, the diffusion and imaging gradients are not separable (see Fig. 2). However, the definition of h given in Eq. (2) implies that h(G_D + G_I) = h(G_D) + h(G_I). Therefore V can be separated into three parts by expanding Eq. (6):

$$V=V_D+V_I+V_C$$ (17)

with the detailed definition of the matrices given in Eq. (40). V_D and V_I represent the effect of diffusion gradients and imaging gradients respectively, and V_C describes the cross–terms between the two types of gradients.

In the ideal case, where the gradients have rectangular shapes (rather than trapezoids), the imaging and diffusion gradients are factorized as the product of a scalar function of time, β_*(ξ), which describes the switching times and duration of the gradients, and a vector (not necessarily of unit norm for the diffusion gradients) that defines the strength of different channels:

$$G_{\ast }(\xi )={\beta }_{\ast }(\xi )g_{\ast }={\beta }_{\ast }(\xi )[g_{\ast x}{g}_{\ast y}{g}_{\ast z}].$$ (18)

The asterisk can be any of the labels ro, pe, ss (read–out, phase–encode, slice–select) for imaging or D for diffusion gradients. Define

$${\mu }_{\ast }(\zeta )={\int }_0^{\zeta }{\beta }_{\ast }(\xi )d\xi -2u(\zeta -\tau ){\int }_0^{\tau }{\beta }_{\ast }(\xi )d\xi .$$ (19)

to obtain from Eq. (2)

$$h(G_{\ast },\zeta )={\mu }_{\ast }(\zeta )g_{\ast }={\mu }_{\ast }(\zeta )[g_{\ast x}{g}_{\ast y}{g}_{\ast z}].$$ (20)

This formulation is well suitable for defining optimization problems with the objective of decoupling the imaging and diffusion gradients [14]. Even if the gradient functions are not boxcars, the factorization given in Eq. (18) will still be a good approximation for gradient amplifiers with short rise times. The calculations for trapezoidal gradients are straightforward but tedious so the rectangular gradients will be adapted for the remainder of the manuscript.

3.1. Calculation of V_D

For ease of notation, denote g_iD, the i^th diffusion gradient vector by g_i. The product of the separated timing and vector component is written as:

$$G_{iD}(\xi )={\beta }_D(\xi )g_i.$$

Using Eq. (19) and Eq. (20), V_D in Eq. (40) can also be factored into a scalar time function and a matrix, which is a function of the diffusion gradient vectors, as follows. Define a nonlinear function w that maps the vector g_i = [g_ix g_iy g_iz] in IR³ to a vector in IR⁶ :

$$w(g_i)=[g_{ix}^2{g}_{iy}^2{g}_{iz}^{2}2g_{ix}{g}_{iy}2g_{iy}{g}_{iz}2g_{ix}{g}_{iz}].$$ (21)

Let g = (g₁, …, g_m) denote the ordered set of the diffusion gradient vectors. The expression for V_D in Eq. (40) and the definition Eq. (2) give

$$V_D=b_t{V}_g$$ (22)

where V_g on the right hand side is the nonlinear map

$$\begin{array}{c}{\mathit{\text{IR}}}^{m\times 3}\to {\mathit{\text{IR}}}^{m\times 6}\\ g=\left[\begin{array}{ccc}{g}_{1x}& g_{1y}& g_{1z}\\ ⋮& ⋮& ⋮\\ g_{mx}& g_{my}& g_{mz}\end{array}\right]\mapsto V_g=\left[\begin{array}{c}w(g_1)\\ ⋮\\ w(g_m)\end{array}\right]\end{array}$$ (23)

or more explicitly V_g is the m × 6 matrix

$$\left[\begin{array}{cccccc}{g}_{1x}^2& g_{1y}^2& g_{1z}^2& 2g_{1x}{g}_{1y}& 2g_{1y}{g}_{1z}& 2g_{1x}{g}_{1z}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ g_{mx}^2& g_{my}^2& g_{mz}^2& 2g_{mx}{g}_{my}& 2g_{my}{g}_{mz}& 2g_{mx}{g}_{mz}\end{array}\right]$$ (24)

and b_t is calculated using Eq. (19) and Eq. (20):

$$\begin{array}{l}{b}_t={\int }_0^t{\left({\int }_0^{\zeta }{\beta }_D(\xi )d\xi -2u(\zeta -\tau ){\int }_0^{\tau }{\beta }_D(\xi )d\xi \right)}^{2}d\zeta \\ ={\int }_0^t{\mu }_D^2(\zeta )d\zeta .\end{array}$$ (25)

For example, the scalar factor of rectangular diffusion gradient pulses is $b_t={\delta }^2(\mathrm{\Delta }-\frac{1}{3}\delta )$ and for trapezoidal pulses it is ${\delta }^2(\mathrm{\Delta }-\frac{1}{3}\delta )-\frac{1}{6}\delta t_{\mathit{\text{rise}}}^2+\frac{1}{30}{t}_{\mathit{\text{rise}}}^3$ where δ is the length of the pulses, Δ is the time between them as shown in Fig. (1), and t_rise is the time for the gradients to reach a specified value. Since $(b_t-{\delta }^2(\mathrm{\Delta }-\frac{1}{3}\delta ))\approx O(t_{\mathit{\text{rise}}}^2)$, if t_rise ≪ δ, trapezoidal gradients can be approximated by rectangular functions of time.

Note that b_t is different than the usual definition of b–value given in the literature. It does not include the gradient strengths and γ². In this manner, the design of DTI experiments based on the diffusion encoding gradient schemes is turned into a geometric search problem as in the formulation of the optimization problems in [14].

3.2. Calculation of V_I

Although V_I is theoretically eliminated from the estimation in Eq. (13), its derivation below plays an essential role for the derivation of the cross–terms matrix V_C as well exposing some of the difficulties with the DTI model. Moreover, V_I appears in Eq. (15) for the total fitting of S_p.

During an experiment, once the slice thickness, position and orientation are selected, they do not change. This implies that the imaging part of V, V_I, has all of its rows equal to each other in Eq. (40). The time dependent imaging gradient vector G_I can be written as a linear combination of three unit vectors, corresponding to read–out, phase–encode and slice–select directions:

$$\begin{array}{l}{G}_I(\xi )={\beta }_{ro}(\xi )g_{ro}+{\beta }_{pe}(\xi )g_{pe}+{\beta }_{ss}(\xi )g_{ss}\\ =[{\beta }_{ro}(\xi ){\beta }_{pe}(\xi ){\beta }_{ss}(\xi )]\left[\begin{array}{lll}{g}_{ro,x}& g_{ro,y}\hfill & g_{ro,z}\\ g_{pe,x}& g_{pe,y}& g_{pe,z}\\ g_{ss,x}& g_{ss,y}& g_{ss,z}\end{array}\right].\end{array}$$ (26)

In this case, the vector's coefficients, which are scalar functions of time, incorporate the strength of the gradients. By the linearity of h, Eq. (19), Eq. (20) and Eq. (26) the following is obtained:

$$\begin{array}{l}h(G_I,\zeta )={\mu }_{ro}(\zeta )g_{ro}+{\mu }_{pe}(\zeta )+g_{pe}+{\mu }_{ss}(\zeta )g_{ss}\\ =[{\mu }_{ro}(\zeta ){\mu }_{pe}(\zeta ){\mu }_{ss}(\zeta )]\left[\begin{array}{lll}{g}_{ro,x}& g_{ro,y}& g_{ro,z}\\ g_{pe,x}& g_{pe,y}& g_{pe,z}\\ g_{ss,x}& g_{ss,y}& g_{ss,z}\end{array}\right].\end{array}$$ (27)

The matrix on the right hand side is an orthogonal matrix because the imaging directions are orthogonal in MRI. If the coordinate frame is chosen to be the imaging frame, the matrix on the right hand side of Eq. (26) and Eq. (27) becomes the identity matrix. The calculation of V_I, which only requires one row, v_I, is accomplished by integrating w([μ_ro μ_pe μ_ss]):

$$v_I={\int }_0^t[{\mu }_{ro}^2{\mu }_{pe}^2{\mu }_{ss}^{2}2{\mu }_{ro}{\mu }_{pe}2{\mu }_{pe}{\mu }_{ss}2{\mu }_{ro}{\mu }_{ss}]d\zeta .$$ (28)

If the imaging gradients are not aligned with the coordinate frame, the calculations are lengthy but straightforward. For instance the first entry of the row vector is calculated as:

$${\int }_0^t{h}_x^2(G_I)d\zeta ={\int }_0^t{({\mu }_{ro}{g}_{ro,x}+{\mu }_{pe}{g}_{pe,x}+{\mu }_{ss}{g}_{ss,x})}^{2}d\zeta .$$

3.3. Calculation of V_C

V_C can be computed in a straightforward manner using the functions given in the previous sections, especially Eq. (27). The matrix consists purely of the cross–terms of the imaging and diffusion parts of h. For example, when the imaging gradients are aligned with the coordinate axes, the calculation of the i^th row requires the following (see Eq. (40)):

$${\int }_0^t{h}_k(G_{iD})h_l(G_I)d\zeta =\left({\int }_0^t{\mu }_{iD}(\zeta ){\mu }_l(\zeta )d\zeta \right)g_{ik}{g}_l$$

where k is any of the labels x, y, z; l is any of x, y, z on the left–hand side and is the corresponding label (i.e. one of ro, pe, ss) on the right–hand side. The calculations result in:

$$V_C=2{\int }_0^t\left[\begin{array}{ccc}{\mu }_{1D}{\mu }_{ro}{g}_{1x}{g}_{ro,x}& \cdots & {\mu }_{1D}({\mu }_{ss}{g}_{1x}{g}_{ss,z}+{\mu }_{ro}{g}_{1z}{g}_{ro,x})\\ ⋮& & ⋮\\ {\mu }_{mD}{\mu }_{ro}{g}_{mx}{g}_{ro,x}& \cdots & {\mu }_{mD}({\mu }_{ss}{g}_{mx}{g}_{ss,z}+{\mu }_{ro}{g}_{mz}{g}_{ro,x})\end{array}\right]d\zeta .$$ (29)

Under boxcar conditions, as in Eq. (22), all μ_iD's are the same for all of the acquisitions: μ_D ≐ μ_iD and the matrix can be calculated as a function of diffusion gradients, V_C(g) :

$$V_{C(g)}=2{\int }_0^t{\mu }_D\left[\begin{array}{cccccc}{\mu }_{ro}{g}_{1x}& {\mu }_{pe}{g}_{1y}& {\mu }_{ss}{g}_{1z}& ({\mu }_{pe}{g}_{1x}+{\mu }_{ro}{g}_{1y})& ({\mu }_{pe}{g}_{1y}+{\mu }_{ss}{g}_{1z})& ({\mu }_{ss}{g}_{1x}+{\mu }_{ro}{g}_{1z})\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ {\mu }_{ro}{g}_{mx}& {\mu }_{pe}{g}_{my}& {\mu }_{ss}{g}_{mz}& ({\mu }_{pe}{g}_{mx}+{\mu }_{ro}{g}_{my})& ({\mu }_{pe}{g}_{my}+{\mu }_{ss}{g}_{mz})& ({\mu }_{ss}{g}_{mx}+{\mu }_{ro}{g}_{mz})\end{array}\right]d\zeta .$$ (30)

When the image orientations are not aligned with the coordinate frame, similar to the case of V_I, tedious but routine computations must be carried out. For example, (1, 1) entry of V_C can be calculated as

$$2{\int }_0^t{h}_x(G_{1D})h_x(G_I)d\zeta =2{\int }_0^t{\mu }_{1D}{g}_{1x}({\mu }_{ro}{g}_{ro,x}+{\mu }_{pe}{g}_{pe,x}+{\mu }_{ss}{g}_{ss,x})d\zeta .$$ (31)

4. Deficiencies of the DT–MRI Model

Although the analytical derivations are carried out without any hurdles, a significant problem arises when the numerical values of V_I (specifically for the total fitting in Eq. (15)) and V_C need to be calculated. For each image, the read–out and the slice–select gradient magnitudes are constant but the strength of the phase–encoding gradient changes at each k–space line. This implies that there is a range of gradient strength choices to use in β_pe for the calculation of μ_pe, h, V_I and V_C. In [13], β_pe is chosen to be 0, corresponding to the center of k–space. This specific choice is equivalent to completely neglecting the effect of the phase–encoding gradients, defying the purpose of obtaining a complete model.

Moreover, in Eq. (1) the estimation of D is based on the intensity values at each pixel that originate from the entirety of the k–space data, not from a single point. During the data collection, the read–out gradient is active. The gradient makes the diffusion of the spins affect all of the k–space points. Since the phase–encode and read–out gradient integrals do not possess null moments, their integrals, $\underset{0}{\overset{T_E}{\int }}{\mu }_{ro}^{2}d\zeta$ and $\underset{0}{\overset{T_E}{\int }}{\mu }_{pe}^{2}d\zeta$, do not form a plateau around T_E as shown in Fig. 3. Therefore the diffusion effect on the k–space points is not uniform and at a fundamental level the DTI model fails to take into account this property.

5. Center Symmetric Diffusion Gradients: NoCroT and CroTO

The modeling ambiguities described in Section 4 affect V_I and V_C. V_I is theoretically eliminated by replacing S_p in Eq. (1) with S₀. This section presents a theoretical way of eliminating the necessity to compute V_C.

The cross–terms can be completely avoided by using the properties of V_C and a specific organization of gradients. Equation (24) and Eq. (29) show that when the sign of the diffusion gradients is changed, V_D remains the same, because V_g = V_(−g) while the cross–terms matrix changes sign, V_C(−g) = −V_C(g). Experiments performed with center–symmetric diffusion gradients, i.e. with the gradient set $(g,-g)=(g_1,\dots ,g_{\frac{m}{2}},-g_1,\dots ,-g_{\frac{m}{2}})$ result in:

$${\gamma }^2\left[\begin{array}{c}{b}_t{V}_g+V_{C(g)}\\ b_t{V}_{(-g)}+V_{C(-g)}\end{array}\right]d=\left[\begin{array}{c}{p}_1\\ p_2\end{array}\right].$$ (32)

The direct approach would be to use least squares estimation by solving the following equation using the pseudoinverse:

$$2{\gamma }^2({\mathit{\text{V}}}_D^T{V}_D+{\mathit{\text{V}}}_C^T{V}_C)d={\mathit{\text{V}}}_D^T(p_1+p_2)+{\mathit{\text{V}}}_C^T(p_1-p_2).$$ (33)

On the other hand, the sum and the difference of Eq. (32) yield

$$\begin{array}{l}2{\gamma }^2{b}_t{V}_{g}d=\left[\begin{array}{c}2ln{S}_0-ln{S}_1-ln{S}_{(\frac{m}{2}+1)}\\ ⋮\\ 2ln{S}_0-ln{S}_{\frac{m}{2}}-ln{S}_m\end{array}\right]\\ =p_1+p_2(\text{NoCroT})\end{array}$$ (34)

$$\begin{array}{l}2{\gamma }^2{V}_{C(g)}d=\left[\begin{array}{c}-ln{S}_1+ln{S}_{(\frac{m}{2}+1)}\\ ⋮\\ -ln{S}_{\frac{m}{2}}+ln{S}_m\end{array}\right]\\ =p_1-p_2(\text{CroTO}).\end{array}$$ (35)

In this manner Eq. (33) is partitioned according to Eq. (34) and Eq. (35). V_C does not appear in Eq. (34), hence the name ‘No Cross Terms’: NoCroT; in contrast to Eq. (35) which consists of ‘Cross Terms Only’: CroTO.

Under ideal experimental conditions, assuming that the correct choice of the phase encoding gradient to use for V_C (and V_I) is known, Eq. (32), Eq. (33), Eq. (34) and Eq. (35) give rise to the same solution for d. NoCroT has the advantage of solving the estimation problem without calculating V_C.

This approach does require, however, using a minimum number of 12 measurements. Since the center–symmetric gradient pairs point in the same direction, the first necessary condition given in [17] for V_D to have full rank is violated. The correct way to choose the center–symmetric diffusion gradients is to first select 6 vectors that will ensure the full rank condition on V_g [17]. More gradients can be added after this requirement is fulfilled. The center–symmetric counterparts are included afterwards to obtain V_(g,−g) with full rank. This implies that the minimum number of NoCroT diffusion gradients is 12.

The solution of NoCroT, Eq. (34), is given by the use of pseudoinverse in:

$${\gamma }^2{\mathit{\text{V}}}_D^T{V}_{D}d=\frac{1}{2}{\mathit{\text{V}}}_D^T(p_1+p_2)$$ (36)

which shows that the NoCroT method is not equivalent to the complete model of Eq. (33), since half of the equations, i.e. Eq.(35), is discarded from the estimation. This is the cost paid for the advantage offered by NoCroT.

Moreover, Eq. (36) is also the least squares solution of the following set of inconsistent equations where the imaging gradients are completely ignored:

$${\gamma }^2\left[\begin{array}{c}{V}_D\\ V_D\end{array}\right]d=\left[\begin{array}{c}{p}_1\\ p_2\end{array}\right].$$ (37)

This is shown by multiplying Eq. (37) from the left with $[{\mathit{\text{V}}}_D^T{\mathit{\text{V}}}_D^T]$ to obtain the pseudoinverse matrix, which results exactly in Eq. (36). Therefore when center–symmetric gradient schemes are used, NoCroT is equivalent to completely neglecting the imaging gradients from the equations.

When the gradient schemes are not center–symmetric, the valid equation for a complete DTI model is Eq. (13) and there is no justification such as the one provided by NoCroT for neglecting the cross–terms.

In the special case where the minimum number of 6 gradient pairs (m = 12) are used V_D is a square matrix in Eq. (34) and Eq. (36). The NoCroT equation is solved by matrix inversion and therefore d is perfectly fitted to $\frac{1}{2}(p_1+p_2)$.

The central assumption behind the NoCroT strategy is that when the sign of the diffusion gradients is changed, the matrix V_C will change sign regardless of how the imaging gradients are modeled and how they appear in the equations. Practically, for the method to work properly, the gradient system must be able to invert the diffusion gradients exactly.

6. Description of the Experiments and the Analysis

First and foremost, the estimation procedures must work properly for the simplest case of diffusion with known characteristics: an isotropic sample. For that reason, a polypropylene centrifuge tube by FisherBrand (Cat. No. 05–539–6) filled with tap water at room temperature, with an inner diameter at the slice of 2.5 cm was chosen as the phantom.

6.1. Experimental Setup

The experiments were carried out on a 4.7 Tesla MR scanner (Varian NMR Systems, Palo Alto, CA, USA) with a gradient system of bore size of 15 cm, maximum gradient strength of 45 gauss/cm and rise time of 0.2 ms using a quadrature birdcage coil (Varian NMR Systems, Palo Alto, CA, USA) with 108/63 mm diameter sizes. DTI data were obtained using the standard spin–echo multi–slice sequence with in–house modifications that store all of the relevant parameters, including the timing and amplitudes of all of the crusher gradients. The images were 128 × 128 pixels with a field of view 64 × 64 mm² and 0.5 mm slice thickness. The repetition time T_R = 2 s, echo time T_E = 35 ms, diffusion pulse separation Δ = 18 ms, diffusion pulse duration δ = 6 ms were used.

Center–symmetric diffusion gradient schemes with 12 diffusion gradient vectors were used to obtain data. The gradient schemes were constructed by appending to the 6 vector gradient schemes listed in [24] their central symmetric part: Tetrahedral (geometrically, the scheme is build on the four tetrahedral vectors of [32] by adding two more elements and is different from the scheme presented in [32]), Cond6, Jones noniso (without the last vector) renamed as Cond* because it yields to a V_g with a good condition number, Jones (N = 6), Muthupallai (which is equal to Icosahedron (ICOSA6) scheme from [25]), Downhill Simplex Minimization (DSM), Dual Gradient. Also a modified version of the Muthupallai scheme, denoted by MUTM is included in the experiments. For convenience, the gradient schemes are also provided in Table 1 with the modified entries of MUTM in bold. A maximum diffusion gradient strength of g_diff = 12 gauss/cm was used. With the boxcar approximation, at maximum diffusion gradient the value of the scalar coefficient is ${\gamma }^2{b}_t{g}_{\mathit{\text{diff}}}^2=593.61\text{s}/{\text{mm}}^2$.

Table 1.

Diffusion Gradient Schemes

cond6			cond*			dsm			dualgr
0.755	0.26	0.602	1	0	0	0.91	0.416	0	0.707	0.707	0
-0.479	0.711	0.515	0	1	0	0	0.91	0.416	0.707	0	0.707
-0.394	-0.63	0.669	0	0	1	0.416	0	0.91	0	0.707	0.707
-0.616	0.262	0.743	0.707	0.707	0	0.91	-0.416	0	0.707	-0.707	0
0.558	-0.741	0.375	0	0.707	0.707	0	0.91	-0.416	0.707	0	-0.707
-0.954	-0.067	0.292	0.707	0	0.707	-0.416	0	0.91	0	0.707	-0.707

jones6			mutm			muthup			tetra
1	0	0	0.851	0.526	0	0.851	0.526	0	0.577	0.577	0.577
0.446	0.895	0	0.851	-0.526	0	0	0.851	0.526	-0.577	-0.577	0.577
0.447	0.275	0.851	0	0.526	0.851	0.526	0	0.851	0.577	-0.577	-0.577
0.448	-0.723	-0.525	0	-0.851	-0.526	0.851	-0.526	0	-0.577	0.577	-0.577
0.447	-0.724	0.526	-0.526	0	0.851	0	0.851	-0.526	0.707	0.707	0
-0.449	-0.277	0.85	0.526	0	0.851	-0.526	0	0.851	0.707	0	0.707

6.2. Analysis of the Experimental Results

In–house Mathematica® (Wolfram Research, Champaign, IL USA) code was used to compute components of V, as described in Section 3, using the parameter values written to the hard disk by the pulse sequence. Integrals were computed using trapezoidal shapes rather than rectangular ones. The calculations included all of the crusher gradients. In–house Matlab® (Mathworks, Natick, MA USA) programs were utilized for the estimation of d at each pixel and for the graphical representation and maps of related results. Standard Matlab® Image Processing Toolbox® routines, Sobel edge detection and morphological reconstruction were used to detect the signal region of the phantom in non-diffusion–weighted images for each gradient scheme. The edges were removed to obtain a region free of susceptibility artifacts and the intersection of all regions was taken to obtain the circular area with 1944 pixels.

Among several estimation methods including weighted and non–weighted least squares for Eq. (14), total fitting [31] and nonlinear estimation (constrained and unconstrained) for Eq. (10), non–weighted least squares is chosen because of its speed and simplicity.

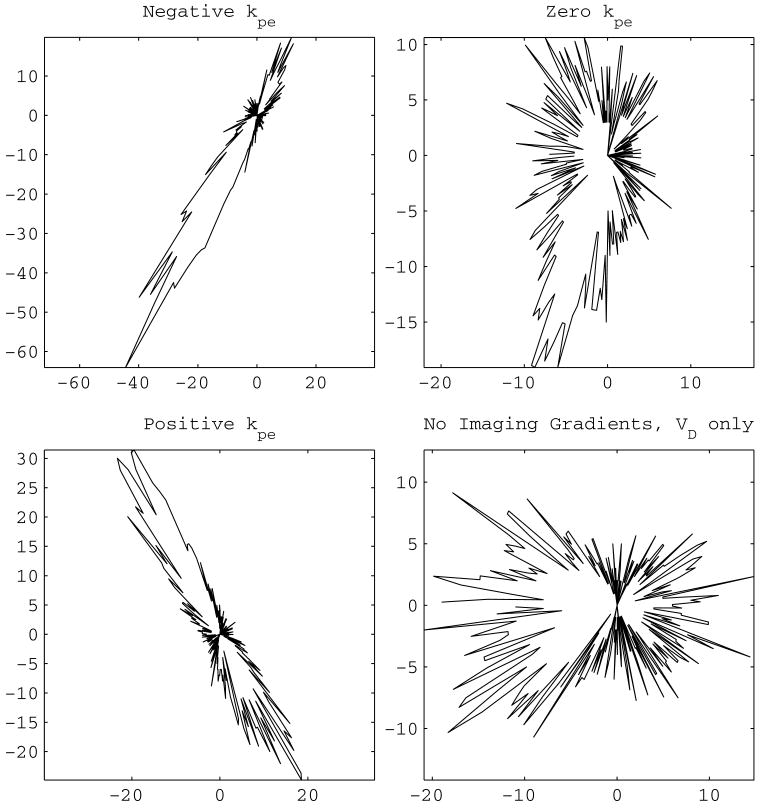
Eight standard diffusion gradient schemes listed in Section 6.1 were used for measurements. In the computation of V_C and V_I the phase–encoding gradient value of 0 was selected based on the observations from Fig. 4 that the eigenvectors show a bias towards the orientation of the phase–encoding gradient. The contrast is visible on the first column of Fig. 4 where upper and lower limits of phase–encoding gradient values are used. It should be clear that this choice does not resolve the existing phase–encoding value ambiguity.

Figure 4.

Polar histogram of the eigenvector corresponding to the largest eigenvalue. The distance of each point from the origin is the number of eigenvectors with their slice plane component pointing in the direction of that point. Under perfect conditions an isotropic sample would result in a circle representing a uniform distribution. The vertical axis is the phase–encode direction. The eigenvectors align according to the phase–encode gradient value used in the estimation equations. This is demonstrated with contrast on the left column: the histograms of the eigenvectors originating from using the most negative (top left corner) and most positive of the phase–encode gradient strengths are ‘orthogonal’. The choice of zero strength (top right corner) creates a histogram aligned in between the ones of the left column. In the case the imaging gradients are excluded from the calculations, general orientation is horizontal.

7. Analysis Results

The analysis was achieved by investigating the variation of different DTI quantities over the uniform sample. The calculations were carried out using two different coefficient matrices: V_DC (all gradients) of Eq. (32) and V_D (diffusion only, equivalent to NoCroT since center–symmetric gradients¹ were used) of Eq. (37). The results are presented in respective rows of the Table 2 as mean±standard deviation. Exclamation points indicate the presence of negative eigenvalues in the Tetrahedron diffusion gradient scheme for ‘all gradients’.

Table 2.

Summary of Analysis Results

		cond6	cond*	dsm	dualgr	mutm	jones6	muthup	tetra
$\overline{FA}$	VDC	0.199 ± 0.0317	0.128 ± 0.0287	0.094 ± 0.0191	0.162 ± 0.0264	0.574 ± 0.0476	0.112 ± 0.0206	0.112 ± 0.0229	!-!
	VD	0.0799 ± 0.0386	0.0639 ± 0.023	0.0506 ± 0.0166	0.0526 ± 0.0189	0.101 ± 0.0584	0.0494 ± 0.0163	0.0502 ± 0.0169	0.111 ± 0.0542
λ̄1	VDC	2.51 ± 0.114	2.12 ± 0.0584	2.04 ± 0.0524	2.08 ± 0.0674	3.84 ± 0.269	1.99 ± 0.053	1.99 ± 0.0506	3.19 ± 0.113
	VD	2.26 ± 0.0928	2.11 ± 0.0677	2.02 ± 0.0473	2 ± 0.0546	2.06 ± 0.132	1.96 ± 0.0511	1.96 ± 0.0482	2.07 ± 0.11
λ̄2	VDC	2.18 ± 0.108	1.95 ± 0.0731	1.92 ± 0.0483	1.97 ± 0.0672	1.66 ± 0.0556	1.88 ± 0.0502	1.88 ± 0.0487	2.99 ± 0.117
	VD	2.1 ± 0.0554	1.98 ± 0.0567	1.93 ± 0.0417	1.9 ± 0.0506	1.88 ± 0.0477	1.87 ± 0.0447	1.86 ± 0.0409	1.87 ± 0.0831
λ̄3	VDC	1.67 ± 0.0611	1.64 ± 0.0799	1.69 ± 0.0493	1.51 ± 0.0621	1.11 ± 0.0855	1.6 ± 0.0563	1.6 ± 0.0578	-0.252 ± 0.13
	VD	1.93 ± 0.104	1.86 ± 0.0669	1.83 ± 0.0463	1.8 ± 0.0575	1.69 ± 0.15	1.78 ± 0.0462	1.78 ± 0.0448	1.67 ± 0.108

The first row group shows the mean of the pixel fractional anisotropy index [33], $\overline{FA}$, from the signal region. The fractional anisotropy is a function of the pixel eigenvalues (λ₁ ≥ λ₂ ≥ λ₃):

$$\mathit{\text{pFA}}=\frac{\sqrt{{({\lambda }_1-{\lambda }_2)}^2+{({\lambda }_2-{\lambda }_3)}^2+{({\lambda }_3-{\lambda }_1)}^2}}{\sqrt{2({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)}}.$$ (38)

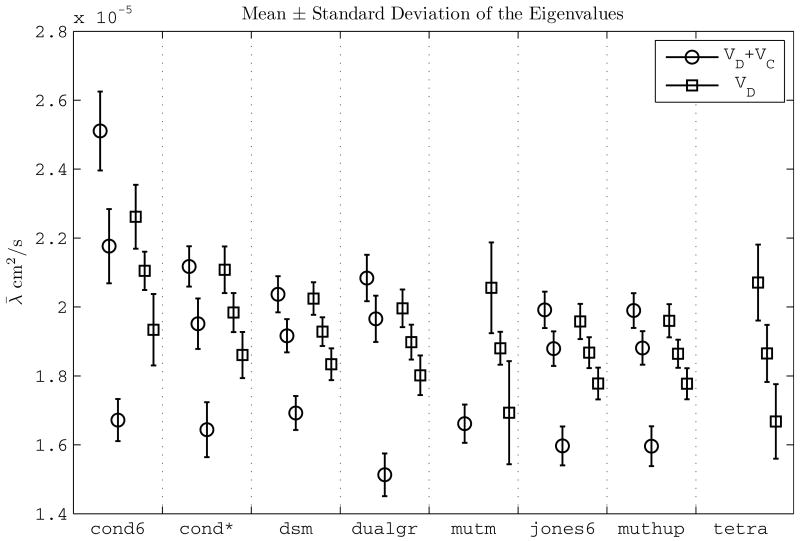
In the experimental results, $\overline{FA}$ is the lowest when all of the imaging gradients are neglected from the calculations (row 2, Table 2). Quantitatively, the decrease varies between from 46.77% (DSM scheme) up to 83.31% (Mutm scheme). Figure 5 portrays that the increase in the fractional anisotropy for V_DC is mainly due to the separation of the smallest eigenvalue from the other two.

Figure 5.

The mean of pixel eigenvalues obtained with different methods: V_D + V_C (‘all gradients’) and V_D (‘diffusion gradients only’). The eigenvalues obtained with V_D + V_C show a larger dispersion meaning a higher anisotropy compared to the ones obtained with V_D. The scheme Tetrahedron exhibit negative eigenvalues for V_DC and they are not shown. The eigenvalues for Mutm scheme obtained by ‘all gradients’, 3.84 ± 0.269, 1.11 ± 0.0855, are also omitted for clarity of presentation.

The standard deviation of the fractional anisotropy does not change drastically between the methods. The difference of the precision values between the methods is not significant enough to draw conclusions.

Since the only known fact is the isotropic nature of the sample, the accuracy criterion for the experiments is the closeness of the eigenvalues. Theoretically, in an isotropic sample the fractional anisotropy is zero because of all of the eigenvalues are equal in the numerator of Eq. (38). The eigenvalues of the estimation using all of the gradients are more dispersed than the ones of the other two methods, which is also visible in Fig. 5. The estimation with V_DC indicates a less isotropic sample and therefore is less accurate.

In addition, the Tetrahedron scheme exhibits negative eigenvalues (see Section 2.1) using V_DC resulting in a ratio of number of pixels with negative eigenvalues to total number of pixels 0.998 (n_roi = 1944). This indicates that the inclusion of imaging gradients can perturb significantly the solutions depending on the gradient scheme sensitivity.

The precision of the eigenvalues does not significantly change between the methods.

The decisive criterion for the performance of any model matching method is the error between the measurements Ŝ_i and the model. For DTI, χ̄ is the mean of the pixel residual error, ‖χ‖ :

$${\Vert \chi \Vert }_2^2=\frac{1}{m}\sum _{i=1}^m{(S(v_{i}d)-{\widehat{S}}_i)}^2.$$ (39)

In the case of nonlinear estimation [18], the solution for d is found by minimizing ${\Vert \chi \Vert }_2^2$, equivalent to using Eq. (1). In the case of Eq. (13), d estimated by the pseudoinverse matrix and the least squares fitting error is not the model matching error of Eq. (39).

The numerical results for the model matching error are presented in Table 3. Notably, there is an increase in the model matching error when the imaging gradients are included in the calculations. This is inline with the observation that the FA increases for the same method: larger residual error, less accurate results.

Table 3.

The Model Matching Error

		cond6	cond*	dsm	dualgr	mutm	jones6	muthup	tetra
χ̄	VDC	529.7 ± 63.86	489.5 ± 52.99	495.4 ± 45.64	481.7 ± 38.59	445.1 ± 32.79	489.9 ± 31.95	483.6 ± 31.43	334.9 ± 25.92
	VD	262.8 ± 36.32	293.4 ± 35.87	272.7 ± 30.68	273.4 ± 28.94	276.7 ± 27.13	272.7 ± 25.37	269.4 ± 26.9	304.9 ± 27.82

8. Conclusion and Future Directions

In the light of the discussion of Section 4 about the severe theoretical and numerical inadequacies for incorporating the imaging gradients to obtain a complete model, and of the experimental results presented in Section 7, the following is concluded:

The decrease of the accuracy for the inclusion of all of the gradients validates the existence of modeling incongruities in Diffusion Tensor Imaging model.

Although there are quantitative variations between the results obtained from different diffusion gradient schemes, qualitatively the conclusion holds regardless of the scheme. Moreover, the usage of nonlinear estimation methods instead of least squares estimation does not change the conclusion [18].

In an effort to minimize the effect of the imaging gradients, the NoCroT method devised by the assistance of the linear algebraic framework avoids the cross–terms in the calculations. The theoretical advantage of the center–symmetric gradient schemes is the elimination of the total impact of imaging gradients on a broader scale. The center–symmetric gradients make NoCroT method mathematically equivalent to estimation using the equations that involve only the diffusion gradients, in other words just the coefficient matrix V_D. Without the center–symmetry, there is no justification for neglecting the cross–terms in a complete model.

An important consequence of the introduction of the imaging gradients into the picture is the creation of the direction awareness for the gradient schemes or equivalently for the sample orientation with respect to the imaging coordinate frame. Concisely speaking, without the involvement of the imaging gradients in the model, the rotation of the gradient scheme or the rotation of the sample should not change the experimental results. Each imaging gradient affects the signal according to the component of the spin motion along its axis. Such effect could result to misleading outcomes for the estimation of the eigenvalues and eigenvectors, and consequently for the fiber tracking algorithms. Therefore, it is important to design robust and sample–independent gradient schemes that would be minimally affected by the imaging gradients. These investigations are carried out in [14] by developing further the linear algebraic setup into a normed vector space structure that permits devising appropriate optimization problems.

A. The components of V, Diffusion Gradient Schemes and the Numerical Values of the Analysis Results

The detailed definition of the different coefficient matrices corresponding respectively to diffusion, imaging and cross term components is:

$$\begin{array}{l}V={\int }_0^t\left[\begin{array}{ccc}{h}_x^2(G_{1D})& \cdots & 2h_x(G_{1D})h_z(G_{1D})\\ ⋮& & ⋮\\ h_x^2(G_{mD})& \cdots & 2h_x(G_{mD})h_z(G_{mD})\end{array}\right]d\zeta \\ +{\int }_0^t\left[\begin{array}{ccc}{h}_x^2(G_I)& \cdots & 2h_x(G_I)h_z(G_I)\\ ⋮& & ⋮\\ h_x^2(G_I)& \cdots & 2h_x(G_I)h_z(G_I)\end{array}\right]d\zeta \\ +2{\int }_0^t\left[\begin{array}{ccc}{h}_x(G_{1D})h_x(G_I)& \cdots & h_x(G_{1D})h_z(G_I)+h_x(G_I)h_z(G_{1D})\\ ⋮& & ⋮\\ h_x(G_{mD})h_x(G_I)& \cdots & h_x(G_{mD})h_z(G_I)+h_x(G_I)h_z(G_{mD})\end{array}\right]d\zeta \\ =V_D+V_I+V_{C.}\end{array}$$ (40)