Abstract
Background
Movement of the optical interface used to collect noninvasive near-infrared spectra is known to dramatically increase prediction errors for glucose concentration measurements within the interstitial fluid of living rat skin. Prediction errors increase by more than 2.5-fold when the interface is moved before each non-invasive measurement compared to measurements where the interface position is constant throughout. Chemical heterogeneity of the skin matrix is examined as a possible mechanism for the strong sensitivity to the interface placement during noninvasive measurements conducted from transmission near-infrared absorption spectroscopy.
Method
Microspectroscopy was performed over a region of the near-infrared spectrum (4000–5000 cm−1) to map the concentrations of water, collagen protein, fat, and keratin protein within the skin tissue matrix through which noninvasive spectra are collected. Maps were created for multiple samples of skin excised from male and female animals. Sets of near-infrared spectra were constructed to simulate noninvasive spectra in accord with the basic tissue composition found from the microspectroscopic maps with added information corresponding to a span of glucose concentrations ranging from 5 to 35 mM and Gaussian-distributed noise.
Results
Microspectroscopic maps of rat skin reveal similar patterns of heterogeneity for major chemical components of skin samples excised from both male and female animals. These maps demonstrate concentration domains with dimensions similar to the size of the fiber interface used to collect noninvasive spectra. Partial least squares calibration models generated from sets of simulated spectra demonstrate increases in prediction errors for glucose when the spectral matrix is changed in accord with the degree of chemical heterogeneity displayed in the skin maps. Prediction errors typically increase between 100 and 1000% when comparing errors generated from spectra that represent a single tissue composition versus spectra that represent a varied skin composition in accord with the distribution displayed in the skin maps.
Conclusions
The distribution of the major components of skin is not uniform, but establishes domains within the skin matrix that strongly impact prediction errors for the noninvasive spectroscopic measurement of glucose within the interstitial fluid of rat dermis tissue. The observed increase in prediction error (>2.5-fold) determined from actual noninvasive measurements is within the lower range of prediction error increases demonstrated by this simulation study. These findings implicate that chemical heterogeneity within the tissue matrix is a major factor in the sensitivity of the location of the fiber interface used to collect noninvasive spectral data.
Keywords: interstitial fluid, microspectroscopic mapping, near-infrared spectroscopy, noninvasive glucose sensing, partial least squares regression, skin heterogeneity
Introduction
Our approach to noninvasive glucose sensing involves transmitting a selected band of near infrared light through a fold of skin and extracting the corresponding in vivo concentration of glucose from a multivariate analysis of the resulting spectrum.1–4 In this configuration, the analytical information is derived primarily from the interstitial fluid (ISF) as the incident light propagates through the skin matrix. In practice, the resulting ISF glucose concentration is related to the corresponding blood glucose concentration through a calibration process that assumes a direct and constant relationship between glucose concentrations in blood and ISF.5–8
The utility of measuring glucose by noninvasive near-infrared transmission spectroscopy has been demonstrated in an animal model, where glucose concentrations are obtained by multivariate methods based on either a direct net analyte signal approach or by the partial least squares (PLS) algorithm.3,4 A careful analysis of these methods verifies that in vivo glucose is the origin of the chemical information used in these multivariate calibration models. In these measurements, an optical fiber launches the incident light into one side of the skin-tissue fold and a second fiber directs the transmitted light to a detector element for quantification. Minimal variations were observed in the measured glucose concentrations when the position of this fiber optic was constant throughout the measurement. Large variations in the glucose concentration predictions were observed, however, when the fiber optic interface was repositioned between each measurement. Standard errors for glucose concentration predictions increased 2.5-fold when the interface was repositioned.3 Clearly, such a sensitivity of the position of the interface is a critical issue for noninvasive measurements and is a known obstacle to achieving universal calibrations for many noninvasive techniques.9
Microspectroscopy can be used to gain a better understanding of the origin of this interface sensitivity. We have reported the use of microspectroscopy over the combination region of the near infrared spectrum (4900–4200 cm−1) to construct concentration maps for the principal chemical components of the skin matrix.10 These maps clearly reveal chemical domains within the tissue matrix where regions on the order of 500–800 μm are composed of different amounts of water, fat, collagen protein, and keratin protein. The size of these domains is significant in comparison to the size of the optical fibers used to collect the noninvasive spectra. In our noninvasive measurements, fibers with outer diameters of 1.8 mm were used to both launch and collect the probe radiation. The chemical information obtained from this optical geometry corresponds to the integrated composition of the skin matrix over the volume of skin probed by the propagating light. This volume can be estimated as a cylinder with a diameter of 1.8 mm and a length of 1 mm. The microspectroscopic measurement, on the other hand, provides a resolution of 200 μm and involves transmitting the incident light through a single layer of skin with a thickness ranging between 0.5 and 1.0 mm. This resolution is governed by the step size of the stage used to position the tissue slice under the microscope objective. The superior resolution of the microspectroscopic image permits identification of concentration domains within the tissue matrix. On the basis of the size of these domains relative to the optical geometry, we have speculated that chemical heterogeneity within the skin matrix is an important factor in the position sensitivity of the interface used to collect noninvasive spectra for the measurement of glucose concentrations in ISF.10
In this article, the impact of skin heterogeneity is further explored in two ways. First, the chemical heterogeneity described in our previous paper was restricted to male rat skin and here we expand our investigation to include rat skin excised from female rats. Second, a simulation study is used to quantify the impact of skin heterogeneity on variations in noninvasive glucose measurements. Spectral simulation is necessary in this case because the signal-to-noise ratio (SNR) of the microspectroscopic measurements is insufficient for measuring glucose directly in the tissue matrix. In this simulation study, sets of noninvasive near-infrared spectra are constructed mathematically as linear combinations of pure component absorption spectra for each of the major chemical components of the skin matrix (water, fat, collagen protein, and keratin protein). The relative amount of each component spectrum is taken from the chemical distribution maps determined from our microspectro-scopic analysis of actual skin samples from both male and female rats. In addition, these simulated noninvasive spectra include a concentration weighted spectrum of glucose as well as randomly distributed Gaussian noise. PLS calibration models for glucose are generated and analyzed from sets of these simulated spectra.
The impact of tissue heterogeneity is assessed by generating PLS calibration models from simulated spectra corresponding to one region of a given slice of tissue and then using this model to predict the concentration of glucose represented in simulated spectra that correspond to a different region within the same tissue slice. More specifically, each tissue matrix is divided into four quadrants, each of which is approximately the size of the fiber-optic interface used to collect noninvasive spectra. The calibration model is generated from the set of simulated spectra for one quadrant and then this model is used to predict glucose concentrations in the other three quadrants. The ratio is computed between prediction errors for glucose concentration predictions in the three noncalibration quadrants relative to prediction errors in the calibration quadrant. The scheme outlined in Figure 1 illustrates the basic steps involved in this analysis. Finally, the ratios determined from these simulated spectra are compared to the ratio of prediction errors measured with and without repositioning the fiber-optic interface during actual noninvasive glucose measurements.
Figure 1.
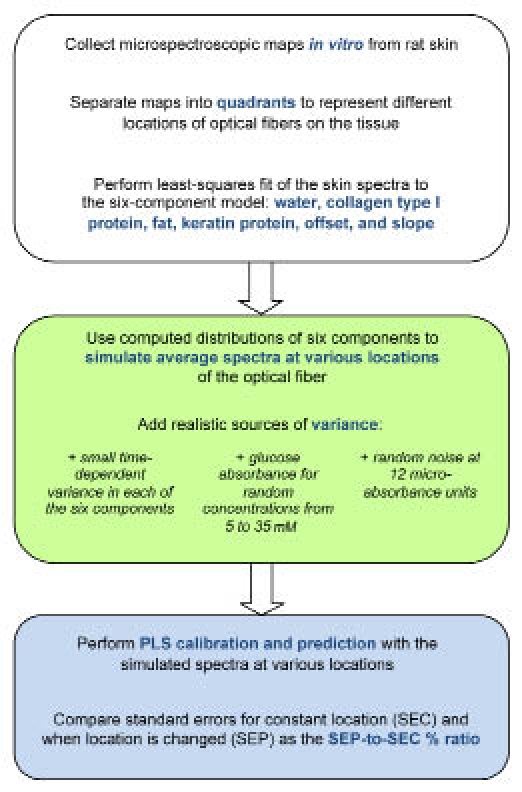
Summary of approach to quantify the influence of tissue heterogeneity on noninvasive glucose predictions. White block addresses processing of in vitro spectral data from rat skin slices, green block explains simulation of spectra at various locations across the skin matrix, and blue block describes PLS procedures.
Methods
Rat Skin Mapping
Procedures for spectral mapping are described in detail elsewhere.10 Briefly, samples of whole skin (epidermis and dermis) were excised from the back of the neck region from 4 male and 4 female healthy Harlan Sprague-Dawley rats immediately following sacrifice. The skin biopsies were taken from male rats that were retired male breeders and weighed between 400 and 500 g, and from female rats that were two months old and weighed between 300 and 350 g. Skin was submerged in phosphate buffered saline, snap-frozen in liquid nitrogen, and stored in a freezer. This procedure was approved by the University of Iowa Animal Care and Use Committee. Prior to collection of the spectra, a 6 × 6 mm2 skin slice was positioned between two sapphire windows inside a compression cell as detailed before.10 Four separate skin slices were investigated per animal giving a total of 32 spectral maps (4 males × 4 slices/animal + 4 females × 4 slices/animal).
Absorbance maps were collected by using a Nicolet Magna 560 Fourier transform infrared (FTIR) spectrometer (Thermo Nicolet Corp., Madison, WI) coupled with an IR-Plan Advantage microscope (Spectra-Tech, Inc., Shelton, CT). The instrumentation was modified by installing a liquid nitrogen-cooled InSb detector in the microscope housing. This detector was equipped with a K-band interference filter to restrict measurements over the combination region of the near-infrared spectrum (4000–5000 cm−1 or 2.0–2.5 μm). As described before, each map was constructed from a 10 × 10 array of near-infrared spectra collected over a 3.6 × 4.8 mm2 rectangle with the step size of the motorized XY-stage being 360 and 480 μm, respectively. The physical thickness was between 0.5 and 1.0 mm for each skin tissue sample as confined by the compression cell.10 In this manner, each map was constructed from the analysis of 100 spectra collected over approximately 3 hours. Every 30 minutes, the stage was moved to the central position on the tissue slice and a set of spectra were recorded as a means to track location-independent changes in the skin sample for reference purposes. The dimensions used for each skin map (3.6 × 4.8 mm2) represented a convenient size of sample for microscopic analysis. In addition, this size of tissue slice permitted the collection of all spectra required across the array of the tissue without concern of dehydration.
All spectra were collected as 8k, double-sided interfero-grams with 128 replicates coadded. Incident radiant powers were maximized by removing external apertures within the microscope. During the course of data collection, no temperature control was exercised and the largest degree of ambient temperature change was between 21 to 24 °C. Air reference spectra used to compute tissue absorbance spectra were collected by using a blank compression cell equipped with a 0.92 mm Teflon spacer with air trapped between two sapphire windows. Data collection and processing were performed with OMNIC® Atlus™ software (Thermo Nicolet Corp., Madison, WI) and MATLAB® 7.0 (The Mathworks, Inc., Natick, MA) was used for all multivariate and statistical analyses.
Analysis of Noninvasive Spectra
The amount of each skin component (water, fat, collagen protein, and keratin protein) was determined by fitting each spectrum in the 10 × 10 spectral array collected for each tissue slice. Each measured skin spectrum was fitted by least squares to a set of pure component spectra for each of these skin components. As described in detail elsewhere,10 these pure component spectra were collected with Type I reagent grade water (18 Mohm) in a 1-mm thick sample cell equipped with sapphire windows, collagen type 1 protein in a 1 mm thick pellet of potassium bromide, keratin protein taken as a fingernail from a human volunteer, and bovine fat in a 1-mm thick sample cell with sapphire windows. Two additional terms were added to this fitting procedure to account for spectral offsets and sloping baselines. This fitting procedure was performed over a spectral range of 4900–4200 cm−1 according to the following expression:10
| (1) |
where βw, βc, βf, βk, βo, and βs correspond to the regression coefficients for each tissue component, Askin represents the measured absorption spectrum for a given location along the 10 × 10 spectral array for the skin sample, and Awater, Acollagen I, Afat, Akeratin, Aoffset, and Aslope, are the pure component absorption spectra for each skin component (water, collagen I protein, fat, keratin protein, spectral offset, and baseline slope), respectively.10 Lastly, e represents the residual absorbance not accounted for by the model.
The fitting procedure generates six regression coefficients for each location on the tissue map. Combined, these regression coefficients provide a measure of the composition of each 360 × 480 μ m2 area within the skin matrix. More specifically, the magnitude of a given coefficient gives a measure of the amount of that component located in the volume of tissue through which the incident light passes during the microspectroscopic measurement. After this fitting procedure, a skin sample can be represented as six 10 × 10 matrices of regression coefficients and the distribution of these components can be obtained by displaying a map of the regression coefficients along the tissue array. Examples of such spatial distributions for skin samples excised from male and female rats are presented in Figure 2 as false-color contour maps.
Figure 2.
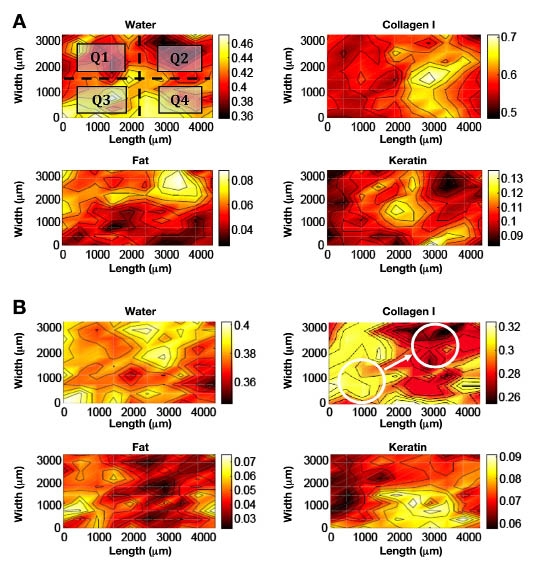
Spatial distribution maps for four chemical components. Darker colors on the maps correspond to lower coefficient values, whereas the solid black contour lines denote every 10% of the total change in the specific component. (A) Example of male rat skin (the two-dimensional map for water is shown separated into quadrants, each of the four being an independent fiber location); (B) example of female rat skin (white circles illustrate interface relocation and correspond to 1.8 mm-diameter optical fibers).
For comparisons between animals and sexes, weighted percent coefficients were calculated for each of the four chemical components according to the following equation:
| (2) |
where βcomp (%)i is the relative amount of a given chemical component at location i on the skin map, βcomp is the measured regression coefficient for this component, and βw, βc, βf and βk represent the measured regression coefficients for each of the four chemical components of the tissue model (water, collagen I protein, fat, and keratin protein, respectively).
Simulated Noninvasive Spectra
Simulated noninvasive spectra were constructed as linear combinations of the absorption spectra corresponding to the fitted skin components (water, collagen I protein, fat, keratin protein, offset, and slope) as well as glucose. In order to model noninvasive spectra collected through the fiber-optic interface, the full 3.6 × 4.8 mm2 tissue matrix was divided into quadrants, as illustrated in Figure 2. The size of each quadrant is indicated in the upper left corner of Figure 2A and the size of the optical fibers is illustrated in the upper right corner of Figure 2B. Each quadrant corresponds to a 5 × 5 subset of the collected 10 × 10 spectral array and represents an area of 1.8 × 2.4 mm2. There is no overlap in the spectral data associated with each quadrant.
A set of simulated noninvasive spectra was constructed for each quadrant. These spectra were generated by summing the individual pure component spectra for each skin component (water, collagen I protein, fat, keratin protein, offset, and slope) after applying a weighting factor derived from the corresponding regression coefficients. The weighting factor for each skin component was the average of the 25 regression coefficients obtained from the fitting procedure for each spectrum of the 5 × 5 matrix elements in the quadrant. In other words, the chemical composition of each quadrant was represented as six regression coefficients computed as the average of the 25 regression coefficients for that quadrant. From this analysis, a base simulated-skin spectrum was generated for each quadrant according to the following expression:
| (3) |
where is the base skin spectrum for quadrant q, and and represent the weighted pure component absorption spectra of water, collagen I protein, fat, keratin protein, spectral offset, and baseline slope, and the weighting coefficients correspond to the average regression coefficient determined from the fitting procedure for the 25 tissue locations within the quadrant.
The base spectrum for each quadrant was further modified to produce the set of simulated spectra needed to produce PLS calibration models for glucose. These additional modifications included (1) adding a spectrum of glucose corresponding to a specific concentration of glucose, (2) adding spectral variance associated with the six major matrix components, and (3) adding Gaussian-distributed noise.
Glucose spectra were added to instill glucose-specific information within the simulated noninvasive spectra. Glucose concentration spectral information was added according to the following equation:11,12
| (4) |
where is the component of the solution spectrum corresponding to glucose, ɛwℓwCw is the absorbance due to water, ɛglucoseℓwCglucose is the absorbance due to glucose, and ℓwCglucose is a term that accounts for changes in the measured absorbance caused by the displacement of water molecules in the optical path by glucose. Conventional terms are used where ɛw and ɛglucose represent molar absorptivities (mm−1 × mM−1) for water and glucose,11 respectively, ℓw is the effective aqueous path length (mm) for the light propagating through the tissue slice,2 Cw and Cglucose correspond to the concentrations (mM) of water and glucose, respectively, and is the water displacement coefficient for glucose. The value for ℓw is taken as the fitted coefficient for water from Equation 1. The water displacement coefficient is a measure of how many water molecules are displaced from the light path for each molecule of glucose dissolved, and has the value of 6.24.11
Spectral variance was added to the base spectrum on the basis of the observed variations for the six major skin components at the central reference point. As noted above, a spectrum was collected at the center point in the 10 × 10 array every 30 minutes. The mean and standard deviation (SD) were computed for each of the six regression coefficients to provide a measure of the relative variation for each component. Variation of the regression coefficients used for the simulated spectra for each quadrant was determined according to the following expression:
| (5) |
where (ςcomp)q is the SD for a given tissue component in quadrant q, is the measured relative SD for this component at the central point of the map, and is the regression coefficient for this component in quadrant q (calculated as the average of 25 coefficients in the quadrant). In constructing simulated spectra, regression coefficients were selected randomly for each tissue component from the normal distribution with a mean value of and a SD of (ςcomp)q. Each resulting regression coefficient was multiplied by the respective pure component absorption spectrum to provide the individual component spectrum for simulating noninvasive tissue spectra. These variations mimic changes to the skin tissue present when the fiber interface is constant and account for instrumentation variations as well as environment factors, such as dehydration and temperature.
Random noise was the final element incorporated into the simulated spectra. Gaussian-distributed noise was added to each spectrum at a level that provided RMS (root mean square) noise on 100% lines of 12 μAU (microabsorbance units) over the 4400–4600 cm−1 spectral range.3 This level of noise is representative of values obtained from actual noninvasive spectra collected from our animal model.
For each quadrant, a set of 40 simulated spectra was generated. Each spectrum in the set included (1) the linear combination of the six pure component spectra, (2) a glucose spectrum corresponding to a randomly selected concentration of glucose between 5 and 35 mM, and (3) Gaussian-distributed noise. In each case, the six pure component spectra were multiplied by the average regression coefficient for that quadrant with variation added according to the relative SD of the center position for that tissue slice. All three sources of variance were combined to generate 40 unique simulated noninvasive spectra for each quadrant of all 32 maps.
PLS Calibration Models
PLS calibration models were generated for each quadrant. Each PLS model was computed by using all 40 of the simulated spectra for a given quadrant. In each case, six latent variables or factors were used in constructing the model. A PLS model generated with spectra in one quadrant was then used to predict the concentration of glucose using the 40 simulated spectra in each of the other three quadrants in the same tissue slice. Errors in the concentration of glucose predicted from the resulting PLS calibration model were quantified as the standard error of calibration (SEC) for the calibration quadrant and as the standard error of prediction (SEP) for the noncalibration quadrants or prediction quadrants. These parameters were computed according to Equations 6 and 7:
| (6) |
| (7) |
where SEC and SEP are in units of mM, Ca and Cp are the actual and predicted concentrations of glucose for each spectrum, respectively, Nc and Np are the number of spectra in the calibration and prediction data sets, respectively, and f is the number of factors used in the PLS regression analysis.
Statistical analysis was performed by computing 10 unique sets of simulated spectra for each quadrant and assessing the resulting PLS calibration models. Each set of 40 simulated spectra included different regression coefficients, glucose concentrations, and noise according to the procedures described above. A unique PLS calibration model was calculated for the 10 data sets in each quadrant, which resulted in 10 SEC values for each quadrant. In addition, each calibration model was used to predict the concentration of glucose in each of the 10 unique sets of 40 simulated spectra for the remaining three non-calibration quadrants in the tissue map, thereby generating 30 SEP values for each calibration model. This procedure was repeated for all four quadrants, thereby accumulating 40 SEC values and 120 SEP values per map. As noted above, four maps were generated per animal, which created 160 SEC values and 480 SEP values per animal.
Results
Characterization of Spatial Tissue Heterogeneity
Measured regression coefficients for the six skin components, as described in Equation 1, are summarized in Table 1 for each animal. This table lists the mean and SD values for each animal. Previously performed analysis of variance has shown that results from this animal model must be treated as separate distributions.10 The relative values for these tissue components are presented in Table 2, according to Equation 2.
Table 1.
| Component | Male animals | |||
|---|---|---|---|---|
| Rat 1 | Rat 2 | Rat 3 | Rat 4 | |
| Water | 0.42 ± 0.03 | 0.43 ± 0.05 | 0.40 ± 0.04 | 0.40 ± 0.07 |
| Collagen type I | 0.57 ± 0.07 | 0.53 ± 0.05 | 0.44 ± 0.04 | 0. 34 ± 0.09 |
| Fat | 0.12 ± 0.03 | 0.04 ± 0.03 | 0.04 ± 0.02 | 0.03 ± 0.03 |
| Keratin | 0.09 ± 0.02 | 0.10 ± 0.01 | 0.10 ± 0.02 | 0.09 ± 0.03 |
| Offset | 0.65 ± 0.06 | 0.6 ± 0.2 | 0.6 ± 0.2 | 0.5 ± 0.1 |
| Slope | −0.025 ± 0.007 | −0.017 ± 0.008 | −0.001 ± 0.009 | −0.005 ± 0.006 |
| Component | Female animals | |||
|---|---|---|---|---|
| Rat 1 | Rat 2 | Rat 3 | Rat 4 | |
| Water | 0.33 ± 0.04 | 0.26 ± 0.06 | 0.31 ± 0.05 | 0.32 ± 0.06 |
| Collagen type I | 0.27 ± 0.04 | 0.26 ± 0.04 | 0.26 ± 0.05 | 0.31 ± 0.05 |
| Fat | 0.03 ± 0.01 | 0.05 ± 0.02 | 0.06 ± 0.03 | 0.05 ± 0.03 |
| Keratin | 0.06 ± 0.01 | 0.052 ± 0.006 | 0.053 ± 0.07 | 0.066 ± 0.009 |
| Offset | 0.5 ± 0.1 | 0.46 ± 0.08 | 0.57 ± 0.07 | 0.6 ± 0.1 |
| Slope | −0.014 ± 0.007 | −0.027 ± 0.009 | −0.020 ± 0.007 | −0.02 ± 0.01 |
Mean value (±SD) with 396 degrees of freedom for each value.
Data for male rats 1 and 2 are identical to an earlier report.10
Table 2.
Relative β (%) Regression Coefficientsa for Major Chemical Components for Four Maleb and Four Female Animals
| Component | Male animals (%) | |||
|---|---|---|---|---|
| Rat 1 | Rat 2 | Rat 3 | Rat 4 | |
| Water | 35 ± 4 | 39 ± 3 | 41 ± 3 | 48 ± 6 |
| Collagen type I | 48 ± 3 | 48 ± 4 | 45 ± 3 | 39 ± 3 |
| Fat | 10 ± 2 | 4 ± 2 | 4 ± 2 | 2 ± 3 |
| Keratin | 8 ± 2 | 9 ± 1 | 10 ± 2 | 11 ± 2 |
| Component | Female animals (%) | |||
|---|---|---|---|---|
| Rat 1 | Rat 2 | Rat 3 | Rat 4 | |
| Water | 47 ± 3 | 42 ± 4 | 46 ± 4 | 43 ± 3 |
| Collagen type I | 39 ± 3 | 42 ± 4 | 37 ± 3 | 41 ± 2 |
| Fat | 3 ± 1 | 5 ± 2 | 6 ± 3 | 5 ± 3 |
| Keratin | 9 ± 1 | 9 ± 1 | 8 ± 2 | 9 ± 2 |
Mean value (±SD) with 396 degrees of freedom for each value.
Data for the male rats 1 and 2 are the same as those reported before.10
Inspection of the values in Table 1 reveals that the amounts of water and collagen type I protein are less in the female rats, while levels of keratin and fat are essentially the same for both sexes. It should be noted that low levels of fat tissue are observed in rat skin tissue taken from the back of the neck, which might account for small differences in fat observed between sexes. Overall, the skin is thicker for male rats compared to female rats. Less difference is noted for the relative coefficients, however.
Lateral distribution of the measured chemical components across the skin is best visualized by false-color contoured maps. Example maps are presented in Figure 2 for one male (Figure 2A) and one female (Figure 2B) rat. These maps provide a two-dimensional view over an area of 3.6 × 4.8 mm2. Domains of high and low content for the chemical components are instantly visible on such maps. It must be noted that these maps represent three-dimensional structures as the probing near infrared light is transmitted through the tissue slice.
Figure 2 illustrates the chemical heterogeneity of the skin matrix for both male and female rats. These maps are representative of all the maps measured for these four animals. Although the size of these chemical domains varies for different animals and for individual skin slices, generally, the domain size is a large fraction of the dimensions of the fiber interface, which is illustrated as the white circles in Figure 2B. No major difference in the domain size or distribution is evident by inspecting maps collected from male and female animals.
Simulation of Spectra at Various Locations
The fiber interface used previously to measure glucose concentrations in the ISF of rat skin has a working diameter of 1.8 mm.3 Consequently, this interface collects radiation over a larger area than that resolved by microspectroscopic imaging. Moreover, the SNR for the microspectroscopic measurements is three orders of magnitude lower compared to the SNR used for our reported noninvasive glucose measurements in living rats.3,10 The low optical throughput of the microscope results in low radiant powers and poor SNR's for the microspectroscopic spectral data. As a result, the actual microspectroscopic data cannot be used to measure glucose concentrations in these samples and cannot be used directly to assess the impact of tissue heterogeneity on accuracy of multivariate calibration models for measuring glucose in these skin matrices. For this reason, simulated spectra are necessary to evaluate the impact of tissue heterogeneity on noninvasive glucose measurements.
As described above, each skin map is split into four quadrants comparable in size to the fiber interface, as demonstrated in Figure 2A. Each quadrant then represents a unique location of the fiber interface. Simulated spectra are then generated based on the average matrix components for a given quadrant, as defined by the regression coefficients listed in Table 1. These simulated spectra include variance related to each of the skin components, spectral information related to different concentrations of glucose, and random noise. In all, these simulated spectra are designed to mimic noninvasive spectra collected in our previous ISF measurements.
Effect of Fiber Relocation on Glucose Concentration Predictions
The PLS algorithm produces a calibration vector that is used to predict the concentration of glucose from subsequent noninvasive tissue spectra. The concentration of glucose is obtained as the dot-product between this calibration vector and the noninvasive spectrum.13–15 Representative PLS calibration vectors are presented in Figure 3 where these calibration vectors were generated from an analysis of sets of 40 simulated spectra for each quadrant of one male (Figure 3A) and one female (Figure 3B) animal. Similarities are noteworthy between these calibration vectors. Each vector possesses a combination of sharp bands between 4500–4200 cm−1 and broader bands around 4700 cm−1. No major differences are evident between vectors generated from spectra derived from male and female skin.
Figure 3.
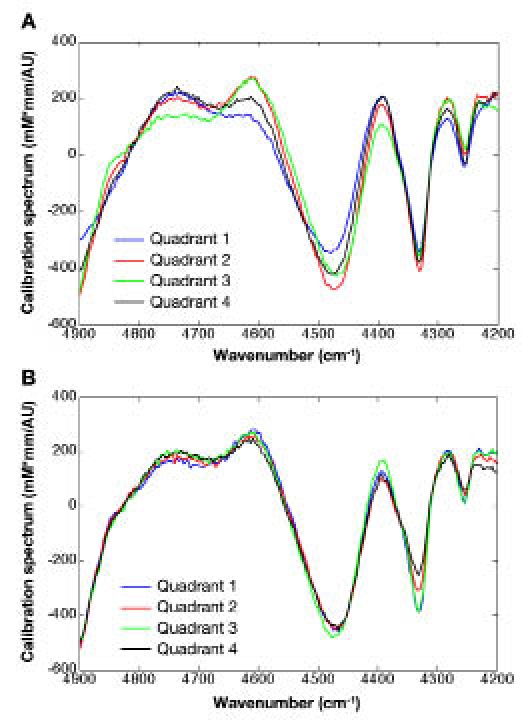
Partial least squares calibration vectors for each quadrant of a sample map collected across a slice of (A) male skin and (B) female skin. The dot product of such a vector with a skin spectrum at a specific location and a water path length gives the glucose concentration in mM units.
The impact of chemical heterogeneity was assessed by applying the calibration vector determined from simulated spectra associated with one quadrant to simulated spectra for a different quadrant. The results are presented in Table 3, where the SEC values reported for each animal correspond to the average SEC (± 1 SD) of 160 individual SEC values determined for 4 slices/animal × 4 quadrants/slice × 10 sets of simulated spectra/quadrant. Likewise, the reported SEP values correspond to the average of 4800 individual SEP values computed for 160 calibration models × 3 noncalibration quadrants/calibration model × 10 sets of simulated spectra/noncalibration quadrant.
Table 3.
Standard Errors of Calibration and Prediction for Glucose with PLS Summarized as Mean ± SD for Male and Female Animals
| Male rats | ||||
|---|---|---|---|---|
| Rat 1 | Rat 2 | Rat 3 | Rat 4 | |
| SEC (mM) | 2 ± 1 | 2 ± 1 | 1 ± 1 | 2 ± 1 |
| SEP (mM) | 9 ± 11 | 12 ± 12 | 14 ± 17 | 7 ± 8 |
| Female rats | ||||
|---|---|---|---|---|
| Rat 1 | Rat 2 | Rat 3 | Rat 4 | |
| SEC (mM) | 1 ± 1 | 1.5 ± 0.9 | 1.2 ± 0.7 | 2 ± 1 |
| SEP (mM) | 2 ± 1 | 7 ± 6 | 3 ± 3 | 4 ± 5 |
The SEC values listed in Table 3 correspond to prediction errors expected if the fiber interface remains stationary during all measurements, while the SEP values represent prediction errors when the calibration vector is generated with the interface in one position and the predictions are performed at a different location along the tissue matrix. The values in Table 3 indicate that the SEP is greater than the corresponding SEC. These SEC values are similar in magnitude to the reported SEC values for noninvasive measurements when the interface is not moved between measurements with a stationary animal.3 The SEP values in this table indicate that moving the interface position increases the prediction error by factors ranging from 2 to 14.
The impact of spatial heterogeneity is further illustrated by the statistical data presented in Figure 4. For this figure, the SEP/SEC ratio was determined for each tissue slice and the results are presented in the form of box plots for each animal tested. A ratio of 100% corresponds to the situation where SEC = SEP and there is no impact on the ability to predict glucose concentrations from the matrix of the noncalibration quadrant. Ratios close to 100% are expected when the two quadrants possess similar compositions.
Figure 4.
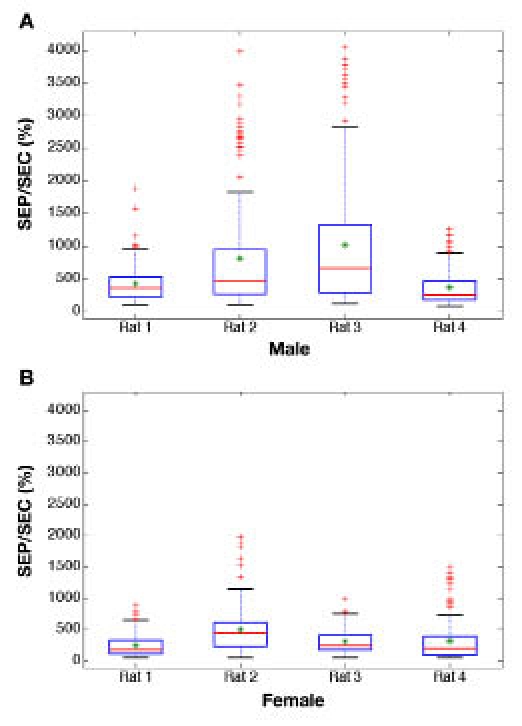
Box plots of distributions of standard error ratios (SEP/SEC, %) for male (A) and female (B) rat skin. For each animal, the red line represents the median, the green star shows the mean value, the blue box includes 75% of all observations (i.e., data points between the 1st and 3rd quartiles), the black whiskers indicate extreme values within three semi-interquartile ranges below 25% and above 75%, and more extreme values are presented as red crosses.
As is evident in Figure 4, most of the SEP/SEC percent ratios range between 100 and 1000%. In most cases, the additional error introduced by a difference in the skin matrix is 2- to 10-fold. In extreme cases, as denoted by red crosses in Figure 4, standard errors increase up to 40-fold for male rats and up to 20-fold for female animals. Such high standard errors suggest that this particular pair of quadrants had drastically different compositions.
Previously presented results for actual in vivo noninvasive glucose measurements3 indicate that the SEP/SEC percent ratio is 2.58-fold when the fiber interface is repositioned before each measurement. This percent ratio is well within the upper and lower quartiles in the box plot distributions presented in Figure 4. These findings support the postulate that tissue heterogeneity is responsible for the degradation in model performance caused by repositioning of the interface for each measurement.10
Discussion
Noninvasive spectroscopic measurements through living tissue are complicated by the complexity of the living skin matrix. Skin heterogeneity is characterized by several factors, including (1) the partitioning of glucose between blood and ISF, (2) differences in the concentration of glucose inside and outside metabolizing skin cells, and (3) the existence of spatially relevant chemical domains of protein, fat, and water, as illustrated in Figure 2. Furthermore, a glucose concentration gradient has been demonstrated where the percentage of glucose in skin ISF relative to blood glucose of 5 mM increases gradually starting at the outer surface of skin and is at its highest (98%) at a depth of approximately 600 μm, which corresponds to the dermis layer.6
The animal model presented here involves transmission of the incident near-infrared light through a fold of skin as a means to model transmission measurements across a fold of skin on the back of the hand of human subjects. Such measurements through human skin will reduce the impact of skin heterogeneity by restricting measurements to the epidermis and dermis layers of skin, thereby avoiding fat containing subcutaneous layers. In addition, this measurement site provides a sample thickness of approximately 1–1.5 mm, which others report to be optimal for measuring glucose in an intralipid phantom.16 Still, spatial chemical domains like those reported here can adversely impact measurement accuracy.
In Vitro Skin Spectra
The experimental procedure used to collect the micro-spectroscopic image involves compressing the soft skin tissue between two sapphire plates. Other researchers have demonstrated the utility of this experimental procedure for collecting transmission-based micro-spectroscopic FTIR images of complex multilayered samples.17,18 Examples include paint samples, which are similar to skin in the sense that paint samples consist of micrometric layers of organic and inorganic components, including proteinaceous compounds, fats, and resins. Although pressing layered paint samples between diamond windows has been shown to distort the geometry of layers somewhat, this procedure keeps the sample structure intact and free of contaminants.18 Alternative methods (preparation of KBr pellets, gluing and embedding techniques, etc.) either involve complete destruction of the sample structure or introduction of strong absorbers.17
Other approaches have been published for using spectroscopy to characterize the heterogeneity of skin tissue related to the photon migration. In this previous work, incident light is launched into the skin through one fiber and a separate collection fiber is used to detect light that has propagated a certain distance into and through the skin matrix. Meglinsky and Matcher have used this approach to characterize optical differences as the photons travel into the tissue.19–21 These photon migration measurements are significantly different compared to the measurements preformed here because our maps characterize tissue heterogeneity laterally across the surface of the tissue matrix while the past photon migration work measures heterogeneity of layers vertically into the skin structure.
Mid-infrared spectroscopy has also been used to characterize the distribution of skin components,22–24 but mid-infrared wavelengths are limited to a penetration depth of a few tens of microns into the tissue matrix owing to the strong absorption properties of water and other matrix components. For this reason, the results reported here are unique, as they characterize the heterogeneity through a larger volume of the tissue as defined by the 0.5–1.0 mm thickness of the samples.
The tissue compression procedure used here permits rapid data collection with SNR's suitable for quantifying the six major components of these skin spectra. The 1 mAU RMS noise levels on 100% lines acquired with our microscope setup are suitable for measuring the principal skin components, but such noise levels are much too high for measuring glucose in a noninvasive experiment.3,4
A notable difference between the in vitro spectra collected in these microspectroscopic experiments and the in vivo spectra collected in our noninvasive experiments is the passage of the incident radiation through one versus two layers of the epidermis and dermis. For in vitro measurements, the tissue lies flat on the transmission window and the radiation passes once through a single layer of epidermis and a single layer of dermis tissue. For in vivo measurements, on the other hand, the skin tissue is folded onto itself and the incident radiation passes through two separate epidermis and dermis layers as it propagates through the fold of skin. The modeling of glucose prediction errors does not consider a two-pass model, but only addresses the single-pass experiment. Although not confirmed experimentally, the inclusion of two skin layers as a fold of skin should reduce the spatial heterogeneity of the skin components, thereby improving prediction ability and reducing prediction errors of the calibration model.
Impact of Animal Sex
Little difference is noted between the chemical hetero-geneity based on the sex of the animal. Similar chemical domains were observed for both male and female animals, as illustrated in Figure 2. The major differences between male and female skin is the overall thickness, with thicker skin for male rats.
Impact of Tissue Heterogeneity on PLS Model Accuracy
Selectivity of PLS regression for glucose measurements has been demonstrated for both complex in vitro mixtures25,26 and in our transient study with a living animal.4 Overall, the lowest standard error we have observed for noninvasive measurements is 0.7 mM (per results of samples collected in our laboratory during the study. Data are unpublished). In this example, the noninvasive spectra were obtained from an anesthetized animal with a stationary interface throughout. A prediction error of 0.7 mM is within the limits of clinical applicability.27
The impact of tissue heterogeneity can be significant, as illustrated in Table 3 and Figure 4. In our noninvasive experiment, the SEP increases by 2.58-fold when comparing measurements where the interface is held in the same position relative to values when the interface is repositioned before each measurement.3 This percentage increase is within the span of SEP/SEC ratios established here from the simulated quadrant data.
It must be noted, however, that the interface was not positioned in a completely new location before each measurement during the reported in vivo experiments. Indeed, the experimenters tried to place the interface in nearly the same position before each measurement.3 One would expect that each interface position was not completely different than the others, so our calculations using quadrants with no spectral overlap represents the worst case scenario in this regard. This fact might explain why the measured increase in prediction errors is on the low side of the ratios computed here from the simulated data.
A strategy is needed to remove or reduce the impact of skin heterogeneity on the performance of the calibration model. One approach is to incorporate more sources of the underlying skin tissue spectral variance into the calibration model. This can be accomplished by purposely moving the interface to several different positions during the calibration phase of the experiment. This way, more of the tissue variance will be incorporated into the calibration model, thereby making the model less sensitive to the exact placement of the interface. Alternatively, the sources of skin spectral variance can be incorporated directly into the calibration model by using pure component spectra from model compounds, such as fatty tissue, keratin protein, and collagen protein.
Conclusions
Effects of repositioning the fiber interface used to collect noninvasive spectra of living skin tissue were explored by using a model based on microspectroscopic near-infrared analysis of both male and female rats. Spatial domains of protein, fat, and water were observed from this analysis and the degree of heterogeneity is essentially the same for skin excised from male and female animals. These chemical heterogeneities create increases in the prediction errors for PLS calibration models when simulated measurements are made through regions of skin not used to generate the calibration model for glucose. These findings suggest that chemical hetero-geneity within the skin tissue matrix is at least partially responsible for previously measured increases in glucose prediction errors when the fiber interface is repositioned before each measurement. Still, the basic structure of the calibration vectors is similar both across skin quadrants and between animals, as shown in Figure 3. The similarity in these calibration vectors suggests that the accuracy of such glucose concentration predictions depends strongly on the exact features of these vectors and subtle differences can have a profound impact on measurement performance.
Preliminary experiments with samples of skin excised from two human subjects demonstrate similar chemical heterogeneity as we have reported for rat skin (per results of samples collected in our laboratory during the study. Data are unpublished). Both skin samples, one from a male subject and one from a female subject, display chemical domains on the order of several hundred microns, similar to those illustrated in Figure 2. In addition, these skin samples were collected from different regions of the body (male knuckle and female upper leg), which suggests that these spectral domains are similar over different areas of the body. Of course, more detailed experimentation is required to verify these preliminary observations. These preliminary human skin maps underscore the significance of this rat model for solving the principal issues that limit noninvasive glucose measurements.
Acknowledgments
The authors acknowledge Dr. Jonathon T. Olesberg of the Optical Science & Technology Center at the University of Iowa for his assistance with the design of the instrumentation used for microscopic mapping. The authors also thank Ms. Terry Graham in the Department of Chemistry at the University of Iowa for her gracious help with collecting skin samples.
Abbreviations
- μAU
micro absorbance units
- FTIR
Fourier transform infrared
- ISF
interstitial fluid
- PLS
partial least squares
- RMS
root mean square
- SD
standard deviation
- SEC
standard error of calibration
- SEP
standard error of prediction
- SNR
signal-to-noise ratio
References
- 1.Arnold MA, Olesberg JT, Small GW. Cunningham D, Stenken JA, editors. Near-infrared spectroscopy for noninvasive glucose sensing. Analytical Chemistry of In Vivo Glucose Measurements. Wiley Chemical Analysis Series. 2010:357–390. [Google Scholar]
- 2.Arnold MA, Small GW. Noninvasive glucose sensing. Anal Chem. 2005;77(17):5429. doi: 10.1021/ac050429e. 5439. [DOI] [PubMed] [Google Scholar]
- 3.Olesberg JT, Liu L, Van Zee V, Arnold MA. In vivo near-infrared spectroscopy of rat skin tissue with varying blood glucose levels. Anal Chem. 2006;78(1):215–223. doi: 10.1021/ac051036i. [DOI] [PubMed] [Google Scholar]
- 4.Arnold MA, Liu L, Olesberg JT. Selectivity assessment of noninvasive glucose measurements based on analysis of multivariate calibration vectors. J Diabetes Sci Technol. 2007;1(4):454–462. doi: 10.1177/193229680700100402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stout PJ, Racchini JR, Hilgers ME. A novel approach to mitigating the physiological lag between blood and interstitial fluid glucose measurements. Diabetes Technol Ther. 2004;6(5):635–644. doi: 10.1089/dia.2004.6.635. [DOI] [PubMed] [Google Scholar]
- 6.Groenendaal W, Schmidt KA, von Basum G, van Riel NA, Hilbers PA. Modeling glucose and water dynamics in human skin. Diabetes Technol Ther. 2008;10(4):283–293. doi: 10.1089/dia.2007.0290. [DOI] [PubMed] [Google Scholar]
- 7.Cengiz E, Tamborlane WV. A tale of two compartments: interstitial versus blood glucose monitoring. Diabetes Technol Ther. 2009;11(Suppl 1):S11–S16. doi: 10.1089/dia.2009.0002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schmidtke DW, Freeland AC, Heller A, Bonnecaze RT. Measurement and modeling of the transient difference between blood and subcutaneous glucose concentrations in the rat after injection of insulin. P Natl Acad Sci USA. 1998;95(1):294–299. doi: 10.1073/pnas.95.1.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Khalil OS. Non-invasive glucose measurement technologies: an update from 1999 to the dawn of the new millennium. Diabetes Technol Ther. 2004;6(5):660–697. doi: 10.1089/dia.2004.6.660. [DOI] [PubMed] [Google Scholar]
- 10.Alexeeva NV, Arnold MA. Near-infrared microspectroscopic analysis of rat skin tissue heterogeneity in relation to noninvasive glucose sensing. J Diabetes Sci Technol. 2009;3(2):219–232. doi: 10.1177/193229680900300202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Amerov AK, Chen J, Arnold MA. Molar absorptivities of glucose and other biological molecules in aqueous solutions over the first overtone and combination regions of the near-infrared spectrum. Appl Spectrosc. 2004;58(10):1195–1204. doi: 10.1366/0003702042336136. [DOI] [PubMed] [Google Scholar]
- 12.Chen J, Arnold MA, Small GW. Comparison of combination and first overtone spectral regions for near-infrared calibration models for glucose and other biomolecules in aqueous solutions. Anal Chem. 2004;76(18):5405–5413. doi: 10.1021/ac0498056. [DOI] [PubMed] [Google Scholar]
- 13.Small GW. Chemometrics and near-infrared spectroscopy: avoiding the pitfalls. Trends Anal Chem. 2006;25(11):1057–1066. [Google Scholar]
- 14.Haaland DM, Thomas EV. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information. Anal Chem. 1988;60(11):1193–1202. [Google Scholar]
- 15.Shih WC, Bechtel KL, Feld MS, Arnold MA, Small GW. Cunningham D, Stenken JA, editors. Introduction to spectroscopy for noninvasive glucose sensing. Analytical Chemistry of In Vivo Glucose Measurements. Wiley Chemical Analysis Series. 2010:331–356. [Google Scholar]
- 16.Jeon KJ, Hwang ID, Hahn S, Yoon G. Comparison between transmittance and reflectance measurements in glucose determination using near infrared spectroscopy. J Biomed Opt. 2006;11(1) doi: 10.1117/1.2165572. 014022. [DOI] [PubMed] [Google Scholar]
- 17.Van der Weerd J, Heeren RMA, Boon JJ. Preparation methods and accessories for the infrared spectroscopic analysis of multi-layer paint films. Stud Conserv. 2004;49(3):193. 210. [Google Scholar]
- 18.Cotte M, Susini J, Sole VA, Taniguchi Y, Chillida J, Checroun E, Walter P. Applications of synchrotron-based micro-imaging techniques to the chemical analysis of ancient paintings. J Anal Atom Spectrom. 2008;23:820–828. [Google Scholar]
- 19.Meglinsky IV, Matcher SJ. Modelling the sampling volume for skin blood oxygenation measurements. Med Biomed Eng Comp. 2001;39(1):44–50. doi: 10.1007/BF02345265. [DOI] [PubMed] [Google Scholar]
- 20.Meglinsky IV, Matcher SJ. Analysis of the spatial distribution of detector sensitivity in a multilayer randomly inhomogeneous medium with strong light scattering and absorption by the Monte Carlo method. Opt Spectrosc. 2001;91(4):654–659. [Google Scholar]
- 21.Meglinsky IV, Matcher SJ. Computer simulation of the skin reflectance spectra. Comp Meth Prog Biomed. 2003;70(2):179–186. doi: 10.1016/s0169-2607(02)00099-8. [DOI] [PubMed] [Google Scholar]
- 22.Garidel P, Boese M. Mid infrared microspectroscopic mapping and imaging: a bio-analytical tool for spatially and chemically resolved tissue characterization and evaluation of drug permeation within tissues. Microsc Res Tech. 2007;70(4):336–349. doi: 10.1002/jemt.20416. [DOI] [PubMed] [Google Scholar]
- 23.Lasch P, Naumann D. Spatial resolution in infrared microspectroscopic imaging of tissues. Biochim Biophys Acta. 2006;1758(7):814–829. doi: 10.1016/j.bbamem.2006.06.008. [DOI] [PubMed] [Google Scholar]
- 24.Garidel P. Insights in the biochemical composition of skin as investigated by micro infrared spectroscopic imaging. PCCP. 2003;5(12):2673–2679. [Google Scholar]
- 25.Li BY, Kasemsumran S, Hu Y, Liang YZ, Ozaki Y. Comparison of performance of partial least squares regression, secured principal component regression, and modified secured principal component regression for determination of human serum albumin, gammaglobulin, and glucose in buffer solutions and in vivo blood glucose quantification by near-infrared spectroscopy. Anal Bioanal Chem. 2007;387(2):603–611. doi: 10.1007/s00216-006-0977-1. [DOI] [PubMed] [Google Scholar]
- 26.Liu L, Arnold MA. Selectivity for glucose, glucose-6-phosphate, and pyruvate in ternary mixtures from the multivariate analysis of near-infrared spectra. Anal Bioanal Chem. 2009;393(2):669–677. doi: 10.1007/s00216-008-2475-0. [DOI] [PubMed] [Google Scholar]
- 27.Oliver NS, Toumazou C, Cass AE, Johnston DG. Glucose sensors: a review of current and emerging technology. Diabet Med. 2009;26(3):197–210. doi: 10.1111/j.1464-5491.2008.02642.x. [DOI] [PubMed] [Google Scholar]


