Microtesla MRI with dynamic nuclear polarization

Abstract

Magnetic resonance imaging at microtesla fields is a promising imaging method that combines the pre-polarization technique and broadband signal reception by superconducting quantum interference device (SQUID) sensors to enable in vivo MRI at microtesla-range magnetic fields similar in strength to the Earth magnetic field. Despite significant advances in recent years, the potential of microtesla MRI for biomedical imaging is limited by its insufficient signal-to-noise ratio due to a relatively low sample polarization. Dynamic nuclear polarization (DNP) is a widely used approach that allows polarization enhancement by two-four orders of magnitude without an increase in the polarizing field strength. In this work, the first implementation of microtesla MRI with Overhauser DNP and SQUID signal detection is described. The first measurements of carbon-13 NMR spectra at microtesla fields are also reported. The experiments were performed at the measurement field of 96 microtesla, corresponding to Larmor frequency of 4 kHz for protons and 1 kHz for carbon-13. The Overhauser DNP was carried out at 3.5 –5.7 mT field using rf irradiation at 120 MHz. Objects for imaging included water phantoms and a cactus plant. Aqueous solutions of metabolically relevant sodium bicarbonate, pyruvate, alanine, and lactate, labeled with carbon-13, were used for NMR studies. All the samples were doped with TEMPO free radicals. The Overhauser DNP enabled nuclear polarization enhancement by factor as high as −95 for protons and as high as −200 for carbon-13, corresponding to thermal polarizations at 0.33 T and 1.1 T fields, respectively. These results demonstrate that SQUID-based microtesla MRI can be naturally combined with Overhauser DNP in one system, and that its signal-to-noise performance is greatly improved in this case. They also suggest that microtesla MRI can become an efficient tool for in vivo imaging of hyperpolarized carbon-13, produced by the low-temperature dissolution DNP.

1. Introduction

Magnetic resonance imaging is characterized by inherently low sensitivity, resulting from the fact that the energy of a nuclear spin in a typical MRI magnetic field is considerably lower than its thermal energy at room temperature. For a system of I=1/2 nuclear spins with gyromagnetic ratio γ_I, the thermal equilibrium polarization, i.e. the difference between populations of the two Zeeman energy levels divided by the sum of their populations, in magnetic field B₀ at temperature T is P_th ≈ γ_IћB₀/(2kT). This value is very low under conventional MRI conditions. For example, for proton spins at 3 T field and room temperature, P_th ~ 1·10⁻⁵ . The sample magnetization, M₀ ≈ Nγ_I²ћ²B₀/(4kT), where N is the number of spins per unit volume, scales linearly with B₀ and quadratically with γ_I. Because the signal, induced in a Faraday receiver coil, increases linearly with Larmor frequency ω₀=γ_IB_0, the signal-to-noise ratio (SNR) in conventional NMR/MRI is proportional to γ_I³ B₀², if the noise is frequency independent. If the noise is dominated by the receiver’s thermal noise, which increases with frequency because of the skin effect, the SNR scales as γ_I^11/4B₀^7/4 at high fields [1]. The approximately cubic dependence of the SNR on γ_I means that the sensitivity of conventional NMR/MRI to ¹³C spins is 64 times lower than to proton spins (γ_C/γ_H=0.251) at the same magnetic field, temperature, and spin concentration.

Various physical approaches have been proposed to improve SNR of NMR/MRI in liquids and biological tissues without increasing the strength of the magnetic field B₀. They typically employ a combination of two different magnetic fields. In the well known pre-polarization technique [2], the sample is pre-polarized by a magnetic field B_p, and NMR signal is measured at a lower measurement field B_m after the pre-polarizing field is rapidly removed. The SNR in this technique is proportional to γ_I³B_pB_m for Faraday detection, and is improved compared to conventional NMR at the low field B_m. This method has been traditionally used to perform NMR/MRI in the Earth magnetic field of ~50 µT (e.g. [3–5]).

Recently, a new approach to enhance SNR of magnetic resonance at low fields was introduced [6, 7]. It is referred to as SQUID-based microtesla NMR/MRI or ultralow-field (ULF) NMR/MRI. This approach combines the pre-polarization technique and broadband signal reception using SQUID sensors [8, 9] with untuned input circuits that act as frequency independent flux-to-voltage transducers. Modern low-T_c SQUID systems provide frequency independent noise performance above ~1 Hz with magnetic field noise levels as low as ~1 fT/Hz^1/2. The sensitivity of SQUID signal detection in ULF NMR/MRI does not depend on Larmor frequency in the measurement field B_m, so the SNR is proportional to γ_I²B_p, and is enhanced substantially compared to the approach with pre-polarization and Faraday detection at low fields. Moreover, because the NMR line broadening due to magnetic field inhomogeneity scales linearly with the field strength (for a fixed relative inhomogeneity), narrow NMR lines with high SNR [6] can be obtained at a microtesla-range B_m field generated by a simple and inexpensive coil system. The NMR sensitivity for ¹³C in this method is 16 times lower than for ¹H under the same conditions. Significant progress was made in recent years in the development and applications of both ULF NMR [10–17] and ULF MRI [18–25]. However, the potential of ULF MRI for medical imaging is limited by the efficiency of pre-polarization. For example, polarization of proton spin populations at the pre-polarizing field of 30 mT, used for human brain imaging in [21], is ~1·10⁻⁷, i.e. 100 times lower than at 3 T field of conventional MRI. It becomes increasingly difficult to generate pulsed B_p fields above ~0.1 T within large sample volumes using resistive coils, because of the higher energy consumption and heat dissipation.

Dynamic nuclear polarization (DNP), based on the well known Overhauser effect [26], is an efficient way to substantially enhance nuclear polarization without increasing the strength of the polarizing field. The DNP procedure usually involves addition of unpaired electron spins (e.g. free radicals) to the studied sample and rf (microwave) irradiation of the resulting two-spin system at the frequency of the electron spin resonance (ESR). Saturation of the ESR resonance leads to a transfer of polarization from electron to nuclear spins, and creates a non-equilibrium nuclear polarization, that can be much larger than the thermal equilibrium polarization at the same magnetic field [27, 28]. The DNP enhancement factor is proportional to (γ_S/γ_I)·F(B_p), where γ_S is the gyromagnetic ratio for electron, and F(B_p) describes dependence of the enhancement on the magnetic field strength, the spin system properties, and the degree of saturation of the ESR resonance. If the NMR/MRI procedure includes DNP enhancement at the field B_p and signal measurement at the field B_m, the SNR scales as γ_Sγ_I²B_pB_m for Faraday detection, and as γ_Sγ_IB_p for SQUID detection. These estimates are based on the assumption that F(B_p) is a slow varying function of B_p, at least for a field range of interest, and noise is frequency independent. Because the electron gyromagnetic ratio γ_S is much larger by absolute value than γ_I for protons (|γ_S|/γ_H=658), DNP allows enhancement of ¹H polarization by two orders of magnitude. The sensitivity of DNP-enhanced NMR/MRI for ¹³C is improved further, and can be as high as 1/4 of its sensitivity for ¹H (under the same conditions) when SQUID detection is used. Moreover, the broadband SQUID reception allows simultaneous measurement of ¹H and ¹³C NMR signals with the same sensor.

Overhauser-enhanced MRI (e.g. [29–33]), also referred to as proton-electron double resonance imaging (PEDRI), is an imaging technique based on Overhauser DNP in liquids, which combines the advantages of ESR and proton MRI. DNP in this method is typically performed at a magnetic field of several mT using rf irradiation frequency of the order of 100 MHz. The specific absorption rate (SAR) is thus sufficiently low to allow in vivo DNP. One application of Overhauser-enhanced MRI is in vivo imaging of free radicals, either endogenous or injected [30]. Another important application is dynamic in vivo oxymetry, which can be used for detection and monitoring of oxygen deficiency in tumors [32].

Recently, a new and very promising implementation of DNP, that allows important imaging applications, was proposed [34]. It is called DNP hyperpolarization or dissolution DNP. In this approach, DNP is performed for a sample in solid state at a low temperature (~ 1 K) and strong magnetic field (~3 T) using microwave irradiation frequency of the order of 100 GHz [34]. Because the thermal equilibrium polarization P_th is inversely proportional to kT, the reduction in temperature from ~300 K to ~1 K increases the thermal polarization by two orders of magnitude. Combined with the DNP polarization enhancement by another two orders of magnitude, this leads to an overall polarization increase by more than 10000 times over the thermal polarization level at 3 T field and room temperature [34]. The predominant DNP mechanism in this case is thermal mixing [35]. Rapid dissolution of the sample preserves the nuclear polarization in liquid phase, and produces a hyperpolarized liquid that can be separated from the free radicals and injected in the bloodstream. Applicability of this technique is limited to nuclear spins with long relaxation time T₁ in liquid state (>20 s), such as ¹³C and ¹⁵N at certain positions within organic molecules. ¹³C polarization levels as high as 40% have been demonstrated after the DNP hyperpolarization and sample dissolution [34]. The hyperpolarization technique has been successfully used for angiography, perfusion mapping, and interventional MRI with unprecedented SNR levels [36]. It has also enabled real-time metabolic imaging [37], in which relative concentrations of metabolites of an injected hyperpolarized endogenous substance, such as [1-¹³C] pyruvate, are monitored by means of MRI spectroscopy of ¹³C. Such imaging has shown promise for cancer research, where it can be used for noninvasive detection and grading of tumors, and for early assessment of tumors’ response to treatment (e.g. [38]).

It has been suggested that DNP mechanisms “promise to form a perfect complement to microtesla MRI” [39]. In this work, we demonstrate microtesla MRI with Overhauser DNP enhancement and SQUID signal detection. We also report Overhauser-enhanced NMR of ¹³C in metabolically relevant substances at microtesla magnetic fields. Finally, we present a detailed argument for integration of the DNP hyperpolarization technique with SQUID-based microtesla MRI.

2. Methods

2.1 Overhauser enhancement

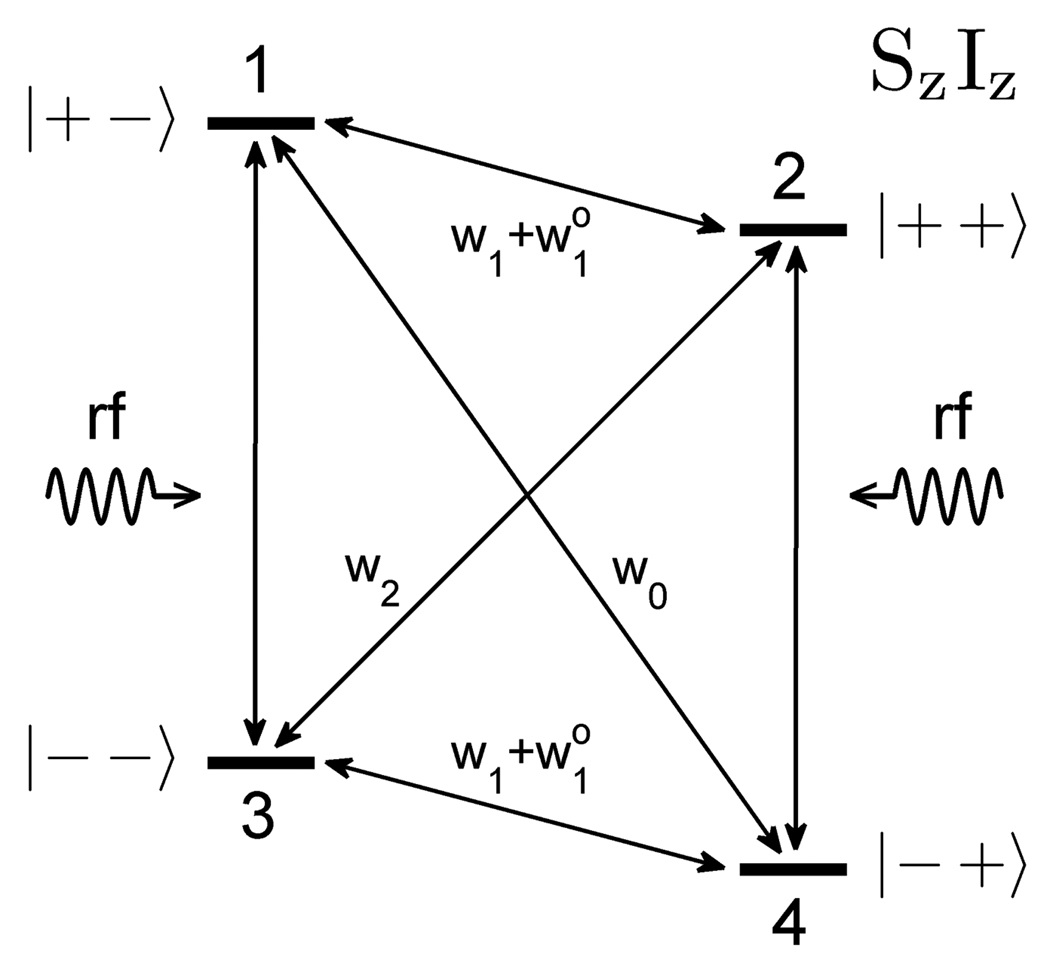
It is instructive to begin the discussion of Overhauser DNP by considering the standard four-state diagram [27, 28] that shows energy levels for a system of two 1/2 spins in a strong magnetic field (Fig. 1). Here, S is the unpaired electron spin (γ_S<0), and I is a nuclear spin. The diagram in Fig. 1 also includes spin-flip processes and the corresponding transition probabilities. Irradiation of this system at the ESR frequency equilizes electron spin populations of levels 1 and 3, as well as 2 and 4, and saturates electron spin-flip transitions 1↔3 and 2↔4. This leads to a relaxation via transitions 1↔4 and 2↔3, that involve flipping of both spins, provided that either w₀ or w₂ transition probability is sufficiently high. Such cross-relaxation enables transfer of polarization from electron to nuclear spins.

Fig. 1.

Diagram of energy levels and transitions in a system of two spins (S=½, I=½) in a strong magnetic field.

According to the theory of Overhauser effect, the expectation values 〈I_z〉 and 〈S_z〉 for the spin system in Fig. 1 are related as follows [27, 28]:

$$\frac{\langle I_{\mathrm{z}}\rangle -I_0}{I_0}=-\rho f\left(\frac{\langle S_{\mathrm{z}}\rangle -S_0}{I_0}\right)$$ (1)

Here, I₀ and S₀ are expectation values of I_z and S_z in thermal equilibrium, ρ is the coupling factor, and f is the leakage factor. These two factors are defined by the following expressions:

$$\rho =\frac{w_2-w_0}{w_0+2w_1+w_2}$$ (2)

$$f=\frac{w_0+2w_1+w_2}{w_0+2w_1+w_2+w_1^0}=1-\frac{T_1}{T_{10}}$$ (3)

The coupling factor ρ ranges from −1 for pure scalar coupling (w₀ > w₂) between the electron and the nuclear spins to +0.5 for pure dipolar coupling (w₂ > w₀). The leakage factor f takes values between 0 and 1, and depends on the ratio of the longitudinal relaxation times for nuclear spins in the presence (T ₁) and in the absence (T₁₀) of unpaired electron spins.

To describe the degree of saturation of the ESR resonance upon rf irradiation, the saturation factor s is commonly introduced:

$$s=\frac{S_0-\langle S_{\mathrm{z}}\rangle }{S_0}$$ (4)

The saturation factor changes between 0 for thermal equilibrium and 1 for complete saturation of all ESR transitions, i.e. 〈S_z〉 = 0. It depends on the power of rf irradiation, the relaxation properties of the electron spins, and the structure of the ESR spectrum at a given magnetic field strength.

The enhancement of nuclear spin polarization due to Overhauser effect is typically characterized by the enhancement factor E, defined as E = 〈I_z〉 /I₀. It can be expressed as follows:

$$E=1-\rho fs\frac{\left|{\gamma }_{\mathrm{s}}\right|}{{\gamma }_{\mathrm{I}}}$$ (5)

This expression is obtained from Eq. (1) using Eq. (4) and an assumption that both I₀ and S₀ correspond to the same magnetic field B₀. This assumption is often violated in real systems at low magnetic fields. When it holds, Eq. (5), predicts the maximum polarization enhancement for protons to be 659 in the case of pure scalar coupling and −328 for pure dipolar coupling. The negative E means that the non-equilibrium magnetization vector, created by Overhauser DNP, has the direction opposite to that of the thermal equilibrium magnetization in the external magnetic field B₀.

Because only one ESR transition can, in practice, be effectively saturated at a time, the maximum achievable enhancement is lower, if the ESR spectrum has several lines. Assuming that the ESR lines are Lorentzian and saturation of one transition does not affect the others, one can use the following approximate expression for the saturation factor [40]:

$$s=\frac{1}{n}\left(\frac{\alpha P_{\text{rf}}}{\text{1}+\alpha P_{\text{rf}}}\right)$$ (6)

Here, n is the number of lines in the ESR spectrum, P_rf is the rf irradiation power, and α is a constant related to relaxation properties of electron spins and the rf resonator characteristics. For n=3, a complete saturation of one ESR resonance, 〈S_z〉 = (2/3)S₀, leads to the saturation factor value s=1/3 and provides the maximum enhancement of −109 in the case of pure dipolar coupling.

2.2 Overhauser DNP at low fields

Nitroxide free radicals [41, 42] have been widely used as sources of unpaired electron spins for ESR and DNP, and their Overhauser DNP properties have been investigated in detail (e.g. [40, 43–45]). The readers are referred to [43] for a rigorous analytical treatment, and to [44] for a thorough physical discussion of the low-field case.

In nitroxide radicals, such as TEMPO (C₉H₁₈NO), the unpaired electron spin S is coupled to the nuclear spin of the nitrogen atom (K=1 for ¹⁴N), and the energy spectrum is split into six levels. As the external magnetic field B₀ is reduced below several mT, the hyperfine term AS·K becomes comparable to and eventually dominates the Zeeman term –γ_SS_zB₀ in the Hamiltonian. The unpaired electron spin experiences a strong local magnetic field from the nitrogen spin, and the energies of the six levels are no longer proportional to B₀. The equilibrium expectation value S₀ in Eq. (1) is no longer the expectation value in the field B₀, and Eq. (5) for Overhauser enhancement does not hold. Because the expectation value I₀ for the nuclear spins in solution scales linearly with B₀, the enhancement factor E increases drastically as the magnetic field is lowered, according to Eq. (1). It was predicted to be as high as ±2000 in the Earth magnetic field [43]. This effect has limited practical significance, however, because the absolute polarization levels, achieved with Overhauser DNP at microtesla-range magnetic fields, are nevertheless quite low.

The electron and nitrogen spins in TEMPO are strongly coupled at low magnetic fields, and this two-spin system has 10 allowed ESR transitions [43, 44]. Eight of them are π transitions that can be induced by rf magnetic fields perpendicular to the static magnetic field B₀. The other two are σ transitions that are induced by rf irradiation fields parallel to B₀. However, only three transitions (T_16π, T_25π, and T_34π) out of ten have significant transition probabilities at magnetic fields above ~2 mT. Thus, the ESR spectrum of TEMPO free radicals in the field range 2 – 10 mT, most commonly used for Overhauser DNP, has three main resonance lines. The maximum polarization enhancement E_max for solvent water protons, obtained via a complete saturation of any one of these resonances, is predicted to be of the order of −100 [43].

2.3 Instrumentation

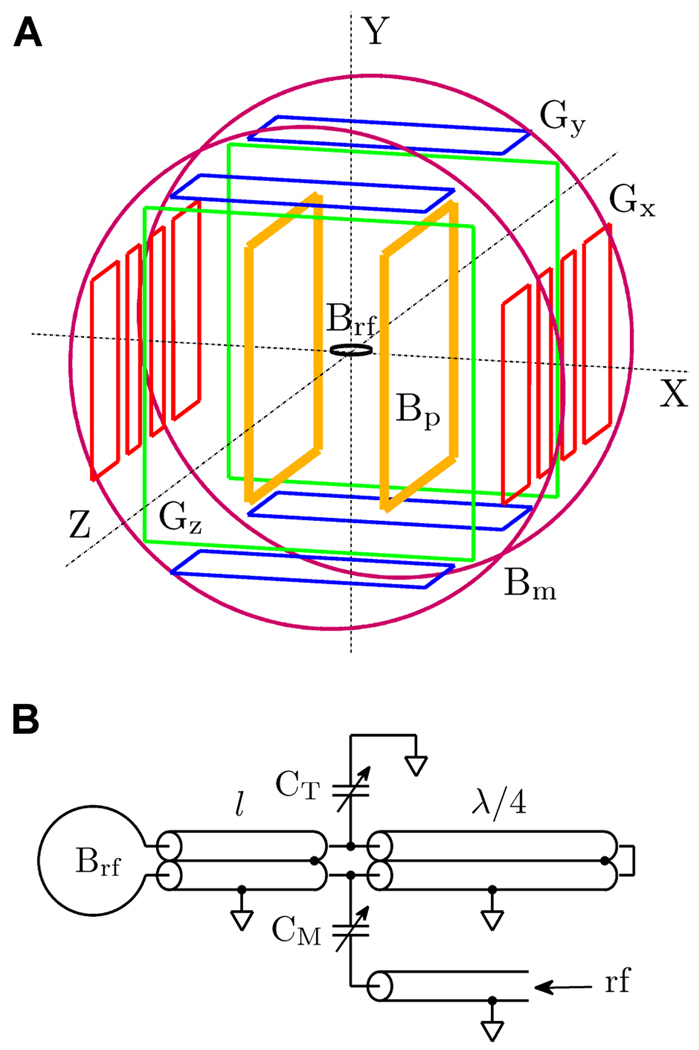
Our instrumentation for 3D ULF MRI has been described in detail before [19–22]. We have used this system to acquire images of the human brain [21] and study parallel imaging at microtesla fields [20]. The system includes seven SQUID channels in a liquid He cryostat. They are characterized by magnetic field noise as low as 1.2 fT/Hz^1/2 at 1 kHz inside a magnetically shielded room (MSR). The modified system for ULF MRI with DNP, employed in the present work, is depicted schematically in Fig. 2. Its main difference from the previously used set-up is that the relatively heavy pre-polarization coils, cooled with liquid nitrogen [19, 22], are replaced with a pair of light Helmholtz coils and a thin rf antenna.

Fig. 2.

A) Schematic of the coil system for 3D ULF MRI with DNP. B) Schematic of the antenna used for rf irradiation of the sample.

The new B_p coils are designed to generate a magnetic field of several mT. They are square with the side length of 61 cm, 2.5 cm × 2.5 cm cross section, and 33.5 cm spacing (Fig. 2A). The relative non-uniformity of the B_p field is less than 0.1% within 10 cm wide sample space, and the field strength is 0.57 mT at 1 A. Because the magnetic field stability is essential for DNP experiments, the B_p coils are driven by dc power supplies (Sorensen DLM 40-15) in current control mode. The B_p current is turned on and off with specially designed solid state switches [19]. An additional mechanical relay is used in the present set-up to completely disconnect the B_p coils from the power supplies before each measurement (after the pre-polarization), and thus prevent the power line noise from entering the system. The other four sets of coils in Fig. 2A are used to generate the µT-range measurement field B_m and three gradients, G_x=dB_z/dx, G_y=dB_z/dy, and G_z=dB_z/dz, for 3D Fourier imaging as described previously [19].

The rf antenna is used for irradiation of the sample at the ESR frequency of 120 MHz. Its schematic is shown in Fig. 2B. We chose the antenna design with a surface coil and a parallel transmission line [33, 46], that is widely used in ESR and Overhauser-enhanced MRI. The resonant circuit in this design is formed by the inductance of the surface coil and the distributed capacitance of the parallel line, which consists of two coaxial cables of length l. The parallel line has an open-circuit termination and is balanced by the λ/2 balun, formed by two coaxial pieces of λ/4 length (Fig. 2B). The balun ensures that voltages at the ends of the parallel line are opposite and symmetric with respect to the ground. The C_T capacitor is used for frequency tuning, and C_M – for impedance matching.

Because larger surface coils allow irradiation of larger objects, we built three rf antennas with coil diameters of 20 mm, 40 mm, and 60 mm, using the standard RG 223/U coaxial cable. Parameters of the antennas were calculated according to formulas in [46]. The parallel transmission line length was computed to be l=320 mm, 199 mm, and 95 mm at 120 MHz for the 20 mm, 40 mm, and 60 mm antennas, respectively. The balun included two cable pieces of λ/4=412 mm length each. To reduce heating, the antenna coils were made of 2 mm thick copper wire, and the outer insulation layer was removed from the coaxial cables. Variable 0.8… 10 pF rf-rated air capacitors were used for C_T and C_M.

To measure generation efficiency of the antennas, we employed a small (3 mm diameter) probe coil in series with a small-size 50 ohm resistor, placed in front of the antenna and connected via a λ/2 length cable to a high-frequency spectrum analyzer (HP 8566B). The power of the rf signal induced in the probe coil is related to the amplitude of the B_rf field produced by the antenna. The generation efficiency of the unloaded antenna coils was measured to be 28 µT/W^1/2, 14 µT/W^1/2, and 8.4 µT/W^1/2 at 120 MHz for the 20 mm, 40 mm, and 60 mm antennas, respectively. The measured values of the quality factor Q for the three antennas were, respectively, 90, 101 and 78. The 120 MHz signal for rf irradiation was provided by a general-purpose signal generator (HP 8662A) and amplified by a high-power rf amplifier (Amplifier Research 1000LP). A directional coupler (–30 dB) was installed at the output of the amplifier to monitor the applied rf power with the spectrum analyzer. High-power rf relays were used to turn the signal on and off, with one relay included between the rf generator and the amplifier, and the other – between the amplifier and the antenna. To reduce interference penetration, the latter relay was placed in the feed-through opening of the MSR, and its rf ground was electrically connected to the MSR wall.

To optimize DNP performance of the system, it is essential to maximize the rf power supplied to the sample by properly tuning the antenna. The tuning was performed in three steps before each experiment. First, the antenna was positioned outside the ULF MRI system, and the small probe coil, connected to the spectrum analyzer, was placed in front of it. The C_T and C_M capacitors were adjusted to tune the resonance frequency and maximize the rf signal induced in the probe coil. Second, the antenna was installed inside the ULF MRI system, and further adjustments were made while the probe coil signal was observed. Third, the sample was placed inside (or around) the antenna, and the C_M capacitor was adjusted again to maximize the DNP-enhanced ULF NMR signal, measured by the SQUID instrumentation and monitored with a general-purpose spectrum analyzer (Stanford Research Systems SR760). This last step requires that the B_p field strength be set to a value close to a DNP resonance.

2.4 Experimental parameters

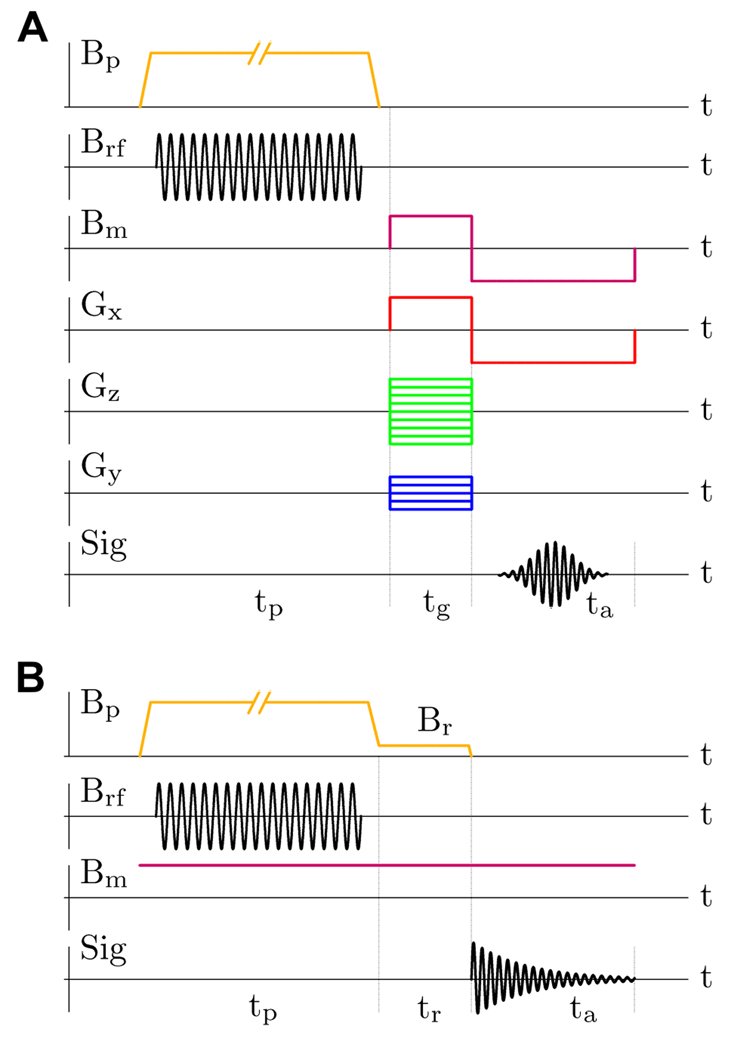
The experimental protocol, used in the present work for Overhauser-enhanced ULF MRI, is illustrated in Fig. 3A, and the protocol for ULF NMR of ¹³C is shown in Fig. 3B. In both protocols, each measurement step begins with the pre-polarization stage, during which the sample is subjected to rf irradiation in the presence of the constant pre-polarizing field B_p. The typical rf power of 100 W was supplied to the antenna during the irradiation. The pre-polarization field strength was B_p=3.52 mT in ¹H imaging experiments, and B_p=5.75 mT in ¹³C NMR measurements. The switch-off time for the B_p field was 2 ms at 10 A current. The measurement field B_m in all the experiments was set to 96 µT, corresponding to the Larmor precession frequency f_H=4096 Hz for ¹H and f_C=1030 Hz for ¹³C.

Fig. 3.

A) Experimental protocol for ULF MRI with Overhauser DNP. B) Protocol for ULF NMR with DNP.

The antenna coil was positioned horizontally (XZ plane) during the imaging experiments, and the object was placed inside the coil as shown in Fig. 4 (left). The measurement field B_m was applied after the removal of the B_p field perpendicular to the polarization vector, inducing spin precession [19]. The echo signal was formed by simultaneous reversal of the B_m field and the frequency encoding gradient G_x (Fig. 3A). The pre-polarization time t_p used for ¹H imaging was either 1.0 s or 1.5 s. The gradient encoding and signal acquisition times were t_g=0.25 s and t_a=0.5 s, respectively. The frequency encoding gradient G_x changed between ±47 µT/m (±20 Hz/cm for ¹H). The phase encoding gradient G_z had N_z=65 different values, that were equally spaced and symmetric with respect to G_z=0, with the maximum value G_z,max = −G_z,min= 47 µT/m (20 Hz/cm). These imaging parameters provided 1 mm × 1 mm resolution in the horizontal plane. In 3D imaging experiments, N_y=11 phase encoding steps were taken with the maximum gradient value G_y,max = −G_y,min= 9.4 µT/m (4.0 Hz/cm for ¹H), providing 5 mm resolution in the vertical (Y) direction. The measured signal was digitized at 21.3 kS/s sampling rate. All ULF MR images with Overhauser enhancement were acquired in a single scan, i.e. without any signal averaging. Because the samples were relatively small (Fig. 4), the data from only one SQUID channel (Ch 1) out of seven were used in the analysis.

Fig. 4.

Left: position of the rf antenna for imaging experiments (the 60 mm antenna is shown). Right: position of the rf antenna for NMR measurements of carbon-13 (the 40 mm antenna is shown).

For the ¹³C NMR measurements, the antenna coil was positioned vertically in the XY plane. The sample consisted of four vials, each containing 2 ml of solution, placed on both sides of the coil as shown in Fig. 4 (right). A forced air flow around the sample was used for cooling. The measurement field B_m was kept constant throughout the experiment (Fig. 3B), and spin precession was induced by rapidly switching off the B_p field (or the B_r field if t_r>0). This approach was chosen for the NMR measurements, because the rapid application of the B_m field in the ULF MRI procedure (Fig. 3A) leads to a magnetic relaxation of the MSR in the direction of B_m, which remains sufficiently strong for about 100 ms to cause a visible drift in Larmor frequency. This drift is not important for imaging, because of the relatively strong G_x gradient (Fig. 3A), but it affects the shape of the measured NMR line. The B_p switching off in 2 ms was non-adiabatic for ¹³C spins (f_C~1 kHz), because virtually no ¹³C signal loss was observed in the case of steady B_m field compared to the protocol with pulsed B_m. The signal from proton spins (f_H~4 kHz), however, decreased by a factor of 2 at the steady B_m, and this effect was taken into account when comparing the NMR signal strengths for ¹H and ¹³C. The relaxation field B_r, generated by the same B_p coils during a variable delay time t_r, was used to measure the longitudinal relaxation time T₁ at the B_r field as in [22]. The pre-polarization time t_p was 5 s for ¹³C sodium bicarbonate, and 10 s for the other ¹³C-labeled chemicals. Each NMR measurement was repeated 50–100 times, and the resulting spectra were averaged.

2.5 Materials

The Overhauser DNP experiments, described in this work, were performed using TEMPO (2,2,6,6-tetramethylpiperidine 1-oxyl) free radicals, purchased from MP Biomedicals (www.mpbio.com). We also used ¹³C labeled substances, including ¹³C sodium bicarbonate NaHCO₃, [1-¹³C] sodium pyruvate CH₃COCOONa, [1-¹³C] L-alanine CH₃CH(NH₂)COOH, and [1-¹³C] sodium L-lactate CH₃CH(OH)COONa. The pyruvate, alanine, and lactate were labeled with ¹³C in the carboxyl -COO-position (also referred to as C₁) with isotopic enrichment of 99%. These materials were purchased from Cambridge Isotope Laboratories, Inc. (www.isotope.com). As mentioned in Sec. 1, the hyperpolarized [1-¹³C] pyruvate is used in metabolic imaging studies, where its conversion to alanine and lactate is monitored as a function of time [37]. The T₁ relaxation time for the carboxyl ¹³C in pyruvate is longer than 20 s. All the chemicals were dissolved in de-ionized water (without degassing), and a fresh solution was prepared before each experiment.

The ³J_CH and ²J_CH coupling constants for the carboxyl ¹³C in [1-¹³C] pyruvate, alanine, and lactate are in the range of 3–5 Hz. Because these values are three orders of magnitude lower than the difference in Larmor frequencies between ¹H and ¹³C (~3 kHz in our experiments), these systems are weakly coupled, and analysis of their ¹³C spectra is straightforward. In pyruvate, interaction of ¹³C with three protons in the methyl CH₃– group (also referred to as C₃ or C_β group) leads to a quartet of lines with ³J_CH~1.3 Hz [47]. In alanine, ¹³C is coupled to three methyl protons with ³J_CH~4.2 Hz and to a proton in the methine –CH– group (C₂ of C_α) with ²J_CH~5.0 Hz [47]. Thus, the ¹³C spectrum of alanine is an octet. For lactate, the corresponding coupling constants are ³J_CH~4.2 Hz and ²J_CH~3.5 Hz [47], so the spectrum is also an octet with a slightly smaller splitting. Because three pairs of lines at the center of the octet spectrum have line separations of only ~0.8 Hz for alanine and ~0.7 Hz for lactate, the ¹³C spectra of these two systems may appear as quintets when the spectral resolution is not very high. In [48], the J-coupling spectra of ¹³C in [1-¹³C] alanine and lactate, measured at 3 T with 1 Hz resolution, look like quintets with J~4.5 Hz and J ~3.75 Hz line splittings, respectively. These data suggest that alanine and lactate can be distinguished based on their J-coupling spectra. A much higher spectral resolution at microtesla-range magnetic fields [4] should allow highly accurate measurements of ¹³C J-coupling spectra for these materials.

3. Results

3.1 Overhauser DNP performance

Fig. 5A exhibits the resonance structure of Overhauser DNP probed as a function of the pre-polarizing field B_p. It was measured for 2 mM (i.e. 2 mM/liter) water solution of TEMPO free radicals at a fixed rf irradiation frequency of 120 MHz using the 40 mm antenna at 20 W input power. The three peaks at 2.15 mT, 3.52 mT, and 5.77 mT fields result from the hyperfine splitting of the TEMPO radicals’ ESR resonance, and correspond to the T_16π, T_25π, and T_34π transitions (Sec. 2.2). We performed similar measurements for 1M water solution of ¹³C sodium bicarbonate, doped with 16 mM of TEMPO. The ¹³C resonances were broader, but their peak positions were very close to those for ¹H, with the tallest peak at B_p=5.75 mT.

Fig. 5.

A) DNP resonance structure for 2 mM water solution of TEMPO free radicals. B) Absolute value of the polarization enhancement factor E measured as a function of applied rf power.

Fig. 5B compares the DNP enhancement factors for the three antennas of 20 mm, 40 mm, and 60 mm diameter. Each antenna was placed horizontally 25 mm below the cryostat. A small vial (9 mm diameter, 2 ml volume) with 2 mM TEMPO solution was put at the center of the antenna, and its position with respect to the cryostat was always the same. The enhancement factor E was determined as the ratio of the ULF NMR signal intensities measured at B_p=3.52 mT with and without rf irradiation. The pre-polarization time in these experiments was t_p=1.5 s, and the T₁ relaxation time for 2 mM TEMPO solution was measured to be 0.79±0.05 s at 3.52 mT. According to Fig. 5B, the polarization enhancement depends strongly on the antenna coil size at low power levels, with the 20 mm antenna providing E as large as –29 at 5W. As the input power increases, however, the saturation regime is gradually approached, and the differences in E among the three antennas become less pronounced. Therefore, both the 40 mm and the 60 mm antennas can be efficiently used for ULF MRI with DNP, provided that the applied rf power is sufficiently high. The largest polarization enhancement, observed for ¹H at B_p=3.52 mT using the 20 mm antenna, was E= –95, which corresponds to the equivalent polarization field of 0.33 T. The DNP experiments, reported below in Sec. 3.2 and Sec. 3.3, were carried out at either 3.52 mT or 5.75 mT field rather than at 2.15 mT to facilitate real-time monitoring of the unenhanced ¹H signal and achieve more accurate tuning of the system as described in Sec. 2.3.

The plots of 1/(1–E) vs 1/P_rf using the data in Fig. 5B yielded straight lines with the same intercept 1/(1–E_max), corresponding to E_max= –101. The leakage factor was f=0.8 according to Eq. (3). Using Eq. (5) and Eq. (6), we then determined the ratio (ρ/n)=0.194. For n=3, this gives the coupling factor value ρ=0.58, which is higher than the theoretical value ρ=0.5 for pure dipolar coupling. Such discrepancy has been observed before (e.g. [40]). It reflects the fact that Eqs. (5) and (6) are based on the four-level model in Fig. 1, which is not entirely accurate for nitroxide radicals even at high magnetic fields, as discussed in [45].

The strong rf pulses, employed in the present work, did not have any negative effect on the performance of the SQUID instrumentation. This is because the cryostat in our ULF MRI system is screened with an rf shield made of gold-plated mylar (Fig. 4), and special cryoswitches [19] are used to disconnect the pick-up coils from the SQUID sensors during the pre-polarization. However, the λ/2 balun part of the antenna (Fig. 2B) provides a return path for Johnson currents, which causes an increase in thermal noise level. For example, when the unloaded antenna coil was placed horizontally 25 mm below the bottom of the cryostat (Fig. 4, left), the magnetic field noise spectral densities were measured to be 1.25 fT/Hz^1/2, 1.52 fT/Hz^1/2, and 1.88 fT/Hz^1/2, for the 20 mm, 40 mm, and 60 mm diameter antennas, respectively. When the antenna was moved up to 18 mm below the cryostat, these noise values increased, respectively, to 1.34 fT/Hz^1/2, 1.82 fT/Hz^1/2, and 2.36 fT/Hz^1/2. In the absense of an rf antenna, the noise spectral density for Ch 1 was 1.2 fT/Hz^1/2 at 1 kHz. Thus, the actual SNR improvement in ULF NMR/MRI with Overhauser DNP is somewhat lower than the polarization enhancement E. This effect can be mitigated by positioning the rf antenna coil vertically (Fig. 4, right). For the 40 mm antenna, the noise level was measured to be 1.38 fT/Hz^1/2 in this case. Such configuration was successfully used for ¹³C NMR measurements (Sec. 3.3), but it is not always convenient for imaging. Modifications to the antenna design that could reduce its thermal noise without compromising its rf generation efficiency would be beneficial.

3.2 Overhauser-enhanced ULF MRI

The first images, acquired by Overhauser-enhanced MRI with SQUID signal detection, are exhibited in Fig. 6. Three vials of 14 mm, 30 mm, and 47 mm internal diameter were filled with 2 mM water solution of TEMPO, and placed inside the 20 mm, 40 mm, and 60 mm antennas, respectively. The imaging experiments were performed as described in Sec. 2.4 with the pre-polarization time t_p=1.5 s. According to Fig. 6, the DNP enhancement leads to a dramatic improvement in image quality. The image of the 47 mm phantom shows some signal reduction toward the phantom edges, because sensitivity of the 37 mm diameter SQUID pick-up coil is decreased in those areas [19]. The DNP images in Fig. 6 are characterized by enhancement factors |E|~60…80 (near the image center), which, at B_p=3.52 mT, correspond to equivalent polarization fields of 0.2…0.3 T. These results demonstrate that Overhauser-enhanced ULF MRI, implemented with a pair of light Helmholtz coils and a thin rf antenna, can produce images that would require the use of a heavy and energy-consuming pre-polarization magnet in conventional ULF MRI.

Fig. 6.

DNP-enhanced 2D images of phantoms containing water solution of TEMPO. The images were acquired at 96 µT field in a single scan with 1 mm × 1 mm resolution. The image without DNP was obtained by averaging 20 scans.

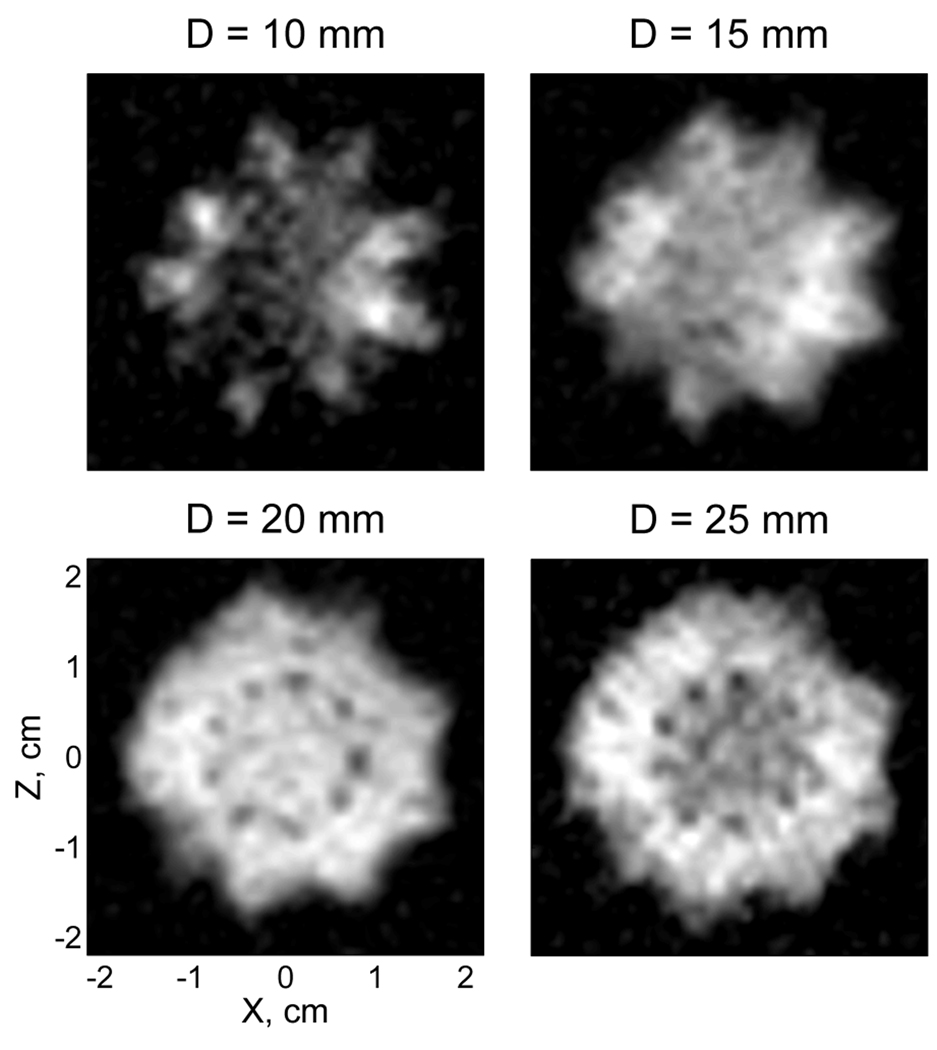
We also used our system for ULF MRI with Overhauser DNP to perform 3D imaging of the insides of a cactus. We chose a cactus plant, because it contains a soft tissue that readily absorbs water. A healthy moon cactus (Gymnocalycium mihanovichii Hibotan), that had been regularly watered, was injected with 6 mM water solution of TEMPO, and placed under the bottom of the cryostat inside the 60 mm antenna (Fig. 4, left). The pre-polarization time at each imaging step was t_p=1.0 s. Because 11 image layers were acquired with 1 mm × 1 mm in-plane resolution and 5 mm resolution in the vertical dimension, the total imaging time for a single scan was about 20 min. Fig. 7 exhibits the resulting image, which reproduces the cactus shape and shows some details of its internal anatomy.

Fig. 7.

DNP-enhanced 3D image of the moon cactus, injected with TEMPO solution. The image was acquired at 96 µT field in a single scan with 1 mm × 1 mm in-plane resolution. D is the depth of a given 5 mm thick layer under the bottom of the cryostat.

In order to estimate time dependence of the polarization enhancement factor E, we monitored the NMR signal from a similar cactus, also injected with TEMPO. The initial enhancement value was found by extrapolation to be |E|~24. The actual enhancement was likely to be higher, because the maximum DNP enhancement occurred at the antenna level 25 mm below the cryostat, while most of the measured unenhanced signal came from the regions closer to the cryostat bottom, where the SQUID pick-up coil has greater sensitivity [19]. The DNP-enhanced NMR signal was found to decay as approximately a linear function of time, dropping by a factor of 3 in 20 min. Such quasi-linear decrease in signal intensity has been observed in ESR studies involving nitroxide free radicals [42]. It is due to a gradual reduction of nitroxides in biological systems (for example, via conversion to hydroxylamines), which results in the loss of paramagnetism [42]. Because such reduction depends on chemical environment, it has been used as a sensitive tool to study various biochemical processes [41]. Our experiment shows that ULF MRI with Overhauser DNP can be successfully used for imaging small animals and plants. It also suggests that 3D Fourier encoding is too time-consuming for this purpose, and imaging sequences with slice selection should be used instead.

3.3 Overhauser-enhanced ULF NMR of carbon-13

As mentioned in Sec. 1, ULF NMR with its broadband SQUID-based signal reception allows simultaneous measurement of NMR signals from ¹H and ¹³C at microtesla-range magnetic fields. NMR of ¹³C, however, is considerably more challenging. For a substance that is labeled with ¹³C in one position within the molecule and has a typical concentration of 1 M in water solution, the ¹³C magnetization is ~1700 times lower than the magnetization of protons in water. Nevertheless, the DNP polarization enhancement makes it possible to perform NMR spectroscopy of ¹³C at microtesla fields.

The first NMR measurement of ¹³C at microtesla fields is demonstrated in Fig.8. The experiment was performed as described in Sec. 2.4. TEMPO concentration of 16 mM was found to provide the strongest ¹³C signal for 1 M concentration of sodium bicarbonate. The ¹³C NMR signal could only be observed with DNP enhancement. We estimated the unenhanced ¹³C signal indirectly using the unenhanced signal from the solvent water protons as a reference, and taking into account the difference in spin concentration, N(¹H)/N(¹³C)~110, the difference in magnetization (for the same concentration), γ²(¹H)/γ²(¹³C)~16, the difference in measured linewidth, T₂*(¹³C)/T₂*(¹H)~17, and the decrease in ¹H signal during the field switching (Sec. 2.4). The polarization enhancement factor for ¹³C was thus estimated to be E ≈ –200. For B_p=5.75 mT, this corresponds to the equivalent polarization field of 1.1 T. The longitudinal relaxation time for ¹³C in sodium bicarbonate with 16 mM TEMPO was measured to be T₁=3.0±0.1 s at 96 µT and T₁=3.5±0.1 s at 5.75 mT. The pre-polarization time was t_p=5.0 s. The described estimation of the unenhanced ¹³C signal from the unenhanced ¹H signal corresponded to t_p ≫ T₁ , as for the water protons in the presence of 16 mM TEMPO. If the same condition held for ¹³C in the DNP experiment, the measured ¹³C NMR signal would likely be ~30% higher, leading to a larger estimated enhancement factor E ≈ −260.

Fig. 8.

Simultaneous measurement of proton and carbon-13 NMR signals at 96 µT field using Overhauser DNP.

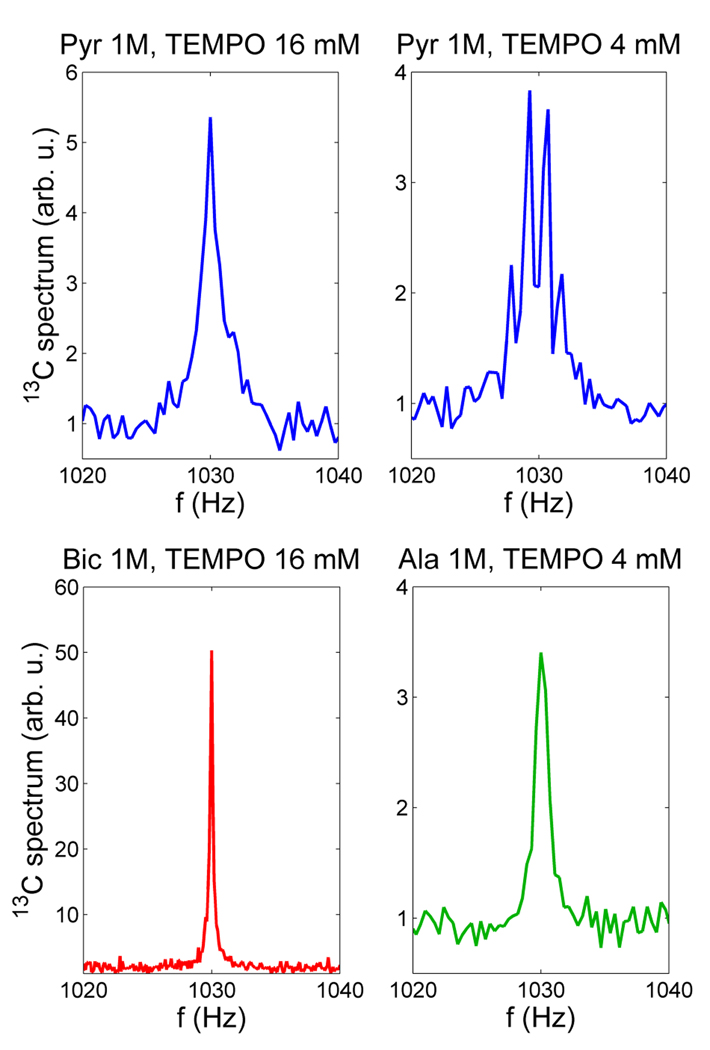
¹³C NMR spectra of [1-¹³C] sodium pyruvate and [1-¹³C] L-alanine at the 96 µT field are exhibited in Fig. 9, together with the ¹³C sodium bicarbonate spectrum from Fig. 8. All the spectra are plotted with the same vertical scale. The quartet splitting for pyruvate at 4 mM TEMPO in Fig. 9 is about 1.4 Hz, which is close to the value of ³J_CH ~1.3 Hz reported in [47]. The first observation one can make is that the J-coupling spectrum of pyruvate changes drastically with the concentration of free radicals: the quartet at 4 mM TEMPO becomes the broadened singlet at 16 mM. This behavior can be attributed to the effect of spin exchange (see, e.g. [49]). As the free radical concentration increases, the T₁ relaxation time for ¹H spins (as well as for the ¹³C spin) in the pyruvate molecule is reduced. This leads to a faster ¹H spin flipping between its two states, so the effect of J-coupling between ¹H and ¹³C is increasingly averaged out. As a result, the sharp multiplet in the limit of 1/T₁^H ≪ 2πJ_CH (slow spin exchange) becomes a sharp singlet in the 1/T ₁^H ≫ 2πJ_CH limit (fast spin exchange). In the intermediate regime, the multiplet lines are broadened and their splitting is reduced, until the multiplet collapses into a broadened singlet, which becomes sharper as the spin exchange rate is increased [49]. Such “chemical exchange spin decoupling” has been observed and studied before [50–52].

Fig. 9.

Carbon-13 spectra of sodium bicarbonate, sodium pyruvate, and alanine, measured at 96 µT field using DNP. The effect of TEMPO concentration on J-coupling spectrum is clearly observed in the case of pyruvate. Similarly, the J-coupling spectrum of alanine, normally a multiplet, appears as a singlet in the figure (see text for details).

Another result to be noted in Fig. 9 is that the ¹³C spectrum of L-alanine is a broadened singlet instead of the expected octet (Sec. 2.5) even at 4 mM TEMPO concentration. This means that the decoupling effect of TEMPO is stronger for alanine than for pyruvate, which can be explained as follows. Nitroxide free radicals are known to form hydrogen bonds with protons in –NH₂, –OH, and –COOH groups [53]. Such bonding causes faster T₁ relaxation for ¹H and ¹³C in the case of alanine, leading to the stronger decoupling effect. Relaxation enhancement due to hydrogen bond formation has also been observed with paramagnetic agents ([54], p.226). This explanation for the appearance of the alanine spectrum in Fig. 9 is further supported by T₁ measurements for ¹³C. For pyruvate, T₁ values were determined to be 3.4±0.3 s (at 96 µT) and 5.0±0.3 s (at 5.7 mT) for 16 mM TEMPO concentration. These values increased to 6.2±0.5 s (96 µT) and 8.7±0.5 s (5.7 mT) for 4 mM TEMPO. In the case of alanine, the corresponding T₁ values were measured to be 3.9±0.4 s (96 µT) and 4.6±0.4 s (5.7 mT) at 4 mM TEMPO. Because the NMR signals from pyruvate and alanine were very weak (Fig. 9), these numbers are rather coarse estimates obtained by fitting an exponential function to only three data points as in [22]. Comparison of the T₁ relaxation times suggests that the 4 mM TEMPO concentration has approximately the same effect on ¹³C relaxation properties of alanine as the 16 mM of TEMPO – on the relaxation properties of pyruvate.

We also tried to carry out Overhauser-enhanced ULF NMR of [1-¹³C] sodium lactate, but were unable to detect any ¹³C signal. This negative result can be attributed to the lower DNP enhancement [55], and, possibly, stronger broadening effects of TEMPO free radicals in the case of the lactate.

4. Discussion

Our results demonstrate that Overhauser DNP at mT-range magnetic fields can be naturally combined with ULF NMR/MRI in one system. This approach greatly improves SNR of ULF NMR/MRI by increasing nuclear spin polarization by two orders of magnitude without an increase in the pre-polarizing field strength.

Our results also suggest that one should exercise caution when evaluating DNP performance based on the enhancement factor E. In Sec. 3.1, polarization enhancement with E= −95 was observed for protons at B_p=3.52 mT (T_25π transition). If the same measurements were carried out at 2.15 mT (T_16π transition) and 5.77 mT (T_34π transition), and the resulting non-equilibrium polarizations were compared to the thermal polarizations at those fields, the enhancement factors would likely be around −150 and −60, respectively. However, the absolute polarization levels in all three cases would be similar (Fig. 5A), corresponding to the thermal polarization at ~0.3 T magnetic field. Values of the factor E may be more confusing when the DNP-enhanced polarization at one magnetic field is compared to the thermal equilibrium polarization at a different field strength. In [44], for example, the authors performed Overhauser DNP at 2.7 mT field (T_16π transition at 131.5 MHz), compared the resulting NMR signal to the unenhanced signal at the Earth magnetic field of ~54 µT, and reported E= −3100. If the same 2.7 mT magnetic field were used as a reference, the enhancement factor value would be E= −62. Therefore, DNP performance is more accurately characterized by the strength of the equivalent magnetic field that would produce the same thermal equilibrium polarization as the measured DNP-enhanced polarization. In our experiments, this equivalent field is 0.33 T for protons, and 1.1 T for ¹³C.

Microtesla MRI with Overhauser enhancement and SQUID signal detection, described in Sec. 3.2, has an important advantage over conventional Overhauser-enhanced MRI, which relies on Faraday signal detection. Because sensitivity of Faraday detection scales linearly with Larmor frequency, a stronger detection field is applied in conventional Overhauser-enhanced MRI after the Overhauser DNP at a low magnetic field. In [31], for instance, the DNP was performed at 60 µT and MR images were acquired at 6.8 mT. In the most advanced system, designed for in vivo imaging of free radicals [30], Overhauser DNP at each imaging step is carried out at 5 mT, and the magnetic field is then ramped up to 0.45 T for MRI signal detection. In our approach, imaging is performed at the microtesla-range measurement field B_m(Fig. 3A) using highly sensitive SQUIDs, so a stronger detection field is not needed. This allows development of more efficient systems for Overhauser-enhanced MRI, utilizing magnetic fields no higher than a few mT.

The NMR experiments, described in Sec. 3.3, show that the combination of Overhauser DNP with SQUID signal detection makes it possible to perform NMR of ¹³C at microtesla-range magnetic fields. Very few studies have been reported in which ¹³C NMR signals were measured below 1 T. In [56], Overhauser DNP and NMR of ¹³C were carried out at 7.4 mT field, but that work used ¹³C containing solvents rather than water solutions of ¹³C chemicals. More recently, Overhauser-enhanced NMR measurements of ¹³C labeled materials in aqueous solutions were reported at 0.35 T magnetic field [57]. The NMR spectroscopy of ¹³C at microtesla fields, demonstrated here for the first time, can be used to measure J-coupling constants for ¹³C spins in various substances with very high (mHz range) spectral resolution. Moreover, because SQUID sensors with untuned input circuits enable broadband signal reception, NMR spectra of various nuclear spins, including ¹³C, ¹⁵N, ³¹P, ¹⁹F, and ¹H, can be measured simultaneously with the same detection sensitivity. Magnetic relaxometry of these spins can provide important information about molecular dynamics. Clearly, both J-coupling and magnetic relaxation properties of ¹³C are strongly affected, if free radicals are present in the solution (Fig. 9). This limitation can be overcome in continuous flow systems, in which a solution of ¹³C labeled material under study is pumped through a special porous media (gel) chemically labeled with stable radicals [58]. This would allow the studied solution to be separated from the radicals after the DNP stage and before the NMR measurement.

The potential of microtesla MRI in combination with DNP is not limited to the case of Overhauser DNP. The most promising integration approach, in our opinion, is combination of SQUID-based microtesla MRI (without pre-polarization) with the ¹³C hyperpolarization method [34]. Because the hyperpolarization is performed outside an MRI scanner using a separate NMR-style hyperpolarizer, such as HyperSense® from Oxford Instruments (www.oxford-instruments.com), high magnetic fields of conventional MRI systems offer little advantage in terms of achievable ¹³C polarization. The same applies to the pre-polarizing field B_p of conventional ULF MRI. It has been suggested that “the use of hyperpolarized substances should make it possible to perform imaging at magnetic field, lower than the one used in clinical routine of today, and still generate images with high SNR” [37]. We propose to perform imaging of an injected hyperpolarized material labeled with ¹³C using a novel type of MRI scanner (Fig. 10), that employs only microtesla-range magnetic fields.

Fig. 10.

Conceptual drawing of an ultimate low-field MRI scanner for imaging hyperpolarized substances. It uses only microtesla-range magnetic fields, and is open, portable, and inexpensive. Color coding for the coil sets is the same as in Fig. 2A.

The scanner in Fig. 10 has several features that could make it an attractive option for imaging hyperpolarized ¹³C (or ¹⁵N). First, it can be much more open, portable, and inexpensive than conventional MRI machines. Moreover, because a DNP hyperpolarizer can produce a large (~100 ml) amount of the hyperpolarized solution [59], several microtesla MRI scanners can be operated simultaneously after a single hyperpolarizer’s run. Second, because this scanner only employs magnetic fields below ~1 mT, SQUID sensors of any type can be successfully used for MRI signal detection without the risk of trapping magnetic flux. This greatly simplifies the SQUID system design, because the special cryoswitches, employed in ULF MRI to protect the SQUIDs from trapping flux during the strong B_p pulses [19], are no longer needed. Third, because hyperpolarized ¹³C provides a strong MRI signal for a relatively short time, parallel imaging with a large SQUID array can be efficiently used to accelerate image acquisition [20]. Modern magnetoencephalography (MEG) systems include as many as ~300 SQUID channels, and their technology is well developed. The image acquisition can be accelerated even further if the MEG-style source localization by a large sensor array is used in place of the conventional MRI encoding. Even though chemical shift information is not available in the low-field limit, metabolites of an injected hyperpolarized substance can, in principle, be distinguished by means of J-coupling spectroscopy and/or magnetic relaxometry of ¹³C at microtesla fields. Our experimental results in Sec. 3.3, together with the published low-resolution spectra for [1-¹³C] alanine and lactate [48] suggest that this might indeed be possible. Therefore, the proposed ultimate low-field MRI scanner (Fig. 10) can potentially be used not only for angiography and perfusion mapping, but also for real-time metabolic imaging with hyperpolarized ¹³C.

5. Conclusion

Based on our experimental results, presented in this work, we conclude that combination of DNP with SQUID detection greatly enhances SNR performance of low-field NMR/MRI. This approach can be used to develop new types of research instruments for in vivo imaging and in vitro materials studies. They include: i) an efficient system for Overhauser-enhanced MRI, with Overhauser DNP at a mT-range and image acquisition at a µT-range magnetic field; ii) a continuous flow system for Overhauser-enhanced NMR of ¹³C, suitable for both J-coupling spectroscopy at µT fields and T₁ relaxometry in the µT – mT field range; iii) an open MRI scanner for imaging DNP hyperpolarized ¹³C using only µT-range magnetic fields. Such instruments could have important applications, particularly in studies of metabolism involving free radicals or endogenous substances labeled with ¹³C.