Atomic Hydrogen as High-Precision Field Standard for High-Field EPR

Abstract

We introduce atomic hydrogen trapped in an octaisobutylsilsesquioxane nanocage (H@iBuT₈) as a new molecular high-precision magnetic field standard for high-field EPR spectroscopy of organic radicals and other systems with signals around g = 2. Its solid-state EPR spectrum consists of two narrow lines separated by about 51 mT and centered at g ≈ 2. The isotropic g factor is 2.00294(3) and essentially temperature independent. The isotopic ¹H hyperfine coupling constant is 1416.8(2) MHz below 70 K and decreases slightly with increasing temperature to 1413.7(1) MHz at room temperature. The spectrum of the standard does not overlap with those of most organic radicals, and it can be easily prepared and is stable at room temperature.

Introduction

Many paramagnetic systems feature relatively narrow spectra centered around g = 2. Among these, organic radicals form a major subgroup. They are pervasive in biological systems, fulfilling crucial roles in electron transfer and in enzymatic redox reactions. Such radicals can occur on substrates, cofactors (flavins, quinones), and amino acids (tyrosine, tryptophan, cysteine, glycine).

The g tensors of these organic radicals can be resolved and determined with high-field EPR, acquired at frequencies at and above about 95 GHz. High-resolution high-field EPR spectra of organic radicals were reported up to 670 GHz and 24 T [1–3].

The g-tensor components are sensitive to structural details such as the microenvironment, protonation state, electron spin density distribution and total charge of the radical [4–8]. In combination with quantum chemical modeling based on density functional theory, they are an important structural diagnostic tool that can reveal these details [9–11].

To this end, precise g values are needed, ideally with a relative uncertainty of 10⁻⁵ or less. Such levels can only be obtained if both the magnetic field and the microwave frequency of the EPR experiment are precisely known. Whereas the frequency can be routinely measured to a relative precision of 10⁻⁹, the relative uncertainty associated with the magnetic field is much larger, sometimes up to 10⁻². This has two reasons: First, due to hysteresis effects, the magnetic field at the sample resulting from a given current input into the coils of a resistive or superconducting magnet depends on the prior history of the magnetic field sweep. As the magnetic field is varied during an EPR experiment, this can vary substantially from sweep to sweep. Second, the spatial inhomogeneity of high-field magnets may cause a non-negligible offset between the fields at the sample position and the point where the field is measured. Field measurement can be done to high precision with NMR-based teslameters such as described in [12] or developed commercially. However, the use of these teslameters in high-field EPR still remains limited.

Ideally, the magnetic field is measured at the same point in time and space as the sample of interest. To this end, one can add a well-characterized paramagnetic compound as a field standard to the sample container. Its spectrum should have a few sharp lines that preferably do not overlap with the spectrum of interest. Its magnetic parameters should be accurately known for all temperatures of interest. Also, it should be an easily available, inert and stable compound. A variety of paramagnetic field standards are currently being employed for high-field EPR, satisfying some of these criteria. The most common are LiF:Li [13],with one very narrow metallic resonance line with g = 2.002293(2) at room temperature, and MgO:Mn²⁺ [14], with six hyperfine lines with g = 2.00101(5) and A = –243.9(1) MHz. Other standards occasionally used include Si:P (featuring one line with g = 1.998 at high P donor concentrations, and two lines separated by 4.4 mT at low donor concentration) [15–17], CaO:Mn²⁺, 2,2-diphenyl-1-picrylhydrazyl (DPPH) [18–20], potassium nitrosodisulfonate (Frémy’s salt) [21; 22], aromatic hydrocarbon radicals such as the perylene radical cation[23], and K₃CrO₈ [24]. Mn²⁺ in MgO and CaO as well as DPPH suffer from poor sample-to-sample and lab-to-lab reproducibility [19]. Standards with a single line (LiF:Li and Si:P) cannot be used directly to calibrate the magnetic field axis over a field range. Frémy’s salt and perylene radical cations are only used in solution, so they are limited to room-temperature measurements. The spectra of most field standards overlap with the g ≈ 2 signals of interest. In addition, for all of these standards, the temperature dependence of the magnetic parameters has not been characterized.

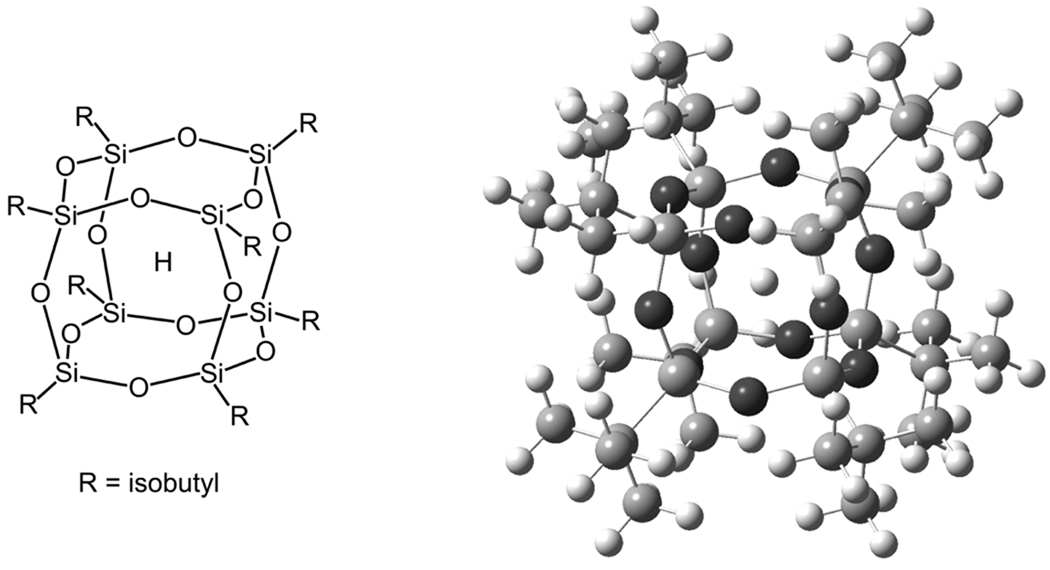
Here, we introduce H@iBuT₈ as a new high-precision field standard for high-field EPR that has distinct advantages compared to the standards mentioned above. It is atomic hydrogen trapped in octaisobutylsilsesquioxane iBuT₈ [25], a cuboidal silicate cage part of the POSS (polyhedral oligosilsesquioxane) family [26; 27]. Its molecular structure is shown in Fig. 1. In the following, we precisely determine the g value and the hyperfine coupling constant of the trapped hydrogen atom and characterize the temperature dependence of these parameters, both of which are isotropic. We then discuss the utility of this standard and illustrate it with high-field EPR spectra from some systems of current biological interest.

Fig. 1.

Structure of H trapped in the cage cavity of octaisobutylsilsesquioxane (H@iBuT₈).

Experimental

Octaisobutylsilsesquioxane (iBuT₈, (C₄H₉)₈Si₈O₁₂, CAS 221326-46-1) was purchased from Sigma-Aldrich and used without further purification. Hybrid Plastics Inc (Hattiesburg, MS) is an alternative supplier. Trapped atomic hydrogen was generated according to published procedures [28; 29]. 42 mg of iBuT₈ together with 4.5 mg of I₂(s) was dissolved in cyclohexane andirradiated in a home-made cave-type ⁶⁰Co source of the “Wisconsin type” described earlier [30] at a dose rate of 50.5 Gy/min for a full week (165h). The iodine was added to quench unwanted secondary radicals that develop during irradiation. The solution was sealed in a 25 mL round bottom Pyrex test tube with a rubber stopper and Parafilm. The tube was placed into a custom-made sample holder which was then inserted into the irradiation chamber of the source. The tube had an OD of 0.5 inch and its center was placed at a distance of 22.9 mm from the source. The dose rate at that distance was determined using the standard Fricke dosimetry approach[31; 32]. After γ-irradiation the solution was purified over a silica column using cyclohexane as the mobile phase. The fractions containing the paramagnetic H@iBuT₈ compound as determined by EPR spectroscopy were recovered and the solvent dried off at ambient pressure in a fume hood before sealing the compound in small Teflon capsules which are stored in the freezer at −20°C when not in use. The compound was found to show a stable EPR signal over more than two years under these conditions.

Two different samples of LiF:Li were used (kindly provided by Andre Stesmans, University of Leuven, and Roger Isaacson, University of California San Diego). The spectra of the two samples consist of one line and are identical, with a g value of 2.002293(2) as determined by Stesmans in 1989 [13]. Commercial MgO with a Mn²⁺ impurity was used (>95% fused MgO, Aldrich), with a g value of 2.00100(5), and a ⁵⁵Mn hyperfine coupling constant of −243.6(5) MHz, as determined previously [33].

X-band cw EPR measurements were performed at the CalEPR center at UC Davis, with a Bruker ECS106 cw EPR spectrometer equipped with a rectangular TE₁₀₂ cavity (flushed with N₂), an EIP 548A frequency counter and an Oxford ESR900 liquid-helium cryostat. The magnetic field was calibrated using a Bruker ER036TM proton NMR teslameter with an in-cavity probe and an accuracy of about 1 µT. All spectra were recorded after a spectrometer warm-up period of at least 12 h to ensure stability. Q-band cw EPR measurements were performed with a Bruker EleXsys 580 spectrometer equipped with an ER5106QT probe. The magnetic field was calibrated with the teslameter after removal of the probe.

High-field EPR spectra above 400 GHz were recorded at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee FL, using a homodyne transmission-mode spectrometer with a non-resonant probe and a 17 T superconducting magnet [34].

Results

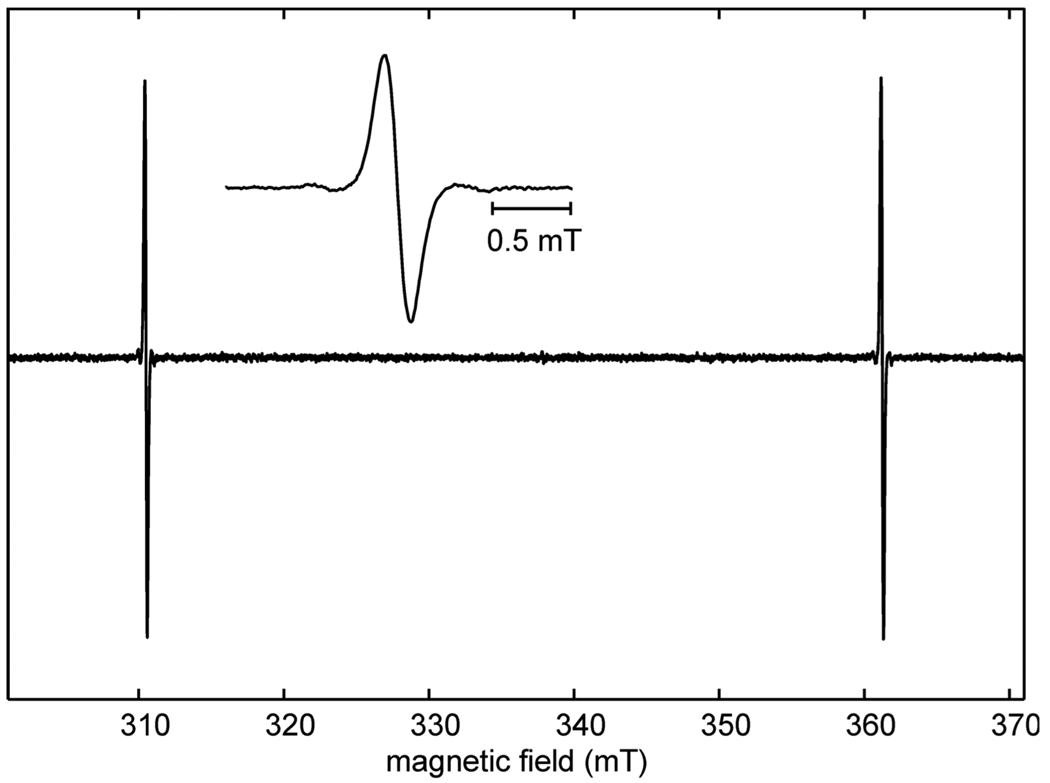
The X-band spectrum of H@iBuT₈ at room temperature is shown in Fig. 2. It exhibits two intense lines separated by about 50.7 mT, corresponding to the EPR transitions for the m_I = ±1/2 states of the trapped hydrogen atom. Each line is flanked by two satellite peaks separated from the central line by the ¹H Larmor frequency (0.47 mT for the low-field line and 0.55 mT for the high-field line). These lines are due to forbidden transitions involving spin-flips of the alkyl ligand protons [28]. Since there are 72 protons in iBuT₈, the transitions are quite intense. They saturate less easily than the central line. At fields higher than X band, the satellite lines vanish, since the transition moments become negligibly small. Hyperfine splittings due to ²⁹Si (I = 1/2, 4.7% natural abundance) are not resolved, since they are smaller than the line width: The silicon nuclei are about 2.8 Å from the atomic hydrogen nucleus, corresponding to a dipolar hyperfine coupling below 1 MHz in the point-dipolar approximation. The isotropic ²⁹Si coupling is about 4.2–4.5 MHz [28; 35; 36].

Fig. 2.

Experimental X-band spectrum of H@iBuT₈, acquired at 9.4801 GHz and 292 K with 0.1 mT modulation amplitude. Inset: enlarged low-field line.

The g factor and hyperfine coupling constant at room temperature (292 K) were determined from X-band cw EPR spectra of a sample containing both H@iBuT₈ and LiF:Li simultaneously as follows. Separate narrow (2 mT) and slow field (25 µT/s) sweeps with 0.01 mT modulation amplitude gave the two resonance lines of the hydrogen standard, at measured spectrometer frequencies ν₁ and ν₂. A similar sweep was applied to the resonance line of LiF:Li, giving B₀ and ν₀. The lines were least-squares fitted with Gaussian lineshapes and gave nominal line centers B_1nom, B_2nom and B_0nom. After removing the sample, the probe of the teslameter was placed in the cavity at the sample position and the field set to B_1nom, B_2nom and B_0nom. The field values B_1tm, B_2tm and B_0tm were read from the teslameter with an accuracy of about 1 µT. The g factor and hyperfine coupling were obtained by least-squares fitting the Breit-Rabi expression for the energy levels of an isotropic S = I = 1/2 spin system [37; 38] to (ν₁, B_1tm) and (ν₂, B_2tm), yielding g_tm and A. The g factor of LiF:Li was obtained from ν_Li and B_Li,tm, yielding a value g_Li,tm very close but not identical to the literature value of g_Li = 2.002293(2) [13]. Over several independent measurements, the deviation of g_Li,tm from g_Li varied randomly but correlated with the variation in g_tm. To reduce the impact of the error, we added the deviation g_Li,tm – g_Li to g_tm and averaged over several measurements. The final analysis gave g = 2.00294(3) and A = 1413.7(1) MHz, practically identical to the literature values for H in other octaalkylsilsesquioxane hosts [39]. The largest source of uncertainty are the determination of the line centers, the positioning of the teslameter probe in the cavity, and instrumental drifts in the time between spectral acquisitions and teslameter calibrations. Uncertainties in the teslameter readout (3×10⁻⁶, relative), the measured microwave frequency (<10⁻⁸, relative) and the physical constants used (<5×10⁻⁸, relative) [40] are negligible.

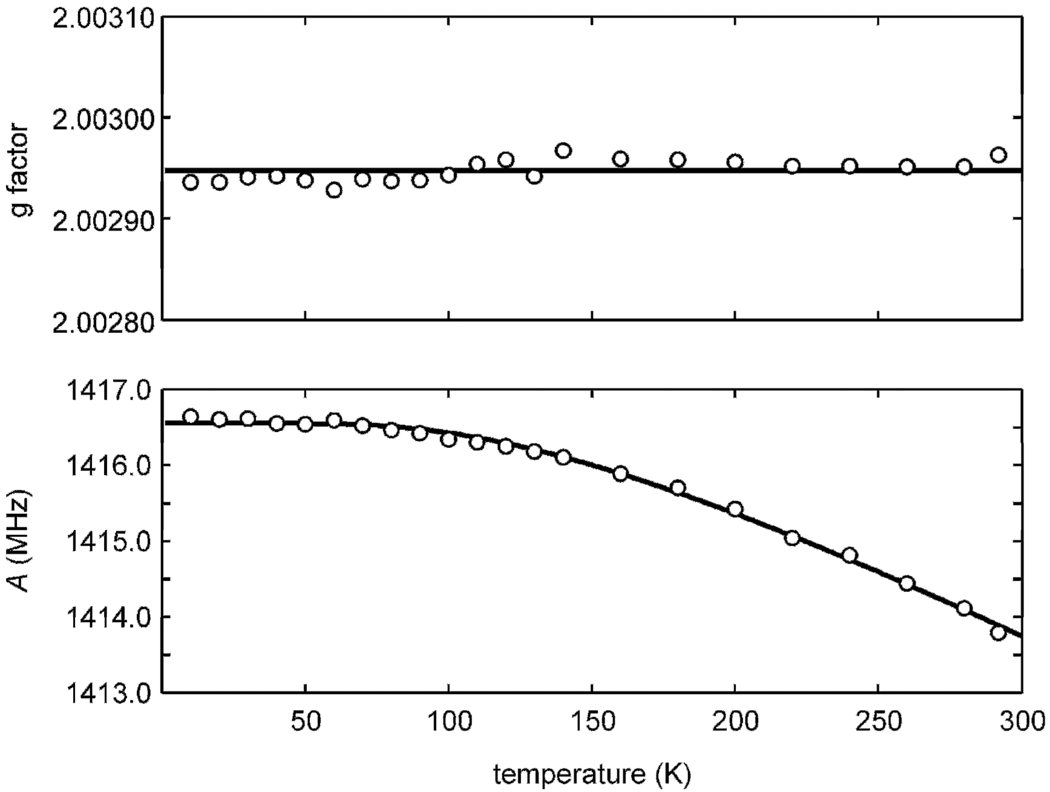
For determining the temperature dependence of g and A below room temperature, the teslameter could not be used, and the hyperfine splittings and g factors were obtained as follows. For each temperature, line centers B_1nom, B_2nom and B_0nom were determined as above. These field values were corrected using a field calibration curve B_nom vs. B_tm obtained with the teslameter at room temperature, yielding B_1tm, B_2tm and B_0tm. g and A were determined by least-squares fitting, and the g factor was again adjusted by comparison of the measured g_Li,tm to the literature value. The results are shown in Fig. 3. The values at room temperature of this temperature-dependent series coincide within experimental error with the independently measured room temperature values from above.

Fig. 3.

Temperature dependence of the g factor and the hyperfine coupling of H@iBuT₈, measured at 9.48 GHz and 1 µW. Dots: Experimental values with errors ±0.00006 for g and ±0.2 MHz for A. Lines: average of g values (2.00294), fit of three-dimensional oscillator model [39] to A values (c₀ = 0.00332, c₂ = –0.89 nm^–2, k = 5.1 N m^–1).

In our measurements, the g factor is temperature independent within experimental error. This is consistent with previous measurements on similar systems [39] and with theoretical calculations [41] that predict an increase of only about 3 ppm between 0 and 300 K. The g factor is always larger than the g value of the free hydrogen atom, 2.00228384(3) [42]. This deviation is almost entirely due to the unpaired spin partially delocalized onto the twelve oxygen atoms of the cage [41], which give a large spin-orbit contribution to the g shift (deviation of g from the free-electron value g_e = 2.0023193…). The temperature independence is due to the fact that any displacement of the hydrogen atom from the cube center will bring it closer to one group of oxygens, but at the same time take it away from another group, so the effect of spin density loss on one group is compensated by the gain on the other.

The hyperfine coupling is temperature independent within experimental error between 10 K and 70 K (1415.8(2) MHz), consistent with previous reports [39; 43]. Above 70 K, the hyperfine coupling starts to decrease noticeably with increasing temperature [35; 39] until it reaches 1413.7(1) MHz at room temperature. Across the entire temperature range, it is slightly smaller than the free hydrogen atom value (1420.405751768(1) MHz [44]). Several effects contribute to this temperature-dependent deviation. Spin delocalization from the hydrogen atom onto the cage reduces the spin density at the nucleus and consequently the hyperfine coupling, but this is partly compensated by the cage-induced compression of the hydrogen atom 1s orbital. The non-zero average displacement of the hydrogen atom from the cube center due to vibrations also reduces the hyperfine coupling compared to the free-atom value, even at zero temperature. At temperatures above about 70 K, higher vibrational states are thermally populated, and the hyperfine coupling decreases linearly with temperature [43].

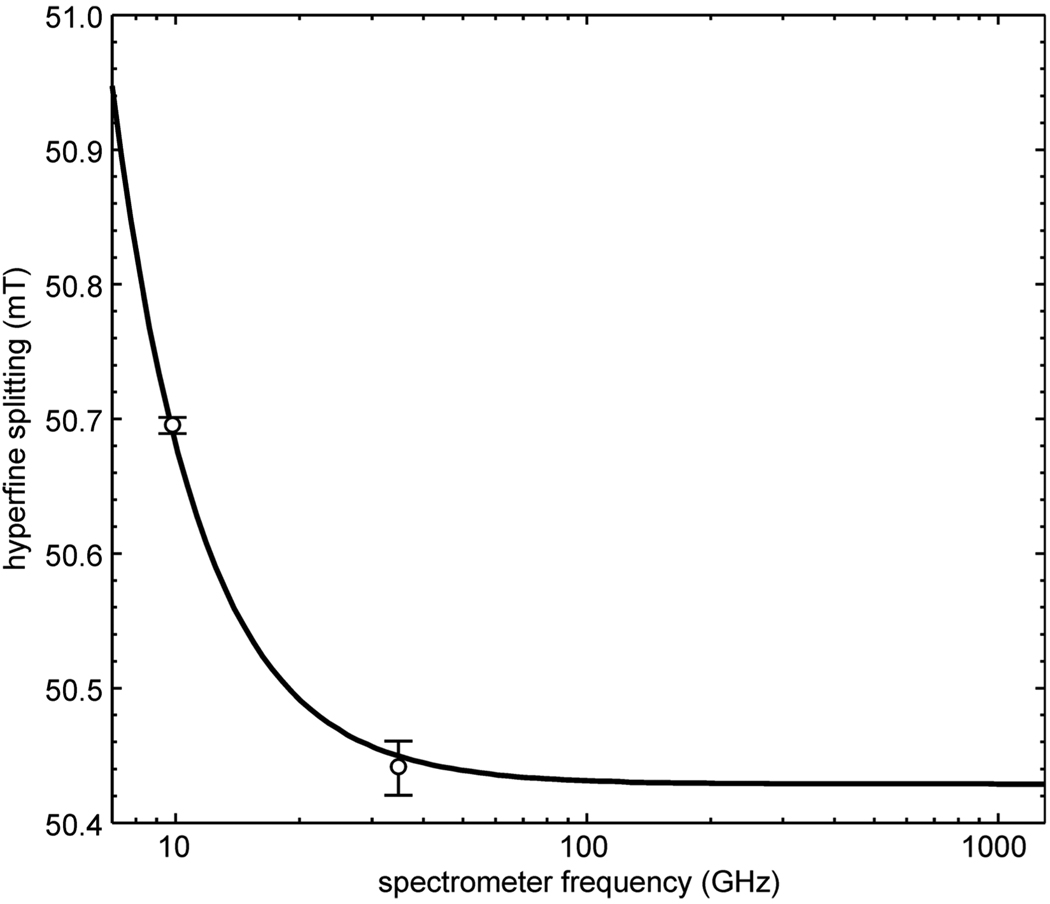
The hyperfine coupling leads to a splitting of 50.4 to 51 mT (at room temperature) depending on the spectrometer frequency, as illustrated in Fig. 4. In the high-frequency limit, it approaches its first-order value of 50.428 mT. The deviation from this value at lower frequencies is due to higher-order effects. For an accuracy of less than 3µT (10⁻⁵ relative), second-order effects are relevant below 80 GHz. Below about 20 GHz, fourth-order terms are significant as well (third-order effects are zero for spin-1/2 nuclei).

Fig. 4.

Spectrometer frequency dependence of the splitting between the two lines of H@iBuT₈. Circles with error bars: experimental values at room temperature, X and Q band. Solid line: Breit-Rabi computation with A(¹H) = 1413.7 MHz and g = 2.00294.

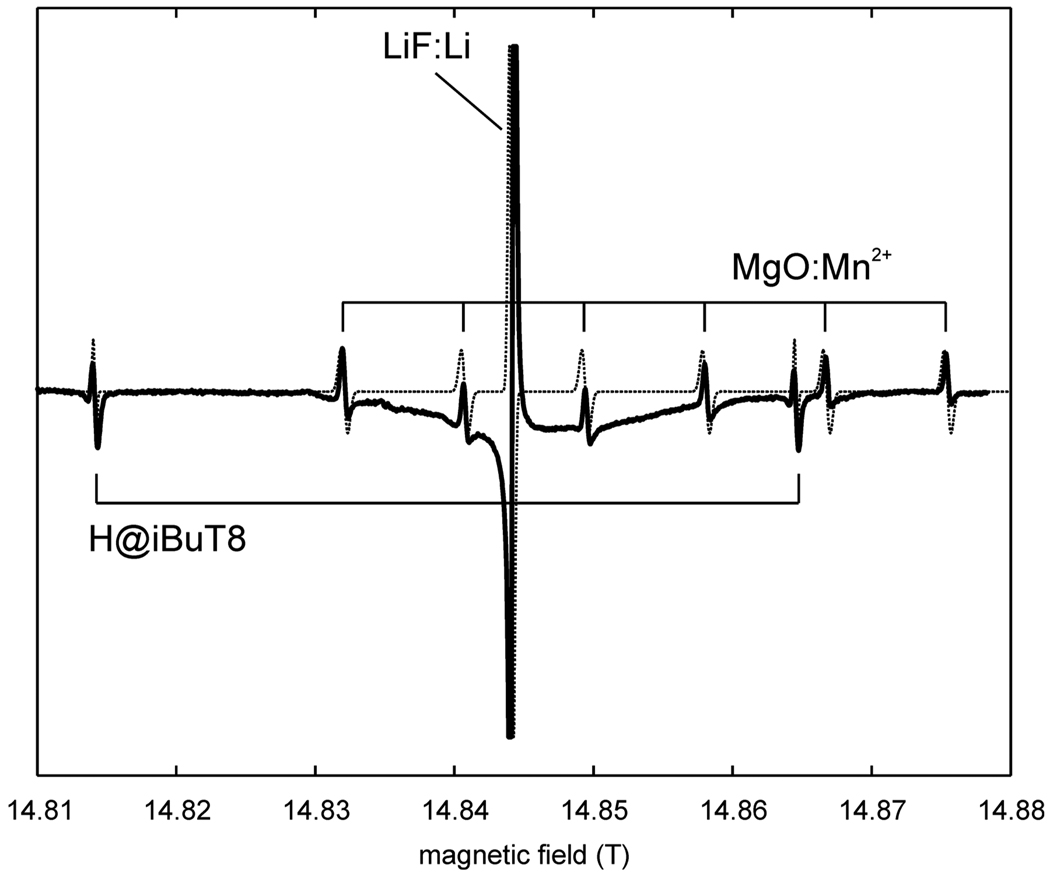
An important question is whether the g value is field independent. Since no high-precision NMR teslameters working above 1.5 T are available, this can only be assessed by comparison of the high-field spectrum of the hydrogen standard to those of other EPR standards for which parameters have also been determined at X band. Fig. 5 shows the 416 GHz spectrum of a sample containing H@iBuT₈, LiF:Li and MgO:Mn²⁺. Rapid passage effects distort the individual line shapes as if often the case in high-field EPR at cryogenic temperatures. However, the positions of all the lines could be accurately simulated using the parameters determined at X band. This shows that the magnetic parameters at X band and at high field of the three standards are internally consistent. A field dependence of the g and A values of the hydrogen standard can therefore be excluded, unless these field dependencies are identical for the three standards. This in turn is not likely given the very different chemical nature of the paramagnetic species (an isolated H atom, a transition metal ion, and a metallic nanocluster). However, further verification of the field independence above 1.5 T has to await the development of high-precision high-field NMR teslameters.

Fig. 5.

416.000 GHz spectra of H@iBuT₈, together with LiF:Li and MgO:Mn²⁺, recorded at 60 K. Sweep rate 0.1 mT/s, modulation 0.1 mT at 50 kHz. Dashed line: simulation.

With the Mn²⁺ standard, we could assess the linearity of the field sweep, which could be compromised due to hysteresis effects. The six lines are equally spaced, and they are centered at a position corresponding to the known g value. Therefore, in the range covered by the six Mn lines, the sweep is linear within experimental error. Note that this assessment is not possible with a standard with only one (LiF:Li) or two (H@iBuT₈) lines.

Apart from unresolved hyperfine splittings from distant ¹H, the lines are broadened by the inhomogeneity of the magnetic field over the sample volume in the magnet of the given spectrometer. Whereas magnets for W-band spectrometers are very homogeneous (giving LiF:Li line widths as small as 0.03 mT), magnets used for measurements above that frequency are less so. The field homogeneity in the magnet used for our 400 GHz measurements is about 0.3 mT over the sample volume which is contained in a cylinder of 2 mm diameter and 3 mm length.

Discussion

The H@iBuT₈ standard is superior to other field standards commonly employed in several respects.

Compared to the “gold” standard LiF:Li, it has broader lines, but the definite advantage that a 51 mT wide field range between its two spectral lines can be calibrated. This is not possible with the one-line standard LiF:Li.

Probably the most distinctive advantage of H@iBuT₈ over other field standards is that it can be measured simultaneously with samples containing organic radicals without overlapping their spectra. The spectra of most biological organic radicals do not overlap with the spectrum of the hydrogen standard until above 650 GHz. Only the spectra of tyrosyl radicals overlap with the low-field line of the H standard above 200–300 GHz, depending on the radical. Even if the low-field line overlaps with part of the spectrum, often the spectrometer frequency can be chosen such that it does not fall on a principal axis feature (g_x) of the spectrum. Due to the large hyperfine splitting of 51 mT, the hydrogen standard is not ideal for organic radicals at low frequencies (X and Q band), since their spectra are usually much narrower than that, and the hydrogen standard would require sweeps much wider than necessary.

Yet another advantage of the hydrogen standard is that the temperature dependences of g and A are known and well understood. In contrast, little is known about the temperature dependence of the magnetic parameters in MgO:Mn²⁺ and in LiF:Li.

H@iBuT₈ is exceptionally stable. Atomic hydrogen atoms have been trapped in many matrices at cryogenic temperatures, but only in octasilsesquioxane are they stable for years. In alkali halides they are unstable above 165 K [45], and in quartz they disappear above 100–120 K [46; 47]. In calcium phosphate their half life at room temperature is about 4 days [48]. In CaF₂ and other alkali-earth fluorides, the signals from interstitial atomic H decay within a few months [49; 50]. Endohedral ¹H atoms in fullerene C₆₀ have been elusive so far [51].

The substituent choice R (see Fig. 1) determines the solubility of the compound. Most alkyl substituted T₈ are soluble in non-polar solvents like cyclohexane and CCl₄. Hydrido-, methyl-and phenyl-T₈ are poorly soluble [28]. The substituent choice also affects the trapping yield. In hydrido-, methyl-, phenyl- and vinyl-T₈, it cannot be increased by addition of scavenger [28]. Ethyl- and propyl-T₈ give the highest yields. Our choice of isobutyl substituents maximizes the amount of substituent protons, which also maximizes the trapping yield. The many ligand protons also enhance relaxation [25], which helps avoid saturation at low temperature. By using per-deuterated substituents, the lines could be narrowed substantially. However, as the trapped hydrogen atoms are partially originating from the substituents and partially from the solvent, it is not possible to produce 100% trapped H (without any D) with perdeuterated substituents. Of course, the use of perdeuterated substituents and/or solvents will allow trapping of ²D in the silica cage [28]. This would be useful in cases where field sweep nonlinearity is an issue and overlap between the signals of the standard and the organic radical to be tested can be tolerated. One would be able to utilize up to five well-defined lines, two from H@iBuT₈ and three from D@iBuT₈ for the field calibration. Trimethylsilyl-D4R (Q₈M₈, used as standard in ²⁹Si solid-state NMR) is an alternative as well, as it gives decent trapping yields [28] and an EPR line width smaller than in H@iBuT₈, at the cost of reduced relaxation. We have not explored this.

On a side note, it is not by chance that the two most reliable g = 2 field standards are based on hydrogen (H@RT₈) and Li (LiF:Li): They are the lightest elements and have very small spin-orbit coupling constants, so that their g shifts are very small.

A class of compounds giving spectra similar to the hydrogen standard are fullerenes encapsulating atomic nitrogen or phosphorous with S = 3/2. However, the hyperfine splittings due to the trapped nuclei, 0.74 mT for ¹⁵N@C₆₀ [52; 53] and 4.92 mT for ³¹P@C₆₀ [54–56], are much smaller than the 50–51 mT observed for the hydrogen standard. Therefore, although endohedral fullerenes could be used as field standards, they do not offer the advantage of not overlapping with the high-field spectra of organic radicals.

Examples

To illustrate the utility of H@iBuT₈, we show two examples of spectra recorded at >400 GHz.

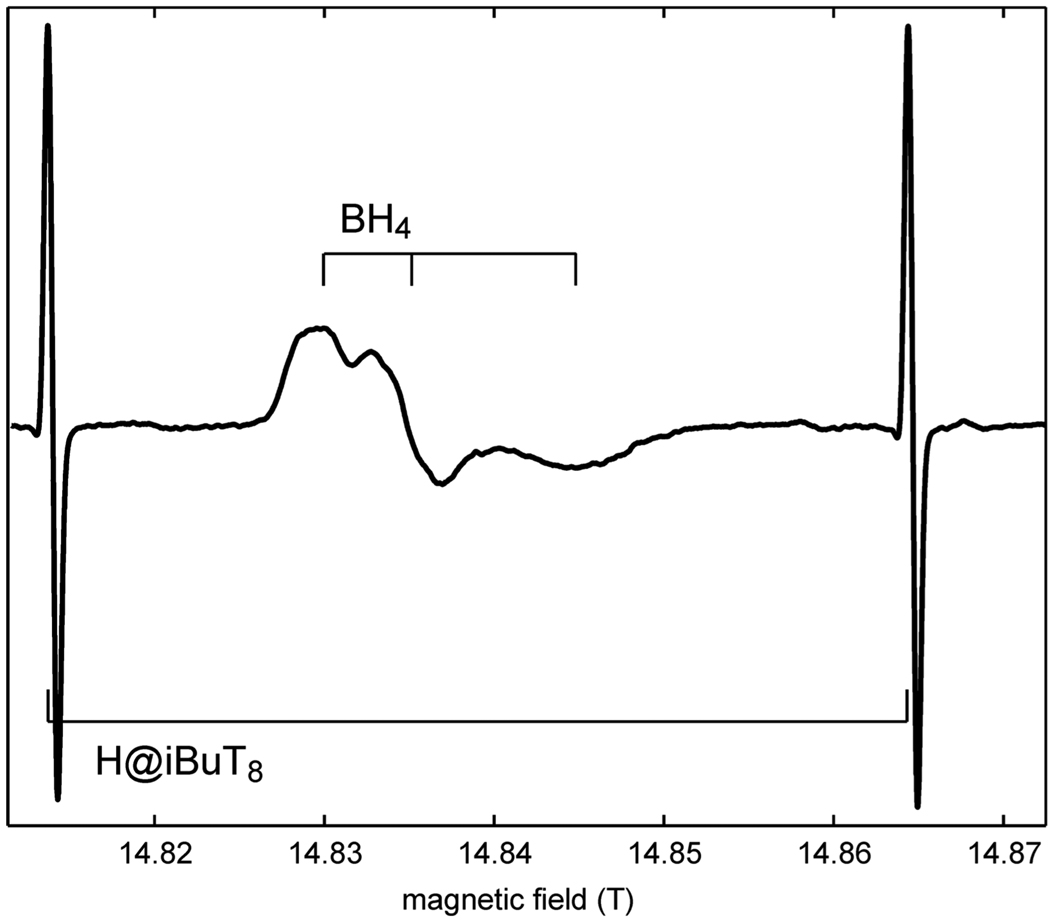
Fig. 6 shows the spectrum of the freeze-quenched transient tetrahydrobiopterin cofactor radical observed during turnover in nitric oxide synthase [57]. This cofactor acts as a reversible electron donor to the heme active site. The hydrogen standard lines frame the radical spectrum without overlapping with it. The g tensor is rhombic, and with the help of the hydrogen standard the principal values were determined as 2.00430(5), 2.00353(5) and 2.00210(9), values very similar to those of anionic flavin radicals (e.g. [58; 59]). From these accurate g values, the protonation state of the cofactor can be determined [60]. Apart from the g anisotropy, the spectrum is broadened due to several unresolved ¹H and ¹⁴N hyperfine couplings.

Fig. 6.

cw EPR spectrum of the tetrahydrobiopterin (BH₄) radical in the heme domain of inducible nitric oxide synthase (iNOS), measured at 416 GHz and 50 K, sweep rate 0.021 mT/s, modulation 10 mA at 50 kHz.

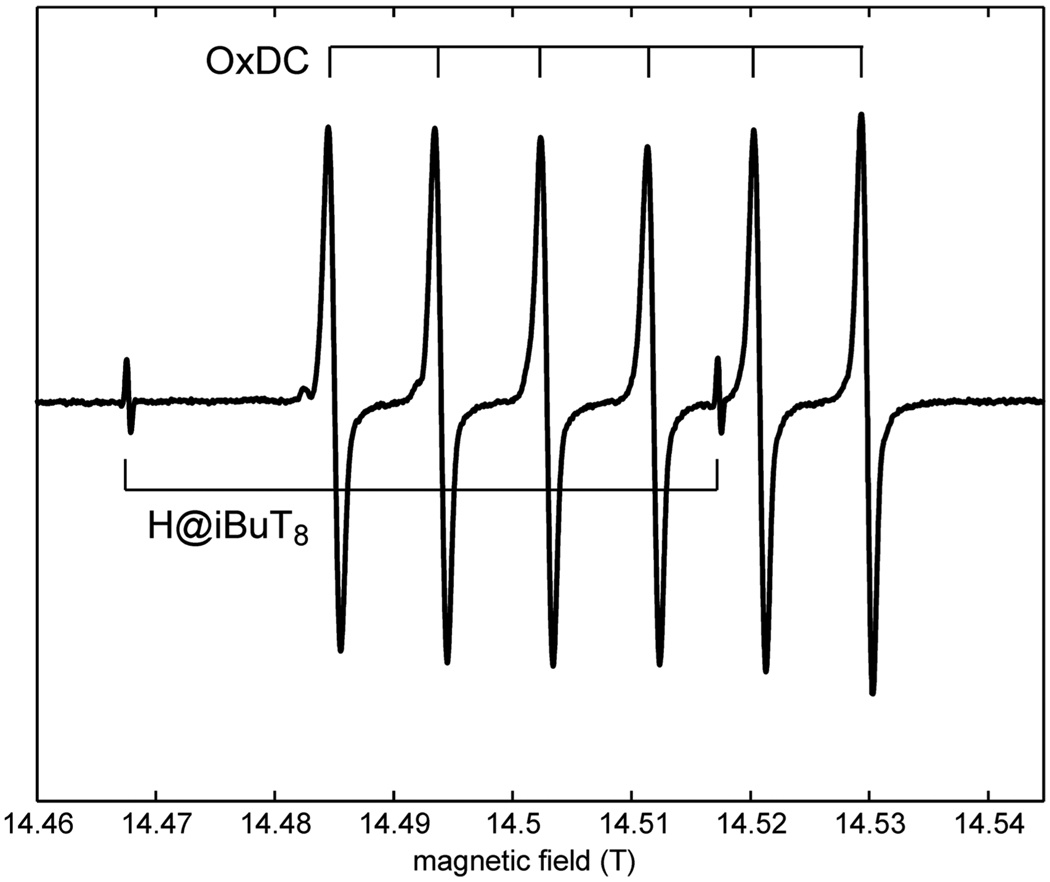
The second example, in Fig. 7, shows the spectrum of oxalate decarboxylase, a Mn-dependent bicupin enzyme. It contains two distinct Mn-binding sites both of which have to be populated for enzymatic activity [61]. High-field EPR has revealed a remarkable number of distinct Mn(II) species dependent on pH and buffer conditions [62; 63]. The obvious advantage of using the H@ iBuT₈ standard in this case over the commonly used Mn(II) standard lies in the fact that it shows only little overlap with the spectrum of interest. By a proper choice of the field/frequency combination the high-field line of the standard can be made to appear between the Mn(II) hyperfine lines as seen in Fig. 7.

Fig. 7.

cw EPR spectrum of oxalate decarboxylase (OxDC) in piperazine buffer at pH 6.3, measured at 406.4 GHz and 20 K, sweep rate 0.1 mT/s, modulation 0.05 mT at 50 kHz.

Conclusions

Atomic hydrogen trapped in octaisobutylsilsesquioxane is an excellent precision internal field standard for high-field EPR since (1) its EPR spectrum has two (and not one) lines allowing the calibration of the field range between the two lines, (2) its two lines are centered at g ≈ 2 and separated about 51 mT and do therefore not overlap with spectra of most organic radicals at high field, (3) its EPR spectrum depends only on two isotropic parameters (g and A) whose values and temperature dependences are accurately known, (4) it can easily be prepared and is a stable solid. A disadvantage of H@iBuT₈ is that it cannot be used to assess field sweep linearity because it only shows two lines. However, this can be easily remedied by the use of a perdeuterated solvent during γ-irradiation.