ADAPTIVE INCREASE IN FORCE VARIANCE DURING FATIGUE IN TASKS WITH LOW REDUNDANCY

Abstract

We tested a hypothesis that fatigue of an element (a finger) leads to an adaptive neural strategy that involves an increase in force variability in the other finger(s) and an increase in co-variation of commands to fingers to keep total force variability relatively unchanged. We tested this hypothesis using a system with small redundancy (two fingers) and a marginally redundant system (with an additional constraint related to the total moment of force produced by the fingers). The subjects performed isometric accurate rhythmic force production tasks by the index (I) finger and two fingers (I and middle, M) pressing together before and after a fatiguing exercise by the I finger. Fatigue led to a large increase in force variance in the I-finger task and a smaller increase in the IM-task. We quantified two components of variance in the space of hypothetical commands to fingers, finger modes. Under both stable and unstable conditions, there was a large increase in the variance component that did not affect total force and a much smaller increase in the component that did. This resulted in an increase in an index of the force-stabilizing synergy. These results indicate that marginal redundancy is sufficient to allow the central nervous system to use adaptive increase in variability to shield important variables from effects of fatigue. We offer an interpretation of these results based on a recent development of the equilibrium-point hypothesis known as the referent configuration hypothesis.

Introduction

Fatigue leads to a decreased ability to produce high force and increased variability of performance [4,5]. However, goal-relevant features of performance may be relatively preserved during fatigue in tasks with redundant sets of elements [1,8,10]. In a recent study [17], we showed that fatigue of a finger leads to higher force variance in all the fingers of the hand during four-finger accurate force production tasks and an increase in co-variation of finger forces across trials such that variance of their total force shows little change. We interpreted this result as pointing at an adaptive neural strategy available due to the motor redundancy of the four-finger system (cf. the lack of such effects in a study with fatigue of all four fingers [10]). In this study, we explored whether the central nervous system (CNS) can use this strategy in a system with smaller redundancy (two fingers) and in a “marginally redundant” system. The latter term reflects a task that has the same number of constraints as the number of elements (so, formally, the system is non-redundant); however, since each constraint is not absolute and allows a degree of variability, there is still an infinite number of possible solutions to such tasks [13].

We used the framework of the uncontrolled manifold (UCM) hypothesis [15,16] to quantify force stabilizing synergies in two-finger accurate force production tasks. According to the UCM hypothesis, the CNS acts in a state space of elemental variables and selects in that space a sub-space (UCM) corresponding to a value of a salient performance variable. Then, the CNS tries to limit variance orthogonal to the UCM (V_ORT) while allowing relatively large variance within the UCM (V_UCM). Effects of changes in the variables within the UCM cancel each other such that the total output remains constant. To quantify synergies, we used an index reflecting the difference between V_UCM and V_ORT [14].

Taken together, the cited studies of the effects of fatigue of an element on performance of a multi-element system suggest that an adaptive neural strategy may involve an increase in variance of non-affected elements with a simultaneous increase in the relative proportion of V_UCM in the total variance. Our first hypothesis is that this strategy will be present even in a task with low redundancy, two elements and one constraint. Such a strategy is by definition unavailable in a non-redundant system, because in such a system UCM is a point and V_UCM = 0. We used two-finger accurate force production as the primary task (redundant, two elemental variables and one constraint) and added a constraint on the moment of force produced by the fingers in a frontal plane [19]. Formally, adding this constraint turns the task into a non-redundant one (two elements and two constraints) although, as mentioned above, the task is rather marginally redundant and allows an infinite number of solutions within a certain error margin. We hypothesized that adding the moment constraint would significantly impair or even eliminate the ability of the CNS to use the mentioned adaptive strategy to fatigue of the index finger.

Materials and Methods

Twelve right-hand dominant participants (eight males) with the age 27.5±4.9 years (mean ± standard deviation), mass 72.3 ± 9.88 kg, and height 1.75 ± 0.09 m participated in the experiment. All participants gave informed consent according to the procedures approved by the Office for the Research Protections of the Pennsylvania State University.

Two setups were used. The first setup (the stable setup) used two unidirectional piezoelectric force sensors (model 208C02; PCB Piezotronic Inc., Depew, NY, USA) that measured the vertical forces produced by the index and middle fingers of the right hand. The two force sensors were placed within an aluminum frame in a groove on a wooden board (Figure 1). In the second setup (the unstable setup) the two sensors were positioned along the two parallel slots (60 mm long) on a Plexiglas plate (150 × 250 mm). There was a groove (120 mm long) underneath the Plexiglas plate parallel to the slots and positioned between them. An aluminum inverted-T-shape bar (110 mm long) was fixed onto the top of the table. The vertical end of the bar was sharpened to reduce the friction when it was fitted into the groove under the Plexiglas plate to act as a pivot. During the experiment, the participants sat in a chair facing the test table with the right upper arm at approximately 45° of abduction in the coronal plane and approximately 45° of flexion in the sagittal plane. The elbow was flexed at approximately 135°. The forearm was strapped to the wooden board with three sets of Velcro straps. A custom-fit support object was placed underneath the palm to help maintain a constant configuration of the hand and fingers. The subject’s hand formed a dome-like structure with all the finger joints slightly flexed. Participants selected comfortable thumb positions during the experiment. A computer monitor was located approximately 0.65 m away from the subject. The non-task fingers, ring (R) and little (L), were taped together to avoid uncontrolled changes in their position; they never touched any external object. In all the tests, the participants were given feedback on the force produced by the instructed finger(s), by a constantly updating plot of the force magnitude (y-axis) against time (x-axis). The data were sampled at 200 Hz.

Figure 1.

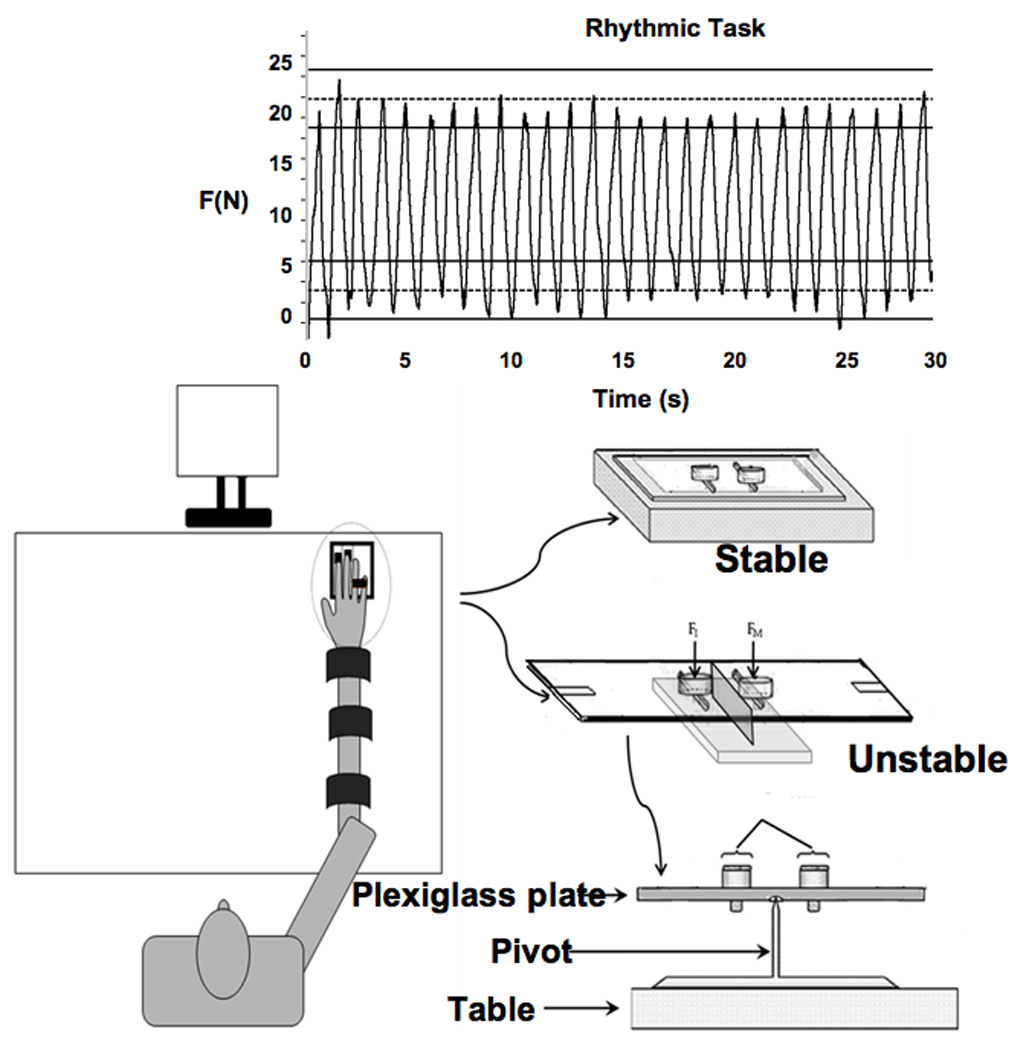
The stable and unstable experimental setups. The upper drawing shows a typical trial within the rhythmic two-finger force production task.

The experiment was run over two successive days. On the first day, the participants were familiarized with the protocol and practiced the accurate rhythmic force production task (described later; see Figure 2).This was done to minimize possible learning effects during the main experiment on the second day. No fatiguing exercise was performed on the first day.

Figure 2.

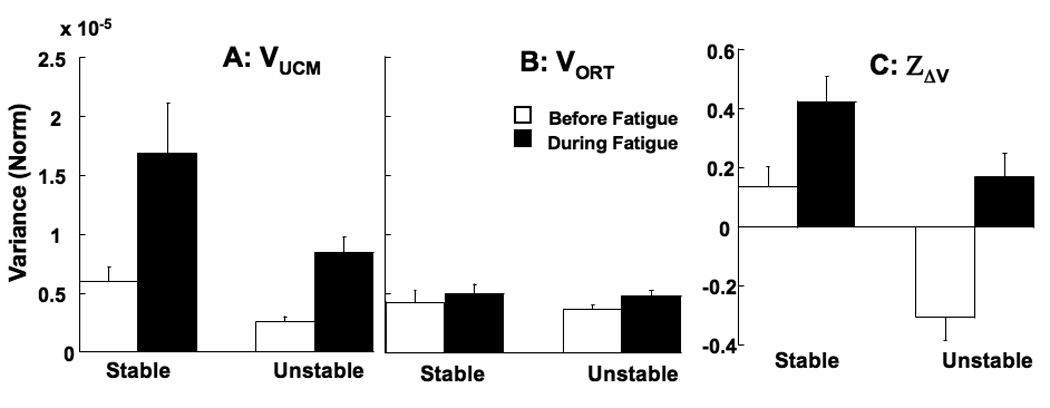
The effects of fatigue on the variance components and synergy index. The amounts of variance within the UCM (V_UCM, A) and orthogonal to the UCM (V_ORT, B) in the finger mode space are shown for the stable and unstable setups. Z-transformed index (Z_ΔV) of the force-stabilizing synergy is shown in panel C. The before-fatigue values are shown as white bars and during-fatigue as black bars. Mean data across the subjects are shown with standard error bars. Note the large increase in V_UCM during fatigue reflected in the higher Z_ΔV.

On day two, several tests were performed. During the maximal voluntary contraction (MVC) trials the participants were required to produce MVC by each of the two task fingers, index (I) and middle (M), and two fingers together (IM). The subjects were asked to relax the two non-task fingers and avoid extending them during any of the tasks. The order of the three MVC tasks was randomized across participants. There were one-minute intervals between trials.

During the one-finger ramp trials, the participants were asked to produce a force profile matching the template on the screen by trying to press with one of the fingers. The template had zero force for the first 5 s and then a slanted line from 0% to 40% MVC over the next 10 s. Participants were instructed not to pay attention to any force production by the other finger and no feedback on force produced by that finger was provided. The data from these trials were used to compute the enslaving matrix E (described later) that was used in the analysis of synergies. There was one trial for each finger, and the order of these trials was randomized across participants. There was a 10-s interval between trials.

During the rhythmic force production, the screen showed two horizontal targets placed at 10% (±3%) and 30% (±3%) of MVC (see Figure 1). The task was to change force profile in a smooth, sine-like fashion in such a way that the crests and troughs lied within the target range. The participants were paced by a metronome at 0.9 Hz. This frequency was selected based on an earlier study [7]. Each trial was 30 s in duration, and three trials were performed for each condition. There were 10-s intervals between trials within a series, and 2-min intervals between series. This task was performed using both fingers on the stable setup (IM_S) and unstable setup (IM_U). The order of the series, IM_S and IM_U, was balanced across participants.

The fatiguing protocol involved a 1-min MVC exercise by the I finger. The “during-fatigue” testing session was identical to the “before-fatigue” session except that additional 20-s MVC fatiguing exercises were performed after each trial [15].

The data were filtered using a second-order zero-lag Butterworth filter with a cutoff frequency of 10 Hz. Peak force (MVC) was measured at the time when the force produced by the task finger(s) reached a maximum. The enslaving matrices (E) were computed for each subject based on the single-finger ramp trials [17]. Each 2×2 E contained regression coefficients for the linear regression between total force and individual finger forces run for each one-finger ramp trial. E was used to convert finger force data into finger mode data in the analysis of synergies [2]. For the rhythmic task, the force data were segmented into the periods of force increase and force decrease as described in earlier publications [7,17]. The start and end of the segments were defined as the times of successive dF/dt = 0. Of the total of over 3850 force cycles analyzed only 6 segments were rejected because the force did not cross the midline. In addition, we rejected segments where the start or end of segment was more than 15% MVC away from the target force or more than 20% of a cycle period away from the metronome tick, as in earlier studies [7, 17]; on average, this resulted in rejecting 3–5% of trials per participant. Each accepted trial was resampled into 100 points using cubic spline interpolation.

The RMS error was computed with respect to the average (across trials) performance. The RMS error was computed at each of the 100 resampled points and then averaged over the 100 points to get a total RMS value Each RMS value was then normalized by 20% of the MVC of the task finger(s) (mid-point of the force range). We also computed the normalized variance in the force, Var(F), produced by the individual fingers in the two-finger tasks. We normalized Var(F) by the squared MVC force of the individual fingers.

The analysis of two-finger synergies stabilizing the total force profile in the IM tasks was performed within the framework of the UCM hypothesis [13–15]. Individual finger forces co-vary because of the phenomenon of enslaving, i.e. unintended force production by fingers when other fingers of the hand produce force [9,18]. Hence, finger modes were used as elemental variables [2,18]. The finger mode variance across trials was quantified within two subspaces, one corresponding to a fixed value of the total force (V_UCM) and the other leading to changes in the total force (V_ORT). A synergy index, ΔV was computed as:

$$\mathrm{\Delta }V=\frac{V_{\mathit{\text{UCM}}}-V_{\mathit{\text{ORT}}}}{V_{\mathit{\text{TOT}}}}$$ (1)

where V_TOT is total variance; all variance indices were computed per degree of freedom. The index ΔV ranges between 2 (V_ORT = 0) and −2 (V_UCM = 0). For statistical analysis, the ΔV values were transformed using a Fisher’s z-transformation adapted to the boundaries of ΔV:

$$Z_{\mathrm{\Delta }\mathrm{V}}=0.5\text{ln}(\frac{2+\mathrm{\Delta }V}{2-\mathrm{\Delta }V})$$ (2)

This analysis was done separately for the force-up and force-down segments.

All statistical analysis was done in the software package R. Standard descriptive statistics were used (mean ± standard error). ANOVAs with repeated measures were run on the outcome variables with factors fatigue-condition (before-fatigue and during-fatigue), fingers (I, M, and IM), direction (up and down) and task-condition (stable and unstable). Level of significance was set at α = 0.05. Bonferroni’s corrections were used.

Results

After fatigue, MVC force of each finger and the IM combination dropped. These changes were significant according to two-way ANOVA with repeated measures with fatigue-condition and fingers as factors. There were main effects of both fingers (F_(2,22) = 92.58; p < 0.001) and fatigue-condition (F_(1,11) = 67.68; p < 0.001). The interaction effect was also significant (F_(2,22) = 7.88, p < 0.01). Post-hoc t-tests with Bonferroni corrections yielded significant effect of fatigue for I (p < 0.001), M (p < 0.001) and IM (p < 0.001). The interaction reflected different effects of fatigue across the fingers as reflected by the 36.8% drop in MVC of the I finger and only the 20.5% drop in MVC of the M finger.

Comparisons between the stable and unstable setups yielded no significant effects of task-condition on any of the outcome variables. Therefore, results of reduced two-way ANOVAs with fatigue-condition and direction as factors are mostly presented. Fatigue caused the RMS error for the IM condition to increase, on average, by about 6.7%. The RMS error for the force-up direction was higher than for the force-down direction by about 14.8%. The effects of fatigue (F_(1,11) = 4.94, p < 0.05) and direction (F_(1,11) = 26.04, p < 0.001) were significant. The two-way interaction was also significant (F_(1,11) = 6.76, p < 0.05) reflecting the fact that fatigue increased the RMS error for the force-up direction significantly (13.2%; p < 0.001) without a significant effect for the force-down direction.

Fatigue increased the variance of both I and M finger forces in the IM task, by about 60% and 30% respectively. Var(F) was higher for the force-up compared to the force-down direction. The ANOVA on Var(F) for the I finger showed significant main effects of fatigue-condition (F_(1,11) = 7.62, p < 0.05) and direction (F_(1,11) = 16.02, p < 0.01) and a significant interaction (F_(1,11) = 7.05, p < 0.05). The interaction reflected larger effects of fatigue on Var(F) for the force-up direction. For the M finger, a two-way repeated measures ANOVA on Var(F) with the same factors showed significant effects of fatigue-condition (F_(1,11) = 5.26, p < 0.05) and direction (F_(1,11) = 11.21, p < 0.01) without an interaction.

Fatigue led to an increase in V_UCM by about 200% while V_ORT increased, on average, only by about 23% (Figure 2A, B). The significantly higher increase in V_UCM was confirmed by three-way repeated measures ANOVA on variance with fatigue-condition, direction and variance-type (V_UCM and V_ORT) as factors. We found a main effect of fatigue-condition (F_(1,11) = 7.60, p < 0.05) and variance-type (F_(1,11) = 5.20, p < 0.05). The interaction between fatigue-condition and variance-type was significant (F_(1,11) = 7.83, p < 0.05). This interaction reflected the fact that fatigue increased V_UCM more than V_ORT. The interaction between fatigue-condition and direction approached significance (F_(1,11) = 3.77, p = 0.08).

The disproportionate effects of fatigue on the two variance indices were reflected in a significant increase of the log-transformed index of force stabilizing synergy, Z_ΔV (Figure 2C). Before fatigue, averaged across the whole cycle and the two setup conditions, Z_ΔV = −0.08±0.06 (average ΔV = −0.14±0.10) while during fatigue Z_ΔV increased to 0.29±0.06 (ΔV = 0.50±0.10). ANOVA on Z_ΔV with fatigue-condition and direction showed a main effect of fatigue-condition (F_(1,11) = 26.57, p < 0.001). None of the other effects were significant.

Discussion

The main result of the study is the increase in the index of force-stabilizing synergy in all conditions after fatiguing exercise performed by the I finger. The substantial increase in finger force variance after fatigue was accompanied by an increase in co-variation of commands (modes) to the fingers such that variance of the total force increased only slightly. Hence, our first hypothesis on an adaptive CNS strategy to fatigue [17] has been confirmed for tasks with minimal redundancy (two-finger force production) and even with marginal redundancy. The finding of a comparable change in the variance components and synergy index in the marginally redundant condition speaks against our second hypothesis. It suggests that the natural margin of error in an apparently non-redundant task gives the system enough flexibility to use the mentioned adaptive strategy. Taken together with the reported lack of such effects when all the fingers are fatigued [10] the results show that marginal redundancy is sufficient and necessary to allow the CNS to use adaptive increase in variability to shield important variables from effects of fatigue. Since absolute constraints do not exist in natural movements, the demonstrated adaptive strategy turns into a universal method of protecting accuracy of movements from detrimental effects of fatigue affecting one (or a few) of the involved elements.

The exercise by the index finger resulted in a MVC drop in the non-exercised, middle finger. This result is not unexpected [3,17]; likely, it reflects the fact that the two fingers share the same multi-tendon extrinsic flexor muscles. We view this factor as strengthening our main conclusion since, even when both fingers showed signs of fatigue, there was increased negative co-variation of commands to the fingers in both low redundancy and marginal redundancy tasks.

We would like to offer an interpretation of the results within the recently developed scheme that combines the idea of synergies with the referent configuration (RC) hypothesis [6,11,12]. Referent configuration is a body configuration at which all the involved muscles would have achieved zero activation levels, while any deviation of actual body configuration from RC leads to non-zero muscle activation. At an equilibrium, actual body configurations commonly deviate from RC because of external forces (including gravity) and/or constraints that may be imposed by external objects (such as rigid obstacles preventing motion of body parts) and the body anatomy. Within the referent configuration hypothesis, the controller uses neural variables (subthreshold depolarization of neuronal pools) to specify a time profile of referent values for salient performance variables. Such a time profile at an upper level of a hypothetical hierarchy maps on a redundant sets of elements at a lower level; this set is organized to facilitate co-variation of elemental variables that stabilizes the performance. Within this scheme, variance of a performance variable is defined primarily by variance in setting its referent values at the upper level of the hierarchy. If performance of one of the elements at the lower level is impaired (shows high variance) due to fatigue, redundancy is vital to mitigate effects of these changes on performance of the whole system. However, the degree of redundancy may not be important.

We have to admit that the study was limited to cyclic force production to avoid performing multiple trials after fatigue; this, however, limits the interpretation of the results because of the documented differences in synergy organization between cyclic and discrete tasks [7].

Research highlights.

Motor redundancy protects important variables from detrimental effects of fatigue;

Fatigue leads to an increase in the relative amount of “good variability”;

Marginal redundancy is sufficient to show neural adaptations to fatigue;

Results can be interpreted within the referent configuration hypothesis.

Abbreviations

UCM

uncontrolled manifold

MVC

maximal voluntary contraction

CNS

central nervous system

I

index

M

middle