Quinidine interaction with Shab K⁺ channels: pore block and irreversible collapse of the K⁺ conductance

Abstract

Quinidine is a commonly used antiarrhythmic agent and a tool to study ion channels. Here it is reported that quinidine equilibrates within seconds across the Sf9 plasma membrane, blocking the open pore of Shab channels from the intracellular side of the membrane in a voltage-dependent manner with 1:1 stoichiometry. On binding to the channels, quinidine interacts with pore K⁺ ions in a mutually destabilizing manner. As a result, when the channels are blocked by quinidine with the cell bathed in an external medium lacking K⁺, the Shab conductance G_K collapses irreversibly, despite the presence of a physiological [K⁺] in the intracellular solution. The quinidine-promoted collapse of Shab G_K resembles the collapse of Shaker G_K observed with 0 K⁺ solutions on both sides of the membrane: thus the extent of G_K drop depends on the number of activating pulses applied in the presence of quinidine, but is independent of the pulse duration. Taken together the observations indicate that, as in Shaker, the quinidine-promoted collapse of Shab G_K occurs during deactivation of the channels, at the end of each activating pulse, with a probability of 0.1 per pulse at −80 mV. It appears that when Shab channels are open, the pore conformation able to conduct is stable in the absence of K⁺, but on deactivation this conformation collapses irreversibly.

Introduction

Quinidine is an alkaloid widely used in clinical cardiology as an antiarrhythmic agent. Quinidine inhibits both Na⁺ and cardiac K⁺ channels, thus affecting both the surge and duration of the cardiac action potential (Roden, 1996). In addition to its clinical use, quinidine (hereafter also referred to as Qd) is also a valuable tool for studying ion channels. Specifically, with regard to K⁺ channels, mechanistic studies of Qd block have been carried out with both Drosophila (Kraliz et al. 1998) and mammalian channels (e.g. see Fishman & Spector, 1981; Nattel & Bailey, 1983; Yatani et al. 1993; Clark et al. 1995; Snyders & Yeola, 1995; Fedida, 1997; Zhang et al. 1998; Caballero et al. 2003; Wang et al. 2003).

Although, Qd is quite unspecific in a broad sense, in terms of Drosophila K⁺ channels it is commonly considered that at micromolar concentrations Qd specifically inhibits Shab channels (e.g. see Singh & Wu, 1989; Kraliz et al. 1998; Singh & Singh, 1999; Gasque et al. 2005; Ueda & Wu, 2006; Frolov et al. 2008). In particular, this work arose from the chance observation that blocking Shab with Qd in the absence of K⁺ only in the external solution (i.e. with physiological K⁺ in the intracellular solution) irreversibly undermined the capability of the channels to conduct K⁺.

Based on the literature regarding the crucial role of K⁺ in the stability of the conductance (G_K) of K⁺ channels (see later), and more specifically in a previous work regarding the irreversible effects of intracellular TEA on the activity of the squid K⁺ channel (Khodakhah et al. 1997), it was suspected that this unexpected, irreversible consequence of Qd block of Shab had to arise from the interaction between Qd and pore K⁺ ions, which should affect K⁺ occupancy of the pore, bringing the latter to a state in which G_K collapses.

It is known that in addition to permeating through the channels K⁺ ions modulate K⁺ channel gating. For example, K⁺ distribution across the membrane strongly determines both entry and recovery rates from inactivation (e.g. see Pardo et al. 1992; Lopez-Barneo et al. 1993; Baukrowitz & Yellen 1995, 1996; Jäger et al. 1998; and for a recent review see Kurata & Fedida (2006) and references cited there). Additionally, it is known that K⁺ ions are also critical to maintain the stability of several K⁺ conductances (i.e. to maintain K⁺ channels in a conformation capable of conducting). For example, K⁺ conductance of both the squid K⁺ channel and the Drosophila Shab channel irreversibly collapses when the channels are placed in 0 K⁺ (no added K⁺) solutions on both sides of the membrane. Interestingly, in both cases G_K drops passively (i.e. while the channels are maintained undisturbed (closed) at the holding potential) during exposure to K⁺-free solutions, indicating that the stabilizing K⁺ easily dissociates from the channels.

Shaker B is another channel whose conductance collapses in 0 K⁺. However, in contrast to the related Shab channels, Shaker G_K does not drop passively in 0 K⁺, but if channels are gated, with the delivery of activating pulses, then G_K collapses. The extent of drop depends on the number of pulses delivered in 0 K⁺ and is fully reversed by prolonged depolarizations.

It has been concluded that the collapse of Shaker G_K occurs when the channels close, at the end of each pulse. Thus, when the channels open in 0 K⁺ they are able to conduct Na⁺, but on deactivation at pulse end, conductance collapses and the channels become unable to conduct any type of ion. In other words: it appears that the K⁺ requirements for the stability of the Shaker conductance (i.e. of the conformation able to conduct) are different when the pore is conducting (open) from when the channels deactivate (Chandler & Meves, 1970; Almers & Armstrong, 1980; Melishchuk et al. 1998; Ogielska & Aldrich, 1998; Loboda et al 2001; Gomez-Lagunas, 1997, 2001, 2007; Ambriz-Rivas et al. 2005).

Studies on the stability of G_K also indicate that K⁺ channels are not uniform regarding the amount of K⁺ that they require to remain functional. For example, Shaker G_K is completely stable (remains constant) for at least 1 h in the absence of only external K⁺ (in Na_o/K_i solutions). However, under the same conditions, Shab G_K decays steadily although slowly (dropping ∼15–20% after 30 min of whole-cell recording) (Ambriz-Rivas et al. 2005 and references cited there), while, as mentioned previously, with 0 K⁺ on both sides of the membrane Shab G_k drops rapidly.

On the other hand, it is known that the KcsA channel adopts a non-conducting pore conformation with 2 mm K⁺ (Zhou et al. 2001b), and the Ca²⁺-activated maxi K channel remains functional and selective on exposure to 0 K⁺ (Vergara et al. 1999), while other channels such as Kv2.1 and Kv1.5 retain a conducting conformation but lose their selectivity in the absence of K⁺ (e.g. see Korn & Ikeda, 1995; Zhuren et al. 2000).

The variable [K⁺] that is required to maintain different channels functional may be physiologically important, particularly under hypokalaemic conditions and/or in the presence of clinically employed drugs that could block K⁺ channels from the cytoplasmic side of the membrane. Many of these drugs are lypophilic cations, such as the commonly used antiarrhythmic drug quinidine that, because of its charge, may interact with pore K⁺ ions, thus affecting K⁺ occupancy of the pore. Conductance then might collapse (depending on the channel), as will be demonstrated here for the case of quinidine-blocked Shab channels. To perform the latter the mechanism of Qd block of Shab will be first reviewed demonstrating that Qd indeed interacts in a mutually exclusive manner with pore K⁺ ions. After this, it will be shown that, as a consequence of this interaction, when Qd blocks Shab in the absence of only external K⁺ the channels irreversibly sink into a non-functional conformation.

Methods

Cell culture and Shab channel expression

Insect Spodoptera frugiperda Sf9 cells were grown at 27°C in Grace's medium (Gibco). Cells were infected, with a multiplicity of infection of 10, with a recombinant baculovirus containing Shab (dShab 11) K⁺ channel cDNA. Experiments were conducted 48–72 h after infection of the cells.

Electrophysiological recordings

Macroscopic currents were recorded under whole-cell patch clamp with an Axopatch 1D amplifier (Molecular Devices (Axon Instruments), Sunnyvale, CA, USA). Unless otherwise indicated, currents were filtered on-line at 5 kHz with the built-in filter of the amplifier, and sampled at 100 μs per point with a Digidata 1322A interface (Molecular Devices). Electrodes were made of borosilicate glass (KIMAX 51) pulled to a 1–1.5 MΩ resistance. Eighty per cent of the series resistance was compensated. Unless otherwise indicated the holding potential (HP) was −80 mV. Experiments were conducted at room temperature.

Solutions

Internal solutions will be identified by subscript i. The K⁺-containing solution will be simply referred to as K_i (either in control conditions or in the presence of quinidine, see Fig. 1). The K_i solution contained (in mm): K_i: 30 KCl, 90 KF, 2 MgCl₂, 10 EGTA-K, 10 Hepes-K. The Na_i solution contained (in mm): 30 NaCl, 90 NaF, 2 MgCl₂, 10 EGTA-Na, 10 Hepes-Na. External solutions will be identified by subscript o, and will be named according to their main cation and quinidine concentration (in mm), e.g. 5K_o+ 0.05Qd stand for a 5K_o solution containing 0.05 mm quinidine. The Na_o solution contained (in mm): 145 NaCl, 10 CaCl₂, 10 Hepes-Na, pH 7.2. The XK_o solution contained (in mm): X KCl, 145 –X NaCl, 10 CaCl₂, 10 Hepes-Na, where X stands for [K⁺]. The pH of all solutions was 7.2.

Figure 1. Quinidine equilibration across the membrane.

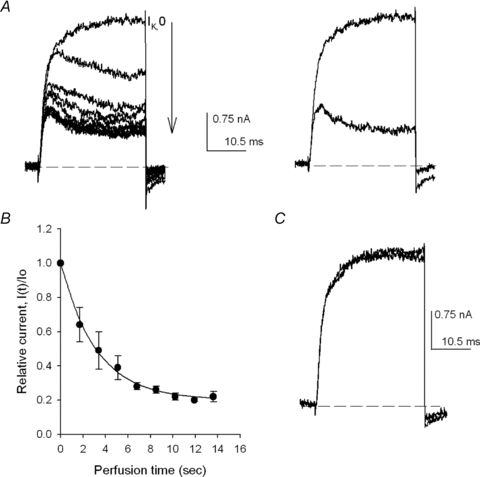
A, left panel, I_K evoked by +40 mV/30 ms pulses applied at 0.6 Hz during the perfusion of the cell with 5K_o+ 0.1Qd solution. I_K changes on each consecutive pulse (indicated by the arrow) as Qd crosses the membrane until steady-state is reached. Right panel, control I_K (largest trace) superimposed on I_K in the presence of Qd (see text). B, relative current I(t)/I_o as a function of the time of perfusion with the Qd-containing solution. I_o is the control I_K and I(t) is the amplitude of I_K, measured at pulse end, at time t of perfusion. The line is the fit of the points with the equation I(t)/I_o= 0.8 × exp(−0.31 ×t) + 0.2 (n= 4 experiments). C, recovery from block. Control I_K superimposed on I_K recorded after washing the cell for 1.25 min with the control 5K_o solution to remove Qd. HP =−80 mV.

Quinidine (sulphate salt, Sigma) was directly dissolved in the Na_o solution at stock concentrations of 1–3 mm. Exchange of solutions was carried out as reported (Gomez-Lagunas, 2007). Unless otherwise indicated, cells were immersed for 45 s in quinidine-containing solutions before activating the channels (to allow Qd equilibration across the membrane). To standardize in all cases cells were exposed to Qd-containing solutions for a total time of 1.5 min.

In the block experiments in which there was K⁺ in the external solution pulses in the presence of Qd were applied every 10 s to allow full recovery from block between pulses (not shown). Regarding the experiments performed without external K⁺, preliminary observations demonstrate that the irreversible drop of G_K is the same if activating pulses are applied every 3 or 10 s; therefore, pulses were applied every 4 s unless otherwise indicated.

Data analysis

Results are expressed as the mean ±s.e.m. of the indicated number of experiments. When necessary, Student's t test was used to evaluate statistical significance. Curves were fitted with SigmaPlot v. 8.0 software (Systat Software Inc., San Jose, CA, USA). The differential equations of the tail kinetic scheme were numerically solved and fitted to the corresponding I_K employing SCoP simulation software (Simulation Resources, Inc., Redlands, CA, USA).

After blocking the channels with Qd, a fraction of the recovered I_K derives from channels that were not blocked upon the exposure to Qd, and the remaining fraction derives from channels that were blocked but did not collapse. Therefore, the fraction collapsed, f_c, was calculated as follows:

where I_c is the control I_K, I_r is the size of I_K after Qd removal and I_q is the size of I_K recorded in the presence of Qd. In all cases I_K was measured at the end of the pulse.

Results

On exposure of the cells to a quinidine-containing external solution, the drug passively permeates across the membrane, blocking Shab channels from the intracellular side of the membrane (see later).

Passive Qd equilibration across the membrane was determined by assessing its inhibitory action on the channels, as illustrated in the left panel of Fig. 1A, which presents a Shab I_K family recorded in physiological 5K_o/K_i solutions (see Methods). I_K were evoked by +40 mV/30 ms pulses delivered every 1.7 s, in the order indicated by the arrow, during cell perfusion with a 0.1 mm Qd-containing external solution (5K_o+ 0.1Qd).

The first trace in Fig. 1A (left panel, labelled I_K,o) was recorded immediately after initiating cell perfusion. I_K,o was the last I_K that did not differ from the previously evoked control I_K (see Fig. 1C and D). Thus, when I_K,o was recorded, the [Qd] inside the cell must have been so small, if not zero, that it can be considered that I_K,o was the last current recorded under the control condition; therefore, its acquisition time was taken as time zero of cell perfusion. Once I_K,o was recorded, the subsequent I_K became progressively smaller and their kinetics changed, until a final amplitude and kinetics were attained after ∼12 s, when equilibrium [Qd] across the membrane (0.1 mm) was reached.

The time course of Qd diffusion into the cell is presented in Fig. 1B, which depicts average normalized I_K measured at the end of each pulse, as a function of the perfusion time of four experiments as in Fig. 1A. Note that, I_K decreases exponentially (line through the points) with a rate constant of 0.34 s⁻¹.

Finally, after steady sate inhibition was achieved, the cell was superfused for 30 s with the control solution. Figure 1C shows I_K recorded after washing the cell superimposed on control I_K. There was a complete recovery. However, it is noteworthy that it is not always possible to achieve a full recovery from block (see later).

The previous observations show that although Qd blocks Shab from the inside (see later), it is useless to study this process employing the inside-out patch-clamp configuration, because Qd will equilibrate within seconds across the membrane. Therefore, block was studied under the whole-cell configuration, in which Shab I_K is fairly stable (Ambriz-Rivas et al. 2005).

The traces in Fig. 1A show that I_k in the presence of Qd presents an apparent ‘inactivation’. The latter is best observed in the right panel, which presents control I_K,o superposed on a steady-state I_K in the presence of Qd (lower trace). Note that I_K in the presence of Qd rises to a peak, with kinetics equal to that of the control I_K, and then declines monotonically to a steady-state value. This indicates that Qd inhibits Shab by blocking the pore from the inside of the membrane, once the activation gate opens; this is similar to the open-pore block of K⁺ channels by TEA derivatives (Armstrong, 1971, 2003; Choi et al. 1993; Holmgren et al. 1997), and also similar to the to the open-pore block that underlies the mechanism of ball-and-chain inactivation of Shaker (for a review see Armstrong, 2003), and to the mechanism of Qd block of mammalian K⁺ channels (see Introduction).

The Qd mechanism of inhibition was further investigated by analysing deactivation tail currents. In order to facilitate the observation of inward deactivation tails with physiological 5 mm, cells with relatively high channel expression were used. Figure 2A presents a control I_K superimposed on I_K recorded in the presence of 0.05 Qd (labelled Qd), in 5K_o/K_i solutions. Due to its size the control current was elicited by a +30 mV/30 ms pulse, while I_K with Qd was evoked by a +50 mV pulse. However, because the membrane was repolarized to −80 mV at pulse end in both cases, the kinetics of their corresponding tails can be compared against each other.

Figure 2. Shab deactivation in the presence of quinidine.

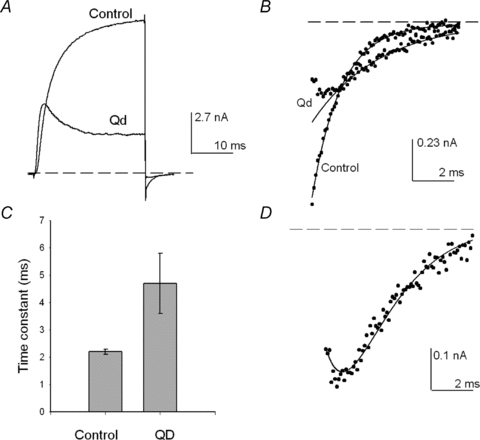
A, superimposed I_K recorded either in control solutions (5K_o/K_i) or with 0.05 Qd present, as indicated. I_K was evoked either by a +30 mV or a +50 mV pulse, respectively (see Text). B, deactivation tails at −80 mV in A shown on an expanded scale. The lines are the single exponential fit of either the control tail or the monotonically declining phase of the tail in the presence of Qd. C, comparison of the deactivation time constant of control I_K (n= 6) against the time constant of the monotonically declining phase of tails with Qd (n= 4) at −80 mV, obtained as in B. D, tail I_K in the presence of Qd in B. The continuous line is the fit of the sample points with the numerical solution of scheme 2(see text). The dotted line indicates the zero current level.

Shab deactivation is best observed in Fig. 2B, which presents the tail currents in Fig. 2A on an expanded scale. Note that while the control tail decays with its known single exponential kinetics, the tail in the presence of Qd possesses a complex time course in which, after an initial jump, I_K first increases to a peak, and thereafter decays in monotonic fashion.

The initial growing phase of tail I_K in the presence of Qd is explained as caused by the initial exit of the blocker toward the internal solution, yielding an increase in the number of open and non-blocked channels, prior to the closing of the activation gate, which produces the subsequent monotonically decaying phase of the tail, as demonstrated by the studies of TEA block of K⁺ channels (Armstrong, 1971; Choi et al. 1993; Holmgren et al. 1997). Additionally, note that the tail with Qd decays at a rate noticeably slower than that of the control. The lines are the fit of the sample points with exponential functions with τ of either 2 or 3.6 ms for the control tail or for the monotonically decaying phase of the tail with Qd, respectively. The latter is summarized in Fig. 2C, which compares the average values of the corresponding time constants. The apparent slow rate of decay of the tail with Qd indicates that the drug must dissociate itself from the pore for the activation gate to close.

The previous observations can be represented with the following kinetic scheme:

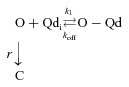In the scheme, O represents the open state of the channels, O-Qd represents the open-and-blocked state, k₁ is the pseudo-first order association rate, k_off is the first order dissociation rate, r is the normal deactivation rate of the channels (i.e. the rate observed in the absence of Qd), and C is the first closed state in the deactivation pathway.

The scheme explicitly states the Qd blocks the open pore of the channels, with a 1:1 stoichiometry (see later), and that channels deactivate after Qd dissociates from the pore. This mechanism is supported by the trace in Fig. 2D, which presents tail I_K with Qd in Fig. 2B fitted with the numerical solution of the kinetic scheme (line through the sample points) with r= 0.58 ms⁻¹, k₁= 0.001 ms⁻¹, and k_off= 0.52 ms⁻¹.

Observe that the slow rate of decay of the tail with Qd (Fig. 2C) is entirely accounted for by the Qd dissociation k_off from the open pore, because the deactivation rate r remains unchanged by Qd.

Qd interaction with Shab was further pursued by studying the block reaction under steady-state conditions, as illustrated in Fig. 3A. First, control I_K were evoked by depolarizing the membrane, from −50 to +50 mV in 10 mV steps (in 5K_o/K_i solutions, left panel). Then, the cell was superfused for 45 s with a 5K_o+ 0.1Qd solution, and I_K was activated every 10 s, to allow recovery from block between pulses, as in the control (middle traces). There was a marked inhibition. Finally, Qd was removed by washing the cell for 1.25 min with the control 5K_o solution, and I_K was recorded as before (right traces). I_K was nearly completely recovered.

Figure 3. Qd block under steady-state conditions.

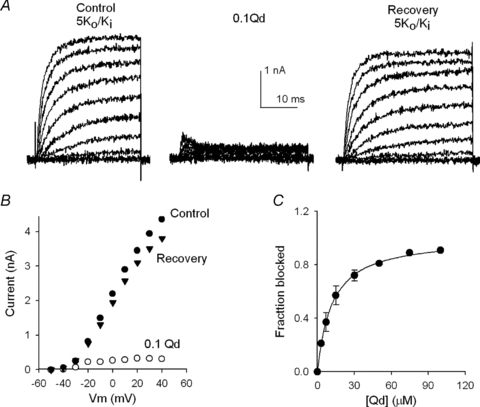
A, left panel, control I_K evoked by 30 ms pulses from −50 to +50 mV applied in 10 mV increments in 5K_o/K_i solutions. Middle panel, I_K in the presence of 0.1 Qd recorded as in the left panel. Right panel, I_K recorded after washing the cell for 1.25 min with the control 5K_o solution. B, I–V relationship of the traces in A. I_K was measured at the end of the pulses. C, fraction of channels blocked (f_b) as a function of [Qd], at +50 mV. f_b= 1 − (I_Qd/I_C), where I_Qd is the current in the presence of the indicated [Qd], and I_C is the corresponding control I_K, measured from at least 4 experiments as in A at each [Qd]. The line is the fit of the points with a Hill equation with Hill number n= 1.03, and an apparent K_d of 11.4 μm.

Qd inhibition is best observed in Fig. 3B, which presents the I–V relationship of the traces in Fig. 3A, obtained by measuring I_K at the end of each pulse. Note that Qd produces a strong rectification, indicating that block is significantly voltage dependent (see later), and that (with 5 mm) recovery from block was nearly complete.

Figure 3C presents the extent of block as a function of [Qd] at +50 mV, obtained from at least four experiments at each [Qd], as in Fig. 3A. The line is the fit of the points with a Hill equation with K_d= 11.4 μm (see Discussion), and Hill number n= 1.03, in agreement with the bimolecular mechanism of block stated in the previous kinetic scheme.

In order to determine the voltage dependence of block, apparent K_d values obtained from complete dose–response curves as in Fig. 3C, were plotted against V_m, within the range of voltages that fully activate the channels (V_m≥ 0 mV) (Gomez-Lagunas, 2007). Figure 4A demonstrates that, as expected from Fig. 3B and the literature regarding mammalian channels, Qd block of Shab is voltage dependent. The line is the fit of the points with a Woodhull equation (Woodhull, 1973) with an electrical distance δ of 0.35 and apparent K_d at 0 mV (K_d(0)) of 22.5 μm.

Figure 4. Effect of K⁺ and voltage on Qd block of Shab.

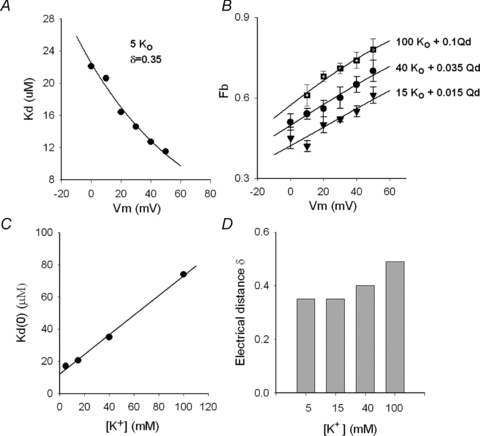
A, apparent K_d against membrane potential V_m. K_d was obtained from complete dose–response curves as in Fig. 3C. The line is the fit of the points with the Woodhul equation: K_d(V_m) =K_d(0)exp(zδFV_m/RT), with z= 1, where K_d(0) (K_d at 0 mV) = 22.5 μm, and δ= 0.35; R, T and F have their usual meaning. B, fraction blocked (f_b) vs. V_m; the points are the average block obtained with either 0.1 mm Qd plus 100 mm (n= 5) or 0.035 mm Qd plus 40 mm (n= 4) or 0.015 mm Qd plus 15 mm (n= 4), as indicated. The lines are the fit of the points with the equation f_b=[Qd]/(K_d(V) +[Qd]), with parameters,100 mm: K_d(0) = 74 μm, δ= 0.49; 40 mm: K_d(0) = 35 μm, δ= 0.40; 15 mm: K_d(0) = 20.6 μm, δ= 0.35. C, K_d(0) vs.[K⁺]_o. The line is the least-squares fit of the points with the equation: K_d(0) = (K_i/K_d,0)[K⁺]_o+K_d,0, with K_d,0 (apparent K_d for Qd at 0 mV and 0 ) = 12.2 μm, and K_i (inhibition constant of ) = 20 mm, r= 0.998; K_d(0) was obtained as the parameter of the curves in either A (5 ) or B (15, 40 and 100 ). D, electrical distance δ at the indicated [K⁺]_o; δ was obtained as the parameter of the curves in either A(5 ) or B (15, 40 and 100 ).

To determine a possible interaction between pore K⁺ ions and Qd, the effect of external K⁺ on the parameters of the Woodhull equation was determined by assessing the extent of block as a function of [K⁺]_o, from experiments as in Fig. 3.

Figure 4B presents the average extent of Qd block as a function of V_m determined at several [K⁺]. The [Qd] employed with each [K⁺] was such that a ∼40–60% blockage was obtained at the less depolarized, fully activating voltage of 0 mV. Observe that in all cases as the voltage becomes more positive, Qd block increases, in a manner that depends on [K⁺], which suggests that a fraction of the effective electrical distance δ originates from the interaction between blocker and permeant ions (e.g. see Neyton & Miller, 1988; Spassova & Lu, 1998). The results in Fig. 4B additionally suggest that as [K⁺] increases the [Qd] needed to obtain a ∼50% blockage at 0 mV also increases.

These previous observations are summarized in Fig. 4C and D, which present the variation of either K_d(0) or δ as function of [K⁺], as indicated (see figure legend). In particular, note that the apparent K_d(0) increases linearly with [K⁺]_o, with the slope of the least-squares line through the points yielding an apparent inhibition constant, K_i, of 20 mm (see figure legend). This indicates that external K⁺ affects Qd block in a manner that operationally resembles the action of a competitive inhibitor in enzyme kinetics.

Taken together the previous observations indicate that Qd interacts with pore K⁺ ions in a mutually destabilizing manner. The following experiments will demonstrate that as a consequence of this interaction when Qd blocks the pore in the absence of only extracellular K⁺ (in Na_o/K_i solutions), Shab G_K irreversibly collapses.

First, as a reference, Fig. 5A illustrates the, previously reported (Gomez-Lagunas, 2007), crucial role of K⁺ ions on the stability of Shab G_K. The figure compares I_K evoked by a 0 mV/30 ms pulse in 40K_o/Na_i solutions before (left panel), and after (labelled After) a 5 min exposure of the cell to 0 K⁺ solutions (Na_o/Na_i solutions) with the channels maintained undisturbed (closed) at the holding potential of −80 mV, as indicated by the arrow. After exposure to 0 K⁺ there is a drastic, and irreversible, reduction of I_K. For completeness, Fig. 5B compares the I_K remaining after a 5 min exposure of the channels to K⁺-free solutions, as in Fig. 5A, against the I_K left after a 25 min recording with K⁺ present on only one side of the membrane, as indicated. Note that in contrast to its behaviour in 0 K⁺ solutions, G_K is fairly stable with K⁺ present on only one side of the membrane (data from Ambriz-Rivas et al. 2005).

Figure 5. K⁺-dependent stability of G_K.

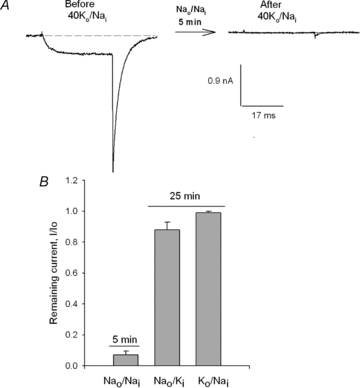
A, left panel, control I_K evoked by a 0 mV/30 ms pulse in 40K_o/Na_i solutions (see Methods). Right panel, I_K left after the immersion of the cell in, 0 K⁺ solutions (Na_o/Na_i) for 5 min, with the channels maintained closed at the HP of −80 mV during the exposure to 0 K⁺ (not shown, indicated by the arrow). B, comparison of the I_K remaining either after 5 min exposure to 0 K⁺, as in A, or after a 25 min recording with K⁺ present on only one side of the membrane, as indicated.

Figure 6 presents the observation that motivated this work: an irreversible drop of Shab G_K which was observed whenever Shab channels were repeatedly blocked by Qd in the absence of only the external K⁺ (in Na_o/K_i solutions).

Figure 6. Quinidine block in the absence of external K⁺.

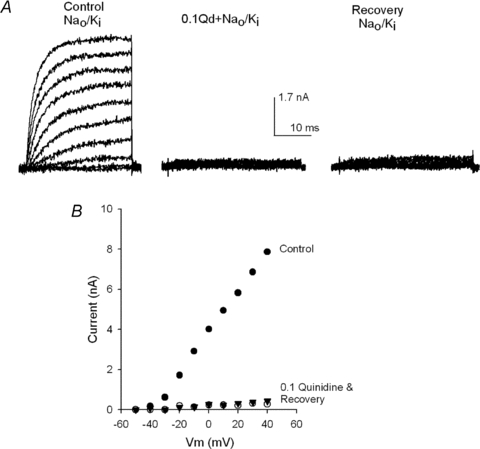
A, left panel, control I_K recorded in Na_o/K_i solutions. I_K was activated by 30 ms pulses from −50 to +40 mV in 10 mV increments. Then the cell was superfused with Na_o+ 0.1Qd solution and 45 s later three I–V pulse protocols were applied, as in the control, the middle panel shows I_K recorded on the third round of pulses. Then, after a total 1.5 min exposure to Qd, the cell was superfused for 1.25 min with the control Na_o solution, and channels were activated as in the control. G_K recovered quite poorly. B, I–V relationship of the traces in A.

In order to block Shab channels with quinidine, a family of control I_k was first recorded in standard Na_o/K_i solutions by applying pulses ranging from −50 to +40 mV in 10 mV increments (Fig. 6A, left panel). Thereafter, the cell was superfused with the Na_o solution containing 0.1 mm Qd (0.1Qd + Na_o), and the channels were activated three times as in the control (see later). The middle panel depicts I_K recorded with the third application of the pulse protocol. I_K had a reduction (∼96% at +40 mV) that was somewhat larger than expected based on the dose–response curve in the similar 5K_o/K_i solutions (Fig. 3). Finally, Qd was removed by extensively perfusing the cell for 1.25 min with the control Na_o solution, a procedure that completely removes Qd in <30 s (Fig. 1, and see later), and subsequently the state of the channels was tested, as in the control. The traces in the right panel show that, unexpectedly, there was an astonishingly poor recovery from block. The latter is best observed in the I–V relationship of the traces in Fig. 6A (Fig. 6B). The unexpected lack of recovery from block documented previously appears more striking when it is compared with the extent of recovery obtained in Figs 1 and 3 after blocking the channels in the presence of only 5 mm.

Loss of Shab G_K after blocking the channels with Qd in Na_o/K_i solutions cannot be due to incomplete removal of the blocker from either the cell and/or the channels, because if that had been the case, (a) the remaining [Qd] should have been sufficiently large to continue to block approximately the same percentage of channels that was blocked on its application (∼90%). In other words, the remaining [Qd] should have been nearly equal to the concentration that was initially applied, as if the extensive washing episode were completely unable to remove the added Qd. The latter hypothetical ineffectiveness disagrees with the ease with which Qd both dissociates from the channels (as indicated by the value of k_off in Fig. 2) and permeates across the membrane (Fig. 1, and see later). Additionally, (b) it should have been observed that I_K recovered with the passage of time after the washing episode and the continued activation of the channels. The latter was never observed in any of the cells tested in this study (≥30), as illustrated later.

Figure 7 demonstrates that the drop of G_K observed after blocking the channels in Na_o/K_i solutions is irreversible and not possibly due to the permanence of Qd either within the cell and/or in the channels, after the extensive perfusion of the cell with the control solution.

Figure 7. Qd-promoted irreversible drop of G_K.

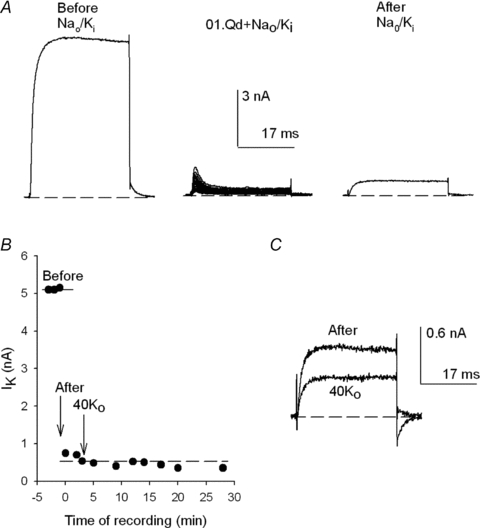
A, control I_K evoked by a +40 mV/30 ms pulse in Na_o/K_i (left panel). After the stability of I_K was tested (see B) the cell was superfused with Na_o+ 0.1Qd for 45 s and 22 +40 mV pulses were applied at 0.25 Hz (middle panel). Then, the cell was superfused for 1.25 min with the Na_o solution and channels were activated as in the control (right panel). B, I_K as a function of the time of recording of the experiment in A, as indicated. The points at t < 0 (labelled Before) are control I_K, prior to the addition of Qd. The points at t≥ 0 (labelled After) are I_K recorded after the washing episode with Na_o (i.e. after Qd removal, as in the right panel in A). At the time indicated by the arrow labelled 40K_o the cell was superfused for 1.25 min with 40K_o solution (and afterward the cell was left in this solution for the remainder of the experiment, as indicated). The dotted line serves to best show the lack of recovery of I_K. C, I_K recovered immediately after washing the cell with Na_o (After in B) superimposed on I_K at the end of the recording (in 40K_o). Addition of 40 mm did not allow the recovery of I_K.

First, control currents were evoked delivering +40 mV/30 ms activating pulses in Na_o/K_i solutions, as illustrated by the trace in the left panel of Fig. 7A (labelled Before; see also the corresponding points in Fig. 7B). Then, the cell was superfused with a 0.1Qd + Na_o solution and subsequently 22 +40 mV pulses were delivered to block the channels repeatedly (middle panel). Finally (after a total of 90 s exposure of the cell to Qd), the cell was extensively superfused for 1.25 min with the control Na_o solution, and the state of the channels was tested as in the control (right panel). Note that (a) again, there was only a scant recovery from block, and that (b) the recovered I_K does not present the time-dependent decline or apparent ‘inactivation’ that signals Qd block at +40 mV (Fig. 1). The latter kinetic feature in itself indicates that no Qd remained in the system (certainly not a sufficient amount to continue to block ∼90% of the channels). This conclusion is strongly supported by the absence of I_K recovery with the passage of time after the washing episode, as illustrated later.

Figure 7B presents the size of I_K at the end of each pulse, as a function of the time of recording after the washing episode (t= 0) of the experiment in Fig. 7A. Note that after Qd removal (i.e. after the washing episode, indicated by the arrow labelled After, at t= 0), the recovered I_K did not increase at all with the passage of time, and the repeated activation of the channels.

Further, at the time indicated by the arrow labelled 40K_o, the cell was extensively superfused for 1.25 min with an external solution containing 40 mm K⁺, and maintained there for the next ∼25 min, a procedure that should have undoubtedly removed any Qd that could have remained within the channels and/or the cell (see Fig. 8A later). Nonetheless, I_K did not increase either at all. The latter is illustrated on the right panel which shows I_K recorded immediately after the first washing episode with Na_o, superimposed on I_K with 40 mm at the end of the recording (smaller trace). In summary, these observations indicate that the drop of G_K after Qd block in Na_o/K_i solutions is irreversible and could not possibly be due to incomplete Qd removal.

Figure 8. Qd removal as a function of [K⁺]_o.

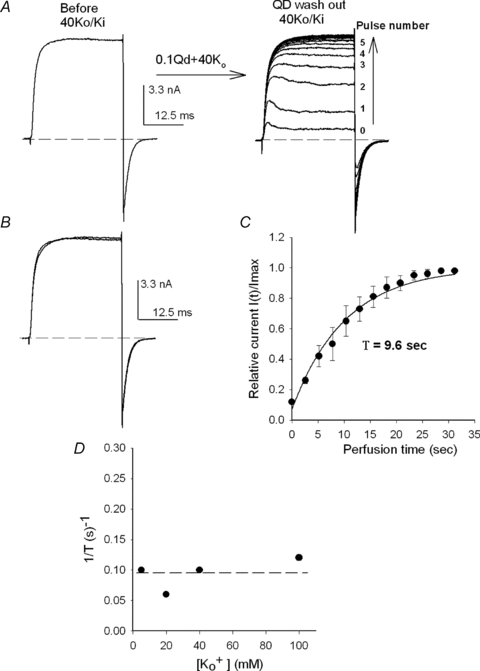
A, left panel, control I_K at +40 mV recorded in 40K_o/K_i solutions. After checking the stability of control I_K, the cell was superfused for 45 s with 40K_o+ 0.1Qd and 22 +40 mV/30 ms pulses were applied to repeatedly block the channels (as in Fig. 7, not shown, indicated by the arrow). Immediately after the last I_K with Qd was recorded (labelled 0, right panel) the cell was superfused with the 40K_o solution while +40 mV pulses were applied at 1.7 Hz, to follow Qd removal (vertical arrow). B, superimposed I_K before (Control) and after Qd removal. There was a complete recovery. C, time course of Qd removal. I(t) is the average amplitude of I_K measured at the end of each pulse at time t of the cell perfusion with 40K_o, as in A right panel, and I_max is the maximal, steady-state I_K (n= 3). The line is the fit of the points with the equation: I(t)/I_max= 1 − exp(t/τ), with τ= 9.6 s. D, 1/τ as a function of [K⁺]_o. 1/τ was obtained from the fit of complete recovery curves as in C (n= 3 at each [K⁺]). The dotted line signals the average rate of Qd removal.

Lack of G_K recovery appears even more striking when the observations in Figs 6 and 7 are compared against the time course of Qd removal. The experiment in Fig. 8A illustrates the rate of Qd withdrawal with 40 mm present. First, control I_K was evoked by a +40 mV/30 ms activating pulse applied in 40K_o/K_i solutions (left panel Figs. 3 & 4). Next, the cell was superfused with 0.1Qd + 40K_o test solution and the channels were repeatedly blocked with the delivery of 22 +40 mV pulses (not shown, indicated by the arrow; the presence of is required to protect G_K during pulsing). The trace labelled 0 on the right panel shows I_K evoked by the last pulse. Finally, immediately after trace 0 was recorded, the cell was superfused back with the control 40K_o solution and Qd removal was followed with the delivery of activating pulses every 2.6 s (indicated by the vertical arrow). Note that I_K increased, and its kinetics changed, with each consecutive pulse until a final steady-state level was attained after only an ∼35 s perfusion, where I_K was indistinguishable from the control I_K, as shown in Fig. 8B, which presents control I_K superposed on I_K recorded once the steady state was reached. This behaviour is in clear contrast with the lack of recovery documented in Fig. 7 upon the extensive perfusion of the cell with 40 K_o.

The time course of Qd removal in 40 K_o is quantitatively analysed in Fig. 8C, which presents the average normalized I_K at the end of each pulse, as a function of the time of perfusion, from three experiments as in Fig. 8A. The line is the fit of the points with an exponential function with a time constant τ of 9.8 s (see figure legend).

Rate of Qd removal (1/τ) as a function of [K⁺] in the washing solution obtained from three experiments at each [K⁺], as in Fig. 8B, is presented in Fig. 8D. Qd withdrawal is roughly independent of the [K⁺]_o and its rate (0.095 ± 0.02 s⁻¹) is much slower than the rate of Qd dissociation k_off from Shab channels (which is of the order of ms⁻¹). This demonstrates that the exit from the cell rather than from the channels constitutes the, K⁺-independent, rate-limiting step of Qd removal, further supporting the conclusion that the lack of I_K recovery after Qd block in Na_o/K_i solutions could not possibly be due to incomplete Qd removal.

Finally, and as mentioned previously, in must be stated that the G_K lost after block was never recovered in any of the cells tested. Moreover, two cells were washed with control solutions in which all Na⁺ was replaced by K⁺ (145 mm), and I_K did not recover at all (not shown). In contrast, when the cells are immersed (for 1.5 min) in 0.1Qd + Na_o and the channels are maintained closed at the HP, to impede Qd blockage, G_k is fully recovered (see later).

Taken together the observations contained in Figs 5–8 demonstrate that the loss of G_K observed after blocking Shab channels in Na_o/K_i solutions is irreversible and not due to incomplete removal of Qd from the cell and/or the channels. Thus, it is concluded that on blocking the channels from the inside of the membrane, on the one hand Qd cuts off communication between the pore and the intracellular K⁺-containing solution and, simultaneously, because of its destabilizing interaction with pore K⁺ ions (Figs. 3 & 4), Qd brings the pore to a virtual 0 K⁺ condition in which G_K collapses, as illustrated in Fig. 5 (see Discussion). The remaining experiments were aimed at characterizing the Qd-promoted irreversible collapse of Shab G_K.

First, the role of the duration of the blocking event in the irreversible G_K drop was examined. To address this point, the outcome of the delivery of 22 30-ms activating pulses applied in the presence of 0.1 Qd (as in Fig. 7A) was compared with the outcome obtained with the delivery of a single pulse of the same total duration (i.e. 660 ms, a duration that on the other hand inactivates only ∼0.12 ± 0.01% (n= 4) of the channels).

Figure 9A illustrates the result of applying a single 660 ms pulse. Control I_K was first evoked by a standard short pulse (+40 mV/30 ms) in Na_o/K_i (left panel). Then, the cell was superfused with Na_o+ 0.1Qd solution, and a single +40 mV/660 ms pulse was applied. The trace in the middle panel shows that ∼90% of the channels were blocked. The peak observed at the beginning of the trace signals Qd entry into the pore, because at this very short time the channels do not inactivate at all. Then, and after a total 1.5 min exposure to Qd, the cell was superfused for 1.25 min with Na_o and the state of the channels was tested, as in the control. The trace in the right panel shows that, surprisingly, despite that the majority of the channels were blocked during the long pulse, only a small fraction of these ceased to conduct.

Figure 9. G_K drop as a function of the pulse duration.

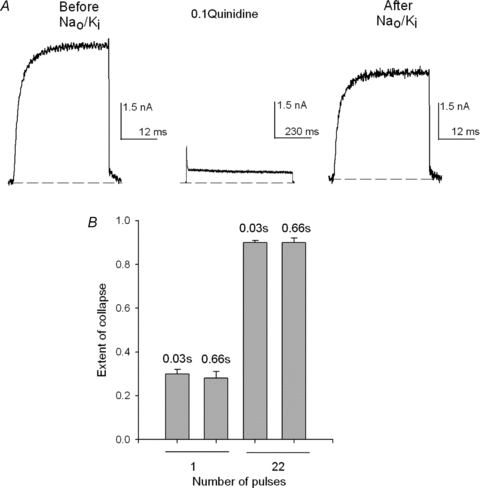
A, left panel, control I_K evoked by a +40 mV/30 ms pulse in Na_o/K_i. Then, the cell was immersed in the Na_o+ 0.1Qd solution and a +40 mV/660 ms pulse was applied (∼90% of I_K was blocked, middle panel). Subsequently, the cell was superfused (1.25 min) with the control Na_o solution and channels were activated as in the control (right panel). G_K drop was small. B, comparison of the average extent of collapse (see Methods) produced by either one or 22 + 40 mV pulses of the indicated duration (numbers above the bars) applied in the presence of Qd, as in A. The bars are the mean ±s.e.m. of at least 5 experiments on each condition.

The meaning of the previous observation is made clear by the bar graph in Fig. 9B which compares the average extent of G_K drop (see Methods) produced by either one or 22 pulses of the indicated duration (numbers above the bars). It is clearly observed that the extent of G_K collapse depends on the number of activating pulses (gating cycles) applied in the presence of Qd, but not on the duration of the pulses, for pulse durations ranging between 30 and 660 ms.

The effect of the number of pulses (gating cycles) in the irreversible drop of G_K is further studied in Fig. 10A, which presents the extent of G_K drop as a function of the number of fully activating (+50 mV/30 ms) pulses, delivered in the presence of 0.1 Qd with the cell bathed in Na_o/K_i solutions. Note that the drop of G_K increases with the number of pulses (filled circles) until ∼100% collapse is attained with ∼20–30 pulses.

Figure 10. G_K drop as a function of the activating pulses.

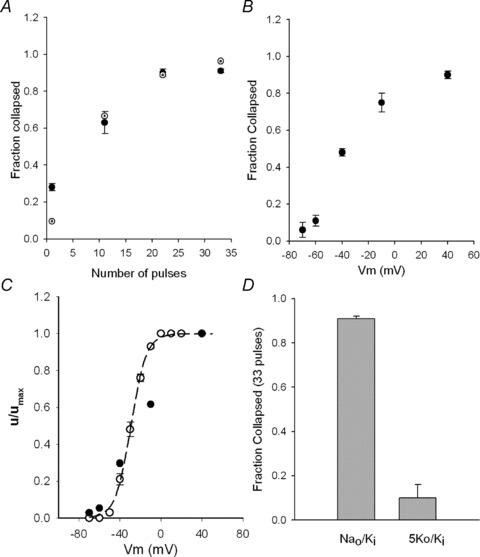
A, fractional G_K drop as a function of the number of +50 mV/30 ms pulses applied in the presence of 0.1Qd (Na_o/K_i) (filled circles). The points are the average of at least 5 experiments at each condition. The dotted circles are the fit of the experimental points with the equation f_c= 1 − (1 −u)ⁿ, with u= 0.1and n= number of pulses (see text). B, average cumulative G_K drop as a function of the pulse potential (V_m), from at least 4 experiments as in A at each voltage (n= 22 pulses). C, normalized extent of G_K drop per pulse (u/u_max) (see text), as a function of V_m (filled circles) compared against the previously reported activation curve of the channels (G_rel=G/G_Max) in Na_o/K_i (open circles). The line is the fit of G_rel with a Boltzmann equation with z= 3.3 and V_1/2=−29 mV (see text). D, extent of collapse after extensively pulsing the channels (33 +50 mV pulses) in the presence of 0.1 Qd in either Na_o/K_i or 5K_o/K_i solution, as indicated.

It is noteworthy that this behaviour resembles the collapse of Shaker G_K observed with K⁺-free solutions on both sides of the membrane (Introduction, and see later). Therefore, the Shab G_K drop was fitted with a model previously applied to characterize Shaker G_K collapse (Gomez-Lagunas et al. 2004), namely if it is assumed that a constant fraction of the channels (fraction of G_K) u collapses with each pulse (with each gating cycle), then the fraction collapsed f_c by n pulses will be f_c(n) = 1 − (1 −u)ⁿ. The dotted circles show that the experimental points (filled circles) are qualitatively well fitted by this model with u= 0.1 (dotted circles, see Discussion).

It was expected that only the pulses that effectively open the channels were capable of promoting G_K collapse. Figure 10B shows that indeed the cumulative drop of G_K (i.e. that produced by 22 pulses, applied with 0.1 Qd present) increases as the pulse potential becomes more positive, reaching a saturating maximal value at potentials that fully activate the channels. The latter is best observed by comparing the effect of pulse potential on the drop of G_K against the activation curve of the channels.

Considering that the extent of G_K drop per pulse u would be quite small at the less depolarized potentials, u was obtained from the cumulative drop in Fig. 9B, utilizing the relationship: u= 1 − (1 −f_c(n))^1/n, with n= 22 pulses; and its normalized value u/u_max was plotted against V_m, along with the previously reported activation curve of the channels (Gomez-Lagunas, 2007) in Na_o/K_i solutions (Fig. 10C, open circles). The line is the fit of the G_rel−V_m points with a Boltzmann equation (see figure legend). Note that u/u_max closely follows the activation curve.

Finally, as quinidine is used in clinical cardiology it was of interest to compare the extent of G_K drop occurring in the absence of external K⁺ against that which possibly occurs with 5 mm. The results in Fig. 10D show that even with physiological K⁺, upon the delivery of 33 fully activating pulses (+50 mV) a small fraction of G_K is irreversibly lost. Although the fraction lost with present is small, and therefore can easily be overlooked in studies in which Qd is utilized to inhibit Shab, it nevertheless may be significant, particularly under hypokalaemic conditions, because it is irreversible.

Discussion

Quinidine is a lipophilic cation that passively equilibrates across the membrane. Here it was shown that Qd inhibits Shab from the inside, blocking the pore in a voltage-dependent manner with 1:1 stoichiometry when the activation gate opens.

The K_d obtained from the dose–response curve (11.4 μm) has a value similar to those obtained at +50 mV in other channels, as for example with Kv1.5 (6.2 μm) (Yeola et al. 1996; Fedida, 1997), HK2 (6.2 μm) (Snyders et al. 1992); Kv1.4 (∼80 μm) (Wang et al. 2003), the transient I_K of rat ventricle (∼6 μm) (Clark et al. 1995), and delayed rectifier currents of Drosophila muscles (∼26 μm, between −10 and +30 mV) (Kraliz et al. 1998).

Because Qd is a lipophilic cation, its binding presents both hydrophobic and electrostatic components (Snyders & Yeola, 1995; Yeola et al. 1996; Kraliz et al. 1998; Zhang et al. 1998). The similarity of the reported K_d suggests that the Qd receptor has a fairly conserved structure and/or that global structural requirements for Qd binding are not very stringent, as in, for example, the binding of inactivation peptides to Shaker (Murrel-Lagnado & Aldrich, 1993; Zhou et al. 2001a). Regarding the latter, it has been shown that mutations of residues located in the middle section of S6 of both Kv1.4 and Kv1.5 affect Qd blockage, indicating that Qd binds within the central cavity of K⁺ channels (Yeola et al. 1996; Zhang et al. 1998; Caballero et al. 2003).

Shab closing in the presence of Quinidine

Tail I_K in the presence of Qd has a complex hook shape due to the exit of the blocker during channel deactivation. With 5 mm the phase that follows the peak of tails with Qd has a rate significantly smaller than the normal deactivation rate, due to the rate of Qd dissociation from the pore, with the Shab closing rate itself being unaffected by Qd, indicating that the activation gate does not close until Qd leaves the pore, in agreement with the conclusions reached by Fedida (1997) studying Kv1.5 gating currents.

Quinidine–K⁺ interaction

In this work it was demonstrated that Qd interacts with pore K⁺ ions, showing the following: (a) the block electrical distance δ varies with [K⁺]_o; (b) the apparent K_d of Qd increases, linearly, with [K⁺]_o; and (c) in the absence of external K⁺ Qd block irreversibly brings about the collapse of Shab G_K.

Qd blocks Shab in a voltage-dependent manner, with a δ of 0.35 under physiological conditions (5K_o/K_i). δ has a value that is slightly greater than those previously reported, which range from 0.2 to 0.3 (see Fedida, 1997). These differences are understood by considering that δ does not indicate the actual location of the blocking site. The latter is clear in the case of Qd, which because of its size (12–14 Å) could not bind within the selectivity filter (of ∼3 Å diameter), the region where the voltage drop occurs in the open conformation (Zhou et al 2001b; Jiang et al. 2002).

Instead of indicating an actual distance, it is known that a variable fraction of δ may arise from the interaction between blocker and permeant ions (Neyton & Miller, 1988; Spassova & Lu, 1998; Thompson & Begenisich, 2005). For example, it is well established that TEA binds in the central cavity of the pore (Armstrong, 1971; Choi et al. 1993; Holmgren et al. 1997; Zhou et al. 2001a), but whereas in Shaker δ takes a value of ∼0.15–0.2 (Choi et al. 1993), in Kir1.1 channels it takes values ranging from ∼0.4 up to 0.9, depending on [K⁺]_o (Spassova & Lu, 1998). In the case of Qd, here it was shown that δ varies with [K⁺]_o, suggesting that the energetic coupling between K⁺ and Qd affects the value of δ.

Qd–K⁺ interaction was additional demonstrated by showing that the apparent Qd affinity at 0 mV varies linearly with [K⁺]_o with a half-inhibition constant K_i of 20 mm, thus suggesting that (a) there is an externally located binding site for , which may be the selectivity filter s1 or s2 site (Zhou et al. 2001b), which in Shab has an apparent affinity for K⁺ of ∼20 mm at 0 mV, and such that (b) K⁺ binding to that site destabilizes Qd block in a manner that is operationally similar to that exerted by competitive inhibitors on enzyme catalysed reactions.

In summary the effect of on the parameters of block clearly shows that K⁺ destabilizes Qd binding. Reciprocally, Qd destabilizes K⁺ dwelling in the pore, thus promoting the irreversible collapse of Shab G_K in Na_o/K_i solutions.

Quinidine collapse of Shab G_K

Blocking Shab channels with Quinidine in Na_o/K_i solutions irreversibly leads to collapse of G_K, regardless of the presence of physiological [K⁺] in the cytoplasm.

The Qd-promoted collapse of Shab G_K presents several characteristics that are similar to the collapse of Shaker G_K observed with 0 K⁺ on both sides of the membrane (Gomez-Lagunas, 1997; Melishchuk et al. 1998; Loboda et al. 2001; Gomez-Lagunas et al. 2004), namely: (a) G_K drop varies with the pulse voltage in a manner that closely follows the activation curve of the channels; (b) the extent of drop depends on the number of pulses (gating cycles) delivered in either Na_o/Na_i (Shaker) or Na_o/K_i (Shab in the presence of Qd) solutions; and (c) G_K drop does not depend on the pulse duration. In the case of Shaker, these observations lead to the conclusion that the collapse of G_k occurred during the closing of the channels at the end of each activating pulse.

Thus based on the observations presented here, and on previous studies with Shaker, it can be conclude that on blocking the channels, on the one hand, Qd halts the flow of intracellular K⁺ through the pore, and on the other hand, through its electrical, destabilizing, interaction with selectivity filter K⁺ ions, brings the channels to a virtual 0 K⁺ condition. Therefore, as the channels close and Qd exits the pore, the fraction of channels that does not manage to be reloaded by the internal K⁺ ceases to conduct. A similar conclusion was reached on applying TEA to the squid channel (Khodakhah et al. 1997).

The observations presented here demonstrate that with each gating cycle a constant ∼10% fraction (u) of the fully activated population of channels is not reloaded by the internal K⁺ upon repolarization to −80 mV, and therefore ceases to function, while the remaining fraction of channels manages to be reloaded, and therefore to close normally, and remain functional. In other words, the probability of Shab G_K collapsing per gating cycle is ∼0.1 at −80 mV.

The previous conclusion gives rise to the interesting possibility that the passive drop of Shab G_K, which develops with 0 K⁺ on both sides of the membrane (as illustrated in Fig. 5), could actually occur during the closing of the channels, at the end of the scant stochastic openings which take place at the holding potential (for a discussion of this point see Gomez-Lagunas, 2007) although, in this case, u would be likely to acquire a value different from that in the presence of Qd. The latter would mean that the mechanism by which G_K collapses in 0 K⁺ could be basically the same in Shab, Shaker and the squid K⁺ channel, and the main difference would be that in the case of Shaker the G_K drop is fully reversible.

Another interesting conclusion is that it appears that while the conducting open-pore does not require K⁺ to remain functional, on closing of the activation gate, the pore sinks into a non-functional conformation in the absence of K⁺.

Considering that quinidine is a commonly used antiarrythmic drug, the observations reported here may also be of physiological interest, because they show that care should be taken with the administration of positively charged lipophilic compounds that permeate across the membrane. These compounds could block, in a non-specific and probably unwanted fashion, K⁺ channels from the inside; thus they could potentially bring some channels to a condition under which G_K might be destabilized, particularly under hypokalaemic conditions.