Statistical Issues in Longitudinal Data Analysis for Treatment Efficacy Studies in the Biomedical Sciences

Abstract

Longitudinally collected outcomes are increasingly common in cell biology and gene therapy research. In this article, we review the current practice of statistical analysis of longitudinal data in these fields, and recommend the “best performing” statistical method among those available in most statistical packages. A survey of papers published in Molecular Therapy indicates that longitudinal data are only properly analyzed in a small fraction of articles, and the most popular approach was analyzing each measurement time point data separately using an analysis of variance (ANOVA) model with Tukey's post hoc tests. We show that first, such cross-sectional ANOVA approach does not utilize all the power that the longitudinal design of a study provides, and second, Tukey's post hoc tests applied at each measurement time separately could result in a false positivity rate as high as 30% using a simulation study. We recommend mixed effects model analysis instead. We also discuss the complexities of multiple comparison adjustment in the post hoc testing that result from within experimental unit correlation existing in longitudinal data. We recommend resampling as a method that readily adjusts the post hoc testing to be limited to only interesting comparisons and thereby avoids unduly sacrificing the power.

Introduction

Longitudinal data consist of outcome measurements repeatedly taken on each experimental unit (e.g., cell line or mouse) over time. Such data are collected to address research questions that are concerned with changes in the mean response or potentially varying mean differences over time, in contrast to cross-sectional data that are concerned with the mean response and mean differences at a single time point. For example, suppose one plans to study an epidermal growth factor receptor inhibitor in a human malignant peripheral nerve sheath tumor (MPNST) xenograft model alone and in combination with inhibitors of the small GTPase protein Rac, a major downstream mediator of epidermal growth factor receptor signaling. Tumor volume will be measured repeatedly in each mouse over, for example, 7 weeks during and after treatment. One may select the baseline and one post-treatment measurement, and analyze changes from the baseline. This does not generally constitute longitudinal data analysis and does not entail the complexities of longitudinal analysis described below. The rigor of such cross-sectional statistical analysis, however, requires determining a priori that post-treatment measurement data will be included in the analysis, forbidding its post hoc determination. Such an a priori decision is often not feasible in practice as the most differential time point may not be predictable. Longitudinal analysis, in contrast, analyzes the entire dataset and compares the mean tumor growth trajectory among treatment groups. It is more powerful as it uses the entire data and can answer research questions such as whether and how long a differential tumor growth, if present, is sustained.

Longitudinal analysis is distinctive from cross-sectional analysis as it addresses dependency among measurements taken on the same experimental unit (e.g., a given mouse). In the above example of the human MPNST xenograft study, tumor volume measurements taken on a given mouse are generally positively correlated and vary less among themselves than tumor measurements taken among different mice. Such positive correlation, if not properly addressed, leads to underestimating the variability of data among experimental units, which may in turn lead to a false significance when treatment group means are compared. The within experimental unit correlation also complicates multiple comparison adjustment in post hoc testing. In the human MPNST xenograft example, the mean tumor growth needs to be compared among treatment groups pairwise to identify a molecule with the most growth inhibiting effect or to compare the effect of a molecule singularly with the effects of its combination with other molecules. Due to the within experimental unit correlation, pairwise comparisons at one time point are positively correlated with pairwise comparisons at another time point. Ignoring this correlation leads to unnecessarily conservative results as we describe in a section below.

We conducted a survey of papers published in Molecular Therapy, with a key word of “longitudinal,” and identified a total of 76 articles and abstracts that were published over the past 10 years. Among them, 47 (62%) have appeared in the past 4 years (December 2005 to December 2009). This indicates an increasing trend of longitudinal data collection in the fields of cell biology and gene therapy, and calls for attention to the aforementioned important statistical issues. In this article, we review the current practice of statistical analysis of longitudinal data in the concerned fields, review statistical models available for longitudinal analysis in most statistical software packages, and discuss multiple comparison adjustment methods with the results from our simulation study.

Results

Statistical models for longitudinal analysis

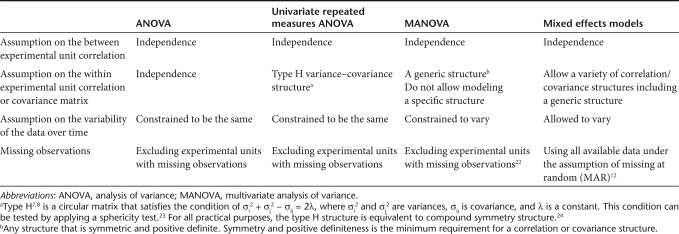
Four statistical models are generally available for the analysis of longitudinal data: univariate repeated measures ANOVA model,¹ multivariate ANOVA (MANOVA) model,² mixed effects model,^3,4 and generalized linear models.⁵ Generalized linear model is quite distinctive from the first three models as it does not require the normality of data and provides robust results against the deviation of the normality in longitudinal data.⁶ The model is fitted to a longitudinal data by generalized estimating equations method. Although well known to statisticians, the generalized estimating equation method is not popular in cell biology or gene therapy research applications, and often is not included in biomedical application–oriented software programs. Thus, we focus on the first three models here. Table 1 summarizes comparative features of these models. We included ordinary ANOVA as well to compare it with univariate repeated measures ANOVA.

Table 1. Comparison of statistical models for longitudinal analysis.

The three models differ primarily by their distributional assumptions on the underlying measurements including assumptions on the “within experimental unit” dependency. The univariate approach of repeated measures ANOVA works with a certain type of the within experimental unit dependency known as Huynh–Feldt (type H) structure,^7,8 although the MANOVA approach is constrained to assume a nonspecific generic structure known as unstructured (see Table 1 for details). Measurements taken on the same experimental unit are often more strongly correlated as their measurement time points are closer and the correlation decays in time as their measurement time points get further apart. Such a time decaying correlation structure does not fit the type H structure and, strictly speaking, cannot be modeled by the univariate repeated measures ANOVA model. Adjustments are available, but their performance varies depending on the sample size and the degree of discrepancy between the true dependency structure of the data and the type H structure.^9,10,11 On the other hand, the MANOVA model does not enable one to model this specific pattern of dependency, failing to incorporate such knowledge in the modeling.

In contrast, the time decaying dependency can be modeled by the mixed effects model. Among many dependency structures available with the mixed effects model in most statistical software packages are an autoregressive of order one and a spatial structure. Both represent diminishing dependency in time with the covariance between measurements in autoregressive of order one following a power of the correlation, a first order autoregression process, and in the spatial structure as an exponential function of distance between two measurement points. Spatial power and spatial sphericity structures also capture such timing decaying correlation. In addition, the mixed effects model allows users to choose a general nonspecific structure (unstructured), independent structure (no dependency), or compound symmetry (constant dependency) and much more.

The mixed effects model even allows the variability of the data to change over time. In the above human MPNST xenograft study example, the variability of the tumor volume data may increase with time as differential growth of tumors becomes more evident with time. Whether the increasing variability of the data can be accommodated is an important consideration in the analysis of these data. The univariate repeated measures ANOVA cannot accommodate increasing variability, whereas the mixed effects and MANOVA models can do so (see Table 1). The mixed effects model also utilizes data more efficiently. It is a likelihood-based method and allows incorporating missing observations under the assumption of missing at random.¹² Missing at random refers to the condition that a missing observation may depend on the observed components of data but not on the unobserved. In designed experimental settings common to cell biology or gene therapy research, missing at random is often not different from missing completely at random, which requires that whether an observation will be missing may not depend on data at all.¹² For example, suppose that three mice in the human MPNST xenograft study have missing values for reasons unrelated to the treatments. A mouse could die of a cage flood or from too aggressive gavage feeding, or a mouse can be killed for pharmacokinetics or pharmacodynamics study. Missing at random or missing completely at random condition is satisfied in these cases, and the mixed effects model will utilize their nonmissing tumor measurement data, whereas the univariate ANOVA and MANOVA approach will exclude the three mice with missing values from the analysis.

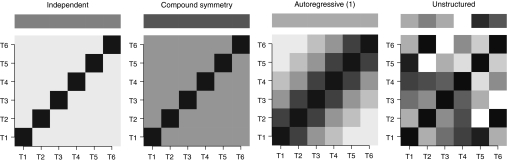
Figure 1 provides a graphical presentation of four commonly used within experimental unit dependency structures to better illustrate different choices. The top panels illustrate the assumptions on the variability of the data at each time point. The nonspecific generic structure (unstructured) allows the variability to change over time, whereas the others do not. The bottom panels illustrate the correlation structures. The diagonals correspond to correlations between measurements at each time point with themselves, which are 1. The off-diagonals correspond to correlations between a pair of measurements. Color gradients are used to show the relative strength of the correlations. Independent structure assumes zero correlations and compound symmetry assumes a constant correlation. Autoregressive of order one assumes a decaying correlation as the time interval between the time points of the concerned measurement pair increases. The general unstructured covariance does not assume a specific structure except the symmetry about the diagonals.

Figure 1.

Illustration of four common variance–covariance structures. When six measurement time points are considered, the top panel illustrates the within experimental unit variances assumed at each time point under the four variance–covariance structure. The bottom panel illustrates corresponding correlation matrices among the measurement time points. Color gradients are used to show the magnitude of the variances and the strength of the correlations. The darker the color grade is, the larger the variance is or the stronger the correlation is.

All three models are available in popular professional statistical software such as SAS (SAS Institute, Cary, NC), JMP (SAS Institute, Cary, NC), SPSS (SPSS, Chicago, IL), S-plus (Insightful, Seattle, WA), and STATA (StataCorp, College Station, TX). On the contrary, biomedical application–oriented software packages only provide the relatively simpler models. For example, only univariate repeated measures ANOVA is available in GraphPad Prism (GraphPad Software, San Diego, CA).

To properly apply these models, the modeling assumptions have to be checked including the normality of data using graphical tools. If the assumptions are violated, mending adjustments need to be made. For example, if data are skewed, log transformation of the data might mitigate the skewness.

Multiple comparison adjustment

Another important statistical issue with longitudinal data analysis is multiple comparison adjustment for post hoc tests. Post hoc tests such as pairwise group comparisons are often conducted to identify pairs of groups that are significantly different and involve more than one hypothesis test. Importantly, the hypotheses tested in the post hoc testing are scientifically associated with one another. In a drug discovery, when a particular biological target is thought to be important in a disease, a group of molecules that act on the same biological target may be tested together. Should the particular biological target not in fact be important, the molecules under investigation collectively will not have any treatment effects, and in this sense, post hoc tests of individual molecules are scientifically associated with one another. Due to this association, for the statistical rigor of post hoc testing results, it is the overall false positivity rate that is called for to be controlled rather than a false positivity rate of individual tests. The overall false positivity rate refers to the probability that at least one test may result in a statistical significance due to chance when no comparisons are in fact scientifically significant. On the other hand, in the previous example of the human MPNST xenograft study, molecules are tested both singularly and as combinations for their antitumor growth effects. Should individual molecules not be effective, their combinations are likely to be noneffective, and pairwise comparisons of treatment groups with the control are scientifically associated.

The overall false positivity rate increases as the number of hypothesis tests entailed increases. In the human MPNST xenograft study, we suppose that a molecule is found to suppress MPNST growth compared to the control. If this finding resulted from one hypothesis test, that is, comparing the molecule-treated group with the control only, the finding is false only 5% of the time. If the finding resulted from comparing two molecules with the control and the molecule is one of the two, the finding is false 9% of the time (based on 10,000 simulations). In other words, we attain at least one false statistical significance 9% of the time by testing each of the molecules against the control at a significance level of 0.05. The overall false positivity rate increases to 12.6% (based on 10,000 simulations) if the comparisons included three molecule groups. This implies that without adjusting the post hoc testing results to control the overall false positivity rate, we do not know how more likely than 5% a significant result can be false and hence cannot compare the importance of unadjusted significant results, when the significant results are found by multiple tests entailing different numbers of hypothesis tests.

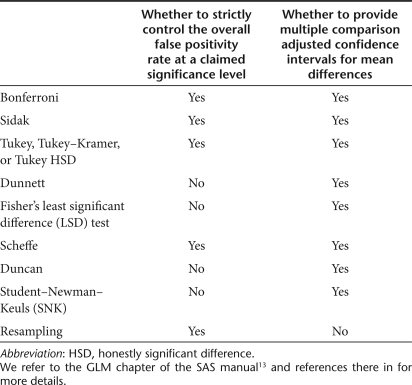
Many statistical methods or tests are available to account for the multiplicity of post hoc tests. Their control of the overall false positivity rate varies as they have different goals. Table 2 summarizes the varying degree of the control for multiple comparison methods and tests available with ANOVA in most of the professional statistical software packages mentioned in the last section. We refer to the GLM chapter of the SAS manual¹³ and references therein for more details. Bonferroni's, Sidak's, Schaffe's, and Tukey's method strictly control the overall false positivity rate at a claimed significance level (usually α = 0.05). When pairwise comparisons are concerned, Tukey's or Tukey–Kramer method is the most powerful. Bonferroni's and Sidak's methods control the upper bound of the overall false positivity rate and hence are conservative compared to Schaffe's and Tukey's method, particularly as the number of groups involved in the post hoc comparison increases. On the other hand, the other tests do not strictly control the overall false positivity rate at the claimed significance level α. For example, with an extensive simulation study, Hoffman and colleagues¹⁴ showed that the overall false positivity rate could be as high as 50% when using Dunnett's adjustment in a longitudinal setting. A resampling-based method¹⁵ also strictly controls the overall false positivity rate.

Table 2. Common post hoc pairwise comparison methods or post hoc comparison adjusted tests.

A challenge with the longitudinal analysis is that most of the existing methods or tests for multiple comparisons are developed for independent data. How to adapt those methods to the analysis of longitudinal data is not straightforward. In the longitudinal analysis, pairwise mean comparisons are often meaningful among groups only at the same measurement time point or across time points within the same groups. However, many statistical software programs compute all possible pairwise mean comparisons by default. When longitudinal analysis includes three treatment groups at three measurement time points, 36 pairwise comparisons are computed by default when meaningful comparisons are 9 or 18 at most (3 pairwise group comparisons per measurement time point and/or 3 pairwise measurement time comparisons per group). The excess number of pairwise mean comparisons leads to unnecessarily conservative results, as the multiplicity adjustment gets more severe as the number of comparisons involved increases. Multiple degree of freedom contrasts can be used to limit the post hoc testing to a subset of interesting comparisons and to control the overall false positivity rate only over the subset. However, they test the comparisons collectively as a group and do not provide adjusted results for individual contrasts involved. Another issue is that due to the within experimental unit correlation, a comparison between a pair of group means at one time point is correlated with comparisons between the same pair at different time points. Ignoring these correlations also leads to unnecessarily conservative results. Many variations of the traditional methods had been proposed to address this problem.^{16,17,18,19,20} However, they are rather specific to particular applications under investigation. The problem of how to adapt the traditional methods to the within experimental unit correlation remains to be discussed.

We recommend resampling method as a method that readily adjusts the post hoc testing to be limited to only interesting comparisons and properly addresses the correlated comparisons.

Numerical experiment results

We focused on the methods that strictly control the overall false positivity rate, and conducted a simulation study to compare their performances. For comparison, we also included Tukey's test applied at each measurement time point separately without adjusting the significance level because it was the most popular choice of tests we found in the survey of current statistical practice on longitudinal data in the concerned fields (to be described in the Materials and Methods section below). We generated 5,000 datasets with two different per group sample sizes (n = 5 or n = 20), assuming equal group size and a correlation of 0.5 among the within experimental unit measurement. This corresponds to a compound symmetry within experimental unit dependency structure with a 0.5 correlation (see Figure 1 for the illustration of the dependency structure). We assumed 3 or 10 treatment groups were considered with 3 or 10 longitudinally measured observations per experimental unit. The simulation parameter combinations considered for (no. of group, no. of measurement time points) were (3, 3), (3, 10), and (10, 3). We assumed pairwise group mean comparisons at the same measurement time points were the only interesting comparisons, and therefore, the number of interesting pairwise comparisons were 9, 30, and 135 for the combinations (3, 3), (3, 10), and (10, 3), respectively. We used R library mvtnorm (R 2.7.2 version) to generate the data.

We conducted mixed effects model analyses for each set of simulated data using the MIXED procedure in SAS (SAS version 9.1.3) and obtained pairwise comparison results of interest that were not yet adjusted for multiple comparison. The adjusted results for Bonferroni's and Sidak's methods were computed by the MULTTEST procedure in SAS. For Tukey's test, we applied the test separately at each measurement time point with the significance level of the test adjusted by Bonferroni's and Sidak's methods for the number of measurement time points. That is, we first adjusted the significance level for the number of measurement time points by Bonferroni's or Sidak's method, and applied Tukey's test for pairwise comparisons at each measurement time point with the adjusted significance level. For example, when three measurement time points were considered, the significance level of our application of the Tukey's test is adjusted to 0.05/3 by Bonferroni's method. The default application of Tukey's test would have used 0.05 significance level but would have considered all possible pairwise mean comparisons instead of mean comparisons at the same measurement time under consideration. As the number of all possible comparisons is much larger than the number of comparisons under consideration, the default application of Tukey's test is more conservative than our application of the Tukey's test. Such adjusted results are denoted by Tukey–Bonferroni and Tukey–Sidak, respectively. Tukey-only denotes results obtained by applying Tukey's test at each measurement time point separately without adjusting the significance level. We considered two resampling methods. Parametric residual resampling method of Westfall and Young¹⁵ was implemented by Glimmix procedure in SAS software (SAS version 9.2). It can be implemented with SAS version 9.1 with a macro add-on. The permutation method was applied with 500 resamplings each. We refer to Westfall and Young¹⁵ for details of these resampling methods.

Figure 2 summarizes the simulation results for the overall false positivity rate. The closer a simulated false positivity rate is to the 5% nominal level, the better a test is. A simulated overall false positivity rate >5% indicates that the test is liberal, whereas a test is conservative if the simulated rate is <5%. The most liberal was Tukey's test applied separately at each measurement time point without adjusting the significance level for multiple times the test is applied (denoted by Tukey-only). The false positivity rate was as high as 30% in our simulation. Among the remaining ones, the more conservative were Bonferroni's and Sidak's methods. This result was expected as they target to control the upper bound of the overall false positive rate. Tukey's test combined with Bonferroni's and Sidak's performed better, whereas the resampling methods outperformed the rest of the methods. The permutation method showed a more reliable performance in all simulation settings, particularly when n = 5 per group, and in this sense, it was slightly better. Westfall's parametric bootstrapping method could be quite liberal in a small sample with many time points (3 groups and 10 time points). A notable point with the sample size is that the overall false positivity rate of the resampling methods will approach the 5% nominal level more closely as sample size increases as assured by statistical theory. This is not the case with the rest of the methods, however, as they will remain either conservative or liberal.

Figure 2.

Overall false positivity rate simulation results based on 5,000 simulated datasets. The panel on the right is the whole plot with all the methods under investigation where Tukey-only method shows a highly inflated overall false positivity rate. The panel on the left shows a zoomed-in bottom part of the right panel where the performance of the other methods can be better depicted.

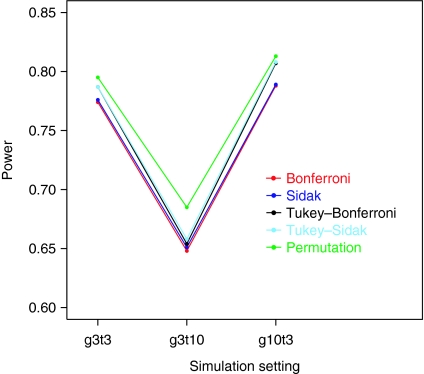
We conducted a separate simulation study to compare the power. We did not include the Tukey-only method because it does not control the false positivity rate as shown above. Using the same experimental settings as above, we considered an alternative hypothesis scenario that the treatment group differences exit in the last measurement time point only. Figure 3 summarized the results based on 1,000 simulated data. The power plot shows similar patterns as with the overall false positivity rate. Bonferroni and Sidak methods have the lowest power. Tukey–Bonferroni and Tukey–Sidak have slightly better power. The permutation method remained as the clear winner. Although the power was greatly affected by the number of time measurement points, its power was higher than the rest as much as 5% at all three settings. We considered different alternative scenarios and obtained similar results.

Figure 3.

Simulation results for the power.

Discussion

In this article, we reviewed the current practice of statistical analysis of longitudinal data and provide a comparative review of the three most popular statistical models and their implementations in statistical software packages. The survey of the current practice indicated that longitudinal data are only properly analyzed in a small fraction of articles, and the most popular approach was analyzing each measurement time point data separately using analysis of variance (ANOVA) model. Such a cross-sectional approach fails to utilize all the power that the longitudinal design of a study provides and is less efficient. In contrast, the survey indicated that slightly >50% of manuscripts adjusted the post hoc testing results for multiple comparison with Tukey's test being the most popular choice. Although we found that applying Tukey's test without modification in the longitudinal setting might result in a false positivity rate of 30%, the survey results are encouraging in that more and more scientists understand and adjust for the increased risk of false positive results with multiple hypothesis testing. At the same time, however, it also indicates that multiple comparison adjustment is not yet as widely accepted and practiced as it should be. An explanation may be that many studies in this field are at an exploratory stage, for example, in drug discovery with interest lying in identifying potent molecules, and the error of false negatives (false nonsignificance) is considered more serious than the error of false positives (false significance). The increased overall false positivity rate due to multiple testing, therefore, may not be a concern to biomedical scientists as much as to statisticians. However, the issue is not that significant findings without multiplicity adjustment can be false >5% of the time. As described in the previous section, the issue is that without the adjustment, we do not know how more likely than 5% a significant result can be false and hence cannot compare the importance of unadjusted significant results, when they are found by multiple tests entailing different numbers of hypothesis tests. The statistical rigor required for multiple comparisons, therefore, is not so much about strictly controlling the false positivity at the usual 5%. It is rather about fairly disclosing and informing the scientific community and regulatory agencies of how likely reported significant results are to be false due to chance and enabling findings from post hoc testing entailing different number of comparisons to be comparable. For this reason, post hoc Tukey's test is also known as Tukey's honestly significant difference test.

A widely held misperception is that no result will remain significant as the number of comparisons increases, and it may contribute to the less desirable acceptance of multiple comparison adjustment. When 20 groups are compared pairwise, the number of possible pairwise comparisons is 190 and a P value has to be smaller than 0.026% or 0.00026 (= 0.05/190) to be significant by Bonferroni's method. The significance level gets smaller linearly as the number of comparisons increase by Bonferroni's method, and this may give such a misperception. However, as explained, Bonferroni's method controls the upper bound of the overall false positivity error rate and hence is inherently conservative. In the same situation, with Tukey's method, the most powerful test for pairwise comparisons, and n = 10 per group, two group means need to be different by 2.04 times of the standard deviation (2.04 SD = 6.467 times of the standard error) to be significant. This shows the importance of a choice of multiple comparison adjustment method. In the longitudinal setting, however, a direct application of Tukey's method is difficult due to the within experimental unit dependency. Based on the simulation study, we recommend resampling methods as methods that best reflect the design structure of longitudinal data and avoid unduly sacrificing the power by adjusting the post hoc testing to be limited to only interesting comparisons. A shortcoming of resampling methods is that confidence intervals are not available (see Table 2). P values may be sufficient if a statistical significance is only of interest. However, in some cases, the magnitudes of mean differences are also of interest and confidence intervals provide such information. We recommend using resampling methods to test for a statistical significance, while using ordinary confidence intervals (unadjusted for multiple comparisons) for the magnitude of mean differences. Although we focused on pairwise group comparisons in the discussion, the recommended resampling-based methods are also applicable to other types of contrasts involved in post hoc testing, as detailed in ref. 15.

Materials and Methods

Current practice of statistical analysis of longitudinal data. We surveyed articles published in Molecular Therapy with a key word “longitudinal” for the past 4 years (December 2005 to December 2009) and with a key word “ANOVA” for the past 3 years (January 2007 to December 2009). We use the search results as a bench mark for the current practice of statistical analysis of longitudinal data in the fields of cell biology and gene therapy.

A total of 67 eligible articles were identified and Table 3 summarizes the findings. Although the majority (93%) conducted statistical analyses, only 18% addressed the within experimental unit correlation and conducted longitudinal analyses. Seventy-five percent conducted cross-sectional analyses, either analyzing only a part of the data (baseline and one post-treatment measurement) or analyzing each measurement time point data separately. The most popular approach was analyzing each measurement time point data separately using ANOVA model with Tukey's post hoc pairwise tests. In general, a cross-sectional analysis does not utilize all the power that the longitudinal design of a study provides and is less powerful.²¹ The loss of statistical power is clear when only a fraction of data such as baseline and one post-treatment measurement time point data are analyzed. When each measurement time point data are analyzed separately, the loss of power can be seen with modestly different group means. Although mean differences at each time point may not reach the magnitude that attains a statistical significance, the pooled mean differences over time may be significant. Other issues exist with the cross sectional approaches. When a fraction of data is analyzed, the rigor of the statistical analysis requires determining which portion of the data to be included in the analysis a priori. When each measurement time point data are analyzed separately by ANOVA, conclusions need to be drawn after adjusting for the multiplicity of the ANOVA analyses to avoid the overall false positivity rate exceeding the widely accepted 5%.

Table 3. Survey summary of the current practice of statistical analysis of longitudinal data.

Our survey also found that 52% acknowledged the multiplicity issue of post hoc multiple comparisons and reported adjusted results. However, their adjustment methods varied. Some controlled the overall false positivity rate, the probability that one or more comparisons attain statistical significance due to the chance when no comparison is significant, too strictly, and some did not control adequately. We will visit this issue with more details in the next section. The overall survey results imply that longitudinal data are not adequately analyzed in the fields of cell biology and gene therapy and an inadequate analysis often leads to a less powerful conclusion.