Kinetic analysis of the effects of H⁺ or Ni²⁺ on Kv1.5 current shows that both ions enhance slow inactivation and induce resting inactivation

Abstract

External H⁺ and Ni²⁺ ions inhibit Kv1.5 channels by increasing current decay during a depolarizing pulse and reducing the maximal conductance. Although the former may be attributed to an enhancement of slow inactivation occurring from the open state, the latter cannot. Instead, we propose that the loss of conductance is due to the induction, by H⁺ or Ni²⁺, of a resting inactivation process. To assess whether the two inactivation processes are mechanistically related, we examined the time courses for the onset of and recovery from H⁺- or Ni²⁺-enhanced slow inactivation and resting inactivation. Compared to the time course of H⁺- or Ni²⁺-enhanced slow inactivation at +50 mV, the onset of resting inactivation induced at −80 mV with either ion involves a relatively slower process. Recovery from slow inactivation under control conditions was bi-exponential, indicative of at least two inactivated states. Recovery following H⁺- or Ni²⁺-enhanced slow inactivation or resting inactivation had time constants similar to those for recovery from control slow inactivation, although H⁺ and Ni²⁺ biased inactivation towards states from which recovery was fast and slow, respectively. The shared time constants suggest that the H⁺- and Ni²⁺-enhanced slow inactivated and induced resting inactivated states are similar to those visited during control slow inactivation at pH 7.4. We conclude that in Kv1.5 H⁺ and Ni²⁺ differentially enhance a slow inactivation process that involves at least two inactivated states and that resting inactivation is probably a close variant of slow inactivation.

Introduction

In response to depolarization, voltage-gated potassium channels from the Kv1 family, of which Shaker is the prototype, rapidly activate, open and then inactivate. Shaker channels have a fast inactivation process that is caused by the block of the inner pore by the N-terminus. Deletion of the N-terminal inactivation domain in the fast inactivation-removed Shaker mutant (ShIR Δ6–46) uncovers a slower process that is referred to as slow or P/C-type inactivation (Hoshi et al. 1990; Kurata & Fedida, 2006). Kv1.5 channels, which are the focus of this report, underlie the ultrarapid delayed rectifier current (I_Kur) in human atrial myocytes and exhibit slow inactivation only (Fedida et al. 1993). Through its effects on action potential duration, Kv1.5 plays an important role in cardiac excitability, particularly in human atrial tissue (Hatem et al. 2010).

Inactivation is a functionally important gating process because the associated loss of channel availability can affect the threshold potential for cell firing and the amplitude and duration of the action potential. Although still poorly understood, a number of studies support the current view that slow inactivation involves a localized constriction of the outer pore mouth (Yellen et al. 1994; Liu et al. 1996; Basso et al. 1998; Kiss & Korn, 1998; Loots & Isacoff, 1998). It is commonly assumed that slow inactivation and channel activation are tightly coupled, such that opening of the activation gate must precede slow inactivation. However, there is some evidence to suggest that activation and slow inactivation of Shaker channels may be uncoupled by certain channel mutations such that an appreciable loss of channel availability occurs at resting potentials in the absence of activation (López-Barneo et al. 1993; Yang et al. 1997; Claydon et al. 2008).

We (Kehl et al. 2002; Fedida et al. 2005; Claydon et al. 2007) and others (López-Barneo et al. 1993; Steidl & Yool, 1999; Pérez-Cornejo, 1999; Jäger & Grissmer, 2001; Trapani & Korn, 2003; Starkus et al. 2003) have shown that low extracellular pH increases the rate and the extent of Kv1.5 and ShIR current decay during a depolarizing pulse. Although the pK_a for this effect differs by over 1 pH unit between Kv1.5 and ShIR, it has nonetheless been attributed in both channel types to an enhancement of the slow inactivation process. Acidification also causes a marked reduction of peak Kv1.5 current, which was attributed by Steidl & Yool (1999) to an activity-dependent accumulation of channels in the slow inactivated state. However, we found that the decline of the peak current persisted at very low stimulus frequencies where cumulative slow inactivation was precluded (Kehl et al. 2002). Thus, we proposed that in Kv1.5 the reduction of the peak current amplitude arises from a H⁺-induced decrease of channel availability at −80 mV, which is defined in this paper as resting inactivation.

An unresolved issue is whether the two effects of H⁺, namely the apparent enhancement of slow inactivation of Kv1.5 and the induction of resting inactivation, are mechanistically related and whether either effect represents modulation of the slow inactivation process observed with depolarization at pH 7.4. (For a detailed definition of the terms used to describe the inactivation processes under control and low pH conditions, please see the Methods.) A number of previous findings imply a possible mechanistic link between the slow inactivation process and the effects of low pH. For example, as with slow inactivation in ShIR (López-Barneo et al. 1993; Baukrowitz & Yellen, 1995; Kiss & Korn, 1998), the resting inactivation induced by low pH is antagonized by elevated [K⁺]_o (K_d = 1 mm; Jäger & Grissmer, 2001; Kehl et al. 2002). Additionally, mutation of a specific outer pore residue (Kv1.5 R487 or ShIR T449) to a valine or tyrosine, markedly attenuates the enhanced current decay and resting inactivation observed at low pH (López-Barneo et al. 1993; Kehl et al. 2002; Trapani & Korn, 2003; Starkus et al. 2003; Claydon et al. 2007). Although in ShIR the site of action for the enhanced slow inactivation observed at low pH has been suggested to be a conserved aspartate residue in the GYGD sequence of the selectivity filter (Pérez-Cornejo, 1999; Starkus et al. 2003), in Kv1.5 the pH sensitivity is dramatically reduced by the mutation to glutamine of the H463 residue in the turret of each α subunit (Steidl & Yool, 1999; Kehl et al. 2002). Based on these findings, and the fact that Ni²⁺, another histidine ligand, qualitatively reproduces most of the effects of extracellular acidification (Perchenet & Clément-Chomienne, 2001; Kwan et al. 2004), we have proposed that H⁺ or Ni²⁺ binding at one or more H463 residues in Kv1.5 facilitates, at rest, a -sensitive process involving the outer pore (Kehl et al. 2002; Kwan et al. 2004), which might be related to slow inactivation.

In the experiments described here we examine the possibility of a mechanistic relationship between the apparent enhancement of slow inactivation and the resting inactivation following exposure to H⁺ or Ni²⁺ ions, and also assess whether either effect represents a modulation of the slow, or P/C-type, inactivation observed at pH 7.4. Our approach involves a comparative analysis of the kinetics of the onset of and recovery from the loss of current evoked by H⁺ or Ni²⁺ either at rest (−80 mV) or during a depolarizing pulse (+50 mV), as well as the recovery time course following control (pH 7.4) slow inactivation at +50 mV. We conclude that the H⁺- or Ni²⁺-induced acceleration of current decay at +50 mV is most simply explained by a concentration-dependent enhancement of slow inactivation, but that H⁺ biases slow inactivation to a state from which recovery is fast and Ni²⁺ biases slow inactivation to a state from which recovery is slow. The H⁺- or Ni²⁺-induced decrease in peak test current and maximal conductance is due primarily to the relatively slower process of resting inactivation. Recovery from the H⁺-induced resting inactivation has a time course similar to that for recovery from the H⁺-enhanced slow inactivation, suggesting that both effects are linked to a similar conformational change.

Methods

Cell preparation

As described previously (Cheng et al. 2008), currents were recorded from a human embryonic kidney cell line (HEK-293, American Type Culture Collection, Rockville, MD, USA) constitutively expressing human wild-type Kv1.5 channels. Cells were dissociated for passage using trypsin-EDTA and maintained at 37°C in an atmosphere of 5% CO₂ in air and in minimum essential medium (MEM) supplemented with 10% fetal bovine serum, 1% penicillin–streptomycin, and 0.5 mg ml⁻¹ geneticin. All tissue culture supplies were obtained from Invitrogen (Burlington, Ontario, Canada).

Recording solutions

The standard, nominally K⁺-free bathing solution contained (in mm): 143.5 NaCl, 2 CaCl₂, 1 MgCl₂, 5 glucose, 10 Hepes and was titrated at room temperature to pH 7.4 with NaOH. Bath solutions containing K⁺ were prepared by substituting KCl for NaCl. Low pH solutions had the same ionic composition as the standard solution, except for the replacement of Hepes by Mes. Ni²⁺ solutions were prepared by dilution of a 1 m NiCl₂ stock solution with the standard pH 7.4 bath solution. At pH 7.4, the concentration of Ni²⁺ that could be used was limited to ≤10 mm by virtue of the solubility product for Ni(OH)₂ (∼2 × 10⁻¹⁶). The standard patch pipette solution contained (in mm): 130 KCl, 4.75 CaCl₂ (pCa²⁺ = 7.3), 1.38 MgCl₂, 10 EGTA, 10 Hepes and was adjusted to pH 7.4 with KOH. When [K⁺]_i was decreased to 35 mm, 10 mm NaCl and 109 mmN-methyl-d-glucamine were used to replace KCl. Chemicals were obtained from the Sigma-Aldrich Chemical Co. (Mississauga, Ontario, Canada).

Fast solution exchange

Rapid changes of the external solution were typically made using a gravity-driven perfusion system in which reservoirs filled with different test solutions were connected to a custom fast application tool (FAT) constructed from polyimide-coated fused silica tubes (0.32 mm inside diameter, ID; Agilent Technologies Canada, Inc., Mississauga, Ontario), which were glued together and fed into a common outlet capillary (0.45 mm ID). While the bath was perfused with control solution (∼2 ml min⁻¹), the FAT outlet was positioned approximately 50 μm from the target cell so that it was exposed to solution flow from the FAT alone. The timing of solution changes was controlled using software-driven transistor-transistor logic (TTL) pulses that switched solenoid valves regulating solution flow between the reservoirs and the FAT. Experiments (not shown) in which the [K⁺]_o was changed from 0 to 140 mm during a pulse to 0 mV showed a latency of 50–100 ms and a time constant for current decay to the zero current level of 50–100 ms. Faster solution changes with shorter latencies were possible but tended to disrupt the whole cell recording.

Definitions of terms

Figure 1 shows simplified schemes, based on evidence summarized in the Introduction, of the putative actions of H⁺ and Ni²⁺ ions on Kv1.5 channels at rest (−80 mV; Scheme I) and at +50 mV (Scheme II).

Figure 1. Simplified gating schemes describing the putative actions of H⁺ or Ni²⁺ ions on Kv1.5 channels at resting and depolarized potentials.

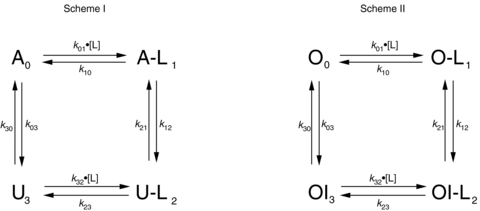
First order rate constants are shown as k_xy, where x and y denote the states (identified by the subscripts 0, 1, 2 or 3) involved in the transition. The concentration of H⁺ or Ni²⁺ ions, also known as the ligand, is shown as [L]; L denotes a ligand-bound state. Scheme I: at rest (−80 mV) channels in the upper row are in the available (A or A-L) state and able to pass current during test depolarizations to +50 mV. Channels in the lower row are in the unavailable or resting inactivated state (U or U-L) and remain non-conductive during test depolarizations. Resting inactivation is defined as the transition at −80 mV from the A to U state or from the A-L to U-L state. See Methods for details. Scheme II: at +50 mV channels are either in the open (O or O-L) and conducting state or in the open-but-slow-inactivated (OI or OI-L) and non-conducting state. Slow inactivation is defined as the transition at +50 mV from the O to OI state, while H⁺- or Ni²⁺-enhanced slow inactivation is defined as the transition from the O-L to OI-L state. See Methods for details.

In Scheme I the upper row represents channels in the available (A₀ or A-L₁) state, meaning that the channel is able to conduct current once the activation gate opens during a test depolarization. The lower row represents channels in the unavailable (U₃ or U-L₂) or resting inactivated state, meaning that channels remain non-conductive even if the activation gate opens. Resting inactivation is defined here as a loss of channel availability occurring at −80 mV, a potential at which channels are assumed, on the basis of gating current measurements in Kv1.5, to be predominantly in the fully deactivated state. Downward and upward transitions in Scheme I represent resting inactivation and recovery from resting inactivation, respectively. Binding and unbinding of Ni²⁺ or H⁺ ions, which is also referred to as ligand (L) binding/unbinding, is represented by the rightward and leftward transitions, respectively, in each row. Under control conditions (pH 7.4, 0 Ni²⁺), the channels gate primarily in the left column of states (i.e. 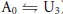) and the reaction equilibrium is strongly biased to the available state. Conversely, the reaction equilibrium of the ligand-bound or right column of states (i.e. 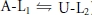) is strongly biased towards inactivation and becomes more dominant as the ligand concentration increases. As described in greater detail below, the availability at −80 mV was typically monitored with 20 ms test pulses to +50 mV.

Scheme II outlines an analogous, simplified relationship for the slow inactivation of channels at +50 mV. We define slow inactivation, sometimes referred to as control slow inactivation, as the current decay observed at +50 mV in control pH 7.4, 0 Ni²⁺ solution. In this scheme channels are either open and conducting (O₀ or O-L₁; upper row) or open-but-slow-inactivated (OI₃ or OI-L₂; lower row). In both columns the gating reaction is biased towards inactivation, but more strongly so for ligand-bound channels. Inactivation was assessed during a seconds-long step to +50 mV, either in the continuous presence of control solution or during a transient application of ligand (low pH or Ni²⁺). For consistency with the terminology used previously by us and others (Steidl & Yool, 1999; Jäger & Grissmer, 2001; Kehl et al. 2002; Kwan et al. 2004), we refer to the low pH- or Ni²⁺-induced acceleration of current decay at +50 mV as enhanced slow inactivation, and will return in the Discussion to a consideration of whether this terminology is justified.

Signal recording and data analysis

In an experiment, a section of glass coverslip to which cells had attached was placed in the recording chamber. Whole-cell currents were recorded at room temperature (20–25°C) using an EPC-8 patch-clamp amplifier and PatchMaster software (HEKA Electronik, Lambrecht/Pfalz, Germany), via an ITC-18 digital interface (Instrutech, HEKA Electronik), which also provided the TTL pulses that synchronized the fast solution change with voltage step commands. Patch electrodes were made from thin-walled 1.2 mm (OD) borosilicate glass (World Precision Instruments, Sarasota, FL, USA) and had resistances of 1.0–2.5 MΩ, measured in the bath with standard external and internal solutions. The circuitry of the amplifier was used to compensate the membrane capacitance and ∼80% of the series resistance. Where applicable, leak subtraction was performed using the online P/N protocol in PatchMaster, for which the holding potential was −100 mV and the scaling factor was −0.25. Current signals were low-pass filtered at 3 kHz (−3 dB, 8 pole Bessel filter) and digitized (18 bit) at a sampling frequency of at least 10 kHz. Voltages were corrected for liquid junction potentials. Holding and test potentials of −80 mV and +50 mV, respectively, were standard. When applicable, current amplitudes were normalized to control measurements made at the beginning of the sweep or experiment. Data from cells showing <80% recovery to control levels after test treatments were discarded.

The similarities between the time courses of recovery from slow inactivation and H⁺- or Ni²⁺-enhanced slow inactivation or resting inactivation were assessed using a simultaneous, or global, fit of data sets to single or double exponential functions. This was performed using the built-in Global Fit function of our analysis software (Igor Pro, Wavemetrics, Portland, OR, USA), in which the fit was constrained such that the time constants of the fitting function were the same for each data set, but the relative amplitudes of the fast and slow recovery components (A_rec,f, A_rec,s) and the initial level of availability (A₀) were allowed to vary. The chi-square (χ²) statistic was used to test for goodness of fit. For other comparisons, a one-way ANOVA and Tukey's test were used to test for statistical significance (P < 0.05). Data are presented as mean ±s.e.m.; n represents the number of cells tested.

Numeric simulation

Macroscopic Kv1.5 currents were simulated in IGOR Pro by calculating state occupancies as a function of time, voltage and ligand concentration from the spectral expansion of the Q-matrix (Colquhoun & Hawkes, 2009) generated from state diagrams described in the text and associated figure legends.

Results

External H⁺ and Ni²⁺ enhance the current decay and reduce peak current

Figure 2A displays a current trace obtained using a 5 s pulse from −80 mV to +50 mV in 0 mm K⁺ solution at pH 7.4. The voltage protocol was then repeated following prolonged exposure to K⁺-free bath solutions at pH 6.9 and 6.4. As reported by others for Kv1.5 and ShIR (Meyer & Heinemann, 1997; Rich & Snyders, 1998), the time course for slow inactivation at pH 7.4 was better fitted to a double exponential. Nonetheless, a single exponential function was used to facilitate a comparison with the current decay at low pH, which was typically mono-exponential. Low pH decreased the peak macroscopic current and the time constant for slow inactivation (τ_inact; Fig. 2A). The small amplitude and non-inactivating time course of the residual current at pH 6.4 point to it being due to endogenous HEK channels (Zhu et al. 1998; Lambert & Oberwinkler, 2005). In 0 the pK_a for the decrease in peak current was ∼6.9 (see figure legend), in agreement with our previous report (Kehl et al. 2002). Increasing [K⁺]_o from 0 to 3.5 mm partially relieved the inhibitory effects of H⁺, so that substantial current was observed even at pH 5.9 (Fig. 2B). Qualitatively similar observations with Ni²⁺ in 0 and 3.5 mM are shown in Fig. 2C and D. These results confirm the previous findings that H⁺ and Ni²⁺ decrease the peak macroscopic current and accelerate the current decay during a pulse in a concentration- and [K⁺]_o-sensitive manner (Steidl & Yool, 1999; Jäger & Grissmer, 2001; Kehl et al. 2002; Kwan et al. 2004). However, the experiment does not distinguish between the reduction in peak current due to enhanced slow inactivation and that due to ligand-induced resting inactivation (see Fig. 1). To address this issue, fast solution changes were used to examine the effects of H⁺ and Ni²⁺ on either open or resting Kv1.5 channels.

Figure 2. Effects of external H⁺ and Ni²⁺ on Kv1.5 current.

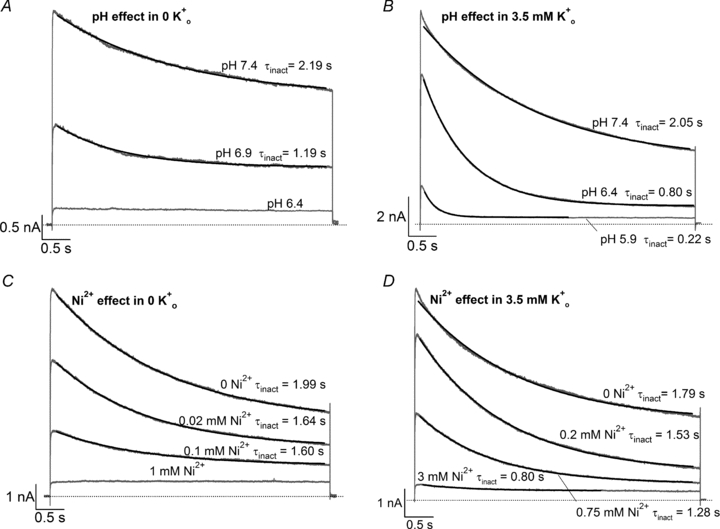
In all panels, superimposed grey traces represent current recorded during 5 s voltage steps to +50 mV from −80 mV following prolonged exposure (20–40 s) to low pH or [Ni²⁺]. Black lines represent the fits of the current decay to a mono-exponential function with a time constant denoted by τ_inact. Each panel represents an experiment on a different cell. A, in 0 mm, low pH decreases both peak Kv1.5 current and τ_inact. Pooled data from 4 cells gave a pK_a of 6.9 and a Hill coefficient of 1.4. B, increasing [K⁺]_o antagonizes the effect of low pH on peak test current. In 3.5 mm the pK_a for the decrease in peak current was 6.2, with a Hill coefficient of 1.8 (n = 4 cells). C, Ni²⁺ also causes a concentration-dependent decrease in peak current but this is associated with relatively smaller decreases of the test current decay rate. From 4 cells, the fit of the [Ni²⁺] dependence of the mean normalized peak current amplitude to the Hill equation gave K_d and Hill coefficient values of 0.034 mm and 0.85, respectively. D, in 3.5 mm the K_d for the [Ni²⁺]-dependent decrease of peak current amplitude was 0.52 mm; the Hill coefficient was 1.2 (n = 4 cells). For reasons unclear to us, these K_d values for the Ni²⁺ effect are lower than those previously reported (Kwan et al. 2004).

Decreasing external pH during a depolarization enhances slow inactivation

To isolate the effects of low pH on open channels, we used fast perfusion to rapidly decrease pH during a step to +50 mV (e.g. Fig. 3A). With this protocol the reduction of peak current that occurs with prolonged application of low pH solutions (Fig. 2) is avoided and the focus is on the effects of H⁺ on the open state and gating transitions as outlined in Scheme II of Fig. 1.

Figure 3. The time course of enhanced slow inactivation and resting inactivation is pH dependent.

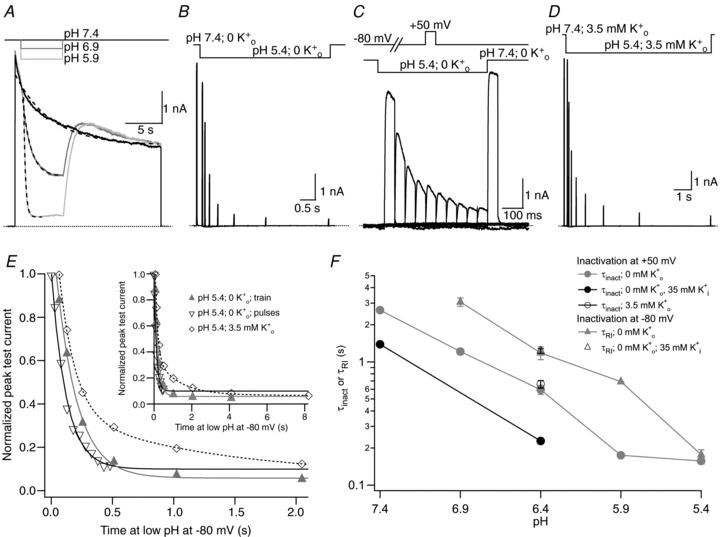
A, superimposed current traces from the same cell showing the enhancement of current decay by low pH. The 0 mm K⁺ bathing solution was rapidly and transiently switched from pH 7.4 to low pH during a 20 s step from −80 mV to +50 mV. Dashed lines represent mono-exponential fits of the current decay with τ_inact values of 4.88 s, 1.11 s and 0.25 s at pH 7.4, 6.4 and 5.9, respectively. B, current trace showing the onset of resting inactivation induced at pH 5.4 in 0 mm. After a 20 ms control pulse to +50 mV at pH 7.4, the external pH was decreased and a pulse train with increasing interpulse intervals was applied during a single sweep. C, resting inactivation was also assessed with multiple (superimposed) sweeps. In each sweep a single test pulse was applied at a known interval after the switch to pH 5.4; the interval was increased for each successive sweep. The final, control, trace was obtained without prior exposure to low pH. D, the onset of resting inactivation induced by pH 5.4 in 3.5 mm was measured as described for B. E, test currents from (B–D) were normalized to their respective controls and plotted against the cumulative time spent at −80 mV at pH 5.4. Inset, the same plot on a longer time scale shows the steady-state level. The continuous and dashed lines represent mono- and bi-exponential fits of the data, respectively; τ_RI at pH 5.4 in 0 was 171 ms and 122 ms measured with a train and single pulses, respectively. In 3.5 mm at pH 5.4, τ_RI,fast and τ_RI,slow were 131 ms and 1.24 s, respectively. F, time constants for low pH enhanced slow inactivation and resting inactivation derived from experiments such as those in A and B are plotted against pH. All data points represent the mean ±s.e.m. from at least 3 cells.

Figure 3A shows superimposed current traces recorded from the same cell in K⁺-free medium at pH 7.4 (control) and with transient exposures to pH 6.9 and pH 5.9. As in ShIR (Starkus et al. 2003), decreasing pH during a depolarizing pulse enhanced Kv1.5 current decay. The mean values for τ_inact measured in this way at pHs ranging from 7.4 to 5.4 in 0 medium are plotted in Fig. 3F (grey circles); the foot of the concentration–response relationship at 100–150 ms may reflect the limiting rate of the solution exchange (see Methods). These results support the hypothesis that low pH enhances slow inactivation of open channels, as outlined in Scheme II.

If it is correct that H⁺ enhances slow inactivation, then an increase of the rate of slow inactivation at pH 7.4 should be paralleled by an increased rate of current decay at low pH. This was tested by taking advantage of the fact that slow inactivation at pH 7.4 is accelerated roughly twofold when the [K⁺]_i is reduced from 130 to 35 mm (compare grey and black circles at pH 7.4 in Fig. 3F), an effect that has been attributed to a decreased flux through the open channel and a consequent reduction of the occupancy of the outer pore site that controls slow inactivation (Fedida et al. 1999; Ogielska & Aldrich, 1999). As predicted, with 35 mm the current decay observed with rapid switching to pH 6.4 at +50 mV was approximately 2.5-fold faster than with 130 mm (grey and black circles at pH 6.4 in Fig. 3F).

In agreement with previous reports that the time course of slow inactivation of open Kv1.5 channels is insensitive to moderate changes in [K⁺]_o (Fedida et al. 1999; Jäger & Grissmer, 2001), the τ_inact at pH 6.4 was unaffected by increasing [K⁺]_o from 0 to 3.5 mm (Fig. 3F, open circles). Thus, as with slow inactivation at pH 7.4, the H⁺-enhanced current decay is sensitive to [K⁺]_i and insensitive to [K⁺]_o, which is consistent with our earlier conclusion that external H⁺ acts on open Kv1.5 channels to enhance slow inactivation during a depolarizing pulse.

Current can recover from a transient decrease in pH during a depolarization

In contrast to findings with ShIR where there is little or no recovery after returning to pH 7.4 (Starkus et al. 2003), in Kv1.5 the transition from low pH back to pH 7.4 during a depolarizing pulse is associated with a substantial recovery current (Fig. 3A). Recovery was occasionally to the same level as the inactivating control current, but in many cells (Fig. 3A) the recovery current crossed and peaked above the control level. In Fig. 3A the rising component of the biphasic recovery current following either the pH 6.9 or the pH 5.9 pulse was well-fitted by a single exponential (τ≈ 1 s in each case). The declining component of the recovery current typically relaxed back to the control current level provided the pulse was long enough. Importantly, single channel studies with both Kv1.5 (Kwan et al. 2006) and ShIR (Claydon et al. 2007) have precluded rapid open channel block as the mechanistic basis for the enhanced decay of current at low pH. As such, the recovery current cannot be ascribed to the reversal of channel block. Instead, the increase of current observed after returning to pH 7.4 solution may reflect channel deprotonation (OI-L₂ → OI₃ of Scheme II of Fig. 1) and subsequent recovery from inactivation (OI₃ → O₀). A further examination of recovery currents at +50 mV is presented below.

The onset of low pH-induced resting inactivation is slow

The time course of low pH-induced resting inactivation of Kv1.5 at −80 mV was next characterized, on the premise that an analysis of the onset and/or recovery kinetics could help elucidate the mechanistic relationship, if any, between slow inactivation at +50 mV and resting inactivation at −80 mV. The protocol involved a 20 ms control step to +50 mV in pH 7.4 solution applied just prior to the beginning of a 4–60 s exposure to low pH solution, during which a train of 20 ms test pulses to +50 mV was applied. For the trace in Fig. 3B, K⁺-free pH 5.4 solution was applied for a 4.3 s duration, during which test pulses were applied. There was a progressive decline of peak test currents as the duration of exposure to pH 5.4 solution increased. A plot of the normalized peak current amplitude against the time spent at low pH at −80 mV (grey triangles in Fig. 3E) shows that the onset of H⁺-induced resting inactivation in K⁺-free medium is well fitted by a single exponential, with a time constant defined as τ_RI. Despite the enhanced slow inactivation during test pulses to +50 mV at pH 5.4 (Fig. 3A), the brevity of the test pulses in this protocol precluded accumulation of slow inactivation as a contributing factor in the decline of the test currents. This is confirmed in Fig. 3C, which shows that the onset of resting inactivation at pH 5.4 is no different when assessed with single test pulses (in multiple, superimposed sweeps) applied after known intervals from the start of the solution change (Fig. 3E; compare ▴ and ▿). The mean values for τ_RI measured with a train of pulses (e.g. Fig. 3B; 161 ± 15 ms; n = 4) and single pulses (e.g. Fig. 3C; 177 ± 17 ms; n = 5) are not significantly different (P > 0.05). Figure 3F (grey triangles) summarizes the pH dependence of τ_RI in 0 measured with pulse trains and also indicates that over the pH range tested, the onset of H⁺-induced resting inactivation was typically slower than for H⁺-enhanced slow inactivation, except at pH 5.4 where the τ_RI and τ_inact converge, possibly due to the limiting rate of the solution change.

Low pH-induced resting inactivation is sensitive to [K⁺]_o but not [K⁺]_i

Because extracellular K⁺ ions antagonize the conductance collapse, or resting inactivation, of Kv1.5 induced by either low pH or Ni²⁺ (Fig. 2; Jäger & Grissmer, 2001; Kehl et al. 2002; Kwan et al. 2004), it was of interest to determine how the time course of H⁺-induced resting inactivation was affected by increasing [K⁺]_o. With 3.5 mm a major kinetic change was that the onset of resting inactivation was bi-exponential (Fig. 3D and E). To facilitate a direct comparison of the time course of resting inactivation in either 0 or 3.5 mm, we calculated the time required for the current to relax to 50% (T₅₀) and 90% (T₉₀) of the maximum current decay. At pH 5.4 with 0 mm, T₅₀ and T₉₀ were 0.11 ± 0.01 s and 0.35 ± 0.03 s (n = 6), respectively, and with 3.5 mm the corresponding values increased to 0.19 ± 0.04 s and 1.66 ± 0.33 s (n = 5). The nearly fivefold increase of T₉₀ with 3.5 reflects the substantial contribution of the slower process to resting inactivation and is consistent with the inhibition by of an inactivation process involving the pore. In contrast to enhanced slow inactivation measured at +50 mV, the time course of pH 6.4-induced resting inactivation in 0 was not affected by reducing [K⁺]_i to 35 mm (Fig. 3F, open triangles), as would be expected since the closed activation gate, which is located on the cytoplasmic side of the channel, would preclude an effect of [K⁺]_i on the occupancy of the permeation pathway.

Transient exposure to Ni²⁺ during a pulse enhances slow inactivation

Figure 4A shows that, like low pH in Fig. 3A, the fast application of Ni²⁺ shortly after the start of a pulse to +50 mV results in an enhancement of the rate and extent of current decay. The concentration dependence of this effect at pH 7.4 with 0 mm is summarized in Fig. 4E (grey circles) and indicates that the Ni²⁺ effect was qualitatively the same as that for low pH. There were additional shared properties of the two ligands. Changing from 0 to 3.5 mm had no effect on τ_inact measured with 2 mm Ni²⁺ (open circles in Fig. 4E), and decreasing control τ_inact (in 0 mm Ni²⁺) by changing [K⁺]_i from 130 to 35 mm was associated with a 2-fold faster rate of inactivation in 2 mm Ni²⁺ (black circles in Fig. 4E). Current recovery was also observed following the return to Ni²⁺-free medium during the pulse, but the recovery time course, although variable, was typically much slower than that following low pH. Thus, like H⁺, Ni²⁺ enhances slow inactivation of Kv1.5 channels at +50 mV.

Figure 4. The time course of enhanced slow inactivation and resting inactivation is also [Ni²⁺] dependent.

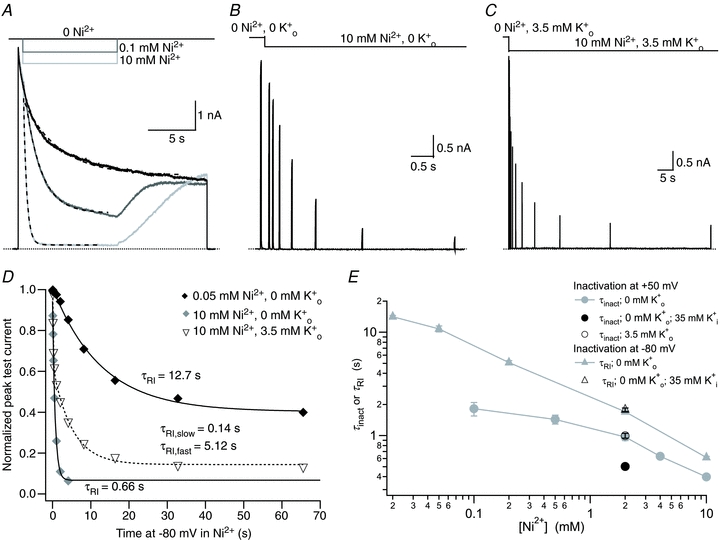
A, superimposed current traces from the same cell showing the enhancement of current decay by external Ni²⁺. During a 20 s step from −80 mV to +50 mV, the control (pH 7.4, 0 mm K⁺) bath solution was rapidly and transiently switched to one containing Ni²⁺. Dashed lines represent mono-exponential fits of the current decay with τ_inact values of 4.08 s, 1.65 s and 0.34 s in 0, 0.1, and 10 mm Ni²⁺, respectively. B, current trace showing the onset of Ni²⁺-induced resting inactivation in 0 mm. After a 20 ms control pulse from −80 mV to +50 mV in 0 mm Ni²⁺, resting inactivation was assessed by switching to 10 mm Ni²⁺ solution and applying a pulse train with increasing interpulse intervals. C, the experimental protocol in B was repeated, albeit on a different time scale, with 3.5 mm. D, test currents from (B and C) were normalized to their respective controls and plotted against the cumulative time spent at −80 mV in Ni²⁺. For comparison, results from an experiment using 0.05 mm Ni²⁺ are also shown. Continuous and dashed lines represent mono- and bi-exponential fits of the data, respectively. E, time constants for Ni²⁺-enhanced current decay and resting inactivation derived from experiments such as those in A and B are plotted against [Ni²⁺]. Data points represent the mean ±s.e.m. of 3–7 cells.

The time course of Ni²⁺-induced resting inactivation is slow

The onset of Ni²⁺-induced resting inactivation in 0 at pH 7.4 was characterized with the same single sweep protocol as for low pH. For the current trace in Fig. 4B, 10 mm Ni²⁺ was present for the duration indicated by the lower horizontal bar; the peak test pulse current decreased exponentially as the duration of exposure to Ni²⁺ at −80 mV increased. A plot of the normalized test current amplitudes for the trace of Fig. 4B and a similar experiment with 50 μm Ni²⁺ show that the extent and the rate of inactivation are concentration dependent (Fig. 4D). At a given [Ni²⁺], τ_RI was the same regardless of whether a single sweep comprising a train of test pulses or several sweeps of single pulses (cf. Fig. 3C) were used (not shown), confirming that the effect is not due to an accumulation of slow inactivation. Figure 4E (grey triangles) summarizes the [Ni²⁺] dependence of τ_RI. The data mimic the pattern observed with H⁺ where the value for τ_RI approaches that for τ_inact as the [Ni²⁺] increases. As observed with low pH, the time course of Ni²⁺-induced resting inactivation was bi-exponential when [K⁺]_o was increased from 0 to 3.5 mm (Fig. 4C and D). With 10 mm Ni²⁺ the T₅₀ and T₉₀ values of the maximum current decay increased from 0.43 ± 0.01 s and 1.42 ± 0.04 s (n = 7) in 0 mm to 1.28 ± 0.16 s and 9.17 ± 0.24 s (n = 8) in 3.5 mm. Thus, consistent with the properties of an inactivation process involving the pore, the addition of external K⁺ dramatically slows the onset of Ni²⁺-induced resting inactivation.

In 2 mm Ni²⁺ there was no significant difference between τ_RI with 130 versus 35 mm (Fig. 4E), which again mirrors the finding with low pH (Fig. 3F). Further support for our contention that resting inactivation involves the pore is provided by the observation that Ni²⁺, as observed at low pH in Kv1.5 (Cheng et al. 2008) and as with slow inactivation in ShIR (Basso et al. 1998), inhibits the movement of Ba²⁺ to and from its deep pore binding site in Kv1.5 at −80 mV (Supplemental Fig. 1).

In summary, the data presented in Figs 2–4 suggest that both external Ni²⁺ and H⁺ enhance slow inactivation at +50 mV in a concentration-dependent manner. Like control slow inactivation at +50 mV, neither the H⁺ nor the Ni²⁺ enhancement of slow inactivation is sensitive to [K⁺]_o but the rate of inactivation with either ligand is augmented by decreasing [K⁺]_i. In contrast, the ligand-induced resting inactivation is inhibited by increasing [K⁺]_o and unaffected by decreasing [K⁺]_i. These properties are consistent with the conclusion that both enhanced slow inactivation at +50 mV and resting inactivation at −80 mV involve an inactivation process involving the pore. However, whether the Ni²⁺- and H⁺-enhanced slow inactivated and resting-inactivated conformations are mechanistically and conformationally related remains unclear. To begin to address that issue, we next turned to a comparative analysis of recovery kinetics following inactivation at +50 mV and −80 mV.

Recovery from H⁺-enhanced slow inactivation or resting inactivation is fast

In this and the following section the time course of recovery following inactivation at +50 mV or −80 mV with low pH or Ni²⁺ is compared to that following control slow inactivation at pH 7.4. Comparisons of control and treated responses were made in the same cell, since, in our experience (e.g. Fig. 2; see also Rich & Snyders, 1998), there is cell-to-cell variability in the rate and extent of slow inactivation. In Fig. 5A single sweeps of a representative experiment show recovery following (from top to bottom) control slow inactivation (5 s at +50 mV at pH 7.4), enhanced slow inactivation (∼5 s at +50 mV at pH 5.4), and resting inactivation (5 s at −80 mV at pH 5.4). In each experimental condition, recovery from inactivation was monitored in 0 , pH 7.4 solution with a train of test pulses to +50 mV.

Figure 5. The kinetics of recovery from H⁺- or Ni²⁺-enhanced slow inactivation or resting inactivation.

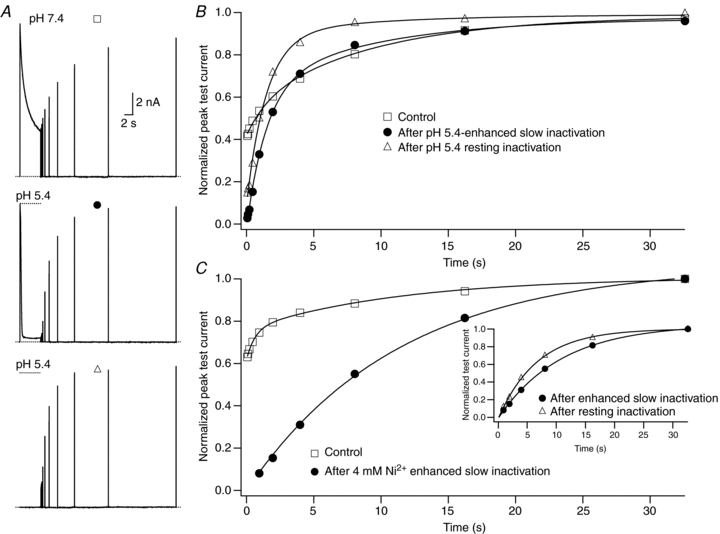
A, current traces recorded in 0 mm from the same cell showing: recovery at pH 7.4 from control slow inactivation (□); recovery at pH 7.4 from slow inactivation enhanced by pH 5.4 (•); and recovery at pH 7.4 from resting inactivation induced by pH 5.4 (▵). The voltage clamp protocol consisted of a 5 s step to +50 mV, except for the resting inactivation trace, followed by a train of 20 ms test pulses to +50 mV. The dotted horizontal lines indicate the duration of the exposure to pH 5.4 solution. B, peak test currents from A, normalized with respect to the peak control current, are plotted against the cumulative recovery time spent at the −80 mV holding potential. The continuous lines represent the simultaneous fit to a double exponential function of the time course of recovery from control slow inactivation (□), H⁺-enhanced slow inactivation (•) and resting inactivation (▵). The resulting values for τ_rec,f and τ_rec,s were 1.48 s and 9.14 s, respectively. C, normalized peak recovery currents measured with the same protocol as in (A), but with 4 mm Ni²⁺ instead of low pH, are plotted against the cumulative recovery time. The recovery from control (□) and Ni²⁺-enhanced (•) slow inactivation were simultaneously fitted to a double exponential function with τ_rec,f = 0.59 s and τ_rec,s = 10.6 s. Recovery from Ni²⁺-enhanced slow inactivation was entirely via the slow phase. The inset graph shows that recovery from Ni²⁺-induced resting inactivation (▵) was faster than that following enhanced slow inactivation. The continuous lines represent separate fits of each data set to a mono-exponential function. τ_rec was 10.8 s for enhanced slow inactivation and 6.7 s for resting inactivation.

For Fig. 5B the peak test current amplitudes from Fig. 5A were normalized to the peak control current and plotted against the cumulative recovery time at −80 mV. In agreement with previous reports, the recovery from control slow inactivation at pH 7.4 was biphasic, which is indicative of at least two inactivated states (Rich & Snyders, 1998; Perchenet & Clément-Chomienne, 2000). Preliminary independent fits (not shown) suggested a similarity of the time constants for recovery from control slow inactivation with those from enhanced slow inactivation and resting inactivation, both at pH 5.4. This motivated simultaneous or global fitting of the three data sets to a bi-exponential function in which the initial level of availability (A₀) and the relative amplitudes of the fast and slow recovery components (A_rec,f and A_rec,s, respectively) were free, while the values for the fast (τ_rec,f) and the slow (τ_rec,s) recovery time constants were constrained to be the same (see Methods). The continuous lines of Fig. 5B show that the outcome of the global fit was excellent (χ² = 0.004). Table 1 summarizes the results from six cells and shows that: (1) during the 5 s pulse the extent (1 −A₀) of either enhanced slow inactivation or resting inactivation at pH 5.4 is greater than that for control slow inactivation at pH 7.4; (2) after slow inactivation at pH 7.4 channels are roughly evenly distributed between the fast and slow recovery pathways; and (3) recovery at pH 7.4 from low pH-enhanced slow inactivation or H⁺-induced resting inactivation is mostly via the fast phase (A_rec,f≫A_rec,s). Together, these findings imply that two major inactivated states are visited following slow inactivation at pH 7.4, and that the same states are also populated after enhanced slow inactivation or resting inactivation at pH 5.4. However, low pH biases inactivation at −80 mV and at +50 mV towards the inactivated state from which recovery is faster.

Table 1.

Low pH biases inactivation to a state from which recovery is fast

	pH 7.4	pH 5.4
	inactivation at +50 mV	inactivation at +50 mV	inactivation at −80 mV
A0	0.53 ± 0.10	0.02 ± 0.01	0.08 ± 0.08
Arec,f**	0.47 ± 0.19	0.71 ± 0.07	0.89 ± 0.04
τrec,f	1.63 ± 0.1 s	*	*
Arec,s**	0.53 ± 0.19	0.29 ± 0.07	0.11 ± 0.04
τrec,s	13.52 ± 2.9 s	*	*

^*Constrained to be the same as control (pH 7.4) values.

^**Presented as proportion of total inactivating current. Data are from experiments described in Fig. 5A and B and are shown as mean ±s.e.m. for 6 cells.

Recovery from Ni²⁺-enhanced slow inactivation or resting inactivation is slow

The time course of recovery following enhanced slow inactivation and resting inactivation in 4 mm Ni²⁺ (Fig. 5C) was assessed using the same stimulus protocols described for Fig. 5A. The main panel of Fig. 5C shows the recovery of the normalized peak test currents, obtained from the same cell, following inactivation in control solution and in 4 mm Ni²⁺ at −80 mV and +50 mV. In this cell both the extent of control slow inactivation at the end of the 5 s pulse to +50 mV and τ_rec,f were less than that described in Fig. 5B; this underscores the cell-to-cell variability of slow inactivation and the rationale for doing within-cell comparisons. In contrast to the situation following enhanced slow inactivation at +50 mV at pH 5.4 (see Fig. 5B), the recovery following Ni²⁺-enhanced slow inactivation was mono-exponential (filled circles in Fig. 5C). However, the time constant (τ_rec) for recovery from Ni²⁺-enhanced slow inactivation was not significantly different from τ_rec,s following control slow inactivation (P > 0.05), and the slow component of control recovery and the mono-exponential recovery following Ni²⁺ treatment were replicated in a global fit (Fig. 5C). In 12 cells, the recovery following control and Ni²⁺-enhanced slow inactivation could be fitted simultaneously (τ_rec,s = τ_rec = 13.84 ± 0.73 s). In the same cells, recovery from Ni²⁺-induced resting inactivation (see Fig. 5C, inset) was also slow and mono-exponential but was consistently faster than recovery following Ni²⁺-enhanced slow inactivation and necessitated separate fits which gave a mean τ_rec value of 7.12 ± 0.42 s (n = 12).

In summary, low pH biases inactivation towards an inactivated state from which recovery is fast. Furthermore, the time constants for recovery from both H⁺-enhanced slow inactivation and resting inactivation are not significantly different, implying shared recovery pathways and similar mechanistic processes. With Ni²⁺, recovery following inactivation at +50 mV is mono-exponential and proceeds with the same time constant as the slow component of recovery from control inactivation at +50 mV, indicating that Ni²⁺ very strongly biases inactivation at +50 mV to the more stable inactivated state visited, albeit to a smaller extent, in control solution. The recovery rates following inactivation in Ni²⁺ at +50 mV and −80 mV differ by roughly 2-fold, suggesting that resting inactivation in Ni²⁺ is to a state that is not visited in control solution.

Recovery from H⁺- and Ni²⁺-induced resting inactivation at depolarized potentials

During a prolonged depolarization to +50 mV there is recovery from ligand-enhanced slow inactivation upon the return to control conditions (Figs 3A and 4A). The results of Fig. 5A and B, which suggest that low pH pushes inactivation towards a state from which recovery is fast, provide a potential explanation for the recovery overshoot shown in Fig. 3A. That is to say, the recovery overshoot may reflect a re-equilibration between two different slow inactivated states upon the return to pH 7.4. Figure 6 presents results from experiments assessing a related question: whether recovery at +50 mV could also be observed following ligand-induced resting inactivation and, if so, how that recovery compared to that following enhanced slow inactivation.

Figure 6. Current recovery during a test depolarizing pulse occurs following either H⁺- or Ni²⁺-enhanced slow inactivation or resting inactivation.

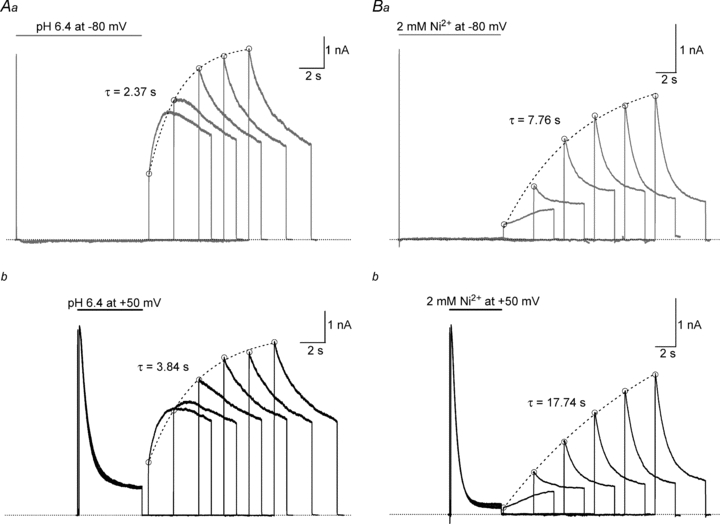
The experimental approach was similar to that used in Fig. 5 except that the test pulse duration was longer and multiple test sweeps were used. An intersweep interval of 60 s allowed for full recovery between sweeps. For the top panels, after a 20 ms control pulse from −80 mV to +50 mV in pH 7.4, 0 mm solution, resting inactivation at −80 mV was induced by a 10 s application of either pH 6.4 (Aa) or 2 mm Ni²⁺ (Ba) solution. To monitor recovery, the test solution was replaced by control solution and the cell held at −80 mV for varying intervals before a 5 s test pulse was applied. For the lower panels, recovery from slow inactivation enhanced by pH 6.4 (Ab) or 2 mm Ni²⁺ (Bb) was assessed in the same way, except that low pH and Ni²⁺ were applied 100 ms after the beginning of a 5 s pulse from −80 mV to +50 mV. For each column, traces were recorded from the same cell. These results show that with either ligand and following either resting inactivation (top panels) or enhanced slow inactivation (lower panels, and see also Figs 3A and 4A) there can be the recovery of current during a depolarizing pulse and that the kinetics of that recovery are qualitatively similar for a given ligand. Dotted lines represent single exponential fits of the amplitude of the fast phase of the test current (○). As shown in Fig. 5, recovery at −80 mV following low pH exposure is faster than that following Ni²⁺ exposure.

The superimposed traces of Fig. 6Aa show the current recovery following resting inactivation at −80 mV induced by a 10 s exposure to pH 6.4 solution. For the first of five successive sweeps there was an interval of 500 ms between the return to pH 7.4 solution and the application of a 5 s test pulse to +50 mV; for each successive sweep the interval between the return to pH 7.4 and the test pulse was increased by 2 s. The first sweep shows an initial fast rise of current (peak demarcated by open circles; τ≈ 2 ms) reflecting the normal opening of channels that either did not inactivate during the pH 6.4 pulse or that had recovered during the recovery interval at −80 mV. The fast component is followed by a more slowly rising phase of current (τ≈ 553 ms). On successive sweeps the amplitude of the initial rapid component increases as more channels recover during the ‘interpulse’ interval. However, even on the second and third test pulses there is also evidence for current recovery during the pulse, revealed either as a slow initial plateau (sweep 2) or as an inactivation rate (sweep 3) that is slower than that of the fourth and fifth test pulses. Figure 6Ab shows six superimposed current traces from the same cell in which slow inactivation was enhanced by switching to pH 6.4 solution 100 ms after the start of a 5 s pulse to +50 mV. Again, test pulses were applied in control solution at varying intervals following the inactivating pulse. The test currents following H⁺-enhanced slow inactivation are qualitatively indistinguishable from those that follow resting inactivation inasmuch as recovery at +50 mV (τ≈ 585 ms) is prominent during the first pulse and is present, but less overt, on the second and third pulses.

Figure 6B shows the results where, using a similar experimental approach and presentation protocol (see figure legend for details), 2 mm Ni²⁺ either induced resting inactivation (Fig. 6Ba) or enhanced slow inactivation (Fig. 6Bb). As with low pH, after resting inactivation and enhanced slow inactivation in Ni²⁺ the test pulse current of the first sweep has an initial rapid rise of current (peak demarcated by filled circles; τ≈ 3 ms). This is followed by a slowly rising phase that can be fitted by a single exponential (τ≈ 4.7 s and τ≈ 5.1 s for resting inactivation and enhanced slow inactivation, respectively) and represents current recovery during the pulse. In subsequent sweeps, as with low pH, current recovery at +50 mV from Ni²⁺-enhanced slow inactivation or resting inactivation is apparent in the lower rate of slow inactivation during the test pulses.

The results of Fig. 6 indicate that recovery from inactivation can occur during a depolarizing test pulse following either enhanced slow inactivation or resting inactivation with either ligand. However, the recovery kinetics following low pH or Ni²⁺ treatment differ in two important aspects. As noted in Fig. 5 and confirmed in Fig. 6 by the open circles and fitted dashed lines, which represent the envelope of the fast phase of current, recovery at −80 mV from either enhanced slow inactivation or resting inactivation is much faster following low pH. Second, the recovery during a pulse at +50 mV, as shown in Figs 3A, 4A and 6A, is also faster following low pH. This again implies that low pH biases inactivation to a state from which recovery, either at −80 mV or +50 mV, is relatively fast, and that Ni²⁺ biases inactivation to a state from which recovery is slow.

The time course for -facilitated recovery from resting inactivation is the same as that for recovery from enhanced slow inactivation

As a further assessment of the relationship between ligand-enhanced slow inactivation and resting inactivation, the effect of increasing [K⁺]_o on the recovery from resting inactivation was examined. These experiments were also motivated by the finding in Kv1.3 H404N (the positional homologue of T449 in ShIR) mutant channels that the time course for recovery from the loss of current induced by removing was much faster than that for recovery from slow inactivation, which was interpreted to mean that the loss of current in 0 K⁺ solution was not due to slow inactivation (Jäger et al. 1998). For these experiments, unlike those in Figs 5 and 6 where recovery was monitored in control solution, recovery from the loss of current in 0 was measured in the continued presence of H⁺ or Ni²⁺. This required the use of cells expressing Kv1.5 channels at a high density so that the residual current, at pH 5.4 or with 2 mm Ni²⁺, was large enough to reliably track recovery kinetics following either enhanced slow inactivation at +50 mV or the induction of a greater level of resting inactivation triggered by removing external K⁺.

Recovery from enhanced slow inactivation at pH 5.4 in 3.5 mm was measured using a single sweep comprising a train of test pulses to +50 mV applied at varying intervals following the inactivating pulse and followed a mono-exponential time course (Fig. 7A). For the sweep of Fig. 7B, which was recorded from the same cell, the control current in pH 5.4, 3.5 mm K⁺ solution was recorded prior to inducing a greater level of resting inactivation by switching to 0 mm K⁺, pH 5.4 solution for 5 s. A train of test pulses was then applied after returning to pH 5.4, 3.5 mm K⁺ solution. The recovery time course, which reflects the re-establishment of the control level of resting channel availability in 3.5 mm K⁺, was also mono-exponential and a plot of the normalized peak test currents from panels A and B against the cumulative recovery time at −80 mV (Fig. 7C) indicates that the two recovery time courses are quite similar. The mean time constants for recovery at pH 5.4 from enhanced slow inactivation and resting inactivation were 2.38 ± 0.15 s and 2.00 ± 0.10 s, respectively, and were not significantly different (P > 0.05; n = 3). Similar voltage and perfusion protocols were used to compare the recovery in 2 mm Ni²⁺ and 3.5 mm (pH 7.4) following enhanced slow inactivation at +50 mV with 3.5 mm or resting inactivation at −80 mV with 0 . Figure 7D shows the normalized peak test currents from a representative experiment. The time courses of recovery following slow inactivation and following resting inactivation in 0 were mono-exponential and the mean recovery time constants of 14.85 ± 1.77 s and 17.51 ± 2.28 s, respectively, were not significantly different (P > 0.05; n = 4). The similarity of the time constants for recovery from enhanced slow inactivation and 0 -induced resting inactivation suggest that slow inactivation and [K⁺]_o-sensitive resting inactivation of Kv1.5 may involve similar kinetic processes.

Figure 7. The time course for recovery from 0 -induced resting inactivation is the same as that for recovery from enhanced slow inactivation.

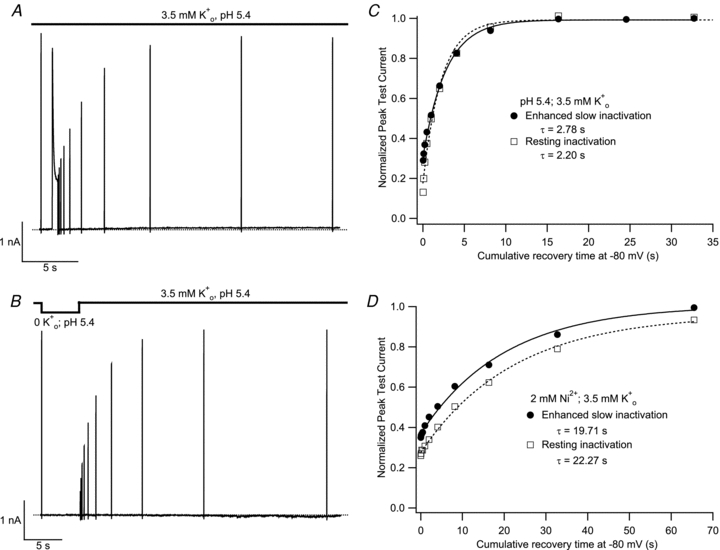
Using cells expressing Kv1.5 channels at high density, current recordings were made in pH 5.4, 3.5 mm K⁺ solution. Following a 20 ms control pulse, the recovery of current in 3.5 mm was monitored, in A, after a 500 ms pulse to +50 mV or, in B, after channel availability was decreased by a 5 s exposure to K⁺-free, pH 5.4 solution. Recovery was monitored using 20 ms test pulses applied at increasing intervals within the same sweep. C, peak test current amplitudes from A and B were normalized with respect to the initial control pulse and plotted against the cumulative recovery time spent at −80 mV. Both data sets were well fitted by a mono-exponential function and had similar time constants. Data shown are from the same cell and are representative of 3 experiments. D, data from another cell (representative of 4 such experiments), where the experiment protocol was analogous to that of panels A and B, and was performed at pH 7.4 with 2 mm Ni²⁺. As with low pH, the time courses of recovery from enhanced slow inactivation and resting inactivation were similar.

Discussion

The two primary questions addressed in this paper are, first, how pH and Ni²⁺ influence slow inactivation of Kv1.5 and, second, whether the H⁺ and Ni²⁺ induced loss of Kv1.5 channel availability represents slow inactivation occurring at rest. We focus first on the effects of H⁺ and Ni²⁺ at +50 mV before discussing the evidence for, and the ramifications of, resting inactivation.

Although the enhanced current decay observed with either ligand at +50 mV could in theory arise from fast open channel block, this explanation is ruled out by previous single channel recordings that revealed no change of the single channel conductance with either ligand (Kwan et al. 2004, 2006). Our results point instead to an enhancement of a complex multistate slow inactivation process as the basis for the accelerated and more complete current decay observed at +50 mV in low pH and Ni²⁺ (Figs 2–4). As has been reported for ShIR channels (Olcese et al. 1997; Klemic et al. 2001; González-Pérez et al. 2008), the time course of the recovery of Kv1.5 channels from control slow inactivation (pH 7.4, 0 mm Ni²⁺) indicates that there are at least two kinetically distinct slow inactivated states (Fig. 5; Rich & Snyders, 1998). Low pH biases slow inactivation to a state from which recovery is fast (Fig. 5B; Table 1), while Ni²⁺ even more strongly biases slow inactivation to a state from which recovery is slow (Fig. 5C). While we cannot rule out an alternative explanation that the slow time course of recovery from Ni²⁺-enhanced slow inactivation reflects the time dependence of Ni²⁺ unbinding, the similarity of the slower recovery time constant following control and Ni²⁺-enhanced slow inactivation suggests this is unlikely. A seemingly similar biasing of slow inactivation has been reported in Kv1.3, where increasing K⁺ occupancy of the outer pore by increasing [K⁺]_o increases the amplitude of a fast component of recovery (Levy & Deutsch, 1996). However, this explanation does not apply in our experiments, since the effects of H⁺ and Ni²⁺ on the recovery time course were observed in 0 mm .

In Kv1.5 the H⁺ or Ni²⁺ binding sites are most likely the H463 residues located in the pore turrets (Kehl et al. 2002; Kwan et al. 2004; Eduljee et al. 2007). An important finding in this connection is that substitutions at these positions (e.g. H463G, H463R) can dramatically accelerate slow inactivation (Kehl et al. 2002; Eduljee et al. 2007). In that light, our observation that ligand binding at this site can enhance slow inactivation in wild-type Kv1.5 bears striking parallels to the action of Cd²⁺ to enhance slow inactivation in ShIR when the threonine at position 449, a site that also influences slow inactivation kinetics, is mutated to cysteine (Yellen et al. 1994). Like Ni²⁺-enhanced slow inactivation in Kv1.5, in ShIR T449C, “‘Cd²⁺-induced inactivation”[at 0 mV] places the channel entirely in the more slowly recovering’ of two inactivated states (Yellen et al. 1994). As noted by Yellen et al. (1994), the ligand-induced enhancement of inactivation during a depolarizing pulse cannot be explained solely by an action to make inactivation an absorbing state; it must also involve an increase of the rate constant for the open to inactivated transition. This is illustrated in Fig. 8B, which shows the outcome of a numerical simulation of a gating scheme incorporating, as required by the experimental data, two open-inactivated states (Fig. 8A, see figure legend for details) in which the O → I transitions are unchanged and inactivation is made to be absorbing by setting the rate for one or both of the I → O transitions to zero. In this scenario, inactivation is complete with sufficiently long pulses but the rate of inactivation is limited by the O → I rate constants and cannot achieve the rates observed experimentally. Much faster slow inactivation is achieved when the rate constant for either one of the O → I transitions is increased (Fig. 8C and D). The simulation results support the conclusion that ligand binding at H463 in Kv1.5, like Cd²⁺ binding at T449C in ShIR, increases the rate constant for the O → I transition. Whether ligand binding does so by causing an allosteric effect, by acting electrostatically to influence the K⁺ concentration at or near the outer pore mouth, or by some other mechanism, remains an open question.

Figure 8. Theoretical outcomes of the modulation of slow inactivation by ligand binding.

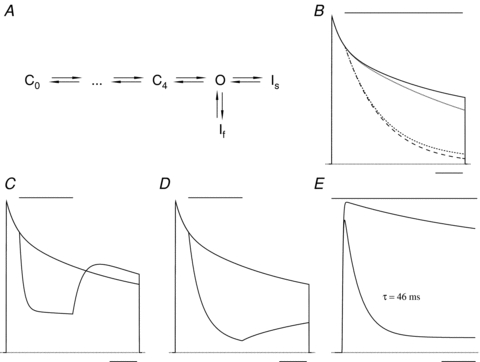
A, the gating model has several closed states in the activation pathway and the open state (O) is coupled to two slow inactivation states, I_f and I_s. For simplicity, the ligand binding/unbinding steps of Scheme II (Fig. 1) are omitted from this revised gating scheme. Although the inactivation rate constants (O → I_f, I_f→ O, O → I_s and I_s→ O of 0.5, 2.2, 0.2 and 0.1 s⁻¹) have been chosen to give macroscopic current behaviour similar to that in Kv1.5 during a 5 s pulse to +50 mV, the simulation is provided for the purpose of illustration only. B, the outcome of the model assuming that ligand application, represented by the bar above the superimposed traces, makes one or both of the inactivation states absorbing (I → O = 0 s⁻¹) but affects neither of the O → I transitions. The relatively modest effect of making I_s (dotted trace), I_f (short dashes trace) or both I_f and I_s (long dashes trace) absorbing emphasizes that rapid current decay, such as that observed in Kv1.5 with H⁺, must involve an increase of the rate constant for the O → I transition. C, the selective enhancement of the O → I_f transition during a 2 s ligand application produces a rapid, mono-exponential decay of current that is followed by a rapid recovery that ‘overshoots’ the control trace. D, ligand application that selectively enhances the O → I_s transition is followed by a slowly recovering current. E, in the model, which does not incorporate inactivation from the resting state, an increase of the O → I_f rate constant and a decrease of the I_f→ O rate constant, which mimics the time course and extent of the current decay in pH 5.4 solution (Fig. 3), causes only a 12% decrease of peak current compared to the control response. This outcome supports the conclusion that the enhancement of slow inactivation makes, at best, a minor contribution to the reduction of peak current observed with Ni²⁺ or H⁺ (e.g. Fig. 2). The calibration bar represents 1 s for panels B–D and 0.1 s for panel E.

Multiple inactivated states can explain the recovery overshoot during a depolarizing pulse

A frequent finding with a transient low pH pulse applied during a depolarizing pulse was a recovery current that overshot the superimposed control current trace (Fig. 3A). The recovery overshoot can be explained given the existence of at least two inactivation processes at +50 mV (Fig. 5). This is illustrated in the numerical simulation of Fig. 8C where an overshoot of the recovery current is obtained when the ligand (i.e. H⁺) causes a selective enhancement of the O → I transition for the inactivated state from which recovery is fast (I_f; Fig. 8A) and which is not directly connected to a more stable inactivated state (I_s). With this constraint, during the ligand application I_f is populated at the expense of I_s and once the ligand is removed there is rapid recovery from I_f, resulting in the recovery overshoot. When the ligand selectively accelerates inactivation to I_s, the recovery kinetics are slow and current does not overshoot the control current level (Fig. 8D), as was usually the case following Ni²⁺ application.

Low pH and Ni²⁺ also induce resting inactivation of Kv1.5 channels

To account for the concentration dependent decline of the peak test current and maximal conductance (Fig. 2), we have proposed that low pH or Ni²⁺ must also trigger a resting inactivation process because enhanced slow inactivation, except at pH values much lower than those used in these experiments, is predicted to have a relatively small effect on peak test currents. To illustrate this point, Fig. 8E shows the outcome of a numerical simulation of the gating scheme in Fig. 8A where the only effect of the ligand is to enhance slow inactivation from the open state by approximately 14-fold, in this case by increasing the rate of the O → I_f transition and decreasing the rate of the I_f→ O transition. Note that despite an increase of slow inactivation at +50 mV to a rate 2- to 3-fold faster than that observed at pH 5.4, the lowest pH we examined, the effect on the peak current amplitude is much smaller than observed in Fig. 2A and B.

Modelling the enhancement of resting inactivation by H⁺ and Ni²⁺

Experimentally, the onset of ligand-induced resting inactivation followed a single exponential time course that was generally slower than enhanced slow inactivation over the range of [H⁺] and [Ni²⁺] tested (Figs 3F and 4E). Figure 9 shows the outcome of a numerical simulation of resting inactivation with Ni²⁺ (Fig. 9A–C) and with low pH (Fig. 9D and E) using a four-state model (Figs 1A and 9F). The critical feature of the model is that resting inactivation is faster (k₁₂ > k₀₃) and the inactivated state is more stable (k₂₁ < k₃₀) for the liganded states. In the fitting procedure, rates were assigned for the forward and reverse transitions between the A and U states and the rates for the transitions were adjusted to match as closely as possible, by eye, the experimental steady-state availability relationship (continuous lines of Fig. 9B and D) and the time dependence of the availability change (continuous lines of Fig. 9C and E) over a range of ligand concentrations. In this iterative approach the values for the rate constants for ligand binding (k₀₁, k₃₂) and unbinding (k₁₀, k₂₃) were also adjusted to optimize the fit to the experimental data. We are unsure if the rate constants in the simulation represent unique solutions and, given the absence of direct information about the binding and unbinding kinetics, this analysis is offered only as a preliminary assessment of the model's plausibility.

Figure 9. Numerical simulation of resting inactivation caused by Ni²⁺ or low pH.

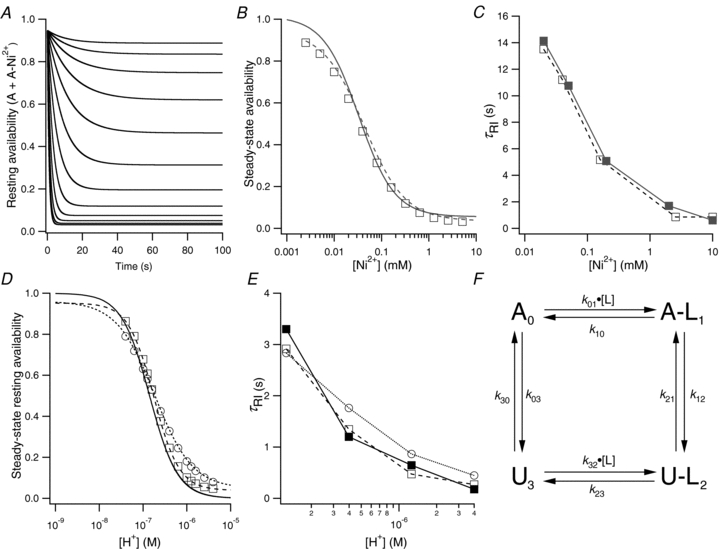
For the simulation with Ni²⁺, the rate constants, based on the scheme in panel F, were: k₀₁ = 110 mm⁻¹ s⁻¹; k₁₀ = 150 s⁻¹; k₁₂ = 1.422 s⁻¹; k₂₁ = 0.036 s⁻¹; k₂₃ = 2.19 s⁻¹; k₃₂ = 1100 mm⁻¹ s⁻¹; k₀₃ = 0.008 s⁻¹; k₃₀ = 0.14 s⁻¹. A, the time dependence of the Ni²⁺-induced decrease of availability, measured as the sum of the proportions of channels in states A and ANi²⁺, was well-fitted by a single exponential. The [Ni²⁺] for the top sweep was 2.5 μm and was doubled for each subsequent sweep. B, the steady-state availability (□), measured from the traces of panel A, is plotted against the [Ni²⁺]. The dashed curve is the fit of the simulated data to the Hill equation (K_d = 36 μm; n_H = 1.0) and the continuous curve is the fit to the experimental data (K_d = 33 μm; n_H = 1.15). C, the values for τ_RI for the simulated (□, from fits of selected traces in A) and experimental (▪) data are plotted against the [Ni²⁺]. For the simulation of extracellular pH induced resting inactivation (D and E), protonation was assumed to trigger an inactivation process different from that induced by Ni²⁺ binding. For ○ in D and E, the rate constants were: k₀₁ = 2 × 10⁹m⁻¹ s⁻¹; k₁₀ = 9000 s⁻¹; k₁₂ = 4.356 s⁻¹; k₂₁ = 0.176 s⁻¹; k₂₃ = 182.3 s⁻¹; k₃₂ = 2 × 10¹⁰m⁻¹ s⁻¹; k₀₃ = 0.03 s⁻¹; k₃₀ = 0.6 s⁻¹ and the binding was assumed to involve a single site (n_H = 1). For □ in D and E, the steepness of the experimental availability curve (n_H = 1.5) was mimicked by changing k₀₁ and k₃₂ to 5 × 10¹²m^−1.5 s⁻¹ and 5 × 10¹³m^−1.5 s⁻¹ and multiplying k₀₁ and k₃₂ by [H⁺]^1.5. The control pH was 7.4 and the test pH ranged from 7.2 to 5.4 in 0.2 pH unit steps. The best fits of the simulated availability data for ○ and □ to the Hill equation are indicated by the dotted line (K_d = 1.8 × 10⁻⁷m; pK_a = 6.73, n_H = 1.0) and the dashed line (K_d = 1.8 × 10⁻⁷m, pK_a = 6.73, n_H = 1.5), respectively. The continuous line is the fit of the experimental concentration dependence (K_d 1.6 × 10⁻⁷m, pK_a = 6.8, n_H = 1.5) taken from Kehl et al. (2002). In panel E the time constants for the loss of availability for the two simulations described for panel D is compared to the experimental values taken from Fig. 3F and represented by ▪. F, the state diagram for resting inactivation at −80 mV. See Fig. 1A for explanation.

The simulation of Ni²⁺-induced resting inactivation shows first, as observed experimentally, a mono-exponential time course for the decrease in channel resting availability, expressed as the sum of the proportion of channels in states A and A-Ni²⁺ (Fig. 9A), and, second, that the fitted time constants correlate well with the mean experimental values (open and filled squares, respectively, in Fig. 9C). There was also good agreement between the simulated (□ and dashed line) and the experimental (continuous line) steady-state availability (Fig. 9B). Simulated recovery (not shown) in 0 mm Ni²⁺ was mono-exponential and the fitted τ_rec of 6.8 s was similar to the experimental value of 7.1 ± 0.4 s.

A similar approach was used to simulate the effects of extracellular acidification (Fig. 9D and E); however, the model explicitly assumed the involvement of a resting inactivation process that differs from Ni²⁺-induced resting inactivation both in its maximum rate (k₁₂) and in the rate of recovery from inactivation (k₂₁). A reasonable fit to the experimental data was obtained when, as with the Ni²⁺ simulation, there was a single binding site (○Fig. 9D and E). Both the fit of the steepness of the steady-state availability relationship and the fit of the time dependence of inactivation were improved when, as implied from the value of 1.5 for the Hill coefficient fitted to the experimental data (Kehl et al. 2002), highly cooperative binding was assumed (□; Fig. 9D and E). The time constant for the simulation of recovery at pH 7.4 following a pulse to pH 5.4 was 3.1 s or roughly twofold slower than the experimentally measured value of 1.6 s (Table 1). This deviation between the simulated and experimental recovery data may reflect a contribution from protonation of residues elsewhere on the channel. In that connection we have noted previously that the shift of the activation curve is much greater for H⁺ than for Ni²⁺ (Kehl et al. 2002; Kwan et al. 2004).

Are the effects of H⁺ or Ni²⁺ on open and resting Kv1.5 channels related?

It seems well-established that both ligands cause resting inactivation and enhance slow inactivation. But is there a mechanistic connection between these two inactivation processes? We consider this possibility first for low pH. The similarity of the time constants for recovery at −80 mV from H⁺-induced resting inactivation and control or H⁺-enhanced slow inactivation (e.g. Fig. 5B) is an argument that H⁺-induced resting inactivation involves the same states visited in H⁺-enhanced slow inactivation and control slow inactivation. An additional argument for a conformational similarity of the enhanced slow inactivated state and the resting inactivated state is the similarities of their recovery kinetics during a depolarizing pulse (Fig. 6A). In other words, at least based on kinetic criteria, H⁺-induced resting inactivation appears to involve a process akin, if not identical, to slow inactivation.

The evidence for conformational similarity between Ni²⁺-induced resting inactivation and enhanced slow inactivation is less compelling. The finding that recovery from Ni²⁺-enhanced slow inactivation proceeds virtually exclusively with the same slow recovery time course that roughly 50% of the inactivated channels follow after control slow inactivation (Fig. 5C) is good evidence that Ni²⁺ steers inactivation at +50 mV to the more stable of the two inactivated states. Additionally, recovery at +50 mV following either enhanced slow inactivation or resting inactivation is comparable (Fig. 6B), which again implies the same inactivated state is involved in inactivation at −80 mV and +50 mV. Evidence against a mechanistic overlap of resting inactivation and enhanced slow inactivation is that recovery at −80 mV (in 0 Ni²⁺) from Ni²⁺-induced resting inactivation was roughly twofold faster than from Ni²⁺-enhanced slow inactivation (Fig. 5C).

Both the onset (i.e. τ_RI) and extent of resting inactivation induced by either ligand were affected by increasing [K⁺]_o from 0 to 3.5 mm (Figs 2–4). Exactly why the addition of causes the onset of resting inactivation to become bi-exponential is unclear, but we suspect that it is related to complexities of the non-competitive interaction between and (Kehl et al. 2002). The sensitivity of resting inactivation to [K⁺]_o (K_d = 1 mm; Kehl et al. 2002) contrasts with the comparative [K⁺]_o insensitivity of slow inactivation of Kv1.5 at +50 mV and is likely to be due to the absence of the mitigating influence of outward K⁺ current. This [K⁺]_o sensitivity might reflect an action of K⁺ to impede the closing of an inactivation gate in the outer aspect of the selectivity filter. Although the [K⁺]_o sensitivity of resting inactivation is reminiscent of the [K⁺]_o sensitivity of slow inactivation in other Kv channels (Baukrowitz & Yellen, 1995; Levy & Deutsch, 1996; Kiss & Korn, 1998) and offers some support for slow inactivation occurring at rest, it is not an infallible benchmark since even with regard to slow inactivation it is a criterion that is not uniformly satisfied (Yang et al. 1997; Fedida et al. 1999). Nonetheless, support for the possibility that resting inactivation does involve a conformational change of the outer pore mouth comes with our demonstration that, as reported for slow inactivated ShIR channels (Basso et al. 1998; Harris et al. 1998), Ba²⁺ movement, at −80 mV, to and from a deep binding site in the Kv1.5 pore is prevented at low pH (Cheng et al. 2008) and by Ni²⁺ (Supplemental Fig. 1).

Evidence from other Kv channels for resting inactivation

As noted above, there are intriguing similarities between the effects of Ni²⁺ on the inactivation of Kv1.5 and the effects of Cd²⁺ on the inactivation of ShIR T449C channels (Yellen et al. 1994). In both cases, divalent cation binding accelerates slow inactivation and induces resting inactivation. The latter phenomenon was not studied in detail in ShIR T449C but it appears, as with Ni²⁺ in Kv1.5, that the onset of resting inactivation is much slower than slow inactivation during a strong depolarization.

In wild-type Kv1.4 channels (Pardo et al. 1992) and the fast inactivating T449A, E and K ShIR mutant channels (López-Barneo et al. 1993) removing causes a loss of current, which in both cases was attributed to a decrease of channel availability at rest. Not only does the same phenomenon occur in Kv1.5 at low pH or in Ni²⁺, as well as in Kv1.5 H463G at pH 7.4 (Kehl et al. 2002), but Fig. 7 illustrates that the time course of recovery from the loss of current induced by either removing or by a depolarization is also the same.

Concluding remarks

As observed by López-Barneo et al. (1993) in fast-inactivating ShIR mutants, in Kv1.5 the enhancement by low pH or Ni²⁺ of slow inactivation (depolarization-induced inactivation) is paralleled by the induction of resting (closed) state inactivation. The data also suggest fairly strongly for low pH and less so for Ni²⁺ that resting inactivation, enhanced slow activation and slow inactivation can involve similar conformational states. Further study is required, but if resting inactivation truly is a variant of slow inactivation it indicates the potential for variability in the degree of coupling between activation and slow inactivation. Complete uncoupling of the type implied here for Kv1.5 appears also to occur in the pore helix mutant ShIR W434F, which has been described as being permanently inactivated at rest (Yang et al. 1997). Resting inactivation in ShIR FWFW channels (i.e. with two W434 residues and two W434F residues; Yang et al. 1997) also shares the [K⁺]_o sensitivity reported here for Kv1.5. As shown for Kv1.5, in the rapidly inactivating FWFW ShIR construct the time course of recovery from the resting inactivated, or unavailable, state is similar to that for recovery from depolarization-induced inactivation (Yang et al. 1997). This raises the possibility that the complex, multistate slow inactivation process, which is normally triggered by a tight coupling between outward voltage sensor movement and a subsequent interaction with the pore domain (Loots & Isacoff, 2000), can proceed independently of activation following mutations in the pore helix (ShIR W434F) or in Kv1.5 by ligand binding at H463 in the pore turret.

Glossary

Abbreviations

A state

available state at −80 mV

A₀

initial level of channel availability

A_rec,f

fast component of current recovery

A_rec,s

slow component of current recovery

A-L state

ligand-bound available state at −80 mV

FAT

fast application tool

ID

inside diameter

O state

open state

O-L state

ligand-bound open state

OD

outside diameter

OI state

open-but-slow-inactivated state

OI-L state

ligand-bound open-but-slow-inactivated state

nh

Hill coefficient

pK_a

apparent acid dissociation constant

ShIR

fast inactivation-removed Shaker mutant

τ_inact

time constant of slow inactivation onset

τ_RI

time constant of resting inactivation onset

U

unavailable state at −80 mV

U-L

ligand-bound unavailable state at −80 mV

Author contributions

Y.M.C. and S.J.K. both contributed to the conception and design of experiments, and the acquisition, analysis and interpretation of the data. S.J.K. performed the numeric simulations. Y.M.C. drafted the manuscript, with critical revision from D.F. and S.J.K. All authors approved the final version for publication. These experiments were performed in the Department of Cellular and Physiological Sciences, University of British Columbia, Vancouver, BC.

Supplemental material

Supplementary Figure 1

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors