Mössbauer, EPR and DFT Studies of Synthetic S = ½ Fe^III-O-Fe^IV=O Complexes. Superexchange-Mediated Spin Transition at the Fe^IV=O Site

Abstract

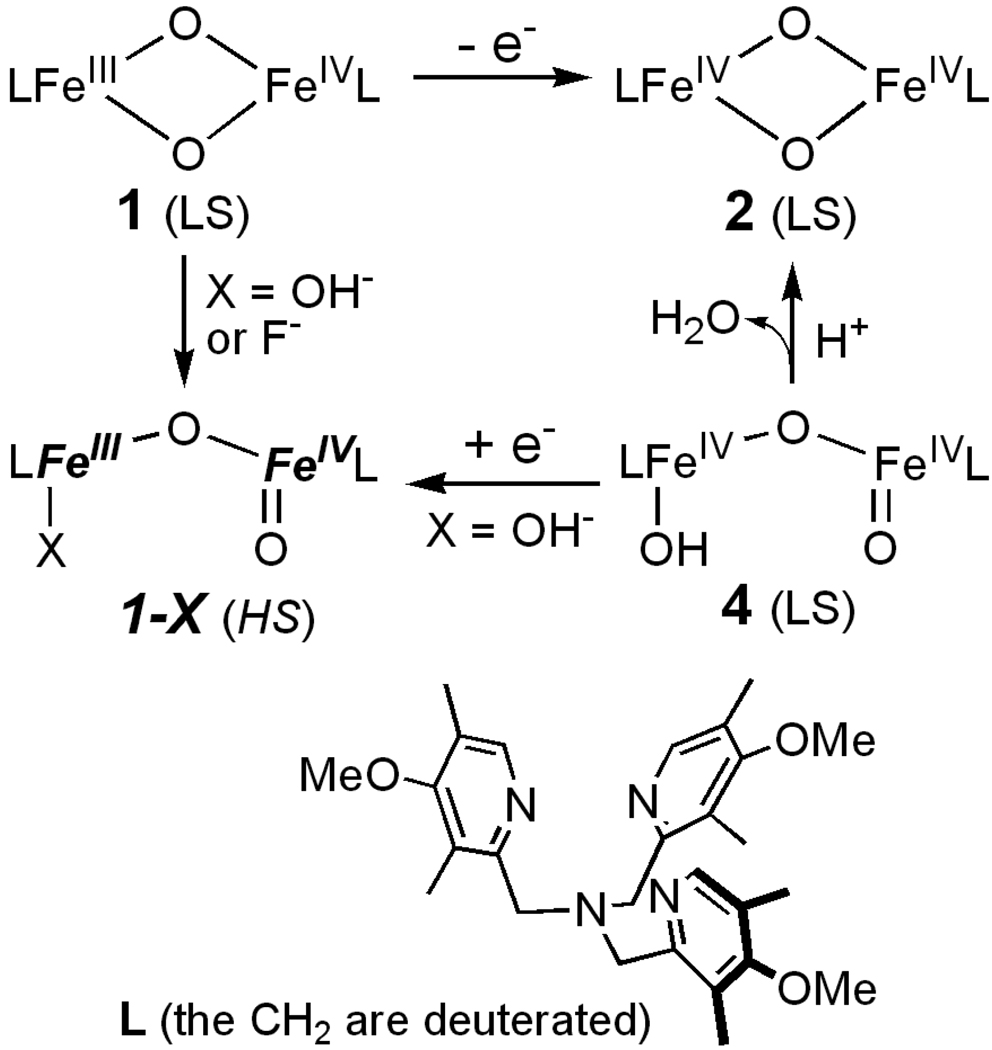
Previously we have characterized two high-valent complexes [LFe^IV(µ-O)₂Fe^IIIL], 1, and [LFe^IV(O)(O)(OH) Fe^IVL], 4. Addition of hydroxide or fluoride to 1 produces two new complexes, 1-OH and 1-F. EPR and Mössbauer studies show that both complexes have an S = ½ ground state which results from antiferromagnetic coupling of the spins of a high-spin (S_a = 5/2) Fe^III and a high-spin (S_b = 2) Fe^IV site. 1-OH can also be obtained by a 1-electron reduction of 4, which has been shown to have an Fe^IV=O site. Radiolytic reduction of 4 at 77 K yields a Mössbauer spectrum identical to that observed for 1-OH, showing that the latter contains an Fe^IV=O. Interestingly, the Fe^IV=O moiety has S_b = 1 in 4 and S_b = 2 in 1-OH and 1-F. From the temperature dependence of the S = ½ signal we have determined the exchange coupling constant J (ℋ= J Ŝ_a·Ŝ_b convention) to be 90 ± 20 cm⁻¹ for both 1-OH and 1-F. Broken-symmetry DFT calculations yield J = 135 cm⁻¹ for 1-OH and J = 104 cm⁻¹ for 1-F, in good agreement with the experiments. DFT analysis shows that the S_b = 1 → S_b = 2 transition of the Fe^IV=O site upon reduction of the Fe^IV-OH site to high-spin Fe^III is driven primarily by the strong antiferromagnetic exchange in the (S_a = 5/2, S_b = 2) couple.

1. Introduction

Non-heme diiron enzymes catalyze the oxidation of various substrates by dioxygen.^1–4 This class includes methane monooxygenase (MMO) and other related monooxygenases, fatty acid desaturases,⁵ and Class I ribonucleotide reductases (RNR).⁶ High-valent intermediates are implicated in the catalytic mechanisms for these enzymes.^{3, 4, 7} For example, intermediate Q of MMO affects the hydroxylation of methane;^8–12 on the basis of EXAFS studies, Q has been proposed to have an [Fe^IV₂(µ-O)₂] diamond-core.¹³ Related diiron(IV) oxidants may be involved in the catalytic cycles of fatty acid desaturases and other diiron monooxygenases resulting from cleavage of the O-O bond in observed peroxo intermediates,^14–16 but direct evidence for such diiron(IV) species has not been obtained. On the other hand, intermediate X of RNR has an S = 1/2 Fe^III-O-Fe^IV core that is responsible for the generation of a catalytically essential tyrosyl radical that initiates ribonucleotide reduction.^{17, 18} A related intermediate has also been observed for the I100W mutant of toluene monooxygenase.¹⁹ For all high-valent diiron intermediates described thus far, the iron(IV) centers are in the high-spin configuration.^{3,8, 17, 19}

In an effort to provide structural, electronic and functional models for the high-valent states of intermediates Q and X, we have synthesized complexes with [Fe^IIIFe^IV(µ-O)₂] (1) and [Fe^IV₂(µ-O)₂] (2) diamond-core structures.^20–22 The complexes of the present study (scheme 1) use tris(3,5-dimethyl-4-methoxylpyridyl-2-methyl)amine as ligand L, which coordinates to each iron via four N donors. The starting material for generating the high-valent complexes is the diferric precursor [Fe^III₂(µ-O)(OH)(H₂O)(L)₂](ClO₄)₃, 3, in which the two iron sites are high-spin. From this precursor we have been able to generate by reaction with H₂O₂ the valence delocalized S = 3/2 Fe^IIIFe^IV complex 1,²⁰ the diamond core diamagnetic diiron(IV) complex 2 (local spins S_a = S_b = 1 are antiferromagnetically coupled to S = 0),²² and the open-core complex [HO-Fe^IV-O-Fe^IV=O], 4, a complex containing S_a = S_b = 1 sites that are ferromagnetically coupled to yield a system with S = 2.^{23, 24} EXAFS studies of 4 indicate a 1.65 Å Fe^IV=O bond and a 3.32 Å Fe-Fe distance (2.73 Å for 2),²² suggesting an open core structure.

Scheme 1.

Interconversion among high-valent diiron complexes. HS (high-spin) and LS (low-spin) refer to the spin states of the individual iron center in each complex.

The iron sites in the nitrogen-rich complexes 1, 2, and 4 are low-spin, which stands in contrast to the high-spin (S_a = 2 or 5/2, S_b = 2) sites in intermediates Q and X.^{3, 25} The high-spin nature of the iron centers in the enzyme intermediates quite likely derives from the fact that the iron ligands are predominantly oxygen donors.¹ Density functional theory (DFT) calculations have suggested that S_b = 2 Fe^IV sites have higher reactivity than S_b = 1 sites, because the former can effectively employ unoccupied σ-frontier orbitals.^26–28 Additional reactivity channels are likely to become available if the diamond core can be opened by transforming one of the bridging oxo ligands, of say 1 or 2, into a terminal oxo functionality.

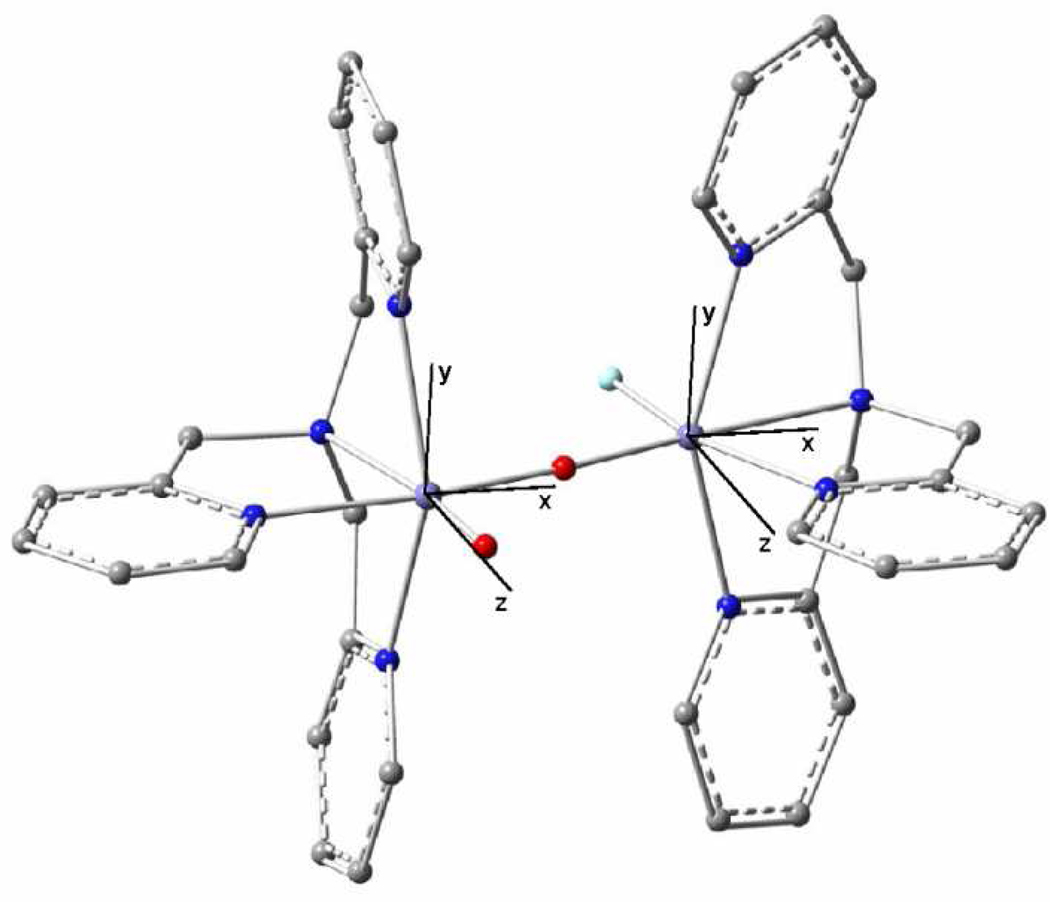
We have recently succeeded²⁹ in transforming 1 into a new complex, 1-OH, with a valence-localized [HO-Fe^III-O-Fe^IV=O] open core for which the iron sites are high-spin (Figure 1). The new short-lived intermediate 1-OH oxidizes the C–H bond of 9,10-dihydroanthracene a million-fold faster than 1. More recently we have also been able to obtain by treatment of 1 with fluoride the related open-core complex 1-F, which has an [F-Fe^III-O-Fe^IV=O] core that is closely related to that of 1-OH. Here we report extensive Mössbauer and EPR studies of the S = ½ ground states of 1-OH and 1-F. By variable temperature EPR we have determined the exchange coupling constants J (in ℋ= J Ŝ_a·Ŝ_b, S_a = 5/2, S_b = 2) to be ≈ 90 cm⁻¹ for both 1-OH and 1-F. Radiolytic reduction experiments of 4 at 77 K, described below, yielded Mössbauer spectra essentially identical to those of 1-OH, suggesting that 4 and 1-OH have the same structure, i. e. the high-spin Fe^IV site in 1-OH has a terminal oxo group. We also report DFT calculations that give insight into the electronic structure of 1-OH and 1-F. In particular, these calculations suggest that exchange interactions are an essential determinant for the transition from S_b = 1 in 4 to S_b = 2 in 1-OH and 1-F.

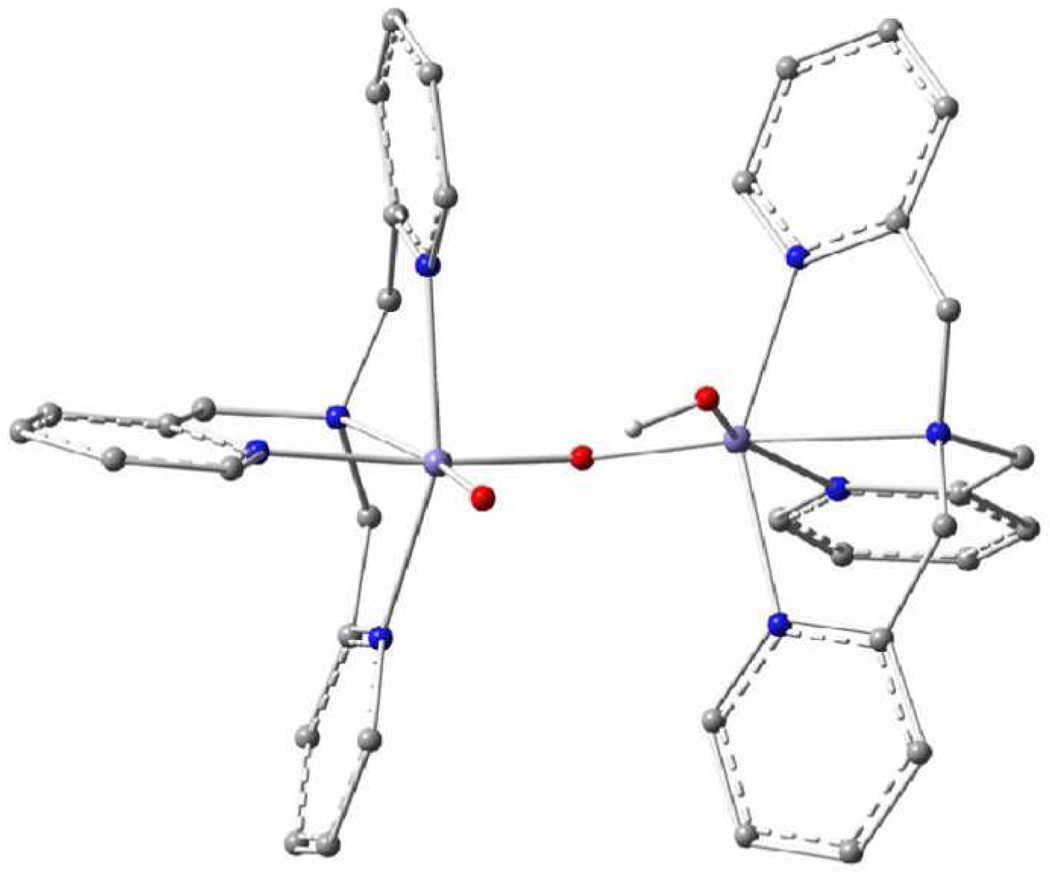
Figure 1.

DFT-optimized structure of 1-OH. In the structure optimization, the Me- and MeO-substituents of ligand L have been replaced by hydrogen atoms. This optimized structure is similar to that of diiron(IV) complex 4.

2. Materials and Methods

2.1 Materials

Tetrabutylammonium fluoride (Bu₄NF) hydrate purchased from Aldrich (98%) was dried under vacuum at 40 °C.³⁰ Butyronitrile (PrCN, 99%+) purchased from Aldrich was purified and dried with reported procedures.³¹ Anhydrous CH₂Cl₂ and MeCN were purchased from Aldrich and used as received. Complexes 1, 4 and 1-OH were prepared following reported procedures.^22,29 The [Fe^III(L)Cl₂]ClO₄ complex was synthesized by modification of a reported procedure for the preparation of the analogue supported by the tris(2-pyridymethyl)amine (TPA) ligand.³² EA: Calcd. for [Fe(L)Cl₂]ClO₄·H₂O (C₂₇H₃₈Cl₃FeN₄O₈): C, 45.75; H, 5.40; N, 7.91; Cl, 15.00. Found: C, 45.57; H, 5.34; N, 7.87; Cl, 14.86.

2.2 Generation of 1-F

To complex 1, solutions (in mixtures of 3:1 PrCN/MeCN or CH₂Cl₂/MeCN to promote glass formation upon freezing) maintained at −80 °C in a UV-vis cell were added 1.5 equivalents of Bu₄NF. The decay of 1 and formation of 1-F were respectively monitored by the absorption decrease at 620 nm and the absorption increase at 385 nm.

2.3 Preparation of EPR and Mössbauer Samples

The frozen samples for EPR and Mössbauer studies typically contain 1.6 to 2.4 mM iron (0.8 mM to 1.2 mM diiron species) in either 3:1 CH₂Cl₂/MeCN or PrCN/MeCN mixed solvents. The samples for Mössbauer were prepared with the latter mixed solvent and contained 95% ⁵⁷Fe isotope. 3:1 MeOH/MeCN was used for preparing the samples for radiolytic reduction, as solvents with high polarity increase the reduction efficiency.

2.4 Physical Methods

Mössbauer spectra were recorded with two spectrometers using Janis Research Super-Varitemp dewars that allow studies in applied magnetic fields up to 8.0 T in the temperature range from 1.5 to 200 K. Mössbauer spectral simulations were performed using the WMOSS software package (WEB Research, Edina, MN). Isomer shifts are quoted relative to iron metal at 298 K. Perpendicular (9.63 GHz) mode X-band EPR spectra were recorded on a Bruker ESP 300 spectrometer equipped with an Oxford ESR 910 liquid helium cryostat and an Oxford temperature controller. The microwave frequency was calibrated with a frequency counter and the magnetic field with an NMR gaussmeter. The quantification of all signals was relative to a Cu-EDTA spin standard. The sample temperature of the X-band cryostat was calibrated with a carbon glass resistor (LakeShore CGR-1–1000) placed at the position of the sample in an EPR tube. The EPR simulation software (SpinCount) was written by one of the authors. All simulations are least-squares fits of the experimental spectra generated with consideration of all intensity factors, which allows computation of simulated spectra for a specified sample concentration. The simulations, therefore, can be used for a quantitative determination of the signal intensities for each complex. The Windows software package (SpinCount) is available for general application to any mono- or dinuclear metal complex by contacting M. P. Hendrich. Samples were γ-irradiated (⁶⁰Co; total dose of 50 kGy) at the γ-irradiation facility of the Breazeale nuclear reactor at Pennsylvania State University. During radiation, samples were maintained at 77 K by immersion in liquid N₂.

In order to generate the data of section 3.7, we have studied the power saturation at each temperature, generated temperature calibration curves using a copper standard and a carbon glass resistor, and repeatedly checked data points that seemed to lie unexpectedly high or too low.

DFT calculations were performed using Becke’s three-parameter hybrid functional (B3LYP) and basis set 6–311G provided by the Gaussian 03 (revision E.01) software package.³³ The ⁵⁷Fe hyperfine parameters were calculated using the properties keyword of the Gaussian code. ⁵⁷Fe isomer shifts, δ, were evaluated from the DFT charge density at the iron nucleus using the calibration give by Vrajmasu et al.³⁴ The coordinates for the optimized structures of the broken-symmetry states for 1-OH_m and 1-F_m are listed in Tables S4 and S5 of the Supporting Information.

3. Results

3.1 Formation of the Open-Core Fe^IIIFe^IV Complexes 1-X

Previously,²⁹ we showed that addition of 3 equivalents of Bu₄NOH to complex 1 at −60 °C resulted in the formation of a new species 1-OH (Scheme 1). 1-OH exhibits an absorption feature near 450 nm and an isotropic S = ½ EPR signal at g = 2.00. The yield of 1-OH estimated by double integration of the g = 2 EPR signal was only 40% with respect to 1, presumably due to its short lifetime at −60 °C, as complete decay occurred within 10 minutes. Attempts to generate 1-OH by this method at lower temperatures were hampered by problems with incomplete conversion and ice formation from water present in the Bu₄NOH, which is obtained as a tridecahydrate. Alternatively, 1-OH can be generated in ~72% yield through one-electron reduction of the [HO-Fe^IV-O-Fe^IV=O] complex 4 at −80 °C. 1-OH generated by reduction of 4 at −80 °C also has a longer lifetime (~1 hour), which facilitates trapping and characterization of this fleeting intermediate.²⁹ However, the presence of a diferric contaminant (~37% of the total iron) in the samples of 4 reduced the overall yield of 1-OH to ~52% with respect to all iron species.

We have found that addition of Bu₄NF to 1 led to the formation of a species closely related to 1-OH. We postulate that F⁻, like OH⁻, binds to 1 and converts it to the open-core complex 1-F (Scheme 1). Because Bu₄NF could be dried to a virtually anhydrous form,³⁰ its use avoided the problems associated with Bu₄NOH·30H₂O at −80 °C. Similar to 1-OH, 1-F shows a near UV absorption feature with λ_max at 385 nm (Figure 2). 1-F was generated in ~74% yield with respect to all iron species, and provided us with a substantially purer sample that facilitated deconvolution of the Mössbauer spectra of the valence-localized Fe^IIIFe^IV complexes. Moreover, the appearance of ¹⁹F superhyperfine splitting in the EPR spectra of 1-F (see below) would be solid evidence for F⁻ binding to 1. Due to the spectral similarities between 1-F and 1-OH, we expect the two complexes to have similar valence-localized X-Fe^III-O-Fe^IV=O open cores.

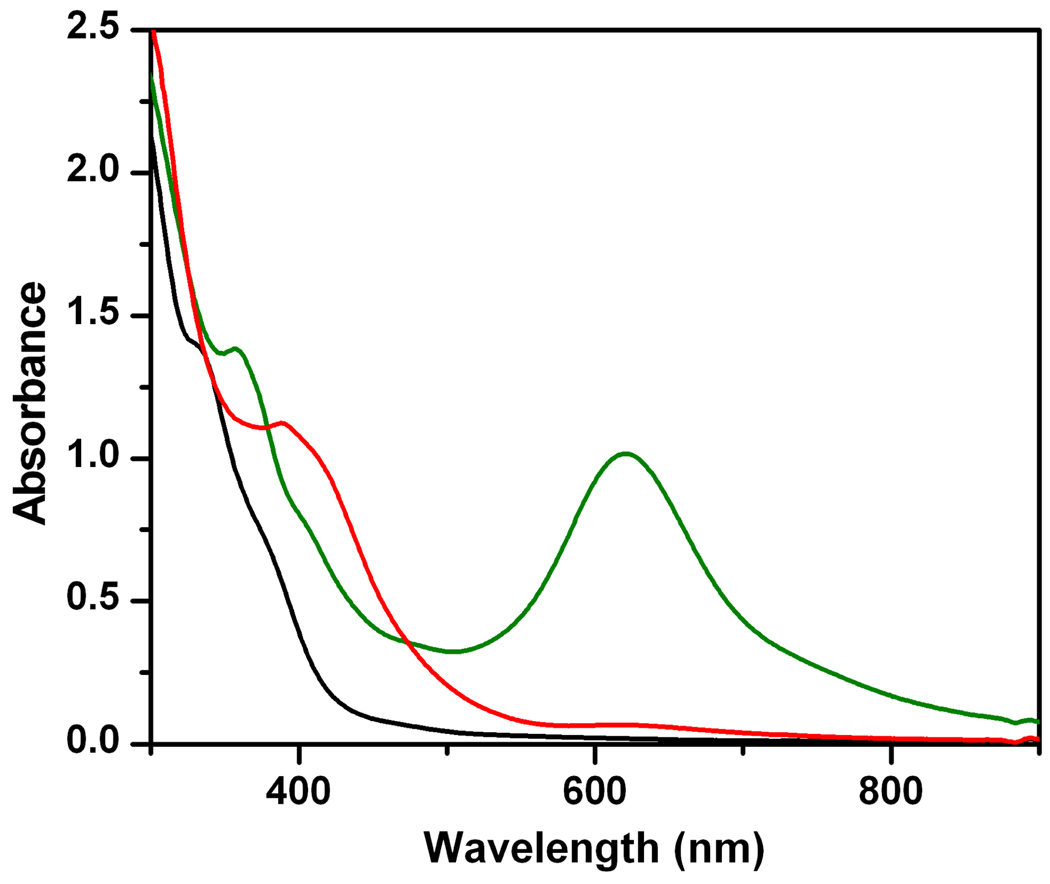
Figure 2.

Spectrophotometric changes observed upon formation and decay of 1-F. The green, red, and black lines respectively represent the spectra of 1, 1-F, and the decay product (after 0.5 hour at −80 °C). Solvent: 3:1 CH₂Cl₂-MeCN.

3.2 EPR Studies

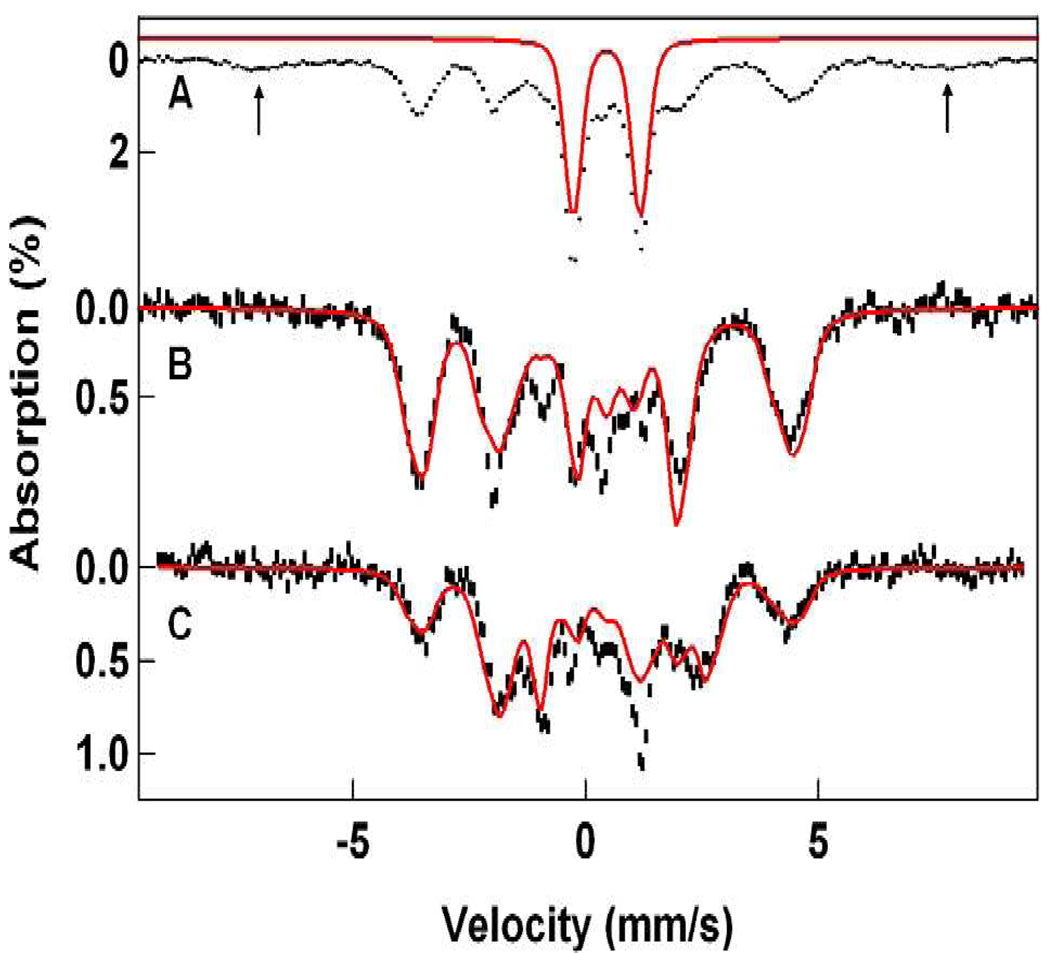
The EPR spectra of 1-OH and 1-F were studied in either 3:1 CH₂Cl₂/MeCN or 3:1 PrCN/MeCN (PrCN = butyronitrile), while only the latter solvent system was used for preparing Mössbauer samples. Both solvent mixtures form frozen glasses, which give rise to sharper EPR and Mössbauer signals, facilitating the spectral analysis. The EPR spectra of 1-OH are essentially identical in both solvent mixtures, suggesting that its structure is not affected by the difference in solvents. The CH₂Cl₂/MeCN mixture, however, produced samples of higher EPR purity (> 96%) and was therefore used for most of the studies (we emphasize that the term “EPR purity” refers to the intensity of signals of interest relative to the combined intensity of all EPR signals). A typical EPR sample of 1-OH was prepared by first reacting 1.2 mM diferric precursor with H₂O₂ to yield 0.9 mM 4 (based on the intensity of its 705-nm band with an ε of 2500 M⁻¹ cm⁻¹)²⁴ and 0.3 mM diferric material (see Mössbauer spectra below), followed by treatment with 0.9 mM ferrocene. The sample of Figure 3A had an S = ½ spin concentration of 0.65 mM, suggesting a 4 → 1-OH conversion yield of 72%. The main contaminant (diferric species) is EPR silent and does not affect the spectral analysis.

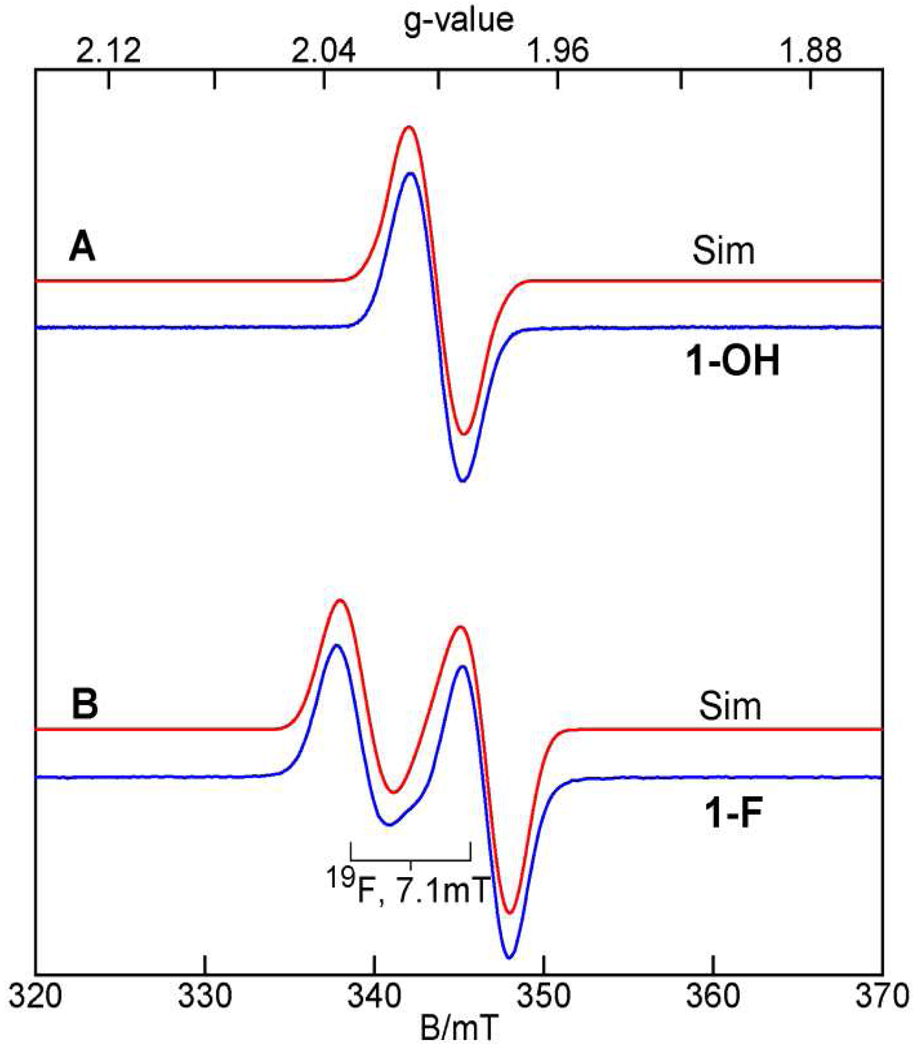
Figure 3.

X-band (9.63 GHz) EPR spectra of (A) 1-OH and (B) 1-F in 3:1 CH₂Cl₂-MeCN. The red lines are least-squares fits with (A) g = 2.002 and (B) = (1.99, 2.01, 2.01), and five equivalent ¹⁴N nuclei with (A) A_14N = 21 MHz and (B) A_14N = 16 MHz. The fit in (B) includes one ¹⁹F nucleus with A = (92, 113, 253) MHz where the coordinate system is suggested by DFT calculations described below. The small shoulder near 342 mT in (B) belongs to a minor contaminant. Experimental parameters: temperature, 27 K; microwave power, (A) 2 µW, (B) 20 µW; modulation, 0.3 mT.

Figure 3A shows an X-band EPR spectrum of 1-OH in 3:1 CH₂Cl₂-MeCN recorded at 35 K. 1-OH exhibits an S = 1/2 resonance centered at g = 2 with a peak-to-trough width of 3.4 mT. Depending on line width assumptions, the spectrum can be fitted with various combinations of g-values that are confined to the range 1.99 – 2.01. Together, the two iron sites of 1-OH have 8 nitrogen ligands (Figure 1), and our DFT calculations (see Figure S5 and Table S3) suggest that 5 of these nitrogens have anisotropic magnetic hyperfine coupling constants of comparable magnitude and anisotropy, with A-tensor components ranging from 14 to 24 MHz, implying that unresolved ¹⁴N hyperfine couplings contribute substantially to the width of the resonance. We have least squares fitted (red line) the spectrum of Figure 3A with an isotropic g-tensor and a hyperfine contribution from five equivalent isotropic ¹⁴N A-tensors; the results are listed in the caption of Figure 3. The best fit shown in Figure 3A was obtained by using A_14N = 21 MHz, which is consistent with the range of A-values from DFT calculations.

Figure 3B shows an EPR spectrum of 1-F. Like 1-OH, this intermediate also has g-values near g = 2. The g = 2 feature, however, is split by substantial ¹⁹F hyperfine interactions,³⁵ showing that fluoride not only causes core isomerization of 1 (see below), but becomes incorporated into the EPR-active complex. Analysis of the spectrum of Figure 3B in a similar manner as for 1-OH afforded a least-squares fit to the spectrum (see red line) with the parameters quoted in the caption of Figure 3. These parameters are very similar to those associated with 1-OH, suggesting similar electronic structures for the two complexes. The g and A_19F tensors are found to be nearly axial, and as with 1-OH, the fit includes five equivalent isotropic ¹⁴N A-tensors with A_14N = 16 MHz. To our knowledge the ¹⁹F hyperfine tensor deduced to be on the Fe^III site is the largest observed to date for an iron complex (e.g., compare A_x ≈ A_y ≈ 63 MHz, A_z = 120 MHz for metmyoglobin fluoride).³⁵ As the Mössbauer data reveal the spin structure of 1-OH and 1-F, we defer variable temperature EPR studies to section 3.7.

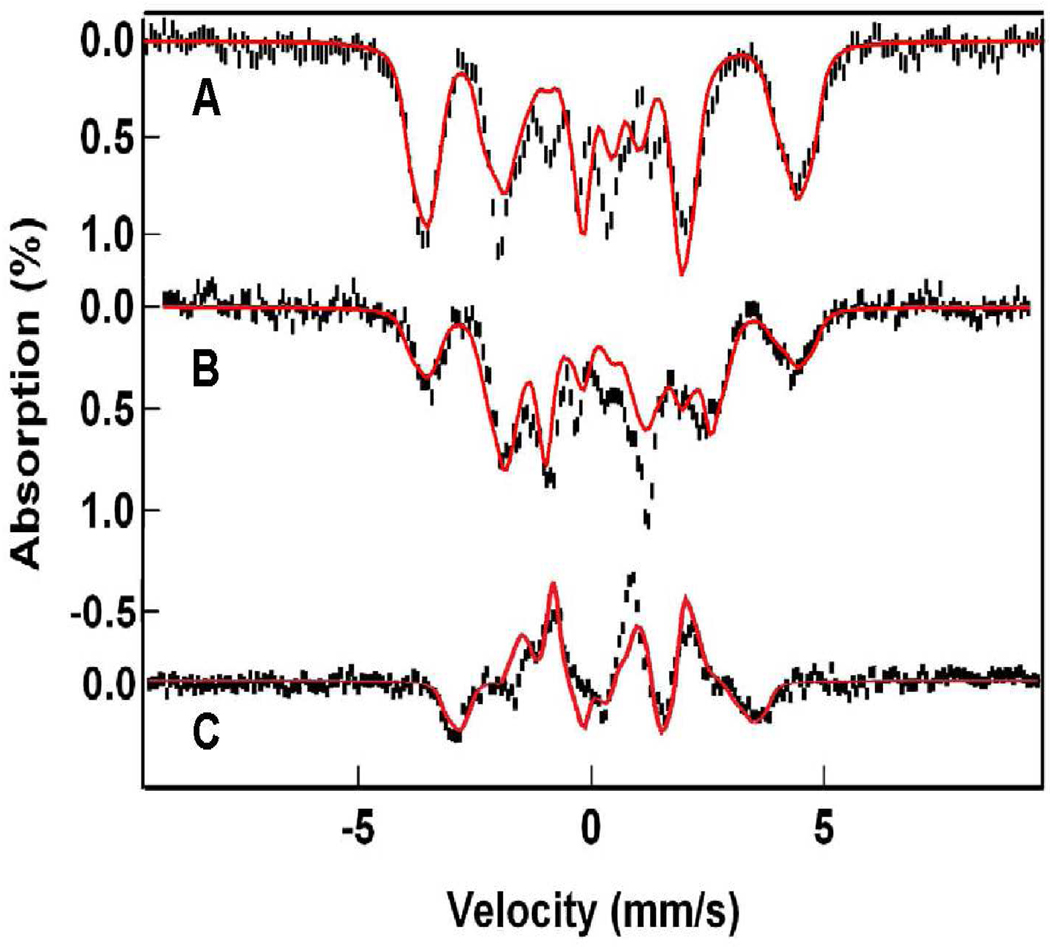
3.3 Mössbauer Spectra of 1-F

Figure 4 shows 4.2 K Mössbauer spectra of 1-F in 3:1 PrCN/MeCN recorded in fields of 50 mT applied parallel (A, B) and perpendicular (C) to the observed γ-rays. The central doublet in Figure 4A with ΔE_Q = 1.5 mm/s and δ = 0.45 mm/s (≈ 22% of total Fe) belongs to a diferric decay product. The spectra of Figures 4B and C, representing 1-F, were obtained by subtracting the contribution of the diferric contaminant from the raw data. The remainder of the absorption belongs to two spectroscopic components (each ≈ 37% of Fe) exhibiting paramagnetic hyperfine structure. The field dependence³⁶ proves that both components are associated with the S = ½ species of Figure 3B. Data recorded in strong applied magnetic fields (see Figure 5) show that the spectral component with the larger splitting, Fe_a, has a magnetic hyperfine tensor, A, with negative components whereas the second site, Fe_b, exhibits positive A-values (in the S = 1/2 representation we use capital letter for the magnetic hyperfine tensors). This type of behavior is well documented and understood for the antiferromagnetically coupled Fe^IIFe^III sites of [Fe₂S₂]⁺ ferredoxins,^37–39 Fe^IIIFe^IV intermediate X of ribonucleotide reductase,¹⁷ and three Fe^IIIFe^IV model complexes (see Scheme 2 and Table 1).^40–42

Figure 4.

Mössbauer spectra of 1-F in 3:1 PrCN/MeCN recorded at 4.2 K in 50 mT fields applied parallel (A, B) and perpendicular (C) to the observed γ rays. The red line in (A) outlines the contribution of a diferric species (22% of Fe; a decay product). The spectra in (B) and (C) were obtained by removing the diferric species from the raw data. The solid red lines in (B) and (C) are spectral simulations for 1-F based on eq 1 using the parameters listed in Table 1. The dashed lines drawn above the data show the contributions of the Fe^III (black) and Fe^IV (blue) sites.

Figure 5.

4.2 K Mössbauer spectra of 1-F recorded in a parallel field of 50 mT (A) and 4.0 T (B). The spectrum shown in (A) is the low field spectrum of Figure 4B. The horizontal arrows indicate the movement of the absorption lines with increasing applied field. Outward moving lines belong to the Fe^IV site. The slanted arrows in (B) mark shoulders belonging to the absorption of the Fe^III site in M_s = + ½ state of the ground doublet. The red solid line is a spectral simulation with eq 1 using the parameters of Table 1.

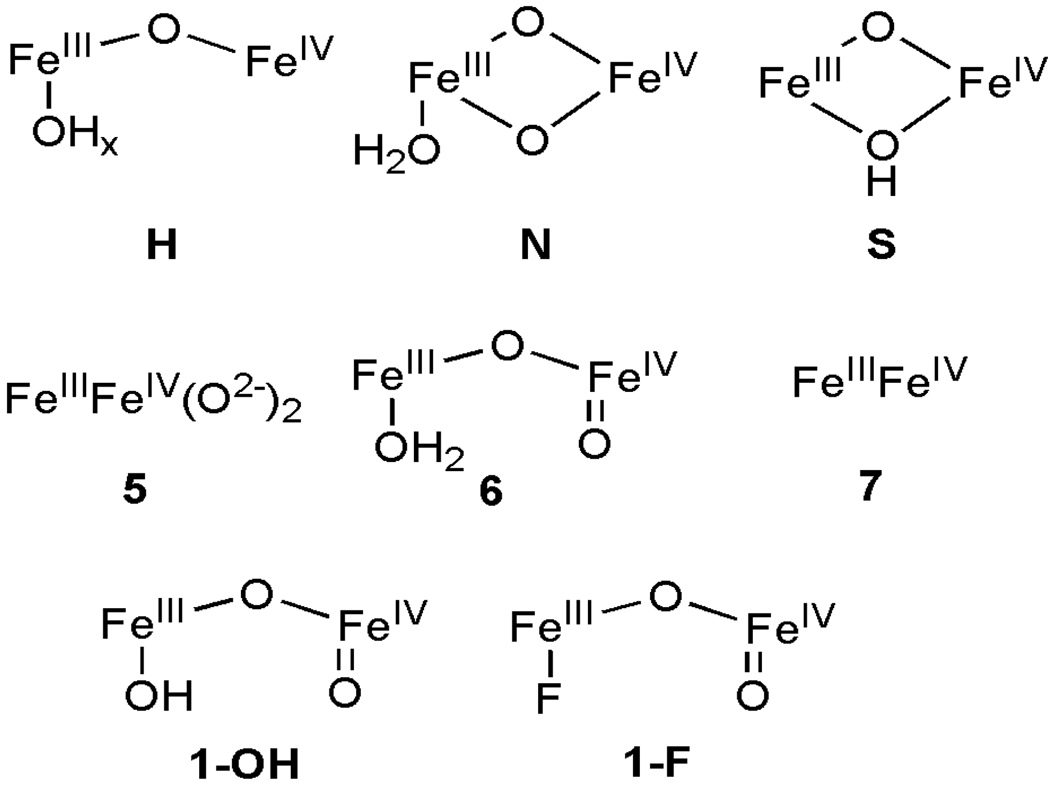
Scheme 2.

The diiron core structures proposed for intermediate X (top) and related synthetic Fe^III-Fe^IV models. Models H, N, and S for X were respectively proposed by Hoffman,⁵³,⁵⁴ Noodleman,⁵⁵ and Solomon.⁵⁶ Due to the limited spectroscopic information, no specific core structure could be proposed for 5 and 7.

Table 1.

⁵⁷Fe hyperfine parameters of 1-F and 1-OH and related complexes. Experimental 4.2 K data were analyzed with eq 1.

Site	System	δ (mm/s)	ΔEQ (mm/s)	η	Ax/gnβn (T)a	Ay/gnβn (T)a	Az/gnβn (T)a	Aiso/gnβn (T)
FeIII	1-F	0.45	1.50	4.3	−52(2)b	−49(2)	−46(2)	−48.7
	1-OH	0.40	−0.60	5.1	−52(2)	−52(2)	−43(2)	−49.2
	RNR R2 Int. Xc	0.56	−0.90	0.5	−54.1	−52.6	−53.4	−53.4
	5d	0.48	1.60	1.0	−47	−47	−47	−47
	6e	0.50	1.30	1.6	−49	−49	−49	−49
	7f	0.56	0.90	−0.3	−55	−51	−55	−53.7
FeIV	1-F	0.10	0.60	−0.7	27(2)b	19(2)	31(2)	25.5
	1-OH	0.09	−0.40	10.0	29(2)	18(3)	23(2)	23.6
	RNR R2 Int. Xc	0.26	−0.60	2.7	20.0	26.8	26.8	24.5
	5d	0.08	0.50	1.0	15	27	27	23
	6e	0.10	1.14	0.1	17	25	20	21
	7f	0.19	0.80	−1.0	19	27	17	21

^aBecause the g-tensors of 1-OH and 1-F are isotropic, the coordinates x, y, and z of the Fe^III and Fe^IV sites cannot be related experimentally for samples containing randomly oriented molecules. However, they become correlated through the D^e/J mixing when the data are analyzed with eq 4. We have labeled the coordinates such that they agree best with the DFT results. The coordinates of complexes 5–7 and intermediate X have not been correlated and are probably better labeled with 1, 2, 3 rather than x,y,z.

^bThe uncertainties of the individual A-tensor components are estimated to be ± 2 T. However, the A_iso values are better than ± 0.5 T.

^cData from ref. 17.

^dData from ref. 40.

^eData from ref. 42.

^fData from ref. 51.

Figure 6A shows a 100 K spectrum of 1-F. At this temperature the relaxation rate of the electronic spin is larger than the nuclear precession frequencies, with the consequence that magnetic hyperfine interactions are (mostly) averaged out; our EPR power saturation studies show that the fast relaxation at 100 K reflects a dominant Raman process.⁴³ As can be seen from the persistence of some broad wings, the system is not quite in the fast relaxation regime (We have tried to get into a faster relaxation regime by warming up the sample to 140 K. Surprisingly, however, the recoilless fraction decreased by almost a factor 5 between 100 K and 140 K and a good spectrum could not be collected. Moreover, long data collection at 140 K leads to substantial decay of 1-F; this complex decays even at 77 K under storage with a half life of roughly six months. We have no indication that 1-OH is unstable at 77 K.). However, we were able to decompose the 100 K zero field spectrum into three doublets corresponding to three different iron environments. The red curve in Figure 6A outlines the diferric component observed in the 4.2 K spectra. Subtracting this component yielded the spectrum of Figure 6B, which contains two doublets with ΔE_Q(a) ≈ 1.5 mm/s, δ(a) ≈ 0.45 mm/s and ΔE_Q(b) ≈ 0.60 mm/s, δ(b) ≈ 0.10 mm/s. The values for δ(a) unambiguously establishes that Fe_a is high-spin ferric, S_a = 5/2 (the value for a_iso/g_nβ_n = −20.9 T, see below, strongly supports this assignment). Since the cluster spin is S = ½, it follows that S_b = 2, and by taking into account the low value for δ(b) it follows that site b is high-spin Fe^IV (a monomeric S = 1 Fe^IV=O complex with the same TPA ligand has δ = 0.01 mm/s; see Table 1 of ref 23).

Figure 6.

Mössbauer spectrum (A) of 1-F recorded at 100 K in a parallel field of 50 mT. The red line in (A) indicates the contribution of a 22% diferric contaminant (same as in Figure 4A). Subtraction of this contaminant yields the spectrum (hashed) of 1-F, shown in (B). The solid line in (B) is the superposition of a doublet representing the Fe^III site (doublet a) with a doublet (b) belonging to the Fe^IV site of 1-F. The broad wings indicate that the electronic system has not yet attained the fast fluctuation limit.

We have analyzed the low-temperature Mössbauer spectra of 1-F and 1-OH with the S = ½ spin Hamiltonian

$$\widehat{\mathscr{H}}=2\mathrm{\beta }\mathbf{B}\cdot \widehat{\mathbf{S}}+{\displaystyle \sum _{\mathrm{i}=\mathrm{a}.\mathrm{b}}\left\{\widehat{\mathbf{S}}\cdot {\mathbf{A}}_{\mathrm{i}}\cdot {\widehat{\mathbf{I}}}_{\mathrm{i}}-{\mathrm{g}}_{\mathrm{n}}{\mathrm{\beta }}_{\mathrm{n}}\mathbf{B}\cdot {\widehat{\mathbf{I}}}_{\mathrm{i}}+{\widehat{\mathscr{H}}}_{\mathrm{Q}}(\mathrm{i})\right\}}$$ (1)

$${\widehat{\mathscr{H}}}_{\mathrm{Q}}(\mathrm{i})=\left(\frac{{\text{eQV}}_{\mathrm{i},\text{zz}}}{12}\right)\left(3{{\widehat{\mathrm{I}}}_{\mathrm{i},\mathrm{z}}}^2-\frac{15}{4}{\mathrm{\eta }}_{\mathrm{i}}\left({{\widehat{\mathrm{I}}}_{\mathrm{i},\mathrm{x}}}^2-{{\widehat{\mathrm{I}}}_{\mathrm{i},\mathrm{y}}}^2\right)\right)$$ (2)

On the basis of the EPR data of Figure 3, we have chosen g = 2 in the electronic Zeeman term. As the g-tensor is nearly isotropic, the Mössbauer spectra (of our frozen solutions) do not correlate to the spatial orientations of the tensors of the two iron sites (We will obtain below, however, a reasonable correlation by working with the full exchange Hamiltonian). The ground state described by eq 1 is the result of antiferromagnetic exchange coupling, ℋ= J Ŝ_a· Ŝ_b, between the high-spin Fe^III site and the high-spin Fe^IV site. Using the appropriate spin projection factors (well known from analyses of [Fe₂S₂]⁺ ferredoxins)³⁸ we can relate the A-tensors of the coupled S = ½ state to the local a-tensors of the individual sites by

$${\mathbf{A}}_{\mathrm{a}}=(7/3){\mathbf{a}}_{\mathrm{a}}\text{and}{\mathbf{A}}_{\mathbf{b}}=-(4/3){\mathbf{a}}_{\mathbf{b}}$$ (3)

Eq 3 holds only in the strong coupling limit (see below). The solid lines in Figures 4–6 are the result of spectral simulations for 1-F based on eq 1 using the parameters listed in Table 1; spectra of the individual sites are outlined by the dashed lines. In general, the magnetic hyperfine interactions of the high-spin Fe^III sites are isotropic; noteworthy exceptions are the ferric sites of exchange coupled [Fe₂S₂]⁺ clusters^{37, 38} and diiron(II,III) centers.^{44, 45} In order to account for the line shape of the Fe^III site of 1-F, we had to allow for considerable anisotropies of the A-tensor, as indicated in Table 1 (we explain this observation below). The value for the local (low case letter) a_iso/g_nβ_n = (a_x+a_y+a_z)/3g_nβ_n = −20.9 T (corresponding to a_iso = −28.6 MHz) agrees within 2% with the a_iso values we have observed for monomeric high-spin ferric species involving TPA-type ligands; for data on [Fe^III(L)Cl₂]⁺ see Figure S3 in Supporting Information.

Given that ΔE_Q of the Fe^IV site is quite small, the line shapes of its low temperature spectra depend essentially on the anisotropy of the A-tensor. After subtracting the diferric contaminant and the contribution of the Fe^III site, we have least squares fitted the spectra of the Fe^IV site making various assumptions about the range of the A-tensor components. The best parameter set for the Fe^IV site is listed in Table 1, where we have used coordinate labels x, y, and z that relate the measured ⁵⁷Fe (and ¹⁹F) A-tensors best to the results of our DFT calculations. Note that the A-tensor of the Fe^IV site is nearly axial and that the largest component of the electric field gradient tensor is perpendicular (along x, y) to the “symmetry” axis of the A-tensor.

Eq 3 shows that the magnetic hyperfine tensor of the Fe^IV site changes sign when expressed in the coupled state (the minus sign in eq 3 results because the smaller spin of the pair, S_b, is oriented antiparallel to the system spin S). Consequently, the magnetic hyperfine splittings of the Fe^III site will decrease with increasing applied field (the components of a_a are negative) while those of the Fe^IV site increase, as seen experimentally in the 4.0 T spectrum of Figure 5.

3.4 Mössbauer Spectra of 1-OH

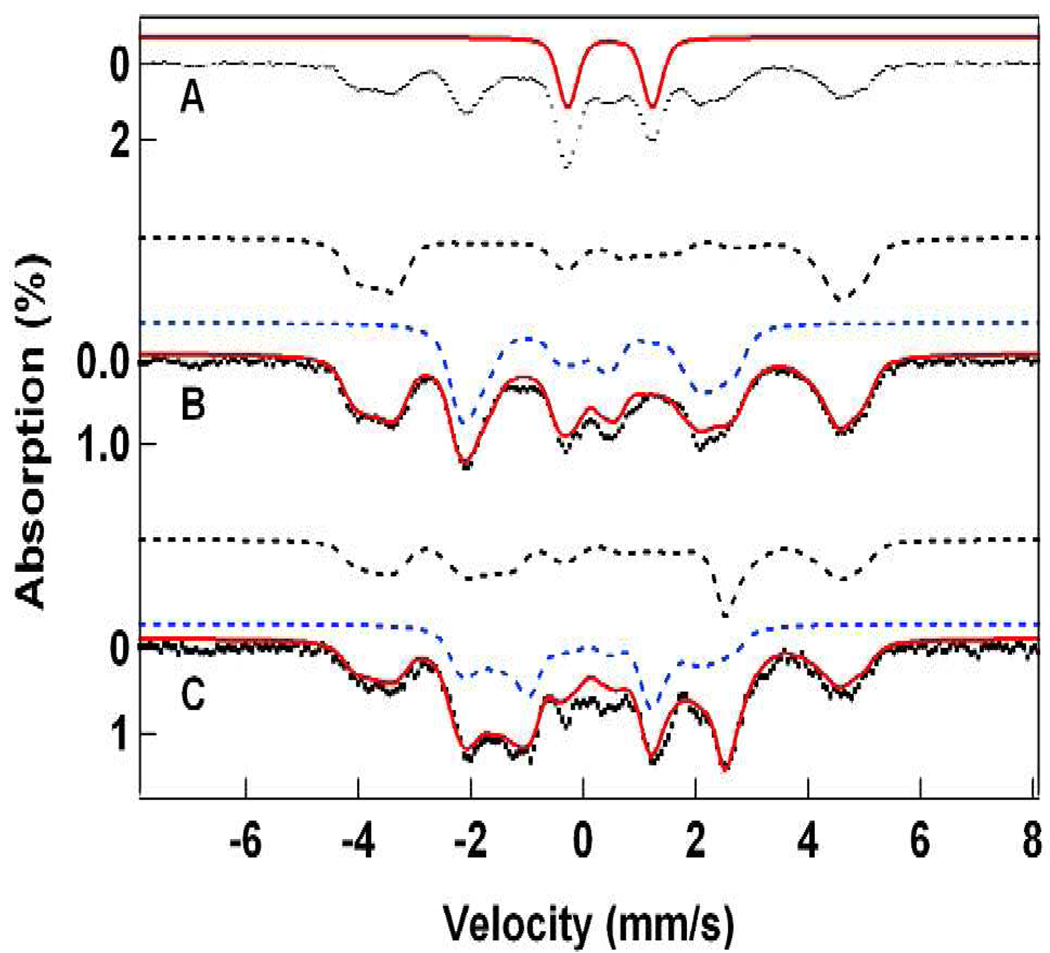
The Mössbauer sample of 1-OH was prepared by 1e–reduction of the diiron(IV) complex 4,²³ which in turn was obtained by reaction of diferric complex 3 with H₂O₂. The spectra of 1-OH contain a high-spin Fe^III contaminant (12% of Fe), representing a collection of species, with broad features (its outer lines are marked by arrows in Figure 7A). Its Mössbauer features are characteristic of precipitated and aggregated Fe^III and the samples did not exhibit EPR features attributable to magnetically isolated high-spin Fe^III. Figure 7A shows a 4.2 K spectrum of a sample in 3:1 PrCN/MeCN containing ca. 52% 1-OH; the solid line outlines the contribution of a 37% diferric contaminant (already present in the diiron(IV) “starting material”), which we have removed from the raw data together with the high-spin Fe^III species to obtain the spectrum of Figure 7B. The transverse field spectrum of Figure 7C was prepared similarly. The solid lines in (B) and (C) are spectral simulations using the parameters listed in Table 1.

Figure 7.

Mössbauer spectra of 1-OH in 3:1 PrCN/MeCN recorded at 4.2 K in 50 mT fields applied parallel (A, B) and perpendicular (C) to the observed γ radiation. The red line in (A) outlines the spectrum of a diiron(III) contaminant; its contribution has been removed in (B) and (C). The solid lines in (B) and (C) are spectral simulations based on eq 1 using the parameters listed in Table 1. See also Figure 8. The arrows in (A) mark the outer lines of a high-spin ferric contaminant.

3.5 Mössbauer Analysis Using the Full Spin Hamiltonian

In the literature, the low temperature Mössbauer and EPR spectra of S = 1/2 Fe^IIIFe^II and Fe^IIIFe^IV complexes with S_a = 5/2 and S_b = 2 are often described by eq 1. Description by the effective S = ½ Hamiltonian, however, is correct only in the strong coupling limit, J ≫ |D_a, D_b|, where D_a and D_b are the zero-field splitting parameters (ZFS) of Fe_a and Fe_b. For |D_a, D_b|/J ≥ 0.1 the ground state properties are noticeably modified through mixing of the ground state with S = 3/2 and 5/2 excited states of the spin ladder by ZFS terms, an effect sometimes referred to as D/J mixing. Mixing is recognized by the observation of sizable anisotropies of A_a in eq 1, as in the case for 1-OH and 1-F; A_b gets modified as well, but as A_b is intrinsically anisotropic the effects of D/J mixing are difficult to recognize. In order to compare the Fe^IV A-tensor with DFT calculations (which ignore spin-orbit coupling), one has to remove the contributions from D/J mixing. This can be accomplished by analyzing the data with the full exchange Hamiltonian

$$\widehat{\mathscr{H}}={\mathrm{J}\widehat{\mathbf{S}}}_{\mathrm{a}}\cdot {\widehat{\mathbf{S}}}_{\mathrm{b}}+{\displaystyle \sum _{\mathrm{i}=\mathrm{a},\mathrm{b}}\left\{{\mathrm{D}}_{\mathrm{i}}[{\widehat{\mathrm{S}}}_{\mathrm{i},\mathrm{z}}^2-{\mathrm{S}}_{\mathrm{i}}({\mathrm{S}}_{\mathrm{i}}+1)/3+({\mathrm{E}}_{\mathrm{i}}/{\mathrm{D}}_{\mathrm{i}})({\widehat{\mathrm{S}}}_{\mathrm{i},\mathrm{x}}^2-{\widehat{\mathrm{S}}}_{\mathrm{i},\mathrm{y}}^2)]+2{\mathrm{\beta }\widehat{\mathbf{S}}}_{\mathrm{i}}\cdot \mathbf{B}+{\widehat{\mathbf{S}}}_{\mathrm{i}}\cdot {\mathrm{a}}_{\mathrm{i}}\cdot {\widehat{\mathbf{I}}}_{\mathrm{i}}-{\mathrm{g}}_{\mathrm{n}}{\mathrm{\beta }}_{\mathrm{n}}\mathbf{B}\cdot {\widehat{\mathbf{I}}}_{\mathrm{i}}+{\widehat{\mathscr{H}}}_{\mathrm{Q}}(\mathrm{i})\right\}}$$ (4)

Using a second-order perturbation approach, Sage et al.⁴⁴ have analyzed D/J mixing for the S = ½ diiron(III,II) state of purple acid phosphatase. The crucial quantity for mixing is the quantity D^e/J, where D^e is a traceless effective ZFS tensor. For collinear ZFS tensors for the two sites, as we have assumed in eq 4, the diagonal components of D^e can be written as

$${\mathrm{D}}_{\text{xx},\text{yy}}^{\mathrm{e}}=8{\mathrm{D}}_{\mathrm{a}}[\pm {(\mathrm{E}/\mathrm{D})}_{\mathrm{a}}-1/3]+3{\mathrm{D}}_{\mathrm{b}}[\pm {(\mathrm{E}/\mathrm{D})}_{\mathrm{b}}-1/3]$$ (5)

$${\mathrm{D}}_{\text{zz}}^{\mathrm{e}}=(16/3){\mathrm{D}}_{\mathrm{a}}+2{\mathrm{D}}_{\mathrm{b}}$$ (6)

While inclusion of D/J mixing introduces at least 5 additional unknowns, the present situation can be simplified because D_b is expected to dominate in eqs 5 and 6. Thus, D ≈ +10 cm⁻¹ and E/D ≈ 0 have been reported for the octahedral sites of the S = 2 complexes (H₂O)₅Fe^IV=O⁴⁶ and Fe^IV=O intermediate J of taurine:αKG dioxygenase,⁴⁷ and the D_a values are expected to be smaller than 1 cm⁻¹. Therefore, eqs 5 and 6 practically reduce to ${\mathrm{D}}_{\text{xx},\text{yy}}^{\mathrm{e}}\approx -{\mathrm{D}}_{\mathrm{b}}$ and ${\mathrm{D}}_{\text{zz}}^{\mathrm{e}}\approx 2{\mathrm{D}}_{\mathrm{b}}$.

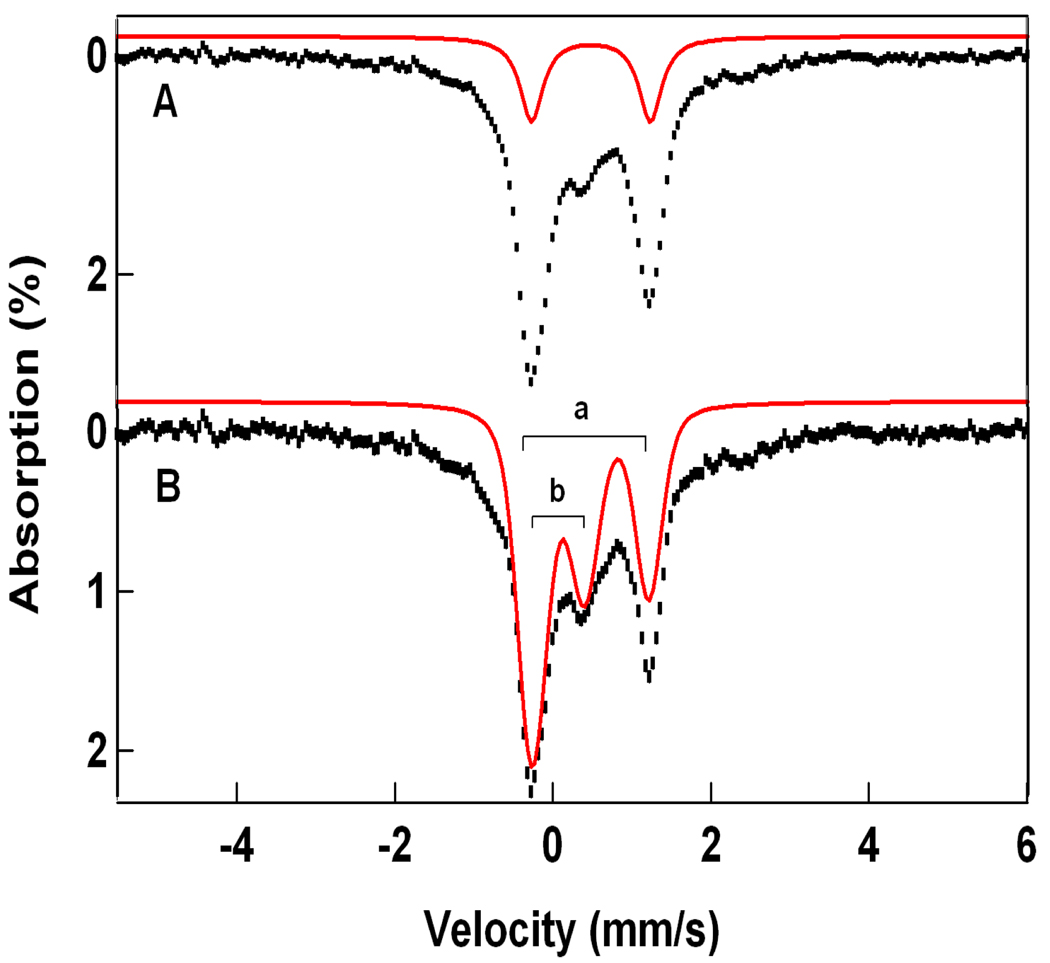
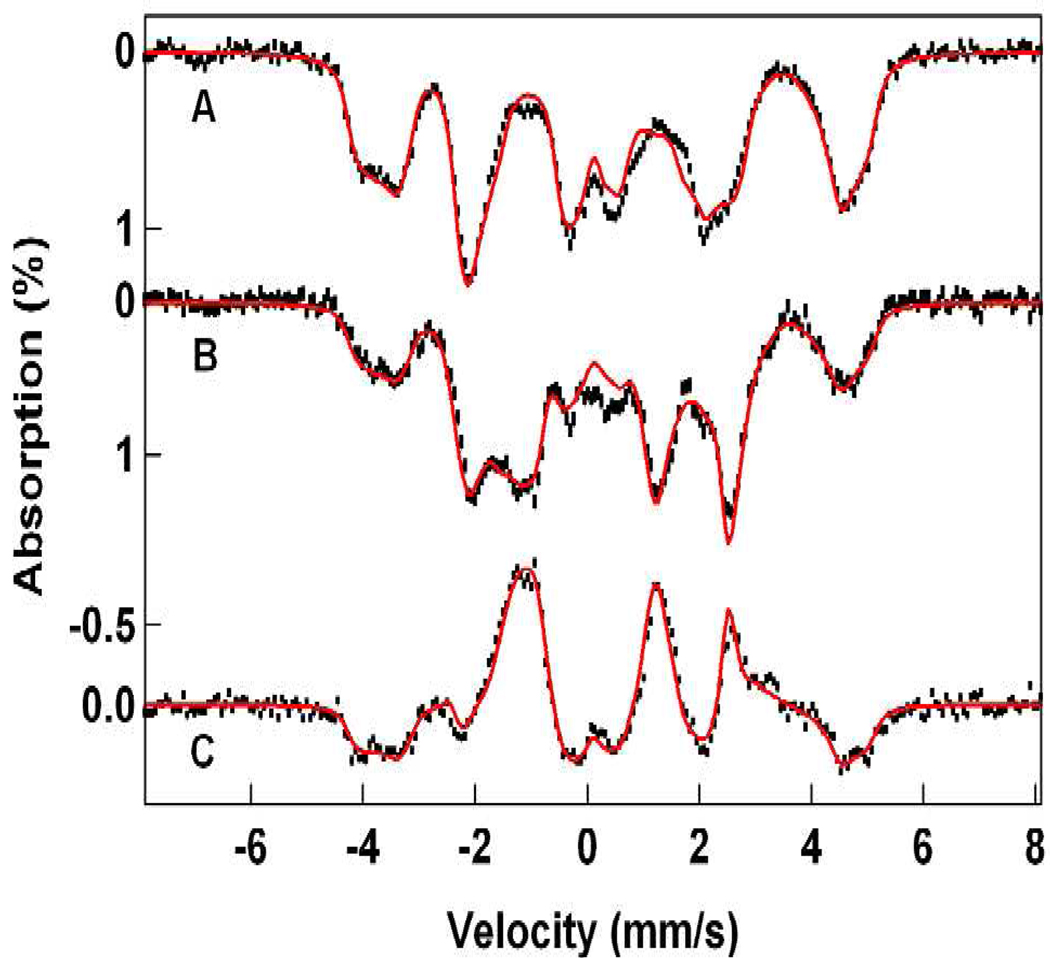
Starting with the solutions obtained with eq 1, we have analyzed the spectra of Figures 4, 5, and 7 with eq 4, using the 2Spin option of WMOSS. Since the 4.2 K spectra depend only on the ratio D^e/J, the problem simplifies to finding the appropriate D_b/J ratio. The A-tensor of the Fe^III site in 1-OH is axial, which fits quite well to the above choice of D^e. In contrast, the Fe^III site of 1-F has a rhombic A-tensor, which can be accommodated by using D_a = 0, D_b ≠ 0 and (E/D)_b ≠ 0 in eqs 5 and 6. Figure 8 shows simulations of the 1-OH spectra using the parameters quoted in Table 2. Although the two Fe^III contaminants in the spectra of Figure 7 can be reasonably well subtracted from the data, the spectral range between −0.5 and + 1.5 mm/s is afflicted with considerable amplitude uncertainties. By taking the difference spectra of the data taken in parallel and transverse applied field (“parallel minus transverse field”, Figure 8C), these contaminants cancel. It can be seen that our simulation of the difference spectrum fits the data quite well. The same procedure gives excellent simulations for 1-F, shown in Figure 9, using the parameters listed in Table 2.

Figure 8.

4.2 K Mössbauer spectra of 1-OH analyzed with eq 4. Spectra in (A) and (B) are the same as in Figure 7. Spectrum in (C) is a difference spectrum obtained by forming the difference spectrum “parallel minus transverse.” In the difference spectrum, the contributions of the two Fe^III contaminants cancel. Solid lines are spectral simulations using the parameters listed in Table 2.

Table 2.

Experimental and DFT (bold) ⁵⁷Fe hyperfine parameters for 1-OH and 1-F. Experimental parameters were obtained from simulations based on eq 4 using J = 90 cm⁻¹ for both complexes.

	System	δ (mm/s)	ΔEQ (mm/s)	η	D (cm−1)	ax/gnβn (T)	ay/gnβn (T)	az/gnβn (T)	aiso/gnβn (T)
FeIII	1-Fm (DFT)	0.45	1.36	0.9		−21.4	−20.8	−20.5	−20.9a
	1-F (Exp.)	0.45	1.50	4.3	0b	−20.9	−20.9	−20.9	−20.9
	1-OHm (DFT)	0.43	1.24	1.0		−21.4	−20.8	−21.1	−21.1a
	1-OH (Exp.)	0.40	−0.60	5.1	0b	−21.1	−21.1	−21.1	−21.1
FeIV	1-Fm (DFT)	0.14	−0.43	0.7		−18.5	−13.6	−26.1	−19.4a
	1-F (Exp.)	0.10	0.60	−0.7	6.3b	−18.6c	−13.4	−26.3	−19.4
	1-OHm (DFT)	0.13	0.20	0.1		−18.5	−12.2	−23.8	−18.2a
	1-OH (Exp)	0.09	−0.40	10.0	12b	−20.0c	−12.0	−22.5	−18.2

^aThe Fermi contact term is generally poorly reproduced by DFT calculations. We have therefore used the experimental a_iso and added the calculated a_SD to obtain “theoretical” a-values.

^bThe anisotropy of A_a is smaller for 1-F than for 1-OH (see Table 1), implying that the quantity D^e/J is smaller for 1-F. We suspect that D_b has about the same value for the Fe^IV=O sites of both complexes. Note that we arbitrarily set D_a = 0. By using different values for D_a (see eqs 5 and 6) we can achieve the required D^e/J values and use the same D_b for both complexes; it is likely that the two Fe^III sites have a different D_a. For 1-OH we used (E/D)_a = 0 for 1-OH and (E/D = = 0.2 for 1-F.

^cErrors for a-tensor components of the Fe^IV=O sites are roughly ± 2 T.

Figure 9.

4.2 K Mössbauer spectra of 1-F analyzed with eq 4. Spectra in (A) and (B) are the same as in Figure 4. Spectrum (C) is a difference spectrum “parallel minus transverse field” using the data of Figure 5A and its transverse field counterpart. Red solid lines are spectral simulations using the parameters listed in Table 2.

3.6 Radiolytic Reduction of 4

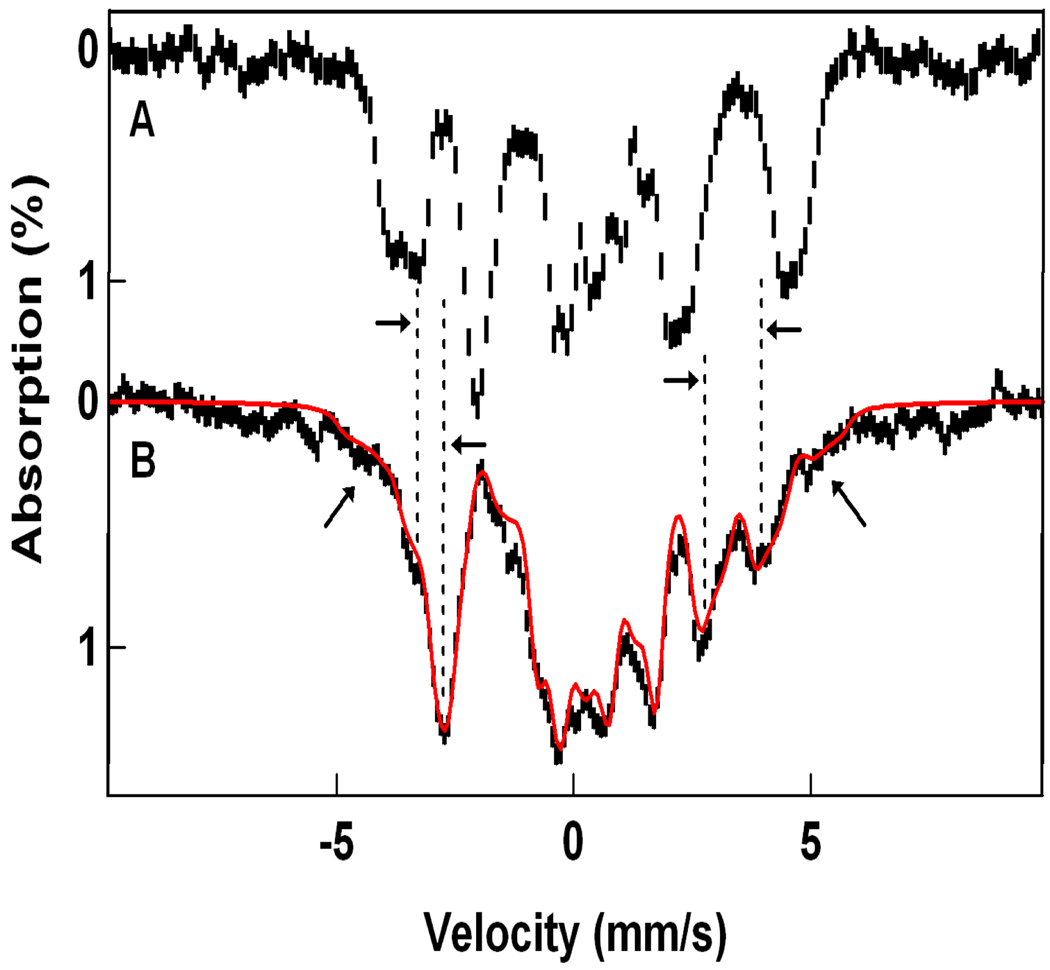
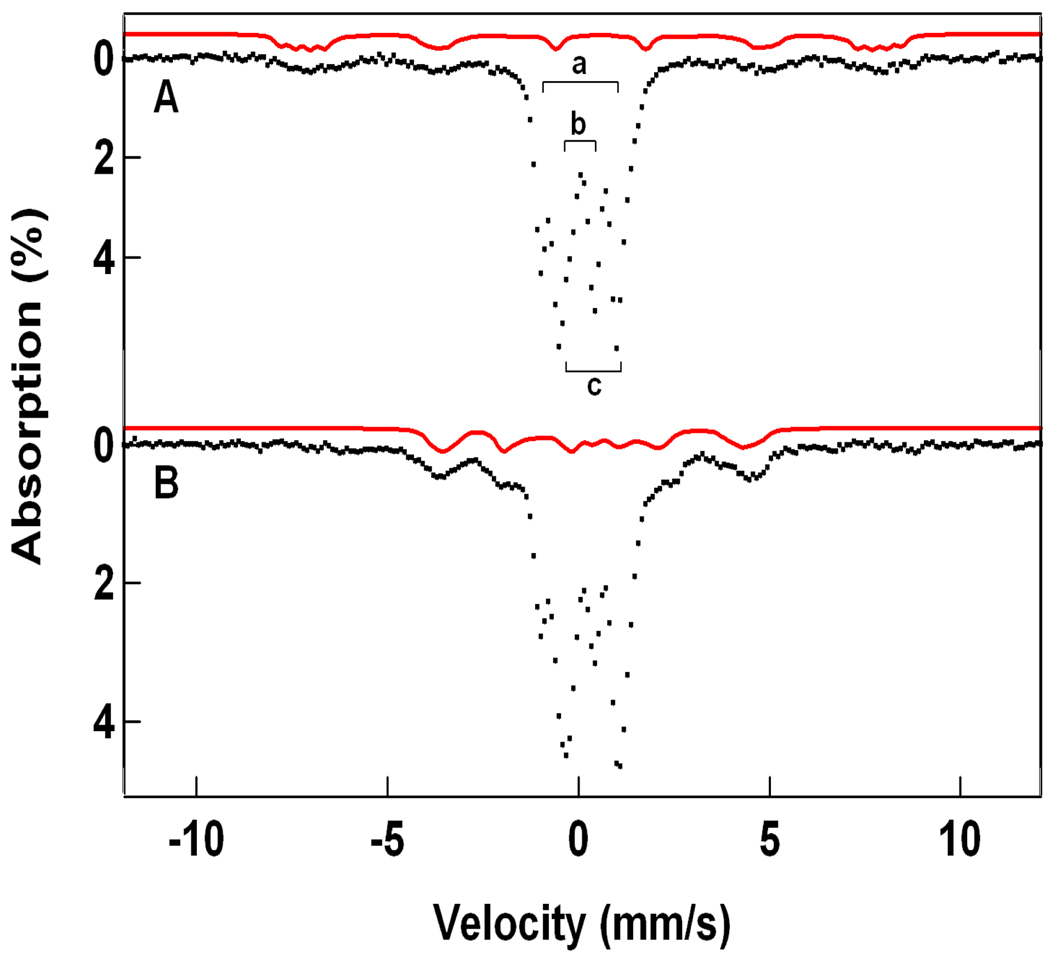
As a means of determining the core structure of 1-OH relative to the HO-Fe^IV-O-Fe^IV=O open core of 4, the latter was subjected to radiolytic reduction at 77 K,⁴⁸ a temperature at which the ligands are expected to be essentially immobile, in order to compare the Mössbauer spectra of the radiolytically reduced species with those derived from ferrocene reduction of 4. Figure 10A shows a 4.2 K Mössbauer spectrum of 4 prior to reduction, prepared as described previously.²³ 65% of the Fe of the sample yields the two doublets of 4, previously labeled a and b,²³ 22% of the Fe contributes a doublet characteristic of a diamagnetic diiron(III) species (most likely due to residual 3 and decay products of 4), and ca. 10% of the Fe belongs to an EPR-silent high-spin ferric species whose broad features are outlined by the simulation of Figure 10A. Figure 10B shows a spectrum of the same sample after a 5 h irradiation (dose 50 kGy) with ⁶⁰Co γ-rays at 77 K. Analysis of the spectrum showed that about half of the iron of diiron(IV) complex 4 was converted to a species that produces the same Mössbauer spectrum as 1-OH; the spectral contribution of this species is outlined by the solid line, the theoretical spectrum of 1-OH shown in Figure 7B. The new species in Figure 10B also exhibits the field dependence (“parallel minus transverse field”) that links it to an isotropic EPR active species (An EPR study of a sample irradiated together with the Mössbauer sample revealed ≈ 14 mM radical species in the g = 2 region that completely masked the S = ½ signal (ca. 0.2 mM) of 1-OH. Annealing at 120 K for 20 min did not measurably diminish the concentration of radicals.). If we make the plausible assumption that the ⁶⁰Co irradiation changes only the oxidation state but not the structure, then the studies just described indicate that 1-OH has essentially the same structure as 4, namely an Fe^IV site with a terminal oxo group (Fe_b) and an Fe^III site with a terminal hydroxo group (Fe_a), a suggestion supported by the DFT studies presented below (see section 4.2).

Figure 10.

Mössbauer spectra of 4 (A) in 3:1 MeOH/MeCN and ⁶⁰Co irradiated 4 (B) recorded at 4.2 K in a 50 mT field applied parallel to the γ-rays. (A) The downward brackets in (A) label the Fe^IV sites of 4; the letter “b” designates the site with a terminal oxo group. The upward bracket marks the lines of the diferric contaminant (22% of Fe). The solid line above the spectrum is a simulated representation of a high-spin Fe^III contaminant, representing ca. 10% of the Fe. The two ferric species were not affected by the irradiation with ⁶⁰Co. (B) Spectrum of the sample of (A) after ⁶⁰Co irradiation at 77 K. The solid red line is the simulation of 1-OH shown in Figure 7B. The high-spin Fe^III contaminant has been removed using the simulation shown in (A).

3.7 Determination of Exchange Coupling Constants by EPR

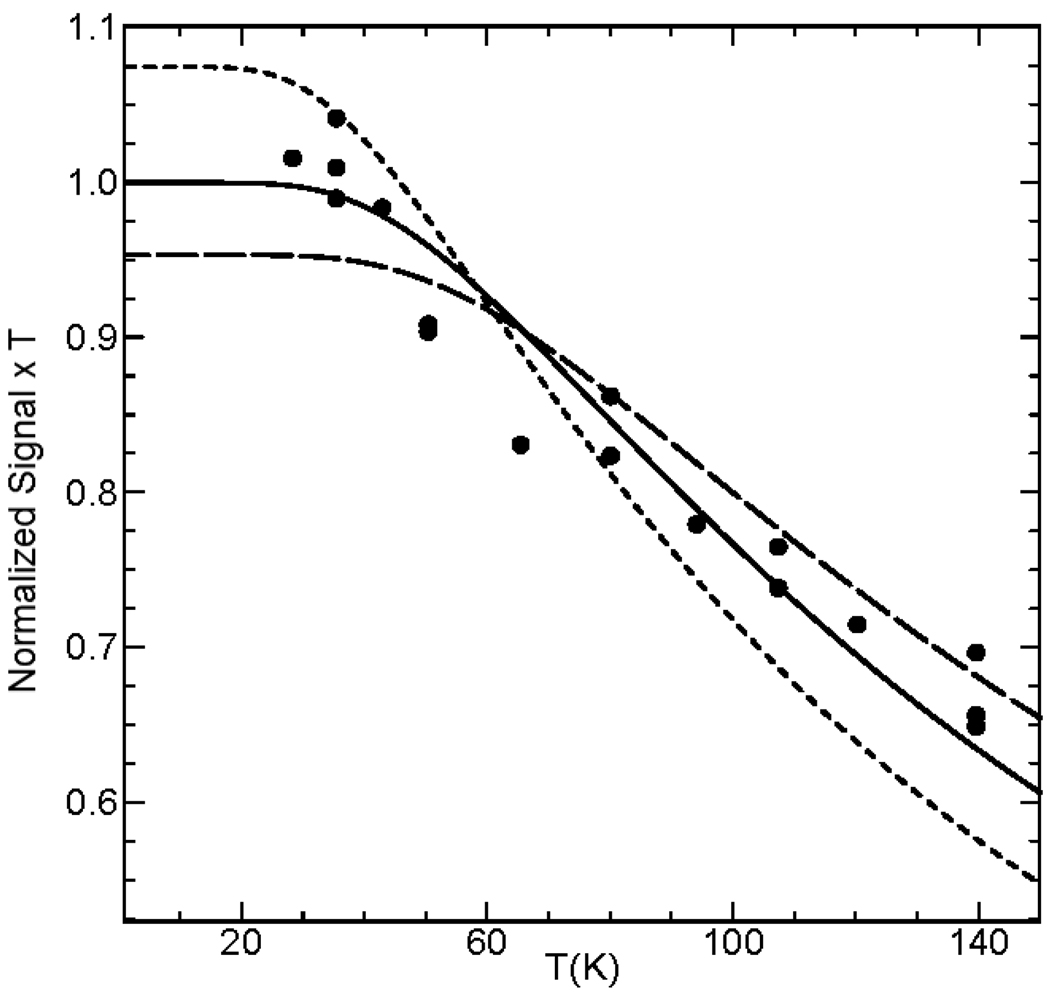
1-OH and 1-F are exchange coupled Fe^IIIFe^IV complexes with an S = ½ ground state. The first excited manifold in the spin ladder, the S = 3/2 multiplet, is at energy Δ = 3J/2. The J values of mixed-valent complexes have been determined by power saturation studies and then analyzed for the presence of an Orbach process for which the rate depends exponentially on Δ.^{49, 50} This method works well provided that Δ is sufficiently small so that the S = 3/2 state becomes thermally accessible before the Raman process with its strong T⁹ dependence dominates the spin-lattice relaxation rate.^{43, 45} For both 1-OH and 1-F we were able to saturate the EPR signal only up to ca. 60 K. A fit to the temperature dependence of the microwave power at half saturation revealed that the Raman process, rather than the Orbach process, dominates the relaxation. We therefore have determined Δ from the depopulation of the S = ½ ground state as a function of temperature. This method is often less reliable because even minor contaminants in the baseline can substantially affect the determination of the spin concentration of the ground state signal.

In the glassy solvent mixture 3:1 PrCN/MeCN, the solvent used to study the Mössbauer spectra of 1-OH, we generally observed a minor S = 1/2 contaminant, exhibiting g-values at 2.07 and 1.93. In a related project we produced this (unknown) species at higher concentrations, obtaining g = 2.07, 1.99 and 1.93. However, by using 3:1 CH₂Cl₂/MeCN we obtained a suitably pure sample, namely the sample of Figure 3A, in which this contaminant represented ca. 4% of the total spin concentration and, moreover, as its g-values were known we could remove its contribution reasonably well. For the CH₂Cl₂/MeCN sample, we were able to analyze the spectra of 1-OH in the temperature range from 27 K to 140 K; a selection of spectra is shown in Figure S1. Figure 11 shows a plot of (signal amplitude × temperature) versus temperature, where the signal amplitude was determined by double integration of the spectrum. The solid line is a fit for J = 90 cm⁻¹; for comparison, additional curves are shown for J = 70 and 110 cm⁻¹. Our analysis suggests that J = 90 ± 20 cm⁻¹. For 1-F (Figure S2) we obtained, within the experimental uncertainties, the same J value.

Figure 11.

Temperature dependence of the population of the S = ½ ground state of 1-OH in 3:1 CH₂Cl₂/MeCN. The solid line is a fit for J = 90 cm⁻¹. The dashed curves were calculated for J = 70 and 110 cm⁻¹. Double and triple entries compare results obtained for repeats on different days. Results for 1-F are shown in Fig. S2 in Supporting Information.

3.8 Summary of Structural and Spectroscopic Properties of 1-OH and 1-F

We have studied here two valence-localized Fe^III-Fe^IV complexes, 1-OH and 1-F. Based on the observations that 1-OH can be generated either by treating 1 with OH⁻ or by radiolytic reduction of 4 at 77 K (see section 3.6), we conclude that 1-OH possesses an HO-Fe^III-O-Fe^IV=O core, with the same ligand arrangement as in 4 as depicted in Scheme 1. We also propose a related F-Fe^III-O-Fe^IV=O core for 1-F, as it shares similar spectroscopic features with 1-OH and can be generated by F⁻ addition to 1. Our spectroscopic studies reveal that both the Fe^III and Fe^IV sites in 1-OH and 1-F are high-spin.

Table 1 lists the ⁵⁷Fe A-tensors of 1-F and 1-OH and compares them with those of E. coli RNR intermediate X and three previously reported synthetic high-spin Fe^III-Fe^IV complexes, 5–7, see Scheme 2 (Note: The A_iso values in Table 1 are not effected by D/J mixing). Complexes 5 and 6 are respectively supported by 6-Me-TPA (6-methyl-2-pyridylmethyl)bis(2-pyridylmethyl)amine)⁴⁰ and 6-Me₃-TPA (tris-(6-methyl-2-pyridylmethyl)amine)⁴² ligands that are closely related to the tetradentate ligand that supports 1-F and 1-OH. On the other hand, 7 derives from a diiron(II) complex having four sterically bulky carboxylate ligands,⁵¹ a ligand set closer to that associated with X. Complexes 5–7 all exhibit similar ⁵⁷Fe hyperfine parameters consistent with an antiferromagnetically coupled high-spin Fe^III-Fe^IV unit. The A_iso (Fe^III) for 7 is comparable to that found for X, but the corresponding values for 1-OH, 1-F, 5, and 6 are ~10% smaller as a result of the larger covalency of the nitrogen-rich Fe^III sites of these complexes relative to the carboxylate-rich Fe^III sites of X and 7. This distinction is also evident in the larger δ-values of X and 7. The trends in A_iso values for the Fe^IV sites are less obvious. In this case, A_iso values for the Fe^IV sites of 1-OH and 1-F are more similar to the value for X than those of 5–7. As the g-tensors of 1-OH and 1-F are isotropic, with Δg_x,y,z < 0.012, there is no reduction of A_iso by orbital contributions, and thus a_iso= −(3/4)A_iso for the Fe^IV=O sites represents the Fermi contact interaction. It is noteworthy that the magnitude of the a_iso values for the high-spin Fe^IV=O sites in 1-OH and 1-F is ca. 5 T larger than the a_iso values for the low-spin (S = 1) Fe^IV=O sites in 4 and [(L)Fe^IV=O(NCMe)].²³

The a_iso values for the reduced site are typical for high-spin Fe^III in N/O coordination. For [Fe^III(L)Cl₂]⁺ we have observed an isotropic a/g_nβ_n = −20.5 T, which is close to the value a_iso/g_nβ_n = −21.0 T obtained for 1-OH. However, the Mössbauer simulations of 1-OH, in the language of eq 1, reveal a substantially larger anisotropy than is usually observed for this half-filled shell ion. As shown in section 3.5 this anisotropy (to a major extent)⁵² can be attributed to mixing of excited S = 3/2 and 5/2 states into the S = ½ ground state by zero-field splitting terms (D/J mixing). Because we have determined J, this mixing provides a measure of the zero-field splitting parameters of the Fe^IV=O site, information which could not be obtained if J were substantially larger than D. Inclusion of D/J mixing into the spectral analysis also allows us to compare the traceless part of the a-tensor of the Fe^IV=O site with the spin-dipolar coupling constant obtained from DFT calculations. As can be seen from Table 2, the agreement between theory and experiment is very good (However, given the limitations in the accuracy of both the simulations and calculations, the striking match found between experiment and theory for the Fe^IV=O site of 1-F must be somewhat fortuitous).

Complexes 1-OH and 1-F are postulated to have an open X-Fe^III-O-Fe^IV=O core structure where the oxo bridge mediates the antiferromagnetic interaction between the high-spin Fe^III and Fe^IV sites. From an analysis of the temperature dependence of the S = ½ signal intensity arising from the ground state, the strength of this coupling, J, has been determined for both 1-OH and 1-F to be 90 cm⁻¹, with an estimated uncertainty of ± 20 cm⁻¹. These values are in good agreement with the DFT results (Tables 4 and S1) described below and serve as the first definitively measured coupling constants between high-spin Fe^III-Fe^IV centers. For comparison, Lippard and coworkers estimated the J value for 7 to be > 100 cm⁻¹ based on the observed Curie law behavior of its S = ½ EPR signal up to 150 K.⁴¹ Solomon and coworkers estimated the J value for RNR intermediate X to be > 70 cm⁻¹ by magnetic circular dichroism spectroscopy based on the absence of any measurable population of the S = 3/2 level at 115 K.⁵⁶ These comparisons suggest that a Fe^III-O-Fe^IV unit may be the minimal common motif for the high-spin Fe^III-Fe^IV complexes described thus far. Lastly, we emphasize that a spin-state change must occur at both iron sites when 1-OH and 1-F are formed from their precursors (1 or 4). For 4, the individual iron sites are best described as intermediate spin S_a,b = 1. A rationale for the unusual S_b = 1 to S_b = 2 transformation is presented in the DFT analysis detailed in the following section, which takes advantage of the rich spectroscopic features of 1-OH and 1-F to describe their electronic structures.

Table 4.

DFT results for the computational model 1-OH_m.

$(\mathrm{S}[{\text{Fe}}_{\text{OH}}^{\text{III}}],\mathrm{S}[{\text{Fe}}_{\mathrm{O}}^{\text{IV}}])\mathrm{S}$	ΔEa (cm−1)	Jb (cm−1)	${\text{Fe}}_{\text{OH}}^{\text{III}}-{\mathrm{O}}_{\mathrm{B}}$ (Å)	${\text{Fe}}_{\mathrm{O}}^{\text{IV}}-{\mathrm{O}}_{\mathrm{B}}$ (Å)	Fe-OB-Fe (°)	${\text{Fe}}_{\text{OH}}^{\text{III}}-\text{OH}$ (Å)
(5/2, 2) 1/2	0	+135	1.887	1.807	129	1.859
(5/2, 2) 9/2	1620		1.907	1.827	129	1.864
(5/2, 1) 3/2	1709	+69	1.861	1.873	129	1.870
(5/2, 1) 7/2	2123		1.858	1.879	131	1.876

^aSystem energies relative to the (5/2, 2) 1/2 ground state.

^bJ values for the (5/2, 2) and (5/2, 1) couples.

4. DFT Analysis

4.1 Spin State Energies

In our previous studies, the application of density functional theory substantially enhanced our understanding of the electronic structure of high-valent diiron complexes, including the ferromagnetically coupled diiron(IV) species 4.²³ Here we have applied DFT to gain further insight into the electronic structures of antiferromagnetically coupled 1-OH and 1-F and, in particular, to understand why the S_b = 1 Fe^IV=O site in 4 becomes S_b = 2 upon reduction of 4 to 1-OH.

Using Gaussian³³ we have performed geometry optimizations for 1-OH_m, ${[(\text{TPA})(\mathrm{O}){\text{Fe}}_{\mathrm{O}}^{\text{IV}}(\mathrm{\mu }-\mathrm{O}){\text{Fe}}_{\text{OH}}^{\text{III}}(\text{OH})(\text{TPA})]}^{2+}$ (Figure 1), and 1-F_m, ${[(\text{TPA})(\mathrm{O}){\text{Fe}}_{\mathrm{O}}^{\text{IV}}(\mathrm{\mu }-\mathrm{O}){\text{Fe}}_{\mathrm{F}}^{\text{III}}(\mathrm{F})(\text{TPA})]}^{2+}$ (Figure 12); to distinguish the computational models, which lack the methyl and methoxy substituents at the pyridines, we have labeled them with subscript m (= model). Since our DFT analysis focuses on a comparison of spin state energies, we have used the hybrid B3LYP functional, which is considered to be most suitable for this purpose.⁵⁷ For this reason, we have performed our calculations with Gaussian instead of the BPVWN functional associated with the ADF program previously used in our study of complex 4.²³

Figure 12.

Geometry optimized structure of 1-F_m. The coordinate system used in this manuscript is drawn into ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ and ${\text{Fe}}_{\mathrm{F}}^{\text{III}}$. The Fe=O and Fe-F bonds are essentially parallel.

The optimized geometry for 1-OH_m (Figure 1) is similar to that reported for 4: the oxo group of the Fe^IV site and the hydroxo group of the Fe^III site are juxtaposed, as in 4, to facilitate hydrogen bonding. The Fe-O_B-Fe angle is 129° (subscript B stands for bridge), the bending being supported by the Fe^IV=O⋯H-OFe^III hydrogen bond. The calculated Fe⋯Fe distance in 1-OH_m is 3.34 Å. In 1-F_m (Figure 12), which contains a fluoride-bound Fe^III site, the Fe-O_B-Fe bond is close to linear (175°) in the absence of a supporting hydrogen bond and the dihedral angle O=Fe-O_B-Fe-F is 180°, rather than 32° in 1-OH_m, minimizing the repulsion between the terminal oxo group and the fluoride. The nearly linear Fe-O_B-Fe unit in 1-F_m results in a longer Fe⋯Fe distance (3.61 Å) than in 1-OH_m. The spin populations of the irons (see Supporting Information) show that 1-OH_m and 1-F_m are valence localized Fe^IIIFe^IV complexes. As anticipated, the DFT solutions for 1-OH_m and 1-F_m place the terminal oxo ligand at the Fe^IV site.

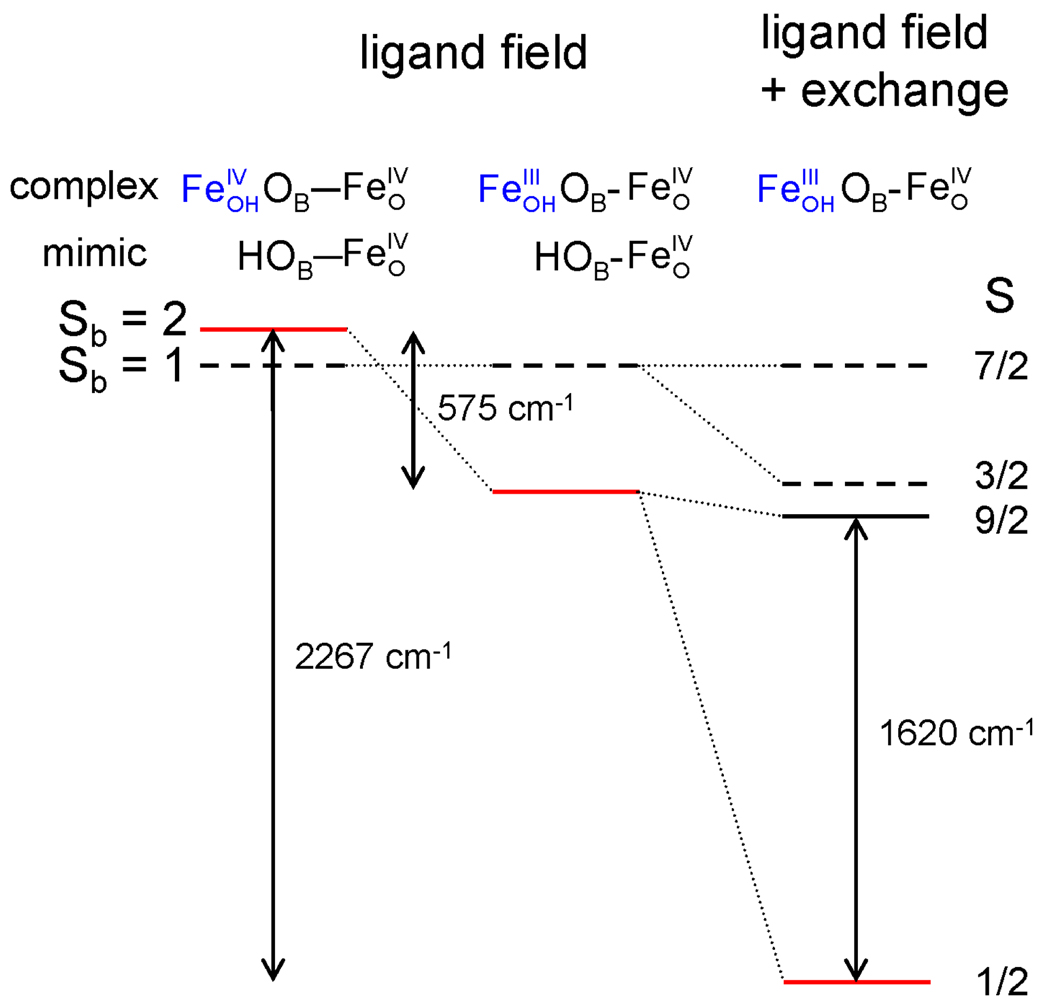
Tables 4 and S1 present the DFT results for 1-OH_m and 1-F_m, respectively. Geometry optimizations were performed for both the ferromagnetic state (F) and the broken-symmetry state (BS) for several local spin combinations. For a given combination, (S_a, S_b), the exchange coupling constant J was obtained from the expression J = (E_F – E_BS)/(2S_aS_b),⁵⁸ assuming the validity of the JŜ_a·Ŝ_b Hamiltonian in these systems. The energy gaps between the ferromagnetic states (S_max = S_a + S_b) and the antiferromagnetic states (S_min = |S_a − S_b|) were evaluated with the expression J[S_max(S_max + 1) − S_min(S_min + 1)]/2, which shows that the total exchange splitting depends on both J and the local spin quantum numbers, S_a and S_b. Using these exchange splittings and the SCF energies for the ferromagnetic states, we obtained the relative state energies (ΔE) listed in Tables 4 and S1. A graphical representation of the energies for 1-OH is given in Figure 13 (right column). For each (S_a, S_b) pair, the energies for the intermediate spin states, S_min < S < S_max, have not been listed but can readily be evaluated using the expression E_S = c + JS(S + 1)/2 for their energies, with c being a constant depending on S_a and S_b. Tables 4 and S1 also present the metric parameters for the Fe-O_B-Fe bridging unit, where we have listed the values obtained from the BS calculations for the antiferromagnetic states. In the following discussion we focus, for clarity, on 1-OH_m; the discussion of 1-F_m, which has similar properties as 1-OH_m, is given in the Supporting Information.

Figure 13.

Energy level scheme showing the effect of the reduction-induced change in the ligand field on the spin state energies of the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site in the absence of exchange interactions (left and middle column) and in combination with the exchange interactions (right column). The spin values indicated are the local spins (S_b) for the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site (left) and the coupled spins (S) for the dinuclear center (right). The (5/2, 1) 7/2 level has been aligned with the S_b = 1 levels for comparison. The splittings in the left and center columns were evaluated using a ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}-\text{OH}$ mimic, using different ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}-\text{OH}$ distances as described in section 4.3. The exchange splittings in the right column correspond to the J(5/2, 2) = 135 cm⁻¹ and J(5/2, 1) = 69 cm⁻¹.

4.2 Results for 1-OH_m

To obtain insight into the electronic state of the Fe^III site, we performed DFT calculations for the high-spin and low-spin states of the mononuclear complex [Fe^III(OH)₂(TPA)]_m, which is derived from 1-OH_m by replacing the entire ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site with a proton. The calculations for this system place the S_a = 5/2 state well below the S_a = 1/2 state, by a margin of about 3000 cm⁻¹, consistent with experimental data showing that the large majority of Fe^III(TPA) complexes with two additional O ligands are high-spin. On the basis of this DFT result and the strong experimental evidence for the high-spin state of the ${\text{Fe}}_{\text{OH}}^{\text{III}}$ site in 1-OH, we did not pursue DFT solutions for 1-OH_m with S_a < 5/2.

Interestingly, the calculations show that the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site is high-spin in the ground state of 1-OH_m (see Table 4), implying that the 1e-reduction of the Fe_OH site in 4 has induced a change in the spin of the adjacent ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site from S_b = 1 in $[{\text{Fe}}_{\text{OH}}^{\text{IV}}{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\mathrm{O}}^{\text{IV}}]$ to S_b = 2 in $[{\text{Fe}}_{\text{OH}}^{\text{III}}{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\mathrm{O}}^{\text{IV}}]$. Concomitantly, the exchange-coupling constant has changed sign, from ferromagnetic in $[{\text{Fe}}_{\text{OH}}^{\text{IV}}{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\mathrm{O}}^{\text{IV}}]$ to antiferromagnetic in $[{\text{Fe}}_{\text{OH}}^{\text{III}}{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\mathrm{O}}^{\text{IV}}]$, leading to an S = 1/2 ground state (see Table 4). As shown graphically in Figure 13, the (5/2, 2) 1/2 ground state is considerably lower in energy than the other three spin states. This is an outcome resulting from the antiferromagnetic exchange interaction in the (5/2, 2) pair, which is substantially larger than for the (5/2, 1) pair. This result establishes that the exchange interaction between the metal ions in 1-OH_m, owing to its dependence on the local spins, is an essential determinant of the spin states of the individual metal ions. To our knowledge, 1-OH (as well as 1-F, see Supporting Information) is the first example of a polynuclear metal complex where the exchange interaction between the paramagnetic sites plays a decisive role in changing the spin at one of the sites.

4.3 Why is the Fe^IV Site Low-Spin in 4 and High-Spin in 1-OH?

In this section, we analyze the spin state change of the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site from S_b = 1 in 4 to S_b = 2 in 1-OH; we treat the slightly more complicated case of 1-F separately in Supporting Information. The following observations are relevant for identifying the roots of the spin transition. The cryoreduction experiment of section 3.6 indicates that the reduction of 4 yields an essentially isostructural 1-OH complex but in which the Fe_OH site has become high-spin Fe^III. According to our DFT calculations, this spin-state change results in a lengthening of the Fe^III-O_B bond and, in compensation, a shortening of the Fe^IV-O_B bond, causing a change in the ligand field at the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site and affecting the energy gap between the S_b = 1 and 2 states; thus there is a ligand-field contribution to the spin transition. Estimating the reduction-induced ligand-field changes in the energy gap between the local spin states is hampered by the simultaneous presence of the exchange interaction between ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ and ${\text{Fe}}_{\text{OH}}^{\text{III}}$. In Figure 13 we propose a scheme for evaluating the difference that the $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{IV}}$ and $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{III}}$ "ligands" exert on the relative spin state energies of ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ to which they are attached. The scheme is based on the use of a O-H diamagnetic mimic for the "ligands" $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{III}}$ and $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{IV}}$. The optimized geometries for the S_b = 1 ground state and S_b = 2 excited state of the mononuclear complex $[(\text{TPA})(\mathrm{O}){\text{Fe}}_{\mathrm{O}}^{\text{IV}}-\{{\mathrm{O}}_{\mathrm{B}}\mathrm{H}\}]$ have ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}-{\mathrm{O}}_{\mathrm{B}}$ distances (1.88 Å and 1.82 Å) that closely match those for the S_b = 1 and 2 states of 1-OH_m (1.87 Å and 1.81 Å). Thus, −O_BH appears to be a faithful, diamagnetic mimic for the paramagnetic $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{III}}$ ligand. As a diamagnetic mimic for the $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{IV}}$ ligand in 4, we have again taken the −{O_BH} ligand, but now with an ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}-\left\{{\mathrm{O}}_{\mathrm{B}}\mathrm{H}\right\}$ distance that is fixed at 1.97 Å in the geometry optimization of $[(\text{TPA})(\mathrm{O}){\text{Fe}}_{\mathrm{O}}^{\text{IV}}-\{{\mathrm{O}}_{\mathrm{B}}\mathrm{H}\}]$, i.e. the value of the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}-{\mathrm{O}}_{\mathrm{B}}$ distance in the optimized structure of 4 (In 4_m this bond is 0.13 Å longer than in 1-OH_m).⁵⁹ Use of the diamagnetic mimics for $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{IV}}$ and $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{III}}$ produces for $[(\text{TPA})(\mathrm{O}){\text{Fe}}_{\mathrm{O}}^{\text{IV}}\{{\mathrm{O}}_{\mathrm{B}}\mathrm{H}\}]$ ground states with spins S_b = 1 and S_b = 2; corresponding excited states with spins S_b = 2 and S_b = 1 are found at 134 cm⁻¹ and 441 cm⁻¹, respectively. Thus, by passing from $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{IV}}$ to $-{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\text{OH}}^{\text{III}}$, the energy gap E(S_b = 2) - E(S_b = 1) is estimated to change from +134 cm⁻¹ to −441 cm⁻¹, representing a total shift of 575 cm⁻¹ (marked in Figure 13) that we attribute to the reduction-induced ligand-field change.⁶⁰ The spin level crossing induced by the ligand-field change is illustrated in the left and middle columns of Figure 13. It can be seen that the reduction-induced ligand-field effect on the spin state energies gives the observed spin crossover in 1-OH_m but fails to reproduce the much larger energy splittings between the (5/2, S_b = 1) 3/2 and (5/2, S_b = 2) 1/2 states (Figure 13, right column). Perhaps the most important feature revealed by the calculations for the diamagnetic mimics is that the S_b = 1 and 2 states of ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ in the ligand environments encountered in 1-OH_m (and 1-F_m) are rather close in energy, creating conditions that make the energy ordering of the local spin states susceptible to weaker interactions, such as the exchange interactions between the irons.^{61, 62} Most importantly, the S_b = 1 → 2 transition adds two unpaired electrons to ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$, leading to a substantial increase of the antiferromagnetic exchange. In the following we outline some of the details of these considerations.

The exchange-coupling constants listed in Tables 4 and S1 for spin pair (S_a = 5/2, S_b = 1) include both positive and negative values and expose intricate dependences on geometrical factors, such as the bond angle and distances of the bridges in these systems. In contrast, the J values for the (S_a = 5/2, S_b = 2) pairs in Tables 4 and S1 are much larger and positive, and resemble those observed in (µ₂-oxo)diiron(III) complexes.^{63, 64} The similarity with the diferric species is not unexpected given that the number of unpaired electrons in the (5/2, 2) complexes differs only by one from the unpaired electron count of ten in (5/2, 5/2). The similarity can be quantified by using the exponential relationship⁶³ between J and the average bridging bond length (denoted P by Gorun and Lippard) for binuclear Fe^III centers bridged by a ligand oxygen atom (µ₂-oxo, µ2-hydroxo, µ₂-alkoxo, etc.) and supported by at least one other bridging ligand. Using this relationship and our calculated bond lengths we obtain for 1-OH_m the values J_{Gorun-Lippard} (5/2, 2) = 122 cm⁻¹ for the P value in the broken symmetry state. This value is remarkably similar to the J (5/2, 2) value listed in Table 4, adding support to the calculated J values.⁶⁵ In the following paragraphs we discuss the anticipated change in J when the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site in 1-OH_m is reduced to high-spin ${\text{Fe}}_{\mathrm{O}}^{\text{III}}$ on the basis of the orbital structure for this site gleaned from the magnetic hyperfine interactions.

We can use the ⁵⁷Fe spin dipolar coupling tensor (A_SD ≈ A - A_iso) to gain insight into the exchange pathways added by the transition S_b = 1 to S_b = 2. The calculated A_SD for the high-spin Fe^IV site has a vanishing component along x and negative and positive values with approximately equal magnitudes along y and z, respectively. As the S_b = 2 state has a t_2g³e_g¹ configuration, the dominant valence contribution to A_SD can be ascribed to the e_g electron. The calculated A_SD components correspond to an orbital of the form |d_e> ≈ −0.26 |z²> + 0.97 |x²−y²> with z||Fe_O=O and x||Fe⋯Fe (see Figure 12). The experimental A_SD is nearly axial along z and not as rhombic as in the calculation, suggesting that the d_e orbital in the molecule is less admixed, i. e. |d_e> ≈ |x²−y²> (Given the complexity of the system, the agreement between the experimental and theoretical A_SDis quite reasonable).

Using this knowledge of the orbital configuration, we now address the difference in the J values for the (5/2, 1) and (5/2, 2) pairs on the basis of the pathway model for J.^{66, 67} For each singly occupied 3d orbital at an ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ of a given symmetry, there is a matching partner in the half-filled 3d shell of the Fe^III site. The local spin change S_b = 1 → 2, due to the transfer xy^β → d_e^α, adds two additional unpaired electrons and associated antiferromagnetic pathways for which J_π, ∝ t_π²/U and J_σ′ ∝ t_σ′²/U, where t_π = <xy_b|h|xy_a> and t_σ′ = <(d_e)_b|h|(3x²-r²)_a> are transfer integrals between the two metals, labeled (a) for ${\text{Fe}}_{\text{OH}}^{\text{III}}$ and (b) for ${\text{Fe}}_{\text{OH}}^{\text{IV}}$. These additional contributions rationalize why the J values for the (5/2, 2) pair are larger than for (5/2, 1). As |d_e> ≈ |x²-y²> = 3^1/2/2 |3x²-r²> − 1/2 |y²-z²>, we obtain for the unpaired electron in d_e the exchange parameter J_σ′ = 3/4 J_σ with J_σ ∝ t_σ²/U and t_σ = <(3x²-r²)_b|h|(3x²-r²)_a>. Thus, the channel sum J ∝ (3/4 J_σ + 2 J_π)/10 for mixed-valent (5/2, 2) differs from J ∝ (J_σ + 2 J_π)/12.5 for the diferric (5/2, 5/2) only by 0.005 J_σ − 0.040 J_π, which rationalizes the similarity in the J values for the Fe^III_HS-O-Fe^IV_HS and Fe^III_HS-O-Fe^III_HS bridges. The J values for the excited states with (5/2, 1) parentage contains the antiferromagnetic contribution J_π ~ t_π²/U with t_π = <yz_b|h|yz_a>. The overall exchange splitting, i.e. the energy gap between S_min and S_max, for (5/2, 1) is 414 cm⁻¹ in 1-OH_m and is about four times smaller than the corresponding values 1620 cm⁻¹ for the (5/2, 2) couple. Similar or even smaller overall exchange splittings than for (5/2, 1) are present in the $[{\text{Fe}}_{\text{OH}}^{\text{IV}}{\mathrm{O}}_{\mathrm{B}}{\text{Fe}}_{\mathrm{O}}^{\text{IV}}]$ core of 4.²³

Conclusions

As illustrated by Figure 13, the antiferromagnetic exchange in the (5/2, 2) pair of 1-OH gives rise to splittings within the (5/2, 2) manifold that are larger than both the exchange splittings within the (5/2, 1) manifold and the reduction-induced ligand-field changes on the energy gap between the local S_b = 1 and 2 states. The reduction-induced spin transition of the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site emerges from this discussion as a process that is not primarily driven by the conventional mechanism that proceeds through changes in the ligand field, but by one that is based on the reduction-induced enhancement of the exchange interaction with an adjacent acceptor site. The change in the spin of the Fe_b site from S_b = 1 in the diiron(IV) complex 4 to S_b = 2 in the iron(III)iron(IV) complex 1-OH (S_b = 2) indicates that the corresponding spin states of the uncoupled Fe^IV(O)(L)(O-X) unit are close in energy. Unlike 1-OH, Wieghardt’s bis(carboxylato)-bridged Fe^III-O-Fe^IV complexes⁶² have S = 3/2 ground states that derive from the (5/2, 1) couple. In these cases, the Fe^IV centers are S = 1 despite being coupled to S = 5/2 Fe^III ions. Whatever the explanation for this difference, the 1e-reduction of 4 to generate 1-OH not only engenders a change in the spin state of the ${\text{Fe}}_{\mathrm{O}}^{\text{IV}}$ site but also enhances its H-atom abstraction ability a thousand-fold,²⁹ providing a compelling rationale for Nature’s choice of high-spin iron(IV) centers to carry out such transformations in nonheme iron enzymes.

Table 3.

Experimental and theoretical ¹⁹F hyperfine parameters of 1-F.

	Ax (MHz)	Ay (MHz)	Az (MHz)
EPR	92	113	253
DFT	+50	+106	+260