A full 3-D reconstruction of the entire porcine coronary vasculature

Abstract

We have previously reconstructed the entire coronary arterial tree of the porcine heart down to the first segment of capillaries. Here, we extend the vascular model through the capillary bed and the entire coronary venous system. The reconstruction was based on comprehensive morphometric data previously measured in the porcine heart. The reconstruction was formulated as a large-scale optimization process, subject to both global constraints relating to the location of the larger veins and to local constraints of measured morphological features. The venous network was partitioned into epicardial, transmural, and perfusion functional subnetworks. The epicardial portion was generated by a simulated annealing search for the optimal coverage of the area perfused by the arterial epicardial vessels. The epicardial subnetwork and coronary arterial capillary network served as boundary conditions for the reconstruction of the in-between transmural and perfusion networks, which were generated to optimize vascular homogeneity. Five sets of full coronary trees, which spanned the entire network down to the capillary level, were reconstructed. The total number of reconstructed venous segments was 17,148,946 ± 1,049,498 (n = 5), which spanned the coronary sinus (order −12) to the first segment of the venous capillary (order 0v). Combined with the reconstructed arterial network, the number of vessel segments for the entire coronary network added up to 27,307,376 ± 1,155,359 (n = 5). The reconstructed full coronary vascular network agreed with the gross anatomy of coronary networks in terms of structure, location of major vessels, and measured morphometric statistics of native coronary networks. This is the first full model of the entire coronary vasculature, which can serve as a foundation for realistic large-scale coronary flow analysis.

the coronary venous system has the largest volume (18, 21, 33), compliance (55), and number of vessels (20, 27, 38) in the coronary network. The coronary venous system drains the capillary bed and conveys the deoxygenated blood to the right atria (through the coronary sinus) and directly into the heart cavities (through the Thebesian veins) via numerous intricate routes (4, 39, 45) and, thus, determines the back pressure of the network. The anatomy of the coronary venous system has a complex three-dimensional (3-D) geometry and branching pattern consisting of higher asymmetry with more abrupt changes in diameters compared with the coronary arterial tree. Whereas the latter is mostly dichotomous (4, 34, 38, 41), the former is characterized by abundant trifurcations, quadrifications, and quintifications (38).

The properties of coronary veins, including their larger diameters, greater elasticity, and lower pressures, lead to a complex venous pressure-flow relationship. Similar to coronary arterioles, the venules have phasic diameters through the cardiac cycle (59) as well as a myogenic response (44). They account for ∼15% of the total myocardial vascular resistance at rest (42, 60), and there may be significant hemodynamic interactions between arterial and venous flows (65). Furthermore, flow in the venous system may be of importance in the flow-dependent countercurrent exchange of metabolites (“venular-arteriolar communication”), which may play a role in arteriole vasodilation (19, 27). These structure and pressure-flow characteristics of the coronary venous system underline the importance of the coronary venous flow to the function of the entire coronary system (16). Accordingly, modeling the 3-D structure of the coronary venous network is of fundamental significance for any realistic simulation of coronary perfusion and metabolic supply and their distribution, both locally and globally.

Anatomic models of the coronary system with 3-D structure, based on detailed morphometric data (41), have been previously developed for the full arterial tree by Beard and Bassingthwaighte (8) in a cylindrical heart model and by Smith et al. (54) in a finite-element model of the heart for the largest six generations of the coronary arterial tree. Our group (32) has previously generated a 3-D reconstruction of the entire coronary arterial network of the porcine heart down to the capillary level in a prolate model of the left ventricle (LV) based on detailed statistical data of the coronary vasculature (37, 40, 41). The model was used to investigate spatial heterogeneity of coronary blood flow and pressure, which were in good agreement with experimental measurements (24).

The previous models have been limited to the arterial system. There is currently no realistic anatomic model of the coronary venous system. Here, our previous 3-D reconstruction of the arterial coronary tree (32) was augmented with a large-scale 3-D reconstruction of the venous network. The present venous reconstruction spanned the entire network down to the venous capillary based on detailed morphometry and asymmetry data of the coronary venous system (31, 37, 38, 40).

METHODS

The reconstruction was based on a set of rules stemming from gross and qualitative anatomic features (3, 4, 28, 45) and quantitative statistical morphometric data on the coronary sinusal tree (11, 38). Details are outlined below.

Network Hierarchy

The coronary venous network was partitioned into three major branches in parallel to the respective arterial left anterior descending coronary artery (LAD), left circumflex artery (LCx), and right coronary artery (RCA) subtrees. According to the capillary network database (37), there are 3.18 ± 0.118 capillaries fed directly by arterioles (0a arterial capillaries) for each order 1 arteriole in the LAD and LCx branches and 2.75 ± 0.082 in the RCA branch. On the other hand, there are 2.56 ± 0.073 capillaries drained directly into venules (0v venous capillaries) for each order 1 venule in the sinusal tree. The latter is the main route by which the venous blood returns to the heart and empties into the right atrium (38). These values, when combined with the observed average of 2 venules/arteriole (7), yield an average ratio between the number of venous and arterial functional capillaries (0v-to-0a ratio) of 1.61:1 (2 × 2.56/3.18) for the LAD and LCx and 1.86:1 (2 × 2.56/2.75) for the RCA. Similar to the coronary arterial tree (32), each venous branch is partitioned longitudinally into the functional epicardial subnetwork (order −9 to −12 vessels), transmural network (order −5 to −8 vessels), and perfusion network (order −4 to 0v vessels). This classification is based on differences in the functional design of these subnetworks (9, 17, 18, 58, 69).

Another feature of the network relates to the asymmetry of the branching geometry, which is expressed in the branching angles: the higher the diameter asymmetry, the larger is the asymmetry in the branching angle (67). Accordingly, it was assumed in the present study that in a asymmetrical bifurcation, the branching angle of the larger daughter branch relative to its parent vessel decreases with the increase in vessel order.

Database

The reconstruction used detailed morphometric data on the sinusal tree (38, 40). Briefly, the data were organized along the diameter-defined Strahler scheme [an ordering system for assigning order numbers to vessels, which is a modification that Kassab et al. (41) introduced to the original Strahler scheme, thus assuring that diameter ranges of successive orders have no overlap], and the network segments were divided into elements (one or more segments in series). The data include statistics of diameters and lengths of segments, the segment-to-element ratio (S/E), connectivity of vessels, and longitudinal position of vessels. The latter two are represented by the connectivity matrix (CM) and by the longitudinal position matrix (LPM), respectively. An analytic form of the distribution functions of the measured morphometric data was generated based on the β-distribution function, which was found to fit the asymmetric features. The family of β-distributions [unlike the normal distribution used previously (8, 54)] is appropriate for the present reconstructions since it accounts for asymmetric distributions and is also bounded.

Weak correlations between successive segment lengths and diameters in the coronary arterial network have been previously reported (61, 69). The database (38, 40, 41) has addressed the correlations (dependence) between successive segments at branching in terms of diameters, lengths, and other features through the CM and LPM. Accordingly, the correlation between successive segment lengths and diameter was introduced through the implementation of the order generation algorithm (as described in the Supplemental Material, Supplement S1, Eq. S1-1).¹ The algorithm determines the order of the daughter segment given the order of its mother element based on CM and LPM features from the database.

Reconstruction Scheme

The venous network reconstruction was formulated as a large-scale optimization process subject to local and global constraints based on the set of rules shown in Table 1. The optimization criteria enforced optimal coverage of the surface covered by the epicardial arterial subnetworks and drainage compatibility with the arterial capillary network subject to the constraints on the 0v-to-0a ratio as well as capillary length and orientation. It was assumed that vessels in each of the LAD, LCx, and RCA subnetworks independently follow the respective arterial major vessels, i.e., there is no connection between the three venous subnetworks. The reconstruction scheme is common to all three subnetworks and was carried through the following steps (detailed in appendices a–c and Supplements S1–S5):

Table 1.

Summary of the basic assumptions underlying the reconstruction of the coronary venous tree

Subject	Description of the Assumption
Heart geometry
1.1	Represented by a prolate spheroid (57)
Network partitioning
2.1	Hierarchical design (9, 31, 35, 58, 68)
2.2	Epicardial subnetworks: orders −12 to −9 (9, 31, 35, 68)
2.3	Transmural subnetworks: orders −8 to −5 (35)
2.4	Perfusion subnetworks: capillaries of orders −4 to 0v (31, 35)
Network design
3.1	The network has a tree-like structure (37)
3.2	Veins accompany their arterial counterparts (18, 27, 33)
3.3	Ratios of 1.61:1 and 1.86:1 are maintained, on average, between the venous (0v) and arterial (0a) capillaries for the venous LAD, LCx, and RCA, respectively (7, 37)
3.4	Venules and venous capillaries can run obliquely between parallel sheets (4, 49)
3.5	Arterial major branches are drained only by their venous counterparts, i.e., there is no communication between major branches, neither arterial nor venous
3.6	No arcading or anastomoses in the venous network
Network morphometry
4.1	No correlation between successive segment lengths and diameters
Three-dimensional reconstruction scheme
5.1	Relation between diameter asymmetry (34) and branching angles: the higher the diameter asymmetry, the larger the asymmetry in the branching angle (9, 17, 18, 29, 68)
5.2	Functional capillaries are oriented along the direction of the myocytes (9, 17, 18, 29, 49, 68)
5.3	Perfusion and transmural venous vessels can cross each other and arterial vessels as well (4, 30, 45)

LAD, left anterior descending coronary artery; LCx, left circumflex artery; RCA, right coronary artery.

Repetitive stochastic generation of the “primitive” epicardial network.

Repetitive stochastic generation of the primitive epicardial network (orders −12 to −9) was performed independently of the rest of the network (orders −8 to 0). A primitive tree has vascular morphometry (orders and lengths) but no geometrical structure, i.e., all tree segments are aligned in the same arbitrary direction (Supplement S1). The generation used the statistical morphometric database (37, 38, 40).

Selection of the anatomically compatible epicardial subnetwork.

Selection of the anatomically compatible epicardial subnetwork was guided by the length of the network, number of vessels, and location of the major branches (Supplement S2).

Assignment of two-dimensional structure.

Assignment of two-dimensional (2-D) structure to the epicardial subnetwork by large-scale optimization is highly nonlinear. For this problem, the conventional gradient-based optimization schemes (e.g., Gauss and Newton-Raphson) are ineffective, and the simulated annealing algorithm is a better alternative (53). Accordingly, a simulating annealing search was applied subject to constraints of similarity to the geometry of the arterial epicardial subnetwork, of avoidance of intersection between segments, and of branching angle rules, which assume that the branching angle of the daughter segment increases with the branching asymmetry (detailed in Supplement S3).

Transformation of the 2-D epicardial subnetworks to the 3-D epicardial geometry.

Transformation of the 2-D epicardial subnetworks to the 3-D epicardial geometry of the assumed truncated prolate spheroid (Supplement S3) was approximated to the LV and right ventricular (RV) geometry with dimensions that corresponded to a 150-cm³ heart [the size of the heart used in the morphometric study (32)].

Generation of transmural and perfusion subnetworks.

Transmural and perfusion subnetworks (orders −8 to 0v), which connect to the reconstructed 3-D venous epicardial subnetwork on one end and to the previously reconstructed (32) arterial capillary mesh on the other, were generated. This was done based on a stepwise top-down-top scheme (appendix a and detailed description in Supplement S4). Briefly, the reconstruction direction was alternated between upward and downward steps, toward the stem and distal part of the generated crowns, respectively. This was subject to three major constraints: 1) association of 0v capillaries with 0a capillaries, 2) avoidance of excessively populated regions, and 3) attraction of transmural venous vessels toward the epicardial venous subtree.

Pruning of unassociated segments.

Once the population of arterial capillaries was associated with venous counterparts [ratios of 1.61:1 for the LAD and LCx and 1.86:1 for the RCA between the 0v (venous) and 0a (arterial) capillaries (7, 37)], the reconstruction was terminated. The remaining arterial capillaries were left unassociated due to distance gaps that were too large to be covered by the venous capillaries. These arterial capillaries (accounting for <0.5% of the total network capillaries) were pruned. Likewise, venous capillaries that were left unassociated with arterial counterparts were pruned as well. The pruning procedure was carried out iteratively, i.e., vessels that were left without daughters were also pruned.

Diameter assignment.

Diameter assignment was done for the venous network (Supplement S5) based on venous data (38) and on the asymmetry features extracted from the raw data (appendix c). Briefly, the assignment was done in a top-down direction starting with the network stem and moving toward the 0v capillaries.

RESULTS

Five sets of coronary venous networks were reconstructed, with each coupled to the reconstructed sets of the coronary arterial trees (32). The total number of reconstructed venous segments was 17,148,946 ± 1,049,498 (n = 5), which spanned capillaries from orders −12 to 0v. Combined with the reconstructed arterial network, the number of vessel segments for the entire coronary network added up to 27,307,376 ± 1,155,359 (n = 5). The epicardial portion of the venous network (orders −12 to −9) accounted for a total of 6,678 ± 601 vessel segments compared with 934 ± 58 vessel segments in the corresponding arterial network.

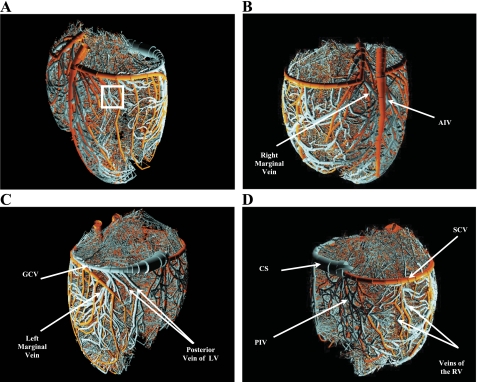
Figure 1, A–D, shows a rendering of the appearance of the combined coronary venous network together with its arterial counterpart with a total of 10,318,878 segments for orders −12 to +11, excluding the 0v and 0a capillaries. The close-up images in Fig. 2A show the dense structure of the network at the midwall. Figure 2B shows a sheet of 0a arterial capillaries drained by a dense array of 0v venous capillaries, where the entire mesh is protruded by transmural vessels. Figure 2C shows a comparison between epicardial, transmural, and perfusion vessels at the subepicardium region. Also shown are the transmural vessels, both arterial and venous, branching from the epicardial network at an almost right angle toward the deeper layers to deliver and drain blood from the microcirculation, respectively. The further close-up image in Fig. 2D shows typical connections between 0a and 0v capillaries with 0a capillaries drained by one or two 0v capillaries. The observed variable directions for the 0v capillaries correspond to the arrangement of the 0a capillaries along the fiber direction, which varies based on their transmural location in the myocardial wall (51).

Fig. 1.

Rendering of the reconstructed arterial and venous trees (orders 1 to 11 and −1 to −12) as viewed form four different aspects: anterolateral left (A), anterolateral right (B), posterolateral left (C), and posterolateral right (D). The rendering was done using POVWIN Raytracer. White rectangle in A marks the location chosen for the close-up image in Fig. 2, A–D. Orange, arterial; cyan, venous. AIV, anterior interventricular vein; GCV, great cardiac vein; LV, left ventricle; CS, coronary sinus; PIV, posterior interventricular vein; SCV, small cardiac vein; RV, right ventricle.

Fig. 2.

Magnified views of the reconstructed arterial and venous trees: a dense mesh of arterial and venous midwall transmural and perfusion vessels (A), perspective view from the epicardium to the endocardium (B), subepicardial transmural and perfusion vessels (C), and view of 0a to 0v capillary connections (D). Orange, arterial; cyan, venous.

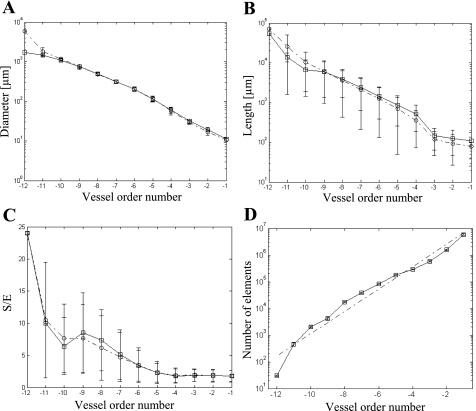
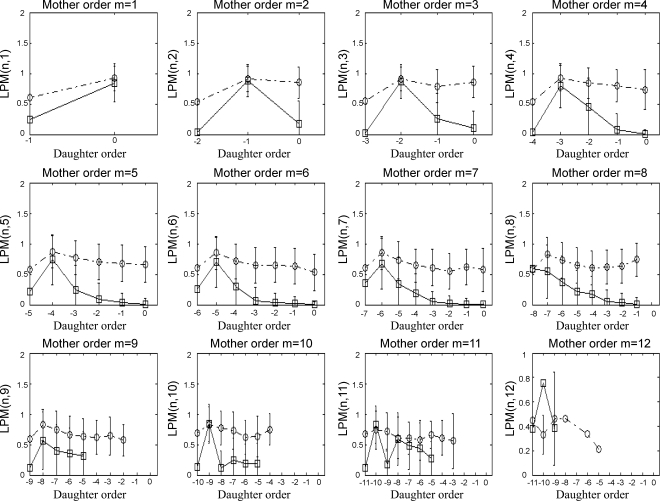
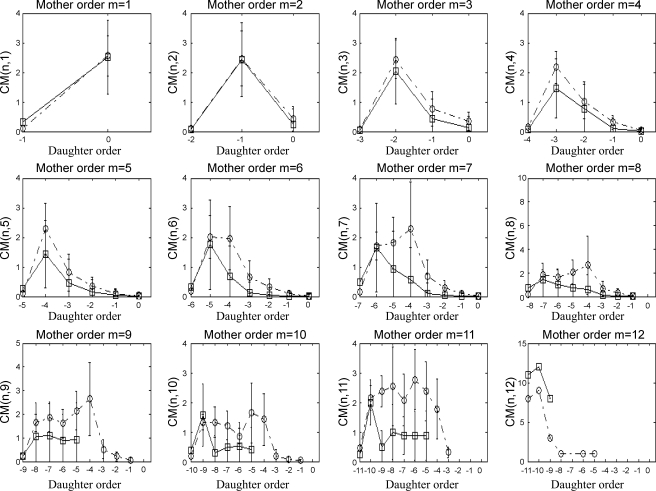
Quantitative characterization of the reconstructed coronary venous network (Figs. 3–5)p provides a comparison of morphometric statistics between the reconstructed venous network and measured data for element diameters (Fig. 3A), element lengths (Fig. 3B), S/E (Fig. 3C), number of vessel elements (Fig. 3D), CM (Fig. 4), and LPM (Fig. 5), all as functions of vessel order number.

Fig. 3.

Comparisons of the data (39) (○) with the reconstruction (□) in terms of vessel order distribution: element diameter (A), element length (B), segment-to-element ratio (S/E; C), and element number (mean and SD; D) together with the corresponding linear regression curve (dashed-dotted line).

Fig. 5.

Reconstructed longitudinal position matrix [LPM(m,n)] (□) compared with the database (39) (○). Each subplot represents the relative location of a bifurcation of a daughter element of order n along a mother element of order m.

Fig. 4.

Connectivity matrix [CM(m,n)] for the reconstructed venous trees (□) compared with the database (39) (○). Each of the subplots shows the probabilities of obtaining a daughter element of order n from a mother element of order m.

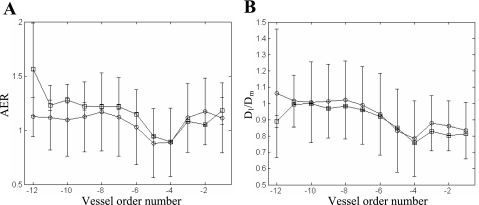
Further quantitative analysis of the reconstructed venous network relates to the order distributions of the area expansion ratio (AER; Fig. 6A) and of the branching asymmetry (Fig. 6B), with the latter quantified by the diameter ratio of the largest daughter segment to the mother segment (D_l/D_m) as a function of order. AER is defined as follows: (D_l²+ D_s²)/D_m², where D_l, D_s, and D_m are the diameters of the large daugter vessels, small daughter vessel, and mother vessel, respectively.

Fig. 6.

Comparison of the order distribution of the reconstruction (□) versus that calculated from the database (39) (○) of the area expansion ratio (AER; A) and diameter asymmetry (D_l/D_m; B).

The averages and SDs of the 0v-to-0a capillary ratio for the entire reconstructed venous network were found to be 1.63 ± 0.02:1 and 1.87 ± 0.005:1 for the venous LAD/LCx and RCA, respectively, compared with the estimated values of 1.61:1 and 1.86:1. The percentage of branching types was found to be 85.4 ± 0.34, 13.3 ± 0.29, 1.10 ± 0.04, and 0.18 ± 0.01 for bifurcations, trifurcations, quadrifications, and quintifications, respectively, compared with 86%, 12.8%, 1%, and 0.2% in the native trees (38).

The calculated mass-normalized cumulative blood volumes (CBV) for the reconstructed venous LAD, LCx, and RCA, excluding the capillaries, were 3.4 ± 0.34, 1.9 ± 0.25, and 3.7 ± 0.39 ml/100 g (n = 5), respectively, which added up to a mass-normalized CBV of 9.0 ± 0.46 ml/100 g for the entire sinusal tree compared with 4.9 ml/100 g calculated for the native coronary venous tree (38). The calculated mass-normalized CBV for the venous functional capillaries was 0.24 ± 0.01 ml/100 g, based on the total number of functional capillaries with a functional length (0a to 0v) of 1,000 μm, which are maximally dilated [diameter of 9 μm (21)].

The LV was divided into slabs with an average volume of 0.017 ml. The number of capillaries in each slab was computed and averaged over the subepicardium, midwall, and subendocardium to yield mean transmural values. The calculated ratio of the mean number of capillaries between the subendocardium and subepicardium was 1.33 ± 0.11 (n = 5).

The calculated distribution of blood volume over the LV, septum, and RV is shown in Table 2 and was compared with both the volume distribution of the corresponding reconstructed arterial network (32) and with the data of Weaver et al. (63) on the arterial tree. The results were in good agreement.

Table 2.

Distribution of the predicted venous blood volume (for the LV, RV, and septum as a percentage of the venous total volume) compared with the corresponding predictions of the reconstructed coronary arterial network (32) as well as the data of Weaver et al. (63)

	LAD			LCx			RCA
	Generated venous	Generated arterial	Weaver et al. data	Generated venous	Generated arterial	Weaver et al. data	Generated venous	Generated arterial	Weaver et al. data
LV total	44.3 ± 1.4	47.0 ± 14.2	49	43.3 ± 2	30.3 ± 6.1	35	12.3 ± 1.2	22.7 ± 8.4	25
Septum	37.3 ± 2.8	39.7 ± 10.0	58				62.3 ± 2.9	60.2 ± 10.0	42
RV total	4.6 ± 3.5	19.7 ± 20.9	0				95.4 ± 3.5	80.2 ± 20.9	72
Ratio of total volume	37.7 ± 1.8			19.8 ± 1.1			41.1 ± 2.2

Values are means ± SD and are ratios of branch volumes relative to the cumulative volume (in %). LV, left ventricle; RV, right ventricle.

DISCUSSION

This is the first full model of the entire coronary vasculature that integrates the coronary arteries and veins as well as the microvasculature, including functional capillaries. The reconstructed coronary venous network demonstrates excellent qualitative and quantitative resemblance to the morphometry of native coronary venous trees. The limitations and future applications of the full circulatory model of the heart are contemplated below.

To develop a realistic 3-D reconstruction of the entire coronary vasculature, a stochastic representation of the anatomy is required due to the variability and irregular structure of the network (3, 4, 10, 49) as well as the highly asymmetric branching patterns (38, 40, 41). In the present study, the 3-D porcine coronary venous network was statistically reconstructed based on measured morphometric features (37, 38, 40), on diameter asymmetry of vessel junctions extracted from the data (appendix c), and in line with the previously reconstructed coronary arterial tree (32). The reconstruction was based on a functional hierarchical division of the network into functional subnetworks, which was supported by morphometric data (34, 38) and by the diameter asymmetry in the coronary venous network (appendix c). The anatomic model was validated as follows.

Comparison of the 3-D model to Observed Anatomic Features

High variability exists in the native network structure at the level of large vessels in terms of left-right dominance and the location of the major branches (3, 4, 45, 46, 49).The epicardial and septal vessels are aligned along the prolate spheroid surfaces (57) of the LV and RV (Fig. 1). The major venous epicardial vessels (Fig. 1) follow the correct course and provide coverage of the entire epicardial surface perfused by corresponding reconstructed arterial epicardial vessels (LAD, LCx, and RCA) (4, 18, 27, 33) and drain their respective networks (45, 49). This includes the small cardiac vein, which follows the route of the RCA artery and branches off to the posterior interventricular vein, which accompanies the posterior interventricular artery. Similarly, the great cardiac vein follows the LCx and gives rise to the lateral LV veins, posterior vein of the LV, and anterior interventricular vein, which runs in parallel to the anterior interventricular artery. Finally, the coronary sinus, which drains most of the epicardial ventricular veins (45), is situated at the posterior region of the coronary sulcus and drains the great cardiac vein, small cardiac vein, posterior vein of the LV, and posterior interventricular vein. The septal veins originate anteriorly and posteriorly from the anterior interventricular vein and posterior interventricular vein, respectively (4).

All the major veins give rise to smaller veins that run on the LV and RV surfaces (orders −12 to −9) and penetrate the myocardium at an almost right angle upon reaching orders −8 to −5 (Fig. 2C). The reconstructed transmural venous branches are independent of their arterial counterparts in terms of both their location and disposition (Fig. 2, B and C), while only some of the principle epicardial vessels coincide with the arrangement of the principle arteries (Fig. 1, A and B), similar to anatomic observations (4). The venous branches are more numerous than the arterial ones (3, 38, 45) (Figs. 1 and 2), as evident by both the opaque appearance of the combined network [in line with anatomic observations (4, 30, 49)] and from quantitative evidence. For example, the reconstructed venous network encompasses 1.69 ± 0.10 times the number of vessels than in the reconstructed coronary arterial tree.

Statistical Analysis of the Reconstructed Network Morphometry

Statistical analysis of the reconstructed network morphometry is an inevitable test since the coronary network is stochastic in nature, characterized by a heterogeneous (6) and highly asymmetric structure (34, 38), and due to the branching nature of the network (37, 38), which leads to an overwhelming number of vessels as the network further diverges toward the capillaries.

The comparison of reconstructed tree statistics with the raw data of native trees (Figs. 3, A–C, 4, and 5) demonstrated excellent agreement in mean and SD values for all orders in terms of segment lengths, diameters, and S/E. The agreement with the connectivity data was generally good. The network statistics relating to the branching asymmetry (Fig. 6) showed excellent agreement with the statistics of the reconstructed venous network (appendix c).

Averages and SDs of the 0v-to-0a capillary ratios.

Averages and SDs of the 0v-to-0a capillary ratios of the reconstruction were found to be 1.63 ± 0.02:1 and 1.87 ± 0.005:1, which were in good agreement with the database-expected ratio values of 1.61:1 and 1.86:1 for the LAD/LCx and RCA, respectively. The percentages of reconstructed branching types of 85.4 ± 0.34, 13.3 ± 0.29, 1.10 ± 0.04, and 0.18 ± 0.01 for bifurcations, trifurcations, quadrifications, and quintifications, respectively, conformed with reported values of Kassab et al. (38): 86%, 12.8%, 1%, and 0.2%, respectively.

A system that demonstrates self-similarity is termed “fractal” and obeys Horton's law, which suggests that a geometric relationship exists between system attributes. The coronary system was found to have fractal characteristics (69). Kassab et al. (38) reported for the sinusal network a mean element length ratio (R_L; mean ratio of element length between successive generations) of 1.77 for veins of orders −4 and above and 1.18 for orders −1 to −3. Furthermore, the reported mean element branching ratio (R_N; mean ratio of the number of elements between successive generations) was 3.37, and the ratio between the major axis mean diameters of successive generations (R_D) was found to be 1.72. The corresponding values of the reconstructed venous networks of R_L were 2.1 ± 0.91 and 1.16 ± 0.009, and the values obtained for R_N and R_D were 3.30 ± 0.03 and 1.67 ± 0.17, respectively.

Validation of Branching Symmetry, Vessel Numbers, Distribution of Vascular Volumes and Cross-Sectional Areas, and Network Topology

Reconstructed network asymmetry.

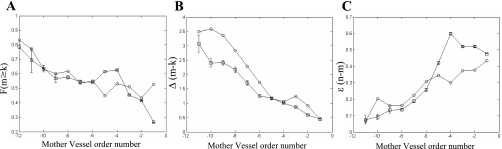
The reconstructed network asymmetry was compared with the features reported by Kalsho and Kassab (34). The first feature (Fig. 7A) was the order-categorized fraction of larger daughter vessels that also have longer lengths than their smaller sister vessels. It was evaluated as follows:

$$F=\frac{N(l_m\ge l_k)}{N(l_m\ge l_k)+N(l_m<l_k)}$$

where m > k is the order of the larger and smaller daughters and N(l_m ≥ l_k) and N(l_m < l_k) are the numbers of bifurcations with the larger daughter vessel having longer vessel length and smaller vessel length, respectively.

Fig. 7.

A: comparison of reconstructed network asymmetry (○) with the data (34) (□) of a fraction of the larger daughter vessel having also a longer vessel length than the smaller daughter as a function of the order of the mother vessel [F(m ≥ k)]. B: relationship between the reconstructed order difference between the two daughter vessels as a function of the order of the mother vessel [Δ(m − k)]. C: relationship between the reconstructed order difference between the mother and larger daughter vessels as function of the order of the mother vessel [ε(n − m)].

Additional features.

Additional features compared were the mother order-categorized ratio of the larger/smaller daughter order difference and the mother/larger daughter order difference, respectively (Fig. 7, B and C). The results conformed with the data (34) and showed that the highest orders are the most asymmetric while the degree of asymmetry decreases with the order.

The order distribution of vessel count (Fig. 3D) was nearly linear. The total number of venous capillaries in the present reconstructed model was 8,533,002 ± 520,007. Together with the coronary arterial tree, the total number of capillaries added to 13,627,776 ± 689,541, nearly half the total number of coronary vessels.

An estimation of the total number of capillaries in the coronary network was done based on measurements of capillary density (7) and, alternatively, based on direct measurements as performed by Wieringa et al. (66), who reported a density estimation of 10⁷ capillaries per 100-g heart in the rat for 15-μm arterioles, and by Eng et al. (14), who reported a value of 43 × 10⁵ capillaries per 100-g heart for 25-μm arterioles. Combining these estimates with the connectivity data of Kassab et al. (38, 41) yielded an estimate for the total number of capillaries per 100-g heart of 8.4 × 10⁷ and 10⁸ based on Refs. 66 and 14, respectively.

The overwhelming high number of capillaries precludes the possibility of a detailed reconstruction of the entire capillary network. In the present reconstruction, representation of the capillary network was simplified by using a single functional capillary to represent a cross-connected mesh, which encompassed between 18 and 30 capillaries (37). Accordingly, the total number of capillaries obtained for the reconstructed network, when the ratio between the functional capillary and cross-connected mesh of 18–30 was incorporated, yielded a total capillary count of 2.5 × 10⁸ to 4 × 10⁸, which was in line with the estimate of ∼10⁸. This value (an average of 3 × 10⁸ capillaries) assumed a ventricular mass of 113 g [86.2 and 26.8 g for the LV and RV, respectively (32)], i.e., 1.13 × 10⁵ voxels of 1 mm³, leading to a capillary density of 2,774 capillaries/mm³ (having a functional length of 1 mm), a value that conformed with the reported values of 2,000–5,000 (21, 52) and is equivalent to an average spacing of 19 μm between capillaries, which was in good agreement with the reported mean capillary distance of ∼18 μm (9).

The reconstructed venous network mass-normalized CBV of 9.0 ± 0.46 ml/100 g was more than twice higher than the mass-normalized CBV of 4.1 ± 0.23 ml/100 g (n = 5) of the reconstructed arterial tree (32). This was in line with the ratio of vessel numbers between the two networks. If we account for the 0.24- and 0.14-ml volume of the functional venous and arterial capillaries, respectively, by a factor of 23, which was taken as the average ratio between the functional capillary and cross-connected mesh, the venous and arterial mass-normalized capillary volumes were 5.22 ± 0.23 and 3.22 ± 0.31 ml/100 g, respectively, which added up to a total capillary volume of 8.74 ± 0.32 ml/100 g, which conformed with the reported data of 4–6% of myocardial wall volume (47, 55).

The total volume for the venous and arterial trees was obtained by adding the capillary volume to the volumes of the venous and arterial trees. Accordingly, the total mass-normalized CBVs obtained for the venous and arterial trees were 14.6 ± 0.56 and 7.32 ± 0.31 ml/100 g, respectively, and, accordingly, the total myocardial mass-normalized CBV was 21.9 ± 0.64 ml/100 g. This estimate, which is within the bounds of reported data (15, 21, 52, 55), was nearly twice the CBV estimated from the morphometric database (38). The difference, in absolute volume, between the reconstruction and database was consistent with the 1.8 difference in the number of vessels between the reconstruction and database. Reports (15, 21, 52, 55) on measured volumes of the coronary system have large variation, which may stem from biological variability and experimental error. Similarly, large variability exists in estimates of the number of coronary vessels (38, 41, 56). In addition, some variability is expected in stochastic reconstructions, depending on the range of distribution parameters in the statistical database. Further future validation is clearly needed to address the issue of total volume.

Currently, there are no data on the distribution of venous blood volume between regions of the heart, similar to the data of Weaver et al. (63) on the arterial tree. Nevertheless, the distribution of the blood volume of reconstructed trees over the LV, septum, and RV (by the venous LAD, LCx, and RCA) were compared with the data of Weaver et al. on the arterial tree. The validity of this comparison was based on two inherent assumptions: 1) drainage of each arterial branch is made by its corresponding venous counterpart and 2) there is no communication between the branches, i.e., the volume distributions of the coronary venous branches are proportional to their corresponding arterial counterparts. The results are shown in Table 2 and demonstrated overall good agreement with the distribution obtained for the previously reconstructed arterial networks and with the data of Weaver et al. (63). The calculated ratio of 1.33 ± 0.11 of the mean number of capillaries between the subendocarium and subepicardium agreed with the reports of greater coronary blood volume in the subendocarial layer than in the subepicardial layer in the LV and was similar to the reported values of 1.10–1.55 for the endocardial-to-epicardial ratios of red blood cell content (13, 23, 50, 64).

In summary, the reconstructed venous trees showed good fit to the measured data both quantitatively and qualitatively, i.e., the overall fit followed the general behavior of the database and usually fell within ±1 SD of the measured data. The effect of these small deviations on local hemodynamics and flow distribution is likely to be small since these deviations were primarily affected by the asymmetry of the network (D_l/D_m and D_s/D_m), a feature of the reconstructed tree that demonstrated excellent fit to the database. Furthermore, the reconstructed trees demonstrated similarity in their native 3-D structure. Finally, there were additional measures of fit, such as Horton ratios for diameter, length, and number of vessels at branching, diameter asymmetry parameters, total number of vessels, and volume distribution (Table 2). All these results serve as validation of the anatomic model.

Validation Via Flow Analysis

The previously generated 3-D coronary arterial network (32), which served as the “template” for the present venous model, was previously used for hemodynamic flow simulation (24). The simulation results were tested experimentally with the use of fluorescent microspheres. Predictions of the regional myocardial flow heterogeneity of the arterial 3-D model were in good agreement with the experimental data in terms of average myocardial flow, relative flow dispersion, and fractal characteristics. Furthermore, the longitudinal distribution of pressure showed agreement with epicardial and endocardial pressure measurements.

Since the present 3-D venous network is based on the structure of the 3-D arterial network, the integrative arteriovenous reconstructed network is expected to preserve the spatial heterogeneity characteristics of flow and pressure. An extensive hemodynamic validation will be carried in future studies based on the present quantitative anatomic platform.

Critique of the Model

Several assumptions were made (Table 1) to ameliorate the overwhelming computational burden associated with the reconstruction of the huge number of the vessels in the coronary venous network and the inherent structural complexity. First, the assumption regarding the admissibility of vessels intersection, considered for the perfusing and transmural vessels to simplify the reconstruction, has no implication on future hemodynamic studies as it is computationally transparent. Second, the Thebesian vessels were not considered to adhere to the tree-like structure of the network. The Thebesian system accounts for only 5–10% of the total venous drainage (9, 38, 56), and Thebesian vessels are more abundant in the atria and interatrial septum but are of lesser significance for the drainage of the LV, RV, and interventricular septum. Third, it was assumed that all the major coronary veins drain via the coronary sinus into the right atrium. This assumption relies on the observation that the coronary venous system is dominated by the coronary sinus in both human (4) as well as porcine (12) hearts. Fourth, the model does not account for anastomoses or arcades. In reality, arcading exists at the epicardial surface of the coronary venous system, and numerous anastomoses exist between the coronary veins (38, 49), with the highest-diameter anastomoses occurring around the cardiac apex on the posterior and anterior surfaces of the heart (4, 30, 49). Nevertheless, the coronary venous network has a dominantly tree-like structure (38), which was captured in the present model. Finally, the capillary cross-connection mesh (28, 37, 49) between arterioles and venules was represented by a single functional capillary. This assumption was made since the complexity of the coronary network structure and the overwhelming size precluded reconstruction of the entire capillary network. The representation of a functional capillary as an equivalent for a capillary cross-connection mesh reduced the complexity of the network by an order of magnitude and should not affect flow results since the location of the cross-connection mesh is confined to a region (“a layer”) in which the gradients of stress and intramyocardial pressure are small and relatively homogenous.

Significance of the Model

Biophysical modeling of the coronary circulation is of substantial significance given the experimental difficulties of in vivo hemodynamic measurements, especially in the deeper layers of contracting myocardium. Most previous coronary models have primarily focused on the arterial portion of the system, either ignoring the venous portion by assuming either constant (8, 25, 26, 36, 54, 61) or variable (48) boundary pressures at the outlet of the arterial bed based on a simplified 2-D venous model (62) or by implementing lumped models based on a single element (55) or a limited number of elements (43, 70). This approach lacks the 3-D spatial geometry of the vasculature and ignores the transmural distribution of venous pressure (1) and its influence on flow dynamics. Since myocardial blood flow is heterogeneous, both temporally and spatially, and highly dependent on the branching pattern and 3-D geometry of the coronary vasculature (2, 5, 6, 8), any realistic coronary flow analysis must be based on an accurate description of the anatomy and geometric structure of the entire coronary network. The present model provides an extensive and integrated anatomic model for realistic hemodynamic analysis of the coronary circulation.

GRANTS

This work was supported by United States-Israel Binational Science Foundation Grant 2003-095 and by National Heart, Lung, and Blood Institute Grant HL-055554-11.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

APPENDIX A: TOP-DOWN-TOP SCHEME

The top-down-top scheme is based on subtrees, or “crowns,” as basic building blocks. A crown of a venous vessel segment (the “stem”) is the entire subtree that it drains. The direction of the vessel generation was iteratively alternated. Starting with a venous capillary (0v capillary; see below), the latter was first associated with an arterial capillary (0a capilloary; in the top-down direction). The generation was then reversed to the down-top direction toward the end venule segment feeding this capillary. After assigning it with order and length following the database [specifically, the inverse of the CM (ICM) data], the progress was reversed again to the top-down direction toward another 0v capillary, which may be drained by this venule. This capillary was then associated with an arterial (0a) capillary. The progress was reversed once more to the down-top direction up to the mother vessel segment of the end venule, which was assigned an order following the statistics of the ICM data. In the next step, the other daughter of the mother segment was generated in the top-down direction based on the data of CM and LPM, and this top-down progress was continued toward the capillaries of the other daughter that were associated with arterial 0a capillaries. The progress was then reversed again to the down-top direction, and this top-down-top process was iteratively maintained until the epicardial branch points were reached. The detailed process is described in Supplement S4.

APPENDIX B: ICM

To assign an order to a venous mother element given its daughter's order, one needs to construct the ICM. ICM quantifies the probability of the order number of the mother element given the order number of its daughter segment. This are new data, which were extracted from the raw (unpublished) database.

The database was organized as a list of mother vessels and their corresponding daughter vessels and included the lengths, diameters, and order numbers for each vessel. The raw data consisted of two samples of sinusal branches: the first contained 12,258 segments, covering orders −1 to −12, and the second branch contained 1,817 segments, covering orders −4 to −11.

The generation of the ICM was based on the following scheme. Daughter vessels were sorted based on their order number, i (−11 ≤ i ≤ 0), and the number of their corresponding mother vessels having order j (−12 ≤ j ≤ −1) was counted. These numbers were arranged in a matrix format, where row i (−11 ≤ i ≤ 0) in the matrix represented daughter vessels of order i and column j (−12 ≤ j ≤ −1) represented mother vessels of order j. Accordingly, cell (i,j) in the matrix contained the total number of mother vessels of order j for a given daughter vessel of order i. ICM was obtained by dividing the values in each row by the total sum of the row, which yielded a histogram of the probability for a mother order given its daughter orders.

Table 3 shows the mean values of ICM and the corresponding SD values, respectively, after the averaging of the two branches.

Table 3.

Inverse connectivity matrix extracted from the raw morphometric data of the sinual tree (38)

	Order of the Mother Vessel
Order of Daughter Vessel	−1	−2	−3	−4	−5	−6	−7	−8	−9	−10	−11	−12
0	0.9746	0.0235	0	0	0.002 ± 0.002	0	0	0	0	0	0	0
−1	0.0321	0.2188	0.0844	0.302 ± 0.166	0.224 ± 0.054	0.099 ± 0.003	0.035 ± 0.012	0.002 ± 0.002	0.001 ± 0.001	0.001 ± 0.001	0	0
−2		0.0112	0.0671	0.320 ± 0.103	0.340 ± 0.014	0.17 ± 0.044	0.057 ± 0.025	0.024 ± 0.005	0.003 ± 0.003	0	0	0
−3			0.0024	0.252 ± 0.061	0.445 ± 0.024	0.208 ± 0.036	0.062 ± 0.038	0.025 ± 0.005	0.005 ± 0.005	0	0	0
−4				0.0453 ± 0.007	0.407 ± 0.054	0.29 ± 0.003	0.132 ± 0.00	0.076 ± 0.025	0.033 ± 0.017	0.010 ± 0.009	0.001 ± 0.001	0
−5					0.091 ± 0.028	0.464 ± 0.042	0.266 ± 0.023	0.100 ± 0.009	0.055 ± 0.027	0.021 ± 0.012	0.002 ± 0.00	0
−6						0.156 ± 0.048	0.466 ± 0.063	0.226 ± 0.030	0.102 ± 0.051	0.034 ± 0.028	0.016 ± 0.001	0.001 ± 0.001
−7							0.187 ± 0.071	0.459 ± 0.092	0.242 ± 0.092	0.097 ± 0.069	0.015 ± 0.001	0
−8								0.280 ± 0.063	0.462 ± 0.024	0.156 ± 0.060	0.098 ± 0.017	0.005 ± 0.005
−9									0.318 ± 0.057	0.361 ± 0.014	0.277 ± 0.027	0.043 ± 0.043
−10										0.267 ± 0.133	0.667 ± 0.067	0.067 ± 0.067
−11											0.750 ± 0.250	0.250 ± 0.250

Values are means ± SD. Columns 1 3 were based on one sample (n = 1) and therefore represent the mean value only; the rest of values in the matrix are based on two samples (n = 2). An element (m,n) in the mth row and nth column is the probability for a mother vessel of order n given a daughter vessel of order m.

APPENDIX C: DIAMETER ASYMMETRY

The diameter assignment algorithm was based on the branching asymmetry at branching points along the tree. For this purpose, branching asymmetry statistics (means ± SD) were calculated from the raw database (38) for the coronary sinusal tree in terms of AER, D_l/D_m, and D_s/D_m as a function of order number. A distinction was made between intraelement and interelement segments. For the intraelement case, the mother and large daughter vessels are of the same order. Accordingly, D_l/D_m, D_s/D_m, and AER statistical data were represented as a function of the element order number (Supplement S6, Suppl. Table S6-1), whereas D_s/D_m data were represented by an asymmetry ratio matrix, which describes the diameter asymmetry of daughter vessels to mother vessels as a function of the mother and sister segment order (Suppl. Table S6-2). For the interelement case, all the daughter vessels belong to different elements, and, therefore, both D_l/D_m and D_s/D_m were represented similarly to the asymmetry ratio matrix. Hence, the former (intraelement) can be viewed as an index of vessel taper, whereas the latter (interelement) represents branching asymmetry. The data shown in Table 4 demonstrates a significant “deep” in both in D_l/D_m and AER, found at a mother vessel of order −4, whereas for D_s/D_m, there was a monotonic trend for the smaller orders (−1 to −8). Accordingly, the data can be subdivided into three subregions: the epicardial and transmural subnetworks (orders −5 to −12) and the perfusion subnetwork (orders −1 to −4).

Table 4.

Statistics for D_l/D_m, D_s/D_m, D_s/D_l, and AER as a function of vessel order

	Dl/Dm		Ds/Dm		Ds/Dl		AER
Order	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Sample Size for the Mother Vessel	Sample Size for the Larger Daughter Vessel	Sample Size for the Smaller Daughter Vessel
−1	0.834	0.174	0.628	0.149	0.769	0.164	1.114	0.322	193	193	177
−2	0.862	0.153	0.619	0.136	0.722	0.167	1.173	0.308	156	165	149
−3	0.879	0.170	0.546	0.152	0.637	0.187	1.115	0.318	135	137	127
−4	0.784	0.233	0.469	0.198	0.626	0.222	0.887	0.316	833	892	656
−5	0.833	0.255	0.374	0.184	0.475	0.232	0.881	0.318	3,354	3,627	2,617
−6	0.934	0.251	0.313	0.180	0.288	0.157	1.030	0.347	3,391	3,496	2,849
−7	0.989	0.238	0.270	0.173	0.209	0.117	1.122	0.362	1,999	1,919	1,765
−8	1.023	0.240	0.248	0.174	0.172	0.097	1.168	0.360	896	816	801
−9	1.014	0.227	0.189	0.141	0.132	0.079	1.123	0.323	297	257	265
−10	1.007	0.248	0.218	0.153	0.149	0.078	1.094	0.331	65	57	55
−11	1.015	0.159	0.248	0.211	0.175	0.101	1.117	0.298	54	53	58
−12	1.062	0.395	0.252	0.198	0.139	0.073	1.123	0.182	7	7	5

D_l/D_m, larger daughter-to-mother vessel diameter ratio; D_s/D_m, smaller daughter-to-mother vessel diameter ratio; D_s/D_l, smaller daughter-to-larger daughter vessel diameter ratio; AER, area expansion ratio. AER is defined as follows: (D{l2} + D{s2})/D{m2}, where D_s, D_l, and D_m are the diameters of the smallest daughter vessel, largest daughter vessel, and mother vessel, respectively.

To determine the statistical significance of the order differences, especially the deep in D_l/D_m, we carried out a statistical analysis that included both order-independent and -dependent tests. The order-independent test was based on a cubic-spline smoothing of D_l/D_m data as a function of the logarithm of the diameter of the mother vessel (Suppl. Fig. S6-1). The generated venous network demonstrated a stochastic nature, similar to the native one, as clearly shown in Suppl. Fig. S6-2, with the minimum of D_l/D_m located at 67 μm.

To evaluate the significance of the deep of the spline fitting, a t-test was performed on a population of samples of D_l/D_m located in the vicinity of the deep. The “deep population” sample size varied between 2.5% and 25% of the entire population size. The hypothesis that the mean of the deep population is a random sample of the entire population was rejected (P < <0.001) (Suppl. Table S6-3). Results of the order-dependent analysis are shown in Suppl. Table S6-4. The population of D_l/D_m was found to be non-normally distributed for orders −4 to −9 and also −11 based on Kolmogorov-Smirnov tests (22) and for orders −3 to −11 based on the Lilliefors test (22). The hypothesis that adjacent order populations have the same mean was rejected for orders −4 to −7 based on all the nonparametric tests [i.e., Wilcoxon-Mann-Whitney, Kruskall-Wallis, and Kolmokorov-Smirnov (22)], indicating that the deep found at order −4 was statistically significant (Suppl. Table S6-4).