Context-Dependent Partitioning of Motor Learning in Bimanual Movements

Abstract

Human subjects easily adapt to single dynamic or visuomotor perturbations. In contrast, when two opposing dynamic or visuomotor perturbations are presented sequentially, interference is often observed. We examined the effect of bimanual movement context on interference between opposing perturbations using pairs of contexts, in which the relative direction of movement between the two arms was different across the pair. When each perturbation direction was associated with a different bimanual context, such as movement of the arms in the same direction versus movement in the opposite direction, interference was dramatically reduced. This occurred over a short period of training and was seen for both dynamic and visuomotor perturbations, suggesting a partitioning of motor learning for the different bimanual contexts. Further support for this was found in a series of transfer experiments. Having learned a single dynamic or visuomotor perturbation in one bimanual context, subjects showed incomplete transfer of this learning when the context changed, even though the perturbation remained the same. In addition, we examined a bimanual context in which one arm was moved passively and show that the reduction in interference requires active movement. The sensory consequences of movement are thus insufficient to allow opposing perturbations to be co-represented. Our results suggest different bimanual movement contexts engage at least partially separate representations of dynamics and kinematics in the motor system.

INTRODUCTION

Humans show a remarkable ability to learn motor tasks. Such learning has been studied in the laboratory using experiments in which subjects are presented with dynamic or visuomotor perturbations. For example, subjects readily adapt to a single perturbation applied unimanually (Shadmehr and Mussa-Ivaldi 1994) and can adapt when opposing perturbations are applied to each arm during bimanual movements (Tcheang et al. 2007). In contrast, when two opposing perturbations are presented unimanually in succession, dramatic interference is often seen (Bock et al. 2001; Brashers-Krug et al. 1996; Caithness et al. 2004; Goedert and Willingham 2002; Karniel and Mussa-Ivaldi 2002; Krakauer et al. 2005; Krakauer et al. 1999; Miall et al. 2004; Shadmehr and Brashers-Krug 1997; Wigmore et al. 2002). However, if a different sensory context is associated with each perturbation, and learning takes place over an extended period, some modest reduction in interference has been observed (Imamizu et al. 2007; Osu et al. 2004; Wada et al. 2003). It has also been shown that the context of bimanual movements can reduce interference (Howard et al. 2008; Nozaki et al. 2006). For example, if the opposing dynamic perturbations are uniquely associated with unimanual and bimanual movements, interference is reduced (Nozaki et al. 2006). Similarly, interference is reduced when opposing dynamic perturbations are each associated with a different bimanual context, whereby the arms either act independently or are linked together as though acting on a single object (Howard et al. 2008). However, in these previous studies, it is unclear whether the observed context-dependent reduction in interference depends on differences in the motor act associated with each context or from their distinct sensory consequences.

Studies that have shown interference between opposing perturbations have led to the conclusion that a single neural resource is shared by both perturbations during the task (Karniel and Mussa-Ivaldi 2002). More recent studies showing a context-dependent reduction in interference suggest that, in some cases, partially separate representations can be engaged by different sensorimotor contexts (Lee and Schweighofer 2009; Nozaki et al. 2006). We hypothesize that such separate representations may exist for movement contexts that are experienced frequently during everyday life. For example, a recent analysis of the statistics of bimanual arm movements showed that translations of the hands in either the same or in opposite directions in space (symmetrical and asymmetrical movements) are particularly common (Howard et al. 2009a). In this study, we examine whether interference between opposing dynamic or visuomotor perturbations is reduced when each is associated with these different bimanual movement contexts.

Subjects performed bimanual reaching movements in which the direction of either a dynamic or visuomotor perturbation changed across short blocks of trials. The bimanual context of the movement was either kept constant across the blocks or alternated in synchrony with the switching perturbations. Only in this latter condition, where each direction of perturbation was associated with a different bimanual context, was interference reduced. Furthermore, we examined a condition in which one arm was moved passively. In this case, switching contexts did not reduce interference, suggesting that it is the motor act rather than the sensory consequences of movement that allows opposing perturbations to be learned.

METHODS

A total of 64 right-handed subjects took part in the study. They provided written informed consent and were naïve to the aims of the experiment. The protocol was approved by a local ethics committee, and all subjects completed an Edinburgh handedness questionnaire.

All experiments were performed using two vBOT planar robotic manipulanda, with associated virtual reality C-rig and air table (Howard et al. 2009b). Subjects were seated at the apparatus and held one robot handle in each hand (Fig. 1A). Their forearms were supported by air sleds that constrained movements to the horizontal plane. The vBOT is a custom-built back-drivable planar robotic manipulandum that exhibits low mass at its handle. Position was measured using optical encoders sampled at 1,000 Hz, and torque motors allow translational forces to be applied at the same rate. The left vBOT was fitted with a force transducer (Nano 25, ATI) mounted below the handle to measure force. A virtual reality system was used to overlay images of targets and cursors in the plane of movement. Subjects were prevented from viewing their hands directly.

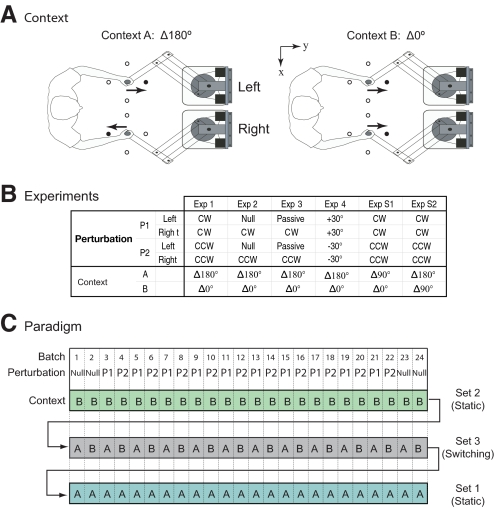
Fig. 1.

The experimental paradigm. A: bimanual movement contexts in dynamic and visuomotor leaning experiments. Center out-and-back movements to 1 of 4 targets were performed either in context A (shown here as Δ180°) or in context B (shown here as Δ0°). Filled targets show an example of a single movement context trial. B: table showing the perturbation and bimanual movement contexts used in experiments 1–4 and S1–S2. C: the experimental paradigm showing perturbation (P1 or P2) and bimanual movement context (A or B) for each batch. Each experiment was comprised of 3 sets, each containing 24 batches of 16 trials. The 1st and last 2 batches in each set were in the null condition. On batches 3–22 of each set, the perturbations always alternated between P1 and P2. Two of the sets were static context sets (A or B). The other set was a switching context set in which the context switched synchronously with the perturbation on each batch. In the example shown here, the 1st set is in context B (static context set), the 2nd is the switching context set (A/B), and the 3rd set is in context A (static context set).

All experiments required subjects to perform out-and-back movements that consisted of a continuous movement out to a target and immediately back to the home position. Each arm reached to one of four targets (circles of 1 cm radius) that were equally spaced around a 10-cm-radius circle (Fig. 1A). The start positions (circles of 1.5 cm radius) were 18 cm left and right of the midsagittal plane for the left and right arms, respectively, and ∼30 cm below the eyes and 30 cm in front of the chest. The right and left arms controlled red and green cursors (circles of 0.5 cm radius), respectively.

At the start of each trial, the vBOTs ensured that each cursor was within the start position, applying a force the move the handles if required. A trial began when each cursor had remained within its start position at speeds <0.1 cm/s for 0.5 s. The left and right targets appeared, and subjects were cued to start the movement by an acoustic tone that was used as a go signal. Subjects were required to achieve the movements with both arms within 600 ms and were warned if their movements were too slow. The average intertrial interval was ∼1 s.

Bimanual context switching experiments

A total of 36 subjects performed the context switching experiments, with 6 subjects randomly assigned to each of six experimental groups (which included 2 control groups; see Supplementary Material).¹ Figure 1B shows the perturbations and bimanual movement contexts used in these experiments.

Each experiment included three sets, with each set consisting of 24 batches and each batch consisting of 16 out-and-back movement trials, for a total of 1,152 trials (Fig. 1C). Within every sequence of four trials, each target was presented once in a pseudorandom order such that each target appeared four times within a batch.

Each set began with a pre-exposure phase consisting of two batches in the null condition (no forces). Subjects performed an exposure phase consisting of 20 batches in which each arm was exposed to two different perturbations that alternated across consecutive batches. These perturbations could be the null condition or a dynamic or visuomotor perturbation, depending on the particular experiment (Fig. 1B). On odd numbered batches, the left and right arms experienced perturbation P1, and on even numbered batches, the arms experienced perturbation P2 (Fig. 1C). Finally, each set finished with a postexposure (wash-out) phase consisting of two batches performed in the null condition. During dynamic perturbations, catch trials were included to assess learning, whereby each vBOT simulated a channel between the starting location and the target (Scheidt et al. 2000) with a wall stiffness of 2,000 N/m. For each subject, one catch trial was pseudorandomly chosen in the first four trials and also in the last four trials of each batch. The catch trial directions were randomly assigned (not counterbalanced) over all four movement directions.

Each experiment involved two distinct bimanual movement contexts (context A and context B; Fig. 1C). Two of the sets were static context sets (the first in context A and the other in context B), in which the context remained constant throughout the set. The third set was a switching context set in which the context alternated across consecutive batches (context A for odd batches and context B for even batches). As such, in the switching set, each perturbation (P1 or P2) was associated with a different bimanual context (A or B). Each subject performed the three sets in a different, randomly assigned order (one example is shown in Fig. 1C).

Data analysis

Data were collected from the manipulandum at 1,000 Hz and logged to disk for offline analysis using Matlab (Matlab, The MathWorks, Natick, MA). We used a two-tailed paired t-test across subjects to determine statistical significance (Matlab).

EXPERIMENT 1: DYNAMIC SWITCHING Δ180°/Δ0°.

The first experiment studied whether associating opposing dynamic perturbations with distinct bimanual movement contexts would reduce interference.

The left and right target positions were chosen for context A so that the relative angle between the movements of the arms was 180° (solid targets in Fig. 1A, left). We refer to this movement context as Δ180°. In context B, the target positions were chosen so that the relative angle between the movements was 0° (solid targets in Fig. 1A, right). We refer to this movement context as Δ0°. In the switching context set, subjects alternated between a batch in context A (Δ180° for 16 trials) and a batch in context B (Δ0° for 16 trials).

During the exposure phase of each set, subjects (n = 6) experienced a dynamic perturbation that changed between odd and even numbered batches. One half the subjects (n = 3) experienced a clockwise viscous curl field (CW) on each arm for odd-numbered batches

$$\left[\begin{array}{c}{F}_{\text{x}}^{\text{R}}\\ F_{\text{y}}^{\text{R}}\end{array}\right]=\left[\begin{array}{cc}0& -10\\ +10& 0\end{array}\right]\left[\begin{array}{c}{\dot{x}}_{\text{R}}\\ {\dot{y}}_{\text{R}}\end{array}\right]\text{and}\left[\begin{array}{c}{F}_{\text{x}}^{\text{L}}\\ F_{\text{y}}^{\text{L}}\end{array}\right]=\left[\begin{array}{cc}0& -10\\ +10& 0\end{array}\right]\left[\begin{array}{c}{\dot{x}}_{\text{L}}\\ {\dot{y}}_{\text{L}}\end{array}\right]$$

and a counterclockwise field (CCW) on each arm for even-numbered batches

$$\left[\begin{array}{c}{F}_{\text{x}}^{\text{R}}\\ F_{\text{y}}^{\text{R}}\end{array}\right]=\left[\begin{array}{cc}0& +10\\ -10& 0\end{array}\right]\left[\begin{array}{c}{\dot{x}}_{\text{R}}\\ {\dot{y}}_{\text{R}}\end{array}\right]\text{and}\left[\begin{array}{c}{F}_{\text{x}}^{\text{L}}\\ F_{\text{y}}^{\text{L}}\end{array}\right]=\left[\begin{array}{cc}0& +10\\ -10& 0\end{array}\right]\left[\begin{array}{c}{\dot{x}}_{\text{L}}\\ {\dot{y}}_{\text{L}}\end{array}\right]$$

For the other half of the subjects (n = 3), the order was reversed, such that they experienced CCW and CW fields on odd and even batches, respectively.

Performance on each trial was defined as the maximum deviation of the hand path on the outward movement, measured from a straight line between the start and target positions. We refer to this as the maximum perpendicular error (MPE). We analyzed only the outward movements because this minimizes the influence of online feedback compensation. To ensure that comparisons between the different conditions were balanced in terms of perturbation direction, we computed an error measure across pairs of batches. For each subject, we computed the average of the absolute MPE from all exposure trials in two successive batches. As such, each batch pair included one batch in the CW field and one in the CCW field. Because absolute MPE was used for this analysis, the different directions of the perturbations could be ignored. We then calculated the mean and SE for each batch pair across subjects. Each arm was analyzed separately. To assess whether subjects were learning to compensate specifically for the dynamic perturbation or were co-contracting, we examined the forces they produced on randomly presented catch trials in which the manipulandum simulated a channel, as described above. We analyzed the force produced by subjects into the wall of the channel at the point of peak outward velocity. To quantify the amount of specific compensation at the end of each set, we examined the catch trial forces over the final four batches of exposure. This includes two batches for each of the perturbations (CCW and CW) and two catch trials per batch to give a total of eight catch trials. The sign of the force associated with the CCW field was changed. We used the mean of these eight values for each subject as a measure of compensation. This will be a positive value if subjects are generating the appropriate forces to compensate for the respective perturbations.

To test the generality of the results to different movement contexts, two control experiments were run on separate groups of subjects. One control group trained with a Δ0°/Δ90° context pair and the other trained with a Δ90°/Δ180° context pair (see Supplementary Material for details).

EXPERIMENT 2: DYNAMIC SWITCHING, NULL LEFT ARM.

The second experiment studied whether any reduction of interference observed in experiment 1 would depend on both arms experiencing a dynamic perturbation. It was identical to experiment 1, except that the left arm always moved in a null field, whereas the right arm alternated between CW and CCW fields as above.

EXPERIMENT 3: DYNAMIC SWITCHING, PASSIVE LEFT ARM.

The third experiment studied whether any reduction of interference observed in experiment 1 would depend on both arms generating active movements. It was identical to experiment 1, except that movement of the left arm was passively driven by movement of the right arm. Specifically, we used the vBOT to passively move the left arm in the same or opposite direction of the right arm, based on the bimanual context (either Δ0° or Δ180° as in experiment 1). The subject's left arm was supported in a plastic mold attached to the left vBOT handle. This arrangement transferred force to the left arm without the need for subjects to firmly grip the handle. Subjects were told to completely relax the left arm. We simulated a stiff two-dimensional virtual spring (spring constant 3,000 N/m) between the left and right vBOT handles, with an appropriate offset and coupling direction.

Subjects were provided with feedback to encourage them to maintain their left arm in a relaxed state. During each trial, the acceleration and force measured at the handle in the direction of the target were recorded. When the arm is passive, the forces recorded by the force transducer at the base of the handle arise primarily (ignoring friction and viscosity) because of the acceleration of the mass of the subject's arm (with a small contribution caused by the mass of the handle). In this case, the measured force should be a scaled version of the acceleration (with the scaling factor representing the effective mass). To estimate whether there was such a scaling relationship, force and acceleration measurements over the course of a trial were first normalized to have the same peak-to-peak values. The mean of the absolute differences between theses normalized values was calculated across the trial. For a passive movement these two curves should be very similar leading to a low difference measure. We applied a threshold value (determined experimentally), below which movement was considered passive. If this threshold was exceeded on a trial, a warning message was displayed that indicated that subjects should relax their left arm. Although it is theoretically possible that subjects could make semiactive movements of reduced force, piloting showed that it was very difficult to “fool” the algorithm in this way. Critically, our results show a dramatic effect of this passive condition on the degree of interference (see results), suggesting that the movements were indeed qualitatively different from active ones.

EXPERIMENT 4: VISUOMOTOR SWITCHING Δ180°/Δ0°.

The fourth experiment studied whether associating opposing visuomotor perturbations with distinct bimanual movement contexts (Δ180° and Δ0°) would reduce interference.

During this experiment, no forces were applied by the manipulanda, and there were no catch trials. The perturbation consisted of introducing a rotation between the position of the hand and the cursor, which provided visual feedback of the hand. To simplify the requirements of visual attention, the left and right cursors and associated start and target positions were offset relative to the corresponding handle positions by 10 cm in the x-axis toward the center of the visual display. To ensure the left and right targets did not overlap, they were also shifted by 2 and −2 cm in the y-axis, respectively. The targets were identified by a line drawn to their respective start positions. As in experiment 1, contexts A and B corresponded to Δ180° and Δ0° movements, respectively. However, the perturbation now alternated between visuomotor rotations of +30° and −30°.

To quantify learning, we measured the initial direction of movement for each cursor at a displacement of 1 cm from the start position. We refer to this measure as the starting angle error (SAE), which will be zero if subjects have perfectly compensated for the visuomotor rotation. As described above for MPE on dynamic perturbations experiments, we similarly computed the average of the absolute SAE from all trials over successive pairs of batches for each subject. We calculated the mean and SE for each batch pair across subjects. Each arm was analyzed separately.

Transfer experiments

A total of 16 subjects performed the transfer experiments, with 8 subjects in each of two experimental groups that experienced either dynamic of visuomotor perturbations.

EXPERIMENT 5: DYNAMIC TRANSFER.

The fifth experiment studied transfer of learning of a dynamic perturbation from the Δ180° bimanual context to the Δ0° context. This order was chosen because results from experiment 1 showed that the Δ0° context is easier for subjects to perform than the Δ180° context. Thus any increase in MPE on transition from Δ180° to Δ0° could be attributed to a lack of transfer and not an increase in difficulty. Subjects performed a pre-exposure phase of two batches in the null field. One half the subjects (n = 4) performed an exposure phase of 10 batches in a CW curl field in the Δ180° context followed by 10 batches in the same field in the Δ0° context. The other half of subjects (n = 4) performed the identical paradigm but in a CCW field. Finally, subjects performed a post-exposure (wash-out) phase in the null field, with the first batch in the Δ0° context and the second batch in the Δ180° context. For each subject, we computed the signed average of the MPE from every four trials. The sign of the MPE for subjects who experienced the CCW field was changed. We computed the mean and SE across all subjects. Each arm was analyzed separately.

EXPERIMENT 6: VISUOMOTOR TRANSFER.

The sixth experiment studied transfer of learning of a visuomotor perturbation from the Δ180° bimanual context to the Δ0° context. It was identical to experiment 5 except that the perturbations were visuomotor rotations of +30° and −30°, and we computed the signed average of the SAE.

Extended learning experiments

The issue of subject fatigue placed limitations of the length of each of the three sets in experiments 1–4. To study learning over a larger number of trials in the switching context set, extended training experiments were carried out for both the dynamic and visuomotor perturbations. A total of 12 subjects performed the extended learning experiments, with two groups of 6 subjects experiencing either dynamic or visuomotor perturbations.

EXPERIMENT 7: EXTENDED DYNAMIC LEARNING.

Subjects performed a pre-exposure phase of two batches in the null field, followed by an exposure phase of 68 batches. The exposure phase was identical to the switching context set of experiment 1, except for its extended duration. That is, curl field direction switched concurrently with alternating Δ180° and Δ0° movement contexts. One half the subjects experienced a CW curl field for odd number batches and CCW for even numbered batches. This order was reversed for the other half of subjects. Finally, subjects performed a post-exposure (wash-out) phase in the null field, with the first batch in the Δ180° context and the second batch in the Δ0° context. For each subject, we computed the signed average of the MPE for all trials in a batch. The sign was adjusted for the half of subjects who experienced the field directions in reverse sequence. We computed the mean and SE across all subjects. Each arm was analyzed separately.

EXPERIMENT 8: EXTENDED VISUOMOTOR LEARNING.

The eighth experiment was identical to experiment 7 except that the perturbations were visuomotor rotations of +30° and −30°, and we computed the signed average of the SAE, as described above for MPE.

RESULTS

Bimanual context switching experiments

In experiments 1–4, subjects were exposed to alternating perturbations (P1 and P2; Fig. 1, B and C), whereby the perturbation switched at the end of each batch of 16 trials. Subjects performed three sets of 24 batches with the order of the sets counterbalanced across subjects. Two of the sets were static context sets in which the arms moved either in the opposite direction in Cartesian space (bimanual context A, Δ180°) or in the same direction (bimanual context B, Δ0°). In the switching context set, the movements alternated between contexts A and B at the end of each batch, such that each perturbation was associated with a distinct bimanual context.

EXPERIMENT 1: DYNAMIC SWITCHING Δ180°/Δ0°.

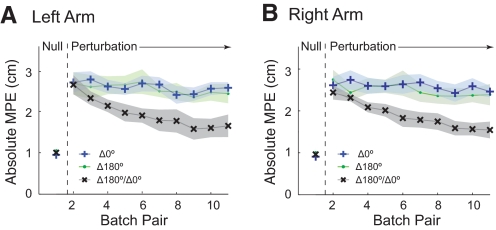
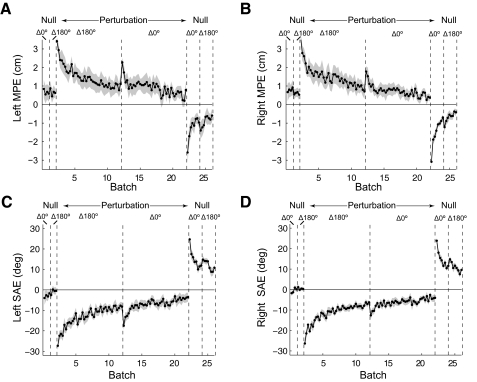
Results for experiment 1 are summarized in Fig. 2, which shows the batch-pair MPE for the three sets for the left and right arms (Supplementary Fig. S1 shows signed MPE for each set and Table S1 contains detailed data for both arms). In the null field pre-exposure phase, subjects made roughly straight-line movements characterized by a low MPE. On introduction of the field, MPE increased for both arms. In the static context sets (Δ180° and Δ0°), the MPE did not change significantly between the initial and final exposure batch pairs for either the left (Δ180°, P = 0.32; Δ0°, P = 0.44) or right arm (Δ180°, P = 0.052; Δ0°, P = 0.40). However, in the switching context set (Δ180°/Δ0°), MPE decreased significantly for both arms (left: P = 0.001, right: P < 0.001). Moreover, the final exposure batch pair MPE was significantly lower for the switching context set than for either of the static context sets for both arms (P < 0.033 for all comparisons). This suggests that associating a different bimanual movement context with each perturbation allows subjects to learn opposing fields.

Fig. 2.

Dynamic perturbation experiment 1 with both arms experiencing the switching dynamic perturbations and bimanual movement contexts of Δ180° and Δ0°. A: left arm mean absolute maximum perpendicular error (MPE; solid lines) and SE (shading) for pairs of batches, averaged over all 6 subjects. The results for the 3 sets are plotted on the same graph. B: MPE for the right arm plotted as in A.

To determine whether decreases in MPE were caused by specific compensation of the perturbation, we analyzed the forces produced by subjects on catch trials (see methods). Significant compensatory forces were observed only in the switching context set [Δ180°/Δ0° left: 4.6 ± 1.1 (SD) N, P = 0.0001; right: 2.50 ± 0.84 N, P = 0.0007]. The compensatory forces were not significant either in the Δ180° static context set (left: −0.29 ± 1.81 N, P = 0.72; right −0.55 ± 2.84 N, P = 0.65) or in the Δ0° static context set (left 0.703 ± 2.32 N, P = 0.49; right 1.90 ± 2.0 N, P = 0.07).

Control experiments, using additional groups of subjects, were also run with perpendicular movement directions (Δ90°) to examine other bimanual movement contexts (Supplementary Material). Results from experiments S1 (Δ0°/Δ90° context pair) and S2 (Δ90°/Δ180° context pair) show that the ability to co-represent opposing dynamic perturbations is not limited to the Δ180°/Δ0° movement context pair.

These results show that associating opposing dynamic perturbations with different bimanual movement contexts allows subjects to partition their representations of each perturbation, thereby reducing the interference that is observed when the movement context remains static.

EXPERIMENT 2: DYNAMIC SWITCHING, NULL LEFT ARM.

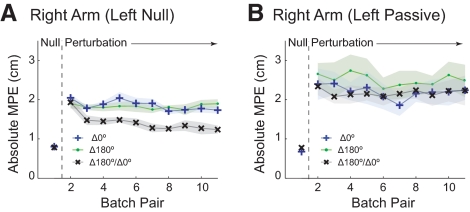
Results for experiment 2 are summarized in Fig. 3A (plotted for the right arm as in Fig. 2B; Supplementary Table S1 contains detailed data for both arms). In the null field, subjects made roughly straight-line movements as indicated by the low MPE. On introduction of the field, the MPE increased. Between the initial and final exposure batch pairs, no significant reduction in MPE was seen for the Δ180° static context set (P = 0.94), whereas a small, but significant, decrease in MPE (down 0.32 cm) was seen for the Δ0° static context set (P = 0.001). In contrast, in the switching context set (Δ180/Δ0°), between the initial and final exposure batch pairs, subjects exhibited a substantial decrease in MPE (down 0.69 cm; P = 0.0001). The final exposure batch pair MPE for the switching context set was significantly lower than for either of the static context sets (P < 0.0002 for both sets).

Fig. 3.

Dynamic perturbation experiments 2 (left null) and 3 (left passive). A: right arm mean absolute MPE (solid lines) and SE (shading) for bimanual movement contexts Δ180° and Δ0°, with the left arm experiencing a null field and the right arm experiencing the switching dynamic perturbations. B: right arm mean absolute MPE with the left arm moving passively and the right arm experiencing the switching dynamic perturbations, plotted as in A.

As in the previous experiment, significant compensatory catch trial forces were observed only in the switching context set (Δ180°/Δ0° 3.20 ± 0.97 N, P = 0.0005; Δ180°, 0.40 ± 0.63 N, P = 0.18; Δ0°, −0.046 ± 1.15 N, P = 0.93). Importantly, this suggests that the small reduction in MPE observed in the Δ0° static context set was caused by co-contraction rather than specific compensation.

Results of this experiment, in which the left arm always moved in the null field, show that the ability to co-represent opposing dynamic perturbations does not require both arms to experience the same dynamic environment.

EXPERIMENT 3: DYNAMIC SWITCHING, PASSIVE LEFT ARM.

Results for experiment 3 are summarized in Fig. 3B (plotted for the right arm as in Fig. 2B; Supplementary Table S1 contains detailed data for both arms). Again, in the null field, subjects made roughly straight-line movements as indicated by the low MPE. On introduction of the field, the MPE increased for the right arm. There was no significant decrease in MPE between the initial and final exposure batch pairs in either of the two static context sets (Δ0°, P = 0.52; Δ180°, P = 0.30) or in the switching context set (Δ0°/Δ180°, P = 0.76). Moreover, MPE at the end of the switching context set was not significantly different from the two static context sets (P > 0.34). Similarly, analysis of catch trials showed no significant compensatory forces in any of the sets (Δ180°/Δ0° −0.98 ± 2.70 N, P = 0.41; Δ180° −0.43 ± 2.01 N, P = 0.62; Δ0° 0.057 ± 1.37 N, P = 0.92).

This suggests that a bimanual context involving active, rather than passive, movements of the left arm is necessary to allow subjects to co-represent opposing dynamic perturbations.

EXPERIMENT 4: VISUOMOTOR SWITCHING Δ180°/Δ0°.

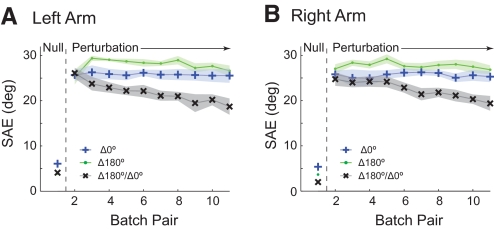
Results for experiment 4 are summarized in Fig. 4 (plotted for both arms as in Fig. 2; Supplementary Table S1 contains detailed data for both arms). In the veridical pre-exposure phase, subjects made roughly straight-line movements with a low SAE. On introduction of the visuomotor rotation to both arms, the SAE increased. In the static context sets (Δ180° and Δ0°), SAE did not decrease significantly between the initial and final exposure batch pairs (P > 0.38 for both arms and sets). However, in the switching context set (Δ180°/Δ0°), SAE decreased progressively. This decrease was significant between the initial and final exposure batch pairs for both arms (left: decrease in SAE of 7.4°: P = 0.002; right: decrease in SAE of 5.4°: P = 0.006). Moreover, the final exposure batch pair SAE was significantly lower for the switching context set than for either of the static context sets for both arms (P < = 0.016 for all comparisons).

Fig. 4.

Visuomotor perturbation experiment 4 with both arms experiencing the switching visuomotor perturbations and bimanual movement contexts of Δ180° and Δ0°. A: left arm mean absolute starting angle error (SAE; solid lines) and SE (shading) for pairs of batches, averaged over all 6 subjects. The results for the 3 sets are plotted on the same graph. B: SAE for the right arm, plotted as in A.

These results show that the ability of distinct bimanual movement contexts to partition learning of opposing sensorimotor perturbations also applies to visuomotor rotations.

Context transfer experiments

The previous experiments showed that the representation of sensorimotor perturbations can be partitioned on the basis of different bimanual movement contexts. In the following experiments, using a transfer paradigm, we examine whether this partitioning is preexisting or whether it develops over the course of learning. Subjects performed two static context sets (Δ180° followed immediately by Δ0°) during which they were exposed to the same dynamic or visuomotor perturbation during both sets. Transfer of learning from the first to the second set was examined.

EXPERIMENT 5: DYNAMIC TRANSFER.

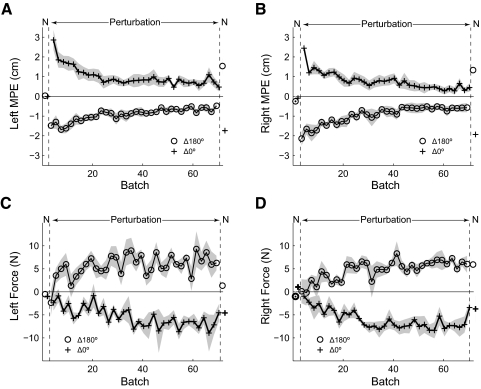
Results for experiment 5 are summarized in Fig. 5, A and B (plotted for both arms; Supplementary Table S2 contains detailed data for both arms). MPE was low in the null field pre-exposure batches. On introduction of the perturbation, MPE increased dramatically and then decreased significantly between the initial and final batches of the first exposure set (Δ180°, left: P = 0.002, right: P < 0.001). On initial transition to the Δ0° movement context, in which the perturbation remained identical to the first, the error increased significantly (change in MPE from last 8 trials in Δ180° to the 1st 8 trials in Δ0° left, 1.06 cm, P = 0.01; right: 0.90 cm, P = 0.001). However, MPE decreased rapidly over the next four batches to preswitch levels. At the end of the Δ0° set, subjects performed 16 post-exposure batches in the null field, with the first 8 batches in the Δ0° context and the final 8 batches in the Δ180° context. MPE rose sharply on initial transition to the null field (left: P < 0.001, right: P < 0.001) and decreased progressively over the eight batches in the Δ0° context. When the context changed to Δ180°, there was no significant change in MPE (left: P = 0.12, right: P = 0.10).

Fig. 5.

Dynamic and visuomotor perturbation transfer experiments 5 and 6. Initial and final 2 batches were in the null conditions. Perturbation direction remained constant throughout the exposure phase. The 1st 10 batches of exposure were in bimanual context Δ180° and were followed by 10 batches in context Δ0°. A: signed mean MPE (solid line) and SE (shading) for the left arm in the dynamic perturbation transfer experiment. Each point is mean across 4 trials and across all 8 subjects. B: right arm MPE, plotted as in A. C: left arm SAE for the visuomotor perturbation transfer experiment, plotted as in A. D: right arm SAE, plotted as in A.

The increase in MPE on transition from the Δ180° to Δ0° movement contexts during exposure to the same dynamic perturbation suggests that there is incomplete transfer between these two contexts.

EXPERIMENT 6: VISUOMOTOR TRANSFER.

Results for experiment 6 are summarized in Fig. 5, C and D (plotted for both arms; Supplementary Table S2 contains detailed data for both arms), and they were very similar to the dynamic transfer experiment. SAE increased dramatically from pre-exposure levels on initial introduction of the perturbation and decreased progressively over the course of the Δ180° set, which was significant on the final batch of the set (left: P < 0.001, right: P < 0.001). On initial transition to the Δ0° context, in which the perturbation remained identical to the first, the error increased significantly (change in SAE from last 8 trials in Δ180° to the 1st 8 trials in Δ0°, left: −7.43°, P = 0.01; right: −4.60°, P = 0.001). However, SAE decreased rapidly over the next four batches to preswitch levels. At the end of the Δ0° set, subjects performed 16 post-exposure batches in the null field, with the first 8 batches in the Δ0° context and the final 8 batches in the Δ180° context. SAE rose sharply on initial transition to the postexposure null condition (left: P < 0.001, right: P < 0.001) and decreased progressively over the eight batches in the Δ0° context. When the context changed to Δ180°, there was a small but nevertheless significant increase in SAE on the right arm only (right: P = 0.05, left: P = 0.32).

The results of the dynamic and visuomotor transfer experiments suggest that there is incomplete transfer of motor learning between different bimanual movement contexts. This is consistent with preexisting separate representations for each context because a context-independent representation would predict 100% transfer. Moreover, the partial transfer observed is consistent with partially overlapping representations for each context.

Extended context switching experiments

In the previous context switching experiments (experiments 1–4, S1, and S2), subjects performed three sets of 24 batches, with two static context sets and one switching set. In the switching set, it was shown that associating a distinct bimanual movement context with each perturbation allowed subjects to learn opposing perturbations, which would otherwise interfere. However, at the end of the switching sets (which lasted ∼20 min), the errors, although significantly decreased, had still not reached asymptotic levels. To examine learning over a longer time course, in the following experiments, subjects performed an extended version (∼1 h) of the switching context set (72 batches) from either experiment 1 (dynamic perturbations) or experiment 4 (visuomotor perturbations).

In these extended learning experiments, we found that subjects were on average 9.5 ± 1.6 (P < 0.001) and 11 ± 2.0 ms (P < 0.01) slower to initiate movements in the Δ180° context compared with the Δ0° context for the dynamic and visuomotor perturbations, respectively (from a baseline reaction time of ∼410–420 ms).

EXPERIMENT 7: EXTENDED DYNAMIC LEARNING.

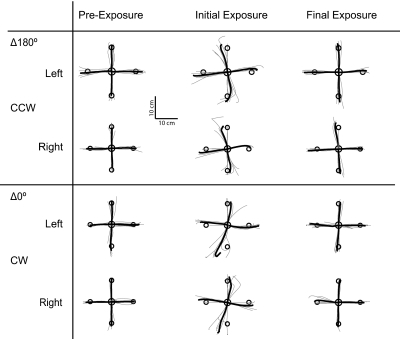
The outward hand paths are shown in Fig. 6, for the first four trials in a batch for each subject (thin lines) and group averages (solid lines). By the end of the pre-exposure phase, subjects made roughly straight-line movements out to the target in both the Δ180° and Δ0° contexts (Pre-exposure column in Fig. 6). On introduction of the dynamic perturbation, trajectories were perturbed in the direction of the field (initial exposure column in Fig. 6). By the end of the exposure period, the movement trajectories had returned to the roughly straight paths observed in the pre-exposure period (final exposure column, Fig. 6).

Fig. 6.

Raw trajectories from the extended dynamic learning experiment 7 with both arms in the switching dynamic perturbations and switching bimanual movement contexts Δ180°/Δ0°. Trajectories for 1st 4 trials for each subject (thin gray line) and mean across subjects (thick black line) are shown for the left and right arms for contexts Δ180° and Δ0°. The 1st column shows the trajectories during pre-exposure (batches 1 and 2), the 2nd column during initial exposure (batches 3 and 4), and the 3rd column during final exposure (batches 69 and 70).

These changes in trajectory were reflected in the MPE values (Fig. 7, A and B, show signed MPE for the left and right arms, respectively). Pre-exposure MPE was low in both the Δ180° and Δ0° contexts and increased on introduction of the perturbation. MPE decreased progressively over the course of the experiment and reached low levels by the final two exposure batches (left CCW: −0.49 ± 0.35 cm, left CW: 0.47 ± 0.54 cm, right CCW: −0.57 ± 0.57 cm, right CW: 0.45 ± 0.53 cm). These low MPE values are consistent with the return to roughly straight-line trajectories seen in Fig. 6 (compare pre-exposure and final exposure columns in Fig. 6).

Fig. 7.

Extended dynamic learning experiment 7, with both arms in the switching dynamic perturbations and switching bimanual movement contexts Δ180°/Δ0°. The 1st and last 2 batches were in the null condition (N). A: signed mean MPE (solid line) and SE (shading) over all 6 subjects for the left arm. B: signed mean MPE for the right arm, plotted as in A. C: mean catch trial forces (solid line) and SE (shading) for the left arm. D: mean catch trial forces for the right arm, plotted as in C.

As in the previous dynamic perturbation experiments, catch trials were used to assess specific compensation. The two catch-trial force values in each batch were averaged together over subjects and are plotted against batch number for the left and right arms in Fig. 7, C and D, respectively. During the initial null pre-exposure phase, the catch-trial forces are close to zero, as expected. Over the duration of exposure, the forces gradually increase in magnitude with a direction appropriate to compensate for the perturbation. This confirms that specific compensatory processes were involved rather than co-contraction. This conclusion is also supported by the context-dependent after-effects in the post-exposure period (Fig. 7, A and B).

EXPERIMENT 8: EXTENDED VISUOMOTOR LEARNING.

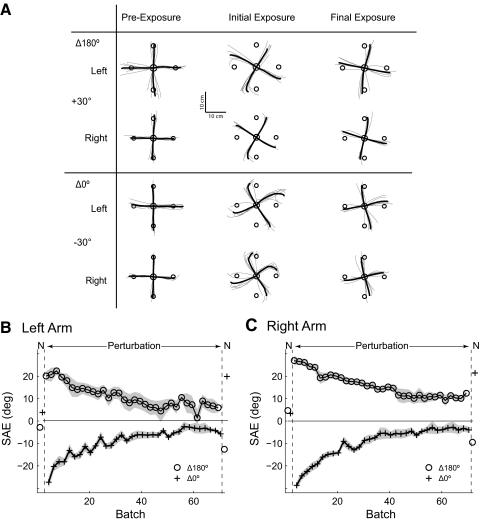
The outward hand paths are shown in Fig. 8A for the first four trials in a batch for each subject (thin lines) and group averages (solid lines). By the end of the pre-exposure phase, subjects made roughly straight-line movements out to the target in both the Δ180° and Δ0° contexts (pre-exposure column in Fig. 8A). On introduction of the visuomotor perturbation, trajectories were rotated with characteristic “correction hooks” at the end (initial exposure column, Fig. 8A). However, by the final exposure batch, movement trajectories were roughly straight paths that were rotated back toward the targets (final exposure column, Fig. 8A).

Fig. 8.

Extended visuomotor rotation learning experiment 8, with both arms experiencing switching visuomotor perturbations and switching bimanual movement contexts Δ180°/Δ0°. The 1st and last 2 batches were in the null condition (N). A: raw trajectories for both arms, plotted as in Fig. 6. Trajectories for 1st 4 trials for each subject (thin gray line) and mean across all 6 subjects (thick black line) are shown for the left and right arms for contexts Δ180 and Δ0°. The 1st column shows the trajectories during pre-exposure (batches 1 and 2), the 2nd column during initial exposure (batches 3 and 4), and the 3rd column during final exposure (batches 69 and 70). B: signed mean SAE (solid line) and SE (shading) over all 6 subjects for the left arm. C: signed mean SAE for the right arm, plotted as in B.

Figure 8, B and C, shows the SAE over the course of the experiment for the left and right arm, respectively. Pre-exposure SAE was low in both movement contexts and increased on introduction of the visuomotor rotation. SAE decreased progressively during the exposure phase and reached a low value by the final two exposure batches (left +30°: 5.90 ± 5.09°, left −30°: −5.75 ± 2.73°, right +30°: 12.38 ± 4.29°, right −30°: −3.95 ± 3.40°). These low final SAE values confirm the observation from movement paths in Fig. 8A that final exposure trajectories were rotated to compensate for the perturbation.

Results from the extended dynamic and visuomotor perturbation experiments show that performance continues to improve over an extended period of learning when opposing perturbations are associated with distinct bimanual movement contexts.

DISCUSSION

We studied the effectiveness of the bimanual movement context to partition the representation of opposing dynamic and opposing visuomotor perturbations. Consistent with previous studies, interference was seen when the context remained constant (Bock et al. 2001; Brashers-Krug et al. 1996; Caithness et al. 2004; Goedert and Willingham 2002; Karniel and Mussa-Ivaldi 2002; Krakauer et al. 2005; Krakauer et al. 1999; Miall et al. 2004; Shadmehr and Brashers-Krug 1997; Wigmore et al. 2002). However, when each perturbation direction was associated with a different bimanual context, interference was dramatically reduced. We examined a variety of context pairs, in which the relative direction of movement of the arms was different across the pair. Interference was reduced when a relative movement of Δ0° (movement of the arms in the same direction) was paired with Δ180° (movement in the opposite direction). This was seen for both dynamic and visuomotor perturbations. In addition, for dynamic perturbations, we showed a reduction in interference when a relative movement context of Δ90° was paired with either Δ0° or Δ180° (see Supplementary Material).

In the case of dynamic perturbations, the reduction in interference did not depend on the perturbation being applied to both arms; when only the right arm experienced the force field, but the left arm moved in a null field, interference in the right arm was similarly reduced. However, when the left arm was moved passively by the manipulandum, there was no reduction in interference. Moreover, in transfer experiments, we found evidence to suggest that the separate representations associated with each bimanual context are partially overlapping. Specifically, after learning a single dynamic or visuomotor perturbation in one bimanual context (Δ180°), subjects showed partial, but incomplete, transfer of this learning when the bimanual context changed (Δ0°), even though the perturbation remained the same. Finally, to examine the extent to which subjects can co-represent opposing perturbations, we exposed subjects to an extended period of training in the Δ180°/Δ0° switching context. For both dynamic and visuomotor perturbations, the error decreased to low levels. Taken together, our results suggest different bimanual movement contexts engage at least partially separate preexisting representations of dynamics and kinematics in the motor system.

Our findings extend previous studies that have shown the ability of subjects to learn concurrent representations of opposing perturbations. In a study of bimanual movements, Tcheang et al. (2007) showed that the two arms can learn separate dynamic representations without interference. In this previous study, the field experienced by each arm remained unchanged throughout the experiment. Therefore, although this study showed a lack of interference between opposing fields concurrently experienced by each arm, it did not address the issue of whether each arm can concurrently represent opposing fields given an appropriate contextual cue. However, Nozaki et al. (2006) showed that opposing dynamic perturbations could be learned when associated with unimanual versus bimanual movements. Moreover, there seems to be distinct representations for bimanual movements that act together on a single object or independently on separate objects (Diedrichsen 2007; Howard et al. 2008).

Our initial motivation for exploring different bimanual movement contexts was twofold. First, bimanual movements have been extensively studied in terms of symmetry bias as seen in rhythmical movement of contralateral body parts, including the arms (Kelso 1984, 1995; Mechsner et al. 2001; Swinnen et al. 1998). This previous work suggests that there is something distinctive about the representation of bimanual symmetric and asymmetric movements, in that these are easier to perform than other phase relations (Howard et al. 2009a). Second, it has recently been shown that the occurrence of symmetric and asymmetric movements are more frequent during everyday life than other phase relations. This suggests that naturalistic tasks are dominated by symmetric and asymmetric movements. In this study, we showed that different classes of bimanual movements have partially separate representations that allow a reduction in interference. Specifically, we compared movement contexts in which the arms moved either in the same or in opposite directions. Depending on their direction with respect to the body (Howard et al. 2009a), movements of the arms in the same direction are considered to be either symmetric (for movements perpendicular to the coronal plane) or asymmetric (for movements perpendicular to the sagittal plane). Similarly, movements of the arms in the opposite direction are considered to be either asymmetric (for movements perpendicular to the coronal plane) or symmetric (for movements perpendicular to the sagittal plane).

A strikingly different result was seen when the left arm was driven passively by the movements of the subject's right arm. Although the passive arm had proprioceptive input because of the movement, as well as tactile input to the hand from the forces applied by the manipulandum, there was no significant learning. This suggests that an effective context must correspond to active rather than passive movement. Specifically, proprioceptive and cutaneous feedback alone does not seem to constitute a sufficient contextual cue for engaging separate representations during motor learning. Therefore the contextual effect of the relative movement between the arms is distinct from a sensory cue because it arises from the differences between the actions performed by the arms. The inability of somatosensory cues to reduce interference is consistent with the results from recent unimanual studies. For example, no reduction in interference was observed when the point of application of force was varied between the different perturbations, with one applied at the hand and the other applied directly to the arm (Davidson et al. 2005). Similarly, interference was not reduced when opposing perturbations were paired with grasping differently shaped objects (Cothros et al. 2008). Our experiment extends these findings by showing that an active movement context can allow opposing perturbations to be learned. This finding parallels similar observations that have shown that active self-generated movements allow the appropriate predictions to be made regarding the consequences of a bimanual action (Bays and Wolpert 2006; Blakemore et al. 1998; Diedrichsen et al. 2003; Witney et al. 1999).

Previous neurophysiological studies support the idea that there are partially separate neural populations for unimanual and bimanual movements. For example, neurons in primary motor cortex (M1) show activity to bimanual movements that is distinct from their activity during unimanual movements (Donchin et al. 1998; Steinberg et al. 2002). Neurons in M1 also show differential activity for ipsilateral and contralateral reaches (Cisek et al. 2003). However, it is unclear whether these representations develop from the extensive training required in nonhuman primate studies or whether they are a natural feature of neural organization. The reduction in interference observed in this study could arise from either preexisting separate representations that are activated by the different contexts or by a single representation that partitions over the course of the experiment because of the requirements of the task. To distinguish between these alternatives, we performed the transfer experiments. If subjects have preexisting separate representations, learning a particular perturbation in one bimanual context should exhibit incomplete transfer to a second context in which the perturbation remains the same. We found evidence for such incomplete transfer for both dynamic and visuomotor perturbations, consistent with preexisting partially separate representations.

Generalization paradigms have been extensively used to study the representation of motor learning. For example, studies have examined the transfer of learning of dynamic (Wang and Sainburg 2004) and visuomotor (Sainburg and Wang 2002) perturbations between the arms in unimanual tasks. Other studies have examined generalization to novel kinematic contexts, such as different locations in the workspace (Shadmehr 2004) or different directions (Pearson et al. 2010) and speed (Goodbody and Wolpert 1998) of movement. In contrast, we examined a bimanual task in which the kinematics of the movements remained unchanged throughout—each arm always reached to the same four targets. Rather, it was the relationship between the movements of the arms (the bimanual context) that changed. Our results showed that the bimanual context influences the pattern of generalization, such that learning in one context exhibited incomplete transfer to another.

In summary, previous unimanual studies of interference in both dynamic and visuomotor learning suggests that common motor resources represent the opposing perturbations. Our results show that interference can be substantially reduced by associating different bimanual contexts with the opposing perturbations, allowing the representation of each to be partitioned based on the relative movement between the two arms.

GRANTS

We thank the Wellcome Trust and The European Project (SENSOPAC IST-2005-028056, //www.sensopac.org) for support.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.