Abstract
Expert musicians show experience-dependent reduced asymmetry in the structure of motor-related brain areas and in the maximum tapping frequency between the hands. Therefore we hypothesized that a reduced hand-skill asymmetry is strongly related to rapid and rhythmical bimanual coordination and developed a dynamical model including a symmetry-breaking parameter Δω, for human bimanual coordination. We conducted unimanual and bimanual drumming experiments to test the following model predictions. 1) The asymmetry in the maximum tapping frequency is more pronounced in nondrummers than that in drummers. If so, 2) a larger number of phase wanderings (i.e., succession of taps by the same hand), 3) larger SD of the relative phase between the hands (SD ϕ), and 4) larger deviation of mean relative phase (mean ϕ) from 180° would be observed in nondrummers than that in professional drummers during antiphase bimanual drumming at the maximum speed. In a unimanual tapping task, the asymmetry in maximum tapping frequency of nondrummers was more pronounced than that of professional drummers. In a bimanual coordination task, phase wanderings were observed only in nondrummers and SD ϕ of the nondrummers is significantly larger than that of professional drummers. On the other hand, there was no significant difference between the mean ϕ of the two groups. All these observations were successfully reproduced by changing Δω, which corresponded to the asymmetry in the maximum tapping frequency. These results support the hypothesis indicating that the prominent bimanual coordination pattern emerges spontaneously after a nonspecific change in Δω or symmetry restoration of the nonlinear dynamical systems.
INTRODUCTION
Expert musicians such as pianists and drummers demonstrate highly skilled bimanual coordination during performance after several years of practice. It is therefore not surprising that neuroscientists have always regarded musicians as the optimal group of people for their investigations into plastic changes in the human brain and behavior, which are related to practicing a musical instrument (Munte et al. 2002; Schlaug 2001; Stewart 2008). An important finding from previous studies is that the size of the primary motor cortex appears to be more symmetrical in the brain of right-handed musicians compared with that in right-handed nonmusicians (Amunts et al. 1997). In addition, when the unimanual tapping was examined at the maximum possible speed, the difference in the tapping rate between the right and left hands was significantly reduced in musicians (Fujii and Oda 2006; Fujii et al. 2009; Jancke et al. 1997). These observations of the bimanual coordination skills suggest that a hemispheric or hand-skill asymmetry is a critical constraint for highly coordinated bimanual performance, in which musicians display less variability compared with that of nonmusicians (Verheul and Geuze 2004; Yamanishi et al. 1980). Therefore we investigated the relationship between the asymmetry in unimanual hand skill and rhythmic bimanual drumming movements as a representative of highly coordinated bimanual performance. To do so, we hypothesized that reduced hand–skill asymmetry is strongly related to stable performance during rapid and rhythmical bimanual coordination and examined the hypothesis from the dynamical systems perspective (Jeka and Kelso 1989; Kelso 1995; Schöner and Kelso 1988a) by extending the Haken–Kelso–Bunz (HKB) model (Haken et al. 1985) for bimanual coordination.
The HKB model (Haken et al. 1985) was developed through the concept of synergetics (Haken 1977), a theory of self-organization in nonequilibrium open systems, and was originally formulated to account for the characteristic behavior in rhythmic bimanual movements reported by Kelso (1984). In the experiment reported by Kelso (1984), participants had been asked to rhythmically move their index fingers or hands under two different initial conditions: one in which homologous muscles contracted synchronously (so-called in-phase pattern) and the other in which homologous muscles contracted in an alternating fashion (so-called antiphase pattern). First, the participants moved their hands in the antiphase pattern, while the frequency of the movement increased (e.g., increased from 1 to 5 Hz). Spontaneous transition from the antiphase pattern to the in-phase pattern occurred at a critical frequency (e.g., 2 Hz) (Kelso 1984). This phase transition phenomenon in bimanual coordination was monitored by means of the relative phase (ϕ), the relative latency of one hand with respect to the other hand. The value of ϕ was equal to 0 or 360° when the hands were in the in-phase pattern and 180° when the hands were in the antiphase pattern (Kelso 1984).
To theoretically describe the observed phase transition phenomenon, Haken et al. (1985) formulated a theoretical model based on the dynamics (i.e., temporal evolution) of the relative phase. The motion equation for ϕ in the HKB model is
| (1) |
where the overdot indicates the derivative of ϕ with respect to time (e.g., the rate at which the relative phase changes) and ξt denotes a Gaussian white noise that functions as a stochastic force of strength Q (see also Schöner et al. 1986). Among the numerical solutions of Eq. 1 for ϕ̇ = 0—which are obtained after excluding the stochastic force—the points corresponding to a negative slope of ϕ̇ are called attractors, and neighboring solutions are attracted in time (Haken 1977; Strogatz 1994). By setting the values of constant a and b so that b/a = 1, attractors exist for ϕ = 0 and 180°, indicating that both the antiphase and in-phase patterns are comparatively stable. In contrast, when the ratio b/a approaches zero and, in particular, when it reaches a critical value of b/a = 0.25, the attractor at ϕ = 180° disappears and only that at ϕ = 0° remains, indicating that the antiphase pattern is no longer stable and a transition from antiphase to in-phase movement occurs (Haken et al. 1985). The change in the strength of the attractors provides a measure of the stability for each coordination pattern, which is indexed according to SD ϕ. The change in the number of attractors in the phase diagram (i.e., attractor layout), leading to a radical change alteration in performance is referred to as bifurcation (Haken 1977). Thus by regarding parameters b/a as movement frequency, the phase transition phenomenon in bimanual coordination was successfully modeled (Haken et al. 1985; Schöner et al. 1986). In the dynamical systems perspective, relative phase (ϕ) is referred to as an order parameter, which could be used to index the order or organization of the hand movements. Furthermore, the ratio of the a and b (b/a) is referred to as a control parameter, which determines the spontaneous pattern change in the order parameter (Jeka and Kelso 1989; Kelso 1995; Schöner and Kelso 1988a). The dynamics of the HKB model is also referred to as intrinsic dynamics, which means that pattern changes emerge as a result of nonspecific changes in the control parameter (Kelso 1995). In our experiment, we used the antiphase movement performed at the maximum possible speed as a bimanual motor task because transitions away from the required pattern are typically observed for the antiphase mode of coordination, but not for the in-phase mode of coordination (Haken et al. 1985) and the differences between experts and nonexperts are more pronounced when they perform a relatively unstable coordination pattern (A Miura, K Kudo, T Ohtsuki, and H Kanehisa, unpublished data).
After the detailed modeling of the phase transition phenomenon, it was confirmed that a transition is observed only when the subjects are instructed not to intervene, even if they feel like they are slipping out of the antiphase pattern (e.g., Lee et al. 1996; see also Kelso et al. 1988; Scholz and Kelso 1990; Schöner and Kelso 1988b). Such an intentional change was modeled by introducing an additional term, which could approximate the intrinsic dynamics of a specific pattern as follows
| (2) |
where c sin (ϕ − ψ) corresponds to the force exerted to stabilize the intended phase pattern (ψ) of a given strength c. We included this intentional term because professional drummers usually do not show phase transition from an antiphase pattern to an in-phase pattern even in very high frequency movements during drum playing. In Eq. 2, when the intentional force exerted to stabilize the antiphase pattern overrides the intrinsic dynamics of a specific pattern (e.g., when ψ = 180°, a = 1, b = 1, and c = 2), the system would be characterized by a single stable pattern at ϕ = 180°, reflecting the capability of the participants to intentionally maintain an antiphase movement (Kelso et al. 1988; Scholz and Kelso 1990; Schöner and Kelso 1988b). Such a specific parametric influence on the order parameter dynamics is referred to as behavioral information (Kelso 1995). It has been confirmed that the behavioral information includes not only a participant's intention, but also other effects such as task-specific environmental events (Byblow et al. 1994; Fink et al. 2000; Kudo et al. 2006), the effect of attentional focus on dual-task performance (Monno et al. 2000; Pellecchia and Turvey 2001; Temprado et al. 2002), and the participant's memory of the specified coordination pattern (Schöner and Kelso 1988c; Verheul and Geuze 2004; Zanone and Kelso 1992).
The models described by Eqs. 1 and 2 are symmetric under the transformation ϕ to −ϕ. In other words, the behavior of the system does not depend on the way in which the left and right hands are labeled. As a consequence, these two models are not sufficient to test the hypothesis on whether a reduced asymmetry in the hand motor skills is strongly related to highly coordinated bimanual performance. Based on recent experimental findings on the difference in the unimanual tapping rate between the right and left hands, which is more pronounced in nonmusicians than that in musicians (Fujii and Oda 2006; Fujii et al. 2009; Jancke et al. 1997), we proposed that Δω should be added into the model as follows
| (3) |
A similar Δω had in the past been introduced to account for the symmetry-breaking dynamics of the system used to examine the coordination between hand and foot (Jeka and Kelso 1995; Kelso and Jeka 1992) or between two handheld pendulums with different eigenfrequencies (Sternad et al. 1995). The introduction of this additional parameter was based on a frequency difference between the system components, which was clearly observed in all these studies. More specifically, these experimental observations led researchers to the assumption that Δω could represent the difference in the uncoupled frequency of the system's individual components or the difference in the intrinsic frequency of each component when it is oscillating alone (Jeka and Kelso 1995). In our previous studies on unimanual tapping at the maximum possible speed, the average tapping frequency across all nonmusician participants was about 6 and 7 Hz for the left and right hands, respectively, whereas the average tapping frequency across the skilled drummers was about 7 Hz for both hands (Fujii and Oda 2006; Fujii et al. 2009). On the basis of these observations, we assumed that Δω corresponds to the asymmetry observed in tapping frequency when unimanual tapping is examined at the maximum speed and that Eq. 3 can predict the bimanual coordination performance in the case of antiphase movement.
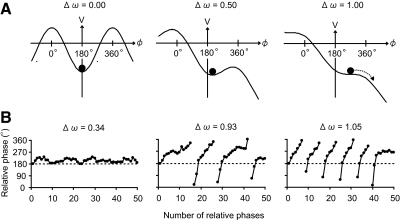
The potential function of the model in Eq. 3 is shown in Fig. 1A (also see the appendix for a detailed description of the potential function). The symmetry of the potential function is broken for a nonzero value of Δω. The left, middle, and right panels of Fig. 1B show typical time series of the relative phase obtained by simulating Eq. 3 for different values of Δω. The model predicts that an increase of Δω would cause a disappearance of the stable fixed point or stationary solution (i.e., local minimum of the potential function) and an appearance of running solution or a phase wandering (see the dotted arrow on the potential function and the line breaks in the time series). These findings indicate that taps of the same hand occurred in succession (e.g., L–R–R–L...) in the case of antiphase (i.e., L–R–L–R–L...) drumming (see Fig. 3). The model also predicts that, as Δω increases, the attractor strength around ϕ = 180° becomes weaker and the SD ϕ in the simulated time series becomes larger. In addition, the stable fixed point deviates from 180°, causing a positive shift in the simulated time series of the mean ϕ from 180°.
Fig. 1.
Schematic diagrams of evolving potential functions and time series of ϕ obtained by simulating Eq. 3. A: potential function. The symmetry in the potential function is broken by increasing the symmetry-breaking parameter from Δω = 0.0 to 0.5, and 1.0 (see left, middle, and right panels). The remaining parameters of the potential function were considered equal to a = 1, b = 0, c = 2, and ψ = 180°. The local minimum of the potential function, indicated by the filled circles, deviates gradually from ϕ = 180° and, finally, phase wandering is observed (see dotted arrow). B: typical examples of simulated time series. The number of phase wanderings (line breaks) increases as the symmetry-breaking parameter increases from Δω = 0.34 to 0.93, and 1.05 (see left, middle, and right panels). The remaining parameters were considered equal to a = 1, b = 0, c = 2, ψ = 180°, and Q = 20°.
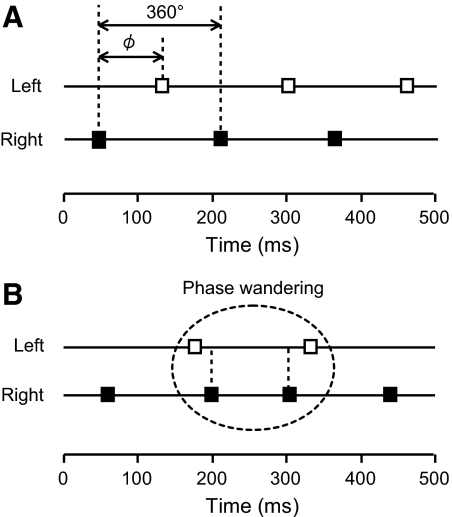
Fig. 3.
Schematic diagrams of ϕ (A) and phase wandering (B). Left and right hand taps are shown by open and filled squares, respectively. When more than one tap of the same hand appeared in succession (e.g., L–R–R–L...), this specific sequence of taps was considered as a phase wandering.
We assumed that the hypothesis put to the test—in other words, that a reduced asymmetry in the hand motor skills is strongly related to highly coordinated bimanual performance—can be regarded as a reduction in Δω in Eq. 3. If Δω denotes the asymmetry observed in maximum tapping frequency between the right and left hands during unimanual tapping, we can obtain the following predictions. 1) The asymmetry in maximum tapping frequency between the right and left hands is more pronounced in nondrummers than that in professional drummers. If so, 2) a larger number of phase wanderings, 3) larger SD ϕ, and 4) larger deviation of mean ϕ from 180° would be observed in nondrummers during antiphase bimanual drumming at the maximum speed. The purpose of the present study was to test these theoretical predictions. For this purpose, we conducted an experiment that includes unimanual and bimanual tasks. The unimanual task aimed to evaluate the difference in the tapping speed asymmetry between the right and left hands during unimanual drumming at the maximum possible speed for nondrummers and skilled drummers. On the other hand, the bimanual task aimed to examine possible differences in bimanual coordination patterns when antiphase bimanual drumming at the maximum possible speed was performed.
METHODS
Participants
A group of right-handed professional drummers (n = 8, men) and another group of nondrummers (n = 8, seven men and one woman) agreed to participate in the experiment. The right-handedness of the participants was assessed according to the Edinburgh Inventory (Oldfield 1971). The mean handedness score of the professional drummers was 82.9 ± 25.0 (mean ± SD) and that of the nondrummers was 87.5 ± 20.5. It should be noted that handedness extends along a continuum from total right-handedness (Oldfield score = +100) to total left-handedness (Oldfield score = −100). No significant difference was detected in the handedness scores of the two groups of participants (z = 0.49, P = 0.62, Mann–Whitney U test). The drummers had 19.6 ± 13.7 yr of experience and the nondrummers had never played drums. The drummers had been practicing the drums since the age of 15.0 ± 1.9 and typically played rock, popular, or jazz music. The mean age of the professional drummers was 34.6 ± 14.1 yr and that of the nondrummers was 24.8 ± 4.4 yr. This study has been approved by the Ethics Committee of the University of Tokyo.
Apparatus
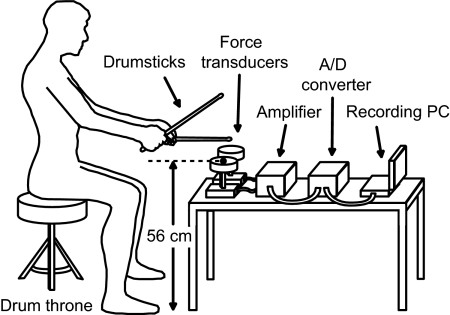
The experimental apparatus is shown in Fig. 2. The height and position of the drum throne were adjusted before participants sat comfortably on it and took the drumsticks in their hands (Manhattan-7A hand-selected hickory drumsticks, VATER). Two strain gauge force transducers (TU-BR200K, TEAC) were located in front of the participants. The tapping point on the force transducers was covered with a cushion made of sponge rubber. The signal of the force transducers was amplified (SA-100D, TEAC), converted from analog to digital at 1,000 Hz, and recorded on a personal computer. Tap timing was determined by analyzing the signal of the force transducers, according to the methodology described in our previous study (Fujii and Oda 2006).
Fig. 2.
Experimental apparatus.
Tasks
During the unimanual task, participants were instructed to hold a drumstick in one hand and perform unimanual tapping as fast as possible for 10 s. During the bimanual task, the participants were instructed to hold a drumstick in each hand and perform bimanual tapping in an antiphase pattern as fast and accurately as possible for 10 s. To ensure accurate execution of the antiphase tapping, the participants received both verbal instructions and a visual demonstration. Furthermore, in both tasks, participants were instructed to repeat the tapping trials three times in total. Before the beginning of each task, the participants were allowed to practice the new tapping tasks for a few minutes. In the unimanual task, the order of the left- and right-hand trials was counterbalanced among the two groups of participants.
Behavioral analysis
In the unimanual task, the number of taps was averaged over all three trials for each hand, and the difference in maximum frequency (ΔΩ) was calculated with use of the following equation
| (4) |
The symbol R denotes the average number of taps across all three trials with the right hand, whereas the symbol L denotes the average number of taps across three trials in the left-hand task. Because the duration for the task was 10 s, we divided the total number of taps by 10 to calculate tapping frequency (tap/s).
In the bimanual task, the coordination between the participant's left and right hands was evaluated by means of ϕ, shown in Fig. 3A, and was calculated using the following equation
| (5) |
The symbol RL denotes the time interval that elapsed from the right hand tap to the next left hand tap and LR indicates the time interval between a left and a right hand tap. The value of ϕ is equal to 180° when participants' taps alternated (Fig. 3A) and 0 or 360° when taps of the right and left hands were simultaneous. When more than one tap of the same hand occurred in succession (e.g., L–R–R–L...), this specific sequence of taps was considered as a phase wandering (Fig. 3B). The number of taps and phase wanderings, the mean ϕ, and SD ϕ were calculated for each trial and then averaged over all three trials for each participant.
Statistics
In the unimanual task, we considered the difference in ΔΩ as a dependent variable. This dependent variable was used, in the present study, to examine 1) whether the asymmetry in maximum frequency during unimanual drumming was more pronounced in nondrummers than that in professional drummers. In the bimanual task, we considered the number of taps, the number of phase wanderings, the mean ϕ, and the SD ϕ as dependent variables. We measured the number of taps and calculated the tapping rate that was voluntarily selected by each individual participant. The other dependent variables were used to test the operational hypothesis about nondrummers showing 2) a larger number of phase wanderings, 3) larger SD ϕ, and 4) larger deviation of mean ϕ from 180° than those of professional drummers, when the antiphase drumming is examined at the maximum possible speed.
Comparisons between professional drummers and nondrummers were made using the Student's t-test in those cases where our measurement data fulfilled all the prerequisites for conducting parametric analyses (the Kolmogorov–Smirnov test applied to test for a normal distribution and the Levene test for homogeneity of variances). When the data did not fulfill the prerequisites for parametric analyses, between-group differences were analyzed with the use of the Mann–Whitney U test. Finally, correlations were assessed using the Pearson's correlation coefficient. All tests were two-tailed and values of P < 0.05 were deemed as statistically significant.
RESULTS
The difference in maximum frequency (ΔΩ) and the number of taps for the right and left hands in the unimanual task are summarized in Table 1. These results confirm that the asymmetry in the mean in maximum tapping frequency between the right and left hands was significantly less pronounced in professional drummers than that in nondrummers (t14 = 5.04, P < 0.001, t-test).
Table 1.
Observed unimanual performance of drummers and nondrummers
| Drummers |
Nondrummers |
|||
|---|---|---|---|---|
| Measurement | Meana | SDb | Meana | SDb |
| Number of taps | ||||
| Right | 72.62 | 5.98 | 74.75 | 7.14 |
| Left | 67.67 | 5.63 | 61.63 | 6.06 |
| Difference in maximum frequency, ΔΩ (Hz) | 0.50 | 0.20 | 1.31 | 0.41 |
Values are means averaged across all participants.
SD between participants.
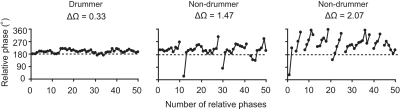
The between-participant mean and SD of each dependent variable in the bimanual task are summarized in Table 2. Professional drummers attained a significantly higher number of taps than that attained by nondrummers (t14 = 3.59, P = 0.003, t-test); the mean tapping frequencies were 6.5 Hz for the professional drummers and 5.5 Hz for nondrummers. A clear difference was observed between professional drummers and nondrummers in the ϕ patterns (see Fig. 4). Interestingly, professional drummers showed no phase wandering pattern, whereas nondrummers showed multiple phase wandering patterns. Correspondingly, nondrummers showed a significantly larger SD ϕ than that of drummers (z = 3.36, P < 0.001, Mann–Whitney U test). However, the mean ϕ was not different between the two groups of participants (t14 = 0.59, P = 0.56, t-test).
Table 2.
Observed bimanual performance of drummers and nondrummers
| Drummers |
Nondrummers |
|||
|---|---|---|---|---|
| Measurement | Meana | SDb | Meana | SDb |
| Number of taps | 129.75 | 8.48 | 109.54 | 13.48 |
| Number of phase wanderings | 0.00 | 0.00 | 4.71 | 1.97 |
| Mean ϕ | 189.69 | 12.16 | 195.45 | 24.66 |
| SD ϕb | 18.14 | 3.44 | 49.45 | 10.29 |
Values are means averaged across all participants.
SD between participants.
Fig. 4.
Typical examples of ϕ patterns observed in bimanual coordination task. Line breaks represent phase wanderings. The value of the symmetry-breaking parameter ΔΩ corresponds to the asymmetry observed in maximum tapping frequency during unimanual tapping task. In the case of a relatively small ΔΩ (left panel), no phase wandering patterns were observed. On the contrary, multiple phase wanderings were observed for relatively large values of ΔΩ (see middle and right panels).
DISCUSSION
We obtained the following four predictions from the previous studies on musicians and theoretical model defined by Eq. 3. 1) The asymmetry in maximum tapping frequency is more pronounced in nondrummers than that in professional drummers. If so, 2) a larger number of phase wanderings, 3) larger SD ϕ, and 4) larger deviation of mean ϕ from 180° would be observed when the antiphase bimanual drumming of nondrummers was examined at the maximum possible speed. With the unimanual task, we confirmed that the asymmetry in maximum tapping frequency between the right and left hands is more pronounced in nondrummers. Subsequently, with the bimanual task, we confirmed that phase wanderings are observed only in nondrummers and, furthermore, that SD ϕ was significantly larger in nondrummers than that in professional drummers. However, contrary to the model prediction, there was no significant difference in the mean ϕ between the two groups of participants. To conclude, the first, second, and third predictions were affirmed, whereas the fourth one was refuted. These results suggested that Eq. 3 cannot accurately describe the patterns observed in the bimanual antiphase drumming of professional drummers and nondrummers and, in particular, in terms of reproducibility of the measured mean ϕ.
Modification of the model
The statistically insignificant difference in the mean ϕ between professional drummers and nondrummers suggests that a correction could have been made so that the mean ϕ would be maintained around the required relative phase (i.e., ϕ = 180°). This correction can be achieved by introducing an additional term, d cos ϕ, into Eq. 3 as follows
| (6) |
The potential function of Eq. 6 has been plotted in Fig. 5A, illustrating that even though Δω increases, the stable fixed point does not deviate far from 180° (compare Fig. 5A with Fig. 1A; also see the appendix for a detailed description of the corrected potential function). This is achieved by assuming that the parameter d increases linearly with increasing Δω, i.e.
| (7) |
where k is an empirical constant. The left, middle, and right panels of Fig. 5B show typical time series of ϕ obtained by simulating by Eq. 6. These time series of ϕ indicate that an increase in Δω leads to the appearance of phase wanderings as well as to a significant variability in ϕ. On the other hand, the mean ϕ does not deviate far from the value of 180°, even though Δω increases. The term added, d cos ϕ, may be related to some behavioral information such as attentional focus of the participants (Amazeen et al. 1997; de Poel et al. 2008) or information that they have memorized (Schöner and Kelso 1988c; Verheul and Geuze 2004; Zanone and Kelso 1992).
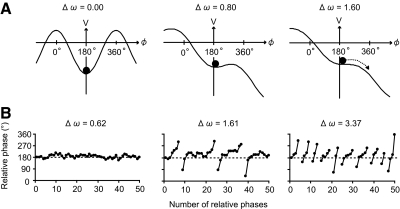
Fig. 5.
Schematic diagrams of evolving potential functions and time series of ϕ obtained by simulating Eq. 6. A: potential functions. The symmetry in the potential function is broken by increasing Δω from 0.0 to 0.8, and 1.6 (see left, middle, and right panels) and, finally, phase wandering is observed (see broken arrow). The remaining parameters were considered equal to a = 1, b = 0, c = 2, and ψ = 180°. However, contrary to Eq. 3, the local minimum of the potential function, indicated by the filled circles, does not deviate far from 180°. B: typical example of simulated time series. The number of phase wanderings (line breaks) increased as Δω increases from 0.62 to 1.61, and 3.37 (see left, middle, and right panels) and the mean ϕ does not deviate far from 180°. The remaining parameters were considered equal to a = 1, b = 0, c = 2, ψ = 180°, k = 0.8, and Q = 20°.
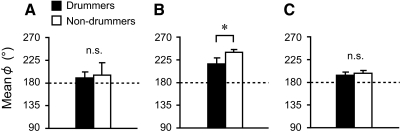
To test the model's validity, we compared the observed mean ϕ with that obtained by simulating both Eqs. 3 and 6 (see Fig. 6 and the appendix for a detailed description of the simulation procedure). In the case of the mean ϕ observed in the bimanual task, we found no significant difference between professional nondrummers and the drummers (Fig. 6A). The mean ϕ estimated by simulating Eq. 3 for nondrummers was significantly larger than that for professional drummers (z = 3.36, P < 0.001, Mann–Whitney U test; see Fig. 6B). In contrast, when simulating Eq. 6, no statistically significant difference could be detected in the simulated mean ϕ between professional drummers and nondrummers (t14 = 1.24, P = 0.23, t-test; see Fig. 6C). Thus the mean ϕ estimated by simulating Eq. 6 was in good agreement with the observed mean ϕ. In other words, for describing the results of the present study, the theoretical model defined by Eq. 6 is more valid than that defined by Eq. 3.
Fig. 6.
Observed and simulated mean ϕ for drummers (black bars) and nondrummers (white bars). A: mean ϕ observed in bimanual coordination task. B: mean ϕ obtained simulated based on Eq. 3. C: mean ϕ simulated based on Eq. 6. The symbol * denotes significant at P < 0.05, whereas n.s. denotes nonsignificant. Error bars represent SD from the mean ϕ. It is worth noting that the mean ϕ simulated based on Eq. 6 was in a good agreement with observations.
Detailed simulation using the modified model
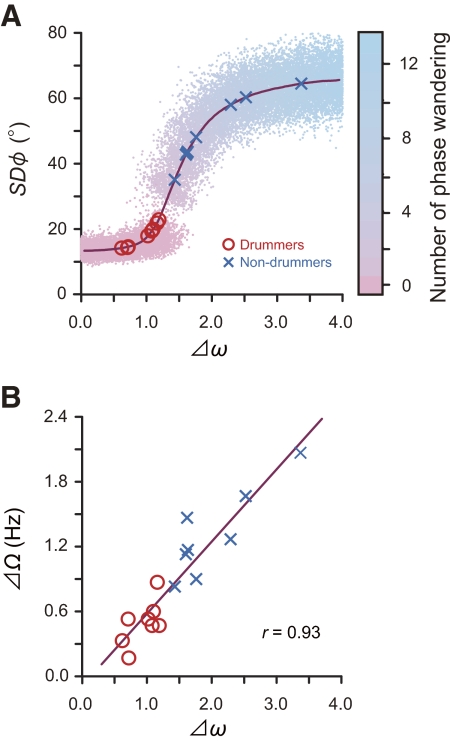
By stimulating Eq. 6, we also examined how a change in parameter Δω induces a change in the SD ϕ (see Fig. 7A). Points in Fig. 7A represent the value of SD ϕ calculated from 50-point simulated time series at a given value of Δω. Because Eq. 6 includes white noise, the value of SD ϕ varies even for the same value of Δω. The line is the smoothed average of SD ϕ as a function of Δω. The sigmoidal (i.e., S-shaped) increase in SD ϕ is a consequence of a qualitative change in the relative phase pattern (i.e., the transition from no phase wandering pattern to phase wandering pattern). The qualitative difference in the relative phase pattern is visualized as a gap between clusters of the points. From a dynamical systems perspective, the sigmoidal curve is a consequence of a saddle node bifurcation, which is the basic mechanism by which fixed points vanish, giving their place to a running solution (Strogatz 1994). Thus the detailed simulation of the corrected model revealed that a change in parameter Δω induces a nonlinear or S-shaped change in the SD ϕ.
Fig. 7.
A: SD ϕ as a function of Δω, calculated based on Eq. 6. Points represent individual simulations, whereas the line gives a smoothed average. The color of each point corresponds to the number of phase wanderings. The observed SD ϕ for each participant in the bimanual coordination task is in good agreement with this best-fit line (red circles for drummers; blue cross for nondrummers). B: the relationship between Δω that has been estimated using the Δω–SD ϕ curve and the observed asymmetry in maximum tapping frequency (ΔΩ) during the unimanual tapping task.
When we plot the SD ϕ observed for each participant on the Δω–SD ϕ curve shown in Fig. 7A, the magnitude of Δω for each participant can be estimated from individual plots. A high correlation was confirmed between the estimated Δω and the observed ΔΩ, the difference in maximum tapping frequency between the hands for unimanual drumming (r = 0.93, P < 0.0001; see Fig. 7B).
Thus we confirmed parameter Δω in the simulation model is strongly related to a difference in uncoupled frequency of the system individual components or a difference in the intrinsic frequency of each component when it is oscillating alone. However, it should be noted that professional drummers and nondrummers might differ not only in the asymmetry underlying unimanual movement but also in the bimanual interaction, which influences asymmetric coupling strength of the limbs (Treffner and Turvey 1995), in terms of callosal communication between the left and right hemispheres or ipsilateral corticospinal pathways convey the same information to bilateral homologous muscles (Aramaki et al. 2010; Cardoso de Oliveira 2002; Serrien 2008; Swinnen 2002).
Effect of musical practice on Δω
One of the main features of motor control in humans is that >85% of the population has the right hand more skillful than the left (Corballis 2003; Coren and Porac 1977; Gilbert and Wysocki 1992; Sun and Walsh 2006; Toga and Thompson 2003). In the general population, the scores from a handedness inventory are linearly related to the difference observed in the speed of executing a unimanual tapping task with the right and left hands. In addition, strongly right handed individuals can attain a significantly higher tapping frequency with the right hand (Nalcaci et al. 2001; Peters and Durding 1978). Previous studies have shown that this asymmetry in the speed of hand movement persists even after several months of intensive practice of unimanual hand skills such as rapid tapping (Peters 1981) and peg moving task (Annett et al. 1974), indicating that the functional asymmetry of hands is a persistent constraint of the human brain. In contrast, the asymmetry in the maximum tapping frequency attained by the expert drummers that participated in our study was significantly reduced when compared with the nondrummers, although the handedness scores were similar between the two groups. Jäncke et al. (1997) previously showed that the asymmetry in the maximum tapping frequency attained by keyboard and string instrument players is reduced when compared with the handedness-matched nonmusicians. In view of these studies, we suggested that the task-specific asymmetry in the maximum tapping frequency (i.e., ΔΩ and Δω) could be reduced through intensive musical practice, whereas the general hand preference assessed according to a handedness inventory may remain the same.
Based on past studies on maximum tapping speed attained by humans, some neuroscientists suggest that it is related to anatomical/structural parameters of the human brain such as the myelin integrity (Bartzokis et al. 2010) or the size of primary motor cortex (Amunts et al. 1997). Others suggest that it is related to functional parameters of the human nervous system such as corticospinal excitability (Koeneke et al. 2006b) or cerebral activation patterns (Koeneke et al. 2006a; Lutz et al. 2005). In addition, the anatomical/structural organization that is specific to a musician's brain was found to be related to the early onset, but not the duration of musical training, indicating that the plastic change in the brain's structure was induced by intense manual training during cerebral maturation in childhood (Amunts et al. 1997; Bengtsson et al. 2005; Imfeld et al. 2009). In the present study, however, the drummers had been practicing the drums since a relatively late (and fairly similar) age ranging from 13.1 to 16.9 yr. Furthermore, only a statistically insignificant correlation between the asymmetry observed in maximum tapping frequency attained with the right and left hands and either the age they started practicing the drums or their years of drumming experience (r = −0.35, P = 0.40 and r = 0.52, P = 0.18, respectively). These findings led us to assume that the neurological correlate of Δω might reflect the asymmetry observed in the functional parameter of the human nervous system rather than an anatomical/structural correlate. However, further studies are needed to determine the precise neural substrate from which Δω originates.
Implication for behavioral and brain science studies on musicians
Because music experts or highly skilled athletes offer an optimal group in which to investigate the process of long-term human learning, recent studies have discovered many differences in behavioral and brain parameters between experts and nonexperts (Munte et al. 2002; Nakata et al. 2010; Schlaug 2001; Stewart 2008; Zatorre et al. 2007). To date, this research on musicians or athletes has mainly focused on the linear relationship between behavioral and neurophysiological/neuroanatomical parameters, typically expressed as correlations (e.g., Amunts et al. 1997; Babiloni et al. 2008; Bengtsson et al. 2005; Elbert et al. 1995; Hutchinson et al. 2003). However, the possibility exists that the relationship is not linear. We suggest that a nonlinear model provides a new perspective for researchers to study experts to reveal more complex relationships among various behavioral/neural parameters as well as to identify critical control parameters. Thus the dynamical system model will be a powerful tool for future studies on the plastic changes of behavior or brain in highly skilled experts.
Conclusions
The present study showed that skilled drummers demonstrate the reduced asymmetry in the maximum tapping frequency between the right and left hands as well as the highly stable performance during rapid bimanual coordination. The organization of stable bimanual coordination was successfully modeled by a nonspecific change in the symmetry-breaking parameter Δω, which is one of the control parameters of such dynamical systems. Our results demonstrated that asymmetry acts as a critical constraint for rapid and rhythmic bimanual coordination performed by professional drummers and nondrummers and indicate that the most prominent bimanual-coordination pattern emerges spontaneously after the symmetry restoration of nonlinear dynamical systems.
GRANTS
This study was supported by a grant for the Fellows of the Japan Society for the Promotion of Science (JSPS) to S. Fujii, JSPS Grants-in-Aid for Scientific Research 17500416 and 21300215 to K. Kudo, and a Grant-in-Aid for Scientific Research (B) 19300216 to T. Ohtsuki.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
ACKNOWLEDGMENTS
We thank H. Tsunoda and the Wild Music School (Tokyo) for support in running this experiment.
APPENDIX
Potential function
The potential function V(ϕ) plotted in Fig. 1A is given by the following equation
| (A1) |
The left, middle, and right panels of Fig. 1A correspond to three different values of the symmetry-breaking parameter: Δω = 0.00, 0.50, and 1.00, respectively. The remaining parameters were considered equal to a = 1, b = 0, c = 2, and ψ = 180°. The potential function V(ϕ) plotted in Fig. 5A is given by the following equation
| (A2) |
The left, middle, and right panels of Fig. 5A correspond to three different values of the symmetry-breaking parameter: Δω = 0.00, 0.80, and 1.60, respectively. The remaining parameters were considered equal to a = 1, b = 0, c = 2, ψ = 180°, and d = 0.8Δω.
Finally, Eqs. 3 and 6 can be derived from Eqs. A1 and A2, by calculating the negative derivative of the potential function
| (A3) |
Simulation of mean relative phase
By plotting the observed SD ϕ on the simulated function of Δω–SD ϕ (i.e., Fig. 7A for Eq. 6), the magnitude of Δω for each participant can be estimated. With the estimated Δω, time series of ϕ were subsequently obtained for each participant through simulations, which can quantitatively reproduce the observed SD ϕ. It should be noted that the values of Δω in Figs. 1B and 5B were estimated according to this procedure to reproduce the observed time series of ϕ (Fig. 4). We also calculated the mean ϕ from each of the simulated time series, which consisted of 50 points for each participant. The simulated time series of ϕ were derived three times for each participant and then used to estimate the between-participant mean ϕ and, finally, the SD of the mean ϕ.
REFERENCES
- Amazeen et al., 1997.Amazeen EL, Amazeen PG, Treffner PJ, Turvey MT. Attention and handedness in bimanual coordination dynamics. J Exp Psychol Hum Percept Perform 23: 1552–1560, 1997 [Google Scholar]
- Amunts et al., 1997.Amunts K, Schlaug G, Jancke L, Steinmetz H, Schleicher A, Dabringhaus A, Zilles K. Motor cortex and hand motor skills: structural compliance in the human brain. Hum Brain Mapp 5: 206–215, 1997 [DOI] [PubMed] [Google Scholar]
- Annett et al., 1974.Annett M, Hudson PT, Turner A. The reliability of differences between the hands in motor skill. Neuropsychologia 12: 527–531, 1974 [DOI] [PubMed] [Google Scholar]
- Aramaki et al., 2010.Aramaki Y, Osu R, Sadato N. Resource-demanding versus cost-effective bimanual interaction in the brain. Exp Brain Res 203: 407–418, 2010 [DOI] [PubMed] [Google Scholar]
- Babiloni et al., 2008.Babiloni C, Del Percio C, Iacoboni M, Infarinato F, Lizio R, Marzano N, Crespi G, Dassu F, Pirritano M, Gallamini M, Eusebi F. Golf putt outcomes are predicted by sensorimotor cerebral EEG rhythms. J Physiol 586: 131–139, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartzokis et al., 2010.Bartzokis G, Lu PH, Tingus K, Mendez MF, Richard A, Peters DG, Oluwadara B, Barrall KA, Finn JP, Villablanca P, Thompson PM, Mintz J. Lifespan trajectory of myelin integrity and maximum motor speed. Neurobiol Aging 31: 1554–1562, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson et al., 2005.Bengtsson SL, Nagy Z, Skare S, Forsman L, Forssberg H, Ullen F. Extensive piano practicing has regionally specific effects on white matter development. Nat Neurosci 8: 1148–1150, 2005 [DOI] [PubMed] [Google Scholar]
- Byblow et al., 1994.Byblow WD, Carson RG, Goodman D. Expressions of asymmetries and anchoring in bimanual coordination. Hum Mov Sci 13: 3–28, 1994 [Google Scholar]
- Cardoso de Oliveira, 2002.Cardoso de Oliveira S. The neuronal basis of bimanual coordination: recent neurophysiological evidence and functional models. Acta Psychol (Amst) 110: 139–159, 2002 [DOI] [PubMed] [Google Scholar]
- Corballis, 2003.Corballis MC. From mouth to hand: gesture, speech, and the evolution of right-handedness. Behav Brain Sci 26: 199–208, 2003 [DOI] [PubMed] [Google Scholar]
- Coren and Porac, 1977.Coren S, Porac C. Fifty centuries of right-handedness: the historical record. Science 198: 631–632, 1977 [DOI] [PubMed] [Google Scholar]
- de Poel et al., 2008.de Poel HJ, Peper CL, Beek PJ. Laterally focused attention modulates asymmetric coupling in rhythmic interlimb coordination. Psychol Res 72: 123–137, 2008 [DOI] [PubMed] [Google Scholar]
- Elbert et al., 1995.Elbert T, Pantev C, Wienbruch C, Rockstroh B, Taub E. Increased cortical representation of the fingers of the left hand in string players. Science 270: 305–307, 1995 [DOI] [PubMed] [Google Scholar]
- Fink et al., 2000.Fink PW, Foo P, Jirsa VK, Kelso JA. Local and global stabilization of coordination by sensory information. Exp Brain Res 134: 9–20, 2000 [DOI] [PubMed] [Google Scholar]
- Fujii et al., 2009.Fujii S, Kudo K, Ohtsuki T, Oda S. Tapping performance and underlying wrist muscle activity of non-drummers, drummers, and the world's fastest drummer. Neurosci Lett 459: 69–73, 2009 [DOI] [PubMed] [Google Scholar]
- Fujii and Oda, 2006.Fujii S, Oda S. Tapping speed asymmetry in drummers for single-hand tapping with a stick. Percept Mot Skills 103: 265–272, 2006 [DOI] [PubMed] [Google Scholar]
- Gilbert and Wysocki, 1992.Gilbert AN, Wysocki CJ. Hand preference and age in the United States. Neuropsychologia 30: 601–608, 1992 [DOI] [PubMed] [Google Scholar]
- Haken, 1977.Haken H. Synergetics: An Introduction. Nonequilibrium Phase Transitions and Self-Organization in Physics, Chemistry and Biology (Springer Series in Synergetics) Berlin: Springer-Verlag, 1977 [Google Scholar]
- Haken et al., 1985.Haken H, Kelso JAS, Bunz H. A theoretical model of phase transitions in human hand movements. Biol Cybern 51: 347–356, 1985 [DOI] [PubMed] [Google Scholar]
- Hutchinson et al., 2003.Hutchinson S, Lee LH, Gaab N, Schlaug G. Cerebellar volume of musicians. Cereb Cortex 13: 943–949, 2003 [DOI] [PubMed] [Google Scholar]
- Imfeld et al., 2009.Imfeld A, Oechslin MS, Meyer M, Loenneker T, Jancke L. White matter plasticity in the corticospinal tract of musicians: a diffusion tensor imaging study. NeuroImage 46: 600–607, 2009 [DOI] [PubMed] [Google Scholar]
- Jancke et al., 1997.Jancke L, Schlaug G, Steinmetz H. Hand skill asymmetry in professional musicians. Brain Cogn 34: 424–432, 1997 [DOI] [PubMed] [Google Scholar]
- Jeka and Kelso, 1989.Jeka JJ, Kelso JAS. The dynamic pattern approach to coordinated behavior: a tutorial review. In: Perspectives on the Coordination of Movement, edited by Wallace SA. Amsterdam: North-Holland/Elsevier, 1989, p. 3–45 [Google Scholar]
- Jeka and Kelso, 1995.Jeka JJ, Kelso JAS. Manipulating symmetry in the coordination dynamics of human movement. J Exp Psychol Hum Percept Perform 21: 360–374, 1995 [DOI] [PubMed] [Google Scholar]
- Kelso, 1984.Kelso JAS. Phase transitions and critical behavior in human bimanual coordination. Am J Physiol Regul Integr Comp Physiol 246: R1000–R1004, 1984 [DOI] [PubMed] [Google Scholar]
- Kelso, 1995.Kelso JAS. Dynamic Patterns. Cambridge, MA: MIT Press, 1995 [Google Scholar]
- Kelso and Jeka, 1992.Kelso JAS, Jeka JJ. Symmetry breaking dynamics of human multilimb coordination. J Exp Psychol Hum Percept Perform 18: 645–668, 1992 [DOI] [PubMed] [Google Scholar]
- Kelso et al., 1988.Kelso JAS, Scholz JP, Schöner G. Dynamics governs switching among patterns of coordination in biological movement. Phys Lett A 134: 8–12, 1988 [Google Scholar]
- Koeneke et al., 2006a.Koeneke S, Lutz K, Esslen M, Jancke L. How finger tapping practice enhances efficiency of motor control. Neuroreport 17: 1565–1569, 2006a [DOI] [PubMed] [Google Scholar]
- Koeneke et al., 2006b.Koeneke S, Lutz K, Herwig U, Ziemann U, Jancke L. Extensive training of elementary finger tapping movements changes the pattern of motor cortex excitability. Exp Brain Res 174: 199–209, 2006b [DOI] [PubMed] [Google Scholar]
- Kudo et al., 2006.Kudo K, Park H, Kay BA, Turvey MT. Environmental coupling modulates the attractors of rhythmic coordination. J Exp Psychol Hum Percept Perform 32: 599–609, 2006 [DOI] [PubMed] [Google Scholar]
- Lee et al., 1996.Lee TD, Blandin Y, Proteau L. Effects of task instructions and oscillation frequency on bimanual coordination. Psychol Res 59: 100–106, 1996 [DOI] [PubMed] [Google Scholar]
- Lutz et al., 2005.Lutz K, Koeneke S, Wustenberg T, Jancke L. Asymmetry of cortical activation during maximum and convenient tapping speed. Neurosci Lett 373: 61–66, 2005 [DOI] [PubMed] [Google Scholar]
- Monno et al., 2000.Monno A, Chardenon A, Temprado JJ, Zanone PG, Laurent M. Effects of attention on phase transitions between bimanual coordination patterns: a behavioral and cost analysis in humans. Neurosci Lett 283: 93–96, 2000 [DOI] [PubMed] [Google Scholar]
- Munte et al., 2002.Munte TF, Altenmuller E, Jancke L. The musician's brain as a model of neuroplasticity. Nat Rev Neurosci 3: 473–478, 2002 [DOI] [PubMed] [Google Scholar]
- Nakata et al., 2010.Nakata H, Yoshie M, Miura A, Kudo K. Characteristics of the athletes' brain: evidence from neurophysiology and neuroimaging. Brain Res Rev 62: 197–211, 2010 [DOI] [PubMed] [Google Scholar]
- Nalcaci et al., 2001.Nalcaci E, Kalaycioglu C, Cicek M, Genc Y. The relationship between handedness and fine motor performance. Cortex 37: 493–500, 2001 [DOI] [PubMed] [Google Scholar]
- Oldfield, 1971.Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9: 97–113, 1971 [DOI] [PubMed] [Google Scholar]
- Pellecchia and Turvey, 2001.Pellecchia GL, Turvey MT. Cognitive activity shifts the attractors of bimanual rhythmic coordination. J Mot Behav 33: 9–15, 2001 [DOI] [PubMed] [Google Scholar]
- Peters, 1981.Peters M. Handedness: effect of prolonged practice on between hand performance differences. Neuropsychologia 19: 587–590, 1981 [DOI] [PubMed] [Google Scholar]
- Peters and Durding, 1978.Peters M, Durding BM. Handedness measured by finger tapping: a continuous variable. Can J Psychol 32: 257–261, 1978 [DOI] [PubMed] [Google Scholar]
- Schlaug, 2001.Schlaug G. The brain of musicians. A model for functional and structural adaptation. Ann NY Acad Sci 930: 281–299, 2001 [PubMed] [Google Scholar]
- Scholz and Kelso, 1990.Scholz JP, Kelso JA. Intentional switching between patterns of bimanual coordination depends on the intrinsic dynamics of the patterns. J Mot Behav 22: 98–124, 1990 [DOI] [PubMed] [Google Scholar]
- Schöner et al., 1986.Schöner G, Haken H, Kelso JA. A stochastic theory of phase transitions in human hand movement. Biol Cybern 53: 247–257, 1986 [DOI] [PubMed] [Google Scholar]
- Schöner and Kelso, 1988a.Schöner G, Kelso JA. Dynamic pattern generation in behavioral and neural systems. Science 239: 1513–1520, 1988a [DOI] [PubMed] [Google Scholar]
- Schöner and Kelso, 1988b.Schöner G, Kelso JA. A dynamic pattern theory of behavioral change. J Theor Biol 135: 501–524, 1988b [Google Scholar]
- Schöner and Kelso, 1988c.Schöner G, Kelso JA. A synergetic theory of environmentally-specified and learned patterns of movement coordination. I. Relative phase dynamics. Biol Cybern 58: 71–80, 1988c [DOI] [PubMed] [Google Scholar]
- Serrien, 2008.Serrien DJ. Coordination constraints during bimanual versus unimanual performance conditions. Neuropsychologia 46: 419–425, 2008 [DOI] [PubMed] [Google Scholar]
- Sternad et al., 1995.Sternad D, Collins D, Turvey MT. The detuning factor in the dynamics of interlimb rhythmic coordination. Biol Cybern 73: 27–35, 1995 [DOI] [PubMed] [Google Scholar]
- Stewart, 2008.Stewart L. Do musicians have different brains? Clin Med 8: 304–308, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strogatz, 1994.Strogatz SH. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Studies in Nonlinearity). Reading, MA: Addison–Wesley, 1994 [Google Scholar]
- Sun and Walsh, 2006.Sun T, Walsh CA. Molecular approaches to brain asymmetry and handedness. Nat Rev Neurosci 7: 655–662, 2006 [DOI] [PubMed] [Google Scholar]
- Swinnen, 2002.Swinnen SP. Intermanual coordination: from behavioural principles to neural-network interactions. Nat Rev Neurosci 3: 348–359, 2002 [DOI] [PubMed] [Google Scholar]
- Temprado et al., 2002.Temprado JJ, Monno A, Zanone PG, Kelso JA. Attentional demands reflect learning-induced alterations of bimanual coordination dynamics. Eur J Neurosci 16: 1390–1394, 2002 [DOI] [PubMed] [Google Scholar]
- Toga and Thompson, 2003.Toga AW, Thompson PM. Mapping brain asymmetry. Nat Rev Neurosci 4: 37–48, 2003 [DOI] [PubMed] [Google Scholar]
- Verheul and Geuze, 2004.Verheul MH, Geuze RH. Bimanual coordination and musical experience: the role of intrinsic dynamics and behavioral information. Motor Control 8: 270–291, 2004 [DOI] [PubMed] [Google Scholar]
- Yamanishi et al., 1980.Yamanishi J, Kawato M, Suzuki R. Two coupled oscillators as a model for the coordinated finger tapping by both hands. Biol Cybern 37: 219–225, 1980 [DOI] [PubMed] [Google Scholar]
- Zanone and Kelso, 1992.Zanone PG, Kelso JAS. Evolution of behavioral attractors with learning: nonequilibrium phase transitions. J Exp Psychol Hum Percept Perform 18: 403–421, 1992 [DOI] [PubMed] [Google Scholar]
- Zatorre et al., 2007.Zatorre RJ, Chen JL, Penhune VB. When the brain plays music: auditory-motor interactions in music perception and production. Nat Rev Neurosci 8: 547–558, 2007 [DOI] [PubMed] [Google Scholar]