Evidence for Opponent-Channel Coding of Interaural Time Differences in Human Auditory Cortex

Abstract

In humans, horizontal sound localization of low-frequency sounds is mainly based on interaural time differences (ITDs). Traditionally, it was assumed that ITDs are converted into a topographic (or rate-place) code, supported by an array of neurons with parametric tuning to ITDs within the behaviorally relevant range. Although this topographic model has been confirmed in owls, its applicability to mammals has been challenged by recent physiological results suggesting that, at least in small-headed species, ITDs are represented by a nontopographic population rate code, which involves only two opponent (left and right) channels, broadly tuned to ITDs from the two auditory hemifields. The current study investigates which of these two models of ITD processing is more likely to apply to humans. For that, evoked responses to abrupt changes in the ITDs of otherwise continuous sounds were measured with electroencephalography. The ITD change was either away from (“outward” change) or toward the midline (“inward” change). According to the opponent-channel model, the response to an outward ITD change should be larger than the response to the corresponding inward change, whereas the topographic model would predict similar response sizes for both conditions. The measured response sizes were highly consistent with the predictions of the opponent-channel model and contravened the predictions of the topographic model, suggesting that, in humans, ITDs are coded nontopographically. The hemispheric distributions of the ITD change responses suggest that the majority of ITD-sensitive neurons in each hemisphere are tuned to ITDs from the contralateral hemifield.

INTRODUCTION

Most of the sounds that are behaviorally relevant to humans, such as speech and music, contain most of their energy in the low-frequency range (i.e., ≲1.5 kHz; Byrne et al. 1994; Sivian et al. 1959). The horizontal localization of such low-frequency sounds is mainly based on differences in sound arrival time at the two ears (referred to as interaural time differences [ITDs]), produced by the path length differences between the ears and the sound source. Humans are sensitive to ITDs of only a few tens of microseconds (for review see Durlach and Colburn 1978). The initial processing of these minute time differences involves brain stem structures that are highly specialized in temporal processing (for review see Grothe 2003; Joris and Yin 2007; Oertel 1999). Traditionally, it was assumed that these structures convert ITDs into a topographic (or rate-place) representation, based on an array of neurons tuned to different ITDs (represented by different colored lines in Fig. 1, A and B; Jeffress 1948), where the ITD of the incoming sound is inferred from the maximum or centroid of the distribution of activity across the array. Although the topographic model seems to be appropriate for owls (Carr and Konishi 1990; Sullivan and Konishi 1986; for review see Konishi 2003) and chickens (Overholt et al. 1992), physiological results suggest that it may not be generally applicable to mammals. These results have shown that, in mammals with small heads and thus a small range of naturally occurring ITDs (referred to as “physiological range”), most ITD-sensitive neurons respond best to ITDs outside of that range (Fitzpatrick et al. 2000; McAlpine 1996, 2001). This has led to the suggestion that, in these species, ITDs may be coded by a nontopographic population rate code, involving only two opponent channels, broadly tuned to ITDs from the left or right hemifields. In this opponent-channel model, all neurons representing the left- or right-tuned channel (represented respectively by the blue- and red-shaded lines in Fig. 1, E and F) are assumed to produce an increasing response with increasing ITD toward the left or right side, respectively, and the ITD of the incoming sound is assumed to be inferred from the relative balance of overall activity between the two channels (Colburn and Latimer 1978; Harper and McAlpine 2004; McAlpine et al. 2001; van Bergeijk 1962; von Békésy 1930; for review see McAlpine 2005).

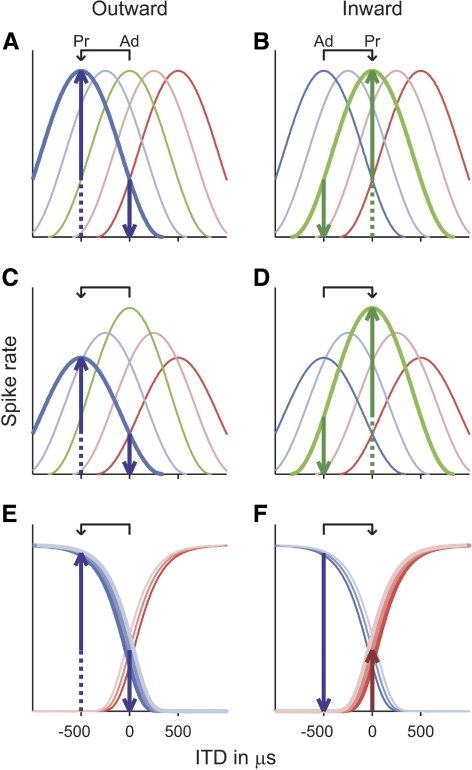
Fig. 1.

Schematic representation of neural interaural time difference (ITD) tuning curves in the topographic (A to D) and opponent-channel (E and F) models. The topographic model is shown either with equal numbers of neurons at all best ITDs (A and B) or with more neurons tuned to ITDs near zero than to large ITDs (represented by the heights of the tuning curves in C and D). The solid upward-pointing arrows show the predicted size of the transition response to an ITD change away from (“outward”; left panels) or toward (“inward”; right panels) the midline (between 0 and −500 μs in this example; see arrows above panels). The predictions are based on the assumptions that 1) only neurons responding more strongly to the probe than to the adaptor contribute to the transition response (indicated by bold tuning curves) and 2) the size of the transition response reflects the differential between the probe and adaptor responses of these neurons (upward- and downward-pointing arrows, respectively). Ad: ITD of the adapting sound; Pr: ITD of the probe sound.

It remains unclear which of the two models applies to humans. A recent modeling study suggests that, if the distribution of the best ITDs of ITD-sensitive neurons were freely adaptable to ecological constraints, the ITD coding mechanism pertaining to a given species would depend on the species' head size and the spectral range over which the ITD information is used (Harper and McAlpine 2004). If this were the case, ITD processing in humans would be expected to be based on a topographic or intermediate code for all but the lowest frequencies (≥250 Hz). Alternatively, the ITD coding mechanism may be a characteristic of the phylogenetic class that a given species belongs to (e.g., mammals vs. birds; for review see McAlpine and Grothe 2003) because it might be determined by the physiological mechanism by which the internal delays in the input to ITD-sensitive neurons are generated (see, e.g., Brand et al. 2002; Joris et al. 2006). In this case, ITD processing in humans would be expected to be based on an opponent-channel code.

The current study investigates this question with electroencephalography (EEG) and a specialized stimulation paradigm, which makes it possible to isolate the response of those neural elements in auditory cortex specifically involved in ITD processing (Chait et al. 2005, 2007b; Dajani and Picton 2006; Halliday and Callaway 1978; Jones 1991; Jones et al. 1991; McEvoy et al. 1990, 1991; Ross 2008; Ross et al. 2007a,b; Ungan et al. 1989, 2001). The paradigm involves presenting a short probe sound (black in Fig. 2A) immediately after a prolonged adapting sound (gray), differing only in ITD, and measuring the response to the transition between the adaptor and the probe. If the adaptor is long enough to allow the transient response to its onset to subside before the onset of the probe, the transition response would be assumed to reflect the activity of neurons that are more strongly activated by the probe than by the adaptor. Under the assumption that the size of the transition response reflects the differential between the probe (upward-pointing arrows in Fig. 1) and adaptor responses (downward-pointing arrows) of these neurons, the response size for a given ITD change between the adaptor and probe (represented by the arrows above the panels in Fig. 1) would be expected to depend on the mechanism by which ITDs are coded in auditory cortex. In the topographic model, the size of the transition response would be expected to be mainly determined by the degree to which neurons responding maximally or near-maximally to the probe (bold dark blue and green tuning curves in Fig. 1, A and B, respectively) are also activated by the adaptor; the less the adaptor-related activation, the larger the transition response (represented by the solid upward-pointing arrows in Fig. 1). If one assumes a homogeneous density of best ITDs across all ITDs (as depicted in Fig. 1, A and B), the size of the transition response would thus be expected to be mainly determined by the size of the ITD change and be scarcely influenced by its direction. In particular, the response to an ITD change away from the midline (“outward” change; Fig. 1A) should have the same or similar size as that of the response to the reverse change, toward the midline (“inward” change; Fig. 1B). ITD discrimination tends to be more accurate around the midline (for review see Durlach and Colburn 1978). In the topographic model, this has been explained by assuming a greater density of neurons with best ITDs near zero (depicted by higher tuning curves in Fig. 1, C and D; Colburn 1973; Stern and Shear 1996). Under this assumption, the response to the inward ITD change might be expected to be larger than the response to the outward change (compare solid upward-pointing arrows in Fig. 1, C and D). In contrast, the opponent-channel model would predict the response to an inward ITD change to be smaller than the response to the corresponding outward change. For instance, if the outward change is from zero ITD (midline) to a strongly lateralized ITD in the left hemifield (−500 μs in the example shown in Fig. 1E), a large transition response should be produced by the neurons representing the channel tuned to the left hemifield (blue-shaded lines in Fig. 1E) because these neurons would respond much more strongly to the probe (upward-pointing arrow) than to the adaptor (downward-pointing arrow). The situation would be reversed for the corresponding inward ITD change (from −500 to 0 ITD; Fig. 1F), which means that the left-tuned neurons should produce little or no response in this case. Thus the response to the inward change would be expected to reflect whatever little activity the probe ITD elicits in the channel tuned to the hemifield opposite to the adapting ITD (the right-tuned channel, represented by the red-shaded lines, in the example shown in Fig. 1F). The current experiment was designed to test these opposing predictions.

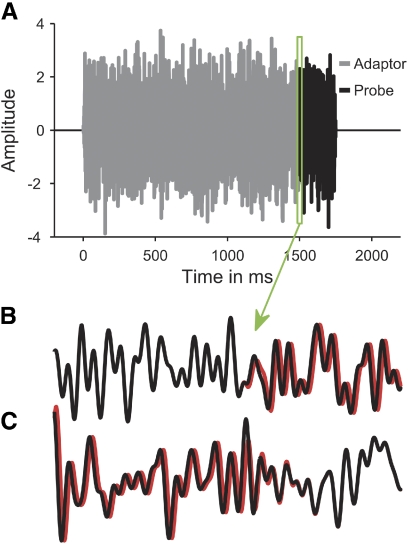
Fig. 2.

Temporal waveform of an example stimulus (A). The gray and black lines show the adaptor and probe portions of the stimulus, respectively. B and C: the left- (black) and right-ear (red) waveforms of an outward (B) and inward (C) ITD change between 0 and −250 μs in a highly magnified section around the transition from the adaptor to the probe (green rectangle in A).

METHODS

Stimuli

The stimuli consisted of a 1,500-ms adapting sound and a 250-ms probe sound, and were presented with an interstimulus interval of 1,500 ms. Both the adaptor and probe consisted of random Gaussian noise, freshly generated for each trial. The ITD was fixed throughout the adaptor and changed to a different static value for the duration of the probe, creating the perception of an abrupt shift in the intracranial position of the stimulus at the transition from the adaptor to the probe. The adaptor and probe were generated separately and concatenated without gap (Fig. 2A). Within each sound, the ITD was generated by advancing the waveform to the right ear by half the ITD and delaying the waveform to the left ear by the same amount. The time shifts were introduced by applying a linear phase gradient across frequency to avoid onset time differences between the left- and right-ear waveforms (Henning 1983). For illustration, Fig. 2, B and C shows the left- (black) and right-ear waveforms (red) of an outward and inward ITD change (between 0 and −250 μs in these examples), respectively, in a highly magnified section around the transition from the adaptor to the probe (green rectangle in Fig. 2A).

Six different stimulus conditions were tested. In the “outward” conditions, the ITD change was from a more medial to a more lateral position (away from the midline). There were three outward conditions with ITD changes from 0 (midline) to −250 (lateralized about halfway to the left ear; Toole and Sayers 1965) or −500 μs (practically fully lateralized toward the left ear) and from −250 to −500 μs. In the other three conditions, referred to as “inward” conditions, the ITD changes were reversed (−250 to 0 μs, −500 to 0 μs, and −500 to −250 μs). We used ITDs only in the left hemifield (i.e., ITDs leading at the left ear) because previous neuroimaging and electrophysiological studies have shown that, in humans, the response to left-lateralized sounds is more contralateral, similar to animals, and is often larger than the response to right-lateralized sounds (for a review of recent imaging data in humans, see Krumbholz et al. 2007 and for animal data see Fitzpatrick et al. 2000).

To ensure that all spectral components of the current stimuli would convey unambiguous ITD cues (i.e., component interaural phase differences were never greater than π), stimuli were low-pass filtered at 1 kHz using a 16th-order Butterworth IIR filter (with a −48-dB per octave filter roll-off). Filtering was carried out on the composite stimulus (i.e., after concatenating the adaptor and probe) to avoid audible clicks at the transition between the adaptor and probe. The composite stimuli were gated on and off with 5-ms cosine ramps, which were synchronous at two ears to avoid envelope ITD cues. Previous psychophysical work has shown that envelope ITDs are ineffective at low frequencies (Henning 1983; Henning and Ashton 1981). Furthermore, it has been suggested that envelope and low-frequency carrier ITDs might be processed by different neural substrates and might thus be subject to different encoding mechanisms (see, e.g., Dreyer and Delgutte 2006). All stimuli were presented at an overall level of 70 dB SPL.

Stimuli were generated digitally with a 25-kHz sampling rate using TDT System 3 (Tucker Davis Technologies, Alachua, FL) and Matlab (The MathWorks, Natick, MA). They were D/A converted with a 24-bit amplitude resolution (TDT RP2.1), amplified (TDT HB7), and presented over headphones (K240 DF; AKG, Vienna, Austria). The participant was seated on a comfortable chair in a double-walled, sound-attenuated room. The experiment was divided into four runs of about 20 min each, with short breaks in between. Each of the six conditions was presented a total of 248 times (62 times within each run). Conditions were presented in a random order within each run.

Data acquisition

Auditory-evoked potentials were recorded with 33 Ag/AgCl sintered ring electrodes, mounted in an elastic cap according to the standard international 10–20 arrangement (Easy Cap, Herrsching, Germany), and amplified with a BrainAmp DC (Brain Products, Munich, Germany) EEG amplifier. The ground electrode was placed centrally on the forehead (AFz position) and the vertex channel (Cz) was used as recording reference and later reconstructed by re-referencing to average reference (see the following section). Recording was continuous with a sampling rate of 500 Hz and on-line filtering between 0.1 and 250 Hz. Participants watched a self-chosen silent movie with subtitles to maintain vigilance during recording.

Data analysis

Preprocessing of the raw data was performed with the EEGLAB toolbox (Delorme and Makeig 2004), which runs under Matlab. The data were 1) low-pass filtered at 35 Hz using a −48-dB per octave, zero-phase band-pass filter (by applying an 8th-order Butterworth filter in both forward and reverse time order), 2) resampled at 250 Hz to reduce computation time, 3) re-referenced to average reference, and 4) divided into stimulus-locked epochs covering the period from −250 to 3,000 ms relative to stimulus onset. Epochs with nonstereotypic artifacts were then rejected automatically using the “joint-probability” function in EEGLAB, which identifies artifacts by looking for unusually large potentials across many electrodes. On average, about 12% of epochs were rejected by this method. Stereotypic artifacts (electroocular and electrocardiac activity) were then eliminated by applying an independent component analysis (ICA) based on the infomax algorithm (Bell and Sejnowski 1995; see also Delorme and Makeig 2004) to the remaining epochs and manually rejecting artifactual components based on inspection of the components' activity time courses, field maps, and event-related average waveforms. The corrected data were then back-projected and baseline-corrected to the 200-ms period preceding stimulus onset.

Responses to the adapting sounds exhibited a sustained response (SR in Fig. 3D), on which the transient response at the onset of the probe sound (labeled change response [CR]) was superposed. The sustained response decayed back to baseline between about 600 and 700 ms after the onset of the probe sound (1,600–1,700 ms relative to stimulus onset; see Fig. 3). Thus to avoid creating a phantom “mirror image” of the sustained response at the end of the epoch (i.e., after the sustained response had decayed), the data were corrected for a baseline that was constant and equal to the average of the 200-ms period just before the onset of the probe sound (1,300–1,500 ms) for times ≤2,100 ms and then decreased linearly to zero between 2,100 and 2,150 ms (for a similar procedure see Krumbholz et al. 2007).

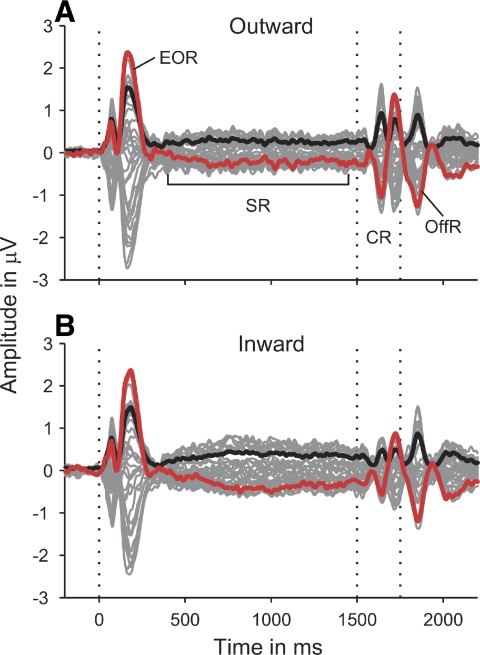
Fig. 3.

Electroencephalographic (EEG) responses to the outward (A) and inward (B) ITD change stimuli, averaged over all 3 ITD change conditions within each group and across participants. The thin gray lines show the responses from the 33 recording electrodes; the black lines show the root mean square (rms) amplitude of the responses; and the red lines show the vertex (Cz) response. The vertical dotted lines mark the stimulus onset, the change in ITD between the adapting and probe sounds (at 1,500 ms), and the stimulus end (at 1,750 ms). The responses were baseline-corrected to the 200-ms period prior to stimulus onset. EOR: energy onset response; SR: sustained response; CR: change response; OffR: offset response.

To assess the left- and right-hemisphere contributions to the ITD change responses, a source model was fitted to the responses, consisting of two equivalent current dipoles, one in each hemisphere, and the current strength of each dipole (referred to as “source waveform”) was calculated by multiplication of the channel data with the inverse of the lead-field matrix (Scherg and von Cramon 1986). The source model was based on a four-shell ellipsoidal volume conductor as head model and was conducted using the Brain Electrical Source Analysis software (BESA, version 5.1.8; Megis, Gräfelfing, Germany). The international 10–20 electrode arrangement mainly covers the upper half of the head surface and is thus unsuitable for accurate source localization of auditory cortical responses (Michel et al. 2004). Moreover, although source waveforms depend strongly on dipole orientation, they are relatively insensitive to variations in dipole location (e.g., a shift in source location of as much as 2 cm has little effect on the source waveform, as long as the dipole orientation is kept fixed; see Scherg et al. 2002, 2010). For these reasons, only the dipole orientations were fitted to the data. The dipole locations were fixed at the centroid of primary auditory area TE1.0 [Talairach coordinates: −47.5 −21.7 13.1 (left) and 50.5 −17.9 10.1 mm (right); Morosan et al. 2001], the MNI (Montreal Neurological Institute) coordinates of which were calculated with the SPM Anatomy toolbox (www.fz-juelich.de/ime/spm_anatomy_toolbox; Eickhoff et al. 2005) and converted to Talairach space using the nonlinear transformation proposed by Brett et al. (2002; http://imaging.mrc-cbu.cam.ac.uk/imaging/MniTalairach). Previous results suggest that responses elicited by changes in ITD arise from a region near medial Heschl's gyrus (Krumbholz et al. 2007), which is where area TE1.0 is located.

The responses to both the stimulus onset and the transition from the adaptor to the probe exhibited a typical triphasic shape (see Figs. 3 and 4, A and B), with one vertex-negative deflection (referred to as N1 or cN1, respectively) flanked by two vertex-positive deflections (referred to as P1/2 or cP1/2, see results). For statistical analysis, the peak amplitudes and latencies of these deflections were measured by finding the largest peaks in the individual vertex (Cz) responses and/or source waveforms within the 80-ms time windows around the deflections' peak latencies in the relevant grand-average responses.

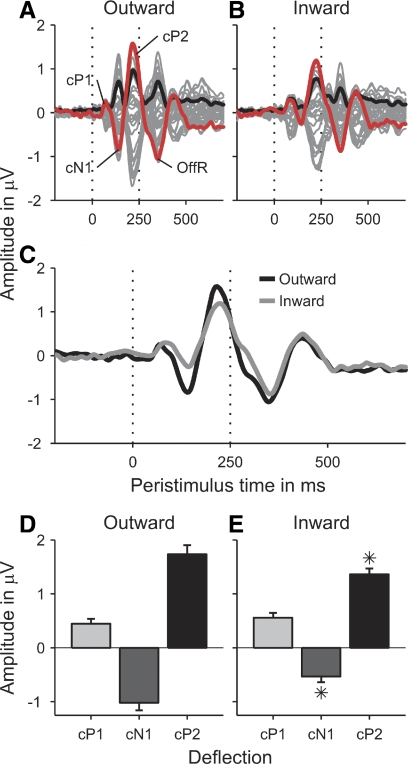
Fig. 4.

Grand-average ITD change responses to the outward (A) and inward (B) conditions as a function of time relative to the transition between the adaptor and probe (at 1,500 ms). As in Fig. 2, the responses were averaged over all conditions within each group and across participants. In this case, however, baseline-correction was to the 200-ms period prior to the onset of the probe (see Data analysis in methods). C: a direct comparison of the vertex responses (red lines in A and B) to the outward (black) and inward conditions (gray). D and E: the peak amplitudes of the cP1 (light-gray bars), cN1 (dark-gray bars), and cP2 (black bars) deflections in these responses. Error bars show the SE. Stars mark significant differences between the outward and inward conditions.

Participants

A total of 10 participants (6 female and 4 male; age range: 19–34 yr) took part in the experiment after having given written informed consent. All participants were right-handed (laterality indices ≥57), as assessed through a modified version of the Edinburgh inventory (Oldfield 1971), and had no history of audiological or neurological disease. The experimental procedures conformed with the Code of Ethics of the World Medical Association (Declaration of Helsinki) and were approved by the Ethics Committee of the University of Nottingham Medical School.

RESULTS

Comparison of outward and inward ITD change responses

The responses to both the outward (Fig. 3A) and inward conditions (Fig. 3B) exhibited a transient response to the onset of the adapting sound (labeled energy onset response [EOR] in Fig. 3A), a sustained response (SR), which remained roughly constant throughout the rest of the stimulus, a transient response to the ITD change at the transition from the adaptor to the probe (labeled change response [CR]) and an off-response following the end of the stimulus (OffR). The off response does not occur for shorter probe sound durations (Hewson-Stoate et al. 2006; Krumbholz et al. 2007) and would thus be assumed to represent an independent response rather than part of the change response.

The energy onset response exhibited a typical triphasic shape, with an initial vertex-positive deflection peaking at an average latency of 72 ms after stimulus onset (P1), a negative deflection at 104 ms (N1), and another positive deflection at 180 ms (P2). In agreement with previous studies using noise stimuli, the N1 was very small (Chait et al. 2004, 2005, 2007b). Whereas the energy onset response did not show any significant amplitude or latency differences between the outward and inward conditions [tested by paired t-comparisons of the P1, N1, and P2 vertex (Cz) amplitudes and latencies between the average responses to the three outward and inward conditions], the sustained response was significantly larger for the inward than that for the outward conditions [confirmed by a paired t-test of its root mean square (rms) amplitude, averaged over the time period from 800 to 1,500 ms poststimulus onset: t(9) = 2.731, P = 0.023; compare Fig. 3, A and B].

Like the energy onset responses, the ITD change responses (shown enlarged and appropriately baseline-corrected in Fig. 4, A and B) comprised three deflections: a small positive deflection peaking at an average latency of 72 ms after the transition from the adaptor to the probe (labeled “change”-P1, or cP1; Fig. 4A), followed by a larger negative (cN1) and another larger positive deflection (cP2) peaking at 140 and 220 ms, respectively. Comparison of Fig. 4, A and B, which show the average outward and inward ITD change responses, respectively, suggests that, particularly the cN1, and to a lesser degree also the cP2, were larger for the outward than those for the inward conditions. To analyze the statistical significance of these differences, the vertex amplitudes and latencies of the cP1, cN1, and cP2 deflections to the six individual ITD change conditions were tested for a main effect of ITD change direction by submitting them to separate two-way repeated-measures ANOVAs with factors ITD change direction (outward and inward) and ITD change condition (ITD change between 0 and −250, 0 and −500, and −250 and −500 μs). Both the cN1 and cP2 amplitudes showed a significant main effect of ITD change direction [cN1: F(1,9) = 12,350, P = 0.007; cP2: F(1,9) = 6.287, P = 0.033] and there were no significant effects of ITD change direction on the cN1 and cP2 latencies. Conversely, the cP1 amplitude showed no significant effect of ITD change direction, but the cP1 latency was significantly shorter for the outward than that for the inward conditions [F(1,9) = 38.876, P < 0.001]. Figure 4C suggests that this was due to the later portion of the outward cP1 being wiped out by the larger and partially overlapping cN1 deflection to the outward conditions.

Response patterns for individual ITD change conditions

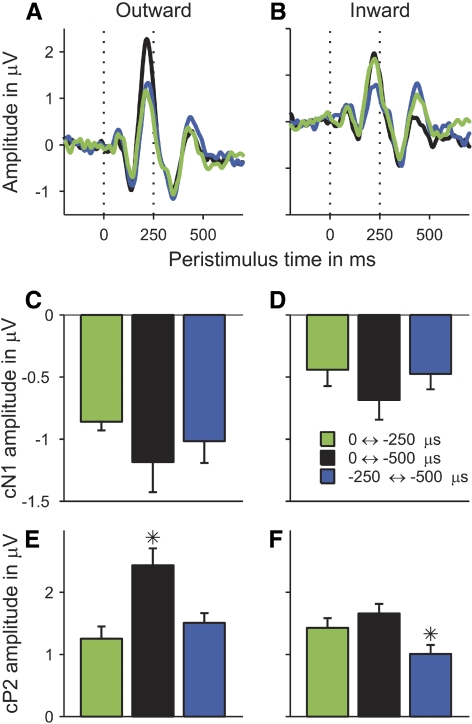
Whereas both the cN1 and cP2 deflections had shown significant effects of ITD change direction, Fig. 5 suggests that only the cP2 showed any effects of ITD change condition. For the outward conditions, the amplitude of the cP2 seemed to depend mainly on the size of the ITD change, with the largest change from 0 to −500 μs producing the largest cP2 response (black line and bar in Fig. 5, A and E, respectively), and the changes from 0 to −250 and from −250 to −500 μs producing smaller and similar-sized responses (green and blue lines and bars in Fig. 5, A and E). In contrast, for the inward conditions, the cP2 amplitude seemed to be mainly determined by the ITD of the probe sound, with the change from −500 to −250 μs producing the smallest response (blue line and bar in Fig. 5, B and F) and the changes from −250 and −500 to 0 μs producing larger and similar-sized responses (green and black lines and bars in Fig. 5, B and F). The cN1 deflection, on the other hand, seemed to show little effect of ITD change condition (Fig. 5, C and D). The statistical significance of these effects was tested using the same ANOVAs as used in the previous section. Whereas the cP2 amplitude showed a highly significant main effect of ITD change condition and interaction between ITD change condition and direction [main effect: F(2,18) = 10.854, P < 0.001; interaction: F(2,18) = 12.335, P < 0.001], these effects were not significant for any of the other response measures (cP1 and cN1 amplitudes, and all latencies). Paired t-test of the cP2 amplitudes for the outward conditions confirmed that the cP2 response to the largest outward ITD change (from 0 to −500 μs) was significantly larger than the responses to the two smaller outward ITD changes [from 0 to −250 μs: t(9) = 4.947, P < 0.001; from −250 to −500 μs: t(9) = 4.156, P = 0.003] and that the latter did not differ significantly from each other [t(9) = 1.151, P = 0.279]. For the inward conditions, the cP2 responses to the two conditions involving the 0-μs probe ITD (from −250 and −500 to 0 μs) did not differ significantly from each other [t(9) = 1.274, P = 0.235], but were both significantly larger than the response to the condition involving the −250-μs probe ITD [from −500 to −250 μs; t(9) = 2.429, P = 0.038; t(9) = 2.986, P = 0.015].

Fig. 5.

Grand-average vertex (Cz) responses to the individual outward (A) and inward (B) ITD change conditions, plotted as a function of time relative to the probe onset. Different conditions are marked by different colors (see legend in D). C–F: the peak amplitudes of the cN1 (C and D) and cP2 deflections (E and F) in these responses. Error bars show the SE. Stars mark significant differences between the different ITD change conditions.

The responses to the individual ITD change conditions also showed that the cN1 and cP2 responses to the −250-μs probe ITD were significantly larger when this probe was preceded by the 0-μs than by the −500-μs adaptor [cN1: t(9) = −2.462, P = 0.036; cP2: t(9) = 2.401, P = 0.04; compare green and blue bars in Fig. 5, C and D (cN1), respectively, and in Fig. 5, E and F (cP2)]. This shows that the differences between the responses to the outward and inward conditions described in the previous section cannot be explained by differences in the probe ITD.

Hemispheric distribution of ITD change responses

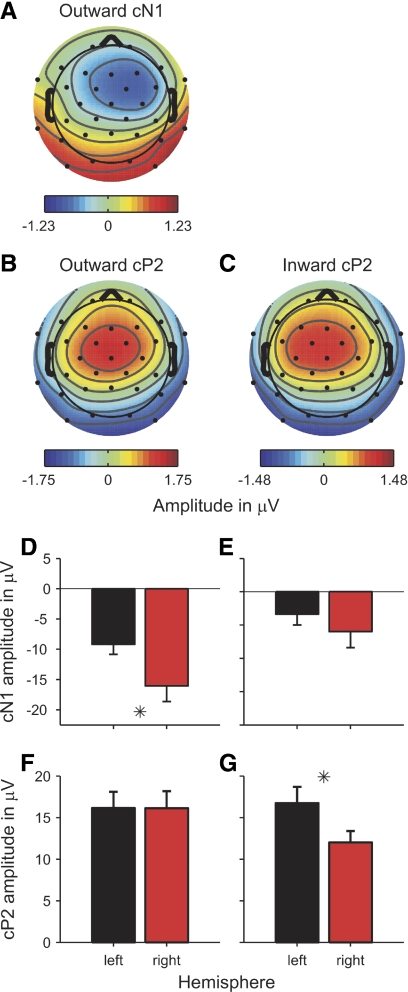
The scalp distribution maps of both the cN1 and cP2 responses were broadly consistent with a source in the region of auditory cortex on the supratemporal plane (Fig. 6, A, B, and C; scalp maps were averaged over the 40-ms windows around the deflections' vertex peaks in the grand-average responses to the relevant conditions). Furthermore, the scalp maps also suggest that that the ITD change responses were distributed asymmetrically across the two cerebral hemispheres and that the hemispheric distribution depended on the ITD change direction. For instance, the scalp map of the cN1 deflection in the average change response to the three outward conditions (Fig. 6A) suggested a strong bias toward the right hemisphere (i.e., contralateral to the probe ITD). Unfortunately, the cN1 response to the inward conditions was too small to result in a meaningful map (the vertex potential of the average inward cN1 hardly crossed the zero baseline; see Fig. 4B). The scalp maps of the cP2 deflections suggested a bilateral hemispheric distribution for the average outward response (Fig. 6B) and a bias toward the left hemisphere (i.e., ipsilateral to the adapting ITD) for the average inward response (Fig. 6C). The scalp maps for the individual outward and inward ITD change conditions were broadly consistent with this pattern (data not shown).

Fig. 6.

Grand-average scalp distribution maps (A–C) and source amplitudes (D–G) of the average outward (left panels) and inward ITD change responses (right panels). The scalp maps were averaged over the 40-ms time windows around the vertex peaks of the cN1 (A) and cP2 deflections (B, C). The cN1 deflection of the average inward response was too small to yield a meaningful map. D–G: black and red bars show the source amplitudes of the left- and right-hemisphere dipoles, respectively. D and E: the source amplitudes of the cN1 deflection. F and G: the cP2 source amplitudes. Error bars show the SE. Stars mark significant differences between the left- and right-hemisphere source amplitudes.

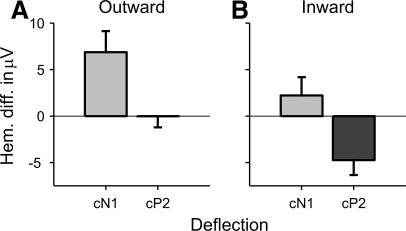
To quantify these effects, an equivalent dipole source model was used to estimate the source strengths of the ITD change responses within the two hemispheres (see methods). The dipole model was fitted to the grand-average ITD change response across all participants and conditions. The fitting was performed within the time window ranging from the start of the cN1 to the end of the cP2 deflection (based on the respective rms minima; for a similar approach see Lütkenhöner et al. 2003). Paired t-comparisons between the left- and right-hemisphere source amplitudes of the cN1 and cP2 deflections revealed a significant right-hemisphere bias of the average outward cN1 deflection [t(9) = −3.014, P = 0.015; Fig. 6D], a bilateral hemispheric distribution of the both the inward cN1 [t(9) = −1.236, P = 0.248; Fig. 6E] and outward cP2 deflections [t(9) = −0.021, P = 0.984; Fig. 6F] and a significant left-hemisphere bias of the inward cP2 deflection [t(9) = 2.960, P = 0.016; Fig. 6F]. These results suggest that 1) the cP2 was generally more left-lateralized than the cN1 and 2) both deflections were more left-lateralized for the inward than outward conditions. To test the statistical validity of these conclusions, we calculated the difference in the absolute values of the source amplitudes between the right and left hemispheres (|right| − |left|) as an index of response lateralization (see Fig. 7; division by the sum of |right| and |left|, as in the classical lateralization index calculation, yielded erratic results for the inward cN1 due to the small size of this deflection and thus division by near-zero values for many participants) and submitted the resulting values to a two-way repeated-measures ANOVA with factors deflection (cN1 and cP2) and ITD change direction (outward and inward). As expected, both factors had significant main effects [deflection: F(1,9) = 16.010, P = 0.003; ITD change direction: F(1,9) = 11.573, P = 0.008] and their interaction was not significant [F(1,9) = 4.420e-4, P = 0.984].

Fig. 7.

Hemispheric differences in the cN1 (light-gray bars) and cP2 (dark-gray bars) source amplitudes of the average outward (A) and inward (B) ITD change responses. Positive differences show lateralization toward the right hemisphere. Error bars show the SE.

DISCUSSION

The aim of the current study was to use EEG with the continuous stimulation paradigm to test whether ITDs are coded by the spatial distribution in a topographic array of ITD-tuned neurons (topographic model) or by the relative activity levels in two channels, broadly tuned to the left and right hemifields (opponent-channel model). The results showed that an ITD change toward the midline (inward change) produces a considerably smaller response than a change away from the midline (outward change). This was true even when the endpoint of the ITD change (the probe ITD) was kept fixed. This finding is consistent with the predictions of the opponent-channel model and is incompatible with the topographic model (see introduction). More generally, the finding that inward ITD change responses are smaller than outward change responses contravenes the existence of channels tuned to ITDs on or close to the midline (i.e., neurons responding more strongly to small than to large ITDs).

Detailed pattern of responses to individual ITD change conditions

The detailed pattern of the responses to the individual ITD change conditions was also more consistent with the opponent-channel than with the topographic model. According to the opponent-channel model, the response amplitude to outward ITD changes should increase with the size of the ITD change because the stimulus would be moving further along the increasing ITD-response function of the channel tuned to the probe ITD (Fig. 1E). The current data accord with this prediction in that the ITD change from 0 to −500 μs produced the largest response and the changes from 0 to −250 and from −250 to −500 μs yielded smaller and similar-sized responses. The topographic model would predict the same result if one assumes a homogeneous density of best ITDs across all ITDs (Fig. 1A). However, under the assumption that a greater number of neurons are tuned to ITDs near zero (Fig. 1C) the response amplitude to the outward conditions would be expected to depend not only on the size of the ITD change but also on its endpoint (the probe ITD), which is in contrast to the current data. According to the opponent-channel model, responses to inward ITD changes should be mainly generated by neurons belonging to the channel tuned to the hemifield opposite to the adapting ITD (the red channel in Fig. 1F). The amplitude of inward change responses should thus be mainly determined by how effectively this channel is activated by the probe ITD and be largely independent of the adapting ITD. The current results are consistent with this prediction in that the responses to the ITD changes from −500 and −250 to 0 μs were of a similar size and larger than the response to the −500- to −250-μs change. In contrast, the topographic model would wrongly predict either the same pattern of response as that for the outward conditions (with the assumption of homogeneous density of best ITDs) or a graded progression of response amplitudes, with the largest response to the −500- to 0-μs ITD change, a median-sized response to the −250- to 0-μs change, and the smallest response to the −500- to −250-μs change (with the assumption of a greater density of best ITDs near zero).

Comparison of cN1 and cP2 deflections

The ITD change response exhibits a similar triphasic shape as that of the response evoked by sound onset (energy onset response). Unlike the initial vertex-positive deflection (here referred to as cP1), both of the subsequent deflections (cN1 and cP2) depended markedly on the start and endpoints of the ITD changes (the adaptor and probe ITDs). Although there was some covariance between the cN1 and cP2 (both deflections were smaller for the inward than for the outward ITD changes), they also showed dissociation, in that only the cP2 showed an effect of ITD change condition. Although this dissociation does not necessarily mean that the processes underlying the cN1 were completely independent of ITD change condition because the cN1 effect may have been cancelled out by a larger effect of opposite polarity in the partially overlapping cP2, it does suggest that the cN1 and cP2 reflect at least partially independent processes. This is consistent with findings for the N1 and P2 deflections in the energy onset response. High-precision magnetoencephalographic (MEG) measurements indicate that the source of the P2 is located anterior and medial to the source of the N1 (Lütkenhöner and Steinsträter 1998; see also Hari et al. 1987), suggesting that the two deflections arise from different auditory fields (Heschl's gyrus and planum temporale, respectively). Alternatively, the P2 might receive contributions from nonauditory regions. Furthermore, the N1 and P2 show dissociation with respect to sleep state, development, and aging (for review see Crowley and Colrain 2004). These results indicate that the N1 and P2 receive contributions from anatomically and functionally distinct sources. The current results suggest that the same is true for the cN1 and cP2.

Hemispheric distribution of ITD-sensitive channels

The source strength analysis of the ITD change responses showed that the responses to the outward ITD changes were more lateralized toward the right hemisphere (i.e., contralateral to the ITDs used in the current experiment) than the inward change responses (or: the inward change responses were more lateralized toward the left, or ipsilateral, hemisphere than the outward responses). This suggests that ITD channels tuned to the left and right hemifields are distributed asymmetrically across the two hemispheres, with a preponderance of neurons tuned to the contralateral hemifield. This finding is consistent with results from previous neurophysiological (Fitzpatrick et al. 2000) and electrophysiological studies (McEvoy et al. 1994). However, Stecker et al. (2005) pointed out that an opponent-channel mechanism involving only one contralateral channel within each hemisphere would require comparisons of activity levels across the two hemispheres. A unilateral lesion would thus be expected to produce localization deficits throughout the entire acoustic field, when, actually, only the contralesional hemifield is affected in most cases (Jenkins and Merzenich 1984; Kavanagh and Kelly 1987; Malhotra et al. 2004, 2008). Thus Stecker et al. proposed a four-channel mechanism, with one contralateral and one ipsilateral channel in each hemisphere. Based on the existing neurophysiological data, the ipsilateral channel would be assumed to be much smaller (involve fewer neurons) than the contralateral channel in nonhuman mammals (Brand et al. 2002; McAlpine et al. 1996). In humans, neuroimaging and electrophysiological data suggest that the balance between contralateral and ipsilateral channels may differ between the two hemispheres, with the right hemisphere responding about equally strongly to ITDs from both hemifields, and the left hemisphere predominantly responding to contralateral ITDs (e.g., Krumbholz et al. 2005; Schönwiesner et al. 2007; for review see Krumbholz et al. 2007; however, see Salminen et al. 2010a). The idea that humans possess three ITD channels, a contralateral and an ipsilateral channel in the right hemisphere and a contralateral channel in the left hemisphere, is consistent with neuropsychological findings showing that right-hemisphere lesions generally lead to spatial processing deficits in both hemifields, whereas patients with left-hemisphere lesions usually perform normally in auditory spatial tasks (Clarke et al. 2000; Zatorre and Penhume 2001; see also Spierer et al. 2009). The current results for the cN1 deflection are consistent with these findings, in that they showed that the cN1 was lateralized toward the right hemisphere for the outward conditions (which would be assumed to activate the left-tuned ITD channel), but was bilateral for the inward conditions (which would be assumed to activate the right-tuned ITD channel). The cP2 results are also consistent, if one assumes that the cP2 exhibits a general (stimulus-independent) left-hemisphere bias. Such a general left-hemisphere bias has previously been described for the P1 deflection in the energy-onset response to noise stimuli (Chait et al. 2004).

The “inverted” topographic model

Some perceptual models of interaural temporal processing assume an “inverted” topographic coding mechanism, whereby ITDs are represented by minima, rather than maxima, in neurons' ITD response functions (Breebaart et al. 2001; Lindemann 1986). Neurons that show a minimum in spike rate at a consistent ITD value across frequencies are known to exist at all levels of the mammalian binaural system (e.g., Fitzpatrick and Kuwada 2001; Fitzpatrick et al. 2002). The ITD response functions of these so-called trough-type neurons look like inverted versions of the schematic tuning curves shown in Fig. 1A. Unlike the original topographic model, the inverted version of the model would be able to account for the observed smaller amplitude of the inward ITD change responses, if it is assumed that there are a greater number of neurons “tuned” (in terms of response minimum) to ITDs near the midline than to more lateral ITDs. However, the model would be inconsistent with the pattern of results found for the individual ITD change conditions tested. According to the inverted topographic model, the amplitude of the ITD change response would be expected to be mainly determined by the proportion of neurons tuned to the adapting ITD. This is because trough-type neurons respond more strongly to ITDs outside than within their receptive fields and so only neurons tuned to the adapting ITD would be expected to respond more strongly to the probe than adapting ITD and thus contribute to the change response. This means that the response amplitude to both the outward and inward ITD changes would be predicted to be mainly determined by the adapting ITD and depend little on the probe ITD. This is inconsistent with the observed pattern of response, where the response amplitude to the outward conditions mainly depended on the size of the ITD change and the response amplitude to the inward conditions mainly depended on the probe ITD. Thus the ITD change responses observed in the current study are unlikely to have arisen from ITD-sensitive neurons with trough-type response characteristics.

Comparison with previous psychophysical results

Some psychophysical studies have investigated how exposure to long adapting sounds similar to those used in the current study changes the perception of the spatial attributes of short probe sounds. Unfortunately, the results from these studies seem too patchy to allow any firm conclusions at this point. Phillips and Hall (2005) found that an adaptor with a large ITD shifts the perceived midline in the direction of the adapting ITD (see also Vigneault-MacLean et al. 2007). Although the finding reported by Phillips and Hall is consistent with the opponent-channel model (see Phillips 2008), it cannot exclude a topographic coding mechanism with broadly, rather than sharply, tuned ITD channels (Baldi and Heiligenberg 1988). This is because their experiment did not include an adaptor with zero ITD (equivalent to the outward change conditions in the current experiment). In contrast, an earlier study by Carlile et al. (2001) did include a medial adaptor, albeit with free-field stimuli rather than pure ITDs. Puzzlingly, the medial adaptor caused the perceived location of probe sounds close to the midline to shift radially away from the midline. According to the opponent-channel model, the medial adaptor should have had little or no effect on the localization of the probes. More systematic psychophysical or combined psychophysical and EEG measurements using pure ITDs would seem to be required to resolve this apparent contradiction.

Comparison with previous electrophysiological results

Some of the previous studies that have measured electrophysiological (EEG or MEG) responses to changes in interaural configuration have also found asymmetries between forward and reverse transitions. In the most recent study, Ross et al. (2008) measured responses to changes in the interaural phase difference (IPD) of pure-tone stimuli. The IPD change was either from 0 to 180° or in the reverse direction. For pure tones, an IPD of 180° represents the maximum possible ITD, corresponding to one half-cycle of the pure tone's repetition period T and leads to the perception of an ambiguous sound image, split between the two ears. In the topographic model, a 180° IPD produces maximal activation of channels tuned to ITDs near ±T/2 and minimal activation in channels tuned to ITDs near zero (Stern and Shear 1996). In the opponent-channel model, a 180° IPD produces strong activation in both left- and right-tuned channels (Hancock and Delgutte 2004). Despite the differences in stimuli (pure tones vs. noise) and perception (the stimuli used in the current study were unambiguously lateralized toward the left hemifield), Ross et al. found a similar asymmetry as observed in the current study, with the IPD change from 0 to 180° producing a considerably larger response than the reverse change. As in the current study, the cN1 deflection showed the greatest difference, whereas the cP1 was largely unaffected by the change direction. Furthermore, the stimulus portions with the 180° IPD also seemed to produce a larger sustained response. This is consistent with the larger sustained response to the more lateralized adaptors in the inward compared with the outward conditions observed in the current study. Although Ross and colleagues did not interpret the asymmetry in terms of ITD coding, their results support our conclusion, in that they favor the opponent-channel over the topographic model.

The current results are also consistent with a recent MEG study by Salminen et al. (2010b) who used a conventional adaptation paradigm with alternating adaptor and probe sounds, presented at a rate of 1/s. Salminen and colleagues showed that a probe ITD of 400 μs was more adapted by a larger than by a smaller adapting ITD.

Surprisingly, earlier comparisons between responses to outward and inward ITD changes failed to find significant differences (Halliday and Callaway 1978; Jones 1991; Jones et al. 1991). The reasons for this are unclear. One possibility is that the studies were underpowered (they used fewer sensors and fewer averages than those used in the current study and those used in the studies by Ross et al.). Alternatively, the discrepancy may be due to differences in stimulus generation procedure (e.g., in all cases, the stimuli included components with IPDs greater than π and some of the stimuli contained envelope ITDs).

Relationship to interaural correlation

Several of the previous studies have measured responses to the transition from interaurally correlated noise (interaural correlation [IAC] of 1) with zero ITD to interaurally uncorrelated noise (IAC = 0) and vice versa (Chait et al. 2005, 2007b; Dajani and Picton 2006; Jones 1991; Jones et al. 1991). Unfortunately, the results from these studies are incongruous. Using MEG and a paradigm similar to that in the current study, with discrete stimuli consisting of a longer adapting and a shorter probe portion and separated by silence, Chait et al. (2005) found that the surface-negative deflection of the IAC change response (cN1 in our terminology) was much larger for the change from interaurally uncorrelated to correlated noise than for the reverse change, whereas the opposite was true for the surface-positive deflections (cP1 and cP2). In contrast, the other studies used continuous stimulation with alternating segments of interaurally correlated and uncorrelated noise and found little or no effect of IAC change direction. From a theoretical viewpoint, the asymmetry observed by Chait et al. (2005) may or may not be related to the asymmetry observed in the current study. Durlach et al. (1986) showed that the processing of IAC plays an important part in the phenomenon of binaural masking release, which refers to the fact that a masked low-frequency signal tends to be more readily detectable when its interaural configuration differs from that of the masker (for review see Durlach and Colburn 1978). It remains unclear whether the processing of IAC for binaural masking release and the processing of ITDs for sound lateralization are based on the same or different neural substrates (Breebaart et al. 2001; Durlach 1963; Stern and Shear 1996).

Do ITD change responses reflect a generic “edge detection” process?

Chait and colleagues pointed out that the asymmetry in the IAC change responses is similar to the asymmetry in the responses to the transition between sequences of tone pips with constant or random frequencies (Chait et al. 2007a, 2008). They conjectured that both types of asymmetry might reflect activity associated with a generic “edge detection” process, which detects the onset of regularity, or “predictability,” in a previously random sound stream and which might thus be involved in the formation of auditory objects or the separation of auditory figure–ground information. According to this interpretation, the response asymmetry observed in the current study might also be the result of such a generic edge detection process. However, this is unlikely for two reasons. First, the adaptor and probe sounds used in the current study differed only in ITD; they had the same interaural correlation (IAC = 1 for both) and were thus equally regular or “predictable.” Second, the hemispheric distribution of the ITD change responses measured in the current experiment depended on the ITDs of the adaptor and probe sounds in a way that was consistent with current knowledge about the hemispheric distribution of ITD-sensitive channels in human auditory cortex. This suggests that the responses reflect activity of neural elements involved in auditory feature coding rather a generic edge detection process.

Conclusions

The current results favor the opponent-channel over the topographic model of ITD coding. They might seem surprising given the finding reported by Harper and McAlpine (2004) that, in humans, a topographic or intermediate ITD code would optimize ITD discrimination performance at all but the lowest frequencies (<250 Hz). However, discrimination performance is only one of several constraints to influence the evolution of binaural processing in humans and opponent-channel coding may be superior to topographic coding for other functions, such as sound localization or signal detection in noise. Moreover, an opponent-channel code of ITDs would allow other stimulus features, such as pitch or loudness, to be encoded by the same population of neurons without the need for interleaved, or nested, feature maps (Knudsen et al. 1987) and thus provide an efficient means for combining spatial with nonspatial information (Stecker et al. 2005). Furthermore, opponent-channel coding would convert ITD information into a similar format as information about interaural level differences (ILDs). Studies of the neural coding of ILDs typically reveal sigmoidal as opposed to “tuned” ILD response functions, with near-zero spike rates for ILDs favoring the ipsilateral ear and increasing spike rate with increasing contralateral ILD (Brugge et al. 1996; Phillips and Irvine 1981). This suggests that ILD coding also involves an opponent-channel mechanism. Results from a recent MEG study by Salminen et al. (2009), which used an adaptation approach similar to that in the current study, support this idea.

GRANTS

This research was supported by the Medical Research Council (UK).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).