Abstract
We assessed synaptic α-amino-3-hydroxy-5-methyl-4-isoxazole propionate receptor (AMPAR) properties during synaptogenesis to describe the development of individual glutamatergic synapses on rat hippocampal CA1 principal neurons. Pharmacologically isolated AMPAR-mediated glutamatergic synaptic currents [evoked by stimulation of the Schaffer Collateral pathway, excitatory postsynaptic currents (EPSCs)], had significantly greater inward-rectification at ages P5–7 compared with P8–18. These inward rectifying EPSCs demonstrated paired-pulse dependent unblocking at positive holding potentials, consistent with voltage-dependent internal polyamine block. Measurements of paired-pulse facilitation did not support altered presynaptic properties associated with inward rectification. Using asynchronous EPSCs (aEPSCs) to analyze populations of individual synapses, we found that quantal amplitudes (Q) increased across early postnatal development (P5-P18) and were directly modulated by increases in the number of activated receptors. Quantal AMPAR decay kinetics (aEPSC τdecays) exhibited the highest coefficient of variation (CV) from P5 to 7 and became markedly less variable at P8–18. At P5–7, faster quantal kinetics coexisted with much slower kinetics; only slower quantal kinetics were found at P8–18. This supports diverse quantal synaptic properties limited to P5–7. Multivariate cluster analysis of Q, CVτdecay, and median τdecay supported a segregation of neurons into two distinct age groups of P5–7 and P8–18, similar to the age-related segregation suggested by inward rectification. Taken together, these findings support synaptic, calcium permeable AMPARs at a subset of synapses onto CA1 pyramidal neurons exclusively at P5–7. These distinct synapses coexist with those sharing the properties of more mature synapses. These synapses disappear after P7 as activated receptor numbers increase with age.
INTRODUCTION
Changes in synaptic α-amino-3-hydroxy-5-methyl-4-isoxazole propionate receptor (AMPAR) activation in the CA1 region of the hippocampus underlie important processes such as learning and memory formation. Thus a better understanding of how the biophysical properties of AMPARs change during synaptogenesis would give insight into the mechanisms for developmental regulation of synaptic maturation. The AMPAR forms as a tetramer composed of homo- and heteromeric combinations of four subunits (GluA1, -2, -3, and -4) (Dingledine et al. 1999) and functions as a synaptically activated channel after postnatal day (P) 0 in rat (Hanse and Gustafsson 2001; Tyzio et al. 1999). It is thought that heteromeric assemblies of these subunits form preferentially in adults rats (P30-40) (Wenthold et al. 1996) and in heterologous expression systems (Mansour et al. 2001), but preferred GluA assemblies in postnatal development have not yet been fully established. Electrophysiological evidence suggests that heterogeneity in AMPAR subunit populations dominate at most developing rat synapses, in that AMPAR GluA1 homomers co-exist at the same synapses as GluA1/2 and/or GluA2/3 heteromeric combinations as well as different splice variants of GluA subunits (Seifert et al. 2000).
Biochemical evidence suggests that GluA subunit transcript levels (Ritter et al. 2002) and protein levels (Petralia et al. 2005) change drastically during synaptogenesis in rodents. For example, GluA4 levels increase from birth to P7 and then decrease thereafter to lower-than-birth levels in rat CA1. GluA1 levels appear to be higher than GluA2 during the first week of life (Monyer et al. 1991; Wisden and Seeburg 1993), but then GluA2 and GluA3 levels dramatically increase around P7-10 (Forti et al. 1997; Petralia et al. 2005; Pickard et al. 2000; Ritter et al. 2002). The total number of AMPARs at each synapse (N) is thought to increase during this period (Baude et al. 1995; Pickard et al. 2000; Tyzio et al. 1999), and supporting this, spontaneous excitatory postsynaptic current (EPSC) amplitude has been shown to increase from P1 up to P8 (Groc et al. 2002). At rat thalamocortical synapses, it has been demonstrated that the number of activated AMPARs modulating quantal amplitude (Q) adjusts with the AMPAR single-channel conductance (γ) to result in a uniform Q during early development (Bannister et al. 2005).
A wide range of AMPAR activation and deactivation kinetics (EPSC τrise and τdecay) and single-channel conductances (γ) have been previously reported (Cull-Candy and Usowicz 1987; Gardner et al. 2001; Mosbacher et al. 1994), and it is likely that these differences arise due to developmental differences in AMPAR expression (Cathala et al. 2005; Seifert et al. 2000). Evidence in the rat cerebellum suggests a speeding of AMPAR-mediated EPSC kinetics as age increases. For example, AMPAR kinetics are slower at ages ≤ P10 versus ages ≥ P40 (Cathala et al. 2005; Wall and Usowicz 1998). Previous studies in CA1 reveal faster τdecay at P45 compared with P15, supporting the idea that EPSC τdecay are faster in the adult (Seifert et al. 2000). Recombinant studies (Oh and Derkach 2005) and evidence in rat hippocampal culture (Thiagrarajan et al. 2005) demonstrate much faster channel kinetics for GluA2-lacking receptors compared with channels that contain the GluA2 subunit, suggesting these changes are influenced by subunit composition. Hippocampal AMPAR-mediated γ values range from 2 to 20 pS (Gebhardt and Cull-Candy 2006). These values could vary depending on differing subunit populations of AMPAR channels because (recombinant) GluA2-lacking receptors have a higher γ compared with GluA2-containing AMPARs (Oh and Derkach 2005). GluA2-lacking AMPARs (or unedited GluA2) are calcium permeable (Bowie and Mayer 1995; Geiger et al. 1995; Kamboj et al. 1995) and highly developmentally regulated. Calcium permeable AMPARs have been found in the rat CA3 region mainly during the first 3 weeks of life (Ho et al. 2007), in neocortical pyramidal neurons until P16, coincident when GluA2s become more prevalent (Kumar et al. 2002), and transiently in primary auditory neurons before the onset of hearing (Eybalin et al. 2004). In CA1, the developmental expression of calcium permeable synaptic AMPARs has been explored, revealing the presence of inward rectifying channels mainly in interneurons (Isa et al. 1996). Detailed analysis of inward rectifying AMPAR on CA1 principal neurons has not been studied during early developmental ages except to note that they are typically not active around P14 (Plant et al. 2006).
It has been shown that AMPAR subunits can be targeted to specific glutamatergic synapses (Craig et al. 1993; Harms et al. 2005; Rubio and Wenthold 1997), and in the cerebellum, this can be due to the activity of calcium permeable AMPARs that direct GluA2-containing receptors into synapses (Lin and Cull-Candy 2002). In CA1 hippocampus, it has been demonstrated that specific targeting of calcium permeable, GluA2-lacking AMPARs aids in the induction and expression of LTP (Plant et al. 2006; but see Adesnik and Nicoll 2007). Similar targeting also occurs in response to pharmacological blockade of AMPARs (Thiagarajan et al. 2005) or in response to hypoxia-induced seizures (Rakhade et al. 2008). This suggests that selective AMPAR properties including calcium permeability are intrinsically necessary in processes that involve precise strengthening or weakening of synaptic neurotransmission. However, it remains unknown if biophysically different AMPARs are segregated to different synapses during basal levels of neurotransmission. We therefore studied both multiquantal and quantal AMPAR-mediated synaptic responses during the formation of synapses in CA1 hippocampus when AMPAR mediated calcium fluxes might affect synaptogenesis. We used whole cell electrophysiological recordings to investigate synaptic AMPAR-mediated multiquantal EPSCs to study inward rectification and quantal aEPSCs (in the presence of extracellular strontium) to study Q, quantal τdecay, γ, and number of activated receptors (N*Po). Our data suggest that neurons at P5–7 expressed two distinct types of synapses: one type expressed inward rectifying AMPARs associated with faster quantal kinetics, whereas the other type expressed nonrectifying (linear) AMPARs associated with slower quantal kinetics, similar to synapses at P8–18. The older neurons (P8–18) had more uniform biophysical properties, yet the number of activated AMPARs significantly increased at the synapse. We therefore speculate that there are AMPAR-mediated calcium fluxes at distinct synapses at P5–7 during early synaptogenesis; as these synapses mature, they then become more biophysically uniform.
METHODS
Ethical approval
All experiments were approved by the University of Colorado at Denver Health Science Center Institutional Animal Care and Use Committee. Data from 122 rat pups were used in this study.
Slice preparation
Sprague-Dawley rats, male and female, P5-18 days old, were decapitated, and the whole brain was rapidly removed and placed in ice-cold cutting solution comprising (in mM) 124 NaCl, 26 NaHCO3, 3 KCl, 1.2 NaH2PO4, 5 MgSO4, 10 d-glucose, and 2 Na ascorbate and bubbled with 95% O2-5% CO2. Sagittal slices were made (300–400 μm thick) using a Leica VT-1200 microtome (Nussloch, Germany), and additional cuts were made with a scalpel to remove the CA3 area of the hippocampus. Hippocampal slices were transferred to a holding chamber and stored for ≥1 h prior to recording in recovery solution (as in preceding text except including 2 mM CaCl2 and substituting 1 mM MgSO4) at room temperature (18–22°C).
Electrophysiological recording
CA1 pyramidal neurons were visually identified by characteristic position and shape in submerged slices using infrared differential interference contrast (DIC) optics under magnification (×40; BX51-WI, Olympus) and patch-clamped in the whole cell configuration. Borosilicate glass (Harvard Instruments, Holliston, MA) recording electrodes were pulled with a Sutter P-97 electrode puller (Sutter Instruments, Novato, CA) with resistance 4–6 MΩ and filled with internal patch solution comprising (in mM) 135 CsMeSO4, 10 HEPES, 0.5 EGTA, 0.3 Na-GTP, 5 QX314, 4 ATP-Na2, 4 MgCl2, and 0.1 spermine, pH 7.25 with 1 M CsOH. For recording, picrotoxin (100 μM), and d-APV (50 μM) were added to the recording solution to block γ-amino butyric acid (GABA) receptor and NMDA receptors, respectively (recording solution).
For rectification experiments, a platinum/iridium bipolar stimulating electrode (FHC, Bowdoin, ME) was placed in the stratum radiatum to evoke a near maximal, synchronous, multiquantal EPSC by using a constant voltage source (Digitimer, DS2A; 7–9 V, 100 μs) every 5 s. In the remainder of experiments, near minimal stimulation of axons in the stratum radiatum to evoke aEPSCs was performed with a glass stimulating electrode (resistance of 6–7 MΩ when filled with recording solution) and placed in a consistent location (30–50 μM distally from the soma and 15–30 μM laterally from the primary apical dendrite) to the recording electrode. A constant voltage (Digitimer, DS2A) or constant current source (WPI, Sarasota, FL) source (1–3.0 V or 8.5–9.9 mA, 100 μs duration) was applied every 5 s. Calcium was replaced with 8 mM Sr2+ in the recording solution to cause asynchronous release of glutamate (Bekkers and Clements 1999; Goda and Stevens 1994) and was introduced following membrane rupture. Resulting asynchronous EPSCs (aEPSC) were collected at a holding potential of −70 mV in a 2.25 s time frame after each single stimulus. EPSCs and aEPSCs were confirmed to be mediated by AMPA receptors by addition of GYKI 52466 (100 μM) across all ages resulting in complete block of current (n = 8). Spontaneous events prior to stimulation were only seen in 2 of 122 recordings; these recordings were not analyzed further; this suggests that aEPSCs in the 2.25 s window after stimulation were not spontaneous events. Series resistance associated with the recording electrode was monitored in every sweep by a −2.0 mV voltage step; recordings were terminated if changes in series resistance of >10% of baseline occurred (see Supplemental Fig. S1).1 Cell capacitance was also determined from this voltage step (Bannister et al. 2005) (see Supplemental Fig. S2). Responses were amplified and filtered at 5 kHz (Axopatch 200B, MDS, Sunnyvale, CA) and digitized at 20 kHz (Digidata 1322A and Clampex 9.2, MDS). No series resistance cancellation was performed. All drugs were purchased from Sigma Aldrich (St Louis, MO) or Tocris Bioscience (Ellisville, MO).
Data analysis
For calculation of rectification index (RI), neurons were voltage clamped at −70 mV for a set of 10–12 EPSCs and then voltage-clamped at +40 mV for a set of 10–12 EPSCs. RI was calculated as the average of absolute peak current at −70 mV divided by absolute peak current at +40 mV for each neuron. In a subset of recordings, voltage was varied from −70 to −40, 0, +20, and +40 mV for ≥10–12 EPSCs each, to obtain peak current-voltage (I-V) relationship, verify minimal voltage offsets (no corrections were performed), and show separation of smaller EPSCs from stimulus artifacts. The voltage-dependent unblocking index (UBI) was calculated by obtaining the paired-pulse ratio (PPR) of averaged amplitudes (≥25 currents) EPSC2/EPSC1 (obtained within a 70 ms interstimulus interval) at +40 mV and divided by the PPR of averaged amplitudes at −70 mV for each neuron (Rozov and Burnashev). The averaged current for EPSC1 at −70 mV was normalized by the averaged amplitude of EPSC1 at +40 mV and compared (Fig. 2C, 1 and 2) to demonstrate degree of unblock for EPSC2 at +40 mV for inward rectifying AMPARs. Because EPSCs are potentially a mixture of inward rectifying and linear AMPARs, then RI is a reflection of that percentage (supplemental text). Because presynaptic-mediated paired pulse ratios will be the same at different postsynaptic holding potentials, UBI can be expressed in terms of the fractional percentage of inward rectifying AMPARs (PRI) as
| 1A |
where, for a pure population of only inward rectifiers, F1 is the maximal block at +40 (EPSC1 at +40 mV/EPSC1 at −70 mV) and F2 is the unblock at +40 (EPSC2 at +40 mV/EPSC1 at −70 mV); unblock at −70 (F4 = EPSC2 at −70 mV/EPSC1 at −70 mV) was assumed to be near unity (see results, Fig. 2B). F1 was extrapolated to be ∼0.05 (based on Rozov et al. 1998, their Fig. 4). For a linear AMPAR conductance, F3 is 0.57 (40/70). F1, F2, and F4 apply only to pure inward rectifiers; F3 applies only to linear AMPARs. The unknown F2 would be expected to be less than or equal to F3, based on the degree of unblock (Rozov et al. 1998). The unblock ratio, the amount of unblock of inward-rectifying AMPARs after single paired pulses, (F2/F3′, where F3′ = 40/70), would be expected to be less than unity for single paired pulses compared with a train of pulses when it would more closely approach unity (Rozov et al. 1998). Furthermore, using
| 1B |
allows an estimate of PRI from RI. This analysis assumes that presynaptic function, as it affects the activation of either pool of AMPARs, is equal.
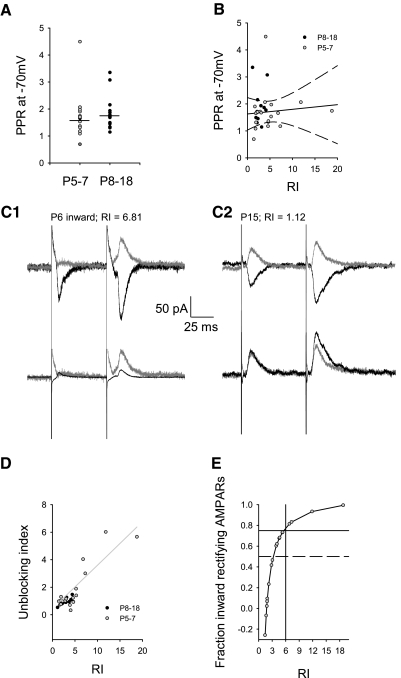
Fig. 2.
Polyamine-mediated voltage dependence of paired-pulse stimulation was restricted to P5–7. A: paired-pulse ratio (PPR) at −70 mV at P5–7 (1.71 ± 0.18, n = 14) compared with P8–18 (1.85 ± 0.18, n = 18, P = 0.45, Mann-Whitney rank sum) were similar. B: at P5–7, there was no correlation of PPR at −70 mV with rectification index (solid line, r2 = 0.009, 95% confidence intervals dashed lines). C: EPSCs evoked by paired-pulse stimulation at +40 and −70 mV were compared (top) in which (PPR at +40 mV)/(PPR at −70 mV) = the unblocking index. C1: inward rectifying AMPARs (P6, RI = 6.81 shown) demonstrated unblocked current in the 2nd pulse at +40 mV (peak current after 1st pulse = 10.54 pA, after 2nd pulse = 65.23 pA, 70 ms interstimulus interval, compared with the −70 mV peak current after 1st pulse = −79.54 pA, after 2nd pulse = −123.59 pA; unblocking index = 3.98). Bottom: the normalized currents from the top overlapped to reveal more unblock at +40 mV (vs. −70 mV) for inward rectifying AMPARs. C2: nonrectifying AMPARs (P15, RI = 1.12 shown) demonstrated little unblock on 2nd pulse at +40 mV, compared with C1 example (peak current after 1st pulse = 45.66 pA, after 2nd pulse = 60.92 pA, 70 ms interstimulus interval compared with the −70 mV peak current after 1st pulse = −53.80 pA, after 2nd pulse = −92.86 pA; unblocking index = 0.77). D: the degree of polyamine unblock correlated with the rectification index of neurons at P5–7 (Eq. 1A, n = 18, r2 = 0.7, P < 0.0001). This correlation predicted an unblocking ratio (F2/F3 = 0.34/0.57) of less than unity (0.6). Minimal unblock was seen at P8–18 (n = 14, F2 = 0.09, r2 = 0.03, P = 0.54, line not shown) suggesting a much smaller unblocking ratio (F2/F3 = 0.09/0.57 = 0.16). E: measurements of RI from D are replotted (Eq. 1B) to demonstrate the relationship of RI to the fraction of inward rectifying AMPARs activated; a fraction of 1 is equivalent to the synaptic activation of only inward rectifying AMPARs. Measurements of RI are relatively insensitive to changes in the fraction of inward rectifying AMPARs <0.5 (dotted line). Fractions >0.75 correlate with RI >6 (solid intersecting lines).
Fig. 4.
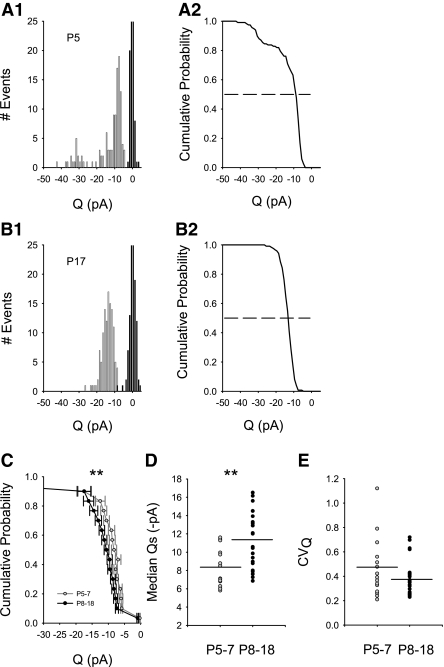
AMPAR-mediated aEPSC quantal amplitudes (Q) across development. A1: probability density of aEPSC amplitudes (Q) from an individual neuron at P5 showed a wide CVQ (0.68) and nonnormal, discontinuous distribution of amplitudes (bin width: 1 pA). Darker vertical bars centered at 0 represent the noise (σn = 1.39 pA). B1: probability density of Q from an individual neuron, at P17 separated from noise (σn = 1.59 pA), exhibited a smaller CVQ (0.26) compared with A1. A2 and B2: median Qs (dotted line at 0.5) were obtained from cumulative distributions of Q for each neuron at P5 and P17, corresponding to probability densities shown at left for each neuron in A1 and B1, respectively. C: cumulative probability distributions of Q at P5–7 (cf. A2) were group-averaged and compared with group-averaged distributions at P8–18 (cf. B2). The average distribution of Q was significantly different (**P = 0.0026, K-S test) for all P5–7 (gray circles, n = 15) neurons compared with all P8–18 (black circles, n = 23). D: median Qs obtained from each individual neuron (cf. A2 and B2) increased during development and were significantly higher for all P8–18 neurons [black circles; mean of median Qs (dark line) = 11.44 ± 0.64 (n = 23)] compared with all neurons at ages P5–7 [gray circles; mean of median Qs (dark line) = 8.22 pA ±0.56 (n = 15), **P < 0.001 Mann-Whitney rank sum test]. E: CVQ was not significantly different between the 2 age groups [P5–7, gray circles: mean of CVQ (dark line) = 0.46 ± 0.065 (n = 15), P8–18, black circles: mean of CVQ (dark line) = 0.386 ± 0.031 (n = 23), P = 0.385, Mann-Whitney rank sum].
AMPAR-mediated aEPSCs were visually detected as peaks arising ≥2.5 times the noise (σn2, average variance 2.04 pA2, range: 0.81–7.84 pA2, n = 38). aEPSCs were analyzed for amplitude (Q) and quantal kinetics (τrise and τdecay) using purpose-written software in which responses were identified based on the point of onset (Benke et al. 1998, 2001). Responses were selected as long as they were not overlapping with another aEPSC in a 10–25 ms window, depending on the rate of aEPSC decay. Each aEPSC peak amplitude was measured as the difference between the average peak value from the middle of a five-sample window (0.25 ms) and a similar window prior to the onset of the aEPSC used to measure the noise. τrise and τdecay for each aEPSC were obtained by fits to the rising phase and decaying phase of individual aEPSCs according to I(t) = a*exp(−t/τrise) – a*exp(−t/τdecay) using a nonlinear least-squares iterative method (see Fig. 3). Median values were calculated from binned cumulative histograms for amplitude, τrise, and τdecay and used for subsequent comparisons across development. Coefficient of variation for amplitude and kinetics for the events from each neuron was estimated as CV = σ/μ, where σ is the SD and μ is the arithmetic mean.
Fig. 3.
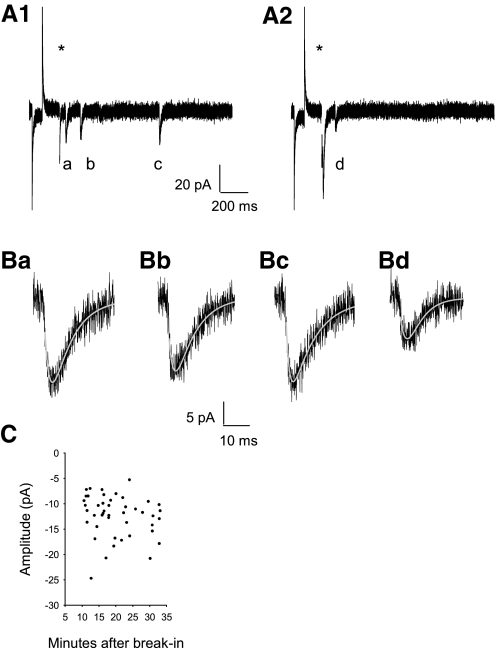
AMPAR-mediated asynchronous EPSCs (aEPSCs) in the presence of extracellular Sr2+. A, 1 and 2: successive traces of AMPAR-mediated aEPSC (a–d) evoked following an electrical stimulus (blanked at *) in the presence of 8 mM Sr2+/0 added Ca2+/1Mg2+ in an example CA1 pyramidal neuron (P13). Series resistance and capacitance were monitored by the current response to the −2 mV voltage step. B: AMPAR-mediated aEPSCs (a–d from A) were distinguished from noise (σn = 2.77 pA, σn2 = 7.67 pA2) and fitted with 2 exponentials (grey, superimposed, see methods); Ba: τrise = 2.1 ms τdecay = 8.5 ms; Bb: τrise = 2.1 ms τdecay = 9.2 ms; Bc: τrise = 1.5 ms τdecay = 10.2 ms; Bd: τrise = 3.1 ms τdecay = 5.8 ms. C: aEPSC amplitudes remained stable for the duration of data acquisition (data from neuron in A and B shown).
Single-channel conductance was determined from an ensemble of aEPSCs from a neuron by using peak-scaled nonstationary fluctuation analysis (NSFA) (Traynelis et al. 1993). This analysis was based on a subset of hand-selected responses (minimum of 14) based on precise alignment around the onset and peak, nonoverlapping aEPSCs (50–70 ms window, depending on the rate of aEPSC decay) and return to baseline in this window (Bannister et al. 2005; Benke et al. 1998, 2001). These limitations prevented analysis on some neurons due to an inadequate number of responses (Benke et al. 2001). Selected individual aEPSCs were averaged to obtain a mean response waveform. This mean aEPSC response waveform was then scaled to the peak of each individual aEPSC peak and subtracted and squared. The variance of fluctuation around the mean was calculated for 10–100 bins of equal current decline from the peak of the mean current until within a time frame five to six times τdecay. The binned variance was plotted against the mean current amplitude and the single-channel current was estimated by fitting the data using a least-squares algorithm according to
| 2 |
where σ2 is the variance, I is the mean current, N*Po is the number of AMPAR activated at the peak of the mean current, i is the single-channel current, and b1 is the background variance (Sigworth 1980; Traynelis et al. 1993). The single-channel conductance, γ, is then γ = i/V where V is the driving force (holding potential of −70 mV, assumed AMPAR reversal potential of 0 mV). To obtain the most accurate estimate for γ, the data were fitted from 0 to 50% of the maximum current (Benke et al. 1998, 2001) with goodness of fit assessed with the Spearman rank-order correlation coefficient (R2sp) (Bannister et al. 2005; Press et al. 1992). Mean current (I) peak amplitude and single-channel conductance infer total AMPAR numbers and peak opening probability according to
| 3 |
where I is the mean current amplitude, N is the average total number of AMPARs across the population of AMPAR clusters activated, Po is the peak open probability of AMPAR opening, γ is the single-channel conductance, and V was the holding potential. NSFA permits calculation of N*Po for individual neurons; peak-scaled NSFA does not allow direct calculation of Po. In the case of quantal aEPSCs, peak quantal current (Qcalc) and peak mean current (I) are theoretically equivalent.
Statistics
For grouped comparisons, data are expressed as mean ± SE and n = number of recordings from individual neurons; Mann-Whitney Rank Sum tests were used for comparisons of two groups, with significance set at P ≤ 0.05 (Sigmaplot, Systat, Point Richmond, CA). Kruskal-Wallis one-way ANOVA on ranks was used to compare three groups with Dunn's method for pair-wise testing of multiple comparisons. Significance was set at P ≤ 0.05. Linear interpolation was used to determine trends with r2 used to assess trend (1 = perfect) and p to assess significance. Median values were interpolated from binned cumulative data distributions as the point at which half of the distribution was above and half below that point. Grouped cumulative distributions were binned along the y axis for averaging. For comparisons of averaged cumulative distributions, the Kolmogorov-Smirnov (K-S) test was used with significance set at P ≤ 0.05 (Press et al. 1992). Hartigan's dip test was used to test for multimodal distributions [significance set at P ≤ 0.1 (Hartigan and Hartigan 1985; Priebe et al. 2004; R Development Core Team 2010)]. Cluster analysis (JMP, SAS, Cary, NC) was used to suggest segregational break points for group comparisons. Levene's test of equal variance (JMP, SAS, Cary, NC) was used for some group comparisons.
RESULTS
Inward rectifying AMPARs exist very early in development at CA1 synapses
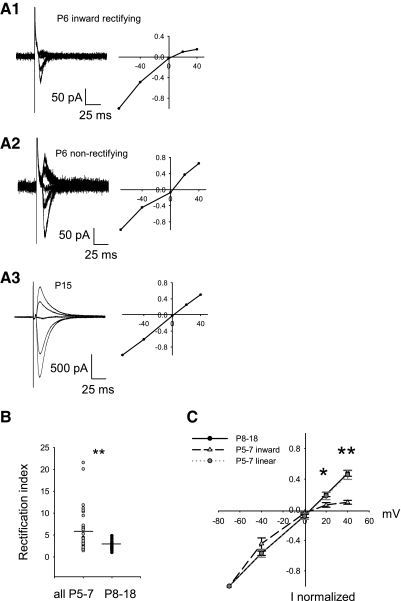
To establish the existence of inward rectifying AMPAR during early development, we conducted whole cell recordings and obtained current-voltage relationships from electrically evoked EPSCs in individual pyramidal neurons. It is known that inward rectifying AMPARs exhibit a voltage-dependent decrease in open probability at positive holding potentials compared with negative holding potentials when in the presence of intracellular polyamines such as spermine (Bowie and Mayer 1995; Kamboj et al. 1995; Rozov et al. 1998). This means inward rectifying channels mediate less current at positive holding potentials compared with negative holding potentials. Figure 1 demonstrates the voltage-dependent properties of EPSCs in the presence of intracellular spermine. An example neuron at P6 (Fig. 1A1) demonstrated minimal outward EPSCs at +20 and +40 mV compared with the robust inward EPSCs at −70 mV to indicate the presence of inward rectifying, synaptic AMPARs. This was not always the case, however, because synaptic AMPARs also demonstrated robust current at both positive and negative holding potentials (Fig. 1A2, example neuron) at this age. I-V curves for neurons between ages P8 and 18 consistently revealed linear synaptic AMPAR conductances (Fig. 1A3, example neuron). Because the largest RI was found at P7 (RI = 21.0), all values of RI after P7 were <5.0, and cluster analysis of RI across all age groups segregated all RI > 6.0, we grouped all neurons at P5–7 and P8–18 (Fig. 1B). Mean RI at P8–18 (2.67 ± 0.15, n = 38) was significantly smaller than mean RI at P5–7 (5.39 ± 0.77, n = 38; P = 0.005, Mann-Whitney rank sum) suggesting the presence of inward rectifying, synaptic AMPARs restricted to P5–7.
Fig. 1.
Inward rectifying AMPARs were only present in some P5–7 pyramidal neurons. A1: inward rectifying excitatory postsynaptic currents (EPSCs) at P6 showed less outward current at +40 mV holding potential (11 traces averaged) compared with inward currents at −70 mV (10 traces averaged) resulting in a high rectification index (RI). A2: nonrectifying EPSCS at P6 with greater outward current at +40 mV (10 traces averaged) and at +20 mV (10 traces) had a lower RI. A3: nonrectifying EPSCs at P15 with robust outward current at +40 mV (35 traces averaged) and at +20 mV (34 traces averaged). B: mean RI at P8–18 (2.67 ± 0.153, n = 38) was significantly smaller than mean RI at P5–7 (5.39 ± 0.77, n = 38; P = 0.005, Mann-Whitney rank sum). C: I-V plots averaged from P5–7 inward rectifiers (light gray triangles, n = 5, RI > 6.5) were significantly different from older P8–18 (black circles, n = 9; +40 mV, **P = 0.004; +20 mV, *P = 0.032 Kruskal-Wallis 1-way ANOVA on ranks, Dunn's post hoc). The P5–7 inward rectifiers were also significantly different from their nonrectifying littermates (dark gray circles, n = 7, RI < 2.9; +40 mV, **P = 0.006; +20 mV *P = 0.032, Kruskal-Wallis 1-way ANOVA on ranks, Dunn's post hoc). Linear P5–7 neurons were not statistically different at any holding potential compared with the older P8–18 neurons (P > 0.05 Kruskal-Wallis 1-way ANOVA on ranks, P > 0.05 Dunn's method).
Because this method of calculating RI can be biased toward higher RI values due to the presence of relatively small EPSCs in developing neurons, especially in the presence of small voltage offsets, full I-V relationships were obtained in a subset of neurons (Fig. 1A). At P5–7, we segregated RI > 6 from the remainder (Fig. 1C) based on cluster analysis and comparison of group means at P5–7 and P8–18 (cf. Fig. 1B); all data sets for which full I-V relationships were available were included. Inward rectifying EPSCs at P5–7 (subset mean RI = 13.13 ± 3.61, range: 6.57–21.57, n = 5) were compared with nonrectifying EPSCs at P5–7 (subset mean RI = 2.51 ± 0.38, range: 1.50–3.76, n = 7) and all (nonrectifying) EPSCs at P8–18 (subset mean RI = 2.20 ± 0.18, range: 1.57–3.23, n = 9). Inward rectifying EPSCs at P5–7 had significantly less total outward current recorded at more positive holding potentials (+40 mV, **P = 0.004; +20 mV, *P = 0.032 Kruskal-Wallis 1-way ANOVA on ranks, Dunn's post hoc). Inward rectifying EPSCs at P5–7 were also significantly different from nonrectifying EPSCs (+40 mV, **P = 0.006; +20 mV *P = 0.032, Kruskal-Wallis 1-way ANOVA on ranks, Dunn's post hoc). EPSCs at P5–7 that were nonrectifying were not statistically different at any holding potential, compared with EPSCs from P8–18 neurons (Fig. 1C), and they both demonstrated the same linear profile. Therefore at younger ages (P5–7), neurons expressed synaptic, inward rectifying AMPARs or nonrectifying (linear) AMPARs, whereas the older age group (P8–18) expressed only linear, synaptic AMPARs. The segregation at P5–7, based on a cut-off of RI > 6, was not significant (Hartigan's dip test, D = 0.039, n = 38, p ≈ 0.9). A parsimonious interpretation is that neurons express synaptic, inward rectifying AMPARs in varying percentage across a continuum rather than in a truly segregated fraction.
To examine this further, we employed the known voltage- and use-dependent properties of intracellular polyamine-mediated inward rectification (Rozov and Burnashev 1999). Delivering a paired-pulse stimulation relieves the intracellular polyamine block of inward rectifying AMPAR channels and to an even greater degree at positive holding potentials (Brill and Huguenard 2009; Rozov et al. 1998). Comparison of paired-pulse ratios (PPR) at positive and negative holding potentials thus reflects the relative contribution of inward rectifying AMPARs to total peak synaptic current. To do this, it was necessary to first calculate the PPR at a negative holding potential for comparison. Similar PPR at −70 mV was found at P5–7 (1.71 ± 0.17, n = 14) compared with P8–18 (1.85 ± 0.17, n = 20, P = 0.43, Mann-Whitney rank sum; Fig. 2A). At P5–7, there was no correlation of PPR at −70 mV with rectification index (r2 = 0.009; Fig. 2B). Because PPR is largely mediated by presynaptic release probability, this suggests that presynaptic function was similar at synapses containing inward rectifying and nonrectifying AMPARs. While there was similar PPR at −70 mV for both inward and nonrectifying EPSCs, inward rectifying EPSCs at P5–7 had more unblock (facilitation) at +40 mV (Fig. 2C1) compared with nonrectifying neurons (Fig. 2C2, e.g., P8–18) with the second pulse. Figure. 2C, 1 and 2, bottom, shows overlapped, normalized currents to demonstrate more unblock at +40 mV (vs. −70 mV) for inward rectifying EPSCs with the second pulse. We then compared the unblocking index (PPR at +40 mV/PPR at −70 mV) to rectification index (Fig. 2D) for neurons at P5–7 and P8–18. As expected for the mechanism of polyamines on inward rectifying AMPARs, at P5–7 the unblocking index correlated with the rectification index of each individual neuron (Fig. 2D, n = 18 neurons, Eq. 1, F2 = 0.34, r2 = 0.7, P < 0.0001). This correlation predicted an unblocking ratio (F2/F3 = 0.34/0.57) of less than unity (0.6), as expected for only two pulses (Rozov et al. 1998). At P8–18, only lower unblocking index and nonrectification were found (Fig. 2D). Minimal unblock was seen at P8–18 (n = 14, F2 = 0.09, r2 = 0.03, P = 0.54) suggesting a much smaller unblocking ratio (F2/F3 = 0.09/0.57 = 0.16). The relationship of rectification index to unblocking index suggested that neurons possibly expressed inward rectifying AMPARs across a continuum. The largest rectification index utilized here (18.8) would be consistent with that for a nearly pure population of synaptically activated inward rectifying AMPARs (Rozov et al. 1998). We used the relationship of UBI to RI (Eq. 1A) to support our estimate of the fraction of inward rectifying AMPARs (Eq. 1B) contributing to each EPSC (Fig. 2E). This relationship suggests that for an inward rectifying fraction of AMPARs <0.5, measurements of RI are relatively insensitive, compared with fractions >0.5. We conservatively estimate from this relationship that an unblocking index >2 and a rectification index >6 is consistent with >75% inward rectifying AMPARs (Fig. 2E). This suggests that 26% (10/38) of neurons at P5–7 express synaptic AMPARs containing >75% inward rectifying AMPARs. However, it is not clear from this analysis whether or not linear and inward rectifying types of AMPARs are mixed together or segregated at individual synapses.
Isolation of quantal AMPAR-mediated EPSCs at immature CA1 hippocampal synapses
Because AMPAR rectification properties changed significantly at P8 in CA1 pyramidal neurons and to address whether AMPAR subtypes might be segregated or mixed at synapses, we further assessed synaptic AMPARs to elucidate other developmental differences to support our findings. We measured peak quantal current (Q), kinetics of deactivation (τdecay), and the underlying single-channel conductance (γ). Calcium was substituted with strontium in the extracellular recording medium to cause asynchronous release (i.e., 1 quantum at a time) of glutamatergic vesicles from presynaptic axonal terminals (Bekkers and Clements 1999; Oliet et al. 1996; Xu-Friedman and Regehr 1999), (Fig. 3, A and B). Near-minimal stimulation allowed the individual quantal activation of a small population of synapses containing AMPARs. By stimulating at a uniform distance from the somatic recording electrode, we approximate that responses emanated from a similar position in the dendritic tree to minimize the contribution of different electrotonic filtering to measurements. It was previously demonstrated that aEPSCs, in contrast to mEPSCs, eliminated discrepancies associated with the activation of synapses throughout the dendritic tree that would likely be differentially filtered (Bekkers and Clements 1999). aEPSCs were AMPAR-mediated responses because in the presence of d-2-amino-5-phosphonopentanoic acid (d-AP5), they were completely blocked by the AMPAR-selective antagonist GYKI 52466 (100 μM) across all ages. (see methods). Response amplitudes of aEPSCs remained stable for ≤35 min (Fig. 3C) following membrane rupture. Response stability allowed us to apply both quantal analysis and peak-scaled nonstationary fluctuation analysis (NSFA) to aEPSCs to report a weighted mean estimate (Cull-Candy et al. 1988) of the underlying AMPAR γ.
Quantal AMPA-mediated aEPSC amplitude during early development
We analyzed AMPAR-mediated aEPSC quantal amplitudes (Q) from each neuron across ages P5-18. We used density and cumulative distribution histograms to assess median Q, mean Q, and relative variability (CVQ) for each neuron (Fig. 4, A and B). Q did not appear to be normally distributed in individual neurons at the younger ages (Fig. 4A, 1 and 2, P5 representative neuron), which necessitated analysis of cumulative distributions and median Q from each neuron. While suggestive, there was not a significant bimodal component for this distribution (Hartigan's dip test, D = 0.030, 117 events, p ≈ 0.7); pooled event data from all P5–7 neurons (not shown) also did not have a significant bimodal component (Hartigan's dip test, D = 0.008, 732 events, p ≈ 0.99). In comparison, distributions of Q from the older age group (P8–18; P17 representative neuron, Fig. 4B, 1 and 2) typically appeared more uniform (Hartigan's dip test, D = 0.014, 290 events, p ≈ 0.5); pooled event data from all P8–18 neurons (not shown) also did not have a significant bimodal component (Hartigan's dip test, D = 0.005 1985 events, p ≈ 0.99).
Due to the significant differences in rectification properties in neurons at ages P5–7 compared with P8–18 (see Fig. 1), we then grouped median Qs at the respective age groups accordingly for direct comparison (Fig. 4, C–E). Even though distributions of Q were (suggestively) more broadly distributed at P5–7, when segregated into groups at P5–7 and P8–18, we found that group-averaged Q distributions for P8–18 were significantly shifted toward larger amplitudes compared with group-averaged Q distributions at P5–7 (Fig. 4C, **P = 0.0026, K-S test). Furthermore, median Qs from each individual neuron (cf. Fig. 4, A2 and B2, dotted lines) were found to be significantly increased between groups during postnatal development [Fig. 4D, P5–7 mean of median Qs = 8.41 ± 0.57 pA (n = 15); P8–18 mean of median Qs = 12.59 ± 0.66 pA (n = 23); **P < 0.001, Mann-Whitney rank sum test]. Also because there was great variability in the occurrence of inward rectifiers (Fig. 1B) and the suggestively broader distributions of Q (Fig. 4A, 1 and 2) at ages P5–7, we examined whether the relative variability of amplitudes (CVQ) was higher at younger ages compared with the older ages. The suggestion of higher variability for AMPAR Q across all neurons at ages P5–7 compared with P8–18 was not significant [Fig. 4E, P5–7: mean of CVQ = 0.46 ± 0.065 (n = 15), P8–18: mean of CVQ = 0.386 ± 0.031 (n = 23) P = 0.385, Mann-Whitney rank sum].
Quantal AMPAR-mediated aEPSC kinetics during early development
Inward rectifying AMPARs display faster kinetics (τrise and τdecay) than linear AMPARs (Oh and Derkach 2005). Collective activation time of an AMPAR synapse is represented in the τrise phase of an aEPSC, while the time it takes for AMPARs to deactivate and desensitize is evident in the τdecay phase of an aEPSC. We measured quantal τrise and τdecay for each aEPSC from each individual neuron across the developmental time points P5-18 and hypothesized the kinetics would be faster for P5–7 when grouped and compared with older animals. Density (Fig. 5, A1 and B1) and cumulative (A2 and B2) distributions of quantal τdecay for each aEPSC (Fig. 3, A and B) from each neuron were analyzed. Analysis of τrise suggested that these distributions were potentially influenced by filtering while τdecay was not (Supplemental Figs. S1 and S2). Similar to our findings of Q per neuron, aEPSC quantal τdecay in each neuron demonstrated wider distributions at P5–7 (representative P7 neuron shown in Fig. 5A, 1 and 2) compared with individual neurons at P8–18 (representative P11 neuron shown in Fig. 5B, 1 and 2). While suggestive, there was not a significant bimodal component for this distribution at P7 (Hartigan's dip test, D = 0.022, 83 events, p ≈ 0.9); pooled event data from all neurons at P5–7 (see Supplemental Fig. S4F) also did not have a significant bimodal component (Hartigan's dip test, D = 0.011, 732 events, p ≈ 0.9). Given the variability of Q and aEPSC τdecay at this age, we compared Q and aEPSC τdecay for each aEPSC at both ages; no correlations were found (Supplemental Fig. S3). In comparison, distributions of τdecay from the older age group (P8–18; P11 representative neuron, Fig. 5B, 1 and 2) typically appeared unimodal (Hartigan's dip test, D = 0.023, 107 events, p ≈ 0.99); pooled event data (not shown) did not have a significant bimodal component (Hartigan's dip test, D = 0.007 1985 events, p ≈ 0.99).
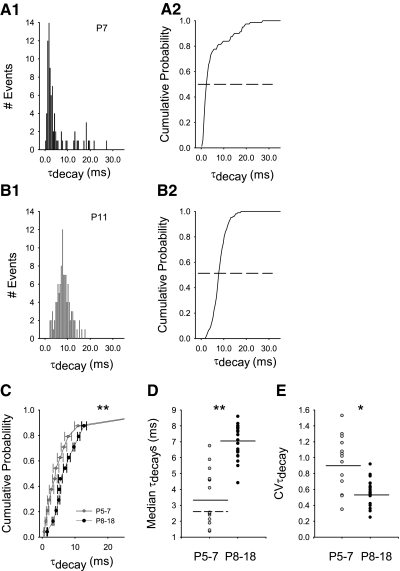
Fig. 5.
Quantal AMPAR-mediated aEPSC kinetics during early development. A1: probability density of quantal aEPSC decay kinetics (τdecay) from a representative neuron at P7 showed a wide CVτdecay (1.53) compared with a representative neuron at P11 (B1) (CVτdecay = 0.36; bin width: 0.5 ms). A2 and B2: median quantal τdecay is indicated by the dotted line from cumulative probability distributions of quantal τdecay for the individual neurons in A1 and B1, respectively. C: cumulative probability distributions of quantal τdecay at P5–7 (cf. A2) were group-averaged and compared with group-averaged distributions at P8–18 (cf. B2). Averaged cumulative probability distributions for all P5–7 (gray circles, n = 15) were significantly different (**P = 0.0022 K-S test) from all P8–18, (black circles, n = 23; horizontal error bars may be smaller than symbols). D: median quantal τdecays were significantly faster for grouped P5–7 [gray circles, mean of median τdecays (dark line) = 3.48 ± 0.467 (n = 15)] compared with all grouped P8–18 [black circles, mean of median τdecays (dark line) = 7.03 ± 0.22 (n = 23), **P < 0.001, Mann-Whitney rank sum test]. Median quantal τdecays were segregated into 2 groups at P5–7 [Hartigan's dip test, D = 0.097, modal break point (dotted line) = 2.6 ms, n = 15, P < 0.1]. E: the distribution of aEPSC quantal τdecay from each neuron at P5–7 (gray circles) had a significantly higher CVτdecay [mean CVτdecay (dark line) = 0.876 ± 0.099, n = 15] compared with neurons at P8–18 [black circles, mean CVτdecay (dark line) = 0.57 ± 0.33, n = 23, *P = 0.023, Mann-Whitney rank sum].
We averaged cumulative probability distributions of quantal τdecay for all P5–7 neurons and compared them to all P8–18 neurons. This revealed that distributions of quantal τdecay for all P5–7 neurons were significantly different from all P8–18 neurons (Fig. 5C, P5–7 n = 15, P8201318 n = 23, **P = 0.0022 K-S test), most likely due to significantly slower channels at P8–18. Median quantal τdecays were much faster for all P5–7 [mean of median τdecays = 3.48 ± 0.467 ms (n = 15)] compared with all P8–18 [mean of median τdecays = 7.03 ± 0.22 ms (n = 23), **P < 0.001, Mann-Whitney rank sum test]. Median quantal τdecays were clearly segregated into two groups at P5–7 (Hartigan's dip test, D = 0.097, modal break point = 2.6 ms, n = 15, P < 0.1). To further determine the source of variability of quantal τdecays, we compared the CVτdecay of each neuron from the two age groups. Consistent with a greater degree of variability in inter-synaptic parameters at P5–7, neurons at P5–7 had a significantly higher CVτdecay when grouped together and compared with all neurons at P8–18 (Fig. 5E, *P = 0.023, Mann-Whitney rank sum). Multivariate cluster analysis of Q, CVQ, CVτdecay, and median quantal τdecays also segregated neurons into groups of P5–7 and P8–18, similar to the grouping suggested by inward rectification.
Single-channel conductance (γ) of AMPARs in developing CA1 neurons
It is known that inward rectifying AMPARs have a higher γ compared with linear AMPARs (Oh and Derkach 2005). We used peak-scaled nonstationary fluctuation analysis (NSFA) to estimate AMPAR γ across P5-18 to determine if γ might decrease during the developmental time points tested. To perform this analysis, a subset of the original aEPSCs (Fig. 6A, 1 and 2) was chosen from each neuron meeting the necessary criteria (see methods; Fig. 6B, 1 and 2). The average γ at P5–7 compared with P8–18 was not statistically different. Similar to rectification and quantal τdecay, the greatest differences in γ occurred at P5–7 [Fig. 6C, P5–7: γ = 9.46 ± 3.10 pS (n = 6); P8–18: γ = 7.52 ± 0.37 pS (n = 15), Levene's F = 10.59, P < 0.0042]. Independent of age, γ was relatively uniform with the corresponding AMPAR median Q for each neuron tested (Fig. 6D). At P6, one neuron demonstrated a very high γ (24.3 pS) and correspondingly low Q (5.0 pA). It is possible that neurons may, indeed, have AMPAR channels that conduct more single-channel current than this plot indicates. However, because only a weighted mean conductance per neuron is possible using peak-scaled NSFA, it is likely that if there are only a few high-conducting channels, then they are most likely obscured by a comparatively greater number of lower-conducting channels. Therefore AMPAR γ was not likely the dominant mechanism regulating AMPAR Q; thus the modest increase in Q during development (P5-18) cannot be explained by an increase in AMPAR single-channel conductance.
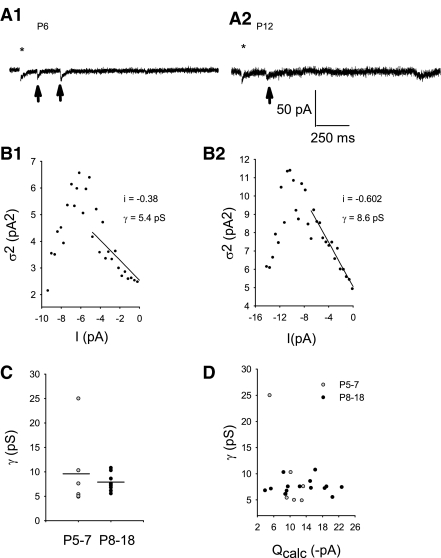
Fig. 6.
AMPAR single-channel conductance (γ) did not change significantly during early postnatal development (P5-18). A1: typical AMPA-mediated aEPSCs (arrows) subjected to peak-scaled nonstationary fluctuation analysis (NSFA) at P6 compared with P12 (A2) that follow the blanked stimulus artifact at *. B, 1 and 2: NSFA resulted in near-parabolic relationships between current variance (σ2) and associated mean current (I) for the selected ensemble of aEPSCs meeting criteria from each of the individual neurons in A, 1 and 2, respectively. Single-channel current (i) was calculated from the initial slope of the parabola and was then used to calculate single-channel conductance (B1: R2sp = 0.92, P ≤ 0.0001; B2: R2sp = 0.99, P ≤ 0.0001). C: γ values when grouped by age were not significantly different between the 2 groups [P5–7: 9.70 ± 3.48 pS (n = 6), P8–18: 7.52 ± 0.38 pS (n = 15); P = 0.76, Mann-Whitney rank sum] but more variable at P5–7 (Levene's F = 10.59, P < 0.0042). D: Qcalc was not correlated with γ (linear regression: n = 21, r2 = 2.86), suggesting γ did not directly modulate Q.
N*Po increases to directly mediate larger AMPAR quantal amplitudes
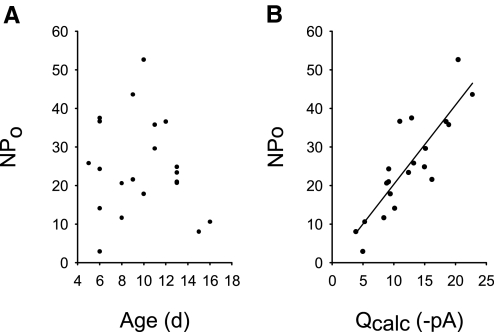
At thalamocortical synapses, Q is tightly controlled across development by regulation of γ and the number of activated receptors (N*Po) (Bannister et al. 2005). Because AMPAR γ demonstrated no direct correlation with Q (Fig. 6D), it was possible that Q was directly associated with the number of activated receptors (N*Po). This can also be determined from peak-scaled NSFA (Eq. 3). When N*Po was examined over the developmental ages P5-18, there was no clearly defined correlation (Fig. 7A). However, N*Po was directly correlated with Q (Fig. 7B, linear regression, r2 = 0.74, P < 0.001). Thus regulation of AMPAR number and/or AMPAR activation most directly influenced Q at these synapses during early postnatal development. Increasing AMPAR number and/or its activation best supports increases in Q from P5–7 to P8–18.
Fig. 7.
AMPAR N*Po increased to support a greater median Q per neuron. A: N*Po across early development was not clearly correlated with age and most likely adjusted withγ to yield Q. B: N*Po directly correlated with amplitude (Q; n = 21, r2 = 0.74, P < 0.001).
DISCUSSION
Development of AMPAR synapses
In the CNS, the hallmark of synaptogenesis is the formation of contacts between presynaptic axons and postsynaptic densities to form a synapse (Cohen-Cory 2002). During this formative phase, which includes the ages studied here (P5-18), anatomical data and microscopy studies have demonstrated significant neuronal growth, both in size and shape (Fiala et al. 1998), as well as an increase in dendritic spine density (Cottrell et al. 2000) and total number of AMPAR clusters per spine (Tyzio et al. 1999). We hypothesized that synaptic AMPAR properties also change significantly during this time period. Under our experimental conditions, Q increased across the developmental time points P5-18. This is an extension of the previous finding that spontaneous EPSCs recorded in this brain region also increase from birth up to P8 (Groc et al. 2002). We determined that these increases in amplitude are directly mediated by increases in the number of activated AMPARs (N*Po) across development. Importantly, our findings suggest that the increases in AMPAR numbers occur across development in a heterogeneous fashion. Inward rectification and faster channel kinetics exclusively at P5–7 suggest that AMPARs mediating these properties are restricted to this developmental window. Furthermore, our data suggest that heterogeneous AMPARs are segregated to distinct synapses prior to P8. After P8, AMPAR synaptic properties are more uniform. These findings have important and novel implications for understanding how AMPAR synapses develop and raise important questions about the role of these distinct synapses in early synaptogenesis.
Neuronal versus synaptic variability in early development
We questioned first whether developing neurons express uniform synaptic AMPAR properties and second if nonuniform, whether these were expressed distinctly or as mixtures across synapses. We suggest that during P5–7, developing hippocampal neurons segregate distinct AMPARs to different synapses leading to pronounced inter-synaptic variability. From P8, synaptic properties change with neuronal development but are more uniform across synapses. Synaptic variability prior to P8 was supported by several findings. First, measurement of the apparent rectification index demonstrated inward rectification only before P8 (Fig. 1B). Comparison with inward rectification after P8 suggested a cut-off value for better visualization (Fig. 1C). Analysis of apparent inward rectification compared with the unblocking index revealed that inward rectifying AMPARs are likely segregated to synapses across a continuum but with some synapses containing nearly all inward rectifying AMPARs. We approximated 26% of synapses contain >75% inward rectifying AMPARs at P5–7. We therefore investigated quantal aEPSCs to further quantify inter-synaptic variability. Second, the range of CVQ at P5–7 was greater than what would be expected for intra-synaptic variability (kinetic variability at an individual synapse) (Liu et al. 1999; McAllister and Stevens 2000). Therefore there was additional inter-synaptic variability in the quantal amplitude, indicating a great degree of variability across synapses. These findings of bimodal Q are reminiscent of those found in the developing Xenopus visual system (Pratt and Aizenman 2007). Prior studies have found that CVQ is low near birth but increases to similar levels to what we have found around P5–7 (Groc et al. 2002; Hanse and Gustafsson 2001); we have extended this to show that CVQ then suggestively decreases and stabilizes after P7. Third, median quantal τdecays at P5–7 demonstrated two distinct populations. Furthermore, CVτdecay was greater at P5–7 than other ages (similar to increased CVQ). This suggests that neurons at P5–7 can simultaneously contain two distinct populations of synapses. If synapses at P5–7 simply contained mixtures of functionally different AMPARs, it would be expected that the median quantal τdecays would be a weighted mean of the relative proportion of each without necessarily increased CVτdecay ( Supplemental Fig. S4). While statistically we did not find evidence of multimodal distributions with the use of Hartigan's dip test, this test has low power for closely spaced modes or pronounced tails (Hartigan and Hartigan 1985) as seen with modeled data (Supplemental Fig. S4.). We therefore suggest that analysis of CV τdecay is more sensitive for detecting intersynaptic variability. The variability of quantal τdecay in individual neurons resulting in CVτdecay >1 at P5–7 can most parsimoniously be explained by the co-existence of biophysically distinct AMPAR synapses; indeed, some mixture of different AMPARs at a synapse was also likely present to some degree. Nevertheless, the finding that there was markedly faster quantal τdecay at P5–7 suggested that younger synapses were biophysically different from older synapses. Taken together, this supports our finding that different AMPAR synapses co-exist at younger ages. Combining our similar estimates from inward rectification and pooled distribution of quantal τdecay (Supplemental Fig. S4F), we conservatively estimate that 30% of synapses prior to P8 may contain >75% inward rectifying AMPARs.
Functionally, inward rectification was not associated with differences in paired-pulse facilitation (Fig. 2, A and B). This suggested that presynaptic function did not contribute to intersynaptic variability and that each population of synapses, although different in numbers, was likely activated with equal probability. Our subsequent analysis to estimate the fraction of inward rectifying AMPARs relied on this assumption. A prior study found two populations of synapses at P6 with different release probabilities linked to different mechanisms of synaptic plasticity (Palmer et al. 2004). This study utilized a minimal stimulation protocol compared with our maximal stimulation protocol used to detect inward rectification. Maximal stimulation was necessary to minimize errors associated with the classification of synaptic failures as inward rectification. Thus the incidence of synapses with low release probability was potentially obscured by the protocol we employed. The prior study did not find that synapses with lower release probability contained higher conductance AMPARs (Palmer et al. 2004), which might have suggested that these synapses contained inward rectifiers, even rarely, as found here (Fig. 6). If taken on its own, however, our estimate from analysis of quantal τdecay at P5–7 suggesting 30% of synapses with inward rectifying AMPARs (Supplemental Fig. S4) could also be consistent with a lower probability of release at these synapses.
AMPARs can have a markedly faster τdecay at P5–7. While we have attributed this to the presence of inward rectifying AMPARs, this is potentially influenced by multiple factors (Conti and Weinberg 1999), such as subunit flip/flop variants (Partin et al. 1994; Quirk et al. 2004), glutamate release/uptake effects (Clements et al. 1992; Liu et al. 1999) on agonist-receptor desensitization/dissociation (Trussell and Fischbach 1989), and subunit composition (Oh and Derkach 2005). Previous studies demonstrated a uniform effect of cyclothiazide across the developmental ages studied here (Seifert et al. 2000), suggesting that flip/flop variability and desensitization effects are minimally contributing at these ages which has been supported by expression studies (Monyer et al. 1991). AMPAR-mediated EPSC CVτdecay has not been previously examined during early development. A previous study at cerebellar inhibitory GABAergic synapses (Nusser et al. 2001), showed an increased CVτdecay (0.1–0.3) that was associated, through modeling studies, with fluctuations in the time-course of GABA in the synaptic space of >55%. CVτdecay measured here was substantially greater than this, supporting our conclusion that the variability was due to the simultaneous presence of functionally different receptor clusters and thus intersynaptic variability. It is unlikely that glutamate concentration cleft dynamics are fluctuating on a trial-to-trial basis to a degree to explain our findings. In support of this, strontium is thought to stabilize synaptic vesicle fusion to favor full, versus partial, release (Elhamdani et al. 2006). Correlation with inward rectification thus favors that faster kinetics are most likely due to inward rectifying AMPAR subunits at the synapse at P5–7 (Oh and Derkach 2005). While inward rectifiers were present at P5–7, they were never detected after P8 (Fig. 1, B and C).
However, not all P5–7 neurons exhibited inward rectification, as some behaved like P8–18 neurons with nonrectifying (linear) AMPARs (Fig. 1C) and slower channel kinetics (Fig. 5, C and D). AMPAR single-channel conductance (γ) was not significantly higher at the younger P5–7 ages (Fig. 6C), though, to support inward rectification at the younger ages. The variance of γ at P5–7 was significantly higher than at P8–18 (Fig. 6C), consistent with the presence of inward rectifying AMPAR channels in some but not all of the P5–7 neurons. As noted, CVτdecay was also comparatively much higher at P5–7 (Fig. 5E) to support the wide variability of rectification at these ages both across neurons as well as synapses within a neuron. Quantal amplitude significantly increased from P5–7 compared with P8–18 (Fig. 3, C and D). This was most consistent, overall, with the developmental increase in AMPAR number (N*Po; Fig. 6B). This increase likely overshadowed any differences in CVQ that might have been expected due to the presence of different AMPAR subtypes. Taken together, while two very different AMPAR synapses exist at younger ages (P5–7), the number of active AMPARs that increase at the synapse up to P18 are less variable in their biophysical properties (CVτdecay and γ), slower, (τdecay) and are never inward rectifying (lower RI). Thus the biophysical properties of increasing numbers of AMPARs across neurons at P8–18 are much more uniform across synapses compared with the younger P5–7 age group.
Inward rectification, because of its association with calcium permeability of AMPARs (Bowie and Mayer 1995; Geiger et al. 1995; Kamboj et al. 1995), and faster kinetics, suggests that younger synapses have uniquely different electrical and chemical signaling properties compared with older synapses. AMPARs lacking GluA2 uniquely have faster kinetics (Oh and Derkach 2005) and greater relative calcium permeability/inward rectification (Geiger et al. 1995; Kamboj et al. 1995; Oh and Derkach 2005). These properties matched the features of synapses seen only at P5–7. Therefore we speculate that prior to P8, many synapses completely lack GluA2, but other synapses prior to P8 seem to contain GluA2; after P8, synapses generally contain GluA2. Immature synapses are thought to initially develop as “silent” synapses, containing relatively calcium permeable NMDA receptors (Liao et al. 1999). AMPAR are acquired through calcium-mediated, activity-dependent signaling (Harms et al. 2005; Isaac 2003; McAllister 2007; Petralia et al. 1999). Our findings temporally link calcium-permeable AMPARs with the synaptic development of principal neurons in hippocampal CA1. However, our findings could be explained by synapse specific clustering of transmembrane AMPAR regulatory proteins (TARPs) to achieve a similar clustering of AMPAR function (Kott et al. 2007; Soto et al. 2007).
Developmental increase in size of AMPAR synapses
Although the total number of activated receptors at the peak (N*Po) of quantal amplitude (Q) was greater to modulate a larger Q, it was not possible to determine which factor of N*Po contributed to the increases in median amplitude with age over the developmental range tested (Fig. 6). Either receptor numbers (N) and/or peak-open probability (Po), as influenced by such factors as cleft glutamate concentration (Liu et al. 1999), could be changing with development. This is due to the nature of peak-scaled NSFA, in that receptor number (N) and peak-open probability (Po) cannot be directly calculated and thus cannot be separated. However, studies suggest that greater numbers of AMPARs are inserted postsynaptically with developmental age (Cottrell et al. 2000; Petralia et al. 1999; Pickard et al. 2000) favoring that increases in Q were primarily mediated by increases in N.
It has been shown that channel conductance can depend on glutamate concentration (Gebhardt and Cull-Candy 2006; Rosenmund et al. 1998; Smith and Howe 2000) although under conditions in which desensitization is minimized. Glutamate concentrations in the synaptic cleft may increase during synaptogenesis (Renger et al. 2001); this would also cause an increase in the quantal amplitude (Franks et al. 2003) via increased Po (Momiyama et al. 2003) if AMPARs were not already saturated. Under our conditions of presumed mono-vesicular, full release in strontium (Elhamdani et al. 2006), this would have to occur by either greater vesicular filling with transmitter or alterations in cleft volume and geometry. If this was the case, then increases in cleft glutamate levels could also then lead to an increase in the number of glutamate molecules bound to AMPAR and thus influence and favor higher AMPAR conductance levels (Cathala et al. 2005). Therefore if our measurements of relatively stable γ across development were an indication of stable cleft glutamate concentrations, this would suggest that Po did not change significantly during the developmental range tested.
Significance of distinctly different AMPAR synapses at very early postnatal ages
Developmental changes in AMPAR subunit composition (Monyer et al. 1991; Pickard et al. 2000) have been demonstrated in the neocortex (Kumar et al. 2002; Shin et al. 2005) and CA3 hippocampus (Ho et al. 2007), but developmental regulation in which these subunits are segregated to different synapses has not been reported. Transient AMPAR subunit composition changes have been described with LTP (Plant et al. 2006), following hypoxia induced seizures (Rakhade et al. 2008), and with synaptic inactivity (Thiagarajan et al. 2005). Developmental changes in AMPAR subunits have been associated with dendritic branch-point maturation in the spinal cord (Inglis et al. 2002). It is assumed that these composition changes result in mixtures of AMPARs at synapses. Therefore and in contrast, the transient expression of different AMPAR at distinct synapses suggested here from P5–7 likely underlies an important developmental process of network maturation in CA1 hippocampus. Indeed the expression mechanisms of synaptic plasticity have been reported to change around P5–7 (Palmer et al. 2004). Further studies will be necessary to determine the exact impact at P5–7 of the faster, inward-rectifying AMPAR synapses that exist with the slower, nonrectifying, mature AMPAR synapses. We speculate in the developing hippocampus that the faster synapses are both GluA2-lacking and calcium permeable, leading to greater calcium accumulations and possibly more finely tuned dynamic signaling, compared with synapses with mixtures of AMPARs. This could have a substantial impact on not only our understanding of synaptic development but also disorders primarily affecting immature synapses (Cornejo et al. 2007).
GRANTS
This was supported by National Institutes of Health Grants NS-056090 to T. A. Benke and T32 GM-007635 to E. A. Stubblefield and by institutional support from the Department of Pediatrics and The Childrens Hospital Research Institute.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
Supplementary Material
ACKNOWLEDGMENTS
Thanks to Drs. John Isaac, Paul Bernard, and Katie Rennie for critical reading of this manuscript.
Footnotes
The online version of this article contains supplemental data.
REFERENCES
- Adesnik and Nicoll, 2007.Adesnik H, Nicoll RA. Conservation of glutamate receptor 2-containing AMPA receptors during long-term potentiation. J Neurosci 27: 4598–4602, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bannister et al., 2005.Bannister NJ, Benke TA, Mellor J, Scott H, Gurdal E, Crabtree JW, Isaac JTR. Developmental changes in AMPA and kainate receptor-mediated quantal transmission at thalamocortical synapses in the barrel cortex. J Neurosci 25: 5259–5271, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baude et al., 1995.Baude A, Nusser Z, Molnar E, McIlhinney RAJ, Somogyi P. High-resolution immunogold localization of AMPA type glutamate receptor subunits at synaptic and non-synaptic sites in rat hippocampus. J Neurosci 69: 1031–1055, 1995 [DOI] [PubMed] [Google Scholar]
- Bekkers and Clements, 1999.Bekkers JM, Clements JD. Quantal amplitude and quantal variance of strontium-induced asynchronous EPSCs in rat dentate granule neurons. J Physiol 516: 227–248, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benke et al., 1998.Benke TA, Lüthi A, Isaac JTR, Collingridge GL. Modulation of AMPA receptor unitary conductance by synaptic activity. Nature 393: 793–797, 1998 [DOI] [PubMed] [Google Scholar]
- Benke et al., 2001.Benke TA, Lüthi A, Palmer MJ, Wikstroem MA, Anderson WW, Isaac JTR, Collingridge GL. Mathematical modeling of non-stationary fluctuation analysis for studying channel properties of synaptic AMPA receptors. J Physiol 537: 407–420, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowie and Mayer, 1995.Bowie D, Mayer ML. Inward rectification of both AMPA and kainate subtype glutamate receptors generated by polyamine-mediated ion channel block. Neuron 15: 453–462, 1995 [DOI] [PubMed] [Google Scholar]
- Brill and Huguenard, 2009.Brill J, Huguenard JR. Sequential changes in AMPA receptor targeting in the developing neocortical excitatory circuit. J Neurosci 28: 13918–13928, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cathala et al., 2005.Cathala L, Holderith NB, Nusser Z, DiGregorio DA, Cull-Candy SG. Changes in synaptic structure underlie the developmental speeding of AMPA receptor-mediated EPSCs. Nat Neurosci 8: 1310–1318, 2005 [DOI] [PubMed] [Google Scholar]
- Clements et al., 1992.Clements JD, Lester RAJ, Tong G, Jahr C, Westbrook GL. The time course of glutamate in the synaptic cleft. Science 258: 1498–1501, 1992 [DOI] [PubMed] [Google Scholar]
- Cohen-Cory, 2002.Cohen-Cory S. The developing synapse: construction and modulation of synaptic structures and circuits. Science 298: 770–776, 2002 [DOI] [PubMed] [Google Scholar]
- Conti and Weinberg, 1999.Conti F, Weinberg RJ. Shaping excitation at glutamatergic synapses. Trends Neurosci 22: 451–457, 1999 [DOI] [PubMed] [Google Scholar]
- Cornejo et al., 2007.Cornejo BJ, Mesches MH, Coultrap S, Browning MD, Benke TA. A single episode of neonatal seizures permanently alters glutamatergic synapses. Ann Neurol 61: 411–426, 2007 [DOI] [PubMed] [Google Scholar]
- Cottrell et al., 2000.Cottrell JR, Dube GR, Egles C, Liu G. Distribution, density, and clustering of functional glutamate receptors before and after synaptogenesis in hippocampal neurons. J Neurophysiol 84: 1573–1587, 2000 [DOI] [PubMed] [Google Scholar]
- Craig et al., 1993.Craig AM, Blackstone CD, Huganir RL, Banker G. The distribution of glutamate receptors in cultured rat hippocampal neurons: postsynaptic clustering of AMPA-selective subunits. Neuron 10: 1055–1068, 1993 [DOI] [PubMed] [Google Scholar]
- Cull-Candy et al., 1988.Cull-Candy SG, Howe JR, Ogden DC. Noise and single channels activated by excitatory amino acids in rat cerebellar granule neurones. J Physiol 400: 189–222, 1988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cull-Candy and Usowicz, 1987.Cull-Candy SG, Usowicz MM. Multiple-conductance channels activated by excitatory amino acids in cerebellar neurons. Nature 325: 525–528, 1987 [DOI] [PubMed] [Google Scholar]
- Dingledine et al., 1999.Dingledine R, Borges K, Bowie D, Traynelis SF. The glutamate receptor ion channels. Pharmacol Rev 51: 7–62, 1999 [PubMed] [Google Scholar]
- Elhamdani et al., 2006.Elhamdani A, Azizi F, Artalejo CR. Double patch clamp reveals that transient fusion (kiss-and-run) is a major mechanism of secretion in calf adrenal chromaffin cells: high calcium shifts the mechanism from kiss-and-run to complete fusion. J Neurosci 26: 3030–3036, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eybalin et al., 2004.Eybalin M, Caicedo A, Renard N, Ruel J, Puel J. Transient Ca2+-permeable AMPA receptors in postnatal rat primary auditory neurons. Eur J Neurosci 20: 2981–2989, 2004 [DOI] [PubMed] [Google Scholar]
- Fiala et al., 1998.Fiala JC, Feinberg M, Popov V, Harris KM. Synaptogenesis via dendritic filopodia in developing hippocampal area CA1. J Neurosci 18: 8900–8911, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forti et al., 1997.Forti L, Bossi M, Bergamashi A, Villa A, Malgaroli A. Loose-patch recordings of single quanta at individual hippocampal synapses. Nature 388: 874–878, 1997 [DOI] [PubMed] [Google Scholar]
- Franks et al., 2003.Franks KM, Stevens CF, Sejnowski TJ. Independent sources of quantal variaiblity at single glutamatergic synapses. J Neurosci 23: 3186–3195, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner et al., 2001.Gardner SM, Trussell LO, Oertel D. Correlation of AMPA receptor subunit composition with synaptic input in the mammalian cochlear nuclei. J Neurosci 21: 7428–7437, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebhardt and Cull-Candy, 2006.Gebhardt C, Cull-Candy SG. Influence of agonist concentration on AMPA and kainate channels in CA1 pyramidal cells in rat hippocampal slices. J Physiol 573: 371–394, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiger et al., 1995.Geiger JRP, Melcher T, Koh DS, Sakmann B, Seeburg PH, Jonas P, Monyer H. Relative abundance of subunit mRNAs determines gating and Ca2+ permeability of AMPA receptors in principal neurons and interneurons in rat CNS. Neuron 15: 193–204, 1995 [DOI] [PubMed] [Google Scholar]
- Goda and Stevens, 1994.Goda Y, Stevens CF. Two components of transmitter release at a central synapse. Proc Natl Acad Sci USA 91: 12942–12946, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groc et al., 2002.Groc L, Gustafsson B, Hanse E. Spontaneous unitary synaptic activity in CA1 pyramidal neurons during early postnatal development: constant contribution of AMPA and NMDA receptors. J Neurosci 22: 5552–5562, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanse and Gustafsson, 2001.Hanse E, Gustafsson B. Quantal variability at glutamatergic synapses in area CA1 of the rat neonatal hippocampus. J Physiol 531: 467–480, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harms et al., 2005.Harms KJ, Tovar KR, Craig AM. Synapse-specific regulation of AMPA receptor subunit composition by activity. J Neurosci 25: 6379–6388, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris and Sultan, 1995.Harris KM, Sultan P. Variation in the number, location, and size of synaptic vesicles provides an anatomical basis for the nonuniform probability of release at hippocampal CA1 synapses. Neuropharmacology 34: 1387–1395, 1995 [DOI] [PubMed] [Google Scholar]
- Hartigan and Hartigan, 1985.Hartigan JA, Hartigan PM. The dip test of unimodality. Ann Stat 13: 70–84, 1985 [Google Scholar]
- Ho et al., 2007.Ho MTW, Pelkey KA, Topolnik L, Petralia RS, Takamiya K, Xia J, Huganir RL, Lacaille JC, McBain CJ. Developmental expression of Ca2+-permeable AMPA receptors underlies depolarization-induced long-term depression at mossy fiber CA3 pyramid synapses. J Neurosci 27: 11651–11662, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inglis et al., 2002.Inglis RM, Crocket R, Korada S, Abraham WC, Hollman M, Kalb RG. The AMPA receptor subunit GluR1 regulates dendritic architecture of motor neurons. J Neurosci 22: 8042–8051, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isa et al., 1996.Isa T, Itazawa S, Iino M, Tsuzuki K, Ozawa S. Distribution of neurons expressing inwardly rectifying and Ca2+ permeable AMPA receptors in rat hippocampal slices. J Physiol 491.3: 719–733, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaac, 2003.Isaac JTR. Postsynaptic silent synapses: evidence and mechanisms. Neuropharmacology 45: 450–460, 2003 [DOI] [PubMed] [Google Scholar]
- Kamboj et al., 1995.Kamboj SK, Swanson GT, Cull-Candy SG. Intracellular spermine confers rectification on rat calcium-permeable AMPA and kainate receptors. J Physiol 486.2: 297–303, 1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kott et al., 2007.Kott S, Werner M, Körber C, Hollmann M. Electrophysiological properties of AMPA receptors are differentially modulated depending on the associated member of the TARP family. J Neurosci 27: 3780–3789, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar et al., 2002.Kumar SS, Bacci A, Kharazia V, Huguenard JR. A developmental switch of AMPA receptor subunits in neocortical pyramidal neurons. J Neurosci 22: 3005–3015, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao et al., 1999.Liao D, Zhang X, O'Brien R, Ehlers MD, Huganir RL. Regulation of morphological postsynaptic silent synapses in developing hippocampal neurons. Nat Neurosci 2: 37–43, 1999 [DOI] [PubMed] [Google Scholar]
- Liu et al., 1999.Liu G, Choi S, Tsien RW. Variability of neurotransmitter concentration and nonsaturation of postsynaptic AMPA receptors at synapses in hippocampal cultures and slices. Neuron 22: 395–409, 1999 [DOI] [PubMed] [Google Scholar]
- Liu and Cull-Candy, 2002.Liu SJ, Cull-Candy S. Activity-dependent change in AMPA receptor properties in cerebellar stellate cells. J Neurosci 22: 3881–3889, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mansour et al., 2001.Mansour M, Nagarajan N, Nehring RB, Clements JD, Rosenmund C. Heteromeric AMPA receptors assemble with a preferred subunit stoichiometry and spatial arrangement. Neuron 32: 841–853, 2001 [DOI] [PubMed] [Google Scholar]
- McAllister, 2007.McAllister KA. Dynamic aspects of CNS synapse formation. Annu Rev Neurosci 30: 425–450, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAllister and Stevens, 2000.McAllister KA, Stevens CF. Nonsaturation of AMPA and NMDA receptors at hippocampal synapses. Proc Natl Acad Sci USA 97: 6173–6178, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Momiyama et al., 2003.Momiyama A, Silver RA, Haeuser M, Notomi T, Wu Y, Shigemoto R, Cull-Candy SG. The density of AMPA receptors activated by a transmitter quantum at the climbing fibre-Purkinje cell synapse in immature rats. J Physiol 549: 75–92, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monyer et al., 1991.Monyer H, Seeburg PH, Wisden W. Glutamate-operated channels: developmentally early and mature forms arise by alternative splicing. Neuron 6: 799–810, 1991 [DOI] [PubMed] [Google Scholar]
- Mosbacher et al., 1994.Mosbacher J, Schoepfer R, Monyer H, Burnashev N, Seeburg PH, Ruppersberg JP. A molecular determinant for submillisecond desensitization in glutamate receptors. Science 266: 1059–1062, 1994 [DOI] [PubMed] [Google Scholar]
- Nusser et al., 2001.Nusser Z, Naylor D, Mody I. Synapse-specific contribution of the variation of transmitter concentration to the decay of inhibitory postsynaptic currents. Biophys J 80: 1251–1261, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh and Derkach, 2005.Oh MC, Derkach VA. Dominant role of the GluR2 subunit in regulation of AMPA receptors by CaMKII. Nat Neurosci 8: 853–854, 2005 [DOI] [PubMed] [Google Scholar]
- Oliet et al., 1996.Oliet SHR, Malenka RC, Nicoll RA. Bidirectional control of quantal size by synaptic activity in the hippocampus. Science 271: 1294–1297, 1996 [DOI] [PubMed] [Google Scholar]
- Palmer et al., 2004.Palmer MJ, Isaac JTR, Collingridge GL. Multiple, developmentally regulated expression mechanisms of long-term potentiation at CA1 synapses. J Neurosci 24: 4903–4911, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Partin et al., 1994.Partin KM, Patneau DK, Mayer ML. Cyclothiazide differentially modulates desensitization of alpha-amino-3- hydroxy-5-methyl-4-isoxazolepropionic acid receptor splice variants. Mol Pharmacol 46: 129–138, 1994 [PubMed] [Google Scholar]
- Petralia et al., 1999.Petralia RS, Esteban JA, Wang Y-X, Partridge JG, Zhao H-M, Wenthold RJ, Malinow R. Selective acquisition of AMPA receptors over postnatal development suggests a molecular basis for silent synapses. Nat Neurosci 2: 31–36, 1999 [DOI] [PubMed] [Google Scholar]
- Petralia et al., 2005.Petralia RS, Sans N, Want Y, Wenthold RJ. Ontogeny of postsynaptic density proteins at glutamatergic synapses. Mol Cell Neurosci 29: 436–452, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickard et al., 2000.Pickard L, Noel J, Henley JM, Collingridge GL, Molnar E. Developmental changes in synaptic AMPA and NMDA receptor distribution and AMPA receptor subunit composition in living hippocampal neurons. J Neurosci 20: 7922–7931, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plant et al., 2006.Plant K, Pelkey KA, Bortolotto ZA, Morita D, Terashima A, McBain CJ, Collingridge GL, Isaac JTR. Transient incorporation of native GluR2-lacking AMPA receptors during hippocampal long-term potentiation. Nat Neurosci 9: 602–604, 2006 [DOI] [PubMed] [Google Scholar]
- Pratt and Aizenman, 2007.Pratt KG, Aizenman CD. Homeostatic regulation of intrinsic excitability and synaptic transmission in a developing visual circuit. J Neurosci 27: 8268–8277, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press et al., 1992.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Statistical description of data. In: Numerical Recipes in C. Cambridge, UK: Cambridge Univ. Press, 1992, p. 609–649 [Google Scholar]
- Priebe et al., 2004.Priebe NJ, Mechler F, Carandini M, Ferster D. The contribution of spike threshold to the dichotomy of cortical simple and complex cells. Nat Neurosci 7: 1113–1122, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quirk et al., 2004.Quirk JC, Siuda ER, Nisenbaum ES. Molecular determinants responsible for differences in desensitization kinetics of AMPA receptor splice variants. J Neurosci 24: 11416–11420, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team, 2010.R Development Core Team R: A language and environment for statistical computing. //www.R-Project.org 2010. Vienna, Austria [Google Scholar]
- Rakhade et al., 2008.Rakhade SN, Zhou C, Aujla PK, Fishman R, Sucher NJ, Jensen FE. Early alterations of AMPA receptors mediate synaptic potentiation induced by neonatal seizures. J Neurosci 28: 7979–7990, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renger et al., 2001.Renger JJ, Egles C, Liu G. A developmental switch in neurotransmitter flux enhances synaptic efficacy by affecting AMPA receptor activation. Neuron 29: 469–484, 2001 [DOI] [PubMed] [Google Scholar]
- Ritter et al., 2002.Ritter LM, Vazquez DM, Meador-Woodruff JH. Ontogeny of ionotropic glutamate receptor subunit expression in the rat hippocampus. Dev Brain Res 139: 227–236, 2002 [DOI] [PubMed] [Google Scholar]
- Robert and Howe, 2003.Robert A, Howe JR. How AMPA receptor desensitization depends on receptor occupancy. J Neurosci 23: 847–858, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenmund et al., 1998.Rosenmund C, Stern-Bach Y, Stevens CF. The tetrameric structure of a glutamate receptor channel. Science 280: 1596–1599, 1998 [DOI] [PubMed] [Google Scholar]
- Rozov and Burnashev, 1999.Rozov A, Burnashev N. Polyamine-dependent facilitation of postsynaptic AMPA receptors counteracts paired-pulse depression. Nature 401: 594–598, 1999 [DOI] [PubMed] [Google Scholar]
- Rozov et al., 1998.Rozov A, Zilberter Y, Wollmuth LP, Burnashev N. Facilitation of currents through rat Ca2+-permeable AMPA receptor channels by activity-dependent relief from polyamine block. J Physiol 511: 361–377, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubio and Wenthold, 1997.Rubio ME, Wenthold RJ. Glutamate receptors are selectively targeted to postsynaptic sites in neurons. Neuron 18: 939–950, 1997 [DOI] [PubMed] [Google Scholar]
- Sakmann and Neher, 1983.Sakmann B, Neher E. Single-Channel Recording. NY: Plenum, 1983 [Google Scholar]
- Seifert et al., 2000.Seifert G, Zhou M, Dietrich D, Schumacher TB, Dybek A, Weiser T, Wienrich M, Wilhelm D, Steinhauser C. Developmental regulation of AMPA-receptor properties in CA1 pyramidal neurons of rat hippocampus. Neuropharmacology 39: 931–942, 2000 [DOI] [PubMed] [Google Scholar]
- Shin et al., 2005.Shin J, Shen F, Huguenard JR. Polyamines modulate AMPA receptor-dependent synaptic responses in immature layer V pyramidal neurons. J Neurophysiol 93: 2634–2643, 2005 [DOI] [PubMed] [Google Scholar]
- Sigworth, 1980.Sigworth FJ. The variance of sodum current fluctuations at the node of Ranvier. J Physiol 304: 97–129, 1980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith and Howe, 2000.Smith TC, Howe JR. Concentration-dependent substate behavior of native AMPA receptors. Nat Neurosci 3: 992–997, 2000 [DOI] [PubMed] [Google Scholar]
- Soto et al., 2007.Soto D, Coombs ID, Kelly L, Farrant M, Cull-Candy SG. Stargazin attenuates intracellular polyamine block of calcium-permeable AMPA receptors. Nat Neurosci 10: 1260–1267, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiagarajan et al., 2005.Thiagarajan TC, Lindskog M, Tsien RW. Adaptation to synaptic inactivity in hippocampal neurons. Neuron 47: 725–737, 2005 [DOI] [PubMed] [Google Scholar]
- Traynelis et al., 1993.Traynelis SF, Silver RA, Culll-Candy SG. Estimated conductance of glutamate receptor channels activated during EPSCs at the cerebellar mossy fiber-granule cell synapse. Neuron 11: 279–289, 1993 [DOI] [PubMed] [Google Scholar]
- Trussell and Fischbach, 1989.Trussell LO, Fischbach GD. Glutamate receptor desensitization and its role in synaptic transmission. Neuron 3: 209–218, 1989 [DOI] [PubMed] [Google Scholar]
- Tyzio et al., 1999.Tyzio R, Represa A, Jorquera I, Ben Ari Y, Gozlan H, Aniksztejn L. The establishment of GABAergic and glutamatergic synapses on CA1 pyramidal neurons is sequential and correlates with the development of the apical dendrite. J Neurosci 19: 10372–10382, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall and Usowicz, 1998.Wall MJ, Usowicz MM. Development of the quantal properties of evoked and spontaneous synaptic currents at a brain synapse. Nat Neurosci 1: 675–681, 1998 [DOI] [PubMed] [Google Scholar]
- Wenthold et al., 1996.Wenthold RJ, Petralia RS, Blahos J, Niedzielski AS. Evidence for multiple AMPA receptor complexes in hippocampal CA1/CA2 neurons. J Neurosci 16: 1982–1989, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wisden and Seeburg, 1993.Wisden W, Seeburg PH. Mammalian ionotropic glutamate receptors. Curr Opin Neurobiol 3: 291–298, 1993 [DOI] [PubMed] [Google Scholar]
- Xu-Friedman and Regehr, 1999.Xu-Friedman MA, Regehr WG. Presynaptic strontium dynamics and synaptic transmission. Biophys J 76: 2029–2042, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.